Abstract
The advent of smart grid technologies has facilitated the integration of new and intermittent renewable forms of electricity generation in power systems. Advancements are driving transformations in the context of energy planning and operations in many countries around the world, particularly impacting short-term horizons. Therefore, one of the primary challenges in this environment is to accurately provide forecasting of the short-term load demand. This is a critical task for creating supply strategies, system reliability decisions, and price formation in electricity power markets. In this context, nonlinear models, such as Neural Networks and Support Vector Machines, have gained popularity over the years due to advancements in mathematical techniques as well as improved computational capacity. The academic literature highlights various approaches to improve the accuracy of these machine learning models, including data segmentation by similar patterns, input variable selection, forecasting from hierarchical data, and net load forecasts. In Brazil, the national independent system operator improved the operation planning in the short term through the DESSEM model, which uses short-term load forecast models for planning the day-ahead operation of the system. Consequently, this study provides a comprehensive review of various methods used for short-term load forecasting, with a particular focus on those based on machine learning strategies, and discusses the Brazilian Experience.
1. Introduction
Recent technological advancements in renewable energy technologies, electric vehicles, energy storage, and electrification in connection with society’s concern with sustainability, decarbonization, and climate change are fueling significant shifts in energy planning and operations across numerous countries worldwide, particularly influencing short-term perspectives. In this context, one of the biggest challenges for independent system operators (ISOs) is to ensure the balance between energy supply and demand, particularly due to the inherent complexity of storing electricity [1]. The rise in renewable energy deployments amplifies the complexity associated with the supply–demand balance, as these sources often introduce additional variability and uncertainty. Thus, electricity load (demand) forecasting becomes critical to properly balance supply and demand in the system, optimize operational costs, and effectively manage electricity generation resources.
By accurately forecasting electricity demand, operators can optimize power systems operations, thereby avoiding potential system overloads or power outages that can affect consumers and economies at the regional and country level. Furthermore, robust, reliable, and timely forecasts of electricity load allow for more strategic planning of renewable energy integration, contributing to a more sustainable and reliable power system. In general, electricity load forecasting problems are classified into four categories: long-term (year to multi years ahead), medium-term (from one week to months ahead) [2], short-term (from hours to days ahead) [3], and very short-term (from minutes to hours ahead) [4].
Long-term forecasts are performed to support system-capacity expansion planning (for example, see the work of [5]), which discusses the importance of such a problem and reviews approaches applied for forecasting 10–50 years ahead. Medium-term load forecasts are needed for fuel-supply scheduling, hydroelectric management, maintenance operations, and interchange planning [6]. Short-term forecasts are usually aimed at scheduling the daily system operation, in tasks such as electricity exchange and demand management [7], and very short-term forecasts are used to quickly respond to intra-hour fluctuations in electricity demand and help to control generation dispatches within real-time operations [8].
In this work, we are particularly interested in providing an overview of the short-term load forecast (STLF) problem and the class of machine learning methods that have been used in this context. STLF plays an important role in supporting system operators in decision making in generation operation planning and coordination, in systems operative reserve, in system security, in dispatch scheduling, in price formation in electricity markets, and in operational cost minimization problems [9]. Nonlinear models, such as Artificial Neural Networks (ANNs) and Support Vector Machines (SVMs), have gained popularity over the years for STLF problems, due to advancements in mathematical techniques as well as improved computational capacity. Computational advances have enabled Deep Neural Networks (DNN), which improve network resource abstraction, allowing better efficiency in the machine learning process for non-linear problems [10]. In this context, many researchers developed alternatives to improve the performance of STLF models, such as the model ensemble and the hybrid models based on methodologies that include meteorological forecasts [11].
The academic literature highlights various approaches to improve the accuracy of these machine learning models, including data segmentation by similar patterns, input variable selection, forecasting from hierarchical data, and netload forecasts. Despite the use of nonlinear models, the use of bi-directional Recurrent Neural Networks (RNNs), and other relevant methods such as transformer neural nets [12] and Bayesian networks [13] remains to be explored in more depth. This paper reviews the main machine learning methods applied to STLF, provides guidance concerning the state-of-the-art methodologies to develop more efficient forecasting models, and discusses the procedures and gaps related to the field. The paper also presents the Brazilian experience with forecasting models applied to the daily operational planning of the Brazilian interconnected power system.
In addition to Section 1, this paper is organized in the following manner: Section 2 presents the main linear and non-linear models of STLF; Section 3 describes the main methodologies that have been used to model and improve STLFs; Section 4 presents how STLF is approached in the Brazilian electricity sector; and Section 5 presents the main conclusions and recommendations for future studies.
2. Short-Term Load Forecasting Models and Methods
Over time, STLF models have greatly advanced for both large-scale energy systems and localized network planning, given their vital role in maintaining an economic equilibrium between consumer needs and utility provisions. Furthermore, in countries or regions that are part of deregulated electricity markets, load forecasts also impact price projections, enabling competitivity [14,15]. In recent decades, STLF has been widely studied, and the main approaches used to represent the problem are classified between linear and non-linear models. Although linear models are sometimes capable of representing physical characteristics such as climate and social variables, they are limited in incorporating the typical non-linearities associated with short-term load behavior [16,17]. The most popular linear models are based on simple (or multiple) linear regressions, semi-parametric additive models, autoregressive-moving-average (ARMA) models, and exponential smoothing approaches. However, hardware and software advancements over time have made viable the use of non-linear models for such a task, including machine learning techniques such as SVMs and ANNs.
2.1. Linear Models
Generally, linear models are based on classical statistical methods, providing a continuous response variable from a function that is characterized by the linear combination of one or more predictor variables [18]. These models can be separated into causal and time series models [15]. Among the most used causal models are multiple linear regressions and semi-parametric additive models [16]. In turn, in time series models, load data are usually modeled as a function of their previously observed values [11,15]. The main models are the ARMA models and exponential smoothing methods.
2.1.1. Multiple Linear Regressions
Linear models possess the ability to include both quantitative and qualitative predictor variables. While their definition implies linearity, certain linear models can be applied to capture non-linear associations between load and predictors [19]. An example is the polynomial regression model (Equation (1)), encompassing predictor variable polynomials. Moreover, multiple linear regression models can also account for the influence of interactions among predictor variables, as shown in (Equation (2)) for a case involving two predictors. In Equations (1) and (2), is the variable to be predicted, βn is the nth regression coefficient, and εi is the normally distributed error term.
For many decades, linear regression models have been used to support STLF problems. In the literature, it is possible to find studies that have used these models to perform STLF for large operators and local network planning, with calendar and temperature variables being the main predictors [19,20,21].
Error analysis has been successfully conducted in the context of regression models over the years. Such a task plays an important role to isolate, observe and diagnose erroneous predictions, helping analysts to understand performance of the models. By conducting error analysis, analysts can diagnose whether the model has adequately captured trends, seasonality’s and other inherent patterns from the time series. For instance, systematic errors might suggest that the model has not fully learned/represented the seasonality in the data. Additionally, error analysis can help in identifying anomalies or outliers that might distort predictions. By understanding the nature and source of these errors, one can refine feature engineering, input variable selection, help to adjust model hyperparameters, or even choose a more suitable model architecture for the task. A discussion about error metrics is further presented in Section 3.7.
2.1.2. Semi-Parametric Additive Models
The primary characteristic of semi-parametric additive models is that they represent the effect of a variable on the response surface as an additive, independent of the effects of other variables. Thus, these models verify the individual contribution of each variable in the forecasting process. Such models allow the use of non-linear and non-parametric methods within their structure [22]. In the STLF process, semi-parametric additive models allow incorporating the past load demands, in addition to calendar variables and temperature data as predictors. Some studies present load forecasts using semi-parametric additive models with a representation of logarithmic load demand data [23,24]. In Equation (3), a simplified example of a semi-parametric additive regression model for STLF is presented, where yt,p represents the load at time t during period p, hp models the effect of calendar variables, fp(wt) models the temperature effects, and models the effects of past load data.
2.1.3. ARMA Models
ARMA models represent a stochastic process using a combination of autoregressive and moving average components [25]. Mathematically, an ARMA (p, q) can be written as in (Equation (4)), where c is a constant, p and q are the data and error term lags, respectively, and and are the model parameters.
In STLF, load series are non-stationary; thus, Autoregressive Integrated Moving Average (ARIMA) models, which are a generalization of the ARMA model, are often used [26,27]. The ARIMA model (Equation (5)) removes the series trend through differentiation; that is, it applies the operator (1 − B) on the series of the ARMA model.
Finally, ARMA models can still include exogenous variables, resulting in ARMAX models (Equation (6)), also used in STLF studies [27,28,29]. Here, are the input parameters of the exogenous variable d.
2.1.4. Smoothing Models
Exponential smoothing models are based on assigning weights to past observations that lose their relevance exponentially over time [28,30]. Thus, they do not depend on explanatory variables, requiring less data than multiple linear regression models. The exponential smoothing method is described by (Equation (7)), where is the exponentially smoothed value, and α is the smoothing constant (0 < α < 1).
Although exponential smoothing models are used in several academic papers about STLF [31,32,33,34], such an approach only accounts for few applications in STLF due to the impossibility to use predicted future temperatures as the input. As weather patterns have a great impact on future load, when weather conditions are volatile, forecasts without considering the predicted temperatures can be significantly affected [14].
2.2. Non-Linear Machine Learning-Based Models
Figure 1 illustrates a flowchart for the STLF process, mapping steps, inputs, outputs and successful machine learning models used to represent the problem.
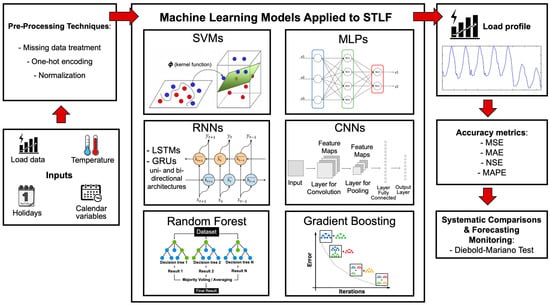
Figure 1.
STLF process on machine learning models.
Machine learning-based non-linear model developments consist of two primary stages: data pre-processing and algorithm processing. In the data pre-processing stage, various tasks are performed on the input data. These include handling missing values, normalizing data, and one-hot encoding. Subsequently, in the algorithm processing stage, the input data are partitioned into training and test sets. During training, the model’s parameters are optimized. Following this, the test set is employed to validate and assess the model’s performance. Once the pre-processing step is concluded, algorithms are trained to generate outputs for the problem at hand.
2.2.1. Support Vector Machines
SVMs with regression capabilities have prominently featured in the literature for their efficacy in forecasting from non-linear data sets. Nonetheless, there are notable challenges associated with their use. For one, the outputs of SVMs can exhibit instability, leading to significant outliers in the forecasted results. Additionally, the intricacies of SVMs configurations, such as kernel selection, kernel parameter tuning, regularization balancing, feature scaling, and handling of imbalanced data, can make the training process complex. Furthermore, the inherent sensitivity of SVMs to hyperparameters and the potential complexity introduced by multi-class problems add layers of challenge in achieving optimal model performance [35].
In regression problems, training includes non-linearity evaluating between the input and output sets of the model. The SVM for regression is based on a hyperplane in multidimensional space to maximize the distance that separates the training data and the loss function, and posteriorly the SVM minimizes the general errors [34].
Let us consider the optimization model defined in Equations (8)–(12), where () constitutes a dataset with , and . Here is the number of samples, is the number of input elements, and is the number of output elements. The decision variables are and , while maps to a hyperspace using a kernel function [36]. Finally, the estimation of for an arbitrary input vector can be mathematically described by Equation (12).
2.2.2. Artificial Neural Networks
In recent years, ANNs have become an important area of discussion and research in the scientific literature, especially when it comes to forecasting problems. This growing emphasis can be attributed to several distinct advantages that ANNs provide. Firstly, their ability to deliver accurate and consistent forecasts sets them apart from many other methods. Unlike many traditional algorithms that may struggle when facing intricate data patterns, ANNs consistently provide forecasts that are not only precise but also reliable across diverse scenarios. This leads to ANNs’ second major strength: their unparalleled configurational flexibility. ANNs’ architectures are not static; rather, they are able to dynamically change and adapt to better suit the application. Depending on the problem at hand, researchers can fine-tune layers, tweak the number of neurons, or adjust activation functions, creating a tailor-made network that resonates with the specific nuances and demands of the task. The third ANN strength lies in their intrinsic ability to generalize. Instead of merely memorizing the characteristics of the training data, ANNs explore deeper, extracting and understanding the underlying patterns, ensuring robust performance even on unseen data. This generalization is particularly vital when one considers the often-non-linear nature of STLF problems [10]. ANNs, with their interconnected structure and capable non-linear activation functions, succeed in such environments by capturing the intricate relationships that define STLF.
A notable characteristic of ANNs is their ability to produce results even when there is limited insight into the specific interactions governing the data [36]. This often makes them considered “black boxes”, where the internal workings might remain obscured to most users, but the outputs are reliably accurate. Within the vast number of ANN types, several architectures stand out for their efficacy and wide application. The Feedforward-based Multi-Layer Perceptron (MLP) is a classic Neural Network structure known for its layered arrangement of neurons and its capability to tackle a vast number of problems. On the other hand, Recurrent Neural Networks (RNNs) introduce a time dimension, allowing for the processing of sequences and offering the ability to “remember” previous inputs in their hidden state, making them ideal for tasks that include temporal dependencies such as STLF. Also, Convolutional Neural Networks (CNNs) have been used in STLF, a structure specially designed for spatial hierarchies, most famously applied in image processing and recognition.
- (a)
- Multi-layer perceptron
The MLP model is the most popular ANN model, and it is capable to be used in STLF tasks [24]. MLPs are characterized by the signal moving forward from the input layer to the hidden layers until it reaches the output layer, where posteriorly the cost function is estimated [36]. Then, a backward propagation is performed based on the cost function partial derivatives, where the weights and bias are used for the parameter update [15].
The computational advance enables Deep Neural Network (DNN) forms of MLPs. DNNs have a higher number of layers than shallow ANNs, which allows MLP models to be trained with larger datasets and contribute to a better generalization behavior [35] as well as a better representation of the non-linear pattern of input and outputs of the dataset [37].
- (b)
- Recurrent Neural Networks
RNNs are networks specialized in exploring temporal dependencies between observations. The name recurrent derives from the fact that a single network structure is used repeatedly to perform forecasts, using as an input the outputs from preceding time stages [37]. In this framework, it is important to create mathematical structures to ensure that information learned from previous stages is not lost during optimization, which commonly happens during simulations with a large number of time discretization [37,38].
Long short-term memory (LSTM) is a type of RNN that tries to address the problem of long-term dependencies using a series of memorization structures inside the network model. Equations (13)–(18) detail how this architecture is mathematically represented. A cell state ( is used as a memorization vector interacting with previous outputs and current stage inputs to identify what elements of the internal vector will be kept or deleted at each time stage. In this architecture, a structure called input gate () interacts with the cell update vector () to integrate new information in the cell state, and a structure called forget gate () interacts with the previous cell state to delete information from the RNN memory. In Equations (13)–(18), wc, wi, wf, and w0 are the weight matrices, bc, bi, bf, and b0 are bias vectors, σ is the logistic sigmoidal function, in the input vector, is the output vector of the present cell, “*” is the Hadamard Product (the element-wise of matrix multiplication), and “” represents a normal matrix multiplication.
After Ct is determined, Equations (17) and (18) are used to estimate the final output at stage ():
Another relevant RNN model is the Gated Recurrent Unit (GRU). The work of [39] applied both LSTMs and Gated Recurrent Unit (GRU) networks to STLF, focusing solely on time series load data. Unlike LSTMs, which use separate gates to control the flow of information, GRUs simplify the model with a blend of reset and update gates. This not only reduces the complexity of the network but also allows it to efficiently capture dependencies over varied time spans. While LSTMs often remain the go-to for deeper sequence complexities, GRUs offer a more compact alternative, adept at handling a wide range of sequential tasks with fewer parameters and often faster training times. The GRU model does not include the cell state and uses the hidden state () to transfer information from previous time series stages [40]. The GRU structure has two gates: the update gate () and the reset gate (). Equations (19)–(22) illustrates the GRU model mathematically.
Traditionally, RNN architectures have a unidirectional flow of information, but another alternative for these models is the bidirectional data flow, called bi-RNNs. Unlike unidirectional RNN models, bi-RNNs process data in two directions (forward in time and backward in time) through different layers [41]. Figure 2a illustrates the unidirectional RNN (uni-RNN) and Figure 2b illustrates the bi-RNN.
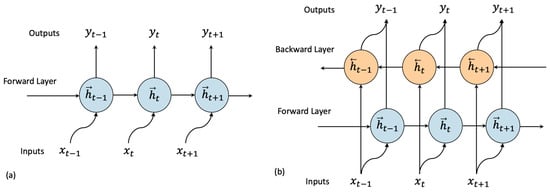
Figure 2.
Uni-RNN and Bi-RNN structures.
According to Yu et al. [42], in the bi-RNN models the forward time sequence is represented by , and the backward time sequence by ; the forward hidden sequence () is computed by Equation (23), and the backward hidden sequence ) by Equation (24), and the output is computed by Equation (25).
where, , , are the weight and biases of the forward layer, , , are the weight and biases of the backward layer, and is a bias parameter for the output.
- (c)
- Convolutional Neural Networks
CNNs have seen a steady increase in STLF over time, as highlighted by numerous recent studies [38,43,44]. This surge in popularity can largely be attributed to the CNN’s ability to process spatial hierarchies in the data. CNNs have the capacity for feature extraction, facilitated by its convolutional layers that systematically identify and prioritize significant patterns in the input data. This makes CNNs exceptionally capable of recognizing and adapting to temporal patterns inherent in STLF tasks, including daily, weekly, or even seasonal fluctuations. Unlike traditional models, which might require manual feature engineering to capture such periodicities, CNNs autonomously discern these cyclic variations, ensuring a more comprehensive and specific understanding of the data.
In CNNs, a convolution layer extracts the input resources, which are output to an activation function. The pooling layer then reduces the resource size, providing robust learning outcomes for the input resources. After several convolution and grouping steps, features are extracted to feed a fully connected layer to perform regression or classification. CNN models use convolution rather than general matrix multiplication in at least one of its layers. Mathematically, the operation for a two-layer CNN can be described by Equation (26) [44], where X is an input matrix and W is a kernel matrix.
Although it is not a very popular architecture for STLF tasks, some studies have considered CNN for this purpose. For example, the work of [45] combines a CNN architecture with input data clustering by k-means. The work of [46] uses CNN for STLF, and observed a good learning result for nonlinear problems such as STLF, but in the case of a set of loads with high volatility and uncertainty, CNN presented inferior results. Other examples of studies that use CNNs to perform STLF can be found in [47,48].
2.2.3. Other Relevant Machine Learning Techniques
Other techniques relevant to the support of STLF tasks discussed below are Bayesian Neural Networks, Transform Neural Networks, Hybrid Neural Networks, Ensemble of Neural Networks, Random Forest, and Gradient Boosting. The literature related to load forecasting as well as renewable energy forecasting studies generally employ support techniques for forecasting models, proposing new advances to improve pre-processing steps, data resource engineering, and machine learning algorithms to improve forecasting performance. For example, the work of [49] systematically reviews and summarizes data characteristics, analysis techniques, research focus, challenges, and future development directions related to wind-energy forecasting.
- (a)
- Bayesian Neural Networks
In forecasting problems where uncertainties play a significant role, the Bayesian Neural Networks (BNNs) emerge as a reliable model for providing reliable predictions. BNNs merge the power of traditional ANNs with Bayesian probability theory [13]. This synergy ensures that the forecasting model remains robust, even when confronted with challenging and unexpected conditions, such as data anomalies, missing values, or outliers. Instead of providing a singular prediction, a BNN offers a probability distribution over possible outcomes. This provides forecasters not just with a prediction but also with valuable statistical insights regarding the uncertainty and confidence associated with those predictions [50]. Such probabilistic forecasts can be insightful, allowing decision makers to have a sense of the risks, understand the model’s level of confidence, and make more informed judgments.
For BNNs, each parameter and b is modeled from a probability distribution. The objective is to estimate all possible different models that are statistically significant from the feature data for the STLF problem observed in the past [13]. Each of these models has a different probability of happening and this probably is also estimated in the training step of the network through the Bayes theorem [51]. In BNNs, the random and epistemic uncertainties are combined. The Bayes theorem and the ensemble of multiple ANNs, given the probability of each ANN, are described in Equations (27) and (28), respectively, where refers to the predicted flow, to the model input vector (for the current forecast), and , is the historical data used in training.
Among examples of recent studies that have applied BNN to STLF tasks is that of [52], which applies this architecture for load forecasting for multiple households. The work of [53] also uses BNN to perform STLF with the support of optimization algorithms to optimize the weights and limits of the Neural Network used. The authors in [54] also used a BNN, but for the STLF with a focus on load forecasting for aggregated and residential load.
- (b)
- Transformer Neural Networks
The transformer architecture is based on an encoder–decoder layer using stacked self-attention and layers connected for both the encoder and decoder [12]. The encoder component is a stack of encoders and is characterized by two main layers: a multi-head self-attention mechanism and a feedforward ANN. The decoder component is a stack of decoders, and besides the multi-head self-attention tool and feedforward ANN, it has a third sub-layer between them that makes multi-head and scaled dot-product attention [55]. Therefore, transformers use scaled dot-production attention to estimate the next vector (Figure 3).
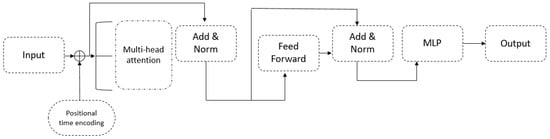
Figure 3.
Transformer Neural Network architecture example.
The scaled-dot production attention is estimated by Equation (29), where Att = attention; Q = WQx; K = WKx; V = WVx on input x = {x1, x2, …, xn}; WQx, WKx and WVx are weight matrices; and Q, K and V are obtained by linear transformation on x.
The process of multi-head attention that allows the model to attend to information from different subspaces in parallel is estimated by Equation (30), where, .
Some recent studies on transformer Neural Networks applied in STLF can be found in the literature. The work of [56] presents a model that contains a similar day-selection approach based on the LightGBM and k-means algorithms. The performance was evaluated by a setup of a series of simulations based on energy consumption data in Australia and obtained better results than traditional RNNs. The work of [57] uses transformer networks in combination with data decomposition strategies, to improve the forecasting of load in a subregion of Spain, showing significant gains in performance through the use of transformer techniques.
- (c)
- Hybrid Neural Networks
When the nature of the pattern of the problem to be approximated is not purely additive or purely multiplicative, it is possible to obtain better performances by considering a hybrid model, with some neurons contributing in an additive way and others in a multiplicative way, producing a hybrid Neural Network [58].
The output of the hybrid Neural Network is given by Equations (31) and (32), where each Θi (i = 1,..., n−1) represents either the sum operator or the multiplication operator, kj (j = 1,…, n−2) represents the weights connecting the cascade of compositions, and the terms zj (j = 1, …, n) are the weighted activation of the jth hidden neuron.
In the literature, several studies with hybrid Neural Network architectures can be found. For example, the work of [59] proposes a hybrid model based on a generalized regression ANN. In [60], a hybrid model composed of two MLPs is presented to perform the integrated load forecast in hierarchical order. The work presented in [61] shows a hybrid model for STLF based on empirical mode decomposition of enhanced ensemble and on a retro-propagation Neural Network. The work presented in [62] proposes a hybrid STLF model based on a BNN.
- (d)
- Ensemble of Neural Networks and Probabilistic Models
At its core, an ensemble approach combines the outputs of multiple models, each precisely fine-tuned prior to integration. This strategy capitalizes on the strengths of individual models while simultaneously compensating for their respective weaknesses. Ensemble methodologies initially relied on calculating a weighted average of outputs from each constituent model. This simplistic approach ensured that more accurate models held greater importance in the final prediction. However, with advancements in technology and a deeper understanding of ANNs, more sophisticated ensemble techniques have emerged [63]. These new methods not only consider the weighted outputs but also factor in the underlying architecture, training data variability, and potential correlation between models. By harnessing multiple and diverse ANNs, ensemble strategies aim to provide a more robust and consistent forecasting tool. The output of a basic ensemble method is mathematically described by Equation (33).
The basic ensemble approach has the potential to enhance the quality of results; however, it overlooks the variation in complexity among input models. Its key strength lies in its direct interpretability and avoidance of increased expected error [64].
An alternative to the basic ensemble is to find weights for each output that minimizes the ensemble error. In this way, the general method of the ensemble is defined by Equation (34), where is chosen to minimize the error concerning the target function f.
There are several studies in which ensembles are applied to solve STLF problems. Some studies have resorted to models of Support Vector Machines (SVMs), fuzzy c-means approaches and particle swarm optimization [65,66]. In [67], ensembles were composed by Random Forest and gradient boosting models and were compared with several linear STLF models.
The work of [68] adopted an enhanced decomposition with integrated autoregressive moving average and wavelet optimized by a fruit fly optimization algorithm. The work of [69] presents a STLF model with the combination of a decomposition, relevance of redundancy and general regression ANN. The work of [70] proposes a hybrid model for STLF combining autocorrelation function and least squares, in addition to SVM combined with a gray wolf optimization algorithm.
Regarding the probabilistic load forecast, these models can be based on scenarios, unless probabilities are assigned to the scenarios. Probabilities can be in the form of quantiles, intervals or probability density functions [14]. There are two intervals that we generally refer to in forecasting: the prediction intervals and the confidence intervals. The prediction interval is associated with a prediction result, while the confidence interval is related to a parameter [14].
Probabilistic load forecasts can provide more comprehensive information about future uncertainties [71]. Quantile regression is one of the main support models for probabilistic load forecasting and can be formulated as an optimization problem to minimize pinball loss, which is a comprehensive index to assess the accuracy and calibration of forecasts [72]. The pinball error is defined for any quantile q ∈ (0, 1) from a weighted absolute error, as in Equation (35), where is the forecasted q-th quantile of the n-th method at time t, is the load at time t, q is the quantile index, and is the pinball loss of n-th method at time t for the q-th quantile.
This type of model is used by many companies in the electricity sector [24], and has also been extensively explored in the literature; for example, the work presented in [73] shows a forecasting model based on semi-parametric regression that uses different temperature scenarios as an input to create a probabilistic load forecast. In [74], the authors developed a model based on multiple linear regression also powered by different temperature scenarios. The authors, in [75], applied a model with quantile regression and generalized additive models for a probabilistic load forecast. In [11], the authors propose a practical methodology to generate probabilistic load forecasts by performing quantile regression averaging on a set of sister point forecasts. In [76], the authors developed a Bayesian model with a probabilistic load forecast framework based on Bayesian deep learning to quantify the shared uncertainties across distinct customer groups while accounting for their differences.
The work of [77] proposes a probabilistic load prediction model based on ANN and probabilistic temperature predictions. The probabilistic load forecast consists of two models to quantify the probabilistic occurrence and magnitude of peak abnormal load. Based on the multilayer Gaussian mixture distribution, the work of [78] proposed a model formulated using quadratic optimization and linear constraints. The work of [79] proposed a model that combines quantile regression with convolutional bi-directional long short-term memory for probabilistic load forecasting. In addition, a combination of interval forecasts obtained by statistical models and machine learning was developed to maintain a high coverage rate, and narrowed interval width in the load interval forecasting, increasing the accuracy results when compared to single models.
- (e)
- Random Forest
Random Forest is a machine-learning technique developed by Breiman [80]. This technique combines the output of multiple decision trees to obtain a single result [81]. A Random Forest can be described as a classifier formed by a set of decision trees {h(X, vk), k, 1, …}, where vk are independent sample random vectors, uniformly distributed among all trees.
The tree-based strategies naturally rank by how well they improve the purity of a node; this implies a decrease in impurity over all trees, namely Gini impurity. The nodes with the greatest impurity decrease are at the beginning of the tree, while the nodes with the least decrease happen at the end of the tree [40].
When developing a Random Forest model, the process begins with the selection of input data using the Bootstrap method. This approach estimates parameters through a simulation based in the asymptotic distribution [82]. Once the dataset is chosen for tree construction, specific features for prediction are then selected. The growth of individual trees in the forest continues until a predefined stopping criterion is met. After the trees have been grown, the model’s performance is evaluated using the out-of-bag error. Essentially, this method leverages the data points that were excluded during the bootstrapping process [80]. The error is computed by comparing the prediction from the highest-scoring tree to the actual value of the left-out data. This approach ensures that the Random Forest model is both robust and validated against unseen data. Figure 4 summarizes the main steps for Random Forest development.
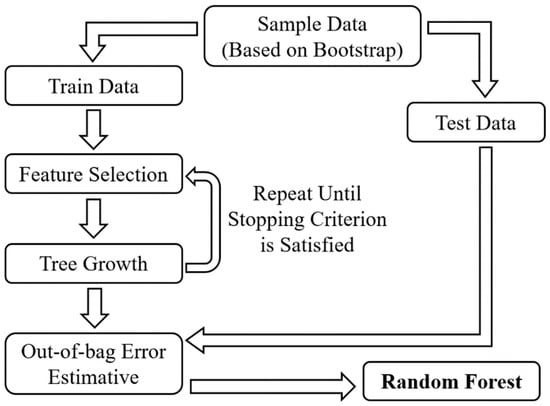
Figure 4.
Random Forest framework.
Random Forest is able to perform, in some cases, better than the classic models in the STLF task, as shown in [83,84]. In [85] the Random Forest is used for STLF, with a focus on data representation and training modes, with high accuracy and low variance, in addition to being easy to learn and optimize. In [86], they also tested the Random Forest method for an STLF problem, and the experiments showed that the prediction accuracy was superior to that of traditional ANN and SVM models.
- (f)
- Gradient Boosting
Gradient Boosting is based on the principle of minimizing a cost function through the aggregation of multiple weak learners [87]. This technique is generally used with decision trees, where one of the benefits is to obtain an estimate of the importance of the characteristics of the trained predictive model. This importance is calculated by the number of times its use improves the tree’s performance measure. Thus, the more a feature is used to make decisions in trees, the greater its relative importance. The final importance of each feature is calculated by averaging its importance in each tree that makes up the model [87].
The objective is to find the minimum value of the cost function so that over the joint distribution of all values of (y, ) the expected value of a predetermined cost function Ψ (y, f (x)) is minimized, as shown in Equation (36).
The boosting method makes an approximation of the function f*(x) from the calculation described in Equation (37), where h (x, am) is the weak learner model, and is the total number of functions. In this equation βm, am are determined using the training data from Equations (38) and (39)
Gradient Boosting using Decision Trees specializes in this method where the generic function h(; ) is a tree with L leaves and is mathematically described in Equation (40). A tree partitions the input space into L disjoint regions R1m, …, RLm and predicts a constant value in each region. In this equation, is the average of in each region Rlm, and is a pseudo-residual, calculated by Equation (41).
Recent studies have applied Gradient Boosting to solve STLF problems: in [88], the Extreme Gradient Boosting (XGboost) was employed to predict load based on similar days using clustering. In [89], XGBoost is proposed, based on the analysis of power-grid-load low big data. In [90], a Gradient Boosting technique is proposed and combined with a CNN. The work of [91] presents a prediction model based on the matching method based on pattern sequence and an XGBoost, splitting the holiday STLF problem into predictions for proportional curve and daily extremum of electricity demand.
2.3. Summary of Model Comparisons
This section briefly summarizes in Table 1 the strengths and weaknesses of the models described in the previous sections from the perspective of the short-term load forecasting literature.

Table 1.
Summary of Strengths and Weakness of Methodologies applied to STLF.
3. STLF State-of-the-Art Procedures
Forecasts based on hybrid models can be executed by ensemble from multiple techniques, and by adopting methodologies that improve data pre-processing, model training, and learning algorithm capabilities [69,92]. Methodologies used in data analysis and modeling such as data segmentation into similar patterns, input variable selection, hierarchical forecasts, measurement station selections, net load considerations, and rolling window techniques are often incorporated into STLF problems. Table 2 describes these methodologies.

Table 2.
Procedures applied to STLF for data manipulation, training and simulation.
3.1. Data Segmentation in Similar Patterns
Similar pattern data segmentation is based on load pattern identification, according to the calendar variables or meteorological conditions [93]. Generally, clustering is the most used tool, with a similarity index estimated by a Euclidean distance. One of the most popular applications is the identification of days where the load presents similar patterns. This procedure is often adopted in studies using SVMs and MLP-ANNs.
Fan et al. [94] reconstruct time series data for a multidimensional perspective, using the Phase Space Reconstruction (PSR) algorithm to perform hourly and semi-hourly forecasts in New South Wales (Australia) from an SVM. Barman et al. [95] performed the STLF for Assam (India) through the SVM, segmenting the load data by similar patterns, including Euclidean distance weighting, to incorporate the temperature and humidity patterns.
In turn, Teeraratkul et al. [96] performed the STLF on an hourly basis for the following day from an ANN; the Dynamic Time Warping (DTW) algorithm was used to group similar load patterns data. Tian and Hao [97] also performed STLF on a semi-hourly basis for New South Wales (Australia) through SVM regression but performed a longitudinal selection to eliminate noise and segment daily similar pattern data. In the study of Dudek [98], although a decomposition regression model was used to perform STLF in a Polish electricity system, similar pattern data are identified using a similarity index.
Clustering is also widely used to identify similar days of load patterns, that is, they can be used to identify patterns by calendar variables (weekdays, seasons, holidays, etc.) and by weather factors, such as temperature data. For example, Papanakidis [99] performed the STLF for a Greek electricity system from an ANN, in which the similarity input pattern is clustered by a fuzzy-C algorithm, where similar load profiles were grouped by temperature data, weekdays, and holidays.
Quilumba et al. [100] utilized the k-means algorithm to cluster load data in similar patterns, drawing insights from temperature information, and employed an MLP-ANN for STLF. Similarly, Jin et al. [101] grouped load data via self-organizing maps and conducted STLF for the markets of Australia, Spain, and New York using MLP-ANNs. In turn, data pattern identification and sequencing are also useful for RNNs [102,103]. In these models, the input sequence is structured by fixed-size vectors, which sequentially input in RNN to training.
Other applications can be found in the work of Liu et al. [104], which introduced long LSTMs coupled with sequenced load data for hourly STLFs in Belgian Electricity systems. In a related approach, Kong et al. [105] employed LSTM-ANNs for the STLF of a smart grid in Australia. In this case, load data were clustered to discern load patterns, sequenced, and then used both for training and forecasting. The work presented in [17] leveraged the k-means algorithm to cluster similar load patterns, subsequently employing sequencing learning based on a combination of load, calendar, and climate data for hourly forecasting using LSTM in New England. The work of [106], focusing on non-residential load forecasting in China, first segmented similar load patterns by days using the k-means algorithm, then explored correlations between these clusters using LSTMs.
In [16], the authors adopted sequencing learning for LSTMs to forecast day-ahead loads on an hourly basis using South Korean data. This effort integrated load data, calendar variables, and temperature as predictors. The work presented in [107] utilized LSTM network for short-term zonal load probabilistic forecasting, considering the correlation of input features and decoding of time dependences. Another contribution presented in [108] applied sequencing learning with LSTMs for day-ahead STLF on a semi-hourly basis and considered an array of data-load, temperature, calendar variables, humidity, and wind speed-from the French electricity system. The work of [109] proposes an approach that uses LSTMs with sequential pattern mining, which is used to extract sequential features that are independent of correlation patterns between load and meteorological data. The proposed model uses load series, temperature, humidity, and wind speed as inputs, among other meteorological data, to create short-term load forecasts in microgrids.
3.2. Input Variable Selection
The input variable selection aims to identify which are the most influential predictors associated with the forecast outputs [110]. In addition to the load data, other variables can be incorporated into STLF models, and among these are calendar variables (time, weekdays, month, day of the year), weather variables (temperature, humidity, cloudiness, wind speed, solar radiation, etc.) [92], and socio-economic indicators (electricity prices, distribution tariffs, income, and others) [111].
Historically, correlation analysis is one of the most used methods for input variable selection that is highly explanatory and independent of other variables [112,113]. However, other techniques have also been considered for the selection process.
Stepwise regression is an input variable selection method that selects main variables for forecast and is considered in studies that use different approaches to load forecasting [23,114,115]. This method defines a procedure for identifying useful predictors to be used in the forecasting model. To do so, stepwise regression systematically adds the most significant variable or removes the least significant variable during each step of the procedure [114].
The mutual information algorithm is another input variable selection method, which is based on evaluating the interdependence between two random variables [116]. If the mutual information results in zero, the two variables are independent and there is no relevant information between them. Some studies apply mutual information algorithms to remove redundancy in the load time series [117,118,119,120,121].
Optimization algorithms, especially genetic algorithms, have also been used in recent studies about STLF [95,108,122] for input variable selection. There are several examples of genetic algorithm applications in the literature, such as ant colony [123], particle swarm [124], evolutionary [125], and colony algorithms [126]. The Xgboost algorithm is also a common technique [17], which is based on the gradient estimation for a decision tree, which performs a variable score, indicating the relevance of each training input.
3.3. Hierarchical Forecasts
Load time series can be disaggregated according to attributes of interest. These time series can be disaggregated into different hierarchies, such as geographic region, time step, and electricity grid, among others.
Hierarchical models are divided into top-down and bottom-up approaches. The top-down approach starts from the most aggregated hierarchy level but ends up losing some time series properties. For example, Quilumba et al. [100] used top-down hierarchy to disaggregate customers from similar load consumption levels. Sun et al. [127] also applied the top-down approach, initially forecasting the load of the top node and then identifying the similarity with the node at the levels below.
In the bottom-up approach, there is no loss of information, but the high dispersion from lower levels is a challenge for load forecasting [128]. The bottom-up approach is quite robust when there is no lack of information at lower levels; otherwise, the forecasts may have higher errors [129].
Forecasts based on hierarchical data can also be run from each hierarchy level. In this case, the sum of forecasts on an aggregated level may not be consistent with the forecasts made on disaggregated levels [130]. Wang et al. [46] used a weighted combination to perform load forecasts in individual clusters, then performed the STLF on a semi-hourly basis, considering individual consumer data from a smart meter. Zheng et al. [17] also used the STLF-weighted for three hundred customers of an Australian utility, which are grouped according to their zip codes into thirty disaggregated hierarchical nodes.
Linear and quadratic programming methods can be used to minimize the error between forecasts based on disaggregated data and aggregate-level data [17]. Other programming models can still be proposed based on an appropriate selection algorithm since different hierarchical levels interact with each other in a complex way, and changes in the data at a level can modify the sequencing at the same level, as well as other hierarchical levels [131,132].
3.4. Measurement Station Selection
In models that disaggregate forecast data into hierarchical levels based on geographic region, the big challenge is to assign measurement information (such as weather variables) for each region. In the recent literature, an emerging alternative has been the employment of combination methods and the aggregation of averages from various weather data stations to pursue a more effective result [133,134,135]. Other studies are also based on defining a linear combination to define the best specific weather stations for each zone, looking for the information that provides the best results [123,124].
According to Hong et al. [136], the procedures for weather-station selection can be divided into the following steps: (i) how many weather stations should be used for the STLF problem in a given region; and (ii) which weather stations should be used to feed the inputs of an STLF model.
To accomplish these steps, initially, several meteorological stations must be heuristically chosen and later, the best stations under the restriction of the previously defined quantity must be identified [137]. Among the more complex methods are the following:
- Linear combination
Linear combination allocates decreasing linear weights to weather stations sorted in ascending order of their Mean Absolute Percent Error (MAPE). The normalized weights are estimated by Equations (42) and (43):
where wi is the normalized vector, n is the number of weather stations, and
- Exponential combination
The exponential combination assigns weights to weather stations inversely proportional to the MAPE of each station. Equations (44) and (45) describe the calculation:
where,
where exp_wi is the exponential weight, and b is the base.
- MAPE-based combination
The MAPE-based combination uses the MAPE of a weather station as weight, like is described in Equation (46):
where is the MAPE of a weather station.
- Geometric mean combination:where xn is the climatic variable profile on the weather station n.
- Twofold combination
The twofold combination takes two iterations to generate virtual stations that indicate the top-ranked stations. The step-by-step of this method is described below:
- (1)
- Rank the original stations in ascending order based on their in-sample fit error of the load forecasting model;
- (2)
- Create virtual stations based on the simple mean of top stations;
- (3)
- Forecast the validation using each virtual climate variable profile, and calculate MAPE for each forecast;
- (4)
- Select the virtual stations based on the best MAPE order;
- (5)
- Create the secondary virtual stations;
- (6)
- Forecast the validation again using the climate variable profile of each secondary virtual station, and calculate MAPE for each forecast;
- (7)
- The secondary virtual station with the smallest MAPE value provides the climate variable profile.
- Genetic Algorithm combination
This considers the weather-station selection as an optimization problem, where the genetic algorithm finds the weights that can minimize the forecast errors. The methodology follows the following steps:
- (1)
- Initialize the problem with randomly assigned weights, where each weight is individually assigned to each individual in a population, and capture a set of possible weights for each station;
- (2)
- Create virtual stations using the weight set;
- (3)
- Evaluate the goodness of fit using MAPE;
- (4)
- Produce the next set in evolution, allowing each unit in the set to mate and mutate;
- (5)
- After all iterations, the desired virtual station will be the one where the weights led to the smallest MAPE.
3.5. Net Load
The analysis of weather-related behavior plays a crucial role in studies focusing on the net-load effect, defined as the difference between the global load and the load stemming from renewable energy sources. These studies seek to comprehend the impact of renewable energy penetration on the net load pattern. A greater presence of renewable sources can significantly influence the distribution, management, and operating costs of the electrical system, as they alter the traditional consumption and production dynamics [138].
Net load forecasting has become fundamental for the operation of modern networks with strong penetration of renewable energy sources [139,140,141]. Brazil has been one of the countries that have paid attention to this, considering the production of photovoltaic distributed generation in its daily operation schedule [142]. In addition to the impact on operation, some approaches have focused on commercial microgrids with high solar photovoltaic penetration [143,144]. Furthermore, recent studies about net load forecasting are found in the literature, in which forecasts were performed by different load segmentations related to several markets and systems with different demand patterns, and analyzing the renewable sources’ impacts on the STLF [145,146,147,148,149,150,151,152].
The procedure for performing net load forecasting depends on data availability and the attributes of the sought solution, such as accuracy and granularity. Thus, the net load prediction can be approached indirectly, where the prediction is the difference between the load and renewable generation forecast, and in a direct way, which directly forecasts the net load without further intermediate steps [153].
Some studies use weather data and renewable generation data to estimate renewable power generation [154]. In this way, they use the renewable generation and the net load forecast to estimate the total load at each time [153]. Others determine the impact of renewable penetration on the STLF, estimating the renewable generation using weather data and calculating the total load [155]). There are still studies that have evaluated both the direct and indirect approach, using machine learning models for net load predictions [156,157].
The main steps for net load forecasting consist of (a) data acquisition, and the assessment of quality and input-feature selection; (b) the implementation and optimization of the machine learning model; and (c) performance evaluation and monitoring. Figure 5 illustrates the main steps for net load STLF.
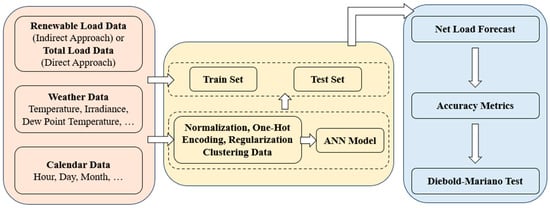
Figure 5.
Net load STLF procedures.
3.6. Rolling Window Forecasting
In the rolling window STLF, the univariate time series spans through the selected time of the window and is considered as input for the next forecasting evaluation; thus, the rolling window uses the output as input for the next point forecast [158]. In the academic literature, some studies have presented the use of rolling window forecasts for different time intervals. Chalapathy et al. [158] predicted building cooling load in six different windows. Ahani et al. [159] performed rolling window predictions in up to one window up to ten windows ahead. Li et al. [160] performed forecasts in four forward windows, and in the study, the forecasts for short-term windows showed higher accuracy.
The rolling window forecast is illustrated in Figure 6, where n is the number of original input datasets and l is the forecast window. When l is equal to 1, it is a one-step forecast.
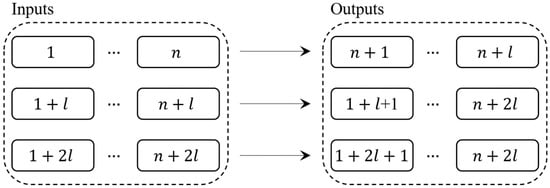
Figure 6.
Rolling window forecasting.
For the STLF rolling window, a univariate time series of load forecast described by l = (l [0], l[1], …, l[T]) feeds load forecasts for a window of periods ahead. Mathematically, the load inputs xt and outputs yt in a rolling window forecast can be described by Equations (48) and (49) [158]:
where xt is the regressor vector at time t; yt is the true output vector for the input sequence at time t; nT is the window size of the regressor vector; and n0 is the time horizon for the forecast.
For simplicity, it is possible to express the input and output vectors concerning the time window. Thus, we can rewrite the input vectors at discrete times using Equations (50) and (51) [158]:
where x[t] is the input vector of the load and other features at time t.
The output vector can be described by Equation (52):
The forecast vector also can be denoted by Equation (53):
where is the vector of parameters estimated by optimized weights of the sequential models.
3.7. Forecast Monitoring, Model Performance and Systematic Comparisons
Forecasting monitoring is an essential step to check whether the performance of any mathematical model remains stable over time, or if it needs interventions. On the other hand, comparisons are also pertinent, aiming towards superior performance results for STLF tasks. There are several accuracy metrics that are generally used to monitor and compare the performances of STLF models. Among them, the Mean Average Percentage Error (MAPE), the Mean Error Absolute (MAE), the Mean Square Error (MSE), the Average Error (AE) and the Nash–Sutcliffe Error (NSE) can be mentioned [3,97]. While error analysis has been conducted in different forms over the years for applications in renewable energy forecasting), to our knowledge most of the STLF literature that has used using machine learning methods has focused on discussing error metrics such as MAPE, MAE, MSE, and others on selecting the appropriate model.
Although these metrics are consolidated benchmarks for monitoring model performance, care must be taken when using them to compare performance across models. In some cases, there may be no statistically significant difference between the models’ performance, leading to incorrect conclusions. An alternative to circumvent this risk is the application of the test presented by Diebold and Mariano (1995) [161], which is capable of statistically validating whether there is a statistically significant superiority between a model in relation to its benchmark.
In a Diebold-Mariano test, the , are the forecasts results from the models (), and (), and , are the forecast errors of each model. The estimated errors for each model are introduced into a loss function, and the statistical value of the Diebold-Mariano test is estimated, where is a consistent estimator of the asymptotic variance [159]:
Finally, the Diebold-Mariano hypothesis test can be described as
- : the loss function generates predictions that are not statistically different ();
- , where model has better prediction performance than ;
- , where model has better prediction performance than .
The Diebold-Mariano test has been applied in several recent studies that have involved the comparison of new STLF models with already-consolidated applications. The work presented in [3] applied the test to evaluate and compare different ANN architectures. The work presented in [160] used the Diebold-Mariano test to compare the performance of architectures that use machine learning and wavelet transformed for the STLF task. In [162], the test is used to validate a new approach using LSTM with five other benchmarking models, including other approaches involving LSTM.
In [163], a decomposition structure is proposed and subsequently evaluated using different non-linear and linear STLF models; for the comparison between the models’ performances the Diebold-Mariano test is also applied. In [164], the Diebold-Mariano test is applied to assess the impact of Kalman filters and fine-tuning for load forecasts to adapt to new electricity consumptions during the COVID-19 pandemic without requiring exogenous information.
3.8. Summary of Studies about STLF Procedures
Table 3 summarizes the studies related to the procedures highlighted in Section 3. The methodologies for data segmentation in similar patterns and input variable selection can be observed; it is also noted that studies on net load have gained popularity due to the growth of the penetration of renewable energy sources in different energy matrices.

Table 3.
Summary of studies.
4. STLF in the Brazilian Power System
The Brazilian electrical power system has unique characteristics in composition due to its vast continental dimensions. The country’s load centers are typically situated at considerable distances from major generation resources, leading to the diverse availability of power generation and transmission assets [165]. The system encompasses four large and distinct submarkets: southeast/central–west, south, northeast, and north, each exhibiting different electricity demand patterns. These submarkets are interconnected by large blocks of transmission lines forming the so-called National Interconnected System (SIN), which makes it possible to export and import energy between regions and optimize the use of the country’s generating portfolio.
The SIN is distinctively characterized by hydropower dominance, which accounts for approximately 65% of the total generation capacity, making Brazil one of the largest hydro-dominant countries in the globe. The country has been actively attempting to diversify its energy portfolio in the last few decades, with significant investments in wind, solar, and biomass, reflecting a shift towards a more diverse energy matrix. With the increasing penetration of wind and photovoltaic sources in the country and associated variability in generation [166], it has become essential to plan energy operations in the very short term in order to satisfy the system demand at minimum costs while optimizing the use of available resources.
The Brazilian independent system operator (ONS) utilizes computational algorithms designed to optimize the operational scheduling of the power generation assets in order to satisfy the system demand. This process aims to minimize the total operational costs in different planning horizons [3]. For mid-term operational scheduling, the NEWAVE model performs system optimization considering a 5-year horizon with monthly decision periods (discretization). Among the results from the NEWAVE run, the monthly locational marginal prices (LMPs) and the future cost function (associated with the dispatch) are obtained. In turn, the DECOMP model aids in defining the optimal operational scheduling considering a short-term horizon (two to twelve months ahead) with weekly discretization. DECOMP simulation uses the future cost function from NEWAVE and defines the weekly LMPs that have been used over the years as a basis to determine the electricity prices in the Brazilian electricity market.
More recently, ONS, in an attempt to enhance very short-term operational planning in the Brazilian interconnected power system, started to adopt the DESSEM model [167,168]. DESSEM aims to plan the daily operation scheduling of a hydrothermal system at half-hour intervals, and estimate the LMPs on an intra-hourly basis. In this horizon, half-hour-interval STLFs for the day ahead in each submarket are used as the input of DESSEM, optimizing the scheduling of generation to satisfy demand at the lowest cost. DESSEM was designed to minimize the day-ahead operational costs of the hydrothermal system dispatch, considering a horizon up to two weeks ahead with semi-hourly discretization. STLF and power generation data, including non-dispatchable sources, are among the main inputs for the DESSEM model. Figure 7 illustrates the planning horizons, optimization models, and time discretization of the problems considered by ONS.
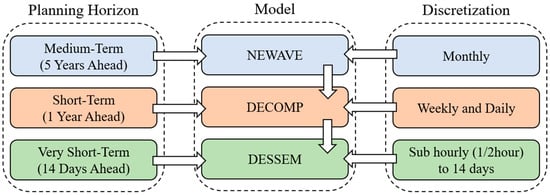
Figure 7.
Planning horizons, optimization models, and time discretization of the problems considered by ONS for generation scheduling and resource coordination.
ONS recently started to use machine learning algorithms for creating STLF models for the Brazilian system. The outputs of these models are used as input for the optimization of the day-ahead generation scheduling using DESSEM. The main STLF model is named PrevCargaDESSEM, and performs semi-hourly load forecasts for the following day, in addition to producing a load curve per level in a weekly horizon. PrevCargaDESSEM is based on a linear combination between a linear SVM, a radial SVM, and an ANN model.
The PrevCargaDESSEM predictors are load data series (on an hourly basis); verified temperature history (for an hour); temperature forecast (on an hourly basis); a list of holidays and special days; DST (start and end); forecast horizon (start and end); and loading times. The input data (divided in a set of data files) and daily forecast are available on ONS online database called SINtegre [169].
The STLF performed in PrevCargaDESSEM are divided into steps 1 to 3, also illustrated in Figure 8:
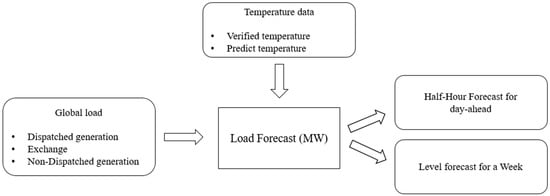
Figure 8.
PrevCargaDESSEM flowchart.
- (1)
- Global load forecast in MW for each weekday, using the following predictors: daily load series; holidays and special days; average, minimum, and maximum daily temperature; and month;
- (2)
- Global load forecast (p.u) for each day type (normal day, holiday eve, holiday, day after holiday, and special days). The predictors are month; DST; weekday and hourly load series; and temperatures;
- (3)
- With the global load average (MW) and the load profile forecast (p.u), the global load forecast in MW is obtained by multiplying the forecasts for each ½ hour segment of the following day for the other weekdays.
In the PrevCargaDESSEM model, it is possible to discretize the load data in half-hour and hourly intervals. Forecasts are made for scheduling the operation for the following day (D + 1), where half-hour discretization is adopted to obtain a very short-term operation planning and information for estimating the intra-hour electricity price. The models’ accuracy is evaluated using MAPE and the root-mean-square error (RMSE).
The DESSEM model considers the power system composed of hydroelectric power plants and thermoelectric power plants, in addition to renewable power plants (wind, biomass, solar, etc., whose dispatch is not optimized by the model). To represent the power system network, power plants are arranged in submarkets (subsystems) that are interconnected by a set of transmission lines. Thus, the PrevCargaDESSEM forecasts are performed for the four Brazilian submarkets (Southeast/Midwest, South, Northeast, and North).
The global load series for the four submarkets includes the dispatched generation data, the exchange between submarkets, and the non-dispatchable generation on an hourly basis. Then, load data are discretized on a half-hourly basis by a cubic monotonic spline. The hourly load profile by energy source is also estimated from the hourly generation of each source, to obtain the daily load profile forecast.
Verified temperature data from the Air Force Command Meteorology Network (REDEMET) [170] are used as input for PrevCargaDESSEM. Other temperature data used by the model are obtained from operational models from the Center for Weather Prediction and Climate Studies (CPTEC/INPE) and prediction models from the National Centers for Environmental Prediction (NCEP) [171].
For the predicted temperature in each submarket, a proxy series called equivalent temperature is adopted. This proxy is obtained from data from two or more locations and their respective weights. Weights are estimated using optimization algorithms, such as genetic algorithms, to maximize the correlation between load and temperature data.
PrevCargaDESSEM is based on fourteen different forecast models together, which is differentiated by predicted temperature data, not considering the predicted temperature, average temperature, maximum temperature, and the maximum and minimum temperatures [172]. In addition, predictions can be run from SVM linear kernels, SVM radial kernels, or over ANN feedforward and two linear dynamic regressions, one considering mean temperature data as input and the other with maximum temperature data. Posteriorly, an ensemble is defined with the best-settings weighting, and finally, a final forecast is produced.
The PrevCargaDESSEM set of input files contains the load series; temperature series; load levels; predicted temperature; holidays; start and end date of forecasts; and an optimizer that looks for the best match among the twelve predictions. Figure 9 illustrates an overview of the PrevCargaDESSEM framework.
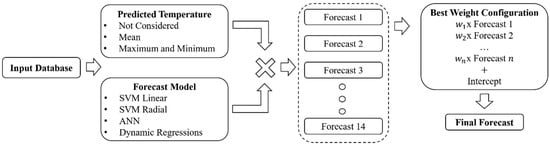
Figure 9.
PrevCargaDESSEM overview.
To consolidate the STLF, ONS also uses the Artificial Neural Network Short-Term Forecast Load (ANNSTLF), from the Electric Power Research Institute (EPRI) [173]. ANNSTLF (6.0) is a Windows software that uses historical load, temperature information, and predicted temperature for STLF.
ONS uses ANNSTLF for generating forecasts for a ten-day-ahead horizon. The predictors considered in the ANNSTLF model are the load series, verified temperature, predicted temperature, holidays and special days, DST (start and end), and unusual load days. The ANNSTLF forecaster consists of three models, two ANNs for load forecasting, a Base Load Forecaster (BLF) that forecasts the hourly load for the following day, and a Change Load Forecaster (CLF) that forecasts the hourly load variation from one day (k) to the next day (k + 1). A module then combines the predictions using a recursive least squares algorithm. Figure 10 illustrates the ANNSTLF overview.
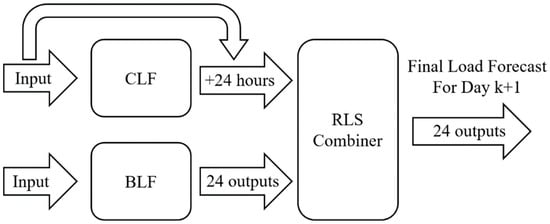
Figure 10.
ANNSTLF overview.
ONS also validates the STLF with an ensemble of linear and non-linear time series models, which uses the mean, minimum, and maximum error in the model ranking. The linear models are ARIMA and Holt–Winters, which include weekly seasonality and previous-day loads, providing weekly variations. Dynamic regression models are also used, in which temperature data are included, as well as dummies for weekdays and holidays. Another linear model used is a quantile regression, which uses load and temperature information as the input. In turn, among the non-linear models are ANN feedforward and SVMs with linear and radial kernels, which include load and temperature information from the seven previous days.
Every week, the ONS presents the performance of its load forecasts on a semi-hourly horizon, where the average MAPE of the forecasts and also the percentage of semi-hours in which the forecasts were above an MAPE of 3% are evaluated [174]. In case of frequent mismatches in the performance of the models, ONS organizes working groups that investigate treatment alternatives for the models’ input data, as well as the use of new architectures for STLF. Since the introduction of daily planning using the DESSEM model, ONS has started to use machine learning models to execute STLF. As their developments are still recent, there are opportunities for testing RNN models (e.g., LSTMs and GRUs) as part of the PrevCargaDESSEM ensemble. LSTMs and GRUs in their uni- and bi-directional forms have shown promising accuracy results for STLF for the Brazilian southeast/central–west submarket in [3], with NSE achieving values up to 0.98 and MAPE of 1.2%, respectively. In addition, there are other things to explore such as weather-station selections for temperature information, the use of other climate variables as predictors, and the incorporation of better forecasts for distributed energy resources that impacts the system net load.
In addition to models used by ONS, the literature also presents other studies about STLF and machine learning models, focused on the Brazilian system. For example, Silva et al. [166] developed an ANN feedforward for seven subsequent days, in which the predictors are the month, weekdays, load forecast one and two hours ago, load variation during the day, and a weighted metric with the climatic variables of temperature, wind speed, and relative humidity. The authors obtained MAPE results around 1.66% with their ANN applied to the Brazilian south submarket using 2016 data. Silva et al. [174] compared three STLF models: an ARIMA; an LSTM; and a GRU ANN. The authors considered the following information as an input: months; weekdays and holidays; GDP growth; regional temperatures expressed as weighted load; and a trend factor for population growth. Machine learning models developed in [171] and applied to the Brazilian southeast/central–west submarket achieved MAPE from 1.75% to 2.5% considering data up to 2019.
Ribeiro et al. [175] presented an RNN of the Echo State Network (ESN) type. ESN is an RNN with a simple architecture, a sparsely hidden layer, and with synaptic weights fixed and randomly assigned. The main ESN feature is that the only fixed weights that are modified in training are the synapses that connect the hidden-layer neurons with the output layer. In the study, this approach was used for the STLF in Brazil’s southern region, using the load data for the first four weeks.
In the literature related to STLF in Brazil and the framework adopted by ONS, machine learning models have started to be employed over the last few years. However, a handful of machine learning models (e.g., RNNs, BNNs, GRUs, etc.) have not yet been adopted by ONS. Moreover, many of the classical procedures for data processing, training, and simulation remain largely unexplored. Therefore, there are still opportunities to investigate these techniques and procedures, signaling potential areas for future research and innovation that can potentially improve the quality of STLFs and consequently the power-generation operational dispatch planning in the country.
5. Conclusions
This paper provided a comprehensive review of machine learning-based methods used for short-term load forecasting and have discussed the Brazilian experience, with applications of such methods to provide forecasts for the Brazilian interconnected power system. The main characteristics of STLF include the non-linearity behavior of the time series and the influence of calendar and weather variables in conjunction with load information. The advancement in computational capabilities has facilitated the consolidation of non-linear models based on machine learning, owing to their ability to process large datasets through pattern identification and improved generalization.
Modern STLF models frequently utilize hybrid approaches, either through ensemble techniques or methodologies that enhance data pre-processing and/or model training. These methods can include strategies such as similar pattern data identification, handling patterns by calendar or climate variables, sequencing learning, input variable selection, hierarchical forecasts, weather station selection, and net-load consideration.
Recently, the Brazilian ISO has started to use machine learning algorithms for STLF, including ANN feedforward and SVMs, via model ensemble techniques. However, the absence of state-of-the-art pre-processing methodologies is noteworthy. Substantial effort is directed toward constructing input datasets containing load, temperature, holiday, and special days data. The selection of airports considered for the acquisition of temperature data, as well as the weighting of the acquired data, also requires attention. Another eminent challenge is to integrate the load from distributed generation into the daily schedule. Over the years, Brazil has experienced an increasing fluctuation effect in load patterns originating from the higher penetration of distributed wind and solar generation and their associated variability. This growing issue will probably require that STLF models consider a better representation of these resources, including their associated climate variables, e.g., wind speed and solar irradiation, in order to create more accurate net load forecasts.
Given the vast and diverse nature of the Brazilian submarkets, each with specific characteristics, methodologies involving similar pattern data, input variable selection, and meteorological station selection can substantially improve frameworks to perform STLF. Finally, it is worth noting that other state-of-the art machine learning techniques could be tested in the context of the Brazilian system, aiming to improve STLF accuracy.
Author Contributions
Conceptualization, G.A. and A.R.d.Q.; investigation, G.A., L.B.S.M., V.A.D.d.F. and A.R.d.Q.; writing—original draft preparation, G.A.; writing—review and editing, G.A., L.B.S.M., V.A.D.d.F. and A.R.d.Q.; supervision, J.W.M.L., L.M.M.L. and A.R.d.Q. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by Energisa on the ANEEL R&D project PD-06585-2003/2020, the Brazilian National Council for Scientific and Technological Development (CNPq): CNPq Fellow–Brazil (300943/2020-2), and the SemeAD (FEA-USP) of Foundation Institute of Administration and Cactvs Payment Institution (SemeAD Scholarship, PQjr - Notice 2021.01).
Data Availability Statement
The authors confirm that the data supporting the findings of this study are available within the article.
Acknowledgments
The authors thank Energisa for the financial support on the ANEEL R&D project PD-06585-2003/2020. This study was also partially thank by the Brazilian National Council for Scientific and Technological Development (CNPq) for the CNPq Fellow–Brazil (300943/2020-2) and the SemeAD (FEA-USP) of Foundation Institute of Administration and Cactvs Payment Institution for the fellow SemeAD Scholarship, PQjr - Notice 2021.01.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Jetcheva, J.G.; Majidpour, M.; Chen, W.P. Neural network model ensembles for building-level electricity load forecasts. Energy Build. 2014, 84, 214–223. [Google Scholar] [CrossRef]
- Mocanu, E.; Nguyen, P.H.; Gibescu, M.; Kling, W.L. Deep learning for estimating building energy consumption. Sustain. Energy Grids Netw. 2016, 6, 91–99. [Google Scholar] [CrossRef]
- Morais, L.S.; Aquila, G.; de Faria, V.A.D.; Lima, J.W.M.; Lima, L.M.M.; de Queiroz, A.R. Short-Term Load Forecasting Using Neural Networks and Global Climate Models: An Application to a Large-scale Electrical Power System. Appl. Energy 2023, 348, 121439. [Google Scholar] [CrossRef]
- Charytoniuk, W.; Chen, M.S. Very short-term load forecasting using artificial neural networks. IEEE Trans. Power Syst. 2000, 15, 263–268. [Google Scholar] [CrossRef]
- Lindberg, K.B.; Seljom, P.; Madsen, H.; Fischer, D.; Korpås, M. Long-term electricity load forecasting: Current and future trends. Util. Policy 2019, 58, 102–119. [Google Scholar] [CrossRef]
- Matrenin, P.; Safaraliev, M.; Dmitriev, S.; Kokin, S.; Ghulomzoda, A.; Mitrofanov, S. Medium-term load forecasting in isolated power systems based on ensemble machine learning models. Energy Rep. 2022, 8, 612–618. [Google Scholar] [CrossRef]
- Rahman, S. Formulation and Analysis of a Rule-Based Short-Term Load Forecasting Algorithm. Proc. IEEE 1990, 78, 5. [Google Scholar] [CrossRef]
- Liu, K.; Subbarayan, S.; Shoults, R.R.; Manry, M.T.; Kwan, C.; Lewis, F.I.; Naccarino, J. Comparison of very short-term load forecasting techniques. IEEE Trans. Power Syst. 1996, 11, 877–882. [Google Scholar] [CrossRef]
- Shahidehpour, M.; Yamin, H.; Li, Z. Market Operations in Electric Power Systems: Forecasting, Scheduling, and Risk Management; John Wiley & Sons: Hoboken, NJ, USA, 2003. [Google Scholar]
- Bengio, Y.; Courville, A.; Vincent, P. Representation Learning: A Review and New Perspectives. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 35, 1798–1828. [Google Scholar] [CrossRef]
- Nowotarski, J.; Liu, B.; Weron, R.; Hong, T. Improving short-term load forecast accuracy via combining sister forecasts. Energy 2016, 98, 40–49. [Google Scholar] [CrossRef]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, L.; Polosukhin, I. Attention is all you need. arXiv 2017, arXiv:1706.03762. [Google Scholar]
- Kiartzis, S.; Kehagias, A.; Bakirtzis, A.; Petridis, V. Short-term load forecasting using a Bayesian combination method. Int. J. Electr. Power Energy Syst. 1997, 19, 171–177. [Google Scholar] [CrossRef]
- Hong, T.; Fan, S. Probabilistic electric load forecasting: A tutorial review. Int. J. Forecast. 2016, 32, 914–938. [Google Scholar] [CrossRef]
- Hippert, H.S.; Pedreira, C.E.; Souza, R.C. Neural networks for short-term load forecasting: A review and evaluation. IEEE Trans. Power Syst. 2001, 16, 44–55. [Google Scholar] [CrossRef]
- Kwon, B.S.; Park, R.J.; Song, K.B. Short-Term Load Forecasting Based on Deep Neural Networks Using LSTM Layer. J. Electr. Eng. Technol. 2020, 15, 1501–1508. [Google Scholar] [CrossRef]
- Zheng, J.; Xu, C.; Zhang, Z.; Li, X. Electric Load Forecasting in Smart Grids Using Long-Short-Term-Memory Based Recurrent Neural Network. In Information Sciences and Systems; IEEE: Piscataway, NJ, USA, 2017. [Google Scholar]
- Kutner, M.H.; Nachtsheim, C.; Neter, J. Applied Linear Statistical Models; McGraw-Hill/Irwin: New York, NY, USA, 2004. [Google Scholar]
- Hong, T. Short-Term Electric Load Forecasting; North Carolina State University: Raleigh, NC, USA, 2010. [Google Scholar]
- Charlton, N.; Singleton, C. A refined parametric model for short-term load forecasting. Int. J. Forecast. 2014, 30, 364–368. [Google Scholar] [CrossRef]
- Hong, T. Energy forecasting: Past, present, and future. Foresight Int. J. Forecast. 2014, 32, 43–49. [Google Scholar]
- Ruppert, D.; Wand, M.P.; Carroll, R.J. Semiparametric Regression; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- Fan, S.; Hyndman, R.J. Short-term load forecasting based on a semi-parametric additive model. IEEE Trans. Power Syst. 2012, 27, 134–141. [Google Scholar] [CrossRef]
- Hyndman, R.J.; Fan, S. Density forecasting for long-term peak electricity demand. IEEE Trans. Power Syst. 2010, 25, 1142–1153. [Google Scholar] [CrossRef]
- Brockwell, P.J.; Davis, R.A. Introduction to Time Series and Forecasting, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Juberias, G.; Yunta, R.; Moreno, J.G.; Mendivil, C. A new ARIMA model for hourly load forecasting. In Proceedings of the 1999 IEEE Transmission and Distribution Conference (Cat. No. 99CH36333), New Orleans, LA, USA, 11–16 April 1999; Volume 1, pp. 314–319. [Google Scholar]
- Wei, L.; Gang, Z.Z. Based on the time sequence of the ARIMA model in the application of short-term electricity load forecasting. In Proceedings of the 2009 International Conference on Research Challenges in Computer Science, Shanghai, China, 28–29 December 2009; pp. 11–14. [Google Scholar]
- Christiaanse, W.R. Short-term load forecasting using general exponential smoothing. IEEE Trans. Power App. Syst. 1971, 2, 900–911. [Google Scholar] [CrossRef]
- Yan, H.T.; Huang, C.M. A new short-term load forecasting approach using self-organizing fuzzy ARMAX models. IEEE Trans. Power Syst. 1998, 13, 217–225. [Google Scholar]
- Nakamura, M. Short term load forecasting using daily updated load models. Automatica 1985, 21, 729–736. [Google Scholar] [CrossRef]
- Wu, J.; Wang, J.; Lu, H.; Dong, Y.; Lu, X. Short-term load forecasting technique based on the seasonal exponential adjustment method and the regression model. Energy Convers. Manag. 2013, 70, 1–9. [Google Scholar] [CrossRef]
- Taylor, J. Short-term load forecasting with exponentially weighted methods. IEEE Trans. Power Syst. 2012, 27, 458–464. [Google Scholar] [CrossRef]
- Taylor, J.W.; Mc Sharry, P.E. Short-Term Load Forecasting Methods: An Evaluation Based on European Data. IEEE Trans. Power Syst. 2007, 22, 2213–2219. [Google Scholar] [CrossRef]
- Taylor, J.W. Short-term electricity demand forecasting using double seasonal exponential smoothing. J. Oper. Res. Soc. 2003, 54, 799–805. [Google Scholar] [CrossRef]
- Deng, Z.; Wang, B.; Xu, Y.; Xu, T.; Liu, C.; Zhu, A.Z. Multi-Scale Convolutional Neural Network with Time-Cognition for Multi-Step Short-Term Load Forecasting. IEEE Access 2019, 7, 88058–88070. [Google Scholar] [CrossRef]
- Haykin, S. Neural Networks: A Comprehensive Foundation, 2nd ed.; Bookman: Grand Haven, MI, USA, 2007; 900p. [Google Scholar]
- Graves, A. Generating Sequences with Recurrent Neural Networks; Computer Science: Kraków Poland, 2013. [Google Scholar]
- Choi, H.; Ryu, S.; Kim, H. Short-Term Load Forecasting based on ResNet and LSTM. In Proceedings of the 2018 IEEE International Conference on Communications, Control, and Computing Technologies for Smart Grids (SmartGridComm), Aalborg, Denmark, 29–31 October 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 1–6. [Google Scholar]
- Kumar, S.; Hussain, L.; Banerjee, S.; Reza, M. Energy Load Forecasting using Deep Learning Approach-LSTM and GRU in Spark Cluster. In Proceedings of the 2018 Fifth International Conference on Emerging Applications of Information Technology (EAIT), Kolkata, India, 12–13 January 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 1–4. [Google Scholar]
- Veeramsetty, V.; Reddy, K.R.; Santhosh, M.; Mohnot, A.; Singal, G. Short-term electric power load forecasting using random forest and gated recurrent unit. Electr. Eng. 2022, 104, 307–329. [Google Scholar] [CrossRef]
- Bianchi, F.M.; Maiorino, E.; Kampffmeyer, M.C.; Rizzi, A.; Jenssen, R. Recurrent Neural Networks for Short-Term Load Forecasting: An Overview and Comparative Analysis; Springer: Berlin/Heidelberg, Germany, 2017. [Google Scholar]
- Yu, Z.; Ramanarayanan, V.; Suendermann-Oeft, D.; Wang, X.; Zechner, K.; Chen, L.; Tao, J.; Ivanou, A.; Qian, Y. Using Bidirectional Lstm Recurrent Neural Networks to Learn High-Level Abstractions of Sequential Features for Automated Scoring of Non-Native Spontaneous Speech. In IEEE Workshop on Automatic Speech Recognition and Understanding; IEEE: Piscataway, NJ, USA, 2015. [Google Scholar]
- Kim, J.; Moon, J.; Hwang, E.; Kang, P. Recurrent inception convolution neural network for multi-short-term load forecasting. Energy Build. 2019, 194, 328–341. [Google Scholar] [CrossRef]
- Chen, K.; Chen, K.; Wang, Q.; He, Z.; Hu, J.; He, J. Short-term load forecasting with deep residual networks. IEEE Trans. Smart Grid 2018, 10, 3943–3952. [Google Scholar] [CrossRef]
- Dong, X.; Qian, L.; Huang, L. Short-Term Load Forecasting in Smart Grid: A Combined CNN and K-Means Clustering Approach. In Proceedings of the 2017 IEEE International Conference on Big Data and Smart Computing (BigComp), Jeju, Republic of Korea, 13–16 February 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 119–125. [Google Scholar]
- Wang, Y.; Chen, Q.; Gan, D.; Yang, J.; Kirschen, D.S.; Kang, C. Deep learning-based socio-demographic information identification from smart meter data. IEEE Trans. Smart Grid 2018, 10, 2593–2602. [Google Scholar] [CrossRef]
- Amarasinghe, K.; Marino, D.L.; Manic, M. Deep Neural Networks for Energy Load Forecasting. In Proceedings of the 2017 IEEE 26th International Symposium on Industrial Electronics (ISIE), Edinburgh, UK, 19–21 June 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 1483–1488. [Google Scholar]
- Kuo, P.H.; Huang, C.J. A high precision artificial neural networks model for short-term energy load forecasting. Energies 2018, 11, 213. [Google Scholar] [CrossRef]
- Zhao, E.; Sun, S.; Wang, S. New developments in wind energy forecasting with artificial intelligence and big data: A scientometric insight. Data Sci. Manag. 2022, 5, 84–95. [Google Scholar] [CrossRef]
- Hilborn, C.G.; Lainiotis, D.G. Optimal estimation in the presence of unknown parameters. IEEE Trans. Syst. Sci. Cybern. 1969, 5, 38–43. [Google Scholar] [CrossRef]
- Lainiotis, D. Optimal adaptive estimation: Structure and parameter adaption. IEEE Trans. Autom. Control 1971, 16, 160–170. [Google Scholar] [CrossRef]
- Bessani, M.; Massignan, J.A.; Santos, T.M.; London, J.B., Jr.; Maciel, C.D. Multiple households very short-term load forecasting using bayesian networks. Electr. Power Syst. Res. 2020, 189, 106733. [Google Scholar] [CrossRef]
- Gao, Z.; Shi, J.; Li, H.; Chen, C.; Tan, J.; Liu, L. Power load forecasting based on Bayesian neural network and particle swarm optimization. In IOP Conference Series: Earth and Environmental Science; IOP Publishing: Bristol, UK, 2020; Volume 558, p. 052050. [Google Scholar]
- Bassamzadeh, N.; Ghanem, R. Multiscale stochastic prediction of electricity demand in smart grids using Bayesian networks. Appl. Energy 2017, 193, 369–380. [Google Scholar] [CrossRef]
- Nascimento, E.G.S.; de Melo, T.A.; Moreira, D.M. A transformer-based deep neural network with wavelet transform for forecasting wind speed and wind energy. Energy 2023, 278, 127678. [Google Scholar] [CrossRef]
- Zhao, Z.; Xia, C.; Chi, L.; Chang, X.; Li, W.; Yang, T.; Zomaya, A.Y. Short-term load forecasting based on the transformer model. Information 2021, 12, 516. [Google Scholar] [CrossRef]
- Ran, P.; Dong, K.; Liu, X.; Wang, J. Short-term load forecasting based on CEEMDAN and Transformer. Electr. Power Syst. Res. 2023, 214, 108885. [Google Scholar] [CrossRef]
- Iyoda, E.M.; Von Zuben, F.J. The evolutionary hybrid composition of activation functions in feedforward neural networks. In Proceedings of the IJCNN’99. International Joint Conference on Neural Networks, Proceedings (Cat. No. 99CH36339), Washington, DC, USA, 10–16 July 1999; IEEE: Piscataway, NJ, USA, 1999; Volume 6, pp. 4048–4053. [Google Scholar]
- Sengar, S.; Liu, X. Ensemble approach for short term load forecasting in wind energy system using hybrid algorithm. J. Ambient. Intell. Humaniz. Comput. 2020, 11, 5297–5314. [Google Scholar] [CrossRef]
- Ilić, S.A.; Vukmirović, S.M.; Erdeljan, A.M.; Kulić, F.J. Hybrid artificial neural network system for short-term load forecasting. Therm. Sci. 2012, 16 (Suppl. S1), 215–224. [Google Scholar] [CrossRef]
- Wu, Z.; Zhao, X.; Ma, Y.; Zhao, X. A hybrid model based on modified multi-objective cuckoo search algorithm for short-term load forecasting. Appl. Energy 2019, 237, 896–909. [Google Scholar] [CrossRef]
- Ghofrani, M.; Ghayekhloo, M.; Arabali, A.; Ghayekhloo, A. A hybrid short-term load forecasting with a new input selection framework. Energy 2015, 81, 777–786. [Google Scholar] [CrossRef]
- Perrone, M.P.; Cooper, L.N. When Networks Disagree: Ensemble Methods for Hybrid Neural Networks. In How We Learn; How We Remember: Toward An Understanding of Brain and Neural Systems: Selected Papers of Leon N Cooper; World Scientific: Singapore, 1995; pp. 342–358. [Google Scholar]
- Bishop, C.M. Neural Networks for Pattern Recognition; Oxford University Press: Oxford, UK, 1995. [Google Scholar]
- Hu, L.; Taylor, G. A novel hybrid technique for short-term electricity price forecasting in UK electricity markets. J. Int. Counc. Electr. Eng. 2014, 4, 114–120. [Google Scholar] [CrossRef]
- Nadtoka, I.I.; Balasim, M.A.Z. Mathematical modelling and short-term forecasting of electricity consumption of the power system, with due account of air temperature and natural illumination, based on support vector machine and particle swarm. Procedia Eng. 2015, 129, 657–663. [Google Scholar] [CrossRef]
- Papadopoulos, S.; Karakatsanis, I. Short-Term Electricity Load Forecasting Using Time Series and Ensemble Learning Methods. In Proceedings of the 2015 IEEE Power and Energy Conference at Illinois (PECI), Champaign, IL, USA, 20–21 February 2015; IEEE: Piscataway, NJ, USA, 2015; pp. 1–6. [Google Scholar]
- Zhang, J.; Wei, Y.M.; Li, D.; Tan, Z.; Zhou, J. Short term electricity load forecasting using a hybrid model. Energy 2018, 158, 774–781. [Google Scholar] [CrossRef]
- Liang, Y.; Niu, D.; Hong, W.C. Short term load forecasting based on feature extraction and improved general regression neural network model. Energy 2019, 166, 653–663. [Google Scholar] [CrossRef]
- Yang, A.; Li, W.; Yang, X. Short-term electricity load forecasting based on feature selection and least squares support vector machines. Knowl. Based Syst. 2019, 163, 159–173. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, N.; Tan, Y.; Hong, T.; Kirschen, D.S.; Kang, C. Combining probabilistic load forecasts. IEEE Trans. Smart Grid 2018, 10, 3664–3674. [Google Scholar] [CrossRef]
- Wang, Y.; Gan, D.; Sun, M.; Zhang, N.; Lu, Z.; Kang, C. Probabilistic individual load forecasting using pinball loss guided LSTM. Appl. Energy 2019, 235, 10–20. [Google Scholar] [CrossRef]
- Dordonnat, V.; Pichavant, A.; Pierrot, A. GEFCom2014 probabilistic electric load forecasting using time series and semi-parametric regression models. Int. J. Forecast. 2016, 32, 1005–1011. [Google Scholar] [CrossRef]
- Xie, J.; and Hong, T. GEFCom2014 probabilistic electric load forecasting: An integrated solution with forecast combination and residual simulation. Int. J. Forecast. 2016, 32, 1012–1016. [Google Scholar] [CrossRef]
- Gaillard, P.; Goude, Y.; and Nedellec, R. Additive models and robust aggregation for GEFCom2014 probabilistic electric load and electricity price forecasting. Int. J. Forecast. 2016, 32, 1038–1050. [Google Scholar] [CrossRef]
- Yang, Y.; Li, W.; Gulliver, T.A.; Li, S. Bayesian deep learning-based probabilistic load forecasting in smart grids. IEEE Trans. Ind. Inform. 2019, 16, 4703–4713. [Google Scholar] [CrossRef]
- Xu, L.; Wang, S.; Tang, R. Probabilistic load forecasting for buildings considering weather forecasting uncertainty and uncertain peak load. Appl. Energy 2019, 237, 180–195. [Google Scholar] [CrossRef]
- He, Y.; Cao, C.; Wang, S.; Fu, H. Nonparametric probabilistic load forecasting based on quantile combination in electrical power systems. Appl. Energy 2022, 322, 119507. [Google Scholar] [CrossRef]
- Zhang, D.; Wang, S.; Liang, Y.; Du, Z. A novel combined model for probabilistic load forecasting based on deep learning and improved optimizer. Energy 2023, 264, 126172. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Breiman, L.; Cutler, A. An introduction to the random forest for beginners. Califórnia Estados Unidos Salford Syst. 2014, 71, 24. [Google Scholar]
- Schmidheiny, K.; Basel, U. Panel data: Fixed and random effects. Short Guides Microeconom. 2011, 7, 2–7. [Google Scholar]
- Dudek, G. Short-Term Load Forecasting Using Random Forests. In Proceedings of the Intelligent Systems’ 2014 7th IEEE International Conference Intelligent Systems IS’2014, Warsaw, Poland, 24–26 September 2014; Tools, Architectures, Systems, Applications. Springer International Publishing: Cham, Switzerland, 2015; Volume 2, pp. 821–828. [Google Scholar]
- Dudek, G. A Comprehensive Study of Random Forest for Short-Term Load Forecasting. Energies 2022, 15, 7547. [Google Scholar] [CrossRef]
- Xuan, Y.; Si, W.; Zhu, J.; Sun, Z.; Zhao, J.; Xu, M.; Xu, S. Multi-model fusion short-term load forecasting based on random forest feature selection and hybrid neural network. IEEE Access 2021, 9, 69002–69009. [Google Scholar] [CrossRef]
- Huang, N.; Lu, G.; Xu, D. A permutation importance-based feature selection method for short-term electricity load forecasting using random forest. Energies 2016, 9, 767. [Google Scholar] [CrossRef]
- Friedman, J.H. Greedy function approximation: A gradient boosting machine. Ann. Stat. 2001, 29, 1189–1232. [Google Scholar] [CrossRef]
- Liao, X.; Cao, N.; Li, M.; Kang, X. Research on Short-Term Load Forecasting Using XGBoost Based on Similar Days. In Proceedings of the 2019 International Conference on Intelligent Transportation, Big Data, Smart City (ICITBS), Changsha, China, 12–13 January 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 675–678. [Google Scholar]
- Ren, L.; Zhang, L.; Wang, H.; Guo, Q. An Extreme Gradient Boosting Algorithm for Short-Term Load Forecasting Using Power Grid Big Data. Lect. Notes Electr. Eng. 2018, 528, 479–490. [Google Scholar]
- Ju, Y.; Sun, G.; Chen, Q.; Zhang, M.; Zhu, H.; Rehman, M.U. A model combining convolutional neural network and LightGBM algorithm for ultra-short-term wind power forecasting. IEEE Access 2019, 7, 28309–28318. [Google Scholar] [CrossRef]
- Zhu, K.; Geng, J.; Wang, K. A hybrid prediction model based on pattern sequence-based matching method and extreme gradient boosting for holiday load forecasting. Electr. Power Syst. Res. 2021, 190, 106841. [Google Scholar] [CrossRef]
- Sun, W.; Liang, Y. Research of least squares support vector regression based on differential evolution algorithm in short-term load forecasting model. J. Renew. Sustain. Energy 2014, 6, 53137. [Google Scholar]
- Mu, Q.; Wu, Y.; Pan, X.; Huang, L.; Li, X. Short-term load forecasting using improved similar days method. In Proceedings of the 2010 Asia-Pacific Power and Energy Engineering Conference, Chengdu, China, 28–31 March 2010; pp. 1–4. [Google Scholar]
- Fan, G.F.; Peng, L.L.; Hong, W.C. Short-term load forecasting based on phase space reconstruction algorithm and bi-square kernel regression model. Appl. Energy 2018, 224, 13–33. [Google Scholar] [CrossRef]
- Barman, M.; Choudhury, N.D.; Sutradhar, S. A regional hybrid GOA-SVM model based on similar day approach for short-term load forecasting in Assam, India. Energy 2018, 145, 710–720. [Google Scholar] [CrossRef]
- Teeraratkul, T.; O’Neill, D.; Lall, S. Shape-based approach to household electric load curve clustering and prediction. IEEE Trans. Smart Grid 2018, 9, 5196–5206. [Google Scholar] [CrossRef]
- Tian, C.; Hao, Y. A Novel Nonlinear Combined Forecasting System for Short-Term Load Forecasting. Energies 2018, 11, 712. [Google Scholar] [CrossRef]
- Dudek, G. Pattern similarity-based methods for short-term load forecasting–Part 1: Principles. Appl. Soft Comput. 2015, 37, 277–287. [Google Scholar] [CrossRef]
- Panapakidis, I.P. Clustering-based day-ahead and hour-ahead bus load forecasting models. Int. J. Electr. Power Energy Syst. 2016, 80, 171–178. [Google Scholar] [CrossRef]
- Quilumba, F.L.; Lee, W.-J.; Huang, H.; Wang, D.Y.; Szabados, R.L. Using Smart Meter Data to Improve the Accuracy of Intraday Load Forecasting Considering Customer Behavior Similarities. IEEE Trans. Smart Grid 2016, 6, 911–918. [Google Scholar] [CrossRef]
- Jin, C.H.; Pok, G.; Lee, Y.; Park, H.-W.; Kim, K.D.; Yun, U.; Ryu, K.H. A SOM clustering pattern sequence-based next symbol prediction method for day-ahead direct electricity load and price forecasting. Energy Convers. Manag. 2015, 90, 84–92. [Google Scholar] [CrossRef]
- Sutskever, I.; Vinyals, O.; Le, Q.V. Sequence to sequence learning with neural networks. Adv. Neural Inf. Process. Syst. 2014, 27, 3104–3112. [Google Scholar]
- Marino, D.L.; Amarasinghe, K.; Manic, M. Building energy load forecasting using deep neural networks. In Proceedings of the IECON 2016-42nd Annual Conference of the IEEE Industrial Electronics Society, Florence, Italy, 24–27 October 2016; pp. 7046–7051. [Google Scholar]
- Liu, C.; Jin, Z.; Gu, J.; Qiu, C. Short-term load forecasting using a long short-term memory network. In Proceedings of the 2017 IEEE PES Innovative Smart Grid Technologies Conference Europe (ISGT-Europe), Torino, Italy, 26–29 September 2017; pp. 1–6. [Google Scholar]
- Kong, W.; Dong, Z.Y.; Jia, Y.; Hill, D.J.; Xu, Y.; Zhang, Y. Short-term residential load forecasting based on LSTM recurrent neural network. IEEE Trans. Smart Grid 2017, 10, 841–851. [Google Scholar] [CrossRef]
- Jiao, R.; Zhang, T.; Jiang, Y.; He, H. Short-Term Non-residential Load Forecasting based on Multiple Sequences LSTM Recurrent Neural Network. IEEE Access 2018, 6, 59438–59448. [Google Scholar] [CrossRef]
- Lin, J.; Ma, J.; Zhu, J.; Cui, Y. Short-term load forecasting based on LSTM networks considering attention mechanism. Int. J. Electr. Power Energy Syst. 2022, 137, 107818. [Google Scholar]
- Bouktif, S.; Fiaz, A.; Ouni, A.; Serhani, M.A. Optimal Deep Learning LSTM Model for Electric Load Forecasting using Feature Selection and Genetic Algorithm: Comparison with Machine Learning Approaches. Energies 2018, 11, 1636. [Google Scholar] [CrossRef]
- Jahani, A.; Zare, K.; Khanli, L.M. Short-term load forecasting for microgrid energy management system using hybrid SPM-LSTM. Sustain. Cities Soc. 2023, 98, 104775. [Google Scholar] [CrossRef]
- de Faria, V.A.D.; de Queiroz, A.R.; Lima, L.M.; Lima, J.W.M.; da Silva, B.C. An assessment of multi-layer perceptron networks for streamflow forecasting in large-scale interconnected hydrosystems. Int. J. Environ. Sci. Technol. 2021, 19, 5819–5838. [Google Scholar] [CrossRef]
- Kuster, C.; Rezgui, Y.; Mourshed, M. Electrical load forecasting models: A critical systematic review. Sustain. Cities Soc. 2017, 35, 257–270. [Google Scholar] [CrossRef]
- Koprinska, I.; Rana, M.; Agelidis, V.G. Correlation and instance-based feature selection for electricity load forecasting. Knowl. Based Syst. 2015, 82, 29–40. [Google Scholar] [CrossRef]
- Kouhi, S.; Keynia, F.; Ravadanegh, S.N. A new short-term load forecast method based on a neuro-evolutionary algorithm and chaotic feature selection. Int. J. Electr. Power Energy Syst. 2014, 62, 862–867. [Google Scholar] [CrossRef]
- Xiao, J.; Li, Y.; Xie, L.; Liu, D.; Huang, J. A hybrid model based on selective ensemble for energy consumption forecasting in China. Energy 2018, 159, 534–546. [Google Scholar] [CrossRef]
- Nedellec, R.; Cugliari, J.; Goude, Y. GEFCom2012: Electric load forecasting and backcasting with semi-parametric models. Int. J. Forecast. 2014, 30, 375–381. [Google Scholar] [CrossRef]
- Suzuki, K. Artificial Neural Networks: Methodological Advances and Biomedical Applications; BoD–Books on Demand: Norderstedt, Germany, 2011. [Google Scholar]
- Battiti, R. Using mutual information for selecting features in supervised neural net learning. IEEE Trans. Neural Netw. 1994, 5, 537–550. [Google Scholar] [CrossRef]
- Ghadimi, N.; Akbarimajd, A.; Shayeghi, H.; Abedinia, O. Two-stage forecast engine with feature selection technique and improved meta-heuristic algorithm for electricity load forecasting. Energy 2018, 161, 130–142. [Google Scholar] [CrossRef]
- Amjady, N.; Keynia, F.; Zareipour, H. Short-Term Load Forecast of Microgrids by a New Bilevel Prediction Strategy. IEEE Trans. Smart Grid 2014, 1, 286–294. [Google Scholar] [CrossRef]
- Wi, Y.-M.; Joo, S.-K.; Song, K.-B. Holiday load forecasting using fuzzy polynomial regression with weather feature selection and adjustment. IEEE Trans. Power Syst. 2012, 27, 596. [Google Scholar] [CrossRef]
- Schaffernicht, E.; Gross, H.-M. Weighted mutual information for feature selection. In Proceedings of the International Conference on Artificial Neural Networks, Espoo, Finland, 14–17 June 2011; pp. 181–188. [Google Scholar]
- Eskandari, H.; Imani, M.; Parsa Moghaddam, M. Best-tree wavelet packet transform bidirectional GRU for short-term load forecasting. J. Supercomput. 2023, 79, 13545–13577. [Google Scholar] [CrossRef]
- Niu, D.; Wang, Y.; Wu, D.D. Power load forecasting using support vector machine and ant colony optimization. Expert Syst. Appl. 2010, 37, 2531–2539. [Google Scholar] [CrossRef]
- Hu, Z.; Bao, Y.; Xiong, T. Comprehensive learning particle swarm optimization based memetic algorithm for model selection in short-term load forecasting using support vector regression. Appl. Soft Comput. 2014, 25, 15–25. [Google Scholar] [CrossRef]
- Jalali, S.M.J.; Ahmadian, S.; Khosravi, A.; Shafie-khah, M.; Nahavandi, S.; Catalão, J.P. A novel evolutionary-based deep convolutional neural network model for intelligent load forecasting. IEEE Trans. Ind. Inform. 2021, 17, 8243–8253. [Google Scholar] [CrossRef]
- Sheikhan, M.; Mohammadi, N. Neural-based electricity load forecasting using a hybrid of GA and ACO for feature selection. Neural Comput. Appl. 2012, 21, 1961–1970. [Google Scholar] [CrossRef]
- Sun, X.; Luh, P.B.; Cheung, K.W.; Guan, W.; Michel, L.D.; Venkata, S.; Miller, M.T. An efficient approach to short-term load forecasting at the distribution level. IEEE Trans. Power Syst. 2016, 31, 2526–2537. [Google Scholar] [CrossRef]
- Stephen, B.; Tang, X.; Harvey, P.R.; Galloway, S.; Jennett, K.I. Incorporating practice theory in sub-profile models for short-term aggregated residential load forecasting. IEEE Trans. Smart Grid 2017, 8, 1591–1598. [Google Scholar] [CrossRef]
- Hyndman, R.J.; Athanasopoulos, G. Forecasting: Principles and Practice. 2018. Available online: https://otexts.org/fpp2/ (accessed on 29 October 2023).
- Gamakumara, P.; Panagiotelis, A.; Athanasopoulos, G.; Hyndman, R.J. Probabilistic Forecasts in Hierarchical Time Series; Monash University: Melbourne, Australia, 2018. [Google Scholar]
- He, Y.; Luo, F.; Sun, M.; Ranzi, G. Privacy-preserving and Hierarchically Federated Framework for Short-Term Residential Load Forecasting. IEEE Trans. Smart Grid 2023, 14, 4409–4423. [Google Scholar]
- Fan, S.; Methaprayoon, K.; Lee, W.-J. Multiregion load forecasting for systems with large geographical areas. IEEE Trans. Ind. Appl. 2009, 45, 1452–1459. [Google Scholar] [CrossRef]
- Xie, J.; Chen, Y.; Hong, T.; Laing, T.D. Relative humidity for load forecasting models. IEEE Trans. Smart Grid 2018, 9, 191–198. [Google Scholar] [CrossRef]
- Liu, B.; Nowotarski, J.; Hong, T.; Weron, R. Probabilistic load forecasting via quantile regression averaging on sister forecasts. IEEE Trans. Smart Grid 2017, 8, 730–737. [Google Scholar] [CrossRef]
- Lloyd, J.R. GEFCom2012 hierarchical load forecasting: Gradient boosting machines and Gaussian processes. Int. J. Forecast. 2014, 30, 369–374. [Google Scholar] [CrossRef]
- Hong, T.; Wang, P.; White, L. Weather station selection for electric load forecasting. Int. J. Forecast. 2015, 31, 286–295. [Google Scholar] [CrossRef]
- Sobhani, M.; Campbell, A.; Sangamwar, S.; Li, C.; Hong, T. Combining weather stations for electric load forecasting. Energies 2019, 12, 1510. [Google Scholar] [CrossRef]
- Lew, D.; Brinkman, G.; Kumar, N.; Lefton, S.; Jordan, G.; Venkataraman, S. Finding flexibility: Cycling the conventional fleet. IEEE Power Energy Mag. 2013, 11, 20–32. [Google Scholar] [CrossRef]
- Tziolis, G.; Spanias, C.; Theodoride, M.; Theocharides, S.; Lopez-Lorente, J.; Livera, A.; Makrides, G.; Georghiou, G.E. Short-term electric net load forecasting for solar-integrated distribution systems based on Bayesian neural networks and statistical post-processing. Energy 2023, 271, 127018. [Google Scholar] [CrossRef]
- Jeong, D.; Park, C.; Ko, Y.M. Short-term electric load forecasting for buildings using logistic mixture vector autoregressive model with curve registration. Appl. Energy 2021, 282, 116249. [Google Scholar] [CrossRef]
- López-Lorente, J.; Liu, X.A.; Morrow, D.J. Effect in the Aggregated Demand of Solar-Plus-Storage Prosumers in the Residential Sector. In CIRED 2020 Berlin Workshop (CIRED 2020); IET: London, UK, 2020; Volume 2020, pp. 24–26. [Google Scholar]
- ONS—Brazilian System Operator. Consolidation of Load Forecast for Electro-Energetic Programming. 2023. Available online: http://www.ons.org.br/_layouts/15/WopiFrame.aspx?sourcedoc=%7b1D9DC738-D131-4204-ADF2-37BE33C661C5%7d,file=Revista%20-%20PEN%20SISOL%202022.pdf,action=default (accessed on 29 October 2023).
- Razavi, S.E.; Arefi, A.; Ledwich, G.; Nourbakhsh, G.; Smith, D.B.; Minakshi, M. From load to net energy forecasting: Short-term residential forecasting for the blend of load and PV behind the meter. IEEE Access 2020, 8, 224343–224353. [Google Scholar] [CrossRef]
- Kobylinski, P.; Wierzbowski, M.; Piotrowski, K. High-resolution net load forecasting for micro-neighborhoods with high penetration of renewable energy sources. Int. J. Electr. Power Energy Syst. 2020, 117, 105635. [Google Scholar] [CrossRef]
- Falces, A.; Capellan-Villacian, C.; Mendoza-Villena, M.; Zorzano-Santamaria, P.J.; Lara-Santillan, P.M.; Garcia-Garrido, E.; Fernandez-Jimenez, L.A.; Zorzano-Alba, E. Short-term net load forecast in distribution networks with PV penetration behind the meter. Energy Rep. 2023, 9, 115–122. [Google Scholar] [CrossRef]
- Allipour, M.; Aghaei, J.; Noruzi, M.; Niknam, T.; Hashemi, S.; Lehtonen, M. A novel electrical net-load forecasting model based on deep neural networks and wavelet transform integration. Energy 2020, 205, 118106. [Google Scholar] [CrossRef]
- Mei, F.; Wu, Q.; Shi, T.; Lu, J.; Pan, Y.; Zheng, J. An ultrashort-term net load forecasting model based on phase space reconstruction and deep neural network. Appl. Sci. 2019, 9, 1487. [Google Scholar] [CrossRef]
- Sreekumar, S.; Chand Sharma, K.; Bhakar, R. Gumbel Copula based aggregated net load forecasting for modern power systems. IET Gener. Transm. Distrib. 2018, 12, 4348–4358. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, N.; Chen, Q.; Kirschen, D.S.; Li, P.; Xia, Q. Data-driven probabilistic net load forecasting with high penetration of behind-the-meter PV. IEEE Trans. Power Syst. 2018, 33, 3255–3264. [Google Scholar] [CrossRef]
- Van Der Meer, D.W.; Munkhammar, J.; Widén, J. Probabilistic forecasting of solar power, electricity consumption, and netload: Investigating the effect of seasons, aggregation and penetration on prediction intervals. Sol. Energy 2018, 171, 397–413. [Google Scholar] [CrossRef]
- Chu, Y.; Pedro, H.T.C.; Kaur, A.; Kleissl, J.; Coimbra, C.F. Netload forecasts for solar-integrated operational grid feeders. Sol. Energy 2017, 158, 236–246. [Google Scholar] [CrossRef]
- Kaur, A.; Nonnenmacher, L.; Coimbra, C.F.M. Netload forecasting for high renewable energy penetration grids. Energy 2016, 114, 1073–1084. [Google Scholar] [CrossRef]
- Saeedi, R.; Sadanandan, S.K.; Srivastava, A.K.; Davies, K.L.; Gebremedhin, A.H. An adaptive machine learning framework for behind-the-meter load/PV disaggregation. IEEE Trans. Ind. Inform. 2021, 17, 7060–7069. [Google Scholar] [CrossRef]
- Hafiz, F.; Awal, M.A.; de Queiroz, A.R.; Husain, I. Real-time stochastic optimization of energy storage management using deep learning-based forecasts for residential PV applications. IEEE Trans. Ind. Appl. 2020, 56, 2216–2226. [Google Scholar] [CrossRef]
- Sun, X.; Jin, C. Impacts of Solar Penetration on Short-Term Net Load Forecasting at the Distribution Level. In Proceedings of the 2021 IEEE 4th International Electrical and Energy Conference (CIEEC), Wuhan, China, 28–30 May 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 1–6. [Google Scholar]
- Aponte, O.; McConkey, K. Peak electric load days forecasting for energy cost reduction with and without behind-the-meter renewable electricity generation. Int. J. Energy Res. 2021, 45, 18735–18753. [Google Scholar] [CrossRef]
- Landelius, T.; Andersson, S.; Abrahamsson, R. Modeling and forecasting PV production in the absence of behind-the-meter measurements. Prog. Photovolt. Res. Appl. 2019, 27, 990–998. [Google Scholar] [CrossRef]
- Chalapathy, R.; Khoa, N.L.D.; Sethuvenkatraman, S. Comparing multi-step ahead building cooling load prediction using shallow machine learning and deep learning models. Sustain. Energy Grids Netw. 2021, 28, 100543. [Google Scholar] [CrossRef]
- Ahani, I.K.; Salari, M.; Shadman, A. An ensemble multi-step-ahead forecasting system for fine particulate matter in urban areas. J. Clean. Prod. 2020, 263, 120983. [Google Scholar] [CrossRef]
- Li, D.; Jiang, F.; Chen, M.; Qian, T. Multi-step-ahead wind speed forecasting based on a hybrid decomposition method and temporal convolutional networks. Energy 2022, 238, 121981. [Google Scholar] [CrossRef]
- Diebold, F.X.; Mariano, R.S. Com paring predictive accu racy. J. Bus. Econ. Stat. 1995, 13, 253–263. [Google Scholar]
- Ijaz, K.; Hussain, Z.; Ahmad, J.; Ali, S.F.; Adnan, M.; Khosa, I. A novel temporal feature selection based LSTM model for electrical short-term load forecasting. IEEE Access 2022, 10, 82596–82613. [Google Scholar] [CrossRef]
- Ma, Y.; Yu, L.; Zhang, G. A Hybrid Short-Term Load Forecasting Model Based on a Multi-Trait-Driven Methodology and Secondary Decomposition. Energies 2022, 15, 5875. [Google Scholar] [CrossRef]
- Obst, D.; De Vilmarest, J.; Goude, Y. Adaptive methods for short-term electricity load forecasting during COVID-19 lockdown in France. IEEE Trans. Power Syst. 2021, 36, 4754–4763. [Google Scholar] [CrossRef] [PubMed]
- de Queiroz, A.R.; Lima, L.M.M.; Lima, J.W.M.; da Silva, B.C.; Scianni, L.A. Climate change impacts in the energy supply of the Brazilian hydro-dominant power system. Renew. Energy 2016, 99, 379–389. [Google Scholar] [CrossRef]
- CEPEL, DESSEM Model: Daily Operation Schedule and Hourly Price Formation of Hydrothermal Systems with Detailed Representation of Generating Units, Intermittent Sources, Consideration of the Electric Grid and Safety Restrictions. 2022. Technical Report. Available online: https://www.cepel.br/wp-content/uploads/2022/05/DESSEM_ManualUsuario_v19.0.24.3.pdf (accessed on 29 October 2023).
- Santos, T.N.; Diniz, A.L.; Saboia, C.H.; Cabral, R.N.; Cerqueira, L.F. Hourly pricing and day-ahead dispatch setting in Brazil: The dessem model. Electr. Power Syst. Res. 2020, 189, 106709. [Google Scholar] [CrossRef]
- Veras, R.B.S.; Oliveira, C.B.M.; de Lima, S.L.; Saavedra, O.R.; Oliveira, D.Q.; Pimenta, F.M.; Lopes, D.C.P.; Torres Junior, A.R.; Neto, F.L.A.; de Freitas, R.M.; et al. Assessing Economic Complementarity in Wind–Solar Hybrid Power Plants Connected to the Brazilian Grid. Sustainability 2023, 15, 8862. [Google Scholar]
- ONS—Brazilian Independent System Operator. 2022 SINtegre Platform. Available online: http://www.ons.org.br/topo/acesso-restrito (accessed on 29 October 2023).
- Air Force Command Meteorology Network—REDEMET Aeródromos. Available online: https://www.redemet.aer.mil.br (accessed on 29 October 2023).
- Center for Weather Prediction and Climate Studies. Centro de Previsão do Tempo e Produtos Climáticos. Available online: https://www.cptec.inpe.br (accessed on 29 October 2023).
- Electric Power Research Institute—EPRI. Artificial Neural Network Short Term Load Forecaster (ANNSTLF) Maintenance and Support. Available online: https://www.epri.com/research/products/000000000001024433 (accessed on 29 October 2023).
- Francisco José Arteiro de Oliveira (org.). O Planejamento da Operação Energética no Sistema: Conceitos, Modelagem Matemática, Previsão de Geração e Carga/Francisco José Arteiro de Oliveira; Artliber: São Paulo, Brazil, 2020; 402p. [Google Scholar]
- Silva, L.N.; Abaide, A.R.; Figueiró, I.C.; Silva, J.O.; Rigodanzo, J.; Sausen, J.P. Development of Brazilian Multi Region Short-Term Load Forecasting Model Considering Climate Variables Weighting in ANN Model. In Proceedings of the 2017 52nd International Universities Power Engineering Conference (UPEC), Heraklion, Greece, 28–31 August 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 1–6. [Google Scholar]
- Ribeiro, G.T.; Sauer, J.G.; Fraccanabbia, N.; Mariani, V.C.; Coelho, L.S. Bayesian optimized Echo State Network to short-term load forecasting. Energies 2020, 13, 2390. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).