Abstract
Regulating the load voltage is of major importance for ensuring high transmission efficiency in wireless power transfer (WPT) systems. In this context, this work presents a novel control strategy applied in the dc-ac converter used in the primary side of a WPT system. The performance of a class-DE resonant inverter is investigated considering that such topology presents inherent soft-switching characteristics, thus implying reduced switching losses. The controller relies on an autoregressive with exogenous output (ARX) model based on an adaptive linear neuron (ADALINE) network, which allows for determining the turn-on time of the active switches accurately while providing the system with the ability to adapt to distinct alignment conditions. The performance of the proposed controller is compared with that of a linear controller, which does not prove to be an effective solution if misalignment occurs.
1. Introduction
1.1. Motivation
Electric vehicles (EVs) have drawn significant attention because of the imminent need to reduce fossil fuel consumption and greenhouse gas emissions [1]. Another important issue is urban mobility, which motivated the development of small-size vehicles such as scooters and electric bikes [2]. In this sense, the significant decrease in manufacturing costs, advances in battery energy storage technology, and the introduction of government policies, among other aspects, will contribute to the gradual replacement of traditional internal combustion engine vehicles (ICEVs) with their electric counterparts [3].
Plug-in electric vehicles (PEVs) play an important role in the conception of future smart cities while contributing significantly to the achievement of sustainable energy goals [4]. The large-scale implementation of EV charging stations is also of major importance. In either case, exhaustive research has been developed in terms of fast onboard and offboard chargers, which rely on power electronic converters [5]. Offboard chargers allow for the simultaneous connection of multiple EVs to the three-phase grid in the context of charging stations [6]. Thus, it is necessary to minimize the charging time as much as possible while both ensuring user safety and preserving the battery lifespan [7].
Wireless power transfer (WPT) technology can be classified into several categories [8]. This is an interesting solution for several applications, which include remote monitoring systems, magnetic field communication systems, radio-frequency identification (RFID), aerospace systems, and wireless sensor networks, among many others. Wireless charging systems are of particular interest for EVs because one can charge the batteries without the need for cabling or any physical connection point [9].
Considering the distance between the source and the load, one can classify WPT systems into two major groups: near-field or non-radioactive systems; and far-field or radioactive systems [10]. The first type comprises inductive power transfer (IPT) and capacitive power transfer (CPT) approaches. CPT relies on contactless power transfer through electric field coupling between two pairs of metal capacitive plates, but most modern CPT systems involve low-power applications, for which the transmission distance is only a few millimeters [11]. In turn, it is possible to achieve high power transmission efficiency (PTE) levels for transmission distances on the order of centimeters when using IPT systems [12].
Considering safety issues, some works focused on assessing the influence of foreign metallic elements that may exist close to the magnetic circuit of the WPT system, in particular the primary winding. This is because they affect electromagnetic field distribution between the transmitter and the receiver, with a direct impact on the PTE, quality factor, and mutual inductance, among others. The authors in [13] analyze three methods for detecting metallic objects. The sensor-based approach relies on temperature, pressure, image, and radar sensors, thus being a highly sensitive method that does not depend on power levels, oscillation frequency, or system misalignments. However, it has high costs, complex implementation, and difficulty in detecting non-metallic materials. The parameter variation method is another possible choice that takes into account changes in important parameters like the mutual inductance, quality factor, currents in primary and secondary windings, and efficiency. Prominent advantages include low cost and fast detection, but this solution is susceptible to misalignment while applied to low-power applications only. The sensing pattern-based detection method is also adequate for detecting metallic foreign objects, especially in high-power WPT systems. Even though it can achieve high sensitivity and immunity to misalignment, the main disadvantage is the design of the detection coil, which should not introduce any loss in the power transferred to the load.
A study focused on the safety assessment of EV users in WPT systems is presented in [14]. The results demonstrate that proper shielding can ensure electromagnetic field emissions of less than 7.2 μT inside the vehicles, that is, 28 times less than the limit of 207 μT imposed by IEEE Std C95.6-2002 [15]. As for the operating temperature, the authors in [16] carried out an experimental analysis focused on the thermal profile of a 50-kW WPT system. The results evidenced that the coil, the magnetic core, and the back-cover are the major sources of heat on the primary side. The maximum operating temperature of the inductor could easily reach 150 °C for a 5-mm thick ferrite core while the back-cover temperature above the receiver pad was 57 °C. The experimental tests showed that the steel parts between two and three inches around the charging pad reached a thermally hazardous temperature. This is why they should be shielded by a high-conductivity, low-permeability metal.
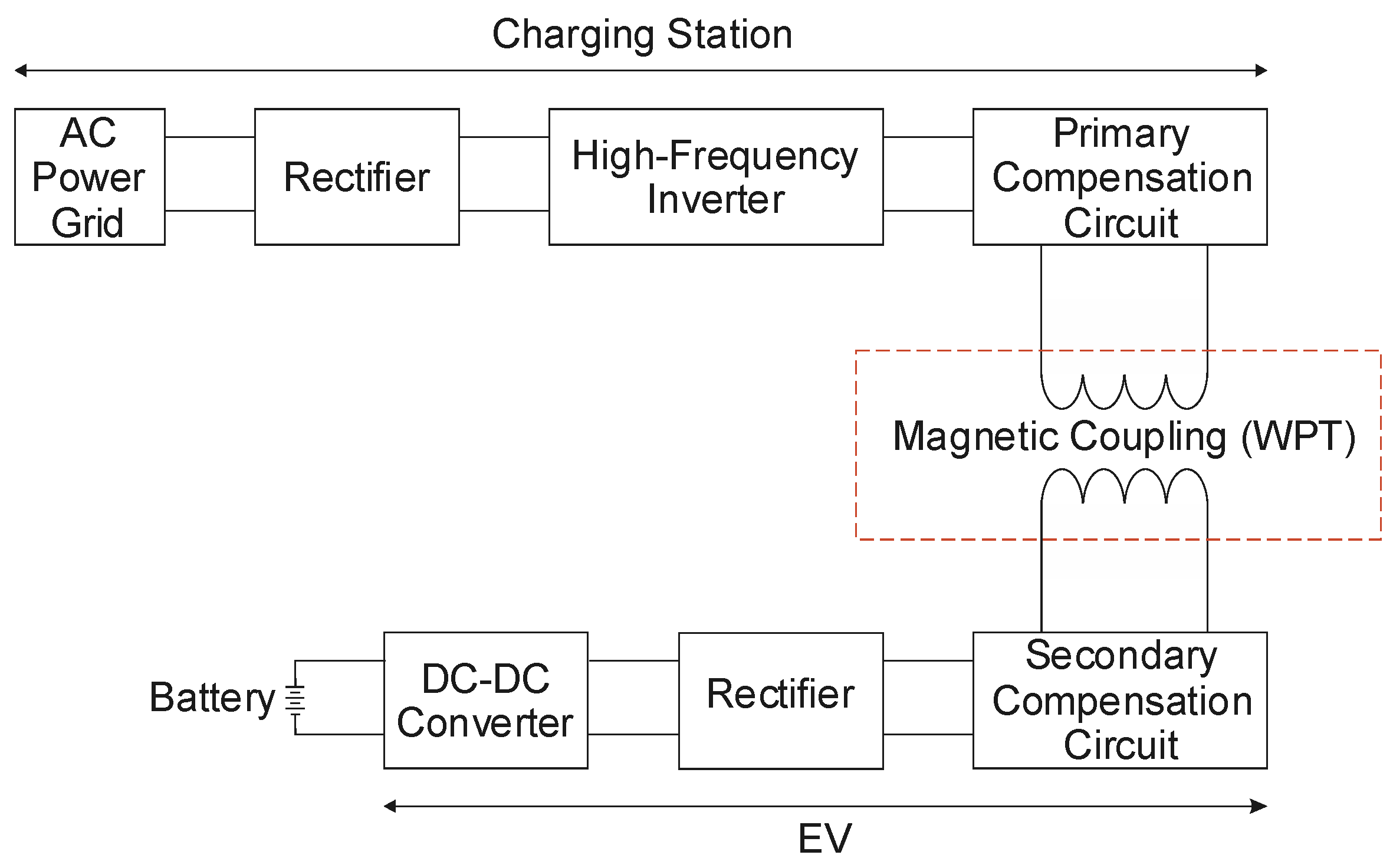
Figure 1 shows a generic IPT system for EV charging applications consisting of basically four conversion stages. A rectifier provides input power factor correction (PFC) and a regulated DC output voltage with a reduced low-frequency ripple. Thus, one can obtain a high-frequency sine wave from a high-frequency inverter, whereas power transmission occurs through a conductive medium with a defined magnetic permeability, that is, the air owing to the magnetic coupling. Another rectifier, whether embedded in the EV or not, is necessary to obtain a DC voltage to supply a DC-DC converter responsible for charging the battery bank. Overall, IPT is a promising technology that involves distinct aspects related to the development of coil structures, efficient and modern energy management strategies, and converter topologies, among others [17].
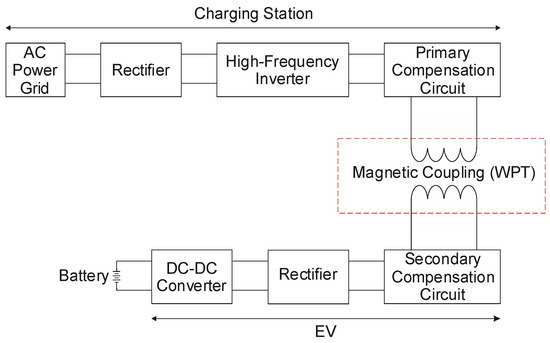
Figure 1.
Generic representation of an MCR-WPT system.
Figure 1 also represents a particular IPT technology named magnetic coupling resonant wireless power transfer (MCR-WPT). In this case, the voltage and current waveforms on the primary and secondary sides are in phase with each other while the circuit behaves as a purely resistive load. This magnetic coupling characteristic has led to improved performance in terms of higher efficiency and longer transmission distances. However, some variables have a direct influence on the efficiency of WPT systems, including misalignment in the magnetic coupling circuit associated with the x axis, the y axis, or both of them.
As a result, switching losses will inevitably exist in the semiconductors operating at a high switching frequency. This issue must be assessed in detail since it affects the overall conversion efficiency.
1.2. State-of-the-Art Review of MCR-WPT Systems
Owing to the heat dissipation in the semiconductors, as well as the variation in the magnetic medium because of the misalignment between the windings, among other factors, the parameters of the resonant circuit may change, undoubtedly compromising the overall performance of the WPT system. The authors in [18] propose a fuzzy logic controller to tune the system by varying the switching frequency, resulting in efficiencies close to 77% and 73% for the primary and secondary circuits, respectively. In this sense, the arrangement performs better than the traditional IPT architecture.
Two transcendental features for designing inductors in WPT systems are the coupling and quality factors. The first one refers to the percentage of electromagnetic flux coming from the transmitter Tx transmitted to the secondary or receiver coil Rx. The second one is a figure of merit that characterizes the inductance invariance as a function of the geometrical characteristics of the winding. An analysis of such quantities is developed in [19] for traditional IPT and MCR-WPT systems. The work demonstrates that the MCR-WPR technology demands higher values for the assessed parameters and involves additional design complexity. The study also shows that the two technologies can reach a theoretical efficiency of up to 98%.
Another important issue when analyzing the coupling factor between the primary and secondary circuits is the constructive characteristics of the windings. An approach based on simulations is presented in [20], in which different manufacturing possibilities for double-sided winding structures with distinct conductor characteristics are analyzed. It is observed that depending on the number of turns and the diameter, a maximum coupling coefficient of around 62% can be obtained. One can adopt it as a reference value since the coupling coefficient is a limiting factor that affects the system efficiency, which in turn does not depend only on the operating frequency.
The work in [21] assesses the PTE in an MCR-WPT system. The authors incorporate two additional circuits into the transmitter and receiver, resulting in a resonant coupling system with four coils. This arrangement leads to an improvement in the coupling coefficient between the inductors, resulting in a higher efficiency of 76.3% for a transmission distance of 1.33 times the diameter of the coils.
Distinct constructive characteristics such as the geometry, conductor type, and core features, among other aspects can be considered in the implementation of the inductors that constitute the transmitter and receiver. This is because all the aforementioned issues influence the quality factor. In this sense, the study carried out by [22] proposes an inductor topology that best suits the magnetically-compensated WPT system, while considering the circular, square, and square superimposed geometries. The study concluded that the planar inductor with a circular geometry is the one that presented the best performance for an MCR-WPT system, achieving an efficiency of 92.4% in terms of energy transferred to the load with a mutual inductance of 1.17 µH.
It is also noteworthy that the higher the mutual inductance, the lower the system efficiency. This is a very important concept when validating a WPT system in which two coils are close to each other. A misalignment between the coils and a variation in the distance between the windings directly affect the resulting mutual inductance between the primary and secondary windings. A two-coil arrangement placed on the primary side is assessed in [23], in which the tests consider overlapping conditions of one-third and one-half the radius, as well as non-overlapped coils. The results show that one-half the radius leads to the best performance in terms of stability in the mutual inductance. Therefore, this issue is likely to influence the conversion efficiency in terms of the power delivered to the secondary side, resulting in a maximum coupling coefficient close to 27% and a mutual inductance of around 100 µH. Thus, one way to overcome the inconvenience of misalignment is undoubtedly the incorporation of an additional coil into the primary side.
A contactless energy transfer system consists of an emitter on the ground and a receiver inside the EV. Thus, the exposure of users to the magnetic field is inherent in the system’s operation. In addition to being efficient, this arrangement ensures proper values of the mutual inductance and coupling factor as previously analyzed. However, they must comply with public health regulations for the maximum levels of non-ionizing radiation tolerated by humans. In this sense, the International Commission for Non-Ionizing Radiation Protection (ICNIRP) established the limits of 27 μT for the magnetic induction and 4.05 V/m for the electric field, which seem to be the most appropriate specifications for MCR-WPT applications involving EVs.
The battery-charging mode in stationary parking avoiding cable connection requires the use of a relatively simple IPT system by properly adjusting the distance to maximize the transmission efficiency. Nevertheless, an interoperability analysis is necessary to define proper standards while considering distinct IPT architectures [24]. In a WPT system, a typical figure of merit is the transmission efficiency between the primary and secondary inductors. The analysis developed in [25] demonstrates that this parameter depends directly on the operating frequency, the coupling coefficient, and the physical characteristics of the inductors. The coupling coefficient is directly related to the mutual inductance ratings, which in turn influence the overall system efficiency. Given the above, the authors state that, for each type of coil, one can determine an optimum distance for which the inductor will operate under the critical coupling coefficient. This parameter is determined mathematically according to the winding’s geometry and specifications. The results showed that optimal distances of 5 cm, 7 cm, and 12 cm are obtained for three distinct inductors with a diameter of 15 cm while varying the cross-sectional area of conductors and the number of turns. Thus, it resulted in critical coefficients of 0.23, 0.14, and 0.07, respectively. In other words, the smaller the critical coefficient of the inductor, the longer the maximum transfer distance.
A study carried out in [26] considers the influence of the transmission medium on the WPT system since at low frequencies the losses caused by the series resistance of the inductors are predominant when compared to the ones generated by the electromagnetic radiation effect. However, the latter portion cannot be neglected at high frequencies since the eddy currents will strongly influence the system’s efficiency. The authors also considered a 5-cm block with different conductivity ratings of the magnetic circuit, that is, varying from 0 S/m to 8 S/m. The results showed that higher operating frequencies are preferred for lower conductivity values. In turn, the best performance in media with a higher conductivity occurs at lower oscillation frequencies. When comparing the traditional IPT and MCR-IPT systems, the latter presented improved performance while considering the same distance and geometry.
As previously mentioned, the best-performing inductor geometry for WPT systems is the plate type. In this way, the work in [27] presents an approach for which the constructive characteristics of a planar inductor of a circular shape are investigated. The external radius of the plate, the diameter of the conductor, and the separation distance are assessed in detail. The authors concluded that a winding with a smaller cross-sectional area and a higher number of turns performs better than one with a higher cross-sectional area and lower number of turns considering the same diameter of the plate. Thus, the coupling coefficient varies because it depends directly on the inductance, resulting in a variation in the resonance frequency. Consequently, the inclusion of a tuning system is a must to ensure the proper coupling of inductors and enhance the system’s performance.
1.3. State-of-the-Art Review of Resonant Inverters for WPT Applications
Another important aspect for ensuring high PTE is the proper choice of power converters for the compensation circuits. Among them, both the side series (S-S) and inductor–capacitor–capacitor (LCC) resonant topologies are interesting choices for WPT systems. This is because the emitter side reaches higher voltages when the resonant circuit presents the S-S series configuration. In turn, the secondary side of the WPT system formed by an LCC resonant circuit behaves as a controlled current source, which is ideal for EV battery charging applications [28].
The high-frequency inverter on the transmitting side is responsible for the generation of sinusoidal current waveforms and ensuring energy transfer between the coils. Half-bridge and full-bridge inverters are simple arrangements that can be used for this purpose, but the operation of semiconductors under hard-switching conditions, the high conduction losses that limit the increase of the operating frequency, and high electromagnetic interference (EMI) levels are of major concern.
To overcome such drawbacks, adopting resonant inverters with soft-switching characteristics is far more attractive owing to the reduced stresses on the switches, higher power density, and higher efficiency. Depending on the arrangement of the resonant tank, one can classify the existing topologies into series, parallel, or series-parallel converters [29]. In this sense, several structures have been considered in the literature for WPT systems. Among them, one can mention the class E, class D, class EF, class EF2, and class DE inverters [30].
The class E resonant inverter is a single-switch topology with reduced losses associated with a low component count [31]. In addition, one can ensure the operation under zero-voltage switching (ZVS) and zero derivate voltage switching (ZDVS). The inverter output voltage can be controlled by varying the switching frequency, changing the DC input voltage, or adjusting the duty cycle, although frequency control is not very effective for light-load conditions. This topology requires a choke inductor, which adds a degree of freedom to its mathematical model and makes the system design somewhat complex. In addition, special attention must be given to the physical implementation of such magnetic elements, which require a high-quality factor and may affect both the mutual inductance and the coupling coefficient of the WPT circuit. Another disadvantage is that the peak voltage across the switch can be up to 3.5 times the DC input voltage. This is why this arrangement is often limited to low-power applications.
The class EF also employs a single active switch like the class E topology. However, the inclusion of an additional capacitor in parallel with the branch composed of an inductor and a capacitor decreases the peak voltage on the switch to 2.5 times the DC input voltage. Additionally, such reactive elements allow modifying the behavior of the switched waveform, while one can employ an optimal duty cycle of around 30% of the switching period. The class EF inverter has a wide operating frequency range on the order of several megahertz, also presenting a high performance and high-power capacity. This type of inverter is less tolerant to misalignment, but operating over a wider power range is possible. A possible drawback is the high component count, which makes its mathematical modeling and control system design more complex.
An inherent advantage of the class DE inverter is that it can ensure soft switching of the active switches in addition to reducing their respective voltage and current stresses. It is also possible to design the control system so that the circuit behaves as a constant voltage source. Thus, load variations that may result from a misalignment between the emitter and receiver are not likely to affect the system’s performance. Since this topology provides high efficiency in high-frequency DC-AC conversion, it is often used in many applications. It can behave as a voltage or a current source when using a series or parallel resonant tank, also ensuring soft-switching of the switches under ZVS or ZVDS conditions during turn-off, respectively [32].
1.4. State-of-the-Art Review of Control Strategies Applied in WPT Systems
The misaligned coils in a WPT system cause the transmission efficiency reduction. To minimize such inconvenience, several techniques based on distinct principles such as proportional-integral (PI) control, perturb and observe (P&O), and sliding mode control have been adopted in the literature to regulate the load voltage [33]. Variable frequency control is a common method used for this purpose, as it relies on adjusting the switching frequency of the resonant inverter to ensure proper magnetic coupling while considering changes in the load resistance. However, the reactive power flow through the system may lead to a significant decrease in efficiency [34].
Another strategy consists of varying the DC input voltage, but adding a front-end DC-DC converter is necessary in this case, thus implying increased losses and costs. The authors in [35] suggest a dual-side control scheme for a WPT system with series compensation for both the transmitter and receiver. By varying the duty cycle in the primary-side inverter, one can track the maximum efficiency point. In turn, the controller on the secondary side can regulate the load voltage accordingly. However, this architecture requires a wireless communication module.
The authors in [36] propose an adaptive frequency tracking control technique based on the detection of the phase angle between the load current and the load voltage. This quantity is used as the input of a neural network, which generates the parameters for tuning a proportional–integral–derivative (PID) controller and adjusting the switching frequency. Another solution based on the traditional dual-loop cascaded control and linear controllers is proposed in [37] for battery charging applications involving eVs. However, the main limitation is the restricted bandwidth of the closed-loop control system.
A control strategy for multifrequency and multi-load MCR-WPT systems is assessed in [38]. It consists of superimposing multifrequency modulation waves to drive the resonant inverter based on the principle of mutual inductance coupling. Thus, one can obtain inductive power transfer with distinct frequencies while considering several multi-resonant networks on the secondary side. In turn, the work in [39] investigates the influence of the mutual inductance and the coupling coefficient between the inductors aiming to maintain efficiency above 80%. The resonant circuit relies on bilateral phase–shift control, in which it is necessary to feed the current induced on the secondary side back into a neural network to obtain the drive signals of the active switches. However, this approach also requires a wireless communication system for data transmission between the primary and secondary circuits. The authors in [40] present a topology without the addition of a resonant compensation circuit. A control strategy capable of providing a variable phase–shift angle allows for regulating the load voltage and operation of active switches under ZVS conditions. In addition, an optimization method is adopted to identify the optimal operating point.
As the transmission distance increases, the transmitted power and efficiency decrease because the coupling coefficient between the inductors becomes extremely low. A first obvious choice could be the use of coils with a high self-inductance by increasing the number of turns, but it will lead to additional losses in the windings associated with increased size, weight, volume, and cost. The authors in [41] aim to optimize the circuit efficiency by minimizing the losses, which occur at the operating point where the primary and secondary currents are equal to each other. This can be achieved by using multilayer coils in both the primary and the secondary circuits, thus leading to an efficiency of 80% for a transmission distance of 100 cm.
Another approach is presented in [42], in which the authors formulate a mathematical model for a WPT system with an LCC compensator circuit for the primary and a resonant series tank for the secondary. One can properly adjust the quantities associated with distance transmission and alignment using genetic algorithms. Thus, the model allows for controlling the load voltage by properly adjusting the duty ratio of the active switch. A hybrid control solution is also presented in [43], in which small variable capacitors are used to regulate the load voltage by varying both the switching frequency and impedance of the resonant tank. However, it relies on a complex strategy for driving the switches associated with the shunt capacitors.
To ensure the operation of a WPT system at its resonance frequency there are some control options described in [36], the author emphasizes the high complexity of implementing a specific frequency tracking model due to its non-linear behavior, this is because the operation with a variable switching frequency may lead to high losses. In this sense, several works focused on bilateral control techniques are available in the literature [44].
1.5. Contributions and Organization of Topics
The overall performance of WPT systems is highly influenced by misalignment between the transmitter and the receiver, as well as the coupling coefficient and mutual inductance between the windings. In addition, such aspects will inevitably cause changes in the impedance of the resonant circuit together with the magnetic circuit associated with the class DE inverter.
As a solution to this inconvenience, this work introduces a novel controller that allows for the class DE inverter to always operate at the resonance condition. Thus, it is possible to control the duty ratio of the active switches and regulate the voltage applied to the transmitter circuit. This control strategy relies on an autoregressive with exogenous output (ARX) model based on an adaptive linear neuron (ADALINE) network [26]. Based on known values for the duty cycle as a function of the load resistance, a learning algorithm is developed to estimate the turn-on time of the active switches while the system can automatically adapt to different alignment conditions of the magnetic circuit. As a result, a discrete-time transfer function is obtained, which will be validated and analyzed through computer simulation.
The remainder of this work is organized as follows. Section 2 describes the resonant class DE inverter in detail. Section 3 addresses the novel control technique based on an ADALINE neural network. Section 4 discusses the results obtained with the proposed solution while comparing them with the ones obtained with a linear controller. Section 5 presents the concluding remarks and future work.
2. Theoretical Analysis of the Class DE Resonant Inverter
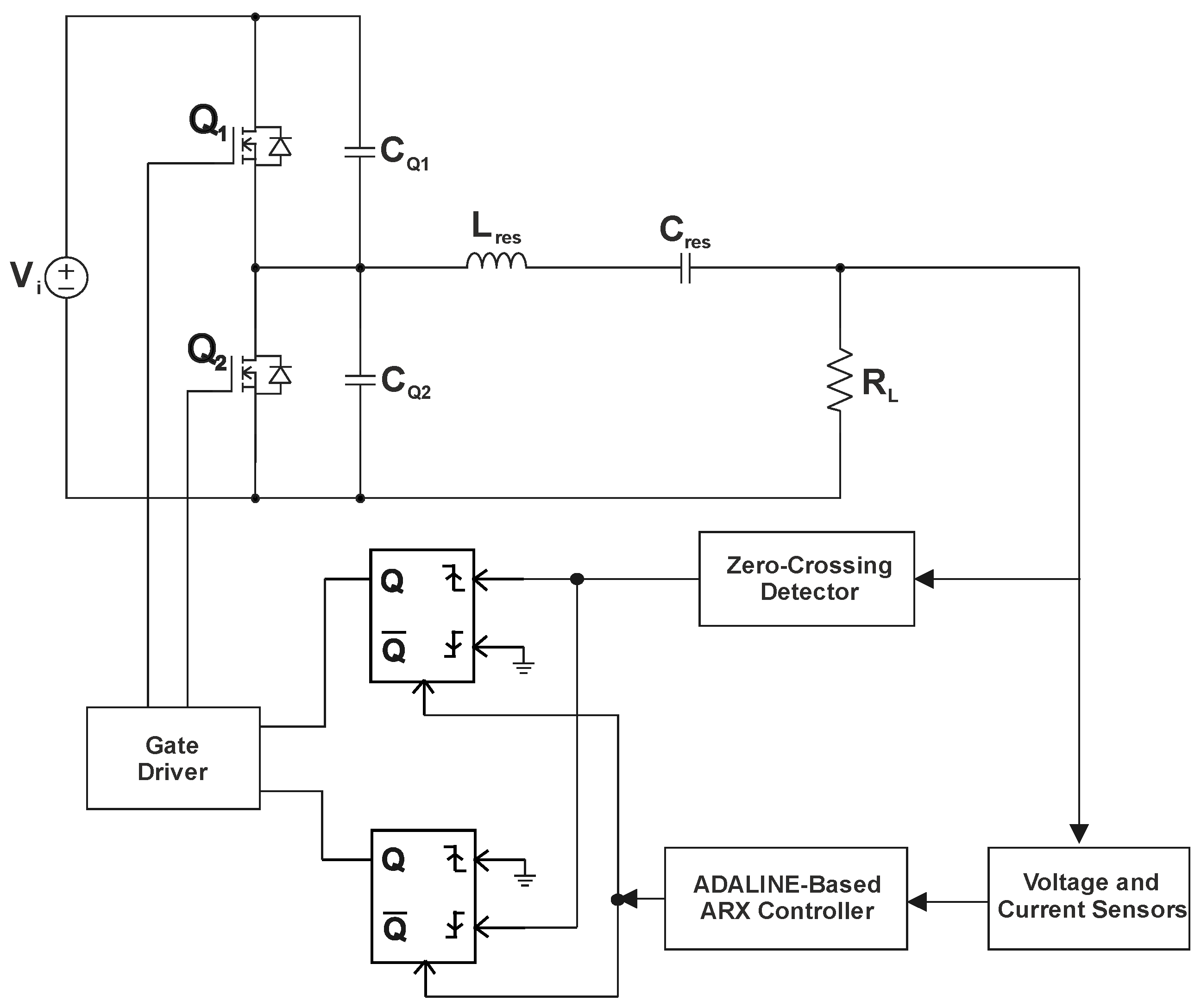
Figure 2 shows the class DE resonant inverter, which is an interesting choice for WPT applications owing to its capacity to operate at high frequencies rated on the order of megahertz. The topology consists of a DC voltage source Vi; two switches Q1 and Q2; two shunt capacitors CQ1 and CQ2; a resonant capacitor Cres; a resonant inductor Lres; and a load resistor RL. In addition, the input-to-output transfer function corresponding to (1) allows for controlling the load voltage and consequently the voltage gain GDE [45].
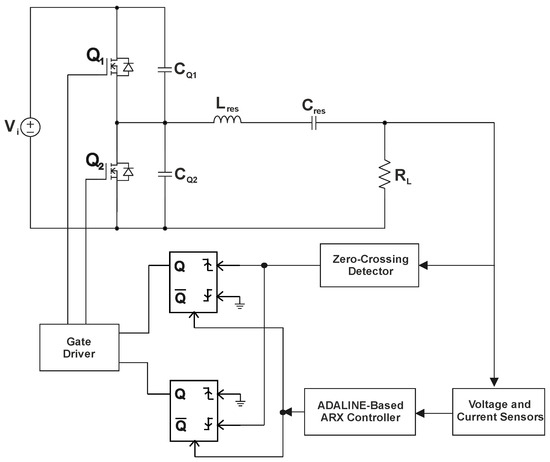
Figure 2.
Class DE resonant inverter.
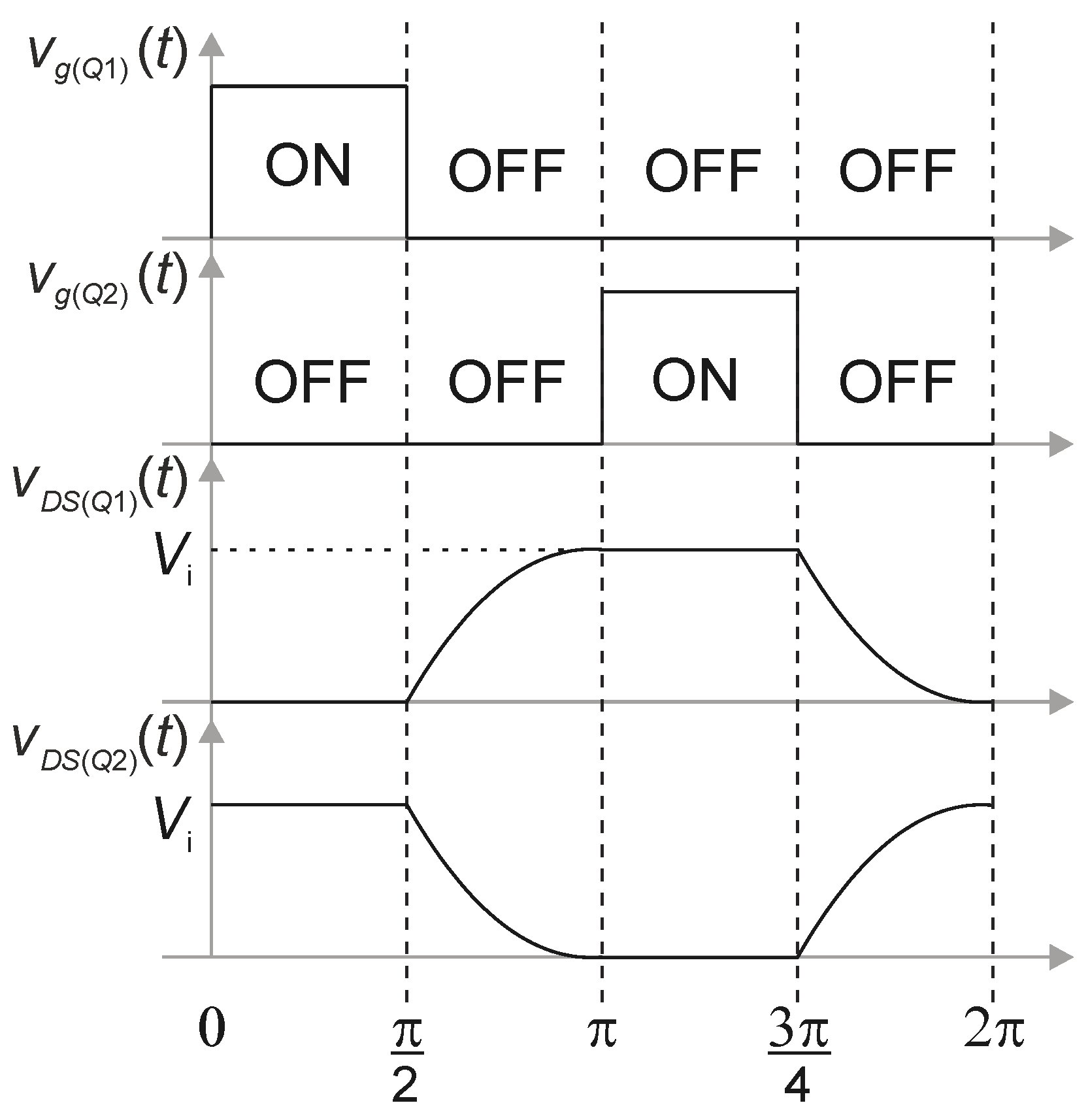
Figure 3 represents the waveforms of the class DE inverter. The drive signals of the active switches corresponding to vgs1(t) and vgs2(t), respectively are shifted by one-fourth of the switching period. Thus, the switches operate under ZVS and ZDVS conditions [46].
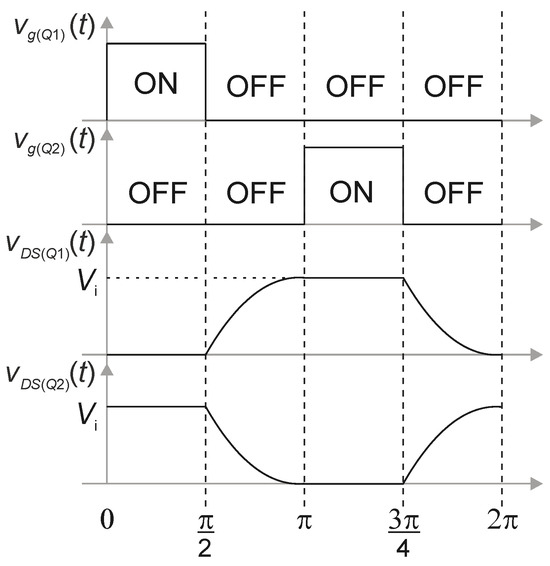
Figure 3.
Main theoretical waveforms of the class DE resonant inverter.
One can design the power stage elements of the converter from (2)–(5).
where Po is the output power, ω0 is the angular resonance frequency, and QDE is the quality factor.
The resonant circuit composed of Lres, Cres, and RL behaves as a band-pass filter that extracts the fundamental component of the instantaneous voltage across CS2 corresponding to vds2(t) according to (6) and (7).
where D is the duty cycle of the active switches and ϕD represents the phase shift caused by the resonant circuit.
One can calculate the voltage gain GDE from (8).
The root mean square (RMS) load voltage is obtained by multiplying (6) by the voltage gain GDE calculated from (8). Thus, one can regulate the load voltage by controlling the duty cycle. It is worth mentioning that this aspect is of major importance because inherent characteristics in the MCR-WPT system such as misalignment, changes in the transmission distance, and the phase–shift angle, as well as variations in the load resistance, may affect the load voltage and the overall efficiency.
3. Proposed Control Approach
The strategy proposed in the present work aims at varying the resistance of the class DE resonant circuit, which in turn is directly associated with the coupling coefficient. Thus, there is no need for a primary compensation circuit because the system operation at the resonance frequency is always ensured. The active switches operate under ZVS and ZVDS conditions by using a zero-crossing detector that relies on an ADALINE-based ARX neural network. Based on (6)–(8), the network generates a two-dimensional data matrix comprising the duty cycle values while considering changes in the load resistance between a given predefined range. The matrix is also used for the learning and training process of the network.
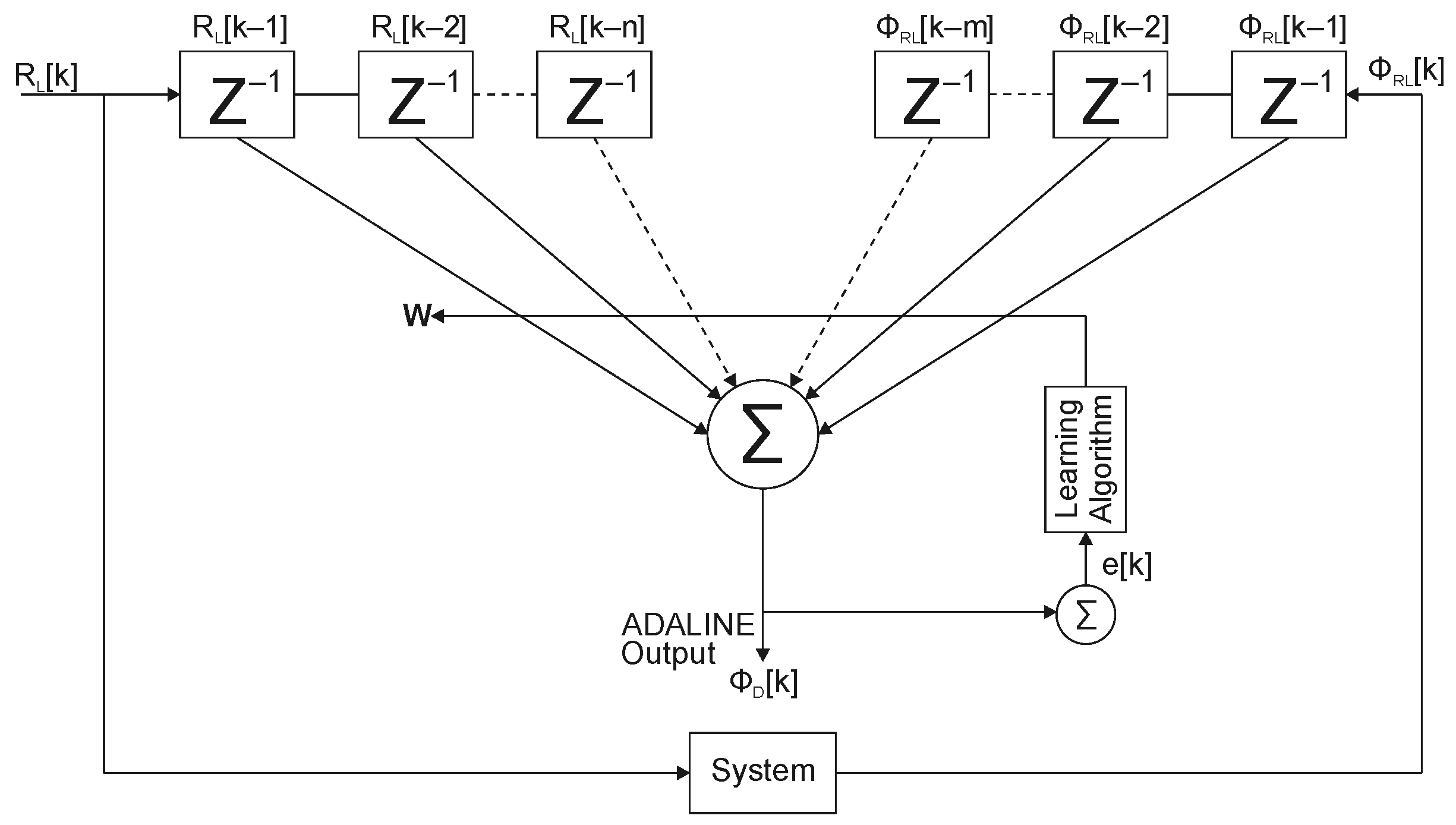
The ADALINE-based ARX model shown in Figure 4 is a neural network used for data prediction purposes from current and past values [47]. It is mathematically described by the differential equation corresponding to (9) and represented as a discrete-time linear system. The known input is the load resistance RL while the resulting output is ϕD, which defines the duty ratio of switches Q1 and Q2 in Figure 2.
where a1, a2,…, an, and b1, b2,…, bm are the polynomials estimated by the ARX neural network; m and n represent the linear regression limits for the input and output vectors respectively; and k is the pointer for an actual value obtained from the input vector RL[k] and the output vector ϕD[k].
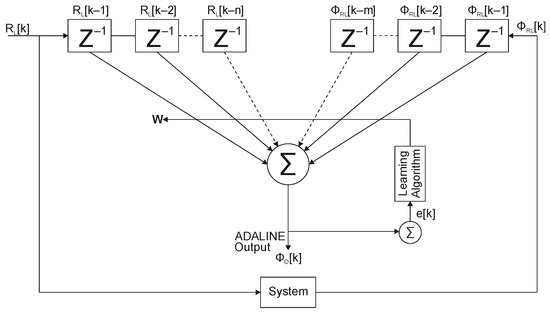
Figure 4.
ADALINE-based ARX model.
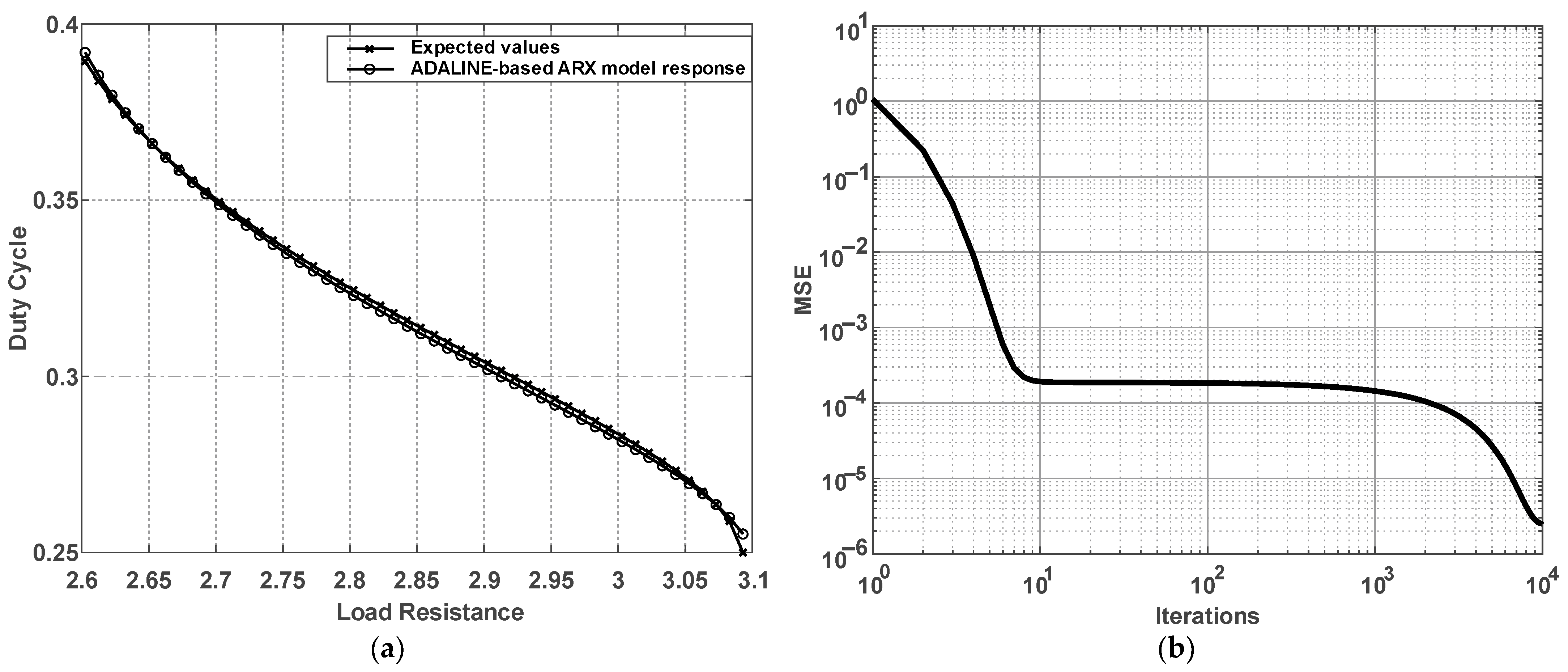
The controller obtained from the learning process of the ADALINE-based ARX neural network reached the minimum convergence error of less than 1 × 10−5. Figure 5 shows the obtained results in terms of the mean square error (MSE) and the expected values compared with the ones provided by the network, resulting in a negligible error.
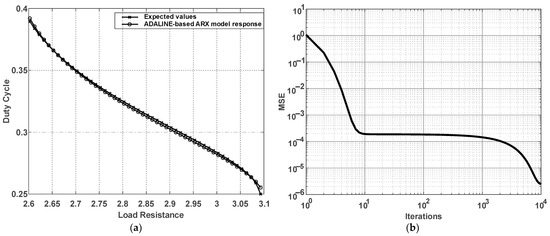
Figure 5.
Fitting process of the ADALINE-based ARX model: (a) duty cycle as a function of the load resistance and (b) MSE as a function of the number of iterations.
Applying the Z transform to (9), one can obtain the discrete-time transfer function of the controller used by the class DE resonant inverter as in (10).
Applying the bilinear transform to (10) yields (11), which is the continuous-time transfer function corresponding to the ADALINE-based ARX controller proposed in this work for the Class DE resonant inverter. The error associated with the linear approximation also influences the second-order transfer function HDE(s). However, some preliminary tests showed that adopting a higher-order model does not lead to a significant decrease in the MSE. Therefore, good tradeoffs between complexity and accuracy result when representing HDE(s) as in (11).
To compare the proposed solution with other similar approaches available in the literature, let us present a brief discussion of traditional control methods applied in WPT while also considering Table 1. Pulse frequency modulation (PFM) is often employed on the primary side to obtain constant current and constant mode control [48]. However, if the switching frequency deviates too far from the resonant frequency, the switches may no longer achieve the soft-switching condition. In turn, pulse width modulation (PWM) applied on the secondary side allows for overcoming such drawbacks. Thus, one can keep the switching frequency constant and close or equal to the resonance frequency to cancel the reactances associated with the leakage inductance and the compensation capacitance, yielding soft-switching operation and a higher efficiency [48].

Table 1.
Comparison of control strategies applied in WPT systems.
The work in [49] compares the performance of consolidated fixed-frequency control techniques, that is, traditional phase–shift (TPS) control, asymmetrical clamped-mode (ACM) control, and asymmetrical duty-cycle (ADC) control. According to the authors, the output voltage is clamped to zero on both sides when TPS control is used. In turn, the output voltage is not clamped to zero or is clamped to zero only on one side if ADC or ACM is adopted instead, respectively. Therefore, it will cause nonuniform switching losses in the active switches while both even and odd harmonics appear in the inverter output voltage.
The well-known P&O algorithm is assessed in [50]. A single-ended primary inductance converter (SEPIC) is incorporated into the secondary side of an MCR-WPT system to achieve maximum power point tracking (MPPT) and match load changes by adjusting the duty cycle of the converter. However, this solution will inevitably imply redundant power processing, higher component count, and increased complexity.
4. Results and Discussion
This section presents some simulation results of a class DE resonant inverter associated with the ADALINE-based ARX controller compared with those obtained with a PI controller. The specifications of the class DE resonant inverter are shown in Table 2.

Table 2.
Specifications of the class DE resonant inverter.
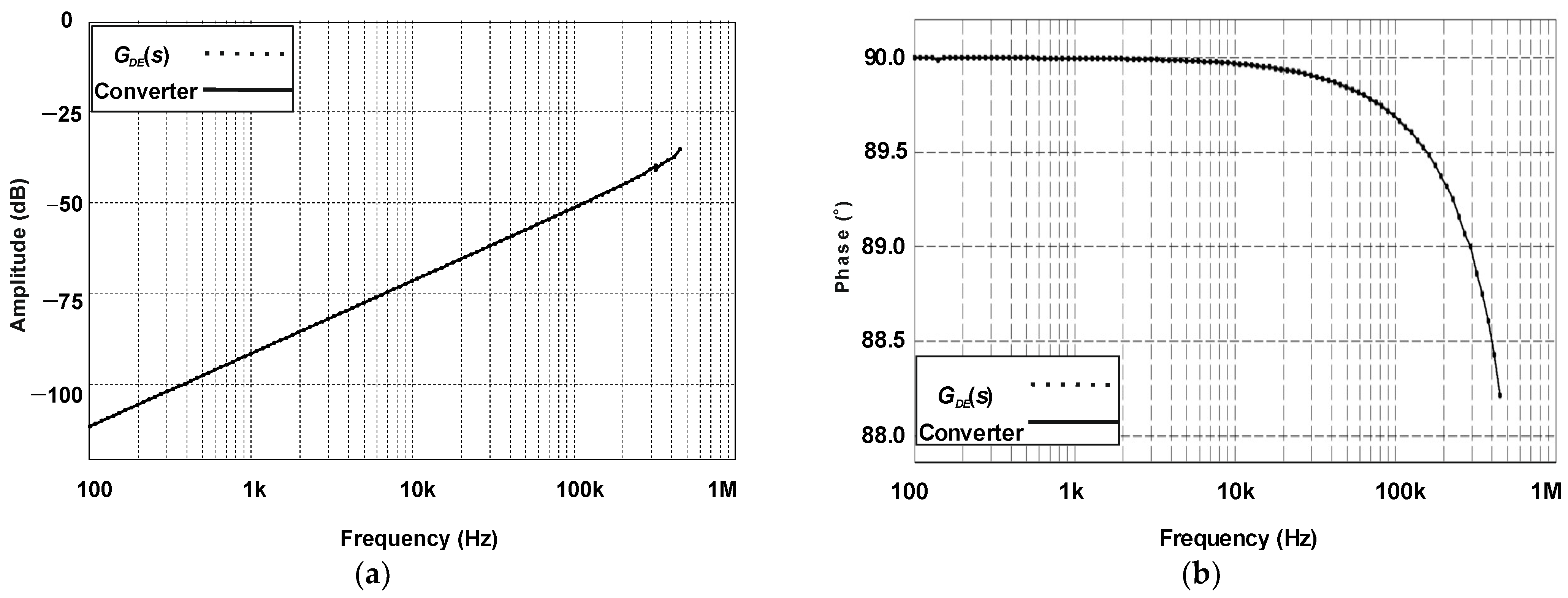
First, it is important to demonstrate that (1) can represent the converter accurately in the frequency domain. Figure 6 shows that the Bode plots of the small-signal model overlap the ones corresponding to the switched converter between 100 Hz and 450 MHz. It is also noteworthy that the small-signal model is valid up to one-half the switching frequency.
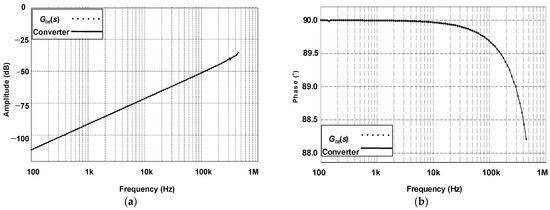
Figure 6.
Bode plots of the class DE inverter and its respective transfer function GDE(s): (a) magnitude and (b) phase.
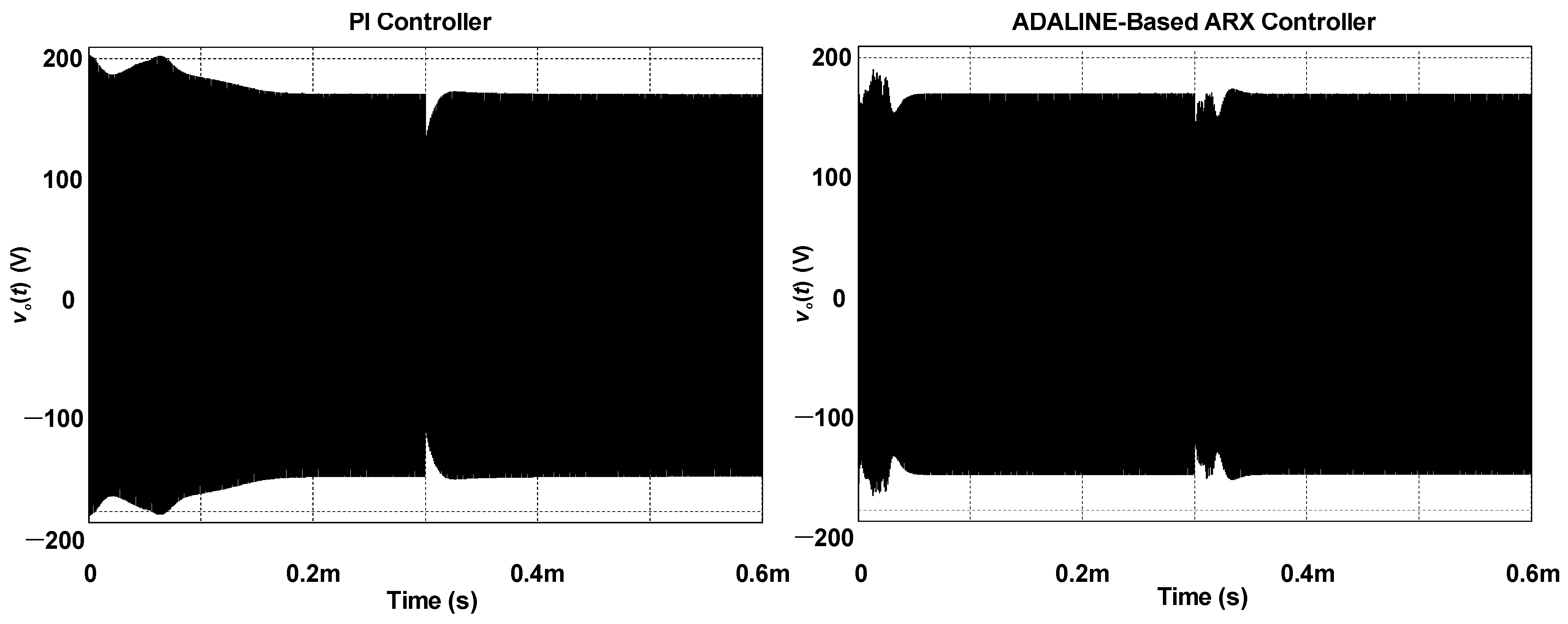
Let us recall that regulating the load voltage is crucial for ensuring the good performance of an MCR-WPT system. To validate the effectiveness of the proposed control approach compared with the PI controller, a load step from 3.1 Ω to 2.6 Ω is applied at t = 0.3 ms in Figure 7. During the startup, the overshoot is 203.17 V and 189.88 V when using the PI and ADALINE-based ARX controllers, respectively. When a load step-up occurs, the resulting overshoot for the PI and ADALINE-based ARX controllers is 171.13 V and 172.76 V, respectively. Another interesting performance metric is the settling time, which is directly related to the duty cycle and the soft-switching characteristic of the active switches. The settling times achieved by the PI and ADALINE-based ARX controllers during start-up are 0.2 ms and 0.04 ms, respectively. After the load power increases at t = 0.3 ms, the system takes 60 µs to reach the steady-state operation when using the ADALINE ARX-based model. In turn, the PI controller will lead to a shorter settling time of 85 µs.
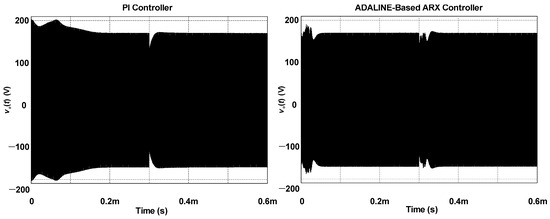
Figure 7.
Behavior of the load voltage when a load step occurs.
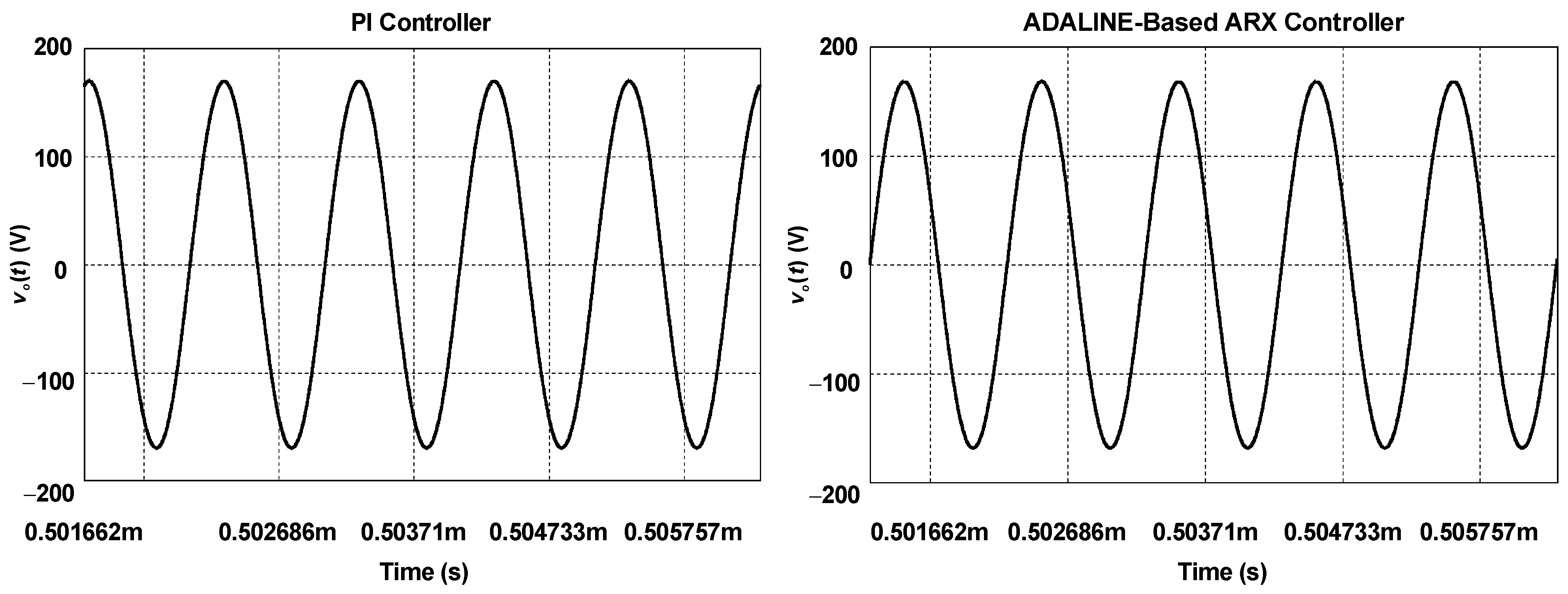
Figure 8 represents the output voltage in a steady-state condition after the load step. The waveforms are not in phase with each other because the PI controller cannot determine the drive signals during the transitions between half cycles accordingly. The period is equal to 1.022 µs, which yields an operating frequency of 0.9784 MHz. Thus, it results in a small deviation of 1.79% around the resonance frequency. The PI controller provides a peak voltage of 169.92 V, while the ADALINE ARX-based controller yields a peak voltage of 168.65 V. The latter controller does not provide the expected value of 169.70 V because the neural network relies on predicting future data based on current and past values. The proposed ADALINE-based ARX model considers a time lag of two intervals, thus yielding a second-order transfer function. A higher-order regression model would undoubtedly allow for obtaining a lower error in the RMS load voltage but at the cost of increasing the implementation complexity.
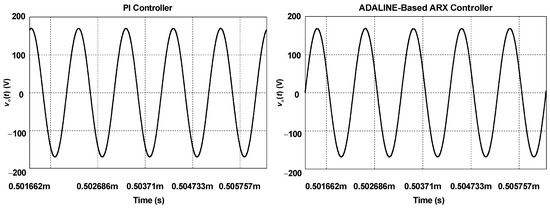
Figure 8.
Detailed view of the load voltage in steady state.
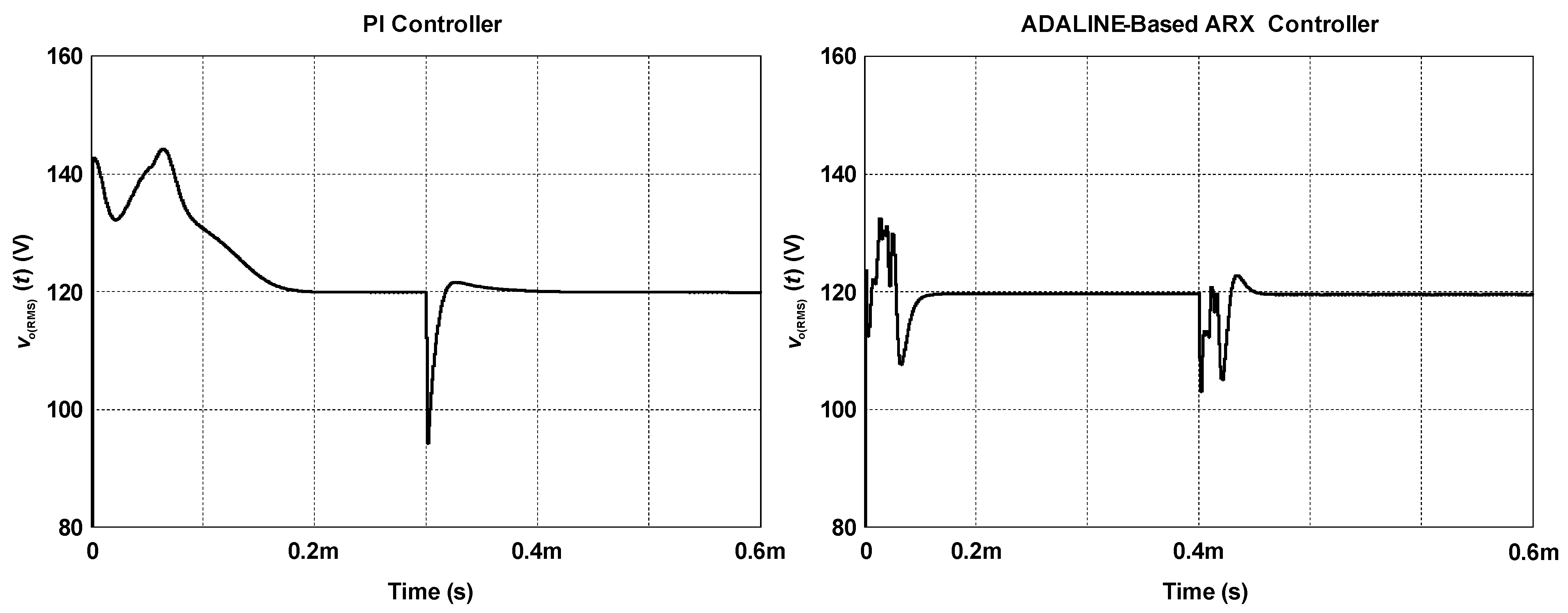
Regulating the RMS output voltage is of major importance for ensuring efficient energy transfer in the WPT system. Figure 9 shows that both controllers can regulate the RMS load voltage at around 120 V during the whole simulation period. However, in the case of the PI controller, the RMS voltage at the load varies between 144.17 V and 94.23 V. In turn, the ADALINE-based ARX controller presents improved performance while keeping the load voltage between 103 V and 132.41 V. In addition, the PI controller takes much longer to regulate the output after the start-up, resulting in higher voltage stresses on the switches when compared with the proposed solution.
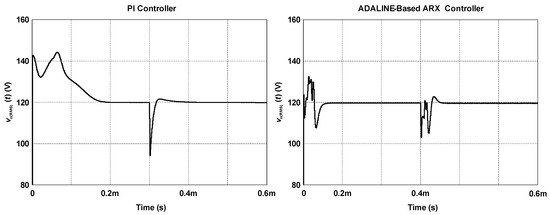
Figure 9.
Behavior of the RMS output voltage.
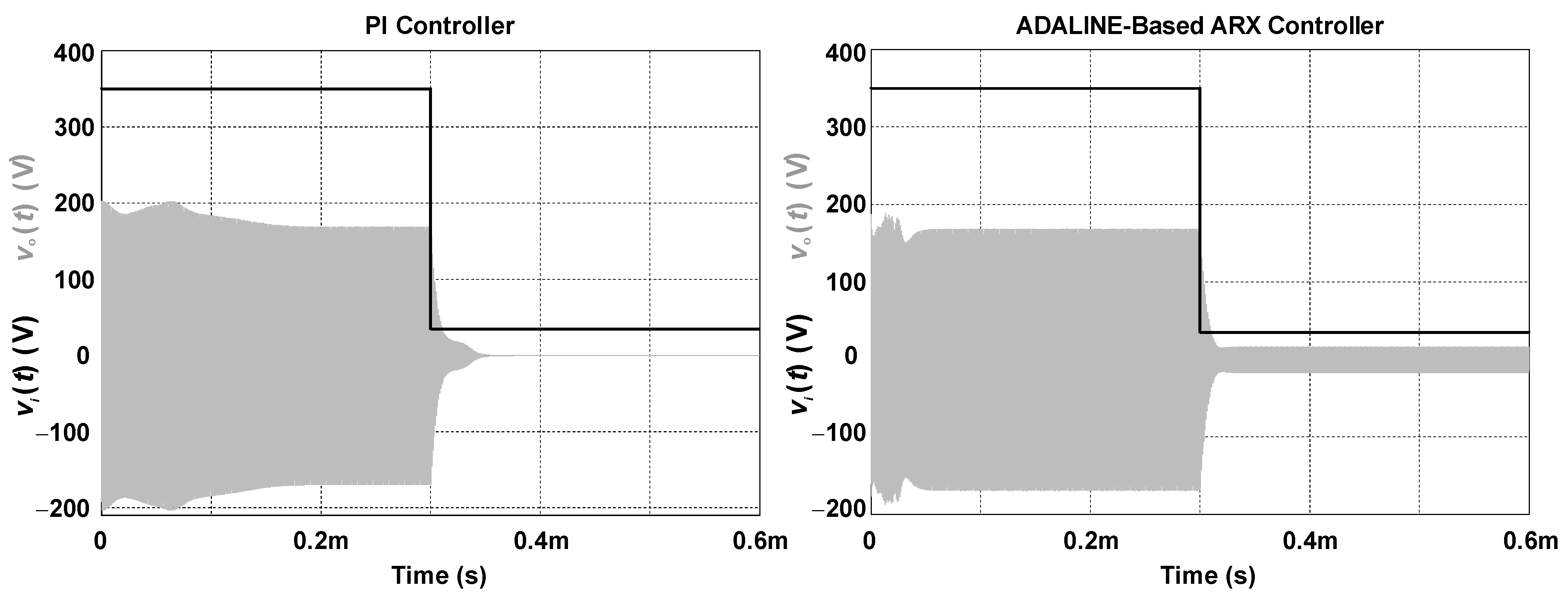
The DC input voltage of the class DE inverter will also play a key role in the overall performance, especially in practical systems where it is often regulated by a front-end DC-DC converter. Figure 10 compares the responses of the PI and ADALINE-based ARX controllers when the input voltage suddenly decreases to only 10% of the rated value. The PI controller becomes untuned while being unable to regulate the load voltage. In turn, the ADALINE-based ARX controller keeps the RMS output voltage regulated at 12.80 V. This result is strictly correct because the load voltage is proportional to the DC input voltage, also considering that Vo(RMS) = 119.85 V results when Vi = 350 V. In other words, the ADALINE-based ARX controller can adapt to any value of the input voltage while being capable of handling different power levels transferred by the WPT circuit.
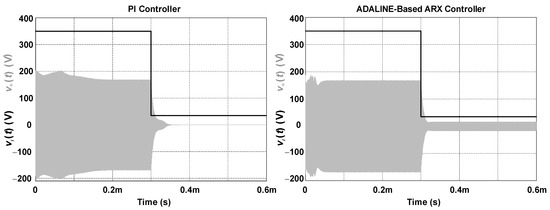
Figure 10.
Behavior of the load voltage when a DC input voltage step occurs.
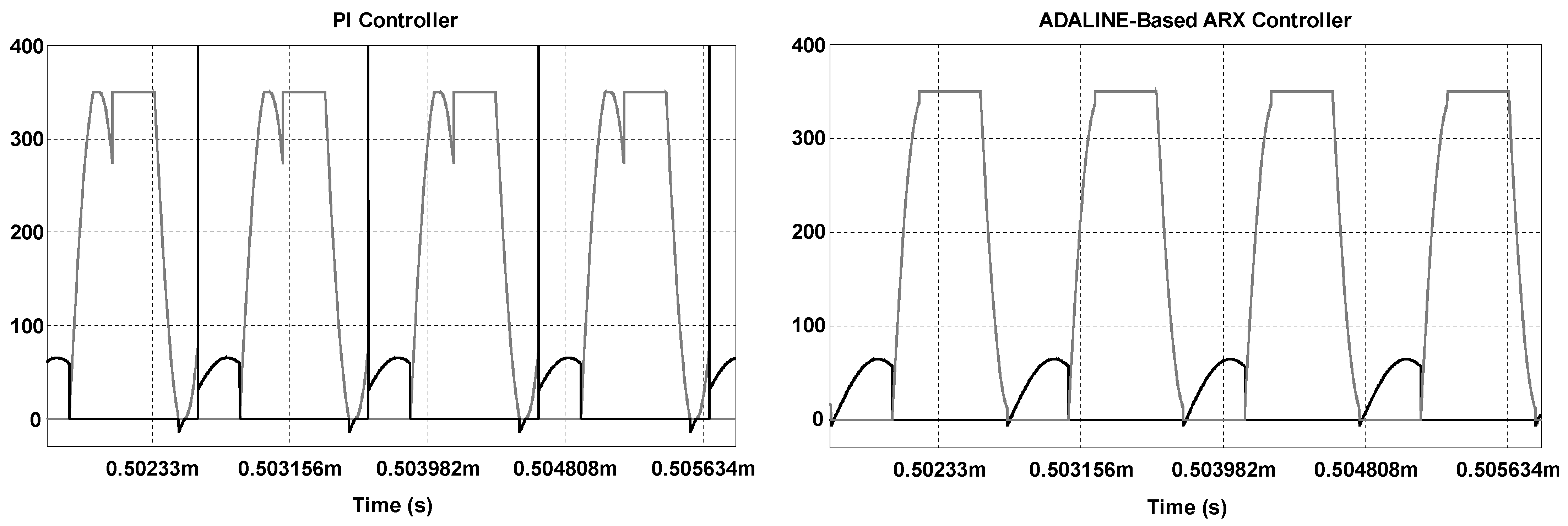
The soft-switching characteristics of Q1 and Q2 are also of major importance to ensure high efficiency. Thus, the turn-on instants of the active switches must coincide with the transitions between the half cycles of the load current. Figure 11 shows that the PI controller cannot ensure the ZVS and ZDVS commutation of the active switches, resulting in very high current spikes because the switches are turned on when the load current is not null. Eventually, it would cause very high switching losses and the failure of semiconductors in practice. Since the ADALINE-based ARX controller is properly tuned after the network is trained for a predefined range of load resistance, the active switches will be turned on accordingly under soft-switching conditions.
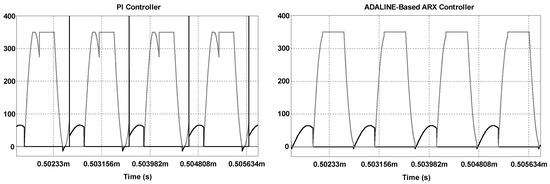
Figure 11.
Behavior of the drain current and drain-source voltage of switch Q1.
The inverter operation at a switching frequency close to the resonance allows for obtaining high transmission efficiency in MCR-WPT systems. Analyzing the harmonic content of the load voltage waveforms obtained from both controllers in steady-state shows that the fundamental frequency is indeed 0.9758 MHz. However, the power transferred to the load when using the ADALINE-based ARX controller is 17.54% higher than that obtained with the PI controller.
According to [51], one can calculate the total harmonic distortion (THD) of the primary-side waveforms in a WPT system corresponding to THD1 from (12), where ki is the coupling factor.
It is observed that increasing the coupling factor causes an increase in the harmonic content. Thus, it is necessary to adjust QDE accordingly. Substituting ki = 0.545 in (12) yields THD1 = 0.8614%, which is strictly in accordance with the result calculated by the simulation software, that is, THD1 = 0.8622%, resulting in a negligible error.
5. Conclusions
This work has presented a robust controller to regulate the AC output voltage of a resonant class DE inverter. The results demonstrate that one can ensure high PTE in WPT systems when misalignment occurs between the transmitter and the receiver as a result of changes in the load resistance. Unlike traditional linear controllers, it can regulate the load voltage accordingly even when drastic changes occur in the operating conditions. In addition, the operation at very high switching frequencies close to the resonance results in reduced dimensions of the resonant tank elements.
The present control approach relies on analyzing the quality factor of the resonant circuit, which affects the harmonic content of the output voltage. It also enables the operation of active switches under soft-switching conditions, thus proving to be an energy-efficient solution that leads to negligible switching losses. Using the ADALINE-based ARX controller allows for changing the resonant circuit characteristic from overdamped to underdamped, resulting in a fast dynamic response.
The introduced ADALINE-based ARX model is an effective and convenient control approach for class DE resonant inverters operating over a wide range of the DC input voltage and load voltage. Unlike other control strategies applied in WPT systems, it will not require any communication architecture associated with the primary or secondary circuits.
Future work includes assessing the inverter performance while considering a parallel resonant tank, which will lead to a completely different mathematical analysis. Another important issue lies in assessing the core losses of the resonant inductor aiming to define the best magnetic material for its physical implementation.
Author Contributions
Conceptualization, methodology, F.L.T. and E.R.R.; formal analysis, investigation, J.P.O.A.; writing—original draft preparation, J.P.O.A.; writing—review and editing, J.P.O.A., F.L.T. and E.R.R.; supervision, F.L.T. and E.R.R. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Coordination for the Improvement of Higher Education Personnel (CAPES). The authors would also like to acknowledge the Brazilian National Council for Scientific and Technological Development (CNPq); the Minas Gerais Research Funding Foundation (FAPEMIG); and the National Institute of Science and Technology in Electric Energy (INERGE) for supporting this work.
Data Availability Statement
Data available on request from the authors.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Zheng, Y.; Wang, Y.; Yang, Q. Two-phase operation for coordinated charging of electric vehicles in a market environment: From electric vehicle aggregators’ perspective. Renew. Sustain. Energy Rev. 2023, 171, 113006. [Google Scholar] [CrossRef]
- Gössling, S. Integrating e-scooters in urban transportation: Problems, policies, and the prospect of system change. Transp. Res. Part D Transp. Environ. 2020, 79, 102230. [Google Scholar] [CrossRef]
- Alsenani, T.R. The participation of electric vehicles in a peer-to-peer energy-backed token market. Int. J. Electr. Power Energy Syst. 2023, 148, 109005. [Google Scholar] [CrossRef]
- Yusuf, J.; Hasan, A.S.M.J.; Garrido, J.; Ula, S.; Barth, M.J. A comparative techno-economic assessment of bidirectional heavy duty and light duty plug-in electric vehicles operation: A case study. Sustain. Cities Soc. 2023, 95, 104582. [Google Scholar] [CrossRef]
- Salkuti, S.R. Advanced technologies for energy storage and electric vehicles. Energies 2023, 16, 2312. [Google Scholar] [CrossRef]
- Acharige, S.S.G.; Haque, M.E.; Arif, M.T.; Hosseinzadeh, N.; Hasan, K.N.; Oo, A.M.T. Review of electric vehicle charging technologies, standards, architectures, and converter configurations. IEEE Access 2023, 11, 41218–41255. [Google Scholar] [CrossRef]
- Narasipuram, R.P.; Mopidevi, S. A technological overview & design considerations for developing electric vehicle charging stations. J. Energy Storage 2021, 43, 103225. [Google Scholar] [CrossRef]
- Niu, S.; Xu, H.; Sun, Z.; Shao, Z.Y.; Jian, L. The state-of-the-arts of wireless electric vehicle charging via magnetic resonance: Principles, standards and core technologies. Renew. Sustain. Energy Rev. 2019, 114, 109302. [Google Scholar] [CrossRef]
- Song, K.; Lan, Y.; Zhang, X.; Jiang, J.; Sun, C.; Yang, G.; Yang, F.; Lan, H. A review on interoperability of wireless charging systems for electric vehicles. Energies 2023, 16, 1653. [Google Scholar] [CrossRef]
- Abou Houran, M.; Yang, X.; Chen, W. Magnetically coupled resonance WPT: Review of compensation topologies, resonator structures with misalignment, and EMI diagnostics. Electronics 2018, 7, 296. [Google Scholar] [CrossRef]
- Wang, Z.; Sun, Y.; Yang, R.; Zhang, M. Frequency splitting characteristics analysis of capacitive wireless power transfer. Electr. Eng. 2023, 105, 1299–1305. [Google Scholar] [CrossRef]
- Barsari, V.Z.; Thrimawithana, D.J.; Kim, S.; Covic, G.A. Modular coupler with integrated planar transformer for wireless EV charging. IEEE Trans. Power Electron. 2023, 38, 9206–9217. [Google Scholar] [CrossRef]
- Lu, J.; Zhu, G.; Mi, C.C. Foreign object detection in wireless power transfer systems. IEEE Trans. Ind. Appl. 2022, 58, 1340–1354. [Google Scholar] [CrossRef]
- Lin, J.C. Safety of wireless power transfer. IEEE Access 2021, 9, 125342–125347. [Google Scholar] [CrossRef]
- C95.6-2002; IEEE Standard for Safety Levels with Respect to Human Exposure to Electromagnetic Fields, 0–3 kHz. IEEE: Piscataway, NJ, USA, 2002; pp. 1–64. [CrossRef]
- Mohammad, M.; Onar, O.C.; Pries, J.L.; Galigekere, V.P.; Su, G.J.; Wilkins, J. Thermal analysis of a 50 kW three-phase wireless charging system. In Proceedings of the 2021 IEEE Transportation Electrification Conference & Expo (ITEC), Chicago, IL, USA, 21–25 June 2021; pp. 1–6. [Google Scholar]
- Rayan, B.A.; Subramaniam, U.; Balamurugan, S. Wireless power transfer in electric vehicles: A review on compensation topologies, coil structures, and safety aspects. Energies 2023, 16, 3084. [Google Scholar] [CrossRef]
- Zheng, Z.; Wang, N.; Ahmed, S. Adaptive frequency tracking control with fuzzy PI compound controller for magnetically coupled resonant wireless power transfer. Int. J. Fuzzy Syst. 2021, 23, 1890–1903. [Google Scholar] [CrossRef]
- Yousuf, M.A.; Das, T.K.; Khallil, M.E.; Aziz, N.A.A.; Rana, M.J.; Hossain, S. Comparison study of inductive coupling and magnetic resonant coupling method for wireless power transmission of electric vehicles. In Proceedings of the 2021 2nd International Conference on Robotics, Electrical and Signal Processing Techniques (ICREST), Khaka, Bangladesh, 5–7 January 2021; pp. 737–741. [Google Scholar]
- Wang, S.; Sun, X.; Feng, W.; Ma, X.; Jing, Y.; Li, S. Optimization of magnetic coupling resonance coils. In Proceedings of the 2021 IEEE 16th Conference on Industrial Electronics and Applications (ICIEA), Chengdu, China, 1–4 August 2021; pp. 793–796. [Google Scholar]
- Ali, A.; Yasin, M.N.M.; Rambe, A.H.; Adam, I.; Ramli, N.; Rahim, H.A.; Sabapathy, T.; Norizan, M.N.; Sobri, S.A. Analysis of symmetric two and four-coil magnetic resonant coupling wireless power transfer. Appl. Comput. Electromagn. Soc. J. 2022, 37, 497–506. [Google Scholar] [CrossRef]
- Pei, Y.; Le Bihan, Y.; Bensetti, M.; Pichon, L. Comparison of coupling coils for static inductive power-transfer systems taking into account sources of uncertainty. Sustainability 2021, 13, 6324. [Google Scholar] [CrossRef]
- Sun, G.; Yang, Y.; Zhang, J.; Cao, Y.; Tan, X.; Pei, J. Modeling and optimization of pavement scale-model for magnetically coupled resonant in wireless power transmission systems. Constr. Build. Mater. 2022, 319, 126066. [Google Scholar] [CrossRef]
- Razek, A. Review of contactless energy transfer concept applied to inductive power transfer systems in electric vehicles. Appl. Sci. 2021, 11, 3221. [Google Scholar] [CrossRef]
- Kim, M.; Choi, J. High-frequency, mid-range wireless power transfer system using critical coupling coefficient adjustment. In Proceedings of the 2021 IEEE Applied Power Electronics Conference and Exposition (APEC), Virtual Conference, 14–17 June 2021; pp. 714–719. [Google Scholar]
- Pham, T.S.; Nguyen, T.D.; Tung, B.S.; Khuyen, B.X.; Hoang, T.T.; Ngo, Q.M.; Hiep, L.T.H.; Lam, V.D. Optimal frequency for magnetic resonant wireless power transfer in conducting medium. Sci. Rep. 2021, 11, 18690. [Google Scholar] [CrossRef] [PubMed]
- Shehata, E. Design of high efficiency low frequency wireless power transfer system for electric vehicle charging. Electr. Eng. 2022, 104, 1797–1809. [Google Scholar] [CrossRef]
- Kiyani, M.; Abdollahi, S.E.; Abdollahi, S.R.; Baigzadehnoe, B. Investigation of resonant tank topologies performance in wireless power transfer applications. Int. J. Electron. 2023. [Google Scholar] [CrossRef]
- Gomaa, E.; Shawky, A.; Orabi, M. Wireless charging techniques and converter topologies for light EVs, e-bikes, e-chairs and e-scooters: A review. In Proceedings of the 2023 IEEE Conference on Power Electronics and Renewable Energy (CPERE), Luxor, Egypt, 19–21 February 2023; pp. 1–8. [Google Scholar]
- Shi, L.; Rodriguez, J.; Carrizosa, M.J.; Alou, P. ZVS tank optimization for class-D amplifiers in high frequency WPT applications. In Proceedings of the 2021 IEEE Applied Power Electronics Conference and Exposition (APEC), Virtual Conference, 14–17 June 2021; pp. 1593–1598. [Google Scholar]
- Thiagarajan, K.; Deepa, T. A comprehensive review of high-frequency transmission inverters for magnetic resonance inductive wireless charging applications in electric vehicles. IETE J. Res. 2021, 69, 2761–2771. [Google Scholar] [CrossRef]
- Kondo, T.; Koizumi, H. Class DE voltage-source parallel resonant inverter. In Proceedings of the IECON 2015—41st Annual Conference of the IEEE Industrial Electronics Society, Yokohama, Japan, 9–12 November 2015; pp. 002968–002973. [Google Scholar]
- Yang, L.; Li, X.; Liu, S.; Xu, Z.; Cai, C. Analysis and design of an LCCC/S-compensated WPT System with constant output characteristics for battery charging applications. IEEE J. Emerg. Sel. Top. Power Electron. 2021, 9, 1169–1180. [Google Scholar] [CrossRef]
- Sriprom, T.; Namin, A.; Tammawari, W.; Yachiangkam, S.; Janjommanit, S.; Kamnarn, U.; Thongpron, J.; Karnjanapiboon, C.; Thounthong, P.; Takorabet, N. Variable frequency control for constant current constant voltage inductive wireless EV charging system. In Proceedings of the 2022 International Power Electronics Conference (IPEC-Himeji 2022-ECCE Asia), Himeji, Japan, 15–19 May 2022; pp. 1481–1488. [Google Scholar]
- Yang, L.; Shi, Y.; Wang, M.; Ren, L. Constant voltage charging and maximum efficiency tracking for WPT systems employing dual-side control scheme. IEEE J. Emerg. Sel. Top. Power Electron. 2022, 10, 945–955. [Google Scholar] [CrossRef]
- Liu, Y.; Liu, F.; Feng, H.; Zhang, G.; Wang, L.; Chi, R.; Li, K. Frequency tracking control of the WPT system based on fuzzy RBF neural network. Int. J. Intell. Syst. 2022, 37, 3881–3899. [Google Scholar] [CrossRef]
- Jaman, S.; Chakraborty, S.; El Baghdadi, M.; Geury, T.; Hegazy, O. Small-signal average switch modeling and dual-loop control of bidirectional integrated converter for G2V and V2G applications in battery EVs. In Proceedings of the 2021 23rd European Conference on Power Electronics and Applications (EPE’21 ECCE Europe), Virtual Conference, 6–10 September 2021; pp. 1–12. [Google Scholar]
- Xia, C.; Wei, N.; Zhang, H.; Zhao, S.; Li, Z.; Liao, Z. Multifrequency and multiload MCR-WPT system using hybrid modulation waves SPWM control method. IEEE Trans. Power Electron. 2021, 36, 12400–12412. [Google Scholar] [CrossRef]
- Zhao, J.; Wu, C. Research on control method and variable topology design of wireless power transmission system with coil offset. IEEJ Trans. Electr. Electron. Eng. 2022, 17, 1495–1505. [Google Scholar] [CrossRef]
- Jiang, Y.; Wang, L.; Fang, J.; Li, R.; Han, R.; Wang, Y. A high-efficiency ZVS wireless power transfer system for electric vehicle charging with variable angle phase shift control. IEEE J. Emerg. Sel. Top. Power Electron. 2021, 9, 2356–2372. [Google Scholar] [CrossRef]
- Zhou, M.; Liu, F.; Li, S.; Chen, X. A 1-kW and 100-cm Distance Magnetically Coupled Resonant WPT System Achieving 80% Efficiency. IEEE Trans. Transp. Electrif. 2022, 8, 4001–4013. [Google Scholar] [CrossRef]
- Gong, W.; Xiao, J.; Wu, X.; Chen, S.; Wu, N. Research on parameter identification and phase-shifted control of magnetically coupled wireless power transfer system based on Inductor–Capacitor–Capacitor compensation topology. Energy Rep. 2022, 8, 949–957. [Google Scholar] [CrossRef]
- Yuan, Z.; Fu, P.; Lu, G.; Cao, P. Wireless power transfer system based on frequency and impedance matching hybrid adjustment against system detuning. J. Phys. Conf. Ser. 2021, 2108, 012035. [Google Scholar] [CrossRef]
- Lu, W.; Zhao, J.; Chen, X.; Fan, Q.; Zhang, C. Bilateral control strategy based on LCL-S compensation network wireless charging system without communication. Int. J. Automot. Technol. 2023, 24, 171–178. [Google Scholar] [CrossRef]
- Hui, S.-Y.R.; Yang, Y.; Zhang, C. Wireless power transfer: Paradigm shift for the next generation. IEEE J. Emerg. Sel. Top. Power Electron. 2023, 11, 2412–2427. [Google Scholar] [CrossRef]
- Tong, Z.; Ye, Z.; Rivas-Davila, J. Class DE switch-mode power amplifier using GaN power HEMTs. IEEE Microw. Mag. 2022, 23, 72–79. [Google Scholar] [CrossRef]
- Seeliger, K.; Ambrogioni, L.; Güçlütürk, Y.; van den Bulk, L.M.; Güçlü, U.; van Gerven, M.A. End-to-end neural system identification with neural information flow. PLOS Comput. Biol. 2021, 17, e1008558. [Google Scholar] [CrossRef]
- Pamungkas, L.; Tampubolon, M.; Lin, Q.; Chiu, H.J. Performance comparison of primary side PFM and secondary side PWM for SS wireless power transfer CC/CV control strategy references. In Proceedings of the 2018 IEEE International Power Electronics and Application Conference and Exposition (PEAC), Guangzhou, China, 4–7 November 2018; pp. 1–5. [Google Scholar]
- Kavimandan, U.D.; Galigekere, V.P.; Onar, O.; Ozpineci, B.; Mahajan, S.M. Comparison of dead-time effects in a WPT system inverter for different fixed-frequency modulation techniques. In Proceedings of the 2020 IEEE Transportation Electrification Conference & Expo (ITEC), Virtual Conference, 23–26 June 2020; pp. 277–283. [Google Scholar]
- Li, J.; Xu, D.; Wang, D. Perturb and observe method of impedance matching for magnetically coupled wireless power transfer system. In Proceedings of the 2018 Chinese Automation Congress (CAC), Xi’an, China, 30 November–2 December 2018; pp. 2513–2517. [Google Scholar]
- Shi, L.; Rodriguezt, J.C.; Alou, P. Modeling and analysis of total harmonic distortion in series-series wireless power transfer system for 6.78 MHz. In Proceedings of the 2020 IEEE Energy Conversion Congress and Exposition (ECCE), Detroit, MI, USA, 11–15 October 2020; pp. 1016–1020. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).