Abstract
Three-phase four-wire voltage inverters are commonly used in energy complexes based on distributed generation sources (solar panels, wind power plants, hydrogen fuel cells) and accumulator batteries. They allow to power loads, including single-phase ones, which require neutral point connection. In these cases, phase voltage formed by spatial pulse-width modulation (PWM) methods considerably differs from sinusoidal waves and has high total harmonic distortions of voltage and current curves. This article is devoted to research into the authors’ control method of a three-phase four-wire inverter, allowing for the rectification of the form of phase voltage supplying the load when applying the most common PWM (SVPWM, DPWMMIN, DPWMMAX, GDPWM) methods. The description of the method and its research results by simulation modeling and test bench are presented in the article. The simulation modeling was carried out by the developed Simulink-model of the three-phase four-wire inverter and its control system. The modeling results showed that the method application ensures sinusoidal voltage form when applying any PWM method. At this, THDU was reduced from 21.56% to 4.39%, while THDI was reduced from 21.16% to 1.69%. Experimental tests were carried out by a test bench featuring an uninterruptible power supply source. The authors researched the inverter operation as a component of the test bench under the control of the proposed method to form neutral point voltage. The experimental test results coincided with the simulation modeling results.
1. Introduction
Three-phase voltage inverters with an additional fourth transistor leg are widely used in various fields of electrical engineering. Such devices are an essential component of hybrid energy complexes with distributed generation sources (solar panels, wind power plants, fuel cells, etc.) [1] and accumulator batteries [2,3]. Their other applications include uninterruptible power supplies [4] and active harmonic filters, aimed at improving electric power quality [5,6,7]. The most popular applications, connection topologies, and control algorithms of four-leg voltage inverters are listed in [8].
When using a three-phase voltage inverter to power a single-phase load, there arises a problem of phase voltage curve distortion. This is attributed to using space vector pulse-width modulation (SVPWM) algorithms. Along with this, the fourth transistor leg allows for the formation of a neutral load point, providing the possibility of rectifying the curve shape into a sinusoidal one, as well as controlling zero sequence current at phase loads asymmetry.
In order to improve electric power quality when a single-phase load is powered by an inverter with four transistor legs, various inverter operation control algorithms are used.
Paper [9] lists an algorithm of voltage inverter operation with four transistor legs, providing simultaneous power supply to three-phase and single-phase AC loads with balanced constant frequency voltage system. The inverter is proposed for transformerless Hybrid Power System applications. The proposed control strategy has the ability to decompose into dq DC quantities, not only the positive and negative current and voltage sequences, but also the homopolar sequence.
A three-phase four-wire voltage inverter control algorithm, based on Scalar PR Controllers, is listed in [10]. The proposed PR control scheme provides good voltage regulation and improves the quality of the APS load voltages in static and dynamic modes when operating on both linear, non-linear, and unbalanced loads.
Zero sequence current impact, when the load is powered by a three-phase four-wire inverter, is given in [11]. The designed four-leg VSI outstands the traditional three-leg VSI in case of network unbalance operating conditions. An additional degree of freedom from the four-leg VSI allows faster fault recovery and a lower MVA requirement can be achieved for unbalanced low-voltage networks.
Paper [12] presents a three-phase four-wire grid-interfacing power quality compensator for compensating voltage unbalance and voltage sag in a microgrid. Functionally, the shunt four-leg inverter is controlled to maintain a set of balanced distortion-free voltages within the microgrid and to regulate power sharing among the parallel-connected distributed generation systems.
Paper [13] presents two novel control strategies for the elimination of common mode conducted emissions in three-phase four-wire four pole inverters connected to an AC distribution bus and operating in grid-following mode. Both methods result in higher switching frequency than typical space vector modulation, so wide bandgap devices should be used to yield comparable switching losses.
A general disadvantage of all the above algorithms is that it is necessary to use voltage and current sensors to build closed control loop circuits.
This paper aims to research the method proposed by the authors [14] which allows for the minimization of the current curve distortions when a single-phase load is powered by an inverter with four transistor legs. The essence of the method is to single out zero sequence voltage from phase load curves. Such an approach ensures compatibility with any space vector PWM-generation algorithm and avoids the necessity of using sensors and providing any voltage or current feedback. These are the main characteristic features and advantages of the developed method.
The paper is organized as follows. Section 2 presents an overview of the most widespread space vector PWM methods. Section 3 gives a description of the developed method to minimize zero sequence voltage impact. The Simulink-model to test the method is described in Section 4. Simulation modeling results and their analysis are listed in Section 5. Section 6 is devoted to the developed method of experimental testing by a special test bench.
2. Materials and Methods
2.1. Space Vector Pulse-width Modulation Methods Overview
Nowadays, the most widespread PWM method is space vector pulse width modulation (SVPWM). It superseded sinusoidal PWM (SPWM), as it provides more use of DC link voltage and smaller output voltage distortions [15]. The so-called discontinuous PWM methods (DPWM) are developed in inverters in order to reduce dynamic losses. A detailed analytical review of various DPWM methods is presented in [16].
A common feature of all PWM methods is that zero sequence voltage is added to the three-phase sinusoidal voltage system. This leads to phase curve distortion. However, in a floating neutral system, for example, these distortions are not observed in induction motors with all line voltages having a sinusoidal form.
The following presents an analysis of algorithms for zero sequence voltage calculation of DPWM methods that enjoy wide coverage in scientific works: DPWMMAX, DPWMMIN, and GDPWM (which is a combination of DPWMMAX and DPWMMIN).
2.1.1. DPWMMAX
When applying DPWMMAX, the zero sequence component is selected in such a way, as to make the maximum at the given moment voltage of the three-phase driving voltage system equal to the level of the DC link positive bar. The expression to calculate zero sequence voltage is as follows:
where UZVS—zero sequence voltage, UA, UB, UC—envelope voltage of phases A, B, C.
DPWMMAX allows for the reduction of dynamic losses of upper inverter switches by 33% because every phase voltage per 120° switching cycle is set to DC link voltage. However, this method application could be difficult or impossible when using transistor drivers with bootstrap power supply, because, due to the high-side transistor being long-time on-state, the bootstrap power supply condenser will be unable to charge and this transistor reclosing will not take place.
2.1.2. DPWMMIN
When applying DPWMMIN, a zero sequence component is selected in such a way as to make the minimum at the given moment voltage of the three-phase driving voltage system equal to the DC link bar zero level. The expression to calculate zero sequence voltage is the following:
This method, the same as DPWMMAX one, allows for the reduction of dynamic losses of lower inverter switches by 33%, but, in its turn, is suitable for bootstrap power supply drivers.
2.1.3. GDPWM
A common expression allowing to switch between DPWMMAX and DPWMMIN at any moment can be derived from Expressions (1) and (2). When combining these methods, zero sequence voltage expression can be written as:
where k—is a generalization coefficient, whose value change makes it possible to select the method, applied at a given moment. For DPWMMAX, k = 1, and for DPWMMIN, k = 0.
It is noteworthy, that when k = 1/2, a three-phase envelope curve system is shaped, corresponding to the SVPWM algorithm. This means that this expression allows for the calculation of the SVPWM algorithm avoiding the use of trigonometric functions.
GDPWM means the method of continuous switchover between DPWMMAX and DPWMMIN. The idea of switchover between two different methods is that it allows for the equal distribution of the time of absence of commutation between lower and upper leg transistors. There are several selection algorithms, commonly called DPWM0, 1, 2, 3 [17]. There is no significant difference between the algorithms. For instance, the DPWM1 algorithm is the following. Three envelope curves of phase voltages are compared to their mean value. If the instantaneous values of two curves are larger than the mean value, DPWMMIN is applied; if only one value is larger than the mean one, DPWMMAX is applied.
In addition, many groups of scientists are developing their own modifications of DPWM algorithms, with the potential to optimize these to be applied in every particular case [18,19,20,21].
2.2. The Description of the Proposed Method to Reduce Zero Sequence Voltage Impact
All the above methods (SVPWM, DPWMMAX, DPWMMIN, GDPWM) of forming a three-phase voltage system have one common feature—they modify zero sequence voltage UZVS and implicitly add this to phase voltage envelope curve. It is insignificant to floating zero load point systems. However, if a zero point is present (which is typical of independent uninterruptible power supply sources and energy complexes based on renewable energy resources), an additional link should be added to the inverter control system, forming zero sequence voltage.
The essence of the method suggested is to single out zero sequence voltage from phase voltage driving curves and to apply it as driving voltage to the fourth transistor leg, forming neutral point voltage.
Figure 1 shows a block diagram of a three-phase four-wire inverter control system based on the method suggested.
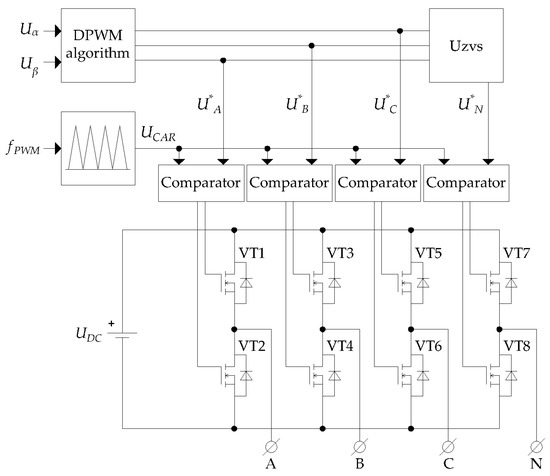
Figure 1.
A block diagram of three-phase four-wire inverter control.
The method starts with the formation of a three-phase envelope curve system by the DPWM algorithm block. In our case, this block generates envelopes corresponding to the following methods: SVPWM, DPWMMAX, DPWMMIN, GDPWM.
The input of the DPWM algorithm block receives signals Uα and Uβ, which are the orthogonal components of the decomposition of the phase A output voltage space vector. Figure 2a shows the input signals Uα and Uβ. Typically, their form can be described by the Equation system (4):
where m—modulation coefficient [0…1]; UDC—DC link voltage, V; f—output voltage frequency, Hz.
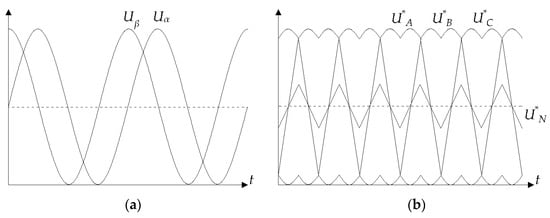
Figure 2.
Diagrams illustrating the operation of a three-phase four-wire inverter control method: (a) setting space vector alpha–beta components; Uα—setting alpha component; Uβ—setting beta component; (b) envelope phase voltage curves and zero phase sequence voltage envelope curve (SVPWM for example); U*A—modified envelope phase A voltage; U*B—modified envelope phase B voltage; U*C—modified envelope phase C voltage; U*N—modified envelope zero phase sequence voltage.
To obtain a three-phase voltage system the inverse Clark transform is used (5):
In order to increase the utilization of the DC link voltage, a common modifying component must be added to each phase voltage. A system of modified phase curves is obtained (6):
The zero sequence voltage can be calculated in various ways. To obtain envelope curves according to the SVPWM, DPWMMAX, DPWMMIN, and GDPWM methods, Expression (3) can be used. To obtain envelope curves corresponding to the DPWMMAX algorithm in Expression (3) it is necessary to take k = 1. To obtain envelope curves corresponding to the DPWMMIN algorithm in Expression (3) it is necessary to take k = 0. To obtain envelope curves corresponding to the SVPWM algorithm in Expression (3) it is necessary to take k = 1/2. To obtain envelope curves corresponding to the GDPWM algorithm it is necessary to change k according to Expression (7):
UZVS block is installed to determine driving zero sequence voltage. This paper considers approaches to space vector PWM generation that involve the calculation of zero-sequence voltage to generate envelope curves. However, not in all cases is the zero-sequence voltage directly calculated when forming the envelope curve. In these cases, the UZVS block is necessary to correctly determine the zero sequence voltage curve shape. The block performs calculations according to the formula:
when the three envelope curves corresponding to the phase voltages are obtained and the zero-sequence voltage has been calculated, the carrier curve must be generated to generate the PWM. In this case, a triangular carrier signal generator is used, which takes as input the desired PWM frequency fPWM and generates a carrier signal UCAR.
Transistor control pulses are generated by a blocks Comparator, which compares the envelope (U*A, U*B,U*C, U*N) and carrier (UCAR) curves for each inverter leg. An example of Comp block operation is shown in Figure 3.
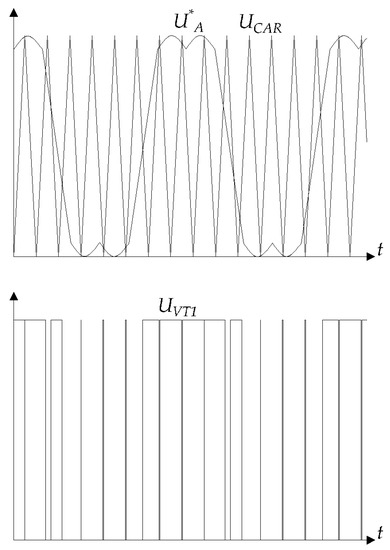
Figure 3.
Diagrams illustrating the operation of a three-phase four-wire inverter control method: UCAR—carrier voltage; U*A—modified envelope phase A voltage; UVT1—transistor control signal.
Thus, a three-phase supply voltage system and zero point voltage are formed at the load. Formation of the correct form zero sequence voltage makes it possible to make line and phase voltages sinusoidal and eliminate zero-sequence currents in symmetrical loads with neutral points.
Further, the implementation of the described control system will be shown in detail using the Simulink-model as an example.
3. Simulink-Model to Test the Method
In order to test the suggested method of reducing zero sequence voltage impact, a Simulink-model of a three-phase voltage inverter with an additional transistor leg and its control system has been developed. The Simulink-model structure is shown in Figure 4.
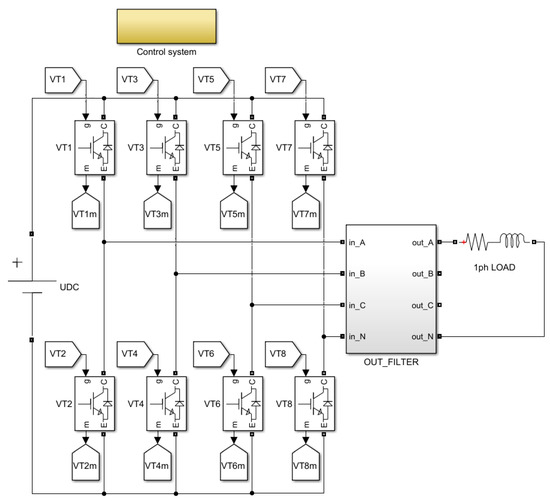
Figure 4.
Simulink-model of three-phase four-wire inverter power circuit, powering single-phase load.
An ideal battery with UDC = 540 V was used as the power supply for the DC link. This voltage level was selected as it is possible to power it when forming a DC link by rectifying the 220/380 three-phase voltage system. A three-phase four-wire transistor inverter is connected to the battery. Transistors are simulated as ideal devices with RON = 0.05 Ohm resistance. An LC-filter, providing output voltage waveform, and phase voltage and current sensors are installed at the inverter output. The output filter Simulink-model structure is shown in Figure 5. RL-network with RLOAD = 22 Ohm, LLOAD = 1 mH parameters are used as load.
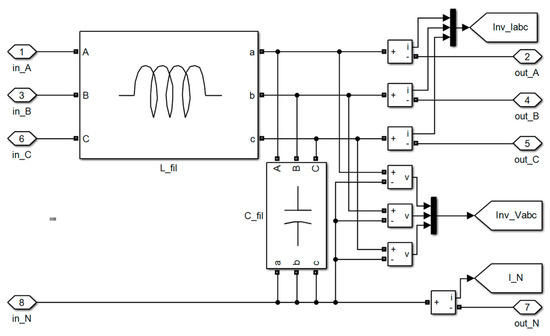
Figure 5.
Simulink-model of output sinusoidal filter and measurement system.
Output filter parameters calculation is performed as follows. Filter inductance is calculated by the formula:
where fsw—transistor switching frequency, Hz; ∆I—maximum pulsation of effective load current value.
If current pulsation is accepted as equal to 20% toward nominal value and the switching frequency is 10 kHz, filter inductance will be equal to:
The necessary capacity is calculated on the basis of the inductance value obtained. As soon as the LC-filter is used, its resonance frequency is equal to:
To provide higher harmonics filtration on PWM frequency, it is accepted that . In this case:
The Simulink-model structure of the inverter control system is shown in Figure 6.
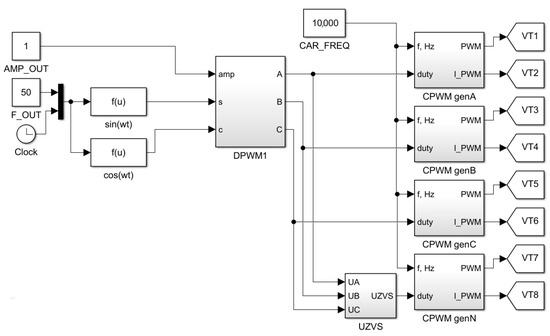
Figure 6.
Simulink-model control system of three-phase four-wire voltage inverter.
Control system drive signals are:
- Output voltage amplitude (AMP_OUT), which is set as a relative value and always accepted as equal to 1;
- Output voltage frequency (F_OUT), accepted as equal to 50 Hz, and transistor switching frequency (CAR_FREQ), accepted as equal to 10 kHz.
Instantaneous values of space vector sine and cosine are calculated by the output frequency value. They are drive signals for the DPWM block, which calculates phase loads curves according to the selected method of forming PWM.
The structure of the DPWM block is shown in Figure 7.
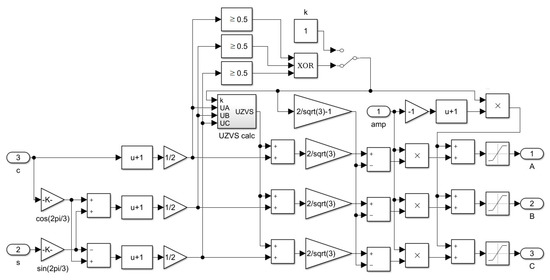
Figure 7.
Simulink-model of DPWM algorithm calculation block.
The block operation algorithm is as follows. The system of three-phase sinusoidal voltages is calculated from the sine and cosine signals using the inverse Clarke transform. Next, these signals are brought from the range [−1…1] to the range [0…1], since the PWM generation unit works with this range. The summation blocks modify the sine waveforms with the generated zero-sequence voltage. The algorithm of zero-sequence voltage calculation is determined by the defined PWM algorithm. In our case, it is possible to use the next algorithms: SVPWM, DPWMMAX, DPWMMIN, GDPWM.
Figure 8 shows the structure of the UZVS calc block.
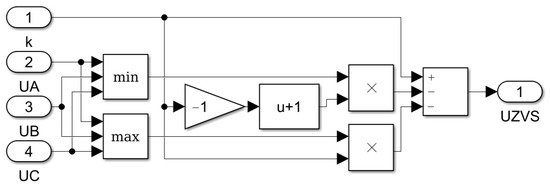
Figure 8.
Simulink-model of UZVS calc block.
This block calculates the zero-sequence voltage shape according to the given phase voltages and the coefficient k, which determines the PWM algorithm. Thus, if k = 1, the DPWMMAX algorithm is realized. If k = 0, then DPWMMIN, and if k = 1/2, then SVPWM.
In order to realize the GDPWM algorithm it is necessary to move the toggle switch to the “down” position. This will activate the algorithm of automatic transition from DPWMMAX to DPWMMIN during the period.
After summation of the initial setting and modifying curves, the resulting voltage is outside the range [0…1], and multiplication by a factor and subtraction of a constant that depends on the current value of k is used to compensate for this deviation. Finally, the obtained curves are multiplied by a given value of the output signal amplitude and centered at 0.5.
A UZVS block is installed in order to single out a zero sequence signal from the envelope curves according to Expression (8).
The generated envelope curves are fed to the PWM signal generation blocks. CPWM blocks genA,B,C,N are aimed at generating transistor control pulses of the corresponding phases, as shown in Figure 9. Each of them consists of two component devices: carrier curve generator and comparator.
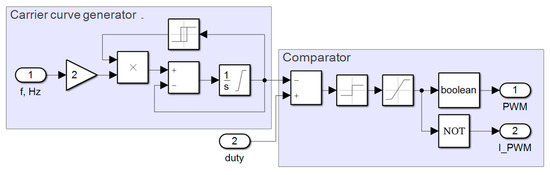
Figure 9.
Simulink-model of CPWM genA,B,C,N blocks.
The Carrier curve generator forms a carrier triangular signal of the specified frequency f. It works as a counter, switching from “up” to “down” counting mode on a command generated by the Relay block.
The comparator subtracts the instantaneous values of the envelope and carrier signals. If the difference is positive, the transistor is activated, if it is negative, the transistor is deactivated.
4. Simulation Modeling Results
The authors have simulated inverter operation, which supplies power to a single0phase load using four different variants of forming PWM (SVPWM, DPWMMIN, DPWMMAX, GDPWM). In the simulation process, phase voltage and current curves’ shapes were compared—with and without zero sequence voltage compensation. When simulating inverter operation without zero sequence voltage compensation, control pulses of fixed relative duration equal to 50% were applied to the fourth leg. Figure 10, Figure 11, Figure 12 and Figure 13 show voltage and current oscillograms, obtained as a result of simulation modeling. In the figures below, the following designations are adopted. UA—envelope phase A voltage (red), UB—envelope phase B voltage (blue), UC—envelope phase C voltage (green), UZVS—envelope zero phase sequence voltage (black), UA_LOAD—load phase A voltage (red), IA_LOAD × 10—load phase A current multiplied by 10 (blue).
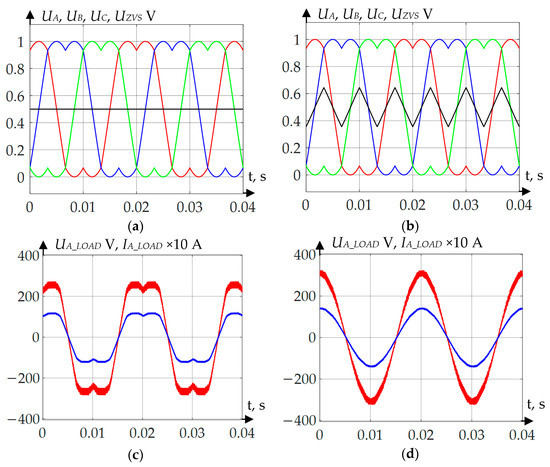
Figure 10.
Voltage and current oscillograms when applying the SVPWM algorithm: (a) curves of phase voltages and zero point voltage without neutral point voltage compensation; (b) curves of phase voltages and zero point voltage with neutral point voltage compensation; (c) load voltage and current without neutral point voltage compensation; (d) load voltage and current with neutral point voltage compensation.
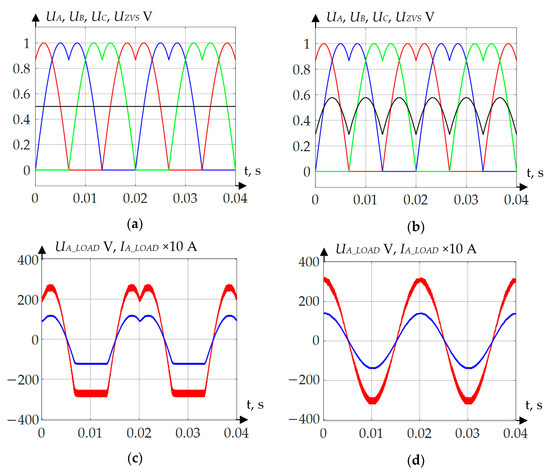
Figure 11.
Voltage and current oscillograms when applying the DPWMMIN algorithm: (a) curves of phase voltages and zero point voltage without neutral point voltage compensation; (b) curves of phase voltages and zero point voltage with neutral point voltage compensation; (c) load voltage and current without neutral point voltage compensation; (d) load voltage and current with neutral point voltage compensation.
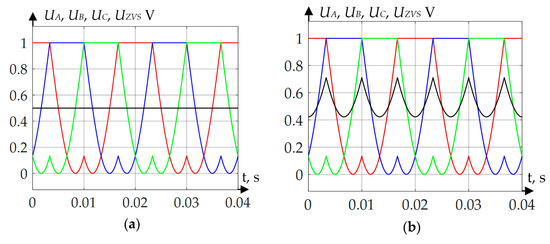
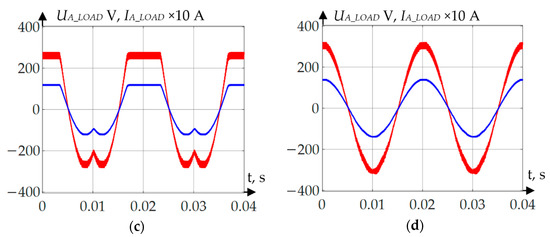
Figure 12.
Voltage and current oscillograms when applying the DPWMMAX algorithm: (a) curves of phase voltages and zero point voltage without neutral point voltage compensation; (b)curves of phase voltages and zero point voltage with neutral point voltage compensation; (c) load voltage and current without neutral point voltage compensation; (d) load voltage and current with neutral point voltage compensation.
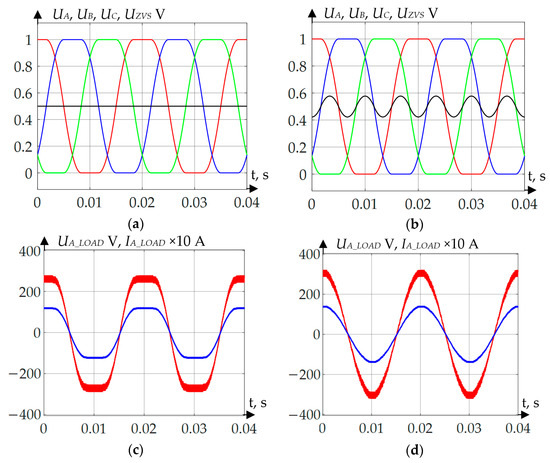
Figure 13.
Voltage and current oscillograms when applying the GDPWM algorithm: (a) curves of phase voltages and zero point voltage without neutral point voltage compensation; (b) curves of phase voltages and zero point voltage with neutral point voltage compensation; (c) load voltage and current without neutral point voltage compensation; (d) load voltage and current with neutral point voltage compensation.
According to Figure 10, Figure 11, Figure 12 and Figure 13, when the calculation and zero point voltage forming are correct, the shape of the curve is rectified, regardless of which PWM forming method is used. Table 1 and Table 2 show the numerical results of inverter operation simulation modeling.

Table 1.
Inverter operation simulation results without neutral point voltage compensation.

Table 2.
Inverter operation simulation results with neutral point voltage compensation.
The results obtained show that a slight reduction of phase voltage and current effective values took place. The maximum voltage reduction was 5.4 V or 2.5% when applying DPWMMIN method. The maximum current reduction was 0.252 A or 2.5% when applying DPWMMIN method. The positive effect of the method proposed is that THDU and THDI are considerably improved. For instance, THDU maximum reduction was 17.17%, while THDI maximum reduction was 19.49%.
5. Experimental Tests
Experimental tests of the proposed method were carried out on a special test bench, and its flow chart shown in Figure 14.
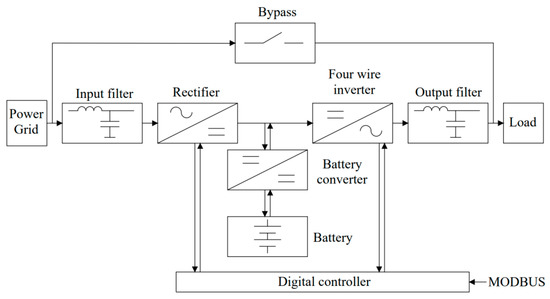
Figure 14.
Flowchart of test bench for experimental testing.
The test bench is an uninterruptible power supply source for essential consumers, built according to the On-Line UPS scheme. The test bench consists of three independent converters, passing each other information about their state and operation mode over an RS-485 interface. The power circuit is unified and built according to a three-phase transistor voltage inverter. A transistor module with integrated M32-75-12-A drivers is used.The control system is based on an STM32F405RGT6 microcontroller. The test bench is designed to power a 6 kVA three-phase four-wire load. The autonomous operation duration is not less than 1 h. Lithium–ferrous–phosphate cells, their full assembly nominal voltage being 600 V, are used as accumulator batteries. Figure 15 shows the physical configuration of the test bench.

Figure 15.
Physical configuration of the test bench for experimental testing: 1—input rectifier and step-up constant voltage regulator; 2—accumulator battery charging converter; 3—three-phase four-wire voltage inverter; 4—phase voltage and current sensors; 5—switchgear and secondary power supply sources; 6—accumulator battery.
Converter 1 functions as a step-up constant-voltage regulator to form a DC link with the required voltage level, as the installation is powered by a three-phase diode rectifier.
Converter 2 functions as an up-down converter to charge the accumulator battery (AB). During the charging process, the converter operates in a step-down mode and stabilizes the current at the pre-set level. When switching to discharge mode, the converter automatically switches to step-up mode and stabilization of voltage.
Converter 3 is a three-phase voltage inverter with an additional external fourth transistor leg to form neutral point voltage. Forming neutral point voltage is necessary because the installation can power both three-phase and single-phase loads. Figure 16 shows a photo of a four-wire voltage inverter, applied as the test bench component. Figure 17 shows the output LC-filter of the three-phase four-wire inverter.

Figure 16.
Three-phase four-wire voltage inverter with additional fourth transistor leg.

Figure 17.
Voltage inverter output LC-filter.
When carrying out experimental tests, the test bench was operating in the following mode:
- The battery was discharged to 540 V;
- The battery converter operated in discharge mode, stabilizing voltage at 570 V level;
- PWM-converters frequency—10 kHz, dead time—1,5 microseconds.
Single-phase active load RLOAD = 62.8 Ohm was connected to phase A and inverter neutral point. Output L-type filter has the following parameters: Lfil = 3 mH, Cfil = 2 uF.
Figure 18 shows the control system phase envelope curve and zero phase sequence curve generated by a microcontroller digital-to-analog converter (DAC).
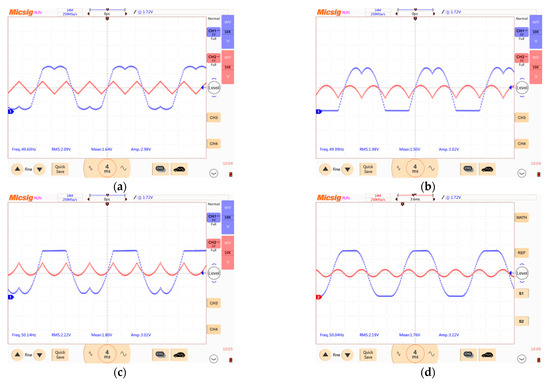
Figure 18.
Envelope phase voltage (blue) and zero phase sequence voltage (red) using different DPWM algorithms: (a) SVPWM; (b) DPWMMIN; (c) DPWMMAX; (d) GDPWM.
Figure 19, Figure 20, Figure 21 and Figure 22 show inverter output voltage oscillograms after the filter when applying SVPWM, DPWMMIN, DPWMMAX, GDPWM algorithms without forming neutral point voltage and when forming neutral point voltage.
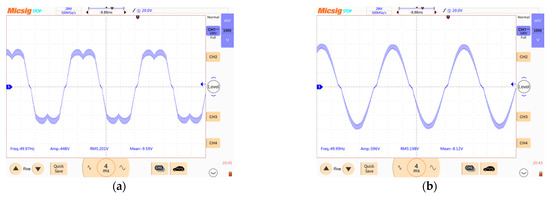
Figure 19.
Output voltage oscillograms when applying SVPWM algorithm: (a) without forming neutral point voltage; (b) when forming neutral point voltage.
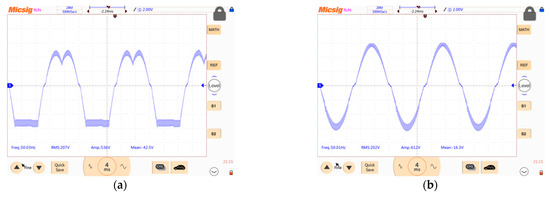
Figure 20.
Output voltage oscillograms when applying DPWMMIN algorithm: (a) without forming neutral point voltage; (b) when forming neutral point voltage.
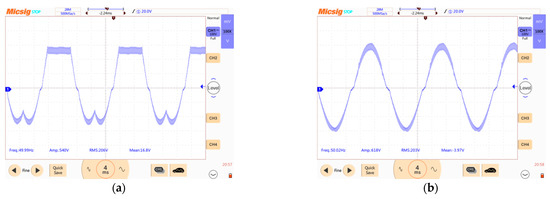
Figure 21.
Output voltage oscillograms when applying DPWMMAX algorithm: (a) without forming neutral point voltage; (b) when forming neutral point voltage.
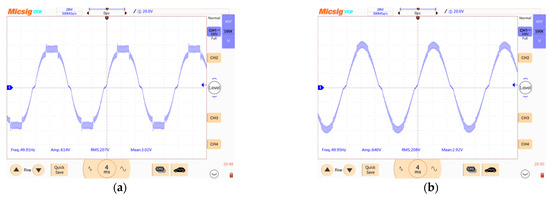
Figure 22.
Output voltage oscillograms when applying GDPWM algorithm: (a) without forming neutral point voltage; (b) when forming neutral point voltage.
Experimental testing of the method proposed showed that the results of forming neutral point voltage, when the single-phase load is powered by a four-wire three-phase voltage inverter, completely coincide with simulation modeling results.
The shape rectification to sinusoidal is possible while the inverter is in operation.
It should be noted that the DPWMMIN, DPWMMAX, and GDPWM methods are not recommended at small relative amplitudes of generated voltage (less than 80% of output voltage maximum effective value). This is connected to the fact that, in this case without zero sequence voltage compensation, considerable distortions of elution curves are observed.
6. Conclusions
Using three-phase four-wire voltage inverters to power single-phase loads remains an acute problem. Herewith, applying modern PWM methods (SVPWM, GDPWM) leads to considerable distortions in voltage and current curves. The fourth transistor leg modulation according to zero sequence voltage form is necessary to solve this problem.
The article presents the authors’ research into the control method of a three-phase four-wire voltage inverter, allowing us to obtain sine phase voltage to power a single-phase load when various PWM (SVPWM, DPWMMIN, DPWMMAX, GDPWM) methods are applied.
In the first stage, the method was researched by a simulation model of a three-phase four-wire inverter and its control system. The simulation results showed that the fourth leg transistors’ modulation by zero sequence driving voltage allows for the rectification of a phase voltage form into a sinusoidal one when any of the PWM methods are applied. This provides the possibility of using PWM methods, which reduce the number of inverter transistor switches (DPWMMIN, DPWMMAX, GDPWM) to power loads, requiring neutral point connection without combining them into a three-phase system. At this, a sinusoidal phase voltage form is sustained. Thus, the simulation results showed that THDU decreased from 21.56% to 4.39%, while THDI decreased from 21.16% to 1.69%.
In the second stage, the method was experimentally tested. For this, a test bench was used, featuring an uninterruptible power supply source with a three-phase four-wire voltage inverter. The inverter operation was researched under algorithms of spatial PWM (SVPWM, DPWMMIN, DPWMMAX, GDPWM) and under the control of the proposed method to form neutral point voltage. The experimental test results completely coincide with simulation modelling results.
Author Contributions
Conceptualization, A.D and A.K. (Andrey Kurkin); methodology, A.D., A.K. (Andrey Kurkin) and A.S. (Anton Sluzov); validation, A.S. (Anton Sluzov) and A.K. (Andrey Kurkin); formal analysis, I.B.; investigation, A.S. (Anton Sluzov), A.K. (Andrey Kurkin), A.K. (Anton Khramov) and I.B.; writing—original draft preparation, A.K. (Andrey Kurkin) and A.S. (Andrey Shalukho); writing—review and editing, A.K. (Andrey Kurkin), A.K. (Anton Khramov), A.S. (Andrey Shalukho) and I.B.; visualization, A.S. (Anton Sluzov); supervision, A.S. (Andrey Shalukho); project administration, A.K. (Andrey Kurkin). All authors have read and agreed to the published version of the manuscript.
Funding
The work is carried out with the financial support of the Ministry of Science and Higher Education of the Russian Federation (state task № FSWE-2022-0006).
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
Abbreviations and Indices
| PWM | Pulse-width modulation |
| SVPWM | Space vector pulse-width modulation |
| SPWM | Sinusoidal pulse-width modulation |
| DPWM | Discontinuous pulse-width modulation |
| GDPWM | Generalized discontinuous pulse-width modulation |
| THD | Total harmonic distortion |
| UPS | Uninterruptible power source |
| AB | Accumulator battery |
| DAC | Digital to analog converter |
| k | Generalization coefficient |
| UDC | DC link voltage |
| UA | Envelope voltage of phase A |
| U*A | Modified envelope voltage of phase A |
| UB | Envelope voltage of phase B |
| U*B | Modified envelope voltage of phase B |
| UC | Envelope voltage of phase C |
| U*C | Modified envelope voltage of phase C |
| UN | Envelope voltage of neutral |
| U*N | Modified envelope voltage of neutral |
| UZVS | Envelope zero phase sequence voltage |
| Uα | Setting alpha component |
| Uβ | Setting beta component |
| UCAR | Carrier voltage |
| UVT | Transistor control pulses |
| fPWM | PWM frequency |
| fSW | Transistor switching frequency |
| RLOAD | Load resistance |
| LLOAD | Load inductance |
| Lfil | Output filter inductance |
| Cfil | Output filter capacitance |
| ffil | Output filter resonance frequency |
| ∆I | Maximum pulsation of effective load current value |
| UA_LOAD | Load phase A voltage |
| IA_LOAD | Load phase A current |
References
- Kulikov, A.; Loskutov, A.; Kurkin, A.; Dar’enkov, A.; Kozelkov, A.; Vanyaev, V.; Shahov, A.; Shalukho, A.; Bedretdinov, R.; Lipuzhin, I.; et al. Development and Operation Modes of Hydrogen Fuel Cell Generation System for Remote Consumers’ Power Supply. Sustainability 2021, 13, 9355. [Google Scholar] [CrossRef]
- Espina, E.; Llanos, J.; Burgos-Mellado, C.; Cardenas-Dobson, R.; Martinez-Gomez, M.; Saez, D. Distributed control strategies for microgrids: An overview. IEEE Access 2020, 8, 193412–193448. [Google Scholar] [CrossRef]
- Mora, A.; Cardenas, R.; Urrutia, M.; Espinoza, M.; Diaz, M. A vector control strategy to eliminate active power oscillations in four-leg gridconnected converters under unbalanced voltages. IEEE J. Emerg. Sel. Topics Power Electron. 2020, 8, 1728–1738. [Google Scholar] [CrossRef]
- Lee, T.; Kinoshita, M.; Sanada, K. High-efficiency large-capacity uninterruptible power supply for 3-phase 4-wire power system. In Proceedings of the 7th International Power Electronics and Motion Control Conference, Harbin, China, 2–5 June 2012; Volume 2, pp. 1131–1136. [Google Scholar]
- Fabricio, E.L.L.; Jacobina, C.B.; Vitorino, M.A.; de Rossiter Correa, M.B. Y-connected three-leg converters applied in three or four-wire shunt compensator. IEEE Trans. Ind. Appl. 2016, 52, 3245–3254. [Google Scholar] [CrossRef]
- Houari, A.; Djerioui, A.; Saim, A.; Ait-Ahmed, M.; Machmoum, M. Improved control strategy for power quality enhancement in standalone systems based on four-leg voltage source inverters. IET Power Electron. 2018, 11, 515–523. [Google Scholar] [CrossRef]
- Chivenkov, A.; Krahmalin, I. Universal converter as a basis for matching the parameters of distributed grid sources with VIE. Intell. Electr. Eng. 2018, 1, 112–115. [Google Scholar] [CrossRef]
- Rojas, F.; Cárdenas, R.; Burgos-Mellado, C.; Espina, E.; Pereda, J.; Pineda, C.; Arancibia, D.; Diaz, M. An Overview of Four-Leg Converters: Topologies, Modulations, Control and Applications. IEEE Access 2022, 10, 61277–61325. [Google Scholar] [CrossRef]
- Vechiu, I.; Curea, O.; Camblong, H. Transient Operation of a Four-Leg Inverter for Autonomous Applications With Unbalanced Load. Power Electron. IEEE Trans. 2010, 25, 399–407. [Google Scholar] [CrossRef]
- Garganeev, A.G.; Aboelsaud, R.; Ibrahim, A. Voltage Control of Autonomous Three-Phase Four-Leg VSI Based on Scalar PR Controllers. In Proceedings of the 2019 20th International Conference of Young Specialists on Micro/Nanotechnologies and Electron Devices (EDM), Erlagol, Russia, 29 June–3 July 2019; pp. 558–564. [Google Scholar] [CrossRef]
- Md Rafi, F.H.; Hossain, M.J.; Rahman, M.S.; Lu, J. Impact of controlling zero sequence current in a three-phase four-wire LV network with PV units. In Proceedings of the 2016 IEEE Power and Energy Society General Meeting (PESGM), Boston, MA, USA, 17–21 July 2016; pp. 1–5. [Google Scholar] [CrossRef]
- Yunwei, L.; Vilathgamuwa, D.M.; Chiang, L.P. Microgrid power quality enhancement using a three-phase four-wire grid-interfacing compensator. IEEE Trans. Power Electron. 2005, 19, 1707–1719. [Google Scholar]
- Julian, A.L.; Oriti, G. Novel Common Mode Voltage Elimination Methods in Three-Phase Four-Wire Grid-Connected Inverters. In Proceedings of the 2021 IEEE Energy Conversion Congress and Exposition (ECCE), Vancouver, BC, Canada, 10–14 October 2021; pp. 2873–2880. [Google Scholar] [CrossRef]
- Dar’enkov, A.; Sluzov, A.; Berdnikov, I.; Sokolov, V.; Kurkin, A. Control Method for a Three-Phase Voltage Inverter. Eurasian Patent Organisation (EAPO). October 2022. Available online: https://www.eapo.org/ru/publications/publicat/viewpubl.php?id=043229&i21=202292616&id=043229&i21=202292616 (accessed on 10 June 2023).
- Llonch-Masachs, M.; Heredero-Peris, D.; Montesinos-Miracle, D.; Rull-Duran, J. Understanding the three and four-leg inverter Space Vector. In Proceedings of the 2016 18th European Conference on Power Electronics and Applications (EPE’16 ECCE Europe), Karlsruhe, Germany, 5–9 September 2016; pp. 1–10. [Google Scholar] [CrossRef]
- Mandrioli, R.; Viatkin, A.; Hammami, M.; Ricco, M.; Grandi, G. A Comprehensive AC Current Ripple Analysis and Performance Enhancement via Discontinuous PWM in Three-Phase Four-Leg Grid-Connected Inverters. Energies 2020, 13, 4352. [Google Scholar] [CrossRef]
- An, S.-L.; Sun, X.-D.; Zhang, Q.; Zhong, Y.-R.; Ren, B.-Y. Study on the Novel Generalized Discontinuous SVPWM Strategies for Three-Phase Voltage Source Inverters. IEEE Trans. Ind. Inform. 2013, 9, 781–789. [Google Scholar] [CrossRef]
- Tcai, A.; Alsofyani, I.M.; Seo, I.-Y.; Lee, K.-B. DC-link Ripple Reduction in a DPWM-Based Two-Level VSI. Energies 2018, 11, 3008. [Google Scholar] [CrossRef]
- Anuchin, A.; Aliamkin, D.; Lashkevich, M.; Shpak, D.; Zharkov, A.; Briz, F. Minimization and redistribution of switching losses using predictive PWM strategy in a voltage source inverter. In Proceedings of the 2018 25th International Workshop on Electric Drives: Optimization in Control of Electric Drives (IWED), Moscow, Russia, 31 January–2 February 2018. [Google Scholar]
- Zhang, Z.; Thomsen, O.C.; Andersen, M.A.E. Discontinuous PWM modulation strategy with circuit-level decoupling concept of three level neutral-point clamped (NPC) inverter. IEEE Trans. Ind. Electron. 2013, 60, 1897–1906. [Google Scholar] [CrossRef]
- Dar’enkov, A.; Sokolov, V.; Sluzov, A.; Berdnikov, I.; Shalukho, A. Research and Development of Adjustable Discontinuous Pulse Width Modulation Method for Three-Phase Voltage Source Inverter. Energies 2022, 15, 7463. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).