Three-Phase Modal Noise Analysis and Optimal Three-Phase Power Line Filter Design

Abstract

Conducted emissions (CE) for three-phase systems are becoming an increasing concern due to the recent exponential growth of three-phase applications, especially linked to the automotive sector. The problem arises because electromagnetic compatibility (EMC) standards only define the methodology to measure the CE generated by the equipment under test (EUT), and they do not provide sufficient information to design a power line filter (PLF) in case of non-compliance. Hence, the design of an optimal PLF is a very difficult task for engineers. The unclear methodology to be followed, unknown load impedances, inadequate equipment, and lack of knowledge of the modal noise are all different reasons that contribute to increasing the PLF design complexity. Common mode (CM) and differential mode (DM) decomposition and PLF design techniques for single-phase EUTs are well discussed and studied in the literature, but the same cannot be stated when it comes to three-phase PLF design. The objective of this paper is to clarify how modal noises behave in a three-phase system and to propose a clear methodology which can be followed to design an optimal three-phase PLF. Additionally, this paper analyses and discusses the modal noises’ intrinsic behavior and provides an understanding of how the PLF components behave when subjected to either a CM or DM noise. Finally, a methodology to design a three-phase PLF, based on accurate insertion loss (IL) estimations and S-parameter measurements, is used to determine the optimal PLF. This approach is tested and validated.

1. Introduction

Due to the recent proliferation of three-phase power electronics and three-phase charging stations [1,2,3], conducted emissions (CE) are becoming an increased concern for manufacturers, who are forced to comply with EMC regulations [4,5,6]. EMC standards dictate the maximum levels of permitted electromagnetic interference (EMI) noise allowed in a certain frequency band. According to these standards, conducted emissions are evaluated in the frequency range of 150 kHz to 30 MHz, also known as band B [4,5,6].

The most common technique to suppress CE noise in order to comply with electromagnetic interference (EMI) standard limitations [4,5,6] is to place a power line filter (PLF) between the equipment under test (EUT) and the power line network (PLN).

Normally, PLFs are selected by relying on the IL values, which are evaluated with 50 Ω impedances at the in-out ports or, to consider the worst-case scenarios, with 100 Ω and 0.1 Ω at the in–out ports respectively, as described in Annex C of CISPR 17 [6].

However, the actual impedance of both the PLN and EUT changes along with the frequency and can also be influenced by parasitic components. Hence, it is impossible to correctly determine the actual IL of a PLF [7,8,9,10,11,12,13,14].

According to the EMC standards, CEs are measured between lines with respect to the ground and, if present, with neutral respect to the ground [4,5]; thus, the actual values of the common mode (CM) and differential modes (DMs) noises remain hidden inside the measured CE. This presents a first and major limitation for optimal PLF design, since each component present in the filter reduces either the CM or DMs. Hence, a detailed knowledge on the CE modal noise is required to design an optimal PLF.

Additionally, commercial three-phase PLFs are found as standardized structures designed to reduce both CM and DMs noises, but they are most likely oversized and more expensive than necessary; almost all structures are comprised by a common mode choke (CMC), at least three $C_x$ capacitors, and at least three $C_y$ capacitors, which might not be strictly necessary [15,16,17,18,19,20,21,22,23,24]. As a result, an oversized PLF is usually implemented. Obviously, an optimal PLF should be optimized in terms of performance, cost, volume, and weight.

Furthermore, it has been demonstrated that an impedance mismatch in the EUT or in the PLF leads to an unexpected energy exchange between DM and CM interference. This modifies the expected PLF performance and leads to unexpected CE levels [16,17,18,19].

Hence, the only way to achieve an optimal PLF design is by designing it.

To the best of authors’ knowledge, the previous literature has not defined a clear and standardized PLF design methodology for three-phase EUTs.

First of all, PLF design for three-phase EUTs is much more complex than for a single phase due to the presence of more lines which lead to completely different modal noise interactions [16,17,18,19,20,21,22,23,24]. Hence, the traditional CM/DM analysis [7,8,9,10,11,12,13,14] cannot be applied in a straightforward manner, and new models and definitions are needed.

A certain amount of research has focused on either CM or DM attenuation [21,22,23,24,25,26,27], without considering modal noise interactions and reflections due to impedance mismatches when implementing the PLF. As a result, a gap is left for optimal PLF design.

Also, certain practices to reduce and optimize the volume and size of the PLF have been proposed in the literature, for instance in [28,29,30]. Anyway, the accuracy of the PLF optimization process is compromised because the modal noises are not measured simultaneously. Furthermore, the methodologies proposed rely on a trial-and-error loop to define the CM and DM components to achieve the required attenuation, resulting in longer times to design the PLF.

Other works [1,2,3,31,32,33,34,35] have focused on evaluating how the modal CE contributes to increase the power grid pollution. Although a comprehensive analysis is proposed on the effects that CE noise have on the system, no specific details on how a PLF can be designed are presented.

In [36,37,38,39,40], external devices called modal separators were used to evaluate the modal noises generated by a three-phase EUT. Although these devices allow CE modal decomposition, they have several disadvantages which limit their implementation for optimal PLF design [8,36]. For instance, ref. [36] proposes a detailed study on how asymmetries, amplitude, and phase mismatches introduced by the modal separator affect the overall modal measurement.

As a result, no methodology has yet been recognized by the EMC community. Hence, most engineers developed their own procedures to design three-phase PLFs based on the available equipment, knowledge, information, and experience. Anyway, the actual PLF design is achieved only after several trial-and-error loops, since the actual PLN and EUT impedance is not known and, on top of that, there is no standard procedure to be followed.

In order to propose a solid and reliable methodology to design an optimal three-phase PLF, this paper defines a generalized model to understand and analyze how the modal components present in the system interact between each other; furthermore, it presents an overview of the available instrumentation that can be used to extract the CE noise, as well as the modal noises.

Then, simulations are carried out to determine the effect that each component present in the PLF has on either CM or DM noise. From these results, it is possible to define a specific and optimized PLF configuration, provided that the modal noises are known.

Finally, a solid design methodology relying on accurate IL estimation of the PLF for both CM and DM is presented and validated to determine the optimal PLF structure for a three-phase EUT.

The main contributions of this research are listed hereafter:

(1)

A clear three-phase modal definition along with a review of the instrumentation capable of extract modal noises;

(2)

A methodology to evaluate the behavior of any PLF component when the system is excited with either CM or DM noises, or a combination of both;

(3)

A detailed PLF design methodology, based on an accurate IL estimation to reduce the CM and DM CE, experimentally tested, and validated in a real case scenario.

To the best of the authors’ knowledge, similar case studies and considerations are not yet available in the literature.

Overall, the results obtained and presented in this paper are useful to understand the nature of the modal noises and to minimize the time and cost to design an optimal PLF. Furthermore, the methodology described can be applied to any EUT without a loss of generality; thus, it sets the basis to become a standard method to be followed to design an optimal PLF for three-phase applications.

This paper is organized as follows: Section 2 proposes a review of the modal noise decomposition for three-phase EUTs. Section 3 proposes a method to analyze the behavior of any component subjected to CM or DM interferences. Section 4 proposes and validates a methodology to design an optimal PLF for a three-phase EUT. Finally, Section 5 summarizes a final discussion of the work.

2. Modal Definition: A Brief Review

Measurements performed according to EMC standards provide information about the total CE level of an EUT, but they do not provide sufficient information to design a PLF in case of non-compliance [7,8,9,10,11,12,13,14].

The following subsections provide a clear model and explanation to understand how the modal noises behave and interact between each other. Although the considerations, equations, and methodology described in this paper could easily be extended for cases where the neutral conductor is present, a more exhaustive analysis considering this scenario should be carried out.

2.1. Three-Phase Modal Definition

Any signal can be characterized in the following ways:

• Circuital: considering the actual phase voltages and currents.
• Modal: considering its modal decomposition, which is, the common mode, along with its voltage and current, and differential modes, along with their voltage and current.

Figure 1 shows how the modal decomposition of the currents can be obtained starting from the actual line currents.

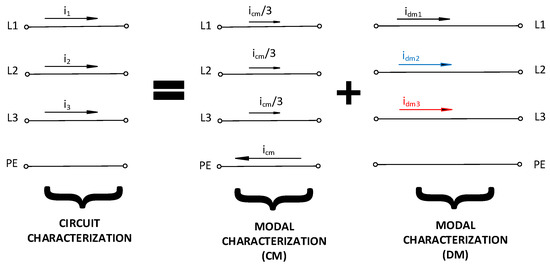
Figure 1. Circuital vs. modal characterization for a three-phase EUT currents.

By analyzing the circuit proposed, the following relationship can be derived:

$$i_i=i_{DMi}+\frac{i_{CM}}{3} ; i = 1, 2, 3.$$

(1)

where $i_{DM,i}$ is the DM current flowing in each phase, $i_{CM}$ is the CM current and $i_i$ is the actual phase current.

By definition, the sum of the DM currents is null [15,16,17,18,19,20,21,22].

$$i_{DM1}+i_{DM2}+i_{DM3}=0$$

(2)

Hence, the CM current is given by:

$$i_{CM}=i_1+i_2+i_3$$

(3)

Figure 1 also shows that CM and DM noise currents are defined by different propagation paths. The CM current flows though the loop formed by all phases and the protective earth line (PE), while DM noise currents flow in one phase and reclose in the other two.

A more detailed representation of this phenomenon is shown in Figure 2. For the sake of exemplification, only $i_{DM1}$ is shown, but the same considerations are valid for $i_{DM2}$ and $i_{DM3}$.

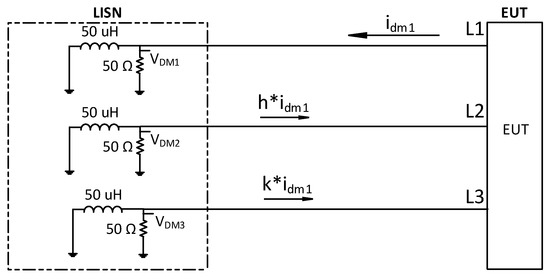
Figure 2. Path followed by $i_{DM1}$ generated by an EUT when connected to a three-phase LISN.

In the figure, $k$ and $h$ depend on the system impedance and can assume different values case by case. Furthermore, the values of $k$ and $h$ for $i_{DM1}$ do not necessarily have to be the same for $i_{DM2}$ and $i_{DM3}$ decomposition.

The complete modal equivalent circuit of a three-phase EUT connected to a LISN is shown in Figure 3. For the sake of simplicity, only the 50 Ω resistance of the LISN is shown.

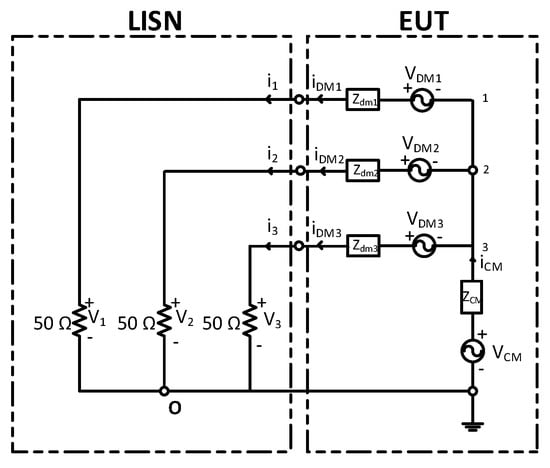
Figure 3. Equivalent circuit of a three-phase EUT connected to a LISN.

As can be seen in Figure 3, a combination of CM and DM voltage sources and their impedances are used to fully model the EUT CE noise; the CM voltage source ${(V}_{CM}),$ which is common to all the three phases, and three independent differential mode voltage sources ($V_{DM,i})$, one for each phase (i = 1, 2, 3) [18,19,20,21,22,23,24,25,26,27,28,29,30].

By applying Kirchhoff’s law to the loops of the circuit shown in Figure 4, the following relationship can be obtained:

$$V_i=V_{DM,i}+V_{CM}; \mathrm{for} i = 1, 2, 3$$

(4)

where $V_i$ represents the voltages generated by the current $i_i$ when passing though the LISN’s resistor. As defined in Equation (1), the current $i_i$ is composed of a DM current ${(i}_{DM,i})$ and a CM current ($i_{CM})$. Hence, $V_i$ is composed of the sum of a differential mode voltage ($V_{DM,i})$ and a common mode voltage ($V_{CM})$.

The CM voltage can be evaluated from the following relationship:

$$V_1+V_2+V_3=\left(i_1+i_2+i_3\right)\times R_{LISN}=i_{CM}\times R_{LISN}=3\times V_{CM}$$

(5)

Thus, one can derive that $V_{CM}=\frac{V_1+V_2+V_3}{3}$.

From these considerations and definitions, it is possible to derive that CM noise can be highlighted as affected by straight capacitances present in the system. In contrast, DMs, which for instance can be generated by the voltage peaks coming from inductive load switching, are not affected by straight capacitances or ground connections [20,36,37,38,39,40,41,42,43].

2.2. Filtering a Predominant Differential Mode Noise

In order to design an optimal PLF, it is necessary to evaluate the contribution that each modal noise has on the overall CE; that is, knowing each $V_{DM,i}$ and $V_{CM}$, which are voltages generated by the DM currents ${(i}_{DM,i})$ and CM current ($i_{CM})$ while flowing though the LISN. Hence, if only one among the three differential modes is prevailing, a different PLF structure than standard ones, for instance composed of three $C_x$ type capacitors, shall be implemented.

For example, if $V_{DM1}$, is found to be the dominant DM noise, the optimal PLF configuration is achieved by inserting two $C_x$ type capacitors between Lines 1–2 and 1–3.

This example is depicted and shown in Figure 4.

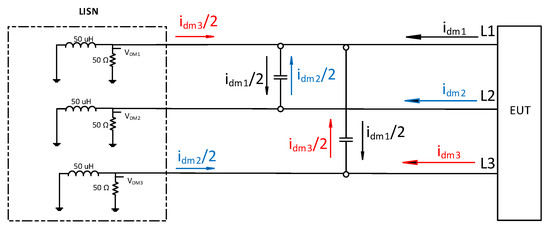
Figure 4. Representation of the differential mode currents flowing in a three-phase system after applying two C_x capacitors. DM1 (black), DM2 (blue), and DM3 (red).

For the sake of simplicity, $k$ and $h$ are assumed to be ½ for each current. This assumption might not be true for all cases, but it is valid for this example. Only DM currents are depicted, since $C_x$ capacitors have no influence on CM currents.

Figure 4 shows how a predominant DM noise ($V_{DM1})$, generated by $i_{DM1}$ flowing through the 50 Ω resistor of the LISN, can be filtered using only two $C_x$ capacitors. It relies on the fact that the current $i_{DM1}$ recloses though the low impedance path offered by the two capacitors and does not flow towards the LISN. Furthermore, as depicted in Figure 4, $i_{DM2}$ and $i_{DM3}$ partially reclose though the low impedance path offered by the capacitors, hence a partial reduction in $V_{DM2}$ and $V_{DM3}$ is also achieved. Throughout the paper, both simulations and measurements results will sustain this statement.

Based on this analysis, it is clear that in order to effectively filter out a single DM noise, only two $C_x$ capacitors are required. The use of any other PLF structure, such as those composed of three $C_x$ capacitors or other components, would only contribute to increase the size and cost of the PLF unnecessarily.

Such a PLF structure implies that:

$$i_{DM1}+i_{DM2}+i_{DM3}\ne 0$$

(6)

This means that at the point ‘O’ shown in Figure 3, the sum of the DM current differs from zero. Hence, part of the DM current will be transformed into a CM current, thus contributing to increasing the overall CM voltage. This energy exchange between modes must be evaluated when implementing such a PLF structure to make sure that the new CM voltage does not cause incompliance. An example will be presented in this paper.

Furthermore, if there is also an imbalance in one of the phase impedances, the CM noise will distribute unevenly among the phases; therefore, part of the CM noise will be transferred to DM noise, this phenomenon is the so-called mixed-mode (MM) noise [15,16,17,18,19,20,21,22,23,24,25]. The same consideration is also valid for DM noise distribution among the phases, but is not further analyzed in this paper.

2.3. General Considerations for CE Testing for Three-Phase EUTs and Consequences in PLF Design

Generally, the EMI receivers available on the market only present one input RF channel. Furthermore, three-phase LISNs are also designed to allow the measurement of only one phase at a time, using an internal switch to commutate to the phase of interest. Therefore, the CE of a three-phase EUT must be performed by at least three subsequent measurements. An example is shown in Figure 5.

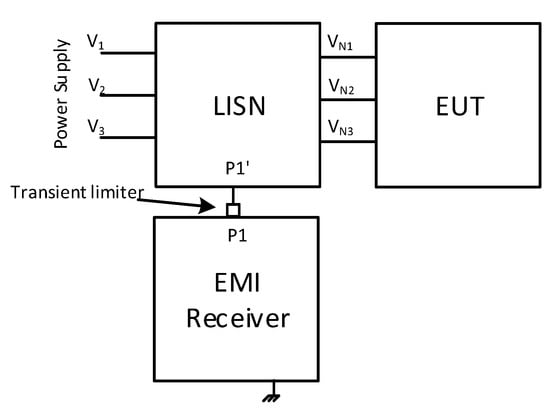
Figure 5. Standard CE set-up for a three-phase EUT.

With the set-up illustrated above, it is not possible to measure the modal noises because only one phase is measured at a time. Hence, designing an optimal PLF becomes a very difficult task because it can be carried out only by following a tedious trial-and-error procedure [15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30].

To overcome this limitation, two main requirements are needed:

(1)

Access to a LISN featuring independent RF outputs for each phase.

(2)

Access to equipment able to extract the modal noises.

To satisfy the recent increasing market demand for Requirement (1), certain LISN manufacturers have begun to offer the possibility to customize a three-phase LISN that features four independent RF outputs instead of only one.

As for Requirement (2), two solutions are possible. The first one would be to use a modal separator, as shown in Figure 6a. In the literature, it is possible to find several examples of these architectures with detailed analysis on their advantages and disadvantages [36,37,38,39,40].

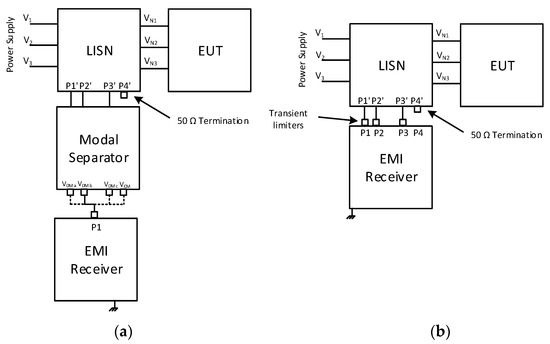
Figure 6. (a) Set-up using a modal separator; (b) set-up using a four-channel EMI receiver.

The second possibility is to have at the project’s disposal a receiver capable of measuring all channels simultaneously and extracting the information of modal noises, as shown in Figure 6b.

The measurements shown in Section 4 are based on this second approach.

When an external separator is used, the following drawbacks must be considered:

• Extra equipment must be bought or developed [8];
• Modal noises cannot be measured simultaneously. This makes the identification of the predominant mode or sporadic interference detection very difficult, especially when a pulsed interference is measured;
• Additional cables and the modal separator itself can behave as an antenna and couple undesired signals into the measurements and add uncertainties into the measurement chain;
• Modal coupling depends on the technology and can change along with the frequency [8,36,37,38,39,40];
• Special care must be taken to avoid impedance mismatches, since reflections can amplify the modal conversion.

The benefits achieved with the set-up illustrated in Figure 6b, composed of an EMI receiver which could measure all the channels simultaneously, are listed hereafter:

• No external modal separator is needed. Whenever an external device is added into the measurement set-up, the possibility of impedance mismatches increases. For example, the impedance of the modal separator placed between a LISN RF output and a receiver RF input might vary in an unknown manner along with the frequency and contribute to providing wrong measurement results [14];
• CM and DM noises can be measured and analyzed simultaneously. A four-channel EMI receiver equipped with a high-speed ADC converts the measured signals in the digital domain. Hence, the modal noises can be evaluated by computing Equations (4) and (5) without external analog devices.

3. PLF Design

The modal noises generated by a EUT, when propagation paths are symmetrical and time invariant, should be decoupled. This means that an equivalent CM source generates only CM noise, and the same is also valid for the DM noise, respectively [15].

Again, this is well-studied for single-phase systems, but there is still a gap for three-phase systems. Hence, it is not possible to correctly understand and determine the effect that each PLF component has on CM or DM reduction.

This section shows how different voltage configurations are used to inject CM or DM noise only into the system. This is to evaluate the response, under known conditions, of the PLF components under study.

The results obtained are important to understand how components react when different noises are generated by the EUT. Furthermore, by following the approach and methodology proposed, simulations considering parasitic parameters and/or multiple components can also be carried out. A detailed analysis of the basic PLF configurations and modal noise analysis is presented hereafter.

3.1. Common Mode Noise Generation

According to the modal definition (Equations (4) and (5)), in order to introduce only a CM noise source into the system, the relationship shown in Equation (7) must be respected; namely, the amplitude and phase displacement of the three vectors must be the same.

V_1n = V_2n = V_3n

(7)

In this case, it holds that:

$$V_{CM}=\frac{V_1+V_2+V_3}{3}=\frac{3\ast V_i}{3}=V_i\ne 0$$

(8)

$$V_{DM,i}=V_i-V_{CM}=V_i-\left(\frac{V_1+V_2+V_3}{3}\right)=V_i-\left(\frac{3\ast V_i}{3}\right)=0; i = 1, 2, 3$$

(9)

Thus, only a CM noise is injected in the system.

3.2. Differential Mode Noise Generation

According to the modal definition (Equations (1) and (3)), in order to introduce a DM noise source into the system the relationship shown in Equation (8) must be respected; namely, the vectors must have the same amplitude and, for example, a phase displacement of 120° each.

V_1n + V_2n + V_3n = 0

(10)

In this case, it holds that:

$$V_{CM}=\frac{V_1+V_2+V_3}{3}=0$$

(11)

$$V_{DM,i}=V_i-V_{CM}=V_i-\left(\frac{V_1+V_2+V_3}{3}\right)=V_i\ne 0; i = 1, 2, 3$$

(12)

3.3. Differential and Common Mode Noise

In order to inject a combination of DM and CM noise, it is simply necessary to set a phase displacement which differs from the conditions indicated in the two subsections above.

3.4. Accurate Estimation of the IL of a PLF

The IL, independently of the noise source present in the system, can be generally computed by solving the following equations:

$$\begin{array}{ll}{\left.IL\right|}_{dB}^{DMi}& =20\times {log}_{10}\left(\frac{V_{DM}^{ref}}{V_{DM}}\right)=20\times {log}_{10}\left(\frac{V_i^{ref}-V_{CM}^{ref}}{V_i-V_{CM}}\right)\\ & =20\times {log}_{10}\left(\frac{V_i^{ref}-\left(\frac{V_1^{ref}+V_2^{ref}+V_3^{ref}}{3}\right)}{V_i-\left(\frac{V_1+V_2+V_3}{3}\right)}\right); i = 1, 2, 3\end{array}$$

(13)

$${\left.IL\right|}_{dB}^{CM}=20\times {log}_{10}\left(\frac{V_{ref}^{CM}}{V_{CM}}\right)=20\times {log}_{10}\left(\frac{\frac{V_1^{ref}+V_2^{ref}+V_3^{ref}}{3}}{\frac{V_1+V_2+V_3}{3}}\right)$$

(14)

where the voltages $V_i^{ref}$ (i = 1, 2, 3) are the voltages at Terminals 1, 2, and 3 of the LISN, respectively, when no PLF is connected, as seen in Figure 7. In contrast, the voltages $V_i$ (i = 1, 2, 3) are the voltages Terminals 1, 2, and 3 of the LISN, respectively, when the signal is filtered, as seen in Figure 8.

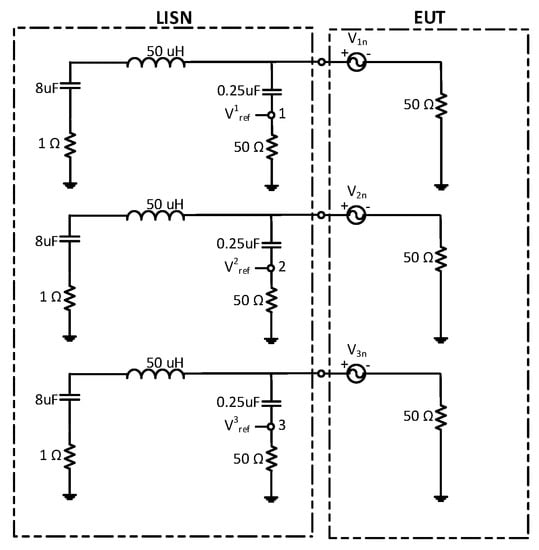
Figure 7. Equivalent circuit of the EUT connected to the equivalent circuit of a three-phase LISN.

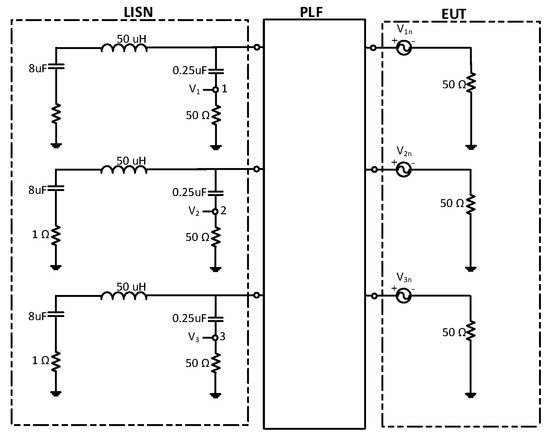
Figure 8. Equivalent circuit of the EUT connected to the equivalent circuit of a three-phase LISN with a PLF.

Both measurement points are placed between the 50 Ω resistor and the 0.25 µF capacitor.

Figure 8 illustrates the equivalent circuit of the EUT connected to the equivalent circuit of a LISN though a general PLF which will be introduced to perform the required evaluations.

In this case, a 50 Ω load is used to represent the impedance of the EUT, while the impedance of the LISN is represented by its internal circuit.

Three voltage noise sources, $V_{1n}$, $V_{2n}$, and $V_{3n},$ are used to provide a fixed amplitude signal at all frequencies of interest, which will be used to compute the attenuation of the PLF as described in the following subsections.

3.5. Models Validation

3.5.1. IL’s Evaluation for C_x Capacitors

Figure 9 shows X-type capacitors ($C_x)$ connected between a three-phase LISN and a three-phase EUT.

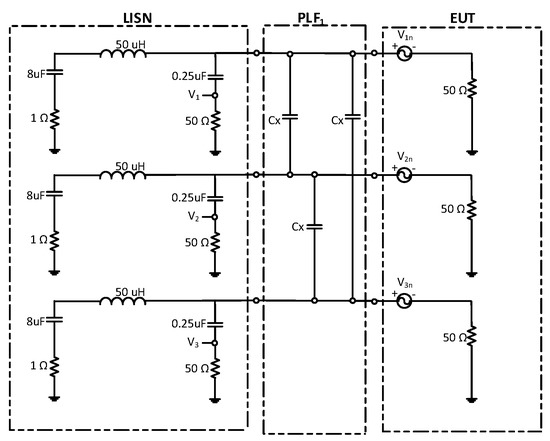
Figure 9. PLF connected between the three-phase LISN and three EUTs consisting of X-type capacitors.

The value of each $C_x$ chosen to carry out the simulation is 0.10 µF. Figure 10 shows the attenuation introduced by PLF₁.

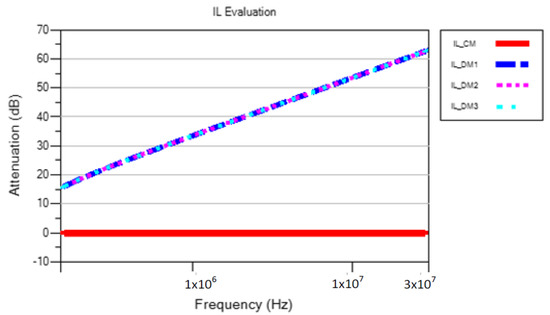
Figure 10. IL of a PLF₁ composed of only $C_x\mathrm{c}\mathrm{a}\mathrm{p}\mathrm{a}\mathrm{c}\mathrm{i}\mathrm{t}\mathrm{o}\mathrm{r}\mathrm{s}$.

As shown in Figure 10, $C_x$ capacitors do not reduce the CM noise and only affect the DM noise.

3.5.2. IL’s Evaluation for CMC

Figure 11 shows a CMC connected between the three-phase LISN and the EUT.

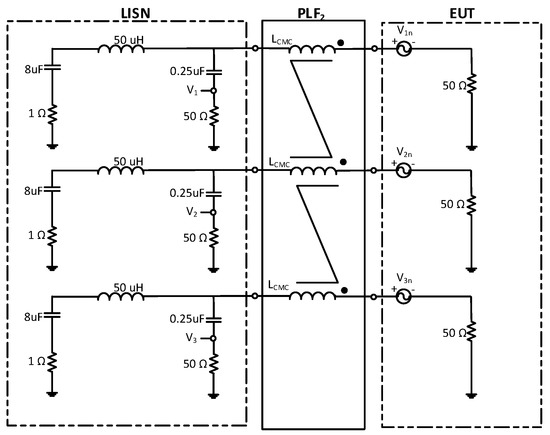
Figure 11. PLF connected between the three-phase LISN and the EUT consisting of a three-phase CMC.

The value of the three-phase CMC selected to carry out this simulation is 1.2 mH. Figure 12 shows the attenuation introduced by PLF₂.

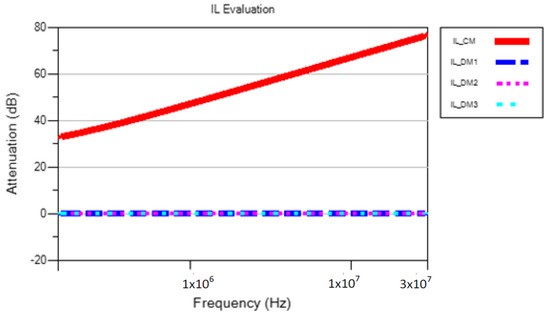
Figure 12. IL of a PLF₂ composed of a three-phase CMC.

As shown in Figure 12, a CMC ideally does not reduce the DM noise and only affects the CM noise.

3.5.3. IL’s Evaluation for C_y Capacitors

Figure 13 shows Y-type capacitors (${\mathrm{C}}_y$) connected between the three-phase LISN and the EUT.

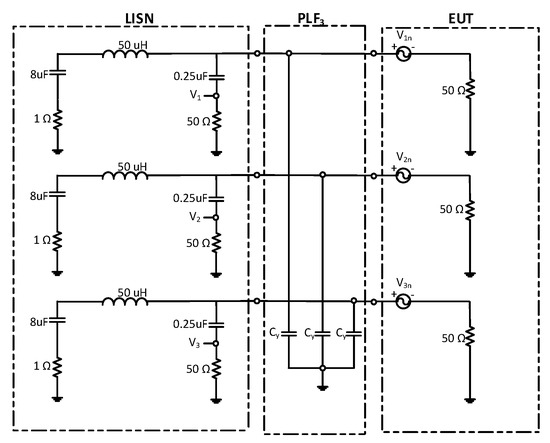
Figure 13. PLF connected between the three-phase LISN and the EUT consisting of X-type capacitors.

The value of each ${\mathrm{C}}_y$ capacitor used to carry out this simulation is 0.05 µF. Figure 14 shows the attenuation introduced by PLF₃.

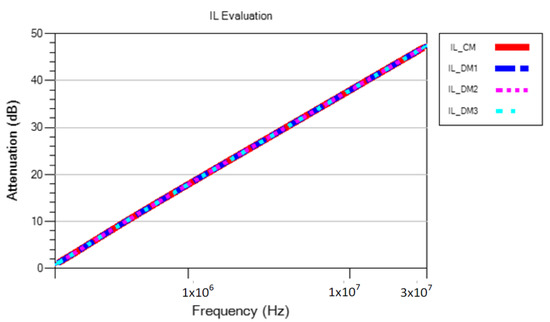
Figure 14. IL of a PLF₃ composed of three ${\mathrm{C}}_{\mathrm{y}}$ capacitors.

As shown in Figure 14, $C_y$ capacitors attenuate both CM and DM noise.

According to the standard IEC 60990 and depending on the application, the maximum leakage current is limited. Thus, extreme care must be taken when using these types of capacitors, since their practical implementation could be strongly limited.

3.6. EUT Characterization—S-Parameter Measurements

It is known that to design an optimal PLF, the input impedance of the EUT must be known [7,8,9,10,11,12,13,14,15]. To this end, the S-parameters of the EUT have been measured. Since only a two-port VNA was available at the laboratory, three subsequent measurements had to be performed (Port 1–2, Port 2–3, and Port 1–3, respectively) and combined together in order to obtain a 3 × 3 matrix characterizing the EUT, as shown in Figure 15.

Figure 15. (a) S-parameter measurement set-up; (b) set-up with 50 Ω termination.

Figure 15a,b show the set-up implemented to measure S-parameters using a two-port VNA and a 50 Ω termination for the remaining line which could not be connected to the VNA.

4. Experimental Validation

The methodology followed to design an optimal PLF of a three-phase EUT is described hereafter:

• Measurement of the EUT’s S-parameters;
• Measurement of the conducted emissions and their modal decompositions. This information is needed to determine the attenuation required to mitigate each mode under a certain limit;
• S-parameters are introduced as a three-port black box in a circuit simulator;
• Implementation of the same circuit by adding the PLF;
• Simulations in frequency domain to obtain the voltage amplitude at the measurement ports of the LISN, that is: $V_1^{ref}{,V}_2^{ref}{,V}_3^{ref},V_1{,V}_2,\mathrm{a}\mathrm{n}\mathrm{d}{V}_3$;
• The CM/DM attenuation is computed using Equations (11) and (12), respectively;
• The determination of the optimal values for each PLF component is conducted using iterative simulations and by selecting the closest available commercial value found. Of course, this methodology could be implemented by means of different optimization techniques.

4.1. CE Measurements

In this subsection, the CE and modal noise measurements obtained are presented.

The set-up for CE measurement described in Section 2 and illustrated in Figure 6b is shown in Figure 16. In this case study, the EUT chosen is a three-phase inverter used for motor control.

Figure 16. CE measurement set-up: an EMSCOPE-RX4 (a four-port EMI receiver, left side), and a four-port LISN (right side, back), with the EUT (right side, front).

Figure 17 shows the CE measurement registered at the line terminals of the LISN using the quasi-peak (QPK) detector.

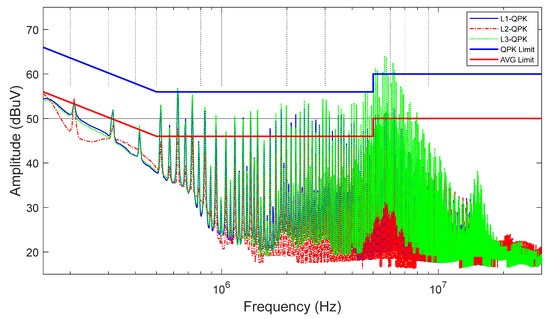
Figure 17. CE measurement of a three-phase EUT with a QPK detector.

It can be seen that at 630 kHz and at 5 MHz, the registered measurement is above the CISPR 32 class B limit [2]. It is clear that the EUT does not comply with the standard limitations and a PLF must be introduced. A minimum mitigation of 20 dB is required to meet the standard limits and make sure that a safe margin is left to compensate possible variations due to slight differences in the set-up and measurement uncertainties when performing the final tests at a third-party EMC lab.

Figure 18 shows the modal decomposition measured with the QPK detector of the CE noise generated by the EUT.

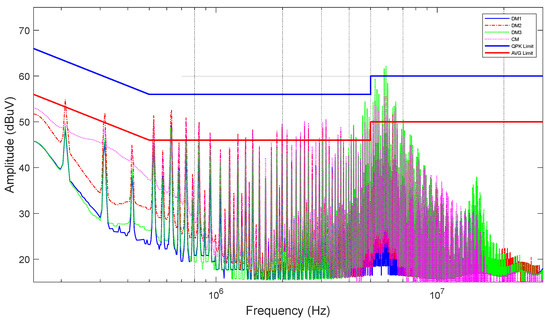
Figure 18. Modal noise measurement of a three-phase EUT measured with a QPK detector.

As can be seen Figure 18, thanks to the modal decomposition, it is possible to determine that DM3 is the dominant mode. This, along with the input impedance of the EUT, is an essential information to design an optimal PLF. Since the other mode noises are below the limit, they do not require special mitigation.

4.2. PLF Design Methodology

In this section, an accurate evaluation of the IL is proposed and then used to determine the optimal PLF for the EUT.

With respect to EMC testing, the LISN, whose internal circuit is known, provides the impedance of the power line network (PLN). Thus, if the EUT impedance is also known, the real IL of any PLF can be evaluated.

Since the S-parameters of the EUT have been measured using the methodology explained in Section 3.6, the EUT impedance is known.

According to the explanation proposed in Section 2, it is clear that two $C_x$capacitors are the correct elements to completely filter the differential mode noise under analysis.

In this case study, since differential mode three (DM3) is above the permitted limit, two X-type capacitors are inserted between Lines 1–3 and 2–3 to reduce the CE. Furthermore, a reduction in DM1 and DM2 will also be achieved.

The value of the $C_{\mathrm{x}}$ capacitors has been obtained by changing the values until the IL introduced achieved the desired attenuation for the case under study.

Figure 19 shows the PLF connected between the EUT and the LISN consisting of two 0.47 uF X-type capacitors placed between Lines 1–3 and 2–3 to mitigate the differential mode noise of interest.

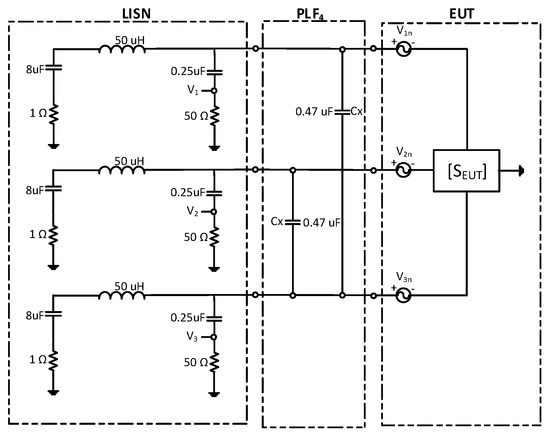
Figure 19. PLF connected between the EUT and the LISN consisting of two X-type capacitors placed between Lines 1–3 and 2–3.

Figure 20 shows the attenuation obtained for each modal noise.

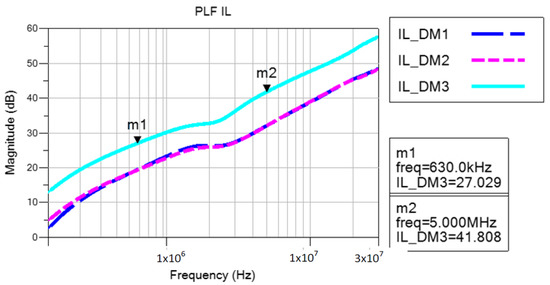
Figure 20. IL of PLF₅.

As can be seen, the reduction obtained at 630 kHz and 5 MHz is enough to make the product comply with the limit imposed by the relative EMC standard [4,5,6].

Figure 21 shows the DM1 recorded before and after applying PLF₅.

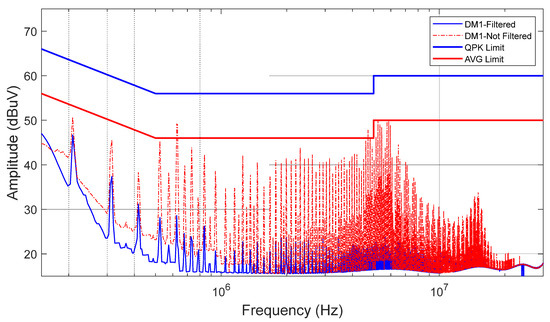
Figure 21. DM1 without PLF₅ (red) vs. with PLF₅ (blue).

As can be seen, reductions of 21 dB and 30 dB are achieved at 630 kHz and 5 MHz, respectively, as expected from the simulation results shown in Figure 20.

Figure 22 shows the DM2 recorded before and after applying PLF₅.

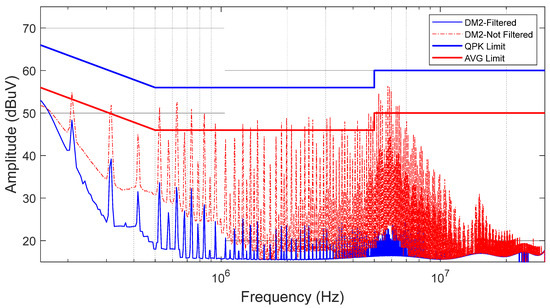
Figure 22. DM2 without PLF₅ (red) vs. with PLF₅ (blue).

As shown in Figure 22, the reductions of 21 dB and 29 dB achieved at 630 kHz and 5 MHz, respectively, are consistent with the estimated value obtained from the simulation results shown in Figure 20.

Figure 23 shows the DM3 recorded before and after applying PLF₅.

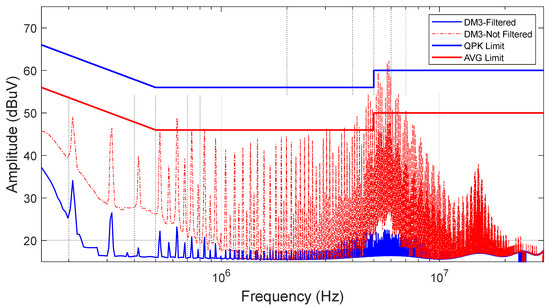
Figure 23. DM3 without PLF₅ (red) vs. with PLF₅ (blue).

As can be seen, the reductions of 26 dB and 38 dB achieved at 630 kHz and 5 MHz are exactly as expected from the simulation results shown in Figure 20.

Figure 24 shows the CMC recorded before and after applying PLF₅.

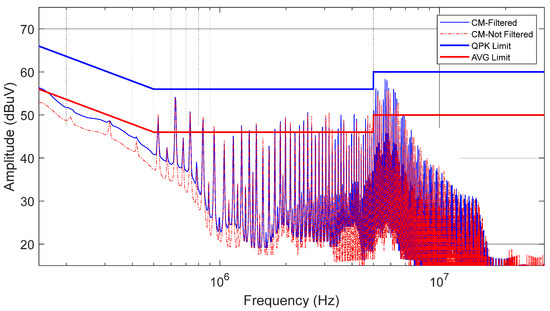
Figure 24. CM without PLF₅ (red) vs. with PLF₅ (blue).

Figure 24 confirms that ${\mathrm{C}}_x$ capacitors do not affect the CM noise, as a confirmation of the simulation carried out in Section 3, Figure 12. The small deviations from the filtered and unfiltered measurements, which can be observed in Figure 24, are due to the modal exchange created by the imbalanced PLF structure implemented, as explained in Section 2.2. Furthermore, the different set-up created when the PLF is added (extra cables, different stray capacitances of the PCB board where the PLF is mounted, etc.) might affect the overall CM noise.

Therefore, the results obtained provide evidence that to design an optimal PLF for three-phase EUTs to meet EMC standards, it is necessary to evaluate the modal noises and, only after that, design a PLF. In this particular case study, a filter composed of two $C_x$ type capacitors was found to be the optimal configuration. Hence, every other component, for instance a $C_x$ capacitor placed between Line 1–2 or a CMC, would have been redundant, and only contributed to increase the size and cost of the PLF.

Most of the current research on this topic discusses modal decomposition; but, when designing a PLF, this information is not taken into account and only static and standardized PLF structures are implemented.

Inevitably, this makes the PLF bigger and more expensive than it should be.

In conclusion, accurate modal noise analysis and EUT characterization are essential information to design an optimal PLF.

From now on, engineers will have a stable and reliable methodology to follow in order to design an optimal PLF for three-phase applications.

5. Conclusions

In this paper, a rigorous methodology for optimal three-phase PLF design is proposed and validated. This study offers an in-depth examination of the modal noises present in three-phase systems, defined through both mathematical expressions and graphical representations. Additionally, this research also outlines the essential testing equipment required to perform these measurements efficiently.

Since each component present in the PLF attenuates either common or differential mode noise, a detailed knowledge on which noise is being generated by the EUT is fundamental to achieving an optimal PLF design. For this, a procedure to evaluate how different PLF components behave when subjected to either common or differential mode noises is validated both from a mathematical and experimental point of view. Then, after having defined the PLF’s components behavior, a methodology to design an optimal PLF relying on accurate IL estimations and modal CE measurements is proposed.

By using a circuit simulator which contains the measured S-parameters of a three-phase EUT and by measuring its modal CE, it was possible to derive the optimal PLF configuration relying on real IL values. Its internal structure is composed of only two $C_x$-type capacitors to reduce the dominant differential mode of interest. The proposed structure differs from a standard structure used in commercial PLFs, which would have implemented at least one CMC and three $C_x$-type capacitors, drastically increasing the number of components implemented in the PLF.

By following the methodology described in this paper, engineers seeking to design an optimal PLF for three-phase applications can reduce the overall cost and time to develop an optimal three-phase PLF and accelerate the time to market of the product.