A Modified Whale Optimizer for Single- and Multi-Objective OPF Frameworks

Abstract

This paper is concerned with an imperative operational problem, called the optimal power flow (OPF), which has several technical and economic points of view with respect the environmental concerns. This paper proposes a multiple-objective optimizer NSWOA (non-dominated sorting whale optimization algorithm) for resolving single-objective OPFs, as well as multi-objective frameworks. With a variety of technical and economic power system objectives, the OPF can be formulated. These objectives are treated as single- and multi-objective OPF issues that are deployed with the aid of the proposed NSWOA to solve these OPF formulations. The proposed algorithm modifies the Pareto ranking and analyzes the optimum compromise solution based on the optimal Euclidian distances. This proposed strategy ensures high convergence speed and improves search capabilities. To achieve this study, an IEEE 30-bus (sixth-generation unit system) is investigated, with eight scenarios studied that highlight technical and environmental operational needs. When compared to previous optimization approaches, the suggested NSWOA achieves considerable techno-economic improvements. Additionally, the statical analyses are carried out for 20 separate runs. This analysis proves the high robustness of the proposed NSWOA at low levels of standard deviation.

1. Introduction

1.1. Motivation

With the massive growth of electrical energy demand, scientific research in the field of electrical power systems becomes increasingly crucial for operation and planning. As per their complexity and non-linear nature, electrical power grids need to be optimally operated without violating their operation constraints. One of the vital approaches which could achieve this goal is the OPF framework. This article aims to solve the OPF problem by considering both single- and multiple-objective frameworks by achieving various power grid requirements from technical and economical viewpoints.

1.2. Literature Review

OPF study was initiated approximately six decades ago [1,2]. OPF study is employed to attain various objectives. These objectives can include fuel cost minimization, bus voltage enhancement, stability enrichment, and optimized reactive power consumption. These cost functions can be realized while single-objective optimization is used. However, if one single-objective optimization—such as fuel cost, for example—is minimized, it can increase the total power loss or voltage deviation. Hence, there is a need for multi-objective optimization to ensure effective compromise in pursuit of the desired objectives. Solution of the OPF can be conquered by conventional (deterministic) techniques such as the simplex method, Newton method, interior point method, and sequential quadratic programming which can be reviewed in [3]. Despite their outstanding convergence characteristics and its industrial popularity, deterministic techniques cannot ensure global optimality and handling of integer variables. Overcoming these shortcomings which are not suitable for OPF solutions and exploiting the rapid growth of computational intelligence in recent years, metaheuristic optimization algorithms are a promising solution for various applications [4,5,6].

In the past decade, organically inspired techniques have been widely adopted for solving the OPF problem. Table 1 summarizes prior methods proposed for the solution of this problem. These methods are classified according to the single- and multi-objectives, SOF and MOF, frameworks, and the main findings of each application.

Table 1. Reported OPF meta-heuristic algorithms in the literature.

Applied Algorithm	Utilized Cost Function		Main Outcomes
	SOF	MOF
Particle Swarm Optimization (PSO) [7,8]	X	X	Wheeling cost minimization
Gravitational Search Algorithm [9]	X		Less-memory utilized
Tabu Search (TS) [10]	X		Quadratic cost curve with sine components
Biogeography Based Optimizer [11]	X		Consider UPFC devices
Differential Evolution (DE) [12]	X	X	Three-constraint handling techniques
Genetic Algorithms [13,14]	X	X	Prohibited zones, valve-point effect, multi-fuels, and emission.
Teaching Learning Based Optimization (TLBO) [15]	X		Applied for small- and large-scale test systems
Cuckoo Search (CS) [16]	X		Consider the valve loading effect
Harris’ Hawk Optimization Algorithm (HHO) [17,18]	X		Consider renewable energy integration
Artificial Bee Colony (ABC) [19]	X		Fast convergence
Hunger Games Search (HGS) [20]	X		Consider renewable energy integration
Heap Optimization Algorithm (HOA ) [21]	X		Consider renewable energy integration with variable nature of load over 24 h
Salp Swarm Optimizer [22]	X		Voltage stability analysis
Jaya Algorithm [23,24]	X	X	Use the Fuzzy Set Theory for the best compromise solution
Fuzzy-Based Grenade Explosion Method [25]	X	X	Handling multi-objectives effectively
Colliding Bodies Optimization Algorithm [26]	X		Prohibited zones constraints
Search Optimization Algorithm [27]	X	X	Consider emission and non-smooth cost functions using
Electromagnetism-Like Mechanism [28]	X		Applied for small-scale test systems
League Championship Algorithm [29]	X		Consider the valve point effect
Differential Search Algorithm [30]	X		Robust, and a superior solution
Quasi-Oppositional Teaching Learning [31]	X	X	Highly distributed non-dominant Pareto optimal solutions
Multi-Objective Harmony Algorithm [32]	X	X	Best compromise solution extraction using fuzzy membership
Multi-Objective Non-Dominated Sorting Opposition Gravitational Algorithm [33]	X	X	A double-objective function is considered
Modified Shuffle Frog Leaping Algorithm [34]	X	X	Run time proportionally increases as the number of control variables increases
Multi-Objective Bees Algorithm [35]	X	X	Utilize fuel cost, emission, and loss
Hybrid Firefly–Bat Algorithm with Constraints-Prior Object-Fuzzy Sorting Strategy (HFBA-COFS) [36]		X	Triple objective function
Adaptive Parallel Seeker Optimization Algorithm (APSOA) [37]	X		Consider thyristor-controlled series compensators (TCSCs)
Adaptive Group Search Optimization [38]	X	X	Consider the N-1 security index
Sine–Cosine Algorithm [39]	X		Modified algorithm
Multi-Objective Differential-Based Harmony Search Algorithm [40]	X	X	Effective initialization method
Differential Search Algorithm [41]	X	X	Use weighting factor for multi-objective
Fruit Fly Optimization Algorithm (FFOA) [42]	X	X	Use weighting factor for multi-objective
Moth Swarm Algorithm (MSA) [43]	X	X	Use Pareto front for multi-objective
Crow Search Algorithm [44,45]	X	X	Economic and environmental objectives
Sine Cosine Optimizer [46]
Differential Evolution [47,48,49]	X	X	Pareto front for MOF

Among the previous methods, one cannot state which are no-free-lunch theorems for optimization [50]. No optimization algorithm can reach the global optimum for all optimization problems as per the no-free-lunch theorem. Therefore, the authors investigate the capability of (NSWOA) to solve single and multi-objective OPF as a non-linear, complex engineering problem. Because of its simple structure, reduced operator requirement, quick convergence characteristics, and improved balancing capabilities between exploration and exploitation phases, the whale optimization algorithm (WOA) has become a widely adopted swarm intelligence technology in a variety of engineering applications. As per this massive application and due to the importance of the OPF, this motivates the use of WOA for solving such highly nonlinear, constrained optimization problems. Instead of covering a vast space, the NSWOA-OPF investigates the search space through the vicinity of the best compromise solution across successive generations and presents the decision-maker with a set of non-dominated alternatives around this preferred solution.

1.3. Contribution

Consequently, the key achievements of this research might be summarized in the following points:

• This research offers a novel optimization method for dealing with the OPF problem in power systems.
• This technique ensures fast convergence and improves search capability by iteratively exploring the neighborhood of the best compromise solution in successive descents.
• Validation of the suggested approach has been employed for single-objective and multi-objective OPF optimizations.
• From the viewpoint of economic and technical benefits, the proposed multi-objective WOA achieves significant improvement in cost minimization and power loss reduction, along with enhancement of bus voltage profile.
• The robustness is demonstrated through statistical evaluations of the lowest, average, maximum, and standard deviation of the obtained results.

1.4. Paper Organization

This manuscript is structured as follows: Section 2 will describe the mathematical formulation of the OPF cost function, while Section 3 will focus on the whale optimization algorithm (WOA) and NSWOA. Section 4 will demonstrate and discuss the simulation results, and Section 5 will provide a summary of the research.

2. Formulation of the OPF Problem

The OPF aims at optimally identifying the system control variables while satisfying various equality and inequality constraints. This is mathematically stated as follows:

2.1. Problem Objectives

In this study, four objectives’ functions are considered. The first objective aims to minimize the total fuel costs of all generators (F₁) as

$$F_1={\displaystyle \sum }_{i=1}^{N_g}{a}_i{Pg}_i{}^2+b_i{Pg}_i+c_i\mathrm{USD}/\mathrm{hr}$$

(1)

Minimization of the system power losses is considered as the second SOF, F₂ (MW), as

$$F_2={\displaystyle \sum }_{i,j\in N_b}{g}_{ij}\left(V_i^2+V_j^2-2V_i{V}_j{\cos \mathit{\theta }}_{ij}\right)$$

(2)

One of the key indications of system security and service quality is load voltage. The voltage profile is being improved in order to reduce voltage deviation (VD) at the load buses from the specified voltage level in p.u. The following equation is used to mathematically characterize the third objective function (F3)

$$F_3=\mathrm{VD}={\displaystyle \sum }_{i=1}^{N_{\mathrm{Load}}}\left|V_i-V_{\mathrm{ref}}\right|$$

(3)

Voltage stability becomes a critical necessity in practice due to the high stress on power systems. As a result, maximization of the voltage stability index (L-index) is crucial for improving voltage stability in reactive power operation. L-index assigns a scalar value to each load bus based on static power flow statistics. This index is set between zero (no-load case) and one (voltage collapse). L-index for each bus j ($L_j$) has been defined as [40]

$$L_j=\left|1-{{\displaystyle \sum }}_{i=1}^{N_g}{F}_{ji}\frac{V_i}{V_j}\angle \left({\theta }_{\mathrm{ij}}+{\delta }_i-{\delta }_j\right)\right|,$$

(4)

$$F_{ji}=-{\left[Y_{\mathrm{LL}}\right]}^{-1}\left[Y_{\mathrm{LG}}\right]$$

(5)

As a result, the fourth objective function ($F_4$) is to minimize (L-index), which is calculated as

$$F_4=\mathrm{Max}\left(L_j\right)j={1,2,\dots ,N}_b$$

(6)

2.2. Constraints

The defined OPF objectives are solved considering the following equality and inequality operational constraints. The first equality constraints are expressed as

$$Q_g{}_i-Q_L{}_i+Q_C{}_i-V_i{\displaystyle \sum }_{j=1}^{N_b}{V}_j\left(G_{ij}{\sin \mathsf{\theta }}_{ij}-B_{ij}{\cos \mathsf{\theta }}_{ij}\right)=0,i={1,2,\dots ,N}_{PQ}$$

(7)

$$P_g{}_i-P_L{}_i-V_i{\displaystyle \sum }_{j=1}^{N_b}{V}_j\left(G_{ij}{\cos \mathsf{\theta }}_{ij}+B_{ij}{\sin \mathsf{\theta }}_{ij}\right)=0,i=1,2,...N_b-\mathit{slack}$$

(8)

Additionally, the following operational inequality limitations are taken into account:

$$P_{gi}^{\min }\le P_{gi}\le P_{gi}^{\max },i={1,2,\dots ,N}_g$$

(9)

$$V_i^{\min }\le V_i\le V_i^{\max },i={1,2,\dots ,N}_b$$

(10)

$$T_k^{\min }\le T_k\le T_k^{\max },k={1,2,\dots ,N}_t$$

(11)

$$0\le Q_{Ce}\le Q_{Ce}^{\max },e={1,2,\dots ,N}_C$$

(12)

$$Q_{gi}^{\min }\le Q_{gi}\le Q_{gi}^{\max },i={1,2,\dots ,N}_{\mathrm{pv}}$$

(13)

$$\left|S_L^{\mathrm{flow}}\right|\le S_L^{\max },L={1,2,\dots ,N}_L$$

(14)

3. Proposed Solution Methodology

3.1. Whale Optimization Algorithm

The whale optimization algorithm (WOA) is one of the swarm-based intelligent meta-heuristic algorithms proposed [51]. It is proposed for complex continuous optimization problems. Various applications of the WOA in power system engineering include reconfiguration of distribution systems [52], parameter estimation of PV modules [53], load frequency control [54], placement of energy storage systems [55], and microgrid operation [56], etc.

The WOA was inspired by the bubble-net chasing move strategy of humpback whales. Humpback whales typically hunt crustaceans or little fish near the water’s surface. They approach their victim by spinning around them and following a distinctive route inside a shrinking circle and creating bubbles in a circular or ‘9’-shaped path.

The WOA is characterized by ease of implementation, robustness, and fewer control parameters. Three functioning processes are used to measure the time-dependent location of whale individuals, which are mathematically described in the following subsections.

• Shrinking Encircling Prey

Humpback whales initiate hunting prey by first encircling it. This mechanism of encircling can be modeled mathematically by the following equations

$$\overrightarrow{D}=\left|\overrightarrow{C}.\overrightarrow{X^{*}}\left(it\right)-\overrightarrow{X^{ }}\left(it\right)\right|$$

(15)

$$\overrightarrow{X^{ }}\left(it+1\right)=\overrightarrow{X^{*}}\left(it\right)-\overrightarrow{A}.\overrightarrow{D}$$

(16)

$$\overrightarrow{A}=2.\overrightarrow{a}.\overrightarrow{r}-\overrightarrow{a}\dots ,\overrightarrow{a}=2-\frac{it}{Max\_iter}$$

(17)

$$\overrightarrow{C}=2.\overrightarrow{r}$$

(18)

where $\overrightarrow{X^{*}}$ refers the whale leader position that refers to the general best solution, $\overrightarrow{X^{}}$ denotes to the position of the selected search agent, $it$ denotes the recent iteration. $\overrightarrow{A}$ and $\overrightarrow{C}$ are two coefficient vectors. The parameter $a$ is a vector and it is linearly decreased from 2 to 0 over the course of iterations, where $r$ is randomly fitted in the interval [0, 1]. The absolute value is represented by the sign $‘\left|\right|\text{’}$.

• Bubble-Net Attacking Method (Exploitation Phase)

Two approaches are employed for mathematical modeling of the bubble-net behavior of humpback whales as:

(a)

The mechanism of shrinking encircling [57]

This mechanism is attained by reducing the value of a $\overrightarrow{a}$ in Equation (17), which will affect the range of $\overrightarrow{A}$ also. Figure 1 shows for a search agent. Its new position is defined in between the original position of the search agent and the position of the current best agent.

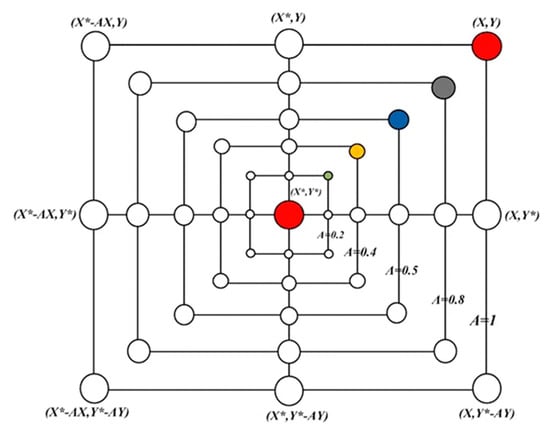
Figure 1. Shrinking encircling mechanism.

(b)

Updating of spiral position

Equation (19) shows the spiral updating equation. To simulate the helix-shaped transition of humpback whales, it will be created between the position of the search agent (whale) and prey. A 50% probability is applied to choose either the shrinking encircling mechanism or the spiral model to update the position of whales that is modeled in Equation (20).

$$\overrightarrow{X^{ }}\left(it+1\right)=\overrightarrow{D^{\prime }}.e^{bl}.\cos \left(2\pi l\right)+\overrightarrow{X^{*}}\left(it\right)\dots ,\overrightarrow{D^{\prime }}=\left|\overrightarrow{X^{*}}\left(it\right)-\overrightarrow{X^{ }}\left(it\right)\right|$$

(19)

$$\overrightarrow{X^{ }}\left(it+1\right)=\{\begin{array}{cc}\overrightarrow{X^{*}}\left(it\right)-\overrightarrow{A}.\overrightarrow{D}& if p<0.5\\ \overrightarrow{D^{\prime }}.e^{bl}.\cos \left(2\pi l\right)+\overrightarrow{X^{*}}\left(it\right)& if p\ge 0.5\end{array}$$

(20)

where $p$ is a random number in the range of [0, 1]. Additionally, $b$ is a constant used to define the logarithmic spiral shape and $l$ is a random value in the range [1, 1].

(c)

Search for prey (exploration phase) [58].

In the exploration phase of WOA, a random candidate solution is selected to lead the other candidate solutions rather than updating their positions according to the position of the best-obtained solution of the current iteration. The vector $\overrightarrow{A}$ is used to force the search agent to move far away from the best-known search agent, as shown in Figure 2. This can be mathematically modeled, as shown in Equations (21) and (22).

$$\overrightarrow{D}=\left|\overrightarrow{C}.\overrightarrow{X_{rand}{}^{ }}-\overrightarrow{X^{ }}\right|$$

(21)

$$\overrightarrow{X^{ }}\left(it+1\right)=\overrightarrow{X_{rand}{}^{ }}-\overrightarrow{A}.\overrightarrow{D}$$

(22)

where, $\overrightarrow{X_{rand}{}^{}}$ is chosen randomly from the current population.

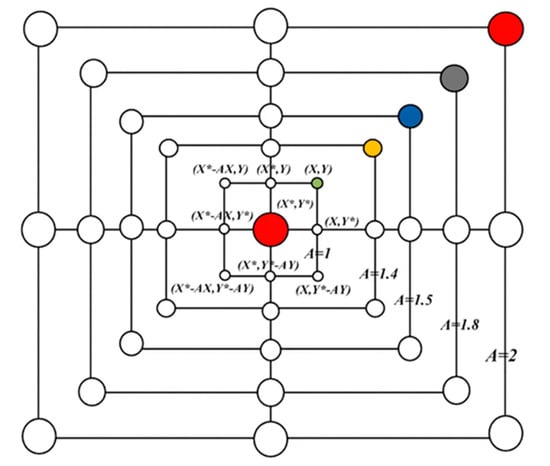
Figure 2. Exploration mechanism in WOA.

The implementation process of the proposed algorithm to solve the OPF problem is illustrated in the flow chart in Figure 3.

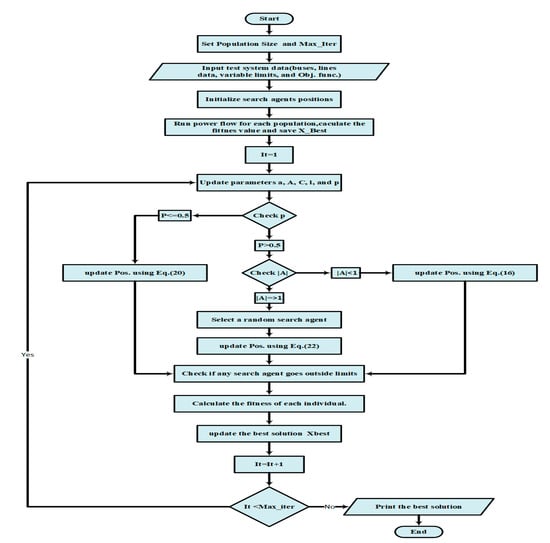
Figure 3. The implementation process of the WOA for the OPF problem.

3.2. Proposed Multi-Objective WOA

Generally, MOF optimization includes more than two objectives that are optimized at the same time. In the proposed multi-objective approach, solutions can be classified into dominant and non-dominant solutions based on the Pareto dominance concept [59]. Based on the following two conditions in Equations (23) and (24), a solution $x_1$ Pareto dominates $x_2$.

$$\forall iϵ\left\{1,2,\dots ,N_{obj}\right\}:F_i\left(x_1\right)\le F_i\left(x_2\right)$$

(23)

$$\exists iϵ\left\{1,2,\dots ,N_{obj}\right\}:F_i\left(x_1\right)<F_i\left(x_2\right)$$

(24)

where $N_{obj}$ is the number of objective functions and $F_i\left(x\right)$ is the cost function value of solution $x$. As a result, within the search space, the non-dominated Pareto optimal solutions are replicated to an outside Pareto set.

The selection of the best compromise solution from the non-dominated solutions set can be determined by several criteria such as the centroid concept, entropy criteria, fuzzy set theory, and the optimal Euclidian distances. The fit compromise solution will be obtained from the non-dominated solutions set using minimal Euclidian distances as

$$D\left(x\right)=\sqrt[ ]{{\displaystyle \sum }_{i=1}^{N_{obj}}\frac{1}{N_{obj}}{\left(\frac{F_i\left(x\right)-F_{i-\min }\left(y_j\right)}{F_{i-min}\left(y_j\right)}\right)}^2}, j=1,2,\dots ,n$$

(25)

4. Simulation Results

The standard IEEE 30-bus test system is employed to check the effectiveness of the proposed algorithm. The single line diagram of the tested system is shown in Figure 4. The generators’ active power limits and cost coefficients are given in Table 2 below. Eight cases are incorporated in this research, as presented in Table 3. SOF and MOF are handled. The SOF cases produce $20,000$ function evaluations.

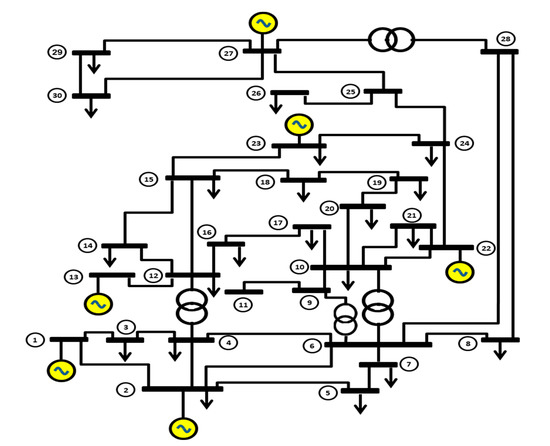
Figure 4. The IEEE-30 bus test system.

Table 2. Generator data of the IEEE-30 bus test system [39].

Bus Number	Active Power Generation (MW)		Generation Cost Coefficients
	Min.	Max.	a	b	c
1	50	200	0.0	2.0	0.00375
2	20	800	0.0	1.75	0.0175
5	15	50	0.0	1.0	0.0625
8	10	35	0.0	3.25	0.00834
11	10	30	0.0	3.0	0.025
13	12	40	0.0	3.0	0.025

Table 3. Summary of various OPF formulations.

OPF Formulation Case		Quadratic Fuel Cost	Active Power Loss	Voltage Deviation	Voltage Stability Index
Mono-objective	Case 1	X
	Case 2		X
	Case 3			X
	Case 4				X
Bi-objective	Case 5	X	X
	Case 6	X		X
	Case 7		X	X
Four-objective	Case 8	X	X	X	X

‘X’ denotes the objective function/s.

4.1. Results for Single-Objective Cases

The proposed algorithm is used to solve the OPF problem considering four SOFs. The obtained results are given in Table 4 and Table 5. In Case 1, the aim is to minimize the quadratic fuel cost as a primary objective function. The proposed WOA reduces the fuel cost to 800.26 USD/h while the active power loss is reduced to 8.82 MW. In Case 2, active power loss minimization is considered the main objective. By using the WOA, the active power loss was reduced to 2.88 MW; however, the fuel cost reaches 967.14 USD/h.

Table 4. Simulation results for a SOF-based OPF.

	Case	Case 1	Case 2	Case 3	Case 4
Cont. Variable
Pg1 (MW)		175.15	51.42	176.02	147.7839
Pg2 (MW)		46.19	80.00	47.17	44.9271
Pg5 (MW)		21.69	50.00	21.66	28.4973
Pg8 (MW)		23.97	35.00	22.17	20.0099
Pg11 (MW)		11.37	30.00	13.84	29.7263
Pg13 (MW)		14.53	40.00	12.13	19.8447
Vg1 (p.u.)		1.06	1.10	1.042	1.0979
Vg2 (p.u.)		1.03	1.10	1.026	1.082
Vg5 (p.u.)		1.01	1.08	1.013	1.0295
Vg8 (p.u.)		1.00	1.09	1.003	1.0484
Vg11 (p.u.)		1.08	1.10	1.065	1.0661
Vg13 (p.u.)		1.00	1.06	0.990	1.0793
Tap6–9		1.05	1.09	1.084	0.9
Tap6–10		0.95	1.01	0.904	1.0973
Tap4–12		0.92	1.08	0.940	0.9033
Tap28–27		0.94	1.04	0.967	0.9
Qc10 (MVAR)		1.92	3.24	4.124	4.9316
Qc12 (MVAR)		2.44	1.10	0.532	3.4673
Qc15 (MVAR)		3.77	4.74	2.991	0
Qc17 (MVAR)		2.93	4.66	1.830	2.6801
Qc20 (MVAR)		1.54	4.43	4.969	3.734
Qc21 (MVAR)		2.09	4.54	4.677	0
Qc23 (MVAR)		5.00	5.00	4.928	0
Qc24 (MVAR)		0.00	4.65	4.952	0
Qc29 (MVAR)		4.68	5.00	2.215	0

Table 5. Fitness functions for Cases 1–4.

	Case	Case 1	Case 2	Case 3	Case 4
Fitness Fun.
Ploss (MW)		8.82	2.88	9.7153	8.4723
VD (p.u.)		0.56	2.00	0.1053	1.0417
L-index		0.14	0.12	0.1371	0.1175
Fuel cost (USD/h)		800.26	967.14	803.3082	814.8988

Case 3 considers the minimization of the voltage deviation as the primary SOF. The voltage profile is enhanced, and the total voltage deviation reaches 0.1781 p.u. while the fuel cost and active power loss are 807.8319 USD/h and 10.964MW, respectively. The last SOF case is Case 4. In this case, the voltage stability index is maximized using the proposed WOA in this case. It reaches 1.0417 and the fuel cost becomes 814.8988 USD/h.

Table 6 shows the effectiveness of the proposed algorithm with previous reported methods. It leads to the best reduction in both economical, fuel costs minimization, and the technical reduction in power losses in Cases 1 and 2, respectively. This is supported by the convergence curves of all utilized performance indices in Figure 5.

Table 6. Comparison of SOF based OPF achieved by various optimization techniques.

Case-1	WOA	CSADHS [60]	MICA–TLA [61]	Case-2	WOA	ABC [62]	EGA–DQLF [13]
	800.26 USD/h	801.59 USD/h	801.05 USD/h		2.88 MW	3.11 MW	3.2 MW
Case-3	WOA	DE [63]	BHBO [64]	Case-4	WOA	ABC [62]	DE [63]
	0.1053 p.u	0.1357	0.1262		0.1175	0.1379	0.1219

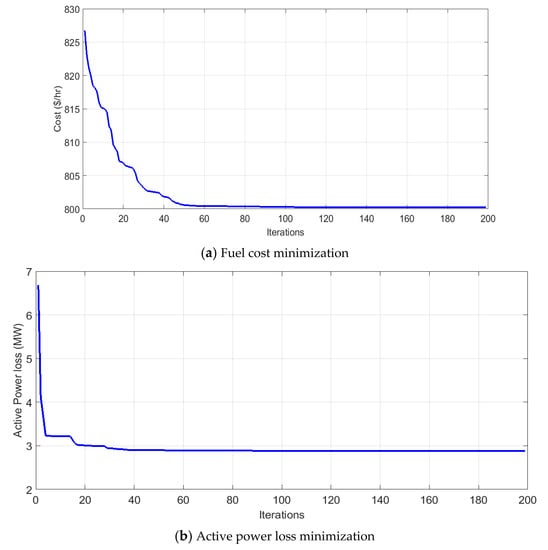
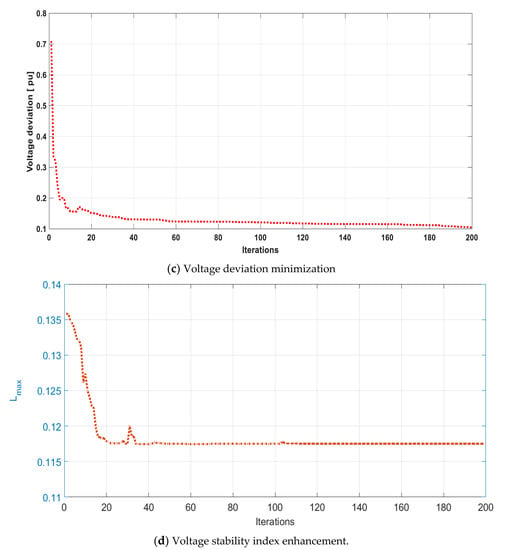
Figure 5. Convergence characteristic curves for the SOF-OPF problem.

4.2. Multi-Objective OPF Simulation Results

Case 5 presents the simultaneous optimization of minimization of fuel costs and power losses. While in Case 6, the reduction in fuel cost and voltage deviation are simultaneously optimized. Minimization of the active power loss and voltage deviation is simulated in Case 7.

Simulation results for Cases 5–7 are presented in Table 7 to show the optimal control variables obtained using the suggested algorithm for bi-objective cases. Figure 6a depicts the Pareto optimum front produced by minimizing fuel costs and losses. The optimum compromise solution is 832.9041796 USD/h and 5.349883577 MW, resulting in a 7.7% reduction in fuel cost and an 11% reduction in loss over the base case. Additionally, the Pareto optimum front produced by minimizing fuel cost and voltage deviation is shown in Figure 6b. The best compromise solution attained from the non-dominated solutions set is 802.5418415 USD/h and 0.173382923 p.u. Finally, Figure 6c shows the Pareto optimum front produced by minimizing the active power loss and voltage deviation. The calculated best compromise solution is 0.578468228 p.u. and 3.14108079 MW.

Table 7. Multi-objective OPF optimizations results.

	Case	Case 5	Case 6	Case 7	Case 8
Cont. Variable
Pg1 (MW)		104.27	177.1531	77.2559	180.45
Pg2 (MW)		55.26	46.2841	78.5356	51.25
Pg5 (MW)		41.20	23.0439	42.8331	17.105
Pg8 (MW)		32.31	20.5680	31.7522	11.065
Pg11 (MW)		27.68	12.4723	20.6790	14.743
Pg13 (MW)		27.16	13.2523	36.5573	19.337
Vg1 (p.u.)		1.10	1.0569	1.0996	1.0663
Vg2 (p.u.)		1.09	1.0351	1.0885	1.0492
Vg5 (p.u.)		1.06	1.0046	1.0630	0.9937
Vg8 (p.u.)		1.07	1.0029	1.0581	1.0299
Vg11 (p.u.)		1.07	1.0185	1.0195	1.1000
Vg13 (p.u.)		1.04	1.0404	1.0282	1.0036
Tap6–9		1.02	0.9906	1.0726	1.0579
Tap6–10		1.05	0.9718	1.0475	1.1000
Tap4–12		1.04	0.9986	1.0165	1.0083
Tap28–27		0.98	0.9617	0.9981	0.9057
Qc10 (MVAR)		1.99	2.6224	4.6249	3.1676
Qc12 (MVAR)		3.43	2.7815	3.6859	5.000
Qc15 (MVAR)		2.29	2.3091	2.5605	4.999
Qc17 (MVAR)		2.60	3.3258	3.1081	4.689
Qc20 (MVAR)		4.03	4.6138	4.0475	5.000
Qc21 (MVAR)		4.70	4.2020	4.1126	5.000
Qc23 (MVAR)		2.30	2.5341	4.7037	4.899
Qc24 (MVAR)		4.23	4.1295	3.1570	2.5508
Qc29 (MVAR)		2.84	2.3603	2.1575	4.2789

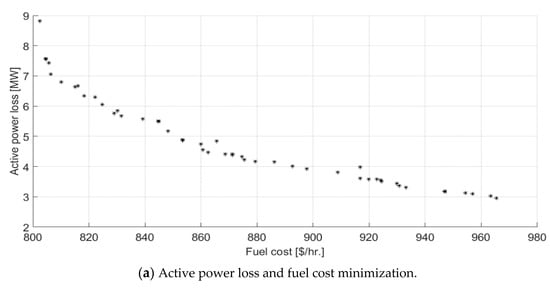
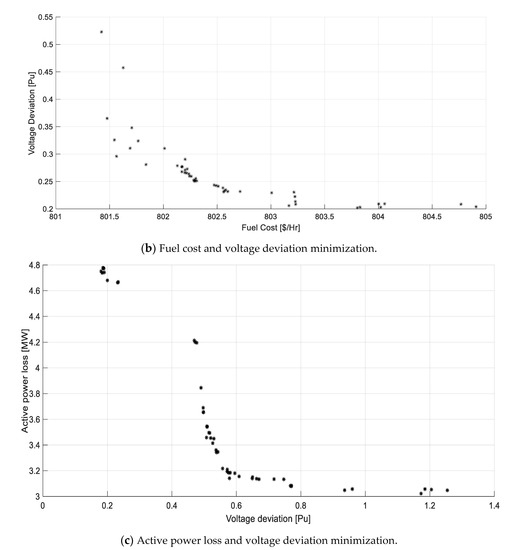
Figure 6. Pareto fronts for bi-objective NSWOA OPF for IEEE-30 bus test system.

In Table 8, the simulation results of the fitness functions are summarized for the multi objective studied cases, Cases 5–8. Table 9 shows the statistical indices for Cases 1–4. As shown, the robustness values of all studied cases are low enough to reflect the robustness of the proposed optimizer. The standard deviation is located in the range 0.000153–0.067411.

Table 8. Simulation results for multi-objective OPF cases.

	Case	Case 5	Case 6	Case 7	Case 8
Fittness
VD (p.u.)		0.88	0.1741	0.4694	0.4985
L-index		0.13	0.1368	0.1328	0.1253
Fuel cost (USD/h)		862.53	802.5395	907.1819	805.0121
Ploss (MW)		4.47	9.4857	4.2134	9.199

Table 9. Statistical indices for the studied cases.

Case No.	Min	Max	Standard Deviation	Average
Case 1	800.26	800.47	0.067411	800.3034
Case 2	2.88	2.889821	0.003713	2.88473
Case 3	0.1053	0.106769	0.000527	0.105965
Case 4	0.1175	0.117975	0.000153	0.117753

In Case 8, the quadratic fuel costs, active power losses, voltage deviation, and voltage stability indices are optimized simultaneously with equal priorities. From Table 10, it can be concluded that the total generation costs are lowered to 805.0121 USD/h with reduction of 10.71%. The total power loss of the transmission lines is increased from 5.05 MW to 9.199 MW, and the voltage variation is reduced to roughly 44%. Furthermore, the voltage stability index is enhanced to reach 0.1253. Moreover, comparative results of NSWOA with recent optimization algorithms are presented in Table 10.

Table 10. Comparison of multi-objective OPF obtained by different optimization algorithms (Case 8).

	Algorithm	PSO	SSA	SCA	CSA	MPA	NSWOA
Fitness Fun.
VD (p.u.)		0.4905	0.4880	0.5280	0.4186	0.5791	0.4985
L-index		0.1212	0.1229	0.1291	0.1256	0.1193	0.1253
Fuel cost (USD/h)		803.4415	803.0555	814.198	804.457	802.8512	805.0121
Ploss(MW)		9.5773	9.9199	9.9970	9.6696	9.2256	9.1620

This demonstrates the suggested algorithm’s advantage in presenting a wide range of output results. These findings are significant from the standpoint of the decision-maker with significant techno-economic benefits. From the previous simulation results, seven cases studied are provided in this study to prove the capability of the proposed non-dominated whale optimization algorithm. These cases reflect various requirements from the viewpoint of the power system operator.

5. Conclusions

This study solves the OPF problem by using a multi-objective NSWOA. The suggested method does not strive to identify the whole set of Pareto optimal solutions, but rather concentrates on only preferred sections of the Pareto set. This can be attained by focusing the search space all over the best compromise option. Moreover, it provides the decision-maker with a collection of Pareto solutions around this chosen one. The obtained findings validated the capabilities of the proposed NSWOA in handling the OPF problem with the optimal compromise for a techno-economic solution. As a result, the authors were self-motivated to extend the NSWOA solution methodology to other power system challenges, such as estimating parameters for smart grid components. Significant improvement in terms of economics were attained, as fuel costs reached 800.12 USD/h; and power losses were reduced by half, reflecting technological gains for power systems. As a result, when compared to other methods in the literature, the suggested method achieves techno-economic gains for power system operations. The simulation results reflect the high robustness of the proposed optimizer with acceptable rates of standard deviations.

The future of this work can be extended to cover many objectives that will be optimized simultaneously. Additionally, the penetration of renewable energies can be considered as a recent trend in OPF problems.