A Wind Power Probabilistic Model Using the Reflection Method and Multi-Kernel Function Kernel Density Estimation

Abstract

This paper proposes a wind power probabilistic model (WPPM) using the reflection method and multi-kernel function kernel density estimation (KDE). With the increasing penetration of renewable energy sources (RESs) into power systems, several probabilistic approaches have been introduced to assess the impact of RESs on the power system. A probabilistic approach requires a wind power scenario (WPS), and the WPS is generated from the WPPM. Previously, WPPM was generated using a parametric density estimation, and it had limitations in reflecting the characteristics of wind power data (WPD) due to a boundary bias problem. The paper proposes a WPPM generated using the KDE, which is a non-parametric method. Additionally, the paper proposes a reflection method correcting for the boundary bias problem caused by the double-bounded characteristic of the WPD and the multi-kernel function KDE minimizing the effect of tied values. Six bandwidth selectors are used to calculate the bandwidth for the KDE, and one is selected by analyzing the correlation between the normalized WPD and the calculated bandwidth. The results were validated by generating WPPMs with WPDs in six regions of the Republic of Korea, and it was confirmed that the accuracy and goodness-of-fit are improved when the proposed method is used.

1. Introduction

Changes in global energy policy have increased the penetration of renewable energy sources (RESs) in power systems. The intermittence and variability of RESs increase uncertainty into power systems. The characteristics of RESs have led to the use of probabilistic approaches to economic dispatch [1], power flow [2], stability evaluation [3], unit commitment [4], optimization problems [5,6,7], and forecasting [8,9,10].

The probabilistic approach requires scenario generation (SG), and the SG method has been proposed in previous studies [11]. SG methods include sampling-based methods [12], prediction-based methods [13,14], and optimization-based methods. Sampling-based methods include the Monte Carlo method and the Latin hypercube method. It is recommended to use different sampling methods according to the given information [15]. The sampling-based method has the advantage of being fast and simple because SG is possible directly from a wind power probabilistic model (WPPM). The prediction-based methods are influenced by historical data and can capture the variability and complex nonlinearity of RESs. The optimization-based method has high scenario approximation accuracy because it captures the characteristics of the RESs well, but it is not suitable for application to large-scale power systems due to the non-deterministic polynomial time problem.

For SG with time series characteristics, using a prediction-based or optimization-based method is a way to reduce uncertainty. Alternatively, scenarios can be hypothesized from models created with wind speed and climate data from surrounding areas [16]. Both methods are realistic for small-scale power systems and have high accuracy. However, both methods require a lot of data and calculations in large-scale power systems. In probabilistic approaches where scenarios with time-series characteristics are not required, it is efficient to use the sampling-based method.

There are two sampling-based methods for the SG. The first is to convert the wind speed scenario generated from the wind speed probabilistic model into a wind power scenario (WPS) using a power curve [17,18], and the second directly generates WPPM from measured wind power data (WPD) and then creates the WPS from the WPPM [19,20]. The first method requires correction because the wind speed distribution and output curve are different depending on the region and climate, even for the same wind power generator [21]. The WPS for use in large-scale power systems requires data from many regions and power curve corrections [22,23], and power curves can be subject to uncertainty [24]. The second method generates WPPM directly from WPD, therefore it requires less calculation and fewer data than the previous method.

A lot of research has been performed to estimate wind speed probabilistic models through parametric [25,26] and non-parametric [27,28] density estimation. It is also used to generate WPPM from WPD. Weibull distribution is one of the parametric distributions and is often used to estimate the distribution of WPD [12]. A representative non-parametric density estimation is kernel density estimation (KDE). For the KDE, it is necessary to calculate a bandwidth suitable for the characteristics of the data. There are various bandwidth selectors to calculate the optimal bandwidth. However, studies directly estimating WPPM from WPD using the KDE are insufficient, and studies on bandwidth selectors suitable for WPD are also insufficient.

WPD has a double-bounded characteristic [29]. The parameter distribution leaks density beyond the second boundary, and KDE leaks density because there is a boundary bias problem. Hong [30] used the delta function to model the double-bounded characteristic in parametric density estimation.

In this paper, WPPM using the reflection method and multiple-kernel-function KDE is proposed. To generate WPPM directly from WPD using the KDE, the optimal bandwidth is required. The first step is to choose the most suitable bandwidth selector by calculating the bandwidth using various bandwidth selectors and analyzing the correlation between the calculated bandwidth and WPD. In the second step, the boundary bias problem due to the double-bounded characteristic of the WPD is corrected using the reflection method and the effect of tied values is minimized using the multi-kernel function.

The main objectives of this study are the following:

(1)

Generate the WPPM directly in WPD by using KDE with the reflection method and multi-kernel function;

(2)

Choose the appropriate bandwidth selector for WPD among six bandwidth selectors by analyzing the correlation between WPD and bandwidth;

(3)

Apply the proposed method for generating WPPM from WPD in six regions in the Republic of Korea. To validate the proposed WPPM, the accuracy and goodness-of-fit are compared with several known methods.

The remainder of this paper is organized as follows. Section 2 analyzes the characteristics of WPD. Section 3 describes Weibull, KDE, and six bandwidth selectors and calculates the optimal bandwidth for WPD. Section 4 proposes the KDE method to overcome the boundary bias problem and tied values of WPD. Section 5 evaluates the accuracy and goodness-of-fit of the proposed WPPM. Section 6 provides concluding remarks and future research directions.

2. Wind Power Data and Analysis

2.1. Wind Power Data

In this paper, data measured from six regions in the Republic of Korea are used and named WPD. The data can be found in the “Public Data Portal” system [31]. The period of all data is one year, the time interval is 1 h, and the unit is kW. If the data are negative, they are corrected to 0. Regions and installed capacity are listed in Table 1, and histograms of WPD for the six regions are shown in Figure 1.

Table 1. Information of six sites: region, installed capacity, and type.

Regions	Installed Capacity	Type
Jeonnam Yeongwang 1 (YG1)	2300 kW	Generator
Jeonnam Yeongwang 2 (YG2)	3000 kW	Generator
Gyeongbuk Gunwi (GW)	11,550 kW	Plant
Incheon Yeongheung (YH)	46,000 kW	Plant
Jeju Seongsan (SS)	20,000 kW	Plant
Jeonnam Hwasun (HS)	16,000 kW	Plant

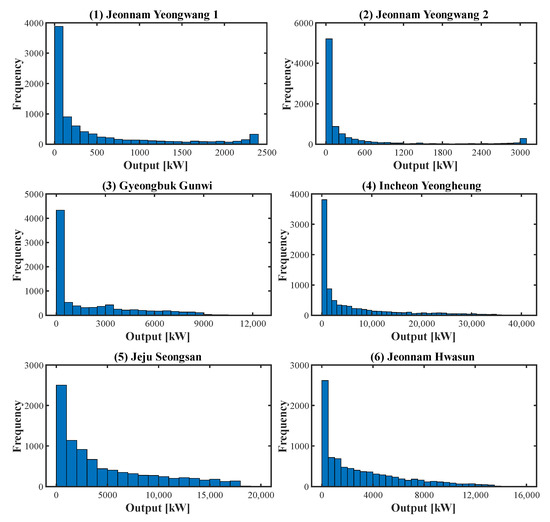
Figure 1. Histogram of WPD for the six regions.

Figure 2 shows the locations where six WPDs were measured on a map of the Republic of Korea. It is shown that the six regions are evenly distributed in the map. Additionally, the WPD measured on Jeju Island is included. By using WPDs from different regions, various WPPMs will be applied and compared.

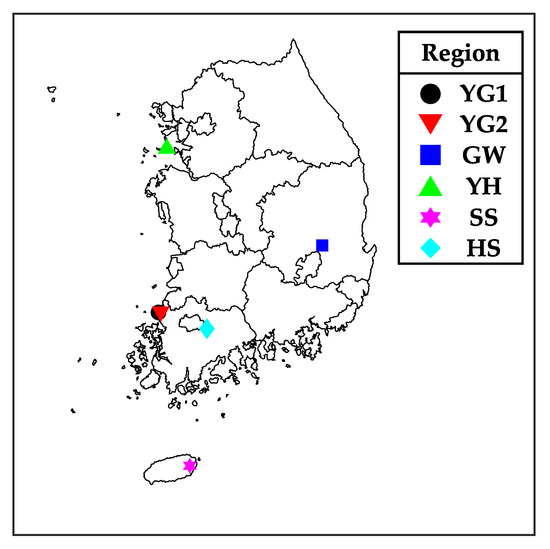
Figure 2. Locations where six WPDs were measured.

2.2. Double-Bounded Characteristics of WPD

WPD has double-bounded characteristics [29]. A boundary exists both when the output is 0 and the output is at installed capacity (i.e., maximum output). The data range is 0 < x < maximum output, and the total probability within the data range must be 1. Figure 3 shows the double-bounded characteristic of the WPD. The first bound means that the wind power generation cannot be negative, and the second bound means that the wind power generation cannot exceed the installed capacity.

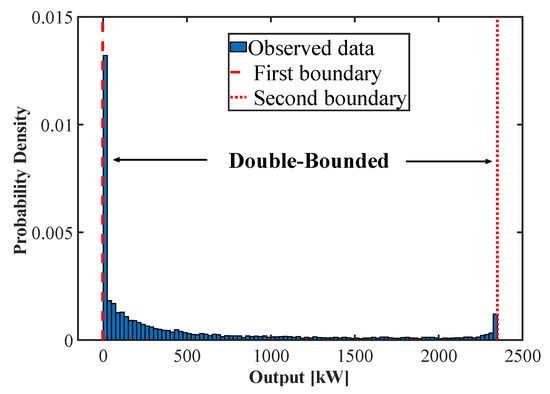
Figure 3. Double-bounded characteristics of the WPD.

2.3. Tied Values at Zero Output

Tied values occur when two are more observations are equal, whether the observations occur in the same sample or in different samples. There are cases where a wind turbine does not produce electricity, and it was recorded as 0 in the data. So in general, WPD has many tied values, but only for values with zero output. Tied values cause leakage density. In order to improve the accuracy of WPPM, the problem of leakage density due to tied values must be addressed.

3. Wind Power Probabilistic Model (WPPM)

A WPPM is generated through a density estimation. The density estimation is to construct an estimate from the observed data, and there are parametric and non-parametric methods. The parametric method estimates parameters by assuming a known probability distribution in order to estimate density. The non-parametric method assumes no pre-specified probability distribution. Histograms and KDEs are representative non-parametric methods.

3.1. Weibull Distribution

The Weibull distribution, which is commonly used for estimating the parametric density emstimation of WPD, is used [12]. The probability density function (PDF) and cumulative distribution function (CDF) of the Weibull distribution are Equations (1) and (2), respectively.

$$f\left(x\right)=\frac{k}{\lambda }{\left(\frac{x}{\lambda }\right)}^{k-1}{e}^{-{\left(\frac{x}{\lambda }\right)}^k}$$

(1)

$$F\left(x\right)=1-e^{-{\left(\frac{x}{\lambda }\right)}^k}$$

(2)

where k is the shape factor of Weibull distribution and $\lambda$ is the scale factor of Weibull distribution.

Table 2 lists the parameters of the Weibull distribution estimated in the six regions [32]. A parametric distribution such as the Weibull distribution cannot model the double-bounded characteristic of WPD. Figure 4 shows the PDF and empirical CDF (ECDF) of WPD and WPPM generated from Weibull distribution (WPPM-Weibull) in YG1. Probability must exist only within the double bounds of the WPD. However, in the Weibull distribution, the probability leaks beyond the second boundary, as shown in Figure 4b, so that total probability is less than 1 within the data range.

Table 2. Parameters of the Weibull distribution estimated for the six regions.

Region	Parameter
	Scale	Shape
YG1	181.963	0.365
YG2	69.366	0.304
GW	866.286	0.372
YH	2490.728	0.388
SS	3409.666	0.549
HS	2072.767	0.510

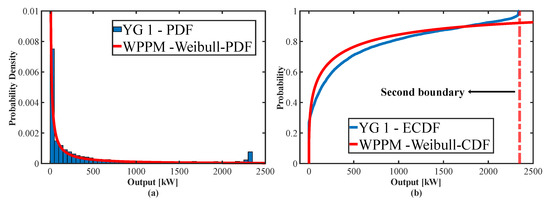
Figure 4. WPD and WPPM-Weibull in YG1. (a) Comparison of YG1-PDF and WPPM-Weibull-PDF. (b) Comparison of YG1–ECDF and WPPM-Weibull-CDF.

3.2. Kernel Density Estimation

KDE is a non-parametric method that estimates PDF directly from observed data. An estimate $\hat{f}$ of the unknown true density $f$ is constructed from the observed data. The procedure by which the observed data is reconstructed through KDE is described in Figure 5. The equation is as follows [33]:

$$\hat{f}\left(x\right)=\frac{1}{nh}{\displaystyle \sum }_{i=1}^{n}K\left(\frac{x-X_i}{h}\right)$$

(3)

where $X_i$ is observed data, n is the number of observed data, h is the bandwidth of the scaling factor that determines the spread of the kernel function. K(u) is a kernel function with $\int K=1$. The Gaussian kernel function and the Dirac delta kernel function are Equations (4) and (5), respectively.

$$K\left(u\right)=\frac{1}{\sqrt{2\pi }}{e}^{-\frac{1}{2}{u}^2}$$

(4)

$$K\left(u\right)=\delta \left(u\right)$$

(5)

where representative kernel functions include Gaussian, box, triangle, and Epanechnikov. In this paper, the Gaussian kernel function and Dirac delta function are used.

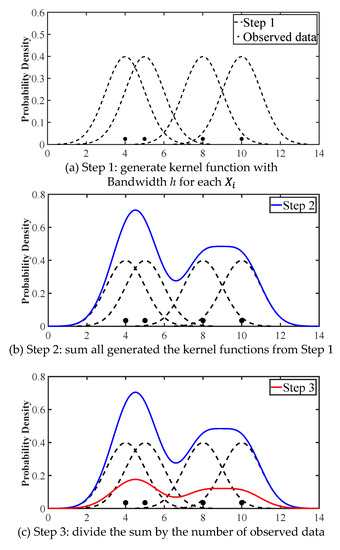
Figure 5. The procedure to obtain probability density through KDE.

3.2.1. Bandwidth Selection

Bandwidth selection is an important issue in KDE. If the bandwidth is selected too small, the fine structure of the data is visible, and if the bandwidth is too large, the overall characteristics of the distribution are blurred [33]. Depending on the bandwidth, PDF with different shapes for the same data may be estimated. The variation of PDF according to the bandwidth is shown in Figure 6, and it confirm that the bandwidth is an important factor in determining the shape of the PDF. The bandwidth selector calculates the optimal bandwidth for data, and there are various bandwidth selectors.

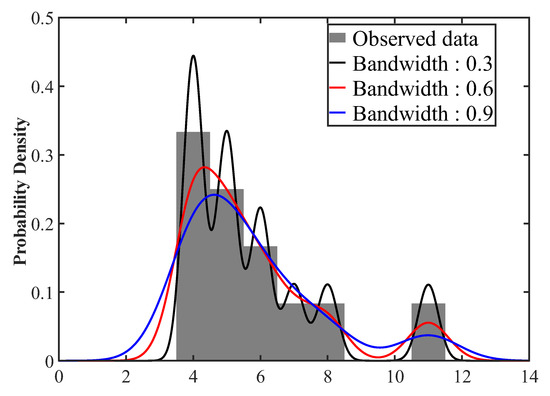
Figure 6. Variation of PDFs according to the bandwidth.

The mean integrated square error (MISE) is used as a method to evaluate the KDE model and expressed as a bias term and variance term. The equation is as follows [34]:

$$MISE\left(\hat{f}\right)=\int bia{s}^2+\int var$$

(6)

where the bias term is described in Equation (7) and the variance term is described in Equation (8).

$$\int bia{s}^2=\frac{1}{4}{h}^4{\mu }_2{\left(K\right)}^{2}R\left(f"\left(x\right)\right)+o\left(h^4\right)$$

(7)

$$\int var=\frac{R\left(K\left(t\right)\right)f\left(x\right)}{nh}+o(\frac{1}{nh})$$

(8)

where ${\mu }_2\left(K\right)=\int z^{2}K\left(z\right)dz$, $R\left(K\right)=\int K{\left(z\right)}^{2}dz$. MISE is expressed as Equation (9).

$$MISE\left(\hat{f}\right)=AMISE\left(\hat{f}\right)+o(\frac{1}{nh}+h^4)$$

(9)

According to the Taylor higher order term in Equation (9), when the bandwidth increases, the bias increases, and when the bandwidth decreases, the variance increases. This is called bias–variance tradeoff, and it means that the error is minimized when the optimal bandwidth is selected rather than when it is too small or too large. The first term on the right side of Equation (9) is called asymptotic MISE (AMISE), and finding the optimal bandwidth means finding the bandwidth that minimizes AMISE, which is expressed as [34]:

$$AMISE\left(\hat{f}\right)=\frac{1}{4}{h}^4{\mu }_2{\left(K\right)}^{2}R\left(f"\left(x\right)\right)+\frac{R\left(K\left(t\right)\right)}{nh}$$

(10)

$$h_{AMISE}=argmin AMISE\left(\hat{f}\right)={\left[\frac{R\left(K\right)}{{\mu }_2{\left(K\right)}^{2}R\left(f"\right)n}\right]}^{0.2}$$

(11)

However, the optimal bandwidth cannot be obtained directly through Equation (11), because R($f"$) calculated from real density cannot be known. Assuming R($f"$) as an arbitrary distribution, Equation (11) can be used to calculate the optimal bandwidth.

3.2.2. Rule of Thumb (ROT)

The ROT bandwidth selector can be calculated by assuming that f in R($f"$) is a normal distribution with standard deviation σ. The optimal bandwidth $h_{ROT}$ is [33]:

$$h_{ROT}={\left[\frac{8{\pi }^{0.5}R\left(K\right)}{3{\mu }_2{\left(K\right)}^{2}n}\right]}^{0.2}\hat{\sigma }$$

(12)

$${\hat{\sigma }}_{IQR}=\frac{Sample IQR}{{\mathsf{\Phi }}^{-1}\left(0.75\right)-{\mathsf{\Phi }}^{-1}\left(0.25\right)}$$

(13)

where ${\mu }_2\left(K\right)$ = 1, $R\left(K\right)=\frac{1}{2\sqrt{\pi }}$, Φ is the inverse cumulative distribution of the normal distribution. It is expressed as:

$$h_{ROT}=1.06n^{-0.2}\hat{\sigma }$$

(14)

where σ is the standard deviation of observation data or ${\hat{\sigma }}_{IQR}$, and n is the number of observed data.

3.2.3. Direct Plug-In (DPI)

The DPI selector can be calculated by substituting ${\Psi }_4$ for the unknown value R($f"$) in Equation (11). $h_{DPI}$ can be calculated by replacing ${\Psi }_4$ with ${\hat{\Psi }}_4\left(g\right)$, and ${\hat{\Psi }}_4\left(g\right)$ can be replaced with ${\hat{\Psi }}_r\left(g\right)$. The equation is as follows [33]:

$$h_{DPI}={\left[\frac{R\left(k\right)}{{\mu }_2{\left(K\right)}^2{\hat{\Psi }}_4\left(g\right)n}\right]}^{0.2}$$

(15)

$${\hat{\Psi }}_r\left(g\right)=\frac{1}{n^2}{\displaystyle \sum }_{i=1}^n{\hat{f}}^{\left(r\right)}\left(X_i;g\right)$$

(16)

where ${\hat{f}}^{\left(r\right)}\left(X_i;g\right)$ is the r-order derivative having the bandwidth $g$ and the kernel function L, and the optimal bandwidth $g$ of this equation is as follows:

$$g_{AMSE}={\left[\frac{-k!K^{\left(r\right)}\left(0\right)}{{\mu }_k\left(L\right){\Psi }_{r+k}n}\right]}^{\frac{1}{r+k+1}}$$

(17)

Calculating ${\hat{\Psi }}_4\left(g\right)$ requires ${\hat{\Psi }}_6\left(g\right)$, and calculating ${\hat{\Psi }}_6\left(g\right)$ requires ${\hat{\Psi }}_8\left(g\right)$. It is calculated assuming ${\hat{\Psi }}_8\left(g\right)$ is a normal distribution, and the equation is as follows:

$${\psi }_r=\frac{{\left(-1\right)}^{\frac{r}{2}} r!}{{\left(2\sigma \right)}^{r+1} \left(\frac{r}{2}\right)!\sqrt{\pi }}$$

(18)

where r is r-order derivative, and $\hat{\sigma }$ calculated as Equation (13). As a result, ${\hat{\psi }}_8^{NS}=\frac{105}{32\sqrt{\pi }{\widehat{\sigma }}^9}$ is calculated.

3.2.4. Sheather–Jones (SJ)

The equation to find the optimal bandwidth of the SJ bandwidth selector is as follows [34]:

$$h_{SJ}={\left[\frac{R\left(k\right)}{{\mu }_2{\left(K\right)}^2{\hat{\Psi }}_4\left(\gamma \left(h\right)\right)n}\right]}^{\frac{1}{5}}$$

(19)

where $\gamma \left(h\right)$ is:

$$\gamma \left(h\right)={\left[\frac{2L^{\left(4\right)}\left(0\right){\mu }_2{\left(K\right)}^2{\hat{\Psi }}_4\left(g_1\right)}{{\hat{\Psi }}_6\left(g_2\right)R\left(k\right){\mu }_2\left(L\right)}\right]}^{\frac{1}{5}} h^{\frac{5}{7}}$$

(20)

where $g_1$ and $g_2$ can be obtained using Equation (17), ${\hat{\Psi }}_4\left(g_1\right)$ and ${\hat{\Psi }}_6\left(g_2\right)$ required to calculate ${\hat{\Psi }}_6$, and ${\hat{\Psi }}_8$ is calculated from Equation (18).

3.2.5. Smooth Cross Validation (SCV)

The rate of convergence increases under a wide range of smoothness conditions. SCV has the advantage of increasing the rate of convergence by presmoothing the data. An integrated bias square (IBS) can be obtained by modifying Equation (7), and the value that minimizes SCV(h) is the optimal bandwidth. The equation is as follows [35]:

$$\mathrm{SCV}\left(h\right)=\frac{R\left(K\right)}{nh}+\widehat{IBS}\left(h\right)$$

(21)

$$\widehat{IBS}\left(h\right)= \int {\left\{K_h\ast {\hat{f}}_L-{\hat{f}}_L\right\}}^2\left(x\right)dx$$

(22)

where ${\hat{f}}_L$ is an estimate having a kernel function L and a bandwidth g, and the equation is as follows:

$${\hat{f}}_L=\frac{1}{n}{\displaystyle \sum }_{i=1}^n{L}_g\left(x-X_i\right)$$

(23)

3.2.6. Least Square Cross Validation and Biased Cross Validation

Least square cross validation (LSCV) (also called unbiased cross validation (UCV) and biased cross validation (BCV)) bandwidth selectors are widely used bandwidth selectors for calculating the optimal bandwidth. LSCV and BCV are numerically analyzed to calculate the optimal bandwidth, and there are several local minimums in this process. To solve this problem, the optimal bandwidth is calculated through the bandwidth grid. However, there is a limitation on the cross-validation method when tied values exist [36].

3.2.7. Optimal Bandwidth of WPD

The optimal bandwidth was calculated using six bandwidth selectors for two data sets. Dataset (1) is the original WPD from the six regions and dataset (2) is the WPD normalized to 1 MW. The reason for calculating the optimal bandwidth of the normalized WPD is to analyze the correlation between WPD and optimal bandwidth. Table 3 shows the bandwidth calculated from dataset (1), the bandwidth calculated from dataset (2), and the ratio of (1) to (2), respectively. The ratio of bandwidth calculated for WPD and normalized WPD equals the size of the installed capacity. This means that the bandwidth calculated by the bandwidth selector has a linear relationship with the installed capacity of the wind power plant. Even if the installed capacity changes due to the expansion or contraction of a wind farm, or the size of the WPD for simulation changes, the bandwidth size only needs to be linearly changed without recalculating the optimal bandwidth.

Table 3. Bandwidth calculated using six bandwidth selectors for six regions.

Region	Dataset	Bandwidth Selector
		ROT	DPI	SJ	LSCV	BCV	SCV
YG1	(1)	83.19	13.16	2.18	X	X	15.93
	(2)	36.17	5.72	0.95	X	X	6.93
	Ratio	2.3	2.3	2.3	X	X	2.3
YG2	(1)	38.06	5.05	0.60	X	X	14.05
	(2)	12.69	1.68	0.20	X	X	4.68
	Ratio	3	3	3	X	X	3
GW	(1)	420.18	62.14	13.83	X	121.52	58.19
	(2)	36.38	5.38	1.20	X	X	5.04
	Ratio	11.55	11.55	11.55	X	X	11.55
YH	(1)	1009.30	160.93	39.86	X	X	189.11
	(2)	21.94	3.50	0.87	X	X	4.11
	Ratio	46	46	46	X	X	46
SS	(1)	840.49	199.20	66.16	X	X	185.76
	(2)	42.02	9.96	3.31	X	252.69	9.29
	Ratio	20	20	20	X	X	20
HS	(1)	570.23	119.22	34.20	X	X	109.10
	(2)	35.64	7.45	2.14	X	116.60	6.82
	Ratio	16	16	16	X	X	16

LSCV and BCV bandwidth selectors are calculated with a bandwidth grid ranging from 0.001–500. The cases where the proper bandwidth in the range was not found are marked with an X. Although the proper bandwidth was found in some cases, it was not found in most. This confirms that the LSCV and BCV bandwidth selectors cannot reliably calculate the optimal bandwidth for WPD.

Figure 7 shows the bandwidth values calculated from the normalized WPD of the six regions. Four bandwidth selectors, ROT, DPI, SJ, and SCV, calculate bandwidths within a certain range regardless of the characteristics of various normalized WPDs. Additionally, the normalization factor for WPD and the optimal bandwidth have a linear relationship.

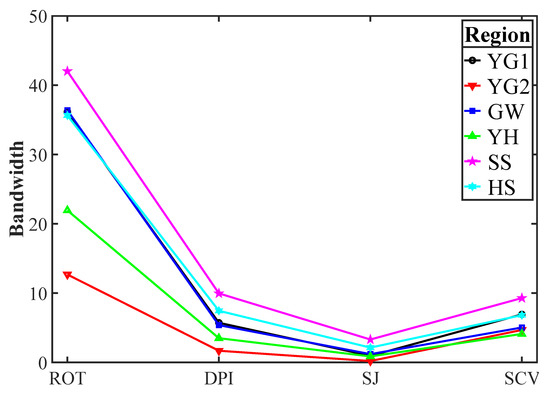
Figure 7. Bandwidths calculated from the normalized WPD of six regions.

4. Proposed Method

4.1. Correction of the Boundary Bias Problem through the Reflection Method

The double-bounded characteristic of WPD cannot be modeled with a parametric distribution, and the boundary bias problem exists in KDE. The boundary bias problem occurs when data exist near the boundary and density leaks over the boundary during the KDE process. A method of solving the boundary bias is called a boundary correction method, of which there are various. The boundary correction method proposed in this paper is a reflection method [33]. The reflection method has the advantage of being simple: it can be used without complicated calculations and assumptions. Figure 8 shows a WPPM generated using KDE (WPPM-KDE) and a WPPM generated via KDE using the reflection method (WPPM-KDE-Reflection). The boundary bias problem is effectively corrected with the reflection method. The equation is as follows [33]:

$$\hat{f}\left(x\right)=\frac{1}{nh}{\displaystyle \sum }_{i=1}^n\left[K\left(\frac{x+X_i}{h}\right)+K\left(\frac{x-X_i}{h}\right)\right]$$

(24)

where $X_i$ is observed data, K is the kernel function with $\int K=1$, h is bandwidth.

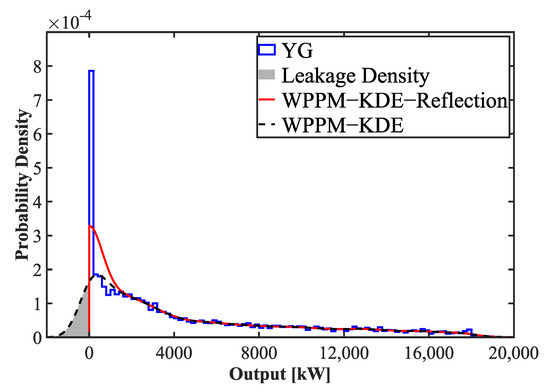
Figure 8. WPPM-KDE and WPPM-KDE-Reflection in YH.

4.2. Minimization of the Effect of Tied Values through the Multi-Kernel Functions

The bandwidth calculated using the bandwidth selector is dependent on the installed capacity, but tied values exist only when the output is 0, regardless of installed capacity. This means that the tied values cause leak density. Unlike the boundary bias that arises from boundaries, this is leakage density caused by too many values connected to a single point. Suga [37] solves this problem with multiple bandwidths. Otherwise, the paper uses the KDE with multi-kernel function to solve this problem. In particular, the Dirac delta function is used as the kernel function to minimize the leakage density in the range with many tied values. The Gaussian function is used in the remaining range. Figure 9 shows WPPM-KDE-Reflection and WPPM-KDE-Reflection using the multi-kernel method (WPPM-PM). The expression of the multi-kernel function method is as follows:

$$K\left(u\right)=\left\{\begin{array}{c} \delta \left(u\right) X_i=0\\ \frac{1}{\sqrt{2\pi }}{e}^{-\frac{1}{2}{u}^2} X_i\ne 0\end{array}\right.$$

(25)

where if $X_i$ is 0, the delta function is used, otherwise the Gaussian kernel function is used.

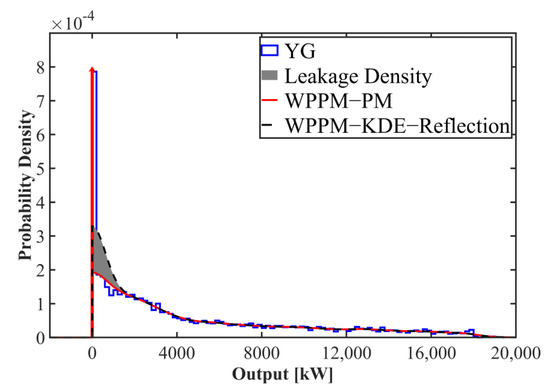
Figure 9. WPPM-KDE-Reflection and WPPM-PM in YH.

4.3. Proposed Model

The proposed WPPM (WPPM-PM) is based on the reflection method and multi-kernel function KDE. The WPPM-PM corrects the boundary bias problem with the reflection method. The influence of tied values can be minimized by using the Dirac delta function. A flowchart of the proposed method is shown in Figure 10.

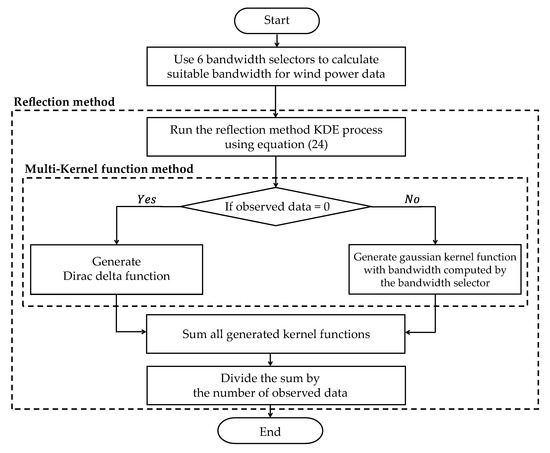
Figure 10. The flowchart of the proposed method.

5. Results and Evaluation

5.1. Evaluation Methods

5.1.1. Mean Absolute Error

MAE is calculated as the average of the absolute errors of the model. The closer the result is to 0, the higher the accuracy. MAE can intuitively identify errors between the model and the WPD. The equation is as follows [38]:

$$MAE=\frac{1}{n}{\displaystyle \sum }_{i=1}^n\left|{\hat{Y}}_i-Y_i\right|$$

(26)

where n is the number of intervals, ${\hat{Y}}_i$ is the i-th value of the generated model, and $Y_i$ is the i-th observation of the WPD.

5.1.2. Root Mean Square Error

RMSE is the square root of the mean of the squared errors of the model and WPD. Compared to MAE, the larger the error, the larger the penalty, and the smaller the error, the smaller the penalty. The equation is as follows [38]:

$$RMSE=\sqrt{\frac{1}{n}{\displaystyle \sum }_{i=1}^n{\left({\hat{Y}}_i-Y_i\right)}^2}$$

(27)

where n is the number of intervals, ${\hat{Y}}_i$ is the i-th value of the generated model, and $Y_i$ is the i-th observation of the WPD.

5.1.3. Kolmogorov–Smirnov Test (K-S Test)

The K-S test is a non-parametric test method. Through the two-sample K-S test, we can test whether the two sets of samples to be compared are drawn from the same probability distribution. If the p-value is greater than 0.05 after comparing the ECDF of two samples, the null hypothesis cannot be rejected, and the two samples are considered to come from the same distribution. The equation is as follows [39]:

$$D=\sup \left|F_1-F_2\right|$$

(28)

where $F_1$ and $F_2$ are the ECDF of the first and second samples, respectively. It is decided whether to reject the null hypothesis by calculating the KS statistic of the two ECDFs.

5.2. Comparison and Results

The results are validated by comparing the WPPM-PM, the WPPM-Weibull, and the WPPM-KDE. When generating the WPPM-PM and WPPM-KDE, the bandwidth is calculated using four bandwidth selectors: ROT, DPI, SJ, and SCV. Accuracy as according to MAE and RMSE is calculated using the ECDF of the WPD and the CDF of WPPM. The K-S test compares the WPD to the WPS generated by WPPM to test the goodness-of-fit.

Table 4 and Table 5 list the MAE and RMSE values. In Table 4 and Table 5, the errors of WPPM-PM and WPPM-KDE are improved compared to WPPM-Weibull, and the average error also confirms this. Compared to WPPM-KDE, the accuracy of WPPM-PM improved by 50% on average for all models, and the results are shown in Table 6. Four bandwidth selectors were applied to propose the best WPPM-PM. The WPPM-PM-SJ shows the highest accuracy in all regions.

Table 4. Results of MAE.

$\mathbf{MAE} ({10}^{-4})$
Region	WPPM-KDE				WPPM-PM				WPPM-Weibull
	ROT	DPI	SJ	SCV	ROT	DPI	SJ	SCV
YG1	111.227	16.172	3.785	19.373	35.461	4.188	1.819	4.864	350.132
YG2	49.428	7.837	2.935	18.286	11.317	1.995	1.154	3.678	16.434
GW	106.926	12.851	3.794	12.135	48.876	4.645	1.951	4.390	619.539
YH	68.762	9.057	3.447	10.482	45.530	4.526	1.330	5.359	389.439
SS	73.502	13.697	5.098	12.793	37.376	5.220	2.285	4.889	538.388
HS	70.994	12.852	4.024	11.829	40.266	6.468	2.189	5.978	591.832
Average	80.1398	12.0777	3.8472	14.1497	36.4710	4.5070	1.7880	4.8597	417.6273

Table 5. Results of RMSE.

$\mathbf{RMSE} ({10}^{-6})$
Region	WPPM-KDE				WPPM-PM				WPPM-Weibull
	ROT	DPI	SJ	SCV	ROT	DPI	SJ	SCV
YG1	836.267	99.492	15.533	121.698	46.711	0.969	0.121	1.272	1954.606
YG2	516.928	56.682	4.126	169.632	12.685	0.354	0.179	15.432	530.007
GW	872.343	56.888	11.745	53.103	212.379	1.711	0.206	1.485	4732.856
YH	501.010	32.811	6.212	40.286	265.007	7.689	0.883	9.987	1952.145
SS	276.515	32.773	9.202	30.075	38.773	0.935	0.118	0.801	3834.946
HS	331.689	36.435	8.492	32.820	91.009	4.892	0.619	4.274	4407.879
Average	555.7920	52.5135	9.2183	74.6023	111.0940	2.7583	0.3543	5.5418	2902.0732

Table 6. Improved rate of MAE.

Region	Improved Rate (%)
	ROT	DPI	SJ	SCV
YG1	68.118	74.103	51.941	74.893
YG2	77.104	74.544	60.681	79.886
GW	54.290	63.855	48.577	63.824
YH	33.786	50.028	61.416	48.874
SS	49.150	61.889	55.179	61.784
HS	43.283	49.673	45.601	49.463
Average	54.2885	62.3487	53.8992	63.1207

Table 7 lists the K-S test results. Only WPPM-PM-SJ passed the K-S test in all regions. WPPM-PM-DPI and WPPM-PM-SCV failed the K-S test according to WPD. WPPM-KDE, WPPM-PM-ROT and WPPM-Weibull failed the K-S test across all regions. Conclusively, the WPPM-PM-SJ guarantees the highest accuracy and goodness-of-fit to stably create WPPM.

Table 7. Results of K-S test.

K-S Test
Region	WPPM-KDE				WPPM-PM				WPPM-Weibull
	ROT	DPI	SJ	SCV	ROT	DPI	SJ	SCV
YG1	0	0	0	0	0.005	0.645	0.997	0.581	0
YG2	0	0	0	0	0.001	0.402	0.487	0.159	0
GW	0	0	0	0	0	0.540	0.802	0.565	0
YH	0	0	0	0	0	0	0.133	0.001	0
SS	0	0	0	0	0.001	0.567	0.792	0.592	0
HS	0	0	0	0	0	0.001	0.077	0.002	0

6. Conclusions

In this paper, a wind power probability model (WPPM) using the reflection method and multi-kernel function kernel density estimation (KDE) is proposed. A boundary bias problem existed due to the double-bounded characteristics of WPD, which was corrected using the reflection method. In addition, the leakage density caused by the effect of tied values at zero output was minimized using the multi-kernel function.

First, because of comparing six bandwidth selectors using wind power data (WPD) from six regions in the Republic of Korea, it was confirmed that the LSCV and BCV bandwidth selectors are inappropriate to calculate the optimal bandwidth of WPD. For the remaining four selectors, the calculated bandwidths were within a certain range regardless of the characteristics of various normalized WPDs. Next, MAE, RMSE, and K-S tests of WPPM-PM, WPPM-Weibull and WPPM-KDE were compared. The accuracy of WPPM-PM and WPPM-KDE was better than that of WPPM-Weibull, and when comparing each bandwidth selector, the accuracy of WPPM-PM was overall better. Only WPPM-PM-SJ passed goodness-of-fit in all regions. The accuracy and goodness-of-fit of WPPM-PM-SJ was the best. As a result, when generating WPPM directly from WPD for WPS generation, a better model can be generated if the method proposed in this paper is used.

Analyzing power systems through a probabilistic approach has become an important task. Through the proposed method, a better WPPM was created than the existing WPPM, and it can be used in various probabilistic approaches.