Numerical Simulation of the Thermally Developed Pulsatile Flow of a Hybrid Nanofluid in a Constricted Channel

Abstract

Heat transfer analysis of the pulsatile flow of a hybrid nanofluid through a constricted channel under the impact of a magnetic field and thermal radiation is presented. Hybrid nanofluids form a new class of nanofluids, distinguished by the thermal properties and functional utilities for improving the heat transfer rate. The behaviors of a water-based copper nanofluid and water-based copper plus a single-wall carbon nanotube, i.e., ($Cu–SWCNT$/water), hybrid nanofluid over each of velocity, wall shear stress, and temperature profiles, are visualized graphically. The time-dependent governing equations of the incompressible fluid flow are transformed to the vorticity-stream function formulation and solved numerically using the finite difference method. The laminar flow simulations are carried out in 2D for simplicity as the flow profiles are assumed to vary only in the 2D plane represented by the 2D Cartesian geometry. The streamlines and vorticity contours are also shown to demonstrate the flow behviour along the channel. For comparison of the flow characteristics and heat transfer rate, the impacts of variations in Hartmann number, Strouhal number, Prandtl number, and the thermal radiation parameter are analyzed. The effects of the emerging parameters on the skin friction coefficient and Nusselt number are also examined. The hybrid nanofluid is demonstrated to have better thermal characteristics than the traditional one.

1. Introduction

Blood flow (pulsatile flow) in the arteries exhibits a periodically echoing time scale that affects the flow-induced mass transfer. This makes the modeling of the physiological processes challenging because the time scales of the characteristics are larger than the pulse period. To address the challenge, researchers look at performing time-averaging over the period to reduce the flow variations within the time period so as to capture a characteristic flow profile. In addition, for discussing the blood flow characteristics in arteries, researchers used constricted channels instead of straight channels because of their geometrical advantages. The phenomena of blood flow through arteries have been associated as an essential factor in hemostasis. For example, many events such as atherogenesis, platelet adhesion, thrombosis, and red blood cell lysis have been connected to various hemodynamic factors.

A nanofluid (NF) is formed by an engineered suspension of nanoparticles (NPs) of a highly conducting substance (such as copper, aluminum, carbon nanotubes, etc.) in a base fluid such as water. The nanofluids are used extensively for their higher thermal conductivity than the base fluids alone. NPs can be categorized into various types by scale, morphology, and physical and chemical properties. As explained by Saidur et al. [1], NFs are in use as heat transfer fluids, biological fluids, pharmaceutical fluids, environmental fluids, etc. Researchers have been analyzing the characteristics of NFs in various applications both experimentally and numerically for even further enhancement in thermal conductivity. Choi [2] was the first one to study the enhancement of thermal conductivity in NFs. Buongiorno [3] simplified the mathematical formulation of the NFs. He described the basic mechanics that lead to the enhancement of the thermal characteristics. This analysis was extended by Kuznetsov and Nield [4] for the boundary layer model of free convective NF flows. Wong and Leon [5] researched NFs as suspensions of NPs in fluids showing substantial improvement in their properties at moderate NP concentrations. Akbar [6] examined the peristaltic flow of incompressible viscous fluid containing metallic NPs in an irregular duct. The combined impact of Lorentz and Kelvin forces in two dimensional $F{e}_3{O}_4$/water NF flow (NFF) was studied by Sheikoleslami et al. [7]. Hayat et al. [8] studied the structures of chemical species on NFF impacted by the rotation of a disc. They reported that the amount of surface shear stress rises with the solid volume fraction of NPs. Paul and Mandal [9] investigated the stretched flow of radiative MHD micropolar NF. Alizadeh et al. [10] studied thermally developed MHD micropolar NFF. They reported that the Nusselt number rises with radiation strength and volume fraction. Dib et al. [11], reported that the presence of NPs enhances heat transfer for their problem of setting the flow between two plates. Cacua et al. [12], demonstrated that NPs improve the thermal characteristics. In practice, NFs might have severe stability issues due to the agglomeration and sedimentation of NPs with time, which limits the applicability of the NFs. To cover the stability issue, Cacua. et al. [12] added surfactants for producing electrostatic or steric repulsion between NPs. Choudhary et al. [13] presented the stability analysis of a $\left(A{l}_2{O}_3\right)$/water NF. They investigated the stability with the help of zeta potential and visual inspection methods. Lim et al. [14,15] used electroosmotic flow with two or more fluids in various microfluidic applications. Shadloo et al. [16] estimated the convection heat transfer coefficient NFF via circular pipes making use of the Support Vector Machine method. For the forced convection flow of $Ti{O}_2$/water NF, Rashidi et al. [17] compared single-phase and two-phase flows in a horizontal tube with a steady wall heat flux as the boundary condition.

A novel class of working NFs, immersed with NPs of two or more solid materials, has come into use during recent years. Such fluids are termed hybrid nanofluids (HNFs). Usually, a material alone does not have all the desirable characteristics needed for a specific purpose; it may have either good thermal or rheological properties. It may be appropriate, however, to have a trade-off between several properties in several practical applications. HNF might serve the desired purpose by combining the properties of its constituent materials. Due to the synergistic impact, HNFs are found to exhibit better thermal conductivity compared with individual NFs [18]. The examples of HNF in use include those formed by the mixing of NPs of two or more of copper $(Cu)$, silver $\left(Ag\right)$, copper oxide $\left(CuO\right)$, aluminium oxide $\left(A{l}_2{O}_3\right)$, Titanium oxide $\left(Ti{O}_2\right)$, single wall carbon nanotubes $(SWCNTs)$, and multi wall carbon nanotube $(MWCNTs)$. Although HNFs have been used in several applications, a lot of research work is still needed for their preparation, characterization, mixing-ratios, and stability [19]. Ahmad and Nadeem [20] discussed the impact of Hall and ion slip with heating for micropolar HNF involving NPs of $SWCNT$ and $MWCNT$. They also studied the effects of radiation, Darcy–Forchheimer, viscous dissipation, and variable viscosity. Khan et al. [21] numerically studied the impact variable viscosity in inclined MHD Williamson NFF over a nonlinearly stretching sheet. They reported that the velocity profile is declined with the rise of inclination angle, Hartmann number, and variable viscosity. The 3D flow of $Cu$-$A{I}_2{O}_3$/water HNF on an expanding surface was studied by Devi and Anjali [22] using the RK-Fehlberg integration technique. The numerical results demonstrated higher heat transfer rate for the HNF than the copper-based NF. Suleman et al. [23] analyzed the effects of Newtonian heating and thermal radiation in chemically reacting silver/water NFF. Nadeem et al. [24] studied the heat transfer feature with heat generation in $SWCNT$–$MWCNT$/water HNF flow. Some examples of relevant studies can be found in [25,26,27,28]. Eshgarf et al. [29] explained that making use of NPs in the conventional fluids to enhance the performance of thermal devices saves energy. Vasua et al. [30] simulated the 2D rheological laminar blood flow via a tapered artery representing mild stenosis. They discussed the effect of various NPs in the blood for pharmacological contexts. Priyadharshini and Ponalagusamy [31] carried out a similar study along with the influence of magnetic field and periodic body acceleration.

In view of the above-mentioned studies, it is notable that no adequate investigations are available in the literature regarding the pulsating MHD HNF flow through a constricted channel subject to thermal radiation. Therefore, to address this research concern, the present study is carried out to analyze the heat transfer of HNF in a constricted channel. The HNF is considered to have NPs of $Cu$ and $SWCNT$ in water. The objective is to examine the cumulative impact of the applied magnetic field and thermal radiation on the wall shear stress (WSS), velocity, and temperature profiles. The effects of various emerging parameters, namely, the Hartman number $\left(M\right)$, Strouhal number $\left(St\right),$ Prandtl number $\left(Pr\right)$, and radiation parameter $\left(Rd\right)$ on the HNF are discussed. The effects of $Rd$, $Pr$, and the Reynolds number $(Re)$ on the Nusselt number ($Nu$) and skin friction coefficient ($C_f$) profiles are also examined. The streamlines and contour graphs are also shown to demonstrate the streamline pattern and flow behviour along the channel. Various comparisons are presented in the present work to observe that which of the NF and HNF possess better thermophysical characteristics. The present study has furnished new insights for the pulsatile flow of a hybrid NF in a constricted channel. The results would provide insight to the relevant researchers and engineers to design concerning products based on the findings. The simulation of the pulsatile flow with nanoparticles is motivated by drug delivery (pharmacology) applications.

The remaining parts of the article are organized in the following manner. The mathematical modeling and its transformation into a solvable form, specifically using the vorticity-stream function formulation, is presented in Section 2. Section 3 discusses the findings and related discussions. Section 4 contains the concluding remarks.

2. Mathematical Model

We consider the pulsatile flow of an incompressible electrically conductive HNF through a rectangular channel. The HNF, having NPs of $Cu$ and $SWCNT$ in water, is assumed to be a uniform and stable fluid. A uniform-magnetic field B is applied perpendicular to the channel walls. We consider a Cartesian coordinate system $\left(\tilde{x},\tilde{y}\right)$ such that the flow direction and the direction of B is along the $\tilde{x}$-axis and $\tilde{y}$-axis, respectively. The channel walls have a pair of symmetrical constrictions. In the transformed system $\left(x, y\right)$, to be discussed later on, the symmetrical constrictions are placed in $\left[-x_0,x_0\right],$ as depicted in Figure 1. We assume that the magnetic-Reynolds number for the flow is very low so that the induced electric and magnetic fields are negligible.

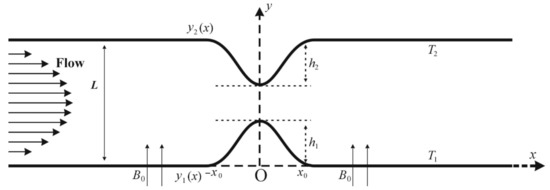
Figure 1. The channel geometry having a symmetric constriction on each of the walls.

The lower and upper walls are defined, respectively, as:

$$\begin{array}{lll}{y}_1\left(x\right)& =& \left\{\begin{array}{cc}\frac{h_1}{2}\left[1+\cos \left(\frac{\pi x}{x_0}\right)\right],& \left|x\right|\le x_0\\ 0, & \left|x\right|>x_0\end{array}\right.\\ y_2\left(x\right)& =& \left\{\begin{array}{cc}1-\frac{h_2}{2}\left[1+\cos \left(\frac{\pi x}{x_0}\right)\right],& \left|x\right|\le x_0\\ 1, & \left|x\right|>x_0\end{array}\right.\end{array}$$

(1)

Here, $h_1$ and $h_2$ denote the respective constriction heights.

The unsteady incompressible Navier–Stokes equations, in $\left(\tilde{x},\tilde{y}\right)$ system, are given by:

The continuity equation:

$$\frac{\partial \tilde{u}}{\partial \tilde{x}}+\frac{\partial \tilde{v}}{\partial \tilde{y}}=0$$

(2)

The momentum equation:

$$\frac{\partial \tilde{u}}{\partial \tilde{t}}+\tilde{u}\frac{\partial \tilde{u}}{\partial \tilde{x}}+\tilde{v}\frac{\partial \tilde{u}}{\partial \tilde{y}}=-\frac{1}{{\rho }_{hnf}}\frac{\partial \tilde{p}}{\partial \tilde{x}}+\frac{{\mu }_{hnf}}{{\rho }_{hnf}}{\nabla }^2\tilde{u}+\frac{1}{{\rho }_{hnf}}{\left(J\times B\right)}_x$$

(3)

$$\frac{\partial \tilde{v}}{\partial \tilde{t}}+\tilde{u}\frac{\partial \tilde{v}}{\partial \tilde{x}}+\tilde{v}\frac{\partial \tilde{v}}{\partial \tilde{y}}=-\frac{1}{{\rho }_{hnf}}\frac{\partial \tilde{p}}{\partial \tilde{y}}+\frac{{\mu }_{hnf}}{{\rho }_{hnf}}{\nabla }^2\tilde{v}$$

(4)

The energy equation:

$$\frac{\partial \tilde{T}}{\partial \tilde{t}}+\tilde{v}\frac{\partial \tilde{T}}{\partial \tilde{x}}+\tilde{v}\frac{\partial \tilde{T}}{\partial \tilde{y}}=\frac{k_{hnf}}{{\left(\rho C_p\right)}_{hnf}}{\nabla }^2\tilde{T}-\frac{1}{{\left(\rho C_p\right)}_{hnf}}\frac{\partial q}{\partial \tilde{y}}$$

(5)

where $q=-\left(\frac{4\sigma }{3k^{\ast }}4T_{\infty }^3\frac{\partial \tilde{T}}{\partial \tilde{y}}\right)$ is the radiative heat flux. Expanding ${\tilde{T}}^4$ about $T_{\infty }$ and ignoring higher-order terms, we get $\begin{array}{ccc}{\tilde{T}}^4& \cong & 4T_{\infty }^3\tilde{T}-3T_{\infty }^4\end{array}$.

Then, $q=-\left(\frac{4\sigma }{3k^{\ast }}4T_{\infty }^3\frac{\partial \tilde{T}}{\partial \tilde{y}}\right)$ and $\frac{\partial q}{\partial \tilde{y}}=-\left(\frac{16\sigma }{3k^{\ast }}{T}_{\infty }^3\frac{{\partial }^2\tilde{T}}{\partial {\tilde{y}}^2}\right)$.

Hence, Equation (5) becomes

$$\frac{\partial \tilde{T}}{\partial \tilde{t}}+\tilde{u}\frac{\partial \tilde{T}}{\partial \tilde{x}}+\tilde{v}\frac{\partial \tilde{T}}{\partial \tilde{y}}=\frac{k_{hnf}}{{\left(\rho C_p\right)}_{hnf}}\left(\frac{{\partial }^2\tilde{T}}{\partial {\tilde{x}}^2}+\frac{{\partial }^2\tilde{T}}{\partial {\tilde{y}}^2}\right)+\frac{16\sigma T_{\infty }^3}{3k^{\ast }{\left(\rho C_p\right)}_{hnf}}\frac{{\partial }^2\tilde{T}}{\partial {\tilde{y}}^2}$$

(6)

where $\tilde{u}$ and $\tilde{v}$ represent the velocity components along $\tilde{x}$- and $\tilde{y}$-axes, respectively, $hnf$ in the subscript represents the nanofluid, $\tilde{p}$ the pressure, $\rho$ the density, $\nu$ the kinematic viscosity, $\tilde{T}$ the temperature, $k$ the thermal conductivity, $C_p$ the specific heat, $J \equiv \left(J_x,J_y,J_z\right)$ the current density, $B \equiv \left(0,B_0,0\right)$ the magnetic field with the uniform strength $B_0$ across the flow, $\sigma$ the electric conductivity,$\mu$ the dynamic viscosity, and ${\mu }_m$ the magnetic permeability of the medium. If $E \equiv \left(E_x,E_y,E_z\right)$ represents the electric field such that the electric current flows along the normal to the plane of the flow, then $E \equiv \left(0,0,E_z\right)$. Next, from Ohm’s law

$$J_x=0,J_y=0,J_z={\sigma }_f\left(E_z+\tilde{u}{B}_0\right)$$

(7)

For the steady flow, Maxwell’s equation $\nabla \times E=0$ implies that $E_z$ is constant. For the current study, we suppose that $E_z=0$. Then, Equation (7) gives, $J_z={\sigma }_f\tilde{u}{B}_0$. Therefore, $J\times B=-{\sigma }_f\tilde{u}{B}_0^2$. Hence, Equation (3) become,

$$\frac{\partial \tilde{u}}{\partial \tilde{t}}+\tilde{u}\frac{\partial \tilde{u}}{\partial \tilde{x}}+\tilde{v}\frac{\partial \tilde{u}}{\partial \tilde{y}}=-\frac{1}{{\rho }_{hnf}}\frac{\partial \tilde{p}}{\partial \tilde{x}}+\frac{{\mu }_{hnf}}{{\rho }_{hnf}}{\nabla }^2\tilde{u}-\frac{1}{{\rho }_{hnf}}{\sigma }_f\tilde{u}{B}_0^2$$

(8)

The following quantities are added for obtaining the non-dimensional form of the governing equations:

$$\begin{gathered} x=\frac{\tilde{x}}{L},y=\frac{\tilde{y}}{L},u=\frac{\tilde{u}}{U}, v=\frac{\tilde{v}}{U},t=\frac{\tilde{t}}{T},\theta =\frac{\tilde{T}-T_2}{T_1-T_2},p=\frac{\tilde{p}}{{\rho }_f{U}^2}, \\ Re=\frac{{\rho }_{f}UL}{{\mu }_f},St=\frac{L}{UT},M=B_{0}L\sqrt{\frac{{\sigma }_f}{{\rho }_f{\nu }_f}},Pr=\frac{{\mu }_f{C}_{p,f}}{k_f},Rd=\frac{16\sigma T_{\infty }^3}{3k^{\ast }{k}_f} \end{gathered}$$

(9)

Here, $L$ is the maximum width of the channel, $T$ is the period of the flow pulsation, $U$ is the characteristic flow velocity, and $k^{\ast }$ is the mean absorption coefficient.

The effective thermophysical properties of HNF [10,22,32] are presented as follows: The HNF’s effective dynamic viscosity ${\mu }_{hnf}$ is given as

$$Rd=\frac{16\sigma T_{\infty }^3}{3k^{\ast }{k}_f}=\frac{{\mu }_f}{{\left(1-{\varphi }_1\right)}^{2.5}{\left(1-{\varphi }_2\right)}^{2.5}}$$

(10)

Here, ${\varphi }_1$ and ${\varphi }_2$ show the volume fractions of NPs $Cu$ and $SWCNT$, respectively.

The HNF’s effective density ${\rho }_{hnf}$ is given as

$${\rho }_{hnf} = \left(1-{\varphi }_2\right)\left[\left(1-{\varphi }_1\right){\rho }_f+{\varphi }_1{\rho }_{s_1}\right] + {\varphi }_2{\rho }_{s_2}$$

(11)

$\mathrm{Here}, s_1$ and $s_2$ in subscripts correspond to the property of $Cu$ and $SWCNT$, respectively. Moreover, $hnf$, $nf$ and $f$ in the subscripts correspond to the property of the hybrid-nanofluid, nanofluid, and base fluid water, respectively. The HNF’s heat capacitance ${\left(\rho C_p\right)}_{hnf}$ is given as

$${\left(\rho C_p\right)}_{hnf} = \left(1-{\varphi }_2\right)\left[\left(1-{\varphi }_1\right){\left(\rho C_p\right)}_f+{\varphi }_1{\left(\rho C_p\right)}_{s_1}\right] + {\varphi }_2{\left(\rho C_p\right)}_{s_2}$$

(12)

The HNF’s effective thermal conductivity $k_{hnf}$ is given as

$$\frac{k_{hnf}}{k_{nf}}=\frac{k_{s_2}+2k_{nf}-2{\varphi }_2\left(k_{nf}-k_{s_2}\right)}{k_{s_2}+2k_{nf}+2{\varphi }_2\left(k_{nf}-k_{s_2}\right)}$$

(13)

where

$$\frac{k_{nf}}{k_f}=\frac{k_{s_1}+2k_f-2{\varphi }_1\left(k_f-k_{s_1}\right)}{k_{s_1}+2k_f+2{\varphi }_1\left(k_f-k_{s_1}\right)}$$

(14)

The thermophysical properties of the base fluid water and the NPs under consideration are shown in Table 1. The properties in Table 1 are given at 24.6 °C. The viscosity of water at 24.6 °C is approximately 0.0000009009 m²/s. Thus, according to Equation (10), ${\mu }_{hnf}=7.940348428\times {10}^{-7}$ m²/s with ${\varphi }_1={\varphi }_2=0.02$.

Table 1. Thermophysical properties of the base fluid water and the two kinds of nanoparticles [10,32].

Physical Property	Base Fluid ${\mathit{H}}_{\mathbf{2}}\mathit{O}$	Nanoparticles
		$Cu$	$SWCNT$
$C_p$ (J/kgK)	4179	385	235
$\rho$ (kg/m3)	997.1	8933	10,500
$k$ (W/mK)	0.613	401	429

Using the quantities from Equations (9) and (12) in Equations (2)–(4) and (6) gives

$$\frac{\partial u}{\partial x}+\frac{\partial u}{\partial y}=0$$

(15)

$$St\frac{\partial u}{\partial t}+u\frac{\partial u}{\partial x}+v\frac{\partial u}{\partial y}=-\frac{1}{{\varnothing }_1}\frac{\partial p}{\partial x}+\frac{1}{Re{\varnothing }_3}{\nabla }^{2}u-\frac{1}{{\varnothing }_1}\frac{M^2}{Re}u$$

(16)

$$St\frac{\partial v}{\partial t}+u\frac{\partial v}{\partial x}+v\frac{\partial v}{\partial y}=-\frac{1}{{\varnothing }_1}\frac{\partial p}{\partial y}+\frac{1}{Re{\varnothing }_3}{\nabla }^{2}v$$

(17)

$$St\frac{\partial \theta }{\partial t}+u\frac{\partial \theta }{\partial x}+v\frac{\partial \theta }{\partial y}=\frac{1}{PrRe}\frac{{\varnothing }_5}{{\varnothing }_4}\left(\frac{{\partial }^2\theta }{\partial x^2}+\left(1+\frac{Rd}{{\varnothing }_5}\right)\frac{{\partial }^2\theta }{\partial y^2}\right)$$

(18)

where

$$\begin{gathered} \begin{array}{ccc}{\varnothing }_1& =& \left(1-{\varphi }_2\right)\left[\left(1-{\varphi }_1\right) + {\varphi }_1\frac{{\rho }_{s_1}}{{\rho }_f}\right] + {\varphi }_2\frac{{\rho }_{s_2}}{{\rho }_f}\end{array} \\ \begin{array}{ccc}{\varnothing }_2& =& \frac{1}{{\left(1-{\varphi }_1\right)}^{2.5}{\left(1-{\varphi }_2\right)}^{2.5}}\end{array} \\ \begin{array}{ccc}{\varnothing }_3& =& {\left(1-{\varphi }_1\right)}^{2.5}{\left(1-{\varphi }_2\right)}^{2.5}\left(\left(1-{\varphi }_2\right)\left[\left(1-{\varphi }_1\right) + {\varphi }_1\frac{{\rho }_{s_1}}{{\rho }_f}\right] + {\varphi }_2\frac{{\rho }_{s_2}}{{\rho }_f}\right)\end{array} \\ \begin{array}{ccc}{\varnothing }_4& =& \left(1-{\varphi }_2\right)\left[\left(1-{\varphi }_1\right) + {\varphi }_1\frac{{\left(\rho C_p\right)}_{s_1}}{{\left(\rho C_p\right)}_f}\right] + {\varphi }_2\frac{{\left(\rho C_p\right)}_{s_2}}{{\left(\rho C_p\right)}_f}\end{array} \\ \begin{array}{ccc}{\varnothing }_5& =& \frac{k_{hnf}}{k_f}\end{array} \end{gathered}$$

2.1. The Boundary Conditions

For the steady case of the flow problem under consideration, the boundary condition, obtained by solving the dimensionless form of Equation (8) and performing some manipulations using Equation (10), are given as follows,

$$u\left(y\right) = \left[\frac{\cosh \left(\frac{M}{2}\right)\left[\cosh \left(\frac{M}{2\sqrt{{\varnothing }_2}}\right)-\cosh \left(\frac{M}{\sqrt{{\varnothing }_2}}\left(y-\frac{1}{2}\right)\right)\right]}{8{\sinh }^2\left(\frac{M}{4}\right)\cosh \left(\frac{M}{2\sqrt{{\varnothing }_2}}\right)}\right]v=0,M\ne 0$$

(19)

When $M=0$, the $u$-velocity at the inlet takes the form:

$$u\left(y\right) = y-y^2,v=0,$$

(20)

The conditions of the outlet boundary are taken as for fully developed flow for all the variables. The flow is presumably sinusoidal for the pulsatile flow:

$$u\left(y,t\right) = u\left(y\right)\left[1+\sin \left(2\pi t\right)\right],v=0$$

(21)

Further, $u=0$ and $v=0$ (i.e., no-slip conditions) are assumed on the walls. In the non-dimensional form, the temperature condition at the lower wall, $\theta =1$ and at the upper wall, $\theta =0$.

2.2. The Vorticity-Stream Function Formulation

The transformation from the primitive variables, $u$ and $v$, to the vorticity-stream functions, $\psi$ and $\omega$, is defined as:

$$u=\frac{\partial \psi }{\partial y},v=-\frac{\partial \psi }{\partial x},\omega =\frac{\partial v}{\partial x}-\frac{\partial u}{\partial y}$$

(22)

The relation for computing the WSS is given by

$$\tau =\mu \widehat{n}\times {\omega }_{wall}$$

Here, $\widehat{n}$ and ${\omega }_{wall}$ denote the normal vector and vorticity at the wall, respectively. As the vorticity and WSS are orthogonal to each other, the WSS can also be determined by the vorticity expression [33].

We differentiate the momentum Equations (16) and (17) with respect to $y$ and $x$, respectively. Then, from their subtraction, we get

$$\begin{gathered} St\frac{\partial }{\partial t}\left(\frac{\partial v}{\partial x}-\frac{\partial u}{\partial y}\right) + u\frac{\partial }{\partial x}\left(\frac{\partial v}{\partial x}-\frac{\partial u}{\partial y}\right) + v\frac{\partial }{\partial y}\left(\frac{\partial v}{\partial x}-\frac{\partial u}{\partial y}\right) \\ = \frac{1}{Re{\varnothing }_3}\left[\frac{{\partial }^2}{\partial x^2}\left(\frac{\partial v}{\partial x}-\frac{\partial u}{\partial y}\right) + \frac{{\partial }^2}{\partial y^2}\left(\frac{\partial v}{\partial x}-\frac{\partial u}{\partial y}\right)\right] + \frac{1}{{\varnothing }_1}\frac{M^2}{Re}\frac{\partial u}{\partial y} \end{gathered}$$

(23)

$$\begin{array}{ccc}St\frac{\partial \omega }{\partial t}+\frac{\partial \psi }{\partial y}\frac{\partial \omega }{\partial x}-\frac{\partial \psi }{\partial x}\frac{\partial \omega }{\partial y}& =& \frac{1}{{\varnothing }_3}\frac{1}{Re}\left[\frac{{\partial }^2\omega }{\partial x^2}+\frac{{\partial }^2\omega }{\partial y^2}\right]+\frac{1}{{\varnothing }_1}\frac{M^2}{Re}\frac{{\partial }^2\psi }{\partial y^2}\end{array}$$

(24)

Additionally, the stream function $\psi$ equation (Poisson equation) is given as

$$\frac{{\partial }^2\psi }{\partial x^2}+\frac{{\partial }^2\psi }{\partial y^2}=-\omega$$

(25)

2.3. Transformation of Coordinates

By incorporating the following coordinate transformation, the constricted portion of the channel is treated as a straight one:

$$\xi =x,\eta =\frac{y-y_1\left(x\right)}{y_2\left(x\right) - y_1\left(x\right)}$$

(26)

In the $\left(\xi , \eta \right)$ system, $\eta =0$ and $\eta =1$ represent the lower and upper walls of the channel, respectively. Moreover, Equations (18) and (24), (25) assume the form as

$$\begin{array}{c}St\frac{\partial \omega }{\partial t} + u\left(\frac{\partial \omega }{\partial \xi }-Q\frac{\partial \omega }{\partial \eta }\right) + vD\frac{\partial \omega }{\partial \eta }\\ =\frac{1}{{\varnothing }_3}\frac{1}{Re}\left[\frac{{\partial }^2\omega }{\partial {\xi }^2}-\left(P-2QR\right)\frac{\partial \omega }{\partial \eta }-2Q\frac{{\partial }^2\omega }{\partial \xi \partial \eta } + \left(Q^2 + D^2\right)\frac{{\partial }^2\omega }{\partial {\eta }^2}\right] + \frac{1}{{\varnothing }_1}\frac{M^2}{Re}{D}^2\frac{{\partial }^2\psi }{\partial {\eta }^2}\end{array}$$

(27)

$$\frac{{\partial }^2\psi }{\partial {\xi }^2} - \left(P-2QR\right)\frac{\partial \psi }{\partial \eta }-2Q\frac{{\partial }^2\psi }{\partial \xi \partial \eta } + \left(Q^2+D^2\right)\frac{{\partial }^2\psi }{\partial {\eta }^2}=-\omega$$

(28)

$$\begin{gathered} St\frac{\partial \theta }{\partial t} + u\left(\frac{\partial \theta }{\partial \xi }-Q\frac{\partial \theta }{\partial \eta }\right) + vD\frac{\partial \theta }{\partial \eta } \\ =\frac{1}{RePr}\frac{{\varnothing }_5}{{\varnothing }_4}\left[\frac{{\partial }^2\theta }{\partial {\xi }^2}-\left(P-2QR\right)\frac{\partial \theta }{\partial \eta }-2Q\frac{{\partial }^2\theta }{\partial \xi \partial \eta }+\left(Q^2+\left(1+\frac{Rd}{{\varnothing }_5}\right)D^2\right)\frac{{\partial }^2\theta }{\partial {\eta }^2}\right] \end{gathered}$$

(29)

where

$$\begin{gathered} P=P\left(\xi ,\eta \right) = \frac{\eta y_2^{″}\left(\xi \right) + \left(1-\eta \right)y_1^{″}\left(\xi \right)}{y_2\left(\xi \right) - y_1\left(\xi \right)},Q=Q\left(\xi ,\eta \right) = \frac{\eta y_2^{\prime }\left(\xi \right) + \left(1-\eta \right)y_1^{\prime }\left(\xi \right)}{y_2\left(\xi \right)-y_1\left(\xi \right)}, \\ R=R\left(\xi \right)=\frac{y_2^{\prime }\left(\xi \right) - y_1^{\prime }\left(\xi \right)}{y_2\left(\xi \right) - y_1\left(\xi \right)},D=D\left(\xi \right) = \frac{1}{y_2\left(\xi \right) - y_1\left(\xi \right)} \end{gathered}$$

(30)

The velocity components $u$ and $v$ in terms of $\left(\xi , \eta \right)$ take the forms

$$u=D\left(\xi \right)\frac{\partial \psi }{\partial \eta },v=Q\left(\xi ,\eta \right)\frac{\partial \psi }{\partial \eta }-\frac{\partial \psi }{\partial \xi }$$

(31)

In the new coordinate system, the initial conditions for $\psi$ and $\omega$ are given by

$$\begin{gathered} \begin{array}{cc}\psi =0,& \mathrm{for} \mathrm{all} t\le 0\end{array} \\ \begin{array}{cc}\omega =0,& \mathrm{for} \mathrm{all} t\le 0\end{array} \end{gathered}$$

Furthermore, the boundary conditions for the walls in $\left(\xi , \eta \right)$ system for $\psi$ and $\omega$ are given as

$$\psi \left(\eta ,t\right) = \left[\frac{\sqrt{{\varnothing }_2}\cosh \left(\frac{M}{2}\right)\tanh \left(\frac{M}{2\sqrt{{\varnothing }_2}}\right)}{8M{\sinh }^2\left(\frac{M}{4}\right)}\right]\left[1+ϵ\sin \left(2\pi t\right)\right],\mathrm{at} \eta =0$$

(32)

$$\psi \left(\eta ,t\right) = \frac{M\cosh \left(\frac{M}{2}\right)}{8\sqrt{{\varnothing }_2}{\sinh }^2\left(\frac{M}{4}\right)}\left[1-\frac{\sqrt{{\varnothing }_2}}{M}\tanh \left(\frac{M}{2\sqrt{{\varnothing }_2}}\right)\right]\left[1+ϵ\sin \left(2\pi t\right)\right],\mathrm{at} \eta =1$$

(33)

$$\omega =-{\left[\left(Q^2+D^2\right)\frac{{\partial }^2\psi }{\partial {\eta }^2}\right]}_{\eta =0,1}$$

(34)

where $ϵ$ denotes the pulsating amplitude. The steady and pulsatile flow conditions are given by $ϵ=0$ and $ϵ=1$, respectively. For the temperature, the boundary conditions after the transformation are given as $\theta =1$ at $\eta =0$ and $\theta =0$ at $\eta =1$.

The other concerning nondimensional physical quantities include the skin friction coefficient and Nusselt number, defined by

$$\begin{array}{cc}{C}_f=\frac{{\tau }_w}{\rho u_w^2},& Nu=\frac{h{q}_w}{k\left(T_1-T_2\right)}\end{array}$$

where ${\tau }_w$ and $q_w$ are defined as

$$\begin{array}{cc}{\tau }_w={\left[\mu \frac{\partial \tilde{u}}{\partial \tilde{y}}\right]}_{\tilde{y}=0},& q_w={\left[\frac{\partial \tilde{T}}{\partial \tilde{y}}\right]}_{\tilde{y}=0}\end{array}$$

After using dimensionless variables from (9) and the coordinate transformation from (26), we get

$$C_f=\frac{1}{u_w^2}{\left[-\frac{1}{Re}D\frac{\partial u}{\partial \eta }\right]}_{\eta =0},Nu={\left[-D\frac{\partial \theta }{\partial \eta }\right]}_{\eta =0}$$

(35)

3. Results and Discussion

The problem Equations (27)–(29) subject to boundary conditions, including (32)–(34), are solved numerically using FDM, as in [34,35,36,37,38,39]. The domain $\left\{\left(\xi ,\eta \right)|\xi \in \left[-x_1,x_1\right] \mathrm{and} \eta \in \left[0,1\right]\right\}$ is discretized by choosing the grid points $\left({\xi }_i,{\eta }_j\right)$ with the step-sizes $\Delta \xi$ and $\Delta \eta$ in $\xi$-direction and $\eta$-direction, respectively. For time integration of the solution, a fixed step size $\Delta t$ is used. The solution at time level $l$ is used to obtain the solution is at time level $l+1$, for $l=0, 1, 2, \cdots$. Firstly, Equation (28) is solved for $\psi =\psi \left(\xi ,\eta \right)$. The linear system obtained through the finite difference discretizations is solved using the Tri-Diagonal Matrix Algorithm (TDMA). Secondly, Equations (27) and (29) are solved using the ADI (Alternating Direction Implicit) method for $\omega =\omega \left(\xi ,\eta \right)$ and $\theta =\theta \left(\xi ,\eta \right)$, respectively. The linear systems obtained through the finite difference discretizations are solved using the TDMA at each of the two half-steps of the ADI method. A detailed description of the algorithm can be found in [38]. The values of the step sizes are taken as follows to ensure the consistency of the numerical scheme: $\Delta t=0.00005$ for the pulsatile flow with $\Delta \xi =0.05$, $\Delta \eta =0.02,$ and $Re=700$. The computations for the present study are performed in a sequential fashion. The results can be found by parallel computing for time-efficient solutions [40].

In the current study, the computational domain, considered as $-10\le \xi \le 10$ and $0\le \eta \le 1$, is discretized by a grid of $400\times 50$ elements. The length of the constriction is considered as $2x_0=4.$ The constrictions on the lower and upper walls are assumed to have heights $h_1=h_2=0.35$; hence, at the throat of the constriction, the channel width remains 30% of the maximum channel width.

The pulsatile motion is modeled by adding in the inflow boundary condition the sinusoidal time-dependent function $\sin \left(2\pi t\right)$. For a comparison of the behaviors of $Cu–SWCNT$/water HNF with $Cu$/water NF, the effects of the physical parameters including $M$, $St$, $Pr$, and $Rd$ are studied on the non-dimensional streamwise velocity $\left(u\right)$ and temperature $\left(\theta \right)$ profiles. We performed simulations for a long enough time that, in most cases, the results are displayed at selected time instants and axial locations, especially $x=0$ (throat of the constriction) and $x=2$ (in the lee of the constriction) where the fluid enters in the low-pressure zone from the high-pressure zone. For a pulse cycle, $0<t<0.25$ is the acceleration phase and $0.25<t<0.75$ is the deceleration phase.

For validation, the present results for the pulsatile flow of the base fluid (i.e., with ${\varphi }_1=0, {\varphi }_2=0$) are compared with those obtained by Bandyopadhyay and Layek [35] in the case of Newtonian fluid without the heat effect. Figure 2 shows a good agreement of the present results, specifically the wall shear stresses, with [35] for $M=5$ and $10$ at $t=0.25$.

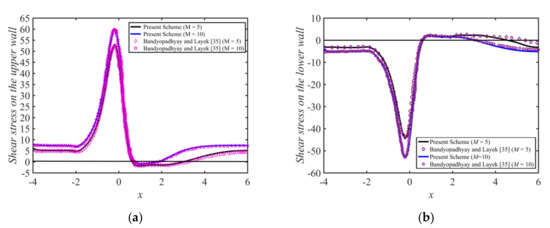
Figure 2. Wall shear stress distributions for the pulsatile flow, for $M=5, 10,$ at $Re=700$, $h_1=h_2=0.35$, $st=0.02$, and $t=0.25$: (a) on the lower wall, and (b) on the upper wall.

The effects of pure water, $Cu$/water, $Cu–SWCNT$/water on the WSS at both walls are computed for a complete pulse cycle while fixing the parameters as $\varphi =0.02$, $M=5$, $St=0.02$, $Pr=1$, and $Rd=0.2$. The results are shown in Figure 3. It is seen that during a complete period, the wall shear stress varies considerably, especially in the vicinity and downstream of the constriction. However, no major changes are observed upstream of the constriction on the WSS. Over the duration $0<t<0.25$, the peak value of WSS decreases and reaches its highest value at $t=0.25$ at peak flow time. The flow separation area rises during this period of the time cycle. After that, during $0.25<t<0.75$, the flow starts to decelerate, and the WSS also decreases, but the area of the flow separation tends to increase. The WSS is oscillating, and its sign changes at zero net flow rate, i.e., at $t=0.75.$

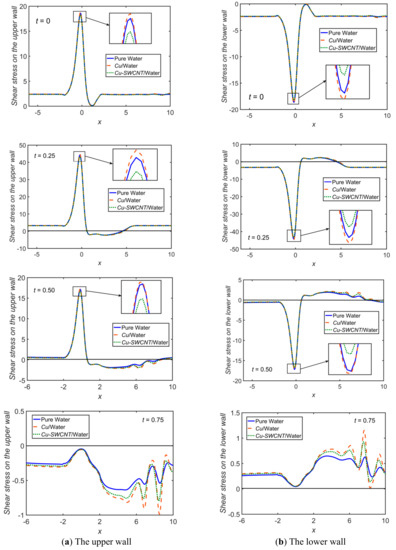
Figure 3. Comparison of pure water, $Cu$/water, and $Cu–SWCNT$/water for WSS with $M=5$, $Pr=1$, $Rd=0.2$, $Re=700$, and $\varphi =0.02$, at $t=0, 0.25, 0.50, \mathrm{and} 0.75$.

Figure 4 presents a comparison among the pure water, $Cu$/water NF, and $Cu–SWCNT$/water HNF by fixing the parameters as $\varphi =0.02$, $M=5$, $St=0.02$, $Pr=1$, and $Rd=0.2$. The velocity profile for pure water is observed to be the highest, followed by the NF and then the HNF. For the HNF, the particle concentration in the fluid is even higher than that of the base fluid and the NF, which causes enhancement of the density and dynamic viscosity. The flow velocity experiences reduction accordingly. The peak value of $u$ tends to rise, and the curves appear to be parabolic for $0\le t\le 0.5$. At $t=0.75$, $u$ is dropped substantially, and backflow occurs near the walls. Figure 5 shows $u$-profiles at $t=0.25$. At $x=2.0$, in the vicinity of the limiting point of the constriction downstream, a backflow is observed.

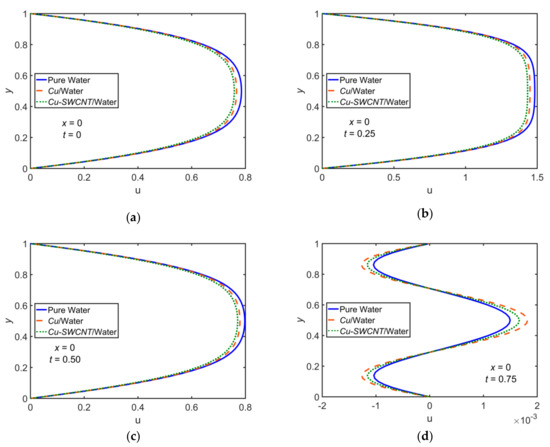
Figure 4. Comparison of pure water, $Cu$/water, and $Cu–SWCNT$/water for velocity profiles for $M=5$, $Pr=1$, $Rd=0.2$, $Re=700$, and $\varphi =0.02$ at (a) $t=0$, (b) $t=0.25$, (c) $t=0.50$, and (d) $t=0.75$.

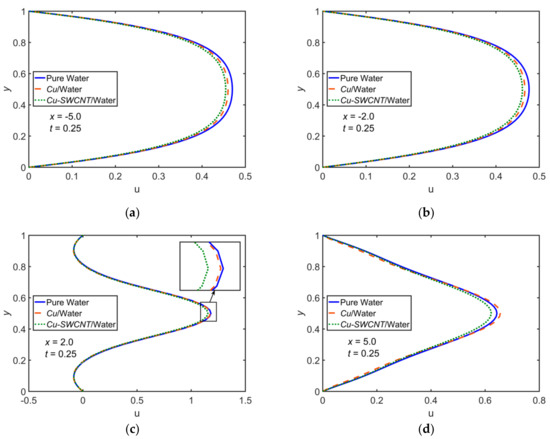
Figure 5. Comparison of pure water, $Cu$/water, and $Cu–SWCNT$/water for velocity profiles for $M=5$, $Pr=1$, $Rd=0.2$, $Re=700$, $\varphi =0.02$, and $t=0.25$ at (a) $x=-5.0$, (b) $x=-2.0$, (c) $x=2.0$, and (d) $x=5.0$.

A comparison among the pure water, $Cu$/water NF, and $Cu–SWCNT$/water HNF for the temperature profiles computed with $\varphi =0.02$, $M=5$, $St=0.02$, $Pr=1$, and $Rd=0.2$. In Figure 6, the profiles are shown at $x=0$ for a complete pulse cycle. However, in Figure 7, the profiles are shown at four different $x$-locations at $t=0.25$. It is noticed that the HNF hits higher temperatures compared to the NF. A rapid rise in temperature is due to the hybrid nature of the nanofluid since it increases the thermal conductivity.

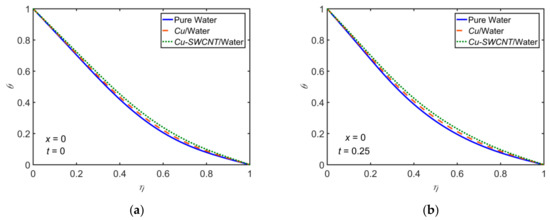
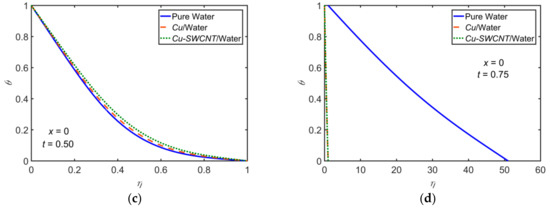
Figure 6. Comparison of pure water, $Cu$/water, and $Cu–SWCNT$/water for the temperature profiles for $M=5$, $Pr=1$, $Rd=0.2$, $Re=700$, and $\varphi =0.02$ at (a) $t=0$, (b) $t=0.25$, (c) $t=0.50$, and (d) $t=0.75$.

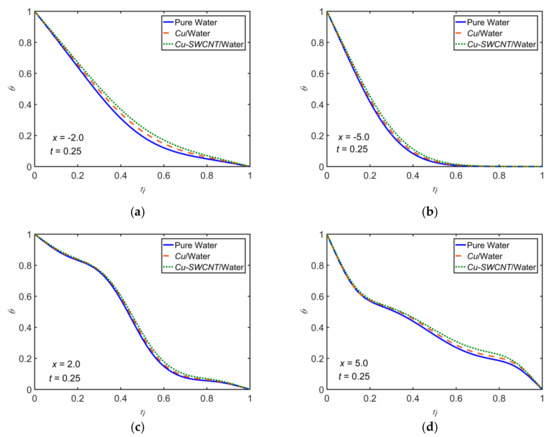
Figure 7. Comparison of pure water, $Cu$/water, and $Cu–SWCNT$/water for the temperature profiles for $M=5$, $Pr=1$, $Rd=0.2$, $Re=700$, $\varphi =0.02$, and $t=0.25$ at (a) $x=-5.0$, (b) $x=-2.0$, (c) $x=2.0$, and (d) $x=5.0$.

Figure 8 and Figure 9 illustrate the behavior of $u$ and $\theta$ profiles, respectively, for the variation of $M$ to make a comparison between the NF and the HNF. The other parameters are fixed as $\varphi =0.02$, $St=0.02$, $Pr=1$, and $Rd=0.2$. It is observed that the velocity is greater for the NF than the HNF. The velocity increases as the magnetic field strength is increased. That is, the viscous boundary layer thickness is decreased for higher values of $M.$ This is due to the production of a resistive Lorentz force, whose strength increases with increasing values of $M$. The HNF temperature profile is slightly higher than that of the NF. The thermal boundary layer thickness decreases, resulting in a decline of the temperature profile with enhancement in the magnetic field strength. The appreciation in $M$ maximizes the velocity gradient and minimizes the temperature gradient at the boundary.

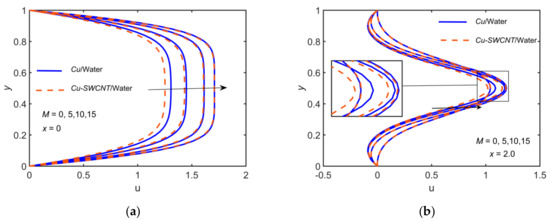
Figure 8. Comparison of $Cu$/water and $Cu–SWCNT$/water for the velocity profiles for $M=0, 5, 10, \mathrm{and} 15$ with $St=0.02$, $Pr=1$, $Rd=0.2$, $Re=700$, $\varphi =0.02$, and $t=0.25$ at (a) $x=0$ (b) $x=2$.

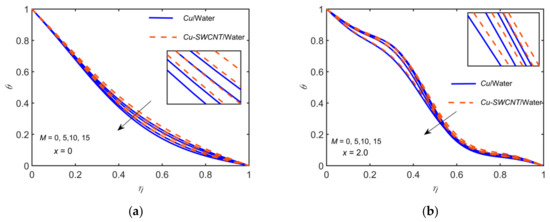
Figure 9. Comparison of $Cu$/water and $Cu–SWCNT$/water for the temperature profiles for $M=0, 5, 10, \mathrm{and} 15$ with $St=0.02$, $Pr=1$, $Rd=0.2$, $Re=700$, $\varphi =0.02$, and $t=0.25$ at (a) $x=0$ (b) $x=2$.

Figure 10 and Figure 11 illustrate the behavior of the velocity and temperature profiles, respectively, for the variation of $St$ to compare the NF and HNF. The other parameters are fixed as: $\varphi =0.02$, $M=5$, $Pr=1$, and $Rd=0.2$. It is observed that the velocity is greater for the NF than the HNF. The velocity decreases with increment in $St$, i.e., the viscous boundary layer thickness increases with $St$. The HNF temperature profile is slightly higher than that of the NF. The thermal boundary layer thickness decreases, resulting in a decrease of the temperature profile with increasing values of $St$. The velocity exhibits a parabolic profile at $x=0$. The profiles are not parabolic as some backflow in the vicinity of the walls is observed at $x=2$. The backflow reduces with an increase in $St$.

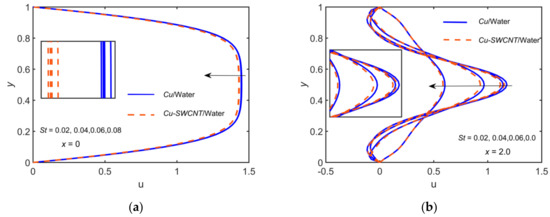
Figure 10. Comparison of $Cu$/water and $Cu–SWCNT$/water for the velocity profiles for $t=0.02, 0.04, 0.06, \mathrm{and} 0.08$ with $M=5$, $Pr=1$, $Rd=0.2$, $Re=700$, $\varphi =0.02$, and $t=0.25$ at (a) $x=0$ (b) $x=2$.

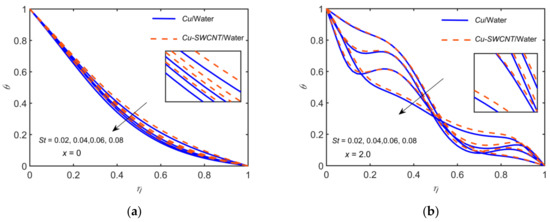
Figure 11. Comparison of $Cu$/water and $Cu–SWCNT$/water for the temperature profiles for $t=0.02, 0.04, 0.06,\mathrm{and} 0.08$ with $M=5$, $Pr=1$, $Rd=0.2$, $Re=700$, $\varphi =0.02$, and $t=0.25$ at (a) $x=0$ (b) $x=2$.

Figure 12 illustrates the behavior of the temperature profiles for the variation of $Pr$ to compare the NF and HNF. The other parameters are fixed as: $\varphi =0.02$, $M=5$, $St=0.02$, and $Rd=0.2$. The HNF temperature profile is slightly higher than that of the NF. The thermal boundary layer thickness decreases as the $Pr$ increases, resulting in a decline in the temperature profile at both locations. The rising values of $Pr$ cause a reduction in thermal diffusivity. Consequently, the temperature of the fluid is lowered.

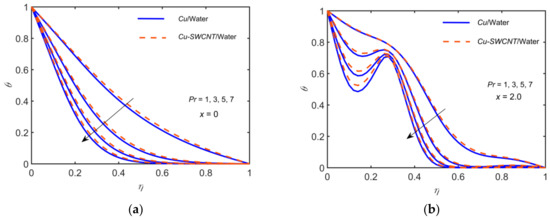
Figure 12. Comparison of $Cu$/water and $Cu–SWCNT$/water for the temperature profiles for $Pr=1,3, 5, \mathrm{and} 7$, $St=0.02$ with $M=5$, $Rd=0.2$, $Re=700$, $\varphi =0.02$, and $t=0.25$ at (a) $x=0$ (b) $x=2$.

Figure 13 illustrates the behavior of the temperature profiles for the variation of $Rd$ to compare the NF and HNF. The other parameters are fixed as $\varphi =0.02$, $M=5$, $St=0.02$, and $Pr=1$. Appreciation in $Rd$ enhances the temperature of the fluids. It is noticed that the temperature profile of the HNF is slightly higher than that of the NF. The thermal boundary layer thickness increases, resulting in the rise of temperature as $Rd$ is increased. Physically it is due to the fact that the mean absorption coefficient decreases, which boosts $Rd,$ thus the radiative heat transfer rate is increased.

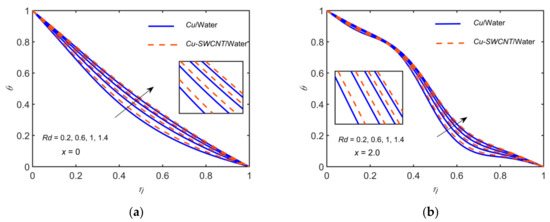
Figure 13. Comparison of $Cu$/water and $Cu–SWCNT$/water for the temperature profiles for $Rd=0.2, 0.6, 1, \mathrm{and} 1.4$ with $St=0.02$, $Pr=1$, $M=5$, $Re=700$, $\varphi =0.02$, and $t=0.25$ at (a) $x=0$ (b) $x=2$.

Figure 14 and Figure 15 illustrate the behavior of the velocity and temperature profiles, respectively, for the variation of solid volume fraction $\varphi$ to compare the NF and HNF. The other parameters are fixed as $M=5$, $St=0.02$ $Pr=1$, and $Rd=0.2$. The velocity is greater for the NF than that of the HNF. We further observe that the velocity decreases for enhancing the solid volume fraction $\varphi ,$ i.e., the viscous boundary layer thickness increases with increasing values of $\varphi$. The temperature distribution and momentum boundary layer thickness show a rising trend with the solid volume fraction. It is also clear from the figure that the HNF exhibits a higher temperature profile than the NF. The velocity exhibits a parabolic profile at $x=0$. The profiles are not parabolic as some backflow in the vicinity of the walls is observed at $x=2$.

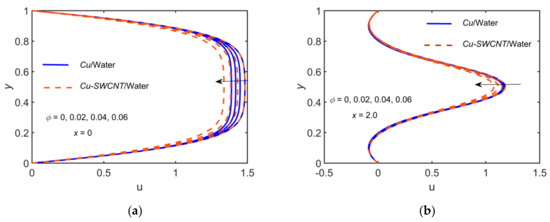
Figure 14. Comparison of $Cu$/water and $Cu–SWCNT$/water for the velocity profiles for $\varphi =0, 0.02, 0.04, \mathrm{and} 0.06$ with $M=5$, $St=0.02$ $Pr=1$, $Rd=0.2$, $Re=700$, and $t=0.25$ at (a) $x=0$ (b) $x=2$.

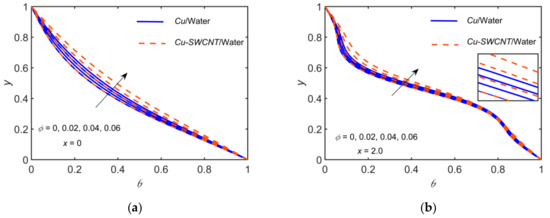
Figure 15. Comparison of $Cu$/water and $Cu–SWCNT$/water for the temperature profiles for $\varphi =0, 0.02, 0.04, \mathrm{and} 0.06$ with $M=5$, $St=0.02$, $Pr=1$, $Rd=0.2$, $Re=700$, and $t=0.25$ at (a) $x=0$ (b) $x=2$.

The effects of $Re=500$ and $700$ for $Cu–SWCNT$/water on the WSS on both walls are computed while fixing the parameters as $\varphi =0.02$, $M=5$, $St=0.02$, $Pr=1$, and $Rd=0.2$. The results are shown in Figure 16, and the streamlines distribution plots are shown Figure 17 for $t=0.25$. As expected, the magnitudes of the peak values of the profiles are lower for the lower $Re$. The profile wave and the eddies downstream of the constriction are weaker for the lower Reynold number.

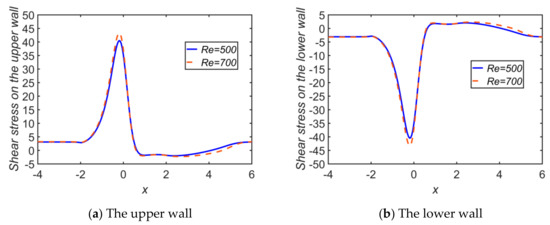
Figure 16. Comparison of WSS for $Re=500$ and $700$ in case of $Cu–SWCNT$/water, setting $M=5$, $Pr=1$, $Rd=0.2$, and $\varphi =0.02$, at $t=0.25$.

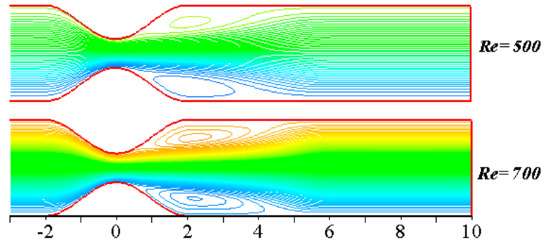
Figure 17. Comparison of the streamlines for $Re=500$ and $700$ in case of $Cu–SWCNT$/water, setting $M=5$, $St=0.02$, $Pr=1$, and $Rd=0.2$, at $t=0.25$.

The effects of $Rd$, $Pr$, and $Re$ on the Nusselt number and skin friction profiles are shown in Figure 18 and Figure 19, respectively. It is observed that the Nusselt number increases for higher values of $Pr$ and $Re$, but decreases for increasing $Rd$. Additionally, the skin friction coefficient increases for an increase in the values of $Re$. However, it remains unchanged for $Pr$ and $Re$.

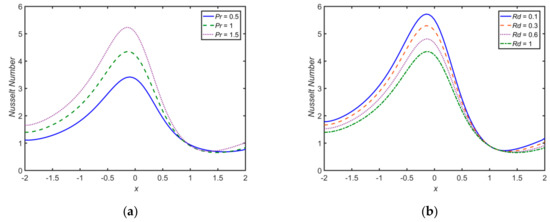
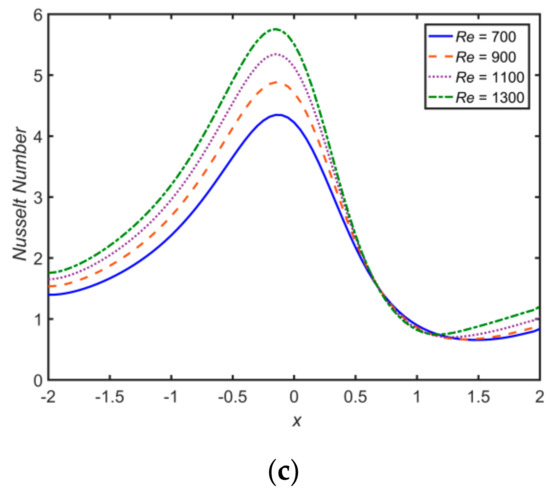
Figure 18. Nusselt profiles for (a) $Pr=0.5, 1$, and $1.5$; (b) $Rd=0.1, 0.3, 0.6$, and $1$; and (c) $Re=700, 900, 1100$, and $1300$; with $M=5$ and $St=0.02$, at $t=0.25$.

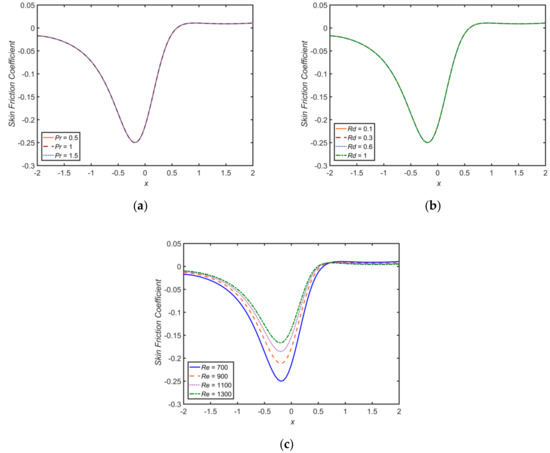
Figure 19. Skin friction profiles for (a) $Pr=0.5$, $1$, and $1.5$; (b) $Rd=0.1$, $0.3$, $0.6$, and $1$; and (c) $Re=700$, $900$, $1100$, and $1300$; with $M=5$ and $St=0.02$, at $t=0.25$.

The streamlines, vorticity, and temperature distribution plots with $\varphi =0.02$, $M=5$, $St=0.02$, $Pr=1$, and $Rd=0.2$ are shown in Figure 20 for comparison among pure water, $Cu$/water NF and $Cu–SWCNT$/water HNF. The formation of vertical eddies in the vicinity of the walls can be observed. Over time, the eddies grow for the HNF and slowly occupy a major part of the channel downstream of the constriction. The inclusion of multiple types of nanoparticles adds more energy. This results in higher increments in the temperature as well as the thickness of the thermal boundary layer. A rapid rise in the temperature is due to the HNF since it increases the thermal conductivity.

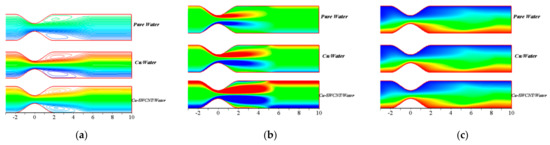
Figure 20. Comparison of pure water, $Cu$/water, and $Cu–SWCNT$/water for (a) Streamlines, (b) vorticity, and (c) temperature distributions with $Re=700$, $M=5$, $St=0.02$, $Pr=1$, and $Rd=0.2$, at the maximum flow rate ($t=0.25$ ).

4. Concluding Remarks

In this research, the comparison between the behavior of a traditional NF and an emerging HNF in the presence of viscous incompressible MHD pulsatile fluid flow over a rectangular channel is numerically investigated. The comparison between the behavior of the pure water, $Cu$/water NF, and $Cu–SWCNT$/water HNF over the velocity, temperature, and WSS distributions are visualized graphically. The impacts of each of $M$, $St$, $Pr$, and $Rd$ on the flow profiles are studied. The summary of the impacts is as follows:

• The effects of the pure water, $Cu$/water, and $Cu–SWCNT$/water on the WSS at both walls are computed. The flow separation area rises during the duration $0<t<0.25$. After that, the flow starts to decelerate, during $0.25<t<0.75,$ and the WSS also decreases, but the area of the flow separation tends to increase.
• Density and dynamic viscosity are the factors of fluid velocity reduction, which is enhanced by hybridity as more immense particles are introduced, so the velocity reduces when comparing the pure water, the NF, and the HNF.
• A rapid rise in temperature is observed due to the HNF since it increases the thermal conductivity when comparing the pure water, the NF, and the HNF. Hence, it is interpreted that the HNF hits higher temperatures compared to the NF.
• The increasing values of $M$ reduce the overall density, which raised the temperature of the HNF within the boundary layer. Finally, the appreciation in $M$ maximizes the velocity gradient and minimizes the temperature gradient at the boundary.
• The HNF temperature profile is slightly higher than that of the NF in the case of varying $St$ and $Pr$. The thermal boundary layer thickness decreases, resulting in a decrease of the temperature profile with increasing values of $St$ and $Pr$. The higher value of $Pr$ number causes a reduction in the thermal diffusivity.
• The thermal boundary layer thickness increases, resulting in the rise of temperature as $Rd$ is increased. Temperature profile and thermal boundary layer thickness are enhanced by increasing the values of $Rd$.
• Velocity decreases for enhancing the solid volume fraction $\varphi ,$ i.e., the viscous boundary layer thickness increases with increasing values of $\varphi$. Additionally, the HNF exhibits a higher temperature profile than the NF.
• The HNF is observed to be a better thermal conductor as compared with the traditional NF.
• The Nusselt number increases for higher values of $Pr$ and $Re$, but decreases for increasing $Rd$.
• The skin friction coefficient increases for an increase in the values of $Re$; however, it remains unchanged for $Pr$ and $Re$.