Abstract
Vertical axis turbines, also called Darrieus turbines, present interesting characteristics for offshore wind and tidal applications but suffer from vibrations and a lower efficiency than the more conventional horizontal axis turbines. The use of variable pitch, in order to control the angle of attack of the blades continuously during their rotation, is considered in this study to overcome these problems. 2D blade-resolved unsteady Reynolds-Averaged Navier–Stokes (RANS) simulations are employed to evaluate the performance improvement that pitching blades can bring to the optimal performance of a three-straight-blade vertical axis tidal turbine. Three pitching laws are defined and tested. They aim to reduce the angle of attack of the blades in the upstream half of the turbine. No pitching motion is used in the downstream half. The streamwise velocity, monitored at the center of the turbine, together with the measurement of the blades’ angle of attack help show the effectiveness of the proposed pitching laws. The decrease in the angle of attack in the upstream half of a revolution leads to a significant increase in the power coefficient () and to a better balance of the torque generated in the upstream and downstream halves. Both torque and thrust ripples are therefore significantly reduced.
1. Introduction
The installed capacity of renewable energy in the world has been increasing continuously over the past fifteen years [1,2]. The will to find energy sources available on a long-term basis with stable costs and lower atmospheric pollutant emissions has led to a growing interest in renewable energies like solar photovoltaics (PV), wind turbines, and biomass (hydro-power was already well developed). Onshore wind and solar PV represent currently the largest additions of installed capacity per year ( GW and GW, respectively, in 2019) and are also forecast to lead the capacity growth until 2025 at least [1,3]. Ocean power consists in only 535 MW of installed capacity at the end of 2019 with an addition of 3 MW during the year [1]. The resource potential of ocean energy is, however, judged “enormous” [1]. Research is thus necessary to help with the development of this source of energy.
Ocean energy comprises tidal, wave, and ocean thermal energy conversion (OTEC) with the tidal branch currently leading the installed capacity. The resource of tidal power around the Channel Islands, one of the most promising tidal site in Europe, is estimated at an average of 1.8 GW electrical power [4], for example. Although it is not very significant compared to the electricity consumption in France or in the UK, tidal energy has the great advantage of being easily predictable.
Tidal turbines can be divided into two sub-categories: horizontal-axis and vertical-axis turbines (HATs and VATs, respectively). This study focuses on VATs, also called Darrieus turbines after Georges Darrieus, the first engineer who patented such vertical-axis rotor in 1931 [5]. Vertical-axis wind turbines (VAWTs) generated a large interest in the 1970s [6,7] before the wind energy industry was dominated by horizontal-axis wind turbines (HAWT). Darrieus turbines have a slightly lower efficiency and generate larger vibrations than HATs because the blades operate with a constantly varying angle of attack, which led to the success of HAWTs. However, VATs have some significant advantages over HATs, which explains why many research studies focused on this technology over the past 15 years: VATs are insensitive to the flow direction (no need of a yawing mechanism); the drive train and generator may be placed close to the water surface (wind turbines) or above the water surface (tidal turbines), making maintenance easier; and they are easily scalable thanks to the absence of varying gravitational loads on the blades and farms of such turbines could reach a significantly higher power density than with HATs [8]. Therefore, VATs seem well adapted for floating offshore and tidal applications.
A way to compensate the low efficiency and high vibrations experienced by VATs is to use variable pitch [9,10]. By changing the pitch angle of a blade continuously during its rotation, it is possible to control its angle of attack and avoid stall. Several studies have been carried out on this topic [11,12,13,14,15,16,17]. Active (using an actuator) or passive blade pitching are generally considered. Active pitching is more efficient as it allows any pitching law to be used but it is mechanically more complicated and may be a source of additional maintenance. This is the solution used in our work as our aim is to study the potential of variable pitch on the performance improvement.
CFD simulations are widely used to predict the performances of VATs. 2D Reynolds-Averaged Navier–Stokes (RANS) simulations [18,19,20,21,22] are an efficient way to obtain relative performance data for a rotor configuration (effect of the airfoil shape or rotor solidity for example). 3D RANS simulations [23,24,25] are more time consuming than 2D RANS but they are more accurate since they include the 3D effects (for example, tip vortices and arm–blade junction losses). They are more adapted to simulate the wake of the turbine due to the importance of the 3D flow structures on the wake recovery. Large Eddy Simulations (LES) [26,27] are even more time-consuming but they allow a significant increase in the accuracy of the performance predictions, especially when the turbine blades experience stall. LES is also well adapted to model the wake of a VAT. In these simulations, the turbine blades are “resolved”, i.e., the outer surface of the blades is meshed and the boundary layer is resolved. Other methods, like the actuator surface [28] or the actuator line [29], model the effect of the blades on the fluid through source terms in the RANS or LES simulations. Lift and drag coefficients are obtained from tabulated data (experiments or high fidelity simulations), which is not the case with the “blade-resolved” simulations. Similar actuator line methods can also be coupled to a Lattice Boltzmann method LES solver [30] in order to obtain a high resolution in the turbine wake.
The present work employs 2D RANS blade-resolved simulations to study the performance improvement that active variable pitch can bring to the optimal working point of a straight-blade vertical axis tidal turbine. Three new pitching laws are defined. They aim at keeping the blades’ angles of attack constant over a given part of the revolution, in the upstream half of the turbine. Similar approaches have been used by other researchers to limit the angle of attack to the stall angle [11] or to keep the circulation around the blade constant [17]. Here, we limit the angle of attack in the upstream half of the turbine to a low value, close to the optimal lift-to-drag ratio. This leads to a better balance of the torque generation between the upstream and downstream halves of the turbine than a fixed pitch turbine.
To make sure the pitching laws operate as expected, we need to determine the angle of attack of the blades. Several methods are available in the literature to extract the angle of attack from the CFD results. One way is to monitor the flow speed along the blade path and average it for one turbine revolution at a given azimuthal angle (excluding data when the blade travels through a given monitor point or is close to it) [31,32,33]. Then, the angle of attack can be calculated with a “free stream” velocity which is more representative of the actual flow field close to the blades. However, this method averages the flow speed at each azimuthal angle, meaning that the unsteadiness of the flow is lost and the velocity used to compute the angle of attack is not exactly the one seen by the blades. A similar method was developed by Elsakka and al. [34], in which they monitor the flow speed at several points that follow the blade during its rotation. They conclude that using two reference points, located 0.5 chord length upstream of the blade and 1 chord length away from each side of the blade, gives an accurate estimation of the angle of attack. Melani et al. [35] benchmark three of these methods and conclude that the “line-average” method is the most accurate. This method, first introduced by Jost et al. [36] for HAWTs, uses a closed line around the airfoil (centered at the quarter chord) to calculate the average undisturbed velocity. This undisturbed velocity is finally used in the velocity triangle to derive the angle of attack. Another approach, developed by Bianchini et al. [37], consists in postprocessing the pressure distribution around the airfoil at a given azimuthal angle and comparing it to the pressure distribution along a fixed blade (placed in a rectilinear flow) at different angles of attack. The fixed airfoil is transformed to take into account the virtual camber effect and Xfoil [38] is used to generate the reference pressure distributions. The method is considered accurate by its authors as long as the blade is not stalled. The method we use in this study was first developed in the PhD of the first author [39]. It is very similar to the previous method as the angle of attack will be determined from the location of the stagnation point on the blade, by comparison to the location of the stagnation point on a fixed blade. The blade used for comparison (fixed angles of attack) has the exact same shape as the turbine blade (i.e., we do not take into account the virtual camber effect) and the 2D RANS method is employed for the reference simulations.
This article is organized as follows. Section 2 gives the details about the turbine studied. Section 3 presents the mesh and numerical parameters used. Section 4 provides a validation study for the numerical set up used, by comparison with experimental results on a fixed airfoil from the literature. Section 5 presents the method that we have developed in order to measure the angle of attack on the blades in the simulation results. Section 6 displays some results for the fixed pitch (Darrieus) turbine in order to identify the optimal operating condition. Section 7 is the core of the article with details about the pitching laws used and the results obtained, before concluding.
2. Turbine
The turbine used in this study is the SHIVA turbine (Figure 1), under development at the French naval academy research institute. It is a 3-bladed vertical-axis tidal turbine with 1m span straight blades. One main motor controls the rotational speed of the turbine and subsidiary motors are mounted on top of each blade to control their pitch angle (Figure 2). This design provides a great flexibility regarding pitching laws (, with the azimuth) that can be tested.
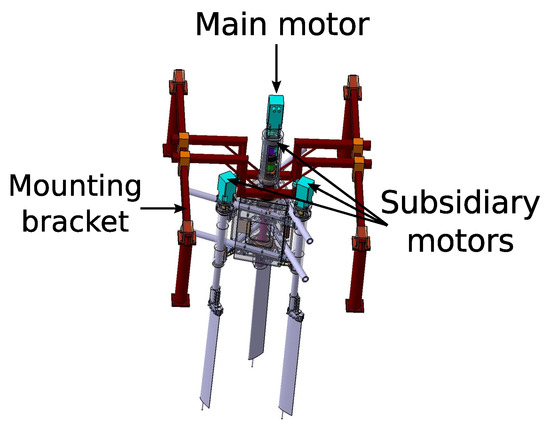
Figure 1.
Computer Assisted Design (CAD) model of the SHIVA turbine.
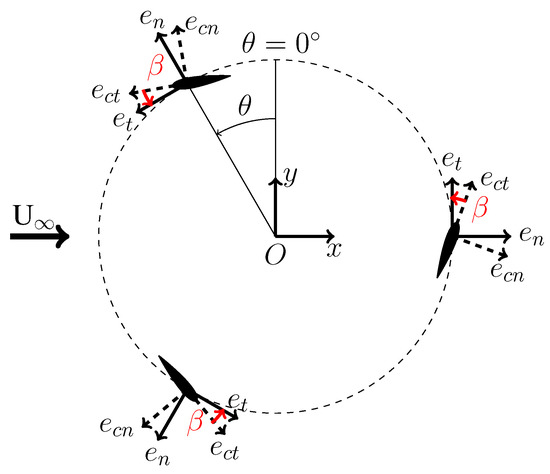
Figure 2.
Definition of the blade pitch angle . (): coordinate frame attached to the blade (i.e., remains parallel to the blade’s chord at all time). (): coordinate frame that follows the blade path with parallel to the tangent to the trajectory of the quarter chord at all time. The pitch angle is the angle between and .
The diameter is 1.6 m and the blade chord length is 0.15 m, which gives a solidity (Table 1). In this study, the flow speed is which is representative of flume tank flows and tidal streams. The blade chord Reynolds number (, with W the relative velocity (m/s) and the kinematic viscosity (m2/s)) varies between and at the tip speed ratio (with the turbine rotational speed). The characteristics of the SHIVA turbine are summarized in Table 1.

Table 1.
SHIVA turbine characteristics.
The turbine performances will be evaluated in terms of the coefficient of power (, Equation (1), with Q the turbine torque, the turbine rotational speed, and the water density, A the rotor swept area and the upstream flow speed), the coefficient of torque (, Equation (2), with R the turbine radius) and the coefficient of thrust (, Equation (3)).
3. Model and Numerical Methods
3.1. Computational Domain and Mesh
The two-dimensional computational domain is meshed with IcemCFD and the resulting multi-block structured grid is divided into three sub domains (Figure 3):
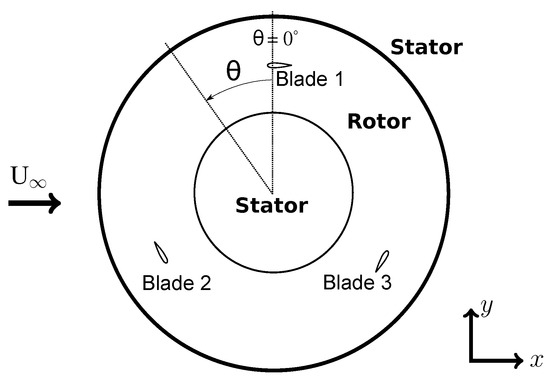
Figure 3.
Computational domain.
- an outer stator (square of side 60 D, not shown in Figure 3 for clarity);
- a rotating ring containing the 3 blades (rotor), located at the center of the outer stator; and
- an inner stator
The size of the outer domain (60 D) results from a sensitivity study carried out to make sure the dependence of the power coefficient to the distance between the turbine and the outer boundaries is negligible. Transient rotor/stator interfaces using the General Grid Interface (GGI) method are employed between the rotor and the 2 stators. Figure 4 shows a close view of the mesh around one blade. Each blade is meshed with 240 cells and the mesh has been refined close to them to reach (maximum value obtained on a blade and over a complete revolution at ) in order to resolve the viscous sublayer sufficiently and obtain a independent solution, according to Maître et al. [18]. The computational domain contains cells in total, which gives a good compromise between accuracy and computational time requirement for the variable pitch simulations.
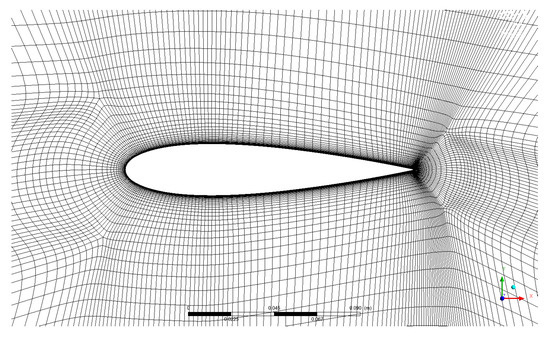
Figure 4.
Mesh in the vicinity of the blade.
3.2. Boundary Conditions and Settings
The inlet velocity is defined by 2 m/s at the inlet boundary. The inlet turbulence intensity is set to 10% with a viscosity ratio . The downstream boundary is set as an outlet boundary with a 0 Pa relative static pressure. Side boundaries are set as symmetry boundaries. Finally, the three blades are set as solid walls.
The time step size used in the simulations corresponds to a variation of the azimuthal angle of the turbine . This time step is widely used in literature and it has been verified that it leads to time step-independent solutions: a time step size corresponding to leads to a decrease in CP by only 0.6% at with a constant pitch (). At the lowest tip speed ratio (), blades experience dynamic stall and the time step is therefore reduced to which was found to provide time step-independent solution at this specific operating condition.
Convergence is defined by a difference between the power coefficient of two consecutive revolutions lower than 0.2% for both fixed pitch and variable pitch simulations.
3.3. Numerical Methods
Incompressible Unsteady Reynolds-Averaged Navier–Stokes (URANS) equations are solved using ANSYS CFX [40]. The (Shear Stress Transport) turbulence model [41] is used to model the Reynolds stress. This model is known to be suitable for lifting body applications when used with a mesh satisfying the criteria . It was shown to be one of the best RANS turbulence models for Darrieus wind turbines applications [21].
Advection terms are discretized using a hybrid first/second order scheme (“High Resolution” scheme in CFX) and the temporal discretization is achieved by using the implicit second-order backward Euler scheme. Calculations are run in double precision and are parallelized on 8 CPUs. The computational time required to simulate one turbine revolution with variable pitch is 3 h and 24 to 30 revolutions are necessary to reach the 0.2% convergence criterion, depending on the pitching law. In the fixed pitch case at 3, 43 turbine revolutions are necessary to reach the same level of convergence.
4. Validation
No experimental data are available at the moment on the turbine studied. It was chosen to validate the mesh and numerical procedure against published data of 2D lift and drag coefficients obtained on an airfoil. The pitching laws used in this study will aim at operating the blades at a constant angle of attack (noted ) over most of the revolution (see Section 7.1), and therefore it was considered relevant to use fixed angle of attack experiments for validation. The experimental work of Timmer [42] was selected as it employs a NACA0018 cross section, the same as the one used by the studied tidal turbine, and Reynolds number is which is close to the Reynolds number calculated on the blades of the turbine ( at ).
The computational domain used in this validation process is shown in Figure 5. The first O-grid around the blade section is kept the same as in the turbine case (see Figure 4), to ensure the validation process is relevant. The structured grid continues inside a 20 c-long-sides box. Between this box and the circular outer boundary located 50 c away from the blade section, an unstructured grid is used. At the inlet boundary, m/s (corresponding to in water, with ). The inlet turbulence intensity is set to 5% with a viscosity ratio . The turbulence intensity decays between the inlet boundary and the blade section to reach % around the blade, which corresponds to the turbulence intensity measured in [42]. All other numerical parameters are the same as detailed in Section 3.
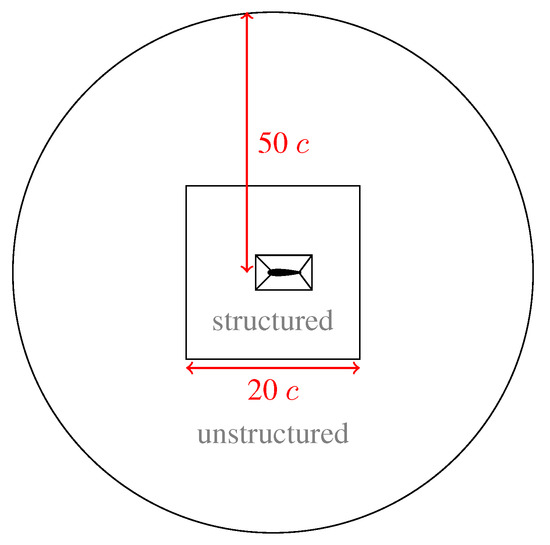
Figure 5.
Computational domain used in the validation step.
Angles of attack range from to . Figure 6 (left) shows that the lift coefficient predicted by the simulations (continuous line) agrees well with the experiments. It starts deviating from the experiments at , beyond the stall angle. The present simulations overestimate the drag coefficient compared to Timmer’s experiments (Figure 6 (right)). This is due to the presence of a laminar boundary layer on most of the airfoil in the experiments: a turbulent boundary layer is triggered by addition of zig-zag tape only on the pressure side at 80% of the chord. The laminar boundary layer is not taken into account in the fully turbulent simulations (SST). However, drag predictions agree well with the experiments carried out by Jacobs et al. [43] at the NACA variable density tunnel (VDT) where the turbulence intensity was higher than in Timmer’s case, which probably led to a much bigger part of the boundary layer to be turbulent [42]. Results show that the mesh used and the numerical settings are well adapted.
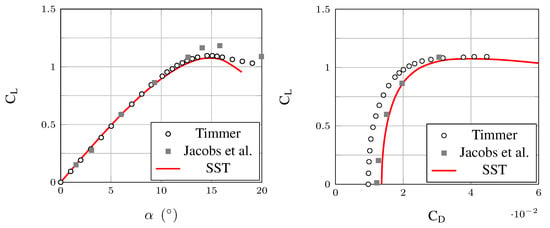
Figure 6.
Lift coefficient as a function of angle of attack (left) and as a function of the drag coefficient (right). Comparison of simulations with experiments from Timmer [42] and from Jacobs et al. [43].
5. Measurement of the Angle of Attack
To have a better understanding of the physics of the turbine and to properly assess whether the pitching laws work as expected, it was considered necessary to find a way to determine the angle of attack of the blades from the CFD results. The angle of attack () is generally calculated from Equation (4) [44], although this equation relies on several strong assumptions that make it not applicable to the downstream half (at least) of a vertical axis turbine.
Several researchers have worked on improving the angle of attack determination. The method we develop in this study is similar to the one found in [37]: we propose to use the location of the stagnation point on a blade (as a function of the reduced chord length ) and to compare it to the location of the stagnation point on the same airfoil at a fixed angle of attack. We can then derive an equivalent angle of attack of the blade at the corresponding azimuthal angle. The stagnation point can be easily located as it corresponds to the mesh node of maximum pressure on the blade. This method requires however to run fixed angle of attack simulations at a Reynolds number representative of the turbine operation and over the expected range of angles of attack that a turbine blade will experience. The interpolation of the fixed angle of attack data ( as a function of the non-dimensioned location of the stagnation point, ) is used to derive the equivalent angle of attack of the turbine blade.
This method is limited by the comparison between a rotating and a fixed blade, i.e., it does not take into account the pitching motion of the blades. However, the stagnation point is a local parameter which directly represents the angle of attack of the blade and allows this method to capture unsteady phenomenons (wake of another blade, wake of a tower). Moreover, in the present study the pitching laws aim to keep the blades’ angle of attack constant. The proposed method is therefore considered well adapted here.
6. Fixed Pitch Cases
In this section, we present results obtained with a constant pitch angle (Darrieus configuration) to evaluate the baseline performance of the turbine. Figure 7 shows that the optimum power coefficient () is predicted at (or close to) .
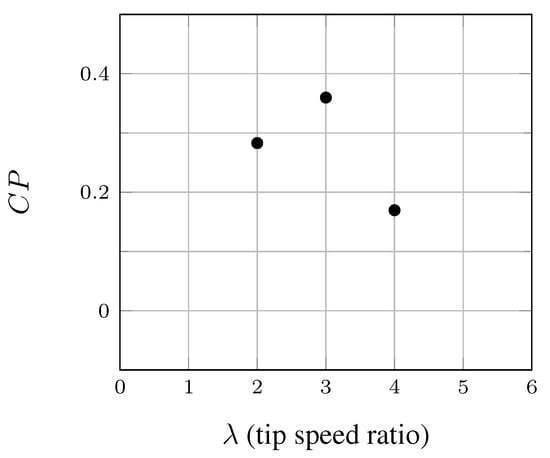
Figure 7.
Power coefficient of the fixed pitch turbine as a function of the tip speed ratio (), .
Figure 8 presents the torque coefficient () calculated for one blade of the turbine at (Blade 1 in Figure 3). Positive (driving) torque is only produced in the upstream half of the revolution. In the downstream half, the blade’s contribution to the torque generation is zero or slightly negative, which means that the blade does not harness power while traveling through the downstream half but slightly brakes the turbine instead. This is due to the significant decrease of the flow speed in the upstream half of the turbine.
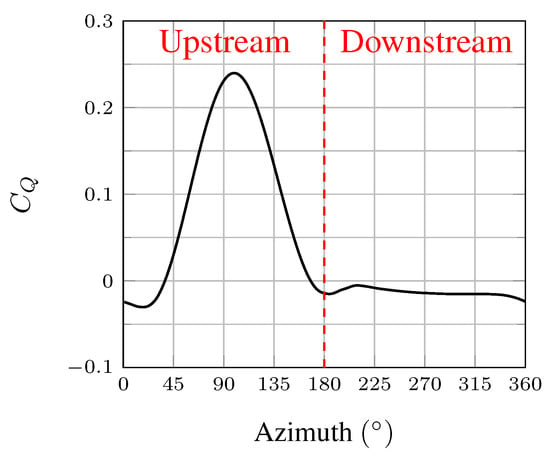
Figure 8.
Torque coefficient () of blade 1 at .
7. Variable Pitch Cases
7.1. Aim, Strategy, and Definition of the Pitching Laws
The aim of introducing a pitching motion to the blades is mainly to improve the turbine efficiency. However, when controlling the blades’ pitch angle, we can also work on reducing both torque ripple and thrust fluctuations, that are major drawbacks of Darrieus turbines. This can be achieved if the torque distribution is balanced between the upstream and downstream halves of the turbine.
Our strategy is to define different pitching laws for the upstream and downstream halves of a revolution. To that end, we split the revolution into four parts (Figure 9): Top, Upstream, Bottom, and Downstream. Specific laws will be defined for the Upstream and Downstream parts in order to achieve the aims defined at the beginning of this section. The Top and Bottom sections correspond to low or even negative torque generation (Figure 8). Pitching laws for these sections are thus cubic splines interpolations between three points to ensure a low drag around the azimuths and as well as the differentiability of the global pitching law. The three points are one end of the Upstream law, for (Top) or (Bottom), and the other end of the Downstream law. Cubic splines generate two polynomials for each Top and Bottom parts (Int 1 and Int 2 or Int 3 and Int 4, respectively, Figure 9). Therefore, the global pitching law (for one revolution) uses six polynomials and is continuous and differentiable.
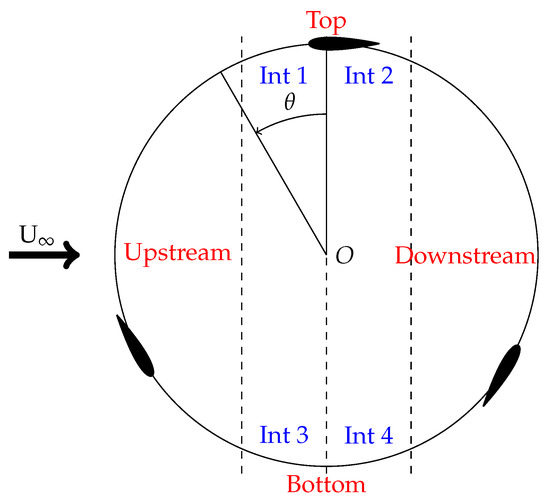
Figure 9.
Cutting up of the pitching laws areas.
Three pitching laws are tested in this study. They consist in limiting the angle of attack of the blades in the upstream half of the turbine to a given value: (PL1), (PL2), and (PL3), while almost not pitching the blades in the downstream half (Figure 10a,b). It means that when the angle of attack of the blade becomes larger than the target value (, or , as defined by Equation (4)) while traveling through the upstream half, the blade pitches to maintain the target value until the azimuthal angle where the angle of attack (as defined by Equation (4)) becomes lower than the target value (Figure 10a). Those pitching laws are based on the simplified angle of attack defined by Equation (4), which is considered valid as we focus on the upstream half only. Outside of the region of limited angle of attack, is modified (increased) by the cubic splines to ensure the differentiability of the global law (Figure 10). In the downstream half, a very small pitching motion (amplitude = ) is imposed (Figure 10b) to keep the mesh deformation active at anytime and avoid discontinuities in the simulations while having a negligible effect on the blades loading. Details of the equations defining the three pitching laws are given in Appendix A. Limiting the angle of attack to a given value is similar to an idea already proposed by Staelens et al. [11]. However, in our case we limit the angle of attack to a value different from the one corresponding to static stall, the global pitching laws are differentiable and different laws are applied in the upstream and downstream halves of a revolution. The approach is also similar to the one followed in [17] that aims to keep the bound circulation constant when blades travel along the upstream or downstream halves of the revolution.
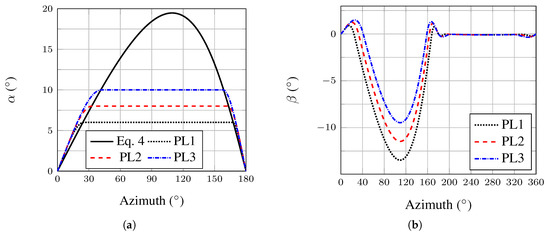
Figure 10.
(a) Blades’ angle of attack of the Darrieus turbine (from Equation (4)) and of the 3 variable-pitch cases; (b) pitching laws studied, .
7.2. Results with Pitch Control
7.2.1. Power Coefficient
The average power coefficient (, average of the instantaneous power coefficient , Equation (1), over one revolution) and its corresponding ripple factor (, Equation (5)), defined as the difference between the maximum and minimum values reached by CP over one turbine revolution, as used by Marsh et al. [24], are presented in Table 2. The three pitching laws proposed lead to a significant increase in power coefficient, with PL2 performing the best ( compared to the fixed pitch case). Figure 11 presents the instantaneous power coefficient over one revolution for all cases. The maximum CP reached by the turbine is approximately the same for all configurations but the cases with variable pitch show a significant increase in the minimum CP. The proposed pitching laws smooth the CP distribution, as was expected.

Table 2.
Power coefficient: average () and ripple factor () values for the fixed and variable pitch cases.
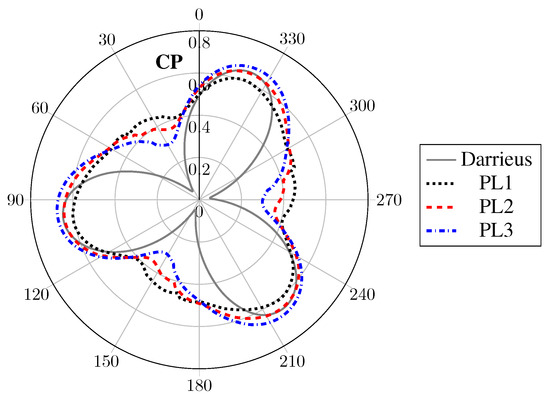
Figure 11.
Results of CP for the Darrieus and the pitching law cases, .
In fact, Table 2 shows that the power coefficient ripple factor is significantly affected by the pitching laws. The lower this value is, the smoother the CP distribution is. Its value is decreased by 37.1% with PL3 and by 66.7% with PL1. Therefore, out of the three pitching laws tested, it can be concluded that the lower the angle of attack in the upstream half of the turbine, the smoother the CP distribution (which also means the smoother the torque distribution as CP is directly related to the torque).
Figure 12 shows that the lower the angle of attack of the blades in the upstream half of the turbine, the lower the torque produced by the blades in the corresponding region but also the higher the torque produced in the downstream half. Even if the blades are not pitching when traveling through the downstream side of the turbine, their loading is significantly affected by the pitching law active on the upstream side. The decrease in peak torque generated in the upstream half is compensated by the gain in the downstream half and the gain in the region of low azimuth. In fact, for , the pitching laws increase the angle of attack of the blades compared to the Darrieus configuration (Figure 10a) which produces a higher torque. It results in an increased average power coefficient (Table 2). Figure 12 also confirms that the proposed pitching laws balance the torque distribution between the upstream and downstream halves of the turbine.
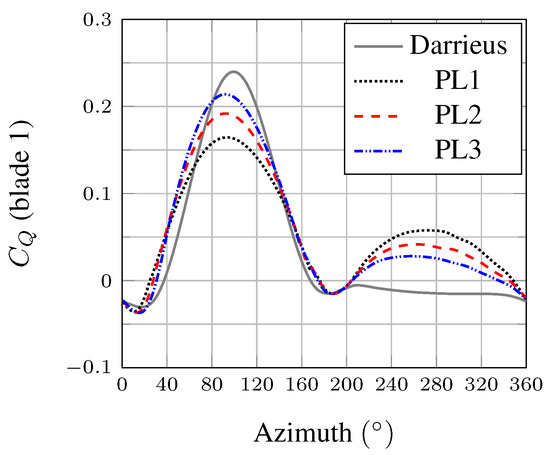
Figure 12.
Torque coefficient () of one blade for the Darrieus and the pitching law cases, .
The power needed to pitch the 3 blades, with PL2, corresponds to an averaged coefficient of power . This is significant as the overall performance is then only slightly better than the Darrieus configuration ( instead of ).
7.2.2. Thrust Coefficient
The thrust coefficient () is plotted in Figure 13 against the azimuth, over one turbine revolution. Similarly to the power coefficient (Figure 11), the proposed pitching laws smooth the thrust distribution. However, the average thrust is approximately the same in all cases (Table 3). Compared to the fixed pitch case, PL1 slightly reduces when PL2 gives a very similar value and PL3 slightly increases it (Table 3).
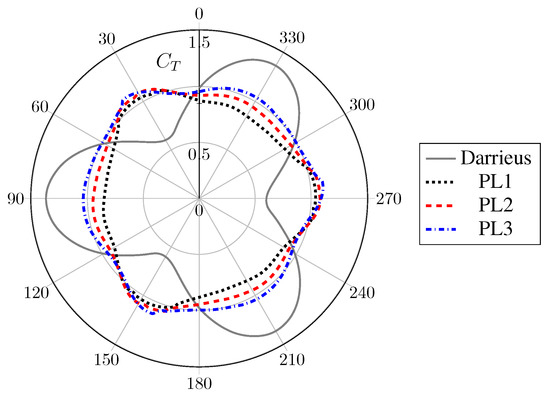
Figure 13.
Thrust coefficient () for the Darrieus and the pitching law cases, .

Table 3.
Thrust coefficient: average () and ripple factor () values for the fixed and variable pitch cases.
The thrust ripple factor (), defined the same way as the power coefficient ripple factor (, Section 7.2.1), is reduced by 74% (PL1) to 79% (PL2) with the proposed pitching laws (Table 3). Although the average thrust coefficient is similar in all cases, such reductions of its fluctuations are of particular interest for the design of the support structures and the foundations because of both the decrease in the maximum thrust generated by the turbine and the lower fatigue experienced by the structure [45].
7.2.3. Flow Field
Figure 14 shows that reducing the angle of attack of the blades in the upstream half of the turbine leads to a significant increase in the flow speed at the center of the rotor compared to the fixed pitch case. More energy is thus available for the blades traveling through the downstream side of the turbine, which explains the balance observed between the upstream and downstream halves in Figure 12. The streamwise velocity at the center of the turbine (Figure 15) is about 30% of the upstream velocity for the fixed pitch case while it varies from 60% (PL3) to 70% (PL1) of the upstream velocity with variable pitch. Although not very large even in the fixed pitch configuration, it can be noted that the velocity fluctuations at the center of the turbine are reduced with the proposed pitching laws (Figure 15).
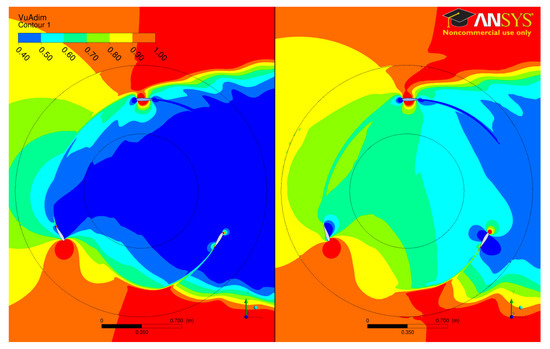
Figure 14.
Isocontours of non-dimensioned streamwise velocity () for the Darrieus (left) and the PL2 (right) cases, . Instantaneous flow field with blade 1 located at .
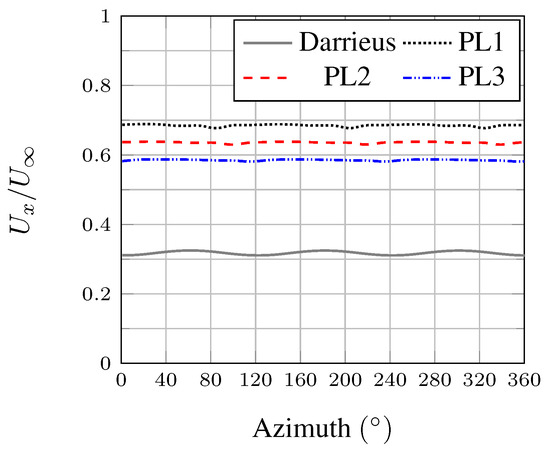
Figure 15.
Non-dimensioned flow speed () at the center of the turbine for the Darrieus and the pitching law cases, .
Figure 16 shows the angle of attack measured on one blade, from the CFD results, following the method presented in Section 5. The result of Equation (4) is plotted for comparison. The fixed pitch case (Darrieus) shows a similar pattern to Equation (4) in the upstream half of the turbine, although the measured angles of attack are lower than the predicted ones. This can be explained by the slower actual flow speed approaching the turbine compared to used in Equation (4), which is especially true with the fixed pitch case (Figure 17). The lower slope observed in the measurements at and may be explained by the fact that the flow speed is not perfectly aligned with the streamwise direction but slightly deviating from the turbine (on both sides), which results in a lateral component of the incoming flow. This lateral component reduces the blades’ angle of attack, particularly at these two azimuthal angles. The accuracy of the method detailed in Section 5, which is not known precisely, can also be questioned, but it is estimated by the authors to be affecting the data less than the two previous points. In the downstream half, the measured angles of attack are significantly lower than what Equation (4) predicts, as expected, due to the significantly slower flow speed at the center of the turbine compared to (Figure 15). The low angles of attack are consistent with the low torque values observed in this range of azimuth (Figure 12). Interestingly, the three variable pitch cases show a limitation of the angle of attack in the upstream half, as was targeted. However, the measured values are lower than the targets ( instead of (PL1), instead of (PL2), and instead of (PL3)). In the downstream half, the angle of attack is significantly increased compared to the fixed pitch case. For PL1, the blades’ angle of attack is even higher in the downstream half of the turbine than in the upstream half. However, the difference of flow speed between the upstream and downstream halves of the turbine makes that the torque generated in the upstream half is higher than in the downstream half. It can be noticed that the three pitching laws give similar angles of attack in the downstream half of the turbine.
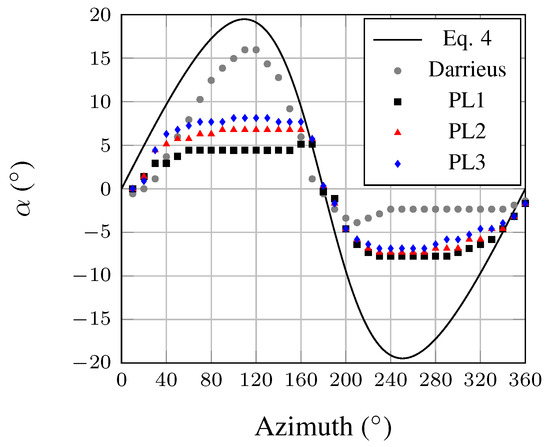
Figure 16.
Measured angle of attack for the Darrieus and the pitching law cases, .
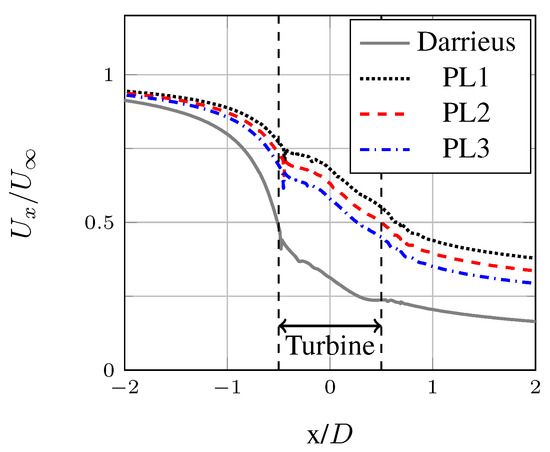
Figure 17.
Non-dimensioned instantaneous streamwise velocity () plotted on a line crossing the center of the turbine ( m) in the streamwise direction. Data for the Darrieus and the pitching law cases, .
Finally, Figure 17 presents the non-dimensioned streamwise velocity (instantaneous) uspstream, inside, and downstream of the turbine. It shows that the velocity is higher when the proposed pitching laws are used. However, inside the turbine, the velocity is slowed down following a very similar slope in all cases. Figure 17 also shows that at the location (in the wake), the streamwise velocity with PL2 is 34% of the far field value, while in the fixed pitch case it is only 16% of the far field value. Unfortunately, the refinement of the mesh used in the far wake does not allow us to conclude about the relevance of the pitching laws for farm applications.
8. Conclusions
2D URANS simulations have been employed to study the performance improvement that pitching blades can bring to a three-straight-blade vertical axis tidal turbine. The numerical procedure employed has been validated, before the fixed pitch () configuration of the turbine was studied to determine its power curve. The optimal tip speed ratio has then been selected to see how much the optimal performance of the turbine can be improved with controlled variable pitch.
The three pitching laws defined aimed to reduce the angle of attack of the blades in the upstream half of the turbine. No pitching motion was used in the downstream half. The decrease in angle of attack in the upstream half of a revolution led to a better balance of the torque generated in the upstream and downstream halves. In fact, when the proposed pitching laws were active, less energy was harnessed by the blades traveling through the upstream half of the turbine and thus, more energy was available in the downstream half, compared to the fixed pitch case.
The streamwise velocity, monitored at the center of the turbine, together with the measurement of the blades’ angle of attack (determined using an innovative method based on the location of the stagnation point) helped showing the effectiveness of the proposed pitching laws. The targeted angles of attack in the upstream half of the turbine were satisfactorily obtained. Those in the downstream half of the turbine were significantly increased compared to the fixed pitch case due to the increase in flow speed at the center of the turbine when the pitching laws are active. Blades were forced to operate close to the angle of attack corresponding to their optimal lift to drag ratio, which can explain the increase in average power coefficient.
Another interesting result of the proposed pitching laws is the significant reduction in both torque and thrust ripples which are of great interest for the mechanical design of such turbine. This is expected to make the support structure and the foundations cheaper. Out of the three pitching laws tested, the intermediate one, PL2, can be considered as the best one as it gives the highest average power coefficient, the lowest thrust ripple and a torque ripple which is decreased by more than 50% compared to the fixed pitch case.
However, the proposed pitching laws assume that the flow is in a specific direction and they should be modified if the flow direction changes (at least the reference azimuth should be updated). This would either require relatively expensive and complex electronic actuators and sensors or limit the applications to river turbines where the flow direction does not change with time. This problem is nevertheless the same whatever the pitching laws are and it is not specific to the ones proposed in this study.
The study has shown that the cost of the selected pitching laws is not negligible. Therefore, it would be interesting to take this parameter into account sooner when new laws are considered.
Further research will focus on the coupling between pitching laws in the upstream and downstream halves of a turbine in order to further improve the average power coefficient and smooth the torque and thrust ripples as much as possible. Studying the impact of such pitching laws on the power density of a tidal farm is also an interesting point that should be addressed.
Author Contributions
Conceptualization, P.-L.D., J.A.A., F.H.; methodology, P.-L.D.; software, P.-L.D., F.D.; validation, P.-L.D.; formal analysis, P.-L.D.; investigation, P.-L.D.; resources, P.-L.D.; data curation, P.-L.D.; writing—original draft preparation, P.-L.D.; writing—review and editing, P.-L.D.; visualization, P.-L.D.; supervision, F.D., J.A.A. and F.H.; project administration, J.A.A. and F.H.; funding acquisition, J.A.A. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. Details of the Pitching Laws
Appendix A provides the details of the three pitching laws proposed in this article: PL1, PL2, and PL3, presented in Table A1, Table A2 and Table A3, respectively. corresponds to the azimuth where the (increasing) blade angle of attack (according to Equation (4)) reaches the target value defined as (PL1), (PL2), or (PL3), in the upstream half of the turbine (see Figure 10a). corresponds to the azimuth where the (decreasing) blade angle of attack (according to Equation (4)) reaches the target value, in the upstream half of the turbine. Similar parameters and are defined in the downstream half although a negligible pitching motion is imposed there. The range of validity of the laws is defined in Table A4.
The aim is to provide a framework as flexible as possible regarding the choice of upstream and downstream laws. and could be different than the values selected in the upstream half of the turbine.
The upstream law, downstream law, Int 1, Int 2, Int 3, and Int 4 equations, together, make the global pitching law: (plotted in Figure 10b).

Table A1.
Details of pitching law PL1 ( is always in degrees () in the expressions).
Table A1.
Details of pitching law PL1 ( is always in degrees () in the expressions).
| [] | 25 |
| Upstream law [] | 6 - |
| [] | 167 |
| [] | 193 |
| Downstream law [] | |
| [] | 335 |
| Int 1 [] | |
| Int 2 [] | |
| Int 3 [] | |
| Int 4 [] |

Table A2.
Details of pitching law PL2 ( is always in degrees () in the expressions).
Table A2.
Details of pitching law PL2 ( is always in degrees () in the expressions).
| [] | 33 |
| Upstream law [] | 8 - |
| [] | 163 |
| [] | 197 |
| Downstream law [] | |
| [] | 327 |
| Int 1 [] | |
| Int 2 [] | |
| Int 3 [] | |
| Int 4 [] |

Table A3.
Details of pitching law PL3 ( is always in degrees () in the expressions).
Table A3.
Details of pitching law PL3 ( is always in degrees () in the expressions).
| [] | 42 |
| Upstream law [] | 10 - |
| [] | 158 |
| [] | 202 |
| Downstream law [] | |
| [] | 318 |
| Int 1 [] | |
| Int 2 [] | |
| Int 3 [] | |
| Int 4 [] |

Table A4.
Range of validity (for ) of each sub-part of the pitching law.
Table A4.
Range of validity (for ) of each sub-part of the pitching law.
| Pitching Law | Range of Validity |
|---|---|
| Int 1 | |
| Upstream law | |
| Int 2 | |
| Int 3 | |
| Downstream law | |
| Int 4 |
References
- REN21. Renewables 2020 Global Status Report; Technical Report; REN21: Paris, France, 2020. [Google Scholar]
- International Renewable Energy Agency. Renewable Energy Statistics 2020; Technical Report; International Renewable Energy Agency: Abu Dhabi, UAE, 2020. [Google Scholar]
- International Energy Agency. Renewables 2020—Analysis and Forecast to 2025 (Executive Summary); Technical Report; International Energy Agency: Paris, France, 2020. [Google Scholar]
- Coles, D.; Blunden, L.; Bahaj, A. Assessment of the energy extraction potential at tidal sites around the Channel Islands. Energy 2017, 124, 171–186. [Google Scholar] [CrossRef]
- Darrieus, G. Turbine Having Its Rotating Shaft Transverse to the Flow of the Current. U.S. Patent 1835018A, 8 December 1931. [Google Scholar]
- Sutherland, H.; Berg, D.; Ashwill, T. A Retrospective of VAWT Technology; Technical Report SAND2012-0304; SANDIA: Albuquerque, NM, USA, 2012. [Google Scholar]
- Templin, R. Aerodynamic Performance Theory for the NRC Vertical-Axis Wind Turbine; Technical Report Rept. LTR-LA-160; NASA: Washington, DC, USA, 1974.
- Dabiri, J.O. Potential order-of-magnitude enhancement of wind farm power density via counter-rotating vertical-axis wind turbine arrays. J. Renew. Sustain. Energy 2011, 3, 043104. [Google Scholar] [CrossRef]
- Kirke, B.; Lazauskas, L. Limitations of fixed pitch Darrieus hydrokinetic turbines and the challenge of variable pitch. Renew. Energy 2011, 36, 893–897. [Google Scholar] [CrossRef]
- Kirke, B.; Lazauskas, L. Enhancing the Performance of Vertical Axis Wind Turbine Using a Simple Variable Pitch System. Wind Eng. 1991, 15, 187–195. [Google Scholar]
- Staelens, Y.; Saeed, F.; Paraschivoiu, I. A straight-bladed variable-pitch VAWT concept for improved power generation. In Proceedings of the 22nd ASME Wind Energy Symposium held in Conjunction with the 41st Aerospace Sciences Meeting & Exhibit, Reno, NV, USA, 6–9 January 2003; pp. 146–154. [Google Scholar]
- Hwang, I.; Lee, Y.; Kim, S. Optimization of cycloidal water turbine and the performance improvement by individual blade control. Appl. Energy 2009, 86, 1532–1540. [Google Scholar] [CrossRef]
- Lazauskas, L.; Kirke, B. Modeling passive variable pitch cross flow hydrokinetic turbines to maximize performance and smooth operation. Renew. Energy 2012, 45, 41–50. [Google Scholar] [CrossRef]
- Paillard, B.; Hauville, F.; Astolfi, J. Simulating variable pitch crossflow water turbines: A coupled unsteady ONERA-EDLIN model and streamtube model. Renew. Energy 2013, 52, 209–217. [Google Scholar] [CrossRef][Green Version]
- Kirke, B.; Paillard, B. Predicted and measured performance of a vertical axis wind turbine with passive variable pitch compared to fixed pitch. Wind Eng. 2017, 41, 74–90. [Google Scholar] [CrossRef]
- Chen, B.; Su, S.; Viola, I.; Greated, C. Numerical investigation of vertical-axis tidal turbines with sinusoidal pitching blades. Ocean Eng. 2018, 155, 75–87. [Google Scholar] [CrossRef]
- De Tavernier, D.; Ferreira, C.; van Bussel, G. Airfoil optimisation for vertical-axis wind turbines with variable pitch. Wind Energy 2019, 22, 547–562. [Google Scholar] [CrossRef]
- Maître, T.; Amet, E.; Pellone, C. Modeling of the flow in a Darrieus water turbine: Wall grid refinement analysis and comparison with experiments. Renew. Energy 2013, 51, 497–512. [Google Scholar] [CrossRef]
- McNaughton, J.; Billard, F.; Revell, A. Turbulence modelling of low Reynolds number flow effects around a vertical axis turbine at a range of tip-speed ratios. J. Fluids Struct. 2014, 47, 124–138. [Google Scholar] [CrossRef]
- Paillard, B.; Astolfi, J.; Hauville, F. URANSE simulation of an active variable-pitch cross-flow Darrieus tidal turbine: Sinusoidal pitch function investigation. Int. J. Mar. Energy 2015, 11, 9–26. [Google Scholar] [CrossRef]
- Balduzzi, F.; Bianchini, A.; Maleci, R.; Ferrara, G.; Ferrari, L. Critical issues in the CFD simulation of Darrieus wind turbines. Renew. Energy 2016, 85, 419–435. [Google Scholar] [CrossRef]
- Guilbot, M.; Barre, S.; Balarac, G.; Bonamy, C.; Guillaud, N. A numerical study of Vertical Axis Wind Turbine performances in twin-rotor configurations. J. Physics Conf. Ser. 2020, 1618, 052012. [Google Scholar] [CrossRef]
- Amet, E. Simulation Numérique D’une Hydrolienne à Axe Vertical de Type Darrieus. Ph.D. Thesis, Institut Polytechnique de Grenoble, Grenoble, France, 2009. [Google Scholar]
- Marsh, P.; Ranmuthugala, D.; Penesis, I.; Thomas, G. Three-dimensional numerical simulations of straight-bladed vertical axis tidal turbines investigating power output, torque ripple and mounting forces. Renew. Energy 2015, 83, 67–77. [Google Scholar] [CrossRef]
- Orlandi, A.; Collu, M.; Zanforlin, S.; Shires, A. 3D URANS analysis of a vertical axis wind turbine in skewed flows. J. Wind Eng. Ind. Aerodyn. 2015, 147, 77–84. [Google Scholar] [CrossRef]
- Li, C.; Zhu, S.; Xu, Y.; Xiao, Y. 2.5 D large eddy simulation of vertical axis wind turbine in consideration of high angle of attack flow. Renew. Energy 2013, 51, 317–330. [Google Scholar] [CrossRef]
- Guillaud, N.; Balarac, G.; Goncalvès, E.; Zanette, J. Large Eddy Simulations on Vertical Axis Hydrokinetic Turbines—Power coefficient analysis for various solidities. Renew. Energy 2020, 147, 473–486. [Google Scholar] [CrossRef]
- Massie, L.; Ouro, P.; Stoesser, T.; Luo, Q. An Actuator Surface Model to Simulate Vertical Axis Turbines. Energies 2019, 12, 4741. [Google Scholar] [CrossRef]
- Zhao, R.; Creech, A.; Borthwick, A.; Venugopal, V. Aerodynamic analysis of a two-bladed vertical-axis wind turbine using a coupled unsteady RANS and actuator line model. Energies 2020, 13, 776. [Google Scholar] [CrossRef]
- Grondeau, M.; Guillou, S.; Mercier, P.; Poizot, E. Wake of a ducted vertical axis tidal turbine in turbulent flows, LBM actuator-line approach. Energies 2019, 12, 4273. [Google Scholar] [CrossRef]
- Edwards, J.; Danao, L.; Howel, R. Novel Experimental Power Curve Determination and Computational Methods for the Performance Analysis of Vertical Axis Wind Turbines. J. Sol. Energy Eng. 2012, 134. [Google Scholar] [CrossRef]
- Gosselin, R. Analysis and Optimization of Vertical Axis Turbines. Ph.D. Thesis, Faculté des Sciences et de Génie, Université Laval, Québec, QC, Canada, 2015. [Google Scholar]
- Raciti Castelli, M.; Englaro, A.; Benini, E. The Darrieus wind turbine: Proposal for a new performance prediction model based on {CFD}. Energy 2011, 36, 4919–4934. [Google Scholar] [CrossRef]
- Elsakka, M.; Ingham, D.; Ma, L.; Pourkashanian, M. CFD analysis of the angle of attack for a vertical axis wind turbine blade. Energy Convers. Manag. 2019, 182, 154–165. [Google Scholar] [CrossRef]
- Melani, P.F.; Balduzzi, F.; Ferrara, G.; Bianchini, A. How to extract the angle attack on airfoils in cycloidal motion from a flow field solved with computational fluid dynamics? Development and verification of a robust computational procedure. Energy Convers. Manag. 2020, 223, 113284. [Google Scholar] [CrossRef]
- Jost, E.; Klein, L.; Leipprand, H.; Lutz, T.; Krämer, E. Extracting the angle of attack on rotor blades from CFD simulations. Wind Energy 2018, 21, 807–822. [Google Scholar] [CrossRef]
- Bianchini, A.; Balduzzi, F.; Ferrara, G.; Ferrari, L. A computational procedure to define the incidence angle on airfoils rotating around an axis orthogonal to flow direction. Energy Convers. Manag. 2016, 126, 790–798. [Google Scholar] [CrossRef]
- Drela, M. XFOIL: An Analysis and Design System for Low Reynolds Number Airfoils. In Low Reynolds Number Aerodynamics; Mueller, T.J., Ed.; Springer: Berlin/Heidelberg, Germany, 1989; pp. 1–12. [Google Scholar]
- Delafin, P.L. Analyse de L’écoulement Transitionnel Sur un Hydrofoil: Application Aux Hydroliennes à Axe Transverse Avec Contrôle Actif de L’angle de Calage. Ph.D. Thesis, Université de Bretagne Occidentale, Brest, France, 2014. [Google Scholar]
- CFX. ANSYS CFX Solver Theory Guide; ANSYS: Canonsburg, PA, USA, 2011; Volume 14.0. [Google Scholar]
- Menter, F. Two-Equation Eddy-Viscosity Turbulence Models for Engineering Applications. AIAA J. 1994, 32, 1598–1604. [Google Scholar] [CrossRef]
- Timmer, W. Two-dimensional low-Reynolds number wind tunnel results for airfoil NACA 0018. Wind Eng. 2008, 32, 525–537. [Google Scholar] [CrossRef]
- Jacobs, E.; Sherman, A. Airfoil Section Characteristics as Affected by Variations of the Reynolds Number; Technical Report, NACA Rept. 586; NACA: Washington, DC, USA, 1937. [Google Scholar]
- Paraschivoiu, I. Wind Turbine Design: With Emphasis on Darrieus Concept; Presses inter Polytechnique: Montréal, QC, Canada, 2002. [Google Scholar]
- Zeiner-Gundersen, D. Turbine design and field development concepts for tidal, ocean, and river applications. Energy Sci. Eng. 2015, 3, 27–42. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).