Abstract
The paper examined Ti3C2Tx MXene (T—OH, Cl or F), which is prepared by etching a layered ternary carbide Ti3AlC2 (312 MAX-phase) precursor and deposited on a polycaprolactone (PCL) electrospun membrane (MXene-PCL nanocomposite). X-ray Diffraction analysis (XRD) and Scanning Electron Microscopy (SEM) indicates that the obtained material is pure Ti3C2 MXene. SEM of the PCL-MXene composite demonstrate random Ti3C2 distribution over the nanoporous membrane. Results of capacitance, inductance, and phase shift angle studies of the MXene-PCL nanocomposite are presented. It was found that the frequency dependence of the capacitance exhibited a clear sharp minima in the frequency range of 50 Hz to over 104 Hz. The frequency dependence of the inductance shows sharp maxima, the position of which exactly coincides with the position of the minima for the capacitance, which indicates the occurrence of parallel resonances. Current conduction occurs by electron tunneling between nanoparticles. In the frequency range from about 104 Hz to about 105 Hz, there is a broad minimum on the inductance relationship. The position of this minimum coincides exactly with the position of the maximum of the phase shift angle—its amplitude is close to 90°. The real value of the inductance of the nanocomposite layer was determined to be about 1 H. It was found that the average value of the distance over which the electron tunnels was determined with some approximation to be about 5.7 nm and the expected value of the relaxation time to be τM ≈ 3 × 10−5 s.
1. Introduction
Mxenotronics is a currently growing discipline [1], within the framework of which the application of MXenes in electronics, electrical devices, and photovoltaics is being carried out. To extend a field of application, new structural features and properties of MXenes need to be considered and reviewed. For example, supercapacitors and batteries are only starting to employ Mxene-based components as substitutes for Li-ion accumulators [2,3].
MXenes in photovoltaics by far were applied for hole/electron transport layers and electrodes. As solar cell elements, they demonstrate much better performance in energy conversion, reduced trap state, and better charge transfer [4,5,6,7]. Yu. Gogotsi et al. demonstrated the possible application of electrospun MXene/Carbon Nanofibers as supercapacitor electrodes for energy storage and opened a wide range of applications [8].
The flexible electronics concept was introduced several decades ago and conductive polymers, organic semiconductors, and amorphous silicon have since found many applications in different areas [9]. Despite the progress in this area, new challenges arise due to the increasing application of implantable systems with high flexibility and biocompatibility [10]. Cardiac patches, electrodes, brain and muscle stimulators, and neural guide conduits require the application of conductive biocompatible polymer membrane with satisfactory electronic properties [11]. Conductive polymers and membranes with conductive materials, including graphene and carbon nanotubes, are widely used in biomedical device development [12,13]. Over the next decade, MXenes was applied to take flexible electronics to a whole new level.
MXenes are a special type of 2D material that consists of thin exfoliated sheets of transition metal carbide or nitride [14]. Typically, to obtain an MXene, a simple method is used: top-down selective etching of MAX phase in hydrofluoric acid to remove the element (Al, Si or Ga). Based on the initial M materials, MXenes are divided into single (Ti2C, V2C, Ti3C2, Ti4N3 and double transition metals (Mo2TiC2, Mo2ScC2). The finite stage of MXene development is intercalation and/or delamination, in which the MXene can improve initial characteristics and achieve even more versatile properties. This t is ensured through contact with surface functional groups (H, F, and O) in the obtained solution [15].
From the practical side, undoubtedly, this material has many crossovers with graphene, including properties [16]. However, in a number of applications, it surpassed the eminent competitor, both in electrical characteristics and manufacturability. Ti3C2, as one of the most popular MXenes, exhibits a high conductivity of 4600 ± 1100 S cm−1 for each individual flake and field effect electron mobility of 2.6 ± 0.7 cm2 V−1 s−1. The electrical resistance of layered Ti3C2 is only one order of magnitude bigger than that of individual flakes that grant an exceptional electron transport between layers in comparison to the majority of other 2D materials [17].
An illustrative case of high technological effectiveness could be the application of MXenes in flexible antennas in the 2.4 GHz band (Wi-Fi and Bluetooth bands) for wearable electronics. They require high flexibility to withstand repeated bending during operation. An MXene solution based on Ti3C2, in this case, is not only mechanically stable but also emits radio signals 50 times better than graphene analogues and 300 times better than antennas with a radiating structure made of Ag. However, the manufacturing of “MXene nanoantenna” is several times easier, and as a bonus, the material is water-dispersable, which are very important for contact with the environment [18,19].
Some research works have demonstrated the application of MXene for deposition on flexible membranes for development of a triboelectric nanogenerator [20]. They reported on a poly(vinylidene fluoride-trifluoroethylene) (PVDF-TrFE)/MXene nanocomposite material with superior dielectric constant and high surface charge density. Application of an electrospun membrane loaded by MXene prevents active material from delaminating the substrate during folding or bending.
The aim of this study was to measure the AC properties (phase shift angle, capacitance and inductance) of a MXene-PCL nanocomposite, analyse the results obtained, and determine the AC conduction mechanism of the MXene-PCL nanocomposite based on them.
2. Materials and Methods
2.1. MXene Synthesis and Characterization
Ti3C2Tx MXene (T—OH, Cl or F) was prepared by etching a layered ternary carbide Ti3AlC2 (312 MAX-phase) precursor with a mixture of hydrochloric (HCl) acid and lithium fluoride (LiF) by the MILD method [21]. The etching solution was prepared as follows: 200 mL of 12M HCl (37%) was added to 50 mL of DI-water to yield 250 mL of 9M HCl; then 16 g of LiF was added under stirring. The mixture was placed in a plastic container (volume 500 mL). 10 g of the Ti3AlC2 powder with mean particle size of less than 40 μm was gradually added to the etching solution. The reaction mixture was held at 25 °C under constant stirring for 24 h. The aluminum layer in Ti3AlC2 was removed by hydrofluoric acid formed an in-situ via reaction between HCl and LiF, leaving Ti3C2 flakes weakly bonded through Van der Vaals interaction. After etching, the obtained MXene slurry was rinsed with DI-water via repetitive centrifugation (10 min each cycle at 3500 rpm) to remove excess acid. After each cycle the acidic supernatant was decanted, followed by the addition of a fresh portion of DI-water, redispersion, and another centrifuging cycle. Rinsing was performed until the pH value of supernatant reached 6. The obtained wet slurry containing MXene was subject to a delamination process in order to separate MXene Ti3C2 flakes into a water-based colloidal solution.
The delamination was assisted by intercalation of Li+ ion between Ti3C2 flakes following separation into the colloidal solution [21]. The solution for the intercalation-assisted delamination was prepared as follows: 2 g of lithium chloride (LiCl) was added to 40 mL of DI-water in a plastic container (volume 50 mL). Two gram of the etched MXene slurry was added to the prepared solution. The process was performed at 35 °C for 24 h under constant stirring. After intercalation in the LiCl solution, the MXene slurry was rinsed via repetitive cycles of centrifuging (10 min each cycle at 3500 rpm), decanting the supernatant, and redispersion in freshy added DI-water until the supernatant turns from transparent to black in color, signaling MXene flakes’ separation into colloidal solution. At this stage, the MXene supernatant after centrifuging is collected and stored. Rinsing is performed until the supernatant after centrifugation becomes transparent again. The collected supernatant containing MXene is centrifuged at 6000 rpm for 1 h to obtain concentrated MXene sediment.
The prepared MXene is characterized by X-Ray Diffraction (XRD) and Scanning Electron Microscopy (SEM) methods. Powder X-Ray diffraction patterns were obtained using the Rigaku Ultima-IV diffractometer (Rigaku Corporation, Tokyo, Japan). The XRD investigation MXene slurry was placed on a square glass samples with a side of 24 mm in the form of a thin non-transparent film and let to dry in vacuum. The SEM investigation was performed using the Tescan Mira 3 LMU (Tescan Orsay Holding, a.s., Brno, Czech Republic) scanning electron microscope. For the SEM investigation, drops of diluted MXene colloidal solution in water were placed on pieces of silicon wafer and let to dry in vacuum.
For crystal structure/phase studies, a TEM-125K (Selmi, Ukraine) was used at the accelerating voltage of 125 kV. In order to create test samples, the Mxenes solution was applied onto NaCl crystals (drop-drying method) with a carbon film that further dissolved in water and was then caught by the microscopic grid made of Cu. The calculation of the selected area’s electron diffraction (SAED) patterns were performed with an Al standard.
2.2. PCL Electrospun Membrane Synthesis
Polycaprolactone (PCL), Mn = 45,000 g/mol, was obtained from Sigma Aldrich (Saint Louis, MI, USA). Chloroform (purity ≥ 99%), ethanol (purity 95.4–96.8%), and acetic acid (purity ≥ 99%) were obtained from Penta Chemicals (Prague, Czech Republic). Polymer solution was prepared as described in [22]. Electrospun fiber mats was produced by the conventional method of electrospinning with the following parameters: 25 kV power, 180 mm distance between the syringe and the collector, and spinning speed of 12 mL/h.
2.3. MXene Deposition on PCL Membranes
The MXene solution was prepared as follows: 0.02 g of thawed concentrated MXene slurry containing about 15% MXene by mass was dispersed in 4 mL DI-water under sonication for 1 min in an ultrasonic bath with power of 50 V at 40 kHz. This solution is used to soak PCL scaffolds. PCL is known to be a hydrophobic polymer; therefore, PCL scaffolds (sized around 5 mm/14 mm) are first treated in 1M Sodium hydroxide (NaOH) solution for four hours at 30 °C in order to improve the hydrophilic properties of the PCL surface and then washed in DI-water for 24 h. As-treated PCL scaffolds are put in small glass containers (20 mL) with 4 mL of the MXene solution. The container was filled with argon to prevent oxidation of MXenes. The container was sonicated for 5 min in an ultrasonic bath with 50 V at 40 kHz and left for 3 h to let MXene soak into the PCL scaffold. Then, the PCL scaffolds were removed from the MXene solution, immersed in DI water for 1 s to remove excess of the solution, and dried on a filter paper. The MXene-PCL nanocomposite scaffolds were subject to the same coating procedure a second time.
The structure of the as-spun and MXene-deposited membranes was assessed using a scanning electron microscope (SEO-SEM Inspect S50-B, FEI, Brno, Czech Republic; accelerating voltage—15 kV) paired with an energy-dispersive X-ray spectrometer (AZ-tecOne with X-MaxN20, Oxford Instruments plc, Abingdon, UK).
3. Experimental
Alternating current measurements of MXene-PCL nanocomposites were carried out using a test stand developed and constructed at the Department of Electrical Devices and High Voltage Technology, Lublin University of Technology (Lublin, Poland). View of the test stand is shown in Figure 1 [23].
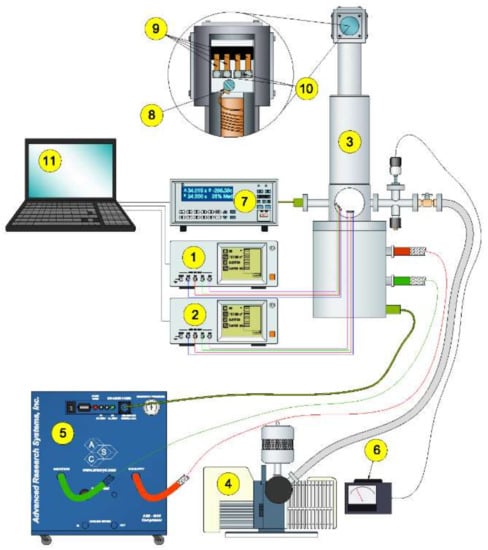
Figure 1.
Test stand for determining electrical parameters [23]: 1 and 2—HIOKI 3532 LCR HiTESTER impedance meters, 3—helium cryostat head, 4—vacuum pump, 5—compressor of helium cryostat, 6—vacuum gauge, 7—LakeShore 335 temperature controller, 8—silicon temperature sensor, 9—test contacts, 10—test samples, 11—computer.
The stand includes the CS 204AE-FMX-1AL helium cryostat (Advanced Research Systems, Inc., Macungie, PA, USA) (3–7), which allows to measure temperatures in the range from 15 K to 450 K with an accuracy of 0.002 K. The entire measurement takes place under vacuum (~0.2 atm.), which is achieved using a vacuum pump (4). The tested nanocomposite sample (11) is placed in the cryostat head (3) and cooled in a closed circuit by means of a helium compressor (5). Temperature detection and control are carried out by a system consisting of a silicon sensor (8), a temperature controller (7), and a connected heater mounted in the cryostat head. Electrical parameters were measured every 1 K in the range 15 K–20 K, every 2 K in the range 20 K–40 K, every 3 K in the range 40 K–151 K, and every 7 K in the range 151 K–305 K. For the AC measurements, 3532 LCR HiTESTER (Hioki, Japan) impedance meters were used (1). The impedance meters have the ability to measure four of the following 14 electrical parameters: Z—impedance, Y—admittance, φ—phase shift angle, tg δ—loss factor, Q—Q factor, CS—static capacitance in series equivalent circuit, CP—static capacitance in parallel equivalent circuit, LS—inductance in series equivalent circuit, LP—inductance in parallel equivalent circuit, RS—effective resistance in series equivalent circuit, G—conductance, RP—effective resistance in parallel equivalent circuit, X—reactance, B—susceptance. The amplitude of the voltage applied to the test sample was U = 0.4 V. The impedance meter and the temperature controller are connected to a computer (11), where the measurement results are saved as xls files.
A program, written in the C++ environment, was developed to control the impedance meters and control and record electrical and temperature parameters. The program has the ability to select any four electrical parameters for simultaneous measurement and allows to enter specific values for measurement voltage and frequency range.
In this study, the AC properties of the MXene-PCL nanocomposite samples were investigated. At both ends of the tested nanocomposite, a thin layer (~10 µm) of silver paste was applied to eliminate the transition resistance at the point between the sample and the contacts (Figure 2).
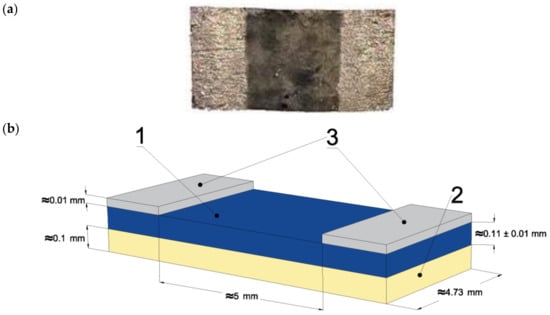
Figure 2.
Photo (a) and view (b) of the nanocomposite sample: 1—MX nanocomposite layer, 2—dielectric substrate, 3—silver paste contacts.
As shown in Figure 2, the AC current applied at the ends of the nanocomposite layer flows between the two contacts. This means that both the real and imaginary components of the current, which consists of capacitive and inductive currents, flow between the same contacts. This means that these three currents flow in parallel in the nanocomposite layer. Therefore, a parallel equivalent impedance meter scheme was chosen to measure the alternating current parameters of the nanocomposite. Measurements were performed in the temperature range of 20 K to 305 K (70 temperatures) and frequencies from 50 Hz to 1 MHz with a step of 50 points per decade (about 240 frequency values). The following parameters were measured: phase shift angle φ, inductance Lp, and capacitance Cp in the parallel equivalent scheme.
As is known [24], there are two components of current in AC parallel circuits consisting of RLC elements. The first one, the real (or resistive) component, is in a phase with applied sinusoidal voltage. Its value is determined by the formula:
where, IR—real component of the current, RP—parallel circuit resistance, U—applied sinusoidal voltage.
The second component of the current, called the imaginary component, is determined by the value of susceptance B:
where, B—susceptance, ω = 2π—circular frequency, CP—parallel circuit capacitance, LP—parallel circuit inductance.
Using the value of susceptance B, the value of the imaginary component of current II is calculated:
where, II—imaginary component of the current.
The vector of the imaginary component is perpendicular to the real current vector. The value of the angle modulus between these vectors is 90°. The sign of this angle depends on which component of susceptance (capacitive or inductive) from Formula (2) is higher. When the capacitive component is higher, the sign of the angle is negative and when the inductive component is higher, the sign of the angle is positive. One of the basic alternating current parameters of the parallel RLC circuit is the phase shift angle between the vector of the real current component and the resultant current vector (Figure 3). The phase shift angle value is calculated from the formula:
where, φ—phase shift angle.
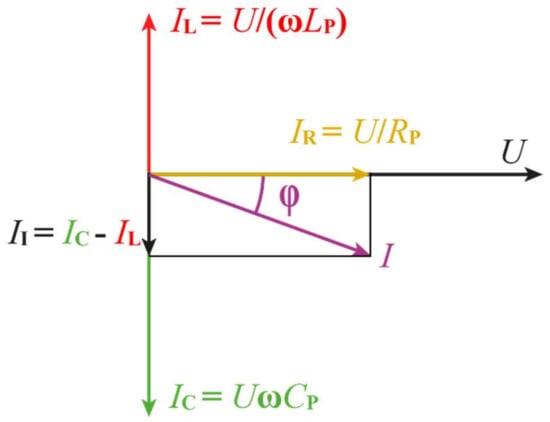
Figure 3.
Phase diagram of the AC sinusoidal current’s real and imaginary components for a parallel RLC circuit in case of IC > IL: U—applied voltage vector, II—real component of imaginary current, IC—capacitive component of imaginary current, IL—inductive component of imaginary current, I—resultant current, φ—phase shift angle, IU = IC−IL—parallel circuit current, RP—resistance, CP—capacitance, LP—inductance.
Figure 3 shows a phasor diagram of the AC sinusoidal current’s real and imaginary components for a parallel RLC circuit in case the capacitive component is larger than the inductive component.
In parallel RLC circuits at the resonant circular frequency ωr = 2πfr, a parallel resonance [25] occurs. From Formula (2) for susceptance, it follows that at the value of resonant circular frequency ωr, the modules of capacitive and inductive components of susceptance are equal and their difference is equal to zero.
The value of the resonant circular frequency for a parallel circuit is determined by the formula:
where, ωr—resonant circular frequency.
Let us now examine how to measure the experimental frequency dependence of the capacitance and inductance of the MXene-PCL nanocomposites using the 3532 LCR HiTESTER impedance meter. The method of measurement and formulas for calculating the parameters are given in the user manual [26]. According to the user manual, after applying sinusoidal voltage U to the tested circuit, in the first stage, the meter calculates the phase shift angle φ between the vectors of voltage U and current I (see Figure 3) and the circular frequency ω = 2πf. In the second stage, based on three values: U, I, and φ, the other parameters of the circuit under test are calculated using the formulas given in the manual. For the purposes of this work, the following formulas are needed:
where, Y—admittance.
where, B—susceptance.
where, CPM—the capacitance value measured by the impedance meter.
We will now determine the relationship between the actual value of the capacitance of the parallel circuit and the value measured by the impedance meter. By substituting into Equation (8) the value of susceptance B from Equation (2) we obtain:
where, CP—actual value of capacitance in the tested parallel circuit, LP—actual value of inductance in the tested parallel circuit.
Formula (9) shows that the measured capacitance is smaller than the actual one. The result of the capacitance measurement coincides with its actual value only if there is no inductance in the circuit under test. The value of the measured capacitance in the case of φ > 0° should not be taken into account.
By substituting the value of the resonant circular frequency (5) into the formula for the measured value of capacitance (9), we obtain:
Formula (10) shows that at the resonant circular frequency, the measured capacitance of the circuit should be zero. When the circular frequency ω approaches the resonant value from the side of lower values, the value of the measured capacitance becomes smaller and smaller, and at the resonant circular frequency ωr, its value, theoretically, is zero. A further increase in the circular frequency will increase the measured capacitance. This means that there will be a clear minimum in the frequency dependence of the measured capacitance. It is one of the criteria that allows to observe the parallel resonance and determine the value of the resonant circular frequency ωr.
According to the user manual, the meter performs the calculation of inductance based on the formula:
By substituting into Formula (11) the value of susceptance given by Formula (2), we obtain:
Formula (12) shows that the inductance of a parallel circuit is measured correctly only in the absence of capacitance.
By substituting the value of the resonant circular frequency (5) into Formula (12) for the measured inductance, we obtain:
As the frequency approaches its resonance value, the measured inductance begins to increase, reaching its maximum value at the resonance frequency. A further frequency increase causes the measured value to decrease.
4. Results and Discussion
Figure 4a–c represented results of XRD and SEM analysis of prepared MXene, respectively. The XRD pattern in Figure 4a indicates that the obtained material is pure Ti3C2 MXene. SEM demonstrates that MXene has a typical shape, with a size from 25 to 500 nm.
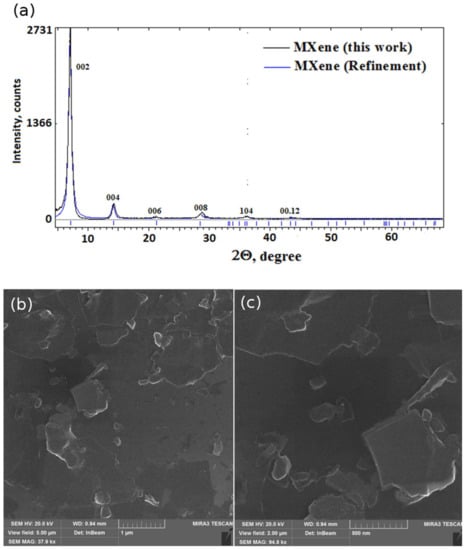
Figure 4.
XRD (a) and SEM (b,c–different magnifications) analyses of the prepared MXene.
Figure 5a,b represents the dark-field images of pure Ti3C2Tx MXene samples. It seems that the samples exhibit good exfoliation. In some regions, MXenes are almost transparent to the electron beam because the thickness is close to several atomic distances [27]. Further analysis of SAED from the flakes revealed the Ti3C2 hexagonal lattice of high crystallinity [28]. Titanium distribution in the crystal lattice ensures good electrical conductivity. Depending on the concentration and thickness (periodicity of layers), the MXenes crystal structure varies from single crystal to polycrystalline-like. Lattice parameters were increased in the tabular Ti3C2 structure (hexagonal P63/mmc symmetry) a = 3.183 Å (atab = 3.071 Å), c = 15.68 Å (ctab = 15.131 Å). Test samples were then exposed to air for two weeks to analyse the oxidation behaviour. As a result of the analysis, the crystallinity of the samples was dropped (Figure 5c). Some flakes exhibit the transition to titanium dioxide, but only local decomposition to oxygen compounds was observed. Moreover, under the thermal effect of the electron beam, the structure of the MXene layers was changed instantly. White areas changed to black, which meant that oxidation of the specimens was only partial and potentially reversible after the thermal annealing.

Figure 5.
TEM images of the structure of Ti3C2 MXenes obtained by the method of dripping onto a substrate and their electron diffraction patterns: high-concentration drips (a), low concentration flakes (b), oxidation test (c).
After MXene was coated on the PCL photomicrograph, an EDS scan was taken (Figure 6). It seems that the distribution of fibers is random, with an average diameter of 1.41 ± 0.33 μm. The structure is similar to pristine PCL with unified MXene flakes along the fibers. MXene nanosheets occupy most of the space, which is very good for electron transport. The chemical composition derived from EDS is consistent with articles by other authors [8,29]. The most intensive signal (~74%) is from the C-Kα line since both PCL and Ti3C2 contains it. O, F, and Cl signals suggest that MXene exhibits a binding with the functional groups. No Al concentration was observed. Thus, it was completely removed during the precursor exfoliation.

Figure 6.
EDS spectrum of the MXene-PCL nanocomposite with element Wt.% distribution (insertion (A)). Insertion (B)—optical (1) and (2) and SEM images (3) and (4) of PCL-MXene composite scaffolds after first and second coating iteration, respectively.
Samples of the MXene-PCL nanocomposites were chosen for the analysis in order to obtain clear and original results.
Figure 7 shows the frequency dependence of the capacitances measured in the parallel equivalent scheme. The figure shows six waveforms in the temperature range of 20 K–305 K, selected from 70 waveforms obtained during the measurements. The measurements, in order to precisely determine the positions of the minima, were performed at 50 points per decade.
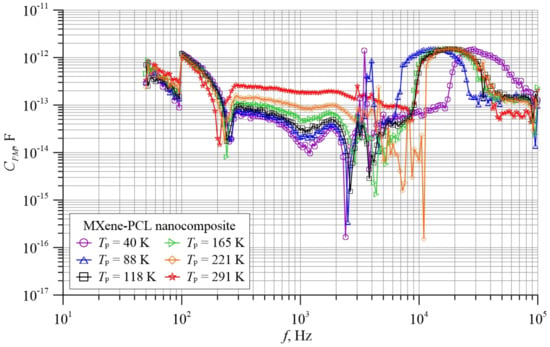
Figure 7.
Frequency dependence of capacitance CPM of the MXene-PCL nanocomposite for six selected temperatures measured in a parallel scheme.
The capacitance values measured in the parallel equivalent circuit diagram slowly decrease with increasing frequency. The values are in the range of 1.7 × 10−12 pF to about 4 × 10−13 pF. Such low capacitance values occur due to the shape of the sample, together with the contacts applied to it (Figure 2). As can be seen from the figure, the area of the measured sample is equal to the cross-sectional area of the nanocomposite layer. The thickness of the dielectric is equal to the distance between the contacts. This results in the capacitance of the sample being very low. From the frequency dependence of the measured capacitances, shown in Figure 7, it can be seen that the MXene-PCL nanocomposite exhibits a series of minima against a background of a slow decrease of capacitance with frequency increase. Some of them are very clear. These are minima at frequencies of around 100 Hz, around 200 Hz, around 1100 Hz and around 2200 Hz. In the frequency range above 2200 Hz, further sharp minima are observed. However, determining the frequency values at which they are observed is relatively difficult due to their very close proximity. The only thing is that these minima practically disappear at room temperature. A broad clear maximum is observed in the frequency range from about 104 Hz to about 105 Hz. The position of the maximum, depending on the temperature, occurs at frequencies from about 1.3 × 104 Hz to about 3 × 104 Hz. In the frequency range above 105 Hz, oscillations of large amplitudes occur that completely interfere with the capacitance measurements. Oscillations of this type were not observed by us for other types of nanocomposites [30,31,32]. The oscillations are probably related to the unique structure of the MXene-PCL nanocomposites. Explanation of their causes requires additional research, far beyond the scope of this article. Accordingly, this paper focuses on the analysis of the behaviour of the minima observed in the frequency range up to 105 Hz. Therefore, in Figure 7, Figure 8 and Figure 9, the frequency range is limited to 105 Hz.
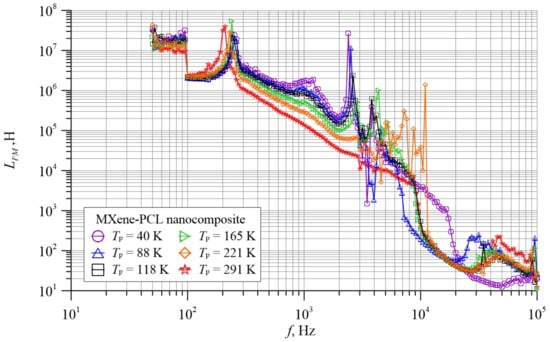
Figure 8.
Frequency dependence of inductance LPM of the MXene-PCL nanocomposite for six selected temperatures measured in a parallel substitution scheme.
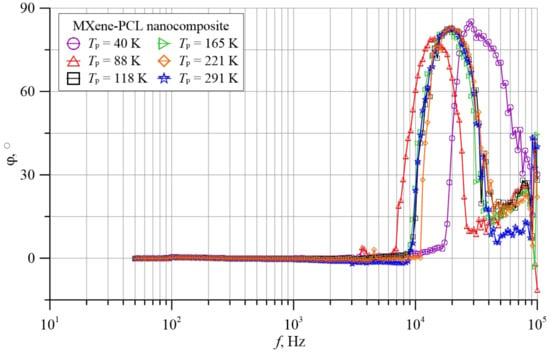
Figure 9.
Frequency dependence of phase shift angle φ of the MXene-PCL nanocomposite for six selected temperatures measured in a parallel substitution scheme.
As can be seen from Equation (10), the capacitance values at the minima should be zero. This is consistent for a parallel RLC circuit, whose resistance is zero. In the case of non-zero resistance, the depth of the minimum is smaller, which is also observed in Figure 7. A second factor, reducing the depth of the minimum, is that measurements were made for 50 points per decade. This means that it was difficult to precisely hit the value of the resonant frequency. As a result of missing such hits, the measured capacitance for a given minimum does not reach zero. The minimum at 2200 Hz is closest to the resonance frequency, and its depth is more than two orders. In conventional parallel RLC circuits consisting of discrete elements, there is only one minimum. This is due to the fact that the values of the discrete elements are constant values. However, in nanocomposites, capacitance and inductance values are functions of the frequency, morphology, and structure of the nanomaterial [33,34]. This allows a greater number of frequencies to occur in the nanocomposite at which parallel resonance is observed.
We will now analyse the effect of temperature on the minima occurring at frequencies of around 100 Hz, around 200 Hz, around 1100 Hz, and around 2200 Hz. It can be seen from Figure 7 that the depth of the minimum at about 100 Hz practically does not depend on the temperature. A similar situation is also characteristic for the minimum at around 200 Hz. An increase in the temperature value causes a slight shift of the minimum position into the area of lower frequencies. The temperature increase practically does not change position of minimum around 1100 Hz, but it clearly reduces its depth. At 291 K, this minimum almost disappears. The next minimum at around 2200 Hz shifts slightly into the higher frequency region as the temperature increases. The depth of this minimum reaches more than two orders and decreases rapidly with increasing temperature. The depth of minima, located in the frequency region (104–105) Hz, also decreases rapidly with increasing temperature and disappears at room temperature. This means that there are at least two types of tunneling between nanoparticles in the nanocomposite, which become apparent in the form of CPM minima. This is evidenced by the different way in which the depth of the minima changes under the influence of temperature. For the minima of the first group (at 100 Hz and 200 Hz), their depth practically does not depend on temperature. For the second group (1100 Hz and 2200 Hz and minima in the frequency region (104–105) Hz)), the depth of the minima decreases very rapidly with increasing temperature. At room temperature, the minima of the second group practically disappear. The two different types of tunneling can be related to the different morphologies and structures of the nanoparticles between which tunneling takes place.
The frequency dependence of the MXene-PCL nanocomposite inductance measured in the parallel equivalent scheme is shown in Figure 8. Only 6 waveforms, selected from 70, obtained during the tests for temperatures ranging from 20 K to 305 K, are shown in the figure. As can be seen from Figure 8, there are a number of maxima on the frequency dependence of LPM(f). Their positions exactly match the positions of the minima on the frequency dependence of the measured capacitances, shown in Figure 7. This means that the frequencies at which inductance maxima occur are the frequencies for which parallel resonance occur. The value of inductance measured at maxima for a circuit not containing resistance should be infinity—Formula (13). The presence of a resistance causes the value at maximum of the measured inductance to be lower. A second factor lowering the value at maximum is that the measurements were made with a step of 50 points per decade. As a result of the simultaneous interaction of these two factors, the inductance at the maximum does not reach infinity. The maximum at 2200 Hz is closest to the resonance frequency. Its amplitude is about two orders. Wide clear minima are observed on the LPM(f) relation at frequencies from about 1.3 × 104 Hz to about 3 × 104 Hz—depending on the temperature. The positions of the minima of the measured inductances (Figure 8) exactly coincide with the positions of the maxima on the frequency dependence of the measured capacitances (Figure 7). In the frequency range above 2200 Hz to about 10,000 Hz, further sharp maxima are observed.
Figure 9 shows 6 selected from 70 frequency dependencies of the MXene-PCL phase shift angle φ, obtained for temperatures ranging from 20 K to 305 K. The measurements, in order to precisely determine the frequencies in which the maximum occurs, were made at 50 points per decade.
The figure shows that up to a frequency of about 103 Hz, the values of the phase shift angle are close to 0°. With further frequency increase practically up to about 104 Hz, the values of the phase shift angle are weakly negative. It follows that in this frequency region, the capacitive component of the conductivity is slightly larger than the inductive component. Beyond a frequency of 104 Hz, the values of the phase shift angle become positive. As can be seen from Figure 9, in the frequency region from about 104 Hz to about 105 Hz, an increase in positive phase angle values is observed and a maximum is reached, the value of which ranges from about 80° to about 85°, depending on the temperature. A further increase in frequency causes a decrease in the value of the phase shift angle—the values of which remain positive. This means that in this frequency range, the inductive component of the conductivity of the MXene-PCL nanocomposite is many times greater than the capacitive component. This phase shift angle behavior occurs in a range of nanocomposites containing conductive phase nanoparticles in dielectric matrices [35,36,37,38,39,40]—both capacitive and inductive components were observed in them.
It should be noted that in conventional RLC circuits, inductance occurs, as a rule, in the form of a coil wound from a thin conductor. In the nanocomposite layers studied, there were no windings (Figure 2). The occurrence of a phase shift in them, characteristic of coils, is related to the conduction mechanism based on the phenomenon of electron tunneling between neighbouring nanoparticles [41]. This paper [41] presents an impedance model and its experimental verification for nanocomposites in which conductivity takes place by electron tunneling between nanoparticles. The model assumes that there are nanometer-sized potential wells in the material where electrons are located (Figure 10). Distances between the wells are also nanometric. This allows the electrons to tunnel between neighbouring wells of the potential, defined by the following formula [42,43]:
where, r—distance over which the electron is tunneling, α—value close to the inverse of the radius of location of the tunneling electron (so called Bohr radius), β—numerical coefficient close to 2 [44], ΔW—activation energy of electron tunneling, k—Boltzman’s constant, T—temperature, P0—numerical factor.
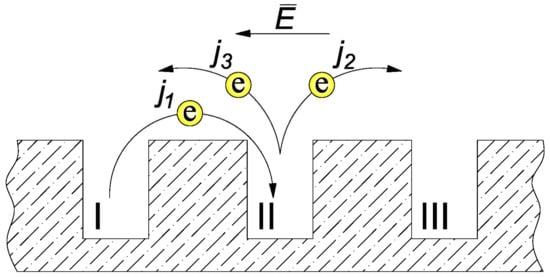
Figure 10.
Potential wells and possible directions of electron tunneling: E—electric field, j1—current of density, j2—second component of the current density, j3—third component of current density.
The electric field forcing the current flow is weak and does not change the probability of electrons tunneling from one neutral potential well to another. The field only leads to an asymmetry of the jumps, related to the Debye factor [44]:
where, e—charge of the electron, r—distance the electron tunneling, E—electric field strength.
The value of a weak electric field can be defined as:
where, E0—amplitude of the electric field strength.
Under the influence of this field (on the tunneling path between adjacent potential wells) flow, a current of density (Figure 10):
where, σ—conductivity.
The electron, after tunneling into the second well, remains there for relaxation time τ. The value of the relaxation time is a function of the temperature and the distance over which the electron tunnels [45]. After the relaxation time, two variants of tunneling are possible. In the first one, the electron with probability p tunnels to the next (third) well in the direction determined by the forcing electric field (Figure 10). This results in a second component of the current density:
In the second variant, the electron after relaxation time τ tunnels from the second well to the first one (Figure 10) with probability (1−p). This results in the appearance of the third component of current density:
Equations (17)–(19) can be used for the temperature region T < 500 K, when values p(T)τ << 1 (see Formula (14)).
This means that the resultant current density, due to electron tunneling, has both a real and an imaginary component.
We will now extract the real and imaginary components of the tunneling current density from Equations (17)–(19). The current density j1 is in the same phase as the forcing electric field and therefore contains only the real component.
The j2 and j3 components are in an equal phase. Hence:
From Formulas (17) and (20), it follows that the real component of the tunneling current density is:
and the imaginary component of the current density due to tunneling is:
The phase shift angle between the real (21) and imaginary (22) components of the current density due to tunneling is:
By substituting the value of θ into Equations (21) and (22), we obtain:
A material of the same composition as the nanocomposite, in the absence of tunneling in it, has a dielectric permittivity εr > 1. This means that, according to Maxwell’s second equation, there will be a component of capacitive current flowing through the material that is not related to electron tunneling. The density of this current component is described by the following formula [46]:
where, εr—relative dielectric permittivity, ε0—dielectric permittivity of vacuum.
The total density of the imaginary component of the current, taking into account Formulas (22) and (26), is:
The phase shift angle between the real and imaginary components of the current density is:
From Equation (28), it follows that the value of the phase shift angle is a function of conductivity σ, dielectric permittivity εr, relaxation time τ and frequency ω. From Equation (28), it follows that in the low frequency region, where:
Formula (28) transforms to the form:
Equation (30) shows that for low frequency values (ωτ << 2σp), the phase shift angle φ is negative and close to zero.
In the paper [41], computer simulations were performed based on Equation (28). They show that with further increase of frequency depending on the conductivity value σ, the following cases can occur:
- (a)
- For low conductivity values in the low frequency range, the phase shift angle φ is approximately equal to 0° and a decrease of the phase shift angle value to about −90° with stabilization at this level is observed. This situation occurs, according to Equation (28), in the high frequency region when:
An indication diagram for this case is shown in Figure 11.
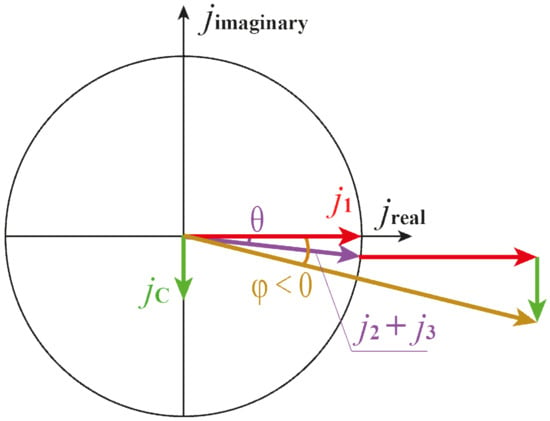
Figure 11.
Indication diagram of current density for the case of dominant capacitive type conduction: j1—current density determined by Formula (17), j2 + j3—current density determined by Formula (20), θ = –ωτ—angle between the vectors j1 and (j2 + j3), φ—phase shift angle determined by Formula (28).
- (b)
- For average conductivity values, the phase shift angle φ waveforms show values close to zero in the low frequency region. An increase of frequency causes an increase of negative values until a minimum is reached. After crossing zero, positive values of the phase shift angle occur, passing through the maximum and then decreasing the phase shift angle. The zero crossing at frequency ωr corresponds to the phenomenon of parallel resonance. From Equations (22) and (28), it follows that φ = 0° occurs when:
An indication diagram for the case of parallel resonance is shown in Figure 12.
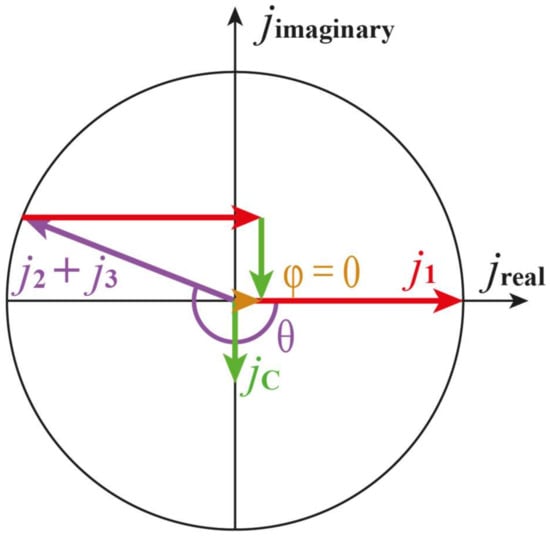
Figure 12.
Indication diagram of current density for the case of parallel resonance: j1—current density determined by Formula (17), j2 + j3—current density determined by Formula (20), θ = –ωτ—angle between the vectors j1 and (j2 + j3), φ = 0°—phase shift angle determined by Formula (32).
- (c)
- For high values of conductivity, when σ >> εrε0ω and medium values of frequency, positive values of the phase shift angle occur. When the maximum is reached, the value of which φmax ≈ 90°, a decrease in the phase shift angle value takes place. An indication graph for this case is shown in Figure 13.
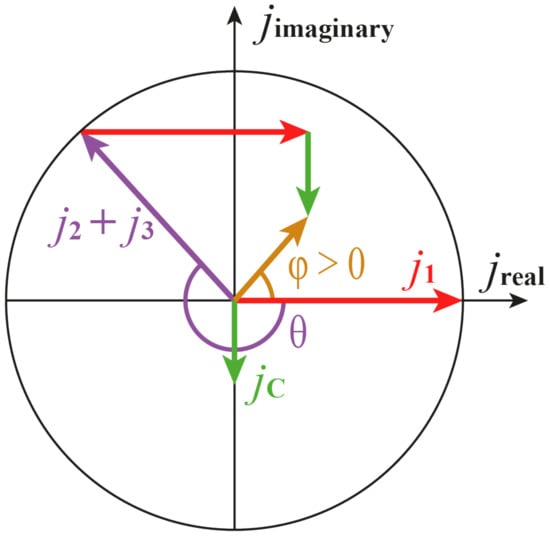 Figure 13. Indication diagram of current density for the case of dominant inductive type conduction: j1—current density determined by Formula (17), j2 + j3—current density determined by Formula (20), θ = –ωτ—angle between the vectors j1 and (j2 + j3), φ—phase shift angle determined by Formula (32).
Figure 13. Indication diagram of current density for the case of dominant inductive type conduction: j1—current density determined by Formula (17), j2 + j3—current density determined by Formula (20), θ = –ωτ—angle between the vectors j1 and (j2 + j3), φ—phase shift angle determined by Formula (32).
Figure 12 shows that the angle θ between the j1 and j2 + j3 components at the resonance frequency is slightly more than −π. From the value of the frequency at the inductance maximum of about 8×104 Hz and using Formula (23), it is possible to determine the values of the relaxation times τ for the individual sharp maxima observed in Figure 8. For maximum at frequency f1 ≈ 100 Hz, τ1 ≈ 5×10−3 s; for f2 ≈ 200 Hz, τ2 ≈ 2.5 × 10−3 s; for f3 ≈ 1100 Hz τ3 ≈ 4.5 × 10−4 s, and for f4 ≈ 2200 Hz, τ4 ≈ 2.3×10−4 s.
As can be seen from Figure 9, in the frequency range f < 104 Hz, there are close to zero values of the phase shift angle. This means that resistive conduction is dominant in this range. The series resonance observed in this range (Figure 7 and Figure 8) prove that apart from resistive conduction, capacitance and inductance are simultaneously present. If the nanocomposite layer had a resistive conductivity and only one of the imaginary components, inductive or capacitive, the resonance of the currents would not occur.
This means that in the MXene-PCL nanocomposite, at least two types of nanoparticles are involved in tunneling in this frequency range. This is due to differences in the behavior of the amplitudes and frequencies of the individual minima induced by the temperature change. The two types of tunneling occurring in this frequency range belong to the case of average conductivity values, described in (b), Formula (28) and (32). An indication diagram is shown in Figure 12. In the region from about 104 Hz to about 105 Hz, there is a broad maximum of the phase shift angle, values in which are 80° ≤ φ ≤ ~85° (Figure 9). The position of the maximum is at frequencies from about 1.3 × 104 Hz to about 3 × 104 Hz, depending on the temperature. This situation is described in (c)—Equation (28). The appearance of a wide maximum at frequencies from about 104 Hz to about 105 Hz means that this is associated with a case of dominant conduction of the inductive type—as shown in case (c). This shows that a third type of tunneling occurs in the MXene-PCL nanocomposite. From the value of the frequency at the maximum of the phase shift angle, the expected value of the relaxation time was determined. At 40 K, it is τM ≈ 8 × 10−5 s. The occurrence of at least three types of tunneling in the MXene-PCL nanocomposite, with different relaxation times, is probably related to differences in the morphology and structure of the nanoparticles between which tunneling takes place and the distances over which electrons tunnel.
From calculations based on the amplitude and frequency of the position of the wide maximum (Figure 8), the actual value of the inductance of the MXene-PCL nanocomposite layer was determined to be LP (4 × 104 Hz) ≈ 1 H. It is important to consider what causes the nanocomposite layer to have such a high inductance. For this, we use the formula for the inductance value of a conventional coil without a ferromagnetic core given in [25]:
where, μ0—magnetic permittivity of vacuum, n—number of coils per unit length, v—volume of coil.
By transforming Equation (33), we obtain the “distance between neighbouring coil windings” from the nanocomposite:
Using this formula, obviously with a high degree of approximation, it is possible to determine the geometric dimensions of a single “coil” formed by the nanocomposite. By substituting into Equation (34) the values of LP (4 × 104 Hz) ≈ 1 H, μ0 and the values of geometrical dimensions of the nanocomposite sample from Figure 2, we obtain the “distance between neighbouring coil windings” of the nanocomposite, which is about ∆l ≈ 5.7 nm. As noted above, conduction in the nanocomposite occurs by electron tunneling between neighbouring nanoparticles. After each jump, the electron remains for a relaxation time τ in the nanoparticle on which it has tunneled and thus causes a phase shift between the real and imaginary components of the current density due to tunneling (see Equations (18)–(23)). There is some analogy here with an induction coil, where each coil affects the phase shift of the current. This may mean that the “distance between neighbouring coil windings” from the nanocomposite obtained from Equation (34) is, to a large approximation, the expected value of the distance over which the electron tunnels.
5. Conclusions
Flaked MXene nanosheets received a single crystal structure of Ti3C2 without intermetallic phases. Preliminary analyses show their relatively fast oxidation rate, so their deposition onto PCL scaffolds was conducted in an inert atmosphere (Ar). EDS chemical analysis of coated PCL membranes confirmed the absence of Al and revealed the uniform distribution of MXenes linked to termination groups.
The studies of capacitance, inductance, and phase shift angle of the MXene-PCL nanocomposite were performed with an impedance meter at 50 points per decade in the measurement frequency range from 50 Hz to 1 MHz at temperatures from 20 K to 305 K.
On the frequency dependence of the capacitance, there are clear sharp minima at about 100 Hz, about 200 Hz, about 1100 Hz, and about 2200 Hz. There is a wide maximum in the area from about 104 Hz to about 105 Hz. The position of the maximum occurs at frequencies from about 1.3 × 104 Hz to about 3 × 104 Hz, depending on the temperature.
Measurements of the nanocomposite inductance have shown that there are clear sharp maxima on its frequency dependence, the position of which exactly agrees with the position of minima for the frequency dependence of capacitance. This indicates the presence of parallel resonances in the nanocomposite.
In the frequency range from about 104 Hz to about 105 Hz, there is a wide minimum in the inductance dependence, the position of which exactly agrees with the position of the maximum of the phase shift angle. Based on the value in this minimum, the actual value of the inductance of the tested nanocomposite layer (about 1 H) was calculated. The expected value of the distance over which the electron tunnels (about 5.7 nm) was also determined with some approximation.
It was found that in the frequency region of up to about 104 Hz, the values of the phase shift angle are close to zero. In the higher frequency region, there is a wide maximum of up to 85° on the φ(f) relationship. From the frequencies in the phase shift angle maximum, the expectation value of the relaxation time was determined. At 40 K, it is τM ≈ 8 × 10−5 s.
At least three types of tunneling between nanoparticles were found to occur in the MXene-PCL nanocomposite. This is due to differences in the behavior of the amplitudes and frequencies of individual parallel resonances induced by temperature changes. This is probably due to differences in the morphology and structure of the nanoparticles between which tunneling occurs and the distances through which electrons tunnel.
Author Contributions
Conceptualization, T.N.K., A.D.P., M.P. and O.G.; methodology, T.N.K., A.D.P., M.P., O.G. and V.Z.; software, P.R. and P.O.; validation, T.N.K. and M.P.; formal analysis, T.N.K. and P.G.; investigation, T.N.K., P.G., K.K, P.R., P.O., V.B. (Vladimir Burranich), K.D., V.Z., V.B. (Vitalii Balitskyi), V.S. and I.B.; resources, P.G. and K.K.; data curation, P.G., K.K., P.R., P.O., K.D., V.B. (Vitalii Balitskyi), V.S. and I.B.; writing—original draft preparation, T.N.K., P.G., V.B. (Vladimir Burranich) and I.B.; writing—review and editing, T.N.K., A.D.P., M.P. and O.G.; visualization, T.N.K., P.G. and V.B. (Vitalii Balitskyi); supervision, T.N.K. and A.D.P.; funding acquisition, T.N.K., K.K., P.R. and P.O. All authors have read and agreed to the published version of the manuscript.
Funding
MXene synthesis and electrospinning membrane preparation were supported by EU Horizon 2020 MSCA RISE grants: 777810, 778157 and by the National Research Found of Ukraine (grant 2020.02/0223). The research was supported by the subsidy of the Ministry of Education and Science (Poland) for the Lublin University of Technology as funds allocated for scientific activities in the scientific discipline of automation, electronics and electrical engineering—grants: FD-20/EE-2/702, FD-20/EE-2/703, FD-20/EE-2/705 and FD-20/EE-2/707.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Shukla, V. The tunable electric and magnetic properties of 2D MXenes and their potential applications. Mater. Adv. 2020, 1, 3104–3121. [Google Scholar] [CrossRef]
- Ling, Z.; Ren, C.E.; Zhao, M.-Q.; Yang, J.; Giammarco, J.M.; Qiu, J.; Barsoum, M.W.; Gogotsi, Y. Flexible and conductive MXene films and nanocomposites with high capacitance. Proc. Natl. Acad. Sci. USA 2014, 111, 16676–16681. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ming, F.; Liang, H.; Huang, G.; Bayhan, Z.; Alshareef, H.N. MXenes for Rechargeable Batteries Beyond the Lithium-Ion. Adv. Mater. 2021, 33, 2004039. [Google Scholar] [CrossRef]
- Agresti, A.; Pazniak, A.; Pescetelli, S.; Di Vito, A.; Rossi, D.; Pecchia, A.; Auf der Maur, M.; Liedl, A.; Larciprete, R.; Kuznetsov, D.V.; et al. Titanium-carbide MXenes for work function and interface engineering in perovskite solar cells. Nat. Mater. 2019, 18, 1228–1234. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Z.; Li, Y.; Liang, C.; Yu, G.; Zhao, J.; Luo, S.; Huang, Y.; Su, C.; Xing, G. In Situ Growth of MAPbBr3 Nanocrystals on Few-Layer MXene Nanosheets with Efficient Energy Transfer. Small 2020, 16, 1905896. [Google Scholar]
- Wang, J.; Cai, Z.; Lin, D.; Chen, K.; Zhao, L.; Xie, F.; Su, R.; Xie, W.; Liu, P.; Zhu, R. Plasma Oxidized Ti3C2Tx MXene as Electron Transport Layer for Efficient Perovskite Solar Cells. ACS Appl. Mater. Interfaces 2021, 13, 32495–32502. [Google Scholar] [CrossRef]
- Yang, L.; Dall’Agnese, Y.; Hantanasirisakul, K.; Shuck, C.E.; Maleski, K.; Alhabeb, M.; Chen, G.; Senehira, Y.; Jena, A.K.; Shen, L.; et al. SnO2-Ti3C2 MXene electron transport layers for perovskite solar cells. J. Mater. Chem. A 2019, 7, 5635–5642. [Google Scholar] [CrossRef]
- Levitt, A.S.; Alhabeb, M.; Hatter, C.B.; Sarycheva, A.; Dion, G.; Gogotsi, Y. Electrospun MXene/carbon nanofibers as supercapacitor electrodes. J. Mater. Chem. A 2019, 7, 269–277. [Google Scholar] [CrossRef]
- Gupta, S.; Navaraj, W.T.; Lorenzelli, L.; Dahiya, R. Ultra-thin chips for high-performance flexible electronics. Npj. Flex. Electron. 2018, 2, 8. [Google Scholar] [CrossRef]
- Martiradonna, L. A solid base. Nat. Mater. 2015, 14, 962. [Google Scholar] [CrossRef]
- Wang, Z.; Sun, L.; Ni, Y.; Liu, L.; Xu, W. Flexible Electronics and Healthcare Applications. Front. Nanotechnol. 2021, 3, 625989. [Google Scholar] [CrossRef]
- Shen, W.; Zhang, X.; Huang, Q.; Xu, Q.; Song, W. Preparation of solid silver nanoparticles for inkjet printed flexible electronics with high conductivity. Nanoscale 2014, 6, 1622–1628. [Google Scholar] [CrossRef]
- Kyrylenko, S.; Kornienko, V.; Gogotsi, O.; Oleshko, O.; Kolesnyk, M.; Mishchenko, O.; Zahorodna, V.; Buranich, V.; Pogrebnjak, A.; Zozulia, Y.; et al. Bio-functionalization of Electrospun Polymeric Nanofibers by Ti3C2Tx MXene. In Proceedings of the 2020 IEEE 10th International Conference Nanomaterials: Applications & Properties (NAP), Sumy, Ukraine, 9–13 November 2020. [Google Scholar]
- Gogotsi, Y.; Anasori, B. The Rise of MXenes. ACS Nano 2019, 13, 8491–8494. [Google Scholar] [CrossRef] [Green Version]
- Hope, M.A.; Forse, A.C.; Griffith, K.J.; Lukatskaya, M.R.; Ghidiu, M.; Gogotsi, Y.; Grey, C.P. NMR reveals the surface functionalisation of Ti3C2 MXene. Phys. Chem. Chem. Phys. 2016, 18, 5099–5102. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Song, Q.; Ye, F.; Kong, L.; Shen, Q.; Han, L.; Feng, L.; Yu, G.; Pan, Y.; Li, H. Graphene and MXene Nanomaterials: Toward High-Performance Electromagnetic Wave Absorption in Gigahertz Band Range. Adv. Funct. Mater. 2020, 30, 2000475. [Google Scholar] [CrossRef]
- Lipatov, A.; Alhabeb, M.; Lukatskaya, M.R.; Boson, A.; Gogotsi, Y.; Sinitskii, A. Effect of Synthesis on Quality, Electronic Properties and Environmental Stability of Individual Monolayer Ti3C2 MXene Flakes. Adv. Electron. Mater. 2016, 2, 1600255. [Google Scholar]
- Sarycheva, A.; Polemi, A.; Liu, Y.; Dandekar, K.; Anasori, B.; Gogotsi, Y. 2D titanium carbide (MXene) for wireless communication. Sci. Adv. 2018, 4, eaau0920. [Google Scholar] [CrossRef] [Green Version]
- Han, M.; Liu, Y.; Rakhmanov, R.; Israel, C.; Tajin, M.A.S.; Friedman, G.; Volman, V.; Hoorfar, A.; Dandekar, K.R.; Gogotsi, Y. Solution-Processed Ti3C2Tx MXene Antennas for Radio-Frequency Communication. Adv. Mater. 2021, 33, 2003225. [Google Scholar] [CrossRef]
- Sohel Rana, S.M.; Toyabur Rahman, M.; Salauddin, M.; Sharma, S.; Maharjan, P.; Bhatta, T.; Cho, H.; Park, C.; Yeong Park, J.Y. Electrospun PVDF-TrFE/MXene Nanofiber Mat-Based Triboelectric Nanogenerator for Smart Home Appliances. ACS Appl. Mater. Interfaces 2021, 13, 4955–4967. [Google Scholar] [CrossRef]
- Alhabeb, M.; Maleski, K.; Anasori, B.; Lelyukh, P.; Clark, L.; Sin, S.; Gogotsi, Y. Guidelines for Synthesis and Processing of 2D Titanium Carbide (Ti3C2Tx MXene). Chem. Mat. 2017, 29, 7633–7644. [Google Scholar]
- Pogorielov, M.; Hapchenko, A.; Deineka, V.; Rogulska, L.; Oleshko, O.; Vodseďálková, K.; Berezkinová, L.; Vysloužilová, L.; Klápšťová, A.; Erben, J. In vitro degradation and in vivo toxicity of NanoMatrix3D® polycaprolactone and poly(lactic acid) nanofibrous scaffolds. J. Biomed. Mater. Res. Part A 2018, 106, 2200–2212. [Google Scholar] [CrossRef]
- Koltunowicz, T.N. Test station for frequency-domain dielectric spectroscopy of nanocomposites and semiconductors. J. Appl. Spectrosc. 2015, 82, 653–658. [Google Scholar] [CrossRef]
- Waygood, A. An Introduction to Electrical Science, 2nd ed.; Routledge: New York, NY, USA, 2019. [Google Scholar]
- Halliday, D.; Resnik, R. Physics, Part 2; Jon Wilej & Sons, Inc.: New York, NY, USA, 1978. [Google Scholar]
- User’s Manual for the HiTESTER Impedance Meter. Available online: https://www.hioki.com/download/32930 (accessed on 15 September 2021).
- Syamsai, R.; Kollu, P.; Kwan Jeong, S.; Nirmala Grace, A. Synthesis and properties of 2D-titanium carbide MXene sheets towards electrochemical energy storage applications. Ceram. Int. 2017, 43, 13119–13126. [Google Scholar] [CrossRef]
- Alnoor, H.; Elsukova, A.; Palisaitis, J.; Persson, I.; Tseng, E.N.; Lu, J.; Hultman, L.; Persson, P.O.A. Exploring MXenes and their MAX phase precursors by electron microscopy. Mater. Today Adv. 2021, 9, 100123. [Google Scholar]
- Awasthi, G.P.; Maharjan, B.; Shrestha, S.; Bhattarai, D.P.; Yoon, D.; Park, C.H.; Kim, C.S. Synthesis, characterizations, and biocompatibility evaluation of polycaprolactone–MXene electrospun fibers. Colloid Surf. A Physicochem. Eng. Asp. 2020, 586, 124282. [Google Scholar] [CrossRef]
- Pogrebnjak, A.; Ivashchenko, V.; Maksakova, O.; Buranich, V.; Konarski, P.; Bondariev, V.; Żukowski, P.; Skrynskyy, P.; Sinelnichenko, A.; Shelest, I.; et al. Comparative measurements and analysis of the mechanical and electrical properties of Ti-Zr-C nanocomposite: Role of stoichiometry. Measurement 2021, 176, 109223. [Google Scholar] [CrossRef]
- Koltunowicz, T.N.; Zukowski, P.; Boiko, O.; Czarnacka, K.; Bondariev, V.; Saad, A.; Larkin, A.V.; Fedotov, A.K. Capacitive properties of nanocomposite (FeCoZr)x(PZT)(100-x) produced by sputtering with the use of argon and oxygen ions beam. J. Mater. Sci. Mater. Electron. 2016, 27, 1171–1176. [Google Scholar] [CrossRef] [Green Version]
- Kołtunowicz, T.N.; Żukowski, P.; Bondariev, V.; Czarnacka, K.; Boiko, O.; Fedotova, J.A.; Kasiuk, J.V. Study of dielectric function of (FeCoZr)x(CaF2)(100−x) nanocomposites produced with a beam of argon ions. J. Alloys Compd. 2015, 650, 262–267. [Google Scholar] [CrossRef]
- Sun, M.; Xiao, Z.; Chai, Y.; Li, Y.; Chan, P.C.H. Inductance properties of silicon-in-grown horizontal carbon nanotubes. In Proceedings of the 60th Electronic Components and Technology Conference, ECTC 2010, Las Vegas, NV, USA, 1–4 January 2010; pp. 1329–1334. [Google Scholar]
- Kołtunowicz, T.N.; Żukowski, P.; Bondariev, V.; Fedotova, J.A.; Fedotov, A.K. The effect of annealing on induction like properties of (FeCoZr)x(CaF2)(100−x) nanocomposite films produced by ion-beam sputtering in the vacuum environment. Vacuum 2015, 120, 44–50. [Google Scholar] [CrossRef]
- Kołtunowicz, T.N.; Bondariev, V.; Żukowski, P.; Fedotova, J.A.; Fedotov, A.K. AC electrical resonances in nanocomposites with partly oxidized FeCoZr grains embedded in CaF2 ceramic matrix—effects of annealing. J. Alloys Compd. 2020, 819, 153361. [Google Scholar] [CrossRef]
- Kołtunowicz, T.N.; Żukowski, P.; Bondariev, V.; Fedotov, A.K.; Svito, I. Voltage and current resonance in nanocomposite (FeCoZr)x(CaF2)(100-x) produced by ion-beam sputtering in pure argon atmosphere. Acta Phys. Pol. A 2015, 128, 897–900. [Google Scholar] [CrossRef]
- Sahraei, A.A.; Ayati, M.; Baniassadi, M.; Rodrigue, D.; Baghani, M.; Abdi, Y. AC and DC electrical behavior of MWCNT/epoxy nanocomposite near percolation threshold: Equivalent circuits and percolation limits. J. Appl. Phys. 2018, 123, 105109. [Google Scholar]
- Cai, H.; Li, H.; Cho, E.Y.; Cybart, S.A. Inductance of YBa2Cu3O7-δ thin-films with and without superconducting ground planes. IEEE Trans. Appl. Supercond. 2020, 30, 7500205. [Google Scholar] [CrossRef]
- Miki, S.; Takeda, M.; Fujiwara, M.; Sasaki, M.; Otomo, A.; Wang, Z. Superconducting NbTiN Nanowire Single Photon Detectors with Low Kinetic Inductance. Appl. Phys. Express 2009, 2, 075002. [Google Scholar] [CrossRef]
- Johansson, J.; Cedergren, K.; Bauch, T.; Lombardi, F. Properties of inductance and magnetic penetration depth in (103)-oriented YBa2Cu3O7−δ thin films. Phys. Rev. B 2009, 79, 214513. [Google Scholar] [CrossRef]
- Żukowski, P.; Kołtunowicz, T.N.; Boiko, O.; Bondariev, V.; Czarnacka, K.; Fedotova, J.; Fedotov, A.K.; Svito, I. Impedance model of metal-dielectric nanocomposites produced by ion-beam sputtering in vacuum conditions and its experimental verification for thin films of (FeCoZr)x(PZT)(100-x). Vacuum 2015, 120, 37–43. [Google Scholar] [CrossRef]
- Mott, N.F.; Davis, E.A. Electron Process in Non-Crystalline Materials; Clarendon Press: Oxford, UK, 1979. [Google Scholar]
- Kirkpatrik, S.S. Amorphous and Liquid Semiconductors. In Proceedings of the 5th International Conference, Garmish-Partenkirchen, Germany, 3–8 September 1973; pp. 183–190. [Google Scholar]
- Shklovsky, B.I.; Efros, A.L. Elecronic Properties of Doped Semiconductors; Springer: Berlin, Germany, 1984. [Google Scholar]
- Żukowski, P.; Kierczyński, K.; Kołtunowicz, T.N.; Rogalski, P.; Subocz, J. Application of elements of quantum mechanics in analysing AC conductivity and determining the dimensions of water nanodrops in the composite of cellulose and mineral oil. Cellulose 2019, 26, 2969–2985. [Google Scholar] [CrossRef] [Green Version]
- Landau, L.D.; Lifshits, E.M.; Pitaevskiĭ, L.P. Electrodynamics of Continuous Media; Elsevier Books; Elsevier: Pergamon, Turkey, 1984. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).