Abstract
The flow field distribution and thermal properties of supercritical hydrogen are crucial factors affecting the quality of neutrons output from spallation neutron source, which may contribute to the optimization design of the moderator. Several sensitivity studies on affecting heat transfer characteristics of liquid hydrogen inside a moderator were executed, and a choice was made to use a computational fluid dynamics method for numerical simulation. The sensitivity degree of factors affecting the heat transfer characteristics of liquid hydrogen are in sequence of inlet mass flow, beam power and operating pressure. Especially when the beam power is 500 kW (the temperature range of liquid hydrogen is about 20~30 K); where the effect of mass flow rate is remarkable, the cooling effect is best in the range of 60~90 g/s × 394 mm2. Meanwhile, the maximum temperature of liquid hydrogen is close to the bottom recirculation zone due to the influence of the flow field and the heat deposition distribution of the poisoned plate. The effect of variable pressure on the temperature of liquid hydrogen is not significant, whereas the sudden rise of wall temperature is observed near the large specific heat region of 15 bar.
1. Introduction
The Chinese Spallation Neutron Source (CSNS) generates intensive neutrons due to the impact of 1.6 GeV high-energy pronton on heavy metal targets. Thermal and cold neutrons after deceleration can be used to study the atomic structure and motion of certain objects [1,2]. The current beam power of a CSNS target station is 100 kW; the phase II target is plans to upgrade this to 500 kW. As the core component of the target station, the moderator slows down the leaking neutrons generated in the spall target for neutron scattering experiments [3]. The Decouple Poison Hydrogen Moderator (DPHM) is taken as the research object owing to its complex internal structure. At the same time, the existence of a poisoned plate inside the container leads to uneven distribution of flow and heat transfer.
During the operation of the target station, special working conditions should be considered, such as power off mode, distortion mode and refrigerator failure, etc., which will lead to a sharp increase in the thermal load of the hydrogen circulation system and a rise in temperature and pressure. In order to protect the cryogenic equipment, liquid hydrogen must be discharged in an emergency. In the above process, the ambient pressure decreases from 1.5 MPa to 0.1 MPa, and the liquid hydrogen in the DPHM changes from a supercritical state to supercooled state [4,5]. Due to the transcritical process, the change of pressure and temperature has a strong influence on the thermophysical properties of liquid hydrogen, for instance density, viscosity and thermal conductivity, which all make the flow heat transfer in the container more complicated [6,7]. In addition, thermal deposition increases significantly with the enhancement of proton beam power at the target station, thus leading to the further rise of the overall temperature of DPHM. To ensure the stable operation of the system, the average temperature of liquid hydrogen and the temperature difference between the inlet and outlet should be maintained in certain extent.
The heat transfer characteristics of supercritical fluid have been investigated extensively, especially the investigation of in tubes have become a focal point of research content [8,9,10,11]. Considering the influence of different factors on heat transfer, Wang et al. [12] found that the buoyancy effect under the non-uniform heat source can effectively alleviate the degree of Heat Transfer Deterioration (HTD). Meanwhile, a modified turbulent model, which can accurately predict the influence of semicircular heating condition on the flow and heat transfer, was also proposed. Zhu et al. [13] conducted a numerical study about the effects of gravity on the heat transfer performance of supercritical CO2 flowing within a vertical tube. They found that the effect of gravity on heat transfer is pronounced and closely related to the variations of thermophysical properties, particularly with low mass flux condition. The experiments on turbulent heat transfer via supercritical CO2 in a vertical tube were carried out by Kim et al. [14]. It is indicated that the distribution of wall temperature, which had a noticeable peak value when the wall heat flux was moderated and the mass flux was low, varied with buoyancy effect and flow acceleration. Nevertheless, it seems that issues such as the heat transfer characteristics of supercritical liquid hydrogen have not received sufficient attention. Youn et al. [15] obtained the variable rules of thermophysical properties of supercritical hydrogen by changing inlet conditions, for example the temperature, pressure, mass flow rate, etc. The evaluations of numerous correlations for heat transfer to supercritical hydrogen flowing turbulently in circular tubes were presented by Locke and Landrum [16]. Furthermore, In comparision with other correlations of supercritical hydrogen, by modifying the relevant parameters of correlations about non-hydrogen supercritical fluid with variable properties, this method can be applied to liquid hydrogen and obtain more accurate prediction results. James [17] described the entire validation process for a model of the heat transfer coefficient and the expected content required to complete the validation. By utilizing the above model, the convection heat transfer coefficient between the supercritical, cryogenic hydrogen and the moderator vessel walls was verified. Xie and Zhang [18,19,20] have carried out a number of studies on enhanced heat transfer of supercritical liquid hydrogen. Specifically, the rib structure was not only added to the wall, but also included some surface grooves and bulges, which were conducive to the enhancement of cooling performance and reducing the influence of the non-uniform distribution on heat transfer. The numerical simulation method of convective heat transfer is also important, which determines the reliability and accuracy of the simulation results. Mosavati et al. [21,22] proposed a novel calculation method for convective heat transfer in a closed cavity, specifically for the distribution factors using backward Monte Carlo method. Moreover, the effects of Rayleigh number, temperature ratio, radiation conductivity and other parameters on heat flux were studied, and the results were compared and analyzed. They conclude that lowering the temperature ratio will make the heat source surface temperature distribution smoother and lead to greater radiation heat transfer flux. At the same time, by increasing the Rayleigh number, the convective heat transfer flux can be significantly improved, and the heat flux on the heat source surface becomes uneven.
Therefore, it is necessary to explore the heat flow characteristics of liquid hydrogen in DPHM under the conditions of changing pressure, heat source and mass flow rate. The study reported here was undertaken to validate the accuracy of the supercritical model by taking the liquid hydrogen in the moderator as the research object. Meanwhile, the corresponding heat sources under different beam power of DPHM were investigated based on the neutron physical-thermal coupling method. Finally, the Computational Fluid Dynamics (CFD) method was used to simulate the flow and heat transfer characteristics of liquid hydrogen by changing the boundary conditions of DPHM.
2. Mathematical and Physical Model
2.1. Physical Model
Due to the internal complexity of the DPHM model, it was simplified for the convenience of numerical simulation analysis, as shown in Figure 1. The main structure of DPHM is made of the inlet-pipe of hydrogen, the outlet-pipe of hydrogen, container and poisoned plate, in which the structure of the pipeline is coaxial multi-layer casing. The distance between the exit of the inlet-pipe of hydrogen and the bottom surface of the container is 5 mm. After the liquid hydrogen flows along inlet-pipe of hydrogen for a distance, the poisoned plate separates the flow of it into two uneven sides, which are injected vertically to the bottom surface of the inner cavity under the action of pressure difference to form a circular jet for cooling [23]. The pressure generated by the impact forces the liquid hydrogen to flow radially along the wall, and then, due to the limitation of the internal structure, it is concentrated upward at the neck of the container and finally discharged by the hydrogen return tube. Due to the thermal deposition caused by neutron collisions, liquid hydrogen is mainly heated by pipelines, poisoned plate and container during flow.
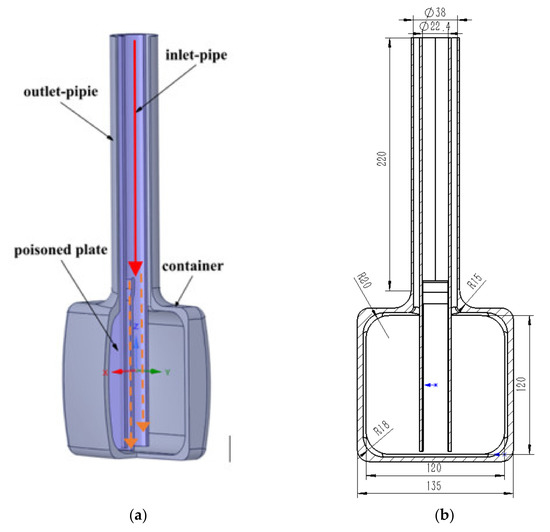
Figure 1.
The Computational Model of DPHM: (a) Model Diagram; (b) Detailed Size (mm).
The MCNPX is a universal Monte Carlo transport program developed by Los Alamos National Laboratory in the United States, which has been proved to be able to accurately simulate the scattering reaction of high-energy particles inside the moderator [24]. In the current work, the external coupling method was used to modify the common parameters of MCPNX 2.5 and CFX 11.0 software [25,26], the heat source distribution of the moderator calculated by the former was taken as the thermal boundary condition of the input of the latter.
2.2. Meshing
The mesh of DPHM generated by commercial software ICEM 14.0 is shown in Figure 2, where the unstructured mesh with strong adaptability was selected to discretize the fluid domain. The overall quality of the grid is detailed; the maximum and average skewness are 0.652 and 0.223 respectively, and the average aspect ratio is 3.124, which proves the reliability of grid division. Considering the influence of boundary layer on the main flow area, the local mesh of areas with large curvature and complex flow, such as inlet, outlet and wall boundary area, was encrypted so as to accurately capture the flow characteristics. In order to accurately predict the turbulent flow field, the height of the first layer of the boundary layer grid is set to be small enough to meet the criterion of y + value close to 1. Five inflation layers are divided in the sensitive region, so the estimation of the thermal gradients can be improved. The selection height of the first layer grid in the calculation model is calculated by the following Equation [27],
where Re, ρ, u, L, μ, Cf, τw and Uτ are the dimensionless number, density, bulk fluid velocity, characteristic length, dynamic viscosity of fluid, boundary layer friction coefficient, boundary layer shear stress and shear velocity. Finally, after calculation, the value of the first layer grid height y + is 2 mm.

Figure 2.
Generation mesh in the computational domain.
2.3. Governing Equations
The liquid hydrogen jet cooling in the moderator belongs to high-speed flow, so the influence of gravity on heat transfer flow can be ignored. In the transcritical process, the pressure has a great influence on the density of liquid hydrogen [28]. Therefore, this article assumes that the liquid hydrogen in the moderator is a compressible fluid, and only the steady flow is studied. The specific governing equations are as follows:
The continuity equation [29]:
The momentum equation:
The energy equation [30]:
where u, τ, p, P, E, T, λeff, τeff and Sh denote the velocity vector, stress tensor, bulk fluid pressure, static pressure, total energy, bulk fluid temperature, effective thermal conductivity, effective stress tensor and volumetric heat source, respectively.
In this paper, the steady-state heat specifies and the material is isotropic, so the Fourier law was employed to describe the heat conduction within the solid wall [31].
where λ is the thermal conductivity of the fluid. The shear stress transport (SST) k-ω turbulence model, which takes into account the transport of turbulent shear stress and has a high accuracy in predicting the complex flow, is used to solve the three-dimensional flow of liquid hydrogen.
2.4. Boundary Conditions
The boundary conditions for each structure of the computational model, including fluid domain and solid domain, should be set before the simulation begins. Moreover, the non-uniform heat source of DPHM is imported into CFX software by compiling User Defined Function (UDF).
- The inlet temperature ranges from 18 to 30 K, the inlet mass flow rate 30 to 150 g/s, the pressure from 11 to 15 bar. It is assumed that the flow at the inlet has been fully developed, and the boundary condition of the entrance is set as the average mass. The outlet boundary condition was set as the pressure outlet according to the standard atmospheric pressure, and the outlet calculation domain was appropriately extended to avoid the backflow phenomenon.
- The standard wall function is used for wall treatment, and the no-slip boundary condition is adopted. The container is set as an adiabatic wall surface, the second-order upwind format is used for the discrete equation, and Semi-Implicit Method for Pressure Linked Equations (SIMPLE) algorithm is selected for the pressure-velocity coupling method. The maximum number of convergent iterations is 8000, and the convergence residual Root Mean Square of the residual values (RMS) value is set to 10−6 to obtain a stable convergent solution.
- The non-uniform heat source of the moderator was obtained by external coupling of MCNPX and CFX software and applied to the moderator. Table 1 lists the comparison of the corrected heat sources between MCNPX and CFX when the proton beam power is 500 kW. Since the models used in the two softwares are slightly different, there are some errors in the calculation values of thermal deposition of materials, but they are within the allowable range, which proves the accuracy and reliability of the coupling results.
 Table 1. Comparison of heat deposition calculation results between MCNPX and CFX (W).
Table 1. Comparison of heat deposition calculation results between MCNPX and CFX (W).
2.5. Verification of Grid Independence
In this paper, the grid independence of DPHM is verified under the conditions of beam power of 100 kW, pressure of 15 bar and inlet flow of 30 g/s. Five groups of grids were selected for comparison, and the three parameters of maximum temperature, maximum pressure of liquid hydrogen and maximum container temperature were detected. The results are shown in Figure 3. It can be seen that the temperature variation tends to be stable when the number of grid elements exceeds 1.68 million, indicating that the independent solution can be obtained for the grid number at this condition. The Grid Convergence Index (GCI) was used to quantify the grid independence [32]. The GCI34 for fine, and medium grids was 1.76%. The GCI45 for medium and coarse grids was 4.61%. The value of GCI45/(rpGCI34) was 1.03, which was approximately 1 and indicates that the solutions were well within the asymptotic range of convergence. Therefore, considering the computational efficiency and accuracy, the fourth group of grids was finally employed for calculation.
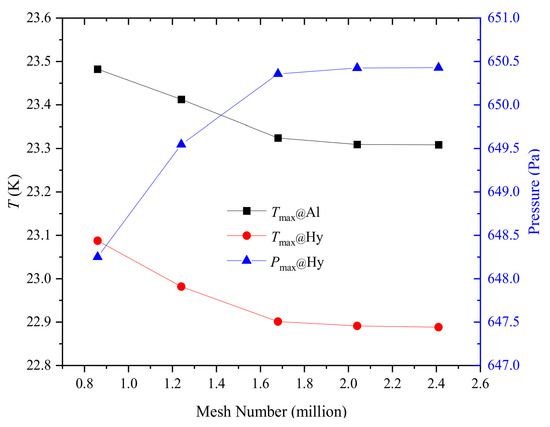
Figure 3.
Grid independence validation of DPHM.
2.6. Verification of Physical Parameters
Pseudo-critical temperature refers to the temperature corresponding to the maximum specific heat capacity of fluid at constant pressure in a supercritical state (Critical pressure and temperature of liquid hydrogen are 12.9 bar and 33.15 K, respectively). In the vicinity of this temperature range, the thermophysical properties of the fluid will change dramatically, thus affecting the flow and heat transfer. As shown in Figure 4a, the density ρ and dynamic viscosity μ decrease with the gradual increase of temperature under 15 bar but converge to a constant value as the temperature is far beyond the critical value. Meanwhile, the change in specific heat cp is most significant, which is further reflected in Figure 4b. There is a prominent phenomenon called the “thermal spike phenomenon”, which is not conducive to the stability of heat transfer. This primary peak in λ and cp of hydrogen disappears with the augment of pressure due to the corresponding Pseudo-critical temperature increasing roughly from 32 to 34 K [33].
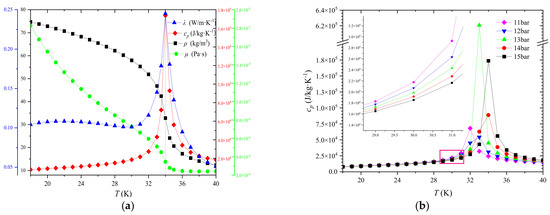
Figure 4.
Variations of thermophysical properties of liquid hydrogen under different pressure: (a) Pressure = 15 bar; (b) Specific Heat (different pressure).
Accurate prediction of the thermal properties of hydrogen is crucial to the reliability of the simulation results. Based on equations of state (EoSs) theory [34,35], the physical parameters of hydrogen, in which the α parameter and pressure–volume–temperature (PVT) relationships have an important influence, can be accurately predicted. In order to more accurately simulate the flow heat transfer of non-ideal fluids under supercritical conditions, under the premise of considering the calculation accuracy and efficiency, this paper adopts the Peng–Robinson (PR-EOS) equation of state [31], which is universal in engineering, to calculate the physical parameters of working fluids:
where
where R, vPR, Tc, pc, and ω are the molecular gas constant, the molar volume, the critical temperature, the critical pressure and the Pitzer acentric factor.
Whereas the prediction results of liquid density obtained by the PR-EOS formula have poor accuracy, especially when the pressure is close to the critical region and in a small temperature range. Khashayar [36] evaluated 11 correlations for predicting hydrogen density and found that the modified Redlich–Kwong EoS by Mathias and Copeman (RKMC) [37] was widely applicable to predict liquid hydrogen properties in various ranges. The deviation between the experimental results and the RKMC EoS equation was small in the temperature range of 14~32 K, which proved the rationality and accuracy of the RKMC EoS equation. Since the liquid hydrogen in this paper belongs to the supercritical state, and the temperature change is located in the above range, the RKMC EOS equation is used for the subsequent calculation in this paper. The specific equation are as follows:
where
where ac is the critical attractive parameter, b is the molar co-volume, α is the temperature dependence function (alpha function), c1,c2,c3 are the coefficients of the Mathias and Copeman alpha function, and Tr is the reference temperature.
Figure 5 shows the density and viscosity distributions at temperatures of 15~40 K at pressures of 5, 10 and 15 bar. In order to verify the accuracy of the above model, a comparison was made with the data of GASPAK [38], the results showing that the two sets of data were well in agreement and that the error was within the allowable range.
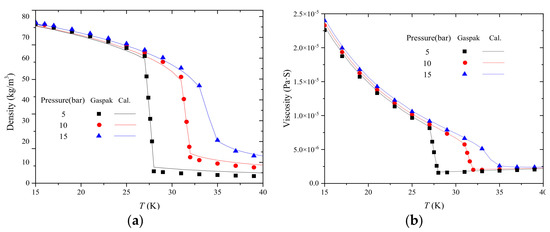
Figure 5.
Comparison of simulation results with GSPAK data of thermophysical properties: (a) Density; (b) Viscosity.
3. Results and Discussion
3.1. The Heat Source Distribution
The cross section of nuclear data, which were used in the simulation calculation with the MCNPX of this paper, are mainly from the databases and form the basis to ensure the correctness of simulation results. A large number of variance reduction techniques are used in the calculation to improve the calculation accuracy and reduce the calculation time. In the process of liquid hydrogen flow heat transfer, its heat source mainly comes from the container (which is all generated by the nuclear reaction on the wall of the moderator), poisoned plate and the background radiation.
Figure 6 shows the heat source distribution of DPHM at 100 kW power obtained by coupling calculation of CFX and MCNPX simulation software, which are, respectively, container (Figure 6a) and poisoned plate (Figure 6b). It can be seen from the contours that the values calculated by the two softwares are slightly different, but the general trend distribution is consistent. A large number of long-wave neutrons elastic scattering reactions, which owing to the narrowing effect of the poisoned plate, result in an energy concentration in the poisoned plate, thus leading to the highest heat deposition at this point (with a maximum value of 3.1 × 106 W/m3).
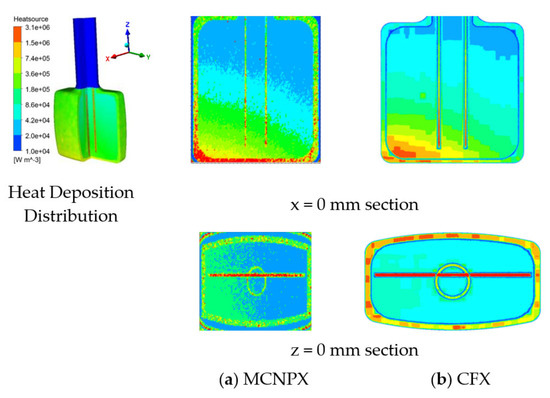
Figure 6.
Comparison of heat deposition calculation results between MCNPX and CFX: (a) MCNPX; (b) CFX.
3.2. Effect of Beam Power on Heat Transfer
The influence of beam power increase on the heat transfer characteristics of liquid hydrogen is characterized by the change of temperature. The temperature distribution with large beam power from 100 kW to 500 kW is shown in Figure 7. As is evident from Figure 7, the temperature of liquid hydrogen in the cavity tends to be symmetrically distributed at different beam power. On the contrary, the temperature at different wall positions of the external aluminum container is quite different, which is manifested in the relatively high temperature values in four corners. The maximum value appears at the lower left corner of the hydrogen container at 500 kW, which is specifically 33 K. And as power increases, the difference becomes more pronounced, due to the irregular heat source of the moderator itself. As shown in Figure 6, the temperature at the wall position corresponding to the high heat deposition is also higher, and the increase of power further highlights this phenomenon. In addition, it can be seen that the liquid hydrogen temperature in the cavity has a partial fluctuation under the power of 300~400 kW, which is thanks to the increase of the overall heat source affecting the physical properties of liquid hydrogen. The overall temperature increases from about 18 K to 20 K corresponding to 500 kW in this range, which is in a transition state, so the liquid hydrogen temperature is unevenly distributed.
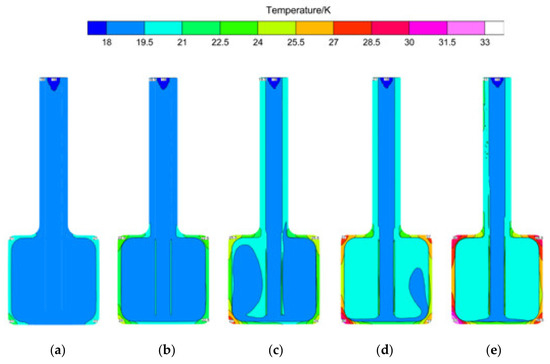
Figure 7.
The temperature distribution of DPHM with various beam power (q = 60 g/s, x = 0 mm): (a) 100 kW; (b) 200 kW; (c) 300 kW; (d) 400 kW; (e) 500 kW.
Considering the neutron performance and hydrogen system safety, the wall temperature of the container is forbidden to exceed the vaporization temperature of the working fluid; thus, the maximum temperature value is the focus of attention and ensures that it is within the safe range. The specific relationship between maximum temperature of container, poisoned plate and hydrogen with beam power is studied in Figure 8; it is found that there is an approximate linear growth relation between them. For the local thermal deposition of DPHM, due to the increase of the Footprint size of the beam, the growth multiple will be smaller than that of the increase of beam power. The latent heat in steady flow is negligible, so the heat change in DPHM is mainly caused by the scattering reaction, which means that the energy generated by per unit volume is proportional to the temperature difference. In this case, the heat deposition increases linearly, resulting in a linear increase in maximum temperature.
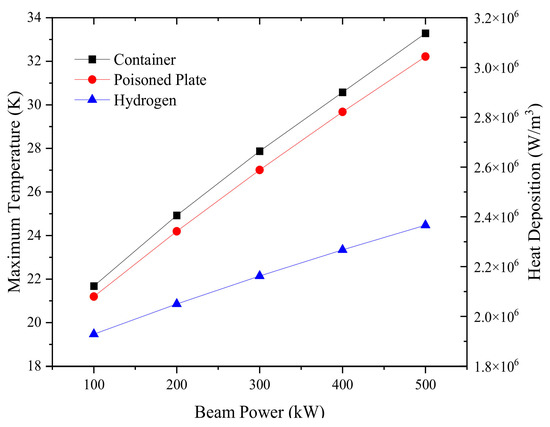
Figure 8.
The variation of maximum temperature with different beam power.
3.3. Effect of Mass Flow on Heat Transfer
The analysis of flowing process mainly includes the selection of flow range and the analysis of pressure loss. The higher the mass flow, the smaller overall temperature rise of liquid hydrogen, and the temperature distribution inside the container is relatively uniform, which is also beneficial to the neutron moderating effect. At the cross section of x = 0 mm, it can be observed, from Figure 9, that the average temperature of the side with lower liquid hydrogen flow is higher due to the uneven segmentation of the cross-sectional area of the import pipeline by the poisoned plate. The velocity contours under different mass flow are also listed, and it can be seen that the temperature distribution is basically unchanged but that the overall temperature decreases gradually with the increase of flow rate.
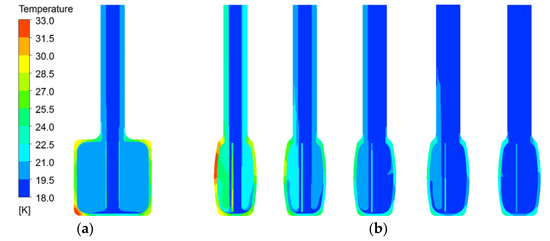
Figure 9.
Temperature distribution of DPHM (beam power = 500 kW): (a) x = 0 mm (60 g/s); (b) y = 0 mm (30, 60, 90, 120, 150 g/s).
Correspondingly, Figure 10 presents the detailed flow of liquid hydrogen inside the cavity under the 60 g/s mass flow when the turbulence viscosity ratio is about 5, which is also one of the important factors affecting heat transfer. There are two distinct symmetrical vortices on both sides of the bottom of the container according to Figure 10a; part of the liquid hydrogen from the exit is involved in the vortex, and the other part is gathered up at the neck by the inertial force. Moreover, it can be seen that due to the separation of the poisoned plate, the size and position of the vortex generated by different flow rates are different but all located near the inner wall of the container, where the intensity of vortex dominates the heat transfer.
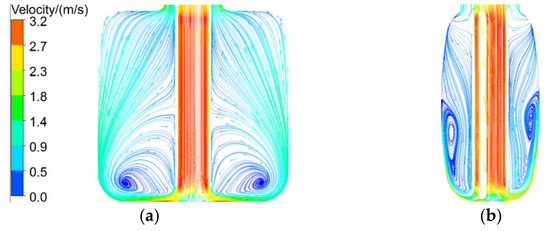
Figure 10.
The streamline in the DPHM: (a) x = 0 mm; (b) y = 0 mm.
The effect of mass flow on maximum temperature under 500 kW beam power is shown in Figure 11. Specifically, the heat transfer effect is significantly improved by distinct increment of turbulence effect in the flow range of 30~60 g/s, while the slope decreases with the increase of mass flow, which proves that the cooling effect reduces gently. It also should be noted that the increase of mass flow is accompanied by the increase of pressure loss, which will be detrimental to the stability of the flow. The intersection point between the temperature curve of liquid hydrogen and the corresponding pressure drop curve is noted, which is in the range of 60~90 g/s, indicating that the cooling effect is the best and the flow is relatively stable.
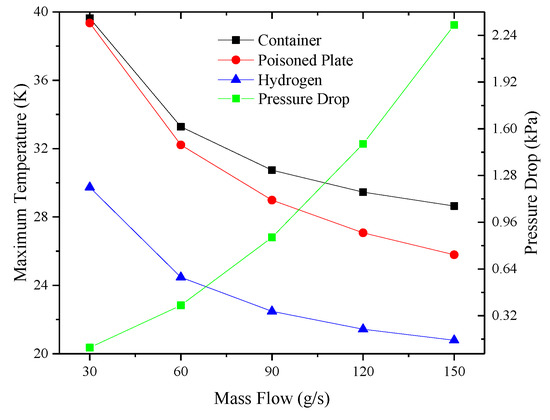
Figure 11.
The variation of maximum temperature with different mass flow.
The liquid hydrogen carries out jet impact on the bottom surface, which was taken as the research object result of its good heat transfer effect, after flowing out of the hydrogen intake pipe with a vertical distance of 5 mm, as shown in Figure 12. For a smooth surface, with the flow of liquid hydrogen reaching the wall, the pressure forces the jet to flow axially along the wall. Combined with the pressure distribution, it can be seen that the target surface located in the impact zone is under the maximum pressure, and then diffuses and decreases along the periphery, leading to a gradual decrease in velocity. The temperature in the center area of the target surface increases slowly with a similar regularity. This is because the viscous boundary layer on the wall gradually thickens and the surface heat transfer coefficient decreases when the liquid hydrogen flows in the radial direction.
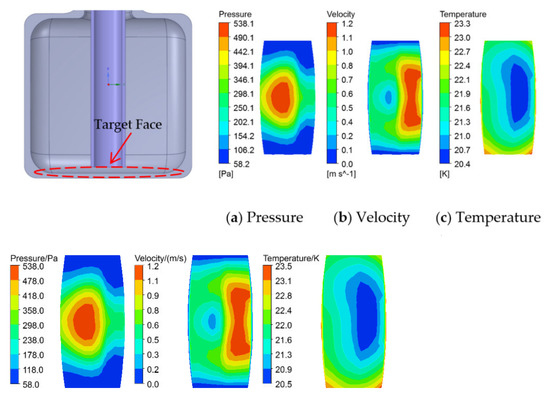
Figure 12.
Physical parameters distribution of target surface: (a) Pressure; (b) Velocity; (c) Temperature.
The local heat transfer coefficient is obtained by the following equations,
where qw, Tw, Tb, w and H are the local heat flux of wall, averaging temperature of wall, bulk fluid temperature, bulk fluid axial velocity and bulk fluid enthalpy.
Figure 13 shows the distribution of the flow heat transfer coefficient h at the bottom target face along the x-axis, corresponding to the temperature distribution. It reaches the maximum value at the position of poisoned plate and then gradually decreases, which is due to the poor heat transfer at this place due to the flow dead zone generated by the shunting phenomenon. After that, the heat transfer coefficient increases gradually with the flow recovery.
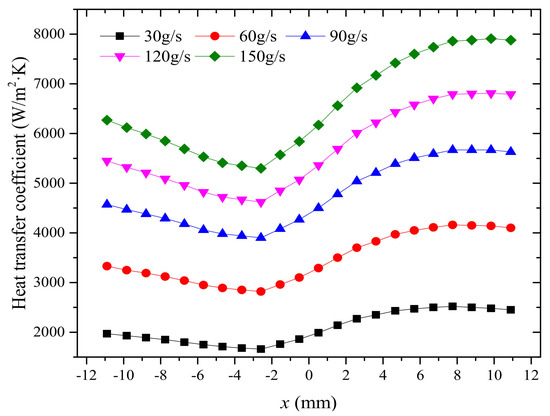
Figure 13.
The distribution of the heat transfer coefficient of the target surface along the x axis.
3.4. Effect of Pressure on Heat Transfer
To explore the influence of law of pressure change in a pseudo-critical region, the inlet temperature of hydrogen is set to 30 K. Figure 14 shows the influence of changing mass flow on the axial distribution of the wall temperature, Tw, of the hydrogen intake tube and the bulk temperature, Tb, of liquid hydrogen inside the tube. The results show that the temperature of both the wall and the liquid hydrogen increases gradually with the deepening of the flow distance. This is because there is no heat source around when the liquid hydrogen flows into the pipeline at the beginning, so the temperature change is not obvious. After that, due to the influence of thermal deposition of the poisoned plate and container, the two kinds of temperature increase significantly, and the temperature rise range of the wall surface is about 3 K. When the pressure is 15 bar, the temperature value will change at the mutation position corresponding to the physical property of liquid hydrogen in Figure 4, while the temperature will not change at a distance from the critical value. Moreover, different pressures have little effect on the average temperature of the fluid in the tube. It can be concluded that under supercritical pressure, the drastic change of physical properties in the critical region will have a great impact on turbulent heat transfer, resulting in the deterioration of convective heat transfer.
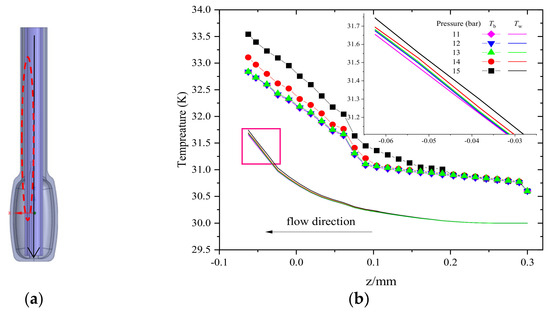
Figure 14.
Variations of temperature along axial direction under different pressures: (a) x = 0 mm; (b) y = 0 mm.
The basic formula of jet impingement heat transfer is the Newton cooling Equation,
where Tj is jet temperature and h is local impact convective heat transfer coefficient. In order to obtain the average h of the whole target surface, the local h curve of the target surface must be obtained, and then the h of each point can be calculated through a surface integral along the radius [39]. The local Nusselt number can be expressed as
where hj, d and λj are local impact convective heat transfer coefficient, diameter of nozzle and thermal conductivity of jet.
In order to more specifically reflect the heat flow characteristics of liquid hydrogen inside the vessel, the relationship between the average Nusselt number on the target surface and the resistance f along the hydrogen inlet pipe and the jet Reynolds number Re was explored under different pressure conditions. As can be seen from Figure 15, Nu increases significantly with the increase of Re and tends to change linearly. Simultaneously, the flow boundary layer in the inlet pipe segment gradually becomes thinner, the flow resistance decreases, the resistance coefficient decreases, and the pressure on the target surface also increases. The intersection point of Nu and f represents the inlet flow of liquid hydrogen corresponding to different pressures when the optimal cooling effect is achieved under the premise of considering the comprehensive characteristics of flow resistance and heat transfer characteristics. On the other hand, with the continuous increase of Re, the variation trend of Nu corresponding to different pressures is the same. At the pressure of 15 bar, the corresponding overall curve of Nu moves down and the heat transfer capacity decreases, which further proves that near the critical region, while the physical property variation caused by the pressure change worsens the turbulent heat transfer.
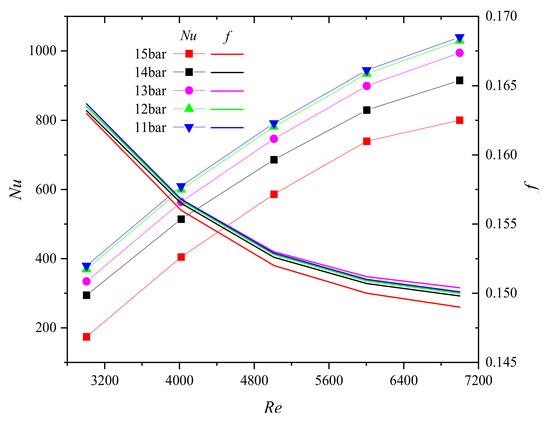
Figure 15.
The variation of Nu with Re at the target surface.
4. Conclusions
In this paper, the heat transfer performance of hydrogen in a decoupled poison hydrogen moderator under supercritical pressure is investigated by numerical method, and the effects of different boundary conditions on flow and heat transfer are compared. The major conclusions are summarized as follows:
- The sensitivity degree of factors affecting the heat transfer characteristics of liquid hydrogen are in sequence of inlet mass flow, beam power and operating pressure.
- The temperature tends to be stable and pressure loss increases gradually when the mass flow rate exceeds a certain range, especially when the beam power is 500 kW (the temperature range of liquid hydrogen is about 20~30 K); the cooling effect is best in the range of 60~90 g/s × 394 mm2.
- With the beam power increasing, the maximum temperature of the container, poisoned plate and hydrogen maintain the linear growth trend. The maximum temperature of liquid hydrogen is close to the bottom recirculation zone due to the influence of the flow field and the heat deposition distribution of the poisoned plate.
- As the pressure increased, there was no significant difference in trends of the bulk temperature, Tb, of liquid hydrogen, whereas, near the large specific heat region of 15 bar, the wall temperature Tw exhibited a sudden enhancement.
Therefore, the concrete influence law of the specific heat of liquid hydrogen on heat transfer is expected for future studies. Meanwhile, it is necessary to establish a 2D model of a moderator for avoiding random errors.
Author Contributions
J.T. and L.Z. are the main authors of this manuscript. All the authors contributed to this manuscript. J.T. and L.Z. conceived the novel idea, and Y.L. (Yiping Lu) and S.D. performed the analysis; J.T. and Y.L. (Youlian Lu) analyzed the data and contributed analysis tools; J.T. and L.Z. wrote the entire paper. J.T., T.L. and S.D. checked, reviewed and revised the paper; J.T., C.Y. and S.W. performed final proofreading and supervised this research. All authors have read and agreed to the published version of the manuscript.
Funding
This article Supported by the Program for Guangdong Introducing Innovative and Entrepreneurial Teams. (Project number: 2017ZT07S225).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| T | bulk fluid temperature, K |
| E | total energy, kJ/kg |
| P | static pressure, Pa |
| R | molecular gas constant, J/(mol·K) |
| L | characteristic length, mm |
| H | bulk fluid enthalpy, kJ/kg |
| Nu | Nussel number, |
| Cf | boundary layer friction coefficient |
| Re | Reynolds number |
| Sh | volumetric heat source, W/m3 |
| Tw | averaging temperature of wall, K |
| Tc | critical temperature, K |
| Tb | bulk temperature of fluid, K |
| Tr | reference temperature, K |
| Uτ | shear velocity, m/s |
| α | temperature dependence function (alpha function) |
| ac | critical attractive parameter, MPa·m6·k·mol−2 |
| b | molar co-volume, m3·k·mol−1 |
| p | ideal gas pressure, Pa |
| u | bulk fluid velocity, m/s |
| h | heat transfer coefficient, W/m2·K |
| f | resistance coefficient, - |
| w | bulk fluid axial velocity, m/s |
| ρ | density, kg/m3 |
| λ | thermal conductivity of the fluid, W/m·K−1 |
| ω | acentric factor, - |
| μ | dynamic viscosity, Pa·S |
| τ | shear stress, N/m2 |
| pc | critical pressure, K |
| Cp | Specific heat capacity, J/kg·K−1 |
| vPR | the molar volume, L |
| λeff | effective thermal conductivity, W/m·K−1 |
| τeff | effective stress tensor, N/m2 |
| τw | boundary layer shear stress, N/m2 |
| c1,c2,c3 | coefficients of the Mathias and Copeman alpha function |
References
- Wei, J.; Chen, H.S.; Chen, Y.W.; Chen, Y.B.; Chi, Y.L.; Deng, C.D.; Dong, H.Y.; Dong, L.; Fang, S.X.; Feng, J.; et al. China Spallation Neutron Source: Design, R&D, and outlook. Nucl. Instrum. Methods Phys. Res. A 2009, 600, 10–13. [Google Scholar]
- Wang, F.W.; Jia, X.J.; Liang, T.J.; He, C.H.; Yin, W.; Zhang, S.Y.; Zhu, T.; Yu, Q.Z.; Wang, P. Physical design of the target station and spectrometers for a spallati-on neutron source. Physics 2008, 34, 449–453. [Google Scholar]
- Wang, F.W.; Yan, Q.W.; Liang, T.J.; Yin, W.; Zhang, P.L.; Fu, S.N.; Tang, J.Y.; Fang, S.S.; Zhang, Z.; Zhang, J. Netron Scattering and Spallation Neutron Source. Physics 2005, 34, 731–738. [Google Scholar]
- Wang, G.P.; Xiao, J.; He, K.; Li, S.P. Conceptual design of cryogenic system for Chinese Spallation Neutron Source. Cryogenics 2009, 5, 27–30. [Google Scholar]
- He, C.C.; He, K.; Wang, G.P. Hydrogen safety design of cryogenic system for Chinese Spallation Neutron Source. Cryogenics 2010, 6, 1–5. [Google Scholar]
- Zhao, K.; Yang, G.P.; Shen, J.; Zhang, Z.; Chen, J. Experimental study on adjustment system of liquid hydrogen density. Cryogenics 2018, 2, 45–50. [Google Scholar]
- Wang, G.P.; Xiao, J.; Zhang, Y.; Qiu, Y.N.; Hu, Z.J.; Ding, M.Y.; Sang, M.J.; Li, S.P. Pressure control design of Chinese Spallation Neutron Source supercritical hydrogen circulation system. Vacuum&Cryogenics 2011, 1, 251–256. [Google Scholar]
- Huang, D.; Wu, Z.; Sunden, B.; Li, W. A brief review on convection heat transfer of fluids at supercritical pressures in tubes and the recent progress. Appl. Energ. 2016, 162, 494–505. [Google Scholar] [CrossRef]
- Mohseni, M.; Bazargan, M. A New Correlation for the Turbulent Prandtl Number in Upward Rounded Tubes in Supercritical Fluid Flows. J. Heat Transf. 2016, 138, 081701. [Google Scholar] [CrossRef]
- Du, X.; Lv, Z.; Yu, X.; Cao, M.; Zhou, J.; Ren, Y.; Qiu, Q.; Zhu, X. Heat transfer of supercritical CO2 in vertical round tube: A considerate turbulent Prandtl number modification. Energy 2020, 192, 116612. [Google Scholar] [CrossRef]
- Qiu, Q.; Du, X.; Zhao, S.; Zhu, X.; Shen, S. Numerical study on heat transfer of SCW near the pseudo-critic-al temperature in a hexagon sub-channel. Nucl. Eng. Des. 2018, 331, 263–273. [Google Scholar] [CrossRef]
- Wang, Z.W.; Qi, G.L.; Li, M.J. Numerical Investigation of Heat Transfer to Supercritical Water in Vertical Tube under Semicircular Heating Condition. Energies 2019, 12, 3958. [Google Scholar] [CrossRef] [Green Version]
- Zhu, X.J.; Zhang, R.Z.; Yu, X.; Cao, M.G.; Ren, Y.X. Numerical Study on the Gravity Effect on Heat Transfer of Supercritical CO2 in a Vertical Tube. Energies 2020, 13, 3502. [Google Scholar] [CrossRef]
- Kim, D.E.; Kim, M.H. Experimental study of the effects of flow acceleration and buoyancy on heat transfer in a supercritical fluid flow in a circular tube. Nucl. Eng. Des. 2010, 240, 3336–3349. [Google Scholar] [CrossRef]
- Youn, B.; Mills, A.F. Flow of Supercritical Hydrogen in a Uniformly Heated Circular Tube. Numer. Heat Transfer Part A Appl. 1993, 24, 1–24. [Google Scholar] [CrossRef]
- Locke, J.M.; Landrum, D.B. Study of Heat Transfer Correlations for Supercritical Hydrogen in Regenerative Cooling Channels. J. Propul. Power 2008, 24, 94–102. [Google Scholar] [CrossRef]
- Freels, J.D. COMSOL Validation Progress on Supercritical Hydrogen Heat Transfer. In Proceedings of the COMSOL Multiphysics Conference 2007 Proceedings, COMSOL, Boston, MA, USA, October 2007; Dravid, V., Ed.; pp. 341–347. [Google Scholar]
- Xie, P.Y.; Zhang, X.B. A method of rib-bed plate enhancing heat transfer in hydrogen rocket engine chamber wall. Int. J. Hydrogen Energy 2019, 44, 20504–20515. [Google Scholar] [CrossRef]
- Xie, P.Y.; Zhang, X.B. Enhancement heat transfer analysis of supercritical hydrogen fuel in small-scale channels with spherical concave. Int. J. Therm. Sci. 2020, 152, 106287. [Google Scholar] [CrossRef]
- Xie, P.Y.; Zhang, X.B. Turbulent heat transfer analysis in supercritical hydrogen fuel flow considering thermal stratification. Numer. Heat Transfer Part A. Appl. 2020, 77, 913–929. [Google Scholar] [CrossRef]
- Mosavati, B.; Mosavati, M.; Kowsary, F. Solution of radiative inverse boundary design problem in a combined radiating-free convecting furnace. Int. Commun. Heat Mass 2013, 45, 130–136. [Google Scholar] [CrossRef]
- Mosavati, B.; Mosavati, M.; Kowsary, F. Inverse boundary design solution in a combined radiating-free convecting furnace filled with participating medium containing specularly reflecting walls. Int. Commun. Heat Mass 2016, 76, 69–76. [Google Scholar] [CrossRef]
- Bolek, A.; Bayraktar, S. Flow and heat transfer investigation of a circular jet issuing on different types of surfaces. Sadhana Acad. P. Eng. 2019, 44, 242–252. [Google Scholar] [CrossRef] [Green Version]
- Tong, J.F.; Wang, J.L.; Zhang, H.C.; Ji, Y.; Tan, H.P. Three dimensional numerical simulation of thermal-hydraulic behaviors of CSNS decoupled poisoned hydrogen moderator with non-uniform heat source. In Proceedings of the ASME 2016 24th International Conference on Nuclear Engineering, Charlotte, NC, USA, 26–30 June 2016; pp. 1–6. [Google Scholar]
- Pelowitz, D.B. MCNPX User’ S Manual Version 2.5.0; Los Alamos National Laboratory: Los Alamos, NM, USA, 2005. [Google Scholar]
- ANSYS Inc. ANSYS CFX Reference Guide, Release 11.0; ANSYS Inc.: Canonsburg, PA, USA, 2006. [Google Scholar]
- Versteeg, H.; Malalasekra, W. An Introduction to Computational Fluid Dynamics: The Finite Volume Method, 2nd ed.; Prentice Hall: Hoboken, NJ, USA, 2007. [Google Scholar]
- Bae, J.H.; Yoo, J.Y. Direct numerical simulation of turbulent supercritical flows with heat transfer. Phys. Fluids 2005, 17, 105104. [Google Scholar] [CrossRef]
- Hirsch, C. Numerical Computation of Internal and External Flows. In Fundamentals of Computational Fluid Dynamics, 2nd ed.; Hirsch John Wiley & Sons Ltd.: New York, NY, USA, 2007; Volume 1. [Google Scholar]
- Tao, W.Q. Numerical Heat Transfer, 2nd ed.; Xi’an Jiaotong University Press: Xi’an, China, 2001. [Google Scholar]
- Yan, X.; Baugn, J.W.; Mesbath, M. The effect of reynolds number on the heat transfer distribution from a flat Plate to an impinging jet. In Proceedings of the ASME Winter Annual Meeting, Anaheim, CA, USA, 1992; Volume 226, pp. 1–7. [Google Scholar]
- Roache, P.J. Perspective: A method for uniform reporting of grid refinement studies. J. Fluids Eng. 1994, 116, 405–413. [Google Scholar] [CrossRef]
- Tong, J.F.; Wang, S.L.; Yin, W.; Lu, Y.L.; Yu, Q.Z.; Hu, C.M.; Yu, C.J.; Du, W.T.; Yao, C.J.; Liang, T.J. Neutronics/Thermal-Hydraulic Coupling for CSNS Decoupled Posioned Hydrogen Moderator. J. Eng. Thermophysrus. 2013, 34, 905–909. [Google Scholar]
- Boublik, T. The BACK equation of state for hydrogen and related compounds. Fluid Phase Equilib 2005, 240, 96–100. [Google Scholar] [CrossRef]
- Peng, D.Y.; Robinson, D.P. A new two-constant equation of state. Ind. Eng. Chem. Fundam. 1976, 15, 59–64. [Google Scholar] [CrossRef]
- Khashayar, N. Comparative study of eleven equations of state in predicting the thermodynamic properties of hydrogen. Int. J. Hydrogen Eng. 2010, 35, 3802–3811. [Google Scholar]
- Mathias, P.M.; Copeman, T.W. Extension of the Peng-Robinson equation-of-state to complex mixtures: Evaluation of the various forms of the local composition concept. Fluid Phase Equilib 1983, 13, 91–108. [Google Scholar] [CrossRef]
- McCarty, R.D.; Arp, V.; Fox, J.R. GASPAK Version 3.35/3.45; CRYODATA Inc.: Littleton, CO, USA, 2007. [Google Scholar]
- Flourusse, L.J.; Peters, C.J.; Pamies, J.C.; Vega, L.F.; Meijer, H. Solubility of hydrogen in heavy n-alkanes: Experiments and SAFT modeling. AIChE. J. 2003, 49, 3260–3269. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).