Abstract
Intermittent power interruptions and blackouts with long outage durations are very common, especially on weak distribution grids such as in developing countries. This paper proposes a hybrid photovoltaic (PV)-battery-system sizing optimization through a genetic algorithm to address the reliability in fragile grids measured by the loss of power supply probability (LPSP) index. Recorded historical outage data from a real stochastic grid in Ethiopia and measured customer load is used. The resulting hybrid-system Pareto solutions give the flexibility for customers/power utilities to choose appropriate sizes based on the required reliability level. To evaluate the sizing solutions’ robustness, this work considers and compares grid outage modeling through two different approaches. The first is a Markov model, developed to be minimally implemented with limited outage data available. The second is a Weibull model, commonly used to describe extreme phenomena and failure analysis. It is more faithful in reproducing the dispersion of outage events. Using these models, the effectiveness and performance of the PV-battery system is verified on a large number of simulated outage scenarios, to estimate the real performance of the optimized design. It leads to a more accurate evaluation of the behavior of a renewable power system to a weak and unreliable electrical grid.
1. Introduction
Monotonous power interruptions and blackouts even in modern electrical power systems are customary throughout the world, from which both the power utility operators and customers are suffering a lot. Distribution networks are the constituent elements of the power system, which make up the major outages and interrupting events world-wide. They account for more than 80% [1,2] of customer reliability issues, and could even reach to 90% [3].
In modern economies, there are virtually no economic or any other activities in any country without energy services, i.e., predominantly, no activities can be carried out under power interruptions. Grid outages are crucial, with impacts on both consumers and suppliers. Whether interruptions are planned or unplanned, they entail high costs and socio-economic losses for different consumer categories [4,5]. Interruptions are either sustained (long) interruptions or momentary (short durations). The aftermath of interruptions highly differs with consumer types, such as for hospitals or residences; time of outage occurrence; and outage durations [5]. For instance, direct costs such as investing on diesel backup generators can make up as much as 40% of consumers’ energy bills [4]. The use of the diesel backup units is also environmentally damaging and the less cost-efficient option. This added consumer cost depends on different factors, such as the behavior of the grid outage.
The first step to improve power supply reliability is the study and detailed assessment of such reliability issues, which are essential for judicious evaluation of mitigation solutions and investment decisions. Several research studies are made on reliability evaluation with respect to incessantly growing and changing power demands, supply imbalances, and weather-caused interruptions. Apart from the severe weather effects, causes of outages could include operational (overvoltage, short circuit, maintenances, etc.), aging and component failures, human actions, overgrown or fallen trees, inadequate maintenance, other nature factors, and so on.
To begin with the broader sense of reliability studies, the impact of integrating distributed generations (DG), both from conventional and renewable resources, has been studied in several works, such as in [2,6,7,8,9,10,11,12]. With an hourly time-step, these works investigated the reliability benefits of DGs tested on IEEE distribution test systems. System reliability indices are evaluated on different bases, e.g., the basis of randomly generated Poisson distribution average failure rates [6]; exponential average failure rates [9,10]; and an average time to repair, modeled by Rayleigh distribution [9]. Some of these publications also include other potential reliability improvement techniques such as load demand management [7,9]. Aside from their universal reliability analysis on DG-based structure, some authors have also featured DGs’ start times [2], grid supply or local integration [8], and their locations in the network for the improvement of reliability and supply restoration for fault-upstream load points [11,12]. Overall, the average interruption durations and frequencies, unsupplied energy or lost loads are some of the reliability measures considered in those works. The reliability concern due to the inclusion of such DGs as solar and wind sources in isolated power systems is also studied [13].
On the other hand, either to recommend power distribution system design configurations or to include DGs for reliability improvements, an overall grid reliability assessment was presented in [14,15]. The system topology and subsystem failure behaviors with their corresponding historical data were used for the reliability analysis model. The Markov model is used for the failure and restoration of the system from the decomposed subsystems data. The authors applied component-level historical interruption, and reliability data profiles such as for switches, breakers, line sections, and fuses were used to construct the Markov technique. These components’ features were then applied by taking into account the distribution system topology and coordinated operation of those devices. Also in [16,17], reliability evaluation is carried out by considering an exponential distribution family for the failure times of system components. The latter papers tried to incorporate aging in the analysis, where a log-normal distribution was used for the downtimes of components. Moreover, a similar approach was reported by [18] for reliability analysis of a system characterized by an artificially created failure history based on individual components’ failure and repair information. In these above papers, components such as lines, transformers, switches, breakers, and feeders are considered.
Reliability assessment studies often use the Monte Carlo simulation for reliability indices’ characteristics analysis, despite its computational demand [19,20,21]. The models of component life relating to the time to failure and time between failures are explored respectively using the exponential and Poisson distributions [21]. Meanwhile, in [20], the probabilities of interruption durations of components are replaced by the Weibull distribution for the reliability evaluation. Similarly, a probabilistic reliability assessment by estimating a probability function for power restoration in a transmission system is examined in [22]. The probability function fit is based on the failure event databases in selected power systems.
Extreme and severe weather impacts, such as from hurricanes, storms, floods, tornados, and so on are the predominant causes in distribution system outages in countries such as the US that have advanced systems [23,24]. Various studies in the literature, such as in [23,24,25,26,27,28], developed system outage predictions to estimate the probable operational or damaged states of components under weather-caused interruptions. The authors reported that the input data for the predictive models are principally the weather information, historical extreme weathers, other environmental parameters or historical outages with their associated factors, such as seasonal birds. Some of the recommended purposes of the prediction include either to facilitate grid restoration, to locate fault areas, or to plan maintenance.
On the other hand, grid outages in developing countries, where either the system is weak or supply is inadequate, are serious, and customers experience very frequent power-supply interruptions [4,29]. For customers with such frail distribution systems, a rather more resilient and reliable solution is required. Optimal energy storage systems are examined for improving distribution network reliability in reducing the unsupplied energy for a radial distribution network [30], and for enhancing the reliability due to momentary interruptions [31]. Moreover, a residential PV-battery backup system is presented for reliable power generation under scheduled grid outages [32,33]. In one case [32], a blackout caused by the supply capacity’s shortage to meet the demand, whereby the scheduled outage is known to customers, is studied. Whereas in another case, a similarly predetermined outage in terms of a fraction of the total simulation is investigated. Two conditions, harsh and moderate, are defined with a corresponding 52% and 34% of outage time from the total simulation period with a 1-h time step. A rural residential setting in Lebanon is where this case study is applied, with a blackout schedule that seems to be rather severe. Additionally, a diesel/solar hybrid system is investigated for a similarly scheduled outage context [34].
Due to the stochastic nature of the unplanned random outages that are very common in developing and emerging countries [29], demand-side solutions usually fail to alleviate these outage problems. It is thus essential to have a supply-side mitigation like in this work, with a more in-depth rational study of the distribution outages and projected grid supply.
Regarding the reliability issue, various approaches in addressing reliability assessment, the added impact of DGs, weather-caused outage predictions, and the sizing and operation of hybrid systems have been explored. However, as explained above, and according to our observation in developing countries like in Ethiopia, the distribution system outages are sporadic in nature, i.e., unscheduled sustained interruptions, and the causes are mainly not linked to weather or environmental factors. Among those, very old and weak grid infrastructure, poor grid architecture, and inadequate maintenance are some of the key causes [35]. Hence, an adapted practical approach for reliability evaluation and improvement is required.
This paper proposes a methodology for modeling and simulating the grid state in scrutinizing its outage phenomena. Unlike others, a 1-min sampled actual stochastic grid interruption rather than a hypothetically synthesized interruption data is considered in this study. Such interruptions or outages are representatives of distribution networks outages under similar circumstances, including radial arrangement, aged networks, geographical places, networks lacking sufficient redundancy, and comparable average outage durations. Hence, this study may be extended to distribution systems under such similar conditions. Furthermore, sizing a hybrid PV-battery system using a multi-criteria optimization for an enhanced reliability index and lower investment is investigated. The idea in this study, partially developed in [36], is to assess the suitability of power system sizing based on a limited number of measured outage sequences, by testing it on a much larger set of data reconstructed through stochastic modeling. Here, a method to simulate a stochastic cloud cover is formulated for a solar radiation-based sizing of a standalone photovoltaic system. In this work, two different modeling approaches are proposed. The first is a Markov model, which can minimally be implemented with limited outage data available. The second is a Weibull model, which is commonly used to describe extreme phenomena and failure analysis. It is more faithful to reproduce the dispersion of the events, both on their duration and on their frequency of occurrence. However, it also requires a larger initial data set. Based on these two modeling approaches, the effectiveness and performance of the PV-battery system is then verified on a large set of simulated outages (equivalent to one thousand years), to try to estimate the real performance of the optimized design. Comparisons of the performances of a sizing are then possible, and open the discussion on the best way to consider outages in a sizing process.
The proposed paper is structured as follows. In Section 2, the technical and economic models with the multiobjective optimization for the proposed hybrid PV-battery system are presented by considering the grid reliability and cost of energy. A nearly one-month-recorded load profile and outage data sampled at 1 min is used as the basis for the sizing. Additionally, the genetic algorithm optimization method, and the solar irradiation and ambient temperature input datasets for a considered case study are also detailed in this section. It also explains the distribution grid outage predictive modeling and simulation approaches based on five years of data, taking into account any periodicities and correlations among the outage parameters. Section 3 presents the Pareto front solutions of the results for the hybrid-system sizing optimization. The grid outage simulations, the test evaluation of these outage profiles on different optimal systems, and overall associated performances on larger scale are also detailed. Finally, the summarized optimal hybrid system and outage simulation findings conclude this paper in the last section.
2. Proposed Methodology
A PV-battery system for an actually measured grid outage sequence is considered as a primary step. Here, the optimization problem is approached through the sizing of the power system, by considering the PV area and the number of batteries. A sizing is then evaluated on its cost and on the quality of the provided services (i.e., enhancing of the reliability), and for a given energy management strategy. Besides this, the load demand combined with grid outage profile for a conventional university building in Addis Ababa, Ethiopia, was measured and is a case study for this work. The battery also allows an extra degree of freedom for supplying energy during the interruptions and in the case of unbalanced solar power production.
A main problem for the sizing of such an auxiliary power system is the stochastic nature of the outages, which represent the main part of the energy to supply when installed on weak distribution systems, such as in developing countries. Thus, faced with this problem of forecasting network outages, this work proposes to link a sizing optimization approach, carried out on the basis of a sample of measurements, and to try to verify the effect of the random nature of the outages on the power system quality. In the end, the idea is that for a given sizing it becomes possible to predict its behavior from a statistical point of view. Then, two different methods are proposed in order to model and simulate possible grid outages, according to short, historical recorded data. To evaluate these models, long-term projected outage profiles (from five years of measurement) are used, which permit a comparative performance analysis of the PV-battery system with the actual historical outage data of a real radial distribution network. This further provides a twofold advantage, which consists of the test of the performance of the optimal power system in reducing interruptions on the one hand, and the validation of the simulated outage behavior with actual records on the other hand.
2.1. System Modeling
Considering such an unreliable grid with random outages, a grid-connected photovoltaic system with battery storage is considered in this work—see Figure 1. The techno-economical models include a solar PV generator, a battery storage, the load demand, the random grid unavailability profile due to outages, solar radiation, and ambient temperature data. The sizing optimization enables consideration of the tradeoff between the cost of the system in terms of energy and the improvement of the grid’s satisfactory ratio (i.e., the reduction of the outage issues). This can be achieved using the energy and economic modeling of the aforementioned system elements.
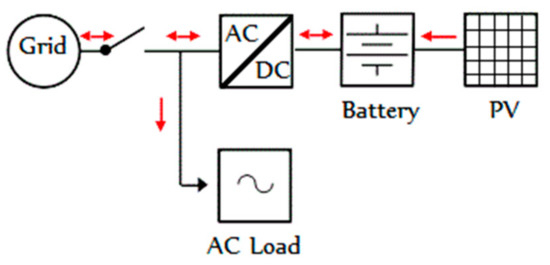
Figure 1.
Simplified system power flow schematic.
Whenever the grid is available, i.e., there are no outages, the grid fully supplies the building load and the PV will charge the battery eventually assisted by the grid, if PV alone is insufficient. During outages, the PV fulfils the demand. If the PV power is inadequate, the storage batteries will flexibly be able to complementarily back up the solar power.
2.1.1. Photovoltaic System Model
The power generated from the photovoltaic panel is defined by the cell temperature as a function of the location’s ambient temperature and the available solar irradiation. The PV power is used to supply the load directly in case of outages, and/or to charge the battery bank. The maximum available power from the PV with maximum power point tracking (MPPT) for a given surface area of the panel, Apv (m2), and the total irradiation hitting the PV surface, Gtot, is mathematically modelled by [36,37,38,39]:
where Ppv is the generated PV power at time step t (a 1-min time step is used) and ηpv is the PV panel efficiency and is given by [36,39]:
where ηm is the module efficiency, βp is the photovoltaic panel power temperature coefficient taken as −0.003/°C for silicon cells. Tcell and Tamb are the cell and ambient temperatures (°C), and Tref is the reference temperature, which is 25 °C. The nominal operating cell temperature (NOCT), module efficiency, and temperature coefficient are variables depending on the selected module, and can be derived from the manufacturers’ datasheets.
2.1.2. Battery Model
During the grid outages and in cases where there is no PV power or there is a deficit in the solar power production, the battery bank supplies the consumer load demand. Considering this key system component to work in connection with the existing grid, a universal sizing method and energy management according to the charging–discharging rule is used [37,38,39,40]. This rule takes into account the grid availability and compares the total (grid + PV) power with the load. Thus, depending on the grid availability together with the total available power and the battery-stored energy, the battery storage system can be modeled by its State of Charge (SoC) at any time instant, t, and given by equations (Equation (4)) for the charging, and (Equation (5)) for the discharging operations:
For discharging:
where Ptot is the total available power from the grid and PV, Pload is the load demand, ηinv and ηbat are the inverter and battery efficiencies, assuming a discharge efficiency of 1, Cbat (kWh) is the battery storage nominal capacity, and Δt is the simulation time-step increment, which is 1 min in this study. Here, note that the total power during outages is only the PV power, as the grid power is zero.
The storage battery ensures the power supply during outages in its operational range of states, SoCmin and SoCmax. These lower and upper limits are here considered to be SoCmin = 0.2 and SoCmax = 0.9. Additionally, for a more rigorous model of the storage, the maximum allowable charging and discharging powers are considered in the energy management model.
2.1.3. Reliability Criteria
The portion of the power that cannot be supplied by the PV-battery system during outages is the reliability metric considered in this study. Apart from this main fraction due to the outage, it also incorporates the intermittency of solar production. This whole portion of power can effectively be described by the widely used parameter, loss of power supply probability (LPSP) [36,37,38,39,40,41], as given by:
where the loss of power supply (LPS) is the power that cannot be met during a sample time Δt, even by the PV-battery system during outages.
This power imbalance is then simply given by the difference of power between the load and the power system:
such that:
where Pbat is the battery power.
The LPSP is normally in the range of [0, 1], in which 0 means that the load is fully satisfied and 1 means that the load can never be met at all.
2.1.4. Economic Model
With the objective of improving the LPSP, the economic evaluation index considers the annualized system cost (Ctot,a) containing the sum of the capital (Ccap), O&M (CO&M), and replacement costs (Crep) of the different components, and grid-charging cost (Ccha.) [36,42]:
where the capital cost covers all the components, the O&M cost is considered for the PV only and the replacement cost for the storage battery only. The system capital recovery factor (CRF), with the discount rate i, is given by [39]:
Finally, we calculated the annualized cost of energy (CoE), which is the average cost (in euros) for the energy actually generated and served (in Wh). It is then defined by:
where Pgen is the total generated power, and N is the project lifetime—considered as 25 years.
The details of the technical and economic parameters of the system components are summed up in Table 1 for a commercially available PV panel and storage battery, taken from literatures, see details in [43].

Table 1.
Considered values for the technical and economic parameters of the system 1.
Figure 2 shows the rule-based energy management strategy implemented in the sizing algorithm based on the grid availability status, the power available from the PV and battery SoC, with other constraints.
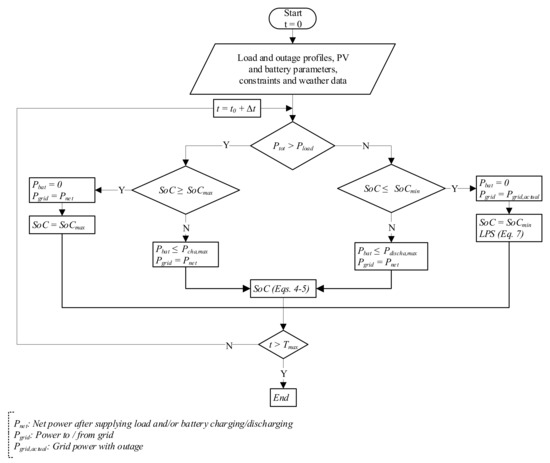
Figure 2.
Rule-based energy management strategy flowchart.
The energy management rule considers the following strategies in the sizing optimization process:
- PV power is preferred over grid to supply loads, when there is no outage;
- The grid covers loads and assists in battery charging, when the grid is available;
- During outage, no power is sent to the grid;
- The algorithm should satisfy the SoC limits and battery charge–discharge constraints;
- The storage-battery charging process starts whenever the total power generation exceeds the load demand;
- Pgrid means the power ‘drawn from’ or ‘sent to’ the electrical grid network.
2.2. Power System Sizing Optimization
As a prime objective for an acceptable robust system configuration, the PV-battery sizing process is formulated as an optimization problem [38,43]. In this problematic, there are two conflicting objectives that will have a set of possible solutions called the Pareto frontier. For these nondominated sets of solutions, for instance, one of the objectives will never be any better without making the other objective worse. This tradeoff will give flexibility to consumers or power utilities to choose any of the combinations of the hybrid system based on their required level of reliability.
The two-objective function considered is: the minimization of the cost of energy (CoE), which is composed of the system and associated costs, as well as grid-charging cost; and the minimization of the LPSP, which is the measure of the reliability improvement by reducing or fully overcoming the grid outages. The optimization algorithm evaluates the area of PV panels (Apv) and number of batteries (Nbat) to be installed either to avoid outages or for minimization. Hence, the area of the PV panels and the number of storage batteries are the sizing parameters in the optimization:
Then, all the possible solutions (Apv, Nbat) of the two decision variables will be evaluated on real load demands and outage profiles recorded at the university building in Ethiopia, namely the Addis Ababa Institute of Technology, located in the capital, Addis Ababa. The system evaluation comprises the Apv and Nbat in wider sizing boundaries to a maximum range of 600 m2 PV panels and 50 batteries, respectively, projected to the project’s lifetime of 25 years. Due to the small number of decision variables, we used an exhaustive search to test all the possible set of solutions in these boundaries.
The nondominated sorting genetic algorithm (NSGA II) was used for optimization of the PV-battery system using the aforementioned monthly load profile and outage data. The optimization Pareto front allows users to choose one of the possible combinations of LPSP and associated CoE, depending on the acceptable reliability degree.
2.2.1. Load and Outage Profile
Nearly a one-month load profile (exactly 28 days, see Figure 3) for a typical public university building in Ethiopia was measured using Fluke 435 power analyzer (series II power quality and energy analyzer). The measurement time-step was 1 s, which was sufficient to register the outage duration and frequency in sensibly high resolution. This demand, the typical one-week data shown in Figure 3a, and one outage profile (Figure 3b) are used for the optimization problem. The grid supply-side LPSP without the inclusion of any backup system, neither diesel nor PV-battery systems, is 5.9%. Additionally, one can also see that the building has an average, maximum, and minimum load power of about 24.5 kW, 50 kW, and 13 kW respectively.
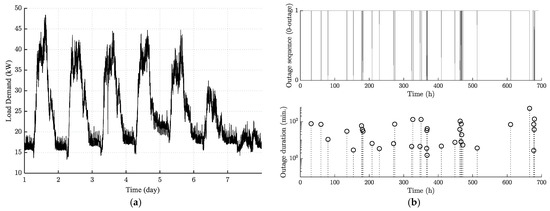
Figure 3.
Load demand and outage profiles measured data: (a) representative one-week (12–18 November 2018) load demand—the first five days represent the weekdays’ load and the last two days for weekends; and (b) outage sequence (upper) and corresponding outage durations (lower) during the measurement period—24 October to 21 November 2018.
Next, five-year outage data for a radial distribution network in Ethiopia were collected, as summarized in Table 2. The data were used for the grid outage modeling and simulation, which will be discussed in detail in Section 2.3. It also served to test the performance of the sizing for a selected year profile by considering a monthly constant load taken from the 1-month measurement. Moreover, the optimization was re-run for the selected year, which was again used to compare with the system testing and performance of the simulated outage. It is worth mentioning here that this distribution outage data is for an 11 kV feeder, which experiences slightly more frequent outages than what are measured at the university node.

Table 2.
Distribution grid outage five-year data.
2.2.2. Solar Resource
The PV power output directly depends on the global solar irradiation incident on the PV panel surface and the ambient temperature of the location. For the site considered in the case study in Ethiopia at a 9.04° N latitude and 38.8° E longitude, the used solar irradiation resource and ambient temperature data are from [44] and given by Figure 4. The dish-shaped irradiation and the temperature minimums in mid-year, are due to the rainy season in the country.
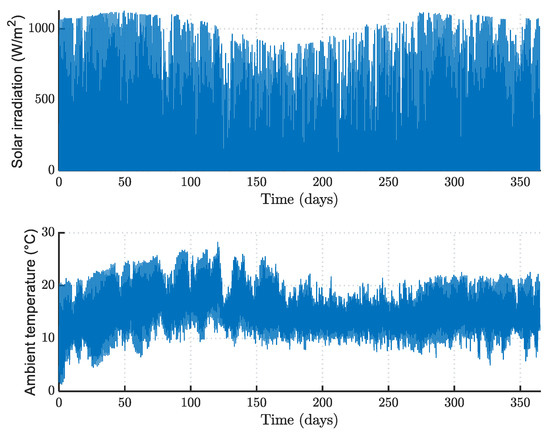
Figure 4.
Solar irradiation and ambient temperature, during one year, in Addis Ababa, Ethiopia.
2.3. Grid Outage Modeling and Simulation
A key part of this work, which proposes to evaluate the influence of the stochastic nature of outage apparition and duration, is the modeling of this stochastic process. Modeling distribution grid outage needs long-term profiles to be accurate and faithful. It then permits us to study the nature of outages in depth for further analysis and reliability improvement solutions. Additionally, it becomes highly important to evaluate the performance of the optimal energy system over a long period of time for techno-economic feasibility. As a reminder, due to a substandard power system infrastructure in developing countries, the existing fragile power-supply service experiences many power outages which greatly affects the service quality [35]. Hence, the modeling technique is very important in that power distribution system measurements, data acquisition, and storage in real-time and for a long time is very costly; and it is hardly even possible to find such datasets for most infrastructures in developing countries.
The Markov model has been used in several power distribution system problems such as in the evaluation and assessment of interruptions taking into account their stochastic nature (see Section 1). It is a probabilistic mathematical model that can sufficiently capture system failures and failure rates in the form of state transitions for most dynamic systems with greater flexibility [2,15].
Alternatively, the Weibull distribution approach is widely used to characterize grid network interruptions. It is one of the statistical approaches used to denote interruption durations or component failure durations, as well as the chain states of interrupting grid components [20,21,45].
Hence, in this paper, the Markov and Weibull models have been applied for the simulation of grid interruptions, as these models can respectively characterize the random probabilistic outages and also be able to signify rare outage occurrences that could be overlooked with a classical approach.
2.3.1. Test for Outage Periodicity, and Correlation between Outage Duration (OD) and Time between Outages (TBO)
In the first step, whether there exist any seasonal variation and other outage periodicity impacts was tested. In addition, other possible periodicities due to such causes as regular maintenance activities, day–night cycles, and mild summer–winter seasonal dependences, as is the case in Ethiopian climate, are tested for their periodic effect, if any exist. For instance, a clear seasonal load difference according to seasonal variation can be observed during winter and summer [32,33].
For this, the frequency representation of the outage sequence data using the fast Fourier transform (FFT) of the autocorrelation function is used. What this basically does is extract the frequency components of the outage data and plot them as a function of time period for observation. This helps either to select an appropriate model for outage simulation or modify currently existing methods. It can also help to determine which DG technologies to consider, depending on resource availability, and integrate any periodicity to the rule-based energy management.
Results are given by Figure 5, where correlations are tested between the TBO and OD as well as the highlight of periodicities in the outage sequence.
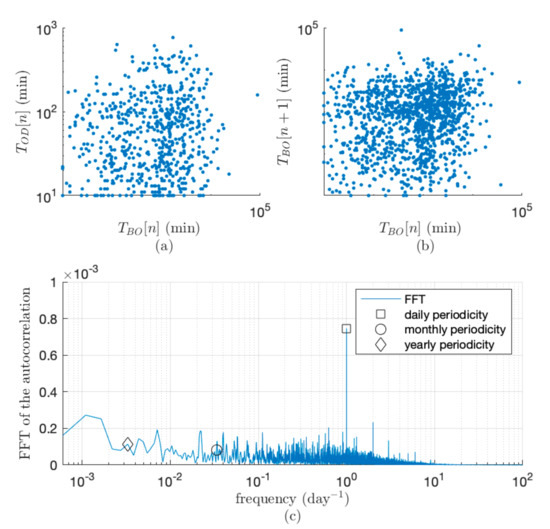
Figure 5.
Correlation diagram between (a) outage duration and time between outages, (b) between two consecutive outages, and (c) frequency analysis to highlight the outage periodicities.
It is quite clear that there are no correlations between the TBO and the OD. It is also interesting to see that the lag between two consecutive outages has a large dynamic and can range from a few minutes to a few hours.
The periodicity check showed that the distribution outage is totally random without any long-term periodicities, concluding that there is no cyclic nature with seasons, nor is there in yearly, monthly, and weekly patterns. In contrast, a clear daily periodicity is visible. Figure 6 shows the time of occurrence of the failures during the day. Most outages occur during the day and seem to be linked to the global load demand. In other words, the probability of outage occurrence is positively correlated to the power requirements of grid users.
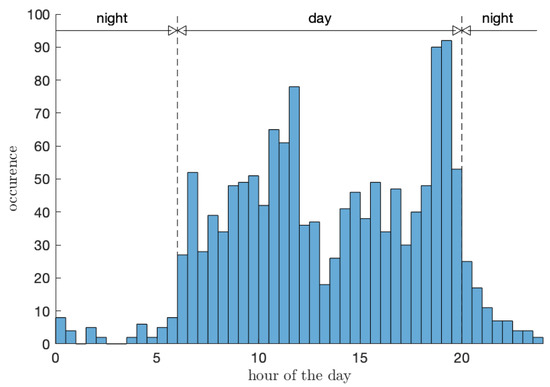
Figure 6.
Histogram of five years’ data of outage occurrences during the day.
2.3.2. Markov Model
It may perhaps be customary to use a historical annual number of outages and corresponding duration data to characterize the distribution grid reliability and further utilize it for various applications, like grid management, outage prediction and adding hybrid systems. To have trustworthy reliability study, long-term historical data is usually required. Hence, it is clear that small data will not be able to adequately describe the distribution system’s reliability. For each year, the sequence of grid availability may not be found, but some global parameters such as the total number of hours of outage, the number of outages in the year, the average duration of an outage, and the average time between two successive outages, can be given.
Here, considering a case in which a small number of data are available, it is proposed to use a relatively simple-to-implement Markov model with the transition probabilities of the grid outage with the binary-state Markov transitions, from/to ‘ON’ and ‘OFF’ states. The Markov model enables the calculation of the probability of system outage states using the analytic matrix computations. This again gives the durations and frequency of outages. The Markov model is important due to its computational minimalism and the capability to be built from global data to develop a full representation of stochastic systems, such as a standalone photovoltaic system sizing based on a stochastic cloud cover, represented by a possible-state values-of-clearness index [36]. Solar irradiation measurement observations were used to label the possible states of the clearness index parameter. The principal indices of the distribution system outage, i.e., outage duration and frequency, were used for the model, and subsequently any desired length of time can be simulated.
To characterize the stochastic grid outage as a Markov process, some steps are followed. Firstly, the state transitions from state to state are enumerated to define the size of the transition matrix (see Figure 7). Secondly, the Markov transition matrix (MTM) is built from the recorded data according to all the transitions encountered. Once this MTM is obtained, simulated scenarios of grid outage can be generated on the base of the MTM probabilities. This Markov probability model assumes that the next outage event is absolutely dependent on the current state only, which is widely used in reliability modeling [16].
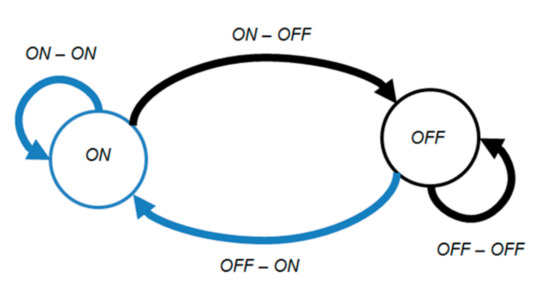
Figure 7.
A schematic representation of MTM transition states.
Here, the power grid description can be limited to only two states, which are ‘ON’ for a working grid, and ‘OFF’ when outage occurs. There are then four possible state transition probabilities to calculate, given by:
where current states are listed in the column and future states in the lines. An easy way to build the transition matrix is to count the total number of each transition. Suppose a measured historical global data with a series of M samples times, and these two possible states. The MTM with a total number of outages N, a total number of samples in OFF state MOFF and deducing the total number of samples in ON state M-MOFF gives (see Figure 8):

Figure 8.
Typical time series of the state of a power grid.
It is interesting to see here that the MTM parameters can be deduced from global data. Indeed, it is common that published data on outages are annual and only the total number of outages and the total duration of the outages for one year are given. For instance, in [46], the average durations of the outages can be deduced per year, as for the total annual outage duration. It is easy to see that these data are enough to build the equivalent MTM. If the total annual outage duration is noted as Toutage, the average outage duration Tavg, and the duration of one year Tyear (8760 h), the MTM can be rewritten as:
To capture the daily occurrence, more adapted Markov transition matrices (MTM) are repartitioned to day and night MTMs, based on the corresponding actual outages occurrences data (see Figure 6). Hence, the above approach enables the MTMs for better simulated predictions and are calculated from the global data (2012–2016); the historical outage data enables us to adapt the MTM simulation model using the said global parameters.
2.3.3. Weibull Model
In the previous section, the Markov transition matrix has been proposed to describe the outage occurrence. It has been shown that this matrix is easily built from global annual data, such as average and total outage durations. The Markov approach also permits us to consider the daily periodicity through the use of two different MTMs, used respectively during the day and the night. In counterpart, the MTM is very limited to take into account the shape of the probability distribution for both parameters, which are the time between outages and the outage duration, because of the limited number of setting parameters with this approach. In particular, it is not possible to take into account the longest outages without changing the step time or the order of the MTM. Then, a second model to address this difficulty is proposed, which is more adapted to approximate the extreme outage events. This time, the outage duration (OD) and time between outages (TBO) are directly based on statistical distributions.
Weibull distribution is able to closely fit with the five-year outage data; consequently for the case study of this paper, the standard two-parameter Weibull distribution has been used to model the distribution grid outage. Outage durations or repair times of a component can be represented by this distribution [20,21], and its cumulative distribution function (cdf) for a random variable x can be given as:
where a and b are the scale and shape parameters; a, b > 0, and are derived from the data.
By fitting a Weibull cdf to the set of historical data, the values of a and b are determined; these characteristic parameters permit us to get a calibrated Weibull distribution with the actual distribution grid outage data. For clarity, the grid outage and restoration sequence are constructed from the simulated TBO and OD—see Figure 8 for grid sequence depiction. Based on those two global parameters, OD and TBO, from the five-year distribution grid operating history, a uniformly distributed pseudorandom number generator in the interval (0, 1) was used to build the distribution of simulated OD and TBO. This once again results in building the grid outage sequence, the grid being in an up state or down state, for the simulation time frame considered.
We have selected the year 2015’s distribution grid outage as a reference year, which has relatively average outage durations, number of outages, and LPSP values. For calculating the LPSPs for each of the five years, we considered the monthly load measurement to be the same in each 12 months. This customer building is assumed to be connected to the 11 kV feeder under consideration, Section 2.2.1.
Finally, the 1000-year simulated outage profiles from both models are tested for their performance with the optimal system sizing.
3. Results and Discussion
3.1. System Configuration and Optimal Sizing Results
Based on the real load demand and outage measurement, a techno-economically optimal solution is developed. The proposed sizing optimization in minimizing the LPSP and CoE enables us to achieve greater reliability improvement. The frequency of outage occurrence and the durations of outages are the two crucial factors dictating the size of the power system components. Longer outages occurring during the night entail bigger battery capacity; conversely, such similar outages during sunny days necessitate a larger PV area. The proposed optimal photovoltaic-battery system sizing analysis was implemented in MATLAB (version R2018a).
The sizing algorithm calculates the desired quality of service measured by the LPSP with the corresponding global energy costs, which are set to be minimized. The nondominated Pareto solutions result in the cost function value and corresponding positions of the optimization variables—in this case, the PV area and number of batteries. This solutions front is the best optimal set from which any of the two objective variables, LPSP or CoE, cannot be further improved without degrading the other. The optimization algorithm is run repeatedly to ensure that the algorithm led to these best results of the Pareto, resulting in similar values.
Figure 9 illustrates the modeling objective targeted at a reduced or zero loss of power is achieved by optimizing the LPSP and CoE for all the possible combinations of the system’s PV area and storage battery capacity. A zero LPSP can be achieved with relatively high battery capacity and PV array, at a cost of energy of 0.17 € per kWh, which corresponds to 182 m2 PV and 39 batteries. The Pareto front set of all the possible solutions indicate that lower costs with a more acceptable choice of LPSP than zero shall give the freedom to choose other PV-battery combinations, for users to make an informed decision in implementing such systems. A customer can select the intended level of comfort (LPSP level) as a primary objective with the best possible value of the corresponding CoE.
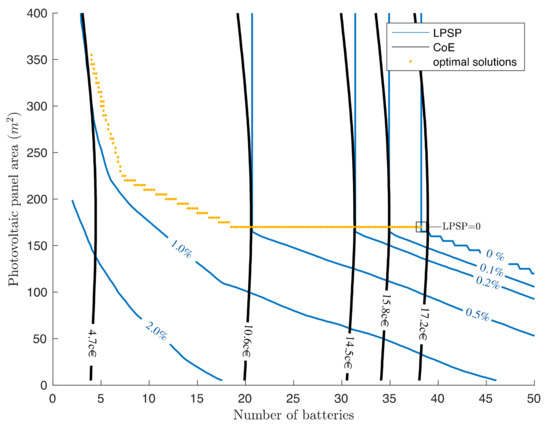
Figure 9.
Photovoltaic-battery system Pareto optimal sizing.
Longer outage duration causes the LPSP to surge, demanding larger system sizes and hence energy costs. Except for the likelihood of slightly enhancing the reliability, the LPSP barely responded to PV area and battery sizes after certain values. A further increase in PV sizes with 10 or more batteries, notably did not further improve the LPSP. This reliability and system sizing optimization result indicated that there is an important sensitivity of the LPSP index to the PV size at a low-cost solution with higher LPSP values. This shows the role of PV in low-cost systems. Increasing the number of batteries from 5 to 20 created a 1% LPSP improvement. At lower LPSPs for improved comfort, the batteries played an important role, with higher system cost as expected. But the LPSP insensitivity beyond this higher battery value highlighted that the outages that occurred during non-PV generation have dictated the sizing process. This means that the compensation for the longest outages, or those that occurred during the night, were provided by the batteries. System sizing would have been primarily ruled by outages if they occurred during a nonzero PV power generation.
3.2. Outage Predictive Modeling: Markov, Weibull
Contrary to the weather conditions that cause distribution systems outage elsewhere in the world, in this paper context there is no wide variation in season and weather conditions. This can be also seen from the two major decisive factors of the PV system design, global irradiation and ambient temperature data (see Figure 4).
For the Markov method, the resulting MTMs of probabilities for the daytime and nighttime are:
and
The transition probabilities apparently show a higher chance of staying in an ‘OFF’ or ‘ON’ state, if the grid is already in those respective states initially. For example, in the daytime MTMd (1, 1), the probability of the grid remaining in its initial position of ‘off’ state is 0.978; refer to Appendix B for a sample simulation based on five years of data with these transition probability matrices compared to actual data.
With regard to the Weibull process, the estimated a and b values with a 95% confidence interval through the maximum likelihood estimates technique are: for TBO: a = 1620 (min), b = 0.77, and for OD: a = 36 (min), b = 0.56.
Figure 10 shows the obtained cumulative distribution functions for both OD and TBO. It is obvious that the Weibull distribution, with only two parameters, is able to accurately reproduce the measurements results. On the contrary, the Markov matrix approach, although it is simpler to implement and can differentiate the day and night phases, does not allow the measured distributions to be accurately followed. In particular, long and unlikely events are very difficult to be captured by the Markov approach. This confirms the idea that using a Markov process to describe grid outages is a simple and accessible way when the data are not available, but that it will not allow to be accurate to the actual outage profiles. Weibull is able to demonstrate a more realistic simulated profile as compared to Markov.
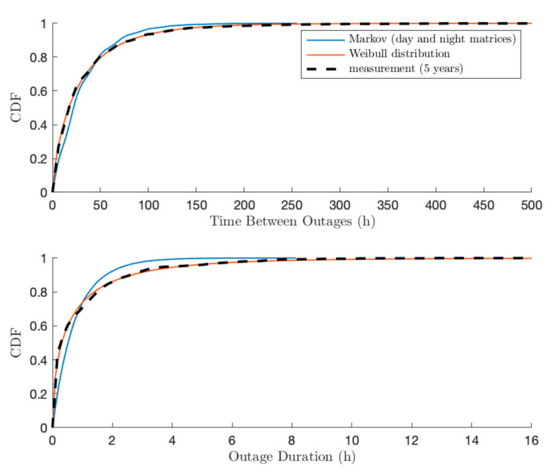
Figure 10.
Cumulative distribution function of outage duration and time between outages, for measurements (five-year data), Markov transition matrices (day and night) and Weibull distribution.
After the proposed models and methods of generating outage profiles were presented, a safe sizing methodology could be developed. On the basis of optimal sizing obtained for a reference year (2015), the method consists of testing it for a large set of simulated outage profiles, and testing its results in the objective plan, which are in this study the LPSP and the cost of the solution. Then, the obtained LPSP results (there are then as many LPSP values as there are years simulated) are statistically compared to the five-year average LPSP value, obtained without any power system (LPSP = 2.53%).
Similarly, according to Figure 11, the Markov model shows a lesser distribution, while Weibull shows better spread—appearing to better cover the data profiles. The outage data without any power system in the years 2012–2016, i.e., the grid-side power supply state without any backup or standby system, is shown in broken vertical lines superimposed on these model simulation probability curves.
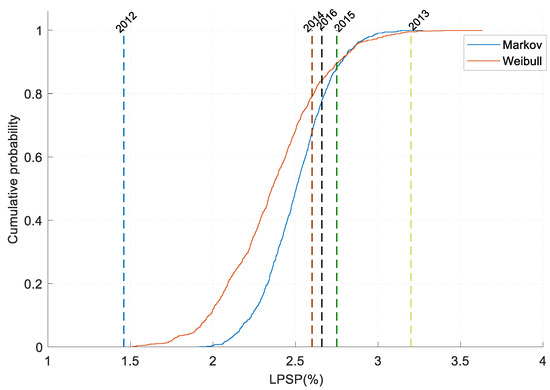
Figure 11.
Cumulative distributions of the simulation of grid outage sequences, without a power system, by using Markov and Weibull models. The LPSP comparison with the 2012–2016 data is shown in broken lines; the mean LPSPs values for the Markov and Weibull simulations are 2.51% and 2.38%, respectively.
The Markov model takes into account a piecewise constant transition probability depending on the hour of the day to develop the outage sequences. Regarding the Weibull model, it gives a more diverse LPSP probability pertaining to its capability to take into account lower frequency outage occurrences or extreme events.
For both models, their mean LPSPs are closer to the five-year average, which is 2.53%, with marginal dispersion, showing the effectiveness of the models. This ensures that the proposed simulation models tend to yield a comparable practical outage scenario. By integrating hybrid systems like in this study, better outage management, system reconfiguration, system planning, and so on can then be examined and reliability will effectively be addressed, based on a sufficient system profile.
3.3. Optimal System Performance Test and Reliability Results
For the robustness criteria, long-term outage sequences are considered in order to test the performance and the robustness of the proposed PV-battery system. To do that, the proposed idea is to test an optimal solution, obtained for a limited measurement data set (few days or few weeks), on a large number of simulated outage scenarios obtained from both Markov transition matrices and Weibull distribution. The methodology is illustrated in Figure 12. Based on a measurement sequence, optimization is achieved and a set of optimal solutions is obtained, on the base of CoE–LPSP objectives.
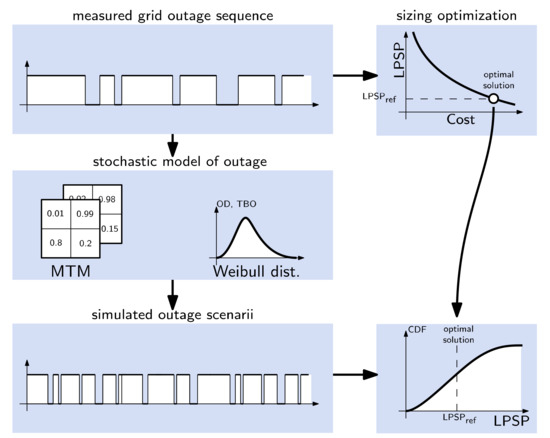
Figure 12.
Proposed methodology for the reliability test of a sizing solution.
In parallel, the measurement data are used to fit the MTM and Weibull distribution parameters. It must be noted that the MTM approach also makes it possible to find the parameters of the transition matrix only from annual global data, as given by equation (15). Next, a sizing solution on the Pareto front is chosen, and tested on a large set of simulated years (for instance a few hundred years). It results, for each simulated year, in a couple of LPSP and CoE, which differ from the values obtained in measurement. It is then possible to build the histogram and the cumulative distribution of both objectives. Finally, for an optimal sizing, it becomes possible to evaluate its robustness with probability values, and especially for the probability value n to have a maximum LPSPn:
To illustrate this methodology with the proposed case study, PV-battery system optimal solutions are adopted, with 0.0%, 0.1%, 0.5%, 1.0%, 1.5%, and 2% LPSPs as reference systems based on 2015. The PV and battery sizes and corresponding energy costs for the reference system are as given below, Table 3.

Table 3.
Reference optimal systems’ PV and battery sizes with their corresponding CoE, based on measurements data of the year 2015.
The next step of the proposed methodology consists of testing the performance of these sizings on the 1000-year simulated outage profiles. It gives a cloud of points of LPSP and CoE that are the two objectives of the optimization problem. These clouds of points are analyzed as statistical distributions of both parameters and are presented in Figure 13.
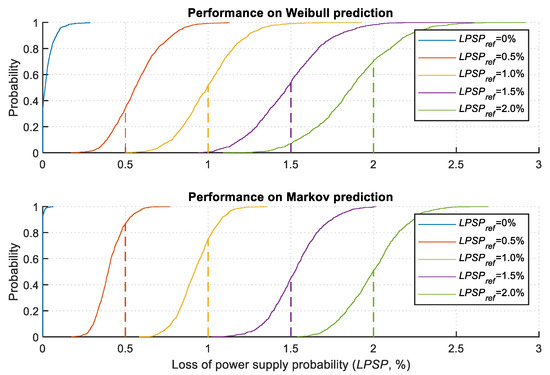
Figure 13.
Power system performance on predictive outage models: Weibull (top); Markov (bottom) cumulative distribution functions of LPSP.
Considering a completely reliable reference system with LPSPref = 0%, this value is equal to zero for about 92% and 32% of simulations for Markov and Weibull respectively. Comparatively, for a relatively higher LPSP reference system, such as 2%, this metric shows an LPSP less than or equal to this value (i.e., 2%) for 51% and 71% in the Markov and Weibull methods. Summing up these figures, for all the different solutions, both Markov and Weibull lead to distributions centered around the reference LPSP values and it can also be deduced that the Markov approach leads to more optimistic results compared to the Weibull distribution results. However, as seen previously, the Weibull distribution approach is more faithful to reality and therefore offers more reliable indicators.
The performance of the two models with selected reference systems with the corresponding LPSPs and CoE are illustrated by boxplots in Figure 14. As explained above, due to the Markov simulation resulting in well above the data average LPSP in lower values, the performance of the PV-battery system ensures a greater reliability under these circumstances. For example, the performance at LPSP = 0.5%, the optimal size line-graph predominantly satisfies load demand under such simulated outages, i.e., the Pareto graph (solid line) crosses above the third quartile (well above the median) of the corresponding boxplot. Note that the red lines inside the box are the median.
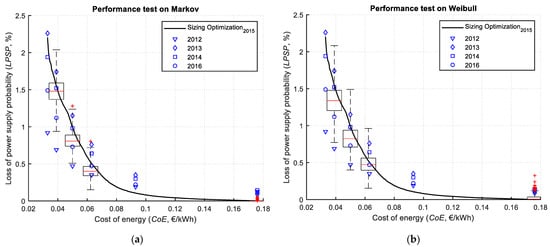
Figure 14.
Optimal PV-battery power system based on 2015 data: performance test on four years’ measured grid outage data is represented by blue symbols, and performance on simulated grid outages is depicted by boxplots; (a) performance of Markov outage prediction; and (b) performance of Weibull outage prediction. Boxplots show the performance of the simulated outage profiles, while the blue marks show the PV-battery system test on the outage data years.
Nevertheless, the Weibull shows the Pareto line crossing through the median for the 0.5% LPSP case. This phenomenon is reversed for higher LPSP values. By taking the 1.5% value, one can see that the point at which the Pareto front crosses the boxplots is vice versa to the above explained case.
In summary, the two pivotal variables in characterizing and sizing the hybrid PV-battery systems are the grid outage durations, which mainly dictate the size of the storage battery via the charge–discharge cycles, and the number of outages. Inherent to these factors is the time of occurrence of outages (time of the day) that further govern the size of the PV panel area required. Others could include the magnitude of the load demand and weather variables. The longer the outage duration and/or if it occurs at night when there is no PV production, the higher the battery size. Additionally, the higher the load demand during the day, the larger the PV area.
Furthermore, the outage modeling by the Markov and Weibull techniques show a very good estimate closer to historical data. The latter, with a minimal computational requirement compared to its counterpart, gives a disperse outage profile weighting in reference to the historical average LPSP. Conversely, the reduced dispersion in Markov offers an advantage for the optimal system to be able to satisfy the load–demand-outage profile to a higher degree of reliability. This is because the simulated outage profiles tend to be situated well below the historical average metric. Its requirement of crude outage data for the modeling is an advantage, but with slightly higher computations than the Weibull.
4. Conclusions and Perspectives
Nowadays, intermittent power interruptions and long outages are very common, especially from distribution systems in developing countries, which are ageing, have poor maintenance practices, substandard infrastructures, capacity shortages, and so on. This consequently affects diverse groups of consumers, with a substantial negative effect for consumers such as hospitals.
In this paper, we proposed an optimal hybrid PV-battery system to improve or wholly achieve the expected reliability. This renewable–based system will also substitute the commonly used diesel backups, which are harmful for the environment and relatively costly options. For practicality, we have used real load consumption and outage data, from Ethiopia, as a case study for the sizing optimization using the NSGA-II algorithm. Moreover, unlike in several papers, a very good resolution simulation time step of 1 min was used, which enables us to consider the power supply dynamics and the outages with a reasonably better accuracy. It was proven that the system can successfully reduce outages and entirely supply the load. The set of optimum solutions gives the freedom for consumers and utility operators to choose a safe system size with the desired reliability index. For instance, consumers connected to a weak distribution network with critical load requirements can have a zero LPSP with 0.17 €/kWh. Conversely, for consumers with tolerable load types, such as households, may choose a system with lower LPSP that perhaps, shall afford partial outages. Let us say that with about 0.11 €/kWh, the system could give 0.5% reliability.
On the other hand, outage evaluations and reliability studies usually demand detailed information about outage-causing factors, sufficiently high data records, and component/subsystem-level contributing elements. However, obtaining such datasets for distribution grids dealing with recurrent outages, such as in developing countries is unlikely. Hence, we developed a methodology to model and extend longtime outage simulation as needed, using global outage parameters and small amount of data. The proposed Markov and Weibull models are able to simulate outage profiles with sound computational effort and effectiveness. Simulated outage profiles can then either be used for various applications, including hybrid system inclusion to a weak grid for outage reductions and hence reliability improvement. Real outage data from a stochastic grid in a developing country is applied for the two modeling approaches. Such sufficiently dispersed outage simulations using the Weibull model will lead to a notable realistic scenario in order to avoid oversized hybrid systems. On the contrary, the PV-battery system on Markov-simulated outage profiles showcased that the reference system seems to perform with above the expected reference LPSP. The effectiveness of the proposed methodology for the optimal system is validated on a large set of simulated outages with these two models. Regardless of the effort to verify the absence of any correlation among the outage parameters and any periodicities, factors such as weather conditions, change in the load demand, future grid maintenance routines, and so on can affect and change the expected LPSP.
Further to these approaches, additional demand-side management techniques and load monitoring, such as load prioritization, could be explored to further improve the cost optimality and increase power supply security during outages. Besides which, sensitivity evaluation on the optimal system and simulated outages under varying load demand outage profiles shall be something to look into. It can obviously be highlighted that a load variation would result in a change of the required system size with a positive correlation, given the same outage profile.
Author Contributions
Conceptualization, F.S.K.; methodology, F.S.K., J.-C.O. and S.B.; software, F.S.K. and J.-C.O.; validation, F.S.K., J.-C.O. and S.B.; formal analysis, F.S.K.; investigation, F.S.K.; resources, M.M.; data curation, F.S.K. and J.-C.O.; writing—original draft preparation, F.S.K.; writing—review and editing, F.S.K., J.-C.O. and S.B.; visualization, F.S.K., J.-C.O. and S.B.; supervision, S.B. and J.-C.O.; project administration, S.B.; funding acquisition, S.B. and J.-C.O. All authors have read and agreed to the published version of the manuscript.
Funding
This research was part of a PhD under a program supported by the French Embassy in Ethiopia and the Ethiopian Ministry of Science and Higher Education.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
The authors would like to thank the Ethiopian Electric Power and Utility for outage data access.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| Apv | PV surface area (m2) |
| Apv,max | Sizing upper boundary/maximum PV area (m2) |
| Cbat | Battery storage nominal capacity (Wh) |
| Cbat,max | Sizing upper boundary/maximum storage capacity (kWh) |
| Ccap,bat | Initial capital cost of the battery bank (€) |
| Ccap,pv | Initial capital cost of the PV (€) |
| Ccha | Battery storage charging cost from grid (€/kWh) |
| CO&M | Operation and maintenance cost (€/yr) |
| CO&M,pv | Annual operation maintenance cost of the PV (€/yr) |
| CoE | Cost of energy generated (€/kWh) |
| Crep | Replacement cost (€/yr) |
| CRF | Capital recovery factor |
| Ctot,a | Annualized total system cost (€/yr) |
| Gtot | Total solar irradiation on tilted surface (Wh/m2) |
| i | Interest rate (%) |
| LPS | Loss of power supply (W) |
| LPSP | Loss of power supply probability (%) |
| N | Project lifetime (yr) |
| Nbat | Number of batteries |
| NOCT | Nominal operating cell temperature |
| Pcha,max | Maximum allowable battery charging power (kW) |
| Pdischa,max | Maximum discharged power from the battery (kW) |
| Pgen | Total generated power (kWh/yr) |
| Pload | Load demand (W) |
| Ppv | Generated power output of the PV (W) |
| Ptot | Total available power from grid and PV (W) |
| SoC | Battery storage state-of-charge (%) |
| SoCmax | Maximum SoC value (%) |
| SoCmin | Minimum SoC value (%) |
| t | Simulation time-step/tth time interval |
| Tamb | Ambient temperature (°C) |
| Tavg | Average grid outage duration (h) |
| Tcell | PV-cell temperature (°C) |
| Toutage | Total annual grid outage duration (h) |
| Tref | Reference temperature (°C) |
| Tyear | Total hours in a year, 8760 h |
| βp | PV module power temperature coefficient (/°C) |
| ηbat | Battery storage efficiency (%) |
| ηinv | Inverter efficiency (%) |
| ηm | PV model module efficiency (%) |
| ηpv | PV panel efficiency (%) |
| Abbreviations | |
| cdf | Cumulative distribution function |
| DG | Distributed generation |
| MTM | Markov transition matrix |
| NSGA-II | Nondominated sorting genetic algorithm II |
| OD | Outage duration |
| PV | Photovoltaic |
| TBO | Time between outages |
Appendix A
Table A1 shows all the detailed technical and economical parameters, and constraints.

Table A1.
Considered values for the technical and economic parameters of the system [43].
Table A1.
Considered values for the technical and economic parameters of the system [43].
| PV Module | Values |
|---|---|
| Reference temperature, Tref (°C) | 25 |
| NOCT (°C) | 47 |
| Module efficiency, ηm (%) | 20.3 |
| Temperature coefficient, βp (%/°C) | −0.30 |
| Capital cost, Ccap,pv (€/m2) | 200 |
| O&M cost, CO&M,pv, (€) | 1% of Ccap,pv |
| PV lifetime (years) | 25 |
| PV simulation boundary (m2) | (0, 600) |
| Storage battery | |
| Nominal capacity, Cbat,nom (kWh) | 7 |
| Efficiency, ηbat (%) | 97 |
| Capital cost, Ccap,bat (€/kWh) | 550 |
| Battery lifetime (years) | 6 |
| Max. charging power, Pcha,max (W) | Cbat,nom/3 |
| Max. discharging power, Pdischa,max (W) | Cbat,nom/2 |
| DOD (%) | 0.8 |
| Battery max. cycle | 2000 |
| Bat. simulation boundary (Nº) | (0, 50) |
| System | |
| Max. grid subscribed power (kW) | 50 |
| Grid elec. cost (€/kWh) | 0.0321 |
| Project lifetime (years) | 25 |
| Discount rate, i (%) | 2 |
Appendix B
Sample grid outage sequence simulation using the Markov approach in comparison with the 2015 measured data. The calculated Markov transition probabilities are also given in the black–white boxes.
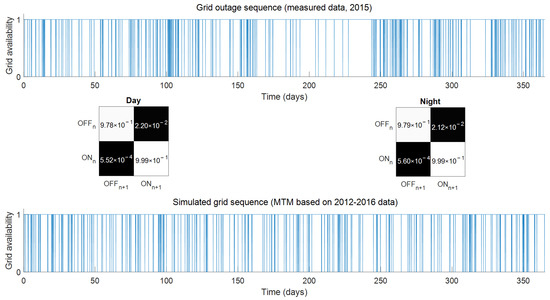
Figure A1.
Markov outage simulation vs. measured data.
References
- Kaduru, R.; Gondlala, N.S. Distribution System Reliability with Distributed Generation Based on Customer Scattering. Power Eng. Electr. Eng. 2015, 13, 64–73. [Google Scholar] [CrossRef]
- Al-Muhaini, M.; Heydt, G.T.; Huynh, A. The reliability of power distribution systems as calculated using system theoretic concepts. In Proceedings of the IEEE PES General Meeting, Minneapolis, MN, USA, 25–29 July 2010; pp. 1–8. [Google Scholar]
- Bourezg, A.; Meglouli, H. Reliability assessment of power distribution systems using disjoint path-set algorithm. J. Ind. Eng. Int. 2015, 11, 45–57. [Google Scholar] [CrossRef]
- Natarajan, V.; Closepet, A. Statistical Analysis of Cost of Energy due to Electricity Outages in Developing Countries. In Proceedings of the Future Computing 2012: The Fourth International Conference on Future Computational Technologies and Applications, Nice, France, 22–27 July 2012; pp. 39–44. [Google Scholar]
- Shivakumar, A.; Welsch, M.; Taliotis, C.; Howells, M.; Jakšić, D.; Baričević, T. Estimating the socio-economic costs of electricity supply interruptions. Rapid Response Energy Br. 2014, 1–10. [Google Scholar]
- Martinez-Velasco, J.A.; Guerra, G. Reliability Analysis of Distribution Systems with Photovoltaic Generation Using a Power Flow Simulator and a Parallel Monte Carlo Approach. Energies 2016, 9, 537. [Google Scholar] [CrossRef]
- Escalera, A.; Castronuovo, E.D.; Prodanović, M.; Roldán-Pérez, J. Reliability assessment of distribution networks with optimal coordination of distributed generation, energy storage and demand management. Energies 2019, 12, 3202. [Google Scholar] [CrossRef]
- Kanitkar, T.; Kosanovic, D. Evaluation of the Contribution of On-Site Generation to Grid and Customer Reliability. Sae Int. J. Mater. Manuf. 2011, 4, 468–476. [Google Scholar] [CrossRef]
- Ndawula, M.B.; Djokic, S.Z.; Hernando-Gil, I. Reliability enhancement in power networks under uncertainty from distributed energy resources. Energies 2019, 12, 531. [Google Scholar] [CrossRef]
- Lin, J.; Wang, X. Reliability Evaluation for Distribution System with Distributed Generation. In Proceedings of the 2010 Asia-Pacific Power and Energy Engineering Conference, Chengdu, China, 28–31 March 2010; Volume 37, pp. 1–4. [Google Scholar]
- Marcos, F.P.; Domingo, C.M.; Román, T.G.S.; Arín, R.C. Location and sizing of micro-grids to improve continuity of supply in radial distribution networks. Energies 2020, 13, 3495. [Google Scholar] [CrossRef]
- Chen, G.; Zhang, F.; You, D.; Wang, Y.; Lu, G.; Zou, Q.; Liu, H.; Qian, J.; Xu, H. Reliability Evaluation of Distribution System with Distributed Generation. IOP Conf. Ser. Mater. Sci. Eng. 2017, 224, 012035. [Google Scholar] [CrossRef]
- Billinton, R.; Karki, R. Maintaining supply reliability of small isolated power systems using renewable energy. IEE Proc. Gener. Transm. Distrib. 2001, 148, 530. [Google Scholar] [CrossRef]
- Brown, R.E.; Gupta, S.; Christie, R.D.; Venkata, S.S.; Fletcher, R. Distribution System Reliability Assessment Using Hierarchical Markov Modeling. IEEE Trans. Power Deliv. 1996, 11, 1929–1934. [Google Scholar] [CrossRef]
- Kovač, Z.; Knežević, G.; Topić, D. Modelling of power system reliability assessment. Teh. Vjesn. 2013, 20, 93–98. [Google Scholar]
- Hagkwen, K.; Singh, C. Reliability Modeling and Simulation in Power Systems With Aging Characteristics. IEEE Trans. Power Syst. 2010, 25, 21–28. [Google Scholar] [CrossRef]
- Asgarpoor, S.; Mathine, M.J. Reliability Evaluation of Distribution Systems with Non-Exponential Down Times. IEEE Trans. Power Syst. 1997, 12, 579–584. [Google Scholar] [CrossRef]
- Bhargava, C.; Murty, P.S. Reliability evaluation of radial distribution system using analytical and time sequential techniques. In Proceedings of the 2016 7th India International Conference on Power Electronics (IICPE), Patiala, India, 17–19 November 2016; pp. 1–6. [Google Scholar]
- Aljohani, T.M.; Beshir, M.J. Matlab Code to Assess the Reliability of the Smart Power Distribution System Using Monte Carlo Simulation. J. Power Energy Eng. 2017, 05, 30–44. [Google Scholar] [CrossRef]
- Van Casteren, J.F.L.; Bollen, M.H.J.; Schmieg, M.E. Reliability assessment in electrical power systems: The Weibull-Markov stochastic model. IEEE Trans. Ind. Appl. 2000, 36, 911–915. [Google Scholar] [CrossRef]
- Tao, S.; Hadjsaid, N.; Xiao, X.; Kieny, C. Power quality & reliability assessment of distribution system considering voltage interruptions and sags. In Proceedings of the 2012 IEEE 15th International Conference on Harmonics and Quality of Power, Hong Kong, China, 17–20 June 2012; pp. 751–757. [Google Scholar]
- Čepin, M. Probability of restoring power to the transmission power system and the time to restore power. Reliab. Eng. Syst. Saf. 2020, 193, 106595. [Google Scholar] [CrossRef]
- Chen, P.C.; Kezunovic, M. Fuzzy Logic Approach to Predictive Risk Analysis in Distribution Outage Management. IEEE Trans. Smart Grid 2016, 7, 2827–2836. [Google Scholar] [CrossRef]
- Eskandarpour, R.; Khodaei, A.; Arab, A. Improving power grid resilience through predictive outage estimation. In Proceedings of the 2017 North American Power Symposium (NAPS), Morgantown, WV, USA, 17–19 September 2017. [Google Scholar] [CrossRef]
- Yue, M.; Toto, T.; Jensen, M.P.; Giangrande, S.E.; Lofaro, R. A Bayesian approach-based outage prediction in electric utility systems using radar measurement data. IEEE Trans. Smart Grid 2018, 9, 6149–6159. [Google Scholar] [CrossRef]
- Jaech, A.; Zhang, B.; Ostendorf, M.; Kirschen, D.S. Real-Time Prediction of the Duration of Distribution System Outages. IEEE Trans. Power Syst. 2019, 34, 773–781. [Google Scholar] [CrossRef]
- Nanadikar, A.A.; Biradar, V.N.; Siva Sarma, D.V.S.S. Improved outage prediction using asset management data and intelligent multiple interruption event handling with fuzzy control during extreme climatic conditions. In Proceedings of the 2014 International Conference on Smart Electric Grid (ISEG), Guntur, India, 19–20 September 2014; pp. 1–7. [Google Scholar]
- Eskandarpour, R.; Khodaei, A. Machine Learning Based Power Grid Outage Prediction in Response to Extreme Events. IEEE Trans. Power Syst. 2017, 32, 3315–3316. [Google Scholar] [CrossRef]
- Cole, M.A.; Elliott, R.J.R.; Occhiali, G.; Strobl, E. Power outages and fi rm performance in Sub-Saharan Africa. J. Dev. Econ. 2018, 134, 150–159. [Google Scholar] [CrossRef]
- Saboori, H.; Hemmati, R.; Jirdehi, M.A. Reliability improvement in radial electrical distribution network by optimal planning of energy storage systems. Energy 2015, 93, 2299–2312. [Google Scholar] [CrossRef]
- Vieira Pombo, A.; Murta-Pina, J.; Fernão Pires, V. Multiobjective formulation of the integration of storage systems within distribution networks for improving reliability. Electr. Power Syst. Res. 2017, 148, 87–96. [Google Scholar] [CrossRef]
- Alramlawi, M.; Gabash, A.; Mohagheghi, E.; Li, P. Optimal operation of hybrid PV-battery system considering grid scheduled blackouts and battery lifetime. Sol. Energy 2018, 161, 125–137. [Google Scholar] [CrossRef]
- Khoury, J.; Mbayed, R.; Salloum, G.; Monmasson, E. Optimal sizing of a residential PV-battery backup for an intermittent primary energy source under realistic constraints. Energy Build. 2015, 105, 206–216. [Google Scholar] [CrossRef]
- Murphy, P.M.; Twaha, S.; Murphy, I.S. Analysis of the cost of reliable electricity: A new method for analyzing grid connected solar, diesel and hybrid distributed electricity systems considering an unreliable electric grid, with examples in Uganda. Energy 2014, 66, 523–534. [Google Scholar] [CrossRef]
- Rentschler, J.; Kornejew, M.; Hallegatte, S.; Braese, J.; Obolensky, M. Underutilized Potential: The Business Costs of Unreliable Infrastructure in Developing Countries. In Underutilized Potential: The Business Costs of Unreliable Infrastructure in Developing Countries; The World Bank: Washington, DC, USA, 2019. [Google Scholar] [CrossRef]
- Bouabdallah, A.; Olivier, J.C.; Bourguet, S.; Machmoum, M.; Schaeffer, E. Safe sizing methodology applied to a standalone photovoltaic system. Renew. Energy 2015, 80, 266–274. [Google Scholar] [CrossRef]
- Mohammad, M.S.; Atsushi, Y.; Tomonobu, S.; Mohammed, E.L.; Masahiro, F. Optimal Economical Sizing of Grid-Connected Hybrid Renewable Energy System. J. Energy Power Eng. 2017, 11, 244–253. [Google Scholar] [CrossRef]
- Maleki, A.; Pourfayaz, F. Optimal sizing of autonomous hybrid photovoltaic/wind/battery power system with LPSP technology by using evolutionary algorithms. Sol. Energy 2015, 115, 471–483. [Google Scholar] [CrossRef]
- Kaabeche, A.; Belhamel, M.; Ibtiouen, R. Sizing optimization of grid-independent hybrid photovoltaic/wind power generation system. Energy 2011, 36, 1214–1222. [Google Scholar] [CrossRef]
- Sharafi, M.; ELMekkawy, T.Y. Multi-objective optimal design of hybrid renewable energy systems using PSO-simulation based approach. Renew. Energy 2014, 68, 67–79. [Google Scholar] [CrossRef]
- Ofry, E.; Braunstein, A. The Loss of Power Supply Probability as a Technique for Designing Stand-Alone Solar Electrical (Photovoltaic) Systems. IEEE Trans. Power Appar. Syst. 1983, PAS-102, 1171–1175. [Google Scholar] [CrossRef]
- Olatomiwa, L. Optimal configuration assessments of hybrid renewable power supply for rural healthcare facilities. Energy Rep. 2016, 2, 141–146. [Google Scholar] [CrossRef]
- Kebede, F.S.; Bouyguet, S.; Olivier, J.-C. Photovoltaic System Sizing for Reliability Improvement in an unreliable Power Distribution System. In Proceedings of the 2020 Fifteenth International Conference on Ecological Vehicles and Renewable Energies (EVER), Monte-Carlo, Monaco, 10–12 September 2020; pp. 1–8. [Google Scholar]
- Huld, T.; Müller, R.; Gambardella, A. A new solar radiation database for estimating PV performance in Europe and Africa. Sol. Energy 2012, 86, 1803–1815. [Google Scholar] [CrossRef]
- Ortmeyer, T.H.; Fisk, B.M. Characterization of Distribution System Interruption Duration. In Proceedings of the 2012 IEEE Power and Energy Society General Meeting, San Diego, CA, USA, 22–26 July 2012; pp. 1–5. [Google Scholar]
- Ethiopian Electric Power. Substation Outage Datalog 2018, Unpublished Raw Dataset (Collected by Authors/Personal Communication). Available online: https://www.eep.com.et/en (accessed on 27 November 2018).
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).