Short-Term Load Forecasting Using Neural Networks with Pattern Similarity-Based Error Weights
Abstract
1. Introduction
1.1. Forecasting Models for TS with Multiple Seasonality
1.2. Neural Networks for STLF
- A hybrid model based on a deep convolutional NN is introduced for short-term photovoltaic power forecasting in [31]. In this approach, different frequency components of the TS are first decomposed using variational mode decomposition, and then, they are constructed into a two-dimensional data, which can be better learned by convolution kernels, leading to a higher prediction accuracy.
- LSTM NN was proposed in [32] for STLF for individual residential households. Forecasting an electric load of a single energy user is fairly challenging due to the high volatility and uncertainty involved. LSTM can capture the subtle temporal consumption pattern persisting in single-meter load profile and can produce the accurate forecasts.
- Deep residual networks were proposed for STLF in [33]. The proposed model is able to integrate domain knowledge and researchers’ understanding of the task by virtue of different NN building blocks. Specifically, a modified deep residual network was formulated to improve the forecast results and a two-stage ensemble strategy was used to enhance the generalization capability of the proposed model. The model can be applied to probabilistic load forecasting using Monte Carlo dropout.
- Stacked denoising autoencoders were used in [34] for forecasting the hourly electricity price. The model was equipped with a unsupervised pre-training process to prevent overfitting. It incorporates concepts of the random sample consensus and stochastic neighbor embedding to further improve the forecasting performance.
- Pooling-based deep recurrent NN was applied in [35] for household load forecasting. A novel pooling-based deep learning was proposed, which batches a group of customers’ load profiles into a pool of inputs. The model aims to directly learn the uncertainty of load profiles by applying deep learning.
- A hybrid model based on randomized NN for probabilistic electricity load forecasting was proposed in [36]. This model includes generalized extreme learning machine for training an improved wavelet NN, wavelet preprocessing, and bootstrapping. It takes into account data noise uncertainties while the output of the model is the load probabilistic interval.
- Second-order gray NN using wavelet decomposition was proposed in [37] to improve the accuracy of load forecasting. In this approach, the load TS is decomposed by wavelet decomposition to reduce the nonstationary load sequence. Then, a second-order gray forecasting model is used to forecast each component of the TS. To obtain the optimal parameters, the NN mapping approach is used to build the second-order gray forecasting model.
- A wavelet echo state network was applied to both STLF and short-term temperature forecasting in [38]. A wavelet transform was used as the front stage for multi-resolution decomposition of the TS. Echo state networks function as forecasters for decomposed components. A modified shuffled frog leaping algorithm is used for optimizing the model.
- A spiking NN for STLF was proposed in [39]. This model employs spike train models that are close to their biological counterparts. An implementation of the proposed model is divided into two phases. In the first phase, spike NN predicts a day-ahead hourly temperature profile. In the second phase, another spike NN predicts a day-ahead load profile based on actual and forecasted temperatures, historical loads, day of the week, and holiday effect.
- Convolutional NNs are combined with fuzzy TS for STLF in [40]. In this approach, multivariate TS data, which include hourly load data, hourly temperature TS, and fuzzified version of load TS, were converted into multi-channel images to be fed to a proposed convolutional NN model.
- Deep residual network with a convolution structure was proposed to STLF in [41]. The authors analyzed and discussed the effectiveness of the convolutional residual network with different hyperparameters and architectures that include depths, widths, block structures, and shortcut connections, with/without dropout.
- Convolutional NNs combined with a data-augmentation technique, which can artificially enlarge the training data, were applied for STLF a single household in [42]. This method can address issues caused by a lack of historical data and improves the accuracy of residential load forecasting, which is a fairly challenging topic because of the high volatility and uncertainty of the electric demand of households.
1.3. Summary of Contributions
- We propose a new univariate multi-step forecasting neural model with pattern similarity-based error weighting for TS with multiple seasonality.
- We empirically demonstrate using challenging STLF problems the statistically significant accuracy improvement and forecasting bias reduction of the proposed approach with respect to the standard approach without error weighting.
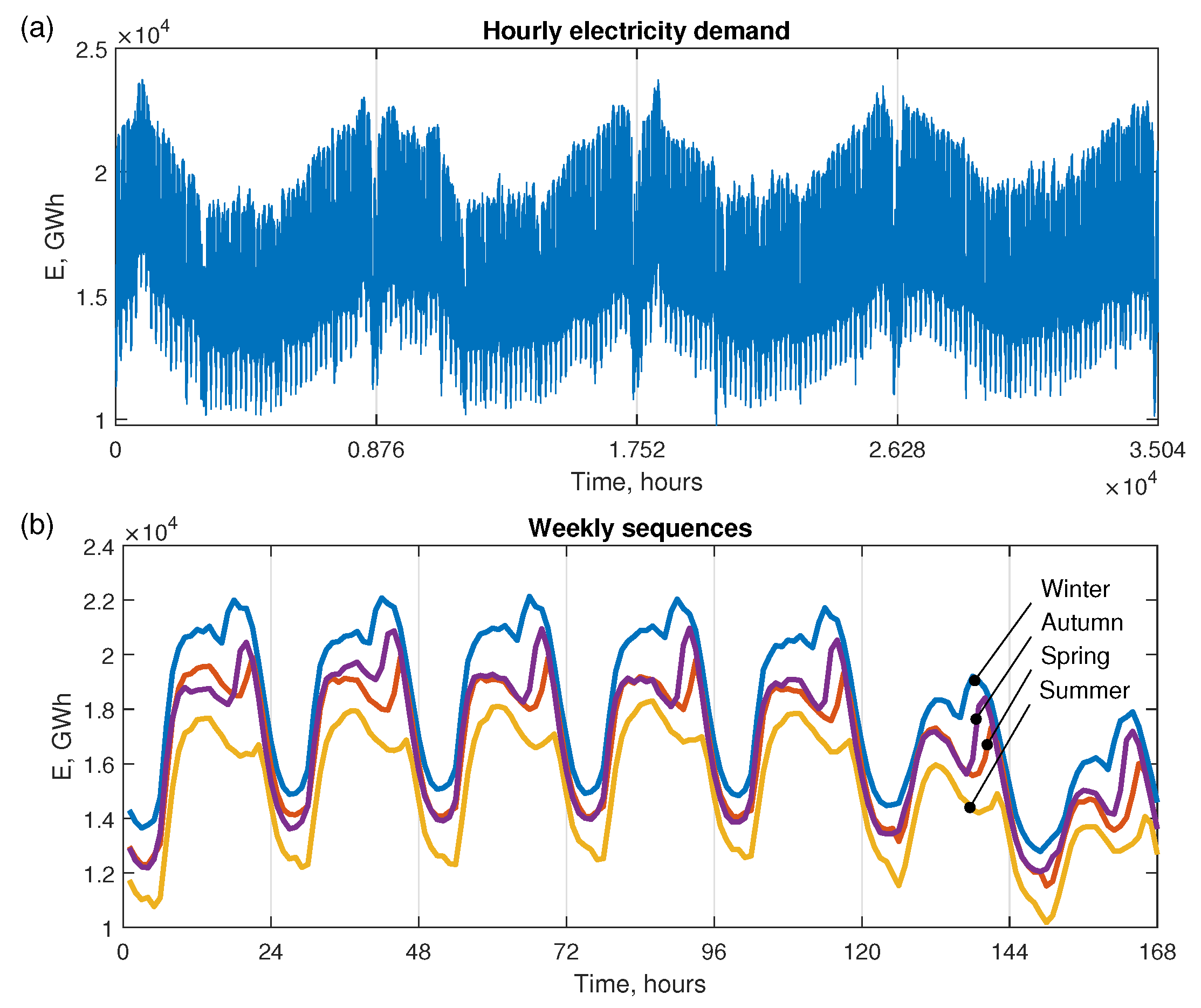
2. Multiple Seasonal Time Series and Their Representation
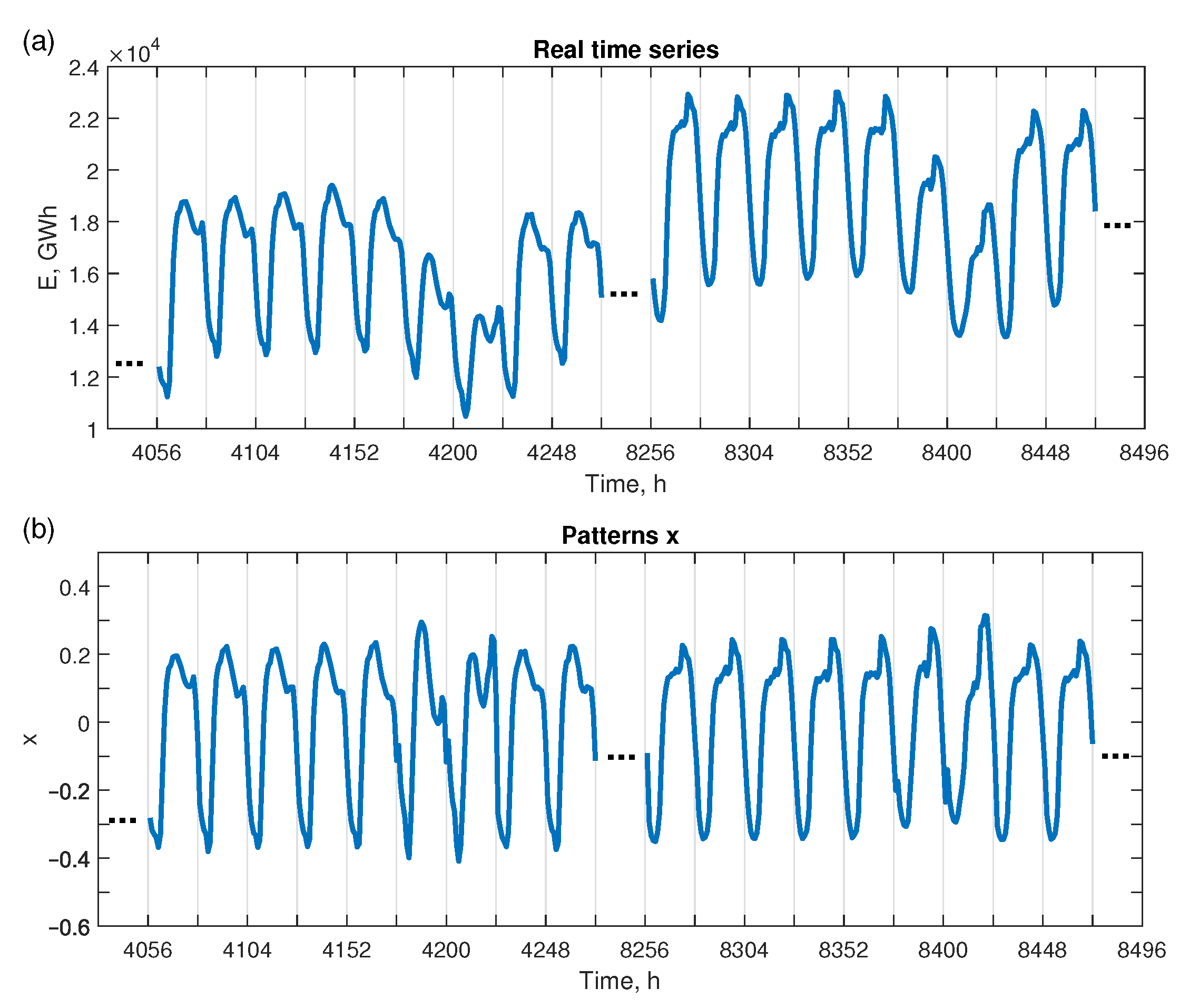
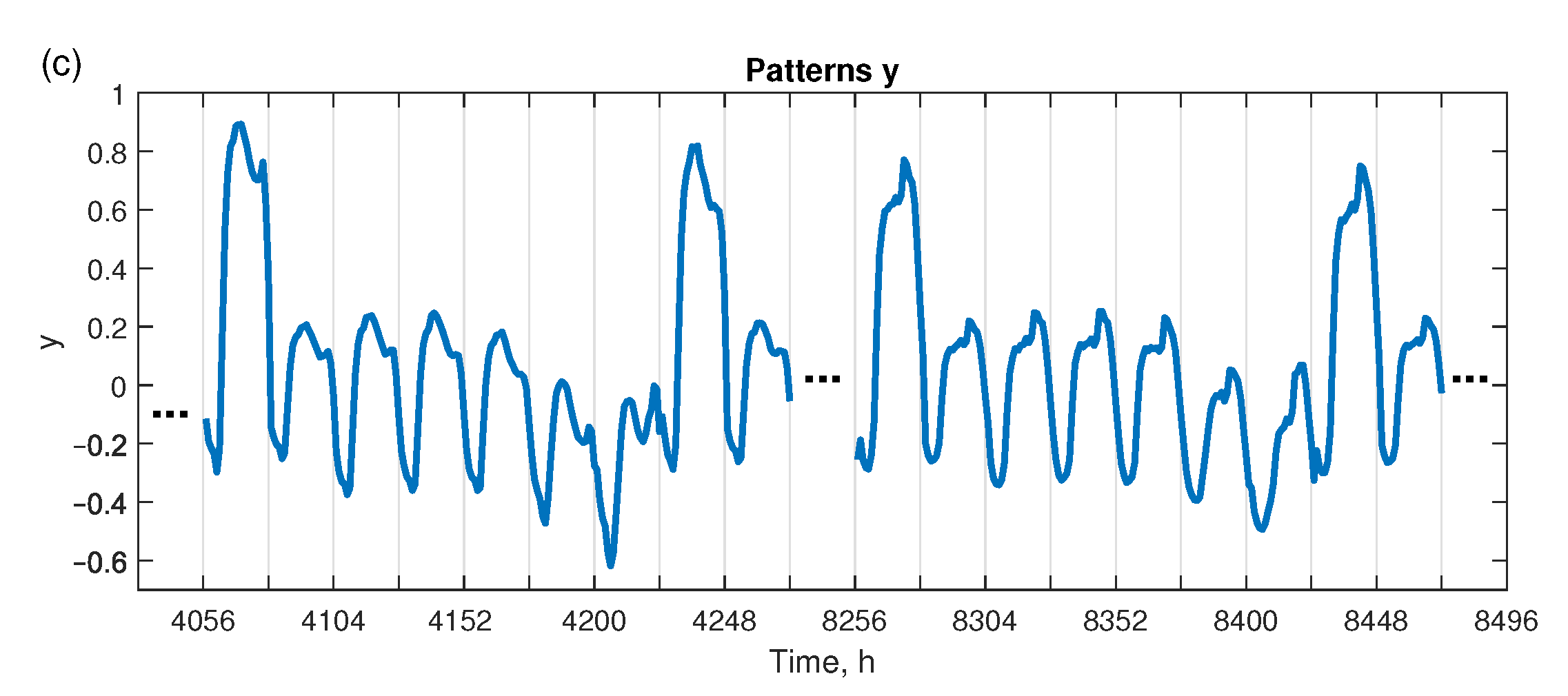
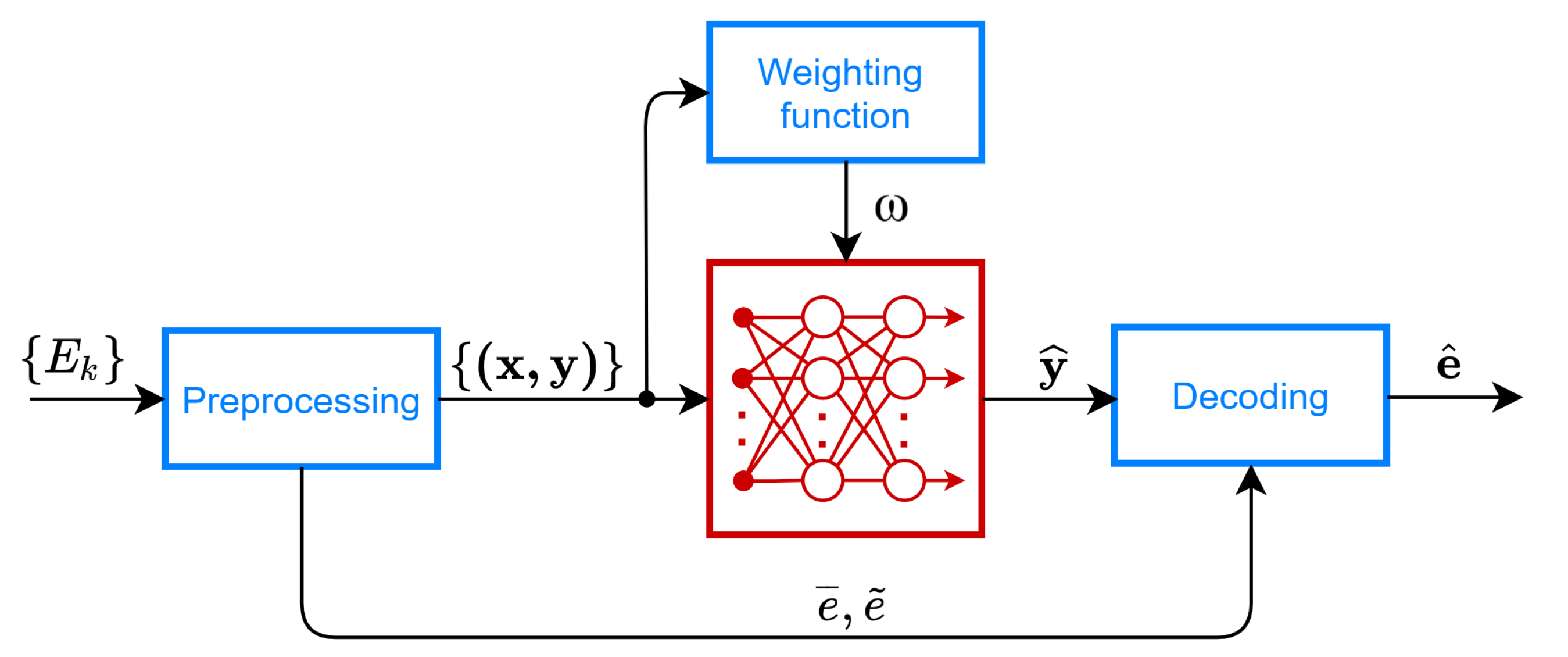
3. Forecasting Model
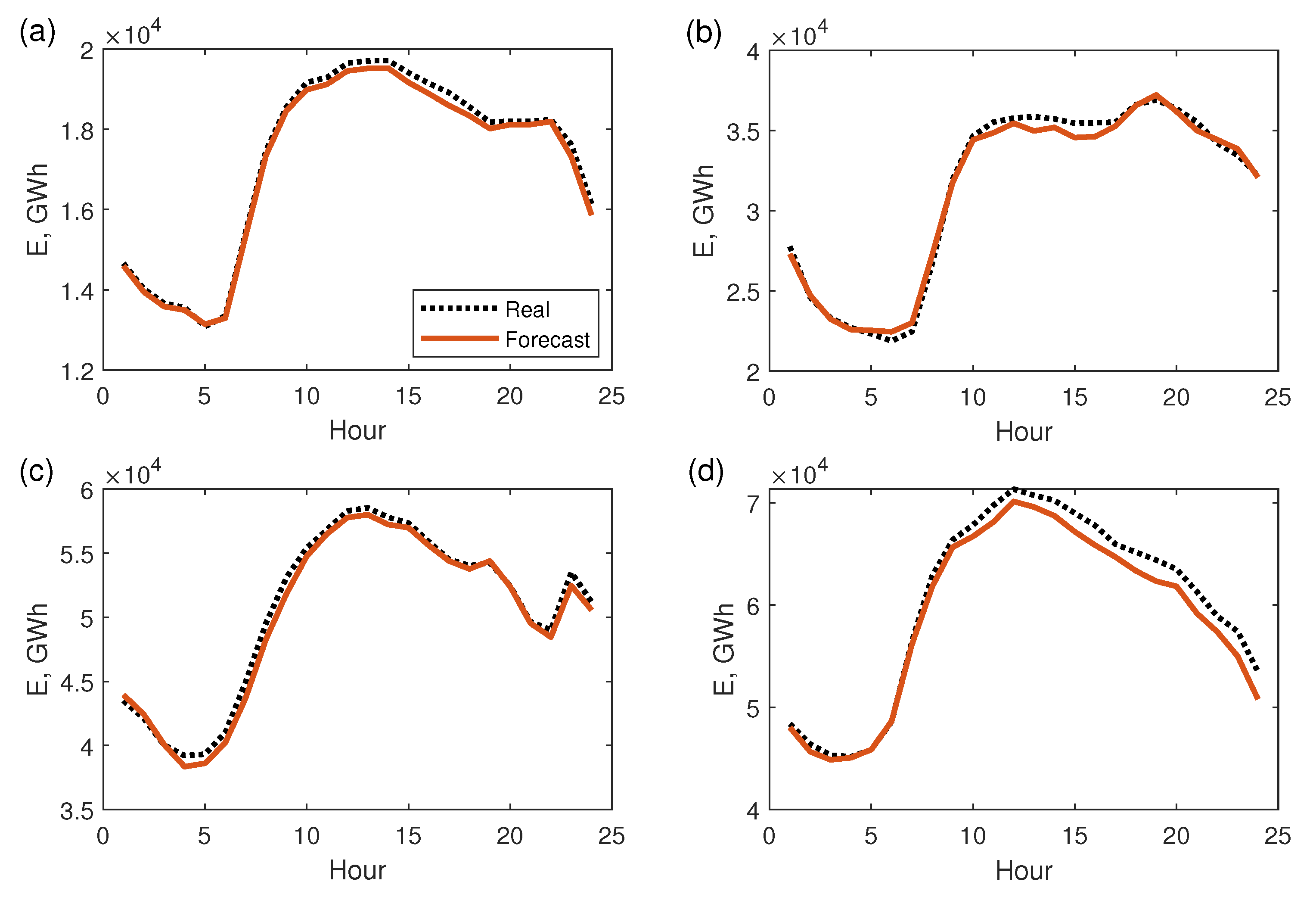
4. Simulation Study
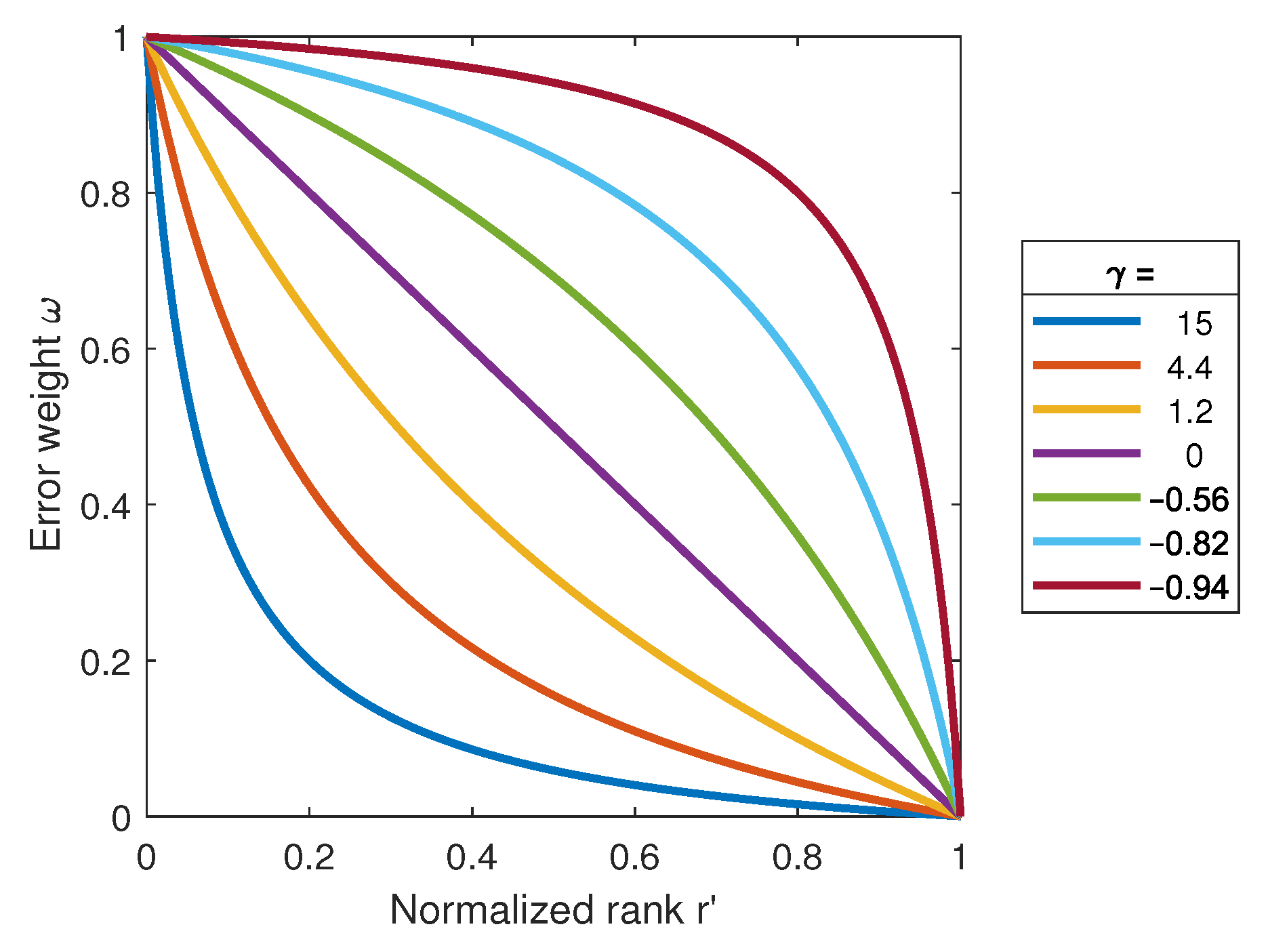
4.1. Tuning of the Error Weights
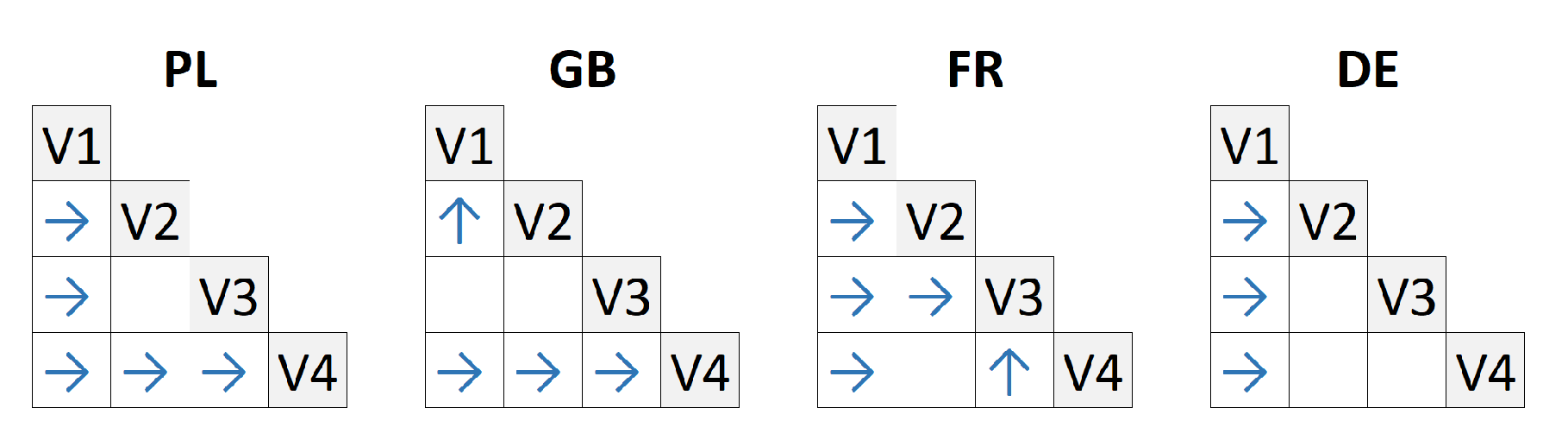
- V1
- learning without error weighting as a baseline for other variants;
- V2
- learning with error weighting, where was selected on the training set, i.e., NN was trained for each , and the minimal training error indicated the selected value. NN with this value was used to produce the forecast for the test pattern;
- V3
- similar to V2, but was selected on the five training patterns most similar to the query test pattern. First, the subset of five training patterns closest (Euclidean distance) to the test pattern was selected. After NN training with , average errors for were calculated. The lowest error indicated the selected value. Then, NN with this was used to produce the forecast for the query test pattern; and
- V4
- learning with fixed .
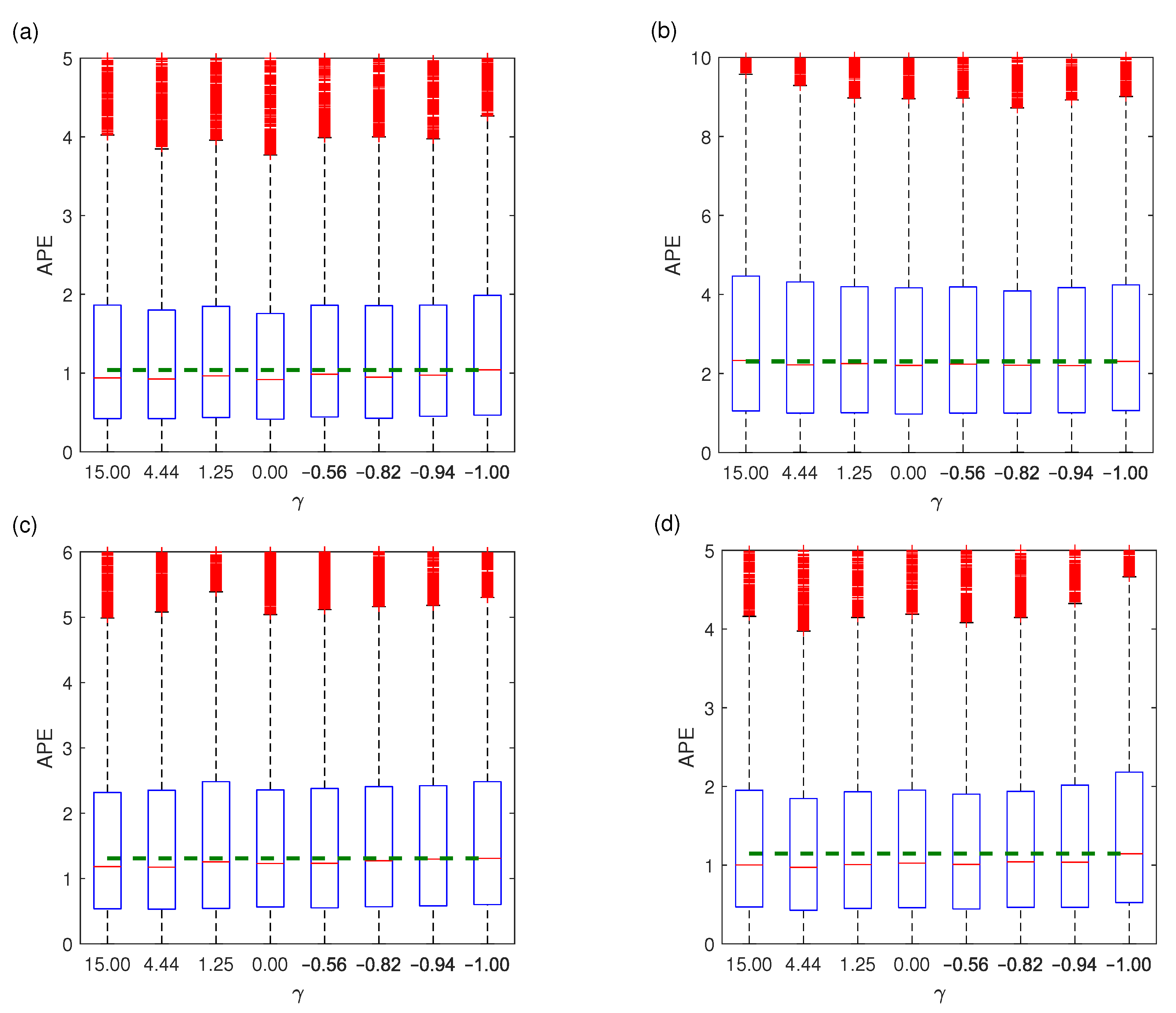
- The baseline variant V1 gave significantly higher errors than other variants in 10 out of 12 cases.
- V4 gave significantly lower errors than the baseline variant V1 for all data sets. It also beat its competitors, V2 and V3, for PL and GB data.
- V2 and V3 gave lower errors than the baseline variant for PL, FR, and DE.
- V3 gave the significantly lowest APE for FR data.
4.2. Tuning of the Number of Hidden Nodes
4.3. Discussion
5. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| APE | Absolute Percentage Error |
| ARMA | Autoregressive Moving Average |
| ETS | Exponential Smoothing |
| LSTM | Long Short-Term Memory Neural Network |
| MAPE | Mean Absolute Percentage Error |
| ML | Machine Learning |
| MLP | Multilayer Perceptron |
| MPE | Mean Percentage Error |
| NN | Neural Network |
| PE | Percentage Error |
| RMSE | Root Mean Square Error |
| STLF | Short-Term Load Forecasting |
| TS | Time Series |
References
- Sowinski, J. The Impact of the Selection of Exogenous Variables in the ANFIS Model on the Results of the Daily Load Forecast in the Power Company. Energies 2021, 14, 345. [Google Scholar] [CrossRef]
- Parol, M.; Piotrowski, P.; Kapler, P.; Piotrowski, M. Forecasting of 10-Second Power Demand of Highly Variable Loads for Microgrid Operation Control. Energies 2021, 14, 1290. [Google Scholar] [CrossRef]
- Popławski, T.; Szeląg, P.; Bartnik, R. Adaptation of models from determined chaos theory to short-term power forecasts for wind farms. Bull. Pol. Acad. Sci. Tech. Sci. 2020, 68, 1491–1501. [Google Scholar] [CrossRef]
- Trull, O.; García-Díaz, J.C.; Peiró-Signes, A. Forecasting Irregular Seasonal Power Consumption. An Application to a Hot-Dip Galvanizing Process. Appl. Sci. 2021, 11, 75. [Google Scholar] [CrossRef]
- Box, G.E.P.; Jenkins, G.M.; Reinsel, G.C. Time Series Analysis: Forecasting and Control, 3rd ed.; Prentice Hall: Englewood Cliff, NJ, USA, 1994. [Google Scholar]
- Taylor, J.W. Short-term electricity demand forecasting using double seasonal exponential smoothing. J. Oper. Res. Soc. 2003, 54, 799–805. [Google Scholar] [CrossRef]
- Taylor, J.W. Triple seasonal methods for short-term load forecasting. Eur. J. Oper. Res. 2010, 204, 139–152. [Google Scholar] [CrossRef]
- Gould, P.G.; Koehler, A.B.; Ord, J.K.; Snyder, R.D.; Hyndman, R.J.; Vahid-Araghi, F. Forecasting time-series with multiple seasonal patterns. Eur. J. Oper. Res. 2008, 191, 207–222. [Google Scholar] [CrossRef]
- De Livera, A.M.; Hyndman, R.J.; Snyder, R.D. Forecasting time series with complex seasonal patterns using exponential smoothing. J. Am. Stat. Assoc. 2011, 106, 1513–1527. [Google Scholar] [CrossRef]
- Taylor, S.J.; Letham, B. Forecasting at scale. Am. Stat. 2018, 72, 37–45. [Google Scholar] [CrossRef]
- Benidis, K.; Rangapuram, S.S.; Flunkert, V.; Wang, B.; Maddix, D.; Turkmen, C.; Gasthaus, J.; Bohlke-Schneider, M.; Salinas, D.; Stella, L.; et al. Neural forecasting: Introduction and literature overview. arXiv 2020, arXiv:2004.10240. [Google Scholar]
- Smyl, S. A hybrid method of exponential smoothing and recurrent neural networks for time series forecasting. Int. J. Forecast. 2020, 36, 75–85. [Google Scholar] [CrossRef]
- Bandara, K.; Bergmeir, C.; Hewamalage, H. LSTM-MSNet: Leveraging forecasts on sets of related time series with multiple seasonal patterns. IEEE Trans. Neural Netw. Learn. Syst. 2021, 32, 1586–1599. [Google Scholar] [CrossRef]
- Salinas, D.; Flunkert, V.; Gasthaus, J.; Januschowski, T. DeepAR: Probabilistic forecasting with autoregressive recurrent networks. Int. J. Forecast. 2020, 36, 1181–1191. [Google Scholar] [CrossRef]
- Oreshkin, B.N.; Carpov, D.; Chapados, N.; Bengio, Y. N-BEATS: Neural basis expansion analysis for interpretable time series forecasting. In Proceedings of the 8th International Conference on Learning Representations, ICLR, Addis Ababa, Ethiopia, 26–30 April 2020. [Google Scholar]
- Li, S.; Jin, X.; Xuan, Y.; Zhou, X.; Chen, W.; Wang, Y.-X.; Yan, X. Enhancing the locality and breaking the memory bottleneck of transformer on time series forecasting. In Proceedings of the Advances in Neural Information Processing Systems (NeurIPS), Vancouver, BC, Canada, 8–14 December 2019. [Google Scholar]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention is all you need. In Proceedings of the Advances in Neural Information Processing Systems (NIPS), Long Beach, CA, USA, 4–9 December 2017; pp. 5998–6008. [Google Scholar]
- Ghaderpour, E.; Vujadinovic, T. Change Detection within Remotely Sensed Satellite Image Time Series via Spectral Analysis. Remote Sens. 2020, 12, 4001. [Google Scholar] [CrossRef]
- Torrence, C.; Compo, G.P. A Practical Guide to Wavelet Analysis. Bull. Am. Meteorol. Soc. 1998, 79, 61–78. [Google Scholar] [CrossRef]
- Chen, D.; Zhang, J.; Jiang, S. Forecasting the Short-Term Metro Ridership With Seasonal and Trend Decomposition Using Loess and LSTM Neural Networks. IEEE Access 2020, 8, 91181–91187. [Google Scholar] [CrossRef]
- Zhang, Z.; Hong, W.C. Electric load forecasting by complete ensemble empirical mode decomposition adaptive noise and support vector regression with quantum-based dragonfly algorithm. Nonlinear Dyn. 2019, 98, 1107–1136. [Google Scholar] [CrossRef]
- Dudek, G. Forecasting daily load curves of power system using radial basis function neural networks. In Proceedings of the 10th Conference Present-Day Problems in Power Engineering, APE 2001, Gdansk–Jurata, Poland, 6–8 June 2001; Volume 3, pp. 93–100. (In Polish). [Google Scholar]
- Dudek, G. Multilayer perceptron for short-term load forecasting: From global to local approach. Neural Comput. Appl. 2019, 32, 3695–3707. [Google Scholar] [CrossRef]
- Dudek, G. Pattern Similarity-based Methods for Short-term Load Forecasting—Part 1: Principles. Appl. Soft Comput. 2015, 37, 277–287. [Google Scholar] [CrossRef]
- Dudek, G. Neural networks for pattern-based short-term load forecasting: A comparative study. Neurocomputing 2016, 205, 64–74. [Google Scholar] [CrossRef]
- Dudek, G.; Pełka, P.; Smyl, S. A hybrid residual dilated LSTM and exponential smoothing model for mid-term electric load forecasting. IEEE Trans. Neural Netw. Learn. Syst. 2021. [Google Scholar] [CrossRef]
- Kuster, C.; Rezgui, Y.; Mourshed, M. Electrical load forecasting models: A critical systematic review. Sustain. Cities Soc. 2017, 35, 257–270. [Google Scholar] [CrossRef]
- Sidorov, D.; Tao, Q.; Muftahov, I.; Zhukov, A.; Karamov, D.; Dreglea, A.; Liu, F. Energy balancing using charge/discharge storages control and load forecasts in a renewable-energy-based grids. In Proceedings of the 38th Chinese Control Conference, Guangzhou, China, 27–30 July 2019; pp. 6865–6870. [Google Scholar]
- Hippert, H.S.; Pedreira, C.E.; Souza, R.C. Neural networks for short-term load forecasting: A review and evaluation. IEEE Trans. Power Syst. 2001, 16, 44–55. [Google Scholar] [CrossRef]
- Kodogiannis, V.S.; Anagnostakis, E.M. Soft computing based techniques for short-term load forecasting. Fuzzy Sets Syst. 2002, 128, 413–442. [Google Scholar] [CrossRef]
- Zang, H.; Cheng, L.; Ding, T.; Cheung, K.; Liang, Z.; Wei, Z.; Sun, G. Hybrid method for short-term photovoltaic power forecasting based on deep convolutional neural network. IET Gener. Transm. Distrib. 2018, 12, 4557–4567. [Google Scholar] [CrossRef]
- Kong, W.; Dong, Z.Y.; Jia, Y.; Hill, D.J.; Xu, Y.; Zhang, Y. Short term residential load forecasting based on LSTM recurrent neural network. IEEE Trans. Smart Grid 2019, 10, 841–851. [Google Scholar] [CrossRef]
- Chen, K.; Chen, K.; Wang, Q.; He, Z.; Hu, J.; He, J. Short-Term Load Forecasting With Deep Residual Networks. IEEE Trans. Smart Grid 2019, 10, 3943–3952. [Google Scholar] [CrossRef]
- Wang, L.; Zhang, Z.; Chen, J. Short-term electricity price forecasting with stacked denoising autoencoders. IEEE Trans. Power Syst. 2017, 32, 2673–2681. [Google Scholar] [CrossRef]
- Shi, H.; Xu, M.; Li, R. Deep learning for household load forecasting—A novel pooling deep RNN. IEEE Trans. Smart Grid 2018, 9, 5271–5280. [Google Scholar] [CrossRef]
- Rafiei, M.; Niknam, T.; Aghaei, J.; Shafie-Khah, M.; Catalao, J.P.S. Probabilistic load forecasting using an improved wavelet neural network trained by generalized extreme learning machine. IEEE Trans. Smart Grid 2018, 9, 6961–6971. [Google Scholar] [CrossRef]
- Li, B.; Zhang, J.; He, Y.; Wang, Y. Short-term load-forecasting method based on wavelet decomposition with second-order gray neural network model combined with ADF test. IEEE Access 2017, 5, 16324–16331. [Google Scholar] [CrossRef]
- Deihimi, A.; Orang, O.; Showkati, H. Short-term electric load and temperature forecasting using wavelet echo state networks with neural reconstruction. Energy 2013, 57, 382–401. [Google Scholar] [CrossRef]
- Kulkarni, S.; Simon, S.P.; Sundareswaran, K. A spiking neural network (SNN) forecast engine for short-term electrical load forecasting. Appl. Soft Comput. 2013, 13, 3628–3635. [Google Scholar] [CrossRef]
- Sadaei, H.J.; e Silva, P.C.d.L.; Guimaraes, F.G.; Lee, M.H. Short-term load forecasting by using a combined method of convolutional neural networks and fuzzy time series. Energy 2019, 175, 365–377. [Google Scholar] [CrossRef]
- Sheng, Z.; Wang, H.; Chen, G.; Zhou, B.; Sun, J. Convolutional residual network to short-term load forecasting. Appl. Intell. 2021, 51, 2485–2499. [Google Scholar] [CrossRef]
- Acharya, S.K.; Wi, Y.-M.; Lee, J. Short-Term Load Forecasting for a Single Household Based on Convolution Neural Networks Using Data Augmentation. Energies 2019, 12, 3560. [Google Scholar] [CrossRef]
- Fernando, K.R.M.; Tsokos, C.P. Dynamically Weighted Balanced Loss: Class Imbalanced Learning and Confidence Calibration of Deep Neural Networks. IEEE Trans. Neural Netw. Learn. Syst. 2021. [Google Scholar] [CrossRef]
- Zhang, K.; Wu, Z.; Yuan, D.; Luan, J.; Jia, J.; Meng, H.; Song, B. Re-Weighted Interval Loss for Handling Data Imbalance Problem of End-to-End Keyword Spotting. Proc. Interspeech 2020, 2567–2571. [Google Scholar] [CrossRef]
- Rengasamy, D.; Jafari, M.; Rothwell, B.; Chen, X.; Figueredo, G.P. Deep Learning with Dynamically Weighted Loss Function for Sensor-Based Prognostics and Health Management. Sensors 2020, 20, 723. [Google Scholar] [CrossRef]
- Dudek, G.; Pełka, P. Pattern similarity-based machine learning methods for mid-term load forecasting: A comparative study. Appl. Soft Comput. 2021, 104, 107223. [Google Scholar] [CrossRef]

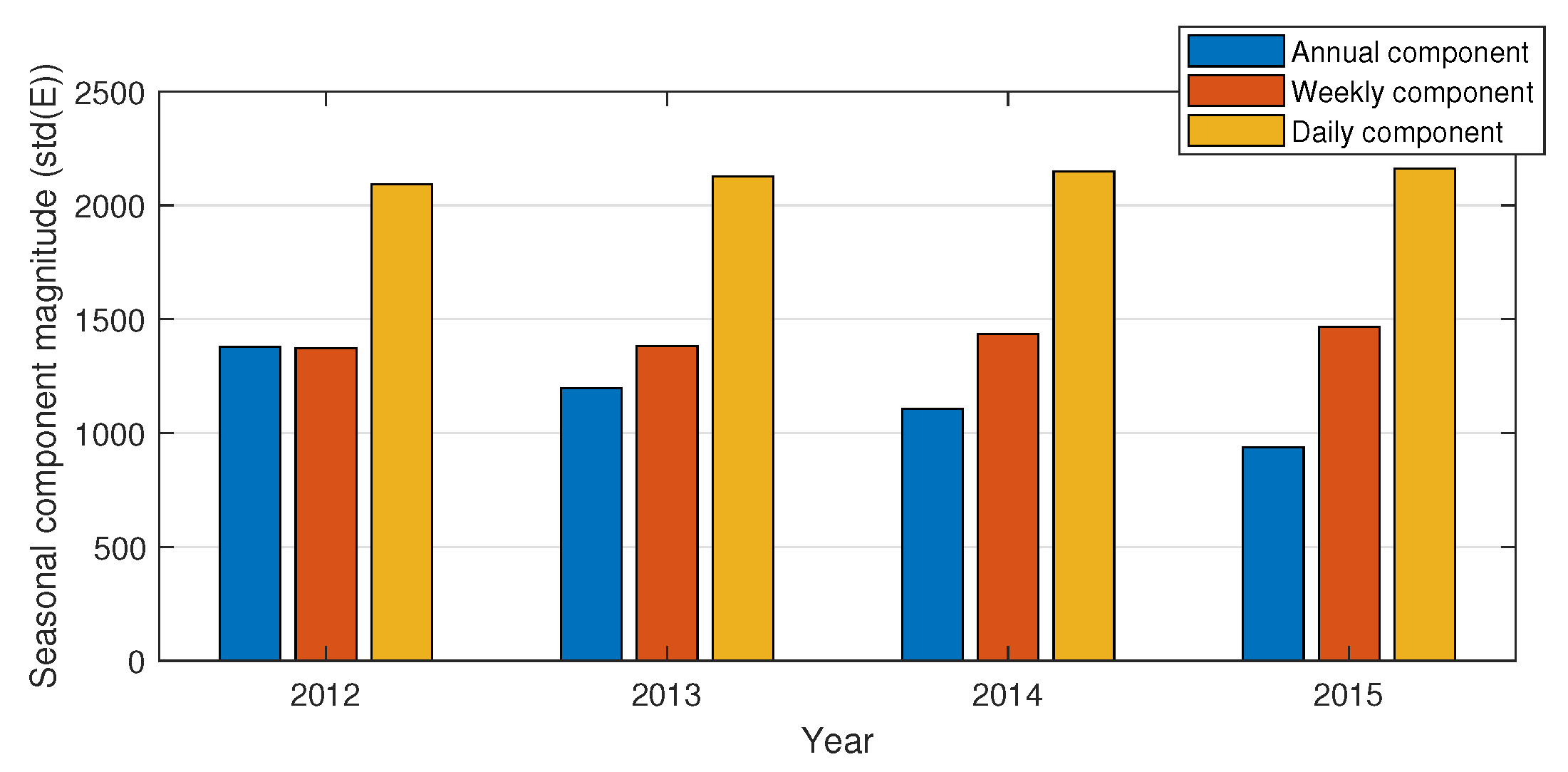

| Symbol | Meaning |
|---|---|
| time series of length K | |
| vector expressing a daily TS sequence of day i | |
| , | mean value and dispersion of sequence , respectively |
| forecasted daily sequence | |
| n | length of the daily sequence; length of the input and output patterns |
| N | number of training samples |
| m | number of hidden nodes |
| , | rank and normalized rank of i-th training sample, respectively |
| input pattern | |
| output pattern | |
| parameter controlling the weighting function shape | |
| forecast horizon in days | |
| training set | |
| error weight for ith training sample |
| Metric | Equation |
|---|---|
| Percentage Error | |
| Mean Percentage Error | |
| Absolute Percentage Error | APE |
| Mean Absolute Percentage Error | |
| Standard deviation of Percentage Error | Std(PE) |
| Root Mean Square Error |
| V1 without Error Weighting | V2 with Selected on Training Set | V3 with Selected on Set | V4 with Linear Weighting | |
|---|---|---|---|---|
| MAPE | 1.48 | 1.35 | 1.35 | 1.28 |
| Median (APE) | 1.00 | 0.90 | 0.90 | 0.88 |
| RMSE | 471 | 397 | 378 | 357 |
| MPE | 0.33 | 0.28 | 0.29 | 0.29 |
| Std (PE) | 2.51 | 2.20 | 2.06 | 2.00 |
| V1 without Error Weighting | V2 with Selected on Training Set | V3 with Selected on Set | V4 with Linear Weighting | |
|---|---|---|---|---|
| MAPE | 3.02 | 3.14 | 3.15 | 2.95 |
| Median (APE) | 2.25 | 2.19 | 2.19 | 2.16 |
| RMSE | 1354 | 1472 | 1488 | 1330 |
| MPE | −0.57 | −0.46 | −0.41 | −0.43 |
| Std (PE) | 4.13 | 4.46 | 4.51 | 4.08 |
| V1 without Error Weighting | V2 with Selected on Training Set | V3 with Selected on Set | V4 with Linear Weighting | |
|---|---|---|---|---|
| MAPE | 1.87 | 1.82 | 1.80 | 1.81 |
| Median (APE) | 1.28 | 1.19 | 1.15 | 1.21 |
| RMSE | 1582 | 1659 | 1603 | 1582 |
| MPE | −0.42 | −0.26 | −0.39 | −0.31 |
| Std (PE) | 2.89 | 2.95 | 2.89 | 2.86 |
| V1 without Error Weighting | V2 with Selected on Training Set | V3 with Selected on Set | V4 with Linear Weighting | |
|---|---|---|---|---|
| MAPE | 1.64 | 1.50 | 1.54 | 1.50 |
| Median (APE) | 1.10 | 0.95 | 0.95 | 0.99 |
| RMSE | 1503 | 1574 | 1647 | 1474 |
| MPE | −0.02 | 0.07 | −0.04 | 0.05 |
| Std (PE) | 2.54 | 2.73 | 2.84 | 2.55 |
| PL | GB | FR | DE | |
|---|---|---|---|---|
| MAPE for m selected on training set | 1.44 | 3.28 | 1.97 | 1.56 |
| MAPE for m selected on set | 1.33 | 3.26 | 1.87 | 1.49 |
| MAPE for | 1.34 | 3.11 | 1.77 | 1.45 |
| MAPE for | 1.29 | 2.91 | 1.73 | 1.43 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dudek, G. Short-Term Load Forecasting Using Neural Networks with Pattern Similarity-Based Error Weights. Energies 2021, 14, 3224. https://doi.org/10.3390/en14113224
Dudek G. Short-Term Load Forecasting Using Neural Networks with Pattern Similarity-Based Error Weights. Energies. 2021; 14(11):3224. https://doi.org/10.3390/en14113224
Chicago/Turabian StyleDudek, Grzegorz. 2021. "Short-Term Load Forecasting Using Neural Networks with Pattern Similarity-Based Error Weights" Energies 14, no. 11: 3224. https://doi.org/10.3390/en14113224
APA StyleDudek, G. (2021). Short-Term Load Forecasting Using Neural Networks with Pattern Similarity-Based Error Weights. Energies, 14(11), 3224. https://doi.org/10.3390/en14113224






