Rate Fairness and Power Consumption Optimization for NOMA-Assisted Downlink Networks

Abstract

This paper considers a non-orthogonal multiple access (NOMA) downlink network, where a hybrid of NOMA and beamforming designs is developed to enhance the channel capacity. We aim to improve the system performance in terms of rate fairness and power consumption. Hence, a multi-objective problem with a joint optimization of user equipment pairing, power control, and quality-of-service requirements is addressed. To efficiently solve the problem, we propose two low-complexity algorithms based on the inner-approximation method, with the first algorithm using the relaxation method and the second one using graph theory. Numerical results are provided to demonstrate the effectiveness of the two proposed algorithms in comparison with the exhaustive search and existing methods.

1. Introduction

Non-orthogonal multiple access (NOMA) can be considered to be a promising multiple access technology for fifth-generation networks for accommodating the rapid growth of data traffic [1,2,3,4]. Unlike orthogonal multiple access, NOMA allows user equipment (UE) to share the same time-frequency resource; hence, the spectral efficiency (SE) and energy efficiency (EE) are improved. The NOMA technique is classified into two main categories: the power domain [5] and code domain [6]. Herein, we focus power-domain NOMA, referred to as NOMA for convenience. The key idea of power-domain NOMA is to allocate a higher power to the UE with poorer channel gain. Meanwhile, a UE with a strong channel gain is equipped with successive interference cancellation (SIC) to remove the signal intended to the UE with poorer channel gain before decoding its own signal [5,7].

1.1. Related Works and Motivation

Recently, many new approaches have been proposed for UE grouping/clustering [8,9,10,11]. The number of clusters is selected based on the cell size and channel gain in [8], whereas a clustering strategy based on channel correlation was investigated in [11]. In [9], a tensor model was proposed to manage UE association, in which clusters of UEs were formed by different circular zones. Owing to the channel conditions and computational capacity of UE, SIC is restricted to limited groups/clusters of UE [8,9].

To ease implementationin a small-sized network, UE pairing is essential. In [12], pairing of one near UE and another far UE was shown to be efficient. A cognitive radio inspired NOMA system with a single-antenna base station (BS) was also investigated in [12], where a cell is divided into inner and outer zones, including cognitive UEs (CUs) with strong channel gain and primary UEs (PUs) with poor channel gain. A two-zone scheme assisted by the multiple-antenna technique was studied in [13], in which each pair comprised one inner-zone UE and the other outer-zone UE. The authors in [14] proposed a distance-based UE pairing scheme to improve the sum throughput, in which the far UEs were paired with an available nearest UEs using a distance threshold. Another pairing scheme based on the vector norms of channel responses was developed for a massive MIMO-NOMA system in [15]. The effect of UE pairing on the performance of NOMA-based systems was studied in [16], in which a CR-NOMA and an F-NOMA system were considered under fixed power allocation.

To fully exploit the advantages of UE pairing, many algorithms have been developed for pairing two arbitrary UEs without separate zones. In addition to random pairing scheme used in [17], UE pairing schemes based on channel condition arrangement have been proposed [17,18,19]. The typical pre-processing step is to place all UE into an unpaired set with sorted channel gains (SCG). Under the setting, various strategies have been proposed to pop and pair two UEs until the SCG is empty or only contains one UE. In [19], two UEs with the best and worst channel gains were popped and paired consecutively. In [18], two best-channel conditions were selected, whereas the first and middle UEs in the SCG were paired together in [17]. Unlike the aforementioned work, a more flexible approach was proposed [20], where any two users in a cell can be dynamically paired together to improve the fairness throughput among all UEs.

Most of the aforementioned works investigated NOMA-based systems to improve SE. In power-domain NOMA, power control is extremely challenging owing to SIC. In addition, the power consumption or EE has been considered to be one of the immediate concerns for the upcoming wireless networks, as indicated by the energy for information and communication technologies, which constitute approximately five percents of the total world’s energy consumption [21,22]. Therefore, power consumption has been recently reported in a few studies. The authors in [10] investigated a joint optimization problem of user assignment and power allocation for a downlink (DL) NOMA network in terms of EE maximization. Another power allocation strategy was proposed in [23] to evaluate the EE of a broadcast DL NOMA network. These studies investigated the sub-channels assignment for UEs; hence, the UE association is still unknown for exploiting the channel capacity using NOMA. This motivates us to develop algorithms with a joint UE pairing and beamforming design that accounts for both the SE fairness and power consumption.

1.2. Contributions

In this paper, we consider a cellular DL NOMA network, where a multi-objective problem for rate fairness among all UEs and power consumption were investigated under the minimum per-UE rate requirement and signal-to-noise ratio (SNR) constraints for decoding the message. To further improve the channel capacity, the NOMA technique can be applied to two UEs in a cell, instead of UE pairing with two near and far groups. The resulting problem belongs to a mixed-integer non-convex class that is difficult to solve. Therefore, we devise two low-complexity algorithms, based on inner approximation (IA) and graph theory. The main contributions of this paper are described as follows:

• First, we investigate a hybrid system comprising NOMA and conventional beamforming to reap their advantages for a unique design. A beamforming design with SIC can be applied to a pair of UE, or conventional beamforming can be used for certain UE depending on the number of UEs and channel conditions. Accordingly, the approach is referred to as dynamic pairing because it enables the pairing of two arbitrary UEs in a cell.
• To manage the dynamic pairing, we introduce a new binary variable matrix for UE association. By using the NOMA principle and sorted channel gains, the computational complexity is reduced with the variables forced into an upper triangular matrix. Next, we formulate a problem for joint optimization of UE pairing and beamforming design, thereby enabling the selection of the objective function: the max-min rate (MMR) and power consumption. However, a strong coupling of binary and continuous variables under non-convex constraints results in a hard class of mixed-integer non-convex programs.
• To efficiently solve the resulting problem, we propose two approaches based on the IA framework as well as the relaxation method and bipartite graph. The first approach is based on a combination of the relaxation and IA methods; it can transform the complicated original problem into a more tractable form without integer variables. Therefore, an iterative algorithm based on the IA framework is derived to obtain a local optimal solution at the least. To further reduce the time complexity, we develop an algorithm in which UE pairing and the beamforming design are managed using a bipartite graph and the IA method. For UE pairing, this approach uses the channel correlation as the weights of edges on the graph, resulting in a linear bottleneck assignment problem. Hence, we apply the binary search and augmenting path algorithm to obtain the UE pair, and then use the solution of the first approach for the beamforming design based on a specified integer variable value.

1.3. Paper Organization and Notation

The rest of this paper is organized as follows. The system model and problem formulation are described in Section 2 and Section 3, respectively. Two proposed solutions based on the IA framework with the relaxation method and graph theory are detailed in Section 4 and Section 5, respectively. For the benchmark purpose, the optimal solution based on exhaustive search is also studied in Section 5. Section 6 presents numerical results, whereas Section 7 concludes the paper.

Notation: Lowercase and uppercase letters in bold indicate vectors and matrices, respectively. ${\mathbf{x}}^H$ is the Hermitian transpose of $\mathbf{x}$. The set of all complex and real numbers are represented by $\mathbb{C}$ and $\mathbb{R}$, respectively. $\parallel ·\parallel$ stands for the Euclidean norm. $\mathbb{E}\{·\}$ is the expectation and $\Re \{.\}$ denotes the real part of a complex number.

2. System Model

We consider a DL NOMA cellular system, where a BS is equipped N transmit antennas to serve K single-antenna UEs. As illustrated in Figure 1, NOMA technique can be applied to a pair of two arbitrary UEs in a set of UEs, denoted by $\mathcal{K}\triangleq \{1,\dots ,K\}$. For simplicity, we denotes the k-th UE by ${\mathrm{UE}}_k$.

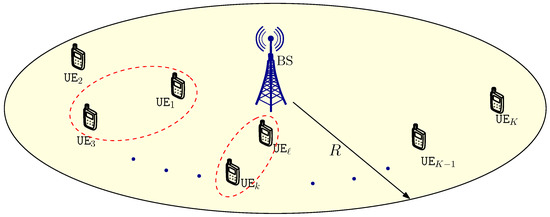
Figure 1. System model.

2.1. Data Transmission Model

The DL channel from BS to ${\mathrm{UE}}_k$ and the corresponding beamforming vector are denoted as ${\mathbf{h}}_k\in {\mathbb{C}}^{N\times 1}$ and ${\mathbf{w}}_k\in {\mathbb{C}}^{N\times 1}$, respectively. Without loss of generality, the channel gains of all UEs are sorted as $\parallel {\mathbf{h}}_1{\parallel }^2\ge \parallel {\mathbf{h}}_2{\parallel }^2\ge \cdots \ge {\parallel {\mathbf{h}}_K\parallel }^2$. The signal received at ${\mathrm{UE}}_k$ can be written as

$$y_k=\sum _{\forall \ell \in \mathcal{K}}{\mathbf{h}}_k^H{\mathbf{w}}_{\ell }{x}_{\ell }+n_k,$$

(1)

where $x_k$ with $\mathbb{E}\left\{\right|x_k{|}^2\}=1$ represents the symbol intended for ${\mathrm{UE}}_k$, and $n_k$ represents the additive white Gaussian noise (AWGN) at ${\mathrm{UE}}_k$. To perform UE pairing, we introduce binary variables ${\alpha }_{k,\ell }\in \{0,1\},\forall k,\ell \in \mathcal{K}$, which are expressed as

$$\begin{array}{c}\hfill {\alpha }_{k,\ell }=\left\{\begin{array}{cc}1,\hfill & \mathrm{if}{\mathrm{UE}}_k\mathrm{and}{\mathrm{UE}}_{\ell }\mathrm{are}\mathrm{paired}\mathrm{with}\mathrm{the}\mathrm{channel}\mathrm{gains}\mathrm{satisfying}\parallel {\mathbf{h}}_k{\parallel }^2\ge {\parallel {\mathbf{h}}_{\ell }\parallel }^2,\hfill \\ 0,\hfill & \mathrm{otherwise}.\hfill \end{array}\right.\end{array}$$

(2)

By defining $\mathit{\alpha }\triangleq {\left[{\alpha }_{k,\ell }\right]}_{K\times K}$, it is clear that $\mathit{\alpha }$ is an upper triangle matrix with the main diagonal of zeros. The signal-to-interference-plus-noise ratio (SINR) at ${\mathrm{UE}}_k$ can be written as

$$\begin{array}{cc}\hfill {\gamma }_k(\mathbf{w},\mathit{\alpha })& =min\left\{{\gamma }_{0,k}(\mathbf{w},\mathit{\alpha }),\underset{\forall \ell \in \mathcal{K}}{min}\left\{{\gamma }_{\ell ,k}(\mathbf{w},\mathit{\alpha })\right\}\right\},\hfill \end{array}$$

(3)

where $\mathbf{w}\triangleq {\left[{\mathbf{w}}_k\right]}_{k\in \mathcal{K}}$. The SINRs for decoding the ${\mathrm{UE}}_k$’s signals at itself and ${\mathrm{UE}}_{\ell }$ are denoted by ${\gamma }_{0,k}(\mathbf{w},\mathit{\alpha })$ and ${\gamma }_{\ell ,k}(\mathbf{w},\mathit{\alpha })$, respectively, which can be expressed as

$$\begin{array}{cc}\hfill {\gamma }_{0,k}(\mathbf{w},\mathit{\alpha })& =\frac{|{\mathbf{h}}_k^H{\mathbf{w}}_k{|}^2}{{\chi }_k(\mathbf{w},\mathit{\alpha })},\hfill \end{array}$$

(4a)

$$\begin{array}{cc}\hfill {\gamma }_{\ell ,k}(\mathbf{w},\mathit{\alpha })& =\frac{|{\mathbf{h}}_{\ell }^H{\mathbf{w}}_k{|}^2}{{\alpha }_{\ell ,k}{\Phi }_{\ell ,k}\left(\mathbf{w}\right)},\hfill \end{array}$$

(4b)

where ${\chi }_k(\mathbf{w},\mathit{\alpha })$ and ${\Phi }_{\ell ,k}(\mathbf{w},\mathit{\alpha })$ are respectively given as

$$\begin{array}{cc}\hfill {\Phi }_k(\mathbf{w},\mathit{\alpha })& =\sum _{\forall \ell \in \mathcal{K}\backslash \left\{k\right\}}(1-{\alpha }_{k,\ell }){\left|{\mathbf{h}}_k{\mathbf{w}}_{\ell }\right|}^2+{\sigma }_k^2,\hfill \end{array}$$

(5a)

$$\begin{array}{cc}\hfill {\Theta }_{\ell ,k}\left(\mathbf{w}\right)& =\sum _{\forall k^{\prime }\in \mathcal{K}\backslash \left\{k\right\}}|{\mathbf{h}}_{\ell }{\mathbf{w}}_{k^{\prime }}{|}^2+{\sigma }_{\ell }^2.\hfill \end{array}$$

(5b)

It is seen that when ${\mathrm{UE}}_k$ and ${\mathrm{UE}}_{\ell }$ are not paired together, i.e., ${\alpha }_{k,\ell }={\alpha }_{\ell ,k}=0,\forall k,\ell \in \mathcal{K}$, only ${\gamma }_{0,k}(\mathbf{w},\mathit{\alpha })$ is involved in Equation (3), since ${\gamma }_{\ell ,k}(\mathbf{w},\mathit{\alpha })\to \infty$.

2.2. Power Consumption Model

To measure power-efficiency, we consider the power consumption for transmission with beamforming, which can be expressed as

$$\begin{array}{c}\hfill P_{\mathrm{T}}\left(\mathbf{w}\right)=\underset{\mathrm{radiated}\mathrm{power}}{\underbrace{{\sum }_{\forall k\in \mathcal{K}}\frac{1}{{\zeta }_{\mathrm{PA}}}{\parallel {\mathbf{w}}_k\parallel }^2}},\end{array}$$

(6)

where ${\zeta }_{\mathrm{PA}}$ is the efficiency of the power amplifier (PA) at the BS. In other words, the power consumption is the power for data transmission from the BS to all the UE in the form of electromagnetic wave radiation. It is clear that $P_{\mathrm{T}}\left(\mathbf{w}\right)$ is a function of beamforming vectors.

Remark 1.

In addition to the power for beamforming, the power consumption in a wireless communication system includes the power for signal processing, device activation, and circuit operation [24,25]. However, these values are constant, and hence can be omitted in the objective function without affecting the search for the optimal solution. For convenience, we consider only the power consumption for beamforming in this paper.

3. Problem Formulation

The achievable rate of ${\mathrm{UE}}_k$ in nats/s/Hz can be expressed as

$$\begin{array}{c}\hfill R\left({\gamma }_k(\mathbf{w},\mathit{\alpha })\right)=ln(1+{\gamma }_k(\mathbf{w},\mathit{\alpha })),k\in \mathcal{K}.\end{array}$$

(7)

We introduce a parameter $\upsilon \in \{0,1\}$ for the objective selection between rate fairness and power consumption optimization. As a result, a multi-objective problem can be formulated as

$$\begin{array}{cc}\hfill \underset{\mathbf{w},\mathit{\alpha }}{max}& \upsilon \underset{\forall k\in \mathcal{K}}{min}R\left({\gamma }_k(\mathbf{w},\mathit{\alpha })\right)-(1-\upsilon )P_{\mathrm{T}}\left(\mathbf{w}\right),\hfill \end{array}$$

(8a)

$$\begin{array}{cc}\hfill \mathrm{s}.\mathrm{t}.& \sum _{k\in \mathcal{K}}\parallel {\mathbf{w}}_k{\parallel }^2\le P_{\mathrm{BS}}^{max},\hfill \end{array}$$

(8b)

$$\begin{array}{cc}\hfill & {\alpha }_{k,\ell }\in \{0,1\},\forall k,\ell \in \mathcal{K},\hfill \end{array}$$

(8c)

$$\begin{array}{cc}\hfill & {\alpha }_{k,\ell }=0,\forall (k,\ell )\in \{\mathcal{K}\times \mathcal{K}|k\ge \ell \},\hfill \end{array}$$

(8d)

$$\begin{array}{cc}\hfill & \sum _{k\in \mathcal{K}}{\alpha }_{k,\ell }\le 1,\forall \ell \in \mathcal{K},\hfill \end{array}$$

(8e)

$$\begin{array}{cc}\hfill & \sum _{\ell \in \mathcal{K}}{\alpha }_{k,\ell }\le 1,\forall k\in \mathcal{K},\hfill \end{array}$$

(8f)

$$\begin{array}{cc}\hfill & {\alpha }_{k,\ell }+\sum _{k^{\prime }\in \mathcal{K}}{\alpha }_{\ell ,k^{\prime }}\le 1\forall (k,\ell )\in \{\mathcal{K}\times \mathcal{K}|k<\ell \},\hfill \end{array}$$

(8g)

$$\begin{array}{cc}\hfill & {\alpha }_{k,\ell }+\sum _{{\ell }^{\prime }\in \mathcal{K}}{\alpha }_{{\ell }^{\prime },k}\le 1\forall (k,\ell )\in \{\mathcal{K}\times \mathcal{K}|k<\ell \},\hfill \end{array}$$

(8h)

$$\begin{array}{cc}\hfill & |{\mathbf{h}}_k^H{\mathbf{w}}_k{|}^2\ge {\rho }_{\mathrm{sn}}{\sigma }_k^2,\hfill \end{array}$$

(8i)

$$\begin{array}{cc}\hfill & R\left({\gamma }_k(\mathbf{w},\mathit{\alpha })\right)\ge (1-\upsilon ){\overline{R}}_k,\forall k\in \mathcal{K}.\hfill \end{array}$$

(8j)

Objective Equation (8a) can be selected for fairness rate maximization (or power consumption minimization) by setting $\upsilon =1$ (or $\upsilon =0$). Constraints Equation (8c–h) correspond to the NOMA criteria for user pairing. Specifically, Equation (8d) ensures that in a certain pair, UE with the better channel employs SIC to remove the interference from the remaining UE. Constraints Equation (8e–h) guarantee that each UE can be paired with at most one other UE. The signal-to-noise ratio (SNR) threshold ${\rho }_{\mathrm{sn}}$ in Equation (8i) is used for detecting the signal at the receivers, whereas constraint Equation (8j) provides the minimum bit rate, ${\overline{R}}_k$, such that UEs satisfy the QoS requirement. Owing to a strong coupling of continuous and binary variables under the non-convex objective function and constraints, Equation (8) is a mixed-integer non-convex problem, and thus, it is hard to obtain a globally optimal solution.

Remark 2.

Although the proposed dynamic pairing approach can further enhance the system performance, it leads to a large number of possible pairing cases. To overcome this issue and to accelerate the application of NOMA technique, the rest of the paper will devise two algorithms which provide low complexity and fast convergence.

4. Proposed Solution Based on Relaxation Method

To convert Equation (8) to a tractable form, the binary variables in constraint Equation (8c) are relaxed to continuous ones as $0\le {\alpha }_{k,\ell }\le 1,\forall k,\ell \in \mathcal{K}$. Then, the optimization problem Equation (8) can be rewritten as

$$\begin{array}{cc}\hfill \underset{\mathbf{w},\mathit{\alpha },\mathit{\lambda },\eta }{max}& \upsilon \eta -(1-\upsilon )P_{\mathrm{T}}\left(\mathbf{w}\right),\hfill \end{array}$$

(9a)

$$\begin{array}{cc}\hfill \mathrm{s}.\mathrm{t}.& 0\le {\alpha }_{k,\ell }\le 1,\forall k,\ell \in \mathcal{K},\hfill \end{array}$$

(9b)

$$\begin{array}{cc}\hfill & R\left({\gamma }_k(\mathbf{w},\mathit{\alpha })\right)\ge {\lambda }_k,\forall k\in \mathcal{K},\hfill \end{array}$$

(9c)

$$\begin{array}{cc}\hfill & {\lambda }_k\ge (1-\upsilon ){\overline{R}}_k,\forall k\in \mathcal{K},\hfill \end{array}$$

(9d)

$$\begin{array}{cc}\hfill & \eta \ge {\lambda }_k,\forall k\in \mathcal{K},\hfill \end{array}$$

(9e)

$$\begin{array}{cc}\hfill & Equation\left(\text{8b}\right),Equation(\text{8d}–\mathrm{i}),\hfill \end{array}$$

(9f)

where $\eta$ is a new variable representing the minimum rate among all UEs and $\mathit{\lambda }\triangleq \{{\lambda }_1,{\lambda }_2,\dots ,{\lambda }_K\}$ denotes the rate of each UE. Furthermore, Equation (9d) is the QoS constraint, which is equivalent to Equation (8j).

It can be observed that constraints Equations (8i) and (9c) are non-convex and thus difficult to solve directly. To deal with the issue, we first introduce some useful IA functions as follows.

• We consider the multiplication function $f_{\mathrm{mul}}(x,z)=xz$. Then an upper bound of $f_{\mathrm{mul}}(x,z)$ is provided in Equation (B.1) in [26]:

  $$\begin{array}{c}\hfill f_{\mathrm{mul}}(x,z)\le \frac{x^{\left(i\right)}}{2z^{\left(i\right)}}{z}^2+\frac{z^{\left(i\right)}}{2x^{\left(i\right)}}{x}^2=f_{\mathrm{mul}}^{\left(i\right)}(x,z),x\ge 0,y\ge 0.\end{array}$$

  (10)
• The logarithm function ${R\left(\right|x|}^2{/z)=ln(1+\left|x\right|}^2/z)$ with $x\in \mathbb{C},y\in {\mathbb{R}}_{+}$, has a lower bound around a feasible point $(x^{\left(i\right)},z^{\left(i\right)})$ [27]:

  $$\begin{array}{c}\hfill ln(1+\frac{{\left|x\right|}^2}{z})\ge R(\frac{|x^{\left(i\right)}{|}^2}{z^{\left(i\right)}})-\frac{|x^{\left(i\right)}{|}^2}{z^{\left(i\right)}}+2\frac{\mathfrak{R}\{x^{\left(i\right)}\ast x\}}{z^{\left(i\right)}}-\frac{|x^{\left(i\right)}{|}^2{\left(\right|x|}^2+z)}{{\left(z^{\left(i\right)}\right)}^2(z^{\left(i\right)}+|x^{\left(i\right)}{|}^2)}.\end{array}$$

  (11)
• A lower bound of the quadratic function $f_{\mathrm{qu}}\left(x\right)={\left|x\right|}^2$ can be expressed as

  $$\begin{array}{c}\hfill f_{\mathrm{qu}}\left(x\right)\ge 2\mathfrak{R}\{(x^{\left(i\right)})\ast x\}-{\left|x^{\left(i\right)}\right|}^2,x\in \mathbb{C}.\end{array}$$

  (12)

Let us convexify the QoS constraint Equation (8c). By using Equation (12), Equation (8c) can be approximated as

$$\begin{array}{c}\hfill |{\mathbf{h}}_k^H{\mathbf{w}}_k{|}^2\ge 2\mathfrak{R}\{({\mathbf{h}}_k^H{\mathbf{w}}_k^{\left(i\right)})\ast \left({\mathbf{h}}_k^H{\mathbf{w}}_k\right)\}-{\left|{\mathbf{h}}_k^H{\mathbf{w}}_k^{\left(i\right)}\right|}^2,\end{array}$$

(13)

resulting in an alternative convex constraints:

$$\begin{array}{c}\hfill 2\mathfrak{R}\{({\mathbf{h}}_k^H{\mathbf{w}}_k^{\left(i\right)})\ast \left({\mathbf{h}}_k^H{\mathbf{w}}_k\right)\}-{\left|{\mathbf{h}}_k^H{\mathbf{w}}_k^{\left(i\right)}\right|}^2\ge {\rho }_{\mathrm{sn}}{\sigma }_k^2,\forall k\in \mathcal{K}.\end{array}$$

(14)

To convexify constraint Equation (9c), we can split Equation (9c) into two sub-constraints as

$$\{\begin{array}{l}R\left({\gamma }_{0,k}(\mathbf{w},\mathit{\alpha })\right)\ge {\lambda }_k, \forall k\in \mathcal{K}, \left(\text{15a}\right)\\ R\left({\gamma }_{\ell ,k}(\mathbf{w},\mathit{\alpha })\right)\ge {\lambda }_k, \forall k\in \mathcal{K}. \left(\text{15b}\right)\end{array}$$

Using Equation (11), a lower bound of ${\gamma }_{0,k}(\mathbf{w},\mathit{\alpha })$ around a feasible point $({\mathbf{w}}^{\left(i\right)},{\mathit{\alpha }}^{\left(i\right)})$ at iteration $(i+1)$ is derived as

$$\begin{array}{c}\hfill R\left({\gamma }_{0,k}(\mathbf{w},\mathit{\alpha })\right)\ge {\mathcal{A}}_{0,k}^{\left(i\right)}+{\mathcal{A}}_{1,k}^{\left(i\right)}\left(\mathbf{w}\right)-{\mathcal{A}}_{2,k}^{\left(i\right)}(\mathbf{w},\mathit{\alpha }),\end{array}$$

(16)

where ${\mathcal{A}}_{0,k}^{\left(i\right)}$, ${\mathcal{A}}_{1,k}^{\left(i\right)}\left(\mathbf{w}\right)$, and ${\mathcal{A}}_{2,k}^{\left(i\right)}(\mathbf{w},\mathit{\alpha })$ are respectively given as

$$\begin{array}{cc}\hfill {\mathcal{A}}_{0,k}^{\left(i\right)}& =R\left({\gamma }_{0,k}^{\left(i\right)}\right)-{\gamma }_{0,k}^{\left(i\right)},\hfill \\ \hfill {\mathcal{A}}_{1,k}^{\left(i\right)}\left(\mathbf{w}\right)& =2\frac{\mathfrak{R}\{({\mathbf{h}}_k^H{\mathbf{w}}_k^{\left(i\right)})\ast \left({\mathbf{h}}_k^H{\mathbf{w}}_k\right)\}}{{\chi }_k^{\left(i\right)}},\hfill \\ \hfill {\mathcal{A}}_{2,k}^{\left(i\right)}(\mathbf{w},\mathit{\alpha })& ={\Theta }_k^{\left(i\right)}{\left|{\mathbf{h}}_k^H{\mathbf{w}}_k\right|}^2+{\Theta }_k^{\left(i\right)}\sum _{\ell \in \mathcal{K}\backslash \left\{k\right\}}(1-{\alpha }_{k,\ell }){\left|{\mathbf{h}}_k^H{\mathbf{w}}_{\ell }\right|}^2+{\Theta }_k^{\left(i\right)}{\sigma }_k^2,\hfill \end{array}$$

with ${\gamma }_{0,k}^{\left(i\right)}\triangleq {\gamma }_{0,k}({\mathbf{w}}^{\left(i\right)},{\mathit{\alpha }}^{\left(i\right)})$, ${\chi }_k^{\left(i\right)}\triangleq {\chi }_k({\mathbf{w}}^{\left(i\right)},{\mathit{\alpha }}^{\left(i\right)})$ and ${\Theta }_k^{\left(i\right)}\triangleq {({\chi }_k^{\left(i\right)})}^{-1}-({\chi }_k^{\left(i\right)}+|{\mathbf{h}}_k^H{\mathbf{w}}_k^{\left(i\right)}{{|}^2)}^{-1}$. Clearly, ${\mathcal{A}}_{2,k}^{\left(i\right)}(\mathbf{w},\mathit{\alpha })$ is still non-convex; hence, we apply Equation (10) to convexify ${\mathcal{A}}_{2,k}^{\left(i\right)}(\mathbf{w},\mathit{\alpha })$ as

$$\begin{array}{cc}{\mathcal{A}}_{2,k}^{\left(i\right)}(\mathbf{w},\mathit{\alpha })\hfill & \le {\Theta }_k^{\left(i\right)}{\tau }_{k,k}+{\Theta }_k^{\left(i\right)}{\displaystyle \sum _{\ell \in \mathcal{K}\backslash \left\{k\right\}}}(1-{\alpha }_{k,\ell }){\tau }_{k,\ell }+{\Theta }_k^{\left(i\right)}{\sigma }_k^2\hfill \\ \hfill & \le {\Theta }_k^{\left(i\right)}{\tau }_{k,k}+{\Theta }_k^{\left(i\right)}{\displaystyle \sum _{\ell \in \mathcal{K}\backslash \left\{k\right\}}}{f}_{\mathrm{mul}}^{\left(i\right)}(1-{\alpha }_{k,\ell },{\tau }_{k,\ell })+{\Theta }_k^{\left(i\right)}{\sigma }_k^2\hfill \\ \hfill & \triangleq {\tilde{\mathcal{A}}}_{2,k}^{\left(i\right)}(\mathbf{w},\mathit{\alpha },\mathit{\tau }),\hfill \end{array}$$

(17)

where $\mathit{\tau }={\left\{{\tau }_{k,\ell }\right\}}_{\forall k,\ell \in \mathcal{K}}$ is introduced as a new variable satisfying the following second-order cone (SOC) constraint:

$$\begin{array}{c}\hfill |{\mathbf{h}}_k^H{\mathbf{w}}_{\ell }{|}^2\le {\tau }_{k,\ell },\forall k,\ell \in \mathcal{K}.\end{array}$$

(18)

Therefore, the convex approximation for constraint Equation (15a) at iteration $(i+1)$ can be written as

$$\begin{array}{c}\hfill {\mathcal{A}}_{0,k}^{\left(i\right)}+{\mathcal{A}}_{1,k}^{\left(i\right)}\left(\mathbf{w}\right)-{\tilde{\mathcal{A}}}_{2,k}^{\left(i\right)}(\mathbf{w},\mathit{\alpha },\mathit{\tau })\ge {\lambda }_k,\forall k\in \mathcal{K}.\end{array}$$

(19)

It can be observed that constraints Equation (15a,b) take the same form. Hence, constraint Equation (15b) at iteration $(i+1)$ is approximated by the same steps as Equations (16)–(19), i.e., Equation (15b) is convexified as

$$\begin{array}{c}\hfill {\mathcal{B}}_{0,\ell ,k}^{\left(i\right)}+{\mathcal{B}}_{1,\ell ,k}^{\left(i\right)}\left(\mathbf{w}\right)-{\tilde{\mathcal{B}}}_{2,\ell ,k}^{\left(i\right)}(\mathbf{w},\mathit{\alpha },\mathit{\tau })\ge {\lambda }_k,\forall \ell ,k\in \mathcal{K},\end{array}$$

(20)

where ${\mathcal{B}}_{0,\ell ,k}^{\left(i\right)},{\mathcal{B}}_{1,\ell ,k}^{\left(i\right)}\left(\mathbf{w}\right)$, and ${\widehat{\mathcal{B}}}_{1,\ell ,k}^{\left(i\right)}(\mathbf{w},\mathit{\alpha })$ are respectively defined as

$$\begin{array}{cc}\hfill {\mathcal{B}}_{0,\ell ,k}^{\left(i\right)}& \triangleq R\left({\gamma }_{\ell ,k}^{\left(i\right)}\right)-{\gamma }_{\ell ,k}^{\left(i\right)},\hfill \\ \hfill {\mathcal{B}}_{1,\ell ,k}^{\left(i\right)}\left(\mathbf{w}\right)& \triangleq 2\frac{\mathfrak{R}\{({\mathbf{h}}_{\ell }^H{\mathbf{w}}_k^{\left(i\right)})\ast \left({\ell }_k^H{\mathbf{w}}_k\right)\}}{{\alpha }_{\ell ,k}^{\left(i\right)}{\Phi }_{\ell ,k}^{\left(i\right)}},\hfill \\ \hfill {\tilde{\mathcal{B}}}_{2,\ell ,k}^{\left(i\right)}(\mathbf{w},\mathit{\alpha },\mathit{\tau })& \triangleq {\Xi }_{\ell ,k}^{\left(i\right)}{\tau }_{\ell ,k}+{\Xi }_{\ell ,k}^{\left(i\right)}\sum _{k^{\prime }\in \mathcal{K}\backslash \left\{k\right\}}{f}_{\mathrm{mul}}^{\left(i\right)}({\alpha }_{\ell ,k},{\tau }_{\ell ,k^{\prime }})+{\Xi }_{\ell ,k}^{\left(i\right)}{\alpha }_{\ell ,k}{\sigma }_{\ell }^2,\hfill \end{array}$$

where ${\gamma }_{\ell ,k}^{\left(i\right)}\triangleq {\gamma }_{\ell ,k}({\mathbf{w}}^{\left(i\right)},{\mathit{\alpha }}^{\left(i\right)})$, ${\Phi }_{\ell ,k}^{\left(i\right)}\triangleq {\Phi }_{\ell ,k}\left({\mathbf{w}}^{\left(i\right)}\right)$, and ${\Xi }_{\ell ,k}^{\left(i\right)}\triangleq {\left({\Phi }_{\ell ,k}^{\left(i\right)}\right)}^{-1}-({\Phi }_{\ell ,k}^{\left(i\right)}+|{\mathbf{h}}_{\ell }^H{\mathbf{w}}_k^{\left(i\right)}{{|}^2)}^{-1}$.

In summary, a successive convex program at iteration $(i+1)$, which provides minorant maximization for Equation (9), can be formulated as

$$\begin{array}{cc}\hfill cc\underset{\mathbf{w},\mathit{\alpha },\mathit{\tau },\mathit{\lambda },\eta }{max}& \upsilon \eta -(1-\upsilon )P_{\mathrm{T}}\left(\mathbf{w}\right),\hfill \end{array}$$

(21a)

$$\begin{array}{cc}\hfill \mathrm{s}.\mathrm{t}.& Equation\left(\text{8b}\right),Equation(\text{8d}–\mathrm{h}),Equation\left(\text{9b}\right),Equation(\text{9d},\mathrm{e}),Equation\left(14\right),Equations\left(18\right)–\left(20\right).\hfill \end{array}$$

(21b)

Clearly, when the iterative algorithm terminates, the value of the relax variable $\alpha$ is approximately the binary value, and not a solution of Equation (8). To address this point, the binary values of $\alpha$ for the optimal solution of Equation (8) is recovered by the rounding function Equation (22), i.e.,

$$\begin{array}{c}\hfill {\alpha }_{k,\ell }^{\star }=\lfloor {\alpha }_{k,\ell }^{\left(i\right)}+\frac{1}{2}\rfloor ,\forall k,\ell \in \mathcal{K},\end{array}$$

(22)

where $\lfloor x\rfloor$ returns the maximum integer that is not larger than $x,x\in \mathbb{R}$.

For implementation purposes, it is necessary to find an initial feasible point for Equation (21). This can be achieved by solving the following sub-problem:

$$\begin{array}{cc}\hfill cc\underset{\mathbf{w},\mathit{\alpha },\mathit{\tau },\mathit{\lambda },\mathit{\omega }}{max}& \omega ,\hfill \end{array}$$

(23a)

$$\begin{array}{cc}\hfill \mathrm{s}.\mathrm{t}.& {\lambda }_k-{\overline{R}}_k\ge \omega ,\forall k\in \mathcal{K},\hfill \end{array}$$

(23b)

$$\begin{array}{cc}\hfill & \omega \le 0,\forall k\in \mathcal{K},\hfill \end{array}$$

(23c)

$$\begin{array}{cc}\hfill & Equation\left(\text{8b}\right),Equation(\text{8d}–\mathrm{h}),Equation\left(\text{9b}\right),Equation\left(\text{14}\right),Equations\left(18\right)–\left(20\right),\hfill \end{array}$$

(23d)

where $\omega$ is a new slack variable. Constraint Equation (23b) guarantees that the initial feasible point can satisfy the QoS requirement. It can be seen that a starting point $({\mathbf{w}}^{\left(0\right)},{\mathit{\alpha }}^{\left(0\right)},{\mathit{\tau }}^{\left(0\right)})$ is obtained when $\omega$ is approximately zero. The proposed iterative algorithm based on the IA method to solve the problem Equation (8) is summarized in Algorithm 1. In particular, the solution of continuous variables for the relaxation problem is found in Phase 1, while Phase 2 is devoted to re-compute the solution for the original problem with a fixed value of the integer variable $\mathit{\alpha }$.

Convergence analysis: Our proposed algorithm based on the IA method has the convergence properties as in [28]. Let ${\mathcal{F}}^{\left(i\right)}$ be the feasible point set of Equation (21) at iteration i, then the properties of IA method indicate that the optimal solution ${\widehat{\mathcal{X}}}^{\left(i\right)}\in {\mathcal{F}}^{\left(i\right)}$ obtained at iteration i satisfies ${\widehat{\mathcal{X}}}^{\left(i\right)}\in {\mathcal{F}}^{(i+1)}$ as well. In addition, ${\mathcal{F}}^{\left(i\right)}$ is a connected set [29]. Therefore, our proposed algorithm can provide at least a local optimal solution that satisfies the Karush-Kuhn-Tucker conditions.

Complexity analysis: The approximated problem Equation (21) includes $5K^2+4K+1$ SOC/linear constraints and $2K^2+NK+1$ variables, which complicates the solving of Equation (21) in terms of the big-O expressed as $\mathcal{O}({(2K^2+NK+1)}^{2.5}({(5K^2+4K+1)}^2+2K^2+NK+1))$ [30].

Algorithm 1 Proposed Algorithm for Solving Problem Equation (8) based on IA Method.

Phase 1: 1: Input-1:${\mathbf{h}}_k$, ${\overline{R}}_k$$(k\in \mathcal{K})$, $P_{\mathrm{BS}}^{\max }$, and ${\rho }_{\mathrm{sn}}$. 2: Initialization: Set $i:=0$. 3: Get an initial point: Execute the sub-problem Equation (23) to obtain an initial point $({\mathbf{w}}^{\left(0\right)},{\mathit{\alpha }}^{\left(0\right)},{\mathit{\tau }}^{\left(0\right)})$ for Equation (21). 4: repeat 5:  Solve the optimization problem Equation (21) to find $({\mathbf{w}}^{\star },{\mathit{\alpha }}^{\star },{\mathit{\tau }}^{\star })$ at the i-th iteration. 6:  Update $({\mathbf{w}}^{(i+1)},{\mathit{\alpha }}^{(i+1)},{\mathit{\tau }}^{(i+1)}):=({\mathbf{w}}^{\star },{\mathit{\alpha }}^{\star },{\mathit{\tau }}^{\star })$. 7:  Set $i:=i+1.$ 8: until Convergence 9: Use the rounding function Equation (22) to recover ${\mathit{\alpha }}^{\star }$. 10: Output-1: The optimal solution ${\mathit{\alpha }}^{\star }$ for the binary variable $\mathit{\alpha }$. Phase 2: 11: Input-2:${\mathbf{h}}_k$, ${\overline{R}}_k$$(k\in \mathcal{K})$, $P_{\mathrm{BS}}^{\max }$, ${\rho }_{\mathrm{sn}}$, and ${\mathit{\alpha }}^{\ast }$. 12: Reset $i:=0$ and repeat steps 1–7 with binary ${\mathit{\alpha }}^{\star }$ to obtain the exact beamforming vector ${\mathbf{w}}^{\star }$. 13: Output-2: The optimal solution (${\mathbf{w}}^{\star },{\mathit{\alpha }}^{\star }$).

5. Proposed Solutions Based on Integer-Variable Reduction

This section presents the reduction in the computational complexity using integer-variable reduction (IVR). Unlike the relaxation method, this approach first determines the value of $\mathit{\alpha }$ for UE pairing; subsequently, power allocation is computed by solving a sub-problem with respect to the given $\mathit{\alpha }$. We investigate two methods to find the UE pairs: (i) a graph-based IVR method to reduce the complexity; and (ii) an IVR using exhaustive search for benchmarking.

5.1. Proposed Solution Using Graph-Based IVR

In this subsection, we propose a low-complexity pairing scheme based on channel vectors. Accordingly, a dynamic pair of UE is determined based on a high channel correlation, to which the SIC technique can be effectively applied. It is observed that when the UEs with high channel correlation are paired to each other, the BS has more degree of freedom for beamforming design to mitigate the inter-pair interference.

To implement this method, we first define a weight matrix $\mathbf{C}\triangleq {\left[c_{k,\ell }\right]}_{\forall k,\ell \in \mathcal{K}}\in {\mathbb{R}}^{K\times K}$, in which each entry $c_{k,\ell }$ denoting the channel correlation between the k-th and ℓ-th UEs is calculated as

$$\begin{array}{c}\hfill c_{k,\ell }=\frac{|<{\mathbf{h}}_k,{\mathbf{h}}_{\ell }>|}{\parallel {\mathbf{h}}_k\parallel \parallel {\mathbf{h}}_{\ell }\parallel },\end{array}$$

(24)

where $<\mathbf{x},\mathbf{y}>$ denotes the inner product of two vectors $\mathbf{x}$ and $\mathbf{y}$. Subsequently, the UE pairs can be determined by solving the following linear bottleneck assignment problem (LBAP):

$$\begin{array}{cc}\hfill \underset{\mathit{\alpha }}{max}& \underset{\forall k\in \mathcal{K}}{min}\sum _{\ell \in \mathcal{K}}{\alpha }_{k,\ell }{c}_{k,\ell },\hfill \end{array}$$

(25a)

$$\begin{array}{cc}\hfill \mathrm{s}.\mathrm{t}.& Equation\left(\text{8c}\right),Equation\left(\text{8e}\right),Equation\left(\text{8f}\right).\hfill \end{array}$$

(25b)

It is noteworthy that when $c_{k,\ell }=0$, no edge exists between the k-th and ℓ-th UEs. To solve problem Equation (25), we use the bipartite graph and binary search methods as follows.

5.1.1. Bipartite Graph for UE Pairing

We employ a balanced bipartite graph $\mathcal{G}=({\mathcal{K}}_1,{\mathcal{K}}_2;\mathcal{D})$, where ${\mathcal{K}}_1$ and ${\mathcal{K}}_2$ are the vertex sets of all UEs with $|{\mathcal{K}}_1|=|{\mathcal{K}}_2|=K$, and $\mathcal{D}$ is the set of edges, i.e., $\mathcal{D}=\left\{\right\{k,\ell \left\}\right|k,\ell \in \mathcal{K}\mathrm{and}k\ne \ell \}$, with the weight of an edge $\{k,\ell \}$ being $c_{k,\ell }$. UE pairing can be performed by using the augmenting path algorithm [31]. Some definitions for developing the pairing algorithm are as follow:

• A matching $\mathcal{M}$ is a subset of $\mathcal{D}$ without any two edges sharing the same vertex. For convenience, we define an unmatched set $\overline{\mathcal{M}}=\mathcal{D}\backslash \mathcal{M}$. Furthermore, a maximum matching corresponds to a special case, in which $\mathcal{M}$ is enlarged to the maximum.
• A free vertex is defined as a vertex not contained in $\mathcal{M}$.
• An alternating path $\mathcal{P}$ is a path in graph $\mathcal{G}$, such that two arbitrary successive edges in $\mathcal{P}$ are from both sets $\mathcal{M}$ and $\overline{\mathcal{M}}$.
• An alternating path $\mathcal{P}$ becomes an augmenting path when both the starting and ending points of $\mathcal{P}$ are free vertexes.

We can use the augmenting path algorithm to expand $\mathcal{M}$ until a maximum matching is obtained. In particular, at each iteration of an iterative algorithm, the augmenting path $\mathcal{P}$ is determined for a given matching $\mathcal{M}$ ($\mathcal{M}=\varnothing$ at the beginning), and then, $\mathcal{M}$ is updated as $\mathcal{M}=(\mathcal{M}\backslash \mathcal{P})\cup (P\backslash M)$. The algorithm terminates when no augmenting path is found. However, a maximum matching with the augmenting path algorithm merely addresses the maximum pairs of UEs, which is insufficient for obtaining the optimal solution for problem Equation (25) under a balanced bipartite graph in a polynomial-time complexity. Hence, the augmenting path algorithm is integrated into a binary search method as will be described in the following subsection.

5.1.2. Binary Search with Augmenting Path Algorithm

The optimal solution for problem Equation (25) is a maximum matching with channel correlation fairness among UE pairs. In other words, the pairs of UEs are determined such that the minimum channel correlation of UE pairs in the achieved maximum matching is maximized. Moreover, the maximal value for the weight fairness is one of the entries in $\mathbf{C}$. Therefore, the binary search algorithm [32] is used to find the solution for Equation (25). The search region is given by an auxiliary vector $\mathit{v}\triangleq {\left[v_i\right]}_{i\in \{1,\dots ,K^2\}}\in {\mathbb{R}}^{1\times K^2}$, of which the components involving all entries of matrix $\mathbf{C}$ are sorted in the ascending order, i.e., $v_1\le v_2\le \cdots \le v_{K^2}$. Let ${\mathrm{id}}_{\min }$ and ${\mathrm{id}}_{\max }$ be the lower and upper indexes for the search region on vector $\mathbf{v}$, respectively. Clearly, ${\mathrm{id}}_{\min }=1$ and ${\mathrm{id}}_{\max }=K^2$ at the initialization. The search region is denoted by $\mathcal{S}\left({\mathrm{id}}_{\min },{\mathrm{id}}_{\max }\right)\triangleq [v_{{\mathrm{id}}_{\min }},\cdots ,v_{{\mathrm{id}}_{\max }}]$. At each iteration, the index of the median in the search region is determined as

$$\begin{array}{c}\hfill {\mathrm{id}}_{\mathrm{med}}=⌊\frac{{\mathrm{id}}_{\min }+{\mathrm{id}}_{\max }}{2}⌋.\end{array}$$

(26)

Subsequently, the augmenting path algorithm is executed on sub-graph $\tilde{\mathcal{G}}=({\mathcal{K}}_1,{\mathcal{K}}_2;\tilde{\mathcal{D}})\subseteq \mathcal{G}$ to find the maximum matching $\mathcal{M}$, where $\tilde{\mathcal{D}}\triangleq \mathcal{D}\backslash \left\{\{k,\ell \}\right|c_{k,\ell }<v_{{\mathrm{id}}_{\mathrm{med}}}\}$. The search region is updated as

$$\begin{array}{c}\hfill \mathcal{S}\left({\mathrm{id}}_{\min },{\mathrm{id}}_{\max }\right)=\left\{\begin{array}{cc}\mathcal{S}\left({\mathrm{id}}_{\mathrm{med}},{\mathrm{id}}_{\max }\right),\hfill & \mathrm{if}\left|\mathcal{M}\right|=K\hfill \\ \mathcal{S}\left({\mathrm{id}}_{\min },{\mathrm{id}}_{\mathrm{med}}\right),\hfill & \mathrm{if}\left|\mathcal{M}\right|<K.\hfill \end{array}\right.\end{array}$$

(27)

The binary search algorithm terminates when $\mathcal{S}\left({\mathrm{id}}_{\min },{\mathrm{id}}_{\max }\right)$ contains only one element, i.e., ${\mathrm{id}}_{\mathrm{med}}={\mathrm{id}}_{\min }={\mathrm{id}}_{\max }$, which results in the value of $\mathit{\alpha }$. After obtaining the value of $\mathit{\alpha }$, we solve the optimization problem Equation (21) with the given $\mathit{\alpha }$ to obtain the solution for Equation (8). The proposed algorithm using graph-based IVR is summarized in Algorithm 2. By applying binary search and augmenting path methods for the bipartite graph, a dynamic pairing solution is computed in Phase 1, at which the binary value of variable $\mathit{\alpha }$ is determined to satisfy the constraints of the original problem. In Phase 2, a convex approximation program is solved under the binary value of $\mathit{\alpha }$ obtained in Phase 1.

Complexity Analysis: The binary search requires $\mathcal{O}\left({log}_2\left(K^2\right)\right)$ steps to find the optimal value $c_{\mathrm{med}}$, while the augmenting path algorithm takes $\mathcal{O}\left(K^3\right)$ [33]. Therefore, the total complexity for finding $\mathit{\alpha }$ in problem Equation (25) is $\mathcal{O}\left(K^3{log}_2\left(K^2\right)\right)$. With a given value of $\mathit{\alpha }$, a sub-problem derived from problem Equation (21) has $K^2+NK+1$ variables and $K^2+3K+\lfloor K/2\rfloor +1$ SOC/linear constraints; consequently, the total complexity of Algorithm 2 is $\mathcal{O}(K^3{log}_2{K}^2+{(K^2+NK+1)}^{2.5}({(K^2+3K+\lfloor K/2\rfloor +1)}^2+K^2+NK+1))$.

Algorithm 2 Proposed Algorithm for Solving Problem Equation (8) using Graph-based IVR.

Phase 1: 1: Input-1:${\mathbf{h}}_k$, $(k\in \mathcal{K})$. 2: Compute the weight matrix C as in Equation (24). 3: Generate an auxiliary vector v which is sorted in an ascending order. 4: Set ${\mathrm{id}}_{\min }:=1$, ${\mathrm{id}}_{\max }:=K^2$. 5: repeat 6:  Compute ${\mathrm{id}}_{\mathrm{med}}$ as in Equation (26). 7:  Build a sub-graph $\tilde{\mathcal{G}}$ using the median $v_{{\mathrm{id}}_{\mathrm{med}}}$. 8:  Apply augmenting path algorithm to find the maximum matching $\mathcal{M}$ in $\tilde{\mathcal{G}}$. 9:  if$\left|\mathcal{M}\right|=K$ then 10:   Set ${\mathrm{id}}_{\min }:={\mathrm{id}}_{\mathrm{med}}$. 11:  else 12:   Set ${\mathrm{id}}_{\max }:={\mathrm{id}}_{\mathrm{med}}$. 13:  end if 14: until  ${\mathrm{id}}_{\min }={\mathrm{id}}_{\max }$ 15: Create $\mathit{\alpha }$ corresponding to the given $\mathcal{M}$. 16: Output-1: The pairing solution ${\mathit{\alpha }}^{\star }$ for the binary variable $\mathit{\alpha }$. Phase 2: 17: Input-2:${\mathbf{h}}_k$, ${\overline{R}}_k$$(k\in \mathcal{K})$, $P_{\mathrm{BS}}^{\max }$, ${\rho }_{\mathrm{sn}}$, and ${\mathit{\alpha }}^{\ast }$. 18: Apply Steps 1–7 in Algorithm 1 with the given value of ${\mathit{\alpha }}^{\star }$ to find the beamforming vector ${\mathbf{w}}^{\star }$. 19: Output-2: The optimal solution (${\mathbf{w}}^{\star },{\mathit{\alpha }}^{\star }$).

5.2. Proposed Solution Based on Exhaustive Search

For benchmarking, this section presents the optimal solution using exhaustive search (ES), where all possible cases of $\mathit{\alpha }$ are considered while satisfying constraints Equations (8c)–(8h). For each case, a sub-problem is derived from Equation (8) by fixing the value of $\mathit{\alpha }$. Instead of only one subproblem, we obtain many sub-problems as in the graph-based method. Subsequently, we use Equation (21) to find the solutions to the sub-problems. The solution $(\mathbf{w},\mathit{\alpha })$ that provides the best performance is selected as the optimal solution. It can be observed that each sub-problem can be solved with a fast convergence since it only needs to handle the continuous variables of the beamforming vectors. However, this approach typical incurs high computational complexity owning to the large number of sub-problems.

Complexity Analysis: The ES method examines ${\sum }_{k=1}^{\lfloor K/2\rfloor }\left(\genfrac{}{}{0pt}{}{K}{k}\right)\frac{\left(2k\right)!}{2^{k}k!}$ sub-problems as all possible cases of $\mathit{\alpha }$. For a given value of $\mathit{\alpha }$, a sub-problem based on Equation (21) contains the same numbers of variables and constraints as in Algorithm 2. Therefore, the total complexity of the ES method is determined as $\mathcal{O}\left(\left({\sum }_{k=1}^{\lfloor K/2\rfloor }\left(\genfrac{}{}{0pt}{}{K}{k}\right)\frac{\left(2k\right)!}{2^{k}k!}\right){(K^2+NK+1)}^{2.5}({(K^2+3K+\lfloor K/2\rfloor +1)}^2+K^2+NK+1)\right)$.

6. Numerical Results

6.1. Parameter and Simulation Settings

We consider a DL cellular system where one BS equipped with N-antennas serves K single-antenna UEs. The BS is located at the center of the cell, whereas the UEs are uniformly distributed within radius R from the cell center. To evaluate the performance of the proposed algorithms, we adopt Monte-Carlo simulations. The channel from the BS to each UE includes the path loss, $\mathrm{PL}\left(d_{\mathrm{BS},\mathrm{UE}}\right)$ with distance $d_{\mathrm{BS},\mathrm{UE}}$, and small-scale fading expressed as a Gaussian random variable $\mathbf{h}\sim \mathcal{CN}(0,\mathrm{PL}\left(d_{\mathrm{BS},\mathrm{UE}}\right)\mathbf{I})$. The other simulation parameters are shown in Table 1,in which the realistic parameters of power consumption and PA efficiency are provided by [24]. We compare Algorithm 1 (Algorithm 1), Algorithm 2 (Algorithm 2) and the ES scheme with the existing schemes. Before UE pairing, we first sort all UEs in descending order of their channel gains. The pairing strategies are described as follows:

Table 1. Simulation Parameters.

Parameter	Value
Noise power spectral density	−174 dBm/Hz
Radius of the cell, R	100 m
Path loss from BS to UEs, ${\mathrm{PL}}_{\mathrm{BS},\mathrm{UE}}$	128.1 + 37.6${log}_{10}\left(d_{\mathrm{BS},\mathrm{UE}}\right)$ dB
The nearest distance from between UEs and BS	10 m
Power budget at BS, $P_{\mathrm{BS}}^{max}$	18 dBm
Rate threshold, ${\overline{R}}_k={\overline{R}}_{\ell }=\overline{R},\forall k,\ell \in \mathcal{K}$	1 bits/s/Hz
Number of UEs, K	6
Number of antennas at BS, N	4
SNR threshold at receivers, ${\rho }_{\mathrm{sn}}$	0 dB
PA efficiency at BS, ${\zeta }_{\mathrm{PA}}$	0.3

• Greedy pairing with difference fairness for channel gains (GP-DFCG): A pair comprises the k-th and $(K-\lfloor K/2\rfloor +k)$-th UEs, resulting in ${\alpha }_{k,K-\lfloor K/2\rfloor +k}=1,1\le k\le \lfloor K/2\rfloor$.
• Greedy pairing with the strongest-to-weakest channel-gain strategy (GP-SWCG): Considering all sorted UEs in an unpaired set, a pair is selected by popping the strongest and weakest channel-gain UEs until the unpaired set is empty or contains one UE, i.e., a pair including the k-th and $(K-k+1)$-th UEs, resulting in ${\alpha }_{k,K-k+1}=1,1\le k\le \lfloor K/2\rfloor$.
• Consecutive pairing (CP): As in [19], the $(2k-1)$-th and $2k$-th UEs are paired together, resulting in ${\alpha }_{2k-1,2k}=1,1\le k\le \lfloor K/2\rfloor$.

Furthermore, we also investigate two other typical schemes: (i) Random pairing, where two UEs in the cell are randomly paired with each other; (ii) Beamforming design, where conventional beamforming is applied to all UEs, resulting in an all-zero matrix $\mathit{\alpha }$. Except for Algorithm 1, the sub-problems, which are derived as the cases of problem Equation (21) for achieved values of $\mathit{\alpha }$, are solved for the beamforming vectors.

6.2. Rate Fairness Performance

To evaluate the effectiveness of the proposed algorithms in terms of rate fairness, the cumulative distribution functions (CDFs) of all schemes are investigated with respect to the MMR. We use 1000 random channels to estimate the CDFs in Figure 2. In general, the GP-based and CP-based schemes exhibit better performance than random pairing and the conventional beamforming design, i.e., gains of 0.4–0.8 bps/Hz at the mid-point. As expected, the proposed algorithms outperform GP- and CP-based schemes. In particular, when comparing to the GP-DFCG scheme at the mid-point, the performance gains of Algorithms 1 and 2 are 0.7 and 0.3 bps/Hz, respectively. Except for beamforming, the other schemes provide high rate fairness for all UEs, exceeding 3 bps/Hz at the 95-percentile points. These CDFs spread in a wide range of MMR (approximately 2 bps/Hz from the 5- to 95-percentile points), adapting to the channel responses. This figure verifies the importance of the channel-gain disparities as well as the strategies of UE pairing for NOMA-based systems.

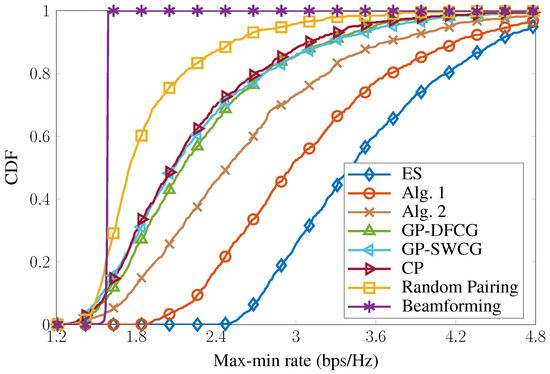
Figure 2. Cumulative distribution function of max-min rate.

Figure 3 depicts the average MMR of the eight schemes along with the change in the budget at the BS. For comparison, the conventional beamforming and ES schemes are also investigated as two baselines. In comparison with the beamforming scheme, the random pairing scheme provides the least MMR gain, whereas the two proposed algorithms outperform the other existing schemes. The performance of Algorithm 1 is approximately 0.5 bps/Hz better than that of Algorithm 2, compensating for the computational complexity of jointly optimizing the mixed-integer variables. Interestingly, the performance of Algorithm 1 is quite close to that of the ES schemes (approximately $0.3$ bps/Hz loss on average), thereby confirming the effectiveness of the proposed scheme.

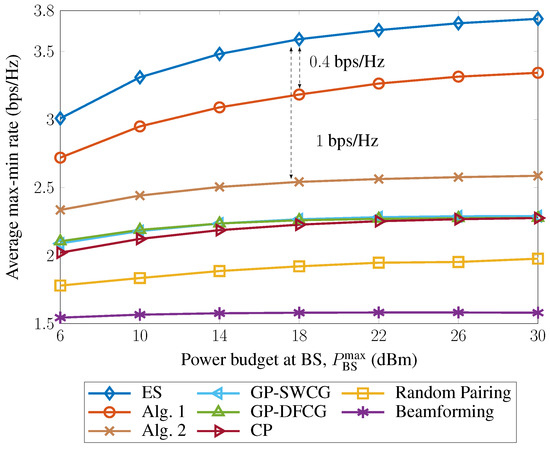
Figure 3. Average max-min rate versus power budget at BS.

6.3. Power Consumption Minimization

We first examine the minimum rate of all UEs and power-consumption percentage at the BS with the various values of power budget at the BS, $P_{\mathrm{BS}}^{max}$, as illustrated in Figure 4. The minimum rates obtained using Algorithms 1 and 2 are only 1 bps/Hz when considering power consumption minimization (i.e., $\upsilon =0$), which is exactly the minimum bit-rate threshold associated with the QoS requirements. This allows the BS to consume sufficient power and hence reduce the major part of the power budget. For example, the power-consumption percentage is lower than $1\%$ of $P_{\mathrm{BS}}^{max}$ and inversely proportional to $P_{\mathrm{BS}}^{max}$. Meanwhile, when the design problem is targeted at the MMR $(\upsilon =1)$, the minimum rate and power-consumption percentage obtained by Algorithms 1 and 2 increase along with $P_{\mathrm{BS}}^{max}$. The minimum rates are equal to MMRs of Algorithms 1 and 2, consistent with the results in Figure 3. As shown, the power-consumption percentages for the MMR are much higher than those for power consumption minimization; however, the entire power budget is not used. Typically, at $P_{\mathrm{BS}}^{max}=18$ dBm, the power consumption percentages of Algorithms 1 and 2 are $56.7\%$ and $97.8\%$, respectively. This supports interference management for achieving rate fairness among all UEs, resulting in a decrease in the power-consumed percentages and MMR saturation at high values of $P_{\mathrm{BS}}^{max}$.

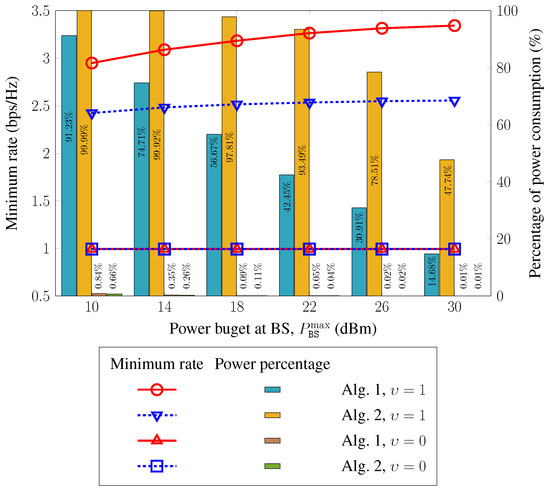
Figure 4. Minimum rate and percentage of power consumption with respect to power budget at BS.

To understand the behavior of the proposed algorithms, Figure 5 depicts the power consumption as a function of the QoS requirement. It is clear that the power consumption of all schemes increases with the minimum bit rate. As expected, the proposed algorithms outperform the others, and satisfy the high level of the minimum bit rate. In particular, from $\overline{R}=2$ (bps/Hz), the proposed algorithms still yield good solution for satisfying the QoS requirement constraint, whereas the other existing schemes could not easily yield the feasible point. Figure 6 demonstrates the power consumption performance versus SNR thresholds. For convenience, we only examine the GP-SWCG scheme, which provides the best performance among the three greedy-based schemes. It is observed that the proposed algorithms provide performance comparable to that of the ES method even at a low SNR threshold. Compared with random pairing, the proposed schemes use approximately 4 dBm, while GP-SWCG provides more than 1 dBm of power saving. These results confirm the flexibility of the proposed methods for the UE pairing to enhance the rate fairness and reduce power consumption.

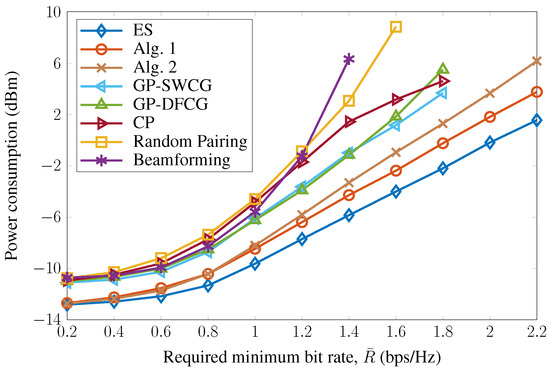
Figure 5. Power consumption versus minimum bit rate.

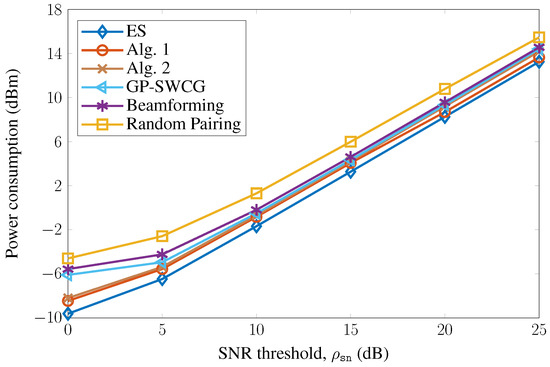
Figure 6. Power consumption versus received SNR threshold.

To further realize the effect of the SNR threshold on system performance, we investigate MMR and power-consumption as a function of SNR threshold, as shown in Figure 7. For power consumption minimization $(\upsilon =0)$, the percentage of consumed power is small and proportional to the SNR threshold, whereas the minimum rate remains almost constant. In this case, both proposed algorithms maintain sufficient consumed power to satisfy the QoS requirement, i.e., the minimum rate of 1 bps/Hz. Specifically, for a low SNR threshold, the power consumption percentage of both Algorithms 1 and 2 are less than $1\%$, whereas the percentage of consumed power for the higher SNR threshold increases to satisfy the requirement for decoding messages, i.e., approximately 15% at ${\rho }_{\mathrm{sn}}=25$ dB. In addition, for the MMR problem $(\upsilon =1)$, the percentage of power consumption differs significantly from that of the power-minimization case. In particular, more than $90\%$ of power budget is required for both algorithms at ${\rho }_{\mathrm{sn}}=25$ dB. Moreover, when ${\rho }_{\mathrm{sn}}$ increases, the MMR performance degrades slightly. This is because the power allocated to each UE is increased to satisfy the SNR threshold at all UEs, resulting in more interference among the UEs and a decrease in the minimum rate. However, between ${\rho }_{\mathrm{sn}}=0$ and ${\rho }_{\mathrm{sn}}=25$ dB, the minimum rates obtained by Algorithms 1 and 2 reduces by only approximately $0.2$ bps/Hz, indicating the adaption of the proposed schemes even under a strict received-SNR condition for NOMA-based beamforming design.

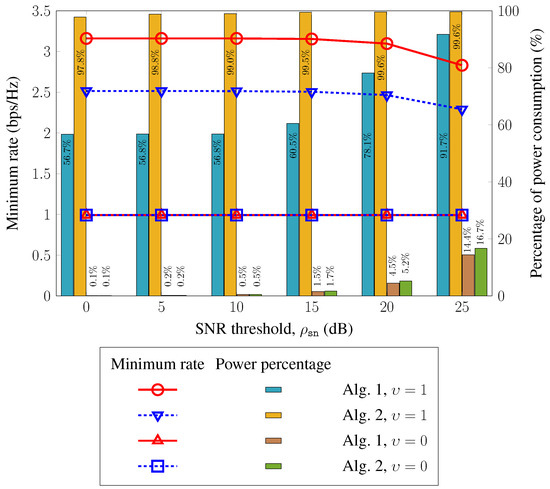
Figure 7. Minimum rate and percentage of power consumption versus SNR threshold.

6.4. Convergence Behaviors

We investigate the convergence behaviors of the proposed algorithms by referencing to the beamforming design. Figure 8 shows the MMR performance of the three schemes at $P_{\mathrm{BS}}^{max}=18$ dBm and ${\rho }_{\mathrm{sn}}=0$ dB. Because the ES method contains many sub-problems, it is difficult to show its convergence behavior; hence, the ES method is omitted in this figure. As previously mentioned, Algorithm 1 includes two phases where the relaxed variable $\alpha$ is rounded after the first phase, and the optimal solution for the original problem is obtained in the second phase. Hence, the convergence line of Algorithm 1 in Figure 8 consists of a bumpy period before reaching the saturation value. Furthermore, the two proposed algorithms achieve 99% performance with fast convergence. In particular, Algorithm 1 converges almost from iteration 13, whereas Algorithm 2 and beamforming require only a few iterations for a faster convergence rate (i.e., convergence at the 10-th iteration). However, it can be concluded that both proposed algorithms provide fast convergence.

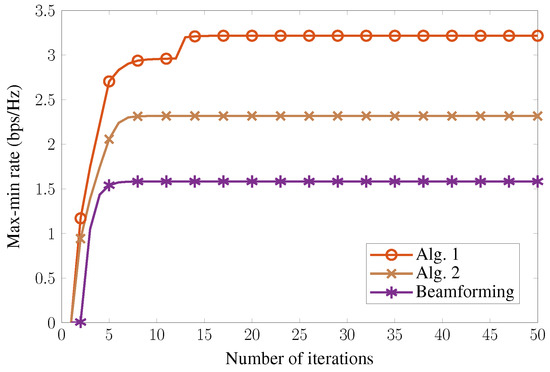
Figure 8. Convergence behaviors of MMR.

7. Conclusions

We studied a hybrid of NOMA and conventional beamforming design, where a dynamic pairing technique was investigated with two arbitrary UEs in a cell that can be paired together. The aim of this paper was to improve the performance in terms of both fairness rate among all UEs and power consumption. To tackle the resulting mixed-integer non-convex problem, we proposed two low-complexity algorithms. The first algorithm was based on a combination of the relaxation and IA methods to jointly optimize UE pairing and beamforming. In the second algorithm, we used the bipartite graph and binary search methods to achieve UE pairing before using the IA method to obtain the beamforming vectors, which can further reduce the computational complexity. Numerical results with realistic parameters demonstrated that the two proposed algorithms outperform the existing schemes in terms of both MMR and the power consumption.

Besides the advantage of novel dynamic UE pairing, some research gaps would be investigated for future works. Even when two proposed algorithms provide good performance and low complexity, an advanced optimization technique for NOMA could be expected to reduce the rate loss. In addition, the channel estimation is not perfect in practice; thus, a robust design under the channel uncertainty would be essential for UE pairing and beamforming in NOMA-based systems. Finally, the effectiveness of dynamic UE pairing in massive device networks is still unknown, which motivates us to develop a new method for the upcoming requirement and environment.