PI Parameter Influence on Underfloor Heating Energy Consumption and Setpoint Tracking in nZEBs
Abstract
1. Introduction
2. Materials and Methods
2.1. The Building
2.2. Outline of the Work
2.3. Input Data
- A sunny week with moderate temperature (19–25.03);
- A cold week with almost no sun (29.01–04.02).
2.4. Model Fitting
2.5. Estimating PI Parameters
- Optimized using GenOpt;
- Tuned in Matlab/Simulink;
- Calculated from an applicable simple method.
| Cohen–Coon (CC): | (3) | (4) | ||
| Skogestad IMC (SIMC): | (5) | (6) | ||
| AMIGO: | (7) | (8) |
2.6. The Evaluation Tests
- The average absolute error (AAE) of the air temperature from the setpoint;
- The heating energy consumption per square meter of the floor area.
2.7. Benchmarks
2.8. PI Implementation in IDA ICE and PI Mechanics
3. Results
3.1. Found Simplified Models
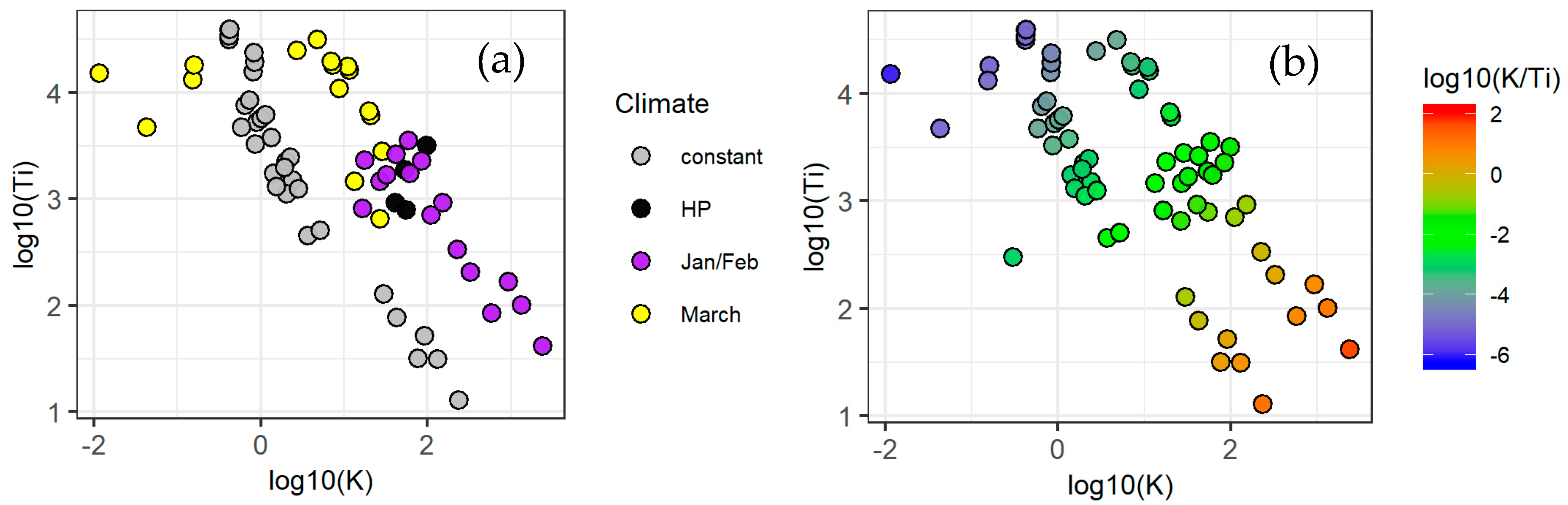
3.2. Identified PI Parameters
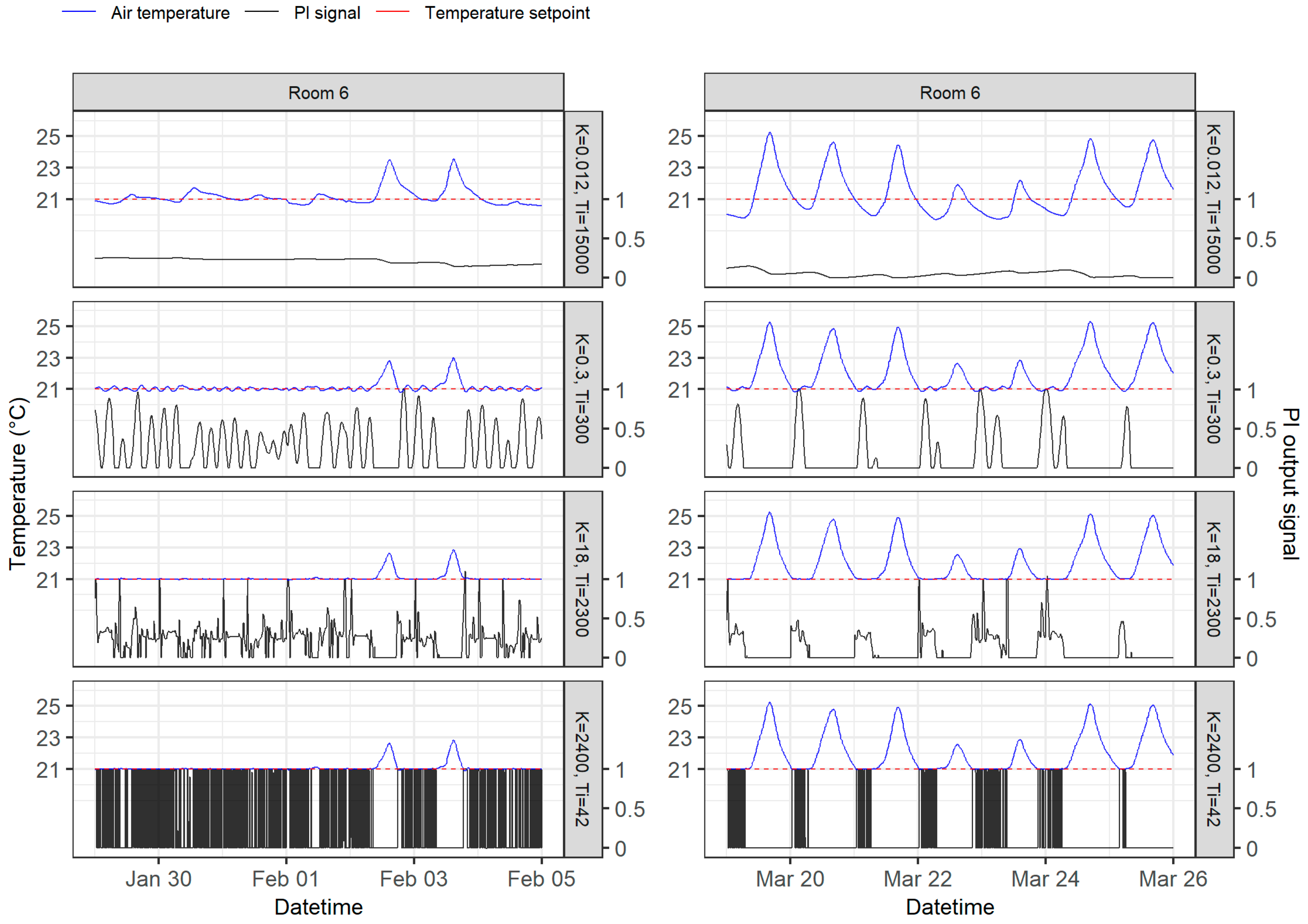
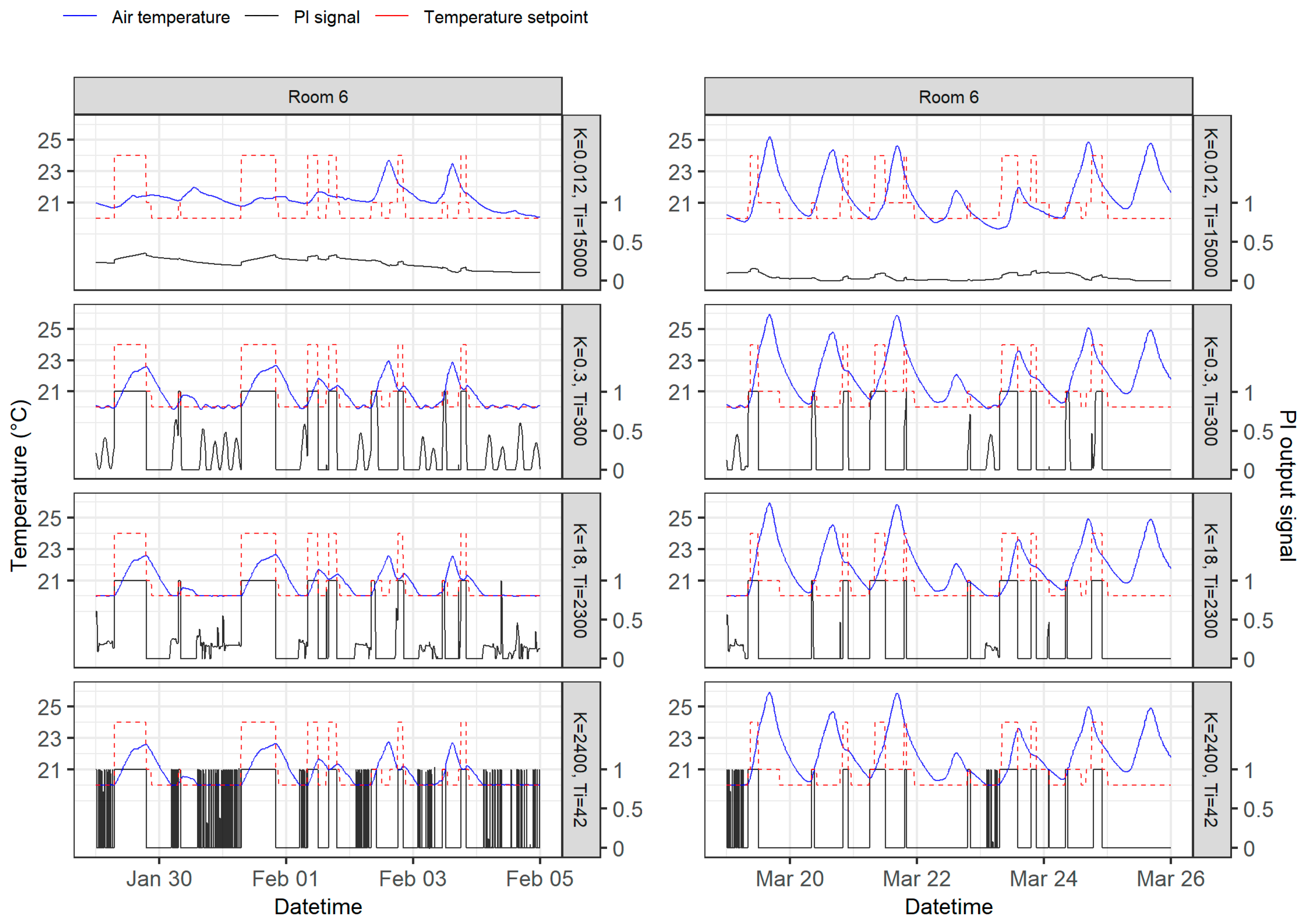
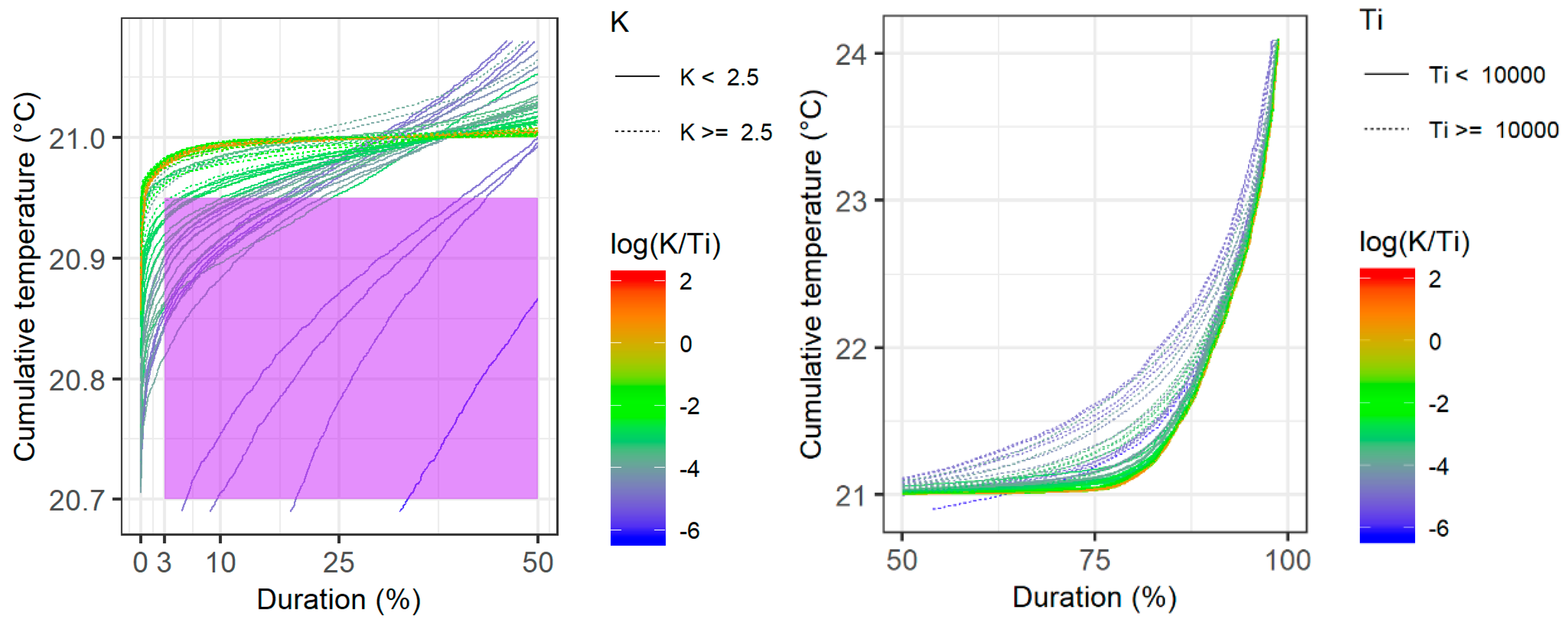
3.3. Setpoint Temperature Tracking and PI Output Signal Behaviour
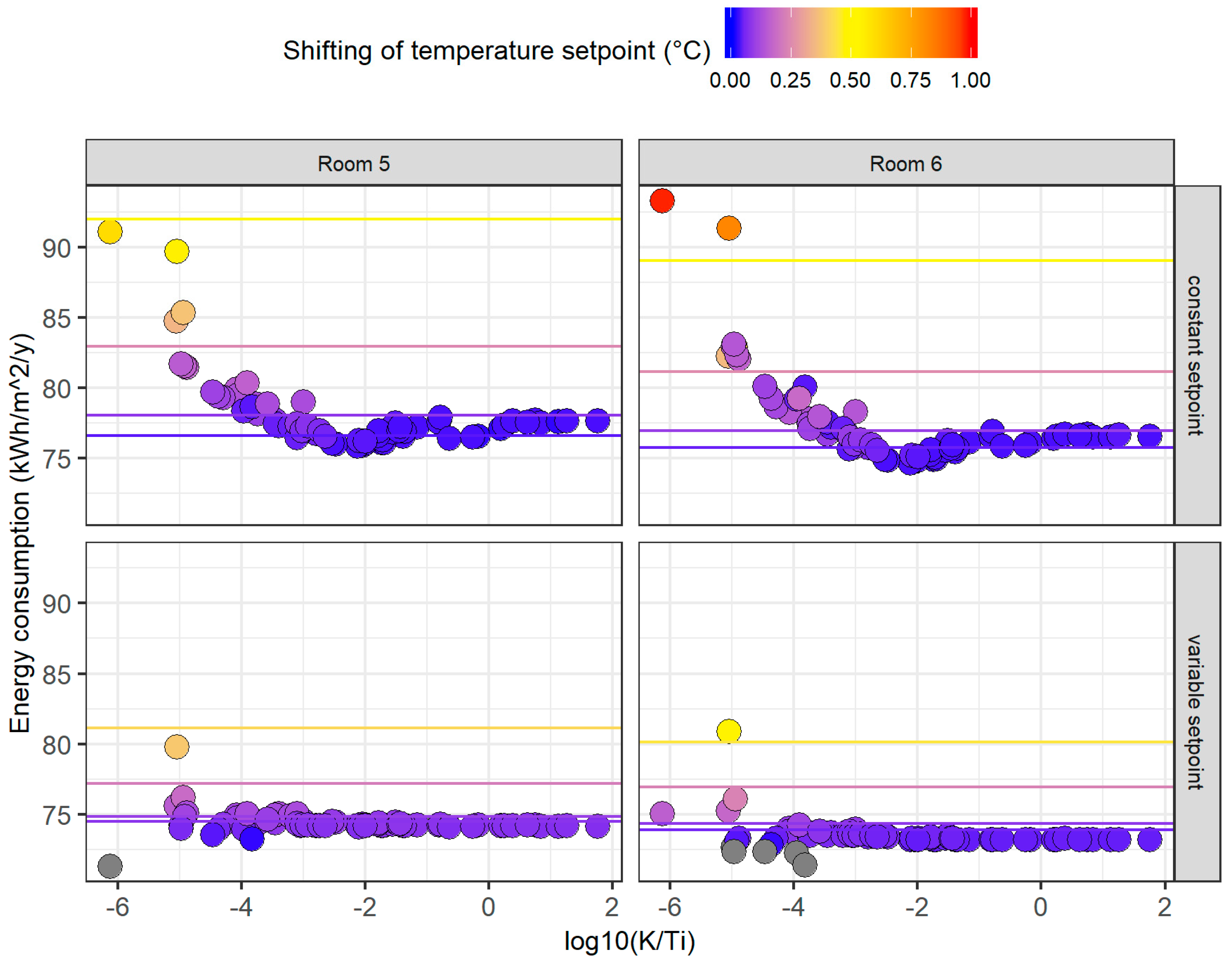
3.4. Setpoint Shifting
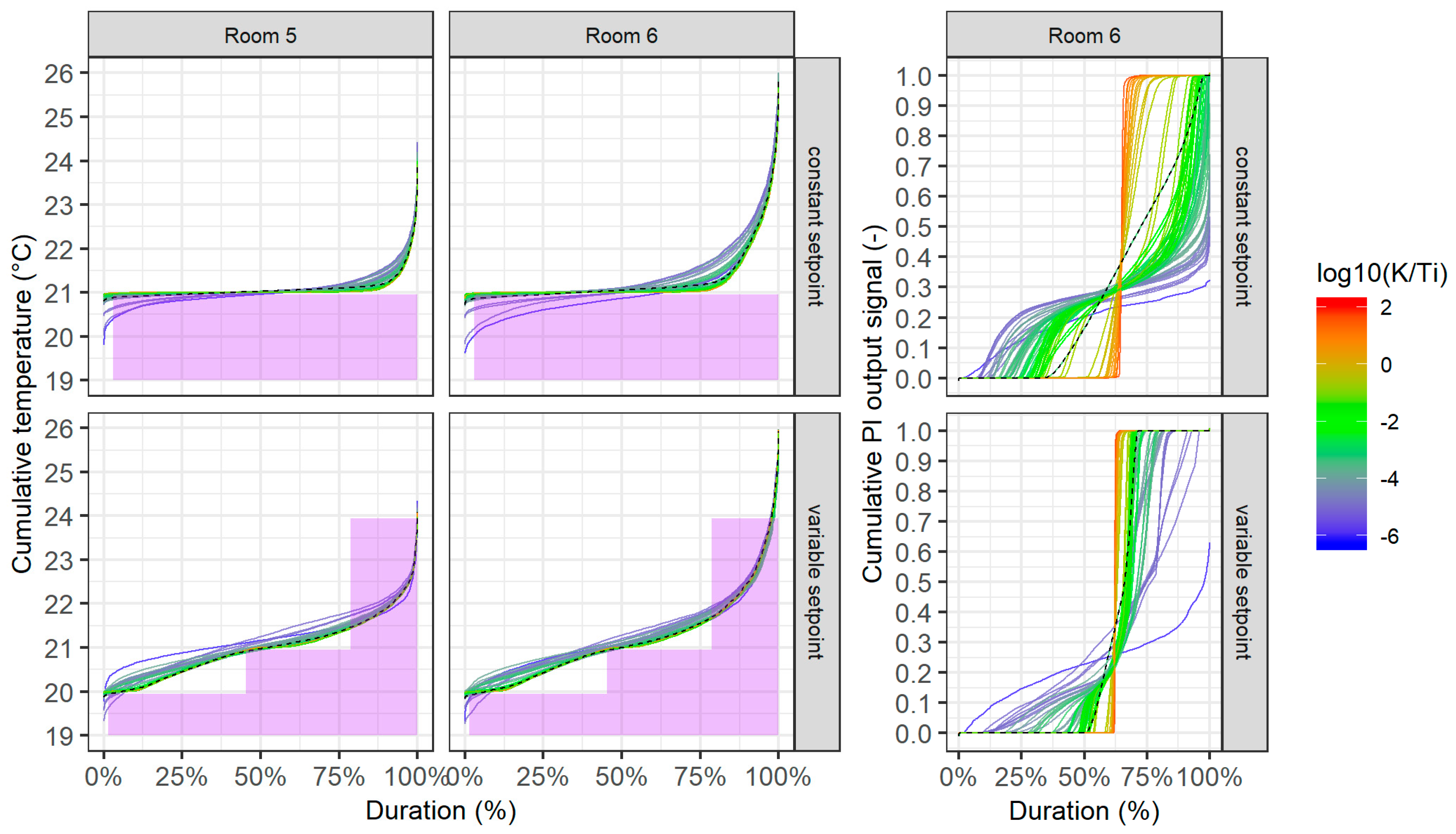
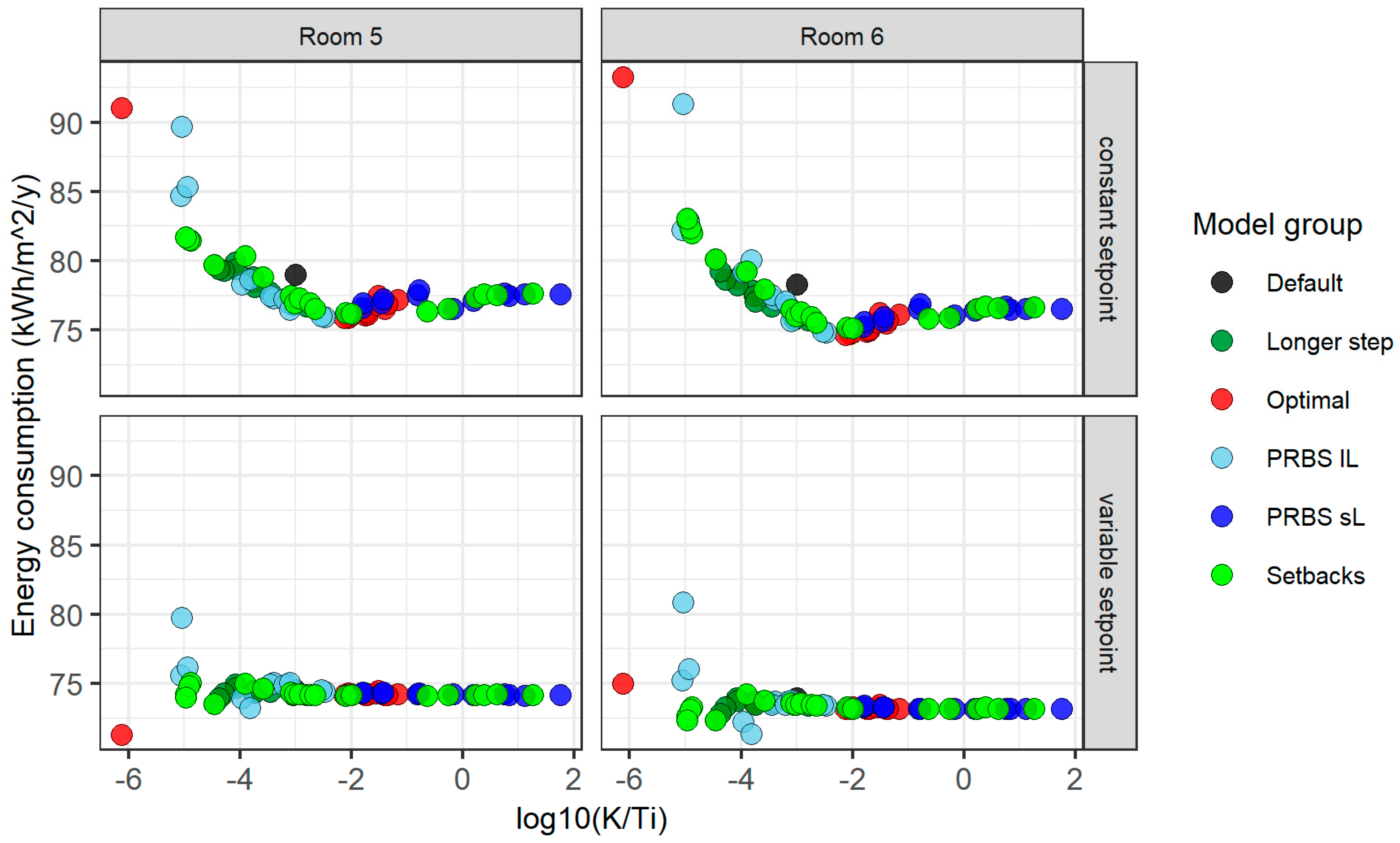
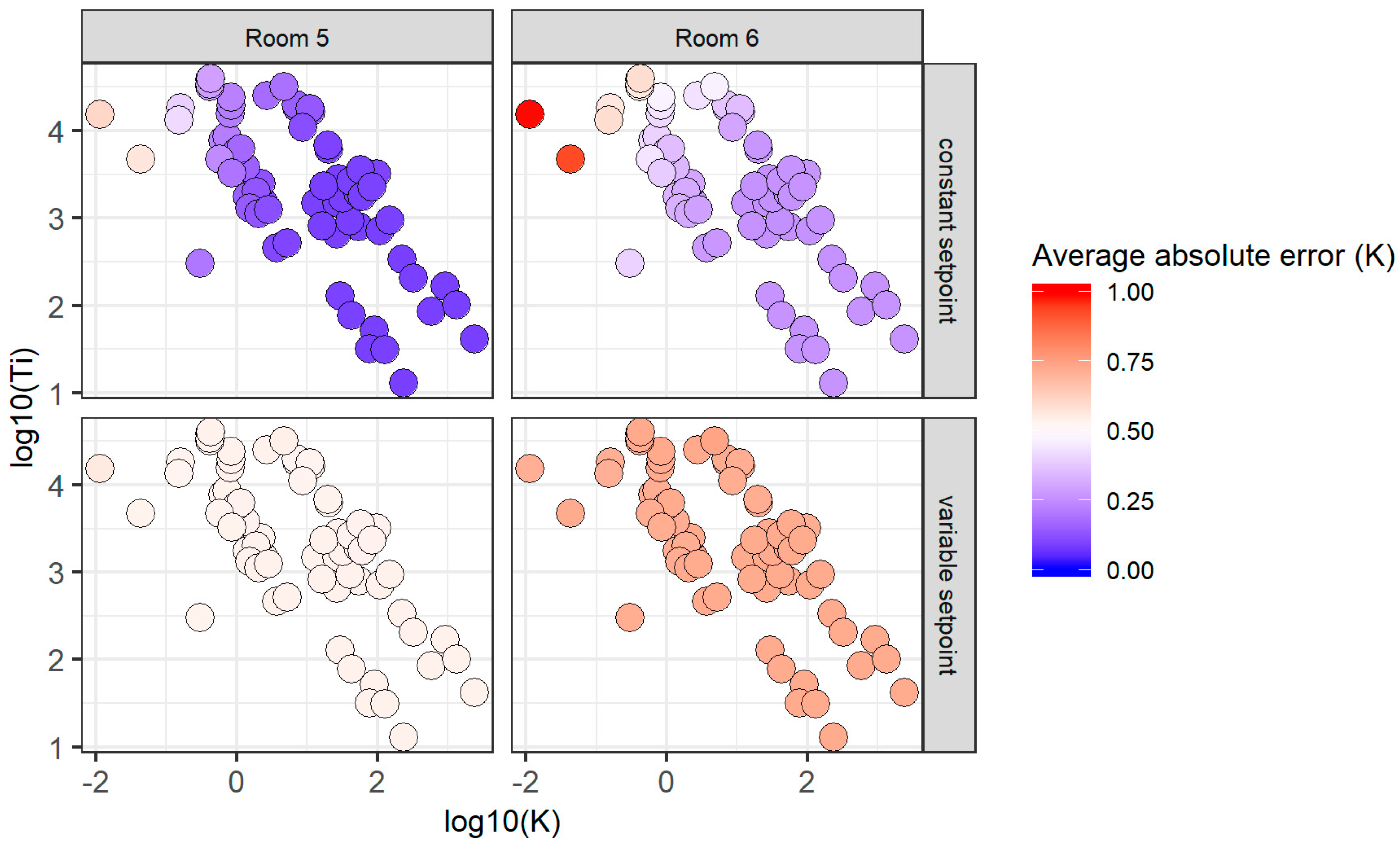
3.5. Energy Performance and Total Setpoint Tracking Accuracy
4. Discussion
5. Conclusions
- For the first time in the scientific literature, it is shown that UFH can operate with determined PI parameters similar to ideal control;
- A performance close to optimal could also be achieved by parameters achieved from shorter tests, e.g., weekend pseudo-random setpoints, and 6- to 24-h setbacks which were shown to be suitable;
- The optimal PI parameters improved the room temperature control accuracy considerably, and that the results show that the UFH PI control with the correct parameters started to work in a predictive fashion and the resulting room temperature curves were practically ideal;
- The optimal PI parameters reduced the energy consumption for heating by up to 9% (7 kWh/m2/year) in comparison with the on–off control (at around 80 kWh/m2/year) and by 5% in comparison with the default PI parameters;
- The variation amplitude of the heating energy needed using different estimated (not random) parameters was more than 15 kWh/m2/year for the constant setpoint, which stresses the importance of having the correct PI parameters;
- The optimal PI parameters included combinations with log10 (K/Ti) between −3 and −1, in these combinations, the proportional gain K ranged from 2 to 100 and the integration time Ti from 500 to 6700 s, and thus higher gain and longer integration time values than are conventionally used are recommended;
- For the variable setpoint, using the PI control had a similar effect to decreasing the dead-band and the variation in the PI parameters did not have a significant further effect on the energy consumption, except for when they were extremely poorly tuned;
- The average absolute error for the air temperatures from the setpoint was well below 0.5 K for the constant setpoints, but above for the variable setpoints.
Author Contributions
Funding
Conflicts of Interest
Appendix A
| K | Ti (s) | Model | Method | Climate | Setpoint | Room | Total Length (Days) |
|---|---|---|---|---|---|---|---|
| 2400 | 42 | 14 | Cohen-Coon | TRY, Jan/Feb week | PRBS | R6 | 7 |
| 235 | 13 | 6 | Cohen-Coon | Const | 1-h setback | equal | 0.25 |
| 1300 | 100 | 14 | SIMC | TRY, Jan/Feb week | PRBS | R6 | 7 |
| 580 | 85 | 13 | Cohen-Coon | TRY, Jan/Feb weekend | PRBS | R6 | 2 |
| 930 | 170 | 14 | AMIGO | TRY, Jan/Feb week | PRBS | R6 | 7 |
| 130 | 31 | 6 | SIMC | Const | 1-h setback | equal | 0.25 |
| 77 | 32 | 5 | Cohen-Coon | Const | 3-h setback | equal | 0.75 |
| 91 | 52 | 6 | AMIGO | Const | 1-h setback | equal | 0.25 |
| 320 | 210 | 13 | SIMC | TRY, Jan/Feb weekend | PRBS | R6 | 2 |
| 230 | 340 | 13 | AMIGO | TRY, Jan/Feb weekend | PRBS | R6 | 2 |
| 43 | 77 | 5 | SIMC | Const | 3-h setback | equal | 0.75 |
| 30 | 130 | 5 | AMIGO | Const | 3-h setback | equal | 0.75 |
| 150 | 940 | 10 | Cohen-Coon | TRY, Jan/Feb week | PRBS | R5 | 7 |
| 110 | 710 | 9 | Cohen-Coon | TRY, Jan/Feb weekend | PRBS | R5 | 2 |
| 1.9 | 2000 | 4 | AMIGO | Const | 6-h setback | equal | 1.5 |
| 2.3 | 2500 | 8 | Cohen-Coon | Actual | 3-day measured | R5 | 3 |
| 2 | 2300 | 7 | Cohen-Coon | Actual | 2-day measured | R5 | 2 |
| 1.4 | 1800 | 2 | AMIGO | Const | 24-h setback | equal | 6 |
| 8.7 | 11,000 | 15 | Cohen-Coon | TRY, March weekend | PRBS | R6 | 2 |
| 11 | 16,000 | 11 | SIMC | TRY, March weekend | PRBS | R5 | 2 |
| 11 | 18,000 | 12 | SIMC | TRY, March week | PRBS | R5 | 7 |
| 7.2 | 18,000 | 11 | AMIGO | TRY, March weekend | PRBS | R5 | 2 |
| 7 | 20,000 | 12 | AMIGO | TRY, March week | PRBS | R5 | 7 |
| 1.3 | 3800 | 1 | SIMC | Const | Ideal step | equal | 60 |
| 0.9 | 3300 | 3 | SIMC | Const | 12-h setback | equal | 3 |
| 1.1 | 6200 | 8 | SIMC | Actual | 3-day measured | R5 | 3 |
| 1 | 5800 | 7 | SIMC | Actual | 2-day measured | R5 | 2 |
| 0.9 | 5300 | 1 | AMIGO | Const | Ideal step | equal | 60 |
| 4.8 | 32,000 | 15 | SIMC | TRY, March weekend | PRBS | R6 | 2 |
| 0.6 | 4700 | 3 | AMIGO | Const | 12-h setback | equal | 3 |
| 2.7 | 25000 | 15 | AMIGO | TRY, March weekend | PRBS | R6 | 2 |
| 0.7 | 8500 | 8 | AMIGO | Actual | 3-day measured | R5 | 3 |
| 0.6 | 7700 | 7 | AMIGO | Actual | 2-day measured | R5 | 2 |
| 0.81 | 16,000 | 1 | tuned in Matlab | Const | Ideal step | equal | 60 |
| 0.83 | 20,000 | 7 | tuned in Matlab | Actual | 2-day measured | R5 | 2 |
| 0.82 | 24,000 | 8 | tuned in Matlab | Actual | 3-day measured | R5 | 3 |
| 0.82 | 24,000 | 2 | tuned in Matlab | Const | 24-h setback | equal | 6 |
| 0.41 | 32,000 | 3 | tuned in Matlab | Const | 12-h setback | equal | 3 |
| 0.41 | 34,000 | 5 | tuned in Matlab | Const | 3-h setback | equal | 0.75 |
| 0.15 | 13,000 | 16 | Cohen-Coon | TRY, March week | PRBS | R6 | 7 |
| 0.43 | 40,000 | 6 | tuned in Matlab | Const | 1-h setback | equal | 0.25 |
| 0.41 | 39,000 | 4 | tuned in Matlab | Const | 6-h setback | equal | 1.5 |
| 0.043 | 4700 | 16 | SIMC | TRY, March week | PRBS | R6 | 7 |
| 0.16 | 18,000 | 16 | AMIGO | TRY, March week | PRBS | R6 | 7 |
| 0.012 | 15,000 | - | genopt | TRY, March week | variable | R6 | Inf |
References
- Salata, F.; Golasi, I.; Domestico, U.; Banditelli, M.; Basso, G.L.; Nastasi, B.; Vollaro, A.D.L. Heading towards the nZEB through CHP+HP systems. A comparison between retrofit solutions able to increase the energy performance for the heating and domestic hot water production in residential buildings. Energy Convers. Manag. 2017, 138, 61–76. [Google Scholar] [CrossRef]
- Becchio, C.; Dabbene, P.; Fabrizio, E.; Monetti, V.; Filippi, M. Cost optimality assessment of a single family house: Building and technical systems solutions for the nZEB target. Energy Build. 2015, 90, 173–187. [Google Scholar] [CrossRef]
- Péan, T.; Salom, J.; Castello, R.C. Review of control strategies for improving the energy flexibility provided by heat pump systems in buildings. J. Process. Control. 2019, 74, 35–49. [Google Scholar] [CrossRef]
- EU Buildings Factsheets. Available online: https://ec.europa.eu/energy/eu-buildings-factsheets_en (accessed on 20 April 2020).
- Thonipara, A.; Runst, P.; Ochsner, C.; Bizer, K. Energy efficiency of residential buildings in the European Union—An exploratory analysis of cross-country consumption patterns. Energy Policy 2019, 129, 1156–1167. [Google Scholar] [CrossRef]
- Kummert, M.; Andre, P.; Nicolas, J. Optimal heating control in a passive solar commercial building. Sol. Energy 2001, 69, 103–116. [Google Scholar] [CrossRef]
- Wolisz, H.; Kull, T.M.; Müller, D.; Kurnitski, J. Self-learning model predictive control for dynamic activation of structural thermal mass in residential buildings. Energy Build. 2020, 207, 109542. [Google Scholar] [CrossRef]
- Astrom, K.; Hägglund, T. The future of PID control. Control. Eng. Pr. 2001, 9, 1163–1175. [Google Scholar] [CrossRef]
- Dounis, A.I.; Caraiscos, C. Advanced control systems engineering for energy and comfort management in a building environment—A review. Renew. Sustain. Energy Rev. 2009, 13, 1246–1261. [Google Scholar] [CrossRef]
- Royapoor, M.; Antony, A.; Roskilly, T. A review of building climate and plant controls, and a survey of industry perspectives. Energy Build. 2018, 158, 453–465. [Google Scholar] [CrossRef]
- Salsbury, T.I. A SURVEY OF CONTROL TECHNOLOGIES IN THE BUILDING AUTOMATION INDUSTRY. IFAC Proc. Vol. 2005, 38, 90–100. [Google Scholar] [CrossRef]
- Rodríguez-Rodríguez, I.; González-Vidal, A.; González, A.R.; Izquierdo, M.A.Z. Commissioning of the Controlled and Automatized Testing Facility for Human Behavior and Control (CASITA). Sensors 2018, 18, 2829. [Google Scholar] [CrossRef] [PubMed]
- Seidel, S.; Haufe, J.; Majetta, K.; Blochwitz, T.; Liebold, E.; Hintzen, U.; Klostermann, V.; Clauß, C. Modelica based Design and Optimisation of Control Systems for Solar Heat Systems and Low Energy Buildings. In Proceedings of the 11th International Modelica Conference, Versailles, France, 21–23 September 2015; Volume 118, pp. 401–410. [Google Scholar]
- Astrom, K.; Hägglund, T.; Wallenborg, A. Automatic tuning of a digital controller. In Proceedings of the 4th IFAC Symposium on Adaptive Systems in Control and Signal, Grenoble, France, 1–3 July 1992; Volume 25, pp. 285–290. [Google Scholar] [CrossRef]
- Wang, Y.-G.; Shi, Z.-G.; Cai, W.-J. PID autotuner and its application in HVAC systems. In Proceedings of the 2001 American Control Conference. (Cat. No.01CH37148), Arlington, VA, USA, 25–27 June 2001; pp. 2192–2196. [Google Scholar] [CrossRef]
- Bi, Q.; Cai, W.-J.; Wang, Q.-G.; Hang, C.-C.; Lee, E.-L.; Sun, Y.; Liu, K.-D.; Zhang, Y.; Zou, B. Advanced controller auto-tuning and its application in HVAC systems. Control. Eng. Pr. 2000, 8, 633–644. [Google Scholar] [CrossRef]
- Ferrarini, L.; Rastegarpour, S.; Petretti, A. An Adaptive Underfloor Heating Control with External Temperature Compensation. In Proceedings of the 14th International Conference on Informatics in Control, Automation and Robotics, Madrid, Spain, 26–28 July 2017; pp. 629–636. [Google Scholar] [CrossRef]
- Curtiss, P.S. Examples of Neural Networks Used for Building System Control and Energy Management. ASHRAE Trans. 1997, 103, 909. [Google Scholar]
- Hasan, A.; Kurnitski, J.; Jokiranta, K. A combined low temperature water heating system consisting of radiators and floor heating. Energy Build. 2009, 41, 470–479. [Google Scholar] [CrossRef]
- Võsa, K.-V.; Ferrantelli, A.; Kurnitski, J. Annual performance analysis of heat emission in radiator and underfloor heating systems in the European reference room. E3S Web Conf. 2019, 111, 111. [Google Scholar] [CrossRef]
- Kukolj, D.D.; Kuzmanović, S.B.; Levi, E. Design of a PID-like compound fuzzy logic controller. Eng. Appl. Artif. Intell. 2001, 14, 785–803. [Google Scholar] [CrossRef]
- Ostermeier, M.; Müller, J. Automated investigation, evaluation and optimisation of simple heating circuits in building automation. E3S Web Conf. 2019, 111, 111. [Google Scholar] [CrossRef]
- Fiducioso, M.; Curi, S.; Schumacher, B.; Gwerder, M.; Krause, A. Safe Contextual Bayesian Optimization for Sustainable Room Temperature PID Control Tuning. In Proceedings of the Twenty-Eighth International Joint Conference on Artificial Intelligence, Macao, 10–16 August 2019. [Google Scholar] [CrossRef]
- Nägele, F.; Kasper, T.; Girod, B. Turning up the heat on obsolete thermostats: A simulation-based comparison of intelligent control approaches for residential heating systems. Renew. Sustain. Energy Rev. 2017, 75, 1254–1268. [Google Scholar] [CrossRef]
- Maivel, M.; Ferrantelli, A.; Kurnitski, J. Experimental determination of radiator, underfloor and air heating emission losses due to stratification and operative temperature variations. Energy Build. 2018, 166, 220–228. [Google Scholar] [CrossRef]
- Võsa, K.-V.; Ferrantelli, A.; Kurnitski, J. Experimental study of radiator, underfloor, ceiling and air heater systems heat emission performance in TUT nZEB test facility. E3S Web Conf. 2019, 111, 111. [Google Scholar] [CrossRef]
- Kull, T.M.; Thalfeldt, M.; Kurnitski, J. Estimating time constants for underfloor heating control. J. Phys. Conf. Ser. 2019, 1343. [Google Scholar] [CrossRef]
- IDA ICE 4.8 SP1, Expert Edition. 2019. Available online: https://www.equa.se/en/ida-ice (accessed on 20 April 2020).
- Kalamees, T.; Kurnitski, J. Estonian test reference year for energy calculations. Proc. Est. Acad. Sci. Eng. 2006, 12, 40–58. [Google Scholar]
- Ljung, L. System Identification Toolbox: User’s Guide; MathWorks Incorporated: Natick, MA, USA, 1995. [Google Scholar]
- Wetter, M. Generic Optimization Program User Manual Version 3.0.0; Lawrence Berkeley National Lab. (LBNL): Berkeley, CA, USA, 2009; pp. 1–108. [Google Scholar] [CrossRef]
- Åström, K.J.; Hägglund, T. Advanced PID Control; ISA-The Instrumentation, Systems, and Automation Society: Research Triangle Park, NC, USA, 2006; Volume 461. [Google Scholar]
- Nord Pool. Available online: https://www.nordpoolgroup.com/historical-market-data/ (accessed on 20 April 2020).
- Clauß, J.; Stinner, S.; Sartori, I.; Georges, L. Predictive rule-based control to activate the energy flexibility of Norwegian residential buildings: Case of an air-source heat pump and direct electric heating. Appl. Energy 2019, 237, 500–518. [Google Scholar] [CrossRef]
- EN 16798-2, Energy Performance of Buildings—Part 2: Indoor Environmental Input Parameters for Design and Assessment of Energy Performance of Buildings Addressing Indoor Air Quality, Thermal Environment, Lighting and Acoustics; EPB Center: AN Rotterdam, The Netherlands, 2019.
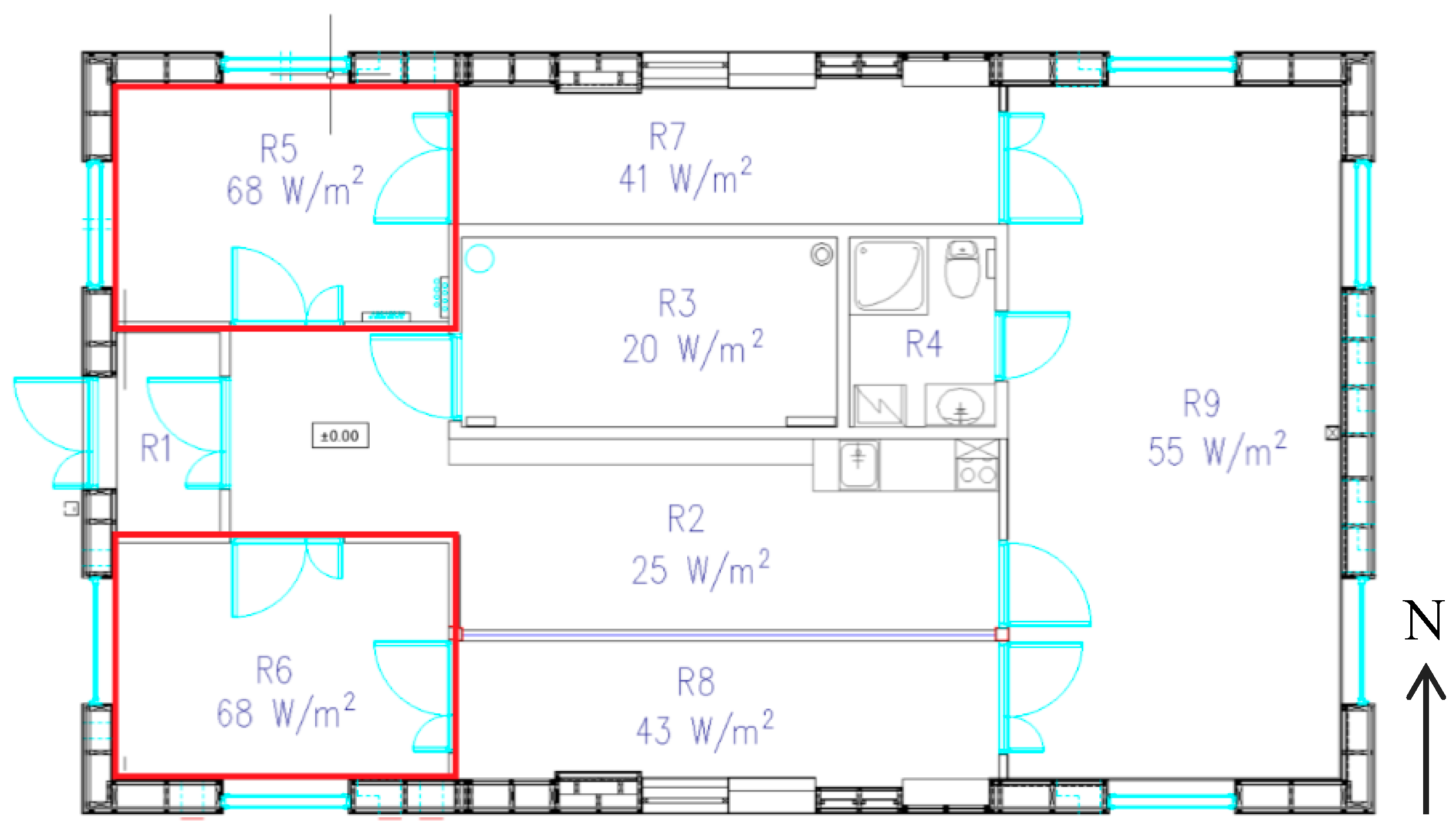

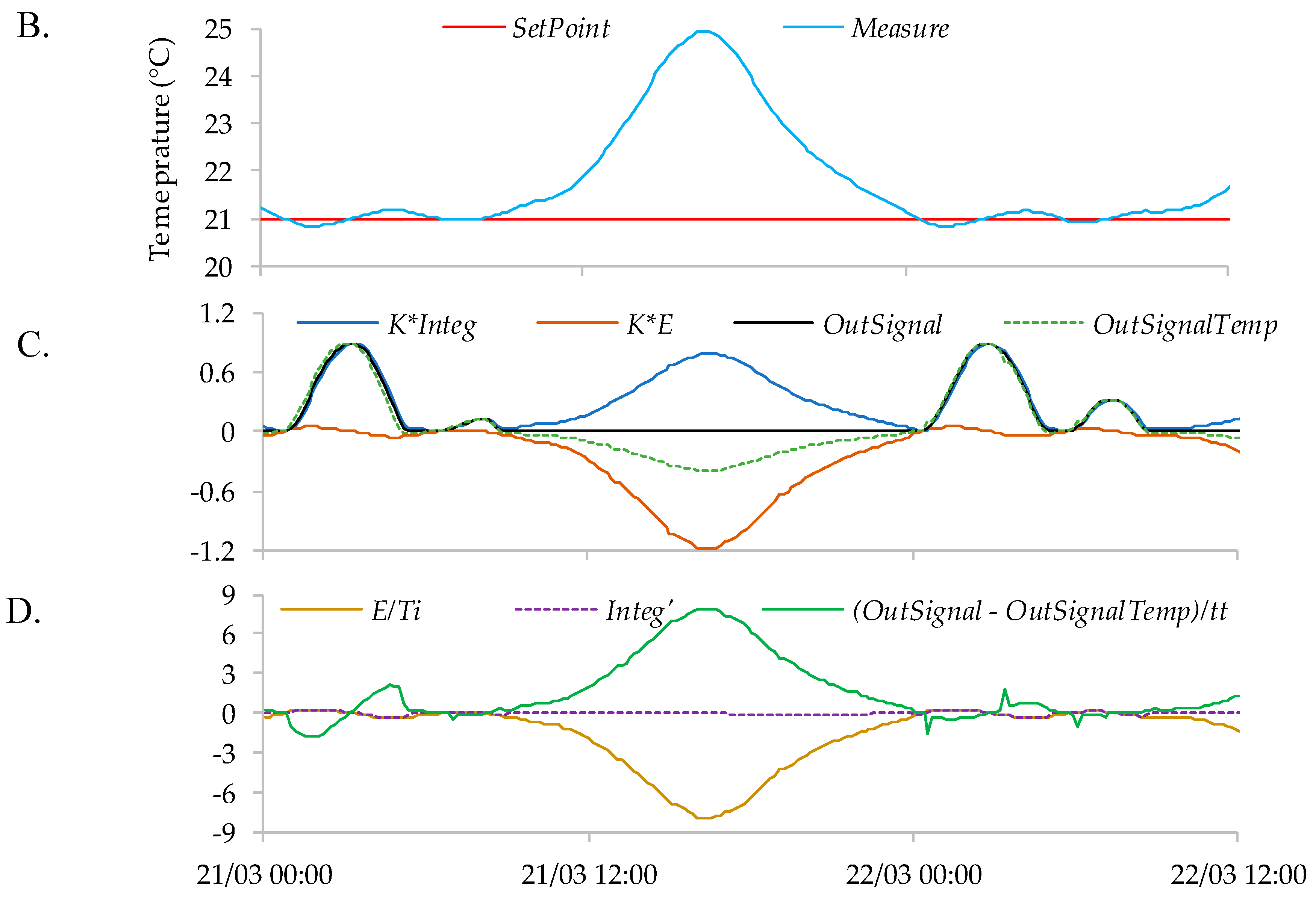
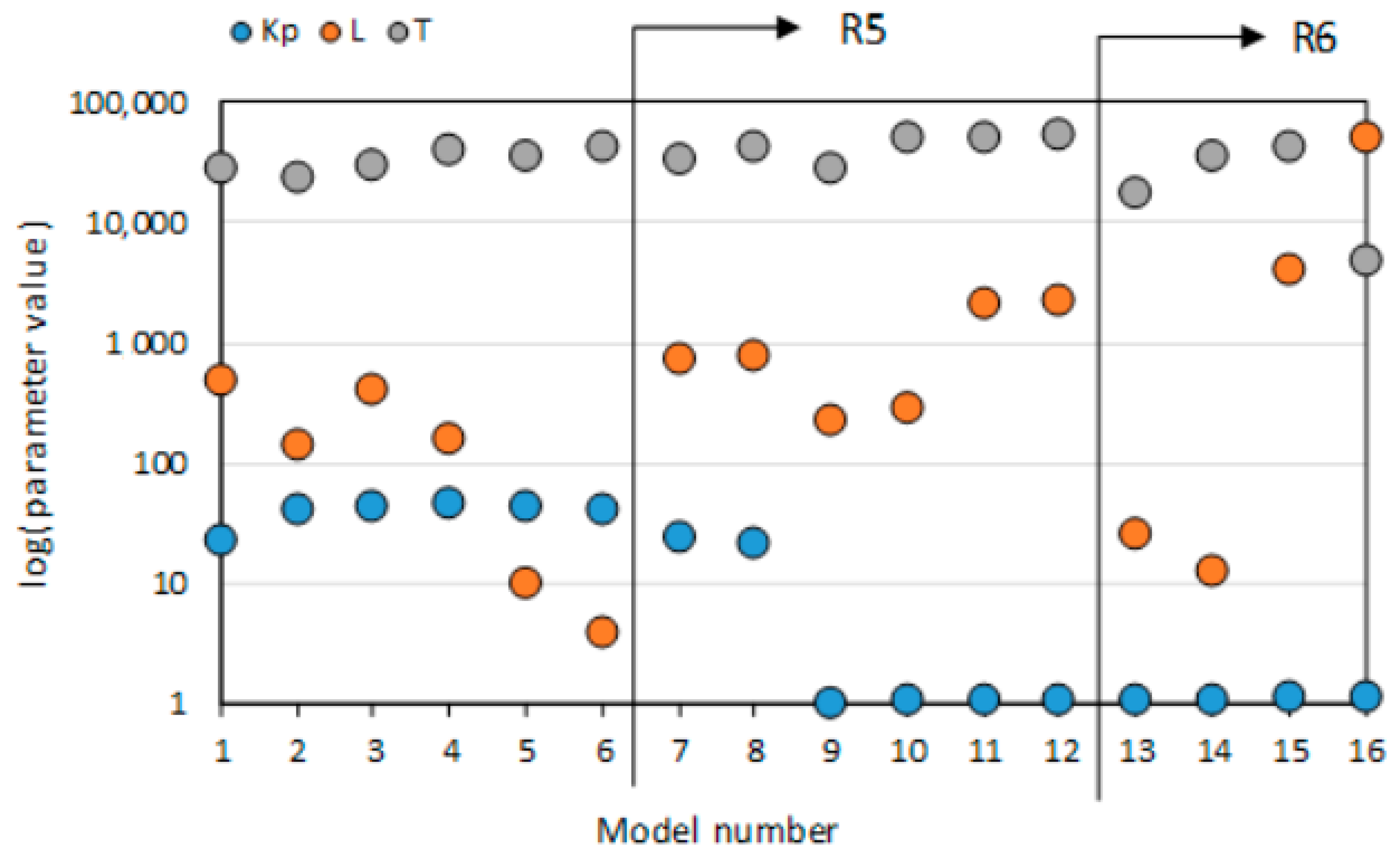
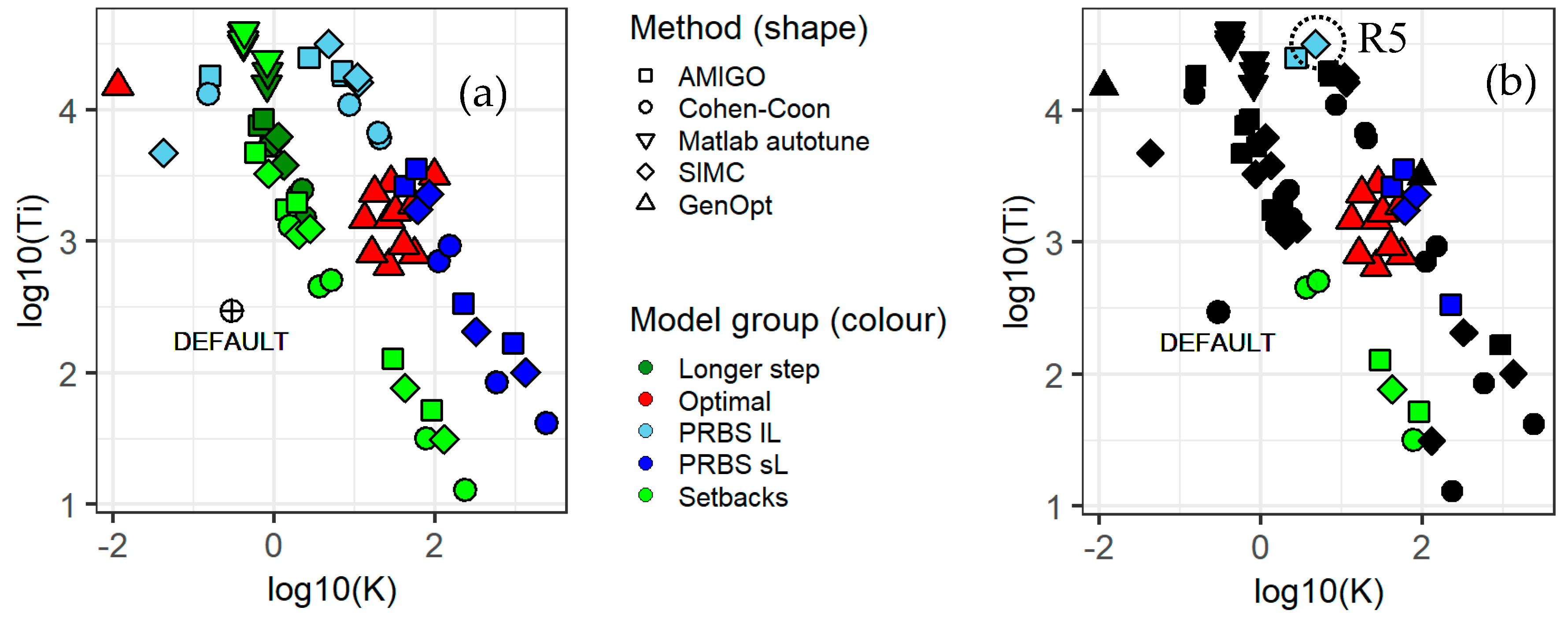
| Climate | Setpoint | Room | Source | Estimation Basis | Method |
|---|---|---|---|---|---|
| Actual | 2-3-day (long) setbacks | R5 | Measured | Simplified model | Calculation methods + tuning in Matlab |
| Constant | Shorter setbacks | R5/R6 (equal) | Simulated | Simplified model | Calculation methods + tuning in Matlab |
| Constant | Infinite/ideal step | R5/R6 (equal) | Simulated | Simplified model | Calculation methods + tuning in Matlab |
| Estonian TRY | PRBS | R5 and R6 | Simulated | Simplified model | Calculation methods |
| Estonian TRY | Constant | R5 and R6 | Simulated | Optimization | GenOpt |
| Estonian TRY | Variable (price-based) | R5 and R6 | Simulated | Optimization | GenOpt |
| Based on Room | Model Number | Model Group | Model Source | Kp | L (Seconds) | T (Seconds) |
|---|---|---|---|---|---|---|
| R5 & R6 | 1 | Longer step | Ideal step | 21.842 | 476 | 27,892 |
| 2 | Setbacks | 24-h setback at 0 ℃ | 41.063 | 141.12 | 23,652 | |
| 3 | Setbacks | 12-h setback at 0 ℃ | 42.649 | 410.58 | 30,141 | |
| 4 | Setbacks | 6-h setback at 0 ℃ | 44.717 | 156.96 | 38,648 | |
| 5 | Setbacks | 3-h setback at 0 ℃ | 42.664 | 9.66 | 35,191 | |
| 6 | Setbacks | 1-h setback at 0 ℃ | 41.446 | 3.9 | 42,130 | |
| R5 | 7 | Longer step | 2-day measured setback | 24.256 | 720 | 33,720 |
| 8 | Longer step | 3-day measured setback | 21.472 | 780 | 41,820 | |
| 9 | PRBS sL | 2-day PRBS in February | 1.0123 | 218.4 | 27,152 | |
| 10 | PRBS sL | 1-week PRBS in February | 1.03 | 286.8 | 50,122 | |
| 11 | PRBS lL | 2-day PRBS in March | 1.0555 | 2034 | 48,950 | |
| 12 | PRBS lL | 1-week PRBS in March | 1.0599 | 2226.6 | 51,845 | |
| R6 | 13 | PRBS sL | 2-day PRBS in February | 1.03 | 25.8 | 17,237 |
| 14 | PRBS sL | 1-week PRBS in February | 1.042 | 12.6 | 34,930 | |
| 15 | PRBS lL | 2-day PRBS in March | 1.0973 | 3996 | 41,990 | |
| 16 | PRBS lL | 1-week PRBS in March | 1.1035 | 50,084 | 4737 |
| K | Ti | Model | Method | Climate | Setpoint | Room | Total Length |
|---|---|---|---|---|---|---|---|
| 18 | 2300 | - | GenOpt | TRY, Jan/Feb week | variable | R6 | Inf |
| 13 | 1500 | - | GenOpt | TRY, March week | constant | R5 | Inf |
| 28 | 2800 | - | GenOpt | TRY, March week | variable | R5 | Inf |
| 21 | 6200 | 11 | Cohen-Coon | TRY, March weekend | PRBS | R5 | 2 days |
| 20 | 6700 | 12 | Cohen-Coon | TRY, March week | PRBS | R5 | 7 days |
| 27 | 1500 | - | GenOpt | TRY, Jan/Feb week | constant | R5 | Inf |
| 16 | 820 | - | GenOpt | TRY, Jan/Feb week | constant | R6 | Inf |
| 32 | 1700 | - | GenOpt | TRY, Jan/Feb week | variable | R5 | Inf |
| 5.2 | 510 | 4 | Cohen-Coon | Const | 6-h setback | equal | 1.5 days |
| 3.7 | 460 | 2 | Cohen-Coon | Const | 24-h setback | equal | 6 days |
| 42 | 2700 | 9 | AMIGO | TRY, Jan/Feb weekend | PRBS | equal | 2 days |
| 27 | 650 | - | GenOpt | TRY, March week | constant | R6 | Inf |
| 54 | 1900 | - | GenOpt | TRY, heating period | variable | R5 | Inf |
| 2.8 | 1300 | 4 | SIMC | Const | 6-h setback | equal | 1.5 days |
| 59 | 3600 | 10 | AMIGO | TRY, Jan/Feb week | PRBS | R5 | 7 days |
| 61 | 1800 | 9 | SIMC | TRY, Jan/Feb weekend | PRBS | R5 | 2 days |
| 41 | 930 | - | GenOpt | TRY, heating period | constant | R6 | Inf |
| 2.4 | 1500 | 1 | Cohen-Coon | Const | Ideal step | equal | 60 days |
| 2.0 | 1100 | 2 | SIMC | Const | 24-h setback | equal | 6 days |
| 85 | 2300 | 10 | SIMC | TRY, Jan/Feb week | PRBS | R5 | 7 days |
| 55 | 800 | - | GenOpt | TRY, heating period | constant | R5 | Inf |
| 98 | 3200 | - | GenOpt | TRY, heating period | variable | R6 | Inf |
| 1.6 | 1300 | 3 | Cohen-Coon | Const | 12-h setback | equal | 3 days |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kull, T.M.; Thalfeldt, M.; Kurnitski, J. PI Parameter Influence on Underfloor Heating Energy Consumption and Setpoint Tracking in nZEBs. Energies 2020, 13, 2068. https://doi.org/10.3390/en13082068
Kull TM, Thalfeldt M, Kurnitski J. PI Parameter Influence on Underfloor Heating Energy Consumption and Setpoint Tracking in nZEBs. Energies. 2020; 13(8):2068. https://doi.org/10.3390/en13082068
Chicago/Turabian StyleKull, Tuule Mall, Martin Thalfeldt, and Jarek Kurnitski. 2020. "PI Parameter Influence on Underfloor Heating Energy Consumption and Setpoint Tracking in nZEBs" Energies 13, no. 8: 2068. https://doi.org/10.3390/en13082068
APA StyleKull, T. M., Thalfeldt, M., & Kurnitski, J. (2020). PI Parameter Influence on Underfloor Heating Energy Consumption and Setpoint Tracking in nZEBs. Energies, 13(8), 2068. https://doi.org/10.3390/en13082068






