Design Method of Dual Active Bridge Converters for Photovoltaic Systems with High Voltage Gain

Abstract

In this paper, a design method for a photovoltaic system based on a dual active bridge converter and a photovoltaic module is proposed. The method is supported by analytical results and theoretical predictions, which are confirmed with circuital simulations. The analytical development, the theoretical predictions, and the validation through circuital simulations, are the main contributions of the paper. The dual active bridge converter is selected due to its high efficiency, high input and output voltages range, and high voltage-conversion ratio, which enables the interface of low-voltage photovoltaic modules with a high-voltage dc bus, such as the input of a micro-inverter. To propose the design method, the circuital analysis of the dual active bridge converter is performed to describe the general waveforms derived from the circuit behavior. Then, the analysis of the dual active bridge converter, interacting with a photovoltaic module driven by a maximum power point tracking algorithm, is used to establish the mathematical expressions for the leakage inductor current, the photovoltaic current, and the range of operation for the phase shift. The design method also provides analytical equations for both the high-frequency transformer equivalent leakage inductor and the photovoltaic side capacitor. The design method is validated through detailed circuital simulations of the whole photovoltaic system, which confirm that the maximum power of the photovoltaic module can be extracted with a correct design of the dual active bridge converter. Also, the theoretical restrictions of the photovoltaic system, such as the photovoltaic voltage and power ripples, are fulfilled with errors lower than 2% with respect to the circuital simulations. Finally, the simulation results also demonstrate that the maximum power point for different environmental conditions is reached, optimizing the phase shift factor with a maximum power point tracking algorithm.

1. Introduction

Fossil fuels have been widely used to supply the increased power consumption caused by the growing of world population. However, fossil fuels are highly polluting and non-renewable sources. Therefore, renewable energy sources are an alternative to supply the power demand and to reduce the environment pollution caused by the generation process. Photovoltaic (PV) systems are one of the most used technologies for power generation based on renewable energy, in fact, in 2017 was installed more power capability in PV systems than in fossil fuels; however, the fossil fuels remain as the main power source [1,2].

PV energy conversion systems are based on PV panels, which are used to convert solar energy into electrical energy. The energy produced by a PV panel depends on the environmental conditions, i.e., irradiation and temperature of the module, therefore a power converter is required to extract the maximum energy available. Such a power converter regulates the PV voltage or current to reach the maximum power point (MPP) of the module, and at the same time, the converter interfaces the PV module with the load. In commercial PV installations it is common that the voltage and power provided by a single PV module are lower than the voltage and power required by the load. Hence, multiple PV modules are connected in different series and parallel configurations to meet the load requirements [3,4]. Also, different power converters topologies are used to adapt the PV voltage to the load requirement; those converters must exhibit high efficiency and, in some cases, high voltage-conversion ratio to feed the loads [5,6]. For example, standalone applications designed for pumping and lighting systems, installed far from the generating point, need to rise the supply voltages to reduce transmission losses [7,8].

To meet the load voltage requirement, series connections between several PV modules are reported in the literature; this solution has a main drawback: if there is a non-uniform irradiation pattern over the PV array, panels with lower irradiation heat up due to the higher currents in the series connection, which damages the modules; that phenomena is known as mismatching [3]. To mitigate that problem, bypass diodes are connected in antiparallel with each module to provide an additional path to the current. However, the activation of those bypass diodes forces the occurrence of local MPP on the power curve of the array, and the bypassed modules operate with small negative voltages, hence consuming power [9]. Moreover, when a power converter is connected to the PV array to perform the maximum power point tracking (MPPT), the MPPT algorithm could be trapped into a local MPP, which significantly reduces the power production. Finally, the power converter ratings must be high enough to support the voltage and current of the whole PV array, which means high current and voltage stresses on the converter elements.

One approach reported literature to address that problem is the use of complex MPPT algorithms designed to find the global MPP, but that solution require high computational cost and high stresses remains on the converter devices [10,11,12]. Another approach to reduce the mismatching impact is known as distributed MPPT (DMPPT), which is formed by DMPPT units [13]. A DMPPT unit (DMMPT-U) is formed by one PV module and one DC-DC converter, which is in charge of extracting the maximum power from the module. To reach high voltage, a DMPPT array is commonly formed by connecting DMPPT-U in series, in which the output voltage depends on the number of unit in the array, then the classical boost converter can be used as DMPPT-U due to the low voltage gain and high efficiency provided. However, if a single DMPPT-U is damaged, the complete DMPPT array could be disconnected. Moreover, under mismatching conditions the output voltage of a DMPPT-U depends on the relation among all the modules power, where the module with the highest power exhibits the highest output voltage, which could cause damages due to overvoltage conditions. In addition, transients on a single DMPPT-U are translated to the other DMPPT-Us, thus the PV voltage of the whole PV modules will change momentarily causing deviation from the MPPs [14,15].

In parallel-connected DMPPT-Us, the power production of the array is not critically dependent of a single unit, and a plug and play system can be developed. The main restriction of this solution is the high voltage gain required for the DC-DC converter in the DMPPT-U, which must also provide high efficiency. For PV systems connected to AC grids, DMPPT parallel arrays are typically implemented using micro-inverters, which is a two-stage converter with the general scheme presented in Figure 1: the first stage is a DC-DC converter that performs the MPPT on the PV module and rise the voltage to the level required by the second stage. The second stage is a grid-connected inverter with both power factor and input voltage controllers [16,17]; and the classical inverters used in this stage require a DC input voltage higher than the peak voltage of the AC grid [7,18,19].

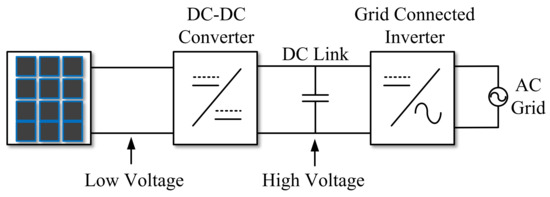
Figure 1. Double-stage PV system with grid connection.

Therefore, considering that many PV applications require converters with high voltage-conversion ratio to supply the load requirements, different converter topologies have been proposed in the literature. The boost converter is the most widely adopted for PV applications, but efficiency is drastically reduced for high voltage-conversion ratios [6,16,20]. The cascade connection of converters with low voltage-conversion ratios is also proposed, but this solution also affects the energy conversion efficiency [19]. Another approach is to use non-isolated topologies with high voltage-conversion ratio for PV applications; this is the case of the three-phase EDR boost converter reported in [17], the dual boost converter and high-gain single-stage boosting converter reported in [19], the coupled-inductor-based converter reported in [21], the Cuk-Derived Transformerless converter described in [22], among others. The main drawback of those solutions is the use of several inductors and capacitors, which reduce both power density and efficiency. Other approach consist of using converters with galvanic isolation [14,16,23,24,25,26,27,28], where the main concerns are the voltage and current stress on the power devices and soft switching capability, but for a well-designed isolated converter, high efficiency and voltage-conversion-ratio are achievable with low stress on the switching devices [29].

The dual active bridge (DAB) converter is one of the most promising topologies for PV applications because it provides galvanic isolation, which decouples the source and load grounds improving the safety of the PV installation [30]. Moreover, the DAB converter could provide a high voltage-conversion ratio based on the transformer turns ratio, and soft switching is achievable to reduce voltage and current stress on the switching devices, providing also high power density due to the use of a high-frequency transformer (HFT) [23,31,32,33]. In the literature, the DAB converter has been used in battery energy storage systems (BESS) [34,35,36], solid-state transformers [37,38,39] and fuel cell applications [40]. Concerning PV systems, the DAB converter has been used in [39,41,42,43,44,45,46,47,48] to interface PV arrays in series connection, but the high voltage-conversion ratio capability has not been exploited in those works. Moreover, although many design considerations have been provided for the DAB converter [32,40,49], there is not reported a design method for a PV system based on the DAB converter. For instance, the work reported in [45] considers a PV array feeding a DC bus through a DAB converter. That work presents modeling and control design procedures aimed at regulating the output voltage, but the converter design for the PV applications is not addressed. The work reported in [39] presents a modified version of the DAB converter for PV applications, focusing on a control design to regulate the DC bus voltage. In that work it is considered an additional boost converter connected between the PV source and the DAB converter which is used to perform the MPPT operation over the PV module, which introduces additional costs and complexity. Moreover, the transistors on the bridge at the load side of the DAB converter are replaced by diodes to avoid bidirectionality, but no converter behavior analysis or design procedure are presented. On the contrary, the work reported in [46] provides a procedure to select both the turns ratio and leakage inductor value of the HFT based on the maximum power of the system. However, such a solution does not take into account the effect of the non-linear behavior of the photovoltaic module on the converter design; instead, the authors model the PV source using an ideal DC voltage source, which is not accurate. In the same way, the work reported in [50] proposes the use a modified DAB converter to perform the MPPT control on a PV array. Such a modified topology does not consider a capacitor at the input of the converter, and it considers a passive filter and an inverter at the output. That work provides a guide to estimate the turns ratio and leakage inductor value of the HFT, but the behavior of the PV module is not taken into account for the selection of the parameters, and the expressions proposed for the design are not explained nor validated. Likewise the authors of [43] use a DAB converter with a three-winding HFT to extract the power from a PV array, where an MPPT algorithm and a PI controller regulate the panel voltage. Although that work describes some considerations for selecting the turns ratio and leakage inductor of the HFT, based on the maximum and minimum array voltages and zero voltage switching (ZVS) operating conditions, it does not take into account the PV model for the design and selection of the converter parameters. Finally, the work reported in [41] proposes a PV system based on a DAB converter controlled by an MPPT algorithm and a PI controller, while the work reported in [42] replaces both MPPT and PI regulators with an artificial neural network (ANN). In those works, the analysis of the converter is performed considering the panel array as a fixed DC voltage source, which is not accurate. Moreover, the design of the DAB converters is not addressed in those works. An additional drawback of the solution reported in [42] concerns the requirement of training the ANN for each type of PV module, requiring also the measurement of both the solar irradiation and PV power in the location where the PV system will be installed. Such a procedure is expensive and time consuming, and the PV power data will be valid only for the particular type of PV module used to collect the data. In conclusion, in the previous revision of the literature has not been found a design method for DAB converters intended to develop PV systems with high voltage gain.

Therefore, the main objective of this paper is to provide a design method for a PV system based on a DAB converter, intended to be part of micro-inverters, which considers high voltage-conversion ratio, high input voltage range, and the operation with basic MPPT algorithms at high efficiency. The behavior of the converter is analyzed in detail to propose analytical expressions for the main variables of the converter, such as PV current, leakage current, among others. Moreover, based on the converter expressions, equations to calculate the passive elements of the converter are proposed, hence a design method of the DAB converter is proposed.

The remain of the paper is organized as follows. Section 2 presents detailed analysis of the DAB converter circuit and operation, providing expressions to describe the currents behavior, and proposing a design method for a PV system based on the DAB converter. Section 3 verifies those analytical predictions using detailed circuits simulated in the power electronics simulator PSIM. Moreover, a design example is used to validate the effectiveness of the proposed design method. PSIM circuital simulations, including a classical perturb-and-observe ($P\&O$) MPPT algorithm, confirm the correct operation of the proposed PV system. Finally, Section 4 discusses the conclusions of the work.

2. Analyses and Methods

The DAB structure is a bidirectional power converter, which could operate at high efficiency with high voltage-conversion-ratio and with the benefits of galvanic isolation, hence this converter will be designed to be the first stage the micro-inverter for PV applications shown in Figure 1. Therefore, this section presents new analyses for the DAB converter interacting with a PV panel. Moreover, this section proposes an analytical design method for PV system based on the DAB converter.

2.1. Analysis of the DAB Circuit

Figure 2 shows the circuital scheme of the DAB converter, where $V_{PV}$ is the source at the low-voltage side (LVS) of the high-frequency transformer (HFT) and $V_{Bus}$ is the load voltage at the high-voltage side (HVS). Bridge 1 and 2 use four transistors: $Q_{LH1}$ to $Q_{LL2}$ and $Q_{HH1}$ to $Q_{HL2}$. Each bridge can operate in inverter or rectifier form depending on the direction of the power flow, i.e., when the power flows from $V_{PV}$ to $V_{Bus}$, bridge 1 works as inverter and bridge 2 works as rectifier; in the other power flow direction the bridge roles change. For PV applications the bidirectionality is not used since the current injection into the PV panel must be avoided, therefore this current flow must be restricted with both diodes and control systems.

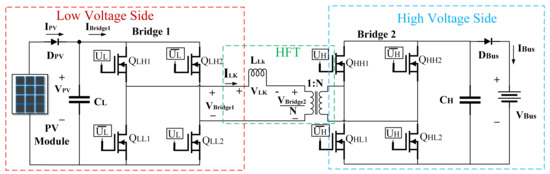
Figure 2. Circuital scheme of the DAB converter.

The HFT provides galvanic isolation and a voltage gain with a ratio 1:N. The leakage inductor ($L_{LK}$) represents the equivalent leakage inductance of both primary and secondary sides. The phase shift $\delta ·\pi$ between the bridge voltages determines power flow direction: when bridge 1 is leading with respect to bridge 2 the power flows from $V_{PV}$ to $V_{Bus}$, but if bridge 1 is lagging with respect to bridge 2 the power flows from $V_{Bus}$ to $V_{PV}$. Thus, the power flow in the DAB converter depends on the phase shift factor $\delta$, which has values between −1 and 1. Multiple techniques have been proposed to perform the power flow control in the DAB converter, where the single-phase shift (SPS) technique is the most widely adopted due to its simplicity [31,32]: in SPS each bridge is controlled by using a PWM signal with a fixed duty cycle (D) equal to $50\%$ to guarantee a zero DC current component in $L_{LK}$, which is necessary to reduce the power losses [31]. Therefore, the phase shift between the bridge PWM signals is the main parameter that determines the power flow on the DAB converter [31,51]. Moreover, to avoid short-circuits in the converter, transistors in the same leg must be controlled using complementary PWM signals. In SPS control, transistors $Q_{LH1}$ and $Q_{LL2}$ are activated using the $U_L$ PWM signal. $\overline{U_L}$ is the complementary PWM signal of $U_L$, and it is used to activate both $Q_{LL1}$ and $Q_{LH2}$. In the same way, transistors $Q_{HH1}$ and $Q_{HL2}$ are activated using the $U_H$ PWM signal, while $Q_{HL1}$ and $Q_{HL2}$ are activated with $\overline{U_H}$, which is the complementary PWM signal of $U_H$.

To analyze the behavior of a DAB converter, Figure 3 shows a simplified version of the circuit referred to the transformer primary side, where a square voltage source $V_{Bridge1}$ models the behavior of both PV module and bridge 1, while $V_{Bridge2}$ divided by N represents the secondary voltage, referred to the primary side, imposed by both the bridge 2 and DC bus. Figure 4 depicts the steady-state waveforms of voltages $V_{Bridge1}$ and $\frac{V_{Bridge2}}{N}$ considering a $\delta ·\pi$ phase shift between those signals. The leakage inductor voltage $\left(V_{LK}\right)$, obtained by subtracting $V_{Bridge1}$ and $\frac{V_{Bridge2}}{N}$, and the leakage inductor current $\left(I_{LK}\right)$ are also reported in Figure 4. Both voltage and current of the leakage inductor are AC signals without DC component, and those waveforms depend on the bridge voltages and phase shift. The figure shows that $V_{LK}$ is a symmetrical signal with respect to time axis; therefore, due to the flux balance on steady-state conditions, the peak value on the positive section of $I_{LK}$ is equal to the peak value of the negative section, i.e., $\left|I_{MAX}\right|=\left|I_{MIN}\right|$. The bridge 1 on the DAB converter can operate in buck mode if $V_{PV}$ is higher or equal than $V_{Bus}/N$, or in boost mode when $V_{Bus}/N$ is higher than $V_{PV}$. In buck mode, the peak current of the leakage inductor $\left(I_{MAX}\right)$ takes place in the middle of the switching period $(T_S/2)$, but in boost mode that peak occurs at $(\delta T_S/2)$ as reported in [32].

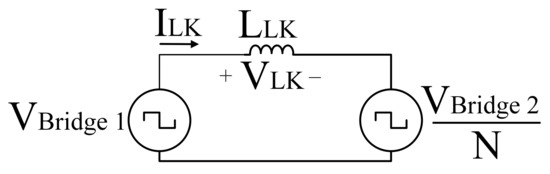
Figure 3. Equivalent DAB Converter.

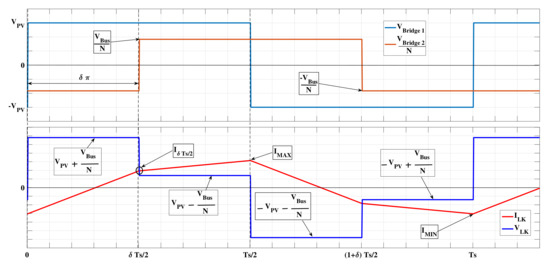
Figure 4. Voltage and Current Signals on Equivalent DAB Converter when $V_{PV}>V_{Bus}/N$.

To analyze the impact of the DAB converter operation on the PV power generation, it is necessary to calculate the active power flowing on the DAB converter. In [51] a Fourier series analysis is presented for $V_{Bridge1}$ and $I_{LK}$, where the instantaneous power $p\left(t\right)$ flowing through $L_{LK}$ is calculated by multiplying those two signals. Starting from the general form of the power in bridge 1 given in [51], the expression for the active power on bridge 1 $P_{Bridge1}$ with SPS control is obtained by averaging $p\left(t\right)$ in one switching period as reported in (1) and (2). The power in the DAB converter can be controlled by modifying $\delta$ for a fixed value of $L_{LK}$. From Equation (2) it is observed that the power is inversely proportional to $L_{LK}$, hence the power capacity of the DAB converter grows by decreasing the leakage inductor value, which can be achieved with a correct design of the transformer.

$$\begin{array}{c}\hfill P_{Bridge1}=\sum _{n=1,3,5,\cdots }^{\infty }{P}_n\end{array}$$

(1)

$$\begin{array}{c}\hfill P_n=\left(\frac{8·V_{PV}·\left(\frac{V_{Bus}}{N}\right)}{{\pi }^2·{\omega }_s·L_{LK}}\right)·\frac{sin\left(n·\delta ·\pi \right)}{n^3}\mathsf{where}{\omega }_s=2·\pi ·F_s\end{array}$$

(2)

For the specific power flow direction, current $I_{Bridge1}$ and $I_{Bridge2}$ are plotted in Figure 5, which shows that both currents have positive and negative values, but the average values of those signals are different from zero. Moreover, if $\delta =0$ or $\delta =1$, the average current value in both bridges is zero, which means that there is not power transfer between the bridges, i.e., $P_{Bridge1}=0$ based on Equations (1) and (2). Negative values in the bridge currents cause problems to unidirectional sources and loads, e.g., a PV module. Therefore, diodes have to be inserted at the input and output terminals of DAB converter, as seen in Figure 2, to avoid current injection into the PV module. For that reason, the diode $D_{PV}$ was inserted between the solar panel and the input capacitor $C_L$ of the DAB converter, thus negative values of $I_{Bridge1}$ flow through $C_L$ instead of the PV source. In the same way, a diode $D_{Bus}$ was inserted between the DC bus and the output capacitor of the DAB converter $C_H$, which prevents current extraction from the load; instead, negative values of $I_{Bridge2}$ flow through $C_H$.

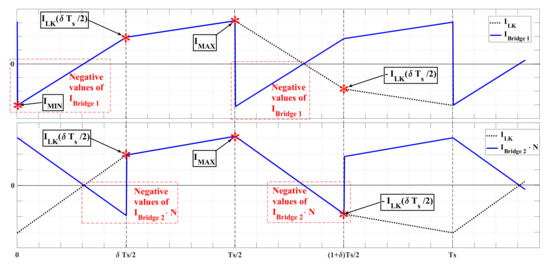
Figure 5. Input and Output Current Signals on DAB Converter.

2.2. Analysis of the PV Module and DAB Connection

Since the PV voltage and power can be modified by varying $\delta$, also the PV current can be controlled with $\delta$. To analyze the phase shift ($\delta$) effect on the PV power extraction, a current analysis in the DAB input node is carry out: Figure 6 shows the connection node of the PV module and DAB converter, and based on the Kirchhoff current law, the PV current ($I_{PV}$) is equal to the current in $C_L$ ($I_{CL}$) plus the bridge 1 current ($I_{Bridge1}$) as reported in (3). Figure 7 depicts the steady-state waveforms of the currents at the input node of the DAB converter for a single switching period $\left(T_s\right)$, i.e., $I_{PV}$, $I_{Bridge1}$ and $I_{CL}$. The figure also depicts the leakage inductor current $I_{LK}$. For the first half period $I_{Bridge1}=I_{LK}$, and for the second half period $I_{Bridge1}=-I_{LK}$. Therefore, the bridge 1 current is formalized using the switched Equation (4), where the switching function $\left(s_1\left(t\right)\right)$ is defined in (5).

$$\begin{array}{c}\hfill i_{PV}\left(t\right)=i_{CL}\left(t\right)+i_{Bridge1}\left(t\right)\end{array}$$

(3)

$$\begin{array}{c}\hfill i_{Bridge1}\left(t\right)=i_{LK}\left(t\right)·s_1\left(t\right)\end{array}$$

(4)

$$\begin{array}{c}\hfill s_1\left(t\right)=\left\{\begin{array}{cc}1\hfill & \mathrm{if}0<t\le \frac{T_s}{2}\hfill \\ -1\hfill & \mathrm{if}\frac{T_s}{2}<t\le T_s\hfill \end{array}\right.\end{array}$$

(5)

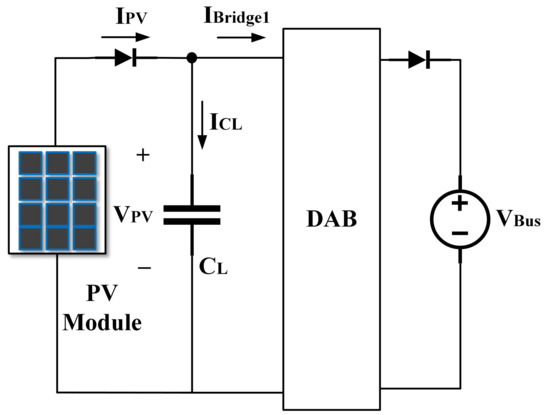
Figure 6. Equivalent circuit of a PV and DAB converter.

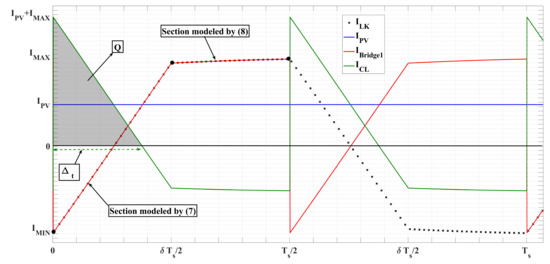
Figure 7. Input node currents on DAB converter with a PV system.

The capacitor charge balance establishes that in steady-state operation, the net change of charge over one switching period must be zero, hence the average capacitor current in steady-state must be zero [52]. Applying the charge balance to $C_L$ in the DAB converter, i.e., when the average value is equal to zero $⟨i_{CL}⟩=0$, enables the obtaining of the average values of (3) as reported in (6). Such an expression shows that the PV current depends on the inductor leakage current.

$$⟨i_{PV}⟩=I_{PV}=⟨i_{LK}\left(t\right)·s_1\left(t\right)⟩$$

(6)

2.2.1. Leakage Inductor Current Analysis

Energy harvested from the PV module flows through the leakage inductor to the DC bus, therefore a detailed analysis of the $I_{LK}$ is developed to determine the relationship between $I_{PV}$ and $\delta$.

The leakage inductor current, shown in Figure 7 for steady-state operation, can be described by two straight lines sections, hence it is represented using a piecewise linear function. The slopes of those linear sections are defined by the inductor voltage divided by the inductance value [52] as follows.

First section equation:

$$\begin{array}{c}\hfill \begin{array}{cc}{I}_{LK}\left(t\right)=I_{MIN}+\left(V_{PV}+\frac{V_{Bus}}{N}\right)·\frac{t}{L_{LK}};& 0<t\le \delta \frac{T_s}{2}\end{array}\end{array}$$

(7)

In such an expression the constant term of the linear equation is equal to $I_{MIN}$, which is the lowest leakage current value in steady-state conditions.

Second section equation:

$$\begin{array}{c}\hfill \begin{array}{cc}{I}_{LK}\left(t\right)=B+\left(V_{PV}-\frac{V_{Bus}}{N}\right)·\frac{t}{L_{LK}};& \delta \frac{T_s}{2}<t\le \frac{T_s}{2}\end{array}\end{array}$$

(8)

In the previous expression the constant term B of the linear equation is obtained evaluating (8) in $t=\delta \frac{T_s}{2}$ and solving for B:

$$\begin{array}{c}\hfill B=I_{LK\left(\delta \frac{T_s}{2}\right)}-\left(V_{PV}-\frac{V_{Bus}}{N}\right)·\frac{\delta ·T_s}{2·L_{LK}}\end{array}$$

(9)

At time $t=\delta \frac{T_s}{2}$ there is an intercept between (7) and (8) equations. Therefore, $I_{LK\left(\delta ·\frac{T_s}{2}\right)}$ is obtained evaluating (7) at $t=\delta \frac{T_s}{2}$:

$$\begin{array}{c}\hfill I_{LK\left(\delta \frac{T_s}{2}\right)}=I_{MIN}+\left(V_{PV}+\frac{V_{Bus}}{N}\right)·\frac{\delta ·T_s}{2·L_{LK}}\end{array}$$

(10)

Replacing (10) into (9) leads to the B value reported in (11).

$$\begin{array}{c}\hfill B=I_{MIN}+\frac{\delta ·T_s·V_{Bus}}{N·L_{LK}}\end{array}$$

(11)

The highest value of the leakage inductor current under steady-state conditions is defined as $I_{MAX}$; for $V_{PV}>\frac{V_{Bus}}{N}$ then $I_{MAX}=I_{LK\left(\frac{T_s}{2}\right)}$. Evaluating (8) in $t=\frac{T_s}{2}$ with the B value (11) leads to the $I_{MAX}$ expression reported in (12), which also takes into account that $\left|I_{MAX}\right|=\left|I_{MIN}\right|$; such a condition is obtained from the flux balance that must be fulfilled in any inductor under steady-state operation.

$$\begin{array}{c}\hfill I_{MAX}=\frac{T_s}{4·L_{LK}}·\left[V_{PV}+\left(2·\delta -1\right)\frac{V_{Bus}}{N}\right]\end{array}$$

(12)

Then, replacing (12) in (10) leads to the $I_{LK\left(\delta \frac{T_s}{2}\right)}$ value reported in (13).

$$\begin{array}{c}\hfill I_{LK\left(\delta \frac{T_s}{2}\right)}=\frac{T_s}{4·L_{LK}}·\left[\left(2·\delta -1\right)·V_{PV}+\frac{V_{Bus}}{N}\right]\end{array}$$

(13)

Solving the equations system formed by (7), (8), (11) and (12) enables the calculation of the $I_{LK}$ expression for a half period reported in (14).

$$\begin{array}{c}\hfill I_{LK}\left(t\right)=\left\{\begin{array}{cc}{I}_{LK1}(t,\delta )\hfill & \mathrm{if}0<t\le \delta \frac{T_S}{2}\hfill \\ I_{LK2}(t,\delta )\hfill & \mathrm{if}\delta \frac{T_S}{2}<t\le \frac{T_S}{2}\hfill \end{array}\right.\mathsf{where}\end{array}$$

(14)

$$\begin{array}{c}\hfill I_{LK1}(t,\delta )=\left(V_{PV}+\frac{V_{Bus}}{N}\right)·\frac{t}{L_{LK}}-\left(V_{PV}+\left(2·\delta -1\right)·\frac{V_{Bus}}{N}\right)·\frac{T_s}{4·L_{LK}}\end{array}$$

(15)

$$\begin{array}{c}\hfill I_{LK2}(t,\delta )=\left(V_{PV}-\frac{V_{Bus}}{N}\right)·\frac{t}{L_{LK}}-\left(V_{PV}-\left(2·\delta +1\right)·\frac{V_{Bus}}{N}\right)·\frac{T_s}{4·L_{LK}}\end{array}$$

(16)

2.2.2. PV Current Analysis

Replacing the previous expression of $I_{LK}$ into Equation (6) leads to the explicit expression reported in (17), where only the first half period of the $I_{LK}$ is taken into account since it is enough information to represent $i_{Bridge1}\left(t\right)$. Then, the average value is multiplied by two to compensate the second half period. This is possible since $i_{Bridge1}\left(t\right)$ is symmetric with respect to $t=\frac{T_s}{2}$ as shown in Figure 7.

$$I_{PV}=\frac{2}{T_s}\left[{\int }_0^{\delta \frac{T_s}{2}}{I}_{LK1}(t,\delta )+{\int }_{\delta \frac{T_s}{2}}^{\frac{T_s}{2}}{I}_{LK2}(t,\delta )\right]$$

(17)

Solving Equation (17), using (15) and (16), leads to Equation (18). Such an expression confirms that the PV current depends on $\delta$.

$$\begin{array}{c}\hfill I_{PV}=\frac{T_s·V_{Bus}·\delta ·\left(1-\delta \right)}{2·L_{LK}·N}\mathrm{if}{I}_{PV}<I_{SC}\end{array}$$

(18)

Finally, since the PV current is lower or equal to the short-circuit current $\left(I_{SC}\right)$ for a given irradiance $\left(S\right)$, the complete expression for $I_{PV}$ is reported in (19), where the PV current is the minimum value between $I_{SC}$ and the value reported in (18).

$$I_{PV(S,\delta )}=min\left\{I_{SC\left(S\right)},\frac{T_s·V_{Bus}·\delta ·\left(1-\delta \right)}{2·L_{LK}·N}\right\}$$

(19)

2.2.3. Range of Operation for the Phase Shift $\delta$

The physical range for the phase shift is $0\le \delta \le 1$ ($0\%$ to $100\%$), but expression (18) of the PV current is symmetric with respect to $\delta =0.5$. This is demonstrated by deriving the previous expression and finding the value in which such a first derivative is equal to zero, such a procedure is reported in (20).

$$\begin{array}{c}\hfill \frac{\partial I_{PV}}{\partial \delta }=\frac{T_s·V_{Bus}·\left(1-2·\delta \right)}{2·L_{LK}·N}=0\Rightarrow \delta =0.5\mathrm{if}{I}_{PV}<I_{SC}\end{array}$$

(20)

Then, the second derivative of (18) is calculated in (21), which is always a negative value. Therefore, it is demonstrated that the maximum value of (18) occurs at $\delta =0.5$.

$$\begin{array}{c}\hfill \frac{{\partial }^2{I}_{PV}}{\partial {\delta }^2}=-\frac{T_s·V_{Bus}}{L_{LK}·N}<0\mathrm{if}{I}_{PV}<I_{SC}\end{array}$$

(21)

The last step is to evaluate (18) with the variable replacement $\delta =1-\delta$, which leads to the same Equation (18). Therefore, the symmetry of (18) with respect to $\delta =0.5$ is demonstrated. Such a condition imply that the same PV current is obtained for both $\delta$ and $1-\delta$ values, e.g., the same PV current occurs for $\delta =0.3$ and $\delta =0.7$. Therefore, it is enough to operate in the range $0\le \delta \le 0.5$ or in the range $0.5\le \delta \le 1$.

However, the RMS value of the leakage inductor current $I_{LKRMS}$ of the DAB converter increases with respect to $\delta$. This analysis is performed starting from the expression for the RMS value of the leakage inductor current reported in [51] and described in (22), where $\alpha ·\pi$ is the phase shift angle between transistors $Q_{LH1}$ and $Q_{LL2}$ from bridge 1, and $\beta ·\pi$ is the phase shift angle between transistors $Q_{HH1}$ and $Q_{HL2}$ from bridge 2.

$$\begin{array}{c}\hfill I_{LKRMS}=\sqrt{\sum _{n=1,3,5...}^{\infty }{\left[\frac{2·\sqrt{2}}{n^2·\pi ·{\omega }_S·L_{LK}}\sqrt{X^2+Y^2}\right]}^2}\mathsf{where}\\ \hfill X=\frac{V_{Bus}}{N}·cos\left(n·\frac{\beta ·\pi }{2}\right)cos\left(n·\pi ·\delta \right)-V_{PV}·cos\left(n·\frac{\alpha ·\pi }{2}\right)\mathsf{and}\\ \hfill Y=\frac{V_{Bus}}{N}·cos\left(n·\frac{\beta ·\pi }{2}\right)·sin\left(n·\pi ·\delta \right)\end{array}$$

(22)

Such an expression must be evaluated for the SPS modulation [51], which means: there is not phase shift between transistors $Q_{LH1}$ and $Q_{LL2}$ from bridge 1, hence $\alpha ·\pi =0$; and there is not phase shift between transistors $Q_{HH1}$ and $Q_{HL2}$ from bridge 2, hence $\beta ·\pi =0$. Therefore, the RMS value of the leakage inductor current becomes:

$$\begin{array}{c}\hfill I_{LKRMS}=\sqrt{\sum _{n=1,3,5...}^{\infty }{\left[\frac{2·\sqrt{2}}{n^2·\pi ·{\omega }_S·L_{LK}}\sqrt{{\left(\frac{V_{Bus}}{N}·cos\left(n·\pi ·\delta \right)-V_{PV}\right)}^2+{\left(\frac{V_{Bus}}{N}·sin\left(n·\pi ·\delta \right)\right)}^2}\right]}^2}\end{array}$$

(23)

Since the ohmic losses in inductors and transformers depend on the square of the current RMS value, the analysis will continue with the square of the current RMS value:

$$\begin{array}{c}\hfill I_{LKRMS}^2=\sum _{n=1,3,5...}^{\infty }{\left[\frac{2·\sqrt{2}}{n^2·\pi ·{\omega }_S·L_{LK}}\sqrt{{\left(\frac{V_{Bus}}{N}·cos\left(n·\pi ·\delta \right)-V_{PV}\right)}^2+{\left(\frac{V_{Bus}}{N}·sin\left(n·\pi ·\delta \right)\right)}^2}\right]}^2\end{array}$$

(24)

The derivative of the previous expression of $I_{LKRMS}^2$, with respect to $\delta$, is given in (25). The non-harmonic component of that expression is always positive since all the terms are positive; however, the sign of the harmonic component must be analyzed.

$$\begin{array}{c}\hfill \frac{\partial \left(I_{LKRMS}^2\right)}{\partial \delta }=\stackrel{Non-harmoniccomponent}{\overbrace{\left(\frac{16·V_{Bus}·V_{PV}}{\pi ·{\omega }_S^2·L_{LK}^2·N}\right)}}·\stackrel{Harmoniccomponent}{\overbrace{\sum _{n=1,3,5...}^{\infty }\frac{sin\left(n·\pi ·\delta \right)}{n^3}}}\end{array}$$

(25)

The convergence value of the harmonic component is reported in (26), where $\Phi \left(z,s,a\right)$ is the Hurwitz-Lerch transcendent function described in [53].

$$\begin{array}{c}\hfill \sum _{n=1,3,5...}^{\infty }\frac{sin\left(n·\pi ·\delta \right)}{n^3}=\frac{i·e^{-i·\pi ·\delta }}{16}·\left[e^{2·i·\pi ·\delta }·\Phi \left(e^{-2·i·\pi ·\delta },3,-0.5\right)-\Phi \left(e^{2·i·\pi ·\delta },3,-0.5\right)\right]\end{array}$$

(26)

Solving ${\sum }_{n=1,3,5...}^{\infty }\frac{sin\left(n·\pi ·\delta \right)}{n^3}=0$ shows that the harmonic component is equal to zero only for $\delta =0$ and $\delta =1$, therefore that harmonic component has the same sign in the range of interest $0\le \delta \le 1$, i.e., always positive or always negative. The extremum value of the harmonic component occurs at $\delta =0.5$ as reported in (27), which is a maximum since the second derivative of the harmonic component is negative at $\delta =0.5$, this is confirmed in (28).

$$\begin{array}{c}\hfill \frac{\partial }{\partial \delta }\sum _{n=1,3,5,\cdots }^{\infty }\frac{sin\left(n·\delta ·\pi \right)}{n^3}=\sum _{n=1,3,5,\cdots }^{\infty }\frac{\pi ·cos\left(n·\delta ·\pi \right)}{n^2}=0\Rightarrow \delta =0.5\mathrm{because}0\le \delta \le 1\end{array}$$

(27)

$$\begin{array}{c}\hfill \frac{{\partial }^2}{\partial {\delta }^2}\sum _{n=1,3,5,\cdots }^{\infty }\frac{sin\left(n·\delta ·\pi \right)}{n^3}=\sum _{n=1,3,5,\cdots }^{\infty }{\left.\frac{-{\pi }^2·sin\left(n·\delta ·\pi \right)}{n}\right|}_{\delta =\frac{1}{2}}=\frac{-{\pi }^3}{4}<0\end{array}$$

(28)

Evaluating the harmonic component (26) into $\delta =0.5$ leads to the maximum value:

$$\begin{array}{c}\hfill max\left(\sum _{n=1,3,5,\cdots }^{\infty }\frac{sin\left(n·\pi ·\delta \right)}{n^3}\right)=\sum _{n=1,3,5,\cdots }^{\infty }{\left.\frac{sin\left(n·\pi ·\delta \right)}{n^3}\right|}_{\delta =0.5}=\frac{{\pi }^3}{32}>0\end{array}$$

(29)

Taking into account that the harmonic component has the same sign for all the physical range $0\le \delta \le 1$, and the maximum value of that harmonic component is positive $\left(\frac{{\pi }^3}{32}\right)$, it is concluded that the harmonic component is always positive. Therefore, since both the non-harmonic and harmonic components are positive, the derivative of $I_{LKRMS}^2$ is always positive, which means that the square of the leakage inductor RMS current increases when $\delta$ increases.

In conclusion, since the PV current Equation (18) is symmetric with respect to $\delta =0.5$, but the square of the RMS value of the leakage inductor current is higher in the range $0.5\le \delta \le 1$, the DAB converter connected to a PV module must be operated in the range $0\le \delta \le 0.5$ to provide lower ohmic losses in the transformer, which ensures higher efficiency: for example, the same PV current occurs for $\delta =0.3$ and $\delta =0.7$, but lower conduction losses will occur for $\delta =0.3$. Therefore, the phase shift will be restricted to $0\le \delta \le 0.5$.

2.3. Design of the DAB Converter for PV Applications

The design of the DAB converter must be carried out based on the PV module capacity. Hence, this subsection proposes a method to properly select the turns ratio of the HFT $1:N$, the leakage inductor value $L_{LK}$ and the PV side capacitor value $C_L$, which are the elements that affect the PV power harvest and its switching ripple.

Figure 8 presents a synthesis of the proposed design method for the DAB converter using a flowchart. The first step is to extract the parameters of the PV module at STC from the manufacturer datasheet; the STC data are used because at those 25 ${}^{\circ }$C and $S=1000$ W/m${}^2$ the maximum PV current $I_{MPP}$ occurs. That information is used to calculate the parameters of the single-diode model used to reproduce the PV module behavior, which is necessary to calculate the value of the PV side capacitor $C_L$. Then, the DC bus voltage is defined by the application, and the switching frequency $(F_S=1/T_S)$ must be selected taking into account that higher $F_S$ reduce the size of the transformer and passive elements on the converter, which is desirable to provide high power density and lower cost. However, taking into account that the switching losses on power converters increase linearly with the switching frequency [52], $F_S$ must be selected to provide a positive balance between power losses and converter size and cost. Next, the selection of turns ratio of the HFT $1:N$ is made to fulfill the restriction $V_{MPP}\cong \frac{V_{Bus}}{N}$, which is needed to obtain the lower peak value of $I_{LK}$, as it is described in [31,32], to produce the lowest current stress and the highest efficiency for the SPS control. Then, $L_{LK}$ is calculated using (32). Subsequently, the PV voltage ripple $\Delta V_{PV}$ is calculated solving (41)–(44) to provide the acceptable value of the PV power ripple $\Delta P_{PV}$. Finally, parameter $C_L$ is calculated using (40).

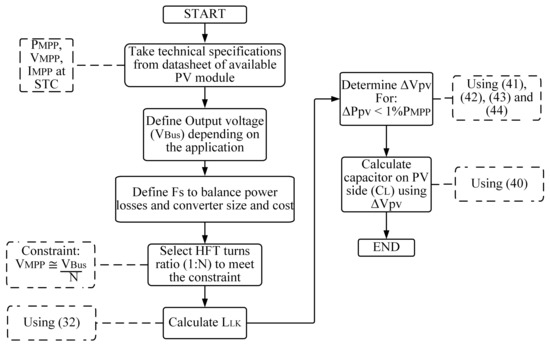
Figure 8. Flowchart of the DAB Design method.

The following subsections provide the mathematical analyses and design equations supporting the proposed design method.

2.3.1. Design of the HFT Equivalent Leakage Inductor

Taking into account that the power delivered by bridge 1 is the PV power, then Equation (1) can be rewritten changing $P_{Bridge1}$ by $P_{PV}$ as given in (30). Term $A_P$ represents a factor that depends on the PV voltage $V_{PV}$, the DC bus voltage $V_{Bus}$, the switching frequency (${\omega }_s=2·\pi ·F_s$), the transformer turns ratio ($1:N$) and the leakage inductance $L_{LK}$. Moreover, the power flowing through the converter is affected by harmonic components that depend on the $\delta$ factor. The expression confirms that for fixed values of $F_s$, $V_{PV}$, $V_{Bus}$ and N, the parameter $L_{LK}$ determines the maximum power extracted from the PV module; hence a higher $L_{LK}$ value implies a lower maximum PV power. Therefore, there is a critical $L_{LK}$ value for each PV module, and using leakage inductances higher that such a critical value makes impossible to extract the maximum power from the PV module.

$$P_{PV}=\stackrel{A_P}{\overbrace{\left(\frac{8·V_{PV}·\left(\frac{V_{Bus}}{N}\right)}{{\pi }^2·{\omega }_s·L_{LK}}\right)}}·\stackrel{Harmoniccomponents}{\overbrace{\sum _{n=1,3,5,\cdots }^{\infty }\frac{sin\left(n·\delta ·\pi \right)}{n^3}}}$$

(30)

Solving (30) for $L_{LK}$ leads to Equation (31), which describes the leakage inductor as a function of $\delta$ and the PV power, among other terms. Therefore, the critical value of the leakage inductor is determined for the maximum PV power $P_{MPP}$ at the maximum irradiance, which is the maximum power that a PV module can provide.

$$L_{LK}=\left(\frac{8·V_{PV}·\left(\frac{V_{Bus}}{N}\right)}{{\pi }^2·{\omega }_s·P_{PV}}\right)·\stackrel{Harmoniccomponents}{\overbrace{\sum _{n=1,3,5,\cdots }^{\infty }\frac{sin\left(n·\delta ·\pi \right)}{n^3}}}$$

(31)

To determine maximum $L_{LK}$ value for a given $P_{MPP}$, ${\omega }_s$, $V_{Bus}$ and N, the phase shift condition maximizing $L_{LK}$ must be calculated. This is done by finding the maximum condition of (31), which requires derivation of such an expression with respect to $\delta$. Taking into account that the harmonic components of (31) are the same harmonic components of (25), the maximum value of those harmonic components also occurs for $\delta =0.5$ with a value equal to $\frac{{\pi }^3}{32}$.

Based on the previous analysis, the critical value for $L_{LK}$ must be determined for $\delta =0.5$. Hence, the value of the harmonic components at $\delta =0.5$, i.e., $\frac{{\pi }^3}{32}$, is replaced into (31) to obtain Equation (32). Such an expression allows calculation of the critical $L_{LKMPP}$ value that ensures the maximum PV power can be extracted with the DAB converter.

$$L_{LKMPP}=\frac{V_{MPP}·V_{Bus}·\pi }{4·N·{\omega }_s·P_{MPP}}$$

(32)

Solving (32) for $P_{MPP}$, as given in (33), shows that a $L_{LK}$ value lower than $L_{LKMPP}$ increases the power capacity of the DAB converter; on the contrary, $L_{LK}$ value higher than $L_{LKMPP}$ reduces the maximum power capacity of the converter, hence the $P_{MPP}$ at higher irradiance conditions cannot be reached for $L_{LK}>L_{LKMPP}$ values. Therefore, leakage inductor must be selected lower or equal than $L_{LKMPP}$.

$$P_{MPP}=\frac{V_{MPP}·V_{Bus}·\pi }{4·N·{\omega }_s·L_{LKMPP}}$$

(33)

2.3.2. Design of the PV Side Capacitor

The PV side capacitor $C_L$ is designed based on the input node current of DAB converter, given in (3), and taking into account the current waveforms depicted in Figure 7. The shadowed area in Figure 7 corresponds to the electrical charge Q accumulated during the capacitor charging process on steady-state operation, which occurs during the time interval ${\Delta }_t$ in which the capacitor current $i_{CL}$ is positive. Such a charge accumulation increases the capacitor voltage in $2·{\Delta }_{Vpv}$ where ${\Delta }_{Vpv}$ is the ripple of the PV voltage. Then, the charge Q is also calculated from the capacitor elemental equation $Q=2·{\Delta }_{Vpv}·C_L$, which leads to Equation (34) [52].

$$Q=2·{\Delta }_{Vpv}·C_L=\frac{1}{2}{\Delta }_t\left(I_{MAX}+I_{PV}\right)$$

(34)

Assuming MPP operation, $I_{MAX}$ and $I_{PV}$ are taken from (12) and (18), respectively. Then, Equation (35) presents the Kirchhoff’s current law for $i_{CL}$, and replacing (4), (14), (15) and (18) into (35) leads to the extended version given in (36).

$$\begin{array}{c}\hfill i_{CL}\left(t\right)=i_{PV}\left(t\right)-i_{Bridge1}\left(t\right)\end{array}$$

(35)

$$\begin{array}{c}\hfill i_{CL}\left(t\right)=\frac{T_s}{4·L_{LK}}·\left[V_{PV}-\left(2·{\delta }^2-4·\delta +1\right)·\frac{V_{Bus}}{N}-\left(V_{PV}+\frac{V_{Bus}}{N}\right)·\frac{4·t}{T_s}\right]\end{array}$$

(36)

The time interval ${\Delta }_t$ is calculated when $i_{CL}\left(t\right)=0$, then solving (36) for that condition results in the $t={\Delta }_t$ expression given in (37).

$${\Delta }_t=\frac{T_s}{4}\left[\frac{V_{PV}-\left(2·{\delta }^2-4·\delta +1\right)·\frac{V_{Bus}}{N}}{V_{PV}+\frac{V_{Bus}}{N}}\right]$$

(37)

Replacing (37), (12) and (18) into (34), and solving for $C_L$, results in the design equation for the PV side capacitor given in (38). Such an expression requires the previous selection of the transformer ratio N, the leakage inductor $L_{LK}$, the switching period $T_s$, and the desired maximum ripple $\Delta V_{PV}$ of the PV voltage.

$$C_L=\frac{T_s^2}{64·\Delta V_{PV}·L_{LK}}\left[\frac{{\left[\frac{V_{Bus}}{N}·\left(2·{\delta }^2-4·\delta +1\right)-V_{PV}\right]}^2}{\frac{V_{Bus}}{N}+V_{PV}}\right]$$

(38)

To ensure a PV voltage ripple lower or equal to $\Delta V_{PV}$, the $C_L$ capacitor must be designed in the operation condition of $\delta$ generating the highest PV voltage ripple. This is analyzed by deriving expression (38) with respect to $\delta$, as it is presented in (39): since $0\le \delta \le 1$ then $(\delta -1)<0$ and $\left[\frac{V_{Bus}}{N}·\left(2·{\delta }^2-4·\delta +1\right)-V_{PV}\right]<0$ if bridge 1 operates in buck-boost mode, i.e., $V_{PV}\cong \frac{V_{Bus}}{N}$, which is the condition required for the highest efficiency of the DAB converter as reported in [32]. Therefore, $\frac{\partial C_L}{\partial \delta }>0$, hence $C_L$ is a monotonically increasing function of $\delta$, which means that the highest PV voltage ripple is exhibited at the highest $\delta$ value.

$$\frac{\partial C_L}{\partial \delta }=\frac{V_{Bus}·\left(\delta -1\right)·T_s^2}{8·\Delta V_{PV}·L_{LK}·N}\left[\frac{\frac{V_{Bus}}{N}·\left(2·{\delta }^2-4·\delta +1\right)-V_{PV}}{\frac{V_{Bus}}{N}+V_{PV}}\right]>0$$

(39)

Taking into account that a high efficiency of the DAB converter requires operation in the range $0\le \delta \le 0.5$, the $C_L$ capacitor must be designed at $\delta =0.5$ where $\Delta V_{PV}$ is maximum. Therefore, the final version of (38), adopting $\delta =0.5$, is given in (40).

$$C_L=\frac{T_s^2}{64·\Delta V_{PV}·L_{LK}}\left[\frac{{\left(\frac{V_{Bus}}{2·N}+V_{PV}\right)}^2}{\frac{V_{Bus}}{N}+V_{PV}}\right]$$

(40)

The selection of $C_L$ depends on the $\Delta V_{PV}$ value. Figure 9 shows the behavior of the PV power and current around the MPP of a PV module: at the MPP, the module voltage is $V_{MPP}$, the current is $I_{MPP}$, and power is $P_{MPP}$. If the PV voltage is increased due to the voltage ripple, i.e., the operating point moves to the right side of the curve, there is a reduction in the PV current. On the contrary, if the operating point moves to the left side, the PV current is increased. Instead, on the PV power curve, the movement at both sides of the MPP voltage causes a power reduction, which is higher when the voltage increases due to the always negative PV current derivative [54]. Figure 9 illustrates the current ripple $\Delta I_{PV}$ and power ripple $\Delta P_{PV}$ caused by the PV voltage ripple $\Delta V_{PV}$ at both sides of the curves.

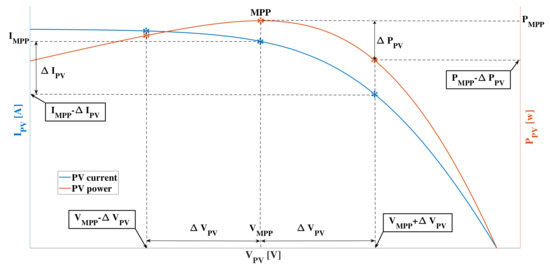
Figure 9. PV current and power vs. PV voltage.

To determine the PV voltage ripple $\Delta V_{PV}$ for an acceptable value of the PV power ripple $\Delta P_{PV}$, Equation (41) reports the minimum PV power around the MPP represented by $\left(P_{MPP}-\Delta P_{PV}\right)$, which is the result of multiplying the maximum PV voltage and minimum PV current around the MPP. Solving (41) for $\Delta P_{PV}$ leads to (42), which shows that the power ripple depends on both PV voltage and current at the MPP, and also depends on both current and voltage ripples. The PV current ripple around the MPP is calculated as the difference between $I_{MPP}$ and the PV current in $V_{MPP}+\Delta V_{PV}$, as it is shown in (43).

$$\begin{array}{cc}\hfill \left(P_{MPP}-\Delta P_{PV}\right)& =\left(V_{MPP}+\Delta V_{PV}\right)·\left(I_{MPP}-\Delta I_{PV}\right)\hfill \end{array}$$

(41)

$$\begin{array}{cc}\hfill \Delta P_{PV}& =\left(V_{MPP}+\Delta V_{PV}\right)·\Delta I_{PV}-\Delta V_{PV}·I_{MPP}\hfill \end{array}$$

(42)

$$\begin{array}{cc}\hfill \Delta I_{PV}& =I_{MPP}-I_{PV}{\mid }_{V_{PV}=V_{MPP}+\Delta V_{PV}}\hfill \end{array}$$

(43)

The PV current is calculated using the single-diode model of the PV module reported in [54], which circuital representation is presented in Figure 10; the corresponding equation is reported in (44), where $I_{PV}$ depends on the photo induced current $I_{ph}$, diode saturation current $I_S$, ideality factor $\eta$, $R_s$ and $R_h$ series and parallel resistances, and $V_{PV}$. Such an expression allows calculation of $I_{PV}$ at any $V_{PV}$ voltage.

$$I_{PV}=\frac{R_h·\left(I_{ph}+I_S\right)-V_{PV}}{R_s+R_h}-\frac{\eta ·V_t}{R_S}·W\left({\Theta }_I\right)$$

(44)

where:

$${\Theta }_I=\frac{\left(R_h\Vert R_S\right)·I_S·e^{\frac{R_h·R_S·(I_{ph}+I_S)+R_h·V_{PV}}{\eta ·V_t·\left(R_h+R_S\right)}}}{\eta ·V_t}$$

(45)

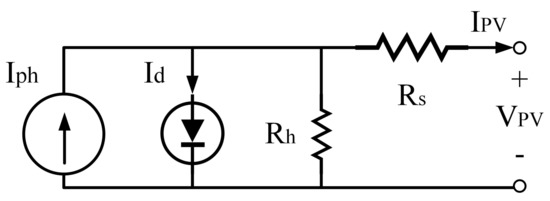
Figure 10. Circuital scheme of the single-diode model.

Therefore, Equation (44) must be used to calculate (43), and $\Delta V_{PV}$ is calculated to produce the acceptable $\Delta P_{PV}$ solving (42) and (41). In this work, $\Delta P_{PV}$ is selected to be lower than the power ripple introduced by the Perturb-and-Observe ($P\&O$) MPPT algorithm, which is needed for a stable operation of the PV system [55]. Finally, considering that a typical $P\&O$ algorithm provides efficiencies around $99\%$ [56,57,58,59], then $\Delta P_{PV}$ must be lower than $1\%$ i.e., $\Delta P_{PV}<1\%·P_{MPP}$.

3. Results and Discussion

This section validates the analytical expressions developed in the previous section for the DAB converter interacting with a PV module. Moreover, this section also validates the method proposed to design the PV system based on a DAB converter. The validation is performed by contrasting the results of detailed circuital simulations carried out in the power electronics PSIM with the predictions provided by the theoretical expressions proposed in the previous section.

3.1. Design Example

To validate the proposed design method for the PV system based on the DAB converter and a PV module, the complete PV system was simulated in PSIM. Figure 11 shows the electrical scheme implemented in PSIM, where the gate signals $U_L$ for bridge one and $U_H$ for bridge two, and their complementary signals, are produced by the “PWM & DELAY GENERATOR” block, which is based on two PWM generators. One PWM produces the $U_L$ gate signal with a $50\%$ duty cycle and a switching frequency $F_s$. A flip flop type-D is used to delay $U_H$ with respect to $U_L$, where the clock signal (CLK) is a complementary PWM, with the $\delta$ value as duty cycle and a switching frequency equal to $2·F_s$. Thus, $U_H$ has the same waveform as $U_L$ but lagging in $\delta \pi$ radians. The $\delta$ value is defined by a $P\&O$ MPPT algorithm which tracks the MPP operation point for any environmental condition. The MPPT parameters, i.e., the changes on $\delta$$(\Delta \delta )$ and perturbation time $\left(T_a\right)$, can be selected based on the criteria given in [55].

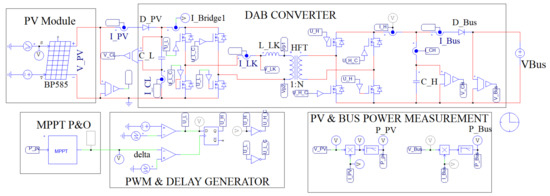
Figure 11. Circuital implementation of the PV system based on a DAB converter and a PV module.

For this validation, the DAB converter is designed for a micro-inverter application following the flowchart depicted in Figure 8. First, the specifications of the BP585 PV module were taken from the manufacturer datasheet [60] and presented in Table 1, and the parameters of the single-diode model were obtained using the procedure described in [61]. On the other hand, the DC bus voltage for a voltage source inverter (VSI), which is one of the most widely used inverter topologies in micro-inverters [62], must be higher than the peak voltage of the AC side [18]. For AC applications with 120 V RMS at 60 Hz, the input voltage for the inverter must be higher than 200 V [63], therefore $V_{Bus}=220$ V was selected to meet this micro-inverter constraint.

Table 1. PV system parameters.

Solar Panel Parameters at STC
Maximum power	$P_{Max}$	85 W
Voltage at Pmax	$V_{MPP}$	18 V
Current at Pmax	$I_{MPP}$	4.72 A
Short-circuit current	$I_{SC}$	5 A
Open-Circuit voltage	$V_{OC}$	22.1 V
Temperature coefficient of $I_{SC}$	${\alpha }_I$	0.065 %/${}^{\circ }$C
Temperature coefficient of voltage	${\alpha }_V$	−80 mV/${}^{\circ }$C
DAB Converter parameters
Input capacitor	$C_L$	33 $\mathsf{\mu }$F
Output capacitor	$C_H$	88 $\mathsf{\mu }$F
Leakage inductor	$L_{LK}$	9 $\mathsf{\mu }$H
Transformer turns ratio	$1:N$	$1:13$
Switching Frequency	$F_S$	50 kHz
DC BUS parameters
DC Bus voltage	$V_{BUS}$	220 V

The switching frequency $\left(F_s\right)$ must be selected higher than 20 kHz to reduce noise in the audible range. Most of the authors in the literature report $F_s$ values between 10 kHz and 500 kHz [40,64,65,66,67,68,69,70,71,72] to provide a positive balance between power losses and converter size and cost. Therefore, this example considers $F_s=50$ kHz, which is common for Si-Mosfets.

Based on the $V_{MPP}=18$ V and the $V_{Bus}$ values, the transformer turns ratio obtained was $1:13$ to fulfill the constraint $V_{MPP}\cong \frac{V_{Bus}}{N}$. Then, leakage inductance $L_{LK}=9$$\mathsf{\mu }$H was calculated using $N=13$ and $P_{MPP}=85$ W from Equation (32). Finally, the PV power ripple $\Delta P_{PV}=425$ mW was defined as $0.5\%$ of $P_{MPP}$. Thus, $\Delta V_{PV}=421$ mV and $\Delta I_{PV}=128.2$ mA were calculated using Equations (41)–(44). Those values are used to calculate the PV side capacitor $C_L=33$ $\mathsf{\mu }$F from Equation (40).

3.2. Verification of the Phase Shift ($\delta$) Optimal Range

Figure 12 shows the changes on the PV voltage $\left(V_{PV}\right)$, PV power $\left(P_{PV}\right)$ and leakage inductor current for changes on $\delta$, without accounting for losses, for different irradiation levels $\left(S\right)$. The maximum power extraction is achieved at $\delta =0.5$ when the irradiance is 1000 W/m${}^2$, as it was predicted by Equation (33), but for lower irradiance values the peak power is reached at different $\delta$ values. Therefore, to extract the maximum power available in the PV module at any irradiance condition, an MPPT algorithm must be used to automatically adjust the optimal phase shift factor. Figure 12 also confirms that both PV voltage and power are symmetric with respect to $\delta =0.5$, hence the MPP for irradiance levels lower than 1000 W/m${}^2$ can be reached with two different $\delta$ values. Moreover, the figure also confirms that the RMS value of the leakage inductor current $\left(I_{LKRMS}\right)$ rises with increments in $\delta$ until the short-circuit current ($I_{SC}$) of the PV module is reached.

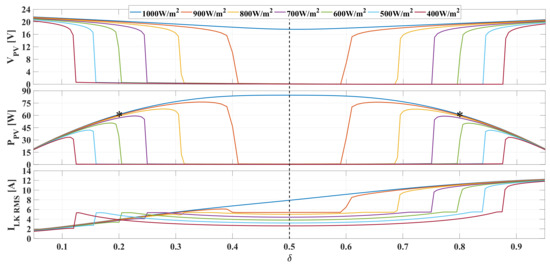
Figure 12. PV voltage, power and leakage inductor current vs. $\delta$ without assuming losses in leakage inductor.

Figure 13 shows the simulation of the PV system taking into account ohmic losses in the HFT, which confirms that the maximum power delivered to the DC bus $\left(P_{Bus}\right)$ is achieved in the range $0\le \delta \le 0.5$ for all irradiance values. In order to clarify this aspect, Figure 13 also reports the power conversion efficiency, which decreases with increments on $\delta$: higher $\delta$ values produce higher $I_{LKRMS}$ values, which increases the power losses. For example, Figure 13 reports that the PV power is $P_{PV}=61.89$ W with $\delta =0.2$ and $\delta =0.8$ for an irradiance level $S=1000$ W/m${}^2$, but the output power is $P_{Bus}=60.22$ W for $\delta =0.2$ and $P_{Bus}=55.81$ W for $\delta =0.8$; hence the conversion efficiency is $97.3\%$ for $\delta =0.2$ and $85.82\%$ for $\delta =0.8$. Therefore, those simulation results confirm that the DAB converter must be operated with phase shift $\delta$ values between 0 and 0.5 to provide the highest efficiency condition.

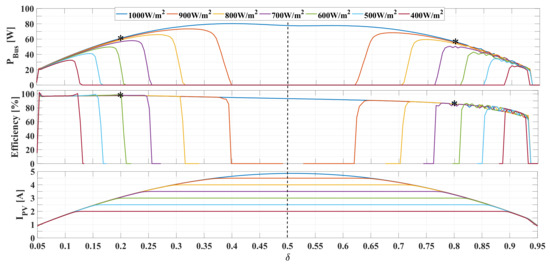
Figure 13. DC bus power, efficiency and PV current vs. $\delta$ assuming losses in leakage inductor.

3.3. Verification of the PV Current Equation

The PV current Equation (19) is validated by contrasting the theoretical predictions of such an expression with the current reported by the PSIM simulation. In such a way, Figure 14 shows the PV current for $\delta$ up to 0.5.: the continuous lines represent the values of $I_{PV}$ calculated using the theoretical expression (19), while the dotted waveforms correspond to the simulation data obtained in the PSIM environment. Those results confirm that Equation (19) correctly predicts the PV current for any irradiance value S, even if $I_{SC}$ is reached. In fact, for $S=1000$ W/m${}^2$ the short-circuit current $I_{SC}$ is not reached since the limit value of $L_{LK}$ was adopted.

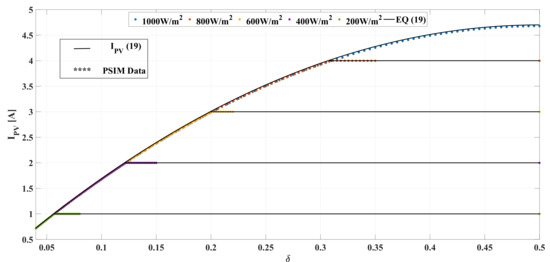
Figure 14. PV current from PSIM simulation vs. Equation (19).

Solving the equations system formed by the single-diode model (44) and (45) and the theoretical PV current expression (19) allows calculation of both $V_{PV}$ and $P_{PV}$ for any irradiance S condition. The PV voltage and power were also simulated in PSIM, and the comparison of both circuital and theoretical data is reported in Figure 15: the continuous lines correspond to the data given by the model and the dotted waveforms correspond to the PSIM data. Such results confirm the accuracy of the theoretical expression for estimating $I_{PV}$ (19) at any irradiance condition.

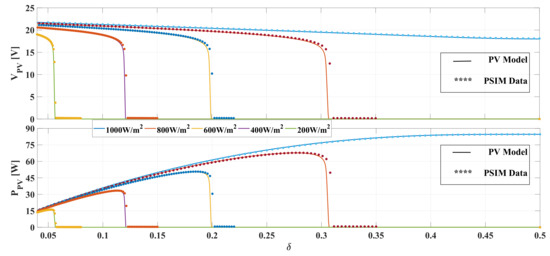
Figure 15. PV voltage and power from PSIM simulation vs. PV single-diode model.

Finally, the previous results confirm that the PV current prediction is accurate. Moreover, those simulations also confirm that the proposed DAB design can be used to extract the maximum power available in the PV module at any irradiance condition, which can be done by varying $\delta$ to track the optimal operation point of the PV module using a MPPT algorithm.

3.4. Verification of the $L_{LK}$ Design Equation

Equation (32) predicts that selecting $L_{LK}=L_{LKMPP}$ calculated at the highest irradiance condition (1000 W/m${}^2$) enables reaching of the MPP with $\delta =0.5$, which is confirmed in the blue trace of Figure 16. If a lower value of $L_{LK}$ is used, the MPP is reached at a lower value of $\delta$; for example, in the yellow trace of Figure 16 it is obtained at $\delta =0.14$ because $L_{LK}=\frac{L_{LKMPP}}{2}$. Instead, if a higher value of $L_{LK}$ is used, e.g., $L_{LK}=2·L_{LKMPP}$, there is not possible to reach the MPP with any value of $\delta$, this is observed in the orange trace of Figure 16. Those behaviors are highlighted by the power-vs-voltage curves of the PV module presented in Figure 16: with $L_{LK}=\frac{L_{LKMPP}}{2}$ the DAB converter enables exploration of all the power-vs-voltage curve; while using $L_{LK}=L_{LKMPP}$ enables the DAB converter to explore the power-vs-voltage curve only up to the MPP condition, which is enough since that is the optimal operation condition of the system; finally, with $L_{LK}=2·L_{LKMPP}$ the DAB converter is able to explore a small section of the power-vs-voltage curve without reaching the MPP, hence the maximum power available in the module cannot be extracted. Those simulation results confirm that the leakage inductor must be selected lower or equal than $L_{LKMPP}$.

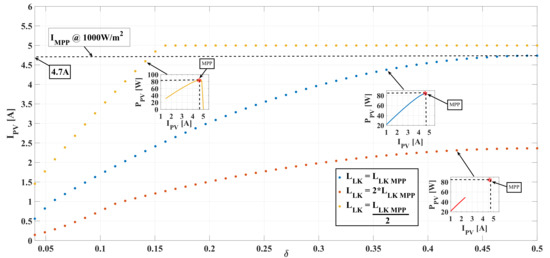
Figure 16. PV current for different values of $L_{LK}$.

The selection of $L_{LK}$ also impact the design of the MPPT algorithm and the sensing circuitry required for that algorithm. Taking into account that the MPPT algorithm must to act on the phase shift factor $\delta$ by adding or subtracting a small differential value $\Delta \delta$, the value of $L_{LK}$ affects the resolution of the MPPT actions on the PV current. For example, adopting $L_{LK}=L_{LKMPP}$ for $S=1000$ W/m${}^2$ and $\Delta \delta =0.01$ for the MPPT implies that the PV current could operate at 50 different values, which defines a resolution of 94 mA for the MPPT algorithm to track the MPP of the module. Instead, if $L_{LK}=\frac{L_{LKMPP}}{2}$ is used for the same $\Delta \delta =0.01$, the PV current could operate at 17 different values, which defines a resolution of 276 mA for the MPPT algorithm, hence a much smaller precision in the tracking of the MPP is available and lower power can be extracted. This can be faced by reducing the $\Delta \delta$ value, but for real implementations that will require circuitry with higher resolution and lower noise, which means a costly implementation.

3.5. Verification of the $C_L$ Design Equation

Figure 17 shows the PV voltage ripple $\Delta V_{PV}$ obtained with different $\delta$ and $C_L$ values using expression (38). Such a simulation confirms that $\Delta V_{PV}$ grows when $\delta$ rises as predicted in (39). Moreover, the simulation confirms that $\Delta V_{PV}$ decreases when $C_L$ is increased, which is evident from (38). Taking into account that a high efficiency of the DAB converter requires operation in the range $0\le \delta \le 0.5$, the simulation confirms that $C_L$ capacitor must be designed at $\delta =0.5$ where $\Delta V_{PV}$ is maximum. Finally, the simulation also confirms that calculating $C_L$ using the final expression (40) provides the desired maximum ripple of the PV voltage (421 mV).

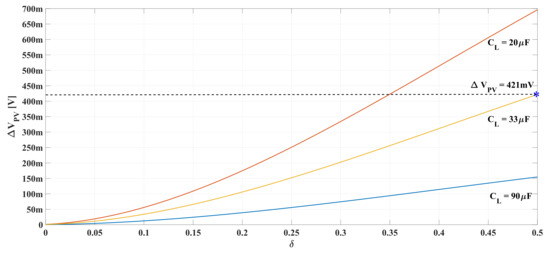
Figure 17. PV voltage ripple vs. $\delta$ for given $C_L$ values.

3.6. Verification of the Steady-State Operation

This subsection validates the proposed design method for $S=1000$ W/m${}^2$ and $\delta =0.5$, which are the conditions used to calculate the converter parameters. Figure 18 and Figure 19 present the circuital simulation of the PV system under those operation conditions. Figure 18 shows the ripples of the PV voltage, current and power: the $\Delta V_{PV}$ of the simulation is equal to $419.7$ mV, which exhibits a $1\%$ error with respect to the theoretical value; this validates the design of $C_L$. Similarly, the simulated $\Delta I_{PV}$ and $\Delta P_{PV}$ are very close to the theoretical values, where $\Delta I_{PV}$ and $\Delta P_{PV}$ exhibit errors of $15\%$ and $2\%$, respectively. In particular, the small error of $\Delta P_{PV}$ guarantees that the value designed for $C_L$ ensure a power ripple lower than the MPPT ripple, as it was described in Section 2.3.2. Figure 18 also shows that the PV power reaches the $P_{MPP}$ two times in a half switching period; this is caused by the operation of $V_{PV}$ and $I_{PV}$ around the MPP, hence $P_{PV}$ is reduced at both the left and right of the MPP. This is a typical behavior when the PV module operates around the MPP with a $P\&O$ algorithm.

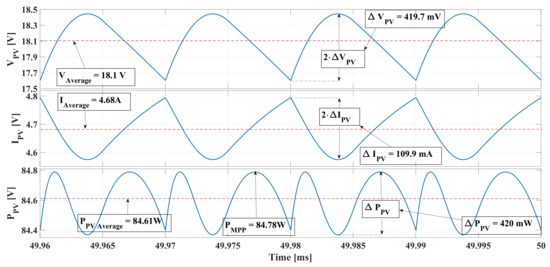
Figure 18. Ripples of the PV voltage, current and power.

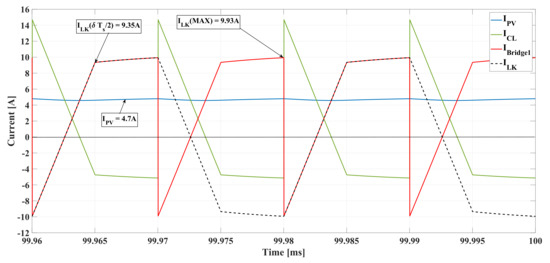
Figure 19. Currents at $C_L$ node.

To validate mathematical analysis presented in the previous section, variables as $I_{MAX}=I_{LK}\left(\frac{T_S}{2}\right)=10$ A, $I_{LK}\left(\frac{\delta T_S}{2}\right)=9.4$ A and $I_{PV}=4.7$ A were calculated using the theoretical expressions (12), (13) and (19) respectively. Figure 19 shows the circuital simulations of $I_{PV}$, $I_{CL}$ and $I_{Bridge1}$ currents at the input node of the DAB converter; where the theoretical values exhibit errors lower than $1\%$ with respect to the PSIM data. The simulations also confirm that the currents at the input node have a period equal to $10\mathsf{\mu }$s, which is a half of the switching period $T_s=20\mathsf{\mu }$s as predicted in the previous sections.

In conclusion, the theoretical expressions developed to calculate $I_{MAX}$, $I_{LK}$ and $I_{PV}$, i.e., Equations (12), (13) and (19), respectively, have been validated. Similarly, the design equations for $C_L$ and $L_{LK}$ are also correct, i.e., expressions (40) and (32), respectively.

3.7. Verification of the Dynamic Operation with a MPPT Algorithm

This set of simulations evaluates the performance of the DAB converter to drive the PV module into the MPP condition for multiple irradiance values. The phase shift factor $\delta$ is automatically adjusted using a classical $P\&O$ algorithm designed following the guidelines given in [55]: the perturbation of the shift factor $\Delta \delta$ is selected as $1\%$ and the perturbation time $T_a$ is selected as 5 ms.

Figure 20, Figure 21 and Figure 22 show the operation of the circuital implementation under the action of the $P\&O$ MPPT algorithm for irradiance values equal to 400 W/m${}^2$, 600 W/m${}^2$ and 800 W/m${}^2$, respectivley. The figures present the phase shift factor $\delta$ provided by the $P\&O$ algorithm, the PV current, voltage and power. The simulations confirm that $I_{PV}$ changes proportionally to the $\delta$ steps, as it was predicted with Equation (19). Moreover, the changes in $V_{PV}$ due to $\delta$ steps are inversely proportional, which is a typical behavior of a PV module. In the three simulation cases the $V_{PV}$ and $I_{PV}$ waveforms describe a three-point-behavior, which ensures that the PV system is operating at the MPP for the corresponding irradiance condition [55], hence the $P\&O$ was able to drive the DAB converter to extract the maximum power from the PV module. This validates the design of $L_{LK}$ since the DAB converter can reach all the $I_{MPP}$ currents. Finally, the three cases also confirm that $\Delta P_{PV}$ is smaller than the PV power perturbations caused by the $P\&O$, which guarantee MPPT stability. This validates the design of $C_L$, which was calculated to ensure a PV power ripple smaller than the power oscillations caused by the MPPT algorithm.

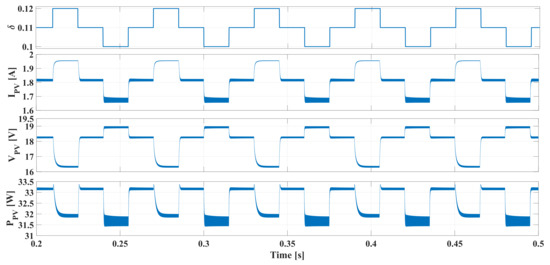
Figure 20. MPPT operation at 400 W/m${}^2$.

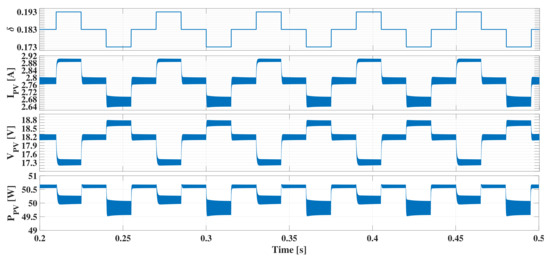
Figure 21. MPPT operation at 600 W/m${}^2$.

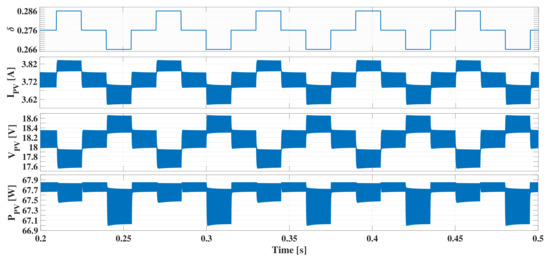
Figure 22. MPPT operation at 800 W/m${}^2$.

The next set of simulations were performed considering dynamic changes on the irradiance condition, which test the performance of the designed DAB converter in a dynamic MPPT operation. Figure 23 shows the circuit behavior for a step irradiance change from 600 W/m${}^2$ to 1000 W/m${}^2$ at 300 ms. Before that change, the PV module was operating at the MPP, producing 51 W with a $\delta$ value around $0.19$. After the irradiance change occurs, the system reaches the new MPP after 500 ms, extracting 85 W with a $\delta$ value around $0.5$. The power-vs-current curves of the PV module in both irradiance conditions are also depicted, and the path followed by the DAB converter is highlighted in red: the PV system travels from the MPP of the first condition (600 W/m${}^2$) to the MPP of the second condition (1000 W/m${}^2$) without deviation, hence, the highest PV power is extracted. The simulation also shows that after 300 ms, due to the step change on the irradiance value, the $V_{PV}$ grows instantaneously to 21 V, and as predicted by Equation (40), the voltage ripple $\Delta V_{PV}$ grows causing an increment on the current ripple $\Delta I_{PV}$. However, as demonstrated in the previous simulations, those ripples fulfill the design requirements imposed to the PV system.

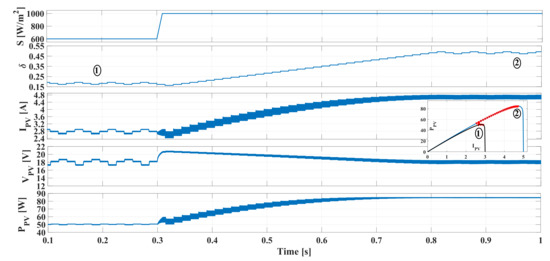
Figure 23. Tracking of the MPP for fast changes on the irradiance.

Finally, Figure 24 shows the behavior of the PV system for slow irradiance changes: first S decreases from 800 W/m${}^2$ to 600 W/m${}^2$ with an slope equal to $-500$ W/(m${}^2$s); then the irradiance rises to 700 W/m${}^2$ with an slope equal to 500 W/(m${}^2$s). Results show that the $P\&O$ MPPT algorithm effectively changes $\delta$ to reach the MPP at any irradiance condition. Moreover, it is observed that changes on $V_{PV}$ and $P_{PV}$ are higher for a positive step change of $\Delta \delta$ and increases when S decreases. This is in agreement with the results presented in Figure 15, where the slope of $V_{PV}$ and $P_{PV}$ curves are higher when the $\delta$ value rises. This can be addressed by developing a PV voltage controller acting on $\delta$ to provide a PV voltage equal to a reference value provided by a MPPT algorithm.

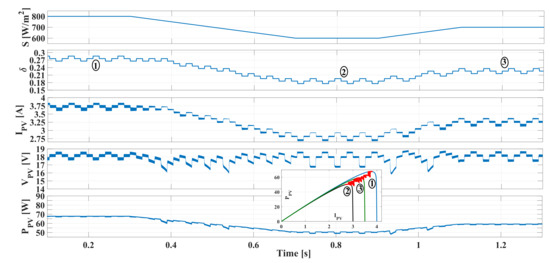
Figure 24. Tracking of the MPP for slow changes on the irradiance.

Finally, the simulations presented in this section confirm the viability of designing a DAB converter to extract the maximum power available of a PV module. Moreover, the simulations also validate both the mathematical analyses and the design method proposed in this paper.

4. Conclusions

A PV system based on a DAB converter and a PV module was proposed in this paper. Because the application of the designed PV system is aimed at interfacing a single PV module with a DC bus, it is also called a distributed MPPT unit or DMPPT-U. The system is aimed at providing the special characteristics of the DAB converter to PV systems, such as high input and output voltages range, high voltage-conversion-ratio and high efficiency, which are desirable to interface low-voltage PV sources with high-voltage DC buses, e.g., a first stage of a photovoltaic micro-inverter.

In particular, in this paper the DAB converter behavior is analyzed in detail. The mathematical analysis was developed to determine the leakage inductor design equation. Based on that equation, the critical value of the leakage inductor is determined to extract the maximum power of the PV panel at any irradiance condition. Moreover, a design equation to calculate the capacitor on the PV side was also obtained. The design criteria to calculate that capacitor is to reduce the voltage ripple in the PV module, which guarantee a high MPPT efficiency. Similarly, the selection of the transformer turns ratio was developed based on the constraints reported in the literature for high efficiency operation of the DAB converter. In the same way, the analysis demonstrated that the phase shift factor must be between 0 and 0.5 to achieve a high efficiency operation of the DAB converter.

For MPPT operation, it was demonstrated that varying the phase shift factor enables control of the PV current, and consequently, also the PV voltage is modified. Taking advantage of those characteristics, a classical $P\&O$ MPPT algorithm was implemented to track the optimal phase shift factor. Circuital simulations where obtained in PSIM for a 85 W PV module and the designed DAB converter feeding a 220 V DC bus, obtaining PV voltage ripples with an error of $1\%$. Moreover, the maximum PV power was achieved for all the irradiance conditions, and changes on the MPP were successfully tracked by varying the phase shift factor value using the $P\&O$ algorithm. Finally, the viability of designing a DAB converter to extract the maximum power available of a PV module was confirmed, and both the mathematical analyses and the design procedure proposed for the DAB were validated.

The main drawback of the adopted MPPT solution concerns the non-linear relation between the phase shift factor and the PV voltage, which produces variable voltage changes for constant perturbations on the phase shift factor. This characteristic produces larger perturbations on the PV power for large PV voltage in comparison with low PV voltages, which reduce the MPPT precision at larger voltages. This problem could be faced by developing a control system to regulate the PV voltage, where the MPPT algorithm imposes constant voltage perturbations. However, such an improvement requires development of a dynamic model for the PV system based on the DAB converter, which is a topic that will be addressed in a future work.