A Virtual Negative Resistor Based Common Mode Current Resonance Suppression Method for Three-Level Grid-Tied Inverter with Discontinuous PWM

Abstract

The output LC filter of a photovoltaic (PV) string three-level grid-tied inverter that connects the filter capacitor neutral point to dc-link capacitor neutral point can reduce the common-mode (CM) current injected to the grid by letting the CM current circulate within the inverter. However, the internal CM current may resonate because of the existence of the resonant frequency of the internal CM LC circuit. Compared with the traditional continuous pulse-width modulation (CPWM), the resonance can be worse if discontinuous pulse-width modulation (DPWM) is applied, for the zero sequence quantity of DPWM contains more harmonics than that of CPWM. In this paper, a virtual negative resistor based common mode current resonance suppression method for a three-level grid-tied inverter is proposed to overcome the CM current resonance problem in DPWM application. Different positions of the virtual negative resistor in the equivalent CM circuit with different feedback variables are analyzed theoretically. The virtual negative resistor connected in series with the inductor in the equivalent CM circuit is selected to damp the CM current resonance for simplification and damping performance. Different from the implementation in CPWM where a pair of small voltage vectors exist and are used to adjust the CM voltage directly, the proposed method for DPWM application is implemented indirectly by adding the CM adjustment quantity to differential-mode (DM) control quantity with appropriate coefficients. Depending on the sector of DM control quantity in the $\mathsf{\alpha }\mathsf{\beta }$ reference frame, the coefficients are calculated using one of three specific voltage vectors. Experimental results are given to demonstrate the effectiveness of theoretical analyses and the proposed method.

1. Introduction

Among all renewable energy sources, photovoltaic (PV) systems have experienced rapid growth both in residential and commercial applications. The power quality of current generated by the PV grid-connected inverter is of importance for the grid. According to IEEE Std 519-2014, the recommended harmonic distortion limit of line-to-neutral voltages is that the voltage total harmonic distortion (VTHD) at the point of common coupling (PCC) is 8% for the bus voltage less than or equal to 1 kV, 5% for the bus voltage between 1 and 69 kV, 2.5% for the bus voltage between 69 and 161 kV, etc., [1]. Switching ripple filters (SRFs), like L, LC, LCL, and LLCL filter, is a significant part of PV grid-connected inverter interfacing with the grid. On one hand, SRFs can maintain a coupling connection and integration between grid and grid-connected inverter. On the other hand, SRFs can filter the switching ripple currents of inverter-side inductor current [2]. However, these filters can potentially cause a harmonic resonance for system operation if not properly designed [3].

In order to suppress the harmonic resonance problems, researchers have proposed passive damping (PD) and active damping (AD) techniques [3,4,5]. PD is a simple and stable technique but increases the damping power loss and volume of an inverter. Compared with PD, AD technique is flexible and does not increase the damping power loss. The three most cited AD techniques in literature are capacitor current feedback based method [6], capacitor voltage feedback based method [7], and notch-filter based method [8]. Different feedback of output filter state corresponds to different impedance position in a LCL filter: the feedback of the converter current forms a virtual impedance in series with the inverter side inductor Lf, capacitor voltage, or current feedback in grid current control forms a virtual impedance in parallel with filter capacitor, grid current feedback forms a virtual impedance in parallel with grid side inductor [9]. In [10], the authors give a comprehensive study of a virtual resistor based AD for the LCL resonance frequency. The virtual resistor based AD technique is simple and effective in damping the LCL resonance current. However, to the best knowledge of the authors, the virtual resistor mentioned above is used only for damping the harmonics resonance of differential-mode (DM) current injected to the grid.

An improved LCL (ILCL) filter is proposed in [11,12] to reduce the leakage current. The ILCL filter is acquired simply by connecting the common point of LCL filter capacitors to the dc-link neutral point without adding any additional components. Letting the common-mode (CM) current circuiting within the inverter, the leakage current injected into the grid can be reduced significantly. However, the CM current circuiting path within the inverter is a LC circuit, in which a LC resonance frequency f_r exists. The CM current resonance suppression methods for inverter using the ILCL filter are proposed in [13,14] to reduce the leakage current injected to gird. In [14], the authors use a PI controller to control the CM current to be zero by real-time adjusting zero-sequence duty ratio in space vector modulation (SVM) technique. In [13], the CM voltage which is injected into DM voltage to extend the inverter modulation index is controlled to suppression CM current resonance. Both the methods are useful and effective, and are based on a pair of small voltage vectors to adjust the CM voltage.

In order to improve the switching efficiency of three-phase rectifier/inverter, discontinuous pulse-width modulation (DPWM) is proposed by researchers [15,16]. The basic idea of DPWM is to select appropriate voltage vectors to compose the reference voltage vector so that the switches have a minimum switching loss. One of its characteristics is that there is no a pair of small voltage vectors, only one of the two small voltage vectors is used to compose the reference voltage vector. Since the CM AD methods in [13,14] are based on a pair of small voltage vectors to adjust the CM voltage, they cannot be used directly in DPWM application.

In this paper, a virtual negative resistor based AD (VNRBAD) method is proposed to damp the CM current resonance for a three-level inverter with an improved LC (ILC) filter in DPWM application. The originality lies in two points: (1) a virtual negative resistor based CM current resonance suppression method and (2) its implementation in DPWM application.

This work is organized as follows. The model of CM current resonance in three-level grid-tied inverter with an ILC filter is presented in Section 2. In Section 3, the comparison of the harmonics of the zero sequence of DPWM and continuous pulse-width modulation (CPWM) is presented. VNRBAD for CM current resonance suppression in DPWM application is proposed in Section 4. Experiments and discussions are given in Section 5 to demonstrate the proposed VNRBAD. In Section 6, conclusions are reached.

2. Model of CM Current Resonance in Grid-Tied Inverter with ILC Filter

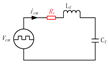
Figure 1 shows the topology of a general PV string three-level grid-tied inverter with an ILC filter [12,17]. Boost converter is usually used as the DC-DC stage to increase the dc voltage and to track the maximum power point of the PV array, the inverter stage is used to convert DC power into AC power and inject it to AC grid. i_CM and v_CM is the CM LC circuit current and voltage respectively, and is defined by Equations (1) and (2). Detailed modeling derivation of CM voltage and current of the topology can be found in [14]. Here, only the CM circuit model is given in Figure 2. Its transfer function G_p and bode diagram is given in Equation (3) and Figure 3, respectively. The CM resonance frequency in the bode diagram is given in Equation (4). The CM current resonance would be excited in the CM current path if no CM current resonance suppression technique is applied. Such resonance current would be more serious when DPWM is used as the modulation algorithm of PV string inverter, which is explained next.

$$i_{\mathrm{CM}}=i_a+i_b+i_c$$

(1)

$$v_{\mathrm{CM}}=v_{Ao}+v_{Bo}+v_{Co}$$

(2)

$${\mathrm{G}}_{\mathrm{p}}=\frac{i_{\mathrm{CM}}}{v_{\mathrm{CM}}}=\frac{C_{f}S}{L_f{C}_f{S}^2+1}$$

(3)

$$f_r=\frac{1}{2\pi \sqrt{L_f{C}_f}}$$

(4)

where, i_CM and v_CM are the CM current and voltage, i_a, i_b, i_c are three-phase inductor current, respectively. v_Ao, v_Bo, and v_Co are three-phase bridge output voltage. G_p and f_r are the model and the resonant frequency of the equivalent CM circuit, respectively. L_f and C_f are the inductance and capacitance of LC filter. S is a complex variable in S domain, and S = $2\pi fi$, f is the frequency of current and voltage.

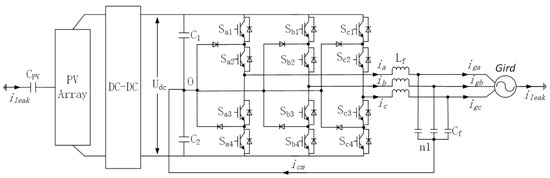
Figure 1. Grid-connected transformer less three-level I-type inverter with ILC filter.

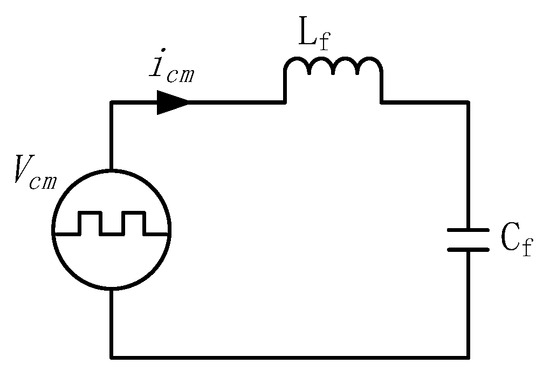
Figure 2. Common-mode (CM) voltage and current equivalent circuit for three-level inverter with ILC filter, without C_pv considered.

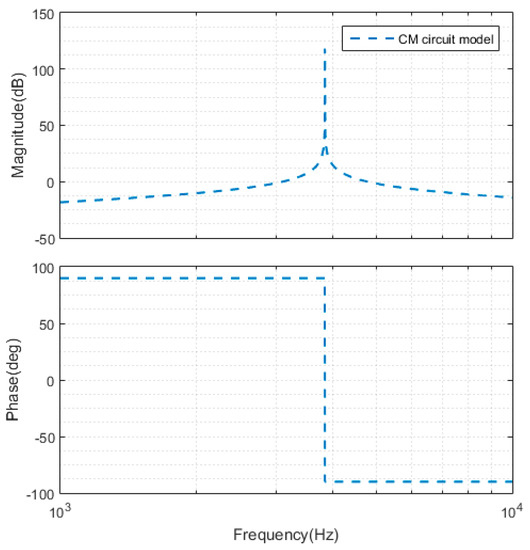
Figure 3. Bode diagram of CM LC circuit.

3. Harmonics Comparison of Zero Sequence Quantity of DPWM and CPWM

The symmetrical PWM [18,19] is used as CPWM in this paper. The zero sequence quantity of symmetrical PWM is given by Equation (5). A detailed description of DPWM used in this paper can be found in [16]. The zero sequence quantity of DPWM used in this paper is given by Equations (6) and (7) [20]. DPWM is widely used in the PV string inverter for its higher efficiency than that of CPWM.

$$V_z=-0.5(V_{max}+V_{min})$$

(5)

$$V_{{}_{\mathrm{x}}}^{\prime }=(V_x+\frac{V_{dc}}{2})\mathrm{mod}(\frac{V_{dc}}{2})-\frac{V_{dc}}{4}$$

(6)

$$V_z=\mathrm{sign}(V_{max}^{\prime })\cdot \frac{V_{dc}}{4}-V_{max}^{\prime }$$

(7)

where V_z is zero sequence quantity, V_x is three-phase voltage,$V_x^{\prime }$ is the intermediate variable, x = a, b, c. $V_{max}^{\prime }$ is the voltage among$V_x^{\prime }$ which have maximum absolute value. (a mod b) delivers the remainder of the division a/b.

The zero sequence quantity of CPWM and DPWM according to different modulation index and time are shown in Figure 4a,c, respectively. Using discrete Fourier transform, the harmonics comparison of zero sequence quantity between CPWM and DPWM are shown in Figure 4b,d respectively, which shows that the zero sequence quantity of DPWM contains more harmonics than that of CPWM. Hence, the zero sequence quantity of DPWM can lead to more serious CM current resonance than that of CPWM. As is shown in Figure 5, when the modulation method is changed from DPWM to CPWM, the resonance of CM current in i_o is alleviated.

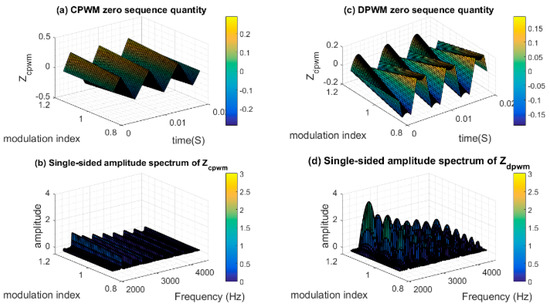
Figure 4. Harmonics comparison between continuous pulse-width modulation (CPWM) and discontinuous pulse-width modulation (DPWM). (a) CPWM zero sequence quantity. (b) PPWM zero sequence quantity. (c) Single-sided amplitude spectrum of Z_CPWM. (d) Single-sided amplitude spectrum of Z_DPWM.

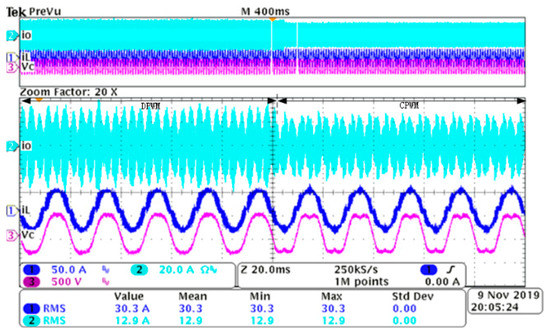
Figure 5. CM current resonance comparison between CPWM and DPWM at 30A i_L.

4. The Proposed VNRBAD Method for CM Current Resonance

4.1. VNRBAD for CM Current Resonance

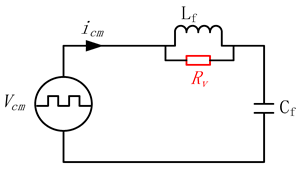
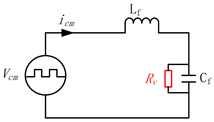
In order to suppress the CM current resonance, VNRBAD is proposed in this subsection. Using the same method as in [10], a general block diagram of the equivalent CM current power stage is proposed, as is shown in Figure 6. Although the same method as in [10] is used, it should be noticed that the analysis equivalent circuit are the major difference: model in [10] is for and only for DM circuit and DM current resonance damping, model in this paper focus on CM circuit and CM current resonance damping. G_ad is a VNRBAD controller and is given by Equation (8). G_t is the transfer function from i_CM to inductor current i_L, capacitor current i_c, or capacitor voltage v_c, and is given by Equation (9). The virtual negative resistor has three positions in the modified equivalent CM circuit, and the feedback variable can be i_L, i_c or v_c. The modified power stage and its corresponding G_ad is given in Table 1 without considering the delay effects.

$$G_{ad}=\frac{G_p-G_{pm}}{G_{pm}{G}_p{G}_t}$$

(8)

where, G_p is the power stage circuit transfer function, G_pm is the modified power stage circuit transfer function, G_t is the transfer function from i_CM to i_L, i_c or v_c.

$${\mathrm{G}}_{\mathrm{t}}=\{\begin{array}{l}\frac{{\mathrm{i}}_{\mathrm{CM}}}{i_L}=1,or\\ \frac{i_{\mathrm{CM}}}{i_c}=1, or\\ \frac{i_{\mathrm{CM}}}{v_c}=CS\end{array}$$

(9)

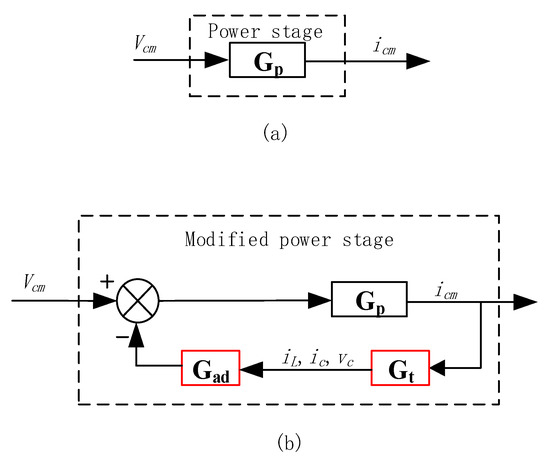
Figure 6. Block diagram of CM power stage. (a) Power stage, (b) modified power stage.

Table 1. Different forms of G_ad(s) with different filter state variables for active damping (AD).

Connection Type of the Virtual Negative Resistor Rv	Modified Power Stage	Variable Feedback for the Active Damping
		iL or ic	vc
	$\frac{\mathrm{CS}}{\mathrm{LC}{\mathrm{S}}^2+R_v\mathrm{CS}+1}$	$R_v$	$R_v\mathrm{CS}$
	$\frac{\mathrm{LC}{\mathrm{S}}^2+R_v\mathrm{CS}}{R_v\mathrm{CL}{\mathrm{S}}^2+\mathrm{LS}+R_v}$	$-\frac{{\mathrm{L}}^2{\mathrm{S}}^2}{\mathrm{LS}+R_v}$	$-\frac{{\mathrm{L}}^2\mathrm{C}{\mathrm{S}}^3}{\mathrm{LS}+R_v}$
	$\frac{R_v\mathrm{CS}+1}{R_v\mathrm{LC}{\mathrm{S}}^2+\mathrm{LS}+R_v}$	$-\frac{1}{R_v{\mathrm{C}}^2{\mathrm{S}}^2+\mathrm{CS}}$	$-\frac{\mathrm{CS}}{R_v{\mathrm{C}}^2{\mathrm{S}}^2+\mathrm{CS}}$

Using the parameters in Table 2, the bode diagram comparison between the original equivalent power stage and the three modified equivalent power stages are given in Figure 7, Figure 8 and Figure 9, respectively. From these bode diagrams, it can be seen that the virtual negative resistor connected in series with the inductor has the best AD performance. Once the connection type of virtual negative resistor is selected, G_ad = R_v is selected from Table 1 for simple implementation purposes.

Table 2. Photovoltaic (PV) string inverter parameters.

Item	Symbol	Value
Filter capacitor	Cf	18 μF
Inverter-side filter inductor	Lf	95 μH at 80A
rate power	P	80 kW
grid line voltage	Vg	540 V
DC voltage	Vdc	800 V
switch frequency	fs	16 kHz

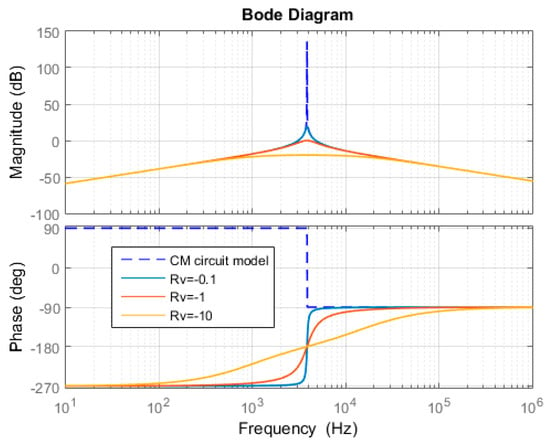
Figure 7. Bode diagram of CM power stage: without R_v and with R_v connected in series with L_f.

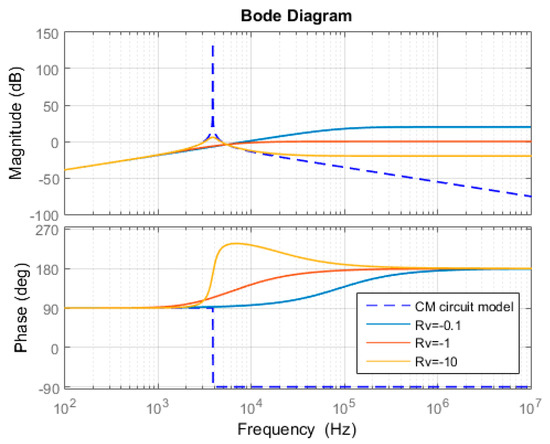
Figure 8. Bode diagram CM power stage: without R_v and with R_v connected in parallel with L_f.

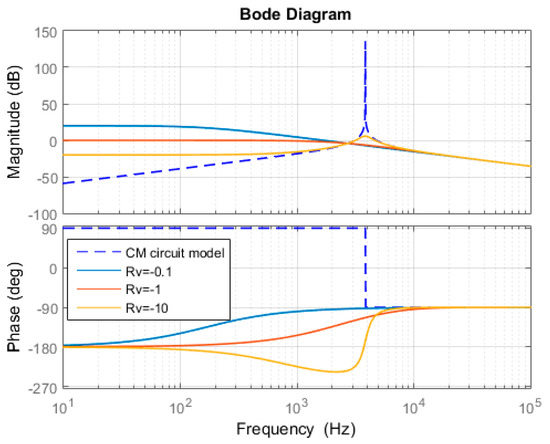
Figure 9. Bode diagram CM power stage: without R_v and with R_v connected in parallel with C_f.

The virtual negative resistor connected in series with the inductor and G_ad = R_v is applied in this paper. The 1.5 times sample period T_s delay is considered, and is given in Equation (10) which composed of computational and PWM delays in the digital control [10]. Since only the harmonics at CM resonance frequency f_r is the harmonics needed to damp and usually it is high-order harmonics, the high pass filter (HPF) is applied to cut off the low frequency harmonics in i_CM, and is given in Equation (11). The cutoff frequency f_c can be chosen as a frequency which lower than f_r. In this paper, f_r is higher than 2000 Hz, and 1000 Hz is used as f_c. The CM current resonance AD control loop with delay and HPF considered is shown in Figure 10. Its bode diagram with different virtual negative resistor values is shown in Figure 11, which shows that the admittance at resonance frequency can be effectively damped with a proper R_v.

$${\mathrm{G}}_{\mathrm{d}}= {\mathrm{e}}^{-1.5\mathrm{Ts}S}$$

(10)

$$\mathrm{HPF}=\frac{S}{S+2\pi f_c}$$

(11)

where, T_s is the sample period, f_c is the cutoff frequency of the first order high pass filter.

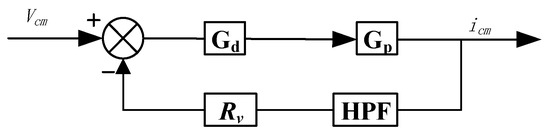
Figure 10. Common mode current suppression control loop.

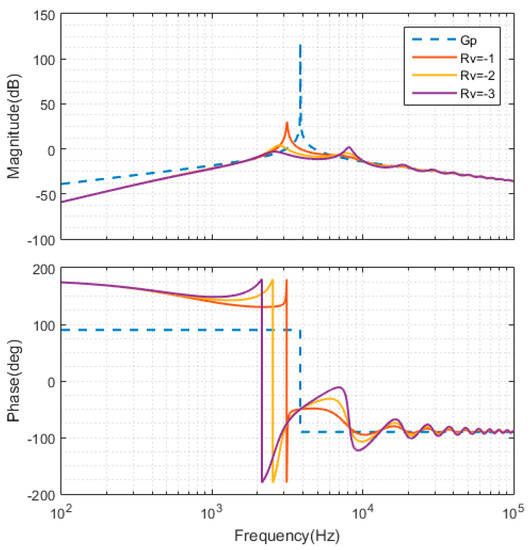
Figure 11. i_L or i_c feedback based virtual negative resistor with delay considered.

4.2. The Implementation of VNRBAD for DPWM Application

In [14], the output of CM current controller d_CM is added into three final modulation quantities in CPWM application, as is shown in Figure 12 and Equation (12). However, it cannot be used in DPWM application. For example, if phase A is clamped to positive bus voltage, m_a is clamped to 1, and d_z can be arrived in Equation (13). Substituting Equation (13) into Equation (12), the final three modulation quantity m_a, m_b, m_c can be calculated in Equation (14). From Equation (14), it can be seen that d_CM have no effects on m_a, m_b, and m_c, which means the d_CM cannot be added directly into three final modulation quantities in DPWM application.

$$\left[\begin{array}{l}{m}_a\\ m_b\\ m_c\end{array}\right]=\left[\begin{array}{l}{d}_{\mathrm{DM}a}\\ d_{\mathrm{DM}b}\\ d_{\mathrm{DM}c}\end{array}\right]+\left[\begin{array}{l}{d}_z\\ d_z\\ d_z\end{array}\right]+\left[\begin{array}{l}{d}_{\mathrm{CM}}\\ d_{\mathrm{CM}}\\ d_{\mathrm{CM}}\end{array}\right]$$

(12)

where, m_a, m_b, m_c are three final modulation quantities, respectively; d_DMa, d_DMb, d_DMc are three-phase components of DM current controller outputs; d_CM is the CM R_v outputs, d_z is the zero sequence quantity of DPWM.

$$d_z=1-d_{\mathrm{DM}a}-d_{\mathrm{CM}}$$

(13)

$$\left[\begin{array}{l}{m}_a\\ m_b\\ m_c\end{array}\right]=\left[\begin{array}{l}1\\ d_{\mathrm{DM}b}+1-d_{\mathrm{DM}a}\\ d_{\mathrm{DM}c}+1-d_{\mathrm{DM}a}\end{array}\right]$$

(14)

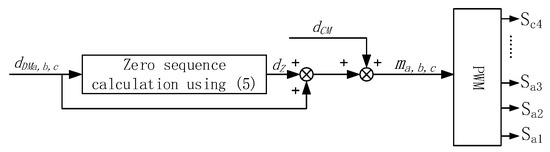
Figure 12. d_CM implementation in CPWM application [14].

The implementation of the proposed method for DPWM application is indirect. Figure 13 show the voltage space vectors in the $\mathsf{\alpha }\mathsf{\beta }$ reference frame for a three-level inverter. Based on voltage vector synthesis principle, once a reference DM voltage vector V_ref in sector I in the $\mathsf{\alpha }\mathsf{\beta }$ reference frame is given as a constant voltage vector, the dwell times t₁, t₁₁ and t₀₁ will be known constant quantities, as is shown in Equation (15) when using CPWM and in Equation (16) when using DPWM. Similarly, the CM voltage V_{CM_cpwm} using CPWM and V_{CM_dpwm} using DPWM is acquired in Equations (17) and (18). From Equation (17), it can be seen that V_{CM_cpwm} can be controlled by adjusting the distribution factor k without needing to adjust dwell times t₁, t₁₁ and t₀₁, which means that there is no coupling relationship between V_{CM_cpwm} and V_ref. In CPWM application, DM duty cycle which controls inductor DM current and CM duty cycle which controls inductor CM current are decoupled by a pair of small voltage vectors. In this example, the small voltage vectors are V_{01_POO} and V_{01_ONN}.

$$V_{ref}=\frac{t_1{V}_1+t_{11}{V}_{11}+k{t}_{01}{V}_{01\_POO}+(1-k)t_{01}{V}_{\mathrm{01}\_ONN}}{T_s}$$

(15)

$$V_{ref}=\frac{t_1{V}_1+t_{11}{V}_{11}+t_{01}{V}_{01\_POO}}{T_s}$$

(16)

$$V_{\mathrm{CM}\_cpwm}=\frac{-t_1\frac{V_{dc}}{2}+t_{01}k\frac{V_{dc}}{2}-t_{01}(1-k)V_{dc}}{T_s}$$

(17)

$$V_{\mathrm{CM}\_dpwm}=\frac{-t_1\frac{V_{dc}}{2}+t_{01}\frac{V_{dc}}{2}}{T_s}$$

(18)

where, V_ref is the DM voltage vector in the $\mathsf{\alpha }\mathsf{\beta }$ reference frame, V_{CM_cpwm} and V_{CM_dpwm} are the CM voltage when using CPWM and DPWM respectively. T_s is the switching period, T_s = t₁ + t₁₁ + t₀₁. t₁, t₁₁, and t₀₁ are the dwell time of voltage vector V₁, V₁₁, and V₀₁ in Figure 13, respectively. V_{01_ONN} and V_{01_POO} are a pair of small vectors V₀₁. k is the distribution factor for V_{01_ONN} and V_{01_POO}, and 0 < k < 1.

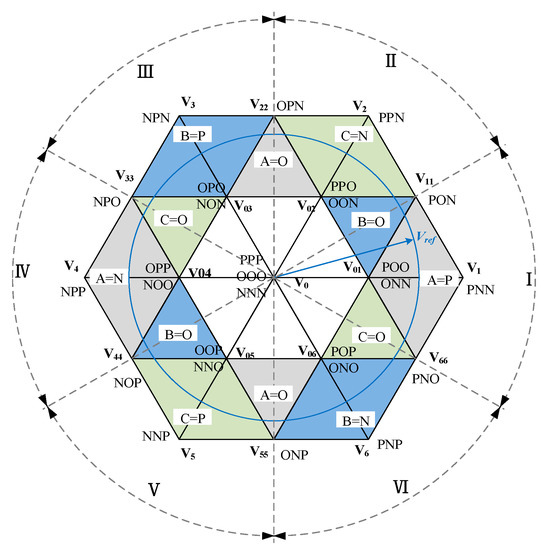
Figure 13. Voltage space vectors for three-level inverter.

In DPWM application, however, there is no a pair of small voltage vectors. According to Equation (16), if V_ref is a given vector, then t₁, t₁₁, and t₀₁ are known constant quantities. According to Equation (18), if t₁, t₁₁, and t₀₁ are known constant quantities, V_{CM_dpwm} will be a constant quantity, which means that there is a coupling relationship between V_{CM_dpwm} and V_ref by dwell time t₁ and t₀₁. The only way to control V_{CM_dpwm} is to adjust t₁ and t₀₁, which means that V_{CM_dpwm} can only be controlled by adjusting V_ref. V_ref can be adjusted by compensating one of the three specific compensating vector V_cpi (i = A,B,C). The three specific compensating voltage vectors are shown in Figure 14a. As is shown in Figure 14b, when phase A is clamped to positive bus voltage, the vector V_cpA can be used to compensate V_ref to increase the dwell time t₁ of voltage vector V₁ in Equation (18) [21], which can decrease V_{CM_dpwm}. In Figure 14c, V_ref is clamped to bus neutral point O. By compensating V_ref with V_cpA, the dwell time of voltage vector V₀₃ is decreased, which can decrease V_{CM_dpwm}. Similarly, when phase A is clamped to negative bus voltage, the vector V_cpA can be used to compensated V_ref to decrease the dwell time of voltage vector V₄, which can decrease V_{CM_dpwm}. To sum up, when phase A is clamped to DC bus positive, negative, or neutral point voltage, the vector V_cpA can be used to compensated V_ref to decrease V_{CM_dpwm}.

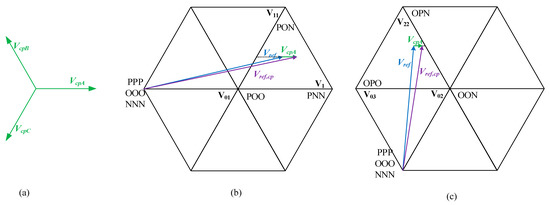
Figure 14. (a) Three compensation vectors for phase A,B,C; (b)V_ref compensation when phase A is clamped to positive bus voltage; (c) V_ref compensation when phase A is clamped to bus neutral point O.

Similar analysis can be implemented when phase B,C is clamped to DC bus positive, negative, or neutral point voltage. It can be arrived that V_{CM_dpwm} can be decreased by compensating V_ref with V_cpi (i = A,B,C) when phase i (i = A,B,C) is clamped to bus positive, negative, or neutral point voltage.

V_ref compensation is implemented in an abc reference frame. As is given in Equation (19), the compensating voltage vector V_cpi (i = A,B,C) in $\mathsf{\alpha }\mathsf{\beta }$ reference frame can be converted to three-phase components d_{CM_DMa}, d_{CM_DMb}, d_{CM_DMc} in the abc reference frame using inverse Clarke transform seen in Equation (20). d_CM is the output CM voltage of R_v and determine the amplitude and sign of V_cpi (i = A,B,C). K_fa, K_fb, K_fc are coefficients which determine the angle of V_cpi (i = A,B,C). As is given in Equation (21), K_fa, K_fb, and K_fc is a value chosen from 1, −0.5, and −0.5 for simplification purposes. The value 1 is for the phase which is clamped to bus positive, negative, or neutral point voltage. The value −0.5 is for the remaining two phases. The judgment of clamped phase is based on sector detection algorithm in [21] and DPWM method in [16]. The final three-phase modulation quantities are given in Equation (22). The implementation diagram of VNRBAD for DPWM application is given in Figure 15.

$$\left[\begin{array}{l}{d}_{\mathrm{CM}}{\_}_{\mathrm{DM}a}\\ d_{\mathrm{CM}}{\_}_{\mathrm{DM}b}\\ d_{\mathrm{CM}}{\_}_{\mathrm{DM}c}\end{array}\right]=d_{\mathrm{CM}}\left[\begin{array}{l}{K}_{fa}\\ K_{fb}\\ K_{fc}\end{array}\right]$$

(19)

$${\mathrm{T}}_{\alpha \beta 2\mathrm{abc}}=\left[\begin{array}{l}1 0\\ -\frac{1}{2} \frac{\sqrt{3}}{2}\\ -\frac{1}{2} \frac{\sqrt{3}}{2}\end{array}\right]$$

(20)

$$\left[\begin{array}{l}{K}_{fa}\\ K_{fb}\\ K_{fc}\end{array}\right]=\{\begin{array}{l}\left[\begin{array}{l}1\\ -0.5\\ -0.5\end{array}\right] (\mathrm{when} \mathrm{A} is clamped)\\ \left[\begin{array}{l}-0.5\\ 1\\ -0.5\end{array}\right] (\mathrm{when} B is clamped)\\ \left[\begin{array}{l}-0.5\\ -0.5\\ 1\end{array}\right] (\mathrm{when} C isclamped)\end{array}$$

(21)

$$\left[\begin{array}{l}{m}_a\\ m_b\\ m_c\end{array}\right]=\left[\begin{array}{l}{d}_{\mathrm{DM}a}\\ d_{\mathrm{DM}b}\\ d_{\mathrm{DM}c}\end{array}\right]+\left[\begin{array}{l}{d}_{\mathrm{CM}\_\mathrm{DM}a}\\ d_{\mathrm{CM}\_\mathrm{DM}b}\\ d_{\mathrm{CM}\_\mathrm{DM}c}\end{array}\right]+\left[\begin{array}{l}{d}_z\\ d_z\\ d_z\end{array}\right]$$

(22)

where, d_{CM_DMa}, d_{CM_DMa}, d_{CM_DMa} are the CM adjust quantity added to d_DMa, d_DMb, and d_DMc, respectively. K_fa, K_fb, K_fc is the coefficient which transfers d_CM into three DM quantity d_DMa d_DMb, and d_DMc, respectively.

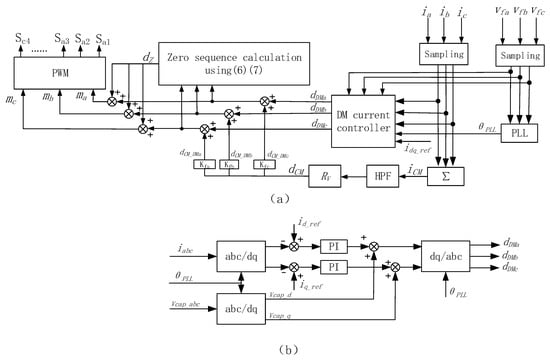
Figure 15. (a) The implementation of virtual negative resistor based AD (VNRBAD) for DPWM application. (b) The DM current controller.

5. Experiments and Discussion

In order to verify the effectiveness of the proposed VNRBAD method, experiments are implemented in a string inverter produced by TBEA Xi’an Electric Technology Co., Ltd. Grid simulators are used as load and PV simulators are used as DC power supply in the experiment. The specification of the inverter and experiment conditions are given in Table 2. Note that the inductance value of L_f is variable with current conducting through it. The value of 95 μH is a measurement value of L_f at 80A. The model number of devices used in the experiment are shown in Table 3.

Table 3. Model number of devices used in the experiment.

Device	Model Number
PV simulator	Chroma 62150H-1000S
Regenerative grid simulator	Chroma 61860
PV String inverter	TBEA TS80KTL_PLUS

5.1. The Value of R_v

As is shown in Figure 11, the smaller R_v value it is, the better CM current resonance suppression performance it is. However, R_v cannot be too small for better CM current resonance suppression, because it will degrade DM current injected to grid. Since the CM voltage is controlled by compensating DM voltage, the CM current resonance will be suppressed better when R_v is smaller, while the DM current will be overcompensated and is degraded. As is shown in Figure 16, when R_v is changed from −3 to −1.5, the CM current in i_o is worse, while the inductor current i_L and grid current i_g are better. Although the damp performance of i_o is better when R_v = −3, an apparent current distortion can be observed in i_L and i_g, which is because the amplitude of the compensated vector is too big. There must be a compromise between the damping performance of i_o and THD of i_g.

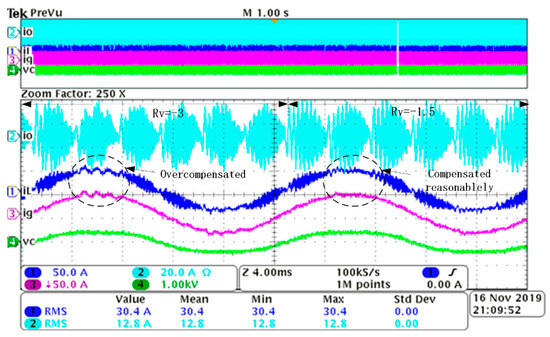
Figure 16. Waveform of i_o, i_L, i_g, and v_c with R_v varied from −3 to −1.5.

In practical application, there exist delays in the control loop which will degrade the CM current resonance suppression performance, so it is suggested that the value of R_v can be adjusted from −3 to 0 by hand.

5.2. Comparison between VNRBAD and Without VNRBAD under Different i_L

Based on the analysis of R_v above, −2 is chosen as the value of R_v in the experiments. The waveform comparison of i_o, i_L, i_g, and v_c between VNRBAD and without VNRBAD under different values of i_L is given in Figure 17 and Figure 18, respectively. Note that the CM current in i_L resonates heavily under 80A i_L when without VNRBAD, and the protection program of the control system is triggered to shut down the inverter. The proposed VNRBAD can suppress the CM current resonance effectively, although not completely. The harmonics of i_L is shown in Figure 19 and Figure 20, respectively. The harmonics at CM resonance frequency is reduced effectively.

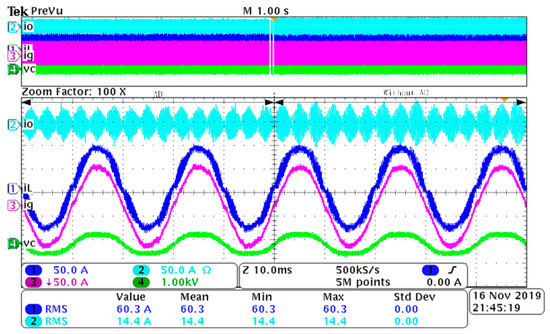
Figure 17. Waveform comparison of i_o, i_L, i_g, and v_c between AD and without AD under 60A i_L.

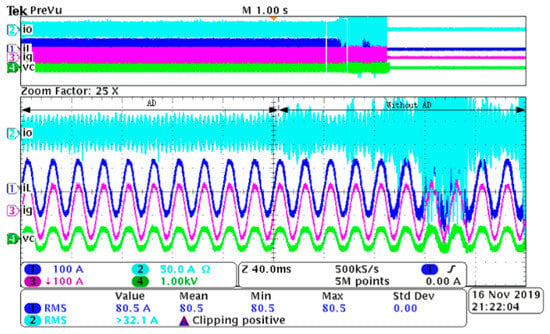
Figure 18. Waveform comparison of i_o, i_L, i_g, and v_c between AD and without AD under 80A i_L.

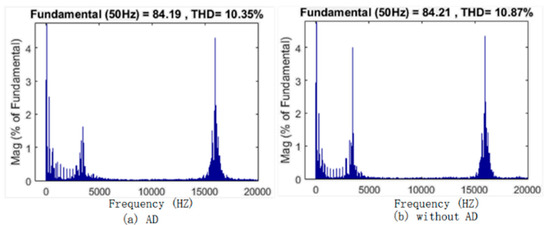
Figure 19. Harmonics comparison of i_L between AD and without AD at 60A i_L.

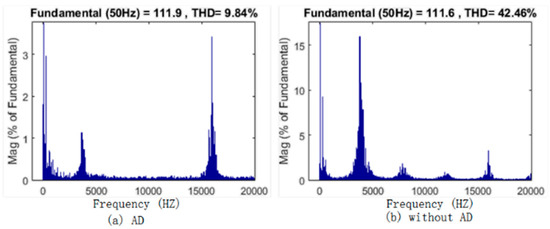
Figure 20. Harmonics comparison of i_L between AD and without AD at 80A i_L.

5.3. Discussion

The PD method with a 0.61 ohm resistor connected in series with the inductor in the CM circuit is also implemented. The waveform of i_o, i_L, and i_g using PD method is shown in Figure 21. The RMS value comparison of i_o of three methods under different i_L is shown in Figure 22. It can be seen that PD has a better CM current suppression performance compared with the proposed VNRBAD method.

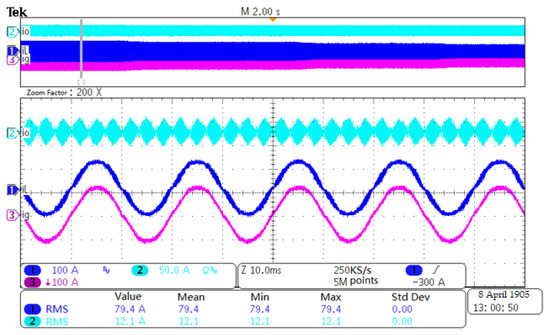
Figure 21. Waveform of i_o, i_L, and i_g under 80A i_L using PD.

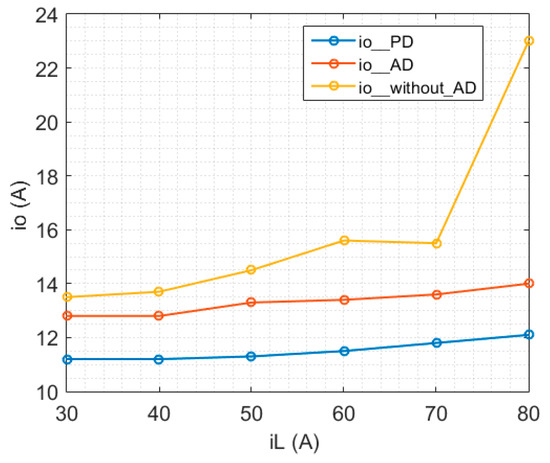
Figure 22. RMS value of i_o of three methods under different i_L.

Two reasons limit the CM resonance suppression performance of the proposed VNRBAD. One is that there is a compromise between the CM current control performance and DM current control performance. If R_v is too small, the CM resonance current damping performance is not good. On the contrary, too small values of R_v overcompensate DM voltage V_ref in $\mathsf{\alpha }\mathsf{\beta }$ reference frame and degrade the quality of DM current i_g. Another reason is the delay in the control loop which can be studied further. Although the damping performance of the proposed VNRBAD method is not as good as PD, VNRBAD can suppress the CM current resonance within an acceptable range to let the inverter operate normally in DPWM application.

6. Conclusions

In this paper, VNRBAD is proposed to suppress the CM current resonance for a three-level grid-tied inverter with DPWM. The harmonics comparison of zero sequence quantity between DPWM and CPWM is presented, which shows DPWM has more harmonics than that of CPWM. In DPWM application, the CM voltage and DM voltage is coupled. VNRBAD is implemented by compensating the DM voltage to control the CM voltage. Experimental results demonstrate the effectiveness of VNRBAD. Although VNRBAD is not as good as PD in the experiments, VNRBAD can suppress the CM current resonance within an acceptable range and does not need additional PD power resistor. Future work will focus on the reduction of the delay in the control loop which can enhance the CM current resonance suppression performance of the proposed VNRBAD method.