Optimal Battery Storage Participation in European Energy and Reserves Markets
Abstract
1. Introduction
2. Literature Review and Contributions
3. Mathematical Formulation
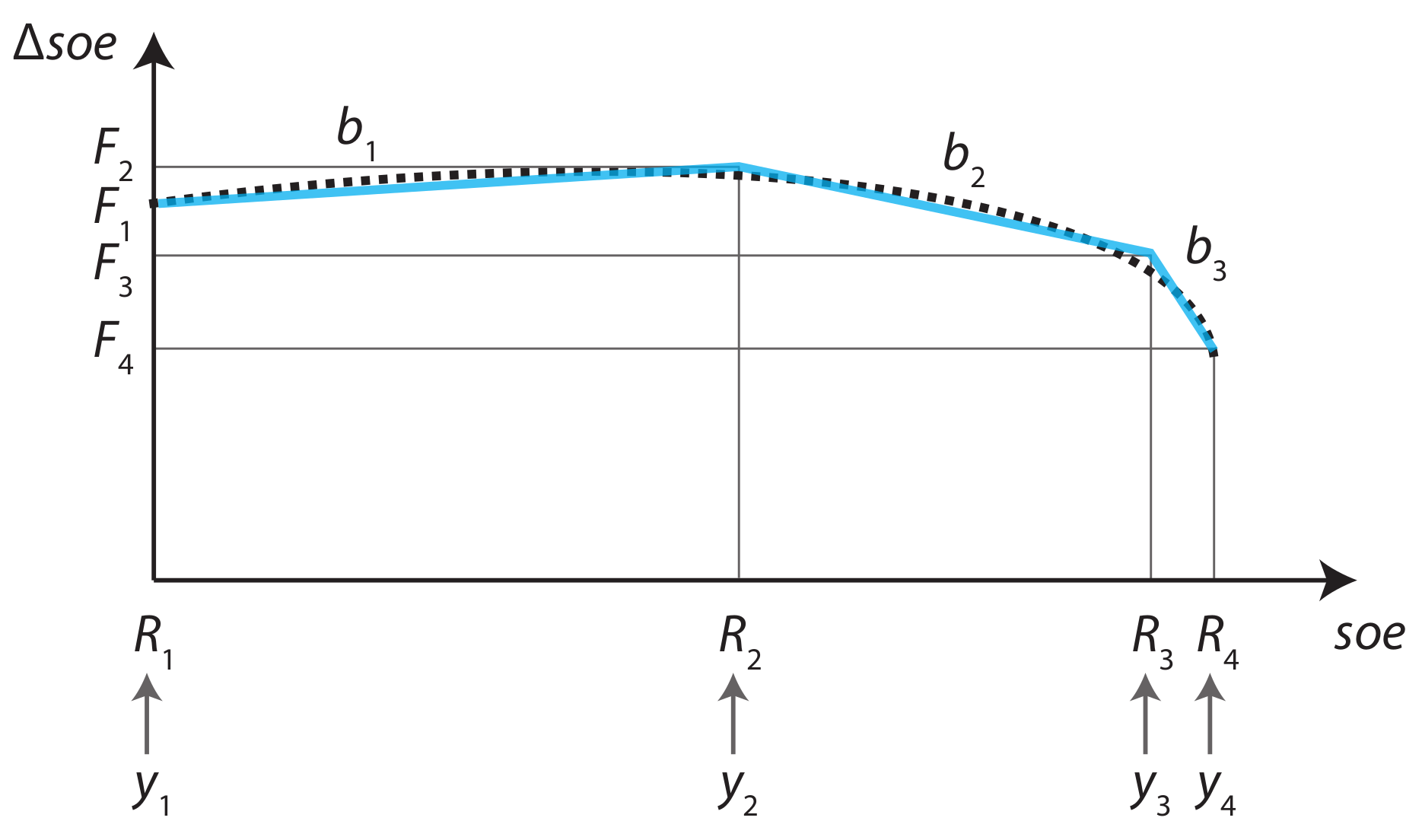
3.1. Nomenclature
| I | Set of generation units, indexed by i. |
| J | Set of battery charging curve linear parts, indexed by j. |
| S | Set of reserve activation scenarios, indexed by s. |
| T | Set of time periods, indexed by t. |
| Generator i down reserve activation price (€/MWh). | |
| Generator i up reserve activation price (€/MWh). | |
| Battery storage down reserve activation price (€/MWh). | |
| Battery storage up reserve activation price (€/MWh). | |
| Battery storage down reserve capacity price (€/MW). | |
| Battery storage up reserve capacity price (€/MW). | |
| Generator i down reserve capacity price (€/MW). | |
| Generator i up reserve capacity price (€/MW). | |
| Generator i maximum down reserve capacity (MW). | |
| Generator i maximum up reserve capacity (MW). | |
| Maximum amount of energy that can be charged at specific state-of-energy breakpoint as a portion of . | |
| P | Battery storage maximum charging and discharging power (MW). |
| Capacity of each state-of-energy segment j as a portion of the maximum state-of-energy . | |
| Required down reserve capacity (MW). | |
| Required up reserve capacity (MW). | |
| Activated down reserve energy (MWh). | |
| Activated up reserve energy (MWh). | |
| Battery storage charging efficiency. | |
| Battery storage discharging efficiency. | |
| Day-ahead market price (€/MW). |
| Generator i activated down energy (MWh). | |
| Generator i activated up energy (MWh). | |
| Generator i down capacity reserved quantity (MW). | |
| Generator i up capacity reserved quantity (MW). | |
| Battery storage down reserve capacity bid (MW). | |
| Battery storage up reserve capacity bid (MW). | |
| Battery storage activated down reserve quantity in scenario s (MWh). | |
| Battery storage activated up reserve quantity in scenario s (MWh). | |
| Battery storage down reserved capacity (MW). | |
| Battery storage up reserved capacity (MW). | |
| Battery storage charging quantity (MW). | |
| Battery storage discharging quantity (MW). | |
| Battery storage state-of-energy (MWh). | |
| Down reserve activation clearing price in scenario s (€/MWh). | |
| Up reserve activation clearing price in scenario s (€/MWh). | |
| Down reserve capacity clearing price (€/MW). | |
| Up reserve capacity clearing price (€/MW). |
3.2. Initial Problem Formulation
3.3. KKT Conditions of the Lower-Level Problem
4. Case Study
4.1. Input Data
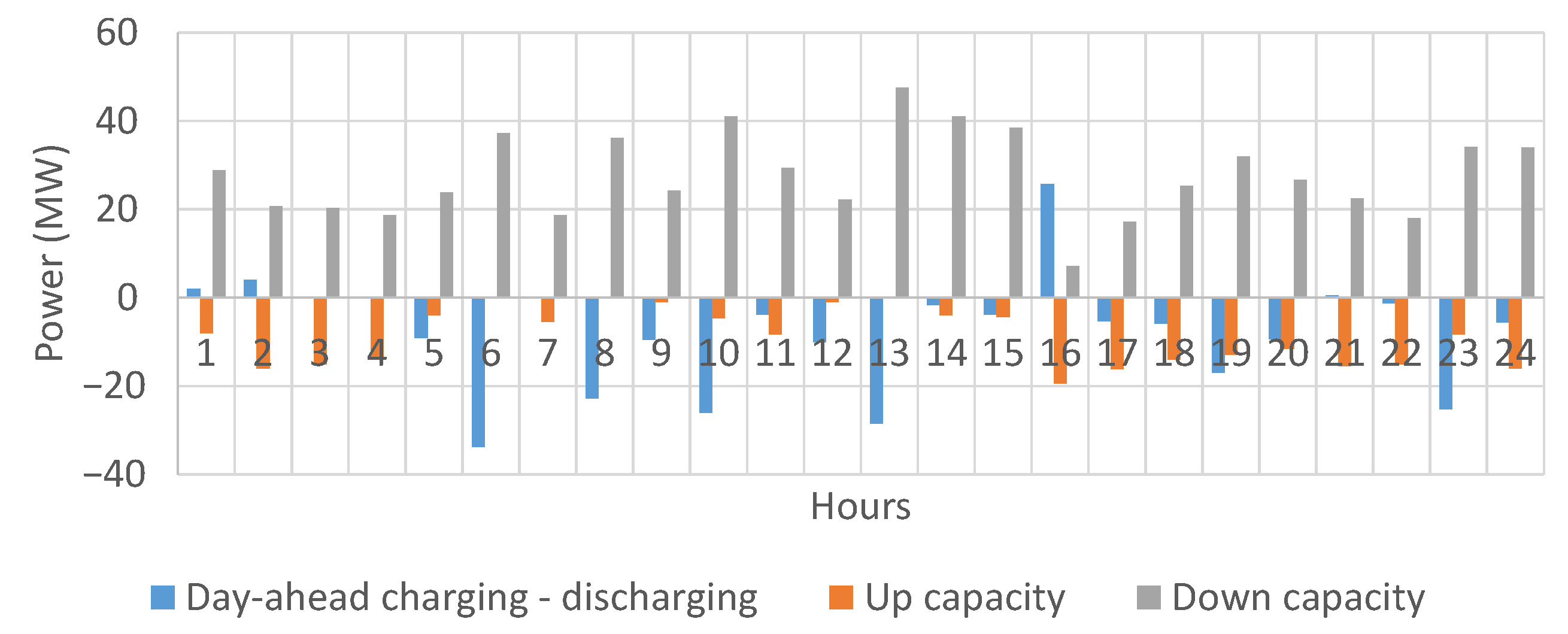
4.2. Results
4.3. Sensitivity Analysis
4.4. Comparison to a Baseline Model
- First we solve only the lower-level problem (2) without battery storage bids, i.e., setting and to zero. This is needed to obtain the capacity reservation and activation prices , , and .
- Then we solve the upper-level problem (1) using the capacity reservation and activation prices , , and from the previous step. Note that the capacity reservation and activation prices are treated as parameters as opposed to being treated as variables in the proposed formulation. The outcome is the battery storage day-ahead and reserves bids.
- Finally, we solve the lower-level problem (2) again, but this time with battery storage bids and from the previous step. This calculation provides actual reserve capacity and activation prices (note that these may differ from those obtained in step 1) as well as cleared battery storage quantities and profit.
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| AESO | Alberta Electric System Operator |
| aFRR | Automatic Frequency Restoration Reserve |
| FCR | Frequency Containment Reserve |
| KKT | Karush–Kuhn–Tucker |
| MILP | Mixed-Integer Linear Program |
| MOL | Merit Order List |
| SOE | State-Of-Energy |
| TSO | Transmission System Operator |
References
- Official Journal of the European Union. Commission Regulation (EU) 2017/2195 of 23 November 2017 Establishing a Guideline on Electricity Balancing; European Commission, Directorate-General for Energy: Brussels, Belgium, 2017. [Google Scholar]
- Koch, C.; Hirth, L. Short-term electricity trading for system balancing: An empirical analysis of the role of intraday trading in balancing Germany’s electricity system. Renew. Sustain. Energy Rev. 2019, 113, 109275. [Google Scholar] [CrossRef]
- Lackner, C.; Nguven, T.; Byrne, R.H.; Wiegandt, F. Energy Storage Participation in the German Secondary Regulation Market. In Proceedings of the 2018 IEEE PES Transmission and Distribution Conference and Exposition (T&D), Denver, CO, USA, 16–19 April 2018; pp. 1–9. [Google Scholar]
- PICASSO Project TSOs. Consultation on the Design of the Platform for Automatic Frequency Restoration Reserve (AFRR) of PICASSO Region, The Platform for the International Coordination of Automated Frequency Restoration and Stable System Operation (PICASSO). 2017.
- Figgener, J.; Stenzel, P.; Kairies, K.P.; Linßen, J.; Haberschusz, D.; Wessels, O.; Angenendt, G.; Robinius, M.; Stolten, D.; Sauer, D.U. The development of stationary battery storage systems in Germany—A market review. J. Energy Storage 2020, 29, 101–153. [Google Scholar] [CrossRef]
- Simon, B. The German Energy Storage Market 2016–2021: The Next Energy Transition. In GTM Research Report; GTM Research: Boston, MA, USA, 2016. [Google Scholar]
- RTE—Le RéSeau de Transport De L’électricité; Electricity Report 2018; Réseau de Transport d’Électricité: Paris, France, 2019.
- Regelleistung.net. Internetplattform zur Vergabe von Regelleistung. 2019. Available online: https://www.regelleistung.net/ext/static/prl (accessed on 5 March 2019).
- Butler, P.C.; Iannucci, J.; Eyer, J. Innovative business cases for energy storage in a restructured electricity marketplace. In Sandia National Laboratories Report; Sandia National Laboratories: Albuquerqe, NM, USA, 2003. [Google Scholar]
- Eyer, J.M.; Iannucci, J.; Corey, G.P. Energy storage benefits and market analysis handbook. In Sandia National Laboratories Report; Sandia National Laboratories: Albuquerqe, NM, USA, 2004. [Google Scholar]
- Sioshansi, R.; Denholm, P.; Jenkin, T.; Weiss, J. Estimating the value of electricity storage in PJM: Arbitrage and some welfare effects. Energy Econ. 2009, 31, 269–277. [Google Scholar] [CrossRef]
- Akhavan-Hejazi, H.; Mohsenian-Rad, H. Optimal Operation of Independent Storage Systems in Energy and Reserve Markets With High Wind Penetration. IEEE Trans. Smart Grid 2014, 5, 1088–1097. [Google Scholar] [CrossRef]
- Kazemi, M.; Zareipour, H.; Amjady, N.; Rosehart, W.D.; Ehsan, M. Operation Scheduling of Battery Storage Systems in Joint Energy and Ancillary Services Markets. IEEE Trans. Sustain. Energy 2017, 8, 1726–1735. [Google Scholar] [CrossRef]
- Fleer, J.; Zurmuhlen, S.; Meyer, J.; Badeda, J.; Stenzel, P.; Hake, J.-F.; Sauer, D. Price development and bidding strategies for battery energy storage systems on the primary control reserve market. Energy Procedia 2017, 135, 143–157. [Google Scholar] [CrossRef]
- Fleer, J. Techno-economic evaluation of battery energy storage systems on the primary control reserve market under consideration of price trends and bidding strategies. J. Energy Storage 2018, 17, 345–356. [Google Scholar] [CrossRef]
- Gomes, I.L.R.; Pousinho, H.M.I.; Melício, R.; Mendes, V.M.F. Stochastic coordination of joint wind and photovoltaic systems with energy storage in day-ahead market. Energy 2017, 124, 310–320. [Google Scholar] [CrossRef]
- Miletić, M.; Pandžić, H.; Yang, D. Operating and Investment Models for Energy Storage Systems. Energies 2020, 13, 4600. [Google Scholar] [CrossRef]
- Alberta Electric System Operator AESO. Comparison Between Sequential Selection and Co-Optimization Between Energy and Ancillary Service Markets; Technical Report; AESO: Calgary, AB, Canada, 2018. [Google Scholar]
- Pavić, I.; Dvorkin, Y.; Pandžić, H. Energy and Reserve Co-optimization—Reserve Availability, Lost Opportunity and Uplift Compensation Cost. IET Gener. Trans. Dis. 2019, 13, 229–237. [Google Scholar] [CrossRef]
- Ehsani, A. A Proposed Model for Co-Optimization of Energy And Reserve In Competitive Electricity Market. Appl. Math. Model. 2009, 33, 92–109. [Google Scholar] [CrossRef]
- Chen, Y.; Gribik, P.; Gardner, J. Incorporating Post Zonal Reserve Deployment Transmission Constraints Into Energy and Ancillary Service Co-Optimization. IEEE Trans. Power Syst. 2014, 29, 537–549. [Google Scholar] [CrossRef]
- Ela, E.; Milligan, M.; Kirby, B. Operating Reserves and Variable Generation. In National Renewable Energy Laboratory Report; National Renewable Energy Laboratory: Golden, CO, USA, 2011. [Google Scholar]
- Chen, Y.; Wan, J.; Ganugula, V.; Merring, R.; Wu, J. Evaluating Available Room for Clearing Energy and Reserve Products under Midwest ISO Co-Optimization Based Real Time Market. In Proceedings of the 2010 IEEE PES General Meeting, Providence, RI, USA, 25–29 July 2010. [Google Scholar]
- Hassan, M.W.; Rasheed, M.B.; Javaid, N.; Nazar, W.; Akmal, M. Co-Optimization of Energy and Reserve Capacity Considering Renewable Energy Unit with Uncertainty. Energies 2018, 11, 2833. [Google Scholar] [CrossRef]
- Zeh, A.; Müller, M.; Naumann, M.; Hesse, H.C.; Jossen, A.; Witzmann, R. Fundamentals of Using Battery Energy Storage Systems to Provide Primary Control Reserves in Germany. Batteries 2016, 2, 29. [Google Scholar] [CrossRef]
- Goebel, C.; Jacobsen, H. Aggregator-Controlled EV Charging in Pay-as-Bid Reserve Markets with Strict Delivery Constraints. IEEE Trans. Power Syst. 2016, 31, 4447–4461. [Google Scholar] [CrossRef]
- Merten, M.; Rücker, F.; Schoeneberger, I.; Sauer, D.U. Automatic frequency restoration reserve market prediction: Methodology and comparison of various approaches. Appl. Energy 2020, 268, 114978. [Google Scholar] [CrossRef]
- Merten, M.; Olk, C.; Schoeneberger, I.; Sauer, D.U. Bidding strategy for battery storage systems in the secondary control reserve market. Appl. Energy 2020, 268, 114951. [Google Scholar] [CrossRef]
- Pandžić, H.; Bobanac, V. An Accurate Charging Model of Battery Energy Storage. IEEE Trans. Power Syst. 2019, 4, 1416–1426. [Google Scholar]
- Conejo, A.J.; Castillo, E.; Minguez, R.; Garcia-Bertrand, R. Decomposition Techniques in Mathematical Programming; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Pandžić, H.; Dvorkin, Y.; Carrion, M. Investments in merchant energy storage: Trading-off between energy and reserve markets. Appl. Energy 2018, 230, 277–286. [Google Scholar] [CrossRef]
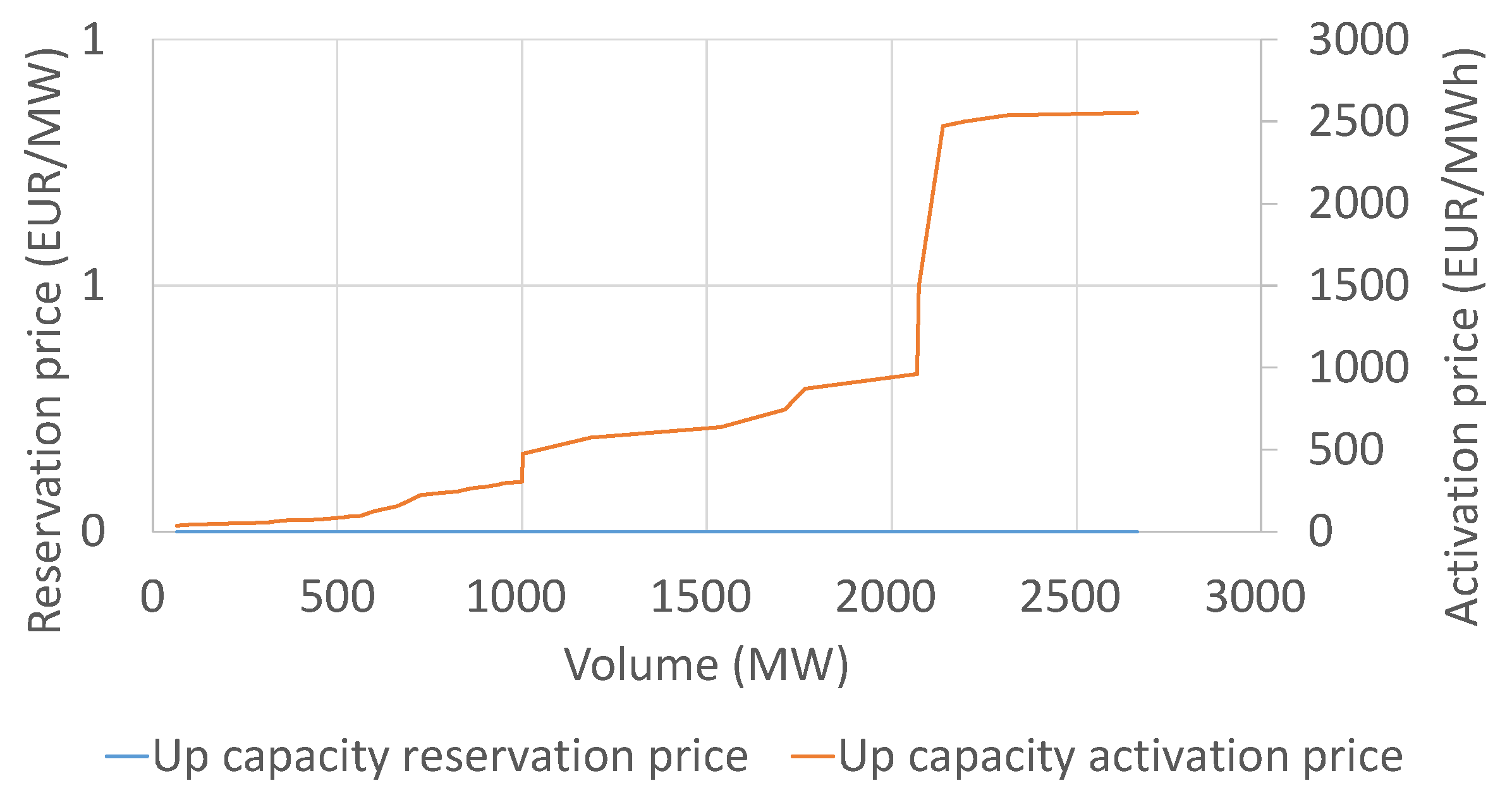


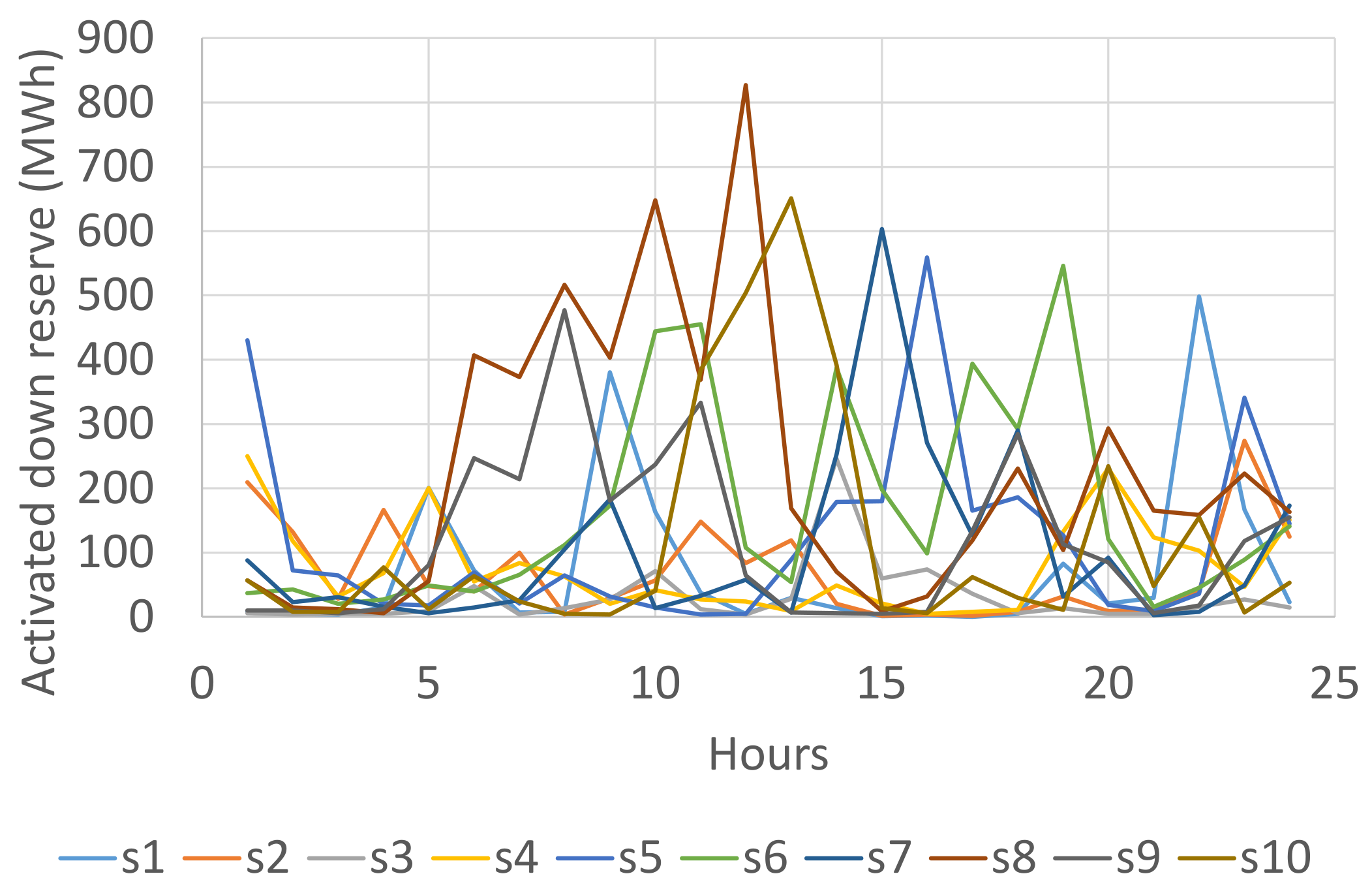
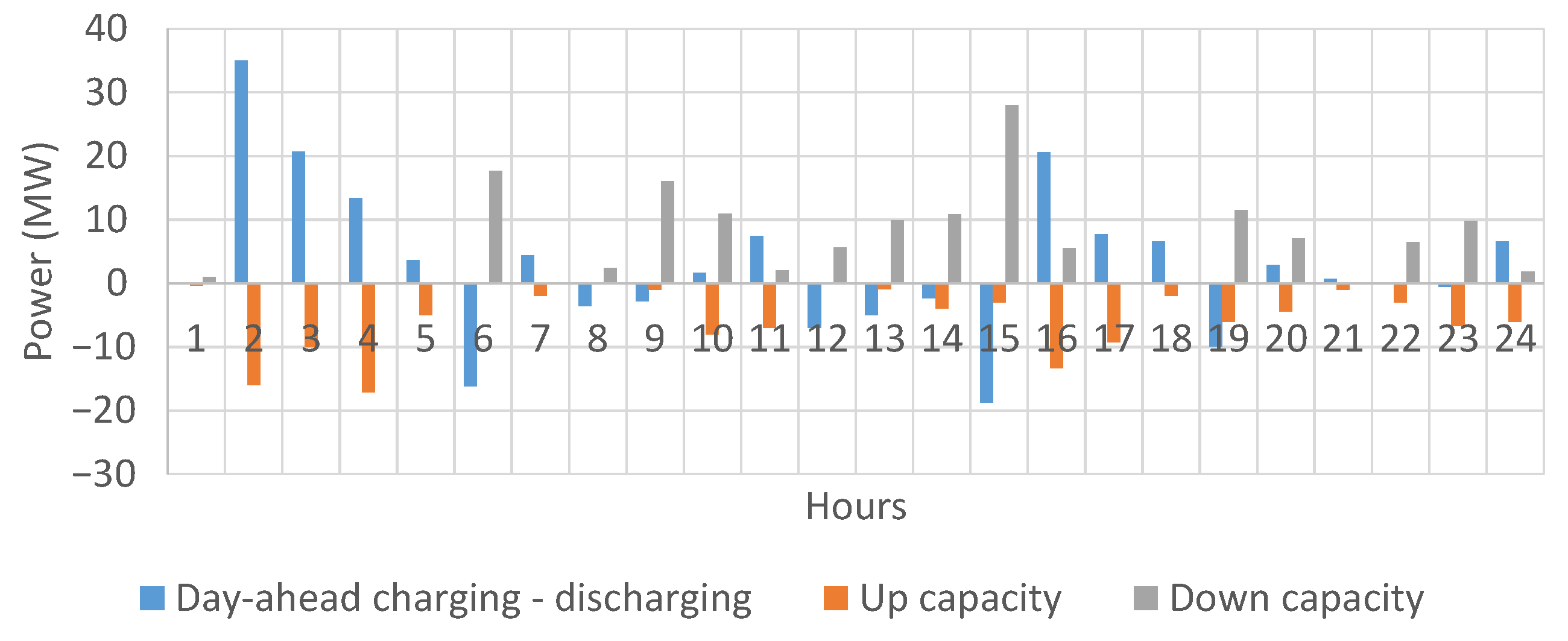
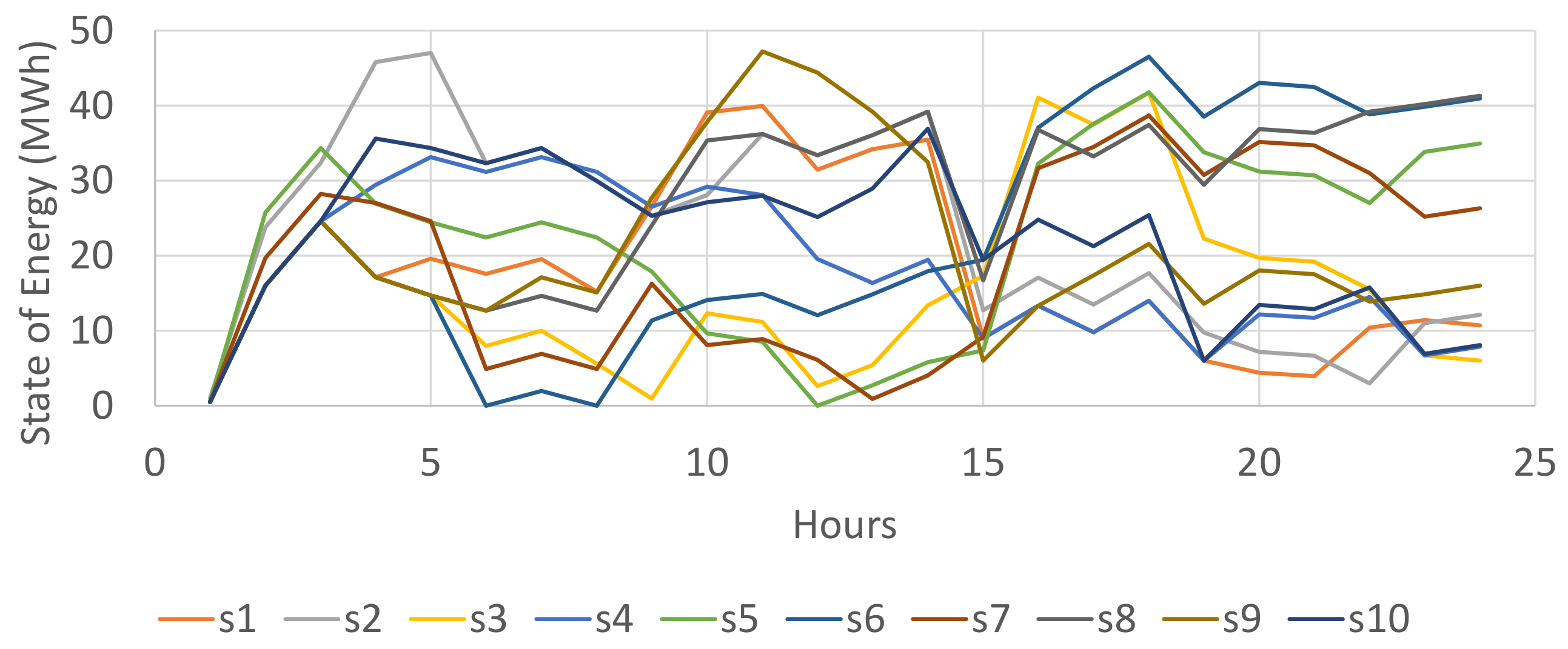
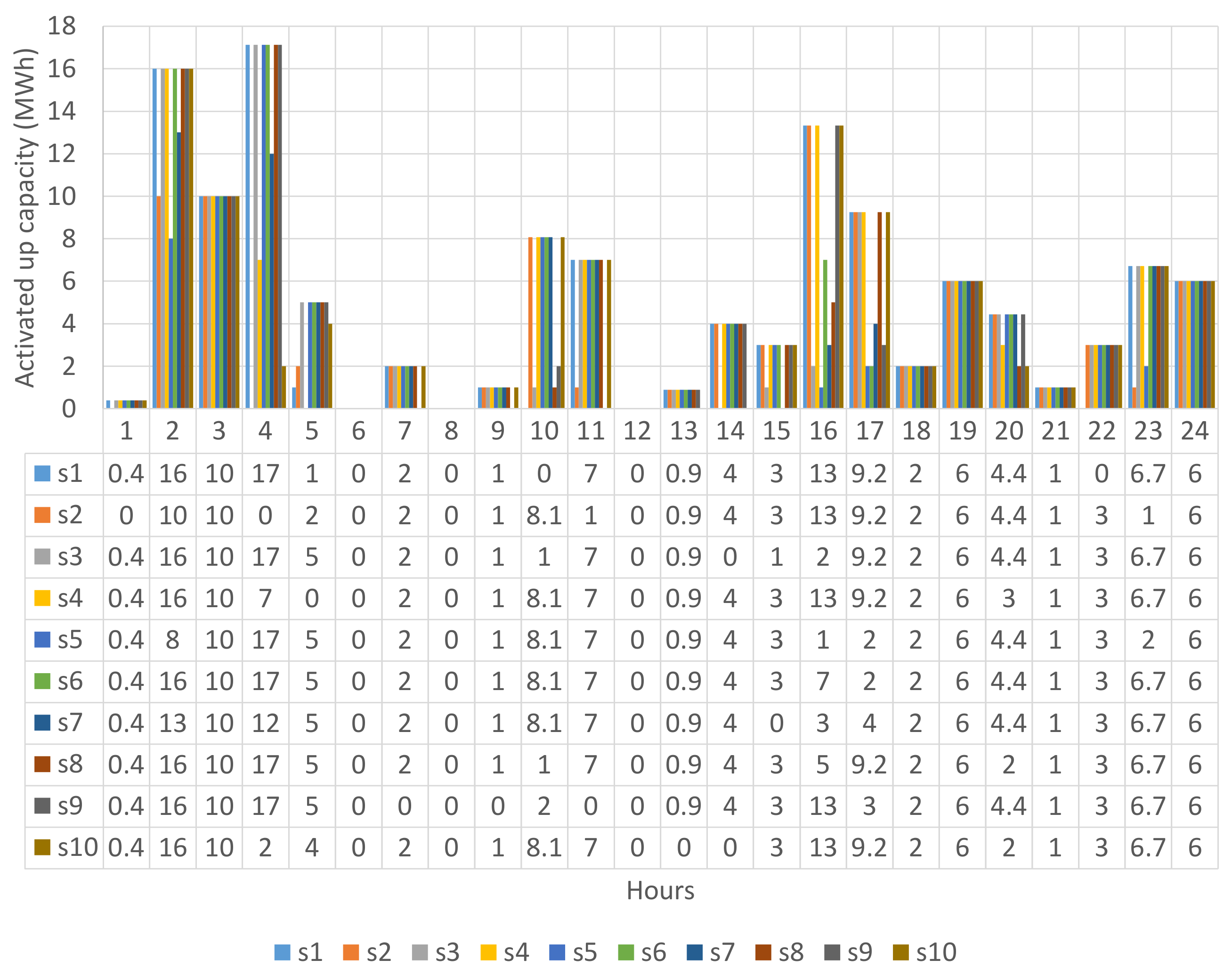
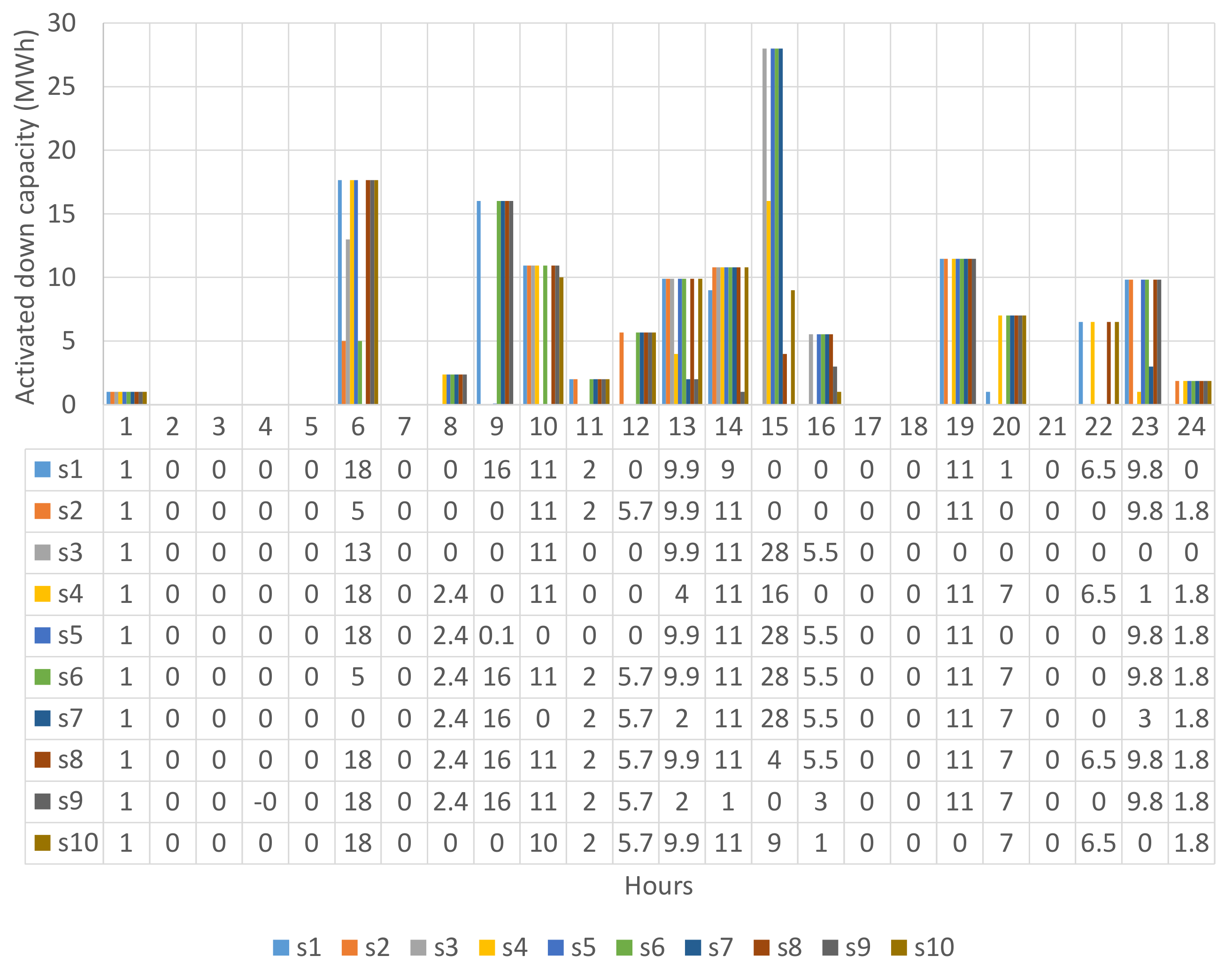
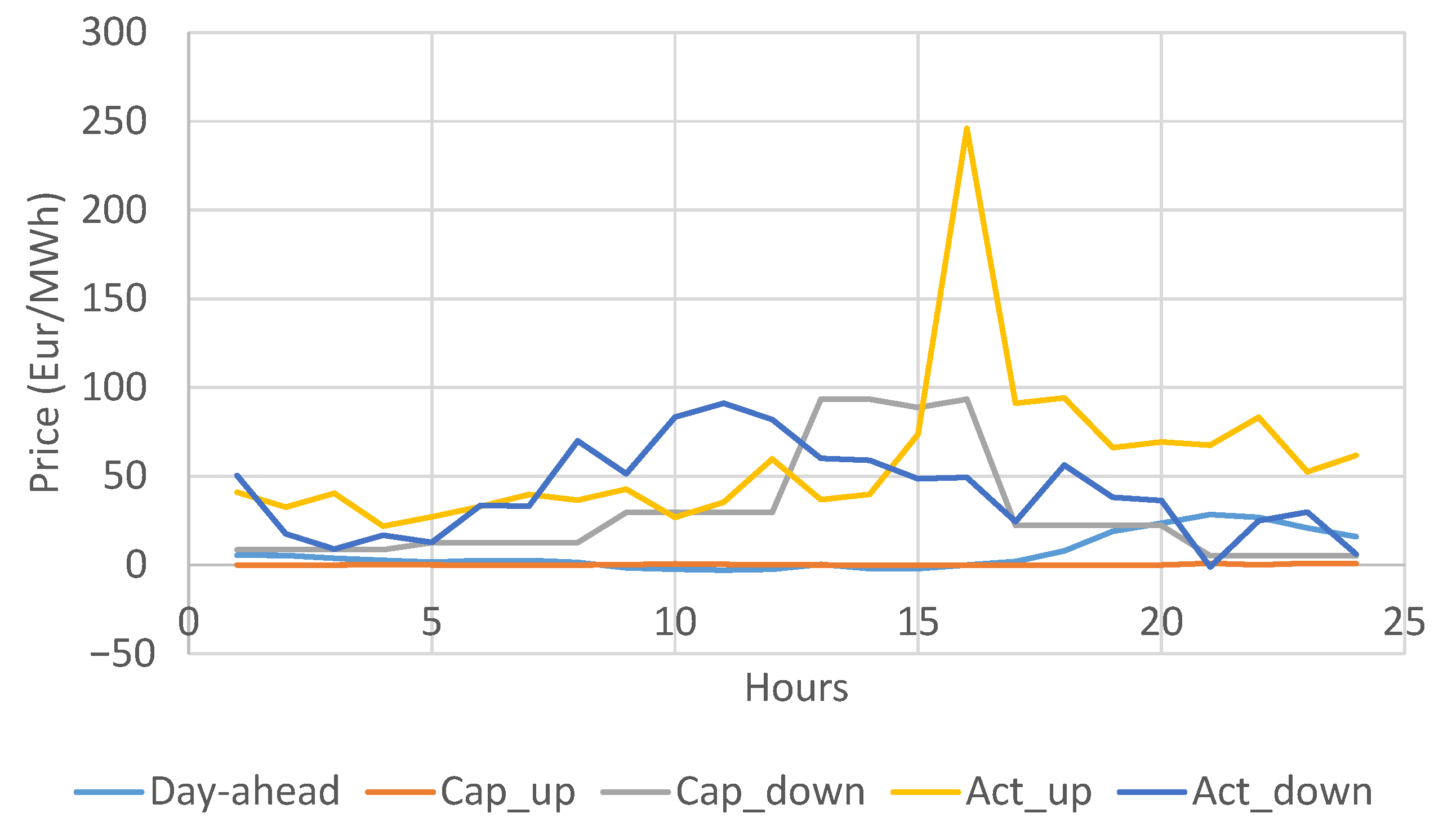
| Hour | Price (€/MWh) | Hour | Price (€/MWh) | Hour | Price (€/MWh) | Hour | Price (€/MWh) |
|---|---|---|---|---|---|---|---|
| 1 | 5.5 | 7 | 2.54 | 13 | 0.35 | 19 | 18.99 |
| 2 | 5.35 | 8 | 1.50 | 14 | −2.04 | 20 | 23.50 |
| 3 | 3.82 | 9 | −1.57 | 15 | −2.06 | 21 | 28.43 |
| 4 | 2.63 | 10 | −2.43 | 16 | −0.04 | 22 | 26.88 |
| 5 | 1.56 | 11 | −2.89 | 17 | 1.95 | 23 | 20.91 |
| 6 | 2.46 | 12 | −2.47 | 18 | 7.88 | 24 | 16.00 |
| Hours 1–4 | Hours 5–8 | Hours 9–12 | Hours 13–16 | Hours 17–20 | Hours 21–24 | |
|---|---|---|---|---|---|---|
| Up reserve (MW) | 2359 | 2334 | 2355 | 2344 | 2357 | 2360 |
| Down reserve (MW) | 2247 | 2295 | 2338 | 2354 | 2316 | 2303 |
| Hour | s1 | s2 | s3 | s4 | s5 | s6 | s7 | s8 | s9 | s10 |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 0.4/400 | 0/0 | 0.4/327 | 0.4/8 | 0.4/2 | 0.4/17 | 0.4/38 | 0.4/116 | 0.4/79 | 0.4/10 |
| 2 | 16/377 | 10/10 | 16/341 | 16/21 | 8/8 | 16/16 | 13/13 | 16/70 | 16/69 | 16/177 |
| 3 | 10/170 | 10/10 | 10/156 | 10/32 | 10/23 | 10/38 | 10/34 | 10/28 | 10/129 | 10/107 |
| 4 | 17/67 | 0/0 | 17/32 | 7/7 | 17/68 | 17/53 | 12/12 | 17/74 | 17/62 | 2/2 |
| 5 | 1/1 | 2/2 | 5/7 | 0/0 | 5/11 | 5/17 | 5/223 | 5/5 | 5/15 | 4/4 |
| 6 | 0/0 | 0/3 | 0/34 | 0/39 | 0/4 | 0/5 | 0/72 | 0/0 | 0/2 | 0/9 |
| 7 | 2/5 | 2/13 | 2/80 | 2/28 | 2/52 | 2/48 | 2/182 | 2/2 | 0/0 | 2/5 |
| 8 | 0/4 | 0/47 | 0/44 | 0/17 | 0/48 | 0/33 | 0/35 | 0/0 | 0/0 | 0/213 |
| 9 | 1/2 | 1/17 | 1/6 | 1/279 | 1/138 | 1/33 | 1/9 | 1/1 | 0/0 | 1/489 |
| 10 | 0/0 | 8/20 | 1/1 | 8/50 | 8/54 | 8/16 | 8/118 | 1/1 | 2/2 | 8/102 |
| 11 | 7/7 | 1/1 | 7/31 | 7/57 | 7/263 | 7/7 | 7/25 | 7/13 | 0/0 | 7/8 |
| 12 | 0/554 | 0/2 | 0/841 | 0/63 | 0/108 | 0/7 | 0/10 | 0/0 | 0/4 | 0/1 |
| 13 | 1/123 | 1/23 | 1/74 | 1/57 | 1/58 | 1/5 | 1/89 | 1/17 | 1/104 | 1/0 |
| 14 | 4/336 | 4/192 | 0/0 | 4/110 | 4/22 | 4/4 | 4/17 | 4/125 | 4/124 | 0/0 |
| 15 | 3/349 | 3/484 | 1/1 | 3/69 | 3/148 | 3/3 | 0/0 | 3/15 | 3/116 | 3/753 |
| 16 | 13/260 | 13/86 | 2/2 | 13/219 | 1/1 | 7/7 | 3/3 | 5/5 | 13/76 | 13/1119 |
| 17 | 9/477 | 9/375 | 9/157 | 9/50 | 2/2 | 2/2 | 4/4 | 9/27 | 3/3 | 9/37 |
| 18 | 2/97 | 2/115 | 2/263 | 2/27 | 2/14 | 2/2 | 2/89 | 2/42 | 2/10 | 2/165 |
| 19 | 6/20 | 6/67 | 6/163 | 6/6 | 6/52 | 6/6 | 6/139 | 6/27 | 6/13 | 6/74 |
| 20 | 4/98 | 4/69 | 4/125 | 3/3 | 4/226 | 4/129 | 4/103 | 2/2 | 4/5 | 2/2 |
| 21 | 1/157 | 1/30 | 1/84 | 1/20 | 1/23 | 1/70 | 1/93 | 1/1 | 1/142 | 1/5 |
| 22 | 0/0 | 3/76 | 3/131 | 3/15 | 3/62 | 3/205 | 3/508 | 3/17 | 3/128 | 3/3 |
| 23 | 7/12 | 1/1 | 7/27 | 7/43 | 2/2 | 7/30 | 7/68 | 7/10 | 7/40 | 7/158 |
| 24 | 6/74 | 6/16 | 6/190 | 6/8 | 6/10 | 6/6 | 6/23 | 6/29 | 6/17 | 6/148 |
| Hour | s1 | s2 | s3 | s4 | s5 | s6 | s7 | s8 | s9 | s10 |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1/8 | 1/209 | 1/6 | 1/250 | 1/430 | 1/37 | 1/88 | 1/57 | 1/10 | 1/57 |
| 2 | 0/5 | 0/132 | 0/4 | 0/118 | 0/72 | 0/43 | 0/23 | 0/15 | 0/10 | 0/8 |
| 3 | 0/4 | 0/28 | 0/5 | 0/32 | 0/65 | 0/20 | 0/31 | 0/12 | 0/6 | 0/8 |
| 4 | 0/15 | 0/166 | 0/5 | 0/68 | 0/20 | 0/27 | 0/16 | 0/6 | 0/12 | 0/77 |
| 5 | 0/201 | 0/48 | 0/9 | 0/200 | 0/18 | 0/49 | 0/6 | 0/56 | 0/81 | 0/12 |
| 6 | 18/72 | 5/40 | 13/48 | 18/55 | 18/69 | 5/40 | 0/15 | 18/407 | 18/247 | 18/64 |
| 7 | 0/7 | 0/100 | 0/4 | 0/84 | 0/21 | 0/66 | 0/26 | 0/373 | 0/214 | 0/24 |
| 8 | 0/8 | 0/4 | 0/14 | 2/63 | 2/65 | 2/112 | 2/105 | 2/516 | 2/477 | 0/5 |
| 9 | 16/380 | 0/29 | 0/27 | 0/20 | 0/32 | 16/173 | 16/183 | 16/403 | 16/181 | 0/4 |
| 10 | 11/163 | 11/57 | 11/71 | 11/42 | 0/15 | 11/444 | 0/14 | 11/648 | 11/237 | 10/41 |
| 11 | 2/38 | 2/148 | 0/12 | 0/27 | 0/4 | 2/455 | 2/33 | 2/369 | 2/333 | 2/384 |
| 12 | 0/5 | 6/84 | 0/4 | 0/24 | 0/5 | 6/108 | 6/58 | 6/827 | 6/65 | 6/504 |
| 13 | 10/30 | 10/119 | 10/28 | 4/9 | 10/89 | 10/54 | 2/7 | 10/169 | 2/7 | 10/651 |
| 14 | 9/14 | 11/20 | 11/246 | 11/49 | 11/179 | 11/387 | 11/253 | 11/70 | 1/6 | 11/392 |
| 15 | 0/1 | 0/2 | 28/60 | 16/21 | 28/180 | 28/198 | 28/603 | 4/9 | 0/5 | 9/14 |
| 16 | 0/2 | 0/4 | 6/74 | 0/5 | 6/559 | 6/99 | 6/271 | 6/32 | 3/8 | 1/6 |
| 17 | 0/0 | 0/2 | 0/36 | 0/8 | 0/165 | 0/394 | 0/127 | 0/119 | 0/134 | 0/62 |
| 18 | 0/5 | 0/8 | 0/6 | 0/11 | 0/186 | 0/292 | 0/290 | 0/231 | 0/284 | 0/30 |
| 19 | 11/83 | 11/32 | 0/14 | 11/133 | 11/127 | 11/546 | 11/32 | 11/104 | 11/113 | 0/11 |
| 20 | 1/21 | 0/9 | 0/5 | 7/231 | 0/19 | 7/121 | 7/92 | 7/293 | 7/85 | 7/234 |
| 21 | 0/30 | 0/12 | 0/5 | 0/124 | 0/9 | 0/16 | 0/3 | 0/165 | 0/6 | 0/48 |
| 22 | 7/498 | 0/40 | 0/16 | 7/103 | 0/36 | 0/45 | 0/8 | 7/159 | 0/18 | 7/155 |
| 23 | 10/167 | 10/274 | 0/27 | 1/47 | 10/341 | 10/89 | 3/49 | 10/223 | 10/118 | 0/7 |
| 24 | 0/23 | 2/125 | 0/15 | 2/151 | 2/145 | 2/141 | 2/173 | 2/163 | 2/155 | 2/53 |
| Day-Ahead Revenue | Up Capacity Res. Revenue | Up Capacity Act. Revenue | Down Capacity Res. Revenue | Down Capacity Act. Revenue | Overall Revenue | |
|---|---|---|---|---|---|---|
| (0,0,0,0) | −372 | 21 | 8507 | 6724 | 7291 | 22,172 |
| (1,1,0,0) | −368 | 22 | 8835 | 6511 | 7163 | 22,162 |
| (1,1,25,0) | −354 | 21 | 8684 | 6804 | 7274 | 22,429 |
| (1,1,25,15) | −366 | 21 | 8316 | 5568 | 5630 | 19,168 |
| (5,5,0,0) | −360 | 22 | 8588 | 6703 | 7205 | 22,158 |
| (5,5,25,0) | −327 | 21 | 8066 | 7162 | 7515 | 22,438 |
| (5,5,25,15) | −360 | 22 | 8096 | 5713 | 5698 | 19,169 |
| (5,5,50,0) | −7 | 5 | 5386 | 5605 | 6352 | 17,342 |
| (10,10,50,−15) | 1033 | 7 | 3585 | 9172 | 12,416 | 26,212 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pandžić, K.; Pavić, I.; Andročec, I.; Pandžić, H. Optimal Battery Storage Participation in European Energy and Reserves Markets. Energies 2020, 13, 6629. https://doi.org/10.3390/en13246629
Pandžić K, Pavić I, Andročec I, Pandžić H. Optimal Battery Storage Participation in European Energy and Reserves Markets. Energies. 2020; 13(24):6629. https://doi.org/10.3390/en13246629
Chicago/Turabian StylePandžić, Kristina, Ivan Pavić, Ivan Andročec, and Hrvoje Pandžić. 2020. "Optimal Battery Storage Participation in European Energy and Reserves Markets" Energies 13, no. 24: 6629. https://doi.org/10.3390/en13246629
APA StylePandžić, K., Pavić, I., Andročec, I., & Pandžić, H. (2020). Optimal Battery Storage Participation in European Energy and Reserves Markets. Energies, 13(24), 6629. https://doi.org/10.3390/en13246629






