Resonance Stability Analysis of Large-Scale Wind Power Bases with Type-IV Wind Generators
Abstract
1. Introduction
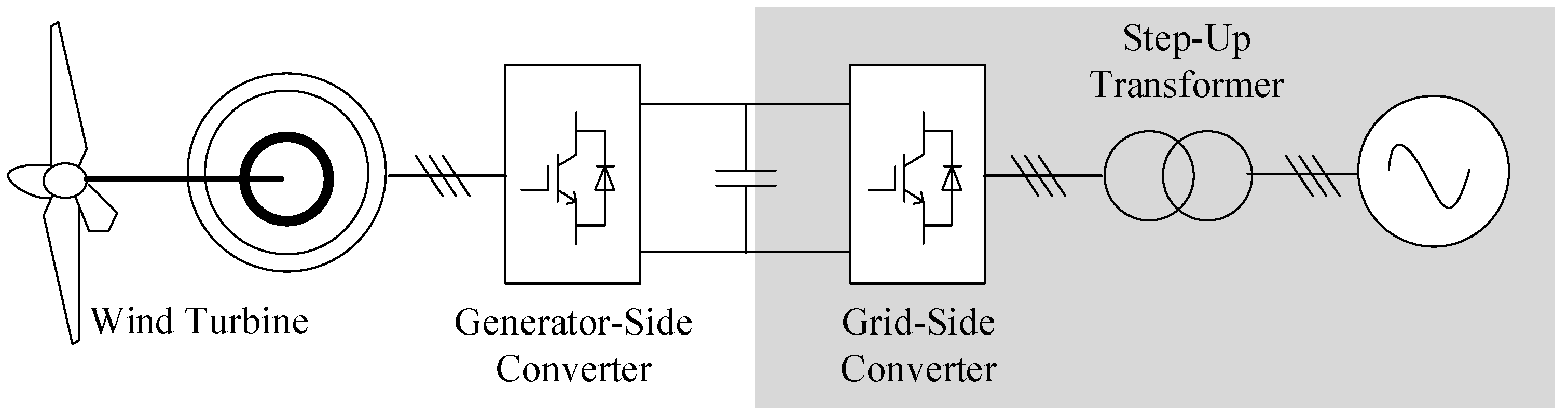
2. Modelling of Type-IV Wind Generators
2.1. Transfer Characteristics of Disturbances in Type-IV Wind Generators
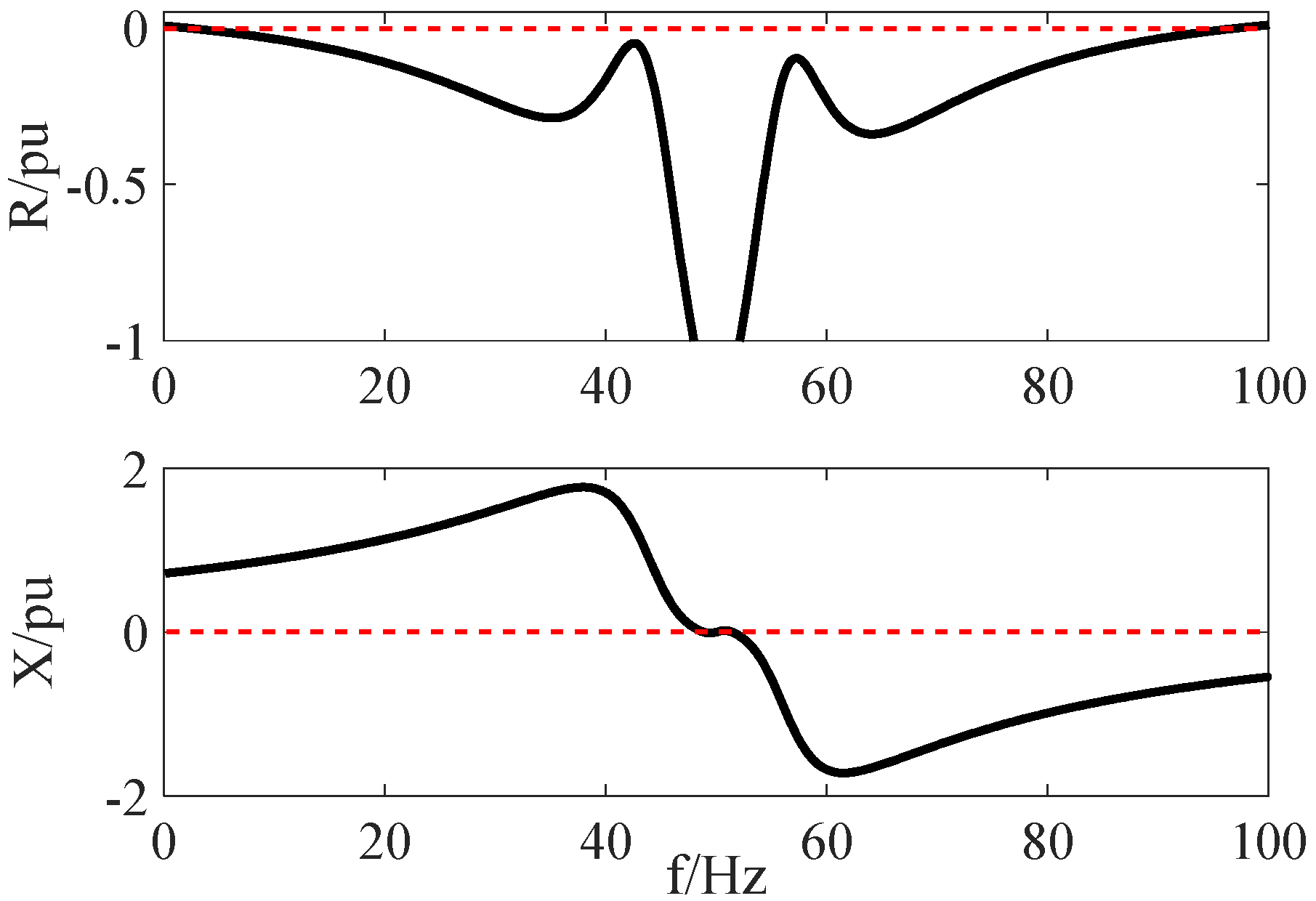
2.2. Impedance Model of Type-IV Wind Generators
3. Resonance Stability Analysis of Wind Power Bases
3.1. System Parameters of Wind Power Bases
3.2. Analysis on Resonance Structure of Wind Power Bases
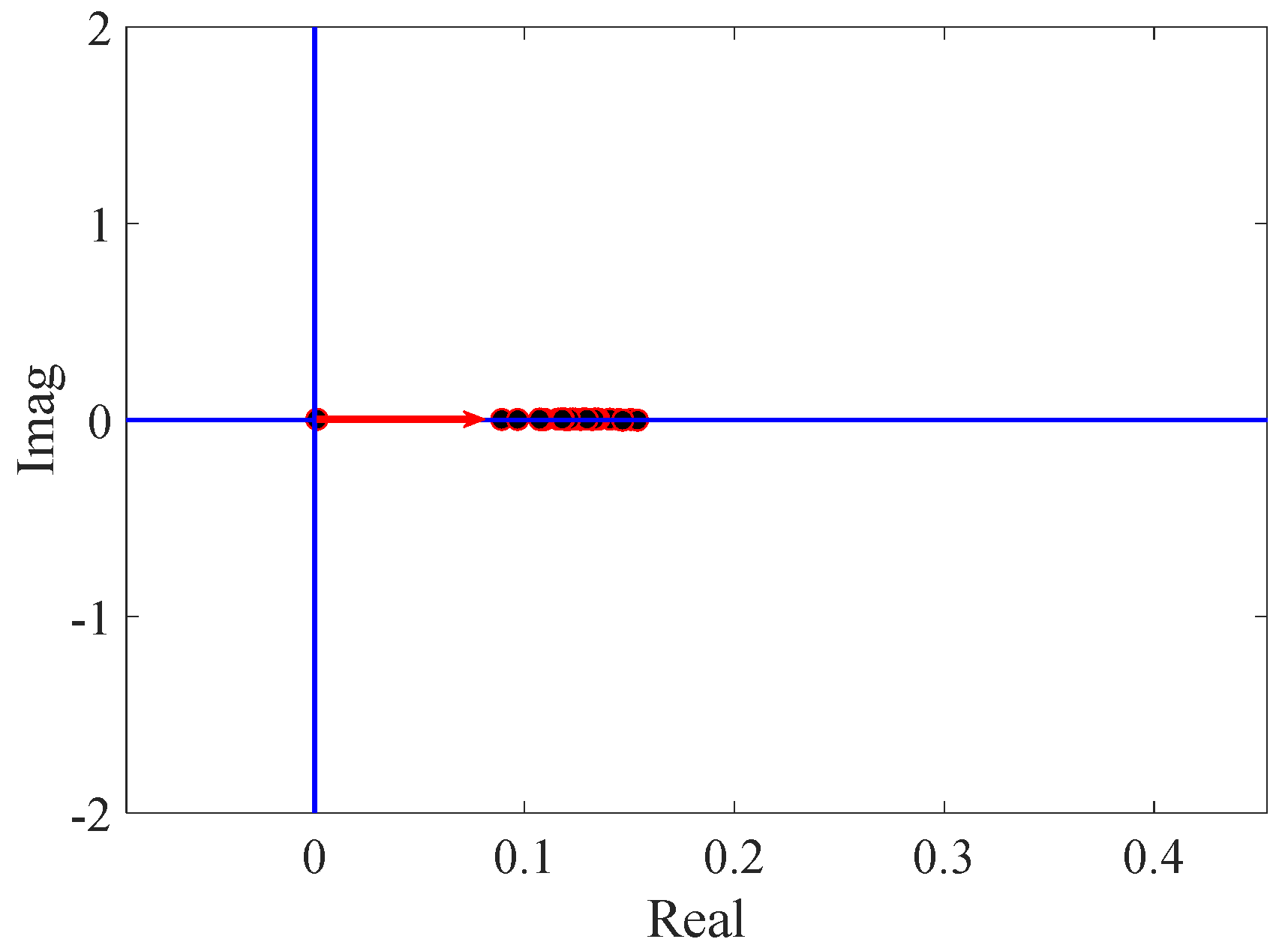
3.3. Mechanism Illustration for Unstable Resonance Mode
4. Verification Based on Electro-Magnetic Transient Simulation
4.1. Verification on Impedance Model of Type-IV WG
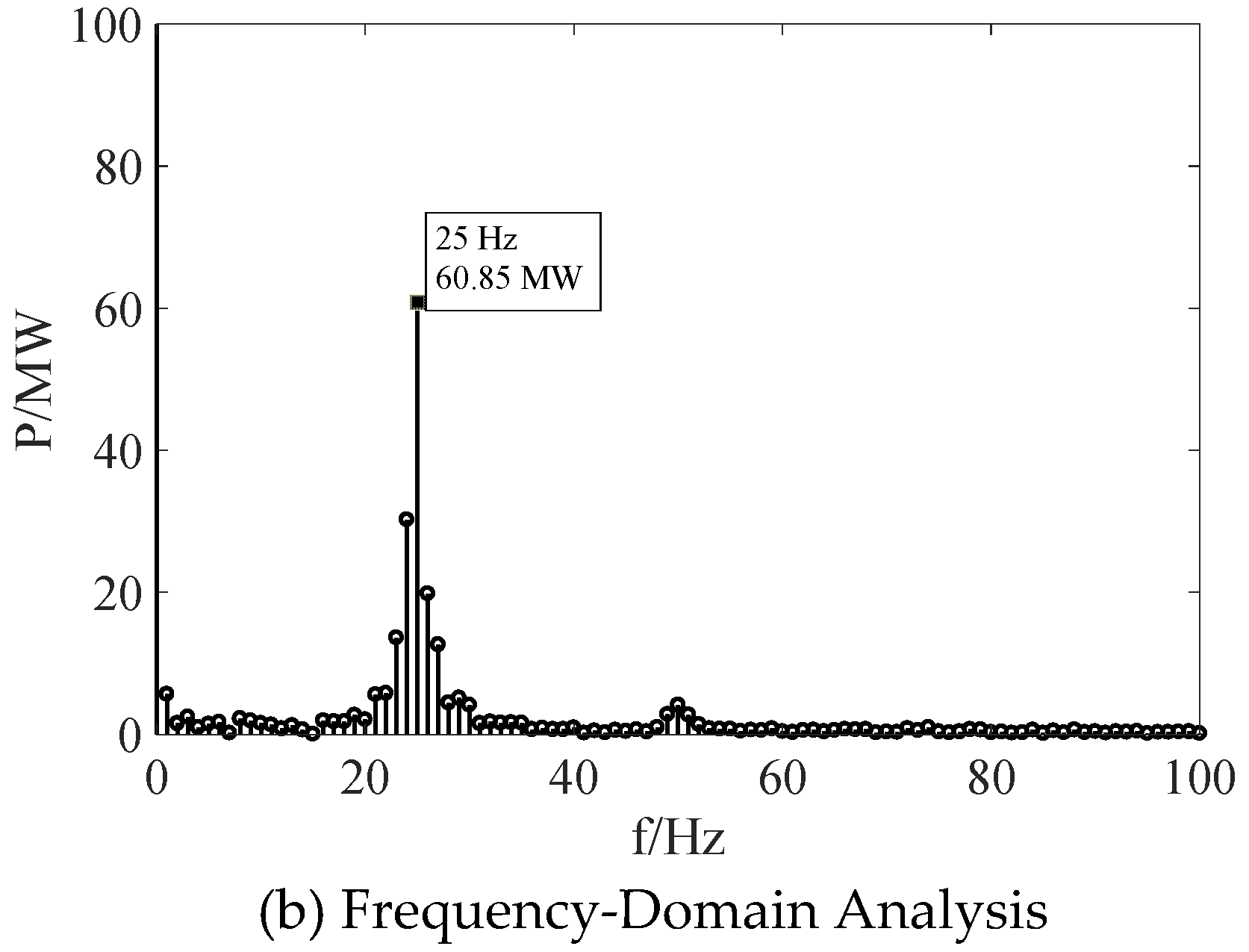
4.2. Verification on Resonance Structure Analysis of Wind Power Bases
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| AC | Alternating current |
| DC | Direct current |
| PI | Proportional integral |
| PLL | Phase-locked loop |
| PSCAD/EMTDC | Power systems computer aided design/Electromagnetic transients including DC |
| PV | Photovoltaic |
| UPS | Uninterruptible Power Supply |
| WG | Wind generator |
| Uabc | The a-, b- and c-phase AC-side voltage |
| Ua(jωp) | The phasor style of the disturbance component of fp frequency in the a-phase AC-side voltage |
| ωp | The frequency of disturbance component |
| Iabc | The a-, b- and c-phase output current of the grid-side converter |
| Ia(jωp) | The phasor style of the disturbance component of fp frequency in the a-phase output current |
| Im | The magnitude of the steady component in the a-phase output current |
| φIa | The phase of the steady component in the a-phase output current |
| Uvabc | The a-, b- and c-phase valve-side voltage |
| Uva(jωp) | The phasor style of the disturbance component of fp frequency in the a-phase valve-side voltage |
| Udq | The d- and q-axis measured voltage in controller |
| Idq | The d- and q-axis measured current in controller |
| Udqref | The d- and q-axis reference voltage from the inner-loop controller |
| Udref, Uqref | The steady component in the d- and q-axis reference voltage |
| Umoddq | The d- and q-axis component correspond to the a-, b- and c-phase modulation voltage |
| Umodabc | The a-, b- and c-phase modulation voltage |
| θPLL | The output phase of the PLL |
| θPLL(j(ωp − ω1)) | The phasor style of the disturbance component of fp − f1 frequency in the output phase of the PLL |
| ω1 | The working-frequency of the system |
| Udc | The DC-side voltage |
| Gv | The standard coefficient in the voltage measurement module |
| Gi | The standard coefficient in the current measurement module |
| HPLL(s) | The transfer function of the PI regulator in the PLL |
| GDelay(s) | The transfer function of the control delay |
| Hin(s) | The transfer function of the PI regulator in the inner-loop controller |
| Kv | The feedforward coefficient of voltage in the inner-loop controller |
| Ki | The decoupled compensation coefficient of current in the inner-loop controller |
| Km | The modulation ratio of amplitude |
| R, L | The resistance and inductance of the connecting circuit |
References
- IEA. Global Energy Review 2019. IEA, Paris. 2020. Available online: https://www.iea.org/reports/global-energy-review-2019 (accessed on 5 April 2020).
- Adams, J.; Pappu, V.A.; Dixit, A. ERCOT experience screening for Sub-Synchronous Control Interaction in the vicinity of series capacitor banks. In Proceedings of the 2012 IEEE Power & Energy Society General Meeting, San Diego, CA, USA, 22–26 July 2012. [Google Scholar]
- Buchhagen, C.; Rauscher, C.; Menze, A.; Jung, J. BorWin1-first experiences with harmonic interactions in converter dominated grids. In Proceedings of the 2015 International ETG Congress, Bonn, Germany, 17–18 November 2015. [Google Scholar]
- Li, M.; Yu, Z.; Xu, T.; He, J.; Wang, C.; Xie, X.; Liu, C. Study of complex oscillation caused by renewable energy integration and its solution. Power Syst. Technol. 2017, 41, 1035–1042. [Google Scholar]
- Kundur, P.; Balu, N.J.; Lauby, M.G. Power System Stability and Control; McGraw Hill: New York, NY, USA, 1994. [Google Scholar]
- Pourbeik, P. Modeling and Dynamic Behavior of Wind Generation as it Relates to Power System Control and Dynamic Performance; CIGRE: Paris, France, 2007. [Google Scholar]
- Li, R.; Lu, Y.; Liu, H.; Han, B. Mechanism analysis on sub-synchronous oscillation caused by grid-integration of doubly fed wind power generation system via series compensation. Power Syst. Technol. 2013, 37, 3073–3079. [Google Scholar]
- Ostadi, A.; Yazdani, A.; Varma, R.K. Modeling and stability analysis of a DFIG-based wind-power generator interfaced with a series-compensated line. IEEE Trans. Power Deliv. 2009, 24, 1504–1514. [Google Scholar] [CrossRef]
- Fan, L.; Kavasseri, R.; Miao, Z.L.; Zhu, C. Modeling of DFIG-based wind farms for SSR analysis. IEEE Trans. Power Deliv. 2010, 25, 2073–2082. [Google Scholar] [CrossRef]
- Sun, J. Modeling and mitigation of harmonic resonance between wind turbines and the grid. In Proceedings of the 2011 Energy Conversion Congress and Exposition (ECCE), Phoenix, AZ, USA, 17–22 September 2011. [Google Scholar]
- Miao, Z. Impedance-model-based SSR analysis for type 3 wind generator and series-compensated network. IEEE Trans. Energy Convers. 2012, 27, 984–991. [Google Scholar] [CrossRef]
- Wu, B.; Lang, Y.; Zargari, N.; Kouro, S. Power Conversion and Control of Wind Energy Systems; Wiley: New York, NY, USA, 2011. [Google Scholar]
- Mei, F.; Pal, B.C. Modal analysis of grid-connected doubly fed induction generators. IEEE Trans. Energy Convers. 2007, 22, 728–736. [Google Scholar] [CrossRef]
- Sun, J. Impedance-based stability criterion for grid-connected inverters. IEEE Trans. Power Electron. 2011, 26, 3075–3078. [Google Scholar] [CrossRef]
- Fan, L.; Miao, Z. Nyquist-stability-criterion-based SSR explanation for Type-3 wind generators. IEEE Trans. Energy Convers. 2012, 27, 807–809. [Google Scholar] [CrossRef]
- Harnefors, L.; Bongiorno, M.; Lundberg, S. Input-admittance calculation and shaping for controlled voltage-source converters. IEEE Trans. Ind. Electron. 2007, 54, 3323–3334. [Google Scholar] [CrossRef]
- Sun, J. Small-signal methods for AC distributed power systems—A review. IEEE Trans. Power Electron. 2009, 24, 2545–2554. [Google Scholar]
- Cespedes, M.; Sun, J. Three-phase impedance measurement for system stability analysis. In Proceedings of the 2013 IEEE 14th Workshop Control and Modeling for Power Electronics, Salt Lake City, UT, USA, 23–26 June 2013. [Google Scholar]
- Xu, Z.; Wang, S.; Xing, F.; Xiao, H. Study on the method for analyzing electric network resonance stability. Energies 2018, 11, 1–8. [Google Scholar]
- Harnefors, L.; Wang, X.; Yepes, A.G.; Blaabjerg, F. Passivity-based stability assessment of grid-connected VSCs—An overview. IEEE J. Emerg. Sel. Top. Power Electron. 2016, 4, 116–125. [Google Scholar] [CrossRef]
- Ino, T.; Mathur, R.M.; Iravani, M.R.; Sasaki, S. Validation of digital simulation of DC links—Part II. IEEE Trans. Power Appar. Syst. 1985, 104, 2596–2603. [Google Scholar] [CrossRef]






| Items | Ref. [19] | This Manuscript |
|---|---|---|
| Main difference | Aims to illustrate the effectiveness of the s-domain nodal admittance analysis method | Aims to analyze the oscillation problems in a practical power engineering |
| Type of wind farm | IEEE 39-bus system with one DFIG | Practical 68-bus system with sixteen Type-IV wind generators |
| Analysis method | s-domain nodal admittance matrix | s-domain nodal admittance matrix |
| Software simulation | Matlab | Matlab, PSCAD |
| Advantages | IEEE standard system | (1) Larger scale of test system and more wind generators (2) Simulation verification of analysis results (3) More detailed analysis on the unstable resonance mode (4) Practical power engineering application |
| Disadvantages | Lack of the simulation verification | / |
| Power Equipment | Items | Values |
|---|---|---|
| Three-winding transformer T1 | Rated capacity | 180/180/180 MVA |
| Nominal voltage | 220/110/37 kV | |
| Leakage impedance 1 | 0.001 + 0.082 pu | |
| Leakage impedance 2 | 0.001 + 0.006 pu | |
| Leakage impedance 3 | 0.001 + 0.051 pu | |
| Three-winding transformer T2/T3 | Rated capacity | 240/180/180 MVA |
| Nominal voltage | 220/110/37 kV | |
| Leakage impedance 1 | 0.001 + 0.062 pu | |
| Leakage impedance 2 | 0.001 + 0.004 pu | |
| Leakage impedance 3 | 0.000 + 0.037 pu | |
| Three-winding transformer T4 | Rated capacity | 180/180/180 MVA |
| Nominal voltage | 220/110/37 kV | |
| Leakage impedance 1 | 0.001 + 0.080 pu | |
| Leakage impedance 2 | 0.001 + 0.006 pu | |
| Leakage impedance 3 | 0.001 + 0.050 pu | |
| Three-winding transformer T5 | Rated capacity | 240/240/120 MVA |
| Nominal voltage | 220/110/37 kV | |
| Leakage impedance 1 | 0.001 + 0.086 pu | |
| Leakage impedance 2 | 0.000 + 0.003 pu | |
| Leakage impedance 3 | 0.003 + 0.042 pu | |
| Transmission line from Bus2 to Bus1 | Line resistance | 0.0071 pu |
| Line reactance | 0.0633 pu | |
| Line susceptance | 0.1178 pu | |
| Transmission line from Bus3 to Bus2 | Line resistance | 0.0018 pu |
| Line reactance | 0.0148 pu | |
| Line susceptance | 0.0269 pu |
| Items | Values |
|---|---|
| Rated capacity | 2 MW |
| Rated frequency | 50 Hz |
| Nominal voltage | 0.69 kV |
| DC-side voltage | ±0.75 kV |
| Resistance in connecting circuit | 0.024 Ω |
| Inductance in connecting circuit | 0.190 mH |
| Rated capacity of step-up transformer | 2.5 MVA |
| Nominal voltage of step-up transformer | 0.69/37 kV |
| Leakage inductance of step-up transformer | 0.12 pu |
| Num. | Damping Coefficient/s−1 | Resonance Frequency/Hz | Resonance Stability |
|---|---|---|---|
| 1 | 2.5518 | 55.7 | Stable |
| 2 | −7.5602 | 77.1 | Unstable |
| Nodes of Injection Current | Nodes of Observation Voltage | Participation Factor |
|---|---|---|
| Wind Farm 4, 0.69 kV Node | Wind Farm 4, 0.69 kV Node | 0.0238∠0.00° |
| Wind Farm 15, 0.69 kV Node | Wind Farm 4, 0.69 kV Node | 0.0233∠0.00° |
| Wind Farm 15, 0.69 kV Node | Wind Farm 15, 0.69 kV Node | 0.0228∠0.00° |
| Wind Farm 4, 0.69 kV Node | Wind Farm 4, 37 kV Node | 0.0227∠0.00° |
| Wind Farm 15, 37 kV Node | Wind Farm 4, 0.69 kV Node | 0.0224∠0.00° |
| Wind Farm 4, 37 kV Node | Wind Farm 15, 0.69 kV Node | 0.0222∠0.00° |
| Wind Farm 15, 37 kV Node | Wind Farm 15, 0.69 kV Node | 0.0219∠0.00° |
| Wind Farm 4, 0.69 kV Node | Wind Farm 16, 0.69 kV Node | 0.0217∠0.00° |
| Wind Farm 4, 0.69 kV Node | Wind Farm 14, 0.69 kV Node | 0.0217∠0.00° |
| Wind Farm 4, 37 kV Node | Wind Farm 4, 37 kV Node | 0.0214∠0.00° |
| Wind Farm 16, 0.69 kV Node | Wind Farm 15, 0.69 kV Node | 0.0213∠0.00° |
| Wind Farm 14, 0.69 kV Node | Wind Farm 15, 0.69 kV Node | 0.0213∠0.00° |
| Wind Farm 15, 37 kV Node | Wind Farm 15, 37 kV Node | 0.0211∠0.00° |
| Wind Farm 4, 0.69 kV Node | Wind Farm 16, 37 kV Node | 0.0209∠0.00° |
| Wind Farm 4, 0.69 kV Node | Wind Farm 14, 37 kV Node | 0.0209∠0.00° |
| Wind Farm 4, 0.69 kV Node | Wind Farm 11, 0.69 kV Node | 0.0209∠0.00° |
| Wind Farm 4, 0.69 kV Node | Wind Farm 8, 0.69 kV Node | 0.0208∠0.00° |
| … | … | … |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xing, F.; Xu, Z.; Zhang, Z.; Dan, Y.; Zhu, Y. Resonance Stability Analysis of Large-Scale Wind Power Bases with Type-IV Wind Generators. Energies 2020, 13, 5220. https://doi.org/10.3390/en13195220
Xing F, Xu Z, Zhang Z, Dan Y, Zhu Y. Resonance Stability Analysis of Large-Scale Wind Power Bases with Type-IV Wind Generators. Energies. 2020; 13(19):5220. https://doi.org/10.3390/en13195220
Chicago/Turabian StyleXing, Facai, Zheng Xu, Zheren Zhang, Yangqing Dan, and Yanwei Zhu. 2020. "Resonance Stability Analysis of Large-Scale Wind Power Bases with Type-IV Wind Generators" Energies 13, no. 19: 5220. https://doi.org/10.3390/en13195220
APA StyleXing, F., Xu, Z., Zhang, Z., Dan, Y., & Zhu, Y. (2020). Resonance Stability Analysis of Large-Scale Wind Power Bases with Type-IV Wind Generators. Energies, 13(19), 5220. https://doi.org/10.3390/en13195220







