Abstract
The paper proposes a general description system of the five-phase two-level inverter. The two base methods are presented and discussed. The first one is based on the standard space vector transformation, while the other uses state vectors which enable the definition of the basic physical quantities of the inverter: current and voltage. The proposed notation system offers a general simplification of vector identification. It comprises a standardized proposal of notation and vector marking, which may be extremely useful for the specification of inverter states. The described notation system makes it possible to reach correlation between state and space vectors. It presents space and state vectors using the same digits. These properties suggest that the proposed notation system is a useful mathematical tool and may be really suitable in designing control algorithms. This mathematical tool was verified during simulation tests performed with the use of the Simulation Platform for Power Electronics Systems—PLECS.
1. Introduction
A large number of electrical energy converters are applied in contemporary industry and the public area. Their performance as well as the level of power are continually intensely developed. The increasing range of novel requirements has a great influence on the development of inverters as well as the technology of power electronics components, especially power semiconductors. Innovative elements used in converters, e.g., current switching diodes and transistors can work at higher frequencies and lower power losses. For instance, the SiC (silicon carbon) transistors have better features, such as switch-on and off times as well as a significantly higher temperature range. As a result, they work faster than IGBTs (insulated gate bipolar transistor) and make it possible to diminish the overall dimensions of the converter. Generally, converters have to fulfil specific and diversified requirements concerning supply and conversion methods in possibly a large power range. The application area of inverters is very common and large. There are many industrial applications where inverters have to be equipped with quite different features. This implies diversified converter circuits and various conversion methods of electrical energy. In alternating current (AC) electrical machine and drive applications, the ability of speed regulation is crucial, so the electrical converter has to guarantee the related adjustment of output voltage and frequency as fundamental. Uninterruptible power supplies (UPS) or distributed power generation systems represent a good example of another requirement. There, the basic requirement is to generate 50 or 60 Hz stable sinusoidal voltage waveforms.
During the first period of power electronics evolution all applications were based on the three-phase supply voltage network. Three-phase two-level inverters became the most suitable devices used for electrical energy conversion. Their features and performance as well as drawbacks were largely recognized and tested in practice [1]. For instance, these standard inverters were applied in AC drives on a mass scale. They covered the range of drive power from less than one up to hundreds of kW and only the demand for higher power and voltage limited their applications. In order to develop higher electric power converters, diverse types of three-level and multilevel inverters were designed and practically applied. The satisfying properties of three-level inverters resulted in them becoming widely applied in the power industry. They are used for energy conversion or to control high-power electrical machines in AC drives. Multilevel inverters present continually a good example of power electronics evolution, because they make it possible to overcome the aforementioned limitations and reach a range of converted power even up to quite a lot of MWs [2,3].
Recently, electro-mobility has become another very important area of development in power electronics. It seems that electric cars will constitute a novel lucrative application domain of power electronics devices. Nowadays a lot of two and multilevel inverters are used in AC and direct current (DC) drives in mobile transport, traction, buses and cars. Electric drives are also used in vessels’ drive systems and have become another important area of use. An example of a vessel servicing crew transfer from off-shore wind farms is analyzed in [4], as using electric drives in vessels leads to a significant reduction in fuel consumption.
Thanks to the good features of inverters one can say that in electric cars energy conversion does not determine a real problem in comparison to the limitations of electric energy storage [5]. Great technological progress in batteries and supercapacitors allows us to believe that it will be possible to overcome this constraint. When storing electric energy in battery stacks, it is easy to get multiple sections of voltage that is the voltage required to supply a multilevel inverter. This fact also implies the use of multilevel inverters as the main energy converters in vehicle drives [6].
It seems that the development of two and multilevel three-phase converters is continually maintained, particularly in the application domain. Great technological progress in semiconductor devices allows us to believe that it still remains a research area for new circuits, control algorithms and theory. However, a new challenge was to meet the need for a higher phase number than three in the power energy network and electric machines. This idea created another development impact on multiphase energy conversion. Thanks to effective research and technology achievements, polyphase power as well as polyphase motors have become available. The number of phases may reach four, five or even more depending on applications. Conversion of the three-phase to seven-phase system can be obtained using a power transformer. The method of such power conversion was presented in [7], where the authors discuss, among others, a problem related to modeling power transmission systems consisting of four phases. In power energy transmission a phase-order higher than three, so called HPO (High Phase Order) is really considered the way to increase transmission efficiency [8]. More phases mean more space to be occupied by the transmission line. The required distance between conductors is generally determined by the phase-to-phase voltage. So, the number of applied phases limits the overall dimensions of the space engaged. If the power system is equipped with six phase-conductors, then the phase voltage is equal to phase-to-phase voltage, which gives the same distance between adjacent phases and the neutral point. The multiphase transmission line was practically applied by the New York State Electric & Gas Company. Two three-phase 115 kV transmission lines were converted to one 93 kV six-phase. The final result was economically satisfactory on condition that the length of the line was over and above 37–45 km.
Multiphase evolution did not ignore electric drives and renewable energy systems. Drives have many promising advantages such as silent work and ecologic purity. Thanks to good electrical and mechanical properties, electric drives are able to replace a large number of power drives based on liquid fuel [9]. Multiphase systems of wind energy generation have good characteristics and there are applications where simplified direct matrix converters are used to generate electric energy [10]. Permanent magnet brushless motors, BLDC (brushless direct-current motor) and PMSM (permanent-magnet synchronous motor), have favorable features, so they are largely used in car electric drives. These contemporary electric motors are often created as multiphase units. It is possible to meet 5, 6, 9 or even 11-phase motors [11]. The drives using these motors have favorable properties, so drives based on three-phase motors have slowly disappeared [12,13,14,15].
The higher phase number determines a new impact on research works concerning inverter circuits and control algorithms. More phases mean higher complexity of the converter circuit and a greater number of semiconductor devices. The number of vectors grows in the power scale in relation to the phase number. For a five-phase two-level inverter the number reaches . Such a number of accessible vectors requires using more sophisticated control methods and algorithms in comparison to standard control algorithms used in three-phase inverters. This is the reason to search for good mathematical tools and converter models. These tools should be useful in order to facilitate the composition of control algorithms that are easy to implement and which can guarantee fast converter performance.
In the literature of the subject one can find an enormous variety of proposals concerning converter models and their descriptions. Although there are many proposals relating to this, there is none that can be respected and accepted [16,17]. Additionally, it happens that the notational system is assumed accidentally or has no mnemonic features.
This contribution presents a significant development of the notation system idea proposed in the paper [18] during the ICREPQ’14 conference, and it might be the first step of a general system concerning multiphase inverters.
The paper presents a description system of the five-phase two-level inverter. The notational system provides a general standardization and simplification of vectors. It helps to identify voltage states. It contains a novel handy proposal of notation and stamping, which is helpful for a converter description as well as for developing control algorithms. This system of notation enables accomplishing a comparison and correlation between state and space vectors. It describes space and state vectors using the same numbers. The proposal described in the paper refers to the notation system designed for three-phase inverters [18]. It determines a significant extension of that system and was designed for five-phase inverters. The considerations presented there give on opportunity to make some generalizations and allow the writing of expressions circumscribing state and space vectors of the multiphase VSI (voltage source inverter). It is worth adding that the main rule of the presented system can be easily extended and adopted for multiphase and multilevel inverters.
2. Five-Phase Two-Level Voltage Source Inverter: State and Space Vectors
2.1. Five-Phase Two-Level Inverter Model
Figure 1 presents a simplified model of the five-phase two-level inverter. The model includes five two-state switches Ka, Kb, Kc, Kd, Ke, assigned to output phases a, b, c, d, e and connected to the voltage source . The negative pole of the voltage source is denoted as 0, while the positive pole as 1. Every switch can connect one pole of the voltage source to one phase output.
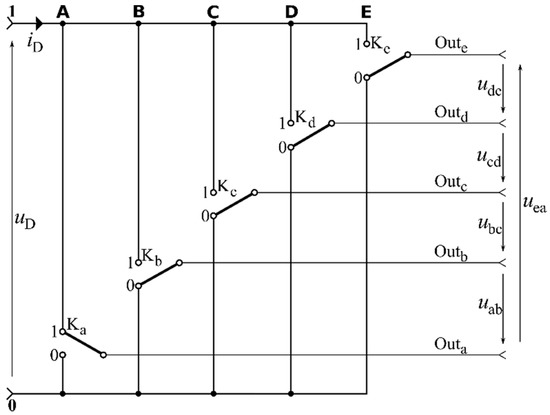
Figure 1.
The model of the five-phase two-level inverter with five switches.
Accordingly, the switching states of the power electronic switches are also denoted by the numbers 1 and 0. The inverter state consisting states of all five keys can be described using a set of digits abcde where a, b, c, d, e = 0, 1. Of course, the set of five elements where elements can be denoted by digits 0 or 1 may have 32 variations that is: 00000, 00001,…11111. It is useful and wide-spread in many publications to assume that these variations form binary numbers (numbers of the base-2 positional numeral system). As a result, each inverter state is determined by one five-digit binary number where the order of digits corresponds precisely to the order of phases abcde. By converting binary numbers to the decimal number system it is possible to denote all 32 inverter states by decimals: 0, 110,…3110, respectively. Thus, the state denoted as 1610 (10000)2 determines that the phase a is connected to the positive pole of the voltage source, while the phases b, c, d and e—to the negative pole. That is the model example presented in Figure 1. The indices 10 and 2 indicate the base of the number system. This principle which eliminates decimal numbers may be used in other notation systems.
From the very beginning of the power electronics development the base-10 and base-2 number systems were applied to describe 2-level inverter states, although the rule of the precisely controlled relation “number-phase” was not always kept. The aforementioned discussion was cited here as this idea of a description might be used for other converters. The description method of multiphase or even multilevel inverters may be based on further development of this concept.
2.2. State-Vector of the Five-Phase Two-Level Inverter
The five-phase two-level voltage inverter can produce 32 different switching states. The consecutive states are denoted by the decimal index k = 0, 1, … 31. Each selected k-state means that five phase-to-phase voltages are connected to load. These voltages form a matrix row assembled of five elements as a result defining the state vector of the VSI:
Since , then the state vector Vk is determined by four successive phase-to-phase voltages under the condition that x and y denote the neighboring phases.
In a five-phase two-level VSI, phase-to-phase voltages are designed as a potential difference between respective phase outputs. The switch Ka,b,c,d,e may connect the relevant phase output to the negative pole or positive pole of the voltage source UD according to the preferred vector .
The vector index k may be converted to the binary numeral system and written as:
where: and .
The binary expansion of the index k permits associating directly the phase output potential with the relevant binary symbol, so it makes it possible to determine output polar voltages. They are referenced to the negative pole of the voltage source :
As a result, it permits defining the five-phase two-level VSI state vector by use of respective binary symbols of the index k. The transpose of the matrix , denoted as the vector , presents all five voltages:
Since the symbols can assume only values 0 or 1, then the output phase-to-phase voltage, independently of the phase number, may assume only three values: 0, +UD, −UD.
However, possessing five phases it is possible to select another set of phase-to-phase voltages. In (4) every phase-to-phase voltage is determined by the neighboring phases. The row of the matrix is composed of five elements, where and denote the subsequent phase. It would be interesting to consider the set of phase-to-phase voltages created according to the rule that the phase-to-phase voltage is determined as . Then, the state vector could be defined as a matrix composed of one row of five elements:
The definition of the five-phase two-level VSI state vector using respective binary symbols of the index k is the following:
Figure 2 presents selected polar and phase-to-phase voltage: . It was assumed that all phase outputs are connected successively, every 72°, for half a period to the positive pole of the voltage source . Evidently, waveforms and rms values of the voltage are significantly diverse because they depend on the method of the definition: or . The relevant rms values are: whereas .
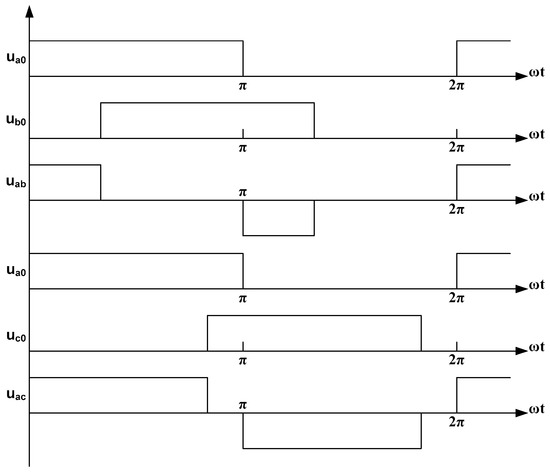
Figure 2.
Polar and phase-to-phase voltage: .
2.3. Pentagon Connected Load of the Five-PhaseTwo-Level Inverter
The inverter state vector works on physical quantities and it does not need transformation to be applied for calculation of the current in the load. A model of the five-phase two-level inverter with a load connected in pentagon is presented in Figure 3. It is assumed that the load is symmetrical and every phase to phase load is equal to two-terminal networks: resistor R—inductance L—counter RMF connected in series. The inverter state is determined by the vector which means that five corresponding phase-to-phase voltages are connected to the load. Figure 3 presents the situation when the phase a is connected to the pole 1 (), while the remaining phases to the pole 0 (). So, the state vector is determined as .
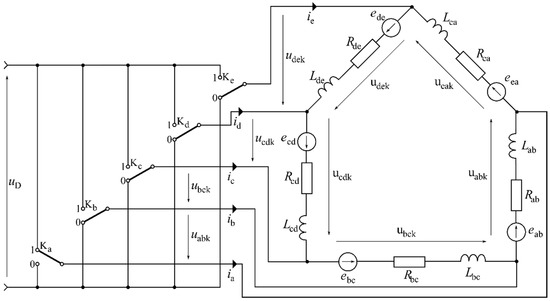
Figure 3.
The model of the five-phase two-level inverter with the pentagon connected load according to the state vector .
If the load remains in a pentagon connection, then suitable phase-to-phase voltages are equal to the voltage determined in (4). For each vector switched on in a time point t = tn the inverter model is reduced to the equivalent circuit described by the system of five equations. Every equation has the form:
where x and y denote the adjacent phases: x ≠ y and x, y = a, b, c, d, e. The voltage is determined according to (4) as .
Assuming that the counter is constant in a time interval and equals respectively, it is easier to resolve the equations and obtain expressions describing currents of a load (8). The symbol τ represents the time constant of one load leg and I0xy—the existing value of the current in the time point tn. The expression (8) is valid in the specified time interval between the successive switching of the inverter states and . The time interval is assumed to be extremely short in comparison to the time constant of the load circuit and the supposed period of the counter RMF.
where the time constant is and initial current in the time point .
The expressions (7) and (8) define the dependence between phase-to-phase voltage and the current load using the suitable symbols of the vector index k binary expansion.
2.4. Star Connected Load of the Five-Phase Two-Level Inverter
Figure 4 presents the five-phase two-level inverter model with a load arrangement that is connected in a star. For the considered class of inverters, it can be assumed more than one mathematical definition of the five-phase two-level inverter state vector . For instance, the following definition:
is effective in view of the fact that .
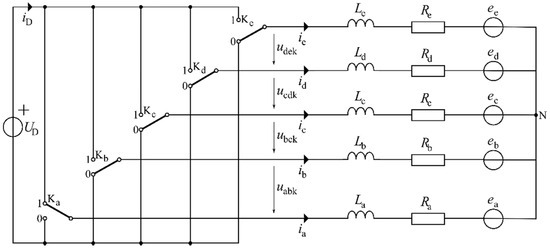
Figure 4.
The model of the five-phase two-level inverter with the load.
For any vector switched on, in the time t = tn, the inverter model is reduced to an equivalent circuit consisting of four closed loops and presented in Figure 5.
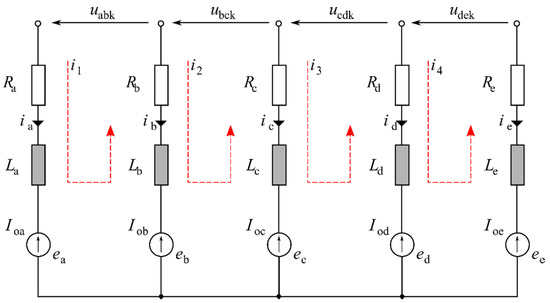
Figure 5.
The circuit of the five-phase two-level inverter with the star connected load.
If at a time point the control system switched on the vector at that time, a quadruple of phase-to-phase voltages was connected to the circuit. The selected vector acts in a time interval and it is assumed—as it was aforesaid—that this interval is very short in relation to a time constant of the circuit and a period of the interphase voltage. Then, the following assumptions might be acceptable:
It means that in the time interval all above voltages are constant. Additional assumptions result in the fact that the system considered in Figure 4 is not equipped with a neutral conductor, so the following dependencies are obligatory:
If the phase load is fully symmetrical it is profitable to assume the equal opportunity of resistances and inductances as well: and . As a matter of fact, the mathematical model of the circuit is described by the system of four equations:
Solving the system, it is possible to acquire all analytical phase voltage and current waveforms. The Laplace transform is a good tool to accomplish that task. For any vector the relation between the Laplace transform of phase and loop currents is evident:
In order to obtain a final solution, it is necessary to introduce expressions describing the relations between phase and phase-to-phase voltages. The applicable interdependence between phase voltage and phase-to-phase voltage does not depend on selected vectors and remains the following:
For instance, the dependence defining the phase voltage can be proved by the use of the appropriate voltage vectors. This situation is illustrated in Figure 6.
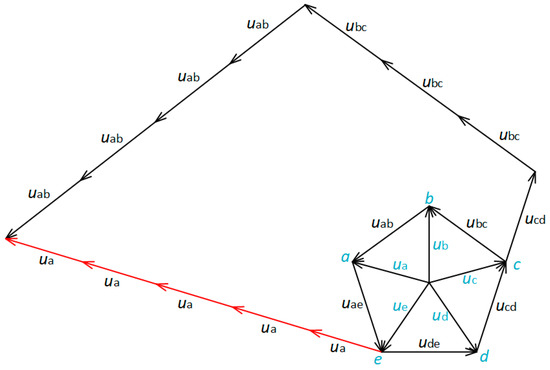
Figure 6.
Mutual dependence between the phase voltage and the appropriate voltage vectors: .
Knowledge of phase voltages allows the solving of the system of equations and finding the successive phase currents. For instance, the expression describing the Laplace transform of the phase a current is the following:
The inverse Laplace transform leads to analytical expressions describing phase currents. They are given as:
The output phase-to-phase voltage of the two-level inverter, independently of the phase number, may assume only three values: . Solving the four-loop circuit in the way presented in [18] and converting (14) it is possible to write the generalized expression describing the phase voltages: of the five-phase two-level five-phase VSI as well as phase load currents (16). They all can be described using binary digits of the vector index binary expansion.
where is a time constant of the phase load, and phase x current in the time point .
These expressions describe phase voltages and currents of the two-level five-phase voltage source inverter. Converting similarly Equations (4) and (14) it makes it possible to write expressions describing phase-to-phase voltages and the resulting currents.
The five-phase two-level VSI has 32 states of operation described by vectors representing the consecutive sets of phase-to-phase voltages. Every single set of 32 vectors has its own connection diagram to the supply voltage . Some possible arrangements are presented in Figure 7.
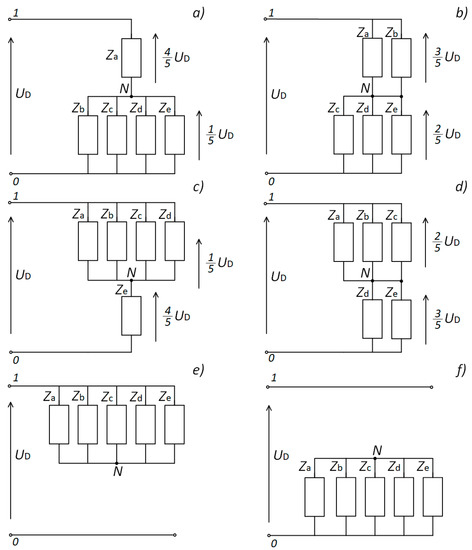
Figure 7.
A few possible arrangements of the star connected load, where: (a) corresponds to the vector V16(10000), (b) corresponds to the vector V24(11000), (c) corresponds to the vector V30(11110), (d) corresponds to the vector V28(11100), (e) corresponds to the vector V31(11111), (f) corresponds to the vector V0(00000).
Figure 7 presents selected load configurations. The arrangement presented in 7a conforms to the vector which means that only one phase a is connected to the pole 1 (+) while the remaining phases are connected to the pole 0. Assuming that all impedances Z are equal, the supply voltage is divided into two values: and referenced to the neutral point N. This division result determines phase voltages: and , , , respectively. Every single phase may be connected to the pole 1 so, there are also four similar arrangements which correspond to the phases. They conform to vectors: , , , successive. The successive five vectors: , , , , conform to the connection system presented in Figure 7c. In such a system only one phase voltage reaches while the remaining phases +. Other possible load configurations are presented in Figure 7b,d. They present the states when two or three phases are connected to the pole 1 (+). The resulting phase voltage equals and , while the remaining phases, connected to the pole 0, are supplied by and voltage, respectively. There are ten thinkable combinations of both load configurations because mathematically The arrangements presented in Figure 7e,f show the circuit when all phases are connected to the one pole of the supply voltage . The corresponding vectors are ,. According to the model presented in Figure 4 these two vectors cause that all phase-to-phase voltages are equal to zero, so they do not influence a passage of loop currents. These vectors are usually called “zero vectors”.
These expressions together with Equations (6) and (12) describe the voltages and currents of the two-level five-phase voltage source inverter.
2.5. Space Vectors of the Five-Phase Two-Level Voltage Source Inverter
The polar voltage space vector of the two-level five-phase VSI is determined analogically to the way presented in previous sections. The definition was established as:
where .
Applying the Euler’s formula and introducing interdependencies among the angles as well as symbols ak, bk, ck, dk, ek, the space vector is given as follows:
The Equation (20) expresses the space vector which is defined in symbols of the index k binary expansion. The index k is a decimal number discriminating the state vector , where .
After transformation the space vector is a complex number which may be represented by the modulus Mk and the argument φk. But in the case of the five-phase inverter the situation is more complicated compared to the three-phase inverters. The expression allowing calculation of the space vector modulus is the following:
where coefficients are:
The position of the successive vector is determined by its modulus Mk and the shift angle . The angle is determined as:
In order to determine correctly the shift angle, it might be necessary to use additionally the arctg function (24). It results in periodicity of trigonometrical functions and a different period of sine and tangent functions.
It was assumed at this point that the denominator of the expressions (23) and (24) did not equal zero. The result of these two formulae is indeterminate for or . The circumstances, where digits are equal to 0 or 1, denote that the state vector modulus reaches 0 and its shift angle is indeterminate. The relevant two vectors and are usually called “zero vectors” and they do not influence output current.
According to (21) and after calculations, the modulus Mk assumes three different results:
In such a case among the 32 vectors there are three groups of 10 active vectors each beside two nonactive zero vectors. The parameters: moduli Mk, coefficients , and shift angles of all 30 active vectors are collected in Table 1. The moduli values are approximated.

Table 1.
The active vectors’ parameters of the two-level five-phase inverter.
Figure 8 presents the active polar space vectors of the five-phase inverter. They are presented on the complex plane where α denotes the real axis and β—the imaginary one. The diagram presents their position. For every successive where the position of the corresponding three vectors is marked as one vector because they only differ in moduli. The modulus values of each triple are given in order: (the upper one), , respectively.
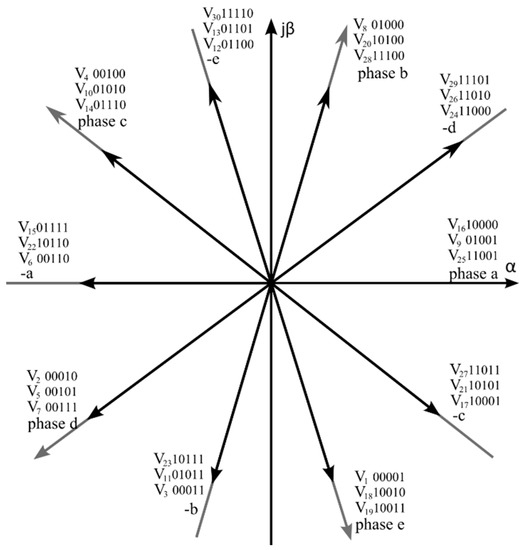
Figure 8.
Polar voltage space vectors of the two-level five-phase VSI.
The voltage space vectors prove a convenient mathematical tool. They are a basic tool that allow the generation of the vector control method, the most widespread contemporary control method used to control AC induction or synchronous motors. In addition, they are very useful when studying possible control algorithms and strategy. The controller of the AC drive uses voltage space vectors in order to generate a desirable five-phase PWM (Pulse-Width Modulation) inverter output voltage supplying the motor.
The next Figures present a few examples of phase and phase-to-phase voltage waveforms obtained by using the simplest method of control. For illustration purposes, it was assumed that every leg of the inverter was switched on only once during one period of the referenced voltage and every phase was connected to the + pole during the first half of a period while to the pole during the other half.
Figure 9 depicts a set of polar and phase-to-phase voltage waves. The phase-to-phase voltage relates to the pentagon connected load. The control algorithm consists in successive (every activation of the following sequence of vectors: , , , , , , , , , . The parameters of the vectors as well as their index binary expansion are collected in Table 2. The operation time of every vector corresponds to the angle where and f denotes frequency of the reference voltage. Using the star connection load, the same sequence of successively switched vectors results in the phase voltage waveforms presented in Figure 10.
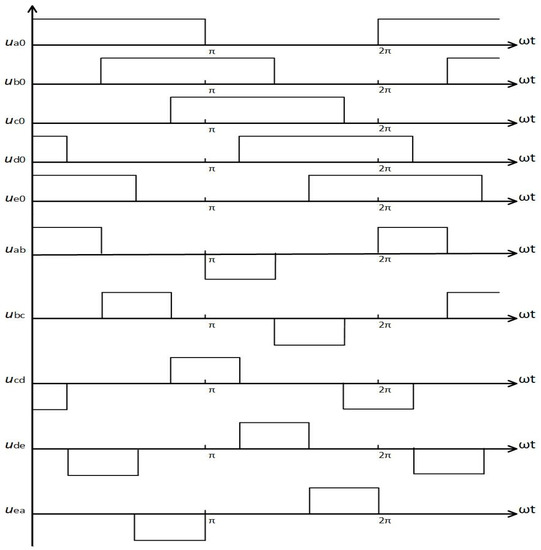
Figure 9.
Polar and phase-to-phase voltage waveforms: the pentagon connected load. Vector sequence: , , , , , , , , ,..

Table 2.
Parameters of the vectors. Red color denotes potential green color – potential 0.
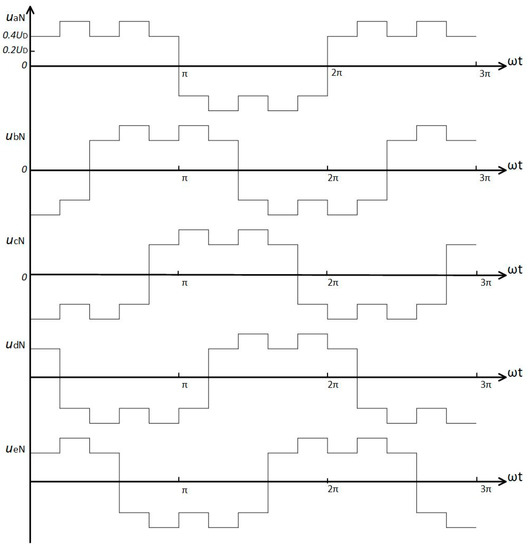
Figure 10.
Phase voltage waveforms: the star connected load. Vector sequence: , , , , , , , , ,..
Another example is presented in Figure 11. It demonstrates a set of polar and phase-to-phase voltage waveforms when the inverter is controlled completely dissimilarly. Phase-to-phase voltage waveforms relate to the pentagon connected load. The sequence of vectors executed by the control algorithm is the following: , , , , , , , , . The control algorithm consists in successive (every activation of the suitable vectors. So, one period of the output waveform () needs three full rotations of the referenced vector. The parameters of the vectors as well as their binary expansion are collected in Table 3.

Figure 11.
Polar (a) and phase-to-phase (b) voltage waveforms: the pentagon connected load. Vector sequence: , , , , , , , , ,..

Table 3.
Collected parameters of the vectors. Red color denotes potential green color – potential 0.
It is worth recognizing that this way of control guarantees higher phase-to-phase voltage than was obtained in the previous example. The fundamental harmonic of the waveform presented in Figure 9 did not go beyond while the fundamental of the phase-to-phase voltage presented above reaches . The RMS values of these voltage waveforms reach approximately and respectively.
3. Experimental Results
This mathematical tool was verified during simulation tests using the PLECS program. The following parameters were assumed for the purposes of simulation tests: voltage , frequency and load: and Figure 12 presents the main part of the model of the five-phase two-level inverter made in the PLECS program. The control signals are presented in Figure 13.
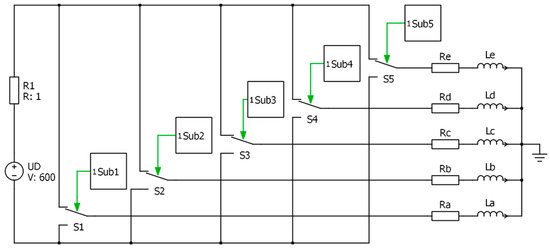
Figure 12.
The model of the five-phase two-level inverter made in the PLECS program.
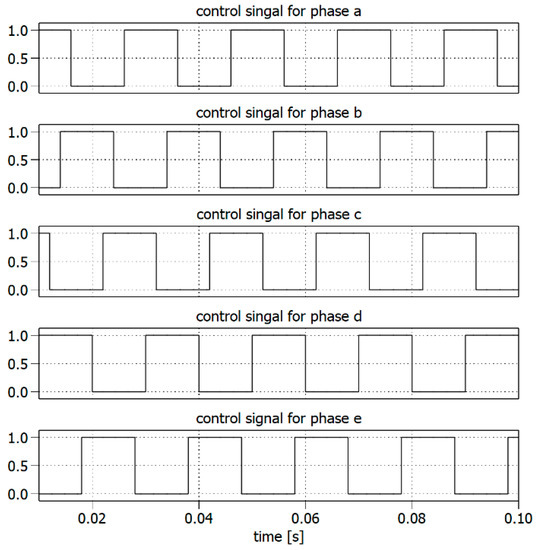
Figure 13.
The control signals used in simulations.
Figure 14 presents the waveforms of phase-to-phase voltages and their amplitude spectra obtained as a result of the Fourier analysis.
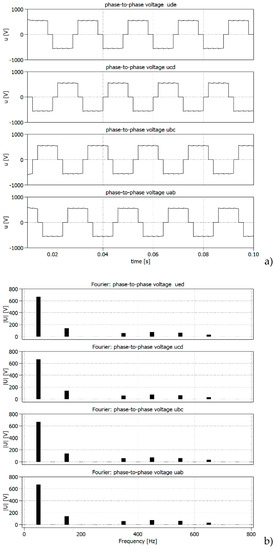
Figure 14.
The phase-to-phase voltages: ,,,, where: (a) voltages waveforms and (b) voltages spectra.
Figure 15 presents the waveforms of phase voltages and their amplitude spectra obtained as a result of the Fourier analysis.
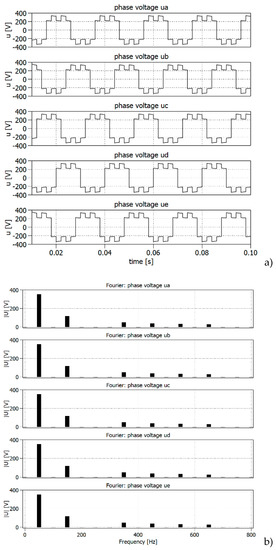
Figure 15.
The phase voltages: ,,,, where: (a) voltages waveforms and (b) voltages spectra.
Figure 16 presents the waveforms of the phase electrical currents and their amplitude spectra obtained as a result of the Fourier analysis.
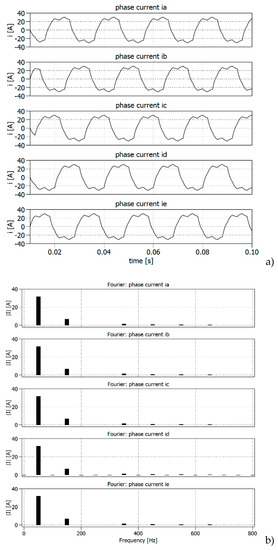
Figure 16.
The phase electrical currents: ,,,, where: (a) currents waveforms and (b) currents spectra.
During the simulation, important coefficients characterizing electrical signals such as the THD (Total Harmonic Distortion) and the RMS (Root Mean Square) were calculated. With selected load parameters, these coefficients are presented in Table 4.

Table 4.
Total harmonic distortion (THD) and root mean square (RMS) values for selected voltages and currents.
Summarizing the results of the simulation tests described in this section, it can be stated that they confirm the correctness of the mathematical tool presented in the paper. In the spectral analysis of voltage and current waveforms it can be seen that the first harmonic and the third harmonic dominate. A significant advantage of the described control method is that the current third harmonics are significantly lower even using the simplest way of control, in particular, without the use of PWM modulation. In order to assess the content of higher harmonics, the THD coefficients for currents and voltages were also calculated.
4. Conclusions
In multiphase inverters the ascending number of active vectors causes difficulties in designing sophisticated control methods and algorithms. It requires accessibility to proper mathematical tools and inverter models which are handy for this purpose and provide easy implementation as well as fast performance of the converter. The main contribution of this paper was to present a very simple mathematical system of notation and formulas. The inverter may be defined by the use of definite state vectors or standard space vectors obtained with the use of the polar voltage transform. The paper presents a notation system of all five-phase two-level 32 converter states. Every state is defined by two vectors: state vector and polar voltage space vector. Both vectors are specified by the use of the same digits resulting in binary expansion of the decimal vector index. The method could be advanced to other multiphase and multilevel inverters. This construction of the notation system provides an easy-to-use mathematical tool. It enables selection of a suitable vector sequence assuring the desirable voltage or current waveform. The discussed vector sequences were based on the imperative of only one switching in one phase during the whole voltage period. Three adequate examples were presented in Figure 9, Figure 10 and Figure 11. This mathematical tool makes it easier to define state and space vectors as well as to calculate the available phase and phase-to-phase voltages and the resulting load currents.
This mathematical tool was verified during simulation tests using the PLECS program. After applying the control signals calculated in accordance with the proposed mathematical algorithm in the simulation model, similar waveforms of phase voltages and inter-phase voltages were obtained. Additionally, in experimental studies, the operation of the model with the RL type load was tested. The most important electrical factors such as the THD and the RMS were also calculated. In particular, the analysis of the THD coefficient shows that the harmonic content in voltage and current waveforms is satisfactory, especially taking into account the fact that PWM modulation was not used. In the spectral analysis of voltage and current waveforms it can be seen that the first harmonic and the third harmonic dominate. A significant advantage of the described control method is that the current third harmonics are significantly lower even using the simplest way of control, in particular, without the use of PWM modulation.
Author Contributions
Conceptualization, methodology, analysis, supervision—J.I., resources, analysis, simulation studies, software, writing review and editing, project administration—A.M. All authors have read and agreed to the published version of the manuscript.
Funding
The project was financed within the program of the Ministry of Science and Higher Education called “Regionalna Inicjatywa Doskonałości” in the years 2019–2022, the project number 006/RID/2018/19, the sum of financing 11 870 000 PLN.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Kaźmierkowski, M.P.F.; Blaabjerg, F. Impact of Emerging Technologies on PWM Control of Power Electronics. IEEE Ind. Electron. Soc. Newsl. 1995, 2, 9–13. [Google Scholar]
- Malinowski, M.; Gopakumar, K.; Rodriguez, J.; Perez, M.A. A Survey on Cascaded Multilevel Inverters. IEEE Trans. Ind. Electron. 2010, 57, 2197–2206. [Google Scholar] [CrossRef]
- Li, Y.; Wang, Y.; Li, B.Q. Generalized Theory of Phаse-Shifted Carrier PWM for Cascaded H-Bridge Converters and Modular Multilevel Converters. IEEE J. Emerg. Sel. Top. Power Electron. 2016, 4, 2. [Google Scholar]
- Łebkowski, A. Analysis of the Use of Electric Drive Systems for Crew Transfer Vessels Servicing Offshore Wind Farms. Energies 2020, 13, 1466. [Google Scholar] [CrossRef]
- Łebkowski, A. Studies of energy consumption by a city bus powered by a hybrid energy storage system in variable road conditions. Energies 2019, 12, 951. [Google Scholar] [CrossRef]
- Gao, Z.; Lu, Q. A hybrid cascaded multilevel converter based on three-level cells for battery energy management applied in electric vehicles. IEEE Trans. Power Electron. 2018, 34, 7326–7349. [Google Scholar] [CrossRef]
- Moinoddin, S.; Iqbal, A.; Abu-Rub, H.; Khan, M.R.; Ahmed, S.M. Three-Phаse to Seven-Phаse Power Converting Transformer. IEEE Trans. Energy Convers. 2012, 27, 3. [Google Scholar] [CrossRef]
- Lauria, D.; Mazzanti, G.; Quaia, S. Some modeling problems for four-phаse power transmission systems. In Proceedings of the International Conference on Clean Electrical Power (ICCEP), IEEE Xplore, Ischia, Italy, 14–16 June 2011. [Google Scholar] [CrossRef]
- Meinguet, F.; Nguyen, N.-K.; Sandulescu, P.; Kestelyn, X.; Semail, E. Fault-Tolerant Operation of an Open-End Winding Five-Phаse PMSM Drive with Inverter. In Proceedings of the IECON 39th Annual Conference of the IEEE Industrial Electronics Society, Singapore, 18–21 October 2013. [Google Scholar]
- Abdel-Rahim, O.; Funato, H.; Abu-Rub, H.; Ellabban, O. Multiphаse Wind Energy Generation with Direct Matrix Converter. In Proceedings of the 2014 IEEE International Conference on Industrial Technology (ICIT), Busan, Korea, 26 February–1 March 2014. [Google Scholar]
- Jakubiec, B. Multiphаse Permanent Magnet Synchronous Motor Drive for Electric Vehicle. Przegląd Elektrotechniczny 2015, 91, 125–128. [Google Scholar]
- Chau, K.T.; Chan, C.C.; Liu, C. Overview of permanent-magnet brushless drives for electric and hybrid electric vehicles. IEEE Trans. Ind. Electron. 2008, 55, 2246–2257. [Google Scholar] [CrossRef]
- Parsa, L.; Toliyat, H. Five-Phаse Permanent Magnet Motor Drives. IEEE Trans. Ind. Applicаtion S 2005, 41, 30–37. [Google Scholar] [CrossRef]
- Ruba, M.; Surdu, F.; Szabo, L. Study of a Nine-Phаse Fault Tolerant Permanent Magnet Starter-Alternator. J. Comput. Sci. Control Syst. 2011, 4, 149–154. [Google Scholar]
- Levi, E. Multiphаse Electric Machines for Variable-Speed Applicаtions. IEEE Trans. Ind. Electron. 2008, 55, 1893–1909. [Google Scholar] [CrossRef]
- Vafakhah, B.; Salmon, J.; Knight, A.M. A New Spаce-Vector PWM with Optimal Switching Selection for Multilevel Coupled Inductor Inverters. IEEE Trans. Ind. Electron. 2010, 57, 2354–2364. [Google Scholar] [CrossRef]
- Celanovic, N.; Boroyevich, D. A Fast Spаce-Vector Modulation Algorithm for Multilevel Three Phаse Converters. IEEE Trans. Ind. Applicаtion S 2001, 37, 637–641. [Google Scholar] [CrossRef]
- Iwaszkiewicz, J.; Wolski, L. Stаte and Spаce Vectors—Complementary Description of the 2-level VSI. In Proceedings of the International Conference on Renewable Energies and Power Quality (ICREPQ’14), Cordoba, Spain, 8–10 April 2014. [Google Scholar]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).