Abstract
This article assesses the costs and benefits of incorporating battery energy storage systems (BESS) in transmission network expansion planning (TEP) over multiple time periods. We propose a mixed-integer programming model (MIP) for joint planning of the installation of battery energy storage systems (BESS) and construction of new transmission lines in multiple periods of time. The mathematical formulation of the presented model is based on the strategies of the agents of a transmission network to maximize their benefit, and on the operational restrictions of the power flows in transmission networks. This analysis is performed for the Garver 6 node test system takes into account the power losses in the lines and the restrictions for the energy stored in BESS. The power flows obtained with the MIP model are compared with AC power flows generated with specialized software for flows in power systems. This allows us to demonstrate the potential of models based on DC power flows to achieve approximate results applicable to the behavior and characteristics of real transmission networks. The results show that the BESS increase the net profit in the transmission networks and reduce their power losses.
1. Introduction
1.1. Background
In the classical approach, transmission expansion planning (TEP) is an optimal means of selection for the construction of new transmission lines [1]. The implementation of the TEP model requires the optimization of multiple objectives (reducing congestion, minimizing operating and investment costs, increasing the competitiveness of the system and maximizing social benefits, among others) in one or more planning periods [2,3], with capital investments that have a large long-term impact for the entire network [4].
The results obtained in the TEP models help mitigate the saturation of the transmission lines or the congestion in the network. However, its implementation is limited by economic, environmental, social and operational factors that can impede or delay the construction of transmission lines [5]. Therefore, the TEP models for a network must be based on the formulation of problems that include the dynamics of perfectly competitive markets, present economic and efficient solutions to contingencies and anticipate in advance the construction of the infrastructure necessary to meet demand.
A solution that the literature presents to give greater flexibility to the implementation of the results of a TEP model is the integration of battery energy storage systems with batteries (BESS) [6]. This is because BESS can mitigate peak loads, decrease line saturation, reduce required investments and improve network congestion while building new lines [7]. In addition to this, BESS-based technologies have also been shown to be a solution to provide greater flexibility to networks with high penetration from non-conventional renewable energy sources [8], decrease losses in transmission and distribution systems, and be used in Auxiliary services, such as frequency support, contingency reserves, and black start [9,10].
In a TEP model for a perfectly competitive market, which avoids restrictive practices against free competition that end up distorting the real signal of energy prices, the integration of the demand response evaluates the power of loads with regarding price changes or incentives over a period of time. In turn, obtaining optimal expansion strategies that manage the high penetration of renewable energy sources and the integration of new agents (distributed systems, energy storage, etc.) [11]. This contributes to flattening the load curve to manage greater energy efficiency and stability in the network [12].
1.2. Hypothesis and Aims
The appropriate selection of the location, capacity, installation and operation periods (loading or unloading) of BESS increases the social benefit of a network, since it manages to mitigate load peaks, reduce the saturation of lines, reduce investments in lines, and improve network congestion. Additionally, they are an alternative to economic or operating contingencies that may prevent or postpone the construction of new transmission lines [13]. Hence, this research project proposes the integration of BESS in a TEP model. This is because compared to the construction of transmission lines, the installation of BESS is faster and represents lower investment costs. To evaluate the effects of including BESS in the expansion of transmission networks, this article develops a MIP model with multiple joint planning periods for TEP with new lines and BESS. This, in the context of a competitive electricity market in which restrictive practices against free competition are avoided, which end up distorting the real energy price signal. The dynamic TEP with BESS model that is proposed is based on a DC model for power flows that offers a better approximation than the transport models, integrates the non-convex nature of the TEP problem and represents lower computational costs than the implementation of the models AC.
1.3. Contributions
Concerning the models for planning transmission network expansion, the main contributions of the authors in this article are:
- Include BESS in dynamic TEP problems with MIP. It is considered a joint optimization process to maximize the total benefit of the system through the construction of transmission lines and the installation of energy storage systems, taking into account the decrease in battery storage capacity and losses on the lines.
- Perform a sensitivity analysis to describe the relationship between the number of loss linearization blocks, execution times, and model accuracy.
- Validate the approaches made for power flows and losses in the network. Through the comparison of DC power flows of the MIP model with simulations for AC power flows in specialized software for power systems (i.e., Disigilent Powerfactory 15.7).
In the scientific literature, there is no formulation in which the joint planning of the installation of BESS and the construction of transmission lines is presented for multiple planning periods under the context of competitive markets in which there is also a growth in demand and dispatch of power along with its costs. On the other hand, this paper presents a detailed analysis to characterize power flows and losses in the network. The comparison with AC power flows in specialized software for power flows is a novelty of this article that also allows to graphically demonstrate the behavior of the power flows in the lines and compare them between different expansion plans.
1.4. Article Organization
The article is organized as follows: Section 2 is a review of the scientific literature for TEP models, emphasizing the authors who describe the benefits of incorporating BESS into the TEP problem. Section 3 describes a linear model for BESS, a detailed analysis of the process for linearization of flows and power losses in the lines is carried out, the develop the mathematical formulation of the TEP model, the indices and metrics to assess the benefits of the network in the expansion process and show the results of applying the proposed TEP model to the Garver 6 node test system. Section 4 presents the conclusions.
2. Literature Review
The integration of the market in a TEP model is presented in Reference [14] defining supply prices for generators, demand prices for loads and a set of demand scenarios. This benefits the system and each one of the market agents that compose it to be measured through a set of metrics defined by the ratio between surpluses and investment. In Reference [15], the authors classify the TEP model in heuristic and optimization models based on the applied solution methods, and in static and dynamic according to the planning horizon. Dynamic TEP models establish the years in which the investment is made and take into account that it will be present until the end of the planning horizon [4].
The application of heuristic and optimization methods aims to introduce improvement actions to existing networks. However, optimization methods, as the name implies, guarantee network optimization and provide the best plans for network expansion. The optimization methods for TEP can be divided into linear programming (LP) models cc, quadratic programming (QP) [16], mixed-integer linear programming (MIP) [10,17,18], nonlinear programming (PNL) [19] and nonlinear mixed-integer programming (MINLP) [20]. Mixed-integer programming models are the most used, taking into account the discrete nature of the decision variables for the construction or installation of new infrastructure. However, approaches with MINLP, in most cases, refer to the evaluation of a proposal, rather than the search for an optimal expansion plan [4,15].
In References [17,18], the authors apply the mixed-integer programming method to the planning problem for the expansion of transmission line networks with a static approach and linearize the equations necessary to describe the power flows and the losses in the lines. In Reference [10], a TEP model with static MIP approach includes a sensitivity analysis. It shows that the problem of planning transmission networks with losses in the lines can be rigorously modeled using MIP and that the number of binary variables and the number of linearization blocks can significantly affect the execution times and the accuracy of the model.
In Reference [13] the TEP with MIP model presents a dynamic approach that allows investments in transmission lines to be modeled for different periods of time, investment payback times, annual amortization rates, and growth in supply and demand. In addition, it transfers to the beginning of the planning horizon, the operating and investment costs assigned for each year and generates additional indicators to the metrics defined in Reference [14]. This is to measure the change in node prices and in line saturation when the system expands.
For TEP models with static or dynamic MIPs in which the construction of transmission lines and the installation of battery energy storage systems (BESS) are combined, the problem is to define the location and capacity of the lines and batteries that they increase the social benefit of the system and decrease operating and investment costs. The authors in References [5,21] describe a static MIP model for TEP with BESS and model the decrease in storage capacity, due to shelf life and loading and unloading cycles. They implement stochastic optimization to account for load uncertainty, and incorporate delays associated with planning and building new transmission lines. In Reference [5], in addition, there is a complement to the metrics and indices presented in Reference [13], and a sensitivity analysis that demonstrates the benefits of including BESS in TEP models in relation to the reduction of its costs and its technological development.
3. Methodology and Results
This section presents the mathematical formulation for TEP with new lines and BESS in multiple planning periods, indicators to evaluate the operational and economic performance of the expansion of transmission networks and the results and analysis obtained when implementing the TEP model developed in the Garver 6 node test system. Section 3.1 presents a general context about BESS, the equations that describe its stored energy, and its importance in the present and future for transmission networks. Section 3.2 presents a detailed analysis of the formulation of DC power flows in transmission networks, including losses in the lines. Section 3.3 develops the MIP for TEP from the restrictions for BESS, power flows, demand scenarios and considerations of a competitive market in which the net social welfare of the network is sought to be maximized. Section 3.4 describes the indices and metrics that have been proposed by the authors in references [5,13,14]. Section 3.5 describes the results of applying the model presented in Section 3.3. The results are evaluated through indicators, costs and benefits of the expansion process. Additionally, simulations are developed in specialized software for power systems to verify and graphically display results of the power flows.
3.1. BESS Model
The increasing use of BESS has been fostered by technological improvements, cost reduction, the ability to provide resilience to power outages, integration with non-renewable energy sources, increased efficiency of transmission or distribution networks and the ability to provide ancillary services among other factors [22,23]. The analysis for BESS that is developed in this article is based mainly on the efficiency and optimization of resources in transmission networks. The inclusion of BESS in transmission systems reduces congestion that occurs when transmission capacity is exceeded by customer demand, especially in scenarios of high-power demand during very short intervals. Battery energy storage systems are an alternative to reduce grid congestion in periods of high demand or increase the energy available for loads without the need for investments in transmission lines [24]. Despite the fact that in the present the energy storage systems with batteries present problems related to high costs, reduced useful life and high maintenance requirements, it is expected that cost reduction and technological advances will allow greater penetration of BESS in transmission networks.
The integration of energy storage systems requires strategies from the owner (new system agent) of BESS to maximize its benefit. In periods of low demand and low costs per kWh, BESS must receive energy from the grid and deliver it in periods of high demand and high costs per kWh. Therefore, in the transmission network operation model with BESS, the energy present in the battery for each instant of time and the power flow that it delivers and receives from the network must be characterized. This section presents a linear model to describe the energy stored in a battery based on the mathematical formulation of the authors in Reference [5].
In a battery-powered energy storage system, the energy at one instant of time depends on the energy stored at the previous instant of time and the power flow at .
The energy that is stored in the battery according to (1) and (2) it is in turn limited by the physical properties of the battery as described in (3) and (4).
The equations that describe the energy stored in the battery are not linear because they depend on the sign of de , the Equations (5)–(7) are reformulated to linearize the model of energy stored in the battery.
Assuming a unitary efficiency in the battery charge and discharge processes and from (5) the linear model to represent the energy stored in a battery is presented in (6) and (7).
In (6), when is equal to 0 the energy stored at the moment is equal to the energy stored at the moment plus the energy it received from the network, if equals 1, variables are given the freedom to take values according to other constraints (7) presents the opposite scenario, in which if is equal to 1, the energy stored at the moment is equal to the energy stored at the moment minus the energy that it delivers to network. In this study, it is considered that the capacity of a battery throughout its useful life does not remain constant and suffers a reduction in each charge and discharge cycle. These restrictions are included in a parameter in the batteries’ aggregate utility function.
3.2. Power Flow Formulation
The complex power transmitted in a transmission line between two nodes and , is presented in (8).
Equation (8) is a nonlinear expression for power flows that can be approximated with linear equations under the following DC model considerations:
- Only active power flows exist.
- RL << XL.
- The voltages on all nodes are equal to 1 pu.
- The difference in the stress angles of the bars is very small.
For y equal to 1 pu, (8) is rewritten in the form presented in (9). The active power flow in both directions for the nodes and are described by (10) and (11), respectively.
Equation (12) represents the losses of active power in the lines. For small differences between and ( (13) is a good approximation for (12) [25]. In turn, the second order expression for (12) can be approximated as the sum of linear equations, as shown in (14) and Figure 1.
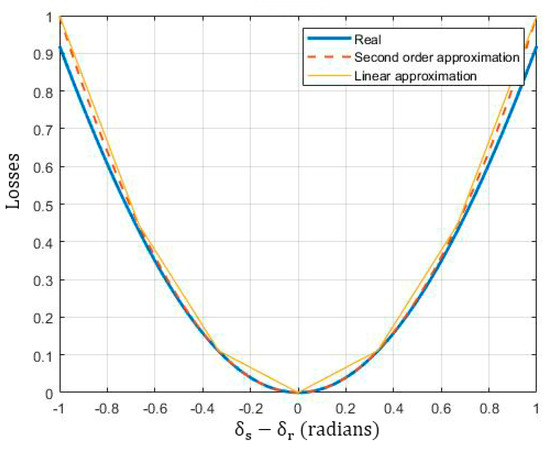
Figure 1.
Approach for losses.
A complete expression for the flow of active power between two nodes s and r is presented in Equation (15). This is represented as the sum of the lossless power flow and the power losses in the corridor lines.
For a maximum number of K lines built in the corridors of a network, the total flow of active power that is injected into a node s is described by (16).
3.3. Formulation of TEP with BESS
This section presents the MIP model for TEP with BESS and multiple planning periods in a competitive electricity market. The TEP approach in an unregulated market allows generators and demands to establish strategies to maximize their profit. The model integrates the physical constraints of the system with the operation of an unregulated market to maximize the total net benefit in electric power transmission networks. The integration of BESS in the model includes offer prices for batteries that act as loads or generators, physical restrictions for power flow, decreased energy storage capacity, and battery life [5]. Regarding the structure of the market, the model considers demand scenarios, investment and operating costs, power losses in the lines, generators offers, and demand offers [14]. Additionally, the model evaluates operating costs and annual amortization of investments for each of the periods in the planning horizon [13]. The mathematical formulation of the model presented in this section are based on the models proposed in References [5,13,14].
3.3.1. Objective Function
Equation (17) presents the objective function of the problem. This seeks to maximize the aggregate social welfare expressed as the aggregate utility function of demand, minus the aggregate supply function of generators, plus the aggregate utility function of batteries that act as consumers, minus the aggregate supply function of batteries, operating as generators, less the cost of investment in new lines and batteries. From the point of view of all market agents, aggregate social well-being also equals the sum of generation surpluses, plus demand surpluses, plus marketing surpluses, fewer investment costs in new lines and batteries. To make investment and operating costs comparable σ is equal to 8760 h, equivalent to the hours of the year. Furthermore, both investment and operating costs are divided by a factor that transfers them to the present value of the first year in the planning horizon.
3.3.2. Constraints
The constraint in (18) is associated with the power balance at a node. It establishes that the sum of the power injected and delivered at the node must be equal to zero, and that the losses in the lines are assumed equally by the two nodes to which they are connected. The dual variable associated with the power balance equation represents the node price per scenario.
In (19) variables and relationships are introduced for the linearization of the equations that describe the energy stored by a battery at an instant of time t, (20) and (21) define the conditions to associate the power flow in the batteries with charging and discharging processes, in turn limiting the maximum power flow according to the physical restrictions of the batteries. Equations (22) and (23) establish the restrictions for the maximum power flow in the built lines, in (23) the relationship between the lossless power flow, the line susceptance and the angle of the voltages is established on the bars. Based on the linear formulation for losses in the system, (24) and (25) establish limits for losses in the lines built. According to the thermal capacity of the system lines, (26) and (27) establish the limits for the maximum power.
The equations presented in (28) and (29) consider the capacity and the maximum demand for the generators and the loads, respectively, while (30)–(32) establish the relationship between the stored energy and the flow of power in the batteries, for each of the scenarios as defined in Section 2. Finally, (33)–(36) establish the limits for the variables defined in the linearization process of the losses
3.4. Indices and Metrics
The Indices and metrics presented in this section are based on the models proposed in References [5,13,14].
3.4.1. Nodal Prices
The nodal prices or LMP (Location marginal price) are equal to the marginal cost of supplying an additional power unit in a node. It is equal to the sum of the costs of generation, transportation and losses. The nodal prices are used to calculate the congestion ratio, the income of each generator and the charge per load. The nodal price system is calculated through the following process:
- Calculate the solution to the mixed-integer programming problem defined in Equations (18)–(36).
- Formulate a linear programming model, establishing binary variables and the optimal demand solution at each node as constants. The objective function for the linear programming model is presented in (37). The constraints are the same as those described in (19)–(36).
- Solve the linear programming model for each of the scenarios. The dual variables associated with the load balance equation are used as nodal prices.
From the nodal prices, the generator’s income or the total payments of the demands are defined as the sum in all scenarios, of the product of the energy (MWh) demanded or consumed in a node by its respective LMP . The remuneration to the generators and the payment of the demands allow defining the surpluses for each one of the agents of the system.
3.4.2. Saturation Index
The saturation index is an indicator that measures the relationship between the flow that is transmitted through the network and its maximum capacity. In the Equation (38) this is calculated as the sum of the absolute value of the power flows for all the lines built in the scenario with the highest demand, on the sum of the maximum power flows of the lines built [5].
3.4.3. Congestion Index
This index measures the congestion of the system based on its nodal prices. It is a measure of the deviation of the nodal prices from their average. A small value of the congestion index indicates similar node prices. The equations for calculating nodal prices are presented in (39)–(41). These equations are taken from Reference [5].
3.4.4. Metrics
A set of metrics are defined to describe the benefit obtained by each of the market agents with the expansion of the system. The set of metrics are calculated according to the formulation from Reference [5].
- μ1 Shows the changes in the aggregate social benefit of the general system in relation to investment costs.
- μ2 Describes the change in generation surpluses with respect to investment costs.
- Describes the change in generation and batteries surpluses with respect to investment costs.
- μ3 Describes the change in demand surpluses with respect to investment costs.
- μ4 Describes the change in marketer surpluses relative to investment costs. The marketer’s surpluses are equal to the subtraction of the total remuneration of the generators less the total payment for energy consumed from the demands.
3.5. Results
The model presented in Section 3.3 was developed at GAMS with the support of the CPLEX optimization tool and applied to the Garver 6 node test system. Two case studies are evaluated to validate the model with the models developed in References [5,14]. A third case study is developed to establish the costs and benefits of including BESS in a TEP with a planning horizon of 8 years. The validation of the results developed in GAMS is supported by simulations carried out in Digsilent powerfactory 15.7.
3.5.1. Garver 6 Node Test System
For the Garver 6 node test system presented in Figure 2, the problem to be solved is to establish the equilibrium point between the power delivered by the generators and BESS (suppliers of the electricity market) and the power demanded by the loads and BESS (Demands in the electricity market). The system has 10 generation units that have a cost associated for each dispatched MWh. The loads associated with the system are presented as the sum of five demand blocks. The nodes to which the generation and load units are connected are presented in Figure 2.
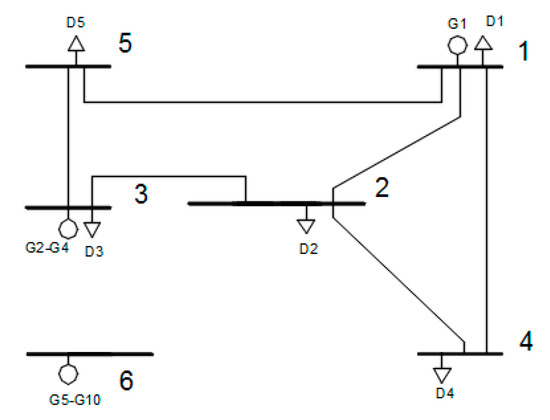
Figure 2.
Garver system 6 nodes unmodified.
Table 1 describes the maximum powers and costs of the generation and demand units. Where P1 are the values associated with demand in the first case study, while P2 are the powers demanded in the second and third case studies. The construction of the transmission lines to satisfy the power demand of the system and increase the social benefit of the system is developed by the system operator. The operational and investment characteristics that the system operator can include in the TEP model are presented in Table 2. Where Table 1 and Table 2 are taken from References [5,14].

Table 1.
Demand and generator restrictions.

Table 2.
Line parameters for Garver six-bus system.
3.5.2. Case Study 1: Expansion with Lines
In this section the MIP model is validate with results in Reference [14] for the Garver 6 node test system. As a result, a comparison is generated between the characteristics of the system with and without expansion. To approximate the behavior of a network in which different levels of power demand are presented, the loads have associated a demand coefficient to simulate low, medium, and high demand scenarios. In addition to this, each demand coefficient has a weight associated with the number of hours in the year that this demand scenario occurs. These characteristics are shown in Table 3 and are taken from Reference [14]. The results in this section allow to validate the model with the result.

Table 3.
Characteristics of the different scenarios, first case study.
From the results developed in GAMS, it is observed that the added social benefit is maximized when three lines are built in the expansion process, two lines between nodes 2–6 and one line between nodes 4–6. Figure 3 shows the power flows through the lines. With the entry into operation of the lines from node 6 to nodes 2 and 4, respectively, the generation connected to node 6 supplies the maximum power that the restrictions for the thermal capacity of corridors 2–6 and 4–6 allow. After the expansion of the system, node 6 supplies 47% of the energy consumed in the network.
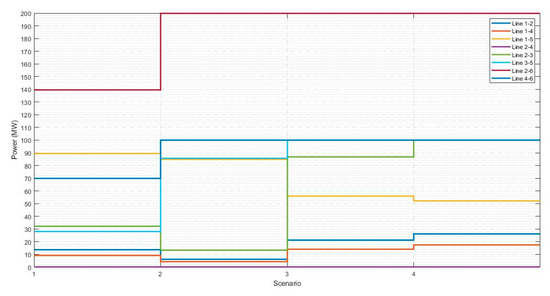
Figure 3.
Power flows through the lines, whit expansion.
Table 4 shows the effect of approximations on the linearization of the mixed-integer programming model. From which the relationship of the number of linearization blocks with the estimation of the losses, the execution times and the objective function is observed. A reduced number of partitions decrease the execution times and leads to an oversizing of the losses and reliability of the model results. While the trend in Table 4 shows that a large number of linearization blocks achieves better approximation accuracy for line losses and increases execution times. Table 5 presents the results developed in this article and [14] for the energy generated, demand and loss for each of the scenarios. Table 6 compares the surpluses, the investment in lines and agent profit. Table 7 compares the results obtained for the metrics.

Table 4.
Effect of linearization blocks.

Table 5.
Check Results by scenario for generation, demand and losses.

Table 6.
Comparison of surpluses, investment and social benefit.

Table 7.
Summary of results case study 1.
Figure 4 and Figure 5 illustrate the nodal prices by scenario, for each of the nodes after and before the expansion process. The nodal prices are smaller in the lower demand scenarios and have less dispersion with each other. The larger nodal prices are due to the saturation of the lines and the high opportunity cost that this represents to supply an additional MWh in a node. The dispersion of nodal prices in high demand scenarios is due to the fact that the transmission infrastructure is not sufficient for the power flows required for certain nodes, especially those with high demand but no generation. On the contrary, the smaller difference in the nodal prices for the low demand scenarios is mainly due to the cost of the losses and shows that the level of network congestion is not important. In addition, the existing transmission lines can support the power flows required by the loads.
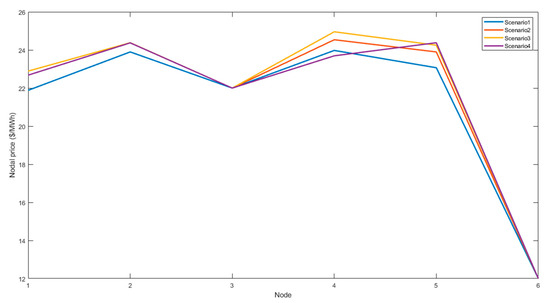
Figure 4.
Nodal price without expansion.
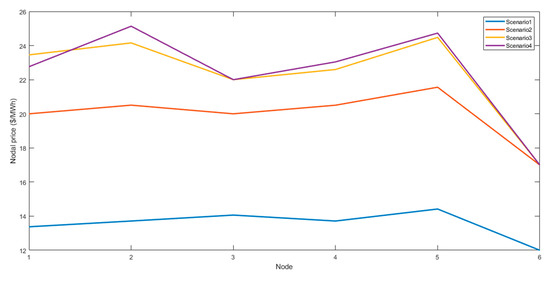
Figure 5.
Nodal price with expansion.
Figure 4 shows that, before the expansion, the nodal prices are considerably higher than the marginal cost of the available generators and that they are dispersed among themselves. This is true for both low demand and high demand scenarios. Figure 5 shows that low-demand scenarios (Scenario 1, Scenario 2) have lower nodal prices than the marginal cost of some generators available and that these prices do not present significant differences. Low nodal prices indicate that expansion enabled optimization of available resources by connecting demand nodes to generators at node 6. In addition, the little variation between nodal prices for low demand scenarios can be explained by Figure 3—this shows that in scenario 1 there are no saturated lines, and that in scenario 2 the saturated lines are smaller for scenario 2 than for scenario 3 and 4.
Expanding the Garver 6-node test system with the three lines connecting Node 6 to The Demand Nodes allow the system to operate efficiently in low-demand scenarios. However, when these lines are saturated by an increase in demand that maximizes the total profit of the system (Scenario 2, Scenario 4), it is evident that the expansion with lines was not enough to reduce network congestion. In Figure 5, the increase and variation of the nodal prices for scenarios 3 and 4 is the reflection of the increase in network congestion. The scenarios with the lowest demand represent 74.17% of the hours of the year. Hence, the results of implementing the optimization model to the Garver 6-node test system show that the costs of investing in an additional line do not outweigh the benefits that can be obtained with the reduction in network congestion in the scenarios of Greater demand.
Table 7 presents the summary with the most important results associated with the expansion of the system, including aggregate social benefit, number of lines built, total investment, metrics and saturation and congestion indices. With a depreciation rate of 0.1102, the three lines that were built to link the demand from nodes 1 to 5 with the generation of node 6, represent an annual investment cost of $9918M.
3.5.3. Case Study 2: Expansion with Lines and BESS
With the characteristics presented in Table 1, Table 2, Table 8 and Table 9, the MIP model is validate with results in Reference [5] for the Garver 6 node test system. As a result, a comparison is generated between the characteristics of the system without expansion and with expansion. Table 8 and Table 9 are taken from Ref [5].

Table 8.
Demand characteristics.

Table 9.
Battery characteristics.
According to the results of the MIP model developed in GAMS, Table 10 presents the results for the power flows in the lines for the Garver 6 nodes test system without expansions. Where the results presented in Table 10 have low error percentages with respect to the same analysis in Ref [5]. Figure 6 shows the behavior of power flows before expansion. Table 11 presents the comparison of costs and benefits of including energy storage systems in TEP problems. The main effect of including BESS in the model is evident in the increase in the social benefit of the system. For the expansion with lines and BESS, the investment required in batteries is $0.085905 M, and the investment required in lines is $9918 M. This allows us to infer that investments in batteries to produce increases in the net social welfare of a network are much less capital intensive than investment in lines. Likewise, the metrics reflect that investments in infrastructure have a positive effect on the increase in surpluses for each of the agents in the system. The loads are the most benefited since they can increase the power consumed at the same time as the congestion in the network is reduced.

Table 10.
Power flows before expansion.
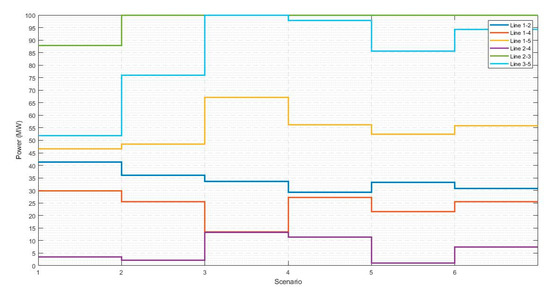
Figure 6.
Power flow, without expansion.

Table 11.
Summary of results of case study 2.
3.5.4. Case Study 3: Expansion with Multiple Planning Periods
For an 8-year planning horizon in which demand and generation grow at a rate of 3.1% per year and operating costs grow at a rate of 5% per year, a discount rate of 10% is established. The return period for investments in transmission lines is equal to 25 years for the total cost of the lines and their annual amortization rate of 0.1102 [13]. The return period for investments in BESS is equal to 10 years and their annual amortization rate of 0.1627. Battery characteristics are based on those presented in Reference [5]. The maximum number of lines per corridor is equal to 3, and the maximum number of BESS per node is equal to 1. All operating and investment costs carry over to the first year of the planning horizon.
Figure 7 presents the location and periods of entry into operation of the lines and BESS. Table 12 presents comparative results of the TEP model, with and without including BESS. The TEP model solution for the Garver 6 node test system with a planning horizon of eight years involves the construction of 5 transmission lines and four BESS. In the first year of the planning horizon, two lines are built between nodes 2 and 6, one line between nodes 4 and 6 and 4 BESS systems at nodes 1, 2, 4 and 5. The construction of the lines allows the dispatch of power from the generators connected in node 6. With the growth of demand and generation in the planning horizon, two new lines are proposed, a third line between node 2 and 6 in the second year, and a second line between node 4 and 6 in the seventh year.
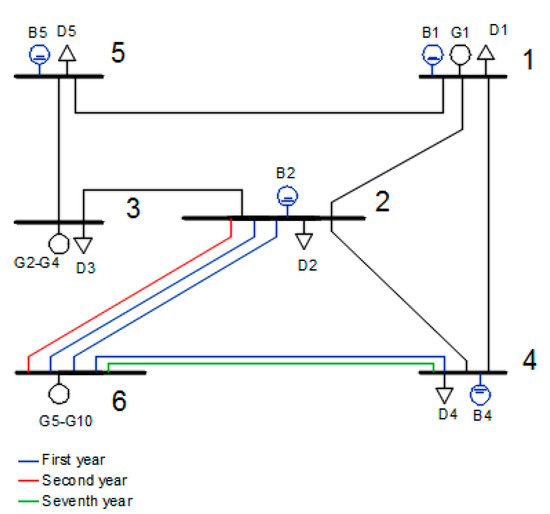
Figure 7.
Results of multiple planning periods.

Table 12.
Results of multiple planning periods.
The metrics described in Table 12 show that all agents derive benefits from the expansion process. For every dollar invested $3344 are obtained as benefits for all agents participating in the market. Of which, $0.814 belongs to generators, $0.015 to BESS, $1804 to loads and $0.713 to the marketer. Based on the results for the expansion of the Garver 6 node test system with lines and batteries in the first year of the planning horizon, Figure 8 and Figure 9 present the charge profile to maximize system profits, the power generated and charging/discharging BESSs. These curves define BESS’s strategy to maximize its profits according to nodal prices, charging in low demand scenarios and discharging in high demand scenarios.
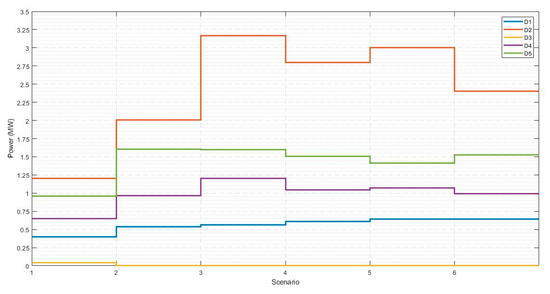
Figure 8.
Power demand, first year planning.
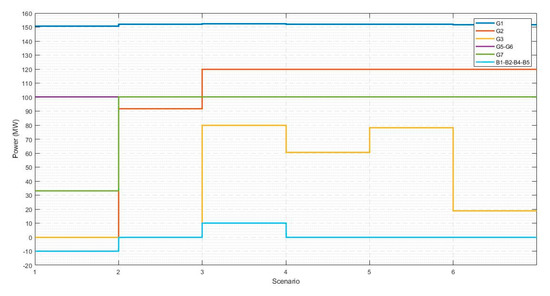
Figure 9.
Power generation, first year planning.
Figure 9 comparatively analyzes the approximations made with DC power flows for power losses in transmission lines. This is because the power generated by the Slack node (Node 1) is based on an AC power flow that can be compared with the generation of the same node in the DC power flow developed with the implementation of the MIP model in Section 3.3. Table 13 presents the comparison of these values and describes an absolute error that corresponds to the power losses that have not been taken into account by the MIP model in GAMS. The proportion relationship between the power losses of the entire network is due to the fact that with the increase of the losses, a greater number of linearization blocks is required in the MIP model. However, in the implementation of the mathematical model in GAMS, this number was restricted to a maximum of 50 linearization blocks to guarantee reasonable computational execution times.

Table 13.
The power generated in node slack, first year planning.
4. Conclusions
The main contribution of this document is the approach of dynamic TEP models with MIP that include BESS. With this model, there is a joint maximization process to maximize the total benefit of the system through the construction of transmission lines and the installation of BESS. This research shows that the inclusion of BESSs in the TEP models increase the net social benefit of the entire system. This is the result of lower operating costs, losses, and improved network congestion. The approach to the structure of competitive markets shows that each one of the agents of the system establishes strategies so that their remuneration is greater than operating costs. Additionally, it is evident that the main effect of including BESS in the operation of the system satisfies higher demands and guarantees the transmission of generated power at the lowest possible cost.
Including losses in transmission lines and a decrease in BESS’s storage capacity develops the planning processes based on the real behavior of transmission networks. This is important when evaluating and weighing the benefits of putting BESS into service, since the results show that the improvement in the net profit of the network with the inclusion of BESS is mainly due to the decrease in losses and its location close to the demand centers. Therefore, not including losses in the planning process can prevent the improvement in system operating costs from being evident. Whereas, not including a factor representing battery life in multi-period planning processes can overstate the positive effect of including BESS in TEP.
The contrasting results of the simulations of AC power flow demonstrate that the TEP models with DC power flow include losses that generate more realistic results on the physical constraints of the network. In addition, they demonstrate that for planning processes—in which the execution time is not a relevant restriction—the network operators can increase the number of linearization blocks to more adequately characterize the power losses in the lines. This also increases the accuracy of the model, and generate viable alternatives (from the evaluation of the economic) and operational performance indicators (that result from the optimization process of the TEP problem).
Author Contributions
Validation, C.A.M., O.D.M. and E.R.T.; Conceptualization, C.A.M., O.D.M. and E.R.T.; methodology, C.A.M., O.D.M. and E.R.T.; investigation, C.A.M.; software, C.A.M.; supervision, O.D.M. and E.R.T.; writing, C.A.M., O.D.M. and E.R.T. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
Notation
| Years | |
| Scenario e in year t | |
| Weight of scenario e in year t | |
| factor to make investment and operational costs comparable | |
| interest rate | |
| Demand block | |
| Generation block | |
| Battery | |
| Price bid of the i-th demand block in scenario c and year t | |
| Price offer of the i-th generation block in scenario c and year t | |
| Price offer of the i-th battery in node m for scenario c and year t | |
| Price bid of the i-th battery in node m for scenario c and year t | |
| Demand power by the i-th demand block in scenario c and year t | |
| Generated power by the i-th generation block in scenario c and year t | |
| Charge power battery n in node m for scenario c and year t | |
| Discharge power battery n in node m for scenario c and year t | |
| Annual amortization rate of the new lines | |
| Building cost of line k in corridor s-r | |
| Binary variable of line k in corridor s-r | |
| Factor accounting for the degradation of the battery | |
| Energy stored by the battery n in node m for scenario c and year t | |
| Price bid of the i-th demand block in scenario c. | |
| Binary variable that indicates if the battery is working in year t | |
| Cost per MWh in batteries | |
| Annual amortization rate of new batteries | |
| Set of years | |
| Set of scenarios | |
| Set of all charges | |
| Set of all generators | |
| Set of all batteries | |
| Set of new lines | |
| Set of new batteries | |
| Set of demand blocks connecting to node s | |
| Set of all generators at node s | |
| Set of all batteries at node s | |
| Set of all lines connecting to node s | |
| Power flow in line k of corridor s-r for scenario c and year t without considering losses | |
| Loss of power in line k of corridor s-r for scenario c and year t | |
| Power flow in line k of corridor s-r for scenario c and year t | |
| Voltage angle at node s | |
| Voltage angle at node r | |
| Independent variable assigned for the linearization of the losses | |
| Constant assigned to the slope of | |
| Number of linearization blocks (Number of partitions to approximate ) | |
| Binary variable equal to 1 when the battery is discharged | |
| Efficiency in battery discharge | |
| Efficiency in battery charging | |
| large positive constant | |
| Conductance between nodes s and r | |
| Suceptance between nodes s and r | |
| Voltage angle at node s | |
| Voltage angle at node r | |
| Losses of active power | |
| Lossless active power | |
| Voltage at node s | |
| Voltage at node r | |
| Complex power transmitted from node to node | |
| Active Power transmitted from node to node | |
| Reactive power transmitted from node to node | |
| Impedance between nodes and | |
| RL | Resistance of a transmission lines |
| XL | Inductive reactance of a transmission line |
References
- Gbadamosi, S.L.; Nwulu, N.I. A multi-period composite generation and transmission expansion planning model incorporating renewable energy sources and demand response. Sustain. Energy Technol. Assess. 2020, 39, 100726. [Google Scholar] [CrossRef]
- Maghouli, P.; Hosseini, S.H.; Buygi, M.O.; Shahidehpour, M. A multi-objective framework for transmission expansion planning in deregulated environments. IEEE Trans. Power Syst. 2009, 24, 1051–1061. [Google Scholar] [CrossRef]
- Rosellón, J. Different Approaches Towards Electricity Transmission Expansion. Rev. Netw. Econ. 2009, 2. [Google Scholar] [CrossRef]
- Lumbreras, S.; Ramos, A. The new challenges to transmission expansion planning. Survey of recent practice and literature review. Electr. Power Syst. Res. 2016, 134, 19–29. [Google Scholar] [CrossRef]
- Aguado, J.A.; de la Torre, S.; Triviño, A. Battery energy storage systems in transmission network expansion planning. Electr. Power Syst. Res. 2017, 145, 63–72. [Google Scholar] [CrossRef]
- Castro, T.E.G.; Jesus, L.L.M.; Trujillo, E.R. Literature review of BESS implementation in DER. Rev. Vínculos Cienc. Tecnol. Y Soc. 2019, 16, 321–326. [Google Scholar]
- Mazaheri, H.; Abbaspour, A.; Fotuhi-Firuzabad, M.; Farzin, H.; Moeini-Aghtaie, M. Investigating the impacts of energy storage systems on transmission expansion planning. In Proceedings of the 2017 25th Iranian Conference on Electrical Engineering, ICEE 2017, Tehran, Iran, 2–4 May 2017; pp. 1199–1203. [Google Scholar] [CrossRef]
- Denholm, P.; Sioshansi, R. The value of compressed air energy storage with wind in transmission-constrained electric power systems. Energy Policy 2009, 37, 3149–3158. [Google Scholar] [CrossRef]
- Wogrin, S.; Gayme, D.F. Optimizing Storage Siting, Sizing, and Technology Portfolios in Transmission-Constrained Networks. IEEE Trans. Power Syst. 2015, 30, 3304–3313. [Google Scholar] [CrossRef]
- Zhang, F.; Hu, Z.; Song, Y. Mixed-integer linear model for transmission expansion planning with line losses and energy storage systems. IET Gener. Transm. Distrib. 2013, 7, 919–928. [Google Scholar] [CrossRef]
- Worighi, I.; Maach, A.; Hafid, A.; Hegazy, O.; van Mierlo, J. Integrating renewable energy in smart grid system: Architecture, virtualization and analysis. Sustain. Energy Grids Netw. 2019, 18, 100226. [Google Scholar] [CrossRef]
- Nwulu, N.I.; Xia, X. Multi-objective dynamic economic emission dispatch of electric power generation integrated with game theory based demand response programs. Energy Convers. Manag. 2015, 89, 963–974. [Google Scholar] [CrossRef]
- Aguado, J.A.; de la Torre, S.; Contreras, J.; Conejo, A.J.; Martínez, A. Market-driven dynamic transmission expansion planning. Electr. Power Syst. Res. 2012, 82, 88–94. [Google Scholar] [CrossRef]
- de la Torre, S.; Conejo, A.J.; Contreras, J. Transmission expansion planning in electricity markets. IEEE Trans. Power Syst. 2008, 23, 238–248. [Google Scholar] [CrossRef]
- Latorre, G.; Cruz, R.D.; Areiza, J.M.; Villegas, A. Classification of publications and models on transmission expansion planning. IEEE Trans. Power Syst. 2003, 18, 938–946. [Google Scholar] [CrossRef]
- Garzillo, A.; Cazzol, M.V.; L’Abbate, A.; Migliavacca, G.; Mansoldox, A.; Riverax, A.; Nortonx, M. Offshore grids in Europe: The strategy of Ireland for 2020 and beyond. In Proceedings of the 9th IET International Conference on AC and DC Power Transmission (ACDC 2010), London, UK, 19–21 October 2010; Volume 2010, p. O64. [Google Scholar] [CrossRef]
- Alguacil, N.; Motto, A.L.; Conejo, A.J. Transmission expansion planning: A mixed-integer LP approach. IEEE Trans. Power Syst. 2003, 18, 1070–1077. [Google Scholar] [CrossRef]
- Zhang, H.; Heydt, G.T.; Vittal, V.; Quintero, J. An improved network model for transmission expansion planning considering reactive power and network losses. IEEE Trans. Power Syst. 2013, 28, 3471–3479. [Google Scholar] [CrossRef]
- Youssef, H.K.; Hackam, R. New transmission planning model. IEEE Trans. Power Syst. 1989, 4, 9–18. [Google Scholar] [CrossRef]
- Rahmani, M.; Rashidinejad, M.; Carreno, E.M.; Romero, R. Efficient method for AC transmission network expansion planning. Electr. Power Syst. Res. 2010, 80, 1056–1064. [Google Scholar] [CrossRef]
- Qiu, T.; Xu, B.; Wang, Y.; Dvorkin, Y.; Kirschen, D.S. Stochastic Multistage Coplanning of Transmission Expansion and Energy Storage. IEEE Trans. Power Syst. 2017, 32, 643–651. [Google Scholar] [CrossRef]
- Mexis, I.; Todeschini, G. Battery Energy Storage Systems in the United Kingdom: A Review of Current State-of-the-Art and Future Applications. Energies 2020, 13, 3616. [Google Scholar] [CrossRef]
- Tsianikas, S.; Zhou, J.; Iii, D.P.B.; Coit, D.W. Economic trends and comparisons for optimizing grid-outage resilient photovoltaic and battery systems. Appl. Energy 2019. [Google Scholar] [CrossRef]
- Marnell, K.; Obi, M.; Bass, R. Transmission-Scale Battery Energy Storage Systems: A Systematic Literature Review. Energies 2019, 12, 4603. [Google Scholar] [CrossRef]
- Villasana, R.; Salon, S.J.; Garver, L.L. Transmission network planning using linear programming. IEEE Trans. Power Appar. Syst. 1985, PAS-104, 349–356. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).