Abstract
Apart from water quality, leakage control and energy consumption management are the most concerning challenges for water treatment plants (WTPs). The joint scheduling of pumps and pressure reducing valves (PRVs) in the water distribution network can reduce excessive pressure and distribute pressure more evenly, which achieves comprehensive reduction of leakages and energy consumption. Taking into account the main shortcomings of the commonly used methods, such as scheduling pumps or PRVs separately, or optimizing PRV settings when their position is given, etc., this paper has taken the PRV (position and setting) and the working status of variable speed pumps (VSPs) as decision variables and the cost savings contributed by leakage reduction and energy consumption savings as the objective function, which maximized the economic benefits brought by PRV and/or VSP scheduling. A genetic algorithm (GA) was used to optimize the solution under multiple working conditions. The performance of three control strategies (PRV-only scheduling, VSP-only scheduling, and joint scheduling of PRVs and VSPs) are compared to each other based on a small network. Joint scheduling has achieved the best economic benefits in reducing the gross cost (contributed by leakage and energy consumption) of the three control strategies, which results in a leakage reduction of 33.4%, an energy consumption reduction of 25.4%, and a total cost reduction of 33.1%, when compared to the original network, and saving about 1148 water (7% of the original consumption) and 722 electric energy (25.4% of the original consumption) per day.
1. Introduction
With the development of cities and global climate change, water resources have been playing an increasingly important role in industrial operation and our daily lives. As a crucial part of the water supply system, the water distribution network undertakes the task of transporting purified water from WTPs to customers. However, its leakage problem has always been one of the major issues that perplexes the water supply department [1]. Due to the differences in countries, regions, and water supply systems, the leakage rate may be as low as 3% (small or medium-sized water distribution networks in the Netherlands [2]), or as high as 50% or more [3,4]. The economic loss caused by long-term and continuous leakage should not be underestimated, and reasonable leakage management will greatly reduce water loss and conserve budget money for the water supply department.
Most of the traditional methods for leakage detection and control are designed for large leakages that have already resulted in serious consequences and can be detected by using leakage detection devices. For small leakages that cannot be easily detected, pressure management shows its advantages [5,6]. Germanopoulos (1985), Savić and Walters (1996), and others have found that there is a clear correlation between leakage and pressure, and have established a mathematical expression between them, which reflects a trend where the degree of leakage declines as the pressure decreases [7,8]. However, in most cases, water distribution networks are designed according to maximal demand. As such, the network suffers excessive pressure during non-peak periods, which makes pressure management more important. In addition to reducing leakages that have already occurred, pressure management can also control the frequency of pipe bursts or lower the risk of deteriorating into a burst [3,9].
The direct or indirect methods of pressure management include: installation and adjustment of PRVs, water distribution network updates (replacing or repairing components, altering unreasonable network topology, adding secondary boosting pumping stations, etc.), optimal scheduling of pumps (changing the outlet pressure or turning it on/off), and network partitioning, according to pressure, etc. [10] The installation of PRVs and scheduling of pumps are generally used more often. They are suitable for most water distribution networks.
Many researchers have made achievements in the field of pressure management. By using PRVs, Nicolini et al. (2009) used a multi-objective genetic algorithm (MOGA) to choose the installation position and setting of PRVs to reduce leakage in a small water distribution network [11]. Creaco and Pezzinga (2015) combined iterative linear programming with a MOGA, which was used to search for the best positions of PRVs (achieved by closing the pipes), while linear programming was used to find the appropriate settings. Their method significantly improved the efficiency of PRV optimization [12]. Gupta et al. (2017) used an improved reference pressure algorithm to better choose PRV locations, while a MOGA was used to find the optimal setting of PRVs with the aim to reduce leakage. Combined with water level optimization of water storage tanks, there was a leakage reduction of 26.51% and 20.81% in two networks, respectively [13].
The optimization on pumps’ operation is mostly aimed at reducing energy consumption. However, there are also some authors focusing on pressure management. Bakker et al. (2014) combined water demand forecasting with pressure management to reduce the pressure and leakage. Dynamic methods were used to control the real-time outlet pressure of pump stations. The comparison before and after the implementation showed that the outlet pressure dropped by 29%, the background leakage decreased by 20%, and the total energy consumption cost of the system decreased by 11.5% on the case network [14]. De Marchis et al. (2016) studied the effect of pumps as turbines (PATs) in networks, by mainly considering the influence of energy changes brought by user behaviors on network pressure recovery and PAT positioning. Simulating different scenarios and taking into account the presence of private tanks, the method can modify the regulation point of PAT with discharge flowing in the network [15]. Page et al. (2018) incorporated hydraulics theory into the VSP controller research. The performance (required parameters, errors, response time, etc.) of different VSP control methods on pressure management was explored [16].
Some researchers also used a combination of pumps and PRVs to manage pressure. Shafiee et al. (2015) used a parallel evolutionary algorithm to redesign a network to reduce background leakage. Pipe replacement, valve installation, and operating rules for tanks and pumps have been optimized based on a single working condition. However, this method has high computational requirements and long computing time. It takes 1450 minutes to calculate with a single core, and 205 minutes with 192 cores [17]. Gupta and Kulat (2018) used PRVs and VSPs to perform pressure management on the North Central Water Distribution System (WDS) of Nagpur city, India. However, the VSP working status is determined before PRV optimization without considering their mutual relationship, and PRV location and setting were selected step-by-step [18]. Monsef et al. (2018) used the pressure-driven method to estimate instantaneous water demand and then used a differential evolutionary algorithm to schedule the installed PRVs and VSPs. However, the number of PRVs and VSPs scheduled in their study was small (two PRVs and one pump station contains three VSPs), and the PRV position was determined in advance [19]. Brentan et al. (2018) predicted real-time water demand based on the particle swarm optimization (PSO) algorithm, and the results were applied to schedule 13 pumps and four PRVs in D-town. However, they still do not take into account the positioning of PRVs [20].
The previously mentioned research has the following shortcomings and deficiencies. First, in most studies, only PRVs for leakage control have been considered and are mostly optimized for existing PRVs, without taking into account positioning problems and linkages with other components. Second, the optimization of the PRV installation position and setting selection is not reasonable, i. e., choosing the PRV settings after deciding the positions [12,13,18], or selecting the PRV position according to a single working condition [17]. To solve them, a new optimization model has been built. We use GA to optimize the position and setting of PRVs and the speed of VSPs simultaneously under multiple working conditions. The objective function is to maximize the cost savings (mainly electric and water costs while PRV cost is considered separately). This model is suitable for those who want to control the leakage and energy consumption by adjusting pumps and PRVs. Three strategies are used for optimization under multiple working conditions: 1. PRV-only scheduling (this is somewhat similar to the method of Nicolini et al. [11]). 2. VSP-only scheduling. 3. Joint scheduling of PRVs and VSPs. Their performance in leakage reduction and energy saving are compared to each other. Moreover, the direct combination of the optimal state of VSP-only scheduling and the optimal state of PRV-only scheduling is also compared. In this way, the best scheduling approach for the largest economic benefit has been found.
2. Model and Methodology
The objective of the optimization model is to maximize the economic benefits brought by PRV and/or VSP scheduling under all kinds of constraints, and the description of this problem is listed in Section 2.1. A genetic algorithm is adopted to optimize this WDS scheduling problem and introduced it in Section 2.2.
2.1. Establishment of the Optimization Model
2.1.1. Objective Function and Decision Variables
Taking into account the cost savings contributed by leakage reduction and the conservation of energy consumption, the objective function is determined as the change of total cost before and after scheduling, which is used to reflect the economic benefits brought by the scheme. The decision variables are the position, setting, and number of PRVs and the speed of VSPs.
The economic benefits caused by leakage reduction is defined by the equation below.
where is the water price coefficient, equal to the water price multiplied by the conversion factor. and are the leakage amount of the period before and after scheduling, respectively. is the number of time steps.
The changes in electric charges resulting from the pump status alteration is defined by the equation below.
where is the quantity of the pump in the pump station in period . is the corresponding head. is the efficiency coefficient, which includes the pump efficiency, the motor efficiency, etc. is the electric price coefficient of the pump station. and are the total number of pump stations and the total number of pumps in the pump station. is the total electric charges before scheduling. The may be negative, which indicates more energy used after scheduling.
The objective function is to maximize the sum of the above two factors.
2.1.2. Constraints
Water Supply Capacity Constraints for Each WTP
Considering the actual water supply capacity of WTPs, it may be necessary to put forward optimization pump schemes under a fixed range of water supply volume per WTP. Therefore, the water volume is limited according to the original plan.
The single-period water supply constraints are shown below.
where and are the water supply volume of the pump station in period after and before scheduling.
24 hours (a whole period) water supply constraints are shown below.
Speed Constraints of VSPs
Due to the motor energy consumption and the constraint of high efficiency range, the speed of VSP is limited in Equation (6).
where is the speed of the pump in the pump station, is the minimum speed, and is the maximum speed, which is always defined as 100%.
Node Pressure Constraints
2.1.3. The Calculation of Leakage
Considering the relationship between leakage and pressure, the following expression is used to calculate the leakage of each node.
where is the leakage constant, is the pressure of node for the t period, is half of the sum length of the pipes connected with node , and is the leakage exponent coefficient.
Thus, the leakage for the whole period is calculated using the formula below.
where is the total number of nodes.
2.1.4. The Simulation of PRV
The simulation of PRV is carried out by changing the head loss of pipes [11].
where is the Hazen-Williams coefficient, is the pipe diameter, is the pipe length, is the pipe flow, and is the diameter multiplier, which simulates the presence of a PRV in the pipe connecting nodes and , and is varied by working conditions.
The is the actual setting of PRV. Equation (11) is used to make a transformation [21,22,23].
2.1.5. The Characteristics of VSP
For the VSPs, the speed can be changed to adapt to the alteration of the water supply volume, and high efficiency can be maintained in different flow ranges to achieve energy savings. The change of outlet pressure will also affect the overall pressure of the network. Assuming that the rated speed is , and the actual speed is , the flow, head, and power comply with the following relationships.
where , , and are the flow, head, and power of VSP at actual speed, respectively. , , and are the flow, head, and power at rated speed, respectively.
According to these equations, the curve at the corresponding speed can be converted from the curve at rated speed for calculation and analysis.
2.2. Genetic Algorithm for Optimization
The genetic algorithm [24] is an optimization method based on a group search strategy. Because it only operates on the chromosome and does not involve the parameters themselves, it has the following features: (1) GA is simple and easy to operate, and is widely used in the optimization of water distribution networks with good evaluation [11,12,13,18,22], (2) compared with the exact or ascendant/descendent algorithm (such as gradient-based algorithm), there is no need to consider complex mathematical backgrounds and nonlinear constraint equations in GA, (3) GA is suitable to handle discrete variables, and 4) GA is a global optimization algorithm and has its advantages in finding global optimal solution. In our model, the decision variables are discrete and a nonlinear problem is generated, since a large number of constraints need to be satisfied. Thus, GA is chosen as a tool to encode and optimize.
A floating-point encoding similar to Nicolini et al. (2009) is adopted [11] (each gene is a random number between 0–1). The following factors have been considered. First, this method is beneficial to joint scheduling, which greatly shortens the number of bits. Second, it can quickly alter the precision or adjust the range, according to the actual situation without changing the code length. The code interpretation process is shown in Figure 1.
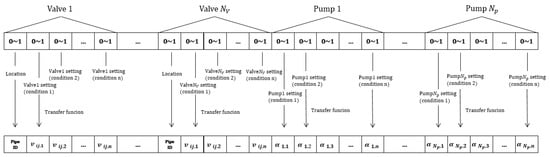
Figure 1.
Encoding mode and interpretation process. is the number of PRVs. is the number of VSPs. The pipe ID is where PRV installs. is the diameter multiplier for condition (from 1 to ). is the speed of the pump for condition .
The length of each string representing an individual is calculated as:
In the process of evolution, a roulette wheel selection scheme is used to choose offspring according to the fitness value after initialization. The arithmetic crossover and boundary nonuniform mutation (generate a random number to replace a gene, Nicolini et al. 2019 [11]) were used for reproduction. The whole process ceases when the generation reaches a reasonable number or the fitness value remains unchanged for a certain period. The penalty function is used to constrain the water supply volume of WTPs and the minimum service pressure of customers. Hydraulic modeling are based on EPANET 2 (Rossman 2000) and optimization is run in MATLAB R2017a.
3. Calculations and Results
The network studied by previous researchers [11,16,21,22,23] is modified to be the case network. For convenience, only the components number of the modified parts and the pipes number are marked in Figure 2, where three VSPs are used to substitute for the reservoirs with constant water heads.
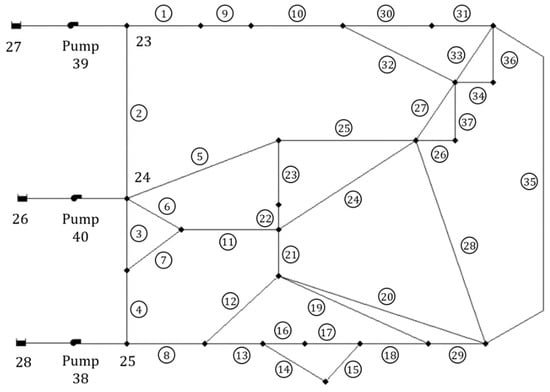
Figure 2.
The modified network.
The network consists of 25 nodes, 37 pipes, three reservoirs, and three VSPs. The elevation of Nodes 23, 24, and 25 is 18 m, 23 m, and 18 m, respectively, and the water demands are all 0 L/s. The heads of reservoirs 26, 27, 28, are 23 m,18 m, and 18 m, respectively. Two types of pumps are chosen according to the maximum water demand.
Pumps 38 and 39 use the curve in Equation (16) and assume an efficiency of 78% at their rated flow. Pump 40 uses the curve in Equation (17) and assumes an efficiency of 80% at its rated flow. The efficiency after changing the speed can be calculated according to Equations (12)–(14).
Numerical simulations have been carried out at this case network. The number of time periods = 24, including three kinds of working conditions. The corresponding demand multipliers are 0.6, 1.0, and 1.4, respectively [21]. The water price coefficient = 3 RMB/m3, and the electricity price coefficient = 0.6 RMB/KWh. Motor efficiency is chosen as 90%. Considering that the solution space increases sharply as the number of PRV increases, the diameter multiplier interval is set to 0.1, with a total of 11 gears. Meanwhile, the node pressure constraint is difficult to satisfy when the pump speed closes to a lower limit (0.75 or 0.8). Thus, 0.85 to 1.0 is selected as the adjustment range of VSPs, with a total of 16 gears. The minimum node pressure = 28 m, the leakage constant , and the leakage exponent coefficient .
In all runs, the algorithm used a population of 100 individuals evolving for 2000 generations. The crossover probability gradually reduced while the mutation probability gradually increased for the first 500 generations. Both remained unchanged for the latter 1500 generations. Most of the process converged in 800 to 1500 generations.
The optimizations of the three strategies are: 1. scheduling PRV-only, 2. scheduling VSP-only, and 3. joint scheduling of PRVs and VSPs together. They were carried out, respectively, under multiple working conditions.
Table 1 represents the results of five better trials out of 10 runs in PRV-only scheduling and joint-scheduling. As for the PRV-only scheduling, the value of fsum first rises significantly as the number of PRVs increases (when the number of PRVs is less than four), and then the increase almost ceases. The same trend is also reflected in fsum1, but fusm2 does not have strong regularity. When the number of PRVs is small, the position selection for the five trials is relatively similar. Pipe 11 is always selected for a single PRV, and (5, 11), (8, 11) for two PRVs, (8, 9, 11) for three PRVs, and (8, 9, 11, 20) for four PRVs. As the number of PRVs increases, these pipe IDs are also included, but the combinations became diverse. It can also be concluded that, if the PRV cost is not considered, installing more PRVs will bring a small benefit. Consideration of the PRV cost will be discussed later.

Table 1.
The results of five trials in PRV-only scheduling and joint scheduling.
As for the joint scheduling, the value of fsum is clearly higher than that of PRV-only scheduling. With an increase of the number of PRVs, better fsum values constantly appear. For the position selection, pipe 11 is still chosen for one PRV, but differentiation begins to occur when more PRVs are used. (9, 11), (11, 13), and (11, 20) are chosen for the two PRV cases, with all containing Pipe 11. The same (11, 20) is contained when three PRVs are selected, and (11, 20, 31) with four PRVs. After that, as the number of PRVs increases, the convergence begins to weaken and the fsum value begins to fluctuate. The determination of the number of PRVs also needs to consider the PRV’s price.
Table 2 shows the results of VSP-only scheduling. It can be found that VSP scheduling can also bring about a significant drop in leakage, which is slightly worse than the optimal solution of installing three PRVs for PRV-only scheduling (fsum1 = 2600 RMB/day, See Table 1). At the same time, it can be noted that the decline in electric charge is better than that of joint scheduling, which indicates that the PRVs increase the energy consumption to a degree. The obtained cost savings brought by VSP-only scheduling is better than PRV-only scheduling but worse than joint scheduling, which shows that the collaboration between PRVs and VSPs can bring better economic benefits.

Table 2.
The results of VSP-only scheduling.
If the PRV cost is taken into account, when the cost for adding a new PRV is greater than the benefits it brings, the new PRV will not be installed. In this study, the cost of one PRV is converted to a daily cost of 100 RMB/day. Thus, installing four PRVs is clearly appropriate when scheduling PRVs. When the 5th PRV continues to be installed, its income of 22 RMB/day is (the optimal value of four PRVs is 2829 RMB/day, and five PRVs is 2851 RMB/day) less than the cost of a new PRV (100 RMB/day).
The variation trend of fsum with and without considering PRV cost is indicated in Figure 3. It can be clearly seen that when the PRV cost is not considered, the value of fsum in Figure 3a remains nearly unchanged after a significant increase, but the value in Figure 3c is still rising. When taking into account the PRV cost, Figure 3b presents a trend of declining after rising, while Figure 3d rises first, then becomes generally flat, and finally falls. There is a clear increase when installing a single PRV in both Figure 3c,d. For selecting the number of PRVs, the maximum values are obtained in Figure 3b,d when the number is four and three, respectively. According to Table 1, the optimal solutions both appear when the number of PRVs is four (2829−400 = 2429 RMB/day for PRV-only scheduling and 3877−400 = 3477 RMB/day for joint scheduling). Thus, the optimization results of four PRVs for further analysis is taken later. At the same time, it can be seen in Figure 3 that the fluctuation of each optimization value near the average value is small, and that convergence is acceptable.
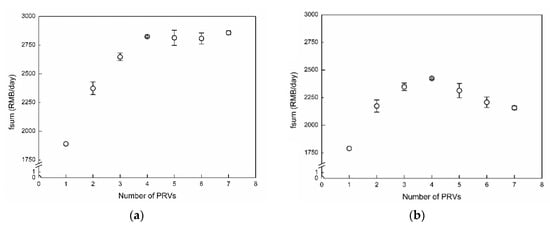
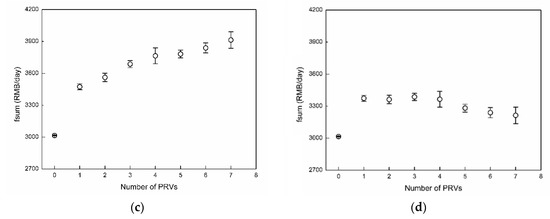
Figure 3.
The value of fsum without and with considering PRV cost: (a) PRV-only scheduling without considering PRV cost; (b) PRV-only scheduling considering PRV cost (100 RMB/day for each); (c) Joint scheduling regardless of PRV cost; (d) Joint scheduling considering PRV cost.
Figure 4 shows the PRV diameter multipliers and VSP speeds under multiple working conditions. Pipe combination (8, 9, 11, 20) is chosen for locating PRVs for PRV-only scheduling strategy, and pipe combination (1, 11, 20, 31) is selected for installing PRVs for a PRV-VSP joint scheduling strategy. The proportion of the white area of the pipe chart in Figure 4 indicates the open degree of a PRV. In contrast, the bar chart indicates the setting of speed of an VSP. It can be found that the setting of the same PRV or VSP under different strategies is different. The PRVs in Condition 1 (the low demand period) are closed more than that in Condition 3 (the peak demand period). The speed of the VSP in condition 1 is lower than that in condition 3. The PRVs’ location for the PRV-only strategy is different from that for the joint scheduling strategy because the VSP can cooperate with PRVs together to manage the pressure.
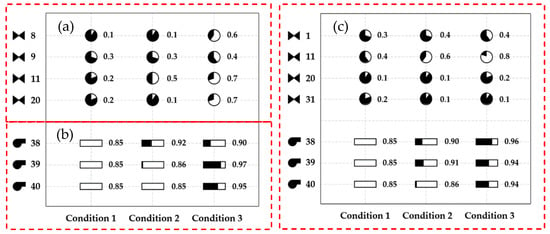
Figure 4.
The PRV setting and VSP speeds when using four PRVs: (a) PRV setting (diameter multipliers) for PRV-only scheduling, (b) VSP speeds for VS-only scheduling, and (c) settings of joint scheduling.
Figure 5 is a comparison of the pressure distribution before and after scheduling. Both PRVs and VSPs make contributions to pressure management. Compared to the original pressure distribution (Figure 5a), the effect of the PRVs is to reduce high pressure area (Figure 5b), especially under the low or intermediate demand period condition (Figure 5a1-a2 Vs Figure 5b1-b2). A significant pressure drop occurs after the position of the PRVs. The effect of VSPs is to reduce the pressure of the whole network (Figure 5c). Because of the limitations of minimal service pressure, high pressure exists in low-elevation areas (the green area in Figure 5c1). The VSP shows global pressure regulation, while the PRV shows flexible local pressure regulation. Joint scheduling combines the advantages of both. The pressure of the entire network is reduced to be uniform in space and stable under all three working conditions (Figure 5d).
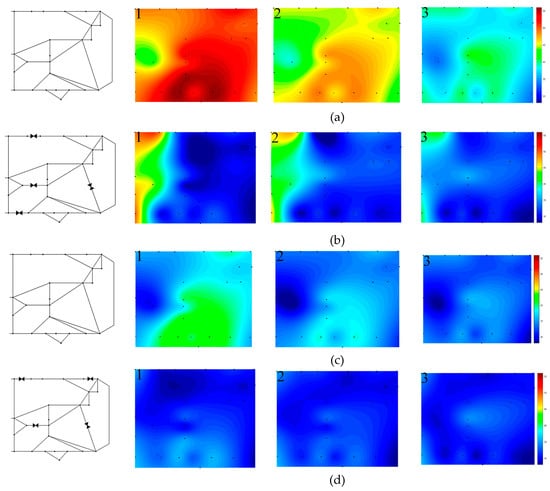
Figure 5.
Pressure distribution before (a) and after (b) PRV, (c) VSP or (d) PRV and VSR joint scheduling. The number 1, 2, and 3 correspond to the low demand period condition, the intermediate demand period condition, and the peak demand period condition, respectively.
Figure 6 shows the cumulative probability distribution (CDF) of nodal pressure before and after scheduling. It can be seen that the proportion of nodes with low-pressure under the three strategies increases significantly when compared to the original network. For the joint scheduling strategy, the pressure distribution is the most uniform and lowest of the three strategies, and the pressure is less than 40 m, which is better than the other two scheduling strategies. The PRV-only scheduling strategy has a higher proportion of pressure below 38 meters than that of the VSP-only scheduling strategy.
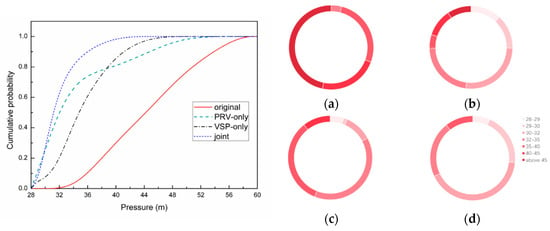
Figure 6.
The distribution of nodal pressure before and after scheduling. The left is the cumulative probability distribution curve of the pressure. The right is the pie chart, (a) original, (b) PRV-only scheduling with four PRVs, (c) VSP-only scheduling, and (d) joint scheduling with four PRVs.
Figure 7 shows the average/maximum/minimum pressure and hourly cost under different optimization strategies. The cost is the actual expense brought by leakage or energy consumption, which is equal to the original cost minus fsum1 and/or fsum2, respectively. Max pressure is the biggest pressure of all the nodal pressure for every time step, while minimum pressure is the smallest one, and the average pressure is the mean value of all the nodal pressure. Regarding the pressure, the decline of maximum pressure for the PRV-only strategy (Figure 7b) is not clear when compared to that of the original network (Figure 7a), while the average and minimum value have a considerable decrease and show stability under the three working conditions. The pressure of VSP-only scheduling is reduced (Figure 7c) compared to that of the original network (Figure 7a). Its max pressure is lower than that of the PRV-only strategy, but its average pressure is higher than that of the PRV-only strategy during a non-peak period (0:00–16:00) and is the minimum pressure during the first eight hours. Joint scheduling achieves the best regulation effect of pressure (Figure 7d). Not only is the pressure lower than the other two, but it is also very uniform under the three working conditions, with a small fluctuation. Regarding the cost, it can be seen that PRV-only scheduling and joint scheduling reduce the leakage cost more significantly and uniformly than VSP-only scheduling. The joint scheduling makes the energy cost slightly higher than the VSP-only scheduling strategy, but still lower than the PRV-only scheduling strategy.
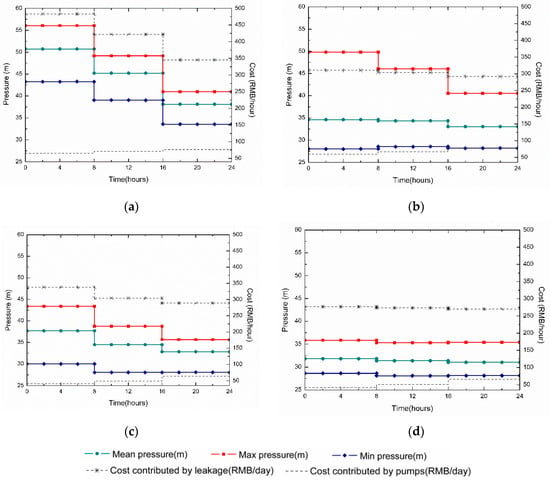
Figure 7.
Average/maximum/minimum pressure and hourly cost under different optimization strategies: (a) Original; (b) PRV-only scheduling with four PRVs; (c) VSP-only scheduling; (d) joint scheduling with four PRVs.
Figure 8 depicts the performance of Pump 39 for the three scheduling strategies. The other two pumps are similar to Pump 39 and are not listed here. The outlet pressure of the PRV-only scheduling strategy has a small rise when compared with the original pressure (Figure 8b) due to the increase in the network’s resistance caused by the PRVs. The outlet pressure is significantly reduced for the VSP-only scheduling. However, it shows instability under multiple working conditions when compared to the joint scheduling strategy, which is unfavorable to the water supply of a water distribution network. Joint scheduling not only makes the outlet pressure significantly reduced, but also presents stability in time. Similarly, the speed of Pump 39 for VSP-only and joint scheduling is lower than that of PRV-only scheduling (Figure 8a). The pump speed of joint scheduling is close to that of VSP-only scheduling during the first eight hours, and then higher during the next eight hours and lower during the last eight hours.
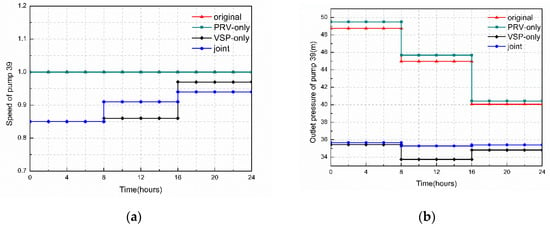
Figure 8.
The speed and outlet pressure of pump 39 under different optimization strategies: (a) speed; (b) outlet pressure.
Through the comparison of the results under three optimization strategies, it can be found that joint scheduling not only has a better effect in controlling and equalizing pressure, but also in reducing energy consumption. The greatest economic benefits are obtained (Table 3), which reduce 34.4% of leakage, 25.4% of energy consumption, and 33.1% of the total cost. This is better than using only PRVs or VSPs, and about 1148 water (7% of the original consumption) and 722 electric energy (25.4% of the original consumption) are saved per day.

Table 3.
The energy conservation and reduction of cost under different strategies.
In particular, considering the reality that PRVs and VSPs are often separately scheduled, we make a simple comparison. The optimal solution for PRV scheduling and the optimal solution for VSP scheduling are simply combined directly. However, the simulation result cannot satisfy the constraints of the water supply capacity of WTPs and minimal node pressure. The manual adjustment is still required, which indicates the necessity of joint scheduling.
4. Discussion
- This paper puts forward a new optimization model for controlling leakage and energy consumption by adjusting pumps and PRVs. The PRVs (location and setting) and VSPs (speed) in a small virtual network was optimized with the aim to reduce leakage and energy consumption. Regardless of the PRV cost, with the number of PRVs growing, the marginal effect of increased PRVs for the PRV-only strategy decreases quickly after incipient rising, while the value of the joint scheduling strategy grows all the time. It was found that joint scheduling not only had clear advantages in pressure control, but also reduced energy consumption (Figure 5, Figure 6 and Figure 7). Under the optimal strategy of joint scheduling, about 1148 water (7% of the original consumption) and 722 electric energy (25.4% of the original consumption) are saved per day. After considering the PRV cost, the actual cost savings began to decline after the number of PRVs reached a certain value.
- Regarding the stability and convergence of optimization results, even though there are some fluctuations in objective function values and changes in PRV locations, it is not clear (See Table 1 and Figure 3). Considering that the location selection is consistent to some degree (e.g., the same combination of 8, 9, 11, and 20 was chosen for the five trials when scheduling four PRVs, and 11, 20, and 30 were always chosen when scheduling four PRVs and VSPs), further refinement of the PRV setting and VSP speed can be redone after the position is selected. When comparing the PRV-only results with Nicolini et al. [11], the consistency of PRV locations for the multiple trials in this paper is better than theirs (identical PRV location combinations appear more times) when the PRV number is less than five (because the maximal PRV number in Nicolini et al. [11] is five).
- The PRVs and VSPs are optimized together under multiple working conditions, and the position and setting of PRVs are decision variables at the same time. This approach is more reasonable than methods that optimize the setting after fixing the positions first [12,13,18]. It can also meet the need to install new PRVs. Meanwhile, the encoding mode can be modified according to the number of working conditions, fixed speed pumps, and VSPs. Considering that fitting too many working conditions may lead to increased calculation difficulty, the maximum, minimum, and intermediate working conditions can be used to simulate when there are too many conditions, and others could be optimized after PRV locations are determined.
- The use of floating-point number coding is mainly based on the fact that it can greatly shorten the number of bits and can perform fast precision conversion and range adjustment, according to the requirements. However, as the number of PRVs, pumps, and working conditions increase, the code length of an individual increases, which results in a dramatic expansion of solution space. This problem makes the optimization in large networks very inefficient and hard [25]. To overcome it, strategies such as improving computer performance, pre-selection of potential PRV locations, and choosing an appropriate range of pump speed should be relied on. In the case network, the computing time varies from about 20 minutes to 360 minutes when the number of PRVs is one to seven, which seems to be accepted when compared with some time-consuming method [17] (due to the difference in model complexity, software, etc., the comparison may not have much meaning).
- The failure of direct combining optimal solutions of the PRV-only strategy and of the VSP-only strategy directly indicates that the joint effects of PRVs and VSPs must be considered. The joint scheduling strategy, which takes into account the interaction among all network components, has its advantages and necessity. Constraints on the water supply volume of each WTP are taken into account in this paper, such that the supplied volume of each WTP can maintain stability before and after optimization. Moreover, the proportion of costs contributed by leakage and by energy consumption may not be reasonable for real water distribution systems. In this case, within the network modified from previous researchers [11,21,22,23], the cost of energy consumption is too low when compared to the cost contributed by leakage, which seems to be unreal. However, it will not influence the application of this proposed method in other water networks.
5. Conclusions
This paper achieves the goal of leakage control and energy consumption reduction by optimizing the PRVs and VSPs in the water distribution network. The PRV will increase energy consumption to some degree, but its effect of reducing leakage is clear. The reasonable scheduling of VSPs plays a role in leakage reduction and energy consumption savings, and can bring significant effects to both. The joint scheduling strategy makes the pressure distribution more uniform, and the average pressure tends to be lower with small fluctuations under the condition of satisfying customer service. The optimal benefit of controlling leakage and energy consumption has also been studied in a small case network, which results in a leakage reduction of 33.4%, an energy consumption reduction of 25.4%, and a total cost reduction of 33.1%, and saves about 1148 water (7% of the original consumption) and 722 electric energy (25.4% of the original consumption) per day. The proposed model can be used to control leakage and energy consumption by adjusting pumps and PRVs. At the same time, because the network used in this paper is a small and simple one, and only three working conditions are considered, the promotion to large networks should still depend on the improvement of computer performance and the optimization model and algorithm themselves, such as pre-selection of the candidate position of PRVs and the range of pump speed, reasonable use of local optimization, and step-by-step optimization methods. Moreover, other better algorithms or the combination of algorithms may be adopted to optimize this WDS scheduling problem. Boosting pumping stations and tanks, which are not considered in this paper, could also be used to WDS scheduling for leakage control and energy saving.
Author Contributions
Conceptualization, Y.S. Formal analysis, X.L. Investigation, T.Y. Methodology, Y.Y. Supervision, Y.S. Validation, S.C. Writing—original draft, Y.Y. Writing—review & editing, Y.S. and X.L.
Funding
This research was funded by The National Key Research and Development Program of China (Grant No. 2016YFC0400600), the National Science and Technology Major Projects for Water Pollution Control and Treatment (Grant No. 2017ZX07502003-05), the National Natural Science Foundation of China (Grant No. 51761145022), and the Fundamental Research Funds for the Central Universities (Grant No. 2019FZA4019).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Gupta, A.; Mishra, S.; Bokde, N.; Kulat, K. Need of smart water systems in India. Int. J. Appl. Eng. Res. 2016, 11, 2216–2223. [Google Scholar]
- Beuken, R.H.S.; Lavooij, C.S.W.; Bosch, A.; Schaap, P.G. Low leakage in the Netherlands confirmed. In Proceedings of the Eighth Annual Water Distribution Systems Analysis Symposium (WDSA), Cincinnati, OH, USA, 27–30 August 2006. [Google Scholar]
- Lambert, A.O. International report: Water losses management and techniques. Water Sci. Technol.-Water Supply 2002, 2, 1–20. [Google Scholar] [CrossRef]
- Mamlook, R.; Al-Jayyous, O. Fuzzy sets analysis for leak detection in infrastructure systems: A proposed methodology. Clean Technol. Environ. Policy 2003, 6, 26–31. [Google Scholar] [CrossRef]
- Vicente, D.J.; Garrote, L.; Sanchez, R.; Santillan, D. Pressure management in water distribution systems: Current status, proposals, and future trends. J. Water Resour. Plan. Manag. 2016, 142, 04015061. [Google Scholar] [CrossRef]
- Walski, T.; Bezts, W.; Posluszny, E.T.; Weir, M.; Whitman, B.E. Modeling leakage reduction through pressure control. J. Am. Water Works Assoc. 2006, 98, 147–155. [Google Scholar] [CrossRef]
- Germanopoulos, G. Technical note on the inclusion of pressure dependent demand and leakage terms in water supply network models. Civ. Eng. Syst. 1985, 2, 171–179. [Google Scholar] [CrossRef]
- Savić, D.A.; Walters, G.A. Integration of a model for hydraulic analysis of water distribution networks with an evolution program for pressure regulation. Comput. Aided Civ. Infrastruct. Eng. 1996, 11, 87–97. [Google Scholar] [CrossRef]
- Ulanicki, B.; Bounds, P.L.M.; Rance, J.P.; Reynolds, L. Open and closed loop pressure control for leakage reduction. Urban Water 2000, 2, 105–114. [Google Scholar] [CrossRef]
- Gupta, A.; Kulat, K.D. A selective literature review on leak management techniques for water distribution system. Water Resour. Manag. 2018, 32, 3247–3269. [Google Scholar] [CrossRef]
- Nicolini, M.; Zovatto, L. Optimal location and control of pressure reducing valves in water networks. J. Water Resour. Plan. Manag. 2009, 135, 178–187. [Google Scholar] [CrossRef]
- Creaco, E.; Pezzinga, G. Embedding linear programming in multi objective genetic algorithms for reducing the size of the search space with application to leakage minimization in water distribution networks. Environ. Modell. Softw. 2015, 69, 308–318. [Google Scholar] [CrossRef]
- Gupta, A.D.; Bokde, N.; Marathe, D.; Kulat, K. Optimization techniques for leakage management in urban water distribution networks. Water Sci. Tech.-Water Sup. 2017, 17, 1638–1652. [Google Scholar] [CrossRef]
- Bakker, M.; Rajewicz, T.; Kien, H.; Vreeburg, J.H.G.; Rietveld, L.C. Advanced control of a water supply system: A case study. Water Pract. Technol. 2014, 9, 264–276. [Google Scholar] [CrossRef]
- De Marchis, M.; Milici, B.; Volpe, R.; Messineo, A. Energy saving in water distribution network through pump as turbine generators: Economic and environmental analysis. Energies 2016, 9, 877. [Google Scholar] [CrossRef]
- Page, P.R.; Abu-Mahfouz, A.M.; Mothetha, M.L. Pressure management of water distribution systems via the remote real-time control of variable speed pumps. J. Water Res. Plan. Manag. 2017, 143, 04017045. [Google Scholar] [CrossRef]
- Shafiee, M.E.; Berglund, A.; Berglund, E.Z.; Brill, E.D.; Mahinthakumar, G. Parallel evolutionary algorithm for designing water distribution networks to minimize background leakage. J. Water Res. Plan. Manag. 2016, 142, C4015007. [Google Scholar] [CrossRef]
- Gupta, A.D.; Kulat, K. Leakage reduction in water distribution system using efficient pressure management techniques. Case study: Nagpur, India. Water Sci. Tech.-Water Supply 2018, 18, 2015–2027. [Google Scholar] [CrossRef]
- Monsef, H.; Naghashzadegan, M.; Farmani, R.; Jamali, A. Pressure management in water distribution systems in order to reduce energy consumption and background leakage. J. Water Supply Res. T 2018, 67, 397–403. [Google Scholar] [CrossRef]
- Brentan, B.; Meirelles, G.; Luvizotto, E.; Izquierdo, J. Joint operation of pressure-reducing valves and pumps for improving the efficiency of water distribution systems. J. Water Res. Plan. Manag. 2018, 144, 04018055. [Google Scholar] [CrossRef]
- Jowitt, P.W.; Xu, C.C. Optimal valve control in water distribution networks. J. Water Resour. Plan. Manag. 1990, 116, 455–472. [Google Scholar] [CrossRef]
- Reis, L.F.R.; Porto, R.M.; Chaudhry, F.H. Optimal location of control valves in pipe networks by genetic algorithm. J. Water Resour. Plan. Manag. 1997, 123, 317–326. [Google Scholar] [CrossRef]
- Vairavamoorthy, K.; Lumbers, J. Leakage reduction in water distribution systems: Optimal valve control. J. Hydraul. Eng. 1998, 124, 1146–1154. [Google Scholar] [CrossRef]
- Holland, J.H. Adaptation in Natural and Artificial Systems; University of Michigan Press: Ann Arbor, MI, USA, 1975. [Google Scholar]
- Pecci, F.; Abraham, E.; Stoianov, I. Model reduction and outer approximation for optimizing the placement of control valves in complex water networks. J. Water Res. Plan. Manag. 2019, 145, 04019014. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).