An Efficient Demand Side Management System with a New Optimized Home Energy Management Controller in Smart Grid

Abstract

The traditional power grid is inadequate to overcome modern day challenges. As the modern era demands the traditional power grid to be more reliable, resilient, and cost-effective, the concept of smart grid evolves and various methods have been developed to overcome these demands which make the smart grid superior over the traditional power grid. One of the essential components of the smart grid, home energy management system (HEMS) enhances the energy efficiency of electricity infrastructure in a residential area. In this aspect, we propose an efficient home energy management controller (EHEMC) based on genetic harmony search algorithm (GHSA) to reduce electricity expense, peak to average ratio (PAR), and maximize user comfort. We consider EHEMC for a single home and multiple homes with real-time electricity pricing (RTEP) and critical peak pricing (CPP) tariffs. In particular, for multiple homes, we classify modes of operation for the appliances according to their energy consumption with varying operation time slots. The constrained optimization problem is solved using heuristic algorithms: wind-driven optimization (WDO), harmony search algorithm (HSA), genetic algorithm (GA), and proposed algorithm GHSA. The proposed algorithm GHSA shows higher search efficiency and dynamic capability to attain optimal solutions as compared to existing algorithms. Simulation results also show that the proposed algorithm GHSA outperforms the existing algorithms in terms of reduction in electricity cost, PAR, and maximize user comfort.

1. Introduction

The traditional grid is facing numerous challenges, including old infrastructure, lack of communication, increasing demand for energy, and security issues. To address these issues, the concept of smart grid has emerged which comprises of information and communication technologies that allow bidirectional communication between the utility and energy consumers. Broadly speaking, smart grid appears as a next generation grid and incorporates advanced technologies in communication, distributed generation, cyber security, and advanced metering infrastructure [1]. These features of the smart grid ultimately enhance the efficiency, reliability, and flexibility of the power grid. The key objective of the smart grid is the transformation of the traditional grid to a cost effective and energy efficient power grid.

Demand side management (DSM) is an essential component in energy management of the smart grid. Generally, DSM refers to manage the consumer’s energy usage in such a way to yield desired changes in load profile and facilitates the consumers by providing them incentives [2]. For this purpose, various DSM techniques have been proposed in literature, including peak clipping, valley filling, load shifting, strategic conservation, strategic load growth, and flexible load shape [3]. Furthermore, DSM is capable of handling the communication infrastructure between end user and utility and also enables the integration of distributed energy resources to optimize energy consumption profile.

Recently, one of the crucial DSM activities is demand response (DR), it is presumed that DR is the subset of DSM in a broader aspect. DR is defined as the tariffs or programs established to influence the end users to reshape their energy consumption profile in response to electricity price [4]. DR program is further categorized into two types: an incentive-based program and price-based program. An incentive-based program provides monetary incentive to the end user on the base of load curtailment. Various incentive programs are discussed in the literature, including direct load control (DLC), curtailable load, demand bidding and buy back, emergency and demand. On the other hand, a price-based program provides the price of electricity during different time intervals. The purpose of the price-based program is to reduce electricity usage when the electricity price is high and thus, reduce demand during peak periods. Price-based programs are: time of use (ToU), RTEP, inclined block rate, CPP, and day ahead pricing. DR is considered as a key feature in smart grid to improve the sustainability and reliability of power grid. However, it is examined in the literature that researchers considered the DSM and DR are interchangeable [5,6].

With the emergence of the smart grid, the consumer and the utility can exchange real-time information based on electricity pricing tariffs and energy demand of the consumer. The two way communication benefits not only the consumers, but also improve stability of the power grid. With this motivation, various models are designed to schedule energy consumption usage. Authors in [7], comparatively evaluate the performance of home energy management controller (HEMC) which is designed to schedule energy consumption on the basis of heuristic algorithms: GA, binary particle swarm optimization (BPSO), and ant colony optimization (ACO). In [8], authors aim to reduce electricity cost while incorporating renewable energy sources (RESs). The appliances are classified into five groups on bases of power ratings and time factor. Multiple knapsack problem (MKP) is used for the problem formulation and an optimization algorithm GA is employed to schedule the load profile. Jon et al. [9], propose HEMS model for energy optimization and categorize the household appliances. The major objective of the proposed model is to tackle the uncertainties related to different kind of loads and reduce the electricity cost. The proposed algorithms are tested with the scrutiny of required home appliances and day-ahead pricing scheme.

Authors in [10], present an improved model for the energy consumption of residential appliances. The desired objective is to minimize the cost by managing energy consumption of the appliances. Fractional programming (FP) is used for scheduling energy consumption by considering RTEP tariff and distributed energy resources. The work in [11] presents HEMS model for energy optimization model at residential sector. The DSM techniques take into account in the presence of distributed generation, time-differentiated prices, and preference of loads. The minimization problem is solved using a constructive algorithm with GA while considering energy cost. Authors in [12], provide a detailed study of HSA algorithm, the primary steps, its adaptation, and its specialty in different fields. Also, authors comparatively discuss the searching criteria of different optimization techniques and HSA. At the end, authors are elaborated the application of HSA in a complex scenarios and various fields. Authors in [13], design day ahead scheduling model for microgrid systems with the integration RESs in order to minimize the start up cost and generation cost of the RESs. A hybrid algorithm is proposed using steps of enhance differential evolution (EDE) algorithm and HSA to achieve desired objective. The improvement in the tuning parameters of EDE and HSA are also carried out which enhances the search diversity. The work in [14], demonstrates the residential load scheduling with the day ahead pricing scheme. A hybrid technique teacher learning genetic optimization (TLGO) is proposed to solve the optimization problem. The major objective of the work is to reduce electricity cost at minimum user discomfort.

Danish et al. in [15], present HEMS model based on heuristic algorithm BSPO. The aim of the authors is to minimize the electricity cost while considering user comfort. Authors in [16], present a generic model of DSM in order to optimize energy consumption in the residential sector. In a home environment, energy management controller (EMC) is used to control energy consumption of the appliances during peak hours. In [17], authors propose a comprehensive model for energy management in homes with multiple appliances. The proposed model consists of six layered architecture and each layer is connected with other in order to achieve better results in terms of cost reduction and PAR.

The work in [18] provides a comprehensive study of WDO technique, the basic concepts, structure its variants, and its application in electromagnetics. A numerical study is presented using uni-modal and multi-modal test functions and results of WDO and other optimization techniques, including GA, BPSO, and differential algorithm (DE). A recent work in [19] proposes a novel approach of DSM with the integration of RESs. The energy provider inspects the load profile and the price of the electricity. Authors aim to reduce the deviation of average load energy demand by scheduling the energy consumption and storage devices. To solve scheduling problem, authors model the energy consumption and storage as a non-cooperative game.

In [20], authors demonstrate the electricity load scheduling problem for multi-resident and multi-class appliances using problem ladson generalized bender algorithm while considering energy consumption constraint. The main objective of the study is to protect the private information i.e., energy consumption profile of the residences and maximize the users satisfaction.

Authors in [21] give an insight of scheduling the energy management in the residential sector and propose two horizon algorithms. The proposed algorithms are efficient to reduce electricity cost with less computational time. Moreover, authors also discuss the implementation of proposed algorithms and challenges related to its implementation. Di Somma et al. in [22], present stochastic programming model for the optimal scheduling of distributed energy resources system. The main aim of the study is to reduce energy cost and $C{O}_2$ emission while, satisfying time-varying user demand. In [23], authors propose a model based on optimal economic choices for the management of the microgrid. The economic model is applied based on GA to the microgrid with traditional power plants and RESs. The work in [24], provides an improved HEMS architecture considering various categories of appliances in the home. Multi- time scale optimization is formulated in order to schedule energy consumption of appliances. A predictive model-based-heuristic solution is proposed and its performance is compared with benchmark algorithms. Table 1 lists the summary of the research work based on heuristic techniques.

Table 1. Heuristic techniques.

Techniques	Aims	Distinctive Attributes	Limitations
Hybrid technique (GA and PSO) [25]	Minimization of cost and PAR	HEMS model is considered with distributed energy resources and energy storage system	User comfort is ignored
EA [26]	Cost reduction	Energy optimization in residential, commercial, and industrial area	System complexity is enhanced
ILP [27]	Cost and PAR minimization	Classification of appliances using day ahead pricing model	PAR is not addressed
DP [28]	Cost and PAR minimization	Optimizes energy consumption behavior with high penetration of RESs	System complexity is increased and user comfort is ignored
GA [29]	Cost reduction and user comfort	Cost reduction by optimizing energy consumption and time slots are divided	System deals with large number of appliances in multiple sector which increases system complexity
GA, BPSO, ACO [7]	Cost and PAR reduction by satisfying user comfort	HEMC schedules the appliances by considering user satisfaction and RESs integration	System complexity and computational time are increased
GA [8]	Cost reduction and user comfor	Optimizes energy consumption behavior with RESs incorporation	Challenges related to RESs are not addressed and PAR is ignored
Hybrid technique (LP and BPSO) [9]	Cost reduction and user comfort maximization	Thermostatically and interruptible appliances are considered with day ahead pricing model	PAR is not considered
FP [10]	Electricity cost reduction	Cost efficient model with distributed energy resources and practical implementation of the model proposed	PAR and user comfort are not taken into account
GA [11]	Cost and PAR reduction	Proposed model is tested using radial residential electrical network	System complexity and computational time are enhanced
HSA [12]	Basic concepts of HSA, its structure, and applications	Improved and hybrid HSA with application	Real time implementation is not considered
Hybrid technique (EDE and HSA) [13]	Startup and generation cost of RESs	Verification is done using IEEE standard bus system	Computational time is increased
BPSO [15]	Electricity cost minimization considering user preference	Simplicity and robustness of BPSO	Computational time is increased as time slot is divided into sub time slots
GA [16]	Minimization of electricity cost, PAR, and waiting time	Generic model of DSM with EMC using RTEP	User comfort is not addressed efficiently
Single knapsack [17]	Energy consumption optimization considering six layer architecture	Comprehensive model for energy management addressing six layer architecture	Complicated architecture in terms of modeling in practical scenario

HEMS is considered as an integral part for the successful DSM of the smart grid [30]. HEMS provides an opportunity for the residential sector consumers to communicate with the household appliances and the utility to improve the energy efficiency regarding electricity tariff and consumer’s comfort. A wide range of research has been made to study scheduling problems in HEMS. A hybrid genetic particle swarm optimization (HGPO) is proposed to schedule the energy consumption of appliances in HEMS with the integration of RESs [25]. However, it is impractical to schedule energy consumption without addressing user comfort. A heuristic optimization algorithm, such as GA is used to schedule appliances for the residential, commercial, and industrial sectors in [26]. However, authors have not addressed the user comfort and also computational time of the algorithm is high. Similarly, in [27,28], integer linear programming (ILP) and dynamic programming (DP) are used to schedule the appliances and reduce electricity cost and PAR. However, these algorithms are inefficient in terms of computational time. In [29], authors propose a general architecture of HEMS based on GA in the presence of RTEP and inclined block rate to reduce electricity cost and PAR. As GA is easy to implement, however, system deals with large number of appliances in multiple sector which increases the computational complexity.

Motivated from aforementioned literature work, we have proposed EHEMC, based on heuristic algorithms. The major contribution of this paper is summarized as follows:

• We have proposed EHEMC with an objective to minimize electricity cost and average waiting time.
• Initially, appliances are classified into three categories: regularly operated appliances, shiftable appliances, and elastic appliances-based upon their energy usage and time of operation. Furthermore, electricity cost and energy usage for each category are calculated using Equations (2)–(7).
• To address our objective efficiently a hybrid optimization algorithm GHSA is proposed, which is later on compared with the existing algorithms, including WDO, HSA, and GA (Section 3).
• We implement the proposed GHSA algorithm for single home (SH) and multiple homes (MHs) and analyze its performance in the presence of pricing tariffs: RTEP and CPP. We observe that as the number of homes is increased computational time of the system also increases. However, our proposed algorithm GHSA effectively address the problem with less computation time.
• In order to flexibly adjust the energy consumption profile different power ratings and operational time slots are assigned in MHs. Specifically, we consider fifty homes in MHs case.
• The effect of electricity cost, energy consumption, and average waiting time is demonstrated by feasible regions (Section 2.10).
• The PAR is minimized to avoid peak power plants.
• Finally, extensive simulations are conducted to validate the effectiveness of proposed algorithm GHSA in terms of electricity cost, PAR, and average waiting of the appliances.

The rest of the paper is structured as follows. Section 2 presents a comprehensive study of the system model. Section 3 describes the simulation results along with the discussion. At the end, we present the conclusion of the paper in Section 4.

Nomenclature

This subsection presents the nomenclature as given in Table 2. The table contains abbreviations, initialism, and pseudo-blends.

Table 2. Nomenclature.

Symbols	Description
$E_{c,TL}$	Total energy consumption in a day
${\varsigma }_{{\mathcal{R}}_a,T_L}$	Energy consumption of regularly operated appliances
${\varsigma }_{{\mathcal{S}}_a,T_L}$	Energy consumption of shift-able operated appliances
${\varsigma }_{{\mathcal{E}}_a,T_L}$	Energy consumption of elastic operated appliances
${\varrho }_{{\mathcal{R}}_a}^{T_L}$	Cost per day of regularly operated appliances
${\varrho }_{{\mathcal{S}}_a}^{T_L}$	Cost per day of shift-able appliances
${\varrho }_{{\mathcal{E}}_a}^{T_L}$	Cost per day of elastic appliances
$\epsilon$	Electricity pricing signal
$\zeta$	ON-OFF states of appliances
$a_{\alpha }$	Starting time of appliance
$b_{\beta }$	Ending time of appliance
$\mathcal{W}$	Waiting time of appliance
$O_t$	Operation time interval
$V_{cur}$	Velocity of air parcel in current iteration
$V_{new}$	Velocity of air parcel in new iteration
${\varsigma }_{a_i}$	Energy consumed by appliance i
$P_{cur}$	Pressure of air parcel in a current location
$x_{new}$	Position of air parcel in the new location
$x_{cur}$	Position of air parcel in the current location
$x_{old}$	Position of air parcel in the previous location
$X_{new}$	Updated value of harmony
${\tau }_r$	Request time of the appliances
${\mathcal{T}}_{max}$	Maximum time of the appliance operation
${\mathcal{T}}_{mini}$	Minimum time of the appliance operation
${{\rm Y}}_{TL}$	Total electricity cost for fifty homes
$\mathsf{\Omega }$	Rotation of the earth
∇	Pressure gradient
$\rho$	Air parcel density
$\mu$	velocity of the wind
$\delta V$	Infinite mass and volume
g	Earth’s gravity

2. System Modeling

As mentioned before, for the effective deployment of smart grid, HEMS is crucial. HEMS can manage, control, and optimize energy consumption in home environment. While an essential element of HEMS, EHEMC is used to schedule energy consumption based on heuristic techniques to effectively reduce electricity cost while considering user preference.

The system model comprises of HEMS architecture, energy consumption model, load categorization, energy cost and unit price, and problem formulation.

2.1. HEMS Architecture

HEMS effectively visualizes the load consumption information in home and contributes towards the energy balancing between the supply and demand side. The primary aim of the HEMS implementation is to reduce electricity expense and PAR. According to utility perspective, its aim is twofold: first, it manages the energy consumption usage of residential sector consumers and secondly, it reduces PAR. While in consumers perspective, it reduces electricity expense. The proposed HEMS architecture comprised of advanced metering infrastructure (AMI), smart meter, EHEMC, In-home display, market pricing, utility, and bulk generation as shown in Figure 1.

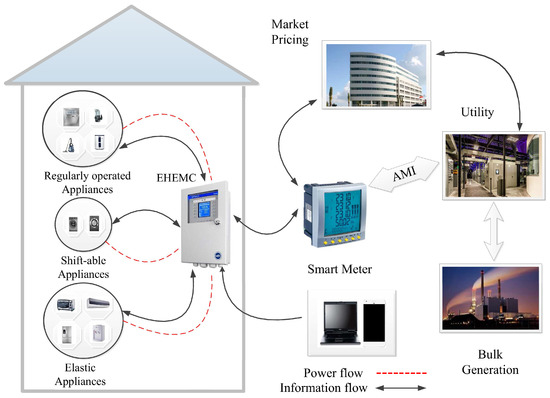
Figure 1. HEMS architecture.

In general, AMI refers to measurement and collection of systems that include smart metering, advanced communications, and data management systems. AMI is also responsible to manage data collection and transmission of energy usage data from the smart meter to the utility. While smart meter acts as a communication gateway between the utility and smart home. The smart meter is associated with processing and sending of energy usage data from EHEMC to the utility via AMI and also processes electricity pricing signal from market pricing and utility. In HEMS architecture, it is assumed that each home is equipped with EHEMC. EHEMC consist of embedded system which schedules the energy consumption profile of the appliances in response to pricing signal and user comfort.

2.2. Energy Consumption Model

We consider a home with a set of appliances $A\triangleq \{a_1,a_2,a_3,\dots ,a_N\}$, such that $a_1,a_2,a_3,\dots ,a_N$ represents each appliance over the time horizon $tϵ\mathcal{T}\triangleq \{1,2,3,\dots ,T\}$. Each time slot represents one hour and the total time interval is 24 h ($T=24$), in accordance with the single day. The total energy consumption of the appliances in a day can be mathematically represented as:

$$E_{c,T_L}=\sum _{t=1}^T\left(\sum _{j=1}^N{E}_{(a_j,t)}\right)\forall tϵ\mathcal{T},aϵA$$

(1)

In smart grid, each home is equipped with EHEMC to optimize energy consumption and reduce electricity cost. Therefore, we categorize the appliances into three groups which are presented in the following subsection.

2.3. Load Categorization

We have categorized each appliance on the bases of energy consumption, operating time, and user preference. Suppose $A_n=\{{\mathcal{R}}_a\bigcup {\mathcal{S}}_a\bigcup {\mathcal{E}}_a\}$ represents a set of appliances, where ${\mathcal{R}}_a$ is regularly operated appliances, ${\mathcal{S}}_a$ shiftable appliances, and ${\mathcal{E}}_a$ elastic appliances. Table 3 shows power ratings and time of operation of the appliances.

Table 3. Load description.

Appliances Group	Appliances	Power Ratings (kW)	Time of Operation (h)
Regularly operated appliances	Vacuum pump	0.6	6
	Water pump	1.18	8
	Dish washer	0.78	10
	Oven	1.44	18
Shift-able appliances	Washing machine	[3.60 0.5 0.38 ]	[5 4 3]
	Cloth dryer	[4.4 2 0.8]	[4 3 2]
Elastic appliances	Refrigerator	[1 0.75 0.5]	[18 16 15]
	AC	[1.5 1.44 1]	[15 13 14]
	Water heater	[4.45 1.2 1]	[7 5 4]
	Water dispenser	[1.5 1 0.5]	[11 10 9]

(1) Regularly operated appliances

These are also called fixed appliances because their energy consumption profile cannot be modified by EHEMC. They are vacuum pump, water pump, dishwasher, and oven. Regularly operated appliances are represented as $\left({\mathcal{R}}_a\right)$ and their energy consumptions are represented by ${\varsigma }_{{\mathcal{R}}_a}$. While power rating of ${\mathcal{R}}_a$ is expressed as ${\xi }_{{\mathcal{R}}_a}$ and the total energy consumption in a day is given as:

$${\varsigma }_{{\mathcal{R}}_a,T_L}=\sum _{t=1}^T\left(\sum _{{\mathcal{R}}_aϵA_n}{\xi }_{{\mathcal{R}}_a}^t\times \zeta \left(t\right)\right)$$

(2)

Similarly, the total cost per day of the ${\mathcal{R}}_a$ is given as:

$${\varrho }_{{\mathcal{R}}_a}^{T_L}=\sum _{t=1}^T\left(\sum _{{\mathcal{R}}_aϵA_n}{\xi }_{{\mathcal{R}}_a}^t\times \epsilon \left(t\right)\times \zeta \left(t\right)\right)$$

(3)

where $\zeta \left(t\right)ϵ[0,1]$ is the operation state of appliances in time interval $tϵ\mathcal{T}$ and $\epsilon$ represents the pricing signal.

(2) Shift-able appliances

These are controllable appliances and their operation time can be shifted to any time slot without performance degradation, however, once they turn ON their length of operation must be completed. They are also named as burst load for example, washing machine and cloth dryer. Shift-able appliances are denoted by $\left({\mathcal{S}}_a\right)$ and power rating of ${\mathcal{S}}_a$ is ${\nu }_{{\mathcal{S}}_a}$. The total energy is computed as:

$${\varsigma }_{{\mathcal{S}}_a,T_L}=\sum _{t=1}^T\left(\sum _{{\mathcal{S}}_aϵA_n}{\nu }_{{\mathcal{S}}_a}^t\times \zeta \left(t\right)\right)$$

(4)

The total cost calculated of ${\mathcal{S}}_a$ in a day is calculated as:

$${\varrho }_{{\mathcal{S}}_a}^{T_L}=\sum _{t=1}^T\left(\sum _{{\mathcal{S}}_aϵA_n}{\nu }_{{\mathcal{S}}_a}^t\times \epsilon \left(t\right)\times \zeta \left(t\right)\right)$$

(5)

(3) Elastic appliances

These are considered as a flexible appliances i.e., their time period and energy consumption profile are flexibly adjusted. They are also named thermostatically-controlled appliances, such as water heater, air condition, water dispenser, and refrigerator. Let us consider ${\mu }_{{\mathcal{E}}_a}$ is the power rating of elastic appliances $\left({\mathcal{E}}_a\right)$ and the total energy of ${\mathcal{E}}_a$ is computed as:

$${\varsigma }_{{\mathcal{E}}_a,T_L}=\sum _{t=1}^T\left(\sum _{{\mathcal{E}}_aϵA_n}{\mu }_{{\mathcal{S}}_a}^t\times \zeta \left(t\right)\right)$$

(6)

The total cost per day of ${\mathcal{E}}_a$ is given as:

$${\varrho }_{{\mathcal{E}}_a}^{T_L}=\sum _{t=1}^T\left(\sum _{{\mathcal{E}}_aϵA_n}{\mu }_{{\mathcal{E}}_a}^t\times \epsilon \left(t\right)\times \zeta \left(t\right)\right)$$

(7)

Let us assume that the total energy consumed $\left({\varsigma }_T\right)$ by appliances in total time interval 24 h is given:

$${\varsigma }_{T_L}={\varsigma }_{{\mathcal{R}}_a,T_L}+{\varsigma }_{{\mathcal{S}}_a,T_L}+{\varsigma }_{{\mathcal{E}}_a,T_L}$$

(8)

Similarly, total cost per day of ${\mathcal{R}}_a$, ${\mathcal{S}}_a$, and ${\mathcal{E}}_a$ appliances is calculated:

$${\varrho }_{T_L}={\varrho }_{{\mathcal{R}}_a}^{T_L}+{\varrho }_{{\mathcal{S}}_a}^{T_L}+{\varrho }_{{\mathcal{E}}_a}^{T_L}$$

(9)

The energy consumption of each appliance in given time period can be mathematically shown in matrix form as:

$$E_c=\left[\begin{array}{ccc}{\varsigma }_{{\mathcal{R}}_a}^{t_1}\dots & {\varsigma }_{{\mathcal{S}}_a}^{t_1}\dots & {\varsigma }_{{\mathcal{E}}_a}^{t_1}\\ {\varsigma }_{{\mathcal{R}}_a}^{t_2}\dots & {\varsigma }_{{\mathcal{S}}_a}^{t_2}\dots & {\varsigma }_{{\mathcal{E}}_a}^{t_2}\\ ⋮& ⋮& ⋮\\ {\varsigma }_{{\mathcal{R}}_a}^T\dots & {\varsigma }_{{\mathcal{S}}_a}^T\dots & {\varsigma }_{{\mathcal{E}}_a}^T\end{array}\right]$$

(10)

2.4. Energy Cost and Unit Price

Various electricity tariffs are proposed to define electricity cost for a day or for a short time period. In our model, we consider RTEP and CPP tariffs.

The RTEP tariff is typically updated for each hour during a day and is capable of contributing better approximation of real time power generation cost. RTEP implementation requires two way of communication in order to interact with the consumer in a real time. Therefore, the aim of RTEP is to reduce demand of consumer during peak demand times. RTEP is also referred as dynamic pricing.

The CPP tariff has resemblance with ToU pricing regarding fix prices in different time intervals. The implementation of CPP during critical event imparts profitable response to the utility [5]. However, due to stress on the power grid, the prices are replaced by the predefined higher rate in order to reduce energy demand. Thus, the aim of the CPP tariff is to assure the reliability and sustainability of the power grid.

In our research work, we consider RTEP and CPP tariffs because in normal operation of power grid, the RTEP behaves more flexibly as compared to other pricing signals. During critical conditions (high electricity demand and low generation) of the power grid consumers have to pay high electricity prices in the respective days or hours. Thus, both pricing signals are considered and electricity cost is reduced by scheduling energy consumption in off-peak hours.

2.5. Problem Formulation

In this research work, we considered SH and MHs with household appliances and our desired objectives are: to reduce electricity cost by scheduling energy consumption in low price hours (off-peak hours), to maintain grid stability by minimizing PAR, and to maximize user comfort level. We formulate our objective function using MKP approach which is based on the following assumptions:

• Assuming $A_n$ as number of items $\left(N\right)$.
• Each of the items comprises of two attributes i.e., weight and the value. The weight of the items expresses the energy usage of the appliances in time interval $\left(t\right)$. In addition, the value of the items denotes the energy cost of the appliances. However, the weight of the appliances is independent of the time interval.
• We consider $\mathcal{N}$ number of knapsacks in order to limit power consumption of each category of the appliances and also to limit the total power capacity $\left({\mathbf{C}}_{\mathbf{g}}\right)$.

By considering aforementioned assumptions, the utility and consumers can actively cooperate in energy demand management in order to reduce electricity cost and PAR. To achieve the grid sustainability, total energy consumption of the appliances in each time interval $tϵ\mathcal{T}$ should not exceed ${\mathbf{C}}_{\mathbf{g}}$. For this reason, we limit the total energy consumption as:

$$0\le {\varsigma }_{T_L}\le {\mathbf{C}}_{\mathbf{g}}$$

(11)

If the constraint in Equation (11) is satisfied the inadequacy of power and stresses on the grid can be eliminated.

2.6. PAR

PAR is the ratio of the maximum aggregated load consumed in a certain time frame and the average of the aggregated load. PAR informs about the energy consumption behavior of the consumers and the operation of the power grid. The high PAR jeopardizes the grid stability and increases the electricity cost. While reduction in PAR simultaneously enhances the stability and reliability of the power grids and reduces the electricity bill of the consumers. Mathematically, it is expressed as:

$$L_{peak}=\underset{tϵ\mathcal{T}}{max}{\varsigma }_T\left(t\right)$$

(12)

$$L_{avg}=\frac{{\sum }_{t=1}^T{\varsigma }_T\left(t\right)}{T}$$

(13)

$L_{peak}$ and $L_{avg}$ show the maximum aggregated load and average load in a time frame (t). While $\varsigma \left(t\right)$ represents the total energy consumption of the appliances in an hour.

$$PAR=\frac{L_{peak}}{L_{avg}}=\frac{T\underset{tϵ\mathcal{T}}{max}{\varsigma }_T\left(t\right)}{{\sum }_{t=1}^T{\varsigma }_T\left(t\right)}$$

(14)

2.7. User Comfort

In energy optimization, the load is shifted from peak hours to off-peak hours in order to reduce electricity cost. In this context, ${\mathcal{R}}_a$ consumption patterns are not changed and they must run with first preference, whereas ${\mathcal{S}}_a$ and ${\mathcal{E}}_a$ operation time interval ($O_t$) are flexibly shifted. ${\mathcal{S}}_a$ and ${\mathcal{E}}_a$ can be delayed to operate during peak hours to reduce electricity cost, however, it incurs discomfort to the consumer. To evaluate waiting time of appliances, we assume starting and ending time instant of appliances $a_{\alpha }ϵ\mathcal{T}$ and $b_{\beta }ϵ\mathcal{T}$, such that $(a_{\alpha }<b_{\beta })$ and ${\tau }_r$ is the request time of an appliance. While $\mathcal{W}$ is expressed as waiting time of the appliances.

$$\mathcal{W}=\left|\right(a_{\alpha }-{\tau }_r\left)\right|$$

(15)

$${\mathcal{W}}_{avg}=\frac{{\sum }_{a=1}^{A_n}\left|(a_{\alpha }-{\tau }_r)\right|}{A_n}$$

(16)

$$W_T=\frac{{\sum }_{t=1}^T{\mathcal{W}}_{avg}\left(t\right)}{{\left({\sum }_{t=1}^T{\mathcal{W}}_{avg}\left(t\right)\right)}_{max}}$$

(17)

Equation (16) shows the average waiting time of the appliances and Equation (17) represents the normalized value of average waiting time.

2.8. Objective Function

The objective is to minimize electricity cost and the average waiting time. The electricity cost is calculated using electricity pricing tariff and energy consumption. The total electricity cost per day is given by:

$$Cost=\sum _{t=1}^T\sum _{a_i}^{An}\epsilon \left(t\right)\times {\varsigma }_{a_i}\left(t\right)\times \zeta \left(t\right)$$

(18)

In Equation (18) ${\varsigma }_{a_i}\left(t\right)$ shows the energy consumption of appliances in time slot t and $\epsilon \left(t\right)$ indicates the electricity pricing tariff in time interval t. Equation (18) is normalized and is given as:

$$Cos{t}_T=\frac{{\sum }_{t=1}^T{\sum }_{a_i}^{An}\epsilon \left(t\right)\times {\varsigma }_{a_i}\left(t\right)\times \zeta \left(t\right)}{{\left({\sum }_{t=1}^T{\sum }_{a_i}^{An}{\varsigma }_{a_i}\left(t\right)\times \epsilon \left(t\right)\times \zeta \left(t\right)\right)}_{max}}$$

(19)

Now, we introduce objective function as:

$$Minimize{w}_1\left(Cos{t}_T\right)+w_2\left(W_T\right)$$

(20)

subjected to:

$${\varsigma }_{T_L}\le {\mathbf{C}}_{\mathbf{g}}$$

(21a)

$$PAR=\frac{T\underset{tϵ\mathcal{T}}{max}{\varsigma }_T\left(t\right)}{{\sum }_{t=1}^T{\varsigma }_T\left(t\right)}\le {\mathrm{T}}_{\max }$$

(21b)

$$\mathcal{T}min\le t\le \mathcal{T}max$$

(21c)

$$\sum _{t=a_{\alpha }}^{b_{\beta }}{\nu }_{{\mathcal{S}}_a}^t={\varsigma }_{{\mathcal{S}}_a,T_L},{\nu }_{{\mathcal{S}}_a}^t=0,\forall tϵ\mathcal{T}\setminus {\mathcal{T}}_a$$

(21d)

$$\sum _{t=a_{\alpha }}^{b_{\beta }}{\mu }_{{\mathcal{E}}_a}^t\le {\varsigma }_{{\mathcal{E}}_a,T_L},{\mu }_{{\mathcal{E}}_a}^t=0,\forall tϵ\mathcal{T}\setminus {\mathcal{T}}_a$$

(21e)

$$0\le {\nu }_{{\mathcal{S}}_a}^t\le {\varsigma }_{{\mathcal{E}}_a,T_L}^t,\forall tϵ\mathcal{T}$$

(21f)

$${\varsigma }_{{\mathcal{E}}_a,T_L}^{mini}\le {\mu }_{{\mathcal{E}}_a}^t\le {\varsigma }_{{\mathcal{E}}_a,T_L}^{max},\forall tϵ\mathcal{T}$$

(21g)

$${\mathcal{W}}_{avg}\le 5$$

(21h)

$$\sum _{t=1}^T{\varsigma }_{T_L}{\left(t\right)}^{unsche}=\sum _{t=1}^T{\varsigma }_{T_L}{\left(t\right)}^{sche},\forall tϵ\mathcal{T}$$

(21i)

In Equation (20) both parts of the objective function i.e., minimization of total cost per day and average waiting time (${\mathcal{W}}_{avg}$) of the appliances are first normalized using Equations (17) and (19) and then simultaneously solved using linear weighted sum method. Equal weights $w_1$ and $w_2$ are assigned to the both parts of the objective function i.e., $w_1$ = $w_2$ = 0.5 [29]. Equations (21a)–(21i) are constraints of the objective function. Equation (21a) shows the total power consumption of appliances should not overreach the power grid capacity. Equation (21b) limits the PAR less than $T_{max}$, and the ideal value of $T_{max}$ is equal to 1. Equation (21c) guarantees that time scheduled by appliances should not exceed the restriction. Equations (21d) and (21e) are constraints representing the energy load balance of ${\mathcal{S}}_a$ and ${\mathcal{E}}_a$ in any time slot $\left(t\right)$. While Equations (21f) and (21g) indicate the maximum and minimum energy consumption of ${\mathcal{S}}_a$ and ${\mathcal{E}}_a$ appliances in each hour of the operation. Equation (21h) shows the maximum time that user postpone the operation of ${\mathcal{S}}_a$ and ${\mathcal{E}}_a$. For our proposed model, we consider ${\mathcal{W}}_{avg}$ of ${\mathcal{S}}_a$ and ${\mathcal{E}}_a$ is equal to or less than 5 h. Whereas, constraint (21i) clearly demonstrates the total energy consumption of the appliances in scheduled case and unscheduled case are always equal i.e., the EHEMC schedules the appliances by taking into account that appliances must complete their length of operation.

2.9. Optimization Techniques

Generally, mathematical techniques provide accurate solutions to the problem which is either feasible or infeasible. However, they are incapable of addressing the complex problems due to the curse of dimensionality, slow convergence rate, and complex calculations. While heuristic optimization algorithms do not guarantee the exact solution and provide approximate solutions, however, they are capable of handling complex calculations. In spite of approximate solutions, optimization algorithms are fair enough to converge faster, reach the desired solution, and applicable in all fields of engineering and computer science [31]. For this purpose, we computed our problem as an optimization problem and four heuristic optimization techniques: WDO, HSA, GA, and GHSA are employed. Each heuristic optimization technique is explained as follows:

2.9.1. GA

GA is an adaptive algorithm based on the biological process [26]. Initially, a set of random solutions is generated called chromosomes and the set of the chromosome is considered as a population. Each chromosome comprises of genes and the value of gene is either binary or numerical value. We consider the value of gene as 1 or 0 which actually shows ON and OFF states of the appliances. The fitness of each chromosome is evaluated using Equation (20) and the stochastic operators crossover and mutation are used to generate new populations. Two point crossover with crossover rate $P_c$ = 0.9 is used and the obtained chromosome is further mutated through mutation process which diversifies the search space of the algorithm, the mutation rate is considered $P_m$ = 0.1. The process of crossover and mutation enables to reach at global optimal results. At the end, binary array [0 0 1 0 0 0 0 0 1 1] is obtained which shows the appliance is ON at 3, 9 and 10 location of the array. We then find out electricity cost and energy consumption to achieve our desired objective. The optimal results are obtained by considering the parameters in Table 4.

Table 4. GA parameters.

Parameters	Values
Maximum iteration	200
Population size	30
$P_c$	0.9
$P_m$	0.1

The process is continued until the best optimal vector is achieved. Additionally, in comparison to other existing optimization techniques, GA is more robust and solves the complex non-linear problem with high convergence rate. GA also exhibits the property of independence of problem domain and imparts divergent solution in a single iteration.

2.9.2. WDO

WDO is the meta-heuristic algorithm which is inspired by the atmospheric motion of wind. In WDO, infinitely small air parcels move in a search space and wind blows to equalize pressure on air parcels using four different forces. These forces are cariols forces, pressure gradient forces, gravitational forces, and the frictional forces. Coriolis force tends to move the wind horizontally i.e., rotate the wind around the earth, while pressure gradient force is defined as; a change in wind pressure over distance covered by the wind. When both coriolis force and pressure gradient force are equal they balance the wind pressure horizontally. Furthermore, the gravitational force pulls the wind towards its center and it is in the vertical direction, while the friction force lowers the speed of the wind which in turn slow down the speed of coriolis force. All of these forces are expressed mathematically as [15]:

$$C_F=-2\mathsf{\Omega }\times \mu ,$$

(22)

$$P_{GF}=-\nabla P\delta V,$$

(23)

$$F_g=\rho \delta Vg,$$

(24)

$$F_f=\rho \alpha \mu ,$$

(25)

At first, the random solution $\left(v_i\right)$ is generated using Equation (26).

$$v_i=V_{max}\times 2\times (rand(populationsize,n)-0.5).$$

(26)

Each of the random solution is evaluated using fitness function and relatively good solutions are reproduced, while bad solutions are neglected. In each step, position and the velocity of the air parcel is evaluated and the new value of velocity is assigned to each air parcel. Equation (27) shows the updated velocity $\left(V_{new}\right)$ of air parcels

$$V_{new}=(1-\alpha )V_{cur}-V_{cur}\times g(R\times T|\frac{1}{j}-1|(x_{new}-x_{old}))+\frac{c{V}_{cur}}{P_{cur}},$$

(27)

$$V_{new}=V_{max}if{V}_{new}>V_{max}$$

(28)

$$V_{new}=V_{min}if{V}_{new}<V_{max}$$

(29)

$$x_{new}=x_{cur}+(V_{new}\times △t),$$

(30)

After updating the velocity of the particle. New generation is obtained using Equation (30) and the process will continue until stopping criteria is reached i.e., optimal scheduling of energy consumption and minimization of electricity cost. The optimal results are obtained by considering the parameters in Table 5.

Table 5. WDO parameters.

Parameters	Values
Maximum iteration	200
Population size	30
$V_{min}$	0.9
$V_{max}$	0.1
RT	3
$\alpha$	0.4
DimMax	5
DimMin	−5
g	0.2

2.9.3. HSA

HSA is the music inspired technique proposed by Zong Woo [12]. In HSA, each musician plays note repeatedly to improve its harmony and generates new random variable according to Equation (28). Tuning parameters are also adjusted to achieve best harmony. The initial population is generated randomly as:

$$X_{ij}=L_i+rand(U_i-L_i)$$

(31)

where $U_i,L_i$ shows upper and lower bound, respectively. Equation (32) shows randomly generated population in matrix form:

$$HM=\left[\begin{array}{cccc}{X}_1^1& X_1^2& X_1^3\dots & X_n^m\\ X_2^1& X_2^2& X_2^3\dots & X_n^m\\ ⋮& ⋮& ⋮& ⋮\\ X_1^n& X_2^n& X_3^n\dots & X_n^m\end{array}\right]$$

(32)

The initial population generated harmony memory (HM) by Equation (32) is compared with the harmony memory consideration rate (HMCR). The HMCR specifies the probability of employing the value of randomly generated matrix. However, suitable HMCR rate is considered as 70% to 90% of the value from the entire pool of HM. The condition for HMCR is:

$$X_{new}=\left\{\begin{array}{c}Xϵ\left\{x_{1i},x_{2i},x_{3i}\dots x_{HM}\right\},WithP\left(HMCR\right)\hfill \\ Xϵ\left\{x_1,x_2,x_3\dots x_N\right\},WithP(1-HMCR).\hfill \end{array}\right.$$

(33)

The values are selected from HM and their pitch are adjusted using pitch adjustment ratio. The pitch adjustment ratio can adjust the frequency of the new harmony and diversify the search space. Par can be adjusted as:

$$X_{new}=\left\{\begin{array}{cc}YES,\hfill & WithP\left(Par\right)\hfill \\ NO,\hfill & WithP(1-Par).\hfill \end{array}\right.$$

(34)

After achieving new harmony vector fitness function is evaluated using Equation (20). If new harmony vector is better than worst harmony replace the worst harmony in the HM. The new harmony is binary coded string and shows the appliances ON/OFF states. The optimal results are obtained by considering the parameters in Table 6.

Table 6. HSA parameters.

Parameters	Values
Maximum iteration	100
Population size	30
HMCR	0.9
$P{A}_{min}$	0.4
$P{A}_{max}$	0.9
$B{w}_{min}$	0.0001
$B{w}_{max}$	0.1

2.9.4. GHSA

We propose heuristic optimization algorithm by combining the attributes of GA and HSA in order to achieve better results as compared to existing algorithms. It is noticed in [12], that HSA has quality to perform searching with high speed i.e., converges at faster rate, while GA has capability to search for global optimal solution. For this reason, we combine the attributes of GA and HSA to achieve global optimal solutions with faster convergence rate.

Initially, GHSA has followed the same steps as the steps of HSA. Equation (31) generates the random values using parameters given in Table 6. The newly generated values are stored and named as harmony memory (HM). HM is binary coded string showing the ON and OFF status of the appliance. After defining HM using Equation (32) the improvisation of HM is done by generating a new harmony vectors based on HMCR using Equation (33). The selected candidate is further modified according to Par. Par calculates the probability of the candidate from HM to be modified and (1-Par) probability of doing else as in Equation (34). However, up to this step, the results achieved by HSA are restricted to only a particular region and the dynamic capability in search of global optimal solution is also confined. In order to overcome this issue, the stochastic operators of GA are introduced i.e., crossover and mutation. These operators not only improve the diversity of the solution but also help to provide higher efficiency towards an optimal solution. As a result, the modified hybrid algorithm GHSA effectively achieve the optimum solution with the faster convergence rate and hence give better results than other algorithms. Therefore, the stochastic operators are employed and the fitness function is evaluated using Equation (20). This new value of the harmony is compared with existing worst harmony in HM and the worst harmony is excluded. The process continues until the termination criteria is met.

The computational time of proposed and existing algorithms for SH and MHs is given in Table 7 and the Algorithm 1 shows working steps of the proposed algorithm GHSA.

Table 7. Computational time of heuristic techniques.

Schemes	Techniques	Computational Time (s)
	WDO	2.61
	HSA	2.01
SH	GA	1.5
	GHSA	1.43
	WDO	100.21
	HSA	96.1
MHs	GA	70.46
	GHSA	60.33

2.10. Feasible Region

Feasible region is defined as the set of optimal points which satisfies all the constraints given in a scenario, including inequalities, equalities, and integer constraints. We consider feasible region of electricity cost versus energy consumption and electricity cost versus ${\mathcal{W}}_{avg}$ for a SH and MHs using RTEP and CPP tariffs.

2.10.1. Feasible Region for SH

In this segment, we figure out the feasible region for electricity cost and energy consumption of SH by considering RTEP and CPP tariffs. Firstly, we consider a SH with RTEP tariff and the electricity cost per hour is given:

$${\xi }_{TL}\left(t\right)=\left(\sum _{a_i}^{A_n}{\varsigma }_{(a_i,t)}\times \epsilon \left(t\right)\times \zeta \left(t\right)\right).tϵ\mathcal{T}$$

(35)

Similarly, the total electricity cost is calculated as:

$${\xi }_{TL}=\sum _{t=1}^T\left(\sum _{a_i}^{A_n}{\varsigma }_{(a_i,t)}\times \epsilon \left(t\right)\times \zeta \left(t\right)\right).tϵ\mathcal{T}$$

(36)

Algorithm 1: GHSA

To minimize Equation (36), we introduce constraints regarding RTEP tariff and energy consumption of the appliances are:

$$\begin{array}{c}\hfill R_1:1.215\le {\xi }_{TL}\left(t\right)\le 3.7\\ \hfill R_2:{\xi }_{TL}\le 21.6\\ \hfill R_3:1.5\le \varsigma \left(t\right)\le 13.84\end{array}$$

In Figure 2a points P${}_1$, P${}_2$, P${}_3$, P${}_5$, and P${}_6$ show the feasible region of electricity cost and energy consumption. The electricity cost is calculated using RTEP tariff and the unscheduled cost per hour is 3.71 cents. The total cost per day is 21.6 cents and based on the parameters electricity cost and energy consumption the constraints are defined. The constraint $R_1$ shows that the electricity cost in hour should not exceed 3.71 cents including peak hours and off-peak hours. Constraints $R_2$ shows total cost per day should not increase than the 21.5 cents as total cost shown here is in the unscheduled case, therefore, the scheduling algorithms must schedule the cost in such way that it should not exceed the limit as in $R_2$. While the constraint $R_3$ shows the total energy consumption of the appliances must be with in limits i.e., between 1.5 and 13.84 kWh to reduce electricity cost. Similarly, Figure 2b shows feasible region for SH considering CPP tariff and the constraints are given as:

$$\begin{array}{c}\hfill C_1:1.215\le {\xi }_{TL}\left(t\right)\le 6.37\\ \hfill C_2:{\xi }_{TL}\le 37.5\\ \hfill C_3:1.5\le \varsigma \left(t\right)\le 13.84\end{array}$$

Figure 2. (a) Feasible region of energy consumption for SH using RTEP; (b) Feasible region of energy consumption for SH using CPP.

Constraints associated with CPP show that the electricity cost of an hour should not exceed 6.37 cents. Constraint $C_2$ shows the cost for a single day should be less than 37.5 cents. While the constraint $C_3$ shows for the optimal scheduling of the energy consumption, energy consumed in an hour should be with in limits of 1.5 kWh and 13.84 kWh.

We also computed feasible region for electricity cost and ${\mathcal{W}}_{avg}$ of the appliances in order to determine the user comfort. User comfort is inversely related with the ${\mathcal{W}}_{avg}$ of the appliances and electricity cost. We consider maximum value of ${\mathcal{W}}_{avg}$ is 5 h for the appliances i.e., allowable delay for the operation of the appliances. In Figure 3a points P${}_1$, P${}_2$, and P${}_3$ show the feasible region for electricity cost and ${\mathcal{W}}_{avg}$ using RTEP tariff. The point P${}_1$ shows that the ${\mathcal{W}}_{avg}$ of the ${\mathcal{S}}_a$ and ${\mathcal{E}}_a$ are restricted to zero, then the electricity cost is reached to a maximum value i.e., 21.5 cents whereas, point P${}_2$ shows the ${\mathcal{W}}_{avg}$ of ${\mathcal{S}}_a$ is 5 h then the cost is reduced to 18.6 cents. While point P${}_3$ shows that ${\mathcal{W}}_{avg}$ of all the appliances, including ${\mathcal{S}}_a$ and ${\mathcal{R}}_a$ is 5 h then the cost is reduced to 10 cents, however, in this case consumers have to pay less cost, but compromise its comfort level. Similarly, in Figure 3b point P${}_1$ shows that the consumers have to pay maximum cost 37.7 cents when ${\mathcal{W}}_{avg}$ is zero. Whereas, point P${}_2$ shows that the cost is reduced to 18.6 cents when the ${\mathcal{W}}_{avg}$ of the ${\mathcal{S}}_a$ is 5 h. While point P${}_3$ presents that the cost is decreased to 15 cents as the ${\mathcal{W}}_{avg}$ of the appliances is increased to 5 h. The feasible region of Figure 3a,b depicts the trade-off between the electricity cost and ${\mathcal{W}}_{avg}$ of the appliances. In order to minimizes the trade-off optimal scheduling of the energy consumption profile is essential in peak hours and off-peak hours.

Figure 3. (a) Feasible region of average waiting time for SH using RTEP; (b) Feasible region of average waiting time for SH using CPP.

2.10.2. Feasible Region for MHs

The feasible region of electricity cost and energy consumption for MHs is determined using RTEP and CPP tariffs. Similar to previous segment, we consider MHs using RTEP and CPP tariffs and the total cost is calculated as:

$${{\rm Y}}_{TL}=\sum _{N=1}^{50}\left(\sum _{t=1}^T\sum _{a_i}^{A_n}{\varsigma }_{(a_i,t)}\times \epsilon \left(t\right)\times \zeta \left(t\right)\right).tϵ\mathcal{T}$$

(37)

Constraints associated with electricity cost and energy consumption for MHs using RTEP are given as:

$$\begin{array}{c}\hfill S_1:50.6\le {\xi }_{TL}\left(t\right)\le 94.4\\ \hfill S_2:{{\rm Y}}_{TL}\le 648.43\\ \hfill S_3:75\le \varsigma \left(t\right)\le 351\end{array}$$

In Figure 4a the shaded region shows the feasible region of electricity cost and energy consumption of MHs using RTEP tariff. Constraint $S_1$ indicates the cost per hour must be restricted with in limits of 50.6 and 94.4 cents. While the cost per day is restricted to 648.43 cents by the constraint $S_2$. Constraint $S_3$ presents that the energy consumption should not exceed upper and lower bound i.e., 75 and 351 kWh respectively. Figure 4b shows the feasible region of the electricity cost and energy consumption for MHs using CPP tariff. The constraints related to electricity cost and energy consumption for MHs using CPP are:

$$\begin{array}{c}\hfill W_1:58.7\le {\xi }_{TL}\left(t\right)\le 156.8\\ \hfill W_2:{{\rm Y}}_{TL}\le 1087\\ \hfill W_3:75\le \varsigma \left(t\right)\le 351\end{array}$$

Figure 4. (a) Feasible region of energy consumption for MHs using RTEP; (b) Feasible region of energy consumption for MHs using CPP.

Similar to prior constraints, the constraint $W_1$ indicates that electricity cost in an hour should be restricted by upper and lower bound i.e., 58.7 and 156.8 cents, respectively. Constraint $W_2$ shows that heuristic algorithm should schedule the cost such that it should not increase 1087 cents. While constraint $W_3$ simply means that for minimization of electricity cost energy consumption of the appliance should not exceed the given values as in $W_3$.

In Figure 5a points P${}_1$, P${}_2$, and P${}_3$ illustrate the feasible region of electricity cost and ${\mathcal{W}}_{avg}$ of MHs using RTEP tariff. The point P${}_1$ shows that the electricity cost is maximum when ${\mathcal{W}}_{avg}$ is zero, while point P${}_3$ represents that at the maximum value of the ${\mathcal{W}}_{avg}$ of the appliances the total cost is minimum i.e., 150 cents. However, at this stage user comfort is decreased. P${}_2$ shows the cost is reduced to 580 cents when the operation time of ${\mathcal{S}}_a$ is delayed to its maximum value i.e., 5 h. Similarly, Figure 5b shows the feasible region bounded by the points P${}_1$, P${}_2$, and P${}_3$ with CPP tariff. The maximum cost in case of CPP is raised to 1087 cents at zero ${\mathcal{W}}_{avg}$. Whereas, P${}_2$ shows the cost when the operation time of ${\mathcal{S}}_a$ is delayed only. While P${}_3$ shows that ${\mathcal{W}}_{avg}$ is maximum for all the appliances the cost is minimum i.e., 150 cents. Moreover, to address the trad-off in a better way, it is important to consider electricity cost and user comfort equally and appropriately.

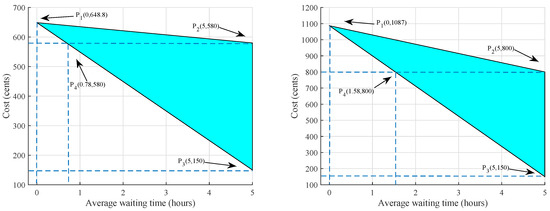
Figure 5. (a) Feasible region of average waiting time for MHs using RTEP; (b) Feasible region of average waiting time for MHs using CPP.

3. Simulation and Discussion

In this section, we inspect the numerical simulation of four heuristic algorithms and their performances are evaluated in terms of electricity cost, PAR, and user comfort. A hybrid algorithm is proposed and simulation results are compared with existing algorithms using software tool MATLAB Ver. 2014b using a processor installed with Intel (R) Core (TM) i5-2450M CPU @ 2.50 GHz and 6 GB of memory on Windows platform.

We assume SH and MHs with household appliances which are categorized into three groups: ${\mathcal{R}}_a$, ${\mathcal{S}}_a$, and ${\mathcal{E}}_a$. While arbitrary operational time and power ratings are assigned to ${\mathcal{S}}_a$ and ${\mathcal{R}}_a$ appliances in the case of MHs. Our objectives are to minimize electricity cost, PAR, and ${\mathcal{W}}_{avg}$ of the appliances. In this regard, heuristic algorithms are incorporated like: WDO, HSA, GA, and proposed algorithm GHSA. Comparative analysis is made among heuristic algorithms and unscheduled case by adopting RTEP and CPP tariffs (as shown in Figure 6a,b) and results are demonstrated the proposed algorithm efficiently addressed the aforementioned objectives. The performance parameters comprise of load profile, cost per hour, electricity cost per day, PAR, and user comfort. The detail of each parameter is provided as follows:

Figure 6. (a) RTEP tariff; (b) CPP tariff.

3.1. Load Profile

The energy consumption of appliances for SH and MHs using RTEP and CPP tariffs is shown in Figure 7a–d. It can be seen that during peak hours i.e., 7 to 15 h each heuristic algorithm performs better than unscheduled case. In Figure 7a maximum unscheduled load during peak hours is 13.84 kWh, and among other heuristic algorithms GA schedules the peak load competently to 5.01 kWh. While in Figure 7b GHSA schedules the peak load to 3.73 kWh which is comparatively less than existing heuristic algorithms and unscheduled load (13.84 kWh). Similarly, Figure 7c,d illustrate the load profile for MHs using RTEP and CPP tariffs and the energy consumed by unscheduled load during peak hours is 351 kWh, however, compared with the existing algorithms GHSA has scheduled the load to 60.29 kWh and 136.09 kWh for MHs using RTEP and CPP tariffs, respectively. The overall results show that proposed algorithm performs better to schedule the load profile for SH and MHs compared to existing algorithms and unscheduled case. Table 8 presents load profile in peak hours of the prices in unscheduled case, scheduled case, percentage decrement, and improvement of heuristic algorithms.

Figure 7. (a) Load profile of SH with RTEP; (b) Load profile of SH with CPP; (c) Load profile of MHs with RTEP; (d) Load profile of MHs with CPP.

Table 8. Cost profile comparison.

Schemes		Techniques
		Unscheduled	WDO	HSA	GA	GHSA
SH with RTEP	Load profile (kWh)	13.84	8.66	6.01	5.01	5.80
	Percentage decrement	—	37.42%	56%	63.80%	63.29%
	Improvement	—	5.18	7.83	8.83	8.76
SH with CPP	Load profile (kWh)	13.84	5.12	6.37	5.10	4.95
	Percentage decrement	—	63.21%	53.97%	63.15%	65.12%
	Improvement	—	9.27	7.47	8.74	10.12
MHs with RTEP	Load profile (kWh)	351	128.88	125.28	241.46	124.29
	Percentage decrement	—	63.28%	65.92%	31.20%	65.72%
	Improvement	—	222.12	290.72	109.54	290.71
MHs with CPP	Load profile (kWh)	351	114.49	140.38	134.68	136.01
	Percentage decrement	—	67.38%	60%	61.6%	61.25%
	Improvement	—	236.51	210.62	216.32	214.99

3.2. Cost Per Hour

The electricity cost per hour is calculated using Equation (32). The results in Figure 8a–d depict electricity cost per hour with the comparison of heuristic algorithms. It is observed that each algorithm tends to schedule the cost in low pricing hours i.e., off-peak hours. In Figure 8a results show that the cost is reduced to 2.61, 1.72, 1.12, and 1.34 cents by WDO, HSA, GA, and GHSA, respectively. Similarly, Figure 8b shows maximum unscheduled cost is 6.83 cents and it is reduced to 2.25, 2.04, 2.02, and 1.60 cents using WDO, HSA, GA, and GHSA, respectively. Figure 8c,d represent results for MHs using RTEP and CPP tariffs. All heuristic algorithms are compared with each other and also with unscheduled case. The unscheduled cost per hour during peak hours for MHs using RTEP and CPP is 94.38 and 156.78 cents while proposed algorithm is reduced it to 20.28 and 58.46 cents, respectively, which represents maximum reduction compared to other existing algorithms.

Figure 8. (a) Cost per hour of SH with RTEP; (b) Cost per hour of SH with CPP; (c) Cost per hour of MHs with RTEP; (d) Cost per hour of MHs with CPP.

3.3. Electricity Cost Per Day

The primary objective of our work is the minimization of electricity cost. The electricity cost is reduced using heuristic algorithms to schedule the energy consumption profile and also with the constraints mentioned in Section 2.8. Figure 9 illustrates the electricity cost per day (total cost) for SH and MHs using RTEP and CPP tariffs. In detail, total cost for SH using RTEP tariff in unscheduled case is 21.53 cents and using heuristic algorithms: WDO, HSA, GA, and GHSA the total cost is reduced to 18.65, 17.04, 16.01, and 15.10 cents, respectively. Likewise, SH with CPP tariff the total cost for unscheduled case is 38.23 cents and the heuristic algorithms: WDO, HSA, GA, and GHSA are reduced the total cost to 25.68, 23.98, 22.63, and 20.21 cents, respectively. In the case of MHs, using RTEP tariff the total cost is reduced from unscheduled case i.e., 648.83 cents to 320.74, 480.36, 445.36, and 284.39 cents by WDO, HSA, GA, and GHSA, respectively as shown in Figure 9. Accordingly, for MHs the total cost associated with CPP tariff is 631.02, 643.18, 608.18, 500.01 cents using WDO, HSA, GA, and GHSA, respectively. The overall effects of the total cost associated with RTEP and CPP rates in the case of SH and MHs are analyzed which show that the proposed algorithm GHSA outperforms the other existing algorithms. Table 9 shows the total cost, percentage decrement, and improvement of heuristic algorithms. Moreover, in order to ensure fairness among heuristic algorithms, electricity cost is also compared in terms of maximum, minimum, and average cost as shown in Table 10. It is worth mentioning that maximum electricity cost of heuristic algorithms is always less than the unscheduled cost (given in Table 9) which shows each heuristic algorithm effectively addresses the objective function and its constraints discussed in Section 2.8.

Figure 9. Electricity cost per day.

Table 9. Total electricity cost per day.

Schemes		Techniques
		Unscheduled	WDO	HSA	GA	GHSA
SH with RTEP	Total cost (cents)	21.53	18.65	17.04	16.01	15.01
	Percentage decrement	—	13.37%	20.58%	25.63%	29.86%
	Improvement	—	2.88	4.49	5.52	6.43
SH with CPP	Total cost (cents)	37.5	25.68	23.98	22.63	20.21
	Percentage decrement	—	31.52%	36.05%	39.65%	46.19%
	Improvement	—	11.82	13.52	14.87	17.21
MHs with RTEP	Total cost (cents)	648.43	320.74	480.36	445.36	284.39
	Percentage decrement	—	50.54%	25.91%	31.31%	56.06%
	Improvement	—	327.69	168.07	303.7	364.04
MHs with CPP	Total cost (cents)	1087	631.02	643.18	608.18	500.21
	Percentage decrement	—	41.94%	40.82%	44.04%	54.04%
	Improvement	—	445.98	443.82	478.82	587

Table 10. Total cost comparison.

Schemes	Cost (cents)	Techniques
		WDO	HSA	GA	GHSA
SH with RTEP	Maximum cost	20.26	19.78	17.39	17.02
	Average cost	19.24	18.41	16.70	16.02
	Minimum cost	18.65	17.04	16.01	15.01
SH with CPP	Maximum cost	33.46	35.76	34.54	31.21
	Average cost	29.57	29.87	28.60	25.71
	Minimum cost	25.68	23.98	22.63	20.21
MHs with RTEP	Maximum cost	446.38	520.63	535.71	408.99
	Average cost	383.56	500.49	490.53	346.66
	Minimum cost	320.74	480.36	445.36	284.39
MHs with CPP	Maximum cost	810.87	904.41	800.70	780.08
	Average cost	720.94	773.79	704.44	640.14
	Minimum cost	631.02	643.18	608.18	500.21

3.4. PAR

PAR describes the behaviour of the consumer’s load profile and directly affects the operation of the power grids. Figure 10 illustrates PAR of scheduled and unscheduled case for SH and MHs with RTEP and CPP tariffs and results show that each heuristic algorithm is competent to reduce PAR compared to unscheduled case. However, it is evident from Figure 10 that GHSA exhibits maximum reduction in PAR compared to the existing algorithms. Moreover, in order to reduce PAR, load profile of the consumer should schedule effectively which ensures the reliability and stability of the power grids. Table 11 represents PAR, percentage reduction of PAR, and improvement of heuristic algorithms.

Figure 10. PAR of SH and MHs with RTEP and CPP.

Table 11. PAR comparison.

Schemes		Techniques
		Unscheduled	WDO	HSA	GA	GHSA
SH with RTEP	PAR	5.01	4.31	3.24	3.73	3.09
	Percentage decrement	—	13.97%	35.32%	25.54%	38.32%
	Improvement	—	0.7	1.77	1.28	1.92
SH with CPP	PAR	5.01	4.68	3.48	3.64	3.13
	Percentage decrement	—	6.58%	30.53%	27.34%	37.52%
	Improvement	—	0.33	1.53	1.37	1.88
MHs with RTEP	PAR	22.46	12.78	14.70	12.70	11.73
	Percentage decrement	—	43.09%	34.55%	43.45%	47.77%
	Improvement	—	11.78	9.84	11.48	12.78
MHs with CPP	PAR	24.54	13.92	12.98	14.01	12.01
	Percentage decrement	—	43.27%	47.01%	42.66%	50.08%
	Improvement	—	10.62	11.56	10.53	12.53

3.5. User Comfort

The ${\mathcal{W}}_{avg}$ of the appliances is calculated which refers to user comfort. User comfort is disturbed when the user faces minimum amount of delay in order to operate the appliance. However, if ${\mathcal{W}}_{avg}$ of the appliances increases eventually cost of electricity reduces. In this vein, there is sort of trade-off between waiting time of appliances and electricity cost. Figure 11 shows ${\mathcal{W}}_{avg}$ for SH and MHs using RTEP and CPP tariffs with heuristic algorithms: WDO, HSA, GA, and GHSA. The maximum allowable delay i.e., ${\mathcal{W}}_{avg}$ of the appliance is 5 h, however, the proposed algorithm GHSA is achieved minimum ${\mathcal{W}}_{avg}$ of the appliances compared with the existing algorithms i.e., 4.3 and 2.4 h, respectively. Similarly, for MHs the proposed algorithm GHSA has achieved minimum delay compared with other heuristic algorithms i.e., 3.7 and 3.5 h , respectively. Among other existing techniques GHSA is capable of minimizing the ${\mathcal{W}}_{avg}$ which in turn increases user comfort. Although it is stated that there is trade-off between electricity cost and ${\mathcal{W}}_{avg}$, however, proposed algorithm GHSA performs efficiently to minimize the trade-off compared to other existing optimization algorithms.

Figure 11. Average waiting time of SH and MHs using RTEP and CPP.

4. Conclusions and Future Work

In this paper, we have proposed a heuristic algorithm GHSA for SH and MHs to reduce electricity expense, PAR, and maximize user comfort. The proposed algorithm is tested in the presence of RTEP and CPP tariffs for SH and MHs. In case of MHs, arbitrary power ratings and time of operations are assigned to the appliances. Extensive simulations are conducted which show the performance of proposed algorithm GHSA is efficient as compared to existing algorithms: WDO, HSA, and GA in terms of electricity cost, PAR, and user comfort. In particular, GHSA reduces the electricity cost to 46.19% in case of SH. While for MHs the electricity cost is reduced to 56.04%. In terms of PAR, GHSA reduces PAR to 38.32% and 50.08% for SH and MHs, respectively. The minimization in electricity cost and PAR reveal benefits to the consumers as well as improve the stability and reliability of the power grid. Moreover, feasible regions are computed to validate the effectiveness of our proposed algorithm GHSA. Thus, it is concluded from above discussion that the proposed EHEMC based on GHSA yields significantly improved performance as compared to existing heuristic algorithms in terms of electricity cost, PAR and user comfort.

In future, we are interested to implement the integration of RESs for both cases i.e., SH and MHs. We are also interested to incorporate distributive algorithms and multi objective problems with convex optimization methods.