Improving Path Loss Prediction Using Environmental Feature Extraction from Satellite Images: Hand-Crafted vs. Convolutional Neural Network

Abstract

There is an increased exploration of the potential of wireless communication networks in the automation of daily human tasks via the Internet of Things. Such implementations are only possible with the proper design of networks. Path loss prediction is a key factor in the design of networks with parameters such as cell radius, antenna heights, and the number of cell sites that can be set. As path loss is affected by the environment, satellite images of network locations are used in developing path loss prediction models such that environmental effects are captured. We developed a path loss model based on the Extreme Gradient Boosting (XGBoost) algorithm, whose inputs are numeric (non-image) features that influence path loss and features extracted from images composed of four tiled satellite images of points along the transmitter to receiver path. The model can predict path loss for multiple frequencies, antenna heights, and environments such that it can be incorporated into Radio Planning Tools. Various feature extraction methods that included CNN and hand-crafted and their combinations were applied to the images in order to determine the best input features, which, when combined with non-image features, will result in the best XGBoost model. Although hand-crafted features have the advantage of not requiring a large volume of data as no training is involved in them, they failed in this application as their use led to a reduction in accuracy. However, the best model was obtained when image features extracted using CNN and GLCM were combined with the non-image features, resulting in an RMSE improvement of 9.4272% against a model with non-image features only without satellite images. The XGBoost model performed better than Random Forest (RF), Extreme Learning Trees (ET), Gradient Boosting, and K Nearest Neighbor (KNN) based on the combination of CNN, GLCM, and non-image features. Further analysis using the Shapley Additive Explanations (SHAP) revealed that features extracted from the satellite images using CNN had the highest contribution toward the XGBoost model’s output. The variation in values of features with output path loss values was presented using SHAP summary plots. Interactions were also observed between some features based on their dependence plots from the computed SHAP values. This information, when further explored, could serve as the basis for the development of an explainable/glass box path loss model.

1. Introduction

Accurate path loss prediction is important in wireless networks. Power distribution within the coverage area can be accurately ascertained during Link Budget, leading to a network with a better quality of service if the predicted values are effectively used during design, expansion, or maintenance [1,2,3]. Deterministic path loss models provide a reasonable accuracy but are computationally expensive and require details that include a 3D model of the environment, building materials, and so on. Empirical models are much easier to use but are prone to errors. Meanwhile, machine learning (ML) models are more accurate than empirical models and sometimes exceed the accuracy of deterministic models. Such ML models were developed with algorithms such as Multiple Layer Perceptron (MLP), Support Vector Regression (SVR), Random Forest (RF), and XGBoost [4,5,6]. Furthermore, a Convolutional Neural Network (CNN) is employed to extract features from images that describe the effects of environment due to the dependence of path loss on the propagation path/environment. Such images include satellite images for a wide area [7], pointwise satellite images [8], segmented images with shadings that represent heights of buildings in an urban environment [9], segmented images based on some parameters, with building height inclusive [10], and pseudoimages representing the fusion of various data types [11].

Most of the models developed are for fixed frequency, antenna height, and environment. However, since path loss varies with the environment, such model prediction will be inaccurate in other scenarios. Considering the fact that path loss prediction is performed before networks are deployed, it is reasonable to develop models that can be used to make accurate predictions for varieties of environments and network parameters. Otherwise, the model will only be suitable for the existing network it was designed for or a network with almost the same parameters in a similar environment. Although ML models make better predictions, empirical models have the advantage of being versatile as they consider a range of frequencies, distances, and antenna heights over which these models are valid. Some of these models have parameters tailored to a specific type of environment, such as COST 231 Hata [12], and Stanford University Interim (SUI) model [13]. Therefore, there is a need to have machine learning path loss models valid for multiple parameters and environments so that they can provide accurate predictions during design and prior to network deployment. This will eliminate the cost of taking measurements under certain network parameters from individual environments and developing individual models specific to the environments and selected network parameters.

Ayadi et al. [14] developed an MLP model for the prediction of a number of frequencies in the Ultra-High-Frequency (UHF) band. The study considered the fact that the propagation path from the transmitter to receiver position varies such that some portions can be classified as either rural, urban, or suburban environments. Thus, distances covered in each type of environment were included as features for model development. The problem with such a model is that it does not capture the micro variations of the environment types along the propagation path; rather, it is developed based on distances covered in each environment type without a detailed description. Nguyen et al. [15] developed a model valid at frequencies between 0.8 and 70 GHz. The model was developed based on the features distance, frequency, propagation scenario, and environment type. The propagation scenario could be either “above rooftop” or “below rooftop”. Above rooftop is a scenario in which one of the antenna heights is above the surrounding rooftops, and below rooftop is when all antenna heights are below the surrounding rooftops. The model does not capture environment details, unlike that in [16], where features extracted from satellite images are included during model development to capture environmental details.

Sani et al. [17] also developed models for multiple frequencies, multiple antenna heights, and multiple environments. A clutter height feature was used in representing the various types of environments such that each type of environment had an integer value representing it. The problem with this method is that it does not take into consideration the micro differences within each type of environment, whereas [16] included satellite images to acknowledge the effects of these micro variations. The ResNet50V2 used in [16] takes time and memory space to train. This work proposes the use of a less complex CNN that will train faster and occupy less memory space.

Another issue to note is the dependence of a CNN’s accuracy on a large volume of data and a large amount of time it takes a CNN to get trained with the data, even though the prediction time is minimal. An alternative is to use hand-crafted feature extraction methods to deal with data limitation as well as the large training time. Sotiroudis et al. used the Segmentation-based Fractal Texture Analysis (SFTA) texture extraction method to extract features from images with grayscale shadings of building heights between the transmitter and receiver and developed three models with features based on RF, Extreme Gradient Boosting Machine (XGBoost), and Light Gradient Boosting Machine (LightGBM) [18]. However, a comparison between the performance of SFTA and CNN was not performed. To the best of our knowledge, their work is the first that incorporated texture feature extraction in a path loss problem. Predictions from a LightGBM model were more accurate, although the hyper-parameter optimization that was carried out in this work was not carried out in theirs to ascertain the optimal hyper-parameters of the algorithms. In other domains, comparisons were made between the performance of hand-crafted features and CNN, in which the CNN-extracted features performed better [19,20]. Combining CNN features and hand-crafted features improved the accuracy [21,22].

The aim of this work is to develop a single ML-based path loss model valid for some network parameters (UHF band and antenna heights) and environments (rural, suburban, urban, and urban highrise) with the effect of terrain/elevation taken into consideration. The essence is to have the ML path loss models valid for various values of network parameters and environment types, similar to existing empirical models. The ability of ML algorithms to model non-linear relationships improves performance over the existing empirical models. Numeric features combined with satellite image features were used as input to the model. Satellite images are used to capture micro and macro variations within the environments, unlike in existing empirical models, where such variations are not captured, resulting in poor predictions in new environments. The performance of features extracted using various methods (hand-crafted and CNN) and their combinations on the model’s output was evaluated. Hand-crafted features were investigated to ascertain the possibility of their use in this application, knowing that they need no training, unlike CNN, which requires training with a lot of data. However, since combining hand-crafted and CNN features was reported to improve accuracy in some applications, we also investigated it, and improvements in accuracy and training time were observed compared to [16]. In addition, the study explores feature importance and analysis. Feature importance was not conducted in all works cited in this paper, except in [17], where only non-image features were considered for model development. Our contributions are:

• Review of path loss prediction based on image processing using CNN.
  Most works presented ML-based image processing approaches for path loss prediction, but to the best of our knowledge, no such comprehensive review of such existing works was supplied.
• Investigation on the use of various hand-crafted feature extraction techniques and their combinations on 2D satellite images in path loss prediction.
• Combining CNN features with hand-crafted features to improve the accuracy of path loss prediction.
  While this has been applied in computer vision tasks, to the best of our knowledge, this has not been applied to the problem of path loss prediction.
• Interpretation of model prediction based on Shapley Additive Explanations (SHAP).
  Most ML-based path loss prediction works do not analyze the features deeply, including the comparison of different types of features.

2. Related Works

The effects of the environment on path loss motivated the incorporation of environment details in the form of 2D satellite images into path loss modeling. A number of works have emerged in which images are processed using CNN. Various image types are being processed that include satellite images, segmented images based on some parameters, pseudoimages, and combinations of various images.

2.1. Satellite Images

Models that take satellite images as input was developed by scholars by either training a customized CNN or by the use of pre-trained CNN models such as VGG-16, ResNet-50, and ResNet50V2 via transfer learning as follows.

2.1.1. Training a Customized CNN with Satellite Images

Thrane et al. [8] predicted path loss in a campus environment (suburban) from a model that integrated satellite image input with other numerical data features. The satellite images are passed through five convolutional layers, and the numerical data are passed through fully connected layers. The outputs of the two networks are concatenated and passed onto an output neural network composed of two fully connected layers and a single node output layer. The data used in training and testing were measurements at 811 and 2630 MHz, with a fixed transmitting antenna height of 30 m and receiving antenna height of 1.5 m. The deep learning model performed better than 3D Ray Tracing and the empirical model. A similar architecture was developed to predict signal strength at 811 and 2630 MHz, but with reduced complexity in the CNN, whereby four convolutional layers were used with a reduced number of filters. A modification was also made to the numerical features used, such that latitude and longitude were removed, the frequency was included, and data from different environments were considered [23]. The model was upgraded in [24] by the addition of the receiver position side view image. Nguyen et al. modified the model in [23] such that the model predicts signal strength corrections of a 3GPP empirical model at 3.5 GHz. The final signal strength is obtained by the addition of the corrections to the signal strength computed using the 3GPP empirical model [25]. However, the image of the receiver position is not sufficient to describe the path of the signal from the transmitter to the receiver position.

2.1.2. Transfer Learning with Satellite Images

In order to train a model with more information about the path from transmitter to receiver location, Sani et al. [16] merged the satellite images of four locations along the path from the transmitter to receiver location into single images and extracted features from the images using a ResNet50V2. The satellite images were also from various environments, as in [23]. The extracted features were merged with eight other features and used for training and testing various regression algorithms. As ResNet50V2 takes a long period of time to train and requires large memory space, a customized CNN with lower complexity should have been used for the purpose.

Ates et al. [26] used VGG-16 and ResNet-50 to predict a path loss exponent and shadowing for 1.8 km ${}^2$ coverage areas using satellite images. Separate models were trained for the path loss exponent and shadowing values resulting from a 3D ray Tracing simulation at a frequency of 900 MHz, a transmitting antenna height of 300 m, and a receiving antenna height of 1.5 m. VGG-16 and ResNet-50 had the same accuracy in path loss exponent prediction, but ResNet-50 was better in terms of shadowing prediction by 1%. A modification of the two CNNs by including a parallel, fully connected layer to learn a histogram of the difference between path loss values and a reference path loss improved their performance by 2%. The process of learning two parameters from a single CNN is called multi-tasking. The prediction of the path loss exponent and shadowing has drawbacks. Both parameters were determined based on curve fitting/least squares regression, and these values contain errors and are not actual values. Training the CNN has its own error as well, thereby compounding the error of the curve fitting/least squares regression. In addition, separate models have to be developed for other frequency bands (for example, 1800 and 2600 MHz) for the same environment. Ahmadien et al. trained a VGG-16 to predict the histogram of path loss. Three models were developed at different single frequency values (900 MHz and 3.5 G Hz) and antenna heights (80 and 300 m) [7]. The prediction of the path loss histogram does not give path loss values location-wise; rather, it gives the ranges of path loss values for a large area. Such information cannot be used in the optimization of cell radius and number of cells during design. A single model should have been developed for the various frequencies and antenna heights. This will save the time needed to train several models and memory allocation if the model is to be implemented in software.

2.2. Segmented Images

Images segmented based on building heights and/or terrain information have been used in path loss model development. Customized CNNs or modified forms of UNet were used for the purpose. The following subsections account for path loss models developed based on segmented images.

2.2.1. Training a Customized CNN with Segmented Images

Lee et al. trained a CNN with 3D Ray tracing simulated data at 28 GHz to predict path loss exponent for 1 km ${}^2$ area based on an image input resulting from the combination of two images. The first image is a segmented image that presents the heights of buildings with respect to the height of the tallest building as shades of red, and the second image is a height above sea level difference between the transmitting antenna and ground level presented in shades of green [10]. However, building height information is available for only a few environments, making the model useless where building height information is unavailable. Though the model is for an urban environment, the effect of vegetation that is present in most urban environments is omitted, especially for a millimeter wave of 28 GHz, which is easily degraded and blocked. Satellite images should have been used to capture such effects, and the model is made versatile. In [9], images containing gray shadings based on building heights between transmitter and receiver were used in training a CNN for path loss prediction at 900 MHz, in which the training data were obtained using 3D Ray Tracing. The performance was comparable to that of a two hidden layer MLP trained with 23 features describing the path from the transmitter to the receiver. The model, however, has to be modified for use at frequencies other than 900 MHz.

Cheng et al. trained an Attention-Enhanced CNN to predict path loss within a suburban environment at 28 GHz. The model’s input is an image segmented based on the Distance Embedded Local Area Multi-scanning (DE-LAMS) algorithm and has an accuracy better than that of a normal CNN, dilated CNN, and a Global Context (GC) CNN [27]. Kim et al. developed a 5G millimeter wave signal strength prediction model based on a 3D CNN, whose inputs are 3D images generated by the 3D-LAMS algorithm based on building and terrain information. Pooling layers in the CNN were avoided so as to prevent information loss. The model, however, neglects the effect of vegetation, which is a very important determinant of path loss/received signal strength and the millimeter frequency/frequencies considered during model development were not specified [28]. Wu et al. developed a path loss prediction model with numerical input characterizing network parameters and image-based inputs characterizing the environment. The images were developed based on grayscale encoding such that each type of land cover between the transmitter and receiver had its own gray level/shade. A CNN was used for image feature extraction, and a fully connected neural network was used for the numeric data. The outputs of the two networks are fused together and passed onto fully connected layers, the output of which is the predicted path loss. The model’s accuracy was better than when a combination of vector-based environment characterization and numeric inputs or when the three input types were combined [29]. The encoding method used does not capture micro variations within each type of environment.

2.2.2. Training Modified UNet Architecture with Segmented Images

Ratnam et al. modified a UNet and trained it to predict an image showing path loss distribution within an area. The training was performed with 3D Ray Tracing data at 28 GHz over areas that are 512 (m${}^2$), with the transmitting antenna at the center. Inputs to the network are terrain information, building information, and foliage information for the area under study encoded as colored images. The inclusion of Line of Sight (LOS) data further improved prediction accuracy, which surpassed distance dependence prediction and conditional least squares. The model is named FadeNet, and it demonstrated faster prediction than 3D Ray Tracing [30].

Zhang et al. trained a UNet model named PLNet. The inputs are images representing the distribution of parameters, clutter, terrain, building, frequency, antenna height, etc., within the region of interest, and the output is an image showing path loss distribution. Predictions by PLNet outperformed those of empirical models and 3D Ray Tracing [31]. The authors did not specify the range of parameter values for which the model is valid. The models in [30,31] are based on UNet, and the output is a segmented image of the path loss distribution. Such a model can only be used for analysis rather than design as numeric path loss values are required.

2.3. Combination of Images

Hayashi et al. used the feature extraction part of AlexNet to process images before passing the images together with numeric features to six fully connected layers. The image inputs include aerial maps, building occupancy maps, and building height maps. For each image type, either image at the receiver location alone or at both transmitter and receiver locations were considered, with each image having a separate CNN for processing. The results showed that for each input type, using images at both transmitter and receiver locations was better and that using the building height map as the input had the highest accuracy [32]. In a similar work, Inoue et al. used the same architecture with some modifications to predict the signal strength at 2.1 GHz. In this case, the building occupancy images were developed from aerial maps with the aid of a trained UNet, and the images at the midpoint between the transmitter and receiver were included as the input. The inclusion of midpoint images improved the model’s accuracy [33]. However, the model is not suitable for other frequency bands since it was trained with single frequency data.

2.4. Pseudoimages

An improvement to [9] is the formation of a pseudo image composed of the building height shadings in grayscale, feature importance of tabular data, and the satellite image of the receiver location. Each of the three images represented a channel in the pseudo image. The model performed better than when only building height information was used for training and when an XGBoost was trained with the tabular/numerical data [11]. However, the model is not versatile as it is for 900 MHz only, and more detailed information about the path should have been used, not the image at the receiver location alone.

2.5. Summary

Works that use different input, model architectures, as well as outputs were reviewed, and the limitations of the works were also highlighted. One of the limitations is that the idea of predicting a path loss exponent based on any of the image input types will result in erroneous path loss prediction. This is because path loss exponents are estimated based on the least squares method. The process of least squares is associated with its error. By further training a CNN that is not 100% accurate in predicting the path loss exponent, the error during path loss exponent computation is compounded with that of the CNN, thereby affecting the final path loss prediction. Furthermore, using an image representing the receiver environment alone, as was performed in many works, is not sufficient to characterize the propagation path. There are works in which predictions of radio maps were performed based on the UNet architecture. Such predictions are for analysis as images representing the distribution of signal strength/path loss are predicted, not the path loss values. Thus, the outputs are not suitable for automated design and optimization.

On a final note, models valid for multiple frequencies, environments, and antenna heights have not been developed. Radio Frequency Planning Tools are used in wireless network design, which has empirical path loss models available for the designer to choose from. ML path loss models have accuracy better than empirical models, and it is likely that they will replace empirical models in these tools in the future. Hence, it is desirable to have ML models valid for a range of frequencies, antenna heights, and environments. Otherwise, many models have to be developed with varying parameters of frequency, antenna height, and environment, leading to large memory occupation, time wastage in training individual models, and confusion on the particular model to select from the end user viewpoint. Thus, the study fills the gap of non-availability of versatile models by developing a model for different environments, frequencies, and antenna heights. This will make the ML models flexible for use in different environments, frequencies, and antenna heights. The model considered takes as its input some numeric features affecting path loss combined with features extracted from images by algorithms (CNN or hand-crafted). The image is composed of four satellite images tiled together in a 2 by 2 grid and is for four different positions along the path from transmitter to receiver position. This gives more information on the propagation path than using the image at the receiver location alone. The effects of various feature extraction methods and their combinations on accuracy were investigated and reported. Improvements were observed compared to our previous work in [16]. However, the work considered some datasets in which measurements were taken from networks operating within the UHF band in environments that included rural, suburban, urban, and urban highrise at some fixed values of transmitting and receiving antenna heights.

3. Methodology

3.1. Dataset

The dataset in [16] is used in this work. It is composed of four datasets combined to form a single dataset, with measurements from different frequencies, environments, and antenna heights. Such a type of dataset combination was performed in [11,23]. Three of the datasets are available at [34,35,36] and have been used in [37,38,39], respectively. The fourth dataset is measurements taken by us. It should be noted that not all samples in [34] were used to maintain a balanced dataset in terms of environment type. The final dataset is made up of 12369 samples, consisting of 8 features and path loss values as the target. The features include elevation at receiver position (elevation), frequency, height of transmitting antenna (ht), height of receiving antenna (hr), latitude difference between transmitting and receiving antenna (distance_x), longitude difference between transmitting and receiving antenna (distance_y), elevation at transmitter position (tantennaelev), and distance between transmitter and receiver (distance). Table 1 presents a summary of the dataset, showing the different types of environments from which the measurements were taken and the parameters under which they were taken that include frequency, transmitting antenna height, and receiving antenna height.

Table 1. Dataset summary.

Environment	Frequency (MHz)	Transmitting Antenna Height (m)	Receiving Antenna Height (m)
Rural	868	0.2, 1.5, 3	12
Suburban	1800	30	1.5
Urban	1835.2, 1836, 1840.8, 1864, 2140	40, 41, 53	1,1.5
Urbanhighrise	868	0.2, 1, 1.5, 3	12

3.2. Image Data

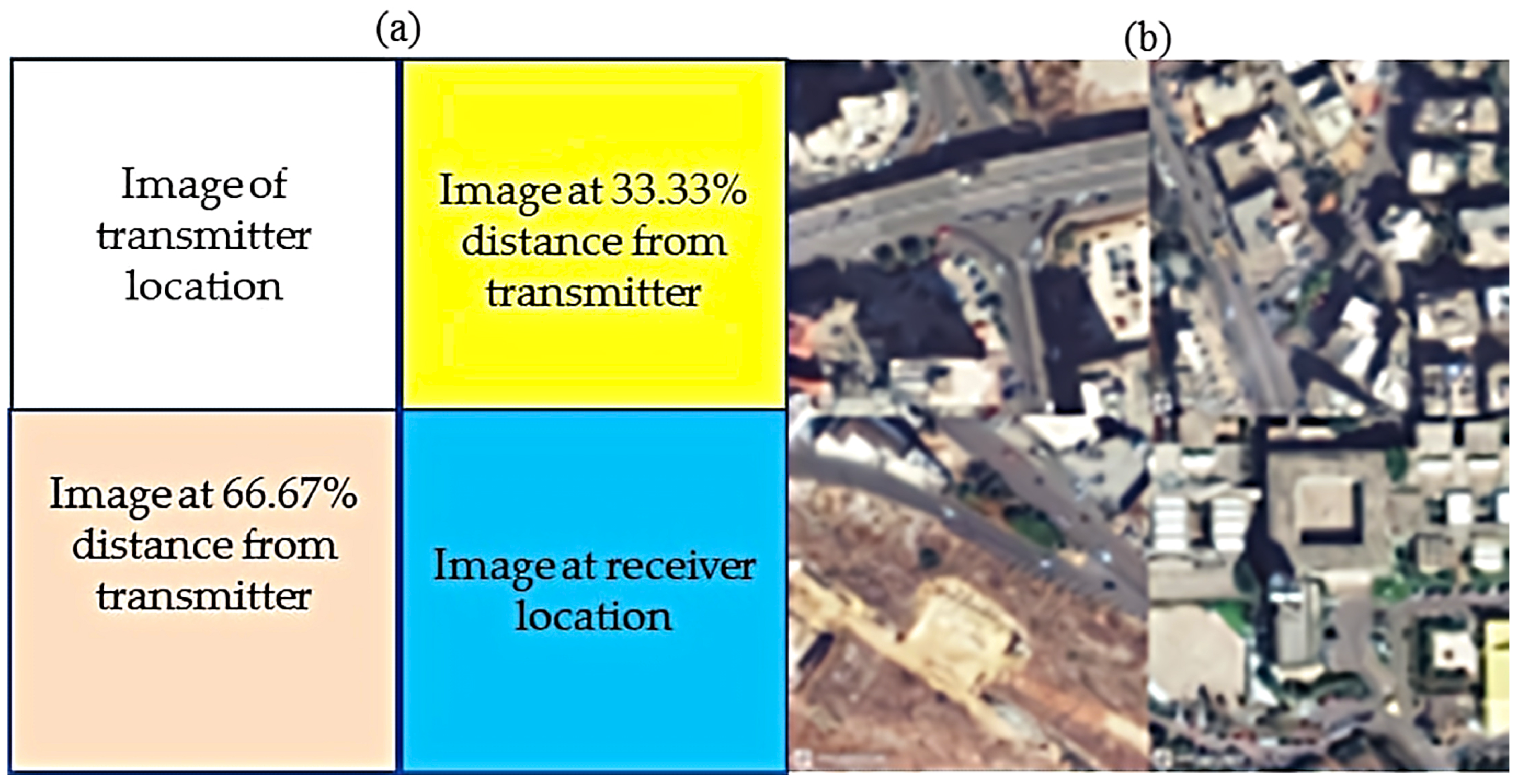
The image used is a concatenation of four satellite images, as illustrated in Figure 1. The images represent various positions along the path from transmitter to receiver locationm as shown in Figure 1a with a sample in Figure 1b. The images were downloaded from Mapbox [40] based on the latitude and longitude values in the dataset.

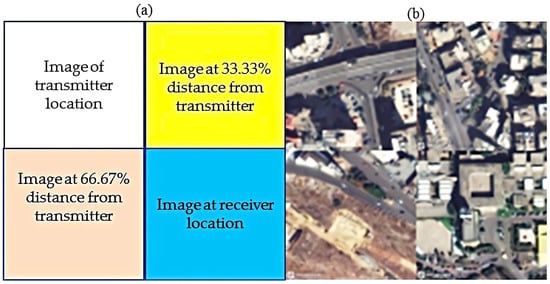
Figure 1. (a) Format of image concatenation. (b) Final concatenated image sample.

3.3. Proposed Method

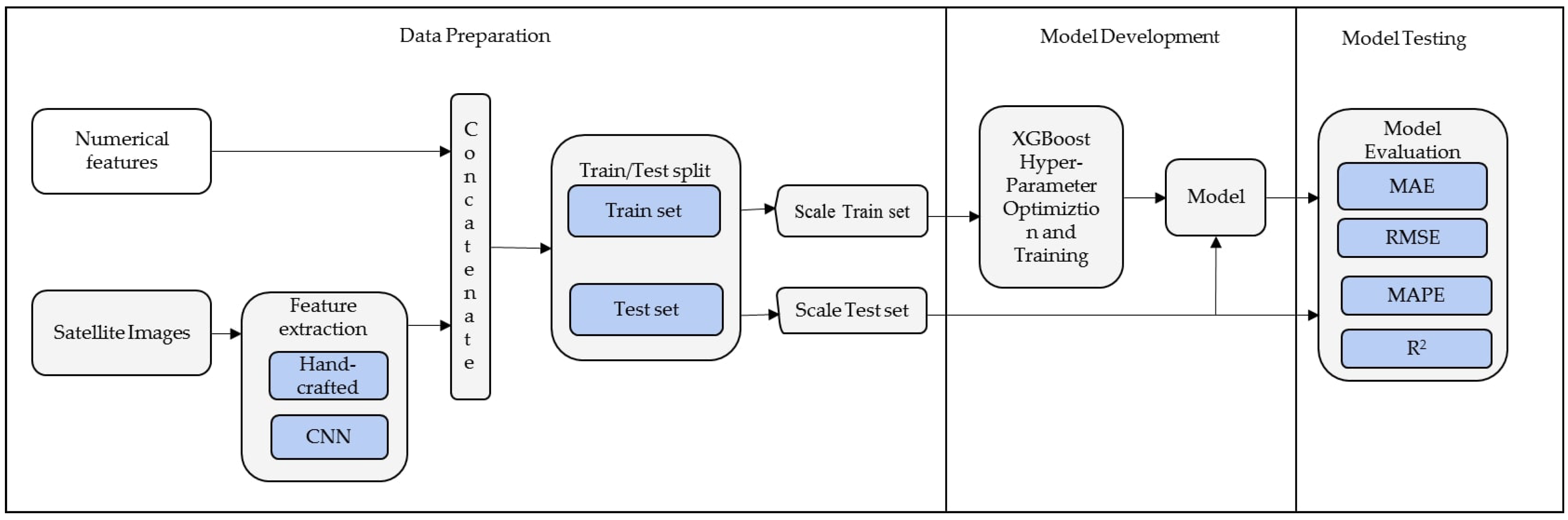
Figure 2 depicts the development process with three main phases; data preparation, model development and model testing.

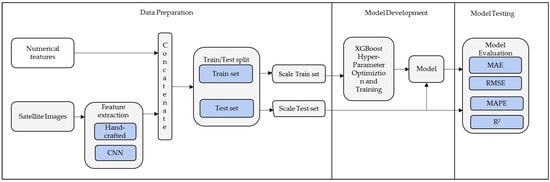
Figure 2. Model development process with three main phases; data preparation, model development, and model testing.

3.3.1. Data Preparation

In the data preparation phase, the features are extracted from satellite images using an algorithm. The extracted features are combined with the numerical features to form a new dataset. The new dataset is then split into the training set and test set with a ratio of 80:20. As a preprocessing step, the two sets of data were scaled with a standard scaler to eliminate magnitude difference amongst features, thereby improving generalization and reducing training time.

3.3.2. Model Development

In the model development phase, hyper-parameter optimization (HPO) was performed on the training set based on XGBoost with hyperband algorithm [41] and then model training was performed with the optimized hyper-parameters.

3.3.3. Model Testing

In this phase, ten different samplings of training and test sets splits were used to train and test an XGBoost fitted with the optimized hyper-parameters. For each of the training and test sets, model performance based on the test set is noted, and the average of the ten samplings was computed.

3.4. Feature Extraction Methods

The following hand-crafted feature extraction methods were applied to the tiled images: Local Binary Pattern (LBP), Histogram of Oriented Gradients (HOG), Gray Level Co-occurrence Matrix (GLCM), and Discrete wavelet transform (DWT). Combinations of GLCM features with other hand-crafted features were considered, as well as a combination of the hand-crafted features with CNN features. The feature extraction methods used are described as follows:

3.4.1. Local Binary Pattern (LBP)

In LBP, a pixel’s intensity is compared with other pixel’s intensities within its local neighborhood, from which a histogram of binary patterns is obtained [42]. It is a less complex texture extraction method that is invariant to rotation. Differences in pixel intensities are presented using a binary encoding method described in Equation (1).

$$LB{P}_{(P,R)}=\sum _{p=0}^{p-1}s(g_p-g_c)2^p$$

(1)

where $g_c$ is the center pixel, and $g_p$ is a neighborhood pixel, P stands for the number of neighbors, R is the neighborhood distance, and $s\left(x\right)$ is computed in Equation (2) and stands for the binary encoding.

$$s\left(x\right)=\left\{\begin{array}{cc}1\hfill & x\ge 0\hfill \\ 0\hfill & x<0\hfill \end{array}\right.$$

(2)

LBP features are computed from histograms of the binary encodings based on Equation (3), where $k=0,1,2,\dots ,K$, K is the maximum value in the computed $LB{P}_{(P,R)}$ within the image with dimension $(M,N)$, and $I\left(x\right)$ has a value of 1 when $LB{P}_{(P,R)})(i,j)=k$, and 0 otherwise. There are various types of LBP [43,44]. A uniform LBP with a p value of 3 and an R-value of 3 was considered in this work.

$$H\left(k\right)=\sum _{i=1}^M\sum _{j=1}^{N}I\left(LB{P}_{(P,R)}\right)(i,j))$$

(3)

3.4.2. Gray Level Co-Occurrence Matrix (GLCM)

In GLCM, a matrix $C(i,j)$ known as the co-occurrence matrix is computed by counting the co-occurrences in gray pixels that occur within a distance, d, and orientation, $\theta$, which takes any value between 0 and ${315}^{\circ }$ at ${45}^{\circ }$ intervals. Features can be extracted from the co-occurrence matrix as a form of dimensionality reduction, with Energy, Inertia, Correlation, Difference Moment, Entropy [45], Contrast, and Homogeneity [46], as the most commonly computed features. Many other features can also be extracted from the co-occurrence matrix [47]. A d value of 3 and a $\theta$ value of ${45}^{\circ }$ were used, with Contrast, Dissimilarity, Homogeneity, Angular Second Moment (ASM), Energy, and Correlation used as features.

3.4.3. Histogram of Oriented Gradients (HOG)

In HOG, each pixel’s magnitude and direction are computed from its x and y gradients. The image is then divided into cells, and histograms are computed for each cell based on gradient values. An aggregation of cells forms a block, and normalization is applied to each block. A combination of the normalized histograms from the blocks forms the HOG features [48]. In this work, the cells are 8 by 8 pixels, and tyebblocks are 2 by 2 cells. The number of orientation bins for the histogram is 9.

3.4.4. Discrete Wavelet Transform (DWT)

In DWT, data are decomposed into low pass L and high pass H components, yielding two sub-bands of $L/H=l_1,l_2,\dots ,l_{(}N/2),h_1,h_2,\dots ,h_2$. For a bidimensional image, decomposition is performed in the vertical and horizontal directions, resulting in four sub-bands. The formed sub-bands are Approximation, Horizontal, Vertical, and Diagonal details and are due to the combination of $LL$, $LH$, $HL$, and $HH$ filters, respectively. Statistical parameters can be computed from each sub-band to have a reduced feature set [43,47]. Methods such as the Line Measure Technique (LMT) [49] are also used to reduce the feature set. The mean, energy, standard deviation, and entropy of each sub-band were used as the extracted features in this work, summing to a total of 16 features.

3.4.5. Segmentation Fractal-Based Texture Analysis (SFTA)

SFTA is a two-staged feature extraction technique where, in the first stage, Two-Threshold Binary Decomposition (TTBD) is applied on a grayscale image to produce binary images. The Multilevel Otsu algorithm is used in TTBD to calculate some threshold values from the image’s gray level distribution. The algorithm first determines a threshold value that ensures that the image’s intra-class variance is minimized. This is applied to all regions of the image to obtain $n_t$ threshold values. Decomposition is carried out by the selection of pairs of threshold values and the application of a two-threshold segmentation, as shown in Equation (4) [50].

$$I_b(x,y)=\left\{\begin{array}{cc}1\hfill & t_1<I(x,y)\le t_u\hfill \\ 0\hfill & otherwise\hfill \end{array}\right.$$

(4)

$I(x,y)$ and $I_b(x,y)$ are pixel intensities of grayscale and binary images, respectively, at $(x,y)$ pixel position. $t_l$ and $t_u$ are the upper and lower threshold values. A total of $(n_t-1)$ binary images are produced based on the procedure. In addition, simple thresholding is applied to produce $n_t$ binary images summing up to $(2n_t-1)$ binary images. In the second step, three features are extracted from each binary image, namely, Area (A), Mean Gray Level (V), and Fractal Dimension (D). Area (A) represents the number of white pixels in the binary image, Mean Gray Level (V) is the average brightness of gray image pixel positions corresponding to white pixel positions in the binary image, and Fractal Dimension (D) is a measure of boundary complexity. A total of $(6n_t-3)$ features are extracted for an input image in SFTA [18]. An $n_t$ value of 8 was used, thereby extracting 45 features from each input image.

3.4.6. Convolutional Neural Networks (CNN)

A CNN is used to process data that is in grid form, such as an image. It is made up of three main layers, the convolutional layer, the pooling layer, and the fully connected layer. Feature extraction is performed at the convolutional and pooling layers, whereas the fully connected layer performs mappings between the extracted features and target values. The convolutional layer is made up of low-dimensional filters that are multiplied by the image pixels by sliding it from left to right and top to bottom based on a stride value. A stride is the number of skips in pixel values for the filter to slide across the image. Each convolutional layer is followed by activation, and the Rectified Linear Unit (ReLU) is commonly used because it is fast and gives a better generalization. The image dimension is reduced when passed through a convolutional layer. The pooling layer is for further dimension reduction to decrease training time and increase immunity against noise, thereby preventing overfitting. Pooling could be carried out by summing the pixel values within a small grid (Sum Pooling), averaging (Average Pooling), or finding the maximum value (Max Pooling). Convolution layers and pooling layers are stacked for feature extraction. The deeper the network, the more sophisticated the process of extracting features. The first convolutional layer extracts features such as lines and edges, and deeper layers extract more detailed information. The fully connected layer is made up of neurons, as in the case of a Multiple Layer Perceptron, where two or more layers could be stacked, with the last layer forming the output layer. Regularization techniques, such as image augmentation, dropout, and batch normalization, are used to improve the accuracy of CNN [51,52,53]. The CNN used in this work is made up of five convolutional layers with batch normalization, and maximum pooling applied after each layer. The output of the last max pooling layer is passed to a fully connected layer with 177 neurons from which the features are extracted. The number of filters in the five consecutive convolutional layers are 24, 38, 83, 98, and 199, respectively, with square filters of sizes 2, 4, 4, 4, and 3, respectively. The maximum pooling layers used are of size 2. The complexity of the CNN is less compared to those of pretrained networks such as VGG-16, ResNet50V2, InceptionV3, EfficientNetB0, and so on. It, therefore, trains faster and occupies less memory space.

3.5. Extreme Gradient Boosting (XGBoost)

XGBoost is an advanced Gradient Boosting with improvements in speed, efficiency, and scalability. It has produced high accuracy in various applications such as prediction of Type 2 diabetes risk [54], hot spots at protein–protein interfaces [55], sales forecasting [56], and has been used in solving various problems in Kaggle competitions [57]. Like any boosting algorithm, it is made up of Classification and Regression Trees (CART) as base learners. Sometimes, linear functions are also used as base learners. The base learners are fitted to minimize a loss function. The loss function determines how well the model performs, and it is minimized during training [58,59]. Minimization of the loss function is achieved through gradient descent [60]. In XGBoost, a regularization term is added to the loss function, and Taylor Series Expansion is used in approximating the modified loss function. Optimization of the tree structure is performed using an approximate greedy algorithm. XGBoost uses column subsampling such that portions of features are collected to grow trees, thereby minimizing overfitting and improving training speed. In addition, it uses a presorting technique and storing mechanism whereby datasets are stored in blocks, and the search for the best split is performed by scanning columns in a block. It also uses techniques such as Block Compression and Block Sharding for out-of-core computations and when fetching data from multiple drives, respectively, thereby enhancing the execution time [58,61]. The boosting system can be composed of normal trees, as in the case of Gradient Boosting, or the use of Dropouts meet Multiple Additive Regression Trees (DART). DART is a process whereby multiple numbers of regression trees are fitted at a low learning rate, and trees fitted earlier are maintained, whereas those fitted later are dropped in order to prevent overfitting [62]. In this work, the number of trees, learning rate, and type of booster were ascertained based on hyperband for each of the combinations of numeric features with one or two feature extraction methods used on the input image, as shown in Table 2.

Table 2. Hyper-parameters of XGBoost for combinations of numeric features and features from one or two feature extraction method(s).

Feature Extraction Method	Number of Trees	Learning Rate	Booster
No Image	248	0.2912	gbtree
LBP	209	0.2698	dart
HOG	260	0.1035	dart
GLCM	251	0.2644	gbtree
DWT	261	0.1375	gbtree
SFTA	202	0.1582	gbtree
GLCM + LBP	263	0.1649	dart
GLCM + HOG	287	0.1178	dart
GLCM + DWT	276	0.2807	dart
GLCM + SFTA	219	0.1994	dart
CNN	100	0.3000	gbtree
CNN + LBP	195	0.1704	dart
CNN + HOG	185	0.0436	dart
CNN + GLCM	293	0.0908	gbtree
CNN + DWT	209	0.0711	dart
CNN + SFTA	199	0.0997	gbtree

3.6. Performance Metrics

The performance metrics used in evaluating the performance of models include Mean Absolute Error (MAE), Root Mean Squared Error (RMSE), Mean Absolute Percentage Error (MAPE), and Coefficient of Determination ($R^2$) [63,64].

$$MAE=\frac{1}{N}\sum _{i=1}^N|P_{m\left(i\right)}-P_{p\left(i\right)}|$$

(5)

$$RMSE=\sqrt{\sum _{i=1}^N\frac{{(P_{m\left(i\right)}-P_{p\left(i\right)})}^2}{N}}$$

(6)

$$MAPE=\frac{100}{N}\sum _{i=1}^N\left|\frac{P_{m\left(i\right)}-P_{p\left(i\right)}}{P_{m\left(i\right)}}\right|$$

(7)

$$R^2=1-\frac{{\sum }_{i=1}^N{(P_{m\left(i\right)}-P_{p\left(i\right)})}^2}{{\sum }_{i=1}^N{(P_{m\left(i\right)}-\overline{P_p})}^2}$$

(8)

$P_m$ is the measured path loss, $P_p$ is the predicted path loss, $\overline{P_p}$ is the mean of predicted path loss values, and N is the number of samples.

4. Result and Discussions

The performance metrics of each model resulting from a combination of non-image features merged with features from one or two feature extraction techniques applied to the images are shown in Table 3. Amongst the hand-crafted features, GLCM had the lowest error metrics and the highest coefficient of determination, but its accuracy is below the case in which no image features were used. The combination of GLCM features with other hand-crafted features further decreased the accuracy below that of GLCM features. The addition of hand-crafted features led to a reduction in accuracy when compared to using only non-image features, as shown by the performance metrics as well as the last column of Table 3, indicating a percentage improvement over using only non-image features. Negative values were observed as percentage improvements, indicating a reduction in performance. However, even with the reduction in performance in models with hand-crafted features, they are expected to perform better when tested with data from a site not used in model training. This is because the model trained with the hand-crafted features has some knowledge of the environments. The performance when CNN-extracted features were used was better than when features extracted based on any of the hand-crafted techniques were used. A combination of CNN features with any hand-crafted feature extraction methods decreased the accuracy compared to when CNN features were used alone, except in the case of LBP and GLCM, where an increase was observed. A combination of CNN-extracted features with GLCM features (CNN + GLCM) had the highest overall accuracy with an $R^2$ of 0.9372, seconded by a combination of CNN with LBP (CNN + LBP) with an $R^2$ of 0.9364 and were ahead of CNN features $\left(R^2=0.9357\right)$. The RMSE value of 3.6682 dB when CNN + GLCM features were used is an indication that the model’s performance is acceptable as it is below the maximum allowed value. The acceptable RMSE for a path loss model is a value less than 7 dB in an urban environment and any value less than 15 dB in suburban and rural environments [65]. The RMSE value achieved is an improvement over the results in [11] with an RMSE of 8.27 dB, [17], 6.8944 dB, [12], 4.4286 dB, [29], 7.61 dB, and [66], 3.89 dB.

Table 3. XGBoost performance on combinations of numeric features and features from one or two feature extraction method(s).

Feature Extraction Method	MAE (dB)	RMSE (dB)	MAPE (%)	${\mathit{R}}^2$	% Improvement
No Image	2.9862	4.0500	2.2985	0.9227	NA
LBP	3.1914	4.2985	2.4589	0.9137	−6.1358
HOG	3.4590	4.7434	2.6751	0.8949	−17.1210
GLCM	3.0964	4.1616	2.3852	0.9191	−2.7557
DWT	3.2247	4.3281	2.4897	0.9125	−6.8667
SFTA	3.2831	4.4040	2.5312	0.9094	−8.7407
GLCM + LBP	3.2035	4.3003	2.4709	0.9136	−6.1803
GLCM + HOG	3.4347	4.7172	2.6530	0.8961	−16.4741
GLCM + DWT	3.2049	4.3393	2.4688	0.9120	−7.1432
GLCM + SFTA	3.2309	4.3358	2.4880	0.9123	−7.0568
CNN	2.6268	3.7106	2.0324	0.9357	8.3802
CNN + LBP	2.6129	3.6909	2.0208	0.9364	8.8667
CNN + HOG	2.7698	4.1205	2.1484	0.9207	−1.7407
CNN + GLCM	2.5848	3.6682	2.0013	0.9372	9.4272
CNN + DWT	2.6305	3.7882	2.0394	0.9329	6.4642
CNN + SFTA	2.6303	3.7655	2.0368	0.9338	7.0247

The results indicated that the hand-crafted features and their combinations could not compete with CNN for feature extraction. As such, the requirement of training a CNN that needs a large volume of data and training time still holds as CNN-extracted features cannot be replaced by hand-crafted features due to the low accuracy of the hand-crafted features. However, the addition of LBP or GLCM features to the CNN features improved model accuracy over CNN features alone. However, since a combination of CNN and GLCM features had the highest improvement; they are recommended for use in this application. Meanwhile, the architecture of the CNN used resulted in an 18-fold speed over the ResNet50V2 used in [16] as it trained in 29.8242 min while the ResNet50V2 trained in 546.5685 min. In addition, a reduction in the RMSE value of 0.7604 dB was observed compared to the results in [16]. Compared to models based on diffraction that require the complete path profile from transmitter to receiver, such as the Walfisch Ikegami and Walfisch Bertoni, the proposed model is cost-effective and saves time as it does not require the additional measurement of parameters such as building heights and street width. In addition, ML models have accuracies better than such models, as seen in [6,67,68] because ML models do capture non-linear relationships.

Deterministic models, which also use the complete profile from transmitter to receiver, as well as the principles of wave transmission, such as reflection, refraction, diffraction, and shadowing, have high computational complexity and are very slow. With the proposed method, predictions are made instantly from the trained model, and the model can be used for similar environments. Meanwhile, in the case of deterministic models, each environment has to undergo the process of computation.

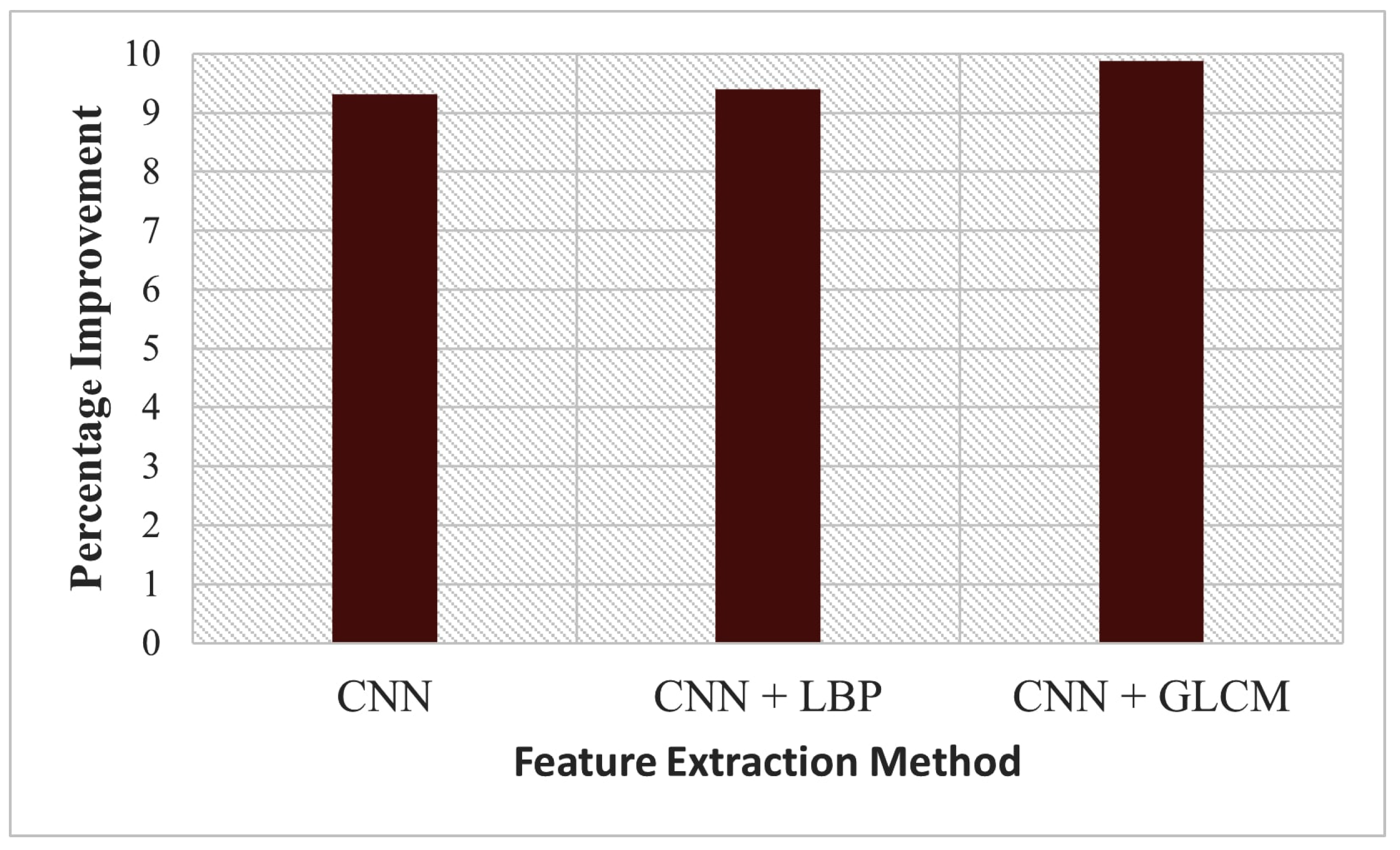
Figure 3 shows the percentage improvement calculated from RMSE values when either CNN, CNN + LBP, or CNN + GLCM features were used in combination with numeric features over when numeric features were used alone. The addition of CNN + GLCM features to the numeric features had the highest improvement of 9.4272%, followed by the addition of CNN + LBP, which resulted in 8.8667%, and lastly, the addition of CNN features improved it by 8.3802%, as shown in line Table 3.

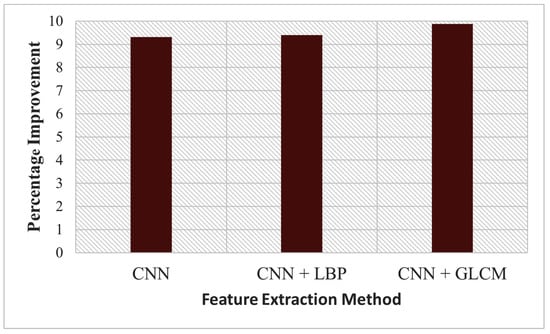
Figure 3. Percentage improvement over non use of images for the top three feature extraction methods; CNN, CNN + LBP, and CNN + GLCM.

4.1. Comparison of XGBoost with Other Algorithms

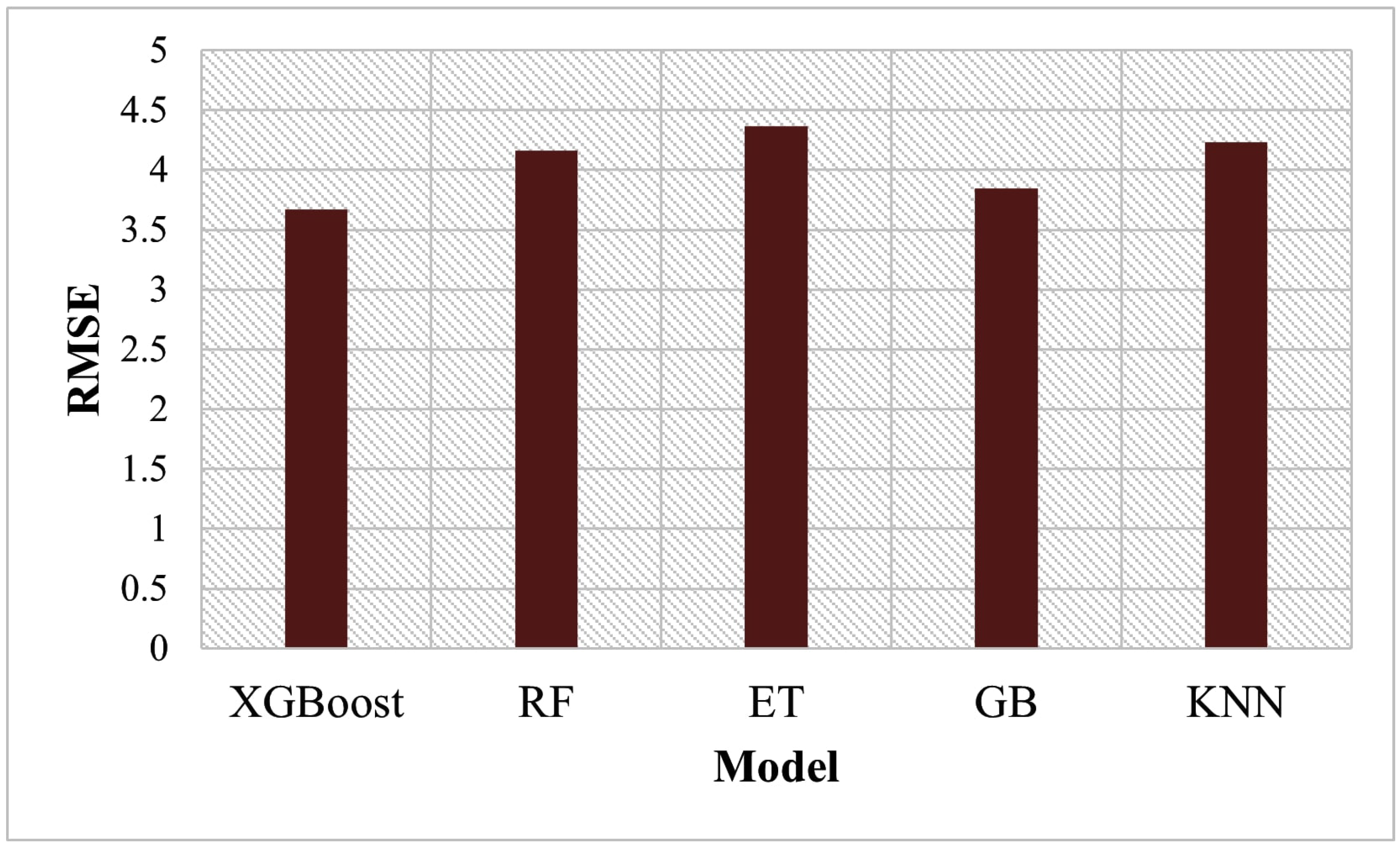
The best features observed were a combination of the numeric features and features extracted using GLCM and CNN. Four other models were developed based on the features using different algorithms, and the performances of the models were compared with XGBoost. The algorithms considered are Random Forest (RF), Extreme Learning Trees (ET), Gradient Boosting (GB), and K Nearest Neighbor (KNN), with hyper-parameter optimization conducted in each case. The average RMSE of each algorithm is presented in Figure 4. It is observed that XGBoost (together with CNN and GLCM extracted features and numeric features) had the lowest RMSE, followed by GB, and ET had the highest value. XGBoost was better because of the regularization term added to its loss function and the column subsampling technique employed in it, which minimizes overfitting. ET had the least performance because it does not employ any optimization process for the determination of splits; rather it chooses the splits randomly.

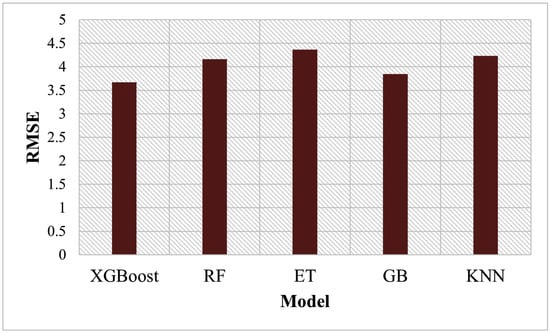
Figure 4. RMSE values of the ML models for a combination of CNN + GLCM features and non-image features.

4.2. Feature Importance

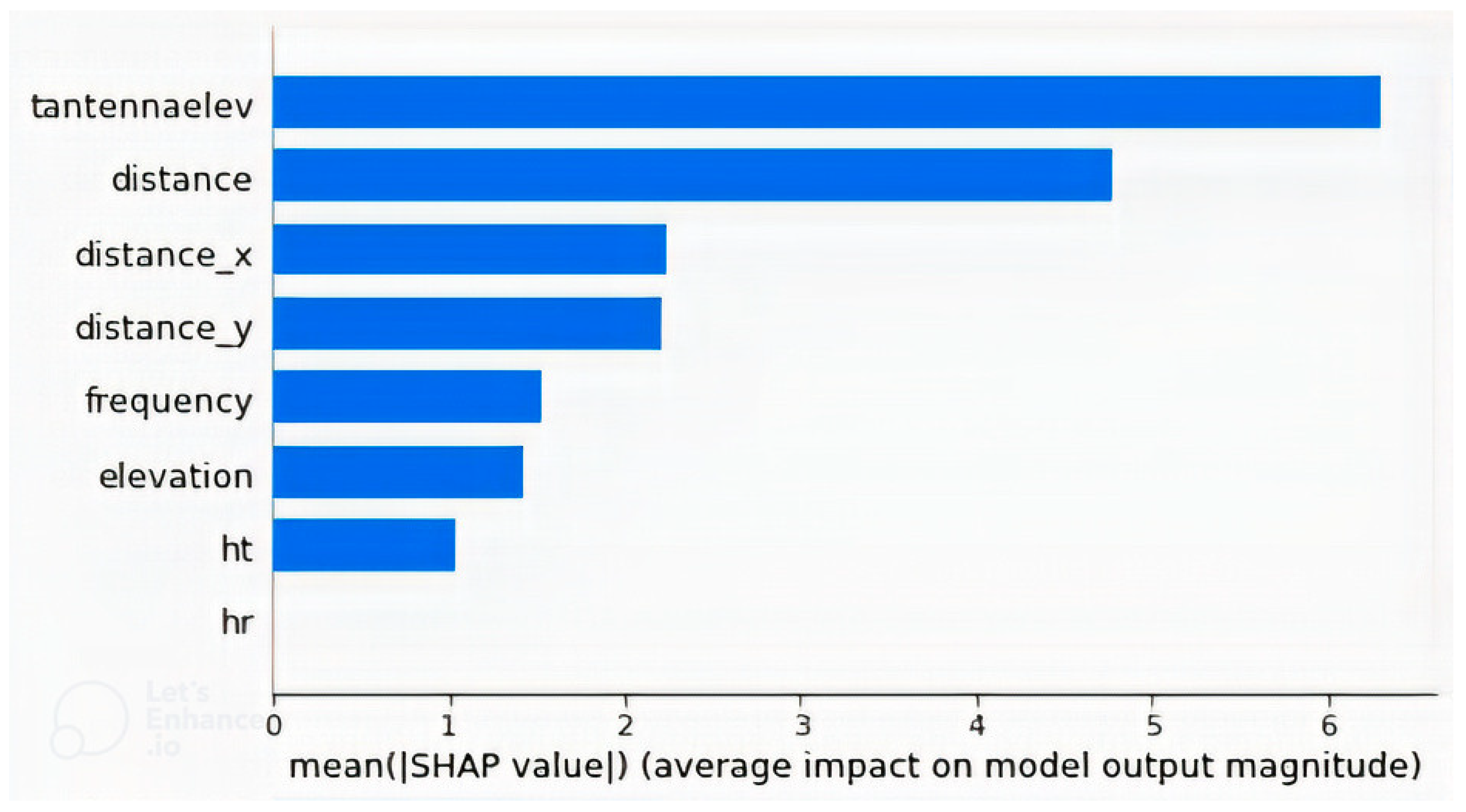
Feature importance of the best model (with CNN + GLCM features), as well as the model that has only non-image features, were determined based on the Shapley Additive Explanations (SHAP). SHAP is a method for interpreting ML models, based on a combination of game theory, Shapley values, and some conditional expectations to compute the importance of each feature [69]. Figure 5, Figure 6, Figure 7 and Figure 8 present explanations of the model with non-image features only. Figure 5 shows the mean importance of each feature, with “tantennaelev” having the highest importance. Next to it is “distance”, as expected, because it is well established that path loss varies with distance. However, “tantennaelev” had the highest impact on the model output because studies have shown that apart from distance, the elevation of a position affects path loss at that position due to variations in height difference between the transmitting and receiving antennas. Thus, for a multiple antenna path loss model, it is wise to include the elevation of the transmitting and receiving antenna positions so that their height difference effect is captured. The “tantennaelev” had an importance that superseded that of “distance” because it was observed by Jimoh et al. [70] that elevation affects path loss to the extent that a position at a further distance from the transmitting antenna but at a high elevation could have lower path loss values than a position closer to the transmitting antenna but at a low elevation. The third and fourth most important features are distances in latitude and longitude, and then the height of the receiving antenna (hr) had the least importance.

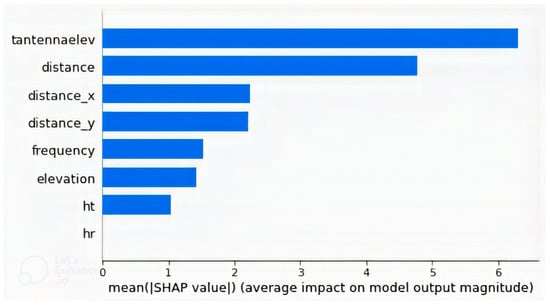
Figure 5. Mean feature importances of the model with non-image features only, with “tantennaelev” having the highest importance and “hr” the least.

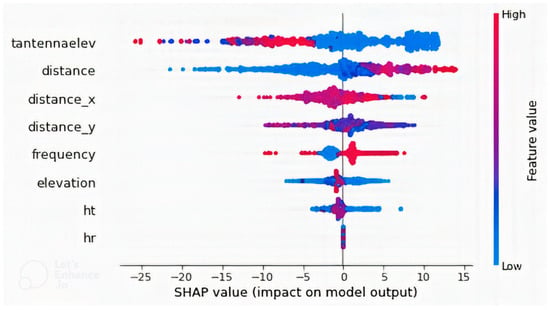
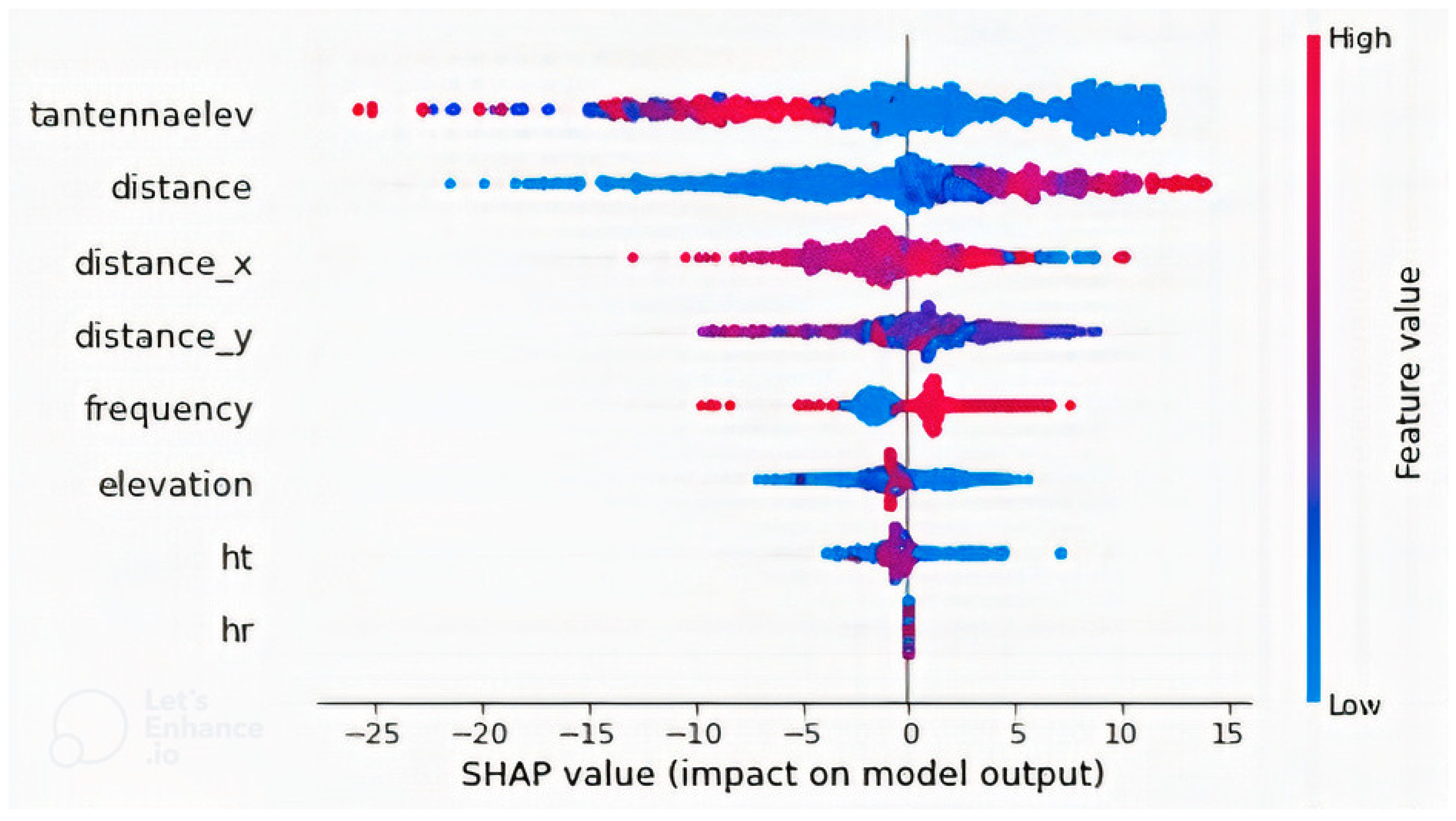
Figure 6. SHAP summary plot of the model with non-image features only, showing the variations in feature values with output path loss value.

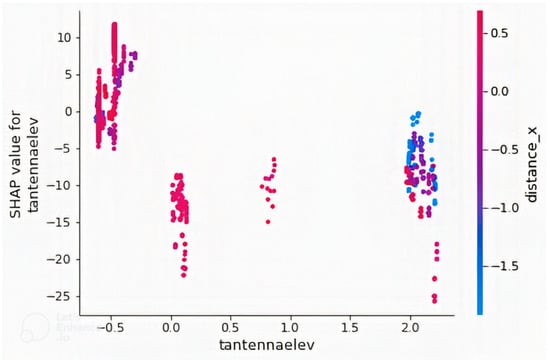
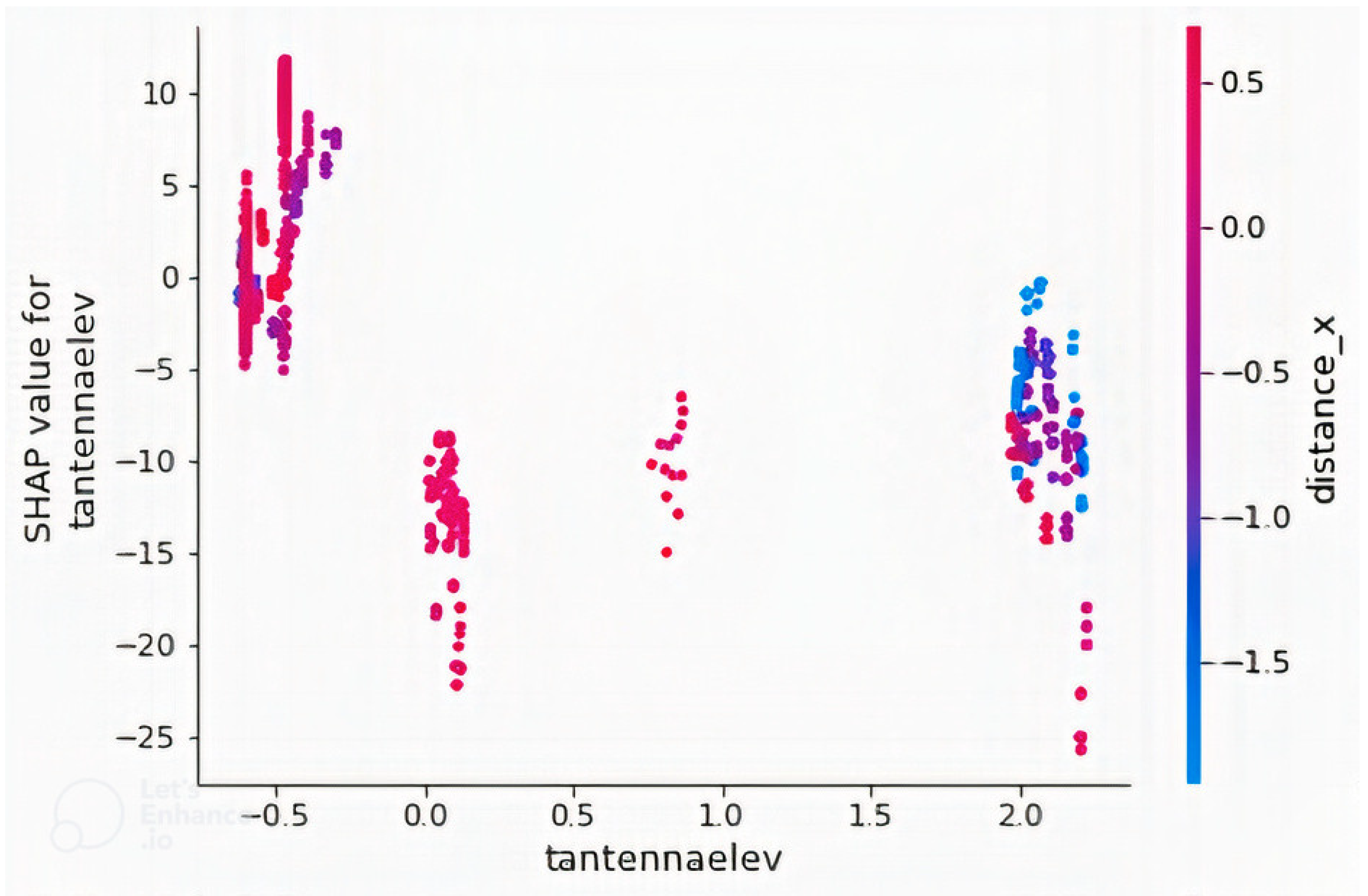
Figure 7. Dependence plot of the feature “tantennaelev” in a model with non-image features only with the feature “distance_x”. Feature “tantennaelev” has the highest interaction index with “distance_x”.

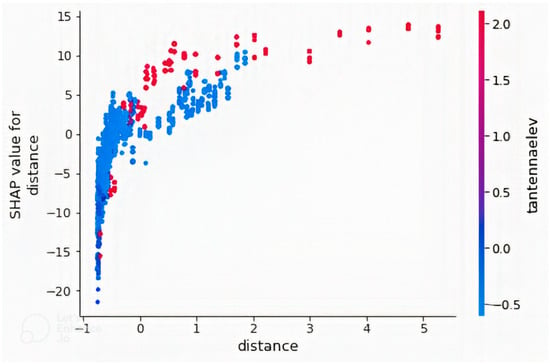
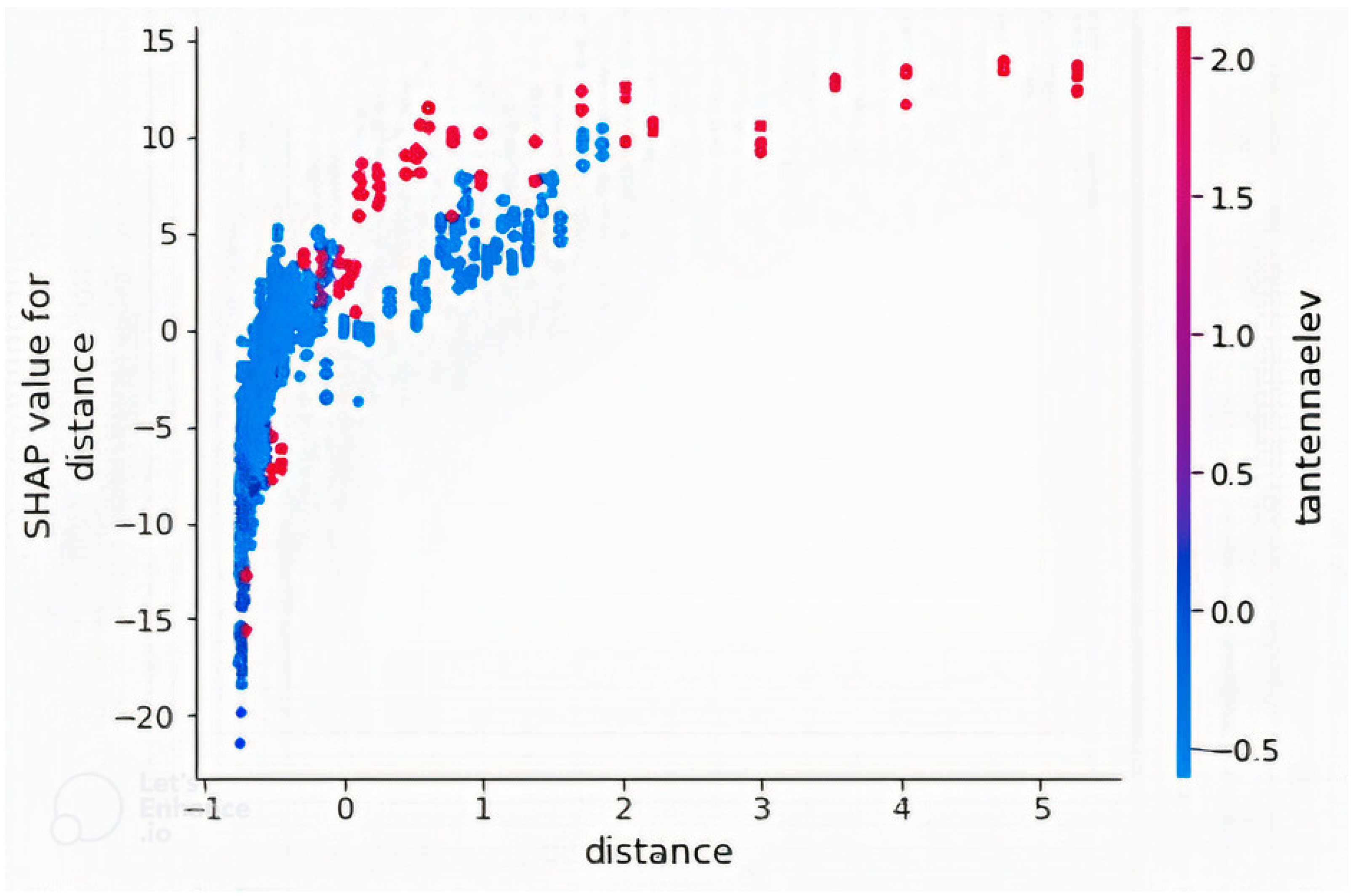
Figure 8. Dependence plot of the feature “distance” in a model with non-image features only with feature “tantennaelev”. Feature “distance” has the highest interaction index with “tantennaelev”.

Figure 6 shows the detailed explanations of the features, with the position of the dots with respect to the horizontal axis showing SHAP values that determine whether the path loss is high or low, and the color indicating the feature value. Positive SHAP values mean that the feature has a positive impact on path loss and negative means it has a negative impact. The results show that for higher values of “tantennaelev”, the path loss value is low, but for lower feature values, the output is high, though with a few instances where the output is low at lower values of “tantennaelev”. This is because the higher the elevation of the transmitting antenna, the wider the signal coverage; therefore, path loss decreases for the distance concerned. Likewise, the lower the elevation, the smaller the coverage, and the higher the path loss values. The fewer points where the low output values were observed might be due to irregularities in elevations of the receiver position as well as clutter. In the case of “distance”, it is observed that at lower distances, the path loss values are low and high at higher distances. Some minor instances in which the linearity is violated are due to the effect of other features. However, not only does the difference between transmitting and receiving antenna altitude (height + elevation) affect the signal coverage. Other antenna parameters such as azimuth and tilt also affect the signal coverage, but the study of their effects is beyond the scope of this work.

The difference in latitude between the transmitting and receiving antenna and that of longitude (distance_x and distance_y) were observed to push path loss values high and moderate, respectively. Higher “frequency” values pushed the path loss values higher as expected, the moderately low values pushed it low, and afew instances in the lowest frequency values pushed the path loss high due to the effect of other factors, such as elevation and/or clutter. The features “elevation” and height of the receiving antenna (ht) were observed to push the path loss values low when they are high or extremely low, whereas the upper part of their low values increased path loss values. This could be due to situations when the transmitting antenna is at a higher elevation.

Dependence plots of the two most important features (tantennaelev and distance) were plotted. Figure 7 shows that “tantennaelev” has some interactions with “distance_x”. Therefore, the effect of “tantennaelev” on path loss is dependent on “distance_x” value. The realization that “distance_x” has interaction with “tantennaelev” is based on the computation of the approximate interaction index between the features, from which the value between “tantennaelev” and “distance_x” was the highest. Confirmation of the presence of interaction is based on the presence of some vertical color patterns. Conclusions about the interactions of these variables cannot be made based on the plot because the data used are not a representation of all latitude and longitude positions on earth. Figure 8 is the dependence plot of “distance”, showing how path loss increases with increasing distance. The presence of vertical color patterns within the plot around the start values of distance indicates an interaction between the features “distance” and “tantennaelev”. As mentioned earlier, path loss at a distance is dependent on elevation. Therefore, path loss at the same distance but different elevation values are unequal.

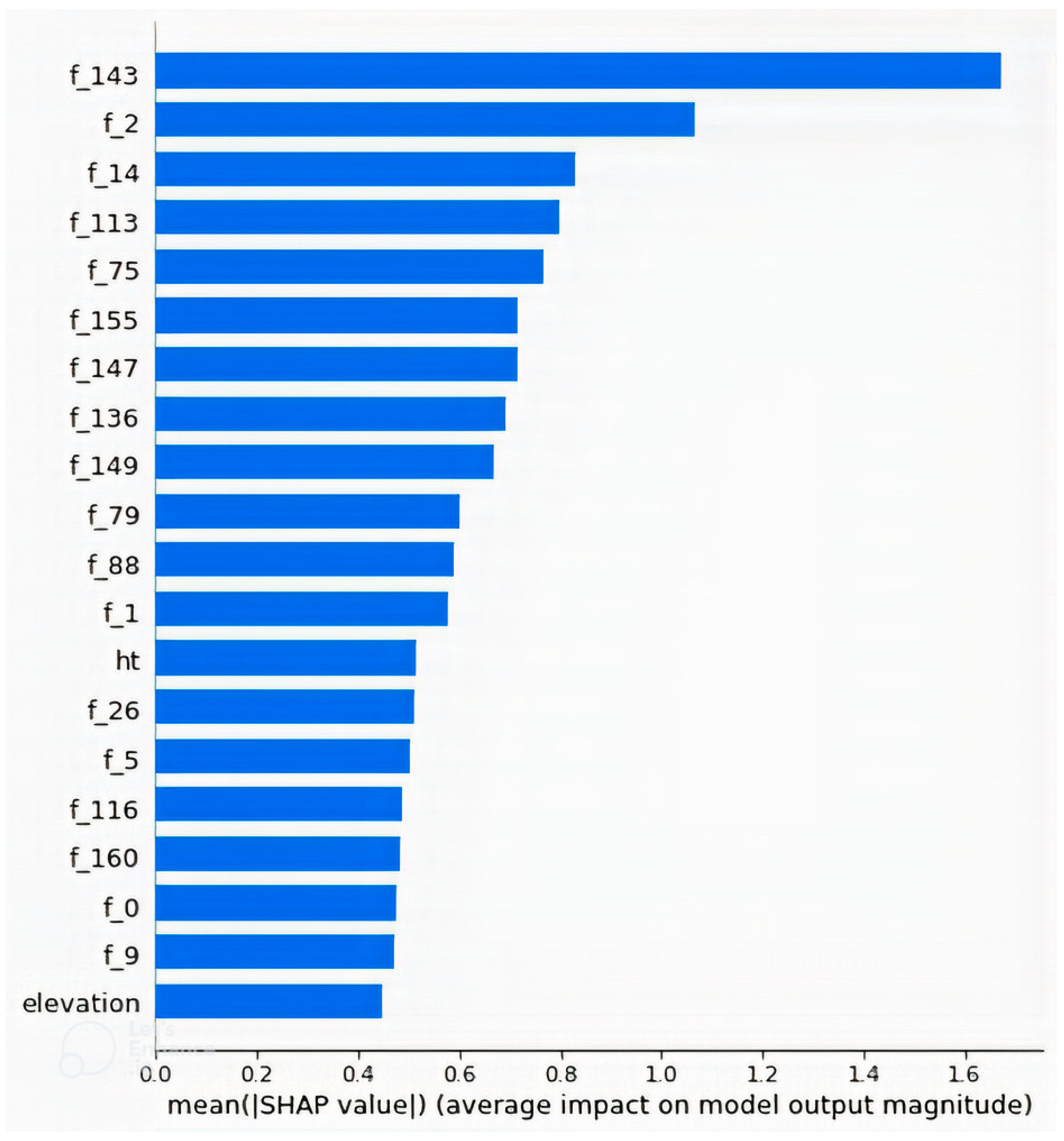
Figure 9 shows the 20 topmost features in terms of mean importance in the model that had non-image inputs as well as combinations of features extracted using CNN and GLCM from the images. Features named “f_x” are the features extracted by the CNN, where x takes values from 0 to 176. It is observed that the 144th feature ”f_143“ had the highest importance, followed by the third, “f_2”. Only two of the non-image features appeared in the top 20, with the height of the transmitting antenna (ht) appearing as the 13th and elevation as the 20th. The most important features are the image features extracted using CNN, and none of the GLCM features appeared in the top 20. Unlike in the case of the non-image input model, where “ht” and “elevation” were the last two, in this case, they were the first two because, in the non-image input model, the model was developed without consideration of environmental factors, and its explanation was similar to that of existing empirical models. The inclusion of features of the satellite images enhances the model’s ability to differentiate between environments. The model is well fitted to differentiate between the environments based on the importance it gives to the extracted features.

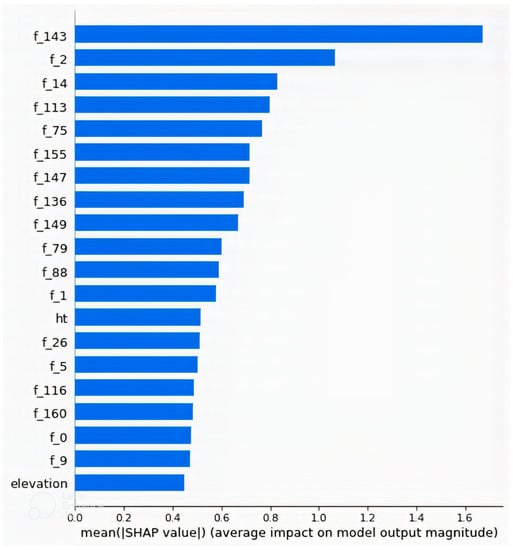
Figure 9. Mean feature importances of the top 20 features in the model with a combination of non-image features and CNN + GLCM features. “f_143”, which is a CNN-extracted feature, has the highest importance, while “elevation”, which stands for elevation at receiving antenna position, has the least importance among them.

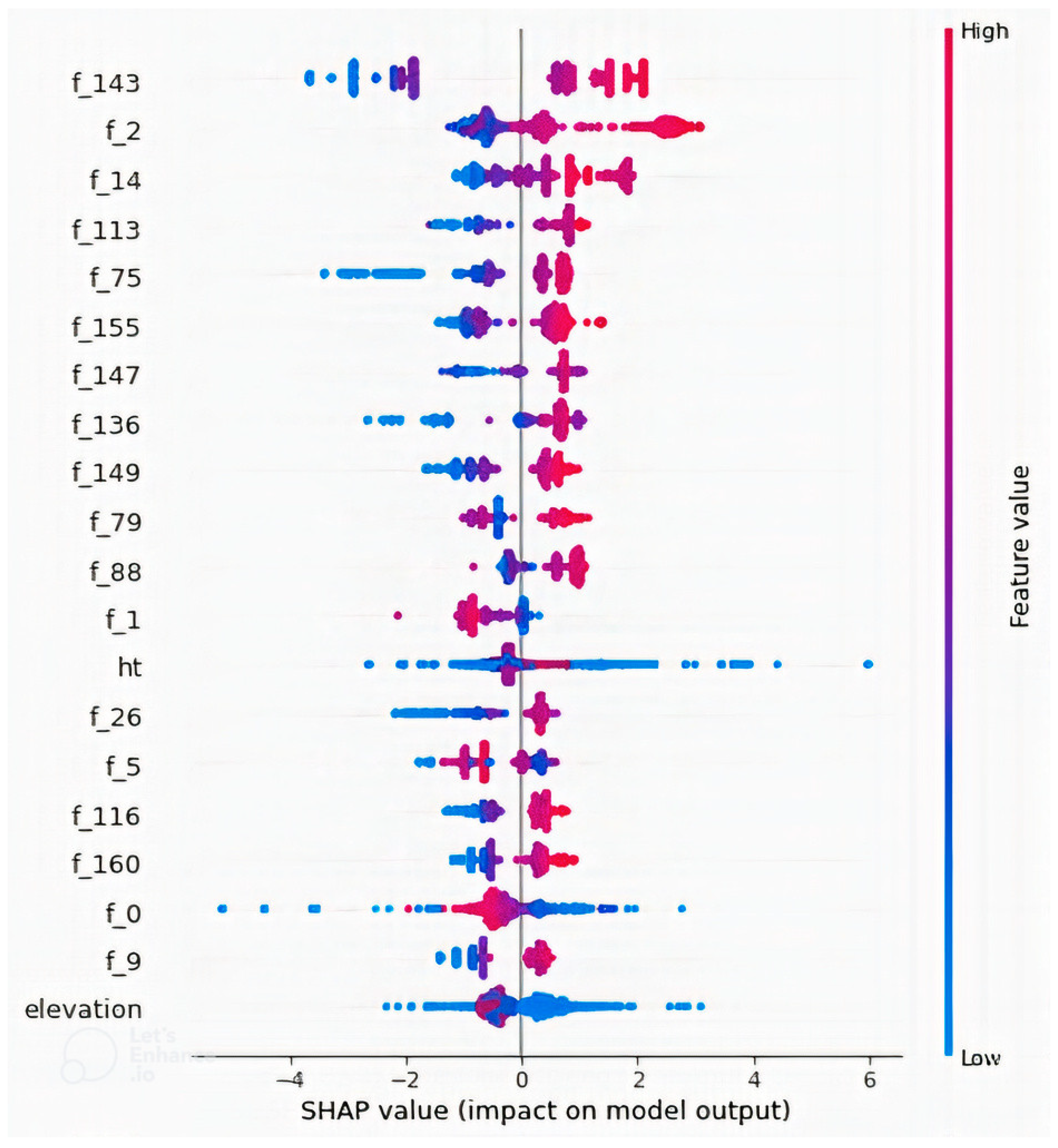
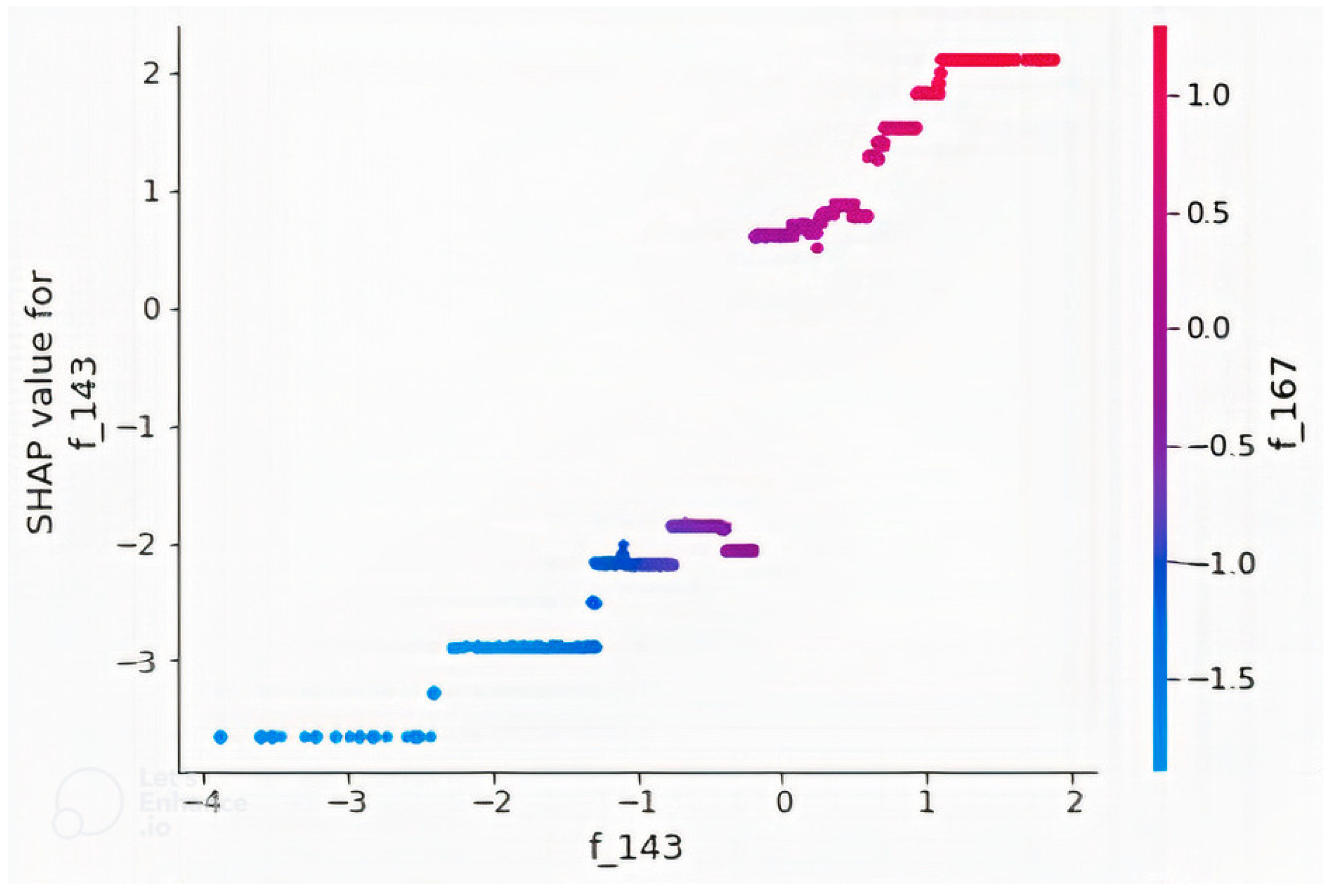
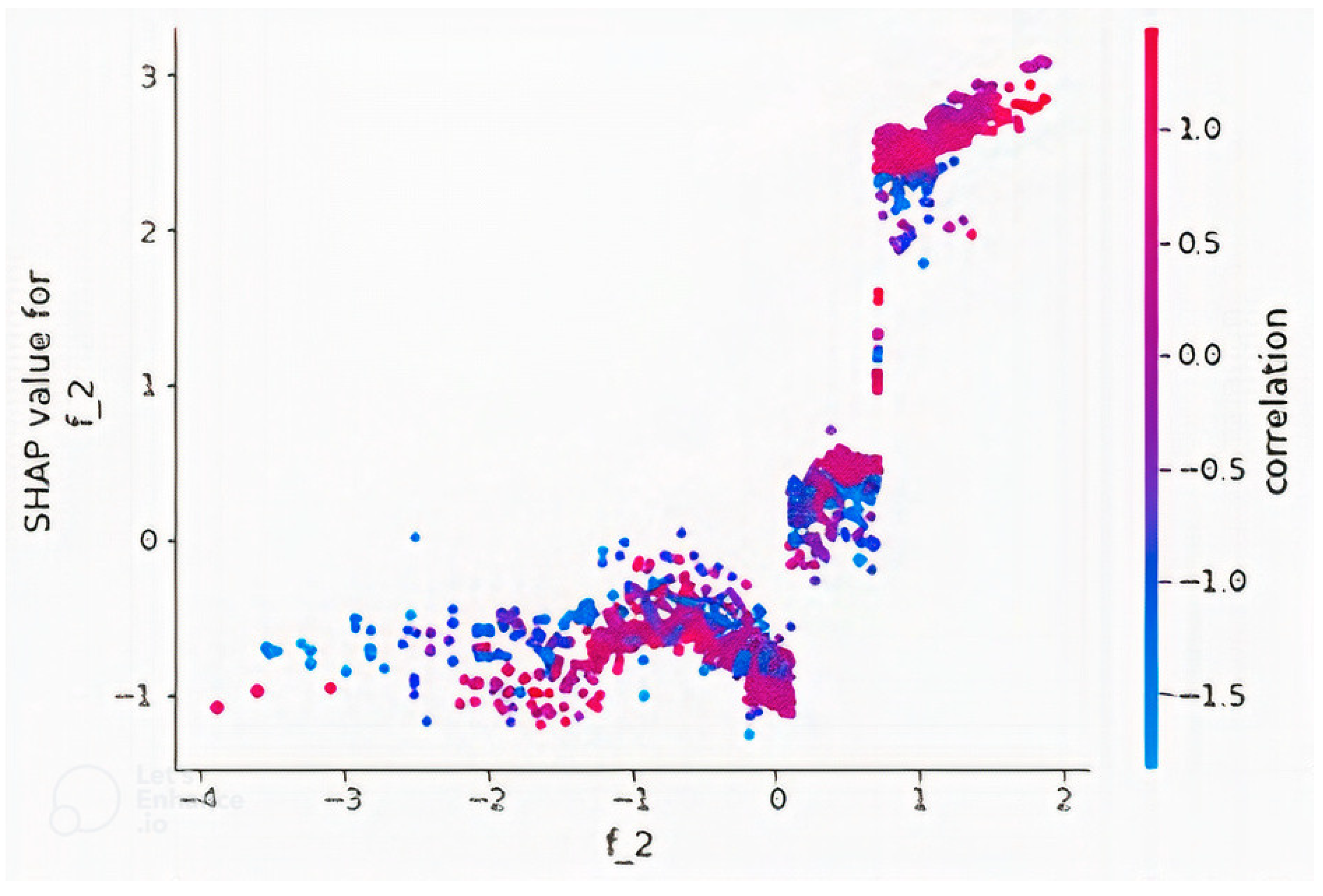
Figure 10 is a summary plot of the 20 most important features. It was observed that higher values of the CNN features produce higher path loss values, and lower values produce lower path loss values, with the exceptions of “f_0” and “f_1”. However, the features were extracted by a CNN, and the reason for this behavior cannot be explained as the features are not physical quantities and were not generated by a known equation but a black box model, unlike other quantities such as “distance” and “elevation” that are physical quantities. However, it is clearly seen that predicted path loss is dependent on these extracted features. Similarly, dependence plots for features “f_143” and “f_2” are presented in Figure 11 and Figure 12, respectively. Figure 11 showed that “f_143” had the highest approximate interaction index with “f_167”, and it was observed that as “f_143” increased, “f_167” also increased, as well as path loss but in a stepwise fashion without interactions even though their partial interaction index is the highest. The pair of feature “f_2” as shown in Figure 12 is “correlation”, which is a GLCM feature. Interactions were found between the variables due to the presence of vertical color patterns, and different portions of the plots show different combination rules that determine path loss values. The vertical color patterns indicate that for the same “f_2” value, the path loss value differs depending on the value of “correlation”. More of such relationships between features could be observed if the dependence plot of the remaining features is plotted. The concept of feature interaction can be explained by Equation (9), where y depends on two variables $x_1$ and $x_2$

$$y={\beta }_0+{\beta }_1{x}_1+{\beta }_2{x}_2+{\beta }_3{x}_1{x}_2+error$$

(9)

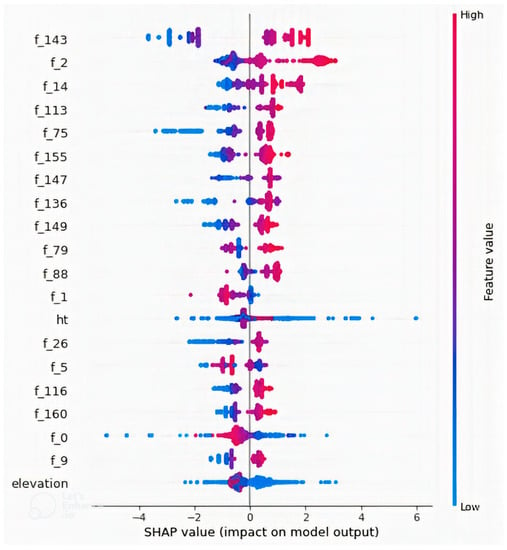
Figure 10. SHAP summary plot of the 20 most important features in the model developed with a combination of non-image features and CNN + GLCM features. It shows the variations in feature values with output path loss value.

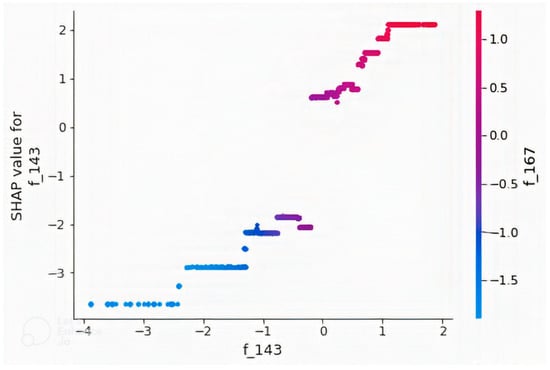
Figure 11. Dependence plot of the feature “f_143” in the model developed with a combination of non-image features and CNN + GLCM features. Feature ”f_143“ has the highest interaction index with ”f_167“.

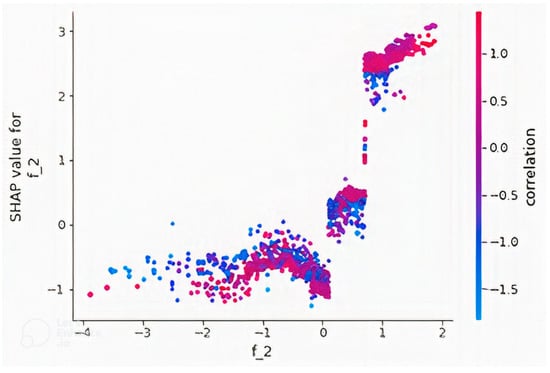
Figure 12. Dependence plot of the feature “f_2” in the model developed with a combination of non-image features and CNN + GLCM features. Feature ”f_2“ has the highest interaction index with the GLCM feature “correlation”.

${\beta }_0$ is an average response, ${\beta }_1$ and ${\beta }_2$ define contributions of features $x_1$ and $x_2$, respectively, and ${\beta }_3$ defines the combined contributions of $x_1$ and $x_2$ beyond their individual explanations alone. Random variations in the values unexplained by the remaining part of the equation are represented by the error term. Thus, the interaction between two features such as “f_2” and “correlation” can be combined and included in an explainable model similar to the ${\beta }_3$$x_1$$x_2$ term in Equation (9) by replacing $x_1$ and $x_2$ with ”f_2“ and ”correlation“, and the dependent variable y with path loss. Further analysis of interactions between the features could result in a glass box path loss model in a form similar to Equation (9) that gives an explanation of how the path loss values are calculated, unlike ML models that are black box models [71,72].

5. Conclusions

A path loss model with a good prediction accuracy is required for the determination of wireless network parameters such as transmitting power, cell radius, antenna height, number of cell sites, and their optimal position. The attainment of the required data rate is dependent on the proper setting of the parameters such that there is good signal coverage and no interference. The dependency of path loss on the environment led to the inclusion of satellite images of network location in developing machine learning path loss models such that the influence of the environment is learned. A path loss predictive model that handles multiple frequencies, multiple antenna heights, and multiple environments were developed in this work. The model takes in a combination of numeric features and features extracted from satellite images to make the path loss prediction. XGBoost was the algorithm used in model development and was selected based on its good performance in several applications. Several hand-crafted feature extraction methods, their combinations, or combinations of hand-crafted features and CNN features, were tested. The hand-crafted feature extraction methods included LBP, HOG, GLCM, DWT, and SFTA. None of the hand-crafted features improved accuracy compared with using numeric features alone; instead, the accuracy was reduced. Combining GLCM with any of the hand-crafted feature extraction methods decreased performance below that of GLCM features. When CNN features were combined with any of the hand-crafted feature extraction methods, combinations with LBP or GLCM resulted in accuracies better than that of CNN features. A combination of CNN and GLCM features from the images had the best performance overall. This resulted in a 9.4272% improvement in RMSE for combined environments over when no satellite image features were used in model development. A comparison was performed to evaluate the performance of other ML algorithms on the combination of numeric, GLCM, and CNN features. Random Forest, Extreme Learning Trees, Gradient Boosting, and K Nearest Neighbor were used for this purpose. XGBoost had the best performance metrics and also has an advantage of a fast training time over them. Features extracted using CNN were observed to have the highest impact on the model’s output based on SHAP. Although the model’s accuracy is good, there is a need for more training data from different environments and network parameters such that a single model can be developed and used for pre-network deployment path loss prediction. Meanwhile, the study demonstrated the possibility of developing such a model because an RMSE value of 3.6682 dB was obtained when combined data were used. This RMSE value is acceptable for a path loss model as it is below 7 dB. In our future work, the model’s performance for the different sub-datasets will be explored, and methods for improving the accuracy of sub-datasets with low accuracy will be addressed.