A Novel Variational Bayesian Method with Unknown Noise for Underwater INS/DVL/USBL Localization
Abstract
1. Introduction
- (1)
- To accurately describe underwater noise, the IW distribution and mixing probability vectors are introduced, and the state transition and the measurement process are derived as hierarchical Gaussian models.
- (2)
- To acquire the optimal position estimation, the IW-VACKF is proposed by using the VB method and cubature sampling rule.
- (3)
- The proposed IW-VACKF has been successfully validated in practical experiments, demonstrating superior performance in enhancing the accuracy and robustness of multi-sensor integrated navigation systems under complex underwater environments.
2. Problems Model and Cubature Kalman Filter
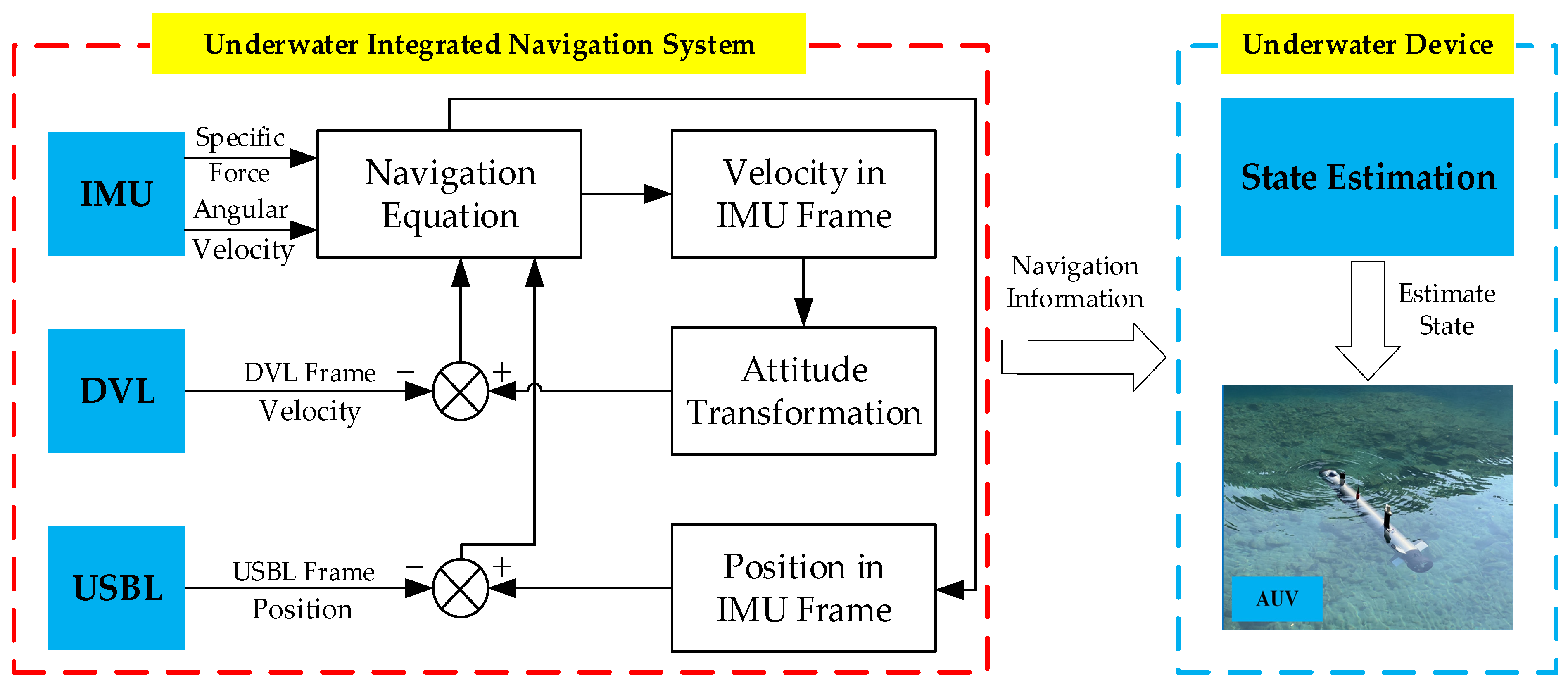
2.1. State-Space Model for INS/DVL/USBL Integrated Navigation
2.2. Cubature Kalman Filter
- (1)
- Time update
- (2)
- Measurement update
3. Inverse Wishart-Based Prior Modeling of System Noise
3.1. Measurement Likelihood PDF
3.2. State Transition Likelihood PDF
4. The Proposed IW-VACKF
4.1. VB Method
4.2. Joint Inference
| Algorithm 1: Time recursion of IW-VACKF |
| Inputs: , , , , , , , , , , , , , , , Time update (1) Calculate and based on cubature sampling rule according to Equations (3)–(6) (2) Update , , by using Equation (25) Measurement update: (3) Initialization: , , , , , for (4) Calculate and by Equations (27)–(29) (5) Update and according to Equation (40) (6) Calculate and employing Equations (32) and (33) (7) Update , , based on Equation (39) (8) Renew the mixing probability vector by Equation (35) (9) Calculate by Equation (41) (10) Renew the concentration parameter vector according to Equation (37) (11) Update and according to Equation (41) (12) If or , iteration is finished end for (13) , , , , , , Outputs: , , , , , , . |
4.3. Discussions
- (1)
- Parameter Selection
- (2)
- Theoretical Advantages and Computational Complexity
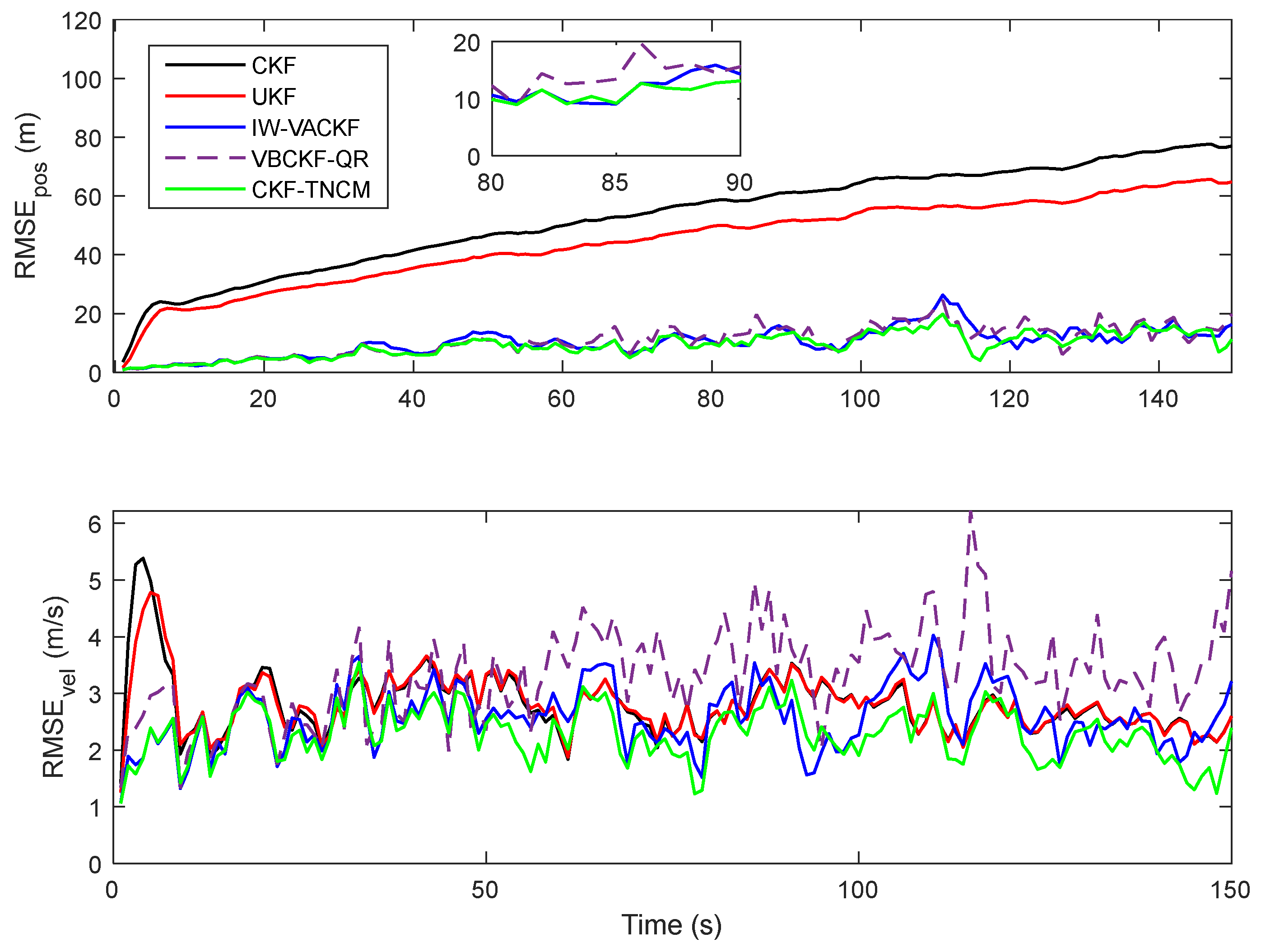
5. Simulation and Experimental Verification
5.1. Simulation Test
- where is the scale factors selected as ; q is an adjust factor for the system state noise strength. In this simulation, by adjusting the factor q, the estimation consistency is verified under different state noise value. T = 150 s is the total simulation time. The measurement process is shown as follows:
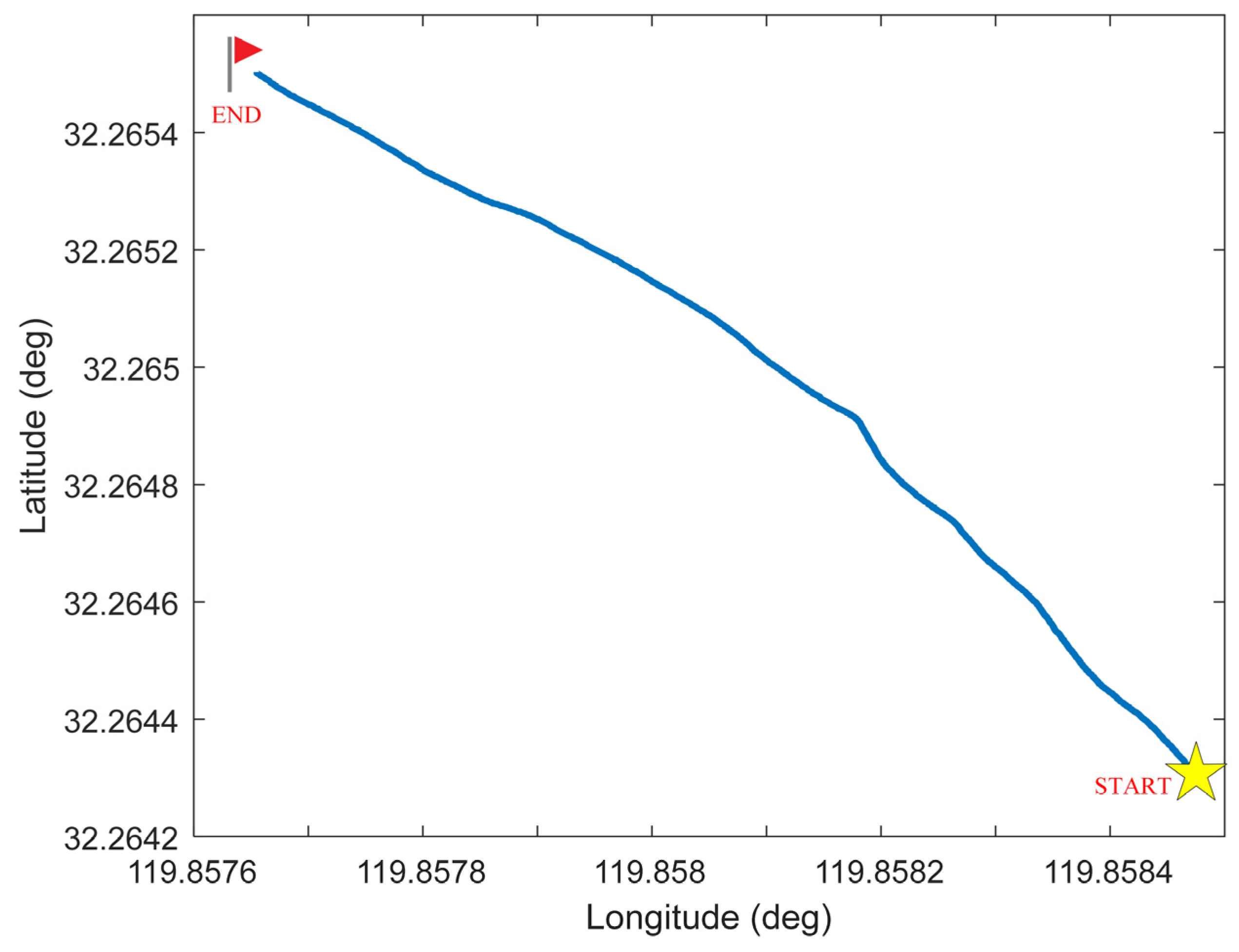
5.2. Experimental Verification on Underwater Vehicle
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- He, H.; Zhu, B.; Tian, G.; Mao, N.; Yu, Y.; Ye, Y. Robust Adaptive SINS/DVL Initial Alignment Method Based on Variational Bayesian Information Filter. IEEE Sens. J. 2024, 24, 6733–6742. [Google Scholar]
- He, X.; Wang, M.; Tang, J.; Wang, B.; Huang, H. A Novel Partitioned Matrix-based Parameter Update Method Embedded in Variational Bayesian For Underwater Positioning. IET Control Theory Appl. 2022, 16, 414–428. [Google Scholar] [CrossRef]
- Huang, H.; Tang, T.; Liu, C.; Zhang, B.; Wang, B. Variational Bayesian-Based Filter For Inaccurate Input in Unwater Navigation. IEEE Trans. Veh. Technol. 2021, 70, 8441–8452. [Google Scholar] [CrossRef]
- Wang, D.; Yao, Y.; Xu, X.; Zhang, T. Virtual DVL Reconstruction Method for an Integrated Navigation System Based on DS-LSSVM Algorithm. IEEE Trans. Instrum. Meas. 2021, 70, 1–13. [Google Scholar] [CrossRef]
- Zhang, L.; Wang, B.; Huang, H.; Wang, S.; Wei, J. A Coarse Alignment Method Based on Vector Observation and Truncated Vectorized κ-Matrix for Underwater Vehicle. IEEE Trans. Veh. Technol. 2023, 72, 3227–3238. [Google Scholar] [CrossRef]
- Xu, X.; Yao, Y.; Wang, D.; Hou, L. An M-Estimation-Based Improved Interacting Multiple Model for INS/DVL Navigation Method. IEEE Sens. J. 2022, 22, 13375–13386. [Google Scholar] [CrossRef]
- Qiu, H.; Gao, F.; Gao, X.; Chen, J.; Deng, F.; Zhang, L. Long-Range Binocular Vision Target Geolocation Using Handheld Electronic Devices in Outdoor Environment. IEEE Trans. Image Process. 2020, 29, 5531–5541. [Google Scholar] [CrossRef]
- Liu, H.H.; Qin, K.; Zhu, B.; Zhu, Y. A Model-Based Approach for Measurement Noise Estimation and Compensation in Feedback Control Systems. IEEE Trans. Instrum. Meas. 2020, 69, 8112–8127. [Google Scholar] [CrossRef]
- Hu, H.; Chen, L.; Wang, S.; Gu, D. Cooperative Localization of AUVs Using Moving Horizon estimation. IEEE/CAA J. Autom. Sin. 2014, 1, 68–76. [Google Scholar] [CrossRef]
- Zhao, H.; Guan, X.; Luo, X.; Yan, J. Privacy Preserving Solution for the Asynchronous Localization of Underwater Sensor NETWORKS. IEEE/CAA J. Autom. Sin. 2020, 7, 1511–1527. [Google Scholar] [CrossRef]
- Pan, X.; Yang, Y.; Dai, M.; Zhang, C.; Li, Z. A Novel Attitude Measurement While Drilling System Based on Single-Axis Fiber Optic Gyroscope. IEEE Trans. Instrum. Meas. 2022, 71, 1–11. [Google Scholar] [CrossRef]
- Tong, J.; Zhu, Y.; Jin, B.; Wang, J.; Zhang, T. Student’s t-Based Robust Kalman Filter for a SINS/USBL Integration Navigation Strategy. IEEE Sens. J. 2020, 20, 5540–5553. [Google Scholar] [CrossRef]
- Wang, D.; Wang, B.; Huang, H.; Zhang, H. A Multisensor Fusion Method Based on Strict Velocity for Underwater Navigation System. IEEE Sens. J. 2023, 23, 18587–18598. [Google Scholar] [CrossRef]
- Song, R.; Tang, J.; Huang, H.; Tang, X. A Novel Matrix Block Algorithm based on Cubature Transformation Fusing Variational Bayesian Scheme for Position Estimation Applied to MEMS Navigation System. Mech. Syst. Signal Process. 2021, 166, 108486. [Google Scholar] [CrossRef]
- Chen, J.; Li, J.; Yang, S.; Deng, F. Weighted Optimization-Based Distributed Kalman Filter for Nonlinear Target Tracking in Collaborative Sensor Networks. IEEE Trans. Cybern. 2017, 1, 1–14. [Google Scholar] [CrossRef]
- Arasaratnam, I.; Haykin, S. Cubature Kalman Filters. IEEE Trans. Autom. Control 2009, 54, 1254–1269. [Google Scholar] [CrossRef]
- Cao, H.; Liu, J.; Tang, J.; Shen, C.; Niu, X.; Wang, C.; Li, J.; Zhao, H. Robust Adaptive Heading Tracking Fusion for Polarization Compass with Uncertain Dynamics and External Disturbances. IEEE Trans. Instrum. Meas. 2023, 72, 1–11. [Google Scholar] [CrossRef]
- Chisci, L.; Dong, X.; Cai, Y. An Adaptive Variational Bayesian Filter for Nonlinear Multi-sensor Systems with Unknown Noise Statistics. Signal Process. 2021, 179, 107837. [Google Scholar] [CrossRef]
- Zhang, Y.; Huang, Y.; Chambers, J.; Li, N.; Wu, Z. A Novel Adaptive Kalman Filter with Inaccurate Process and Measurement Noise Covariance Matrices. IEEE Trans. Autom. Control 2018, 63, 594–601. [Google Scholar] [CrossRef]
- Xu, B.; Wang, X.; Zhang, J.; Guo, Y.; Razzaqi, A.A. A novel adaptive filtering for cooperative localization under compass failure and non-gaussian noise. IEEE Trans. Veh. Technol. 2022, 71, 3737–3749. [Google Scholar] [CrossRef]
- Yang, Y.; Wang, Z.; Wang, B. A Variational Bayesian-based Maximum Correntropy Adaptive Kalman Filter for SINS/USBL Integrated Navigation System. IEEE Sens. J. 2025, 25, 20147–20157. [Google Scholar] [CrossRef]
- Leung, H.; Li, Y.; Zhu, H.; Zhang, G. An adaptive Kalman filter with inaccurate noise covariances in the presence of outliers. IEEE Trans. Autom. Control 2021, 67, 374–381. [Google Scholar] [CrossRef]
- Ge, Q.; Li, Y.; Song, Z.; He, H.; Hu, X. A Novel Adaptive Kalman Filter Based on Credibility Measure. IEEE/CAA J. Autom. Sin. 2023, 10, 103–120. [Google Scholar] [CrossRef]
- Yu, L.; Chu, N.; Wu, P.; Liu, Q.; Shao, Z.; Qin, H. A Bayesian Framework of Non-Synchronous Measurement at Coprime Positions for Sound Source Localization with High Resolution. IEEE Trans. Instrum. Meas. 2023, 72, 1–17. [Google Scholar] [CrossRef]
- Huang, Y.; Zhang, Y.; Zhao, Y.; Chamber, J. A Novel Robust Gaussian-Student’s t Mixture Distribution Based Kalman Filter. IEEE Trans. Signal Process. 2019, 67, 3606–3620. [Google Scholar] [CrossRef]
- Li, J.; Wei, X.; Chen, X.; Wang, A.; Cui, B. Robust Cubature Kalman Filter based on Variational Bayesian and Transformed Posterior Sigma Points Error. ISA Trans. 2019, 86, 18–28. [Google Scholar] [CrossRef]
- Shi, P.; Zhang, Y.; Huang, Y.; Chambers, J. Variational Adaptive Kalman Filter with Gaussian-Inverse-Wishart Mixture Distribution. IEEE Trans. Autom. Control 2021, 66, 1786–1793. [Google Scholar] [CrossRef]
- Zhang, W.-A.; Zhang, J.; Yang, X. A Progressive Bayesian Filtering Framework for Nonlinear Systems with Heavy-Tailed Noises. IEEE Trans. Autom. Control 2023, 68, 1918–1925. [Google Scholar] [CrossRef]
- Meng, Q.; Li, X. Minimum Cauchy Kernel Loss Based Robust Cubature Kalman Filter and Its Low Complexity Cost Version with Application on INS/OD Integrated Navigation System. IEEE Sens. J. 2022, 22, 9534–9542. [Google Scholar] [CrossRef]
- Huang, H.; Zhang, S.; Wang, D.; Ling, K.-V.; Liu, F.; He, X. A Novel Bayesian-Based Adaptive Algorithm Applied to Unob-servable Sensor Measurement Information Loss for Underwater Navigation. IEEE Trans. Instrum. Meas.-Urem. 2023, 72, 1–12. [Google Scholar]
- Huang, Y.; Chen, B.; Zhang, Y.; Bai, M. A Novel Robust Kalman Filtering Framework Based on Normal-Skew Mixture Distribution. IEEE Trans. Syst. Man Cybern. Syst. 2021, 2022, 6789–6805. [Google Scholar] [CrossRef]
- Luan, X.; Huang, B.; Liu, F.; Zhao, S.; Xu, C.; Ma, Y. Sensor Fault Estimation in a Probabilistic Framework for Industrial Processes and Its Applications. IEEE Trans. Ind. Inform. 2022, 18, 387–396. [Google Scholar] [CrossRef]
- Zhou, H.; Zou, C.; Appiah, E.; Bobobee, E.D.; Haque, A.; Takyi-Aninakwa, P.; Wang, S. Improved fixed range forgetting factor-adaptive extended Kalman filtering (FRFF-AEKF) algorithm for the state of charge estimation of high-power lithium-ion batteries. Int. J. Electrochem. Sci. 2022, 17, 221146. [Google Scholar] [CrossRef]
- Bar-Shalom, Y.; Li, X.; Kirubarajan, T. Estimation with Applications to Tracking and Navigation: Theory Algorithms and Software; Wiley: Hobobken, NJ, USA, 2004. [Google Scholar]

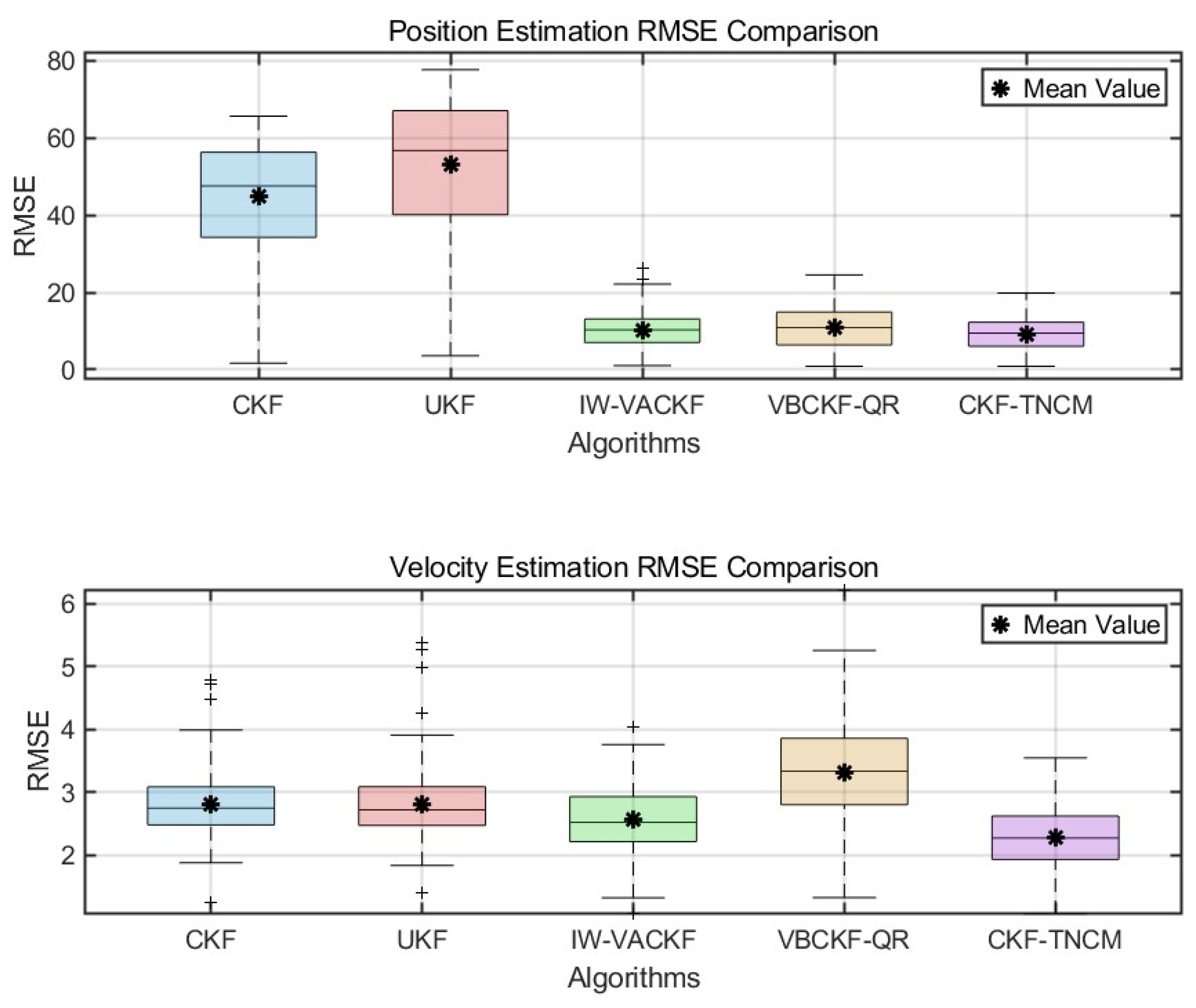


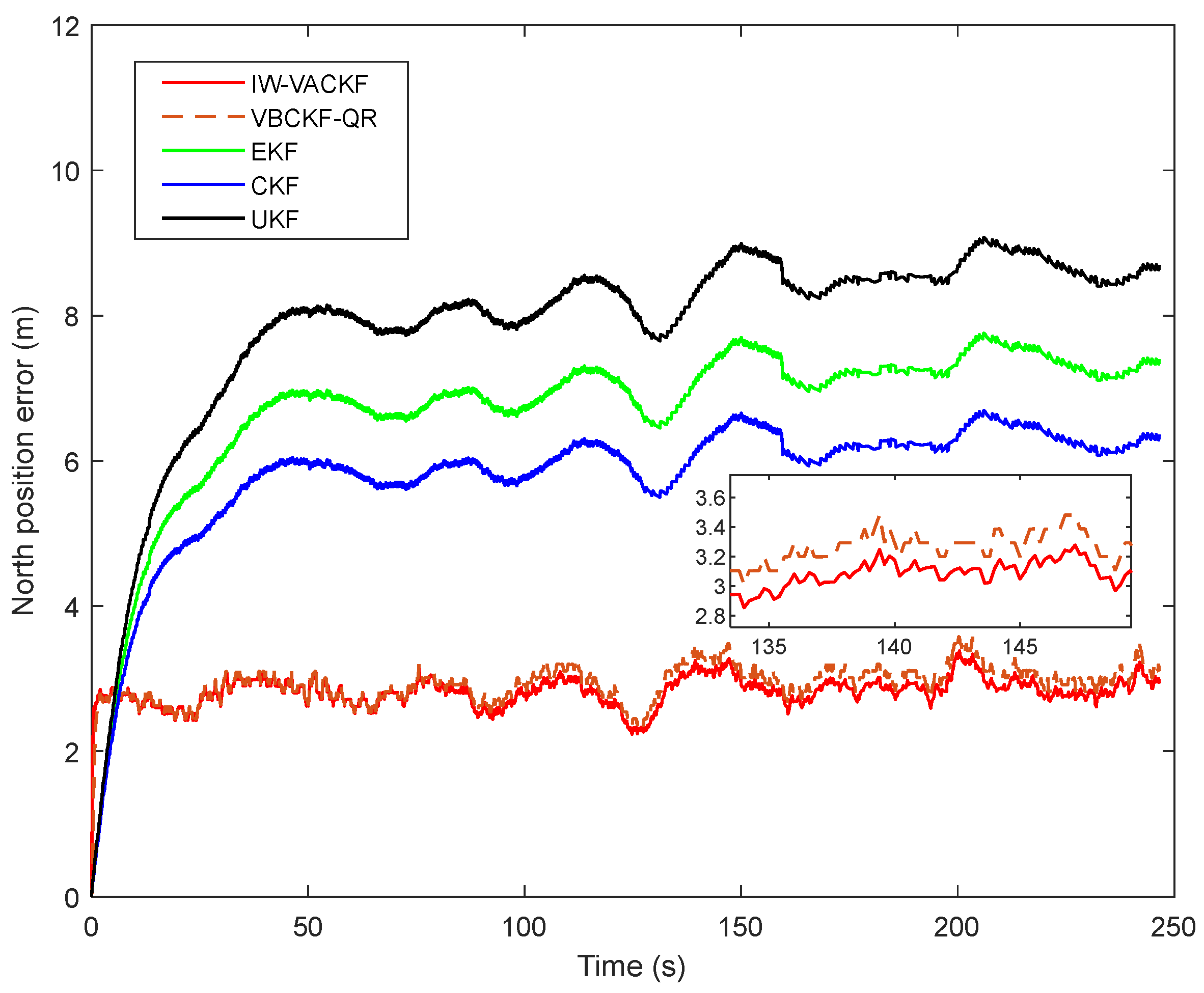


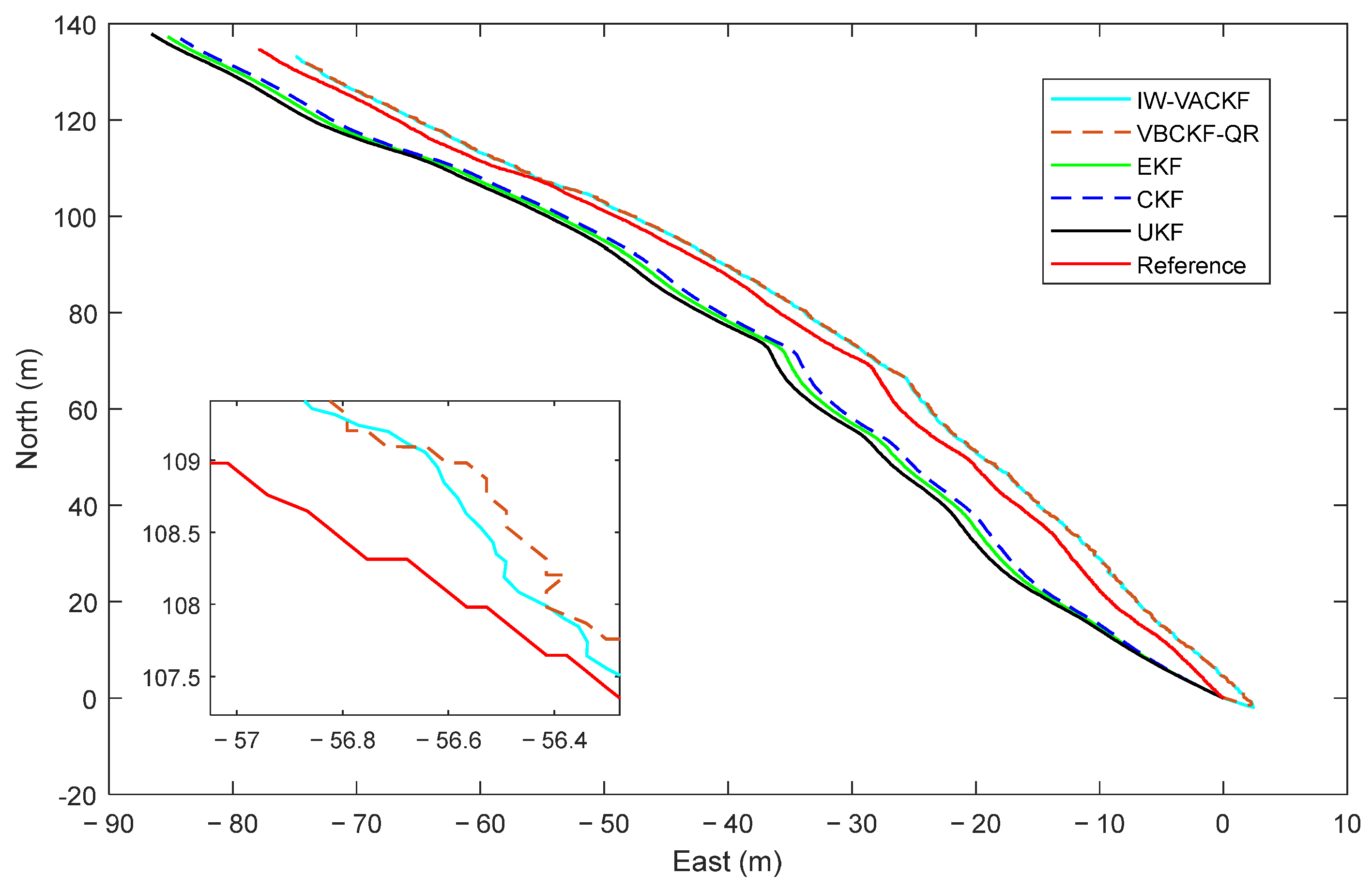
| Parameters | Filter | (m) | (m/s) |
|---|---|---|---|
| UKF | 53.3109 | 2.9186 | |
| CKF | 45.2893 | 2.8961 | |
| VBCKF-QR | 10.8589 | 3.3216 | |
| IW-VACKF | 10.2683 | 2.5733 | |
| CKF-TNCM | 8.9651 | 2.2954 | |
| UKF | 61.9777 | 4.3249 | |
| CKF | 58.6286 | 4.3189 | |
| VBCKF-QR | 12.3005 | 3.6468 | |
| IW-VACKF | 11.2230 | 3.3291 | |
| CKF-TNCM | 10.6104 | 3.0313 | |
| UKF | 73.9291 | 5.5212 | |
| CKF | 96.2329 | 7.2268 | |
| VBCKF-QR | 13.8656 | 4.2379 | |
| IW-VACKF | 11.4812 | 3.1558 | |
| CKF-TNCM | 11.4189 | 3.4854 |
| Items | Gyroscope |
| In run bias stability | 8 |
| Scale factor stability | 500 |
| Angular Random Walk | 0.18 |
| One year bias stability | 0.4 |
| Items | Accelerometers |
| Scale factor stability | 1000 |
| Velocity Random walk | 57 |
| In run bias instability | 14 |
| One year bias stability | 5 |
| Items | GPS |
| Single positional Accuracy | 5 |
| Velocity Accuracy | 3 |
| Items | DVL |
| Velocity Accuracy | 0.001 |
| Algorithms | North Error (m) | East Error (m) | Down Error (m) |
|---|---|---|---|
| IW-VACKF | 2.82 | 1.99 | 0.23 |
| VBCKF-QR | 2.94 | 2.07 | 0.24 |
| EKF | 6.73 | 2.89 | 0.57 |
| UKF | 7.87 | 3.49 | 0.65 |
| CKF | 5.80 | 2.41 | 0.51 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, H.; Dong, C.; Zhang, Y.; Zhang, S. A Novel Variational Bayesian Method with Unknown Noise for Underwater INS/DVL/USBL Localization. Sensors 2025, 25, 3708. https://doi.org/10.3390/s25123708
Huang H, Dong C, Zhang Y, Zhang S. A Novel Variational Bayesian Method with Unknown Noise for Underwater INS/DVL/USBL Localization. Sensors. 2025; 25(12):3708. https://doi.org/10.3390/s25123708
Chicago/Turabian StyleHuang, Haoqian, Chenhui Dong, Yutong Zhang, and Shuang Zhang. 2025. "A Novel Variational Bayesian Method with Unknown Noise for Underwater INS/DVL/USBL Localization" Sensors 25, no. 12: 3708. https://doi.org/10.3390/s25123708
APA StyleHuang, H., Dong, C., Zhang, Y., & Zhang, S. (2025). A Novel Variational Bayesian Method with Unknown Noise for Underwater INS/DVL/USBL Localization. Sensors, 25(12), 3708. https://doi.org/10.3390/s25123708







