Design and Experiment of an Automatic Leveling System for Tractor-Mounted Implements
Abstract
1. Introduction
2. Materials and Methods
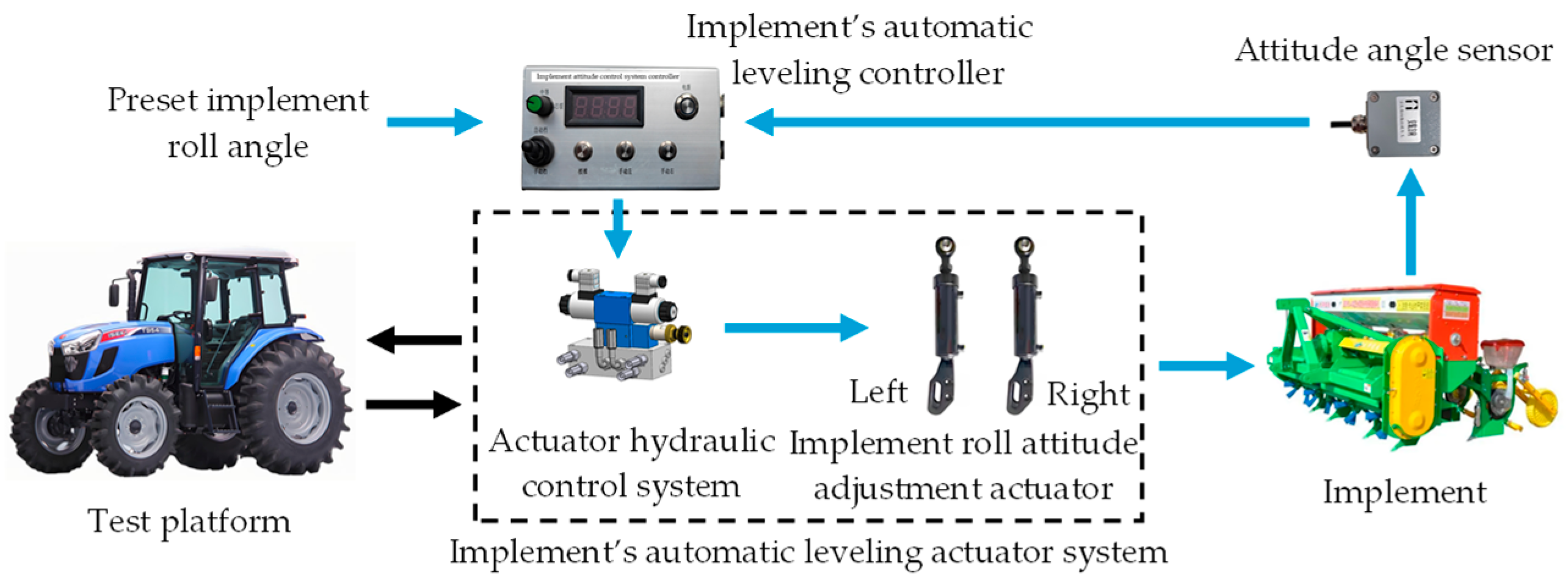
2.1. Implement Leveling System
2.1.1. System Overall Architecture
2.1.2. System Working Overview
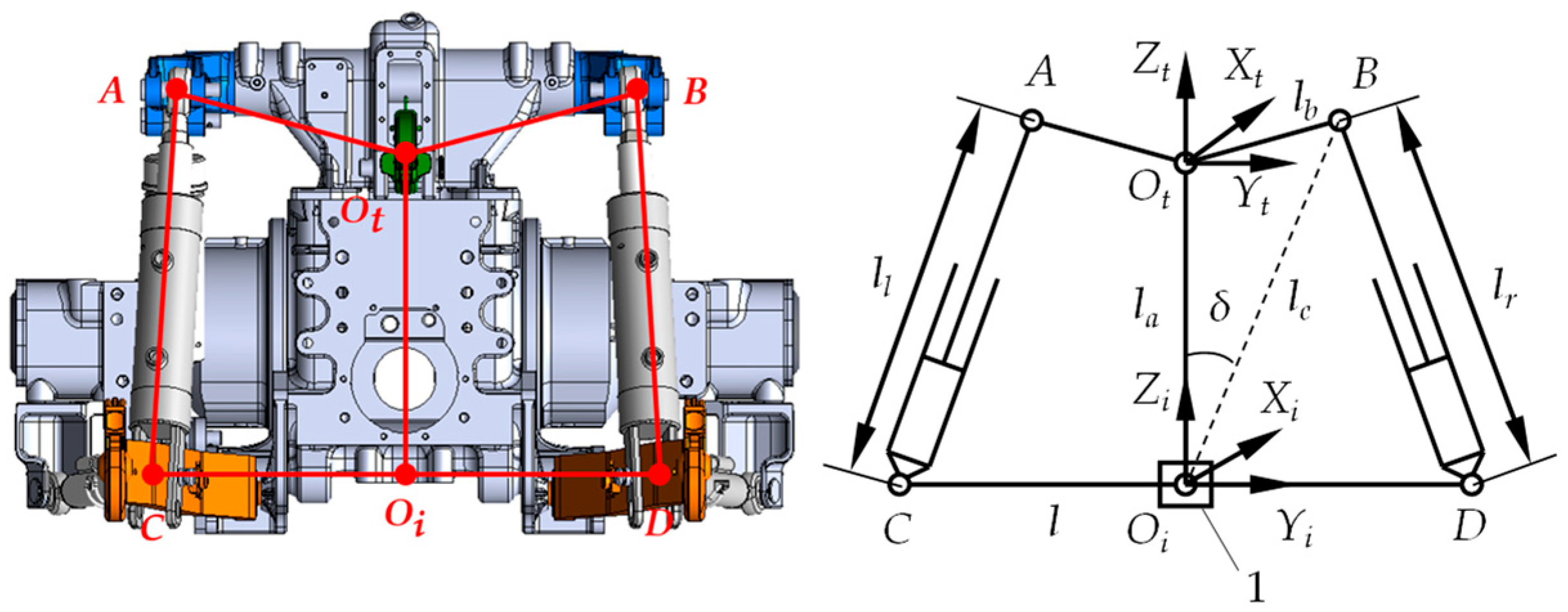
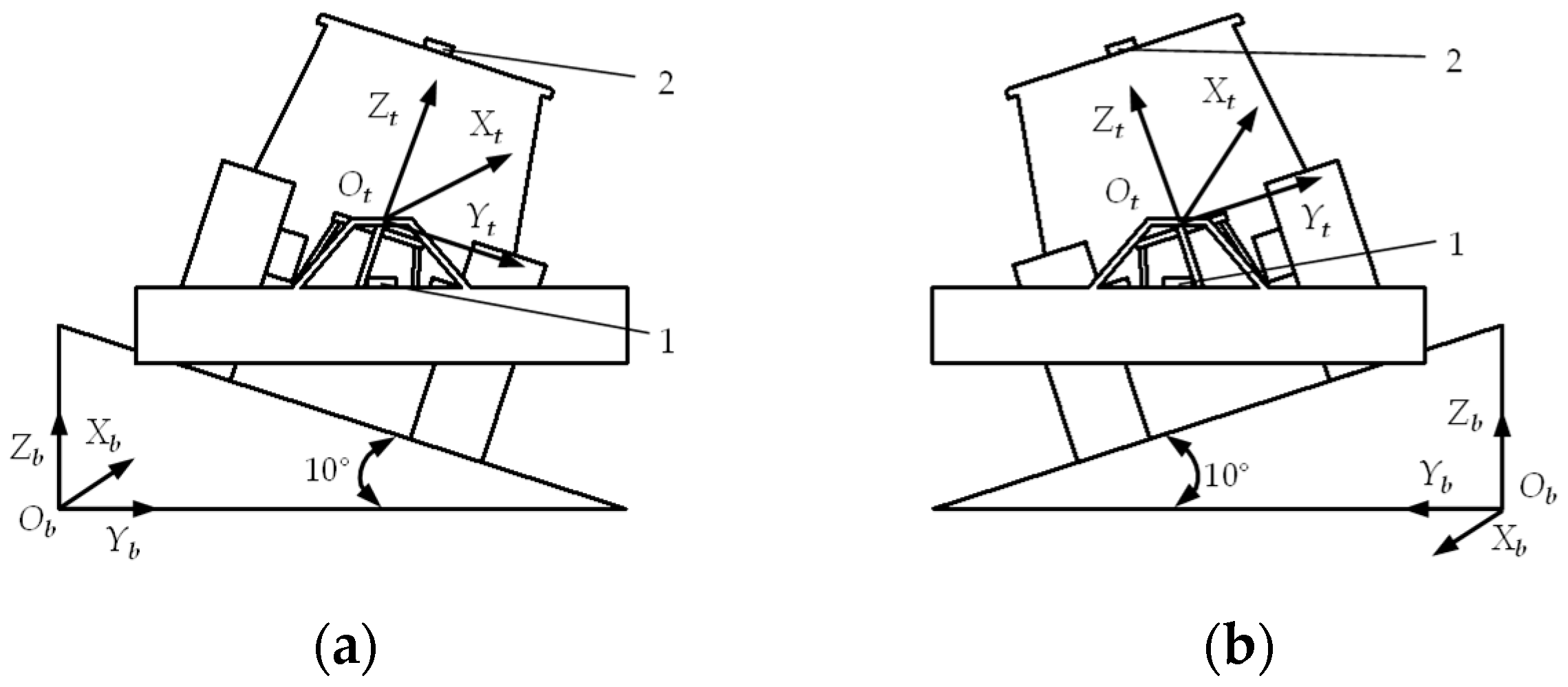
2.2. Design of Implement’s Automatic Leveling Actuator
2.2.1. Kinematic Analysis of Actuator
2.2.2. Analyzing the Relationship of Implement Roll Angle and Actuator Response Time
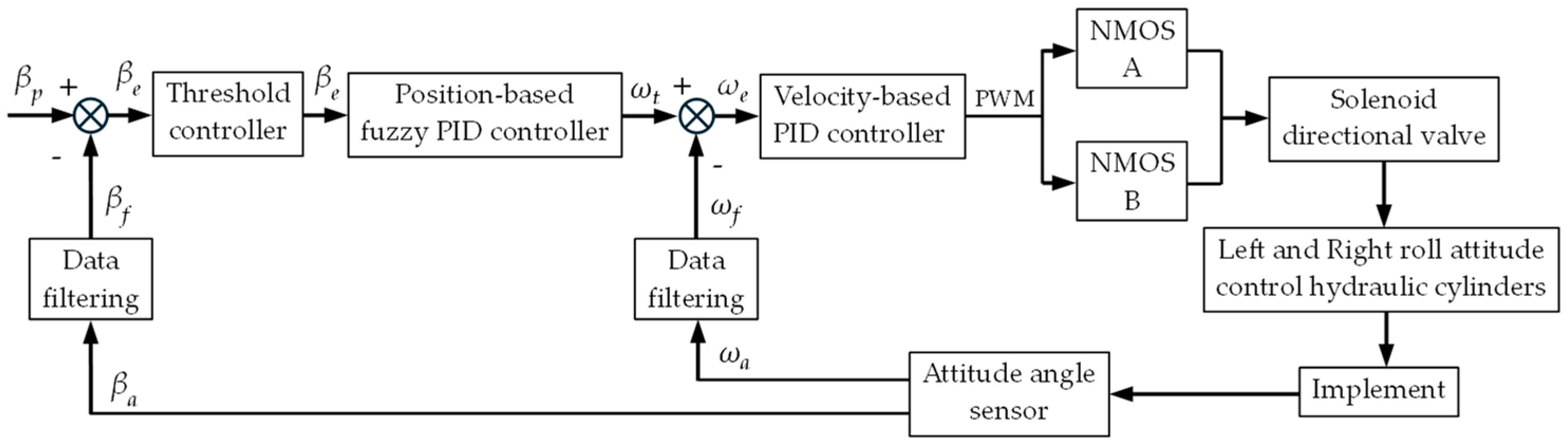
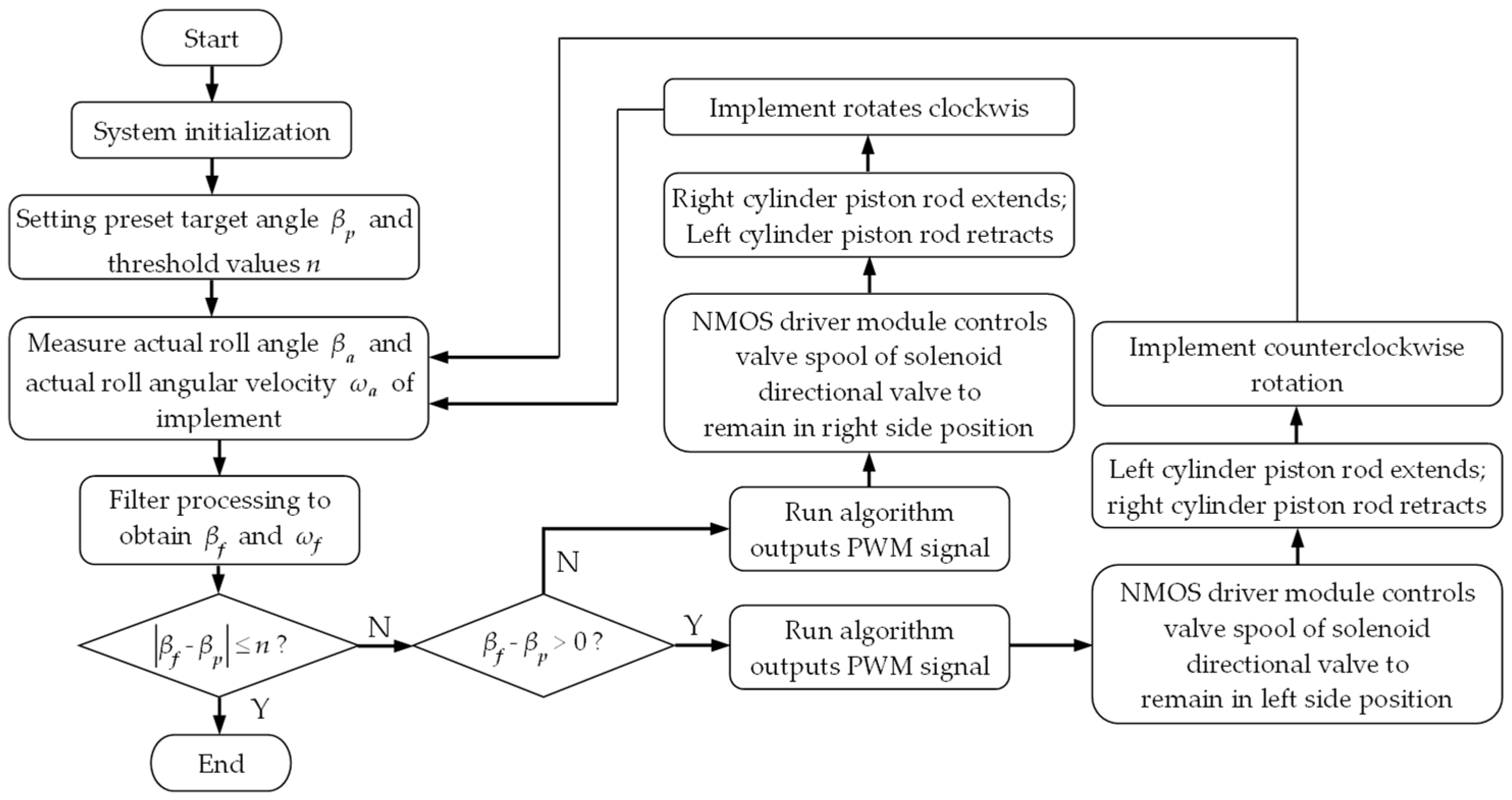
2.3. Design of Implement’s Automatic Leveling Algorithm
2.3.1. Working Principle of Dual Closed-Loop Fuzzy PID
2.3.2. Design of Fuzzy PID Algorithm
2.4. Implement’s Automatic Leveling Controller Design
2.4.1. Hardware Design
2.4.2. Software Design
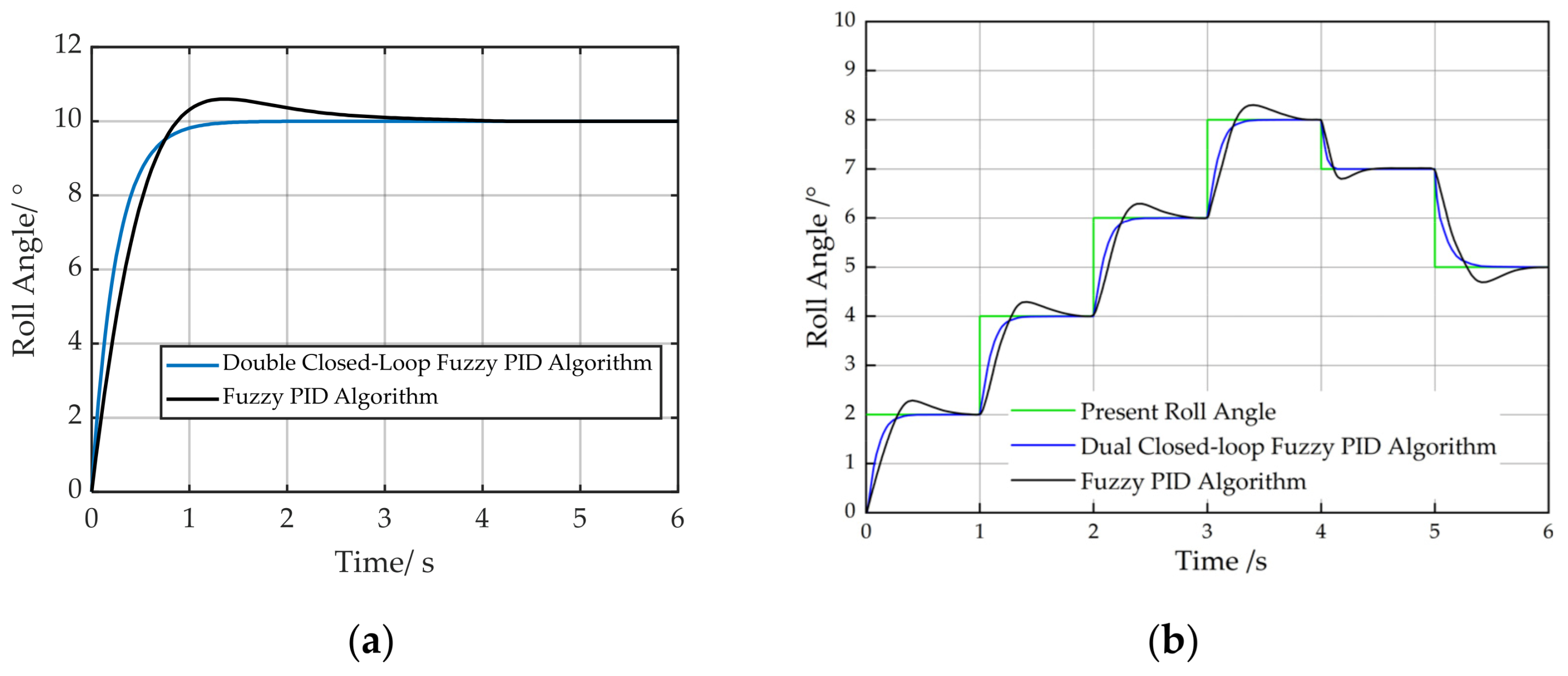
2.5. Simulation Analysis of Tractor-Mounted Implement’s Automatic Leveling Control System
2.5.1. Modeling of the Valve-Controlled Hydraulic Cylinder System
2.5.2. Simulation Analysis of Implement’s Automatic Leveling System
3. Experimental Testing and Analysis
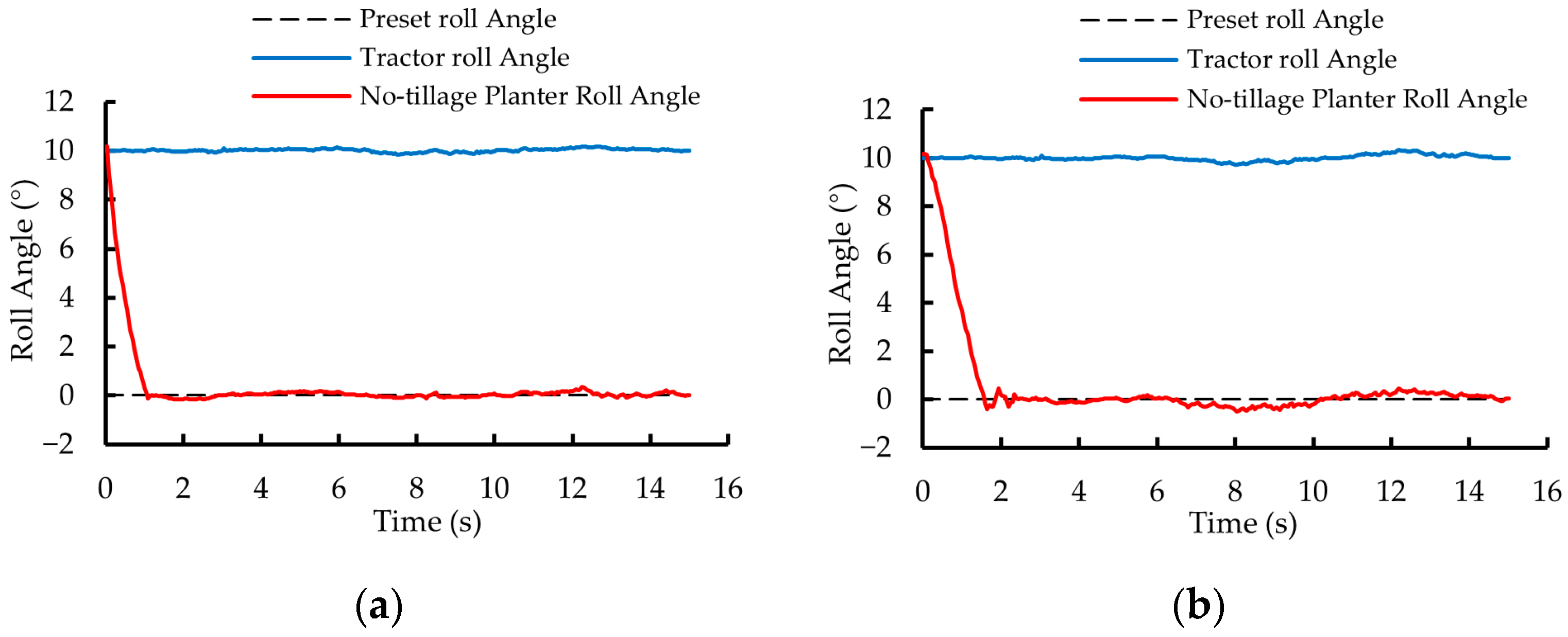
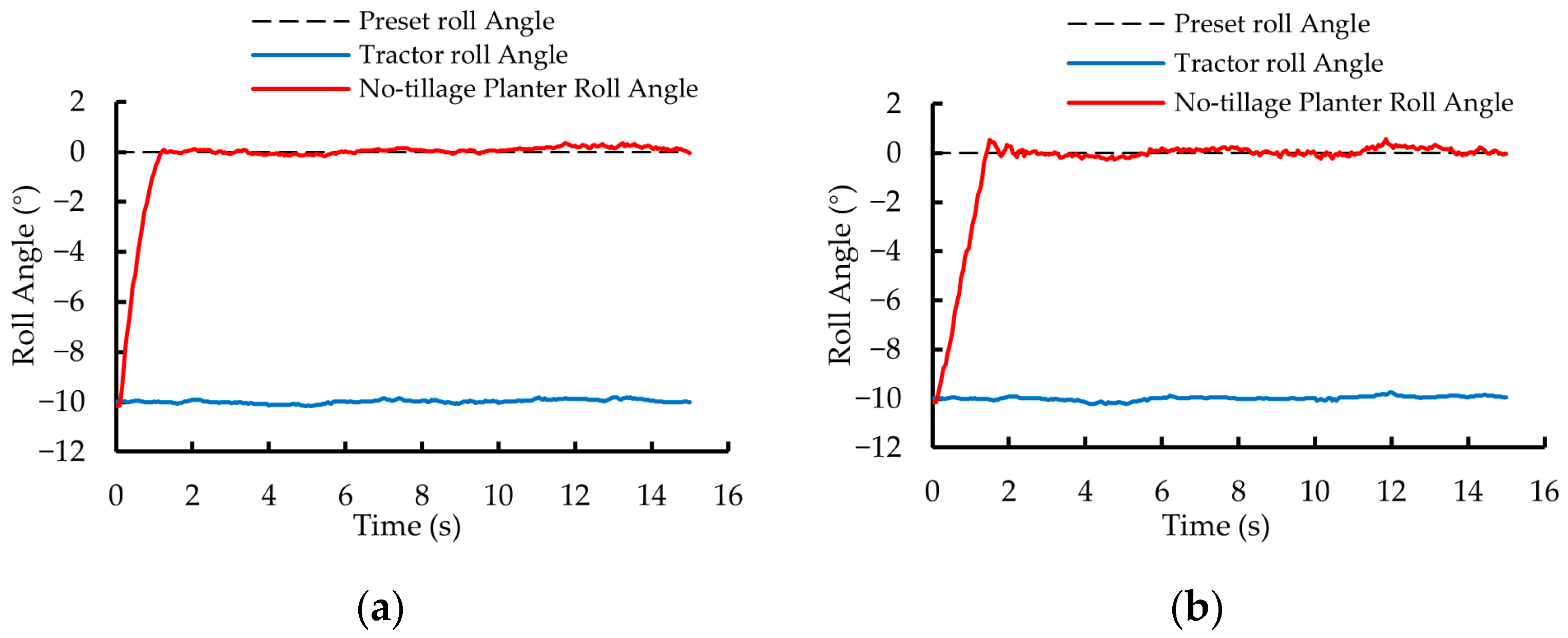
3.1. Static Experiment
3.1.1. Experimental Method and Content
3.1.2. Experimental Results and Analysis
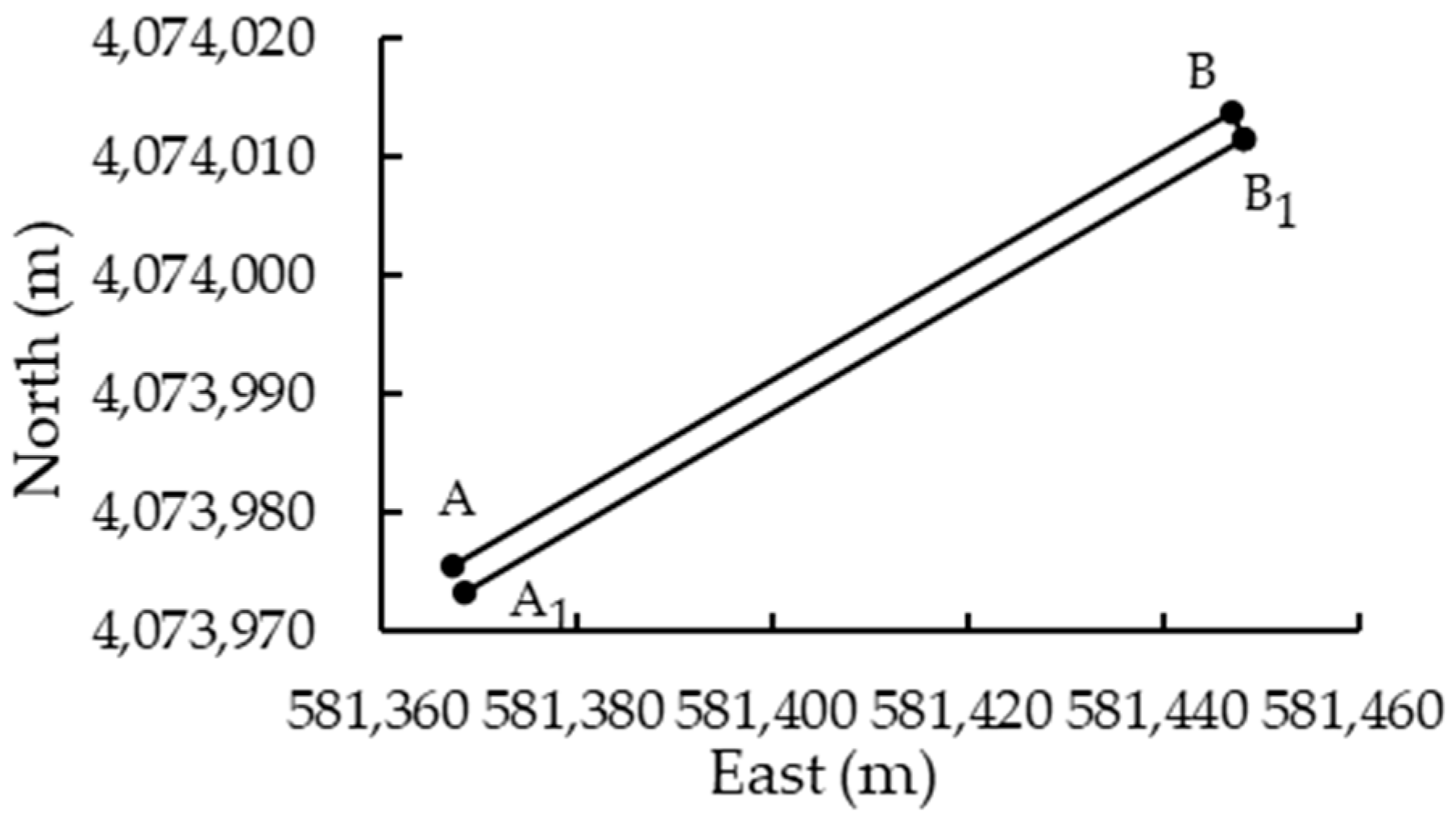
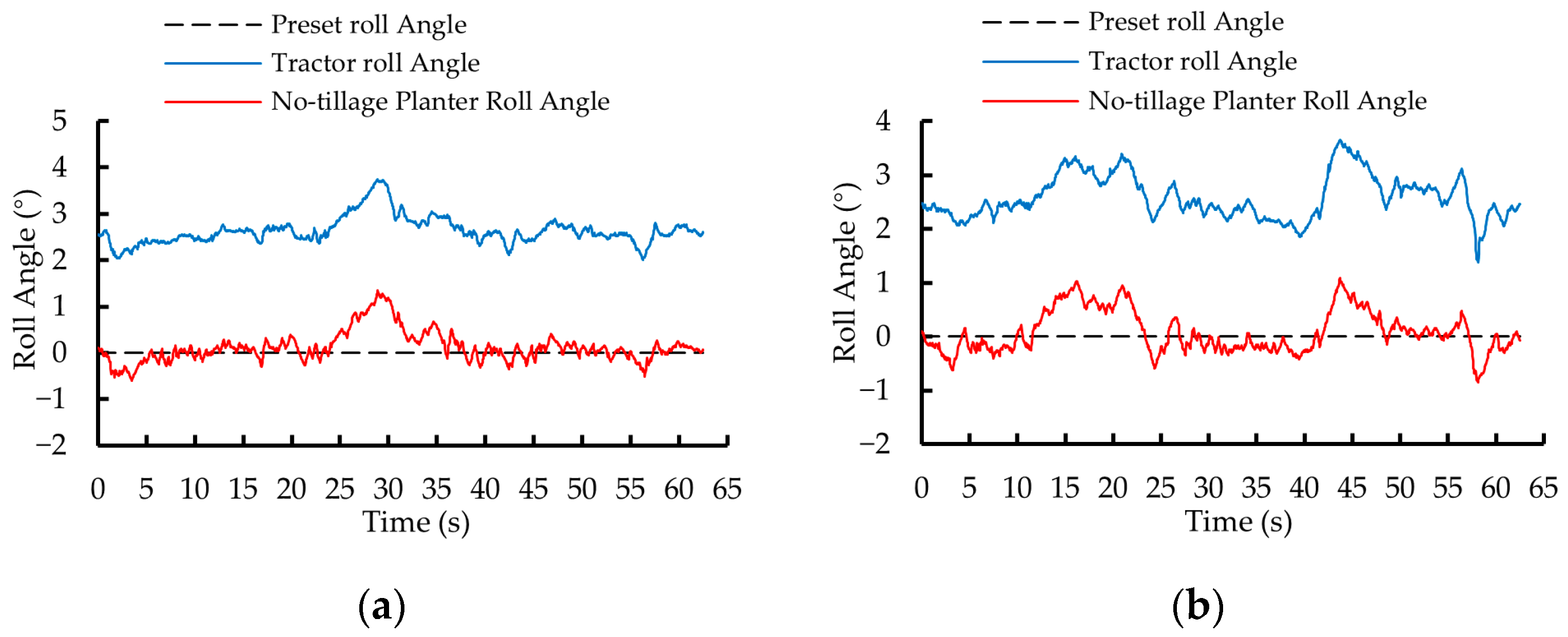
3.2. Field Experiment
3.2.1. Experimental Method and Content
3.2.2. Experimental Results and Analysis
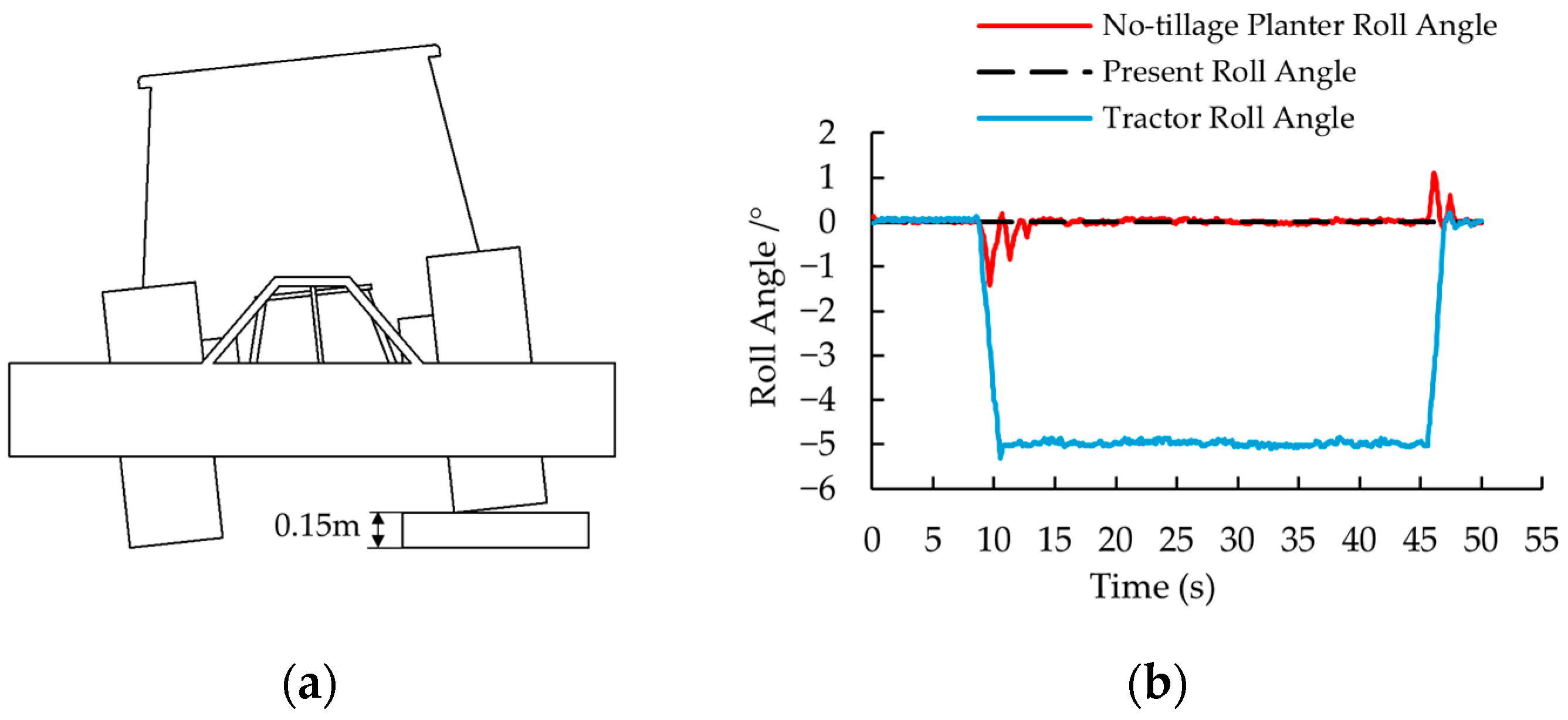
3.3. System Anti-Interference Capability Verification Under Localized Terrain Irregularities
3.4. Experimental Analysis
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Sun, X.; Lu, Z.; Song, Y.; Cheng, Z.; Jiang, C.; Qian, J.; Lu, Y. Development Status and Research Progress of a Tractor Electro-Hydraulic Hitch System. Agriculture 2022, 12, 1547. [Google Scholar] [CrossRef]
- Wang, L.; Wang, Y.; Dai, D.; Wang, X.; Wang, S. Review of electro-hydraulic hitch system control method of automated tractors. Int. J. Agric. Biol. Eng. 2021, 14, 1–8. [Google Scholar] [CrossRef]
- Lysych, M.N. A study of the static lateral stability of a tillage machine-tractor unit on a virtual stand. J. Phys. Conf. Ser. 2020, 1515, 042033. [Google Scholar] [CrossRef]
- Gyarmati, G.; Mizik, T. The present and future of the precision agriculture. In Proceeding of the 2020 IEEE 15th International Conference of System of Systems Engineering (SoSE), Budapest, Hungary, 2–4 June 2020; pp. 593–596. [Google Scholar]
- Xie, B.; Wu, Z.; Mao, R. Development and Prospect of Key Technologies on Agricultural Tractor. J. Chin. Soc. Agric. Mach. 2018, 49, 1–17. [Google Scholar] [CrossRef]
- Zhou, H.; Hu, L.; Luo, X.; Zhao, R.; Xu, Y.; Yang, W. Design and Experiment on Auto Leveling System of Rotary Tiller. J. Chin. Soc. Agric. Mach. 2016, 1, 117–123. [Google Scholar]
- Fan, Y.; Zhai, Z.; Zhu, Z.; Mao, E.; Wang, H.; Chen, Y. Electro-hydraulic Hitch Terrain-adaptive Control System for Hillside Tractors. J. Chin. Soc. Agric. Mach. 2020, 51, 517–524. [Google Scholar] [CrossRef]
- Shao, M.; Xin, Z.; Jiang, Q.; Zhang, Y.; Du, Y.; Yang, H. Fuzzy PID Control for Lateral Pose Adjustment of Tractor Rear Sus-pension. J. Chin. Soc. Agric. Eng. 2019, 35, 34–42. [Google Scholar] [CrossRef]
- İrsel, G.; Altinbalik, M.T. Adaptation of tilt adjustment and tracking force automation system on a laser-controlled land leveling machine. Comput. Electron. Agric. 2018, 150, 374–386. [Google Scholar] [CrossRef]
- Xin, Z.; Jiang, Q.; Zhu, Z.; Shao, M. Design and optimization of a new terrain-adaptive hitch mechanism for hilly tractors. Int. J. Agric. Biol. Eng. 2023, 16, 134–144. [Google Scholar] [CrossRef]
- Chukewad, Y.M.; Chadha, S.; Jagdale, K.S.; Elkunchwar, N.; Rosa, U.A.; Omohundro, Z. Tractor Three-Point Hitch Control for an Independent Lower Arms System. Agriengineering 2024, 6, 1725–1746. [Google Scholar] [CrossRef]
- Yu, J.H.; Park, J.K.; Cheon, S.H.; Byeon, S.J.; Lee, J.W. Development of a rolling angle estimation algorithm to improve the performance of implement leveling-control systems for agricultural tractors. Adv. Mech. Eng. 2022, 14, 16878132221138310. [Google Scholar] [CrossRef]
- Mu, X.; Yang, F.; Duan, L.; Liu, Z.; Song, Z.; Li, Z.; Guan, S. Research Advances and Development Trend of Mountainous Tractor Leveling and Anti-Rollover System. Smart Agric. 2024, 6, 1–16. [Google Scholar] [CrossRef]
- Xiong, L.; Sun, S.; Xiao, M. Agricultural Machinery Automation and Intelligent Research and Application. IOP Conf. Ser. Mater. Sci. Eng. 2018, 452, 042077. [Google Scholar] [CrossRef]
- Liu, C.; Gu, J.; Du, X.; Yang, L.; Du, Y.; Mao, E. A Vibration Reduction Control Method for Tractor Rear Hydraulic Hitch Based on Pressure Feedback. Agriculture 2023, 13, 1546. [Google Scholar] [CrossRef]
- Gao, Y.; Hu, Y.; Yang, Y.; Feng, K.; Han, X.; Li, P.; Zhu, Y.; Song, Q. Optimization of Operating Parameters for Straw Returning Machine Based on Vibration Characteristic Analysis. Agronomy 2024, 14, 2388. [Google Scholar] [CrossRef]
- Knospe, C. PID control. IEEE Control. Syst. 2006, 26, 30–31. [Google Scholar] [CrossRef]
- Filo, G. A Review of Fuzzy Logic Method Development in Hydraulic and Pneumatic Systems. Energies 2023, 16, 7584. [Google Scholar] [CrossRef]
- Chao, C.-T.; Sutarna, N.; Chiou, J.-S.; Wang, C.-J. Equivalence between Fuzzy PID Controllers and Conventional PID Controllers. Appl. Sci. 2017, 7, 513. [Google Scholar] [CrossRef]
- Liu, C.; Zhao, J.; Gu, J.; Du, Y.; Li, Z.; Zhu, Z.; Mao, E. Pressure Control Algorithm Based on Adaptive Fuzzy PID with Compensation Correction for the Tractor Electronic Hydraulic Hitch. Appl. Sci. 2020, 10, 3179. [Google Scholar] [CrossRef]
- Hu, L.; Ling, C.; Luo, X.; Yang, W.; Xu, Y.; Zhou, H.; Zhang, Z. Design and Experiment on Auto Leveling Control System of Agricultural Implements. J. Chin. Soc. Agric. Eng. 2015, 31, 15–20. [Google Scholar]
- Yin, X.; An, J.; Wang, X.; Wang, Y.; Li, J.; Jin, C. Design and Test of Automatic Beam Leveling System for High-clearance Sprayer. J. Chin. Soc. Agric. Mach. 2022, 53, 98–105+115. [Google Scholar] [CrossRef]
- Yang, F.; Niu, H.; Sun, J.; Liu, Z.; Li, Y.; Chu, H. Design and Experiment of Attitude Cooperative Control System of Mountain Crawler Tractor and Farm Tools. J. Chin. Soc. Agric. Mach. 2022, 53, 414–422. [Google Scholar] [CrossRef]
- Matikainen, V.; Backman, J.; Visala, A. Cartesian control of an advanced tractors rear hitch—Geometric solution. IFAC Proc. Vol. 2013, 46, 270–275. [Google Scholar] [CrossRef]
- Che, G.; Liu, W.; Wan, L.; Yi, S.; Liu, H.; Wang, Q.; Lu, B. Design and Experiment of the Automatic Leveling System for the Seedbed Precision Leveler in Rice Seedling Nursery. J. Chin. Soc. Agric. Eng. 2023, 39, 9–17. [Google Scholar] [CrossRef]
- Wang, W.; Wu, K.; Zhang, Y.; Wang, M.; Zhang, C.; Chen, L. The Development of an Electric-Driven Control System for a High-Speed Precision Planter Based on the Double Closed-Loop Fuzzy PID Algorithm. Agronomy 2022, 12, 945. [Google Scholar] [CrossRef]
- Wen, Y.; Tan, J.; Sang, Y.; Zhou, S. Research on fuzzy symmetrical control of valve controlled asymmetric hydraulic cylinder system. J. Intell. Fuzzy Syst. 2021, 41, 4451–4460. [Google Scholar] [CrossRef]
- Liu, F.; Peng, X.W. On application of proportional valve-controlled hydraulic cylinder position servo system. In Proceedings of the 2015 34th Chinese Control Conference (CCC), Hangzhou, China, 28–30 July 2015; pp. 3642–3647. [Google Scholar]
- Zhang, W.; Yuan, Q.; Xu, Y.; Wang, X.; Bai, S.; Zhao, L.; Hua, Y.; Ma, X. Research on Control Strategy of Electro-Hydraulic Lifting System Based on AMESim and MATLAB. Symmetry 2023, 15, 435. [Google Scholar] [CrossRef]
- Sun, X.; Song, Y.; Wang, Y.; Qian, J.; Lu, Z.; Wang, T. Design and Test of a Tractor Electro-Hydraulic-Suspension Tillage-Depth and Loading-Control System Test Bench. Agriculture 2023, 13, 1884. [Google Scholar] [CrossRef]
- Meena, K.; Dhavalikar, M.; Thorat, S. A review on the position control of hydraulic cylinder for accuracy and response time. Mater. Today Proc. 2022, 72, 995–999. [Google Scholar] [CrossRef]

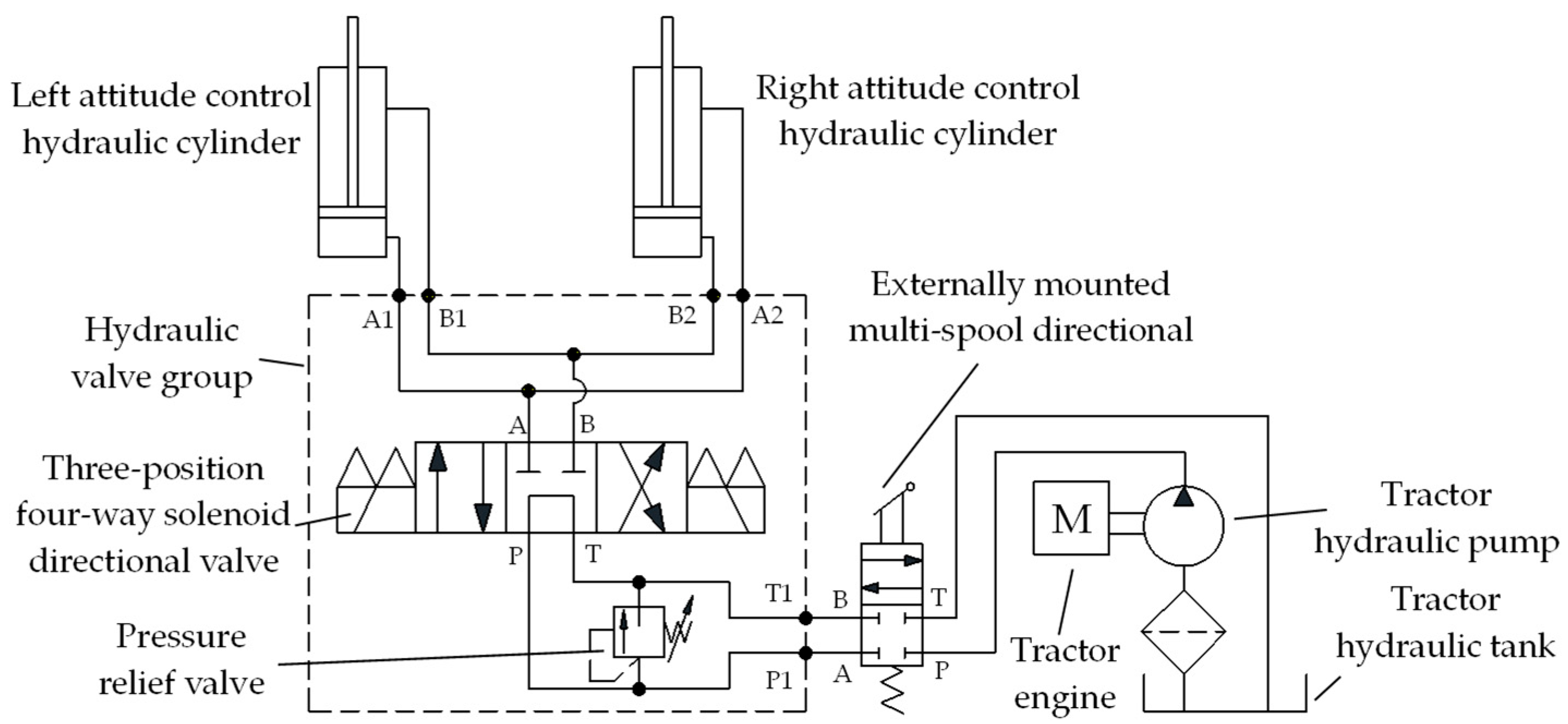







| Name | Model | Principal Technical Specifications | |
|---|---|---|---|
| Maximum Operating Pressure | Maximum Operating Flow Rate | ||
| Three-position four-way solenoid directional valve | 4WE10G-3X/CD12 | 35 MPa | 120 L/min |
| Pressure relief valve | MRV-03P | 25 MPa | 80 L/min |
| Tractor hydraulic pump | DDG1A259F9H9-L165 | 20 MPa | 50 L/min |
| NB | NM | NS | ZO | PS | PM | PB | ||
|---|---|---|---|---|---|---|---|---|
| E | NB | PB/NB/PS | PB/NB/NS | PM/NM/NB | PM/NM/NB | PS/NS/NB | ZO/ZO/NM | ZO/ZO/PS |
| NM | PB/NB/PS | PB/NB/NS | PM/NM/NB | PS/NS/NM | PS/NS/NM | ZO/ZO/NS | NS/ZO/ZO | |
| NS | PM/NB/ZO | PM/NM/NS | PM/NS/NM | PS/NS/NM | ZO/ZO/NS | NS/PS/NS | NS/PS/ZO | |
| ZO | PM/NM/ZO | PM/NM/NS | PS/NS/NS | ZO/ZO/NS | NS/PS/NS | NM/PM/NS | NM/PM/ZO | |
| PS | PS/NM/ZO | PS/NS/ZO | ZO/ZO/ZO | NS/PS/ZO | NS/PS/ZO | NM/PM/ZO | NM/PB/ZO | |
| PM | PS/ZO/PB | ZO/ZO/NS | NS/PS/PS | NM/PS/NS | NM/PM/PS | NM/PBPS | NB/PB/PB | |
| PB | ZO/ZO/PB | ZO/ZO/PM | NM/PS/PM | NM/PM/PM | NM/PM/PS | NB/PB/PS | NB/PB/PB | |
| Parameters | Number of Values |
|---|---|
| Piston rod diameter of the cylinder | 0.05 m |
| Piston diameter of the cylinder | 0.08 m |
| Load capacity of a single cylinder | 1000 kg |
| Natural frequency of three-way four-port solenoid valve | 80 Hz |
| Damping ratio of three-way four-port solenoid valve | 0.8 |
| Steady-state flow gain of three-way four-port solenoid valve | |
| Volume modulus of elasticity of hydraulic fluid | Pa |
| Hydraulic damping coefficient | 0.2 |
| Hydraulic pump operating pressure | 18 MPa |
| Hydraulic pump flow rate | 25 L/min |
| Planned Driving Path | Maxae (°) | (°) | Mae (°) | Rmse (°) | Percentage of Leveling Errors Within 0.5° (%) | |
|---|---|---|---|---|---|---|
| Dual closed-loop fuzzy PID control algorithm | 0.91 | 0.10 | 0.19 | 0.28 | 90.56 | |
| 0.85 | 0.04 | 0.19 | 0.25 | 94.48 | ||
| Fuzzy PID control algorithm | 1.34 | 0.12 | 0.24 | 0.36 | 88.33 | |
| 1.09 | 0.08 | 0.32 | 0.40 | 76.49 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yao, H.; Zhang, E.; Liu, Y.; Du, J.; Yin, X. Design and Experiment of an Automatic Leveling System for Tractor-Mounted Implements. Sensors 2025, 25, 3707. https://doi.org/10.3390/s25123707
Yao H, Zhang E, Liu Y, Du J, Yin X. Design and Experiment of an Automatic Leveling System for Tractor-Mounted Implements. Sensors. 2025; 25(12):3707. https://doi.org/10.3390/s25123707
Chicago/Turabian StyleYao, Haibin, Engen Zhang, Yufei Liu, Juan Du, and Xiang Yin. 2025. "Design and Experiment of an Automatic Leveling System for Tractor-Mounted Implements" Sensors 25, no. 12: 3707. https://doi.org/10.3390/s25123707
APA StyleYao, H., Zhang, E., Liu, Y., Du, J., & Yin, X. (2025). Design and Experiment of an Automatic Leveling System for Tractor-Mounted Implements. Sensors, 25(12), 3707. https://doi.org/10.3390/s25123707







