Can Data-Driven Supervised Machine Learning Approaches Applied to Infrared Thermal Imaging Data Estimate Muscular Activity and Fatigue?
Abstract
1. Introduction
2. Materials and Methods
2.1. Participants
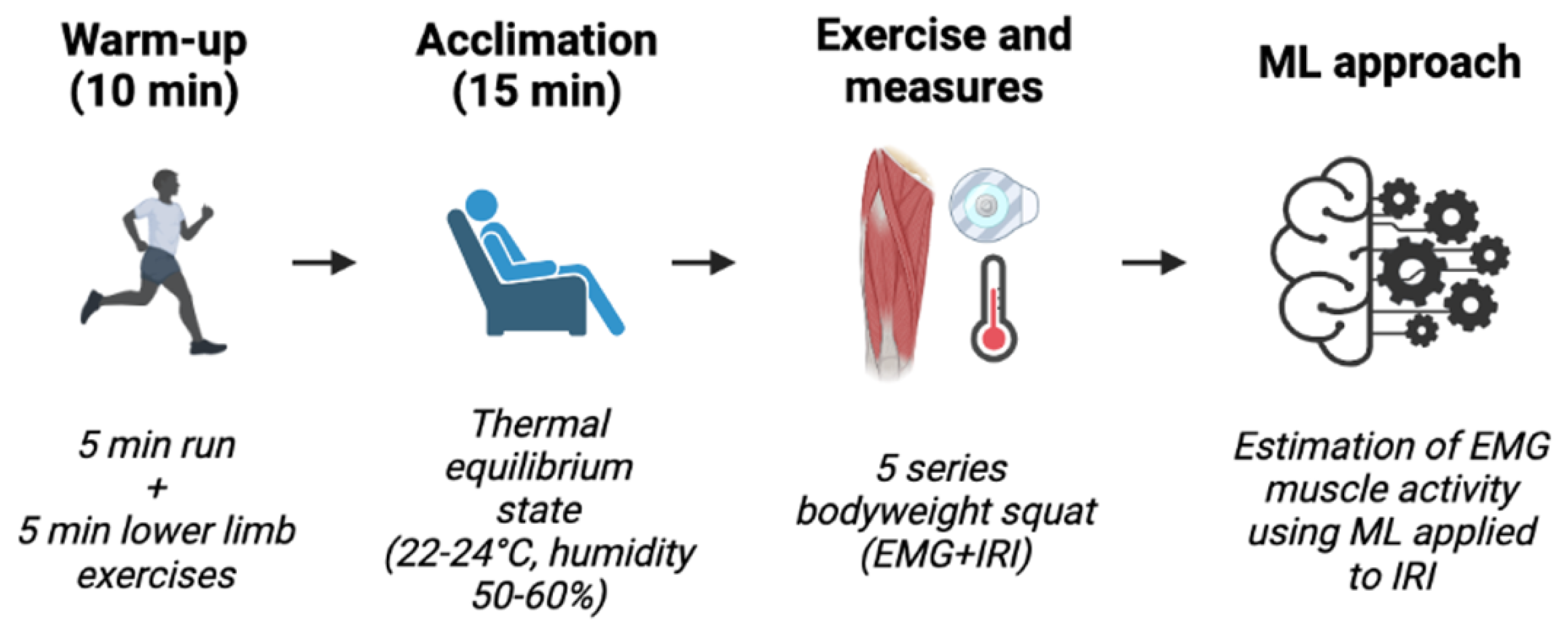
2.2. Experimental Protocol
2.3. Electromyography Recording and Preprocessing
2.4. Infrared Thermal Imaging Recording and Preprocessing
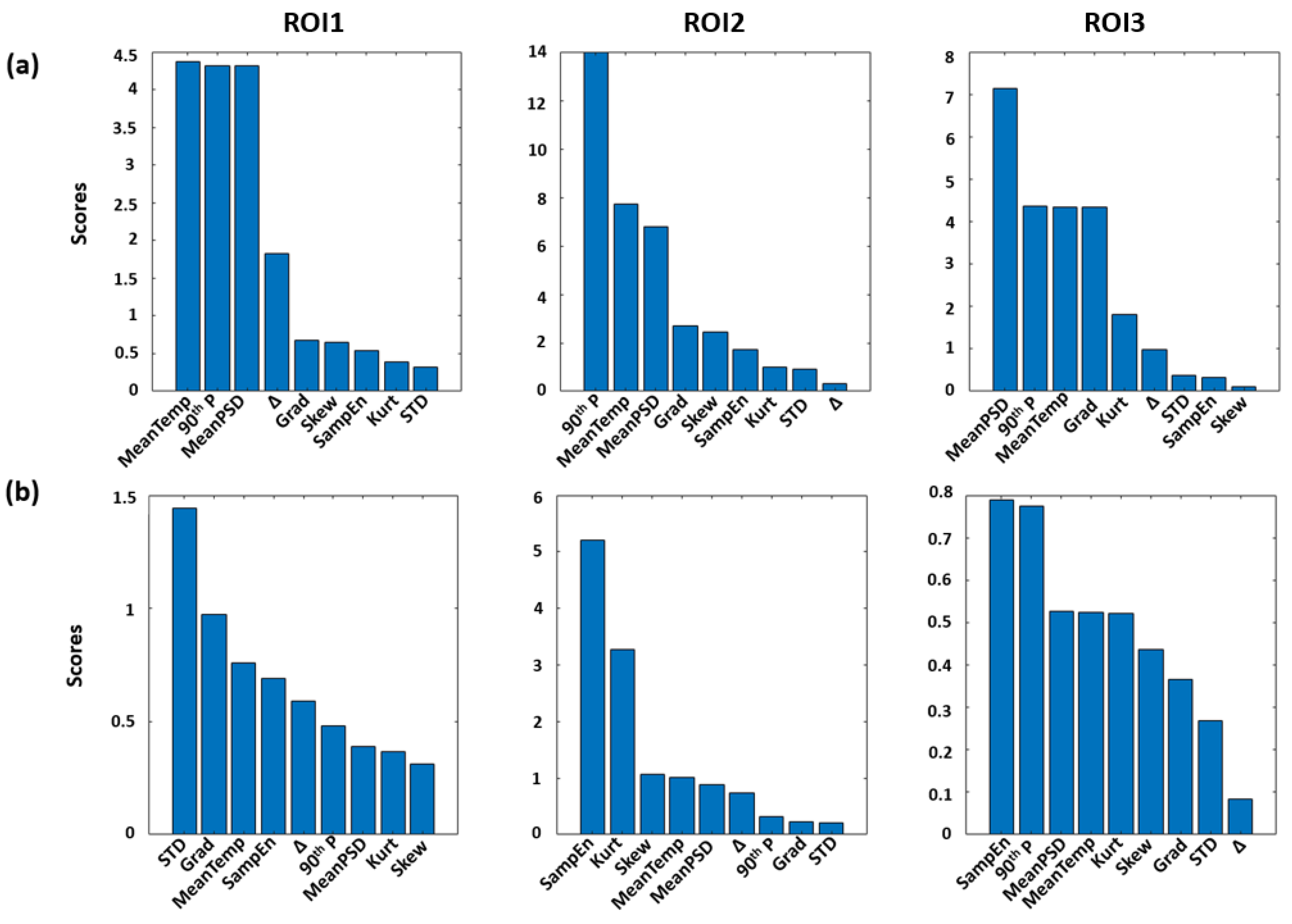
2.5. Features Extraction and Machine Learning Procedures
- Mean value (MeanTemp): average value of the thermal signal T over a temporal window of 10 s after the end of the exercise defined as:where N is the number of samples.
- Standard deviation (STD): standard deviation of the thermal signal T over a temporal window of 10 s after the end of the exercise defined as:where N is the number of samples.
- Mean value of the power spectral density (MeanPSD) of the thermal signal T over a temporal window of 10 s after the end of the exercise. The PSD is defined as the Fourier transform of the autocorrelation matrix of a random process :
- Kurtosis (Kurt): fourth standardized moment, and it is evaluated as follows:where N is the number of samples.
- Skewness (Skew): third standardized moment, and it is evaluated as follows:
- 90th percentile (90th P): it is the temperature value below which the 90% of all temperature frequency distribution are comprised.
- Sample Entropy (SampEn): it is defined as the negative natural logarithm of the conditional probability that signals that the subseries of length m (pattern length) that match pointwise within a tolerance r (similarity factor) also match at the m + 1 point. SampEn of a time series {t1,…,tN} of length N is computed employing the following set of equations:
- Where U is the subseries vector considered and Cm(r) is the probability that any vector Um(j) is within r of Um(i).
- Spatial gradient (Grad): it is evaluated as follow:
- Delta (Δ): difference between the average of the signal in the first 2 s and in the last 2 s of a temporal window of 10 s after the end of the exercise.
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Rodríguez-Tapia, B.; Soto, I.; Martínez, D.M.; Arballo, N.C. Myoelectric Interfaces and Related Applications: Current State of EMG Signal Processing–A Systematic Review. IEEE Access 2020, 8, 7792–7805. [Google Scholar] [CrossRef]
- Naik, G.R.; Selvan, S.E.; Nguyen, H.T. Single-Channel EMG Classification With Ensemble-Empirical-Mode-Decomposition-Based ICA for Diagnosing Neuromuscular Disorders. IEEE Trans. Neural Syst. Rehabil. Eng. 2016, 24, 734–743. [Google Scholar] [CrossRef]
- Taborri, J.; Keogh, J.; Kos, A.; Santuz, A.; Umek, A.; Urbanczyk, C.; van der Kruk, E.; Rossi, S. Sport Biomechanics Applications Using Inertial, Force, and EMG Sensors: A Literature Overview. Appl. Bionics Biomech. 2020, 2020, e2041549. [Google Scholar] [CrossRef] [PubMed]
- Merletti, R.; Rainoldi, A.; Farina, D. Surface Electromyography for Noninvasive Characterization of Muscle. Exerc. Sport Sci. Rev. 2001, 29, 20–25. [Google Scholar] [CrossRef] [PubMed]
- Hatton, A.L.; Dixon, J.; Martin, D.; Rome, K. The Effect of Textured Surfaces on Postural Stability and Lower Limb Muscle Activity. J. Electromyogr. Kinesiol. 2009, 19, 957–964. [Google Scholar] [CrossRef] [PubMed]
- Edwards, L.; Dixon, J.; Kent, J.R.; Hodgson, D.; Whittaker, V.J. Effect of Shoe Heel Height on Vastus Medialis and Vastus Lateralis Electromyographic Activity during Sit to Stand. J. Orthop. Surg. Res. 2008, 3, 2. [Google Scholar] [CrossRef] [PubMed]
- Hibbs, A.E.; Thompson, K.G.; French, D.N.; Hodgson, D.; Spears, I.R. Peak and Average Rectified EMG Measures: Which Method of Data Reduction Should Be Used for Assessing Core Training Exercises? J. Electromyogr. Kinesiol. 2011, 21, 102. [Google Scholar] [CrossRef]
- Rampichini, S.; Vieira, T.M.; Castiglioni, P.; Merati, G. Complexity Analysis of Surface Electromyography for Assessing the Myoelectric Manifestation of Muscle Fatigue: A Review. Entropy 2020, 22, 529. [Google Scholar] [CrossRef]
- Lawrence, M.A.; Leib, D.J.; Ostrowski, S.J.; Carlson, L.A. Nonlinear Analysis of an Unstable Bench Press Bar Path and Muscle Activation. J. Strength Cond. Res. 2017, 31, 1206–1211. [Google Scholar] [CrossRef]
- Martens, J.; Daly, D.; Deschamps, K.; Staes, F.; Fernandes, R.J. Inter-Individual Variability and Pattern Recognition of Surface Electromyography in Front Crawl Swimming. J. Electromyogr. Kinesiol. 2016, 31, 14–21. [Google Scholar] [CrossRef]
- Silva, L.; Vaz, J.R.; Castro, M.A.; Serranho, P.; Cabri, J.; Pezarat-Correia, P. Recurrence Quantification Analysis and Support Vector Machines for Golf Handicap and Low Back Pain EMG Classification. J. Electromyogr. Kinesiol. 2015, 25, 637–647. [Google Scholar] [CrossRef] [PubMed]
- Fricke, C.; Alizadeh, J.; Zakhary, N.; Woost, T.B.; Bogdan, M.; Classen, J. Evaluation of Three Machine Learning Algorithms for the Automatic Classification of EMG Patterns in Gait Disorders. Front. Neurol. 2021, 12, 666458. [Google Scholar] [CrossRef] [PubMed]
- Ng, C.L.; Reaz, M.B.I. Evolution of a Capacitive Electromyography Contactless Biosensor: Design and Modelling Techniques. Measurement 2019, 145, 460–471. [Google Scholar] [CrossRef]
- Ulas, U.H.; Cengiz, B.; Alanoglu, E.; Ozdag, M.F.; Odabasi, Z.; Vural, O. Comparison of Sensitivities of Macro EMG and Concentric Needle EMG in L4 Radiculopathy. Neurol. Sci. 2003, 24, 258–260. [Google Scholar] [CrossRef] [PubMed]
- Laferriere, P.; Lemaire, E.D.; Chan, A.D.C. Surface Electromyographic Signals Using Dry Electrodes. IEEE Trans. Instrum. Meas. 2011, 60, 3259–3268. [Google Scholar] [CrossRef]
- Padmadinata, F.Z.; Veerhoek, J.J.; van Dijk, G.J.A.; Huijsing, J.H. Microelectronic Skin Electrode. Sens. Actuators B Chem. 1990, 1, 491–494. [Google Scholar] [CrossRef]
- Searle, A.; Kirkup, L. A Direct Comparison of Wet, Dry and Insulating Bioelectric Recording Electrodes. Physiol. Meas. 2000, 21, 271. [Google Scholar] [CrossRef]
- Godin, D.T.; Parker, P.A.; Scott, R.N. Noise Characteristics of Stainless-Steel Surface Electrodes. Med. Biol. Eng. Comput. 1991, 29, 585–590. [Google Scholar] [CrossRef]
- McLaughlin, J.A.; McAdams, E.T.; Anderson, J. Novel Dry Electrode ECG Sensor System. In Proceedings of the 16th Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Baltimore, MD, USA, 3–6 November 1994; Volume 2, p. 804. [Google Scholar]
- Oh, T.I.; Yoon, S.; Kim, T.E.; Wi, H.; Kim, K.J.; Woo, E.J.; Sadleir, R.J. Nanofiber Web Textile Dry Electrodes for Long-Term Biopotential Recording. IEEE Trans. Biomed. Circuits Syst. 2013, 7, 204–211. [Google Scholar] [CrossRef]
- Fonseca, C.; Cunha, J.P.S.; Martins, R.E.; Ferreira, V.M.; de Sa, J.P.M.; Barbosa, M.A.; Martins da Silva, A. A Novel Dry Active Electrode for EEG Recording. IEEE Trans. Biomed. Eng. 2007, 54, 162–165. [Google Scholar] [CrossRef]
- Priego-Quesada, J.I.; De la Fuente, C.; Kunzler, M.R.; Perez-Soriano, P.; Hervás-Marín, D.; Carpes, F.P. Relationship between Skin Temperature, Electrical Manifestations of Muscle Fatigue, and Exercise-Induced Delayed Onset Muscle Soreness for Dynamic Contractions: A Preliminary Study. Int. J. Environ. Res. Public Health 2020, 17, 6817. [Google Scholar] [CrossRef] [PubMed]
- Rodriguez-Sanz, D.; Losa-Iglesias, M.E.; Becerro-de-Bengoa-Vallejo, R.; Dorgham, H.A.A.; Benito-de-Pedro, M.; San-Antolín, M.; Mazoteras-Pardo, V.; Calvo-Lobo, C. Thermography Related to Electromyography in Runners with Functional Equinus Condition after Running. Phys. Ther. Sport 2019, 40, 193–196. [Google Scholar] [CrossRef] [PubMed]
- Shakhih, M.F.M.; Ridzuan, N.; Wahab, A.A.; Zainuddin, N.F.; Delestri, L.F.U.; Rosslan, A.S.; Kadir, M.R.A. Non-Obstructive Monitoring of Muscle Fatigue for Low Intensity Dynamic Exercise with Infrared Thermography Technique. Med. Biol. Eng. Comput. 2021, 59, 1447–1459. [Google Scholar] [CrossRef] [PubMed]
- Perpetuini, D.; Trippetti, N.; Cardone, D.; Breda, L.; D’Attilio, M.; Merla, A. Detection of temporomandibular joint disfunction in juvenile idiopathic arthritis through infrared thermal imaging and a machine learning procedure. In Proceedings of the European Medical and Biological Engineering Conference, Portorož, Slovenia, 29 November–3 December 2020; Metzlerarmn, J.B., Cvetko, T., Mahnič-Kalamiza, A., Mityle, A., Eds.; Springer International Publishing: Cham, Switzerland, 2020; pp. 372–381. [Google Scholar]
- Ring, E.F.J.; Ammer, K. Infrared Thermal Imaging in Medicine. Physiol. Meas. 2012, 33, R33. [Google Scholar] [CrossRef] [PubMed]
- Cardone, D.; Pinti, P.; Merla, A. Thermal Infrared Imaging-Based Computational Psychophysiology for Psychometrics. Comput. Math. Methods Med. 2015, 2015, e984353. [Google Scholar] [CrossRef]
- Perpetuini, D.; Formenti, D.; Iodice, P.; Cardone, D.; Filippini, C.; Chiarelli, A.M.; Michielon, G.; Trecroci, A.; Alberti, G.; Merla, A. Central and Peripheral Thermal Signatures of Brain-Derived Fatigue during Unilateral Resistance Exercise: A Preliminary Study. Biology 2022, 11, 322. [Google Scholar] [CrossRef]
- Diakides, M.; Bronzino, J.D.; Peterson, D.R. Medical Infrared Imaging: Principles and Practices; CRC Press: Boca Raton, FL, USA, 2012; ISBN 978-1-4398-7250-5. [Google Scholar]
- Moreira, D.G.; Costello, J.T.; Brito, C.J.; Adamczyk, J.G.; Ammer, K.; Bach, A.J.E.; Costa, C.M.A.; Eglin, C.; Fernandes, A.A.; Fernández-Cuevas, I.; et al. Thermographic Imaging in Sports and Exercise Medicine: A Delphi Study and Consensus Statement on the Measurement of Human Skin Temperature. J. Therm. Biol. 2017, 69, 155–162. [Google Scholar] [CrossRef]
- Muyor, J.M.; Martín-Fuentes, I.; Rodríguez-Ridao, D.; Antequera-Vique, J.A. Electromyographic Activity in the Gluteus Medius, Gluteus Maximus, Biceps Femoris, Vastus Lateralis, Vastus Medialis and Rectus Femoris during the Monopodal Squat, Forward Lunge and Lateral Step-Up Exercises. PLoS ONE 2020, 15, e0230841. [Google Scholar] [CrossRef]
- van Boxtel, A.; Boelhouwer, A.; Bos, A. Optimal EMG Signal Bandwidth and Interelectrode Distance for the Recording of Acoustic, Electrocutaneous, and Photic Blink Reflexes. Psychophysiology 1998, 35, 690–697. [Google Scholar] [CrossRef]
- Boxtel, A.V. Optimal Signal Bandwidth for the Recording of Surface EMG Activity of Facial, Jaw, Oral, and Neck Muscles. Psychophysiology 2001, 38, 22–34. [Google Scholar] [CrossRef]
- Merletti, R. Standards for Reporting EMG Data. J. Electromyogr. Kinesiol. 1999, 9, 3–4. [Google Scholar]
- De Luca, C.J.; Donald Gilmore, L.; Kuznetsov, M.; Roy, S.H. Filtering the Surface EMG Signal: Movement Artifact and Baseline Noise Contamination. J. Biomech. 2010, 43, 1573–1579. [Google Scholar] [CrossRef] [PubMed]
- Welch, P. The Use of Fast Fourier Transform for the Estimation of Power Spectra: A Method Based on Time Averaging over Short, Modified Periodograms. IEEE Trans. Audio Electroacoust. 1967, 15, 70–73. [Google Scholar] [CrossRef]
- Oskoei, M.A.; Hu, H. Support Vector Machine-Based Classification Scheme for Myoelectric Control Applied to Upper Limb. IEEE Trans. Biomed. Eng. 2008, 55, 1956–1965. [Google Scholar] [CrossRef] [PubMed]
- Perpetuini, D.; Cardone, D.; Filippini, C.; Chiarelli, A.M.; Merla, A. A Motion Artifact Correction Procedure for FNIRS Signals Based on Wavelet Transform and Infrared Thermography Video Tracking. Sensors 2021, 21, 5117. [Google Scholar] [CrossRef] [PubMed]
- Richman, J.S.; Moorman, J.R. Physiological Time-Series Analysis Using Approximate Entropy and Sample Entropy. Am. J. Physiol. Heart Circ. Physiol. 2000, 278, H2039–H2049. [Google Scholar] [CrossRef]
- Dreiseitl, S.; Ohno-Machado, L. Logistic Regression and Artificial Neural Network Classification Models: A Methodology Review. J. Biomed. Inform. 2002, 35, 352–359. [Google Scholar] [CrossRef]
- Cervantes, J.; Garcia-Lamont, F.; Rodríguez-Mazahua, L.; Lopez, A. A Comprehensive Survey on Support Vector Machine Classification: Applications, Challenges and Trends. Neurocomputing 2020, 408, 189–215. [Google Scholar] [CrossRef]
- Rokach, L. Ensemble-Based Classifiers. Artif. Intell. Rev. 2010, 33, 1–39. [Google Scholar] [CrossRef]
- Schulz, E.; Speekenbrink, M.; Krause, A. A Tutorial on Gaussian Process Regression: Modelling, Exploring, and Exploiting Functions. J. Math. Psychol. 2018, 85, 1–16. [Google Scholar] [CrossRef]
- Domino, M.; Borowska, M.; Zdrojkowski, Ł.; Jasiński, T.; Sikorska, U.; Skibniewski, M.; Maśko, M. Application of the Two-Dimensional Entropy Measures in the Infrared Thermography-Based Detection of Rider: Horse Bodyweight Ratio in Horseback Riding. Sensors 2022, 22, 6052. [Google Scholar] [CrossRef] [PubMed]
- Perpetuini, D.; Russo, E.F.; Cardone, D.; Palmieri, R.; Filippini, C.; Tritto, M.; Pellicano, F.; De Santis, G.P.; Pellegrino, R.; Calabrò, R.S.; et al. Psychophysiological Assessment of Children with Cerebral Palsy during Robotic-Assisted Gait Training through Infrared Imaging. Int. J. Environ. Res. Public Health 2022, 19, 15224. [Google Scholar] [CrossRef] [PubMed]
- Perpetuini, D.; Formenti, D.; Cardone, D.; Filippini, C.; Merla, A. Regions of Interest Selection and Thermal Imaging Data Analysis in Sports and Exercise Science: A Narrative Review. Physiol. Meas. 2021, 42, 08TR01. [Google Scholar] [CrossRef]
- Cohen, J. Statistical Power Analysis for the Behavioral Sciences, 2nd ed.; Routledge: New York, NY, USA, 1988; ISBN 978-0-203-77158-7. [Google Scholar]
- Schneider, A.; Hommel, G.; Blettner, M. Linear Regression Analysis. Dtsch. Arztebl. Int. 2010, 107, 776–782. [Google Scholar] [CrossRef]
- Vardasca, R. The Influence of Angles and Distance on Assessing Inner-Canthi of the Eye Skin Temperature. Thermol. Int. 2017, 27, 130–135. [Google Scholar]
- Priego Quesada, J.I.; Cibrián Ortiz de Anda, R.M.; Pérez-Soriano, P.; Salvador Palmer, R. Introduction: Historical Perspective of Infrared Thermography and Its Application in Sport Science. In Application of Infrared Thermography in Sports Science; Priego Quesada, J.I., Ed.; Biological and Medical Physics, Biomedical Engineering; Springer International Publishing: Cham, Switzerland, 2017; pp. 1–23. ISBN 978-3-319-47410-6. [Google Scholar]
- Di Credico, A.; Perpetuini, D.; Izzicupo, P.; Gaggi, G.; Cardone, D.; Filippini, C.; Merla, A.; Ghinassi, B.; Di Baldassarre, A. Estimation of Heart Rate Variability Parameters by Machine Learning Approaches Applied to Facial Infrared Thermal Imaging. Front. Cardiovasc. Med. 2022, 9, 893374. [Google Scholar] [CrossRef] [PubMed]
- Magalhaes, C.; Mendes, J.; Vardasca, R. Meta-Analysis and Systematic Review of the Application of Machine Learning Classifiers in Biomedical Applications of Infrared Thermography. Appl. Sci. 2021, 11, 842. [Google Scholar] [CrossRef]
- Angelova, R.A.; Georgieva, E.; Markov, D.; Bozhkov, T.; Simova, I.; Kehaiova, N.; Stankov, P. Estimating the Effect of Torso Clothing Insulation on Body Skin and Clothing Temperatures in a Cold Environment Using Infrared Thermography. Fibres Text. East. Eur. 2018, 26, 122–129. [Google Scholar] [CrossRef]
- Ratovoson, D.; Jourdan, F.; Huon, V. A Study of Heat Distribution in Human Skin: Use of Infrared Thermography. EPJ Web Conf. 2010, 6, 21008. [Google Scholar] [CrossRef]
- Buxton, R.B. Introduction to Functional Magnetic Resonance Imaging: Principles and Techniques; Cambridge University Press: Cambridge, UK, 2009; ISBN 978-1-139-48130-4. [Google Scholar]
- Pinti, P.; Tachtsidis, I.; Hamilton, A.; Hirsch, J.; Aichelburg, C.; Gilbert, S.; Burgess, P.W. The Present and Future Use of Functional Near-infrared Spectroscopy (FNIRS) for Cognitive Neuroscience. Ann. N. Y. Acad. Sci. 2020, 1464, 5. [Google Scholar] [CrossRef]
- Chiarelli, A.M.; Perpetuini, D.; Croce, P.; Greco, G.; Mistretta, L.; Rizzo, R.; Vinciguerra, V.; Romeo, M.F.; Zappasodi, F.; Merla, A. Fiberless, Multi-Channel FNIRS-EEG System Based on Silicon Photomultipliers: Towards Sensitive and Ecological Mapping of Brain Activity and Neurovascular Coupling. Sensors 2020, 20, 2831. [Google Scholar] [CrossRef] [PubMed]
- Longmore, S.K.; Lui, G.Y.; Naik, G.; Breen, P.P.; Jalaludin, B.; Gargiulo, G.D. A Comparison of Reflective Photoplethysmography for Detection of Heart Rate, Blood Oxygen Saturation, and Respiration Rate at Various Anatomical Locations. Sensors 2019, 19, 1874. [Google Scholar] [CrossRef] [PubMed]
- Perpetuini, D.; Chiarelli, A.M.; Cardone, D.; Filippini, C.; Rinella, S.; Massimino, S.; Bianco, F.; Bucciarelli, V.; Vinciguerra, V.; Fallica, P.; et al. Prediction of State Anxiety by Machine Learning Applied to Photoplethysmography Data. PeerJ 2021, 9, e10448. [Google Scholar] [CrossRef] [PubMed]
- Wang, W.; den Brinker, A.C.; Stuijk, S.; de Haan, G. Algorithmic Principles of Remote PPG. IEEE Trans. Biomed. Eng. 2017, 64, 1479–1491. [Google Scholar] [CrossRef] [PubMed]
- Tasli, H.E.; Gudi, A.; den Uyl, M. Remote PPG Based Vital Sign Measurement Using Adaptive Facial Regions. In Proceedings of the 2014 IEEE International Conference on Image Processing (ICIP), Paris, France, 27–30 October 2014; pp. 1410–1414. [Google Scholar]
- Di Credico, A.; Perpetuini, D.; Chiacchiaretta, P.; Cardone, D.; Filippini, C.; Gaggi, G.; Merla, A.; Ghinassi, B.; Di Baldassarre, A.; Izzicupo, P. The Prediction of Running Velocity during the 30–15 Intermittent Fitness Test Using Accelerometry-Derived Metrics and Physiological Parameters: A Machine Learning Approach. Int. J. Environ. Res. Public Heal. 2021, 18, 10854. [Google Scholar] [CrossRef] [PubMed]
- Musa, R.M.; Majeed, A.P.P.A.; Taha, Z.; Chang, S.-W.; Nasir, A.F.A.; Abdullah, M.R. A Machine Learning Approach of Predicting High Potential Archers by Means of Physical Fitness Indicators. PLoS ONE 2019, 14, e0209638. [Google Scholar] [CrossRef]
- Herold, F.; Gronwald, T.; Scholkmann, F.; Zohdi, H.; Wyser, D.; Müller, N.G.; Hamacher, D. New Directions in Exercise Prescription: Is There a Role for Brain-Derived Parameters Obtained by Functional Near-Infrared Spectroscopy? Brain Sci. 2020, 10, 342. [Google Scholar] [CrossRef]
- Formenti, D.; Perpetuini, D.; Iodice, P.; Cardone, D.; Michielon, G.; Scurati, R.; Alberti, G.; Merla, A. Effects of Knee Extension with Different Speeds of Movement on Muscle and Cerebral Oxygenation. PeerJ 2018, 6, e5704. [Google Scholar] [CrossRef]
- Dindorf, C.; Bartaguiz, E.; Janowicz, E.; Fröhlich, M.; Ludwig, O. Effects of Unilateral Muscle Fatigue on Thermographic Skin Surface Temperature of Back and Abdominal Muscles—A Pilot Study. Sports 2022, 10, 41. [Google Scholar] [CrossRef]
- Escamilla-Galindo, V.L.; Estal-Martínez, A.; Adamczyk, J.G.; Brito, C.J.; Arnaiz-Lastras, J.; Sillero-Quintana, M. Skin Temperature Response to Unilateral Training Measured with Infrared Thermography. J. Exerc. Rehabil. 2017, 13, 526–534. [Google Scholar] [CrossRef]
- Church, J.S.; Hegadoren, P.R.; Paetkau, M.J.; Miller, C.C.; Regev-Shoshani, G.; Schaefer, A.L.; Schwartzkopf-Genswein, K.S. Influence of Environmental Factors on Infrared Eye Temperature Measurements in Cattle. Res. Vet. Sci. 2014, 96, 220–226. [Google Scholar] [CrossRef] [PubMed]
- Soroko, M.; Howell, K. Infrared Thermography: Current Applications in Equine Medicine. J. Equine Vet. Sci. 2018, 60, 90–96.e2. [Google Scholar] [CrossRef]
- Cardone, D.; Spadolini, E.; Perpetuini, D.; Filippini, C.; Chiarelli, A.M.; Merla, A. Automated Warping Procedure for Facial Thermal Imaging Based on Features Identification in the Visible Domain. Infrared Phys. Technol. 2020, 112, 103595. [Google Scholar] [CrossRef]

| ROI | IRI Feature | r (ARV) | r (MDF) |
|---|---|---|---|
| 1 | MeanTemp | 0.607 (p = 0.001) | 0.067 (p = 0.749) |
| STD | −0.213 (p = 0.306) | −0.160 (p = 0.444) | |
| Δ | 0.202 (p = 0.331) | 0.240 (p = 0.248) | |
| MeanPSD | 0.5966 (p = 0.002) | 0.106 (p = 0.615) | |
| Kurt | −0.167 (p = 0.426) | −0.122 (p = 0.563) | |
| Skew | −0.015 (p = 0.942) | 0.257 (p = 0.214) | |
| 90th P | 0.5856 (p = 0.002) | 0.049 (p = 0.818) | |
| SampEn | −0.293 (p = 0.155) | −0.160 (p = 0.446) | |
| Grad | 0.034 (p = 0.870) | −0.004 (p = 0.986) | |
| 2 | MeanTemp | 0.490 (p = 0.013) | 0.192 (p = 0.357) |
| STD | −0.052 (p = 0.804) | −0.102 (p = 0.629) | |
| Δ | 0.256 (p = 0.217) | 0.264 (p = 0.203) | |
| MeanPSD | 0.505 (p = 0.010) | 0.195 (p = 0.350) | |
| Kurt | −0.161 (p = 0.441) | −0.257 (p = 0.216) | |
| Skew | 0.082 (p = 0.699) | 0.270 (p = 0.192) | |
| 90th P | 0.487 (p = 0.014) | 0.194 (p = 0.354) | |
| SampEn | −0.270 (p = 0.196) | −0.088 (p = 0.675) | |
| Grad | 0.248 (p = 0.231) | 0.211 (p = 0.312) | |
| 3 | MeanTemp | 0.541 (p = 0.005) | 0.196 (p = 0.349) |
| STD | −0.117 (p = 0.579) | −0.151 (p = 0.473) | |
| Δ | 0.040 (p = 0.849) | −0.064 (p = 0.761) | |
| MeanPSD | 0.540 (p = 0.005) | 0.210 (p = 0.314) | |
| Kurt | 0.068 (p = 0.746) | −0.159 (p = 0.449) | |
| Skew | −0.166 (p = 0.427) | 0.232 (p = 0.264) | |
| 90th P | 0.518 (p = 0.008) | 0.186 (p = 0.375) | |
| SampEn | −0.247 (p = 0.235) | −0.116 (p = 0.581) | |
| Grad | 0.020 (p = 0.924) | 0.121 (p = 0.563) |
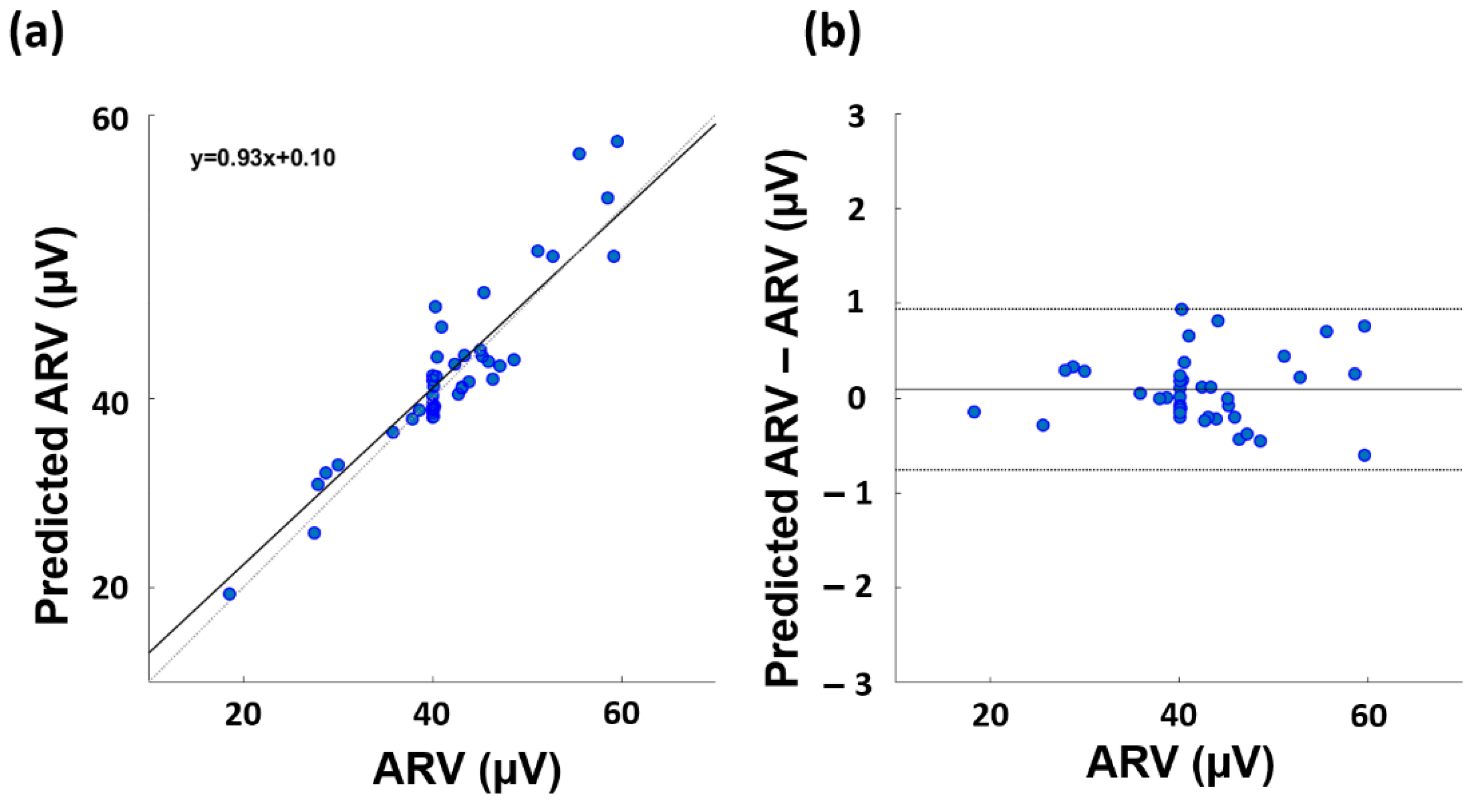
| Model | ROI | RMSE | r |
|---|---|---|---|
| LR | 1 | 0.869 | 0.453 (p = 0.023) |
| SVR (Linear) | 1 | 0.933 | 0.421 (p = 0.036) |
| SVR (Gaussian) | 1 | 0.959 | 0.711 (p = 6.75·10−5) |
| Ensemble | 1 | 0.824 | 0.545 (p = 0.005) |
| Gaussian | 1 | 0.902 | 0.414 (p = 0.040) |
| LR | 2 | 0.926 | 0.327 (p = 0.111) |
| SVR (Linear) | 2 | 1.004 | 0.412 (p = 0.041) |
| SVR (Gaussian) | 2 | 0.969 | 0.555 (p = 0.004) |
| Ensemble | 2 | 0.821 | 0.550 (p = 0.004) |
| Gaussian | 2 | 0.877 | 0.451 (p = 0.024) |
| LR | 3 | 1.051 | 0.377 (p = 0.063) |
| SVR (Linear) | 3 | 0.980 | 0.356 (p = 0.081) |
| SVR (Gaussian) | 3 | 0.977 | 0.457 (p = 0.022) |
| Ensemble | 3 | 0.833 | 0.529 (p = 0.007) |
| Gaussian | 3 | 0.456 * | 0.886 (p = 3.91·10−9) * |
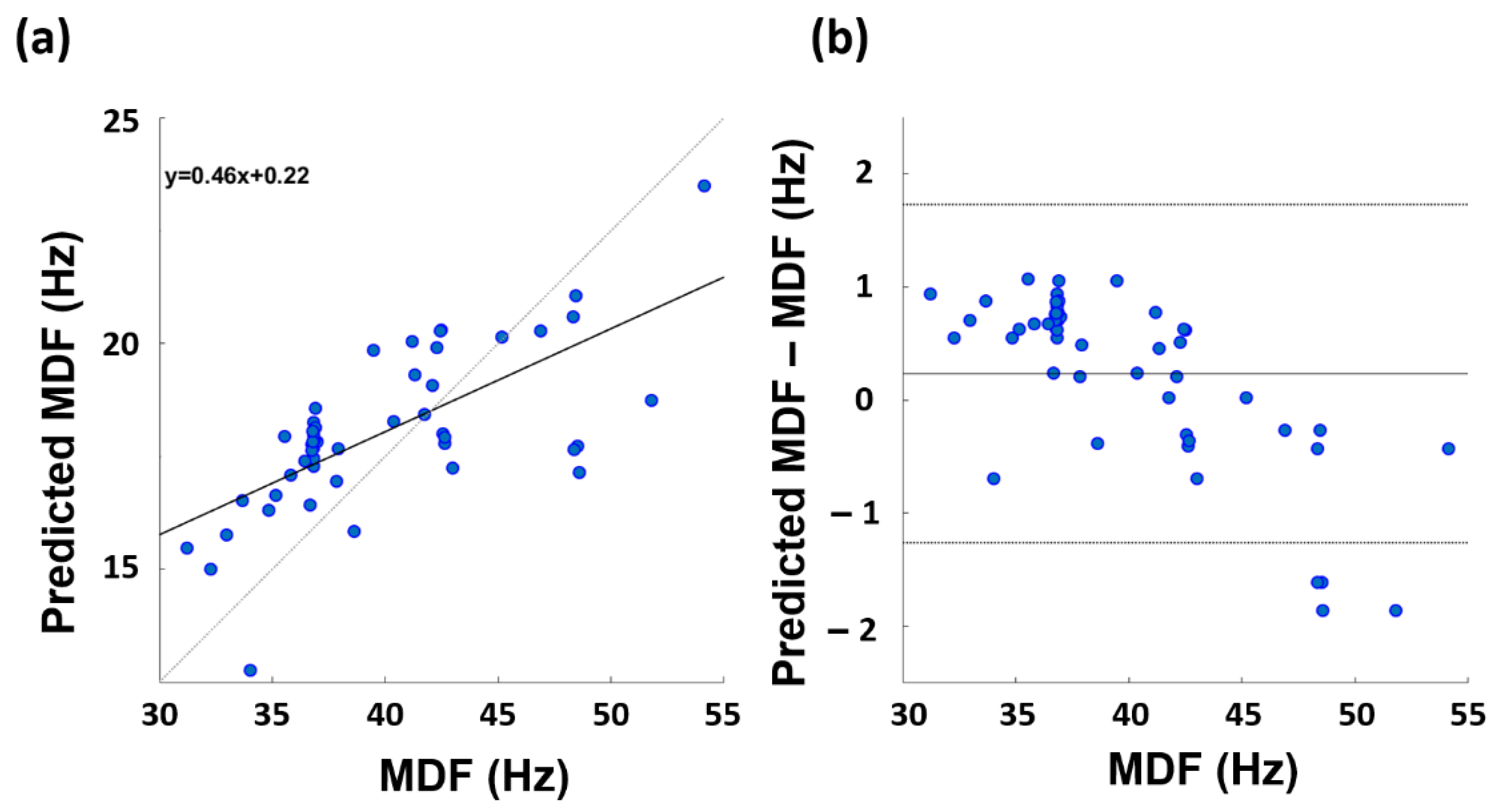
| Model | ROI | RMSE | r |
|---|---|---|---|
| LR | 1 | 1.094 | 0.368 (p = 0.063) |
| SVR (Linear) | 1 | 1.114 | 0.271 (p = 0.239) |
| SVR (Gaussian) | 1 | 0.981 | 0.447 (p = 0.025) |
| Ensemble | 1 | 1.041 | 0.382 (p = 0.059) |
| Gaussian | 1 | 0.854 | 0.509 (p = 0.009) |
| LR | 2 | 1.077 | 0.319 (p = 0.121) |
| SVR (Linear) | 2 | 0.994 | 0.528 (p = 0.007) |
| SVR (Gaussian) | 2 | 1.016 | 0.498 (p = 0.011) |
| Ensemble | 2 | 0.993 | 0.420 (p = 0.037) |
| Gaussian | 2 | 1.017 | 0.464 (p = 0.020) |
| LR | 3 | 1.085 | 0.364 (p = 0.074) |
| SVR (Linear) | 3 | 0.775 | 0.623 (p = 8.85·10−4) |
| SVR (Gaussian) | 3 | 1.026 | 0.335 (p = 0.102) |
| Ensemble | 3 | 1.039 | 0.442 (p = 0.027) |
| Gaussian | 3 | 0.751 * | 0.661 (p = 3.21·10−4) * |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Perpetuini, D.; Formenti, D.; Cardone, D.; Trecroci, A.; Rossi, A.; Di Credico, A.; Merati, G.; Alberti, G.; Di Baldassarre, A.; Merla, A. Can Data-Driven Supervised Machine Learning Approaches Applied to Infrared Thermal Imaging Data Estimate Muscular Activity and Fatigue? Sensors 2023, 23, 832. https://doi.org/10.3390/s23020832
Perpetuini D, Formenti D, Cardone D, Trecroci A, Rossi A, Di Credico A, Merati G, Alberti G, Di Baldassarre A, Merla A. Can Data-Driven Supervised Machine Learning Approaches Applied to Infrared Thermal Imaging Data Estimate Muscular Activity and Fatigue? Sensors. 2023; 23(2):832. https://doi.org/10.3390/s23020832
Chicago/Turabian StylePerpetuini, David, Damiano Formenti, Daniela Cardone, Athos Trecroci, Alessio Rossi, Andrea Di Credico, Giampiero Merati, Giampietro Alberti, Angela Di Baldassarre, and Arcangelo Merla. 2023. "Can Data-Driven Supervised Machine Learning Approaches Applied to Infrared Thermal Imaging Data Estimate Muscular Activity and Fatigue?" Sensors 23, no. 2: 832. https://doi.org/10.3390/s23020832
APA StylePerpetuini, D., Formenti, D., Cardone, D., Trecroci, A., Rossi, A., Di Credico, A., Merati, G., Alberti, G., Di Baldassarre, A., & Merla, A. (2023). Can Data-Driven Supervised Machine Learning Approaches Applied to Infrared Thermal Imaging Data Estimate Muscular Activity and Fatigue? Sensors, 23(2), 832. https://doi.org/10.3390/s23020832












