Abstract
Herein, we have discussed three major methods which have been generally employed for the generation of optical beams with orbital angular momentum (OAM). These methods include the practice of diffractive optics elements (DOEs), metasurfaces (MSs), and photonic integrated circuits (PICs) for the production of in-plane and out-of-plane OAM. This topic has been significantly evolved as a result; these three methods have been further implemented efficiently by different novel approaches which are discussed as well. Furthermore, development in the OAM detection techniques has also been presented. We have tried our best to bring novel and up-to-date information to the readers on this interesting and widely investigated topic.
1. Introduction
Optical beams transporting orbital angular momentum (hereafter expressed as OAM), also known as optical vortices (OVs), have piqued researchers’ interest in recent years due to their unique properties [1]. A helical wavefront and a phase proportional to exp(ilϕ) describe such beams, where l is an integer known as the topological charge, which could take any value. Optical OAM modes form an orthogonal basis that can be utilized to fundamentally enhance the capability of fiber optic [2], free-space, and quantum communications [3]. Also, the phase of optical vortices is utilized in the analysis of the laser field’s polarizing properties. For example, a single fork-shaped phase grating matched with first-order vortices for detecting radially and azimuthally polarized laser beams [4], and more complex multi-order optical elements matched with vortices of different orders, make it possible to uniquely determine various combinations of the cylindrical polarization state and the vortex phase of the laser beam [5,6,7]. Optical tweezers and spanners [8,9,10,11,12], non-diverging speckles [13], imagining and microscopy [14,15,16,17], novel sensing technologies for detecting molecules and nanostructures [18,19,20,21,22], and object motion detection [23,24] are only a few of the applications for optical vortices that have been proposed so far. As a result, there is a growing demand for efficient beam generation methods.
Since Allen and coworkers’ seminal paper [25], light beams carrying OAM have spawned a burgeoning area of study, resulting in a plethora of studies and applications [26], including particle trapping [27], tweezing and manipulation [28], astronomical coronagraphy [29], mode-division multiplexing [30], and security [31]. Discrete optical elements perform most methods of generating optical vortices, which are traditionally divided into two groups: spatial and fiber generating methods [32]. Diffractive optical components [33,34], cylindrical lens mode converters [35], spiral phase plates (SPPs) [36,37], circular and spiral gratings [38], spatial light modulators [39], metamaterials [40], and q-plates [41] are among the devices in the first category. On the millimeter scale, the second category of fiber-based systems, such as fiber gratings [42], chirally coupled core fibers [43], and photonic lanterns [44], seem to provide more promising solutions in terms of system size. In addition, the solutions based on photonic integrated circuits (PICs), due to their energy efficiency, small footprint, and performance reliability, become a sensible option for implementing the OAM-based applications. Furthermore, PIC’s fabrication processes ensure repeatability in the large-scale production of the developed devices. The PIC-based OAM modes generator satisfies the modern trend toward optical integration in terms of practical miniaturization and multiplexing optical signals for transmission in a single propagation medium.
The generation of in-plane or out-of-plane light with OAM is an interesting topic that has been studied by researchers all over the world. The popularity of this topic can be witnessed in Figure 1 where the number of published papers index in the Scopus database is presented from the years 2000–2021. It shows a linear trend in the publication of papers as the topic is developing with time and several new techniques have been proposed for the efficient generation of light with OAM.
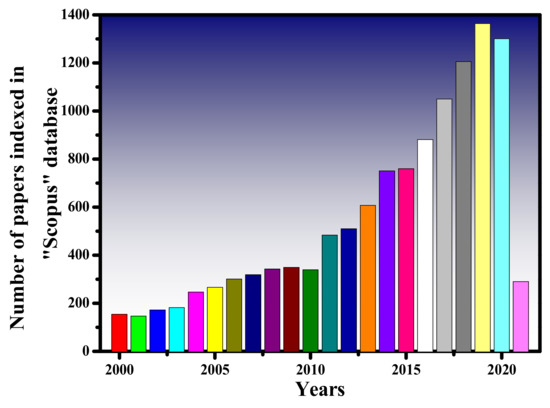
Figure 1.
The number of papers related to the “Orbital angular momentum” topic searched in the Scopus database for the years 2000–2021.
In this paper, the most significant and recent advances in the generation of light with OAM are discussed. We have focused on three different methods that are popular among the scientific community and widely researched in recent times. In Section 2, OAM generation via diffractive optics is discussed. It involves three significant methods, i.e., spiral phase plate (hereafter expressed as SPP), computer-generated holograms (hereafter expressed as CGHs), and diffractive optical elements (DOEs) that are considered in detail. Section 3 is devoted to metasurfaces (hereafter expressed as MSs). In recent times, the adaptable MSs, 2D arrays of subwavelength structures with space-variant phase responses, deliver robust and accessible methods for the generation of OAM. Section 4 discusses recent developments in OAM generation in photonic integrated circuits (PICs). These OAM generators can be separated into two categories; one is that OAM beams are created out-of-plane and transmitted in free space, while the other is that OAM beams are produced in-plane and propagated in waveguides (hereafter represented as WG). The latter has attracted a lot of interest in fully utilizing the distinctive characteristic of OAM beams in guided optics. Nevertheless, to ensure uniform spatial distributions of multi-coupled WGs, the majority of the integrated OAM generators need extremely critical dimension control technology. In the end, a brief overview of the OAM detection methods is discussed in Section 5 followed by the conclusion in Section 6.
Allowing a light beam to transmit through a medium with spiral inhomogeneity in the longitudinal path to produce an integer phase stage along the azimuthal angle is the most explicit method to establish a helical wavefront. The spiral phase plate (SPP), which was first used in 1994, is a straightforward route to assemble a plate with a helical surface [36]. Usually, the helical surface is discretized into various steps as diffractive elements to make the fabrication process simpler. The working wavelength can be slightly tuned by matching the refractive index. Another approach for creating optical vortices is to utilize a computer-generated hologram (CGH) [45,46]. A spiral interfering fringe is produced when an OV beam bearing a spiral wavefront collinearly interferes with a Gaussian beam, with the number and rotating direction of the spiralling arms signifying the number and sign of the topological charge, respectively. As it hits with an off-axis plane wave, it produces a forked grating with a visible defect on the fringes where a phase singularity occurs. These distinctive interference patterns were also commonly used to describe an OV beam’s topological charge. The spiral fringe or the forked grating may be used to create a hologram plate established on the interference property. Commercial spatial light modulators (SLMs) established on pixelate liquid crystals can be programmed to produce holograms through a consumer terminal, and are widely used in this way [47].
Recent advancements in flexible MSs have also accelerated the development of efficient and convenient OAM generation routes [48,49,50,51,52,53]. MS is based on frequency selective surfaces (FSSs) [54]. They are made up of different shaped and oriented subwavelength scatterers [55]. As a result of the high feasibility of tailoring the geometry and orientation of the ultracompact scatterers, they go beyond traditional FSSs. The sudden phase shift at the scatterers causes MSs to change the wave properties locally. Scatterers can cover an entire 2π phase shift by adjusting the geometry or alignment, allowing for arbitrary beam formation [56]. In the meantime, scatterers can be built to adjust the wave front. They may also have a magnetic response in addition to the electric response. Nonperiodic MSs that respond to both electric and magnetic fields have been introduced. These surfaces are referred to as metamaterial Huygens’ surfaces, since their design is based on a rigorous interpretation of Huygens’ principle [57]. The magnetic response aids in compensating for the impedance mismatch at the MS interface, allowing for perfect performance. The design principles for OAM generation lead to one familiar rule: the implementation of the azimuthal phase term eilϕto EM waves, even though there are numerous models in various categories and appropriate for different application circumstances. They are divided into two groups: those that are independent of wave polarization and those that are dependent on it.
Figure 2 demonstrates four different methods used for the creation of light with OAM which are widely used among the researchers [58,59,60,61]. Another device, comprising a mutable amplitude splitter (VAS) and an OAM emitter, has recently been suggested, in which the comparative amplitude of the two OAM states with inverse chirality can be tuned [62]. Furthermore, many methods such as WG-array centered radial grating coupling system [63], hybrid 3D PIC device [64], organic semiconductor μ-disk laser, and micro-scale SPP integrated VSCEL [65] have demonstrated readily OAM generation and (de-)multiplexing (multiple OAM states superposition) functions, which differ from this azimuthal grating coupling system. These devices demonstrated the possibility of developing advanced OAM functions on scalable and dense PICs using on-chip dynamical control of OAM states [66].
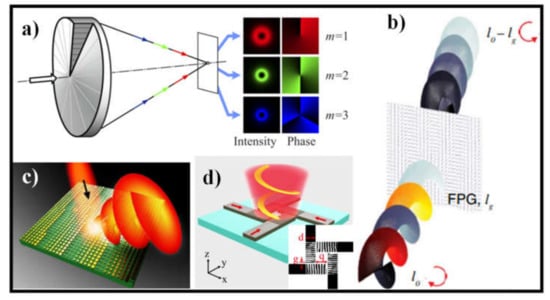
Figure 2.
Methods to generate light with OAM: (a) Shift in the OAM order by illuminating a 3D element with the laser light of different wavelengths [58]; (b) OAM generator via CGH [59]; (c) Schematic of the OV beam generator from MS [60]; and (d) The schematic illustration of the OV beam generator on the embedded multi-WG [61].
2. OAM Emitters Based on Diffractive Optic Elements
Fiber optics are now employed in the backbone part of modern data communications. However, for specific applications, fiber is not practical due to the immobility of the sending and receiving ports connected to the fiber laid down. Free space optical networking, also identified as wireless optical communication, reduces the system’s spatial dependency. Furthermore, applying OAM to a beam of light mitigates some of the shortcomings that would otherwise be present. A significant limiting factor on signal path length is the rate at which light signals spread through the air. An image has been effectively sent 3 km through the air utilizing OAM, despite considerable turbulence along the path length [67].
Since laser beams with OAM are of special interest for data channel multiplexing [2,68,69]. Many studies are devoted to the propagation of OV beams as in free space [70,71,72,73] and in optical fibers [74,75,76]. To implement multichannel information transfer using OAM, a certain superposition of OVs with a given energy and phase distribution in the transmitter must be excited on the transmitting side, so each mode transmits an independent information signal. This can be done using elements of diffractive optics. The design doctrines for OAM production leads to one general rule: the implementation of the azimuthal phase term eilϕ to EM waves, even though there are numerous models in different types and appropriate for distinct application circumstances. The first scheme makes use of isotropic materials like SPPs [77] and CGHs [78]. An SPP is the simplest device for manipulating OAM modes at millimeter frequencies. An SPP is a dielectric slab of material with an azimuthally reliant on thickness that causes incident radiation to undergo an azimuthal phase change [79,80]. The SPP’s total step height, h, is selected so that the total phase change around the SPP’s center is an integer multiple of 2πl, where l is an integer. The azimuthal mode number l of the incident radiation is modified because of this, such that: , where Δn is the refractive index difference between the dielectric material and the surrounding medium, and λ is the incident wavelength.
In addition to SPPs, various DOEs (see Figure 3) are actively used to generate OVs, such as spiral axicons [81,82,83], generating Bessel beams of high orders, and spiral zone plates [84,85,86] which are a combination of a focusing lens and an SPP. Recently, unconventional focusing elements have been used to provide abruptly autofocusing [87,88,89]. The listed elements form OV beams on the optical axis. To generate OV beams at an angle to the optical axis or in different diffraction orders, fork gratings are used [90,91,92,93], as well as curved fork gratings [94,95,96]. Regular fork gratings correspond to plane wave multiplexing, while curved fork gratings provide conical wave multiplexing. More complex elements are also known, for example, for multiplexing Airy beams [97], hypergeometric beams [98], and Laguerre-Gauss modes [99,100,101].
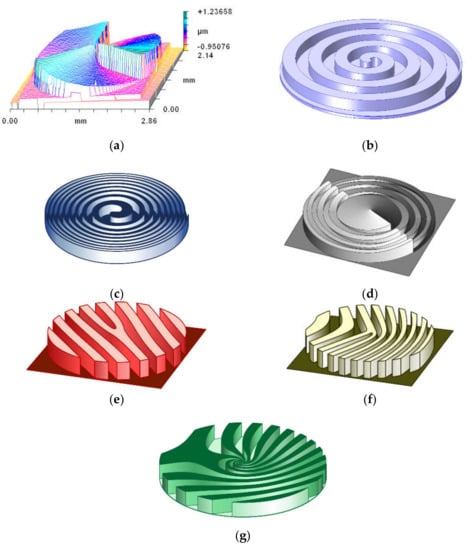
Figure 3.
Elements of singular optics: (a) SPP. Reprinted with permission from ref. [36]. Copyright 1994, Elsevier; (b) spiral axicon; (c) spiral zone plate; (d) OV autofocusing optical element; (e) fork grating; (f) curved fork grating; and (g) grating for OV hyper-geometric laser beams generation.
DOEs are relatively simple optical elements, as shown in Figure 3. To generate a co-axial linear arrangement of a finite number of OV modes with given weights (or information codes) more complex optical elements are used [102,103,104,105], which are calculated using various coding methods [106,107,108,109]. Note, the classical diffraction SPPs are manufactured for a specific laser wavelength. However, refractive (with high relief) SPPs have been successfully used for different wavelengths [110,111] allowing the OVs generation of various orders, including fractional orders [58]. The advantages of SPPs made from solid materials are high damage threshold and efficiency.
The same qualities are inherent in devices based on solid anisotropic crystals, which are often used not only to generate OV beams but also cylindrically polarized beams [112,113,114,115,116]. For example, Figure 4 shows an optical system for the generation of OV Laguerre-Gaussian beams with radial or azimuthal polarization by a combination of DOEs and anisotropic crystals [115]. Spatial light modulators (SLMs) are very convenient and versatile devices for the formation of vector OV beams [117,118,119,120,121]. However, it is known that SLMs are characterized by low efficiency, resolution, and when used with high-power lasers they require additional cooling systems [122]. Thus, the application of DOEs remains relevant.
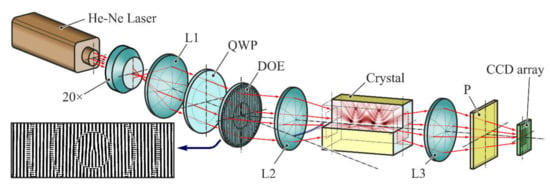
Figure 4.
Optical system for generation of vector OV beams by a combination of DOEs and anisotropic crystals: a He-Ne laser emitting linearly polarized light which was expanded using an objective (L1), a quarter-wave plate (QWP) was utilized to alter the linearly polarized beam into the circularly polarized beam, the diffractive optical element (DOE) generates OV Laguerre-Gaussian modes which are focusing by a lens (L2) into a c-cut CaCO3 crystal, cylindrically polarized beams (with radial or azimuthal polarization) are imaging by a lens (L3) at CCD array and analyzed by a polarizer (P). Reprinted with permission from ref. [115]. Copyright 2017, Elsevier.
3. MSs for Generation of Vector OV Beams
Alternatively, an antenna or antenna array’s excitation may be explicitly modified to fulfill the necessary phase requirement, allowing an OAM wave to be emitted out [123]. The abrupt phase change at scatterers on an MS can also be used to create eilϕ. The resonant frequency of the scatterer is modified by changing its geometry, causing the phase shift to differ at the desired frequency. After optimization, a total of 2π phase shift is achieved, and the effective generation of various OAM states has been demonstrated [124]. Tunable scatterers stocked by varactor diodes have recently been suggested as a convenient way to generate multiple OAM modes [125]. Scatterers can also be rendered anisotropic to regulate various polarizations independently. Even if the scatterer’s responses are polarization-dependent, the helicity of the emitted OAM is independent of the incident wave’s polarization state. In other words, the helicity is fixed.
To generate dual-mode convergent OAM beams, a high-efficiency dual-polarized transmissive MS is presented in [126]. To achieve the phase modulation for the orthogonal polarizations, the recommended transmissive MS consists of dual-polarized MS units made up of four packed stripes coupled through a Jerusalem-cross aperture on the interlayer ground. The MS units are capable of absolute 2π phase modulation with low transmission loss. The suggested transmissive MS for both orthogonal polarizations, which has been proven numerically and experimentally, stimulates converged OAM beams with mode numbers ℓx = +1 and ℓy = −2. The MS prototype with 30 × 30 units was fabricated and tested to authenticate the efficacy of the engineered MS for generating dual-polarized dual-mode converged OAM beams. The measurements are carried out in the near-field anechoic chamber using a 3D platform and an open-ended WG probe, as shown in Figure 5a [126]. Figure 5b,c depicts the measured full hemisphere far-field radiation patterns in magnitude and phase for the two orthogonal polarized OAM modes, with the excessive intensity annular tapered patterns, as well as the typical spiral phase fronts and on-axis phase singularities, obviously visible [126].
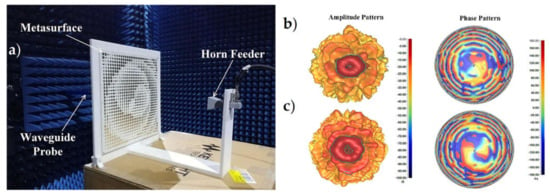
Figure 5.
(a) The fabricated MS and its experimental setup with a WG probe in the near field chamber [126]. Radiation forms of the MS: (b) x-polarization, OAM mode lx = +1 [126]; and (c) y-polarization, OAM mode ly = −2 [126].
The transformation and coupling of SAM and OAM are the basis for the second scheme [127,128]. This occurs in media that are nonuniform and anisotropic, such as q-plates [129]. Q-plates have a spatially shifting optical axis and change the circular polarization state from left to right or right to left. AM conservation law may be used to justify their behavior. SAM changes by a factor of ±2ħ when the circular polarization state is flipped. The cumulative AM is conserved when the q-plate is cylindrically symmetrical so that the output wave must have an OAM of ∓2ħ. When the q-plate is not cylindrically symmetrical, it introduces extra AM into the device, allowing for the generation of different orders of OAM in the output wave. Because of their versatility and anisotropic properties, liquid crystals are commonly used to make q-plates. The birefringent retardation in liquid crystals varies with temperature on external voltage, allowing the conversion efficiency to be tweaked [130]. When the retardation is π, optimum productivity is achieved. The function of q-plates has been implemented using MSs [78,131,132]. The rotation of the optical axis of a q-plate, along with the insertion of a geometric step, is analogous to the flipping of the circular polarization state accomplished by anisotropic scatterers and the rotation of the scatterers. Geometric phase MSs is the name given to this type of MS [133]. Geometric-phase MSs, unlike MSs that use the first scheme, generate OAM in conjunction with a transition in the polarization state of the output wave, which is radically different from the first scheme. The incident SAM determines the handedness of the generated OAM.
Of course, MSs are very promising devices for generating vector OV beams, since they are compact optical elements and can simultaneously perform several operations: to not only generate OV phase and perform polarization conversion, but also focus or multiplexing beams. There are metal MSs (subwavelength structures etched on metal films) [134,135] and dielectric MSs [136,137]. Metal subwavelength gratings operate as a rule in a reflecting mode and are less chemically resilient to an assertive medium. The main disadvantage of subwavelength dielectric gratings is the nonuniformity of amplitude transmission for different polarizations. This drawback can be prevented by merging several functions: polarization transformation by subwavelength gratings and focusing, for orthogonal ridges in adjacent Fresnel zones [138,139].
Large numbers of OAM modes are normally controlled with a diffractive hologram projected on an SLM in optical systems, however, due to the comparatively long wavelengths, comparable systems do not occur for millimeter and radio frequencies. The results of measurements performed on a modular SPP design capable of producing millimeter-wavelength beams with an azimuthal mode number of l ± 10 is offered [140]. The plate is made up of 10 single modules that interlock to form the entire plate assembly, allowing for better machining precision than traditional methods. As a result, this design may be utilized in millimeter-wavelength systems that involve massive OAM mode manipulation. The plate was made of polypropylene and tested at a frequency of 100 GHz. Three near field surfaces behind the plate were measured using a 3D field scanner. The OAM intensity ring was visible in intensity measurements, and phase measurements revealed 10 phase dislocations, indicating appropriate functionality [140].
In [141], an all-fiber high-efficiency OV beam generator is demonstrated experimentally. The generator is created by combining a kinoform spiral zone plate (KSZP) on top of the composite fiber structure, as illustrated in Figure 6a, using fs-laser two-photon polymerization 3D nanoimprinting. By overlaying a spiral phase onto a kinoform lens, the KSZP with spiral continuous-surface relief function is created, allowing an all-incident beam to be efficiently concentrated and transformed into a single-focus OV beam without the unwanted zero-order diffracted light and extra high-order focus. The SEM image of the nanoimprinted KSZP microstructure with topological charge l = −1 is shown in Figure 6b. Experiments show that the all-fiber generators’ focusing efficiency and OV purity are over 60% and 86%, respectively, under arbitrary polarized light incident conditions, which is significantly greater than a typical binary SZP integrated on an optical fiber facet [141]. The simulated and experimental focal spot profiles along with the coaxial interference patterns are shown in Figure 6c. The suggested all-fiber photonic devices have encouraging capacity in optical communication, particle manipulation, and quantum computing applications because of their compact size, versatile nature, polarization insensitivity, superior focusing power, and high OV purity.
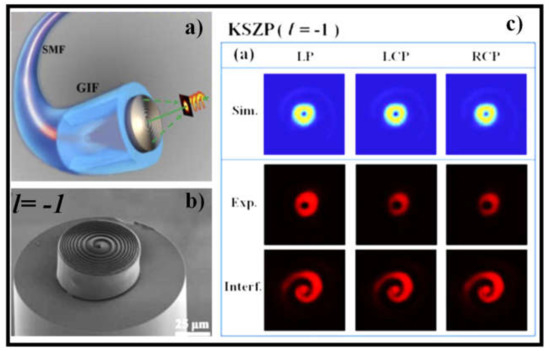
Figure 6.
(a) Graphical design of all-fiber focused OV beam generator [141], (b) SEM image of the nanoimprinted KSZP microstructure with topological charge l = −1 [141], and (c) focal spot profiles acquired from FDTD simulation (top row), experimental measurement (middle row), and the measured coaxial interference forms (bottom row) [141].
4. OAM Beams Generation with Photonic Integrated Circuits
There are two types of PIC solutions for generation and (de)multiplexing of OAM-beams currently available: out-of-plane and in-plane solutions. The out-of-plane approach implies the principles of scattered field generation with a help of single passive PIC elements or integrated with a light source. Most methods for out-of-plane generation and (de)multiplexing demonstrate good potential for scalability. For example, a CMOS-compatible PIC for generating or receiving azimuthally or radially polarized beams is revealed in [63,142], which is based on the SOI platform. The PIC uses annular gratings and a star coupler and can focus the beam on its own, so no external lenses are needed. It was validated, that the device is mode-number scalable, which is obtained by increasing the number of WG arms. The proposed principle was also experimentally demonstrated in [143], in which data transmission using the proposed PIC was performed for two multiplexed OAM states. The annual grating is also used in [144], where the authors show a structure for producing and encoding OAM modes that includes a ring cavity, a bus WG, and eight download units that are evenly connected to the ring and spread evenly around the circle. The electrically controlled thermo-optic effect in [145] demonstrated the dynamic switching of nine OAM modes with azimuthal polarization by using a spatially isolated μ-ring cavity and scattering unit that could be tuned individually. Figure 7a shows an applied cobweb-like unit consisting of a bus WG and a μ-ring hollow with 16 downloading WGs and 16 gratings. The micrograph of the fabricated emitter with the resolution of 200 µm is presented in Figure 7b, and the scanning electron micrograph with the resolution of 5 µm in Figure 7c. As it could be seen, the total diameter of the ring is 400 µm.
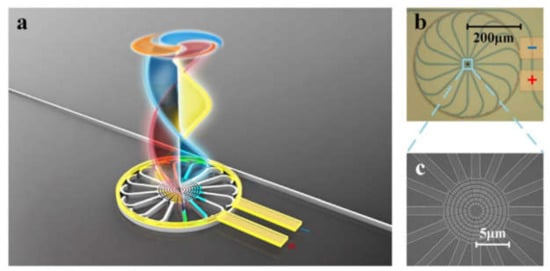
Figure 7.
The integrated photonic emitter: (a) The graphical illustration [145]; (b) the micrograph [145]; and (c) the SEM image of the manufactured device [145].
Another widespread solution is to obtain light enclosed in whispering gallery modes (WGMs) with high OAM into free-space beams with the well-controlled extent of OAM using Si-integrated optical OV emitters and angular gratings. The angular grating’s working theory is like that of second-order gratings, which are generally used as input/output couplers in straight WGs, in which the directed wave is dispersed by the grating elements collectively and a substantial fraction of power is redirected in a specific direction, resulting in constructive interference [146]. WGMs with high OAM can be assisted by circular optical resonators such as μ-rings or μ-disks. The example of silicon nitride μ-disk OAM-resonator was demonstrated in [147], where it was combined with an aluminium nanorod antenna array shaped in periodic rings for generation of a polarization-pure single OAM beam. The proposed unit cell engineering could provide many more possibilities for vector OV beams implementation; however, this approach is not without the disadvantage of simultaneous generating high-order parasitic modes. In [148] a μ-ring is represented by an angular grating structure with a periodic modulation of refractive index in the azimuthal direction which is embedded into the WGM resonator. The wavefront of the radiated light from the μ-ring skew in the azimuthal direction turns into a helix if the WG with grating is bent to form a loop. Theoretical predictions that the emitted beams hold precisely specified and customized OAM were also confirmed by experimental characterization.
The OAM beam emitter constructed on a shallow-ridge silicon μ-ring is proposed in [149] where the azimuthally distributed gratings generate an OAM beam, and each grating element is a hole etched on top of the WG to scatter radially polarized light. The key parameters, i.e., the number of grating elements and the radiation efficiency of a single element, are optimized to enhance the OAM order purity for l up to ±4. A variable amplitude splitter and an OAM emitter based on a μ-ring cavity are presented in [62]. Another research [150] employs a silicon-on-insulator μ-ring with three superimposed gratings, each designed to emit a different OAM order, as a device enabling 3 × 3 optical switching. This approach utilizing the ring resonators with gratings provides good mode purity for OAM-multiplexing, however, the OAM-beams are generated already out of the chip plane in free space and cannot be used or processed at the chip any more.
Finally, a generation of optical beams carrying superposition of OAM states by utilizing superimposed angular gratings embedded into WGM μ-ring resonators is described in [151]. Two sets of angular gratings with distinct period-Λ1 (Figure 8(a1)) and Λ2 (Figure 8(a2)) have been superimposed into a ring resonator in the device, resulting in a superimposed grating envelope with numerous beat perturbations, as illustrated in Figure 8(a3). Figure 8b–d shows far-field images of the two-beat grating device recorded at various resonant wavelengths according to the transmission/radiation spectrum, resulting in various topological charge combinations. The near-field pattern (Figure 8e) and the well-defined spiral interference fringes (Figure 8d) show two crescent-shaped lobes positioned in a circular pattern, showing that the radiated beams are truly emitted from the modulated gratings. Because it does not require any extra couplers or MZIs, the suggested device is quite small. Furthermore, by simply adding more gratings, it may construct superposition states in more than two dimensions. Because all modes are emitted from the same source mode via the same superimposed grating, the used methodology is simple and maintains a fairly constant phase between the OAM states.
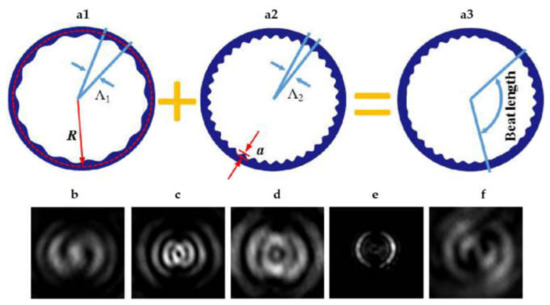
Figure 8.
(a1,a2) Schematic of two single grating (with period of Λ1 and Λ2, respectively) superimposed into multiple-beat modulated device [151]. An unfolded view of resulting the three beats device (a3) [151]. The far-field patterns of the two-beat grating device: (b) 1508.1 nm, topological charges combination +1 and −1; (c) 1518.9 nm, topological charges combination 0 and −2; and (d) 1530 nm, topological charges combination −3 and −1 [151]. The near-field pattern is showing in (e), and the well-defined spiral interference fringe existed at appropriate locations is showing in (f) [151].
Integrated WGs could be also applied in the out-of-plane approach. In [148] optical OV beam with a well-defined and continuously tunable OAM state is generated using the silicon bus WG that forms an open circle. A multi-WG surface holographic gratings composed of four WGs perpendicular to each other with holographic gratings etched on their surfaces is proposed in [61] for high-order OAM generation up to l = +8. In [152,153], the free space OV beam and the in-plane guiding wave can be transferred to each other by placing a holographic grating on top of a dielectric WG. The geometry parameters of this μ-scale holographic grating are extremely stable. Furthermore, multiple generators made up of two holographic gratings on two parallel WGs are investigated, which can modulate the OV beam in an efficient and versatile manner by regulating the phase of the input light. Figure 9a shows a schematic of the proposed OV beam generator, in which incident light from one WG port (in-plane) is transformed to free space (vertical) OV beam by the WG surface holographic grating (WGSHG).
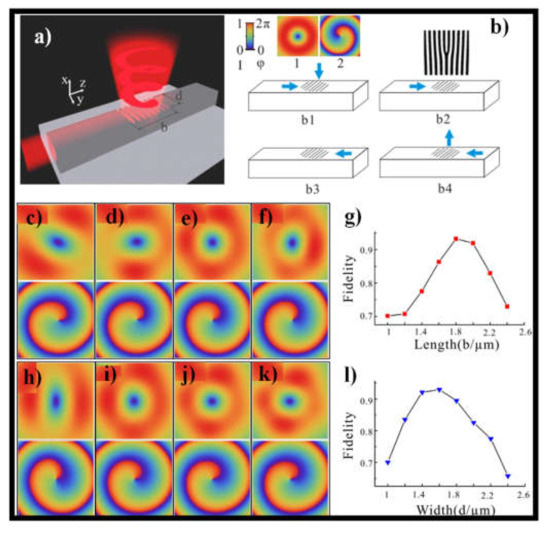
Figure 9.
(a) The graphical image of the OV beam generator, (b) (b1–b4), the basis of the holographic grating on WG. The acquired OV beams by the holographic gratings with different sizes. The intensity and phase distributions are shown in the upper row and down row of the figures, (c–f) consistent to the holographic gratings with a constant width d = 1.5 μm but different lengths b = 1, 1.4, 1.8, 2.2 μm, and (h–k) corresponding to the holographic gratings with a constant-length b = 1.8 μm but dissimilar widths d = 1, 1.4, 1.8, and 2.2 μm, respectively, (g,l) are the fidelities of the attained OV beams as the functions of length b and width d, correspondingly. Reprinted with permission from ref. [152]. Copyright 2016, Elsevier.
The essential idea of holographic grating is shown in Figure 9(b1–b4). Figure 9c–f shows the simulation findings of the acquired beam for holographic gratings with a constant width d = 1.5 μm and different lengths b = 1 μm, 1.4 μm, 1.8 μm, and 2.2 μm. Figure 9g shows the OV beam fidelities as a function of length b, where the fidelities are larger than 0.7 for b in the range [1,2.4] μm. Fidelity is calculated by using the following formula:
where Ao(x,y,z) and At(x,y,z) are the amplitudes of the obtained and target vortex beams, respectively [152]. Fidelity surges with b until it hits a peak, after which it drops with b. The greatest fidelity is 0.93 for b = 1.8 μm, which is the length of the holographic grating in the accompanying figure. The OV beam is formed based on the grating width d and the fixed length b = 1.8 μm, as shown in Figure 9h–l. The field distribution for d = 1 μm, 1.4 μm, 1.8 μm, and 2.2 μm indicate that d has a moderate effect on phase but a considerable effect on amplitude. The fidelity represented in Figure 9l has an optimal F = 0.93 for d = 1.6 μm.
The main disadvantage of the WGMs OAM emitters is that their inherent narrow bandwidths prevent them from being compatible with WDM/FDM techniques. To overcome the μ-ring’s bandwidth restriction, freeform MS was demonstrated in [154], utilizing a novel joint path-resonance phase control concept. The proposed SOI emitter is based on series of subwavelength cavities with low Q resonance, providing phase control and short response time for an ultra-broadband operation. [154] proposes an OV beam generation method based on elliptical nanoholes array designed on the MS with spiral phase distributions.
OAM beams can also be generated directly by adding an integrative OV generator module to the light source’s output port or directly generating a OV beam within the light source cavities [155]. In this manner, integrated micro SPPs and two-dimensional fiber-gratings placed at the output port of a single-mode 860 nm vertical-cavity surface-emitting laser (VCSEL) were utilized in [65] and [156], respectively. This approach has shown robustness and high purity of the generated OAM states, allowing OAM multiplexed data transmission [157,158]. Fabrication of a broadly wavelength tunable MEMS-based Fabry-Perot filter with the sized SPP placed on the filter aperture has been proposed in the papers with our contribution [159,160]. This device divides wavelengths in a controllable manner while also giving a fixed OAM determined by the topological charge of SPP in the output beam. Figure 10a,b shows the construction and top view of a constructed OV emitter that included an anti-reflection coating, a Si substrate, a fixed bottom distributed Bragg reflector (DBR), a changeable air gap, a moveable MEMS DBR, and an SPP. Figure 10c shows a SEM image of the first-order SPP that will be inserted into the circular aperture in the Cr/Au layer of the MEMS DBR.

Figure 10.
(a) Scheme of an OV MEMS Fabry-Perot filter: AR-coating = anti-reflection coating, and DBR = distributed Bragg reflector [160]. (b) Top view of a MEMS tunable Fabry-Perot filter with an integrated SPP [160]. (c) SEM image of a SPP of order lSPP = 1 on a plane Si substrate [160].
Notwithstanding that most of the proposed methods are experimentally verified, telecom applications are demonstrated only for ring resonators with annular grating [61,148,150], fixed SPPs [65,159,160], and lately for a pixel-array structure [154]. The output OAM beam from most out-of-plane generation methods is satisfactory in terms of mode purity; nevertheless, free-space propagation necessitates the use of a lens to concentrate the signal and couple it into the optical fiber, which reduces the final device’s reliability and scale. The minimal potential for multiplexing of OVs with different topological charges is another drawback of this method.
For more complex operations using vortices on a photonic integrated circuit, it is necessary to generate or inject a beam into the chip’s plane, and on-chip WGs must support its propagation. To implement such an operating principle, not only functional methods are important, but also the features of the chosen PIC platform. The most common integrated photonics platforms which are used for in-plane OAM applications are based on Silicon-on-Insulator (SOI) [161,162,163,164] and Silicon Nitride (SiNx) [165,166,167]. Because of the low cost, the high material strength of Si and CMOS compatibility, PICs based on the Si platform are particularly well suited as a medium for integrating with other components. Moreover, in [153,168] a scheme is proposed that uses a hybrid plasmonic WG to produce light beams with selective angular momentum (AM) over a wide wavelength range. AM beams can either propagate through optical WGs or emit into free space. Since it is based on an SOI platform and uses standard CMOS technology, this approach has high fabrication feasibility.
Regarding the propagation, it is experimentally demonstrated in [169,170] that OAM mode transmit over a rectangular polymer WG. Experimental data show that the imperfect shape of the intensity profiles and phase fronts of OV beams is caused not by the distortion of the OV modes propagating along the WG, but by the imperfection of the WG end facet, which affects the measured interferograms. This work provides the prototype illustration that OAM modes can propagate through rectangular on-chip WGs, proficient of traditional lithographic microfabrication.
In our recent work [166] we conducted a computational and theoretical investigation into the prospect of OV modes transmission over dielectric rectangular WGs, as well as the issue of WG structure enhancement for the sustenance of OV modes. The findings show that rectangular WGs can theoretically transmit quasi-TE and quasi-TM modes with high OAM purity states in the dominant field component. The constituent eigenmodes of higher azimuthal orders can only propagate in a phase-matched regime for the quasi-generate mode of azimuthal order ±1, and the OV modes of higher azimuthal orders can only transmit with a particular beat length. Furthermore, the normalized power of the subsequent OAM state in the modal superposition declines as the target azimuthal order increases. Numerical EM simulations of silicon nitride WGs provided field mappings and OAM spectra of the related modal superpositions, confirming the analytical predictions. The normalized intensity distribution, normalized amplitude distribution, and phase mapping of the leading E-field component are shown in Figure 11a–f [166].
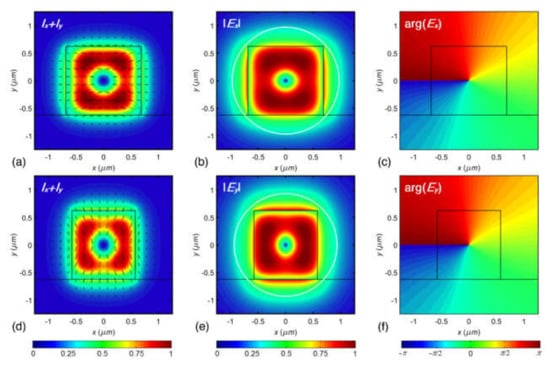
Figure 11.
The normalized transversal field component intensity distribution superimposed with polarization map (a,d) [166], Normalized absolute amplitude mapping of dominant E-field component (b,e) and phase distribution of dominant E-field component (c,f) of the quasi-TE (a–c) and quasi-TM (d–f) quasi-degenerate modes of order l = 1 in the symmetric (silica clad) silicon nitride WGs enhanced for phase-matched propagation of the constituent eigenmodes (β01 ≈ β10) [166].
In [163] SAM and OAM of light in silicon channel WGs was studied, where OV beam carrying OAM represented by a superposition of the TE01 and TE10 modes. Due to the transverse confinement, the SAM and OAM of the OV fields are strongly coupled and the whole space of structure variables of the WG can be separated just into three regimes. These results shed light on the correlation between angular momentum and mode confinement, which is useful for applying OVs in PICs. In the case of higher-order OAM modes propagation, the cross-shaped core WG structure was designed in [161]. Two degenerate driven modes of π/2 l-rotation symmetry can assist the l-th order OAM mode. The designed cross-shaped WG supports OAM modes of ±1 and ±2 topological charges concurrently at a wavelength of 1550 nm with high mode purity. The Hermite Gaussian (HG)-similar guided modes are shown in Figure 12a–d. To fulfil the degeneracy of HG01–HG10 and , which form OAM modes of ±1 and ±2 topological charges, respectively, the geometric variables denoted as W1, L1, W2 and L2 have been optimized (see Figure 12e). The impact of every parameter on neff of the modes is shown in Figure 12f. Additionally, such WG structures were designed for l = ±3 and l = ±4 OAM modes guiding individually, but the purity turned out to be lower and it is challenging to design the WG concurrently supporting the l = ±3 and l = ±4 OAM modes. Probably, a more complex transverse composition is required to further increase the topological charge. Anyway, in-plane operation using higher-order OAM modes is a competitive field.
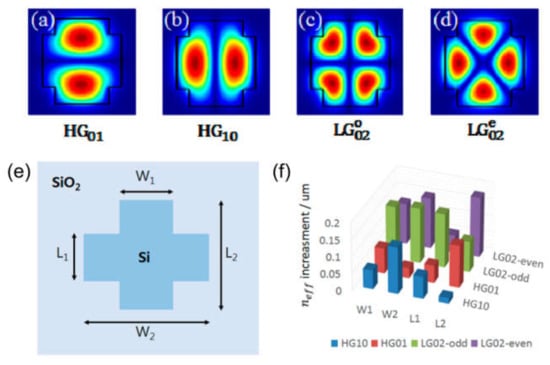
Figure 12.
HG-similar mode field allocations in the WG (a–d) [163], WG configuration for concurrently managing l = ±1 OAM mode and l = ±2 OAM mode (e) [163], mode neff reliance on WG parameters (f) [163].
Furthermore, the same group discovered that an OAM mode directional coupler with fabricable dimensions might be difficult to achieve with a rectangular WG and presented an on-chip device based on the cross-shaped WG structure [164]. The structure is effective in balancing the horizontal direction coupling strength of OAMl=1 mode’s two constitutive eigenmodes. The desired device has a coupling length of 670 μm and exhibits little OAM mode purity loss during the optical power transfer procedure. But again, the design of such a device for the higher-order OAM modes coupling is tricky and still competitive. Figure 13 shows the dependences of the coupling coefficient on the length in the case of the usual directional coupler and on the cutout size t in the case of cross shape WG coupler. As can be seen, the coupling coefficient of the TE10 mode is always higher than the TE01 one in the case of a rectangular WG coupler and does not satisfy a requirement for the OAMl=1 mode directional coupler. But when the directional coupler is made of a cross-shaped WG, there is a cutout size around 490 µm, where TE01 and TE10 modes have the same coupling coefficient. The insertion of the cutoff breaks down the degeneracy between TE10 and TE01 modes in the starting rectangular WG. The particle swarm optimization method can be used to optimize WG’s width and height and the cutoff dimensions of the cross-shaped WG simultaneously [164].
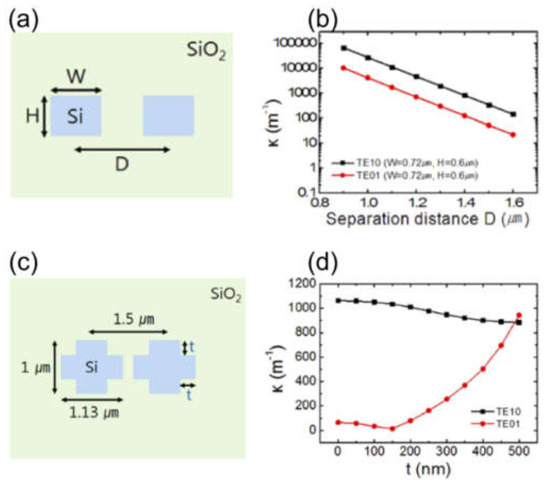
Figure 13.
Cross-section of rectangular WG coupler (a) [164], the coupling coefficient of TE10 and TE01 modes in case of W = 0.72 µm and H = 0.6 µm (b) [164], the cross-section of cross shape WG coupler (c) [164], the coupling coefficient of TE10 and TE01 modes as a function of t (d) [164].
To achieve a compact full-fledged device utilizing in-plane OV beams it is necessary to generate such carrying OAM state wave on an integrated circuit. In [161], it is proposed to produce OAM beams by a simple on-chip integrated structure involving only silicon WGs and couplers, which controls the phase shift of the second-order propagating mode. The idea of getting the necessary distribution at the output of the device already touched upon TE01 and TE10 eigenmodes being mixed with π/2 phase shift. The rectangular WGs assisting multiple transverse modes and keeping symmetry in two orthogonal transverse directions are also proposed in [171].
Another generation method—based on a hybrid plasmonic WG—is proposed in [153,168,172,173]. The main feature of the suggested method is to divide a WG into three sections: the first and third sections are pure dielectric WGs, and the middle section is a hybrid plasmonic WG. Because of the polarization rotation in the asymmetrical WG, the transverse field factors produce a spin angular momentum (SAM). The proposed method for generating an OAM beam in a WG could be useful for on-chip integrated optical tweezers, data processing, and other applications [153]. Later, the application of integrable quarter-wave plates being able to control the OAM of photons within nanophotonic WGs was proposed [174]. Although plates do not act as the generating structure, the fundamental physics embraces fundamental potential and applicability to an extensive variety of applications, such as detection of chiral molecules, nanoscale optical manipulation, integrated computing science, and on-chip managing of quantum information [174].
Finally, an ultra-compact integrated structure to generate OAM modes is proposed by a specially designed single-trench WG in [67]. To implement OAM modes generation, the WG with a trench is designed. A trench can break the original rotation symmetry and split the mode degeneracy. As can be seen from Figure 14a, OAM modes with topological charge ±1 synthesized from two orthogonal LP-like eigenmodes that were excited by second-order TE01 mode at the input of a trench WG. Figure 14b shows a cross-section of a WG. The distributions of eigenmodes of a trench WG are shown in Figure 14c and its combination evolutions are presented in Figure 14d. Moreover, the structure of an on-chip OAM modes (de)multiplexer for x-polarization, utilizing the trench WGs was demonstrated.
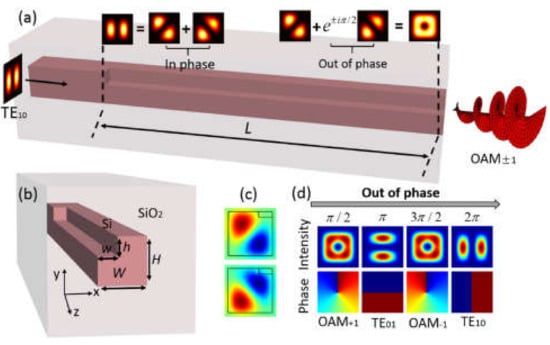
Figure 14.
(a) OAM beam generator principle built on a single-trench WG; (b) A single trench WG in cross-section; (c) Two eigenmodes of a single-trench WG’s field distributions; and (d) For x-polarization, intensity and phase evolutions of a combination of eigenmodes [67].
Another method involves coupling incident radiation into an integral WG through an MS [167]. A Si antenna array on the surface of the Si3N4 WG represents the MS. MS simultaneously realizes OAM excitation and light coupling. The device also generates and adds two high-order TE01 and TE10 modes with π/2 phase difference. The convenience of the MS in simultaneous excitation and mixing of modes at the required phase ratio.
Finally, the authors have recently introduced the principle of vortex mode generation by coherent superposition between two high-ordered TE-like modes excited in one waveguide from the incident radiation using the grating coupler. First, in [175] the approach was demonstrated based on the two waveguides of different widths, which are coupled together by the directional coupler. Next, in [176] the symmetric silica-cladded silicon nitride WG with shallowly etched gratings is provided for the in-plane generation of the vortex mode with azimuthal order l = ±1. The proposed design is beneficial over the previous because it provides the generation of a pure phase vortex of quasi-TE polarization at the PIC output; the device can be implemented as a passive PIC and can be excited by a single standard SMF, which can be coupled in a technologically convenient in-line way. The power coefficients of the target OAM states ±1 are higher than 0.96, which is verified with the numerical simulation. The only drawback is relatively low coupling efficiency compared to the typical values for fundamental TE00 mode excitation, which however could be further increased by properly optimizing the etching depth and other grating coupler parameters.
5. Detection of Light with OAM
OAM detection at the receiver side is needed in communications. Even though OAM detection is simply the reverse of OAM generation, it is significantly difficult because of the deteriorated OAM states after transmission [177]. Mode assessment established on field data [178], the study of OAM induced effects—for instance, the rotational Doppler shift [179,180]—and beam-restoring using holographic technology [181] are the three types of OAM detection. To measure the OAM directly, the first method requires acquiring all three components of E and H-fields [182]. On the other hand, the phase gradient equal to the OAM index l can be calculated. The OAM modes can be anticipated into a measurable Gaussian mode in the third method, which utilizes a hologram [183]. Geometric-phase MSs can be employed to integrate holograms because they have a low profile and a lot of tuning versatility.
Based on DOEs, multi-channel (or multi-order) optical elements have been developed, matched to OVs of different orders [184,185,186,187] and their action is based on the correlation filtering in the Fourier region [188]. Subsequently, these DOEs were used in the problems of fiber-optic multichannel communication utilizing OV beams [4]. More recent studies used SLMs [189,190,191,192,193]. For example, Figure 15 shows detecting results for the phase 13-channel filter, matched with integer and half-integer OVs [193]. Note, DOEs can be employed to recognize not only the singular phase state of structured light beams but also for detection polarization state [4,5,6,194]. However, MSs are more suitable for these purposes [195,196,197,198,199,200].
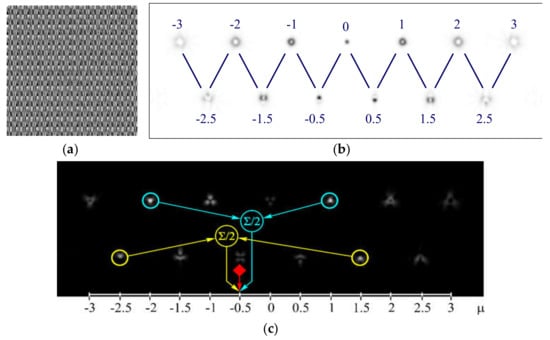
Figure 15.
Detecting OVs: (a) phase of a 13-channel filter; (b) intensity pattern (negative) in the focal plane and correspondence of diffraction orders to OV values; and (c) results of detecting of different OVs in the beam with co-axial superposition exp(−i2φ) + exp(−iφ) (total OAM μ = −0.5) [194].
The additional degree of freedom provided by the OAM state of photons has a wide range of uses. For enhanced fidelity, miniaturization, and reconfiguration of OAM state measurement, which is a fundamental requirement of these applications, photonic integrated devices are required. In [201], a Si-integrated OAM receiver is described that can discriminate between separate and changeable OAM states. Also, the detector’s reconfiguration capability is attained by using a voltage to the GeSe film, which forms gratings with alternate states. By modifying the duty cycle of the gratings, the resonant wavelength for any OAM state is shown to be tunable in a quasi-linear manner. It proposes a viable method for realizing a compact integrated OAM detection system with better functionality, which could have vital applications in optical communications and information processing involving OAM states [199]. Photonic integrated circuits (PICs) perform a wide range of optical functions using light rather than electrons. The spectrum of potential functionalities for these highly integrated optical chips has been extended thanks to recent advances in nanostructures, metamaterials, and Si technologies. Mach–Zehnder interferometric and ring-based modulators, for example, have been published [202,203,204,205,206,207]. Work on an OAM detection system, which includes converting light with distinct OAM states into spatially separated surface plasmon polaritons waves, has begun in recent years. Miniature photonic devices with dimensions significantly smaller than those now accessible are possible thanks to the surface plasmon polariton’s unique features in terms of short equivalent wavelength and excellent spatial confinement. Metaholograms with plasmonic photodiodes, for instance, have been shown to detect OAM in real time [180]. This method allows for the development of a compact, integrated detection system. It is, however, limited to one OAM state. Several methods for the detection of OAM of light has been proposed in recent times [208,209,210,211].
A novel concept of an optomechanical system that enables sensitive transduction of OAM of light has recently been demonstrated [212]. A photonic crystal cavity optomechanical system detects an optically induced twist on the chip. This facilitates the measurement of the OAM of light as photons are absorbed by the mechanical element or detect photons as they are dispersed into new OAM states by a sub-wavelength grating patterned on the device. Such a device will detect optical pulses with l = 1 OAM field and an average photon number of 3.9 × 103 at a repetition rate of 5 MHz, assuming detector noise does not restrict measurement precision. High-order OAM states can be added to this design. A schematic of the OAM detector system reported in [212] is shown in Figure 16. As shown in Figure 16a,b, it comprises of a center suspended pad connected to one side of a slot-mode photonic crystal nanobeam cavity [212].
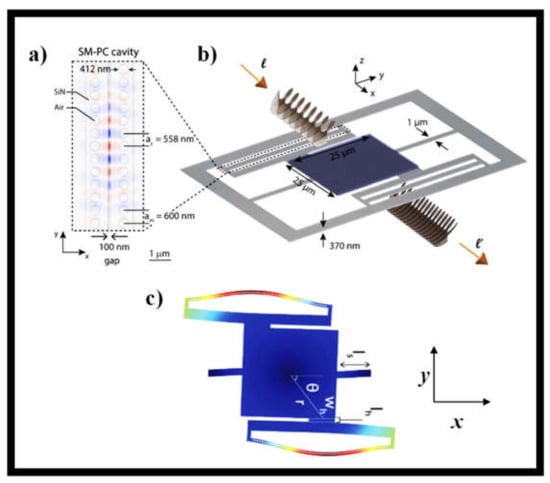
Figure 16.
A diagram of the device’s geometry: (a) Top view of a slot-mode PhC cavity geometry and modeling of the E-field distribution of its fundamental optical mode [212]; and (b) The OAM detector in isometric perspective. The cavity from (a) is attached to the square pad by a hanger whose dimensions wh and lh are indicated in (c) [212]. The pad motion is moved to the nanobeam when excited by a source of torque as exhibited by the simulated displacement profile shown in (c) [212].
The chip that surrounds the cavity is linked to the other half of the cavity. The cavity operates in an air-band mode with a field centered in the space between the nanobeams, making it very sensitive to any nanobeam motion that changes the slot-gap width, causing the cavity mode wavelength to change. The motion of the nanobeam is transformed into the amplitude of light coupled out of the cavity during this dispersive optomechanical coupling phase. Light may be linked into and out of the cavity using an optical fiber taper WG evanescently interfering with the cavity to control this optomechanical transduction. By rotating the central pad and activating the nanobeam’s mechanical bounce mode, optical actuation of the central pad through OAM moves the nanobeam’s center of mass location. Figure 16c shows a simulated displacement profile of the unit when its central pad is operated by an external torque source, displaying several forms of displacement [212]. The OAM of light incident on the device’s central pad may be transformed to torque using a variety of different approaches. The OAM of light changes from l = l′ = 0 as the torsional pad is covered with an absorbent layer and lit up with helical light. A helical beam with OAM number l can be altered during broadcast or reflection to any OAM number l′ supplied by the MS shape if the torsional pad is replicated with an appropriately built MS.
6. Conclusions
In this paper, we have reviewed the most extensively used methods for the generation of orbital angular momentum (OAM) optical beams and their detection. These methods include the usage of diffractive optics, metasurfaces (MSs), and photonic integrated circuits (PICs). Diffractive optics can be further classified in spiral phase plates, computer-generated holograms, and diffractive optical elements. MSs are relatively compact and deliver high performance compared to conventional DOEs. PICs based OAM generators can be divided into two sub-categories: out-of-plane OAM generator and in-plane OAM generator. For the latter, it has attracted a lot of interest in fully utilizing the unique feature of OAM beams in the guided optics. However, to ensure uniform spatial distributions of the multi-coupled waveguide, the majority of the integrated OAM generators need exceedingly critical dimension control technology. The aim of this paper is not to highlight the dominance of one approach over another. We have provided the advantages/disadvantages of each method based on the ease of implementation and performance.
Author Contributions
Conceptualization, D.M.F., M.A.B., E.P.G., R.V.K., I.V.S., N.L.K., S.N.K., V.S.L., A.K.S.; methodology, D.M.F., M.A.B., E.P.G., R.V.K., I.V.S., N.L.K., S.N.K., V.S.L., A.K.S.; validation, D.M.F., M.A.B., E.P.G., R.V.K., I.V.S., N.L.K., S.N.K., V.S.L., A.K.S.; formal analysis, D.M.F., M.A.B., E.P.G., R.V.K., I.V.S., N.L.K., S.N.K., V.S.L., A.K.S.; investigation, D.M.F., M.A.B., E.P.G., R.V.K., I.V.S., N.L.K., S.N.K., V.S.L., A.K.S.; resources, D.M.F., M.A.B., E.P.G., R.V.K., I.V.S., N.L.K., S.N.K., V.S.L., A.K.S.; data curation, D.M.F., M.A.B., E.P.G., R.V.K., I.V.S., N.L.K., S.N.K., V.S.L., A.K.S.; writing—original draft preparation, D.M.F., M.A.B., E.P.G., R.V.K., I.V.S., N.L.K., S.N.K., V.S.L., A.K.S.; writing—review and editing, D.M.F., M.A.B., E.P.G., R.V.K., I.V.S., N.L.K., S.N.K., V.S.L., A.K.S.; visualization, D.M.F., M.A.B., E.P.G., R.V.K., I.V.S., N.L.K., S.N.K., V.S.L., A.K.S.; supervision, D.M.F., M.A.B., E.P.G., R.V.K., I.V.S., N.L.K., S.N.K., V.S.L., A.K.S.; project administration, D.M.F., M.A.B., E.P.G., R.V.K., I.V.S., N.L.K., S.N.K., V.S.L., A.K.S.; funding acquisition, D.M.F., M.A.B., E.P.G., R.V.K., I.V.S., N.L.K., S.N.K., V.S.L., A.K.S. All authors have read and agreed to the published version of the manuscript.
Funding
This work was funded under the grant of the Russian Science Foundation (Project No. 19-49-04112).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Yao, A.M.; Padgett, M.J. Orbital angular momentum: Origins, behavior and applications. Adv. Opt. Photonics 2011, 3, 161–204. [Google Scholar] [CrossRef]
- Bozinovic, N.; Yue, Y.; Ren, Y.; Tur, M.; Kristensen, P.; Huang, H.; Willner, A.E.; Ramachandran, S. Terabit-scale orbital angular momentum mode division multiplexing in fibers. Science 2013, 340, 1545–1548. [Google Scholar] [CrossRef]
- Nicolas, A.; Veissier, L.; Giner, L.; Giacobino, E.; Maxein, D.; Laurat, J. A quantum memory for orbital angular momentum photonic qubits. Nat. Photonics 2014, 8, 234–238. [Google Scholar] [CrossRef]
- Moreno, I.; Davis, J.; Ruiz, I.; Cottrell, D. Decomposition of radially and azimuthally polarized beams using a circular-polarization and vortex-sensing diffraction grating. Opt. Express 2010, 18, 7173–7183. [Google Scholar] [CrossRef] [PubMed]
- Khonina, S.N.; Savelyev, D.; Kazanskiy, N.L. Vortex phase elements as detectors of polarization state. Opt. Express 2015, 23, 17845–17859. [Google Scholar] [CrossRef] [PubMed]
- Moreno, I.; Davis, J.; Badham, K.; Sanchez-Lopez, M.M.; Holland, J.; Cottrell, D. Vector beam polarization state spectrum analyzer. Sci. Rep. 2017, 7, 2216. [Google Scholar] [CrossRef] [PubMed]
- Khonina, S.N.; Porfirev, A.P.; Karpeev, S. Recognition of polarization and phase states of light based on the interaction of nonuniformly polarized laser beams with singular phase structures. Opt. Express 2019, 27, 18484–18492. [Google Scholar] [CrossRef]
- Grier, D.G. A revolution in optical manipulation. Nature 2003, 424, 810–816. [Google Scholar] [CrossRef]
- Padgett, M.; Bowman, R. Tweezers with a twist. Nat. Photonics 2011, 5, 343–348. [Google Scholar] [CrossRef]
- Chapin, S.C.; Germain, V.; Dufresne, E.R. Automated trapping, assembly, and sorting with holographic optical tweezers. Opt. Express 2006, 14, 13095–13100. [Google Scholar] [CrossRef]
- Gong, L.; Gu, B.; Rui, G.; Cui, Y.; Zhu, Z.; Zhan, Q. Optical forces of focused femtosecond laser pulses on nonlinear optical Rayleigh particles. Photonics Res. 2018, 6, 138–143. [Google Scholar] [CrossRef]
- Zhang, Y.; Shen, J.; Min, C.; Jin, Y.; Jiang, Y.; Liu, J.; Zhu, S.; Sheng, Y.; Zayats, A.V.; Yuan, X. Nonlinearity-induced multiplexed optical trapping and manipulation with femtosecond vector beams. Nano Lett. 2018, 18, 5538–5543. [Google Scholar] [CrossRef] [PubMed]
- Reddy, S.G.; Vaity, C.P.P.; Aadhi, A.; Prabhakar, S.; Singh, R.P. Non-diffracting speckles of a perfect vortex beam. J. Opt. 2016, 18, 055602. [Google Scholar] [CrossRef]
- Furhapter, S.; Jesacher, A.; Bernet, S.; Ritsch-Marte, M. Spiral phase contrast imaging in microscopy. Opt. Express 2005, 13, 689–694. [Google Scholar] [CrossRef]
- Tamburini, F.; Anzolin, G.; Umbriaco, G.; Bianchini, A.; Barbieri, C. Overcoming the Rayleigh criterion limit with optical vortices. Phys. Rev. Lett. 2006, 97, 163903. [Google Scholar] [CrossRef]
- Jesacher, A.; Ritsch-Marte, M.; Piestun, R. Three-dimensional information from two-dimensional scans: A scanning microscope with postacquisition refocusing capability. Optica 2015, 2, 210–213. [Google Scholar] [CrossRef]
- Willig, K.I.; Rizzoli, S.O.; Westphal, V.; Jahn, R.; Hell, S.W. STED microscopy reveals that synaptotagmin remains clustered after synaptic vesicle exocytosis. Nature 2006, 440, 935–939. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Y.; Askarpour, A.N.; Sun, L.; Shi, J.; Li, X.; Alu, A. Chirality detection of enantiomers using twisted optical metamaterials. Nat. Commun. 2017, 8, 1–8. [Google Scholar] [CrossRef]
- Xie, Z.; Lei, T.; Si, G.; Du, L.; Lin, J.; Min, C.; Yuan, X. On-chip spin-controlled orbital angular momentum directional coupling. J. Phys. D Appl. Phys. 2017, 51, 014002. [Google Scholar] [CrossRef]
- Xie, G.; Song, H.; Zhao, Z.; Milione, G.; Ren, Y.; Liu, Y.; Zhang, R.; Bao, C.; Li, L.; Wang, Z.; et al. Using a complex optical orbital-angular-momentum spectrum to measure object parameters. Opt. Lett. 2017, 42, 4482. [Google Scholar] [CrossRef] [PubMed]
- Qin, Y.; Li, Y.; Deng, D.; Liu, Y.; Sun, M. Ultracompact biosensor based on a metalens with a longitudinally structured vector beam. Appl. Opt. 2019, 58, 4438–4442. [Google Scholar] [CrossRef]
- Dorrah, A.H.; Zamboni-Rached, M.; Mojahedi, M. Experimental demonstration of tunable refractometer based on orbital angular momentum of longitudinally structured light. Light Sci. Appl. 2018, 7, 40. [Google Scholar] [CrossRef]
- Cvijetic, N.; Milione, G.; Ip, E.; Wang, T. Detecting lateral motion using light’s orbital angular momentum. Sci. Rep. 2015, 5, 15422. [Google Scholar] [CrossRef]
- Lavery, M.P.; Speirits, F.; Barnett, S.; Padgett, M. Detection of a spinning object using light’s orbital angular momentum. Science 2013, 341, 537. [Google Scholar] [CrossRef] [PubMed]
- Allen, L.; Beijersbergen, M.W.; Spreeuw, R.J.; Woerdman, J.P. Orbital angular momentum of light and the transformation of Laguerre-Gaussian modes. Phys. Rev. A 1992, 45, 8185–8189. [Google Scholar] [CrossRef]
- Padgett, M.J. Orbital angular momentum 25 years on. Opt. Express 2017, 25, 11265–11274. [Google Scholar] [CrossRef] [PubMed]
- Cojoc, D.; Garbin, V.; Ferrari, E.; Businaro, L.; Romanato, F.; Fabrizio, E. Laser trapping and micromanipulation using optical vortices. Microelectron. Eng. 2005, 78–79, 125–131. [Google Scholar] [CrossRef]
- Chen, X.; Cheng, W.; Xie, M.; Zhao, F. Optical rotational self-assembly at air-water surface by a single vortex beam. Results Phys. 2019, 12, 1172–1176. [Google Scholar] [CrossRef]
- Barbieri, C.; Tamburini, F.; Anzolin, G.; Bianchini, A.; Mari, E.; Sponselli, A.; Umbriaco, G.; Prasciolu, M.; Romanato, F.; Villoresi, P. Light’s orbital angular momentum and optical vortices for astronomical coronagraphy from ground and space telescopes. Earth Moon Planets 2009, 105, 283–288. [Google Scholar] [CrossRef]
- Huang, H.; Milione, G.; Lavery, M.J.; Xie, G.; Ren, Y.; Cao, Y.; Ahmed, N.; Nguyen, T.A.; Nolan, D.A.; Li, M.-J.; et al. Mode division multiplexing using an orbital angular momentum mode sorter and MIMO-DSP over a graded-index few-mode optical fibre. Sci. Rep. 2015, 5, 14931. [Google Scholar] [CrossRef]
- Fang, X.; Ren, H.; Gu, M. Orbital angular momentum holography for high security encryption. Nat. Photonics 2020, 14, 102–108. [Google Scholar] [CrossRef]
- Zhang, H.; Mao, B.; Han, Y.; Wang, Z.; Yue, Y.; Liu, Y. Generation of orbital angular momentum modes using fiber systems. Appl. Sci. 2019, 9, 1033. [Google Scholar] [CrossRef]
- Ruffato, G.; Massari, M.; Romanato, F. Diffractive optics for OAM-mode division multiplexing of optical vortices design, fabrication and optical characterization. In Proceedings of the IEEE 7th International Conference on Advance Optoelectronics and Lasers (CAOL), Odessa, Ukraine, 12–15 September 2016; pp. 148–150. [Google Scholar]
- Khonina, S.N.; Porfirev, A.P.; Volotovskiy, S.G.; Ustinov, A.V.; Fomchenkov, S.A.; Pavelyev, V.S.; Schroter, S.; Duparre, M. Generation of Multiple Vector Optical Bottle Beams. Photonics 2021, 8, 218. [Google Scholar] [CrossRef]
- Courtial, J.; Padgett, M.J. Performance of a cylindrical lens mode converter for producing Laguerre-Gaussian laser modes. Opt. Commun. 1999, 159, 13–18. [Google Scholar] [CrossRef]
- Beijersbergen, M.W.; Coerwinkel, R.C.; Kristensen, M.; Woerdman, J.P. Helical-wavefront laser beams produced with a spiral phaseplate. Opt. Commun. 1994, 112, 321–327. [Google Scholar] [CrossRef]
- Uchida, M.; Tonomura, A. Generation of electron beams carrying orbital angular momentum. Nature 2010, 464, 737–739. [Google Scholar] [CrossRef]
- Dyson, J. Circular and spiral diffraction gratings. Proc. R. Soc. Lond. Ser. A 1958, 248, 93–106. [Google Scholar]
- Forbes, A.; Dudley, A.; McLaren, M. Creation and detection of optical modes with spatial light modulators. Adv. Opt. Photonics 2016, 8, 200–227. [Google Scholar] [CrossRef]
- Zhao, Z.; Wang, J.; Li, S.; Willner, A.E. Metamaterials-based broadband generation of orbital angular momentum carrying vector beams. Opt. Lett. 2013, 38, 932–934. [Google Scholar] [CrossRef] [PubMed]
- Marrucci, L.; Karimi, E.; Slussarenko, S.; Piccirillo, B.; Santamato, E.; Nagali, E.; Sciarrino, F. Spin-to-orbital conversion of the angular momentum of light and its classical and quantum applications. J. Opt. 2011, 13, 064001. [Google Scholar] [CrossRef]
- Wu, H.; Go, S.; Huang, B.; Feng, Y.; Huang, X.; Liu, W.; Li, Z. All-fiber second-order optical vortex generation based on strong modulated long-period grating in a four-mode fiber. Opt. Lett. 2017, 42, 5210. [Google Scholar] [CrossRef]
- Ma, X.; Liu, C.-H.; Chang, G.; Galvanauskas, A. Angular-momentum coupled optical waves in chirally-coupled-core fibers. Opt. Express 2011, 19, 26515. [Google Scholar] [CrossRef]
- Zeng, X.; Li, Y.; Feng, L.; Wu, S.; Yang, C.; Li, W.; Tong, W.; Wu, J. All-fiber optical angular momentum mode multiplexer based on a mode-selective photonic lantern and a mode polarization controller. Opt. Lett. 2018, 43, 4779. [Google Scholar] [CrossRef]
- Ruffato, G.; Rossi, R.; Massari, M.; Mafakheri, E.; Capaldo, P.; Romanato, F. Design, fabrication and characterization of computer generated holograms for anti-counterfeiting applications using OAM beams as light decoders. Sci. Rep. 2017, 7, 18011. [Google Scholar] [CrossRef] [PubMed]
- Heckenberg, N.R.; McDuff, R.; Smith, C.P.; White, A.G. Generation of optical phase insinglarities by computer-generated holograms. Opt. Commun. 1992, 91, 158–162. [Google Scholar]
- Cohen, G.B.; Pogreb, R.; Vinokur, K.; Davidov, D. Spatial light modulator based on a deformed-helix ferroelectric liquid crystal and a thin a-Si:H amorphous photoconductor. Appl. Opt. 1997, 36, 455–459. [Google Scholar] [CrossRef] [PubMed]
- Genevet, P.; Yu, N.F.; Aieta, Y.F.; Lin, J.; Kats, M.A.; Blanchard, R.; Scully, M.O.; Gaburro, Z.; Capasso, F. Ultra-thin plasmonic optical vortex plate based on phase discontinuities. Appl. Phys. Lett. 2012, 100, 013101. [Google Scholar] [CrossRef]
- Yu, N.F.; Capasso, F. Flat optics with designer metasurfaces. Nat. Mater. 2014, 13, 139–150. [Google Scholar] [CrossRef]
- Zhou, C.; Yang, W.; Xue, Q.; Che, W. Low-profile wideband dual-circularly polarized orbital angular momentum antenna array using metasurface. Microw. Opt. Technol. Lett. 2020, 63, 1207–1212. [Google Scholar] [CrossRef]
- Sun, Z.; Shi, Y.; Sun, X.; Jia, H.; Jin, Z.; Deng, K.; Yang, J. Underwater acoustic multiplexing communication by pentamodemetasurface. J. Phys. D Appl. Phys. 2020, 54, 205303. [Google Scholar] [CrossRef]
- Wang, D.; Liu, F.; Liu, T.; Sun, S.; He, Q.; Zhou, L. Efficient generation of complex vectorial optical fields with metasurfaces. Light Sci. Appl. 2021, 10, 67. [Google Scholar] [CrossRef] [PubMed]
- Guo, Y.; Zhang, S.; Pu, M.; He, Q.; Jin, J.; Xu, M.; Zhang, Y.; Gao, P.; Luo, X. Spin-decoupled metasurface for simultaneous detection of spin and orbital angular momenta via momentum transformation. Light Sci. Appl. 2021, 10, 63. [Google Scholar] [CrossRef]
- Munk, B. Frequency Selective Surfaces: Theory and Design; John Wiley: New York, NY, USA, 2000. [Google Scholar]
- Kazanskiy, N.L.; Butt, M.A.; Khonina, S.N. Carbon dioxide gas sensor based on polyhexamethylene biguanide polymer deposited on silicon nano-cylinders metasurface. Sensors 2021, 21, 378. [Google Scholar] [CrossRef]
- Li, J.; Wu, T.; Xu, W.; Liu, Y.; Liu, C.; Wang, Y.; Yu, Z.; Zhu, D.; Yu, L.; Ye, H. Mechanisms of 2π phase control in dielectric metasurface and transmission enhancement effect. Opt. Express 2019, 27, 23186–23196. [Google Scholar] [CrossRef] [PubMed]
- Pfeiffer, C.; Grbic, A. Metamaterial Huygens’ surfaces: Tailoring wave fronts with reflectionless sheets. Phys. Rev. Lett. 2013, 110, 197401. [Google Scholar] [CrossRef] [PubMed]
- Khonina, S.N.; Podlipnov, V.V.; Karpeev, S.V.; Ustinov, A.V.; Volotovsky, S.G.; Ganchevskaya, S.V. Spectral control of the orbital angular momentum of a laser beam based on 3D properties of spiral phase plates fabricated for an infrared wavelength. Opt. Express 2020, 28, 18407. [Google Scholar] [CrossRef]
- Li, Y.; Kim, J.; Escuti, M.J. Orbital angular momentum generation and mode transformation with high efficiency using forked polarization gratings. Appl. Opt. 2012, 51, 8236–8245. [Google Scholar] [CrossRef] [PubMed]
- Chung, H.; Kim, D.; Sawant, A.; Lee, I.; Choi, E.; Lee, J. Generation of E-band metasurface-based vortex beam with reduced divergence angle. Sci. Rep. 2020, 10, 8289. [Google Scholar] [CrossRef]
- Liu, A.; Wu, M.; Zhuang, R.; Hong, J.; Wang, Q.; Ren, X. On-chip generation of the reconfigurable orbital angular momentum with high order. Opt. Express 2020, 28, 17957. [Google Scholar] [CrossRef]
- Wang, Y.; Feng, X.; Zhang, D.; Zhao, P.; Li, X.; Cui, K.; Liu, F.; Huang, Y. Generating optical superimposed vortex beam with tunable orbital momentum using integrated devices. Sci. Rep. 2015, 5, 10958. [Google Scholar] [CrossRef]
- Fontaine, N.K.; Doerr, C.R.; Buhl, L.L. Efficient multiplexing and demultiplexing of free-space orbital angular momentum using photonic integrated circuits. In Proceedings of the Optical Fiber Communication Conference, OSA Technical Digest, Los Angeles, CA, USA, 4–8 March 2012. [Google Scholar]
- Guan, B.; Scott, R.P.; Fontaine, N.K.; Ferrari, T.C.; Cappuzzo, M.; Klemens, F.; Keller, B.; Earnshaw, M.; Yoo, S.B. Integrated optical orbital angular momentum multiplexing device using 3-D waveguides and a silica PLC. In Proceedings of the Conference on Lasers and Electro-Optics (CLEO), San Jose, CA, USA, 9–14 June 2013. [Google Scholar]
- Li, H.; Phillips, D.B.; Wang, X.; Ho, D.; Chen, L.; Zhou, X.; Zhu, J.; Yu, S.; Cai, X. Orbital angular momentum vertical-cavity surface-emitting lasers. Optica 2015, 2, 547–552. [Google Scholar] [CrossRef]
- Zheng, S.; Wang, J. On-chip orbital angular momentum modes generator and (de)multiplexer based on trench silicon waveguides. Opt. Express 2017, 25, 18492. [Google Scholar] [CrossRef]
- Krenn, M.; Fickler, R.; Fink, M.; Handsteiner, J.; Malik, M.; Scheidl, T.; Ursin, R.; Zeilinger, A. Communication with spatially modulated light through turbulent air across Vienna. New J. Phys. 2014, 16, 113028. [Google Scholar] [CrossRef]
- Yan, Y.; Xie, G.; Lavery, M.P.; Huang, H.; Ahmed, N.; Bao, C.; Ren, Y.; Cao, Y.; Li, L.; Zhao, Z.; et al. High-capacity millimetre-wave communications with orbital angular momentum multiplexing. Nat. Commun. 2014, 5876, 4876. [Google Scholar] [CrossRef]
- Huang, H.; Xie, G.; Yan, Y.; Ahmed, N.; Ren, Y.; Yue, Y.; Rogawski, D.; Willner, M.; Erkmen, B.; Birnbaum, K.M.; et al. 100 Tbit/s free-space data link enabled by three-dimensional multiplexing of orbital angular momentum, polarization, and wavelength. Opt. Express 2014, 39, 197–200. [Google Scholar] [CrossRef]
- Gbur, G.; Tyson, R.K. Vortex beam propagation through atmospheric turbulence and topological charge conservation. J. Opt. Soc. Am. A 2008, 25, 225–230. [Google Scholar] [CrossRef] [PubMed]
- Wang, T.; Pu, J.; Chen, Z.; Wang, T.; Pu, J.; Chen, Z. Beam-spreading and topological charge of vortex beams propagating in a turbulent atmosphere. Opt. Commun. 2009, 282, 1255–1259. [Google Scholar] [CrossRef]
- Malik, M.; O’Sullivan, M.; Rodenburg, B.; Mirhosseini, M.; Leach, J.; Lavery, M.P.; Padgett, M.; Boyd, R.W. Influence of atmospheric turbulence on optical communications using orbital angular momentum for encoding. Opt. Express 2012, 20, 13195–13200. [Google Scholar] [CrossRef] [PubMed]
- Porfirev, A.; Kirilenko, M.; Khonina, S.N.; Skidanov, R.; Soifer, V. Study of propagation of vortex beams in aerosol optical medium. Appl. Opt. 2017, 56, E5–E15. [Google Scholar] [CrossRef] [PubMed]
- Khonina, S.N.; Striletz, A.; Kovalev, A.; Kotlyar, V. Propagation of laser vortex beams in a parabolic optical fiber. Proc. SPIE 2010, 7523. [Google Scholar] [CrossRef]
- Ye, J.; Li, Y.; Han, Y.; Deng, D.; Guo, Z.; Gao, J.; Sun, Q.; Liu, Y.; Qu, S. Excitation and separation of vortex modes in twisted air-core fiber. Opt. Express 2016, 24, 8310–8316. [Google Scholar] [CrossRef] [PubMed]
- Wen, Y.; Chremmos, I.; Chen, Y.; Zhu, G.; Zhang, J.; Zhu, J.; Zhang, Y.; Liu, J.; Yu, S. Compact and high-performance vortex mode sorter for multi-dimensional multiplexed fiber communication systems. Optica 2020, 7, 254–262. [Google Scholar] [CrossRef]
- Kotlyar, V.V.; Almazov, A.A.; Khonina, S.N.; Soifer, V.A.; Elfstrom, H.; Turunen, J. Generation of phase singularity through diffracting a plane or Gaussian beam by a spiral phase plate. J. Opt. Soc. Am. A 2005, 22, 849–861. [Google Scholar] [CrossRef] [PubMed]
- Oraizi, H.; Emamian, H. Generation of orbital angular momentum modes via holographic leaky-wave metasurfaces. Sci. Rep. 2020, 10, 7358. [Google Scholar] [CrossRef] [PubMed]
- Khonina, S.N.; Ustinov, A.V.; Logachev, V.I.; Porfirev, A.P. Properties of vortex light fields generated by generalized spiral phase plates. Phys. Rev. A 2020, 101, 043829. [Google Scholar] [CrossRef]
- Isakov, D.; Wu, Y.; Allen, B.; Grant, P.S.; Stevens, C.J.; Gibbons, G.J. Evaluation of the Laguerre-Gaussian mode purity produced by three-dimensional-printed microwave spiral phase plates. R. Soc. Open Sci. 2020, 7, 200493. [Google Scholar] [CrossRef] [PubMed]
- Khonina, S.N.; Kotlyar, V.V.; Soifer, V.A.; Skinkaryev, M.V.; Uspleniev, G.V. Trochoson. Opt. Commun. 1992, 91, 158–162. [Google Scholar] [CrossRef]
- Musigmann, M.; Jahns, J.; Bock, M.; Grunwald, R. Refractive-diffractive dispersion compensation for optical vortex beams with ultrashort pulse durations. Appl. Opt. 2014, 53, 7304–7311. [Google Scholar] [CrossRef]
- Degtyarev, S.A.; Porfirev, A.P.; Khonina, S.N. Photonic nanohelix generated by a binary spiral axicon. Appl. Opt. 2016, 55, B44–B48. [Google Scholar] [CrossRef]
- Soskin, M.S.; Polyanskii, P.V.; Arkhelyuk, O.O. Computer-synthesized hologram-based rainbow optical vortices. New J. Phys. 2004, 6, 196. [Google Scholar] [CrossRef]
- Yu, J.; Zhou, C.; Jia, W.; Hu, A.; Cao, W.; Wu, J.; Wang, S. Generation of dipole vortex array using spiral Dammann zone plates. Appl. Opt. 2012, 51, 6799–6804. [Google Scholar] [CrossRef]
- Janicijevic, L.; Topuzoski, S. Gaussian laser beam transformation into an optical vortex beam by helical lens. J. Mod. Opt. 2016, 63, 164–176. [Google Scholar] [CrossRef][Green Version]
- Davis, J.A.; Cottrell, D.M.; Sand, D. Abruptly autofocusing vortex beam. Opt. Express 2012, 20, 13302–13310. [Google Scholar] [CrossRef]
- Jiang, Y.; Zhao, S.; Yu, W.; Zhu, X. Abruptly autofocusing property of circular Airy vortex beams with different initial launch angles. J. Opt. Soc. Am. A 2018, 35, 890–894. [Google Scholar] [CrossRef]
- Khonina, S.N.; Porfirev, A.P.; Ustinov, A.V.; Butt, M.A. Generation of complex transverse energy flow distributions with autofocusing optical vortex beams. Micromachines 2021, 12, 297. [Google Scholar] [CrossRef]
- Bazhenov, V.Y.; Vasnetsov, M.V.; Soskin, M.S. Laser beams with screw dislocations in their wavefronts. JTP Lett. 1990, 52, 429–431. [Google Scholar]
- Heckenberg, N.R.; McDuff, R.; Smith, C.P.; Rubinstein-Dunlop, H.; Wegener, M.J. Laser beams with phase singularities. Opt. Quantum Electron. 1992, 24, S951–S962. [Google Scholar] [CrossRef]
- Khonina, S.N.; Kotlyar, V.V.; Soifer, V.A.; Lautanen, J.; Honkanen, M.; Turunen, J. Generating a couple of rotating nondiffracting beams using a binary-phase DOE. Optik 1999, 110, 137–144. [Google Scholar]
- Janicijevic, L.; Topuzoski, S. Fresnel and Fraunhofer diffraction of a Gaussian laser beam by fork-shaped gratings. J. Opt. Soc. Am. A 2008, 25, 2659–2669. [Google Scholar] [CrossRef] [PubMed]
- Topuzoski, S. Generation of optical vortices with curved fork-shaped holograms. Opt. Quantum Electron. 2016, 48, 1–6. [Google Scholar] [CrossRef]
- Saad, F.; El Halba, E.M.; Belafhal, A. Generation of generalized spiraling Bessel beams of arbitrary order by curved fork-shaped holograms. Opt. Quantum Electron. 2016, 48, 454. [Google Scholar] [CrossRef]
- Khonina, S.N.; Usinov, A.V.; Kirilenko, M.S.; Kuchmizhak, A.A.; Porfirev, A.P. Application of a binary curved fork grating for the generation and detection of optical vortices outside the focal plane. J. Opt. Soc. Am. B 2020, 37, 1714–1721. [Google Scholar] [CrossRef]
- Wang, D.; Jin, L.; Rosales-Guzman, C.; Gao, W. Generating arbitrary arrays of circular Airy Gaussian vortex beams with a single digital hologram. Appl. Phys. B 2021, 127, 22. [Google Scholar] [CrossRef]
- Khonina, S.N.; Balalayev, S.A.; Skidanov, R.V.; Kotlyar, V.V.; Paivanranta, B.; Turunen, J. Encoded binary diffractive element to form hyper-geometric laser beams. J. Opt. A Pure Appl. Opt. 2009, 11, 065702. [Google Scholar] [CrossRef]
- Khonina, S.N.; Kotlyar, V.V.; Soifer, V.A.; Honkanen, M.; Lautanen, J.; Turunen, J. Generation of rotating Gauss-Laguerre modes with binary-phase diffractive optics. J. Mod. Opt. 2009, 46, 227–238. [Google Scholar]
- Lerner, V.; Shwa, D.; Drori, Y.; Katz, N. Shaping Laguerre-Gaussian laser modes with binary gratings using a digital micromirror device. Opt. Lett. 2012, 37, 4826–4848. [Google Scholar] [CrossRef] [PubMed]
- Mirhosseini, M.; Magana-Loaiza, O.S.; Chen, C.; Rodenburg, B.; Malik, M.; Boyd, R.W. Rapid generation of light beams carrying orbital angular momentum. Opt. Express 2013, 21, 30204–30211. [Google Scholar] [CrossRef]
- Kotlyar, V.V.; Soifer, V.A.; Khonina, S.N. Rotation of multimodal Gauss-Laguerre light beams in free space and in a fiber. Opt. Lasers Eng. 1998, 29, 343–350. [Google Scholar] [CrossRef]
- Almazov, A.A.; Khonina, S.N.; Kotlyar, V.V. Using phase diffraction optical elements to shape and select laser beams consisting of a superposition of an arbitrary number of angular harmonics. J. Opt. Technol. 2005, 72, 391–399. [Google Scholar] [CrossRef]
- Caley, A.J.; Thomson, M.J.; Liu, J.; Waddie, A.J.; Taghizadeh, M.R. Diffractive optical elements for high gain lasers with arbitrary output beam profiles. Opt. Express 2007, 15, 10699–10704. [Google Scholar] [CrossRef]
- Jia, W.; Chen, Z.; Wen, F.J.; Zhou, C.; Chow, Y.T.; Chung, P.S. Coaxial holographic encoding based on pure phase modulation. Appl. Opt. 2011, 50, H10–H15. [Google Scholar] [CrossRef]
- Gerchberg, R.W.; Saxton, W.D. A practical algorithm for the determination of the phase from image and diffraction plane pictures. Optik 1972, 35, 237–246. [Google Scholar]
- Khonina, S.N.; Kotlyar, V.V.; Soifer, V.A. Techniques for encoding composite diffractive optical elements. Proc. SPIE Int. Soc. Opt. Eng. 2003, 5036, 493–498. [Google Scholar]
- Meister, M.; Winfield, R.J. Novel approaches to direct search algorithms for the design of diffractive optical elements. Opt. Commun. 2002, 203, 39–49. [Google Scholar] [CrossRef]
- Hsu, W.-F.; Lin, S.-C. Iternative pixelwise approach applied to computer-generated holograms and diffractive optical elements. Appl. Opt. 2018, 57, A189–A196. [Google Scholar] [CrossRef] [PubMed]
- Swartzlander, G.A. Achromatic optical vortex lens. Opt. Lett. 2006, 31, 2042–2044. [Google Scholar] [CrossRef]
- Xie, Q.; Zhao, D. Optical vortices generated by multi-level achromatic spiral phase plates for broadband beams. Opt. Commun. 2008, 281, 7–11. [Google Scholar] [CrossRef]
- Fadeyeva, T.A.; Shvedov, V.G.; Izdebskaya, Y.V.; Volyar, A.V.; Brasselet, E.; Neshev, D.N.; Desyatnikov, A.S.; Krolikowski, W.; Kivshar, Y.S. Spatially engineered polarization states and optical vortices in uniaxial crystals. Opt. Express 2010, 18, 10848–10863. [Google Scholar]
- Loussert, C.; Brasselet, E. Efficient scalar and vectorial singular beam shaping using homogeneous anisotropic media. Opt. Lett. 2010, 35, 7–9. [Google Scholar] [CrossRef]
- Khonina, S.N.; Karpeev, S.V.; Alferov, S.V.; Soifer, V.A. Generation of cylindrical vector beams of high orders using uniaxial crystals. J. Opt. 2015, 17, 065001. [Google Scholar] [CrossRef]
- Khonina, S.N.; Karpeev, S.V.; Paranin, V.D.; Morozov, A.A. Polarization conversion under focusing of vortex laser beams along the axis of anisotropic crystals. Phys. Lett. A 2017, 381, 2444–2455. [Google Scholar] [CrossRef]
- Khonina, S.N.; Porfirev, A.P.; Kazanskiy, N.L. Variable transformation of singular cylindrical vector beams using anisotropic crystals. Sci. Rep. 2020, 10, 5590. [Google Scholar] [CrossRef]
- Wang, X.; Ding, J.; Ni, W.; Guo, C.; Wang, H. Generation of arbitrary vector beams with a spatial light modulator and a common path interferometric arrangement. Opt. Lett. 2007, 32, 3549. [Google Scholar] [CrossRef] [PubMed]
- Cancula, M.; Ravnik, M.; Zumer, S. Generation of vector beams with liquid crystal disclination lines. Phys. Rev. E 2014, 90, 022503. [Google Scholar] [CrossRef] [PubMed]
- Hsu, W.-L.; Balakrishnan, K.; Ibn-Elhaj, M.; Pau, S. Infrared liquid crystal polymer micropolarizer. Appl. Opt. 2014, 53, 5252–5258. [Google Scholar] [CrossRef]
- Alpmann, C.; Schlickriede, C.; Otte, E.; Denz, C. Dynamic modulation of Poincare beams. Sci. Rep. 2017, 7, 8076. [Google Scholar] [CrossRef] [PubMed]
- Zhou, H.; Fu, S.; Zhai, Y.; Yin, C.; Gao, C. Spatial light modulator-based programmable J-plate for the arbitrary spin-to-orbital angular momentum conversion of lights. Appl. Phys. B 2019, 125, 42. [Google Scholar] [CrossRef]
- Beck, R.J.; Parry, J.P.; MacPherson, W.N.; Waddie, A.; Weston, N.J.; Shephard, J.D.; Hand, D.P. Application of cooled spatial light modulator for high power nanosecond laser micromachining. Opt. Express 2010, 18, 17059–17065. [Google Scholar] [CrossRef] [PubMed]
- Liu, D.; Gui, L.; Akram, M.R. Generation of OAM radio waves using a slot antenna array. In Proceedings of the Asia-Pacific Microwave Conference (APMC), Nanjing, China, 6–9 December 2015; pp. 1–3. [Google Scholar]
- Yu, S.X.; Li, L.; Shi, G.M.; Zhu, C.; Shi, Y. Generating multiple orbital angular momentum vortex beams using a metasurface in radio frequency domain. Appl. Phys. Lett. 2016, 108, 241901. [Google Scholar] [CrossRef]
- Wang, L.Y.; Shi, H.Y.; Zhu, S.T.; Li, J.X.; Zhang, A.X.; Li, L.M. Generation of multiple modes microwave vortex beams using tunable metasurface. In Proceedings of the 7th IEEE International Symposium on Microwave, Antenna, Propagation and EMC Technologies, Xi’an, China, 24–27 October 2017; pp. 379–381. [Google Scholar]
- Bai, X. High-efficiency transmissive metasurface for dual-polarized dual-mode OAM generation. Results Phys. 2020, 18, 103334. [Google Scholar] [CrossRef]
- Barnett, S.M.; Allen, L. Orbital angular momentum and nonparaxial light beams. Opt. Commun. 1994, 10, 670. [Google Scholar] [CrossRef]
- Devlin, R.C.; Ambrosio, A.; Rubin, N.A.; Mueller, J.P.B.; Capasso, F. Arbitrary spin-to-orbital angular momentum conversion of light. Science 2017, 358, 896–901. [Google Scholar] [CrossRef] [PubMed]
- Yang, C.-H.; Fuh, A.Y.-G. Complex beam shaping based on an equivalent q-plate system and analysis of its properties using digital holography polarization imaging. Sci. Rep. 2017, 7, 2769. [Google Scholar] [CrossRef]
- Karimi, E.; Piccirillo, B.; Nagali, E.; Marrucci, L.; Santamato, E. Efficient generation and sorting of orbital angular momentum eigenmodes of light by thermally tuned q-plates. Appl. Phys. Lett. 2009, 94, 231123. [Google Scholar] [CrossRef]
- Li, G.X.; Kang, M.; Chen, S.M.; Zhang, S.; Pun, E.B.; Cheah, K.; Li, J.S. Spin-enabled plasmonic metasurfaces for manipulating orbital angular momentum of light. Nano Lett. 2013, 13, 4148–4151. [Google Scholar] [CrossRef]
- Zhang, Y.; Lyu, Y.; Liao, D.; Wang, H. Reflective metasurface for generating orbital angular momentum of microwave. In Proceedings of the International Applied Computational Electromagnetics Society Symposium (ACES), Firenze, Italy, 29–30 March 2017; pp. 1–2. [Google Scholar]
- Chen, M.N.; Jiang, L.J.; Sha, W.I. Orbital angular momentum generation and detection by geometric-phase based metasurfaces. Appl. Sci. 2018, 8, 362. [Google Scholar] [CrossRef]
- Yue, F.; Wen, D.; Xin, J.; Gerardot, B.D.; Li, J.; Chen, X. Vector vortex beam generation with a single plasmonic metasurface. ACS Photonics 2016, 3, 1558–1563. [Google Scholar] [CrossRef]
- Mehmood, M.Q.; Mei, S.; Hussain, S.; Huang, K.; Siew, S.Y.; Zhang, L.; Zhang, T.; Ling, X.; Liu, H.; Teng, J.; et al. Visible-frequency metasurface for structuring and spatially multiplexing optical vortices. Adv. Mater. 2016, 28, 2533–2539. [Google Scholar] [CrossRef]
- Yang, Y.M.; Wang, W.Y.; Moitra, P.; Kravchenko, I.I.; Briggs, D.P.; Valentine, J. Dielectric meta-reflectarray for broadband linear polarization conversion and optical vortex generation. Nano Lett. 2014, 14, 1394–1399. [Google Scholar] [CrossRef]
- He, Y.; Li, Y.; Liu, J.; Zhang, X.; Cai, Y.; Chen, Y.; Chen, S.; Fan, D. Switchable phase and polarization singular beams generation using dielectric metasurfaces. Sci. Rep. 2017, 7, 6814. [Google Scholar] [CrossRef] [PubMed]
- Stafeev, S.S.; Kotlyar, V.V.; Nalimov, A.G.; Kotlyar, M.V.; O’Faolain, L. Subwavelength gratings for polarization conversion and focusing of laser light. Photonics Nanostruct. 2017, 27, 32–41. [Google Scholar] [CrossRef]
- Degtyarev, S.A.; Volotovsky, S.G.; Khonina, S.N. Sublinearly chirped metalenses for forming abruptly autofocusing cylindrically polarized beams. J. Opt. Soc. Am. B 2018, 35, 1963–1969. [Google Scholar] [CrossRef]
- Schemmel, P.; Pisano, G.; Maffei, B. Modular spiral phase plate design for orbital angular momentum generation at millimetre wavelengths. Opt. Express 2014, 22, 14712–14726. [Google Scholar] [CrossRef] [PubMed]
- Yu, J.; Bai, Z.; Zhu, G.; Fu, C.; Li, Y.; Liu, S.; Liao, C.; Wang, Y. 3D nanoprintedkinoform spiral zone plates on fiber facets for high-efficiency focused vortex beam generation. Opt. Express 2020, 28, 38127–38139. [Google Scholar] [CrossRef]
- Doerr, C.R.; Buhl, L.L. Circular grating coupler for creating focused azimuthally and radially polarized beams. Opt. Lett. 2011, 36, 1209–1211. [Google Scholar] [CrossRef]
- Su, T.; Scott, R.; Djordjevic, S.; Fontaine, N.; Geisler, D.; Cai, Z.; Yoo, S. Demonstration of free space coherent optical communication using integrated silicon photonic orbital angular momentum devices. Opt. Express 2012, 20, 9396–9402. [Google Scholar] [CrossRef] [PubMed]
- Zhang, D.; Feng, X.; Huang, Y. Encoding and decoding of orbital angular momentum for wireless optical interconnects on chip. Opt. Express 2012, 20, 26986–26995. [Google Scholar] [CrossRef]
- Wang, Y.; Zhao, P.; Feng, X.; Xu, Y.; Cui, K.; Liu, F.; Zhang, W.; Huang, Y. Integrated photonic emitter with a wide switching range of orbital angular momentum modes. Sci. Rep. 2016, 6, 22512. [Google Scholar] [CrossRef] [PubMed]
- Taillaert, D.; Laere, F.V.; Ayre, M.; Bogaerts, W.; Thourhout, D.V.; Bienstman, P.; Baets, R. Grating couplers for coupling between optical fibers and nanophotonic waveguides. Jpn. J. Appl. Phys. 2006, 45, 6071. [Google Scholar] [CrossRef]
- Cognee, K.D.H.L.P.K.A. Generation of pure OAM beams with a single state of polarization by antenna-decorated microdisk resonators. ACS Photonics 2020, 7, 43. [Google Scholar] [CrossRef]
- Cai, X.; Wang, J.; Strain, M.J.; Johnson-Morris, B.; Zhu, J.; Sorel, M.; Brien, J.L.; Thompson, M.G.; Yu, S. Integrated compact optical vortex beam emitters. Science 2012, 338, 363–366. [Google Scholar] [CrossRef]
- Li, R.; Feng, X.; Zhang, D.; Cui, K.; Liu, F.; Huang, Y. Radially polarized orbital angular momentum beam emitter based on shallow-ridge silicon microring cavity. IEEE Photonics J. 2014, 6, 2200710. [Google Scholar] [CrossRef]
- Scaffardi, M.; Malik, M.M.; Lazzeri, E.; Klitis, C.; Meriggi, L.; Zhang, N.; Sorel, M.; Bogoni, A. 3x3 optical switch by exploiting vortex beam emitters based on silicon microrings with superimposed gratings. Opt. Lett. 2017, 42, 3749. [Google Scholar] [CrossRef] [PubMed]
- Xiao, Q.; Klitis, C.; Li, S.; Chen, Y.; Cai, X.; Sorel, M.; Yu, S. Generation of photonic orbital angular momentum superposition states using vortex beam emitters with superimposed gratings. Opt. Express 2016, 24, 3168. [Google Scholar] [CrossRef] [PubMed]
- Liu, A.; Zou, C.-L.; Ren, X.; Wang, Q.; Guo, G.-C. On-chip generation and control of the vortex beam. Appl. Phys. Lett. 2016, 108, 181103. [Google Scholar] [CrossRef]
- Liu, W.; Hu, X.; Jin, L.; Fu, X.; Chen, Q. Generation of in-plane light beam with orbital angular momentum with an asymmetrical plasmonic waveguide. Plasmonics 2016, 11, 1323–1329. [Google Scholar] [CrossRef]
- Xie, Z.; Lei, T.; Li, F.; Qiu, H.; Zhang, Z.; Wang, H.; Min, C.; Du, L.; Li, Z.; Yuan, X. Ultra-broadband on-chip twisted light emitter for optical communications. Light Sci. Appl. 2018, 7, 18001. [Google Scholar] [CrossRef]
- Wang, X.; Nie, Z.; Liang, Y.; Wang, J.; Li, T.; Jia, B. Recent advances on optical vortex generation. Nanophotonics 2018, 7, 1533–1556. [Google Scholar] [CrossRef]
- Zhao, Z.; Fan, S. Design principles of apodized grating couplers. J. Lightwave Technol. 2020, 38, 4435–4446. [Google Scholar] [CrossRef]
- Liu, J.; Li, S.; Ding, Y.; Chen, S.; Du, C.; Mo, Q.; Morioka, T.; Yvind, K.; Oxenlowe, K.; Yu, S.; et al. Orbital angular momentum modes emission from a silicon photonic integrated device for km-scale data-carrying fiber transmission. Opt. Express 2018, 26, 15471–15479. [Google Scholar] [CrossRef]
- Li, S.; Nong, Z.; Wu, X.; Yu, W.; He, M.; Klitis, C.; Zhu, Y.; Gao, S.; Liu, J.; Li, Z.; et al. Orbital angular momentum vector modes (de)multiplexer based on multimode micro-ring. Opt. Express 2018, 26, 29895–29905. [Google Scholar] [CrossRef]
- Paul, S.; Lyubopytov, V.S.; Schumann, M.F.; Cesar, J.; Chipouline, A.; Wegener, M.; Küppers, F. Wavelength-selective orbital-angular-momentum beam generation using MEMS tunable Fabry-Perot filter. Opt. Lett. 2016, 41, 3249. [Google Scholar] [CrossRef]
- Lyubopytov, V.S.; Porfirev, A.P.; Gurbatov, S.O.; Paul, S.; Schumann, M.F.; Cesar, J.; Malekizandi, M.; Haidar, M.T.; Wegener, M.; Chipouline, A.; et al. Simultaneous wavelength and orbital angular momentum demultiplexing using tunable MEMS-based Fabry-Perot filter. Opt. Express 2017, 25, 9634–9646. [Google Scholar] [CrossRef]
- Zhang, D.; Feng, X.; Cui, K.; Liu, F.; Huang, Y. Generating in-plane orbital angular momentum beams with silicon waveguides. IEEE Photonics J. 2013, 5, 2201206. [Google Scholar] [CrossRef]
- Zhang, D. Angular momentum of optical modes in a silicon channel waveguide. Phys. Rev. Res. 2020, 2, 33454. [Google Scholar] [CrossRef]
- Lee, I.J.; Kim, S. On-chip guiding of higher-order orbital angular momentum modes. Photonics 2019, 6, 72. [Google Scholar] [CrossRef]
- Lee, I.J.; Kim, S. Directional coupler design for orbital angular momentum mode-based photonic integrated circuits. Opt. Express 2020, 28, 30085. [Google Scholar] [CrossRef] [PubMed]
- Chen, L.; Zhao, L.; Hao, Y.; Liu, W.; Wu, Y.; Wei, Z.; Xu, N.; Qin, S.; Yang, X.; Liu, H. Metasurface spiral focusing generators with tunable orbital angular momentum based on slab silicon nitride waveguide and vanadium dioxide (VO2). Nanomaterials 2020, 10, 1864. [Google Scholar] [CrossRef]
- Lyubopytov, V.S.; Kutluyarov, R.V.; Bagmanov, V.K.; Neumann, N.; Sultanov, A.K. Modeling and optimization of vortex modes propagation in rectangular dielectric waveguides. IEEE Photonics J. 2020, 12, 6100117. [Google Scholar] [CrossRef]
- Meng, Y.; Liu, Z.; Xie, Z.; Wang, R.; Qi, T.; Hu, F.; Kim, H.; Xiao, Q.; Fu, X.; Wu, Q.; et al. Versatile on-chip light coupling and (de)multiplexing from arbitrary polarizations to controlled waveguide modes using an integrated dielectric metasurface. Photonics Res. 2020, 8, 564. [Google Scholar] [CrossRef]
- Liang, Y.; Wu, H.W.; Huang, B.J.; Huang, X.G. Light beams with selective angular momentum generated by hybrid plasmonic waveguides. Nanoscale 2014, 6, 12360–12365. [Google Scholar] [CrossRef]
- Lyubopytov, V.S.; Chipouline, A.; Zywietz, U.; Chichkov, B.; Sokolovskii, G.S.; Averkiev, N.S.; Savchenko, G.M.; Bougrov, V.E.; Monroy, I.T.; Kuppers, F. Optical vortex propagation in few-mode rectangular polymer waveguides. In Proceedings of the 2017 Opto-Electronics and Communications Conference (OECC) and Photonics Global Conference (PGC), Singapore, 31 July–4 August 2017. [Google Scholar]
- Lyubopytov, V.S.; Chipouline, A.; Sokolovskii, G.S.; Averkiev, N.S.; Savchenko, G.M.; Zywietz, U.; Chichkov, B.; Monroy, I.T.; Bougrov, V.E.; Kuppers, F. Demonstration of optical vortex propagation in on-chip rectangular dielectric waveguides. In Proceedings of the 2017 European Conference on Lasers and Electro-Optics and European Quantum Electronics Conference, Munich, Germany, 25–29 June 2017. [Google Scholar]
- Ma, Z.; Chen, H.; Wu, K.; Zhang, Y.; Chen, Y.; Yu, S. Self-imaging of orbital angular momentum (OAM) modes in rectangular multimode interference waveguides. Opt. Express 2015, 23, 5014. [Google Scholar] [CrossRef]
- Butt, M.A.; Khonina, S.N.; Kazanskiy, N.L. Hybrid plasmonic waveguide-assisted metal-insulator-metal ring resonator for refractive index sensing. J. Mod. Opt. 2018, 65, 1135–1140. [Google Scholar] [CrossRef]
- Butt, M.A.; Khonina, S.N.; Kazanskiy, N.L. Device performance of standard strip, slot and hybrid plasmonic micro-ring resonator: A comparative study. Waves Random Complex Media 2020. [Google Scholar] [CrossRef]
- Liang, Y.; Zhang, F.; Gu, J.; Huang, X.G.; Liu, S. Integratable quarter-wave plates enable one-way angular momentum conversion. Sci. Rep. 2016, 6, 24959. [Google Scholar] [CrossRef] [PubMed]
- Kutluyarov, R.V.; Fatkhiev, D.M.; Stepanov, I.V.; Grakhova, E.P.; Lyubopytov, V.S.; Sultanov, A.K. Design and modeling of a photonic integrated device for optical vortex generation in a silicon waveguide. Comput. Opt. 2021, 45, 324–330. [Google Scholar] [CrossRef]
- Fatkhiev, D.M.; Lyubopytov, V.S.; Kutluyarov, R.V.; Grakhova, E.P.; Sultanov, A.K. A grating coupler design for optical vortex mode generation in rectangular waveguides. IEEE Photonics J. 2021. [Google Scholar] [CrossRef]
- Schulze, C.; Dudley, A.; Flamm, D.; Duparre, M.; Forbes, A. Measurement of the orbital angular momentum density of light by modal decomposition. New J. Phys. 2013, 15, 073025. [Google Scholar] [CrossRef]
- Yu, T.; Xia, H.; Xie, W.; Peng, Y. Orbital angular momentum mode detection of the combined vortex beam generated by coherent combining technology. Opt. Express 2020, 28, 35795–35806. [Google Scholar] [CrossRef] [PubMed]
- Zhang, C.; Ma, L. Detecting the orbital angular momentum of electro-magnetic waves using virtual rotational antenna. Sci. Rep. 2017, 7, 4585. [Google Scholar] [CrossRef]
- Liu, B.; Chu, H.; Giddens, H.; Li, R.; Hao, Y. Experimental observation of linear and rotational doppler shifts from several designer surfaces. Sci. Rep. 2019, 9, 8971. [Google Scholar] [CrossRef]
- Genevet, P.; Lin, J.; Kats, M.A.; Capasso, F. Holographic detection of the orbital angular momentum of light with plasmonic photodiodes. Nat. Commun. 2012, 3, 1278. [Google Scholar] [CrossRef]
- Mohammadi, S.M.; Daldorff, L.S.; Forozesh, K.; Thide, B.; Bergman, J.S.; Isham, B.; Karlsson, R.; Carozzi, T.D. Orbital angular momentum in radio: Measurement methods. Radio Sci. 2010, 45, 1–14. [Google Scholar] [CrossRef]
- Mair, A.; Vaziri, A.; Weihs, G.; Zeilinger, A. Entanglement of the orbital angular momentum states of photons. Nature 2001, 412, 313–316. [Google Scholar] [CrossRef]
- Kotlyar, V.V.; Khonina, S.N.; Soifer, V. Light field decomposition in angular harmonics by means of diffractive optics. J. Mod. Opt. 1998, 45, 1495–1506. [Google Scholar] [CrossRef]
- Khonina, S.N.; Kotlyar, V.; Soifer, V.; Paakkonen, P.; Simonen, J.; Turunen, J. An analysis of the angular momentum of a light field in terms of angular harmonics. J. Mod. Opt. 2001, 48, 1543–1557. [Google Scholar] [CrossRef]
- Moreno, I.; Davis, J.A.; Pascoguin, B.L.; Mitry, M.J.; Cottrell, D.M. Vortex sensing diffraction gratings. Opt. Lett. 2009, 34, 2927–2929. [Google Scholar] [CrossRef] [PubMed]
- Kazanskiy, N.L.; Khonina, S.N.; Karpeev, S.V.; Porfirev, A.P. Diffractive optical elements for multiplexing structured laser beams. Quantum Electron. 2020, 50, 629–635. [Google Scholar] [CrossRef]
- Khonina, S.N.; Karpeev, S.V.; Paranin, V.D. A technique for simultaneous detection of individual vortex states of Laguerre-Gaussian beams transmitted through an aqueous suspension of microparticles. Opt. Lasers Eng. 2018, 105, 68–74. [Google Scholar] [CrossRef]
- Khonina, S.N.; Skidanov, R.V.; Kotlyar, V.V.; Jefimovs, K.; Turunen, J. Phase diffractive filter to analyze an output step-index fiber beam. Proc. SPIE Int. Soc. Opt. Eng. 2004, 5182, 251–259. [Google Scholar]
- Lei, T.; Zhang, M.; Li, Y.; Jia, P.; Liu, G.N.; Xu, X.; Li, Z.; Min, C.; Lin, J.; Yu, C.; et al. Massive individual orbital angular momentum channels for multiplexing enabled by Dammann gratings. Light Sci. Appl. 2015, 4, e257. [Google Scholar] [CrossRef]
- Fu, S.; Zhang, S.; Wang, T.; Gao, C. Measurement of orbital angular momentum spectra of multiplexing optical vortices. Opt. Express 2016, 24, 6240–6248. [Google Scholar] [CrossRef]
- D’Errico, A.; D’Amelio, R.; Piccirillo, B.; Cardano, F.; Marrucci, L. Measuring the complex orbital angular momentum spectrum and spatial mode decomposition of structured light beams. Optica 2017, 4, 1350–1357. [Google Scholar] [CrossRef]
- Fu, S.; Zhai, Y.; Wang, T.; Yin, C.; Gao, C. Orbital angular momentum channel monitoring of coaxially multiplexed vortices by diffraction pattern analysis. Appl. Opt. 2018, 57, 1056–1060. [Google Scholar] [CrossRef]
- Khonina, S.N.; Karpeev, S.V.; Butt, M.A. Spatial-light-modulator-based multichannel data transmission by vortex beams of various orders. Sensors 2021, 21, 2988. [Google Scholar] [CrossRef] [PubMed]
- Wen, D.; Yue, F.; Li, G.; Zheng, G.; Chan, K.; Chen, S.; Chen, M.; Li, K.; Wong, P.; Cheah, K.; et al. Helicity multiplexed broadband metasurface holograms. Nat. Commun. 2015, 6, 8241. [Google Scholar] [CrossRef]
- Arbabi, A.; Horie, Y.; Bagheri, M.; Faraon, A. Dielectric metasurfaces for complete control of phase and polarization with subwavelength spatial resolution and high transmission. Nat. Nanotechnol. 2015, 10, 937–943. [Google Scholar] [CrossRef] [PubMed]
- Mueller, J.P.; Rubin, N.A.; Devlin, R.C.; Groever, B.; Capasso, F. Metasurface polarization optics: Independent phase control of arbitrary orthogonal states of polarization. Phys. Rev. Lett. 2017, 118, 133901. [Google Scholar]
- Bao, Y.; Ni, J.; Qiu, C.W. A minimalist single-layer metasurface for arbitrary and full control of vector vortex beams. Adv. Mater. 2020, 32, 1905659. [Google Scholar] [CrossRef] [PubMed]
- He, Y.; Wang, P.; Wang, C.; Liu, J.; Ye, H.; Zhou, X.; Li, Y.; Chen, S.; Fan, D. All-optical signal processing in structured light multiplexing with dielectric meta-optics. ACS Photonics 2020, 7, 135–146. [Google Scholar] [CrossRef]
- Li, S.; Li, X.; Zhang, L.; Wang, G.; Zhang, L.; Liu, M.; Zeng, C.; Wang, L.; Sun, Q.; Zhao, W.; et al. Efficient optical angular momentum manipulation for compact multiplexing and demultiplexing using a dielectric metasurface. Adv. Opt. Mater. 2020, 8, 1901666. [Google Scholar] [CrossRef]
- Rui, G.; Gu, B.; Cui, Y.; Zhan, Q. Detection of orbital angular momentum using a photonic integrated circuit. Sci. Rep. 2016, 6, 28262. [Google Scholar] [CrossRef] [PubMed]
- Liu, A.; Jones, R.; Liao, L.; Samara-Rubio, D.; Rubin, D.; Cohen, O.; Nicolaescu, R.; Paniccia, M. A high-speed silicon optical modulator based on a metal-oxide-semiconductor capacitor. Nature 2004, 427, 615–618. [Google Scholar] [CrossRef] [PubMed]
- Butt, M.A.; Khonina, S.N.; Kazanskiy, N.L. Ultrashort inverted tapered silicon ridge-to-slot waveguide coupler at 1.55 μm and 3.392 μm wavelength. Appl. Opt. 2020, 59, 7821–7828. [Google Scholar] [CrossRef] [PubMed]
- Butt, M.A.; Khonina, S.N.; Kazanskiy, N.L. 2D-Photonic crystal heterostructures for the realization of compact photonic devices. Photonics Nanostruct.-Fundam. Appl. 2021, 44, 100903. [Google Scholar] [CrossRef]
- Kazanskiy, N.L.; Butt, M.A.; Khonina, S.N. Silicon photonic devices realized on refractive index engineered subwavelength grating waveguides-A review. Opt. Laser Technol. 2021, 138, 106863. [Google Scholar] [CrossRef]
- Khonina, S.N.; Kazanskiy, N.L.; Butt, M.A. Spectral characteristics of broad band-rejection filter based on Bragg grating, one-dimensional photonic crystal, and subwavelength grating waveguide. Phys. Scr. 2021, 96, 055505. [Google Scholar] [CrossRef]
- Butt, M.A.; Kazanskiy, N.L. Narrowband perfect metasurface absorber based on impedance matching. Photonics Lett. Pol. 2020, 12, 88–90. [Google Scholar] [CrossRef]
- Zhou, J.; Zhang, W.; Chen, L. Experimental detection of high-order or fractional orbital angular momentum of light based on a robust mode converter. Appl. Phys. Lett. 2016, 108, 111108. [Google Scholar] [CrossRef]
- Ma, A.; Intaravanne, Y.; Han, J.; Wang, R.; Chen, X. Polarization detection using light’s orbital angular momentum. Adv. Opt. Mater. 2020, 8, 2000484. [Google Scholar] [CrossRef]
- Shen, Y.; Wang, X.; Xie, Z.; Min, C.; Fu, X.; Liu, Q.; Gong, M.; Yuan, X. Optical vortices 30 years on: OAM manipulation from topological charge to multiple singularities. Light Sci. Appl. 2019, 8, 90. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Malaney, R.; Green, J. Detecting orbital angular momentum of light in Satellite-to-Ground Quantum communications. In Proceedings of the IEEE Global Communications Conference (GLOBECOM), Waikoloa, HI, USA, 9–13 December 2019; pp. 1–6. [Google Scholar]
- Kaviani, H.; Ghobadi, R.; Behera, B.; Wu, M.; Hryciw, A.; Vo, S.; Fattal, D.; Barclay, P. Optomechanical detection of light with orbital angular momentum. Opt. Express 2020, 28, 15482–15496. [Google Scholar] [CrossRef] [PubMed]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).