Abstract
In this paper, we describe and present a Virtual Instrument, a tool that allows the determination of the electromechanical, dielectric, and elastic coefficients in polarised ferroelectric ceramic discs (piezoceramics) in the linear range, including all of the losses when the piezoceramics are vibrating in radial mode. There is no evidence in the recent scientific literature of any automatic system conceived and implemented as a Virtual Instrument based on an iterative algorithm issued as an alternative to solve the limitations of the ANSI IEEE 176 standard for the characterisation of piezoelectric coefficients of thin discs in resonant mode. The characterisation of these coefficients is needed for the design of ultrasonic sensors and generators. In 1995, two of the authors of this work, together with other authors, published an iterative procedure that allowed for the automatic determination of the complex constants for lossy piezoelectric materials in radial mode. As described in this work, the procedures involved in using a Virtual Instrument have been improved: the response time for the characterisation of a piezoelectric sample is shorter (approximately 5 s); the accuracy in measurement and, therefore, in the estimates of the coefficients has been increased; the calculation speed has been increased; an intuitive, simple, and friendly user interface has been designed, and tools have been provided for exporting and inspecting the measured and processed data. No Virtual Instrument has been found in the recent scientific literature that has improved on the iterative procedure designed in 1995. This Virtual Instrument is based on the measurement of a unique magnitude, the electrical admittance (Y = G + iB) in the frequency range of interest. After measuring the electrical admittance, estimates of the set of piezoelectric coefficients of the device are obtained. The programming language used in the construction of the Virtual Instrument is LabVIEW 2019®.
1. Introduction
Piezoceramics present the so-called piezoelectric effect, which consists of the polarisation of the material following a certain polar axis when the piezoceramic is subjected to mechanical traction or compression [1,2]. The polarisation of the material causes an accumulation of a charge in one direction or another of its polar axis, manifesting as a potential difference in the faces of the crystals [3,4,5,6,7,8]. This phenomenon is called the direct piezoelectric effect. Piezoceramics also present the inverse piezoelectric effect: if the piezoceramic is subjected to an external electric field, it will be compressed or stretched depending on the value and direction of the electric field [1]. Figure 1 shows a depiction of the piezoelectric effect.

Figure 1.
Piezoelectric effect: (a) Direct effect; (b) Inverse effect.
Piezoceramics are used as sensors and/or generators, and their applications are constantly expanding [9,10,11,12,13], especially in industrial applications and in a wide range of electronic devices. The electromechanical characterisation of these devices must be as reliable and accurate as possible such that the electromechanical behaviour of the sensor or actuator is perfectly described [14,15].
The most extended characterisation method of these types of piezoceramic materials is well-known as the resonance method. It is based on the inverse piezoelectric effect (Figure 1b) that provokes a vibration when an AC electric field in a certain interval of frequencies is applied to the material. This method is described in the ANSI IEEE 176 [2] standard, which provides a procedure to estimate the electromechanical, dielectric, and elastic coefficients in resonant modes from measurements of the impedance/admittance of the sample, assuming low energy losses. Therefore, the values of the coefficients calculated by the ANSI IEEE 176 method are real numerical values (i.e., without an imaginary part). Numerous papers have been published on the characterisation of piezoelectric ceramics based on this standard [16,17]; however, characterisation of the dielectric and elastic coefficients, taking into account material losses, has provided further research motivation for materials scientists and engineers [18,19,20,21,22,23,24,25,26,27,28,29,30,31], which have used both the resonance method and other direct measurements.
In previous works, the authors of this paper exposed some difficulties presented by the ANSI IEEE 176 standard in terms of calculating exact material coefficients when the energy losses are not ignored. For this reason, they proposed an iterative, programmable method, based on Smits’s [22] method, that allows for estimation of the coefficients while taking into account the energy losses in the material by providing an estimate of the coefficients with complex numerical values (i.e., with real and imaginary parts) [18,32,33], as the imaginary part of the coefficients represents the non-negligible losses in the material.
The iterative method consists of searching for resonance frequencies in samples with different geometries (see Figure 2) and measuring the electrical admittance (Y = G + iB) in the frequency range of interest in the laboratory using an impedance analyser. With the expressions of the real and imaginary parts of the electrical admittance, Y, a system of nonlinear equations can be obtained. The resolution of this system of nonlinear equations is solved using an iterative numerical method based on the measurements obtained. The constructed Virtual Instrument consists of hardware for excitation and measurement in the sample as well as software for control and management of the measured data. No Virtual Instrument that performs this type of automatic characterisation of these devices has been found in the recent scientific literature. The authors of this paper have modified the iterative procedure [18] for better accuracy in estimating the coefficients. There is also no evidence in the recent scientific literature of any Virtual Instrument based on an iterative procedure based on a single measure of admittance as a function of frequency.
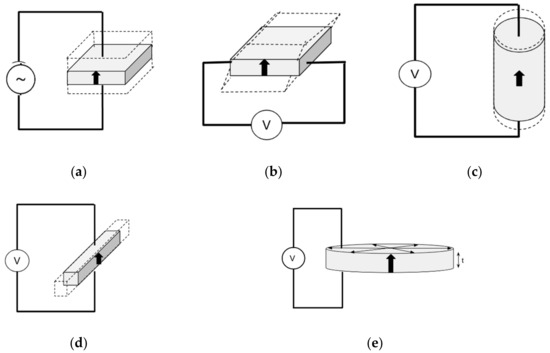
Figure 2.
Schematic of the resonant modes of vibration of ceramic resonators: (a) Thickness extensional of a thickness poled thin plate; (b) Shear of a non-standard thickness poled thin plate; (c) Length extensional of a longitudinally poled cylinder or bar; (d) Length extensional of a thickness poled thin bar; (e) Radial extensional of a thickness poled thin disc.
To carry out estimation of the coefficients using the iterative numerical method, different versions of measured systems have been developed using different programming languages, including QUICKBASIC® (1994), JAVA® (2003), and LabVIEW 2008®. In all previous versions, the number of samples acquired and the iterative method were the same.
The versions mentioned are composed of a set of programs that are independent of each other and that implement the estimation of piezoelectric coefficients under different modes of vibration, as shown in Figure 2. Figure 2 includes a non-standard, thickness poled and longitudinally excited shear plate (Figure 2b), amenable to achieve the monomodal resonance needed for the application of the resonance method [34].
The original versions lack the capabilities provided by modern programming languages, such as libraries of mathematical analysis functions, functionality for the presentation of data, ease of installation of software on different platforms, and ease of exporting data, among others.
Our motivation for building a Virtual Instrument, the tool described in this paper, was to improve upon previous versions, specifically in the following aspects:
- Improve the automatic procedure for the calculation of piezoelectric coefficients in resonant mode.
- Increase the speed of processing and the calculation of constants.
- Increase the accuracy of the results.
- Improve the user interface by making it friendly and intuitive.
- Provide the system with tools for the exploration and export of the acquired and processed data.
- Make the Virtual Instrument software easily readable, expandable, and scalable.
Figure 2 shows the five resonant modes of interest for determination of material coefficients. We chose to construct a Virtual Instrument so that estimation is calculated with respect to the radial resonant mode of a thin disc as it is the most complicated procedure to implement and because there are many electronic devices that use this type of geometry and vibration mode.
The software architecture of the Virtual Instrument designed and developed allows the instrument to be expanded and scaled so that the inclusion of the analogue iterative procedures for the resonant modes’ vibration shown in Figure 2 would not involve interaction with the code already implemented for the thin disc in radial resonant mode.
In addition, LabVIEW 2019® can perform operations with extended length floating-point numbers of 128 bits (real and imaginary), and it allows substantially to improve the speed and processing capacity of the designed tool.
2. Virtual Instrument Description
The system conceived for a Virtual Instrument consists of a hardware part and a software part running on a computerised system (PC). A block diagram of the system is shown in Figure 3.
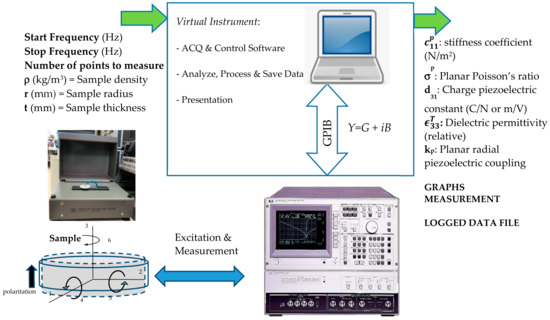
Figure 3.
Block diagram of the proposed measurement system.
The computerised system of a Virtual Instrument includes data acquisition hardware, drivers for the peripherals, and a software application to perform the functions of the measuring instrument [35].
Virtual Instruments, more generally, represent a significant shift from traditional instrumentation systems, which are typically focused on one measurement instrument towards computer systems that can improve productivity, visualisation, digital signal processing, and connectivity capabilities.
A Virtual Instrument adheres to the slogan “software is the instrument” [36,37]. It is the software, using the appropriate hardware, that defines the instrument’s functions.
The input data of a Virtual Instrument are:
- The measured admittance of the sample, which is placed in a 16065A Ext Voltage Bias Fixture HP sample holder connected to an HP4194A impedance analyser. The sample holder has to meet the two conditions of allowing the sample to vibrate freely, by not using rigid terminals that will clamp the sample, and avoiding the addition of admittance components that could modify the measurement of the complex admittance of the sample. Figure 4 shows how the sample is connected:
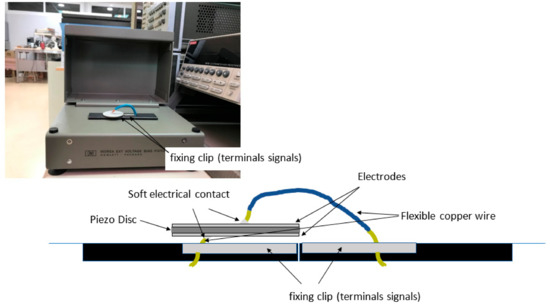 Figure 4. Image of experimental setup and schematic of sample.
Figure 4. Image of experimental setup and schematic of sample. - The start frequency (Hz), that is, the initial excitation frequency.
- The stop frequency (Hz), that is, the final excitation frequency.
- The sample radius a (mm) and sample thickness t (mm).
The data calculated [2,18] and reported by a Virtual Instrument are:
- , the elastic stiffness coefficient (N/m2) in the radial plane:where is the compliance, which is the relationship between the relative deformation in the p-axis and the mechanical stress in the q direction for an electric field E.
- , the planar radial Poisson’s ratio:
- , the relative dielectric permittivity when an electric field is applied in the direction of polarisation (i.e., direction 3) at a constant mechanical stress (T = 0, “free” permittivity). Therefore, , where .
- d31, the proportion between the dimensional variation (Δr) of the piezoelectric material (in meters) and the difference of potential applied in volts in axis 3, as well as between the generation of electric charges and the force applied in the material.
- kp, planar radial piezoelectric coupling:
- Measurement graphs: The Virtual Instrument provides several graphs from the measured data of electrical admittance, Y = G + iB, as well as utilities for data exploration.
- Logged data file: The Virtual Instrument records the measured and calculated data in files that can be exported to other applications. Moreover, all the intermediate steps of the calculations performed in the iterations are recorded.
The electrical admittance of the disc at the radial resonance frequency follows Equation (4), which is Equation (117) of the “IEEE Standard of Piezoelectricity” [2]:
where is a complex variable function called Onoe’s function [18], which follows the expression:
where and are the zeroth- and first-order first-class Bessel functions, respectively, with argument as follows:
With all of the above, along with the information of the conducted measurements, the iterative numerical method is applied, which calculates the coefficients , , , d31, and kp while taking into account the energy losses. The numerical iterative method has been described in detail in [18].
2.1. Virtual Instrument Measurements
The measurements required by the iterative numerical method consist of searching for the singular frequencies of Y = G + iB and the electrical impedance Z = R + iX within a certain frequency range. This frequency range must cover at least one overtone of the mode of interest.
The measurements that a Virtual Instrument must obtain, in order to start the iterative method [18] from the data measured with the impedance analyser (HP4194A), are as follows:
- f1s and f2s, the frequencies where G is maximal in the fundamental tone and in the overtone, respectively. The values of these frequencies are used as initial values in the iterative method.
- fp, the frequency where R is maximal.
- Δfs = |fBmax − fBmin|, where fBmax and fBmin are the frequencies at which B becomes maximal and minimal, respectively, in the fundamental tone. The values of these frequencies are used as initial values in the iterative method.
Therefore, a Virtual Instrument must measure Y within a frequency range, calculate Z from the measured data, and search for the frequencies of interest with an adequate resolution. It is at this point that the design of a Virtual Instrument presents important improvements with respect to that presented in [18], and to the previous software versions mentioned in the Introduction.
The available impedance analyser (HP4194A) was limited to 401 measurement points between the initial sweep frequency, Start frequency (Hz), and the final sweep frequency, Stop frequency (Hz).
Typically, the frequency ranges to be swept on the discs under a study of 10–15 mm radius and approximately 1 mm thickness is around 200 kHz. This means that, if the frequency search were done in a single step, the frequency resolution of the measurement would be very low, which worsens the accuracy of estimates of the coefficients after applying the iterative method. This forces the operator of the previous software to carry on a number of measurements to ensure the precision of this frequency determination.
To solve this problem, all the process has been automated in the Virtual Instrument. We have chosen to implement a solution where the user determines the frequency range in which the frequencies of interest are located. Then, automatically, the VI performs three contiguous frequency sweeps of 400 points (1200 points), and the search for the values of f1s, f2s, fp, fBmax, and fBmin. These values are the initial values to start the implemented iterative method. To do so, there is a previous step of calculation of real and imaginary parts of the measured complex admittance (Y = G + iB) and, also, of its inverse, the complex impedance (Z = R + iX).
Figure 5 presents the procedure.
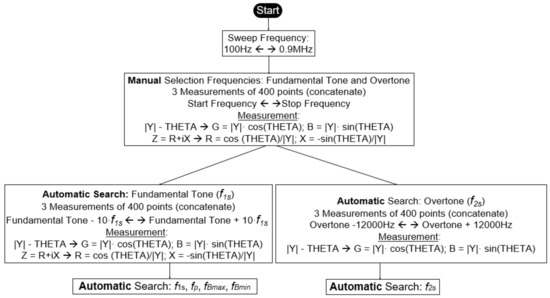
Figure 5.
Procedure for searching for the frequencies f1s, fp, fBmax, and fBmin from the fundamental tone and f2s from the first overtone.
2.2. Virtual Instrument Software
The system software was written using the graphical programming language LabVIEW 2019®, which is the most widely used language for Virtual Instrumentation. The programs developed with LabVIEW 2019® consist of two main windows, the front panel (user interface), and the block diagram (program code). The programming is modular, where each module is built with one or more files called SubVIs [38].
In this work, the Virtual Instrument was designed using a state machine architecture for measurement and control. This design pattern is very suitable for the design of complex measurement equipment in which different functionalities are required, namely, the admittance measurements and calculations for determination of coefficients in the four modes specified in Figure 2. A state is a situation in which the machine can be found. Usually, in a given state, actions or operations associated with this state are performed; furthermore, there will be a decision code to decide what state the machine should evolve to. A machine consisting of states is graphically represented as a diagram of states. The programming language LabVIEW 2019® allows the user to implement a state machine with a simple design pattern, which allows for the development of complex programs, making VI scalable, maintainable, and readable. Figure 6 shows the used LabVIEW 2019® template.
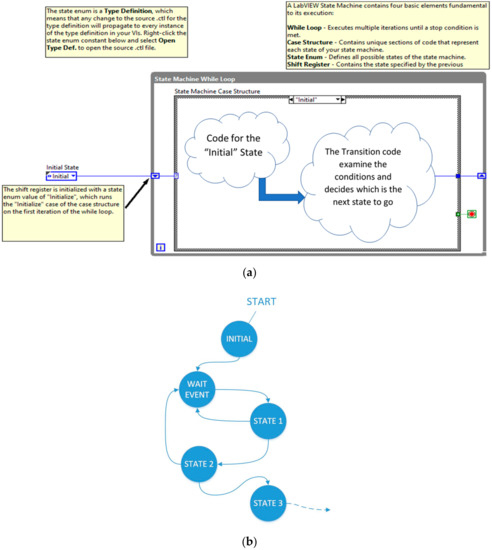
Figure 6.
(a) State machine LabVIEW 2019® template; (b) Typical state diagram.
Figure 7 shows the state diagram of the designed Virtual Instrument software. The state diagram is intended to be self-explanatory for readers with knowledge in the software. The transition between the states is caused by the events produced when the user interacts with the front panel controls.
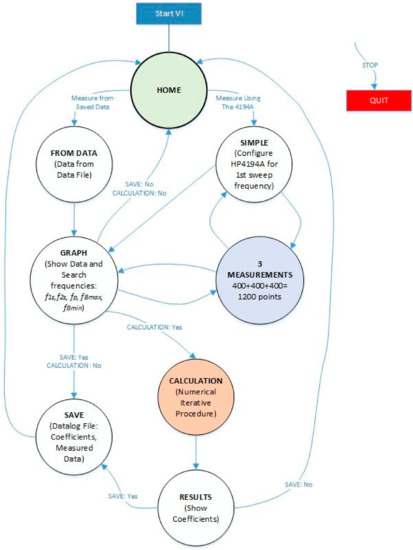
Figure 7.
State diagram of the Virtual Instrument software.
If the STOP control is pressed, the program will stop. In the CALCULATION state, the numerical iterative method is implemented, which provides the coefficients. Figure 8 shows a flowchart of the iterative process, which has been explained in detail in [18]. As can be seen, the iterative calculation can begin with the frequencies described above (f1s, f2s, fBmax, and fBmin).
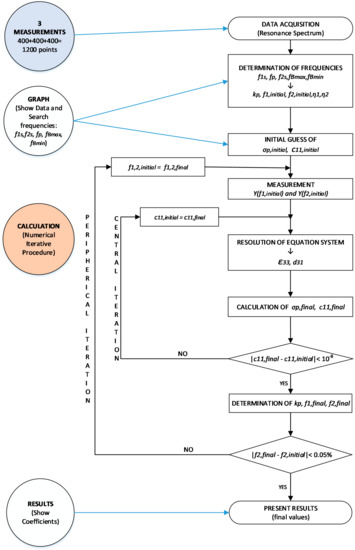
Figure 8.
Flowchart of the iterative method.
With these measurements, we obtain kp,initial, f1,initial, f2,initial, η1, and η2, where:
The initial guess value of σp (σp, initial) and are obtained by solving the system of equations of the Equation (10). The system is solved by the iterative method as described in [18]:
The initial values of σp , and allows to calculate the initial value of as described in [8].
From here, the state machine continues the calculations following the iterative method shown in Figure 8.
3. Experimental Results and Discussion
The following shows and describes the practical realisation of the characterisation of a thin piezoelectric disc using a Virtual Instrument. For this purpose, a commercial disc of soft lead titanate zirconate, with reference PZ27 of Meggit FerropermTM Piezoceramics [39], with a density ρ = 7700 kg/m3, radius = 15 mm, and thickness = 1 mm. Figure 9 shows the front panel of a Virtual Instrument.
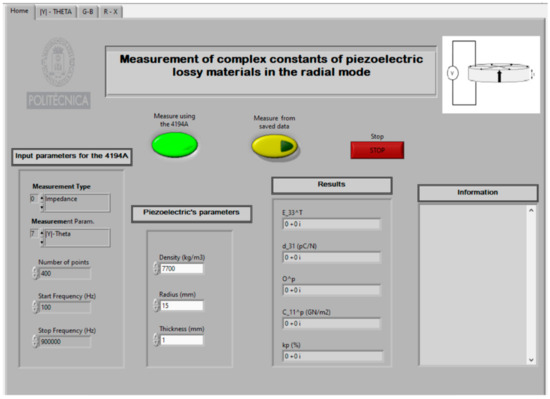
Figure 9.
Virtual Instrument front panel.
Where:
- C_11^p ≡ : stiffness coefficient (N/m2)
- O^p ≡ σp: Planar Poisson’s ratio
- d_31 ≡ d31: Charge piezoelectric constant (C/N or m/V)
- E_33^T ≡ : Dielectric permittivity (relative)
- Kp (%) ≡ kp: Planar radial piezoelectric coupling
The Sweep Frequency was performed between 100 Hz and 0.9 MHz, as indicated in Figure 5. The data obtained in the first sweep are shown in Figure 10.
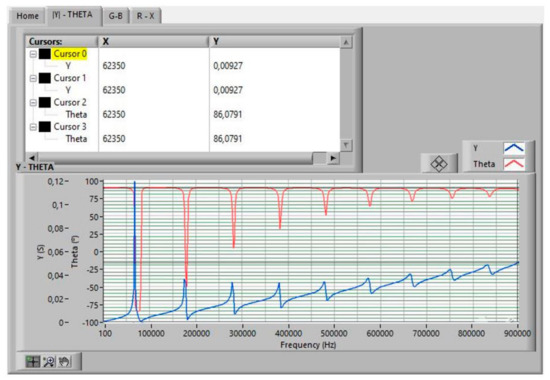
Figure 10.
Sweep frequency data measurement results.
Figure 11, Figure 12 and Figure 13 show the data obtained from a PZT after performing the Automatic Search step, indicated in the flowchart in Figure 5. The data can be viewed by selecting the corresponding tabs in the Virtual Instrument front panel.
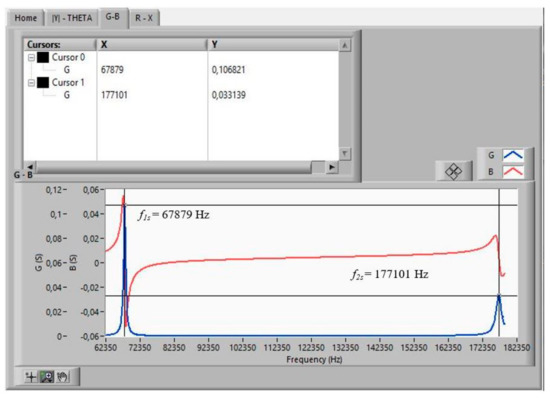
Figure 11.
Searched frequencies after the automatic search step: f1s, f2s.
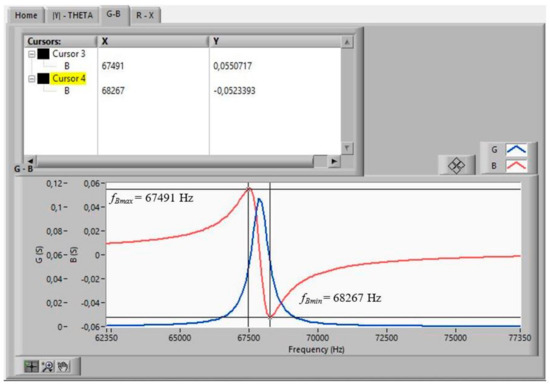
Figure 12.
Searched frequencies after the automatic search step: fBmax, fBmin.
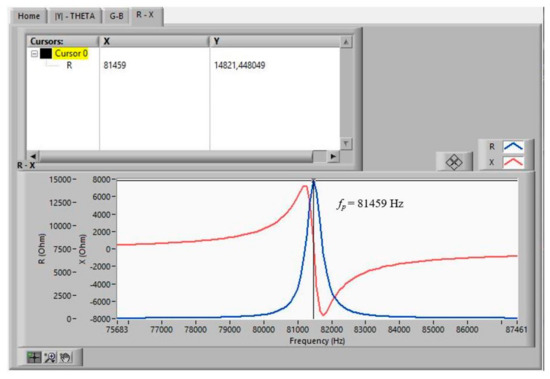
Figure 13.
Searched frequencies after the automatic search step: fp.
With the automatically found values of f1s, f2s, fp, fBmax, and fBmin, the iterative method described in Figure 8 begins. The iterative method is executed in the CALCULATION state (see Figure 7).
In addition, the Virtual Instrument has, as a novelty, the added functionality which allows to save all the intermediate steps of the calculations performed in the iterative procedure. The intermediate steps are shown in the “Information” section of the Virtual Instrument front panel (see Figure 14).
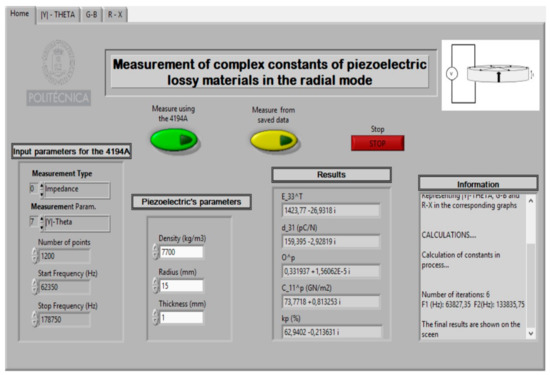
Figure 14.
Results of test.
3.1. Processing/Computation Time
To quantify the time taken by the Virtual Instrument to characterise the tested sample shown in this paper, we used the data acquisition time estimate from the manufacturer of the HP4194A [40] as well as the LabVIEW 2019® Profile Performance tool [41]. The computation time estimate in this section is the sum of the execution time of the states “MEASUREMENTS”, “GRAPH”, and “CALCULATION”.
We considered the maximum time between samples in the HP4194A manufacturer’s specifications for the execution time of the state “MEASUREMENTS”.
Ten runs were carried out to estimate the processing time. Results are shown in Table 1.

Table 1.
Profile performance.
Therefore, it is possible to estimate the average time that the Virtual Instrument took to characterise the sample:
Tcharacterisation (ms) = 4440 + 7.8 + 15.9 × 6 + 2.1 = 4540.5.
3.2. Comparation with JAVA (2003) Software
A comparison was made between the obtained results and those obtained using JAVA software (i.e., using the characterisation program constructed in JAVA in 2003).
Table 2 shows the results of the implemented Virtual Instrument and the JAVA version (2003).

Table 2.
Results of the calculation with the JAVA version and the implemented Virtual Instrument.
The differences in the calculation procedures leading to the values shown in Table 2. were due to the improvements made to the implemented Virtual Instrument, which are summarised below:
- In the Virtual Instrument program, the value of is accepted when the relative value of the difference of two consecutive values of is lower than GN/m2 while in the JAVA (2003) program, it is accepted when it is lower than GN/m2.
- The values of f1 and f2 are accepted in Virtual Instrument when the relative value of the difference of two consecutive values of f2 is lower than 5·10−4 Hz while in JAVA (2003), they are accepted when this is lower than 10−3 Hz. For this reason, the values of were accurately estimated.
- The number of points acquired in the search for the initial values of the numerical method is three times greater. This gives place to high accuracy of calculation for all values.
- The frequencies of interest, f1s, f2s, fp, fBmax, and fBmin, are automatically searched for with an adequate resolution. This improved the accuracy of calculation for all values.
- The calculation and results’ presentation time was much shorter when using the version of Virtual Instrument implemented in this work.
Thanks to these differences, the iterative method can be used with all the benefits of the up-to-date programming advantages of the Virtual Instrument and, as data in Table 2 shows, with great accuracy, lower processing time and very good matching with the results of previous software.
4. Conclusions
The proposed Virtual Instrument improved the procedures of previous versions for the automatic calculation of piezoelectric coefficients from admittance measurements at the radial extensional resonant mode of thickness poled discs.
The software architecture used, in addition to the floating-point resolution of real and complex numbers, substantially improved the speed and processing capacity of the designed tool.
The results in Table 2 and the discussion in Section 3 reveal that, together with highly automatized measurements and all the advantages related to the Virtual Instrument, highly accurate results of the calculation that matches the results from previous software were achieved.
The Virtual Instrument has a simple and friendly user interface. The graphs shown allow for visualisation of the admittance in polar form (Y–theta) or in Cartesian form (Y = G + iB), and of the impedance in Cartesian form (Z = R + iX) as a function of the frequency. These graphs are also equipped with advanced visualisation tools (e.g., focus, zoom, cursors, etc.).
The Virtual Instrument, as implemented in this work, records the measured and calculated data in exportable files (ASCII) for use in other applications. In addition, the Virtual Instrument has, as a novelty, the added functionality which allows all the intermediate steps of the calculations performed in the iterative procedure to be recorded.
The Virtual Instrument has the advantage of making use of the extensively tested iterative method of Alemany et al. [32] which allows characterizing even samples with very weak piezoelectric coefficients, as well as samples with strong losses, something that the method proposed in ANSI IEEE 176 does not allow.
The software architecture used in the Virtual Instrument makes it easily readable, expandable, and scalable. A future line to be developed is to extend the Virtual Instrument to include the implementation of the resonance modes shown in the geometries of Figure 2. In this way, a complete characterisation of the elastic-piezo-dielectric matrix of a material in the geometries typically used in piezoceramic devices could be possible.
Author Contributions
Conceptualisation, A.M.G. and L.P.; methodology, A.M.G. and L.P.; software, F.J.J. and B.G.; validation, F.J.J. and M.V.-R.; formal analysis, F.J.J. and A.M.G.; investigation, F.J.J., A.M.G., L.P., M.V.-R., P.O. and B.G.; resources, F.J.J., A.M.G., L.P., M.V.-R., P.O. and B.G.; writing—original draft preparation, F.J.J.; writing—review and editing, F.J.J., A.M.G., L.P., M.V.-R., P.O. and B.G.; visualisation, F.J.J., A.M.G., L.P., M.V.-R., P.O. and B.G. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the R&D project number MAT 2017 86168R.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available on request from the corresponding author. The data are not publicly available due to privacy.
Acknowledgments
The authors thank the Escuela Técnica Superior de Ingeniería y Sistemas de Telecomunicación of the Universidad Politécnica de Madrid, its staff and the students, Arianna Silva and Ignacio Grijota, for the help provided.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Cady, W.G. Piezoelectricity: An Introduction to the Theory and Applications of Electromechanical Phenomena in Crystals; Mc Graw Hill Book Co.: New York, NY, USA, 1946. [Google Scholar]
- IEEE Standard on Piezoelectricity. In ANSI/IEEE Std 176-1987; The Institute of Electrical and Electronics Engineers, Inc.: New York, NY, USA, 1987. [CrossRef]
- Zhao, Q.; Wang, L.; Zhao, K.; Yang, H. Development of a Novel Piezoelectric Sensing System for Pavement Dynamic Load Identification. Sensors 2019, 19, 4668. [Google Scholar] [CrossRef]
- Kim, K.; Choi, H. High-efficiency high-voltage class F amplifier for high-frequency wireless ultrasound systems. PLoS ONE 2021, 16, e0249034. [Google Scholar] [CrossRef]
- Udalov, A.; Alikin, D.; Kholkin, A. Piezoresponse in Ferroelectric Materials under Uniform Electric Field of Electrodes. Sensors 2021, 21, 3707. [Google Scholar] [CrossRef]
- Teplykh, A.; Zaitsev, B.; Semyonov, A.; Borodina, I. The Radial Electric Field Excited Circular Disk Piezoceramic Acoustic Resonator and Its Properties. Sensors 2021, 21, 608. [Google Scholar] [CrossRef]
- Zhang, X.; Shan, X.; Shen, Z.; Xie, T.; Miao, J. A New Self-Powered Sensor Using the Radial Field Piezoelectric Diaphragm in d33 Mode for Detecting Underwater Disturbances. Sensors 2019, 19, 962. [Google Scholar] [CrossRef] [PubMed]
- Wang, W.; Jiang, Y.; Thomas, P.J. Structural Design and Physical Mechanism of Axial and Radial Sandwich Resonators with Piezoelectric Ceramics: A Review. Sensors 2021, 21, 1112. [Google Scholar] [CrossRef]
- Jaffe, B.; Cook, W.R.; Jaffe, H. Piezoelectric Ceramics; Academic Press: New York, NY, USA, 1971. [Google Scholar]
- Pan, C.; Xiao, G.; Feng, Z.; Liao, W. Electromechanical characteristics of discal piezoelectric transducers with spiral interdigitated electrodes. Smart Mater. Struct. 2014, 23, 125029. [Google Scholar] [CrossRef]
- Guo, Z.; Huang, T.; Schröder, K.-U. Development of a Piezoelectric Transducer-Based Integrated Structural Health Monitoring System for Impact Monitoring and Impedance Measurement. Appl. Sci. 2020, 10, 2062. [Google Scholar] [CrossRef]
- Covaci, C.; Gontean, A. Piezoelectric Energy Harvesting Solutions: A Review. Sensors 2020, 20, 3512. [Google Scholar] [CrossRef] [PubMed]
- Vázquez-Rodríguez, M.; Jiménez, F.J.; Pardo, L.; Ochoa, P.; González, A.M.; de Frutos, J. A New Prospect in Road Traffic Energy Harvesting Using Lead-Free Piezoceramics. Materials 2019, 12, 3725. [Google Scholar] [CrossRef] [PubMed]
- Hwang, S.C.; Lynch, C.S.; McMeeking, R.M. Ferroelectric/ferroelastic interactions and a polarization switching model. Acta Metall. Mater. 1995, 43, 2073–2084. [Google Scholar] [CrossRef]
- Ochoa-Perez, P.; Gonzalez-Crespo, A.M.; Garcia-Lucas, A.; Jimenez-Martinez, F.J.; Vazquez-Rodriguez, M.; Pardo, L. FEA study of shear mode decoupling in non-standard thin plates of a lead-free piezoelectric ceramic. IEEE Trans. UFFC 2020. [Google Scholar] [CrossRef]
- Chinchurreta, F.J.; de Espinosa, F.M. Guides to characterize piezoelectric materials from disk shaped samples. Ferroelectrics 1988, 81, 229–232. [Google Scholar] [CrossRef]
- San Emeterio, J.L. Determination of electromechanical coupling factors of low Q piezoelectric resonators operating in stiffened modes. IEEE Trans. Ultrason. Ferroelec. Freq. Control 1997, 44, 108–113. [Google Scholar] [CrossRef]
- Alemany, C.; Gonzalez, A.M.; Pardo, L.; Jimenez, B.; Carmona, F.; Mendiola, J. Automatic determination of complex constants of piezoelectric lossy materials in the radial mode. J. Phys. D Appl. Phys. 1995, 28, 945. [Google Scholar] [CrossRef]
- González, A.M.; De Frutos, J.; Duro, C.; Alemany, C.; Pardo, L. Changes in the piezoelectric parameters of PZT ceramics during the poling process. Ferroelectrics 1998, 208, 449–457. [Google Scholar] [CrossRef]
- Holland, R. Representation of dielectric, elastic, and piezoelectric losses by complex coefficients. IEEE Trans. Sonics Ultrason. 1967, 14, 18–20. [Google Scholar] [CrossRef]
- Martin, G.E. Dielectric, Elastic and Piezoelectric Losses in Piezoelectric Materials. In Proceedings of the 1974 Ultrasonics Symposium, Milwaukee, WI, USA, 11–14 November 1974; pp. 613–617. [Google Scholar]
- Smits, J.G. Iterative Method for Accurate Determination of the Real and Imaginary Parts of the Materials Coefficients of Piezoelectric Ceramics. IEEE Trans. Sonics Ultrason. 1976, 23, 393–401. [Google Scholar] [CrossRef]
- Arlt, G.; Dederichs, H. Complex elastic, dielectric and piezoelectric constants by domain wall damping in ferroelectric ceramics. Ferroelectrics 1980, 29, 47–50. [Google Scholar] [CrossRef]
- Damjanovic, D.; Gururaja, T.R.; Jang, S.J.; Cross, L.E. Temperature behavior of the complex piezoelectric d31, coefficient in modified lead titanate ceramics. Mater. Lett. 1986, 4, 414. [Google Scholar] [CrossRef]
- Uchino, K.; Zhuang, Y.; Ural, S.O. Loss determination methodology for a piezoelectric ceramic: New phenomenological theory and experimental proposals. J. Adv. Dielectr. 2011, 1, 17–31. [Google Scholar] [CrossRef]
- Mezheritsky, A.V. Efficiency of excitation of piezoceramic transducers at antiresonance frequency. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2002, 49, 484–494. [Google Scholar] [CrossRef] [PubMed]
- Hagiwara, M.; Hoshina, T.; Takeda, H.; Tsurumi, T. Identicalness between Piezoelectric Loss and Dielectric Loss in Converse Effect of Piezoelectric Ceramic Resonators. Jpn. J. Appl. Phys. 2012, 51, 09LD10. [Google Scholar] [CrossRef]
- Cain, M.G.; Stewart, M. Losses in Piezoelectric via Complex Resonance Analysis. In Characterization of Ferroelectric Bulk Materials and Thin Films; Cain, M.G., Ed.; Springer Series in Measurement Science and Technology: New York, NY, USA, 2014; Volume 2. [Google Scholar]
- Liu, G.; Zhang, S.; Jiang, W.; Cao, W. Losses in ferroelectric materials. Mater. Sci. Eng. R. Rep. 2015, 89, 1–48. [Google Scholar] [CrossRef]
- González, A.; García, Á.; Benavente-Peces, C.; Pardo, L. Revisiting the Characterization of the Losses in Piezoelectric Materials from Impedance Spectroscopy at Resonance. Materials 2016, 9, 72. [Google Scholar] [CrossRef]
- Pérez, N.; Buiochi, F.; Brizzotti Andrade, M.; Adamowski, J. Numerical Characterization of Piezoceramics Using Resonance Curves. Materials 2016, 9, 71. [Google Scholar] [CrossRef]
- Alemany, C.; Pardo, L.; Jimenez, B.; Carmona, F.; Mendiola, J.; González, A.M. Automatic iterative evaluation of complex material constants in piezoelectric ceramics. J. Phys. D Appl. Phys. 1994, 27, 148. [Google Scholar] [CrossRef]
- Algueró, M.; Alemany, C.; Pardo, L.; González, A.M. Method for Obtaining the Full Set of Linear Electric, Mechanical, and Electromechanical Coefficients and All Related Losses of a Piezoelectric Ceramic. J. Am. Ceram. Soc. 2004, 87, 209–215. [Google Scholar] [CrossRef]
- Pardo, L.; Reyes-Montero, A.; García, Á.; Jacas-Rodríguez, A.; Ochoa, P.; González, A.M.; Jiménez, F.J.; Vázquez-Rodríguez, M.; Villafuerte-Castrejón, M.E. A Modified Iterative Automatic Method for Characterization at Shear Resonance: Case Study of Ba0.85Ca0.15Ti0.90Zr0.10O3 Eco-Piezoceramics. Materials 2020, 13, 1666. [Google Scholar] [CrossRef] [PubMed]
- Available online: https://www.ni.com/es-es/innovations/white-papers/06/virtual-instrumentation.html (accessed on 30 May 2021).
- Show Daily NIWeek 2003–The Worldwide Conference on Virtual Instrumentation. Available online: http://www.ni.com/pdf/niweek/us/081403_show_daily.pdf (accessed on 31 May 2021).
- Travis, J.; Kring, J. Chapter 1: What in the World Is LabVIEW? In LabVIEW for Everyone: Graphical Programming Made Easy and Fun, 3rd ed.; National Instruments Virtual Instrumentation Series; Prentice Hall: Hoboken, NJ, USA, 2006; pp. 27–33. ISBN 10 0131856723. [Google Scholar]
- Available online: http://www.ni.com/white-paper/3024/en/ (accessed on 31 May 2021).
- Available online: https://www.meggittferroperm.com/material/traditional-soft-pzt-for-sensor-applications/ (accessed on 31 May 2021).
- Available online: http://www.testequipmenthq.com/datasheets/Keysight-4194A-Datasheet.pdf (accessed on 31 May 2021).
- Available online: https://zone.ni.com/reference/en-XX/help/371361R-01/lvconcepts/using_profile_window/ (accessed on 30 May 2021).
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).