Abstract
Common seasonal variations in Global Positioning System (GPS) coordinate time series always exist, and the modeling and correction of the seasonal signals are helpful for many geodetic studies using GPS observations. A spatiotemporal model was proposed to model the common seasonal variations in vertical GPS coordinate time series, based on independent component analysis and varying coefficient regression method. In the model, independent component analysis (ICA) is used to separate the common seasonal signals in the vertical GPS coordinate time series. Considering that the periodic signals in GPS coordinate time series change with time, a varying coefficient regression method is used to fit the separated independent components. The spatiotemporal model was then used to fit the vertical GPS coordinate time series of 262 global International GPS Service for Geodynamics (IGS) GPS sites. The results show that compared with least squares regression, the varying coefficient method can achieve a more reliable fitting result for the seasonal variation of the separated independent components. The proposed method can accurately model the common seasonal variations in the vertical GPS coordinate time series, with an average root mean square (RMS) reduction of 41.6% after the model correction.
1. Introduction
Seasonal signals are always observed in Global Positioning System (GPS) coordinate time series [1], which are thought to be a combination of different factors. The main causes of the seasonal signals in vertical GPS coordinate time series are thought to be the uncorrected mass loading deformations, usually including atmospheric loading [2,3], hydrological loading [4,5,6] and non-tidal loading [7,8]. The effects of different mass loadings vary in different regions due to differences in environmental change. Another factor that causes the seasonal variations in GPS time series is the false periodic signals generated in GPS processing, e.g., the errors in satellite orbit, tropospheric delay, antenna phase center correction models and multipath effects [1,9,10,11]. In addition, the thermal expansion effect of the bedrock is also thought to be one of the reasons for the periodic changes of the vertical GPS coordinates time series [12].
The existence of the seasonal variations in GPS time series will affect the estimation of motion velocities and their uncertainties on sites [13,14], which is not conducive to the study of geophysical applications using GPS, e.g., assessment of glacial isostatic adjustment (GIA) models using vertical GPS observations [15]. Thus, it is very necessary to model or separate the seasonal signals in GPS coordinate time series for many geodetic studies, especially in the vertical direction [1,9,10,16].
An optional measure to estimate the seasonal variations is to quantify the potential periodic signals based on their physical sources. For example, the mass loading displacements can be calculated by convolving the grid surface mass data with Green’s functions [17], and currently, various environmental loading products are available for estimating the mass loading effects [9,11,18,19]. The estimation results would be different due to differences in the Green’s functions, the references frame of the Green’ functions, the reference mass model, and the land–ocean mask [9]; in many studies, the effect of correcting the seasonal variations in GPS observations using mass loading models is limited, due to the complexity of the Earth’s structure and the spatial resolution of grid mass data.
The other idea to estimate the seasonal signals in GPS coordinate time series, is modeling the potential period changes using mathematical fitting methods. The most classic approach is using Least-squares with sine and cosine functions for a specific period [20], prior to—or simultaneous with—some noise assumption [21,22,23]. However, only constant amplitudes and phases can be estimated using this fitting method, which cannot fully describe the actual periodic changes in many cases. True seasonal variations in GPS coordinate time series are not constant from year to year [24], and several approaches have been proposed to model the time-varying seasonal signals, such as non-parametric annual signal [25], Kalman filter techniques [26], piecewise continuous linear polynomials [27], singular spectrum analysis (SSA) [24], ensemble empirical mode decomposition (EEMD) [28], and so on. All the methods above are aimed at the GPS time series at a single GPS site, and are not conducive to the overall analysis of regional GPS observations. Actually, the seasonal signals at regional GPS sites have similar features [29,30]. Gruszczynska et al. [30] used multichannel singular spectrum analysis (MSSA) to model the common seasonal signals in GPS observations in different regions around the world and without influencing the high frequency part of the spectra. Some other data-driven mathematical methods have been proposed to be used in modeling the geophysical signals from regional geodetic time series, e.g., principle component analysis (PCA) and independent component analysis (ICA), which have been widely used in smoothing and modeling GPS time series [15,23,31,32,33,34,35,36,37]. ICA has especially been widely used in the separation of potential sources of seasonal signals in vertical GPS coordinate time series, and the main independent components (ICs) were thought to be consistent with some of the geophysical signals [32,33,34].
In this paper, we conducted a spatiotemporal analysis of vertical GPS coordinates on a global scale with ICA, separating the common seasonal components of all the sites. Further, a varying coefficient (VC) regression method was used to model the separated common seasonal signals. Combining the spatial responses (SRs) achieved in ICA processing, we built a spatiotemporal model to analyze the seasonal signals in all the GPS sites in the case study.
2. Methods
2.1. Spatiotemporal Model Using ICA and VC Regression
ICA is a blind source separation method that can separate statistically independent signals from mixed signals using the higher order statistical characteristics of the source signals [38]. The process of ICA is illustrated in Figure 1.
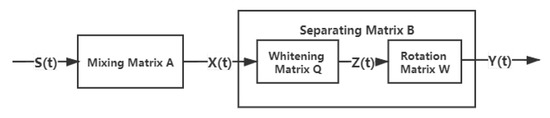
Figure 1.
Process of independent component analysis.
Each observation can be viewed as the mixture of the source signals
with different weights. The purpose of ICA is to obtain a separating matrix , then the signals , the best estimates of . Generally, the process of ICA can be divided into two steps. The first is to whiten the observed variables by and , where is called the whitening matrix. The second step is to obtain a rotation matrix by following the ICA algorithm, then we obtain the . The row vectors in are ICs to be estimated and the column vectors in the inverse matrix of are the spatial resonses of ICs. To obtain each weight vector in the rotation matrix , FastICA algorithm based on negentropy [39,40] was used in ICA analysis. The estimation process of is as follows:
- (1)
- Centralize and whiten the observed data, obtain the whitened data ;
- (2)
- Choose an initial weight vector of unit norm (random) ;
- (3)
- Update by , where is a nonlinear function, such as , and ;
- (4)
- Normalize by ;
- (5)
- Go back to step “3” if not converged.
The vertical GPS coordinate time series are seen as the inputs of ICA and a set of ICs and the SRs can be obtained after ICA processing. Then we can obtain the model of common seasonal variations for the GPS time series by
where are the common independent components extracted from the GPS time series using ICA, and they are thought to represent the common seasonal sources after identification. is the spatial response values in ICA separation. are the modeled result of ICs and they are estimated using the VC regression method by the following equations:
2.2. Varying Coefficient Regression Method
The expression of varying coefficient regression model is as follows [41]:
where is the variable to be fitted, is the regression variables, is the coefficient which is a function of another variable , and is the fitting error. When is defined as a time variable, the Equation (1) would be an expression of temporal varying coefficient regression used in modeling the ICs in Equation (2). Here, we estimated the varying coefficients using local linear fitting [42]. For groups of independent observed data, the sample form of the VC regression model is as follows:
Assume have continuous derivatives with respect to , and the range of is . According to Taylor’s formula, in the range of , for any given , there exists:
Define a kernel function as , and . A Gauss kernel function was used in our following case study. The is the window width parameter, and the determination of will be introduced below. The local linear fitting of the coefficient in VC regression chooses and to satisfy the following condition:
Assuming:
and the solution of the above weighted least squares situation can be expressed as:
Thus, the local linear estimations of the coefficients at can be expressed as:
where and are the unit matrix and zero matrix with order . We define as a 2-dimensional column vector with th element being 1, and the remaining elements being 0, then we have:
The coefficient can be estimated as according to Equation (9), then we can calculate at each design point according to Equation (8):
where is the th variables of . The final result of Equation (10) can be expressed in the style of , where is called the pseudo-hat matrix.
We used the cross-confirmation (CV) method to select the best window width parameter. Taking the range of the window width to be selected for a given step length, with every within the range, we can obtain the fitting results using a local linear fitting method, where represents the pseudo-hat matrix with series selected . The process of cross-validation is as follows: for a given window width parameter , except for the th variable , we can calculate the fitting value of the regression function at for the other data using the local linear fitting method under the given , defined as:
The values of each were calculated and corresponds to the minimum value of which is the optimal window width parameter.
3. Case Study
3.1. GPS Data
The International GPS Service for Geodynamics (IGS) GPS time series processed by the Scripps Orbit and Permanent Array Center (SOPAC) and California Spatial Reference Center (CSRC) were used in our case study (available at http://garner.ucsd.edu/). The outliers and trend item have been removed in the time series products. To perform the ICA analysis, we completed further processing on the vertical GPS time series. We chose GPS time series data which span the eight years from the beginning of 2010 to the end of 2017. Spatiotemporal analysis with ICA works most effectively with data that have few gaps. As such, we only used sites with more than 70% data. Additionally, we removed the sites with obvious offset in the time series using manual methods [43] and the obvious abnormal sites, which would affect the separation of common seasonal ICs. To identify the “abnormal” sites, we computed the correlation coefficients between the series at each site and the series at the four nearest sites. If the correlation coefficients were all less than 0.4, we considered the time series at this site as being affected by local geophysical deformation or equipment changes, and it would be defined as an abnormal site and removed. Finally, a total of 262 GPS sites around the world were chosen in the case study, and the distribution of the sites are shown in Figure 2. After this, a kriged kalman filter technique was used to interpolate the missing data of the 262 vertical GPS time series [44]. We did not complete additional processing in the correction of other potential seasonal signals, including the draconic year effect and bedrock thermal expansion, although we think the mass loadings are the main contribution to the seasonal variation in vertical GPS coordinate time series. Because in the separation of ICA, as long as the existing source signals are statistically independent, the separation of independent components will not be obviously affected by the existence of errors.
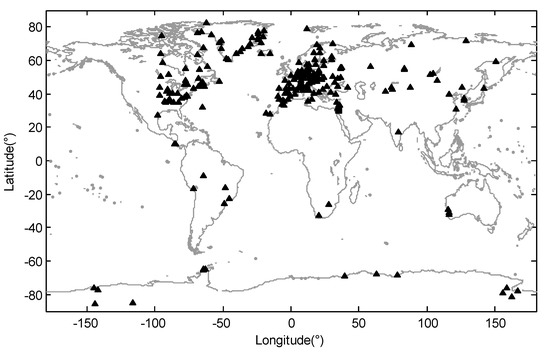
Figure 2.
Distribution of Global Positioning System (GPS) sites used in the case study.
3.2. Spatiotemporal Analysis Using ICA
We acquired 262 sets of complete vertical GPS time series after the selection and processing steps. PCA was used to preprocess the GPS time series before we performed ICA. An appropriate number of PCs need to remain for the following ICA processing. We completed several tests and found that in most cases the choice of the number of remaining PCs had little effect on the separation of the top four ICs. In our study, the top six principle components with more than 80% contribution of variance were retained and used in the following analysis. Then, FastICA was used to separate the ICs from the mixtures, and we received a series of temporal components and their corresponding spatial patterns. Unlike PCA, the order of ICs is random in ICA and we rearranged the ICs according to their contributions based on their ratio values, defined by Liu et al. [33]. To enable comparisons, we divided each spatial response of the independent component by the maximum of its absolute value and the corresponding ICs are multiplied by the scale. As a result, all the spatial patterns are in the range of -100% to 100%. The top four scaled ICs and their spatial responses are shown in Figure 3.
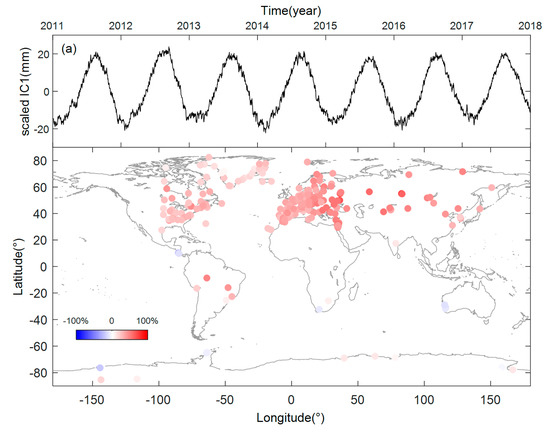
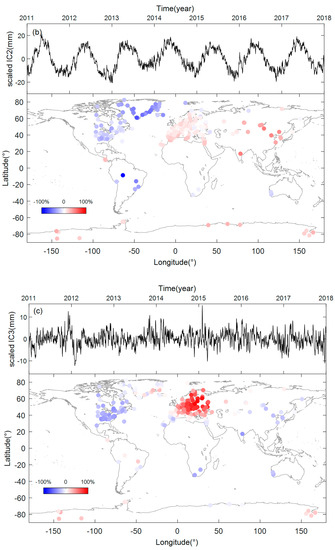
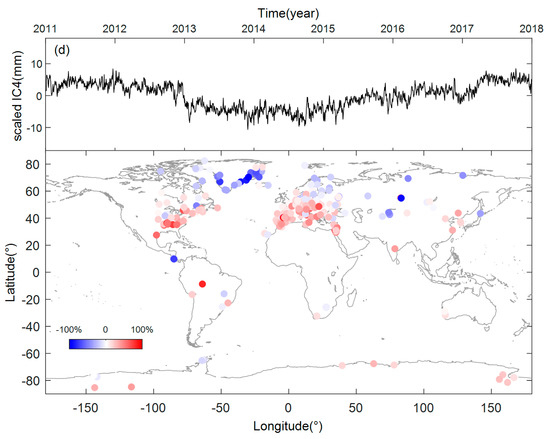
Figure 3.
Top 4 Scaled independent components (ICs) and the spatial responses (SRs). (a) scaled IC1 and SR1. (b) scaled IC2 and SR2. (c) scaled IC3 and SR3. (d) scaled IC4 and SR4.
Note the temporal components in Figure 3a,b, the top two ICs have obvious seasonal signals. Especially for the first independent component, we can see a significant annual period signal and this shows consistent positive spatial responses to almost all of the global GPS sites. We noticed that the SRs of IC1 are most obvious for the sites in northern Asia, northeastern Mediterranean and the area near the Black Sea, but relatively small for the sites in midwestern Europe and North America. The SRs of IC1 are the least obvious for most of the sites in Greenland, Antarctica and the two sites on the west coast of Australia, while the two sites near the Amazon basin in South America have more obvious spatial responses of IC1. IC1 may be a response of common hydrological mass variation.
IC2 and its spatial responses are shown in Figure 3b. It shows seasonal variations, and obvious differences exist in the annual amplitudes, which cannot be described using constant sine and cosine functions. The SRs of IC2 are most obvious for the sites in Greenland, followed by the sites in the Americas, and are least obvious for the sites in west Asia and Europe. The spatial responses of IC2 show special distribution, that is, apart from the sites on the Antarctic Peninsula, IC2 shows obvious opposite responses to the sites in the eastern and western hemispheres. IC2 may be driven by climate or some other environmental factors.
The spatial and temporal patterns of IC3 and IC4 are shown in Figure 3c,d. IC3 looks like a random error series and has opposite responses to the sites in Europe and other regions, especially for the sites in eastern Europe and North America, where this contrast is most obvious. The source of IC3 needs to be further explored. IC4 shows long-term trend changes, which describe the nonlinear long-tern trend change in the vertical GPS time series. We notice that this trend is most obvious in the Greenland site, and it may be related to the short-term ice mass change in Greenland during the period. Considering the negative spatial responses, most GPS sites in Greenland show uplift from early 2011 to 2013 and this is followed by a subsidence from 2014 to 2017, which is consistent with the transient ice mass changes during the period [45,46].
3.3. Modeling Common Seasonal Signals
After the spatiotemporal filtering of vertical GPS time series, the top two ICs are thought to represent the common seasonal signals for all the sites. Thus, the next step is modeling the IC1 and IC2 using a varying coefficient regression method based on Equation (2). As comparisons, the least square regression method (LS) is also used to fit IC1 and IC2. The fitting results for ICs are shown in Figure 4.
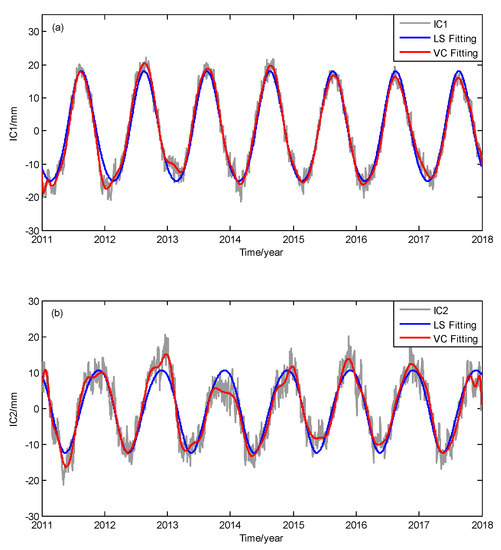
Figure 4.
Fitting results of (a) IC1 and (b) IC2 using least squares (LS) regression and varying coefficient (VC) regression.
As shown in Figure 4, both LS and VC regression models fit the periodic variations of IC1 and IC2. However, the annual amplitudes are time varying for the ICs, especially for IC2 in Figure 4b. We notice that the LS regression can only achieve constant periodic fitting results, both in Figure 4a,b, while the VC regression method can closely fit the seasonal changes in each year, with better flexibility and adaptability. The histogram of residuals of different methods are shown in Figure 5. All the residuals present normal distributions and note that the residuals of VC regression for IC1 and IC2 are more concentrated. The standard deviation (std) values of IC1 fitting residuals using the LS and VC regression models are 2.5 mm and 1.6 mm, respectively, and the std values of IC2 fitting residuals using the LS and VC regression models are 3.4 mm and 2.5 mm, respectively.
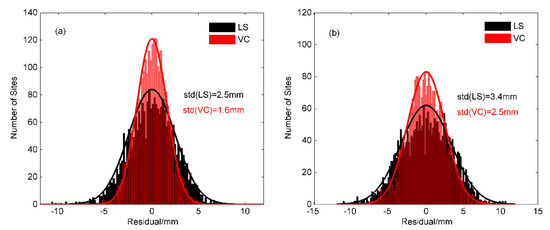
Figure 5.
Histogram of Residual in the fitting model of least squares regression (LS) and varying coefficient regression (VC) for (a) IC1 and (b) IC2, the std of residual are marked.
3.4. Spatiotemporal Modeling and Discussion
We obtained the model of IC1 and IC2 using the varying coefficient regression, which is thought to represent the main common seasonal changes in the vertical GPS time series in our case study. According to Equation (1), by multiplying by the spatial responses we obtained the spatiotemporal model of the main common seasonal signals :
where and are the modeling results of IC1 and IC2 using VC regression. The window width parameter in the VC regression is selected as 39.4 through a cross-confirmation method. We then removed the seasonal model from al the vertical GPS time series and obtained the seasonal corrected series. The correction effects were evaluated using Equation (13). The values for all the sites are shown in Figure 6.
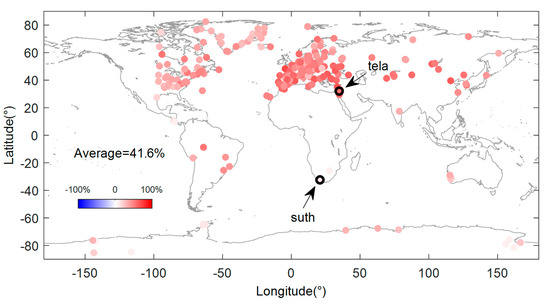
Figure 6.
The root mean square (RMS) reduction in coordinate time series after the model correction for each site, the sites “tela” and “suth” are marked.
It can be seen that the values of all the GPS time series have been reduced by varying degrees after the model correction, with an average correction effect of 41.6%, and the average correction effect decreases to 41.2% when using LS regression to model the ICs. Among them, the most obvious seasonal corrections occurred at the sites in the Eurasian region, followed by the sites in the Americas and Greenland. The corrections effects of several sites in Africa, Australia and Antarctica were the worst. This is related to the insignificant seasonality of these sites. The site with the best correction effect is "tela”, with an improvement of 71.8%, and the lowest improvement rate is only 0.7% at the site ”suth”. The two sites were marked in Figure 6. The fitting effect of the GPS time series of sites “tela” and “suth” are shown in Figure 7. Note that the site “suth” is located in southern Africa, and seasonal variation in its time series is insignificant (Figure 7). The top two ICs did not separate the non-obvious nonlinear changes. Therefore, the fitting effect of the spatiotemporal model is limited for this site.
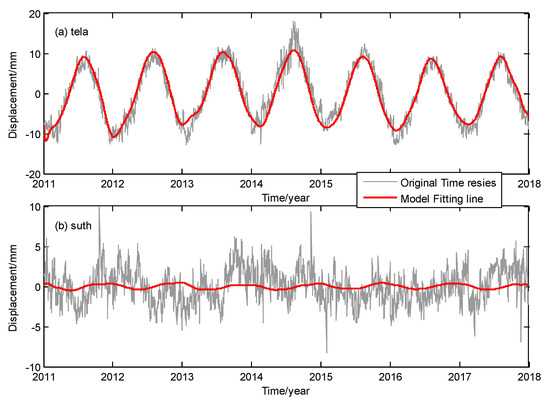
Figure 7.
Vertical coordinate time series and the fitting lines of spatiotemporal model for sites (a) “tela” and (b) “suth”.
To explore the geophysical sources of the IC1 and IC2, we took the site “tela” as an example. We computed mass loading displacements at this site via the International Mass Loading Service [18], including the atmospheric loading (ATML), land water storage mass loading (LWS) and non-tidal loading (NTOL). For ATML and LWS, we use the model of Modern Era Retrospective-analysis for Research and Applications (MERRA2), and for NOTL we use the model of the Ocean Model for Circulation and Tides (OMCT). We averaged the loading series into daily results to make comparisons with the ICs derived displacements (GPS(ICs)). We found the mass loadings are not consistent with the individual ICs, but the sum of mass loadings is highly correlated with the sum of GPS(IC1) and GPS(IC2), with a correlation coefficient of 0.87. The comparison between their displacements is shown in Figure 8. We find that the amplitude of the mass loadings is less than that of GPS(ICs), which indicates the mass loading may be underestimated at the site ”tela”. We further corrected the mass loading effects from the GPS time series at the site “tela” and the is 40.4%, while for the conditions of VC and LS regression fitting for ICs, the correction effect is 71.8% and 68.4%, respectively.
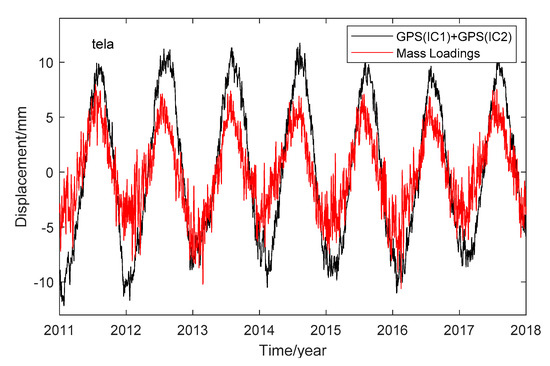
Figure 8.
Comparison between ICs derived displacements (GPS(ICs)) and mass loading displacements at site “tela”.
4. Conclusions
We propose a spatiotemporal model based on ICA and VC regression methods to fit the common seasonal signals in vertical GPS coordinate time series. On the basis of ICA spatiotemporal analysis, a varying coefficient regression method was used to model the common independent seasonal signals, then, combined with the spatial responses of ICs, the fitting model of the seasonal variations for all the vertical time series can be achieved. The use of ICA makes it possible that by modeling a few temporal components, we can achieve the fitting of the seasonal changes in the time series of all GPS sites. The use of VC regression solves the problem that the least squares regression cannot accurately fit the time varying period signals.
The spatiotemporal modeling method was then used in the fitting of seasonal signals in the vertical time series of 262 GPS sites worldwide. We separated several independent components from the GPS time series and analyzed the possible geophysical origin based on their temporal and spatial characteristics. We used VC regression to fit the top two ICs and the results show that VC regression performs a better fitting to the LS regression. We obtained the spatiotemporal model of the common seasonal signals in all the 262 GPS sites and corrected the modeling results from original GPS time series. The RMS values for all the GPS time series have been reduced after seasonal signals correction, with an average reduction of 41.6%. It is also noticed that our proposed spatiotemporal model mainly accounts for the common seasonal variations at the sites, and the local seasonal signals that exist in individual sites are not reflected in the common mode ICs. For the GPS time series contained with local seasonal responses, a better choice would be to model the coordinate time series separately using the varying coefficient regression method.
Author Contributions
Conceptualization, B.L. and X.X.; methodology, B.L.; investigation, B.L.; writing—original draft preparation, B.L.; writing—review and editing, J.T. and Q.X.; funding acquisition, B.L. All authors have read and agreed to the published version of the manuscript.
Funding
This work is funded by the National Natural Science Foundation of China (Grant No. 41904003 and 42074033), the Project supported by the Natural Science Foundation of Hunan Province, China (Grant No. 2020JJ5571) and Open Fund of Engineering Laboratory of Spatial Information Technology of Highway Geological Disaster Early Warning in Hunan Province (Changsha University of Science and Technology) (Grant No. KFJ190602).
Acknowledgments
We thank the Scripps Orbit and Permanent Array Center (SOPAC) and California Spatial Reference Center (CSRC) for providing GPS coordinate time series data.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Dong, D.; Fang, P.; Bock, Y.; Cheng, M.K.; Miyazaki, S.I. Anatomy of apparent seasonal variations from GPS-derived site position time series. J. Geophys. Res. 2002, 107, 2075. [Google Scholar] [CrossRef]
- Vandam, T.M.; Blewitt, G.; Heflin, M.B. Atmospheric pressure loading effects on Global Positioning System coordinate determinations. J. Geophys. Res. Solid Earth 1994, 99, 23939–23950. [Google Scholar] [CrossRef]
- van Dam, T.; Altamimi, Z.; Collilieux, X.; Ray, J. Topographically induced height errors in predicted atmospheric loading effects. J. Geophys. Res. Solid Earth 2010, 115, B07415. [Google Scholar] [CrossRef]
- Fu, Y.; Argus, D.F.; Freymueller, J.T.; Heflin, M.B. Horizontal motion in elastic response to seasonal loading of rain water in the Amazon Basin and monsoon water in Southeast Asia observed by GPS and inferred from GRACE. Geophys. Res. Lett. 2013, 40, 6048–6053. [Google Scholar] [CrossRef]
- Chanard, K.; Avouac, J.P.; Ramillien, G.; Genrich, J. Modeling deformation induced by seasonal variations of continental water in the Himalaya region: Sensitivity to Earth elastic structure. J. Geophys. Res. Solid Earth 2014, 119, 5097–5113. [Google Scholar] [CrossRef]
- Rateb, A.; Hermas, E. The 2018 Long Rainy Season in Kenya: Hydrological Changes and Correlated Land Subsidence. Remote Sens. 2020, 12, 1930. [Google Scholar] [CrossRef]
- van Dam, T.; Collilieux, X.; Wuite, J.; Altamimi, Z.; Ray, J. Nontidal ocean loading: Amplitudes and potential effects in GPS height time series. J. Geod. 2012, 86, 1043–1057. [Google Scholar] [CrossRef]
- Memin, A.; Boy, J.P.; Santamaria-Gomez, A. Correcting GPS measurements for non-tidal loading. GPS Solutions 2020, 24, 45. [Google Scholar] [CrossRef]
- Jiang, W.; Li, Z.; van Dam, T.; Ding, W. Comparative analysis of different environmental loading methods and their impacts on the GPS height time series. J. Geod. 2013, 87, 687–703. [Google Scholar] [CrossRef]
- Jiang, W.; Deng, L.; Li, Z.; Zhou, X.; Liu, H. Effects on noise properties of GPS time series caused by higher-order ionospheric corrections. Adv. Space Res. 2014, 53, 1035–1046. [Google Scholar] [CrossRef]
- He, X.; Montillet, J.P.; Fernandes, R.; Bos, M.; Yu, K.; Hua, X.; Jiang, W. Review of current GPS methodologies for producing accurate time series and their error sources. J. Geodyn. 2017, 106, 12–29. [Google Scholar] [CrossRef]
- Yan, H.; Chen, W.; Zhu, Y.; Zhang, W.; Zhong, M. Contributions of thermal expansion of monuments and nearby bedrock to observed GPS height changes. Geophys. Res. Lett. 2009, 36, L13301. [Google Scholar] [CrossRef]
- Santamaría-Gómez, A.; Memin, A. Geodetic secular velocity errors due to interannual surface loading deformation. Geophys. J. Int. 2015, 202, 763–767. [Google Scholar] [CrossRef]
- Bogusz, J.; Klos, A. On the significance of periodic signals in noise analysis of GPS station coordinates time series. GPS Solutions 2016, 20, 655–664. [Google Scholar] [CrossRef]
- Liu, B.; King, M.; Dai, W. Common mode error in Antarctic GPS coordinate time-series on its effect on bedrock-uplift estimates. Geophys. J. Int. 2018, 214, 1652–1664. [Google Scholar] [CrossRef]
- Ray, J.; Altamimi, Z.; Collilieux, X.; van Dam, T. Anomalous harmonics in the spectra of GPS position estimates. GPS Solutions 2008, 12, 55–64. [Google Scholar] [CrossRef]
- Farrell, W.E. Deformation of the Earth by surface loads. Rev. Geophys. 1972, 10, 761–797. [Google Scholar] [CrossRef]
- Petrov, L. REFAG 2014; Springer International Publishing: Cham, Switzerland, 2014; pp. 79–83. [Google Scholar]
- Li, C.; Huang, S.; Chen, Q.; Dam, T.V.; Fok, H.S.; Zhao, Q.; Wu, W.; Wang, X. Quantitative Evaluation of Environmental Loading Induced Displacement Products for Correcting GNSS Time Series in CMONOC. Remote Sens. 2020, 12, 594. [Google Scholar] [CrossRef]
- Nikolaidis, R. Observation of Geodetic and Seismic Deformation with the Global Positioning System. Ph.D. Thesis, University of California, San Diego, CA, USA, 2002. [Google Scholar]
- Mao, A.; Harrison, C.G.; Dixon, T.H. Noise in GPS coordinate time series. J. Geophys. Res. Solid Earth 1999, 104, 2797–2816. [Google Scholar] [CrossRef]
- Williams, S.D.; Bock, Y.; Fang, P.; Jamason, P.; Nikolaidis, R.M.; Prawirodirdjo, L.; Miller, M.; Johnson, D.J. Error analysis of continuous GPS position time series. J. Geophys. Res. Solid Earth 2004, 109, B03412. [Google Scholar] [CrossRef]
- Serpelloni, E.; Faccenna, C.; Spada, G.; Dong, D.; Williams, S.D. Vertical GPS ground motion rates in the Euro-Mediterranean region: New evidence of velocity gradients at different spatial scales along the Nubia-Eurasia plate boundary. J. Geophys. Res. Solid Earth 2013, 118, 6003–6024. [Google Scholar] [CrossRef]
- Chen, Q.; van Dam, T.; Sneeuw, N.; Collilieux, X.; Weigelt, M.; Rebischung, P. Singular spectrum analysis for modeling seasonal signals from GPS time series. J. Geodyn. 2013, 72, 25–35. [Google Scholar] [CrossRef]
- Freymueller, J.T. Seasonal Position Variations and Regional Reference Frame Realization. In Proceedings of the Geodetic Reference Frames: IAG Symposium, Munich, Germany, 9–14 October 2006; pp. 191–196. [Google Scholar]
- Davis, J.L.; Wernicke, B.P.; Tamisiea, M.E. On seasonal signals in geodetic time series. J. Geophys. Res. Solid Earth 2012, 117, B01403. [Google Scholar] [CrossRef]
- Davis, J.L.; Wernicke, B.P.; Bisnath, S.; Niemi, N.A.; Elosegui, P. Subcontinental-scale crustal velocity changes along the Pacific-North America plate boundary. Nature 2006, 441, 1131–1134. [Google Scholar] [CrossRef] [PubMed]
- Pan, Y.; Shen, W.B.; Ding, H.; Hwang, C.; Li, J.; Zhang, T. The Quasi-Biennial Vertical Oscillations at Global GPS Stations: Identification by Ensemble Empirical Mode Decomposition. Sensors 2015, 15, 26096–26114. [Google Scholar] [CrossRef]
- Tesmer, V.; Steigenberger, P.; van Dam, T.; Mayer-Gürr, T. Vertical deformations from homogeneously processed GRACE and global GPS long-term series. J. Geod. 2011, 85, 291–310. [Google Scholar] [CrossRef]
- Gruszczynska, M.; Rosat, S.; Klos, A.; Gruszczynski, M.; Bogusz, J. Multichannel Singular Spectrum Analysis in the Estimates of Common Environmental Effects Affecting GPS Observations. Pure Appl. Geophys. 2018, 175, 1805–1822. [Google Scholar] [CrossRef]
- Ming, F.; Yang, Y.; Zeng, A.; Zhao, B. Spatiotemporal filtering for regional GPS network in China using independent component analysis. J. Geod. 2017, 91, 419–440. [Google Scholar] [CrossRef]
- Liu, B.; Dai, W.; Peng, W.; Meng, X. Spatiotemporal analysis of GPS time series in vertical direction using independent component analysis. Earth Planets Space 2015, 67, 189. [Google Scholar] [CrossRef]
- Liu, B.; Dai, W.; Liu, N. Extracting seasonal deformations of the Nepal Himalaya region from vertical GPS position time series using Independent Component Analysis. Adv. Space Res. 2017, 60, 2910–2917. [Google Scholar] [CrossRef]
- Yan, J.; Dong, D.; Bürgmann, R.; Materna, K.; Tan, W.; Peng, Y.; Chen, J. Separation of Sources of Seasonal Uplift in China Using Independent Component Analysis of GNSS Time Series. J. Geophys. Res. Solid Earth 2019, 124, 11951–11971. [Google Scholar] [CrossRef]
- Gualandi, A.; Avouac, J.P.; Galetzka, J.; Genrich, J.F.; Blewitt, G.; Adhikari, L.B.; Koirala, B.P.; Gupta, R.; Upreti, B.N.; Pratt-Sitaula, B.; et al. Pre- and post-seismic deformation related to the 2015, Mw7.8 Gorkha earthquake, Nepal. Tectonophysics 2017, 714, 90–106. [Google Scholar] [CrossRef]
- Riddell, A.R.; King, M.A.; Watson, C.S. Present-Day Vertical Land Motion of Australia From GPS Observations and Geophysical Models. J. Geophys. Res. Solid Earth 2020, 125, e2019JB018034. [Google Scholar] [CrossRef]
- Li, W.; Jiang, W.; Li, Z.; Chen, H.; Chen, Q.; Wang, J.; Zhu, G. Extracting Common Mode Errors of Regional GNSS Position Time Series in the Presence of Missing Data by Variational Bayesian Principal Component Analysis. Sensors 2020, 20, 2298. [Google Scholar] [CrossRef]
- Comon, P. Independent component analysis, A new concept? Signal Process. 1994, 36, 287–314. [Google Scholar] [CrossRef]
- Hyvarinen, A. Fast and robust fixed-point algorithms for independent component analysis. IEEE Trans. Neural Networks 1999, 10, 626–634. [Google Scholar] [CrossRef]
- Hyvärinen, A.; Oja, E. Independent component analysis: Algorithms and applications. Neural Networks 2000, 13, 411–430. [Google Scholar] [CrossRef]
- Fan, J.; Zhang, W. Statistical Estimation in Varying Coeficient Models. Ann. Stat. 1999, 27, 1491–1518. [Google Scholar]
- Fan, J.; Zhang, W. Simultaneous Confidence Bands and Hypothesis Testing in Varying-coefficient Models. Scand. J. Stat. 2000, 27, 715–731. [Google Scholar] [CrossRef]
- Gazeaux, J.; Williams, S.; King, M.; Bos, M.; Dach, R.; Deo, M.; Moore, A.W.; Ostini, L.; Petrie, E.; Roggero, M.; et al. Detecting offsets in GPS time series: First results from the detection of offsets in GPS experiment. J. Geophys. Res. Solid Earth 2013, 118, 2397–2407. [Google Scholar] [CrossRef]
- Liu, N.; Dai, W.; Santerre, R.; Kuang, C. A MATLAB-based Kriged Kalman Filter software for interpolating missing data in GNSS coordinate time series. GPS Solutions 2018, 22, 25. [Google Scholar] [CrossRef]
- Bevis, M.; Harig, C.; Khan, S.A.; Brown, A.; Simons, F.J.; Willis, M.; Fettweis, X.; van den Broeke, M.R.; Madsen, F.B.; Kendrick, E.; et al. Accelerating changes in ice mass within Greenland, and the ice sheet’s sensitivity to atmospheric forcing. Proc. Natl. Acad. Sci. USA 2019, 116, 1934–1939. [Google Scholar] [CrossRef] [PubMed]
- Zhang, B.; Liu, L.; Khan, S.A.; van Dam, T.; Bjørk, A.A.; Peings, Y.; Zhang, E.; Bevis, M.; Yao, Y.; Noël, B. Geodetic and model data reveal different spatio-temporal patterns of transient mass changes over Greenland from 2007 to 2017. Earth Planet. Sci. Lett. 2019, 515, 154–163. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).