Abstract
Aiming at the two-dimensional (2D) incoherently distributed (ID) sources, we explore a direction-of-arrival (DOA) estimation algorithm based on uniform rectangular arrays (URA). By means of Taylor series expansion of steering vector, rotational invariance relations with regard to nominal azimuth and nominal elevation between subarrays are deduced under the assumption of small angular spreads and small sensors distance firstly; then received signal vectors can be described by generalized steering matrices and generalized signal vectors; thus, an estimation of signal parameters via rotational invariance techniques (ESPRIT) like algorithm is proposed to estimate nominal elevation and nominal azimuth respectively using covariance matrices of constructed subarrays. Angle matching method is proposed by virtue of Capon principle lastly. The proposed method can estimate multiple 2D ID sources without spectral searching and without information of angular power distribution function of sources. Investigating different SNR, sources with different angular power density functions, sources in boundary region, distance between sensors and number of sources, simulations are conducted to investigate the effectiveness of the proposed method.
1. Introduction
In most applications of array signal processing, traditional DOA estimation is based on point source models which can simplify calculations. Point source models assume that propagations between sources and receive arrays are straight paths and the spatial characteristics of sources can be ignored. In the field of wireless communication, there are obstacles around sources; the propagations from sources to receive arrays are multipath. In the real surrounding of underwater, on the one hand, there exist paths from seabed and sea surface of backscatters; on the other hand, spatial scatterers of targets cannot be ignored when the distances from targets and receive arrays are short. Considering the spatial scatterers and multipath phenomena, point models cannot characterize sources effectively, which should be described by distributed source models [1]. The signal of a source only propagates from a single direction through a straight path under the assumption of point source model. Distributed sources can be regarded as an assembly of point sources within a spatial distribution. The shape of spatial distribution is related to geometry and surface property of a target in underwater detection for instance. Spatial distribution of a distributed source can be generally modeled as Gaussian or uniform with parameters containing nominal angles and angular spreads. Nominal angles represent the center of targets and angular spreads represent the spatial extension of targets.
According to the scatterers coherence of sources, distributed sources can be classified into coherently distributed (CD) sources and incoherently distributed (ID) sources [1]. CD sources suppose that scatterers within a source are coherent whereas scatterers of an ID source are assumed to be uncorrelated. In this paper, ID sources are considered.
For CD sources, representative achievements of DOA estimation are methods extended from point source models through rotation invariance relations with respect to different array configuration under the small angular spreads assumption [2,3,4,5,6,7,8,9,10]. As to ID sources, people have presented subspace-based algorithms such as distributed signal parameter estimator (DSPE) [1] and dispersed signal parametric estimation (DSPARE) [11] which are developed from multiple signal classification (MUSIC). Based on uniform linear arrays (ULA), the authors of [12] have extended Capon method for ID sources, where two-dimensional (2D) spectral searches based on high-order matrix inversion are involved. The authors of [13] have proposed a generalized Capon’s method by introducing a matrix pencil of sample covariance matrix and normalized covariance matrix to traditional Capon framework. A robust generalized Capon’s method in [14] has been proposed by supplementing a constraint function using property of covariance matrix to cost function of algorithm in [12], which has better accuracy without a priori knowledge of shape of ID sources. Maximum likelihood (ML) approaches [15,16,17] have better accuracy but require high computational complexity. The authors of [18] have taken the lead in extending covariance matching estimation techniques (COMET) to DOA estimation of ID sources using ULA. They have converted complex nonlinear optimization to two successive one-dimensional (1D) searches utilizing the extended invariance principle (EXIP). Considering Gaussian and uniform ID sources, number of sensors in experiment of [18] ranges from 4 to 20; they have proved that when sensors is increased to a certain extent with other parameters fixed, estimation tends to be less accurate. Applying Taylor series expansion of steering vector to approximate the array covariance matrix using the central moments of the source, the authors of [19] have elaborated a lower computational COMET for ID sources, which exhibits a good performance at low SNR based on ULA with 11 sensors. The authors of [20] have presented the ambiguity problem of COMET-EXIP algorithm using ULA and proposed an inequality constraint in the original objective functions to solve this problem. The authors of [21] have turned covariance matching problem to retrieve parameters of received covariance by exploiting the annihilating property of linear nested arrays. The authors of [22] have embedded algorithm of [19] into a Kalman filter for DOA tracking problem of ID sources.
The aforementioned DOA estimations of ID sources consider the sources and receive arrays are in the same plane where sources are described by 1D model with two parameters: nominal angle and angular spread. Generally, sources are in different plane with receive arrays, which should be modeled as two-dimensional (2D) models with parameters as nominal azimuth angle, nominal elevation angle, azimuth spread, and elevation spread. With more parameters, there have been relatively few studies on estimation of 2D ID sources. The authors of [23] have extended COMET algorithm to 2D scenarios, which separates variables of each source based on alternating projection technique, then formulate equations set of unknown variables. The algorithm from [23] is applicable to any arrays in three-dimensional spaces but requires considerably high computational complexity. In addition, experiments of [23] have only considered a relatively small number of targets. The authors of [24] have proposed a two-stage approach based on rotation invariance relations of generalized steering vector of double parallel uniform linear arrays (DPULA), where nominal elevation is firstly estimated via TLS-ESPRIT, then nominal azimuth is acquired by 1D searching.
In order to estimate DOA of 2D ID sources, we propose an algorithm based on URA. Through Taylor series expansions of steering vectors, received signal vectors of arrays can be expressed as a generalized form which is combination of generalized steering matrix and generalized signal vector under the assumption of small distance of sensors and small angular spread. Consequently, the rotation invariance relations of constructed subarrays with respect to nominal azimuth and nominal elevation are derived. Constructed subarrays fully use elements of URA, so the estimation accuracy is improved. Then the nominal azimuth and nominal elevation can be calculated respectively by means of an ESPRIT like algorithm. Thus, estimation of multiple 2D ID sources do not need spectral searching and avoid high computational complexity. Lastly, the angle matching method is proposed according to Capon spectral search. Without information of angular power distribution function, the proposed method can detect sources with different angular power distribution functions.
2. Arrays Configuration and Signal Model
As shown in Figure 1, the URA consists of M × K sensors on xoz plane. The distance between sensors along the direction of x and z axes is set at d meters. Azimuth θ and elevation φ are used to describe the direction of signal in a three dimensional space. There are q 2D ID narrowband sources with nominal angles (θi, φi) (i = 1, 2, …, q) denoting nominal azimuth and nominal elevation of the ith sources impinging into arrays. θi , φi . λ is the wavelength of the impinging signal. The additive noise is considered as Gaussian white with zero mean and uncorrelated with sensors.
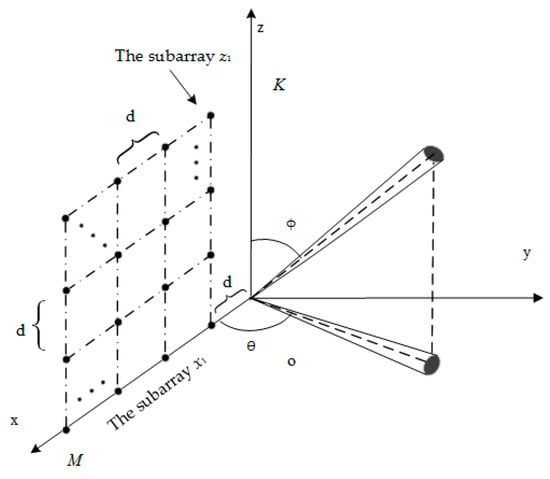
Figure 1.
Uniform rectangular arrays configuration.
The M × 1 dimensional received vector of the M sensors located on the x-axis defined as subarray x1 can be written as
where nx1(t) denotes the noise vector of subarray. The M × 1 dimensional vector α1(θ,φ) denotes the steering vector of subarray x1 with respect to point source, which can be expressed as
si(θ,φ,t) is the complex random angular signal density of the distributed source representing the reflection intensity of the source from angle (θ,φ) at the snapshot index t. Unlike a point source, signal of a distributed source exists not only in the direction of (θi,φi) but also in a spatial distribution around (θi,φi). A distributed source is defined as incoherently distributed if si(θ,φ,t) from one direction is uncorrelated with other directions, which can be modeled as a random process as
where δ(·) is the Kronecker delta function, Pi is the power of the source, fi(θ,φ;ui) is its normalized angular power density function (APDF) reflecting geometry and surface property of a distributed source. APDF is determined by parameter set ui. For a Gaussian ID source, ui = [, , , , ] denoting nominal azimuth, nominal elevation, azimuth spread, elevation spread, and covariance coefficient respectively, APDF can be expressed as
For a uniform ID source, ui = [, , , ] denoting nominal azimuth, nominal elevation, azimuth spread and elevation spread respectively. APDF can be expressed as
The M × 1 dimensional received vector of the kth subarray parallel to x-axis, which is defined as subarray xk, can be written as
where αk(θ,φ) denotes the steering vector of subarray xk with respect to point source, which can be written as
The M × K dimensional received matrix of the URA along the x-axis can be expressed as
The K × 1 dimensional received vector of the K sensors with distance d and parallel to z-axis defined as subarray z1 can be written as
where the K × 1 dimensional vector β1(θ,φ) denotes the steering vector of subarray z1 with respect to point source, nz1(t) denotes the noise vector of subarray z1. β1(θ,φ) can be expressed as
The K × 1 dimensional received vector of the mth subarray parallel to z-axis defined as subarray zm can be written as
where βm(θ,φ) denotes the steering vector of subarray zm with respect to point source, which can be written as
The K × M dimensional received matrix of the URA along the z-axis can be expressed as
3. Proposed Method
This section consists of five parts. First of all, generalized steering matrices are obtained from taking the first-order Taylor series expansions of steering vectors under the assumption of small angular spreads and small distance d of the URA. Then, the rotation invariance relations of generalized steering matrices within subarrays are derived. In the next part, the received signal vectors are transformed as combinations of generalized signal vectors and generalized steering matrices. Next, based on rotation invariance relations of constructed subarrays, nominal azimuth and nominal elevation can be estimated separately by an ESPRIT like algorithm. Afterwards, angle matching method is proposed based on the Capon principle. Lastly computational procedure is summarized and complexity analysis is analyzed with comparison of two existing methods for 2D ID sources.
3.1. Generalized Steering Matrix
Assume that angular spread of distributed sources is small, take the first-order Taylor series expansions of steering vectors of subarrays xk and xk−1 at (θi, φi), we have
where and denote the first-order partial derivatives of θ and φ at (θi, φi), the following relationship can be obtained from Equation (7)
If d/λ 0.5, the second term of the right side of the Equation (18) can be ignored, so Equation (18) can be written as
In the point source model case, steering vectors is used to describe response of an array. Nevertheless, as for distribute sources, generalized steering vectors or generalized steering matrices [5,24] represent response of arrays. Define M × 3q dimensional generalized steering matrix of subarray x1 as . A11, A12, and A13 are expressed as
Define the generalized steering matrix of subarray xk as ,
From Equations (16), (17) and (19) we can obtain the generalized steering matrix of xk subarray as
where Φz is rotation invariance operator, which can be written as
Take the first-order Taylor series expansions of steering vectors of subarrays zm and zm−1 at (θi, φi), we have
Form Equation (12) we have
If d/λ 0.5, the second term of the right side of the Equations (27) and (28) can be ignored, so Equations (27) and (28) can be written as
Define the M × 3q dimensional generalized steering matrix of subarray z1 as ; B11, B12, and B13 are written as
Define the generalized steering matrix of subarray z1 as ,
From Equations (26), (29), and (30), the generalized steering matrix of zm can be expressed as
where Φx is rotation invariance operator, which can be written as
3.2. Generalized Signal Vector
Define generalized signal vector as H; and are written as
where
Substitute Taylor series expansions (15) into Equation (6), we obtain
Thus, received vector of subarray xk can be expressed as a combination of the generalized signal vector and generalized steering matrix
The MK × 1 received vector of the URA along the x-axis can be express as
where nX(t) is the noise vector of the URA along the x-axis, which can be expressed as
Similarly, the received vector of subarray zm can be expressed as
Supposing different ID sources are uncorrelated there exist following relations within generalized signal vectors (see Appendix A)
where Mθi, Mφi can be express as
According to the assumption that different ID sources are uncorrelated, so we have
where Λ, Mθ, and Mφ can be written as
3.3. Nominal Angles Estimation
We construct two subarrays X1 and X2 along the direction of the x-axis. X1 is constituted by arrays from x1 to xK−1; while X2 contains arrays from x2 to xK. Thus, X1(t) is M(K − 1) × 1 dimensional received vector of X1 also equals a vector containing elements from 1 to MK − M row of (t); whereas X2(t) is M(K − 1) × 1 dimensional received vector of X2 containing elements from M + 1 to MK of (t). X1(t) and X2(t) can be written as
nX1(t) is noise vector of X1 containing elements from 1 to MK − M row of nX(t), nX2(t) is noise vector of X2 containing elements from M to MK row of nX(t). is the generalized steering matrix of subarray X1(t), which can be expressed as
is the generalized steering matrix of subarray X2(t). From Equation (22) we can obtain
which proves the rotational invariance relation between the two constructed subarrays X1 and X2. According to the ESPRIT principle, combing the vector X1(t) and X2(t), we obtain a vector with rotational invariance property as
where the generalized steering matrix of the combination X12(t) can be expressed as
The combination of noise vector can be expressed as
ESPRIT framework is based on rotational invariance property of signal subspace, which can be derived from the rotational invariance property of the received signal vector. Signal subspace can be acquired by eigendecomposition of the covariance matrix of received vector X12(t) which can be expressed as
can be replaced by sample covariance matrix with N snapshots as
From Equations (45) and (46) we find that eigenvalues of covariance matrix of received signal vector consist of three parts Λ, MθΛ and MφΛ. The three parts all has q elements. Each part corresponds to respective eigenvectors. Under the assumption of small angular spread, we can obtain Mθi < 1 and Mφi < 1. Therefore, subspace spanned by eigenvectors corresponding to the largest q eigenvalues is equal to subspace spanned by Ax1. Suppose Ex is 2M(K − 1) × q dimensional matrix with columns as the eigenvectors of the covariance matrix corresponding to the q largest eigenvalues. Accordingly, there exists a q × q nonsingular matrix T satisfying the following relation
Let Ex1 and Ex2 denote matrices selecting upper and lower MK − M rows of Ex
So we have
Let
Thus, the eigenvalues of Φx is elements of Фz. Ωx can be obtained as
where (•)+ denotes pseudo-inverse operator, then the nominal elevation of the sources can be get from
where ηi is the ith eigenvalues of Ωx, angle(•) denotes argument of complex variable.
Similarly, we construct two subarrays Z1 and Z2 along the direction of z-axis. Z1 is constituted by arrays from z1 to zM−1; while Z2 contains arrays from z2 to zM.1(t) is K(M − 1) × 1 dimensional receive vector of Z1 containing elements from 1 to K(M − 1) row of (t); whereas Z2(t) is K(M − 1) × 1 dimensional received vector of Z2 containing elements from K + 1 to MK row of (t). nZ1(t) and nZ2(t) have the similar definition as nX1(t) and nX2(t). The received vectors Z1(t) and Z2(t) can be expressed as
where is the generalized steering matrix of Z1(t), which can be expressed as
Form Equation (33), the generalized steering matrix of Z2(t) can be obtained as
which proves the rotational invariance relation between the two constructed subarrays Z1 and Z2. Combing the vector Z1(t) and Z2(t), we obtain a vector with rotational invariance property as
where the generalized steering matrix of Z12(t) can be expressed as
The combination of noise vector of Z1(t) and Z2(t) can be expressed as
The covariance matrices of received signal Z12(t) can be expressed as
which can be replaced by sample covariance matrix with N snapshots as
Suppose Ez is 2K(M − 1) × q matrix with columns as the eigenvectors of the covariance matrix corresponding to the q largest eigenvalues. As the same as Ex, Ez is the same subspace spanned by . Accordingly, there exists a q × q nonsingular matrix Q satisfying the following relation
Let Ez1 and Ez2 denote matrices selecting upper and lower MK − K rows of Ez
So we have
Let
Thus, the eigenvalues of Φz is elements of Фx. Ωz can be obtained as
Then the nominal azimuth of the sources can be get from
where μi is the ith eigenvalues of Ωz.
3.4. Angle Matching Method
After all the eigenvalues of Ωx and Ωz are calculated, we need to match the right θi to right φi. We can obtain cost function by applying Capon principle to subarray x1 firstly. Then angle matching can be obtained by substituting all the possible pairs into the cost function.
The generalized steering matrix of subarray x1 is , the Capon principle with regard to the subarray x1 can be expressed as
where is the covariance matrix of subarray x1. Equation (75) can be solved through minimization of Lagrange function as follows
Take the derivative of the Equation (76) with regard to w and set the result equal to 0, we obtain
Considering constraint condition, we obtain
The optimal vector wopt can be obtained as follows
Then, the cost function can be expressed as
can be replaced by sample covariance matrix with N snapshots as
Suppose that all eigenvalues of Ωx and Ωz are calculated. Now we summarize the angle matching procedure as follows:
Step 1: Calculate nominal elevation φi (i = 1, 2,…, q) from Equation (60). Select one elevation angle form set at random. Superscript ^ denotes the angle already determined. Substitute to the eigenvalues set of Ωz: and calculate q matching azimuth angles from Equation (74). So we get q possible pairs .
Step 2: As the right parameters of sources can meet the objective function in Equation (75). Substitute into cost function (80). Choose the azimuth making reach the maximum as the right azimuth angle matching to , which is labeled as .
Step 3: Delete from set meanwhile delete eigenvalue from set .
Step 4: Set q = q − 1.
Step 5: Repeat steps 1 to 4.
All the nominal azimuth and nominal elevation can be matched after (q + 2)(q − 1)/2 times calculation.
3.5. Computational Procedure and Complexity Analysis
Now, our algorithm can be summarized as follows
Step 1: Compute sample covariance matrices and using Equations (54) and (68).
Step 2: Find the eigenvectors Ex and Ez corresponding to the q largest eigenvalues through eigendecomposition of and . Divide Ex into Ex1, Ex2 and divide Ez into Ez1, Ez2.
Step 3: Obtain Ωx and Ωz from Equations (59) and (73), calculate eigenvalues and (i = 1, 2, …, q) through eigendecomposition of Ωx and Ωz.
Step 4: Calculate nominal azimuth θi and nominal elevation φi from Equations (60) and (74).
Step 5: Compute sample covariance matrix form Equation (81) and take the angle matching procedure.
We analyze the computational complexity of the proposed method in comparison with COMET [23] which can be applied for URA and Zhou’s algorithm [24] which uses DPULA for 2D ID sources. COMET [23] is a method under alternating projection algorithm framework, its computational cost mostly consists of the calculation of the sample covariance matrix which needs O(NM2K2) and the alternating projection technique with respect to cost functions which is O(M4K4 + 2M2K2). Zhou’s algorithm uses TLS-ESPRIT to calculate nominal elevation and 1D searching to find nominal azimuth. Computational cost of Zhou’s algorithm [24] mainly contains calculation of the sample covariance matrix O(4NM2), eigendecomposition and inversion of the sample covariance matrix O(16M3) and 1D searching O(8M3). Computational cost of the proposed algorithm mainly contains calculation of the sample covariance matrix O[N(MK − K)2 + N(MK − M)2], eigendecomposition of and O[8 (MK − K)3 + 8(MK − M)3], eigendecomposition of Ωx and Ωz O(q3) and angle matching O(q2). The main computational complexity of the three algorithms are shown in Table 1.

Table 1.
Computational complexity of different methods
From Table 1, we can conclude that the computational cost of the proposed algorithm is higher than Zhou’s algorithm [24] when K > 2 and lower than COMET algorithm [23] when the two algorithm use same number of sensors.
4. Results and Discussion
In this section, the effectiveness of the proposed algorithm is investigated through five simulation experiments. The array configuration is shown in Figure 1. Root mean squared error (RMSE) is applied for the evaluation of the performance of estimation. RMSEθ and RMSEφ denote the RMSE of nominal azimuth and nominal elevation respectively, which can be expressed as
where MC is the number of Monte Carlo simulations. and are the estimated nominal azimuth and nominal elevation of ith source in th Monte Carlo simulation.
In the first experiment, we examine the performance of the proposed method vesus SNR with regard to two Gaussian ID source with parameters [30°, 45°, 2°, 2°, 0.5] and [50°, 45°, 2°, 2°, 0.5]. The sources are supposed to have the same power. Snapshots number is set at 200, MC = 100, M = K = 8. d = λ/10. Figure 2a,b show RMSEθ and RMSEφ curves with SNR varying from −5 dB to 30 dB. The figures also show the estimation of the COMET [23] using the URA, Zhou’s algorithm [24] using arrays x1 and x2 and the Cramer–Rao lower bound (CRLB). As shown from Figure 2a,b, when SNR changes from −5 dB to 0 dB, COMET [23] presents better performance than the proposed algorithm. As SNR increases, RMSEθ and RMSEφ of all algorithms decrease. The proposed algorithm has better performance than other algorithms with SNR ranging from 10 dB to 30 dB. Thus, it can be concluded that our method has a good performance when SNR is at high levels. Estimation of our method is based on acquiring signal subspace through eigendecomposition of covariance matrix of received vector. The accuracy of eigendecomposition would deteriorate at low SNR, while COMET [23] separates the noise and signal power through covariance matching fitting matrix by alternating projection technique firstly, as a result, perform better at low SNR.
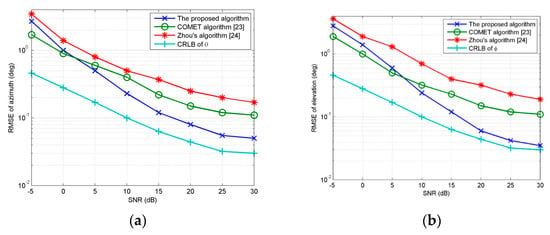
Figure 2.
(a) RMSEθ estimated by three algorithms for 2D ID sources vesus SNR; (b) RMSEφ estimated by three algorithms for 2D ID sources vesus SNR.
In the second experiment, we investigate the estimation of source near the boundary region. Consider a Gaussian and a uniform ID source respectively. Both sources have angular spread 2°. Covariance coefficients of Gaussian sources are set at 0.5. SNR is set at 15 dB and snapshots number is 200, MC = 100, M = K = 8, d = λ/10. Figure 3a shows RMSEθ curves as nominal azimuth changing from 0° to 180° with nominal elevation fixed at 20°, while Figure 3b shows RMSEφ curves as nominal elevation changing from 0° to 180° with nominal azimuth fixed at 20°. As can be seen, both RMSEθ and RMSEφ increase markedly near the boundary region. Generally, the error of the boundary region estimated by our method is acceptable.
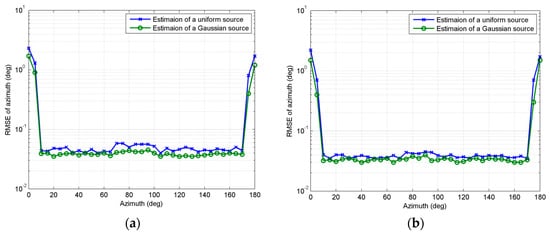
Figure 3.
(a) RMSEθ estimated with θ changing from 0° to 180° while φ is fixed at 20°; (b) RMSEφ estimated with φ changing from 0° to 180° while θ is fixed at 20°.
In the third experiment, we examine the performance of the proposed method with regard to estimation of sources with different APDFs simultaneously. Consider four ID sources with same power and parameters of sources are set as [30°, 45°, 2°, 2°, 0.5], [50°, 45°, 1.5°, 3°, 0.5], [50°, 60°, 2°, 2.5°], and [70°, 60°, 1.5°, 3.5°]. The first and second sources are Gaussian whereas the third and fourth sources are uniform. The experiment set SNR at 15 dB; number of snapshots is 200. MC = 100, M = K = 8, d = λ/10. Figure 4 shows the estimated result of four sources, which indicate that the proposed method can estimate sources with different APDFs effectively.
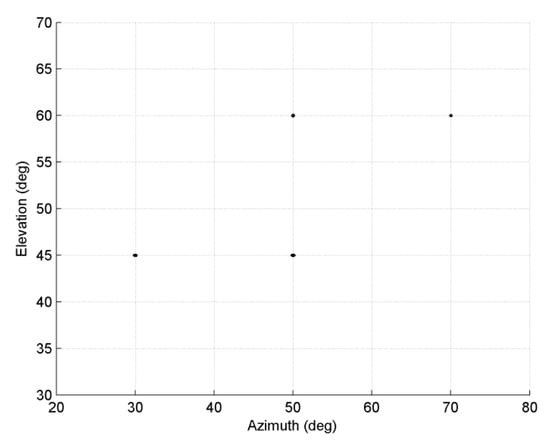
Figure 4.
Estimated results for 2D ID sources with different angular power density functions.
In the fourth experiment, we examine the performance of the proposed method vesus the distance d between adjacent sensors. As the rotational invariance relations of generalize steering matrices are obtained under the small distance d assumption, it is necessary to investigate the influence of d to the estimation. Four sources with the same parameters as the sources in third example are set to be estimated as the d varying from λ/20 to λ/2. SNR is set at 15 dB and snapshots number is 200, MC = 100, M = K = 8. Figure 5 shows that RMSEθ and RMSEφ of both Gaussian and uniform sources increase with the distance d from λ/20 to λ/2. When d is λ/2, RMSEθ and RMSEφ of Gaussian sources reach 0.62 and 0.44, those of uniform sources reach 0.79 and 0.67, which are still satisfactory results. It can be concluded that the proposed algorithm shows satisfactory performance with small distance between adjacent sensors.
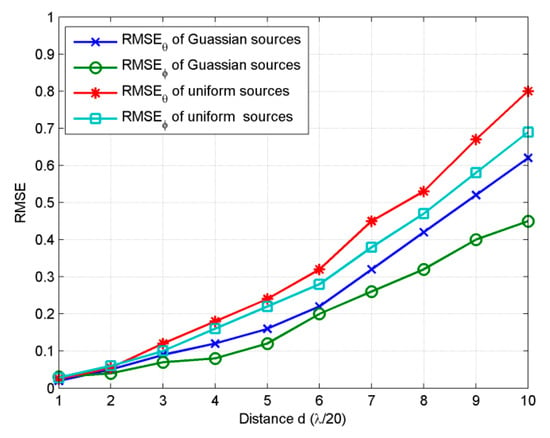
Figure 5.
RMSE estimated for 2D ID sources with different distance d.
According to the result of third example, the smaller distance d is, the higher estimation accuracy is. However, in the same channel the frequency increases, wavelength decreases. High frequency detection needs smaller d than low frequency detection to attain the same estimation accuracy. Actually, when the distance d is small, installation accuracy of sensors will get worse, which would also deteriorate the estimation accuracy. Thus, installation accuracy and the distance d is a matter of balance especially in high frequency detection. In the field of low frequency underwater detection, frequency of sonar can be down to 100 HZ, which means wavelength can reach 14.5 m approximately, on this condition d/λ can reach a small value practically.
In the fifth experiment, we investigate the performance of the proposed algorithm versus the number of sources and sensors. Theoretically, if M = K, the proposed algorithm can estimate M(M − 1) different ID sources and COMET [23] can estimate M2. Utilizing double parallel arrays which contains only 2M sensors can estimate M sources simultaneously. We consider seven URA with M varying from 4 to 10. The total number of sources is set at M2 which is a theoretical upper limit of the trail. The (a, b)th source is set at [20° + (a − 1)10°, 20° + (b − 1)10°]. All sources are Gaussian and have same power. SNR is 15 dB, number of snapshots is 200, MC = 100, d = λ/10, 2°. Covariance coefficients of Gaussian sources are set at 0.5. When all sources are estimated successfully, the difference between estimators is accuracy which can be described by RMSE. When not all sources are estimated successfully, RMSE cannot differentiate performance of estimators. Thus, an indicator reflecting the number of sources detected is needed to measure the performance of different estimators. Estimation is regarded as effective when the estimated angles satisfying 5°. Define detection probability as Nd/M2 where Nd is number of source estimated effectively. So in theory the detection probability of the proposed algorithm is (M − 1)/M, COMET is 1, Zhou’s algorithm [24] is 1/M.
As can be seen from Figure 6, the estimation probability of zhou’s algorithm [24] is consistent with theoretical value within all range of the trail, so are the estimation probabilities of our method and COMET with M < 6. When M ≥ 7, our method perform better than COMET, which means using 7 × 7 or larger arrays our method can estimated more sources than COMET if there are large number of sources that need estimating Involving eigendecomposition of high dimensional matrices, effectiveness of our method deteriorates as the number of sources becomes large. For instance, if M = 8 and total source is 64, the covariance matrix of received vector is 112 × 112 dimensional, Ωx and Ωz is 64 × 64 dimensional, which all need eigendecomposition. The deterioration of COMET [23] is also closely related to the number of sources. COMET [23] separates unknown variables of each source based on alternating projection technique, and then formulate equation sets of unknown variables. In the separating process, 64 inversion operations of a 64 × 64 dimensional matrix are executed on the condition M = 8 and total source is 64. Consequently, the errors of the separating process deliver to equations set and affect the validity of estimation.
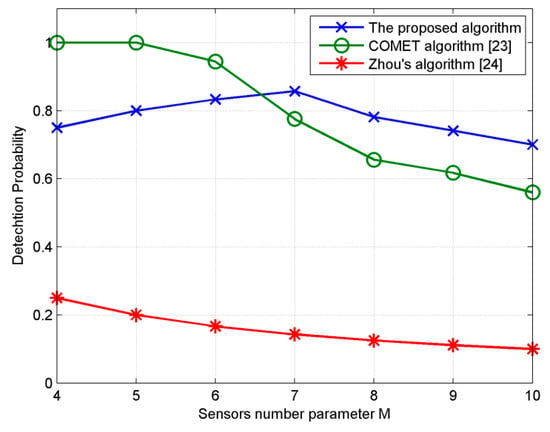
Figure 6.
Detection probability by three algorithms with different numbers of sources and sensors.
5. Conclusions
In this paper, we propose an estimator for 2D ID sources using URA. The received signal vectors can be transformed as combinations of generalized signal vectors and generalized steering matrices through Taylor series expansions. By virtue of the rotational invariance relations of generalized steering matrices within subarrays, an ESPRIT like algorithm are introduced in detail, then angle matching method based on Capon principle is proposed. Simulations demonstrate the effectiveness of the proposed method with regard to sources with different APDF, distance d between sensors, sources in boundary region. Simulation also indicates that our method has better performance when SNR is at high level on the condition that the quantity of sources is relatively small and can estimate more sources in sufficient sources circumstance using large dimensional arrays.
Author Contributions
Conceptualization, Z.D.; Methodology, T.W.; Software, T.W.; Writing—Original Draft Preparation, T.W. and Y.L.; Writing—Review & Editing, Y.H.
Funding
This research was funded by the National Natural Science Foundation of China grant number 61471299 and 51776222.
Acknowledgments
The authors would like to thank editorial board and reviewers for the improvement of this paper.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
Take Gaussian distribution described by (4) for example, if l = n = 0, can be expressed as
If l = n = θ, can be expressed as
where
Similarly, and .
If l ≠ n, there exists six cases, l = 0 with n = θ or φ, l = θ with n = 0 or φ and l = φ with n = 0 or θ. Take l = θ with n = φ and l = 0 with n = φ for example, can be expressed as
References
- Valaee, S.; Champagne, B.; Kabal, P. Parametric localization of distributed sources. IEEE Trans. Signal Process. 1995, 43, 2144–2153. [Google Scholar] [CrossRef]
- Wan, L.; Han, G.; Jiang, J.; Zhu, C.; Shu, L. A DOA Estimation Approach for Transmission Performance Guarantee in D2D Communication. Mobile Netw. Appl. 2017, 36, 1–12. [Google Scholar] [CrossRef]
- Dai, Z.; Cui, W.; Ba, B.; Wang, D.; Sun, Y. Two-Dimensional DOA Estimation for Coherently Distributed Sources with Symmetric Properties in Crossed Arrays. Sensors 2017, 17, 1300. [Google Scholar] [CrossRef]
- Yang, X.; Zheng, Z.; Chi, C.K.; Zhong, L. Low-complexity 2D parameter estimation of coherently distributed noncircular signals using modified propagator. Multidim. Syst. Sign. Process. 2017, 28, 1–20. [Google Scholar] [CrossRef]
- Zheng, Z.; Li, G.J.; Teng, Y. 2D DOA Estimator for Multiple Coherently Distributed Sources Using Modified Propagator. Circuits Syst. Signal Process. 2012, 31, 255–270. [Google Scholar] [CrossRef]
- Zheng, Z.; Li, G.J.; Teng, Y. Low-complexity 2D DOA estimator for multiple coherently distributed sources. COMPEL 2012, 31, 443–459. [Google Scholar] [CrossRef]
- Zoubir, A.; Wang, Y. Performance analysis of the generalized beamforming estimators in the case of coherently distributed sources. Signal Process. 2008, 88, 428–435. [Google Scholar] [CrossRef]
- Han, K.; Nehorai, A. Nested Array Processing for Distributed Sources. IEEE Signal Process. Lett. 2014, 21, 1111–1114. [Google Scholar] [CrossRef]
- Yang, X.; Li, G.; Zheng, Z.; Zhong, L. 2D DOA Estimation of Coherently Distributed Noncircular Sources. Wirel. Pers. Commun. 2014, 78, 1095–1102. [Google Scholar] [CrossRef]
- Xiong, W.; José, P.; Sylvie, M. Performance analysis of distributed source parameter estimator (DSPE) in the presence of modeling errors due to the spatial distributions of sources. Signal Process. 2018, 143, 146–151. [Google Scholar] [CrossRef]
- Meng, Y.; Stoica, P.; Wong, K.M. Estimation of direction of arrival of spatially dispersed signals in array processing. IET Radar Sonar Navig. 1995, 143, 1–9. [Google Scholar] [CrossRef]
- Xu, X. Spatially-spread sources and the SMVDR estimator. In Proceedings of the IEEE SPAWC’2003, Rome, Italy, 15−18 June 2003. [Google Scholar]
- Hassanien, A.; Shahbazpanahi, S.; Gershman, A.B. A generalized capon estimator for localization of multiple spread sources. IEEE Trans.Signal Process. 2004, 52, 280–283. [Google Scholar] [CrossRef]
- Zoubir, A.; Wang, Y. Robust generalised Capon algorithm for estimating the angular parameters of multiple incoherently distributed sources. IET Signal Process. 2008, 2, 163–168. [Google Scholar] [CrossRef]
- Raich, R.; Goldberg, J.; Messer, H. Bearing estimation for a distributed source: Modeling, inherent accuracy limitations and algorithms. IEEE Trans. Signal Process. 2000, 48, 429–441. [Google Scholar] [CrossRef]
- Besson, O.; Vincent, F.; Stoica, P.; Gershman, A.B. Approximate maximum likelihood estimators for array processing in multiplicative noise environments. IEEE Trans. Signal Process. 2000, 48, 2506–2518. [Google Scholar] [CrossRef]
- Trump, T.; Ottersten, B. Estimation of nominal direction of arrival and angular spread using an array of sensors. Signal Process. 1996, 50, 57–69. [Google Scholar] [CrossRef]
- Besson, O.; Stoica, P. Decoupled estimation of DOA and angular spread for a spatially distributed source. IEEE Trans. Signal Process. 2000, 48, 1872–1882. [Google Scholar] [CrossRef]
- Shahbazpanahi, S.; Valaee, S.; Gershman, A.B. A covariance fitting approach to parametric localization of multiple incoherently distributed sources. IEEE Trans. Signal Process. 2004, 52, 592–600. [Google Scholar] [CrossRef]
- Zoubir, A.; Wang, Y.; Charge, P. On the ambiguity of COMET-EXIP algorithm for estimating a scattered source. In Proceedings of the IEEE International Conference on Acoustics, Speech, and Signal Processing, Philadelphia, PA, USA, 23−23 March 2005. [Google Scholar]
- Wen, C.; Shi, G.; Xie, X. Estimation of directions of arrival of multiple distributed sources for nested array. Signal Process. 2017, 130, 315–322. [Google Scholar] [CrossRef]
- Hassen, S.B.; Samet, A. An efficient central DOA tracking algorithm for multiple incoherently distributed sources. EURASIP J. Adv. Signal Process. 2015, 1, 1–19. [Google Scholar] [CrossRef]
- Boujemâa, H. Extension of COMET algorithm to multiple diffuse source localization in azimuth and elevation. Eur. Telecommun. 2012, 16, 557–566. [Google Scholar] [CrossRef]
- Zhou, J.; Li, G.J. Low-Complexity Estimation of the Nominal Azimuth and Elevation for Incoherently Distributed Sources. Wirel. Pers. Commun. 2013, 71, 1777–1793. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).