Abstract
A nanocrystalline SnO2 thin film was synthesized by a chemical bath method. The parameters affecting the energy band gap and surface morphology of the deposited SnO2 thin film were optimized using a semi-empirical method. Four parameters, including deposition time, pH, bath temperature and tin chloride (SnCl2·2H2O) concentration were optimized by a factorial method. The factorial used a Taguchi OA (TOA) design method to estimate certain interactions and obtain the actual responses. Statistical evidences in analysis of variance including high F-value (4,112.2 and 20.27), very low P-value (<0.012 and 0.0478), non-significant lack of fit, the determination coefficient (R2 equal to 0.978 and 0.977) and the adequate precision (170.96 and 12.57) validated the suggested model. The optima of the suggested model were verified in the laboratory and results were quite close to the predicted values, indicating that the model successfully simulated the optimum conditions of SnO2 thin film synthesis.1. Introduction
Metal oxide semiconductors with wide band gaps have many important applications in the optics, electric and electronic industries. Transparent SnO2 thin films have been widely used in the production of transparent electrodes, far-infrared detectors, solar cells and gas sensors [1–4]. Nanocrystalline SnO2 thin films have also garnered attention since higher quality synthesis of SnO2 thin films was achieved.
A variety of methods, such as magnetron sputtering [5], vacuum evaporation [6], sol-gel [7], chemical vapor deposition [8], and sonochemistry [9] have been employed to prepare SnO2 thin films. Among all the methods, the chemical bath deposition technique is very attractive because it is easy to control the growth factors, and crystal quality [10].
Since in the CBD method several effective parameters such as concentration, time, temperature and the pH of the solution exist, too many experiments must be performed for finding the optimum conditions. Besides laborious experimental management, this also requires more chemicals, instruments and labor time. Furthermore, the preparation conditions are critical factors that affect the shape and size of the resulting nanomaterials [11,12], therefore prediction of the optimal conditions seems highly desirable and necessary.
The Taguchi method is a statistical technique used in empirical studies. It is an conomical way to characterize complicated processes, and it requires fewer experiments to optimize reactions. In the methodology, a factorial design was used for experimental design and fitting the performed results with a polynomial equation in the vicinity of the optimum conditions to make a model [13]. The model relates the responses and the variables of the deposition process [14]. Therefore, in this work the optimum conditions were simulated by the TOA and then visualized by 3D plots in vicinity of the reported optimum conditions [15]. The predicted optima of the responses and the variables were the confirmed by the actual responses from laboratory experiments.
2. Experimental
2.1. Materials
Glass slides of 76 × 25 mm2 were used as the substrate. SnCl2·2H2O (Merck, Darmstadt, Germany, 98.1%), Ethylenediaminetetraacetic acid and triethanolamine (Sigma Aldrich, St Louis, MO, USA) were used as the complexing agents. Ethanol, HCl and H2O2 used in this study were of analytical reagent grade.
2.2. Empirical Methodology
The reactions were performed in 100 mL flasks and specified volumes of deionized water were added as the solvent. Different concentrations of tin chloride were mixed with the complexing agents, while different amounts of H2O2, HCl and ethanol were subsequently added to adjust the pH. The reaction was performed in a water bath at different temperatures and for different deposition times, as shown in Table 1. The substrates were preheated to 120 °C and then quickly mounted in cold reaction solution. After that, the reaction vessels were moved to water bath which was maintained at 30–50 °C for 30–90 min. The samples were removed from the bath then dried at room temperature. The surface roughness data was recorded using an atomic force microscope (Quesant Q-scope 250, Ambios Technology, Inc., Santa Cruz, CA, USA). The optical transmission data in the wavelength range of 280–800 nm were recorded using a Lambda 2S Ultraviolet/Visible spectrophotometer (Uberlingen, Germany) at room temperature.

2.3. Statistical Methods
To find the optimum deposition conditions, the experiments were designed by factorial and TOA as shown in Table 1 (the design is codified). The design with four effective variables (Table 2) was run by the Design-expert version 8.0.7.1 software (Minneapolis, MN, USA).

The total number of performed runs was nine. The designed actual responses were fitted to the quadratic cubic models by orthogonal array TOA. The fitting was based on a second order polynomial model by a multiple regression analysis [13]. The significance and adequacy of the model was determined by the statistical evidence that appear in analysis of variance (ANOVA) output of the TOA method. These included Fisher variation ratio (F-value), lack of fit, coefficient of determination R-squared (Rd2), adjusted R-squared (RAdj2), and predicted R-squared (RPred2) and adequate precision of Predicted Residual Error of Sum of Squares (PRESS). Most of these parameters are clearly defined in experimental design texts. RAdj2 and the RPred2 are the measurement of the amount of variation around the mean and the new explained data, respectively. F-value is a statistically valid measure of how well the factors described the variation in the data about its meaning while P-value represents the degree of significance of each variable [13].
3. Results and Discussion
3.1. Analysis of the Model
The model fitting technique showed sufficient correlation between the predicted values to the observed values. The fitting of the data to various models (i.e., linear, quadratic, two factorial and cubic) and their subsequent ANOVA showed that a quadratic response surface model was the most suitable to describe the synthesis of nanocrystalline SnO2. Figures 1 and 2 show the predicted values versus the actual values of the energy band gap and RMS roughness. The coefficients of determination (R2) obtained for the energy band gap and RMS were 0.978 and 0.977, respectively.
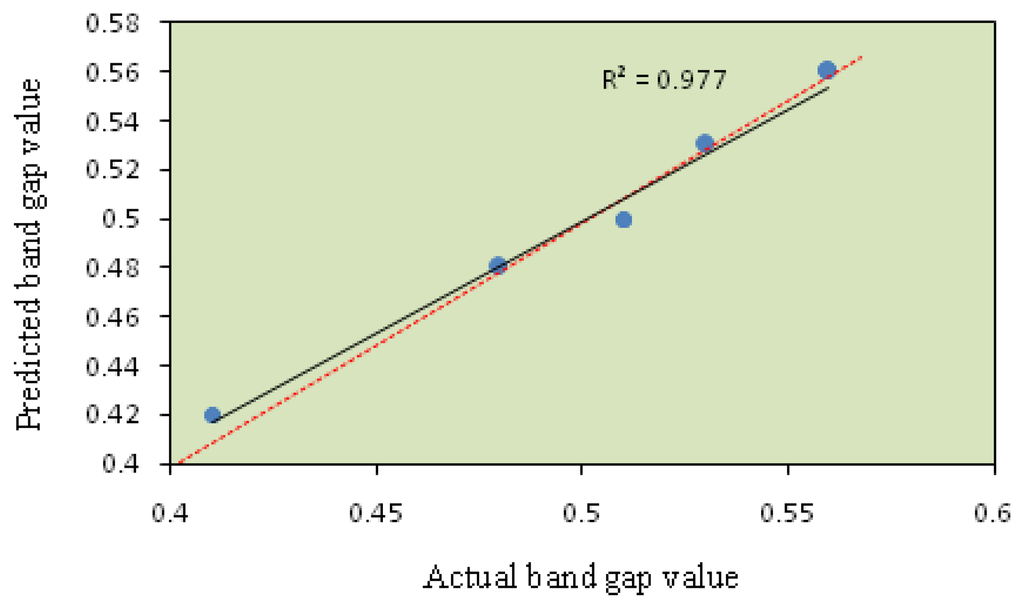
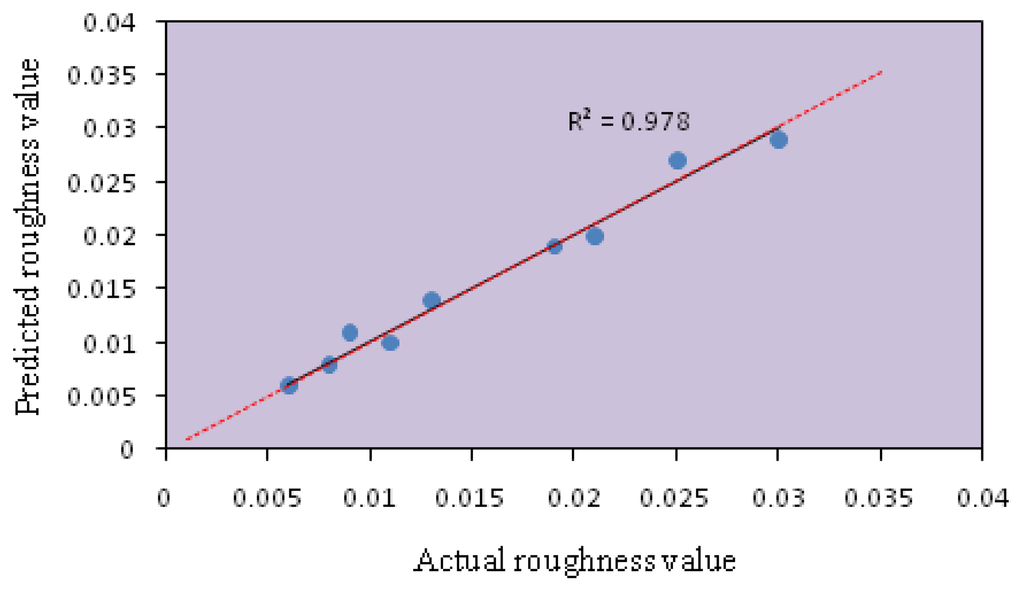
The S/N ratio is a logarithmic function used to optimize the process or product design and minimize the variability. The maximization of S/N ratio allows reduction of variability of the process against undesirable changes in the neighboring environment or uncontrollable factors. To minimize variability, the level of factor which produces the higher value of S/N ratio must be chosen. The S/N ratios were calculated using Equation (1) [16] as follows:
The ANOVA results of the quadratic model for the deposition of SnO2 thin film are presented in Tables 3 and 4. High F-values of 20.27 and 4,112.2 indicate that the model was significant and there was only a 1.2% and 4.78% chance occurrence of noise.


The coefficients of determination (R2) of the model were 0.9838 and 0.9937, which indicated 98.38% and 99.37% of variability in the response could be explained by the model. Therefore, the present R2-values reflected a very good fit (>0.9) between the experimental and predicted values [17].
In addition, the R2Adj (0.9353 and 0.9997) were satisfactory, which confirms the aptness of the model. Moreover, the adequate precision (12.57 and 170.96) shows remarkable signal (≫4). This ensured model (quadratic) was suitable to navigate the design space and provide a satisfactory match of the polynomial model to the experimental data.
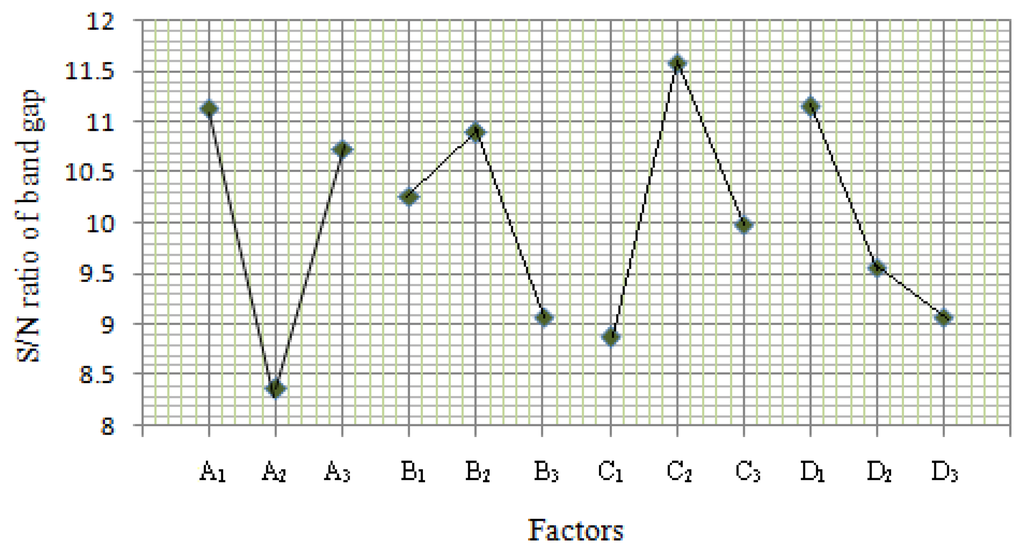
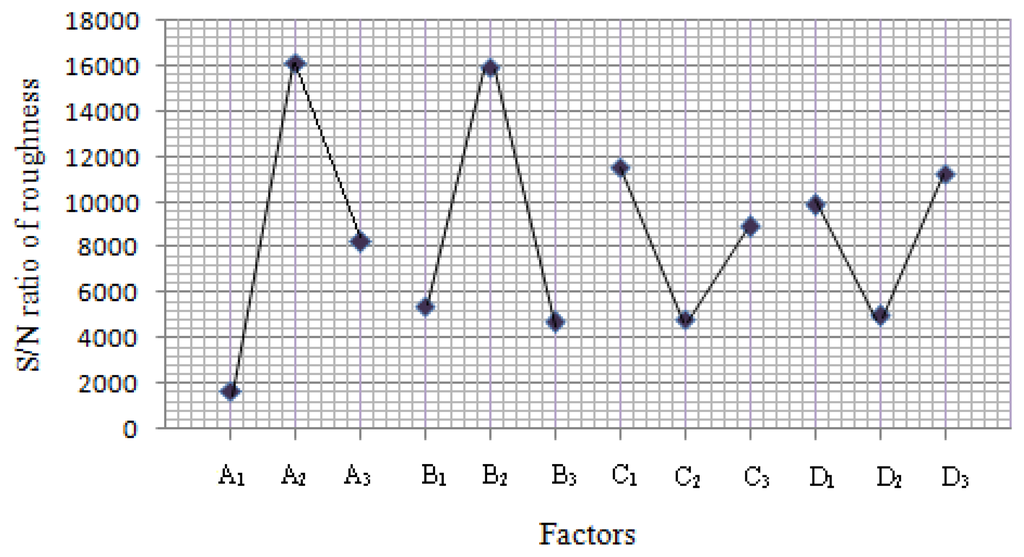
3.2. The Quadratic Expression Model
It is normal to describe experimental data by forming a mathematical relationship between the factors (independent variables) and responses (dependent variables). The final model to describe the relationship of the energy band gap and surface roughness with control factors is shown in Equations (2) and (3), respectively, as follows:
3.3. Response Surface Plots
Based on the validated model, the 3D plots present the numerous predicted (simulated) responses with the four variables and one response (Table 2) of the deposition (Figure 5). The effect of pH, deposition time, temperature and SnCl2 concentration on chemical synthesis of SnO2 thin film was investigated during the deposition as a preliminary study, while two variables in each case were held constant (e.g., Figure 5a). As observed, the deposition illustrated a peak at a particular value of pH, deposition time, temperature and SnCl2 concentration.
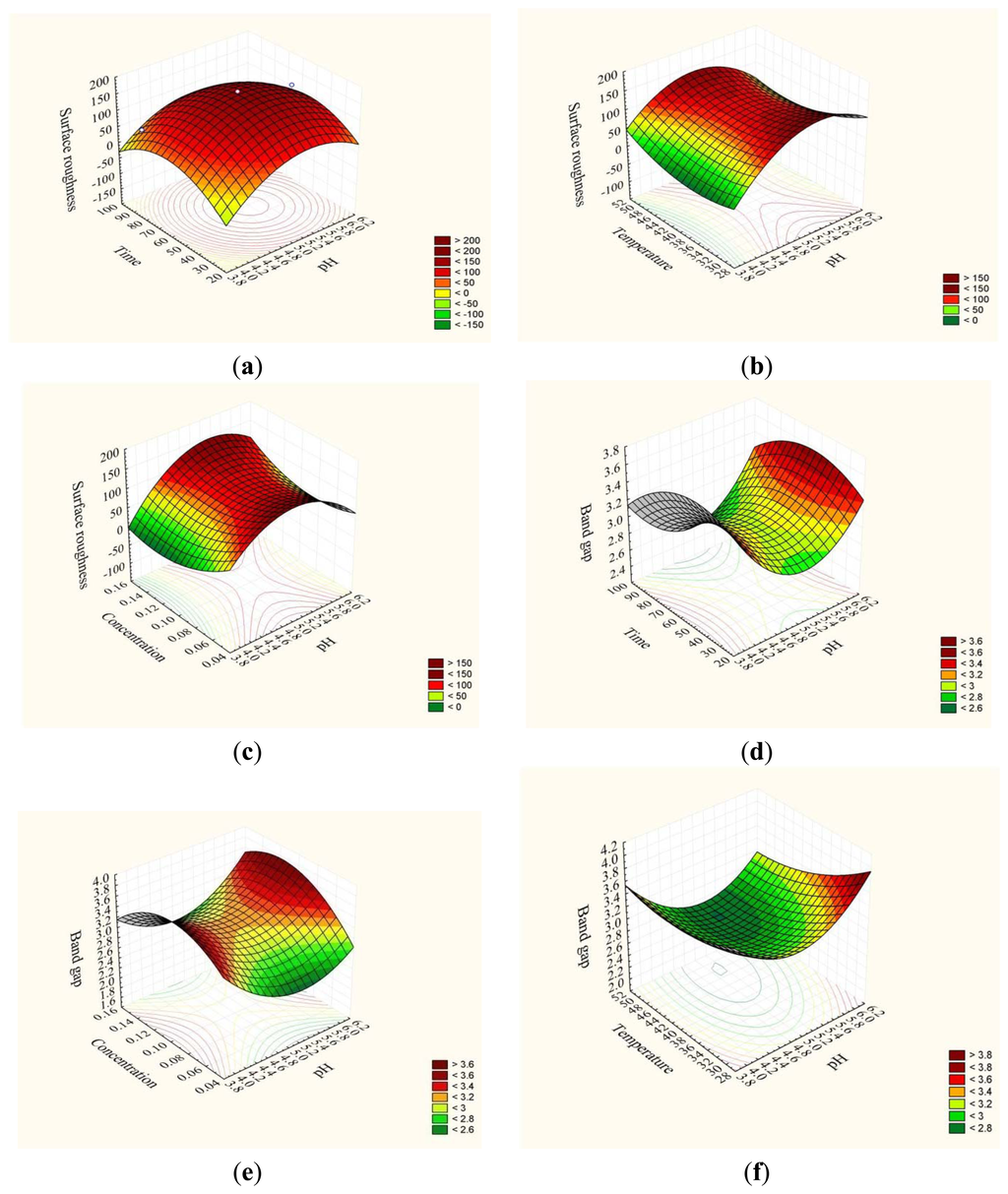
Figure 5a shows the result of the mutual interaction of pH and time with constant temperature and concentration (40 °C and 0.1 M). As shown the RMS roughness of the film increases by increasing the deposition time to 55 minute and the pH value to 5.2, since at acidic pH, the concentration of H+ ions increases in the solution (Equation (5)) and according to Le Chatelier's principle, this reduces the rate of ionization of H2O (Equation (4)) and the crystallization rate accordingly:
Thus, the nucleation occurs by multiple growths and reduces the size and surface roughness of the film:
A decrease in RMS roughness was observed above the optimum. The reduction may be due to the prolonged deposition time which destroys the film.
Figure 5b shows the interaction between pH and tin chloride concentration at constant temperature and time (40 °C and 60 min). As shown, the surface roughness decreased slightly as the concentration increased from 0.05 M to 0.1 M in the studied range of pH. The decrease in the surface roughness may be due to increasing Sn2+ ions in the reaction solution (Equation (6)) and growth centers on the substrate subsequent (Equation (7)). Further increases in concentration increased the roughness of the film. Excess Sn2+ ions would not have the opportunity to react with the OH− ions resulting in cluster growth of the film.
The same trend was observed in Figure 5c for the interaction between pH and temperature at constant concentration and time (0.1 M and 60 min). Generally, as the temperature of the system increases, the number of molecules that carry enough energy to react increases and the rate of reaction increases. Thus the rate of release of precursors and grain growth increase (Equations (4) and (6)), which improves the surface roughness. An optimum temperature point was achieved at 40 °C.
Figure 5d shows the result of the mutual interaction of pH and time with constant temperature and concentration (40 °C and 0.1 M) for the energy band gap. As shown, the energy band gap decreased with increasing pH from pH 4 to 5 over the range of deposition times. This can be related to the deposition of side products, such as SnO and Sn(OH)2 (Equations (7) and (8)) which decrease the energy band gap of the deposited SnO2 thin film. Further increases again increase the energy band gap value.
Figure 5e shows the result of the mutual interaction of pH and concentration with constant temperature and time (40 °C and 60 min) for the energy band gap. An optimum point for the energy band gap was observed at a concentration of 0.1 M in the range of studied pH values. However, a decrease in energy band gap was observed above and below the optimum.
Figure 5f shows the interaction between pH and temperature with constant concentration and time (0.1 M and 60 min). As observed, an acceptable energy band gap was obtained at lower temperatures. Any increase in the temperature resulted in a diminished energy band gap.
As a result, the optimum conditions for energy band gap and surface roughness are somewhat different. Simultaneous optimization led by the model allowed us to evaluate the optimum conditions for both responses. As a result the optimum point for energy band gap and surface roughness were 3.40 eV (average) and 50 nm under the conditions of pH of 6 and tin chloride concentration 0.14 M with 78 min of deposition time and 45 °C bath temperature. The optimum was validated by performing confirmatory experiments.
3.4. Prediction and Confirmation of Properties
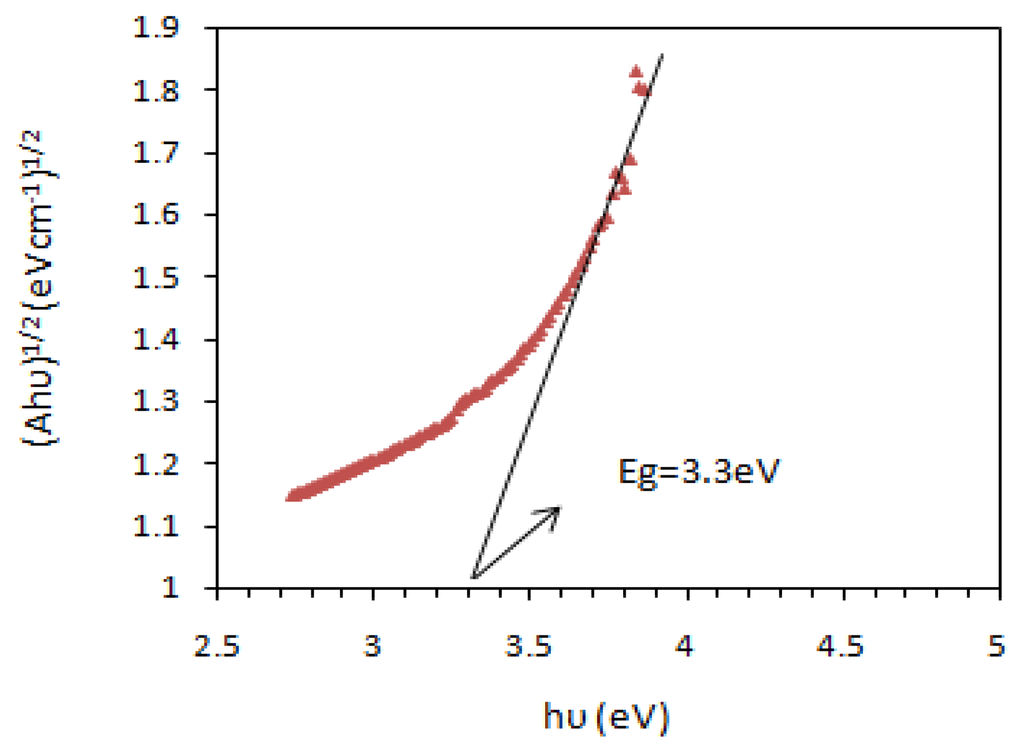
Once the optimum level of the design parameters had been selected, the final step was to predict and verify the improvement of the quality characteristic using the optimum level of the design parameters. Figures 6 and 7 show the surface morphology and energy band gap of nanocrystalline SnO2 thin film at the optimum conditions predicted by TOA. As observed, the experimental values were reasonably close to the simulated values, which indicated the high validity and adequacy of the model. The grain size of the deposited SnO2 film under the optimum conditions according to SEM observation was about 45 nm.

4. Conclusions
Nanocrystalline SnO2 thin film synthesis was optimized and modeled using a Taguchi robust design method with multiple linear regression analysis. The experiments were designed with four effective factors including concentration, pH value, and deposition time and bath temperature. To suggest a model for the deposition, the responses were fitted with a quadratic model. The ANOVA confirmed the high validity of the model as evidenced of the high F-value (20.27 and 4,112.2), non-significant lack of fit, the R2 (98.38% and 99.37%), and the adequate precision (12.57 and 170.96). The results of simulated 3D plots and predicted model for the SnO2 nanocrytalline synthesis were in agreement with the experimental results of a confirmation test. This study indicates the success of an orthogonal array to simulate the optimum condition of SnO2 nanocrytalline synthesis using the chemical bath method.
Acknowledgments
We would like to express acknowledgement with thanks to the Physic department of Faculty Science and atomic force microscopy laboratory.
Conflicts of Interest
The authors declare that there is no conflict of interest.
References
- Leem, J.W.; Yu, J.S. Physical properties of electrically conductive Sb-doped SnO2 transparent electrodes by thermal annealing dependent structural changes for photovoltaic applications. Mater. Sci. Eng. B 2011, 176, 1207–1212. [Google Scholar]
- Mason, M.G.; Hung, L.S.; Tang, C.W.; Lee, S.T. Characterization of treated indium-tin-oxide surfaces used in electroluminescent devices. J. Appl. Phys. 1999, 86, 1688. [Google Scholar]
- Bucher, E. The use of rare earths in photovoltaics. Appl. Phys. 1978, 17, 1. [Google Scholar]
- Kida, T.; Fujiyama, S.; Suematsu, K.; Yuasa, M.; Shimanoe, K. Pore and particle size control of gas sensing films using SnO2 nanoparticles synthesized by seed-mediated growth: Design of highly sensitive gas sensors. J. Phys. Chem. C 2013, 117, 17574–17582. [Google Scholar]
- Nuli, Y.N.; Zhao, S.L.; Qin, Q.Z. Nanocrystalline tin oxides and nickel oxide film anodes for Li-ion batteries. J. Power Sour. 2003, 114, 113. [Google Scholar]
- Laghrib, S.; Amardjia-Adnani, H.; Abdi, D.; Pelletier, J.M. Tin oxide thin layers obtained by vacuum evaporation of tin and annealing under oxygen flow. J. Vacuum 2008, 82, 782–788. [Google Scholar]
- Aziz, M.; Saber Abbas, S.; Wan Baharom, W.R. Size-controlled synthesis of SnO2 nanoparticles by sol-gel method. Mater. Lett. 2013, 91, 31–34. [Google Scholar]
- Szanyi, J. The origin of haze in CVD tin oxide thin films. J. Appl. Surf. Sci. 2002, 185, 161. [Google Scholar]
- Wagner, T.; Kohl, C.D.; Fröba, M.; Tiemann, M. Gas sensing properties of ordered mesoporous SnO2. J. Sens. 2006, 6, 318–323. [Google Scholar]
- Hodes, G.; Dekker, M. Chemical Solution Deposition of Semiconductor Films; CRC: New York, NY, USA, 2002. [Google Scholar]
- Thiandoume, C.; Barjonb, J.; Lusson, A.; Galtier, P.; Sallet, V. Morphology transition of one-dimensional ZnO grown by metal organic vapour phase epitaxy on (0001)-ZnO substrate. J. Cryst. Growth 2009, 311, 4311–4316. [Google Scholar]
- Salazar-Alvarez, G.; Muhammed, M.; Zagorodni, A.A. Novel flow injection synthesis of iron oxide nanoparticles with narrow size distribution. J. Chem. Eng. Sci. 2006, 61, 24625–24633. [Google Scholar]
- Montgomery, D.C. Design and Analysis of Experiments; John Wiley & Sons Inc.: New York, NY, USA, 2008. [Google Scholar]
- Chen, C.S.; Liu, K.J.; Lou, Y.H.; Shieh, C.J. Optimization of kojic acid monolaurate synthesis PS from Pseudomonas cepacia. J. Sci. Food Agric. 2002, 82, 601–605. [Google Scholar]
- Ebrahimiasl, S.; Wan Yunus, W.Z.; Kassim, A.; Zainal, Z. Synthesis of nanocrystalline SnOx (x = 1 – 2) thin film using a chemical bath deposition method with improved deposition time, temperature and pH. J. Sens. 2011, 11, 9207–9216. [Google Scholar]
- Ross, P.J. Taguchi Techniques for Quality Engineering; McGraw-Hill: New York, NY, USA, 1996. [Google Scholar]
- Li, Y.; Lu, J. Characterization of the enzymatic degradation of arabinoxylans in grist containing wheat malt using response surface methodology. J. Am. Soc. Brew. Chem. 2005, 63, 171–176. [Google Scholar]
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/3.0/).