Abstract
From an academic and practical point of view, it is desirable to be able to assess the possibility of the proton exchange of a given molecular system just by knowing the positions of the proton acceptor and the proton donor. This study addresses the difference between intramolecular hydrogen bonds in 2,2′-bipyridinium and 1,10-phenanthrolinium. Solid-state 15N NMR and model calculations show that these hydrogen bonds are weak; their energies are 25 kJ/mol and 15 kJ/mol, respectively. Neither these hydrogen bonds nor N-H stretches can be responsible for the fast reversible proton transfer observed for 2,2′-bipyridinium in a polar solvent down to 115 K. This process must have been caused by an external force, which was a fluctuating electric field present in the solution. However, these hydrogen bonds are the grain that tips the scales precisely because they are an integral part of a large system of interactions, including both intramolecular interactions and environmental influence.
1. Introduction
Non-covalent interactions make our world alive. Of particular importance, at least for biological systems, is hydrogen bonding. Among other things, this interaction is an almost indispensable initial step for the simplest molecular chemical reaction, and at the same time, the most important biological chemical reaction—the proton transfer reaction [1,2]. The rate of this reaction strongly depends on the distance between the proton acceptor and the proton donor groups, as well as on the deviation of the formed hydrogen bond from linearity. From an academic and practical point of view, it is therefore desirable to be able to assess the possibility of the proton exchange of a given molecular system with limited mobility just by knowing the position and mutual orientation of the proton acceptor and the proton donor. One of the ways to solve this problem is to study model systems for which the arrangement of these groups is similar but the characteristics of the hydrogen bond and associated proton exchange are different. 2,2′-bipyridine (BiPy) and 1,10-phenanthroline (Phen) represent a suitable model pair for such a study (Figure 1).
Figure 1.
Substances studied in this work. (a) 2,2′-bipyridine (BiPy), (b) 2,2′-bipyridinium (BiPyH+), (c) 1,10-phenanthroline (Phen), (d) 1,10-phenanthrolinium (PhenH+).
Theoretical calculations show that both the cis and trans conformers of BiPy can be present in the gas phase and solutions [3]. The trans conformer is lower in energy, and the barrier for cis/trans interconversion is small. This conformer is planar in the gas [3] and solid phases [4,5,6] but can be nonplanar in solutions [7]. When adsorbed onto silica, BiPy also adopts the trans conformation. [8]. In contrast, for 2,2′-bipyridinium (BiPyH+), its cis conformer is the low-energy one in the gas phase [3], solution [9], and the solid state [10,11,12,13,14,15,16]. This conformer is planar in the gas phase [3] and, as an exception, in the solid state in the case of non-coordinating anions [17,18,19,20,21,22,23,24,25]. The N…N distance in these structures varies from 2.611 Å [10] to 2.727 Å [23]. A detailed examination suggested that the N…N distance is determined more by the crystal packing than by the planarity of the molecule itself [25].
BiPy can be doubly protonated. In this form, its conformation tends back to the trans orientation, and the torsion angle between its rings varies from 36° to 180° [23,26].
The most stable conformation of other bipyridines often depends on intramolecular interactions [27,28]. For BiPyH+, the stabilization of the cis conformer is intuitively associated with the formation of an intramolecular hydrogen bond. In this regard, it is often compared with 1,10-phenanthrolinium (PhenH+). Indeed, the fundamental coordination [11] and proton-accepting properties of BiPy and Phen are similar.
The N…N distances in Phen and PhenH+ are about 2.71–2.74 Å [10,11,14,16,17,23,29,30]. Phen can be doubly protonated. In this form, the N…N distance is about 2.80–2.90 Å [31,32,33,34,35,36], and the planarity of the molecule can be somewhat distorted. This allows us to make the following assumptions. The molecular structure of Phen is flexible enough to accommodate intermolecular non-covalent interactions. This is evident from the possibility of the double protonation and some contraction in PhenH+.
The difference between the intramolecular hydrogen bonds in BiPyH+ and PhenH+ has been addressed in the past. The following arguments were given as proof of the presence of a strong hydrogen bond in BiPyH+. The ν(NH) stretching frequency at 10 K is 3147 cm−1, while in PhenH+, it is 3279 cm−1 [10]. A lower limit on the strength of the intramolecular hydrogen bond in BiPyH+ was placed at 63 kJ/mol [3]. A fast reversible intramolecular hydrogen bond transfer in BiPyH+ was observed in a polar solvent down to 115 K [9]. This process is consistent with the presence of a strong intramolecular hydrogen bond. However, all these arguments only do not contradict the presence of this interaction, but they do not allow us to evaluate its strength either numerically or in comparison with the hydrogen bond in PhenH+. On the other hand, the difference between the N…N distances in BiPyH+ and PhenH+ is small. If we take into account that both bonds are nonlinear, then the difference between their energies can be insignificant.
This work has the following objectives: (i) to measure the 15N NMR chemical shifts of BiPy, Phen, BiPyH+, and PhenH+ in the solid state and to compare these experimental values with theoretically calculated values to determine the correct hydrogen bond geometry in the condensed state; (ii) to estimate the energy of the intramolecular hydrogen bonds in BiPyH+ and PhenH+; (iii) to theoretically model the intramolecular proton transfer in BiPyH+ and PhenH+ to elucidate the most likely mechanism and barrier height.
2. Results and Discussion
2.1. Hydrogen Bond Geometry and Energy in BiPyH+ and PhenH+
2.1.1. Experimental 15N NMR Chemical Shifts
Figure 2 shows the 15N NMR spectra of polycrystalline samples of BiPy, Phen, BiPyH+, and PhenH+. The numerical values of the isotropic chemical shift, , are collected in Table 1. The values of BiPy and Phen were similar in the solid state and in a solution of tetrahydrofuran. There are two structurally distinct molecules in the crystal structure of Phen [29,30]. The anisotropy of the chemical shift tensors of structurally different molecules is different, which results in the difference in their and spinning sideband patterns [37].
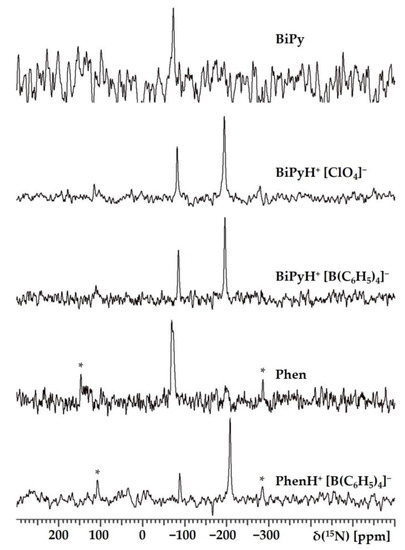
Figure 2.
5N CPMAS NMR spectra of polycrystalline samples of BiPy, Phen, BiPyH+, and PhenH+. Asterisks * denote spinning sidebands.

Table 1.
The experimental values of the isotropic 15N chemical shift.
Hydrogen bonding significantly affects the of pyridines [38]. For symmetrically substituted pyridines, there is a functional dependence between the change in the and the value of the N…H distance [39]. This dependence was successfully used in the past to study the geometry of hydrogen bonds in complex molecular systems [40,41,42]. The maximal difference between the free and protonated forms is approximately the same for all pyridine derivatives and is 125 ppm [43].
The changes observed for BiPy and BiPyH+, as well as for Phen and PhenH+, are completely consistent with the expected changes (Table 1). The of the protonated nitrogen shifted to −200 ppm, while for the other, it changed by only −10 ppm. However, neither for BiPyH+ nor for PhenH+ could these changes be converted into the numerical values of the N-H and H…N distances using the mentioned dependence. The reasons for this limitation are as follows. (i) This dependence was established for linear hydrogen bonds. In BiPyH+ and PhenH+, these bonds are highly bent. (ii) The conformations of BiPy and BiPyH+ are different. (iii) In PhenH+, the electron densities in the two conjugated pyridine rings cannot be considered independent. It is not known how these effects affect the values of the respective . The geometry of the hydrogen bonds in these structures will have to be determined using theoretical calculations.
2.1.2. Calculated 15N NMR Chemical Shifts
Non-covalent interactions cause changes in chemical shifts [44,45]. For solids, the theoretical evaluation of these changes requires either using the GIPAW approach [46,47,48] or fragment-based calculations [46,49,50]. Such calculations require knowledge of the exact crystal structure, which is not always available [51]. However, in many cases, the influence of intermolecular interactions is small, and the required accuracy is achieved using simple adducts or single-molecule calculations [52,53,54].
Figure 3 shows the notations for the selected distances and angles used in this work. The calculated structures discussed below are named S_FB_W_ωM. S stands for the structure. F and B stand for the DFT functional and the basis set used for geometry optimization. F = ω or T for ωB97XD and TPSSh. B = t or q for def2tzvp and def2qzvp. W stands for geometries optimized with the polarizable continuum model approximation (PCM) using SCRF=(Solvent=water). ω and M stand for the DFT functional (ωB97XD) and the basis set used for GIAO NMR calculations, M = t or q or S for def2tzvp, def2qzvp, and pcSseg-3.
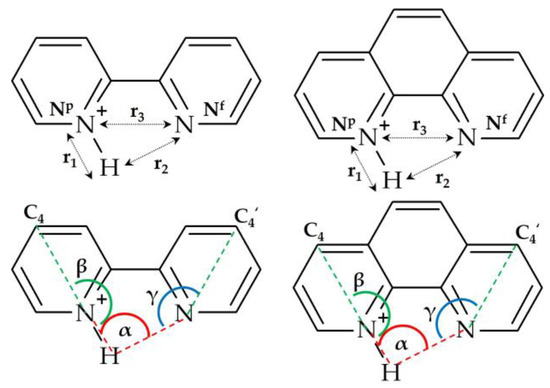
Figure 3.
The notations for the selected distances and angles used in this work.
The structure BiPy_Tq_W_ωt was optimized using the TPSSh/def2qzvp approximation and SCRF=(Solvent=water). The values were calculated using the ωB97XD/def2qzvp approximation and SCRF=(Solvent=water). The selected geometric and NMR parameters for this structure are reported in Table 2. The numerical values of these parameters depend on the approximation used for geometry optimization but not on the approximation used for the NMR calculations; see the structures BiPy_Tq_W_ωq, BiPy_ωq_W_ωt, and BiPy_ωq_W_ωq. The values obtained for all these structures agree with the experimental values reported in Table 1. Therefore, the choice of the preferred approximation is a matter of taste.

Table 2.
Calculated geometries and for the selected structures of BiPy and BiPyH+.
BiPycis_Tq_W_ωt corresponded to the cis form of BiPy, which is a higher-energy stable structure. The of this structure is somewhat different. Therefore, the functional dependence of the
on the N…H distance found for pyridines [39] cannot be used for BiPy since it is not clear whether the chemical shift of the cis or trans conformer corresponds to the limit .
BiPyH+_Tq_W_ωt is the optimized structure of BiPyH+. BiPyHClO4_Tq_W_ωt is a structure in which the positions of all atoms, except for hydrogen atoms, were taken from the experimental XRD structure of BiPyH+ [ClO4]−, while the hydrogen positions were optimized using the TPSSh/def2qzvp approximation and SCRF=(Solvent=water). ZUTDAT_Tq_W_ωt and ZUTDAT01_Tq_W_ωt were constructed in the same way using the experimental XRD structure of BiPyH+ [B(C6H5)4]− listed in the Cambridge Structural Database under ID ZUTDAT [10] and ZUTDAT01 [55]. A comparison of the values for these structures suggests that they do not correlate unambiguously with the r1 and r2 distances. Of course, what is meant is not the obvious difference in the and , but the variation in these values for different structures. These differences cannot be unambiguously attributed to the influence of the intramolecular hydrogen bond. Rather, they arose from differences in the geometries of these structures. On the other hand, protonation led to a significant decrease in the r3 compared to BiPycis_Tq_W_ωt.
It is not a priori obvious which basis set is required for the correct computation of the of Phen. Three basis sets were used to calculate the of Phen structures optimized using the TPSSh/def2qzvp approximation and SCRF=(Solvent=water): Phen_Tq_W_ωt, Phen_Tq_W_ωq, and Phen_Tq_W_ωS (Table 3). All the basis sets gave the same value. OPENAN_Tt_W_ωt and OPENAN01_Tt_W_ωt are structures in which the positions of all atoms, except for hydrogen atoms, were taken from the experimental XRD structures of Phen listed in the Cambridge Structural Database under ID OPENAN [29] and OPENAN01 [30], while the hydrogen positions were optimized using the TPSSh/def2qzvp approximation and SCRF=(Solvent=water). There are two structurally distinct molecules in these crystal structures that have different . The r3 distances in the solid state were less than the calculated one. The calculated values of the approximately coincide, agree with the experimental values, and do not correlate with the r3.

Table 3.
Calculated geometries and for the selected structures of Phen and PhenH+.
Protonation resulted in a shortening of the r3 distance. PhenH+_Tq_W_ωt corresponded to the optimized structure of PhenH+. ZUTDEX_Tq_W_ωt was constructed from the experimental XRD structure of PhenH+ [B(C6H5)4]− listed in the Cambridge Structural Database under ID ZUTDEX [10] in the same manner as described above. The calculated values of are similar and agree with the experimental values (Table 1).
The first objective of this work was achieved. The experimental and calculated values of the for BiPyH+ and PhenH+ agree quite well. Therefore, the calculated geometries of their intramolecular hydrogen bonds are reliable. Protonation resulted in a shortening of the r3 in both species. Although these distances are comparable to the shortest N…N distance measured for the proton-bound homodimers of the pyridines of 2.62 Å [56,57], the intramolecular hydrogen bonds in BiPyH+ and PhenH+ are strongly bent. Their lengths should be calculated as r1 + r2, which gives about 3.08 Å and 3.28 Å, respectively. The difference between the in BiPy and Phen and the of the N-H nitrogens in BiPyH+ and PhenH+ is greater than 120 ppm, the value expected for an uncoordinated pyridinium [43]. Therefore, both the geometries and indicate that these hydrogen bonds are weak.
2.1.3. Hydrogen Bond Energy
What is the energy of the intramolecular hydrogen bonds in BiPyH+ and PhenH+? Given the chemical similarity of these cations to the proton-bound homodimer of pyridine (PyHPy+), this energy can be estimated using simplified model calculations. Figure 4a shows the structure of PyHPy+. This complex has been studied in detail in the past [56,57,58,59,60,61,62,63,64,65]. Its hydrogen bond is moderately strong, it is of the asymmetric N-H…N type and exhibits fast reversible proton transfer in solution. Let us define the energy of the hydrogen bond in PyHPy+, ΔE, as the difference between the electronic energy of PyHPy+ for a given distance, r2, and the sum of the electronic energies of pyridine and pyridinium. At the ωB97XD/def2tzvp approximation and SCRF=(Solvent=water), ΔE is minimal at r2 = 1.645433 Å. This distance is longer than the experimental value of 1.532 Å [57]. The reason for this has been explained elsewhere [66,67]. As the r2 increases, the ΔE increases and tends asymptotically to zero (Figure 4b). The numerical values are collected in Table S1 in the Supporting Information.
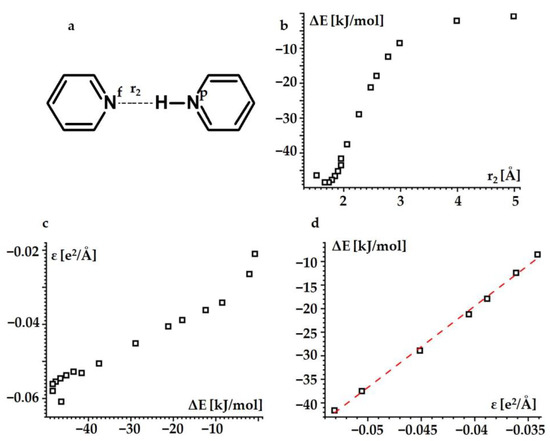
Figure 4.
The hydrogen bond energy of PyHPy+ estimated at the ωB97XD/def2tzvp approximation and SCRF=(Solvent=water). (a) The structure of PyHPy+. (b) The hydrogen bond energy ΔE as a function of r2. (c) The electric potential energy ε associated with the Nf…H interaction as a function of ΔE. (d) The range of the linear dependence between ΔE and ε.
For a large r2, one can expect that the binding energy of the hydrogen-bonded pyridine-Np-H…Nf-pyridine cation is defined by the electric force between the charges located at the Nf nitrogen and the binding proton. As an approximate numerical estimate of these charges, one can use the Mulliken charges of the Nf nitrogen q(Nf) and the binding proton q(H)。 The electric potential energy associated with this interaction is , where q(H) and q(Nf) are in units of the elementary charge e. Figure 4c shows ε as a function of the ΔE. For ΔE values between −41.6 kJ/mol and −8.5 kJ/mol, i.e., for r2 values between 1.95 Å and 3.0 Å, a linear dependence between the ε and ΔE is evident. Thus, for this interval of the r2 distances, the above assumption is correct. This dependence is , where the ΔE is in kJ/mol and the ε in e2/Å (Figure 4d). (Of course, the energy of such hydrogen bonds can alternatively be defined as ε. In this case, however, there is ambiguity in the choice of the value of the relative permittivity, which requires additional assumptions that are difficult to justify.)
For the other approximations, the linearity of the dependence was preserved, but the numerical values of the coefficients changed. For the TPSSh/def2qzvp approximation, (Table S2). For the /def2qzvp approximation, (Table S3).
In BiPyH+ and PhenH+, the r2 was in the range pf 2.0–2.3 Å. Thus, the obtained dependences could be used to estimate the hydrogen bond energy in these cations. The numerical values of ΔE varied depending on the basis set but were the same for the TPSSh and ωB97XD DFT functionals (Table 4). Consequently, the energy values of the intramolecular hydrogen bonds in BiPyH+ and PhenH+ were about 25 kJ/mol and 15 kJ/mol, respectively.

Table 4.
The r2 and r3 distances, the Mulliken charges of the binding proton (q(H)) and the Nf nitrogen (q(Nf)), the electric potential energy , and the hydrogen bond energy ΔE in BiPyH+ and PhenH+ estimated at various approximations and SCRF=(Solvent=water).
2.2. Intramolecular Proton Transfer in BiPyH+ and PhenH+
Proton Transfer Pathway
This section discusses the theoretically modeled intramolecular proton transfer pathway in BiPyH+ and PhenH+. Since the exact numerical values of the considered geometric and energetic parameters are not the subject of this analysis, these calculations were carried out without using the PCM approximation. The proton transfer pathway was modeled as follows. The geometries of BiPyH+ and PhenH+ were optimized using the ωB97XD/def2tzvp approximation. Then, the r1 distance was increased stepwise, and for each of the selected r1 distances, the geometry was optimized again. The final structure, referred to below as a symmetric structure, corresponds to equal r1 and r2 distances. Thus, this model describes the case of proton transfer due to the gradual strengthening of the intramolecular hydrogen bond, in which the geometry of the molecule has time to adapt to this change. The resulting numerical values are reported in Tables S4 and S5.
Figure 5 shows the changes in the selected geometric parameters caused by such proton transfer. These changes are presented as functions of the proton coordinate q1 = ½(r1 − r2). The decrease in q1 caused a contraction of r3 (Figure 5a). The trends of these changes were the same for BiPyH+ and PhenH+, although, in the latter, the r3 was always longer by at least 0.05 Å. The changes in the angles α, β, and γ were the same as well (Figure 5b). Strengthening the hydrogen bond made it more linear, that is, the angle α increased. The convergence of the angles β and γ for a flexible BiPyH+ occurred smoothly. On the contrary, for a rigid PhenH+, the last step to q1 = 0 caused a saltatory change in these angles.
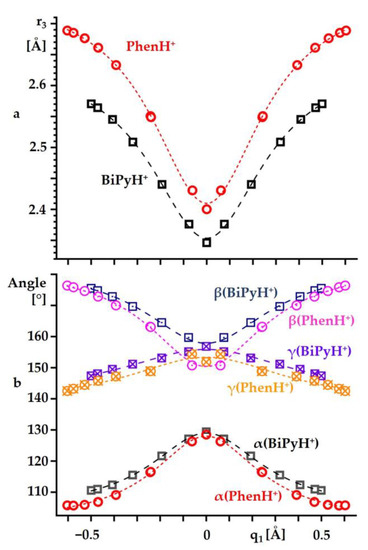
Figure 5.
The changes in the r3 (a) and selected angles (b) caused by the intramolecular proton transfer in BiPyH+ and PhenH+ as functions of the proton coordinate q1 = ½(r1 − r2). Curves describe a trend and serve as a guide for the eyes.
Figure 6 shows the changes in the heavy atom hydrogen bond coordinate q2 = r1 + r2 and the energy values of BiPyH+ and PhenH+ caused by such a proton transfer. As with any other known hydrogen bonds, the decrease in q1 caused a contraction of q2 [68,69,70] (Figure 6a). However, there was also a difference between the BiPyH+ and PhenH+. For a large q1, the q2 changed abnormally in PhenH+ and somewhat increased with a decreasing q1. This fact can be interpreted as an indication that, near the optimal geometry, the intramolecular hydrogen bond in PhenH+ is weak and small changes in its geometry do not significantly affect the geometry of this rigid structure. On the contrary, in the limit of the strong hydrogen bonding at q1 = 0, this bond was only slightly weaker than in BiPyH+. Near the optimal geometry, a small increase in the r1 did not cause a significant energy increase (Figure 6b). However, then the energy rapidly increased in an inverse proportion to q1. For PhenH+, this growth was much steeper than for BiPyH+. As a result, the energies of the symmetric structures at q1 = 0 were 41 kJ/mol and 72 kJ/mol higher than the energies of the lowest energy structures of BiPyH+ and PhenH+, respectively.
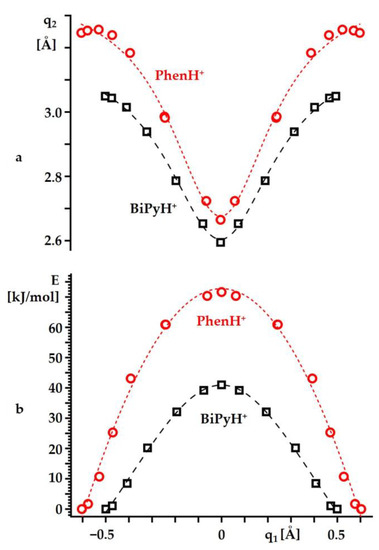
Figure 6.
The changes in the heavy atom hydrogen bond coordinate q2 = r1 + r2 (a) and the energy (b) caused by the proton transfer in BiPyH+ and PhenH+ as functions of q1 = ½(r1 − r2). Curves describe a trend and serve as a guide for the eyes.
The energy required for the proton transfer, calculated above, is quite large. How much will this energy change if the polarity of the solvent is taken into account, SCRF=(Solvent=water)? The geometries of the lowest energy structures and the symmetric structures at q1 = 0 of BiPyH+ and PhenH+ changed somewhat in this approximation (Tables S6 and S7). Their energy differences increased to 51 kJ/mol and 82 kJ/mol for BiPyH+ and PhenH+, respectively.
To obtain a more realistic estimate of the energy required for the proton transfer, the calculation procedure was changed. The geometries were optimized using the ωB97XD/def2tzvp approximation and SCRF=(Solvent=water). Then, the r3 distance was decreased stepwise, and for each of the selected r3 distances, the geometry was optimized. The final structure corresponded to equal r1 and r2 distances. For all these structures, the Np-H stretches were calculated (Table S8). Thus, this model describes the case of proton transfer in which the movement of the proton is much faster than the ongoing changes in the r3 distance and reduces the multi-dimensional potential energy problem [71,72,73] to a one-dimensional one. The only structure with a negative frequency is the structure with the equal r1 and r2 distances. Thus, these calculations show that no intramolecular vibrations can be the cause of the fast reversible proton transfer observed in BiPyH+ in the experiment [9]. This process must be caused by external forces.
3. Materials and Methods
Solid-state 15N NMR measurements were performed on an Infinityplus spectrometer system (Varian Inc., Palo Alto, CA, USA) operated at 7 T and equipped with a Chemagnetics 6 mm pencil CPMAS probe. The 15N{1H} MAS CP NMR spectra were recorded using a 90°−pulse length of 5.0 μsec, a cross-polarization contact time of 15 ms, and relaxation delays of 5–20 s. The spectra were indirectly referenced to CH3NO2 [74] using solid 15NH4Cl (δ = −341.3 ppm [75]). To convert these values to the liquid ammonia scale, add 380.6 ppm to them [75].
The Gaussian 09.D.01 program package was used for geometry optimizations and NMR calculations [76]. The TPSSh and ωB97XD DFT hybrid functionals [77,78] and the def2tzvp, def2qzvp, and pcSseg-3 basis sets were used [79,80,81]. The geometry optimization was performed at the very tight convergence criteria. The NMR calculations were carried out using the GIAO approach. Some calculations were performed using the PCM approximation with water as the solvent [82]. This choice is arbitrary. The outcomes of the PCM approximation are not very sensitive to the value of the dielectric constant [83]. However, this correction is necessary to consider the effect of the crystal field.
To convert the 15N NMR absolute shielding values σ obtained in the theoretical calculations into the chemical shift scale δ used in the experiments, it was necessary to know the reference 15N absolute chemical shielding ref: [84,85]. The numerical value of ref depends on the approximation used to calculate σ [86]. The calculated chemical shifts reported in this work were derived from the calculated absolute shielding values using the following values of ref: 143 ppm, 148 ppm, and 153 ppm [86]. The applicability of this approach was previously confirmed for 31P NMR [54,87,88].
Crystalline BiPyH+ [ClO4]− was obtained from a solution of 2,2′-bipyridine in tetrahydrofuran by adding 70% HClO4. The precipitate was filtered off and recrystallized either from acetonitrile or from nitromethane. X−ray diffraction data for single crystals of BiPyH+ [ClO4]− were collected by Rigaku Oxford Diffraction SuperNova diffractometers (Tables S9 and S10, Applied Rigaku Technologies, Inc., Austin, TX, USA). The crystals were kept at 123.0 K during the data collection. The structures were solved with the ShelXT 2018/2 [89] solution program using dual methods and Olex2 1.5-alpha [90] as the graphical interface. The model was refined with Olex2.refine 1.5-alpha [91] using full matrix least squares minimization on F2. The structures have been deposited at the Cambridge Crystallographic Data Centre (CCDC) with numbers 2266914 and 2266916. The atomic coordinates of the BiPyHClO4_Tq_W, ZUTDAT_Tq_W, ZUTDAT01_Tq_W, OPENAN_Tt_W, OPENAN01_Tt_W, and ZUTDEX_Tq_W structures are available in Tables S11–S16.
Polycrystalline BiPyH+ [B(C6H5)4]− and PhenH+ [B(C6H5)4]− were obtained from a solution of BiPy or Phen in methanol by adding 37% HCl and NaB(C6H5)4. The precipitate was filtered off and washed with water.
4. Conclusions
This study had three objectives. First, it aimed to measure the 15N NMR chemical shifts of BiPy, Phen, BiPyH+, and PhenH+ in the solid state and to compare these experimental values with theoretically calculated values to determine the correct hydrogen bond geometry in the condensed state. These measurements and calculations show equal results. Thus, the calculated geometries were similar to those of the solid state.
The second objective was to estimate the energy of the intramolecular hydrogen bond in BiPyH+ and PhenH+. The model calculations provided for the energy of these interactions were 25 kJ/mol and 15 kJ/mol, respectively. The nature of these hydrogen bonds is purely electrostatic. It would be instructive to make an independent estimate of these energies using the experimental electron density distribution function [92,93,94,95,96].
The final objective was to model the intramolecular proton transfer in BiPyH+ and PhenH+. The analysis showed that neither these interactions nor N-H stretches could be responsible for the fast reversible proton transfer observed for BiPyH+ in a polar solvent down to 115 K. The electrostatic interaction between the mobile proton and the second nitrogen atom was a guide for the transfer, but it was too weak to overcome the transfer barrier. This process was controlled by an external force. This force was a fluctuating electric field present in the solution. Its effects and amplitude have been evaluated in the past for several molecular adducts [66,83,88,97,98]. However, the influence of this field on proton transfer can only be modeled if the transfer occurs along the symmetry axis of the adduct under consideration. Neither BiPyH+ nor PhenH+ has such an axis.
The particular results obtained for the examples of BiPyH+ and PhenH+ allow us to draw the following general conclusion. The hydrogen bonds under discussion are weak. By themselves, they could not have a significant effect on the properties of these molecules. However, these bonds are an integral part of a large system of interactions, which includes both intramolecular interactions and the influence of the environment. Within the framework of such a system, they become the grain that tips the scales.
Supplementary Materials
The supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/ijms241210390/s1.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Hynes, J.T.; Klinman, J.P.; Limbach, H.-H.; Schowen, R.L. Hydrogen-Transfer Reachtions; WILEY-VCH Verlag: Weinheim, Germany, 2007. [Google Scholar]
- Kohen, A.; Limbach, H.-H. Isotope Effects in Chemistry and Biology; CRC Press: Boca Raton, FL, USA, 2006. [Google Scholar]
- Howard, S.T. Conformers, Energetics, and Basicity of 2,2‘-Bipyridine. J. Am. Chem. Soc. 1996, 118, 10269–10274. [Google Scholar] [CrossRef]
- Merritt, L.L., Jr.; Schroeder, E.D. The crystal structure of 2,2′-bipyridine. Acta Crystallogr. 1956, 9, 801–804. [Google Scholar] [CrossRef]
- Chisholm, M.H.; Huffman, J.C.; Rothwell, I.P.; Bradley, P.G.; Kress, N.; Woodruff, W.H. Bis(2,2′-bipyridyl)diisopropoxymolybdenum(II). Structural and Spectroscopic Evidence for Molybdenum-to-Bipyridyl π* Bonding. J. Am. Chem. Soc. 1981, 103, 4945–4947. [Google Scholar] [CrossRef]
- Kühn, F.E.; Groarke, M.; Bencze, E.; Herdtweck, E.; Prazeres, A.; Santos, A.M.; Calhorda, M.J.; Romão, C.C.; Gonçalves, I.S.; Lopes, A.D.; et al. Octahedral Bipyridine and Bipyrimidine Dioxomolybdenum(vi) Complexes:Characterization, Application in Catalytic Epoxidation, and DensityFunctional Mechanistic Study. Chem. Eur. J. 2002, 8, 2370–2383. [Google Scholar] [CrossRef] [PubMed]
- Cheng, C.L.; Murthy, D.S.N.; Ritchie, G.L.D. Molecular conformations from magnetic anisotropies. J. Chem. Soc. Faraday Trans. 1972, 68, 1679–1690. [Google Scholar] [CrossRef]
- Lesnichin, S.B.; Kamdem, N.; Mauder, D.; Denisov, G.S.; Shenderovich, I.G. Studies of Adsorption of 2,2′-Bipyridyl on the Surface of Highly Regulated Silica Matrix of the MCM-41 Type by Means of 15N NMR Spectroscopy. Russ. J. Gen. Chem. 2010, 80, 2027–2031. [Google Scholar] [CrossRef]
- Lesnichin, S.B.; Tolstoy, P.M.; Limbach, H.-H.; Shenderovich, I.G. Counteranion-Dependent Mechanisms of Intramolecular Proton Transfer in Aprotic Solution. Phys. Chem. Chem. Phys. 2010, 12, 10373–10379. [Google Scholar] [CrossRef]
- Bakshi, P.K.; Cameron, T.S.; Knop, O. Crystal chemistry of tetraradial species. Part 8. Mix and match: Cation geometry, ion packing, hydrogen bonding, and π–π interactions in cis-2,2′-bipyridinium(1+) and 1,10-phenanthrolinium(1+) tetraphenylborates—And what about proton sponges? Can. J. Chem. 1996, 74, 201–220. [Google Scholar] [CrossRef]
- Schone, S.; Radoske, T.; Marz, J.; Stumpf, T.; Ikeda-Ohno, A. Synthesis and Characterization of Heterometallic Iron–Uranium Complexes with a Bidentate N-Donor Ligand (2,2′-Bipyridine or 1,10-Phenanthroline). Inorg. Chem. 2018, 57, 13318–13329. [Google Scholar] [CrossRef]
- Kavitha, S.J.; Panchanatheswaran, K.; Low, N.J.; Glidewell, C. 2-(2-Pyridyl)pyridinium perchlorate, redetermined at 120 K: Complex hydrogen-bonded sheets. Acta Crystallogr. Sect. C Cryst. Struct. Commun. 2005, 61, o473–o474. [Google Scholar] [CrossRef]
- Kadarkaraisamy, M.; Engelhart, D.P.; Basa, P.N.; Sykes, A.G. Hexafluorophosphate salts of bis and tetrakis(2,2′-bipyridine)lead(II) complexes. J. Coord. Chem. 2010, 63, 2261–2267. [Google Scholar] [CrossRef]
- Milani, B.; Anzilutti, A.; Vicentini, L.; Sessanta o Santi, A.; Zangrando, E.; Geremia, S.; Mestroni, G. Bis-Chelated Palladium(II) Complexes with Nitrogen-Donor Chelating Ligands Are Efficient Catalyst Precursors for the CO/Styrene Copolymerization Reaction. Organometallics 1997, 16, 5064–5075. [Google Scholar] [CrossRef]
- Kraus, F.; Breu, J. Arene-arene stacking in the revised structure of 2,2′-bipyridinium hexafluorophosphate. Acta Crystallogr. Sect. C Cryst. Struct. Commun. 2002, 58, o254–o256. [Google Scholar] [CrossRef] [PubMed]
- Yoshikawa, N.; Yamazaki, S.; Kato, N.; Kubota, A.; Sawai, M.; Noda, K.; Kanehisa, N.; Inoue, T.; Nakata, E.; Takashima, H. Syntheses, X-Ray Crystal Structures, Emission Properties and DFT Calculations of Monoprotonated Polypyridines. Chem. Sel. 2019, 4, 59–65. [Google Scholar] [CrossRef]
- Buttery, J.H.; Effendy; Junk,, P.C.; Mutrofin, S.; Skelton, B.W.; Whitaker, C.R.; White, A.H. The Structural Systematics of Protonation of Some Important Nitrogen-base Ligands. IV. Some Ethane-1,2-diaminium Univalent Anion Salt/1,10-Phenanthroline (Hydrate) Arrays. Z. Anorg. Allg. Chem. 2006, 632, 1326–1339. [Google Scholar] [CrossRef]
- Jagan, R.; Sathya, D.; Sivakumar, K. A dihydrogen phosphate anionic network as a host lattice for cations in 1-methyl piperazine-1,4-diium bis (di hydrogen phosphate) and 2-(pyridin-2-yl)pyridinium di hydrogen phosphate-ortho phosphoric acid (1/1). Acta Crystallogr. Sect. C Cryst. Struct. Chem. 2015, 71, 374–380. [Google Scholar] [CrossRef]
- Ivanova, B.; Spiteller, M. On the chemical identification and determination of flavonoids in solid-state. Talanta 2012, 94, 9–21. [Google Scholar] [CrossRef]
- Charushnikova, I.A.; Den Auwer, C. 2,2′-Bipyridyl-2-ium aqua(2,2′-bipyridyl-κ2N,N’)-tetakis-(nitrato-κ2O,O’) -praseodymium(III) 2,2′-bipyridyl hemisolvate. Acta Crystallogr. Sect. E Struct. Rep. Online 2004, 60, m1775–m1777. [Google Scholar] [CrossRef]
- Thuery, P. Sulfonate Complexes of Actinide Ions: Structural Diversity in Uranyl Complexes with 2-Sulfobenzoate. Inorg. Chem. 2013, 52, 435–447. [Google Scholar] [CrossRef]
- Mrvos-Sermek, D.; Popovic, Z.; Matkovic-Calogovic, D. Hydrogen Bonding in the 2,2′-Bipyridinium Salt of 1,2,4,5-Benzenetetracarboxylic Acid (Pyromellitic Acid). Acta Crystallogr. Sect. C Cryst. Struct. Commun. 1996, 52, 2538–2541. [Google Scholar] [CrossRef]
- Thuery, P. 2,2′-Bipyridine and 1,10-Phenanthroline as Coligands or Structure-Directing Agents in Uranyl–Organic Assemblies with Polycarboxylic Acids. Eur. J. Inorg. Chem. 2013, 2013, 4563–4573. [Google Scholar] [CrossRef]
- Jurowska, A.; Szklarzewicz, J.; Basta, N.; Hodorowicz, M. Structural and physicochemical characterization of ion-pair salts with dipyridyl cations and [Fe(CN)6]4− and [Fe(CN)5(NO)]2− anions. Inorg. Chim. Acta 2022, 539, 121033. [Google Scholar] [CrossRef]
- Balabanova, S.P.; Buikin, P.A.; Ilyukhin, A.B.; Rudenko, A.Y.; Dorovatovskii, P.V.; Korlyukov, A.A.; Kotov, V.Y. Crystal Structure and Optical Properties of New Hybrid Halobismuthates of 2,2′-Bipyridinium Derivatives. Russ. J. Inorg. Chem. 2022, 67, 1018–1024. [Google Scholar] [CrossRef]
- Jurowska, A.; Szklarzewicz, J.; Hodorowicz, M. Ion pair charge-transfer salts based on protonated bipyridines and [W(CN)6(bpy)]2− anion-structure and properties. J. Mol. Struct. 2022, 1261, 132931. [Google Scholar] [CrossRef]
- Summers, L.A. The Bipyridines. Adv. Heterocycl. Chem. 1984, 35, 281–374. [Google Scholar] [CrossRef]
- Vogler, A.; Shenderovich, I.G. Photochemistry of deprotonated rhenium(I) (3,3′-dihydroxy-2,2′-bipyridine) tricarbonyl chloride. Photoisomerization at the chelate in basic solution. Inorg. Chim. Acta 2014, 421, 496–499. [Google Scholar] [CrossRef]
- Nishigaki, S.; Yoshioka, H.; Nakatsu, K. The crystal and molecular structure of o-phenanthroline. Acta Crystallogr. Sect. B Struct. Crystallogr. Cryst. Chem. 1978, 34, 875–879. [Google Scholar] [CrossRef]
- Gembicky, M. The Cambridge Structural Database Communication ID OPENAN01. University of Buffalo: Buffalo, NY, USA, 2020. [Google Scholar]
- Rojas, Y.; Tadrosse, M.; Assaf, C.; Bernal, I.; Lalancette, R.A. Preparation and structural studies of manganese polychloride anions in three metal charge states [(II), (III), (IV)]—Their stereochemistries. Struct. Chem. 2020, 31, 1309–1316. [Google Scholar] [CrossRef]
- Oswald, I.W.H.; Ahn, H.; Neilson, J.R. Influence of organic cation planarity on structural templating in hybrid metal-halides. Dalton Trans. 2019, 48, 16340–16349. [Google Scholar] [CrossRef]
- Gel’mbol’dt, V.O.; Anisimov, V.Y.; Fonar’, M.S. Interaction between hydrofluorosilicic acid and 1,10-phenanthroline: Hydrolytic stability of chelate complexes of silicon tetrafluoride with bidentate N-donors. Russ. J. Inorg. Chem. 2016, 61, 822–825. [Google Scholar] [CrossRef]
- Ma, G.; Ilyukhin, A.; Glaser, J. 2,2′-Bipyridinium bis(perchlorate). Acta Crystallogr. Sect. C Cryst. Struct. Chem. 2000, C56, 1473–1475. [Google Scholar] [CrossRef] [PubMed]
- Bujak, M.; Frank, W. Crystal structure of 1,10-phenanthrolindiium bis(triiodide) monohydrate, C12H12I6N2O. Z. Kristallogr. -New Cryst. Struct. 2014, 229, 379–380. [Google Scholar] [CrossRef]
- Li, F.; Yin, H.; Simpson, J. catena-Poly[1,10-phen anthroline-1,10-diium [[dichlorido bismuthate(III)]-di-μ-chlorido]]. Acta Crystallogr. Sect. E Struct. Rep. Online 2007, 63, m1746. [Google Scholar] [CrossRef]
- Pelties, S.; Maier, T.; Herrmann, D.; de Bruin, B.; Rebreyend, C.; Gärtner, S.; Shenderovich, I.G.; Wolf, R. Selective P4 Activation by a Highly Reduced Cobaltate: Synthesis of Dicobalt Tetraphosphido Complexes. Chem. Eur. J. 2017, 23, 6094–6102. [Google Scholar] [CrossRef] [PubMed]
- Solum, M.S.; Altmann, K.L.; Strohmeier, M.; Berges, D.A.; Zhang, Y.; Facelli, J.C.; Pugmire, R.J.; Grant, D.M. 15N Chemical Shift Principal Values in Nitrogen Heterocycles. J. Am. Chem. Soc. 1997, 119, 9804–9809. [Google Scholar] [CrossRef]
- Lorente, P.; Shenderovich, I.G.; Golubev, N.S.; Denisov, G.S.; Buntkowsky, G.; Limbach, H.-H. 1H/15N NMR Chemical Shielding, Dipolar 15N, 2H Coupling and Hydrogen Bond Geometry Correlations in a Novel Series of Hydrogen-Bonded Acid–Base Complexes of Collidine with Carboxylic Acids. Magn. Reson. Chem. 2001, 39, S18–S29. [Google Scholar] [CrossRef]
- Brilmayer, R.; Brodrecht, M.; Kaiser, C.; Breitzke, H.; Kumari, B.; Wachtveitl, J.; Buntkowsky, G.; Andrieu-Brunsen, A. The Interplay of Nanoconfinement and pH from the Perspective of a Dye-Reporter Molecule. ChemNanoMat 2020, 6, 1843–1853. [Google Scholar] [CrossRef]
- Sharif, S.; Denisov, G.S.; Toney, M.D.; Limbach, H.-H. NMR Studies of Solvent-Assisted Proton Transfer in a Biologically Relevant Schiff Base: Toward a Distinction of Geometric and Equilibrium H-Bond Isotope Effects. J. Am. Chem. Soc. 2006, 128, 3375–3387. [Google Scholar] [CrossRef]
- Tupikina, E.Y.; Sigalov, M.V.; Tolstoy, P.M. Simultaneous Estimation of Two Coupled Hydrogen Bond Geometries from Pairs of Entangled NMR Parameters: The Test Case of 4-Hydroxypyridine Anion. Molecules 2022, 27, 3923. [Google Scholar] [CrossRef]
- Andreeva, D.V.; Ip, B.; Gurinov, A.A.; Tolstoy, P.M.; Shenderovich, I.G.; Limbach, H.-H. Geometrical Features of Hydrogen Bonded Complexes Involving Sterically Hindered Pyridines. J. Phys. Chem. A 2006, 110, 10872–10879. [Google Scholar] [CrossRef]
- Li, Z.J.; Abramov, Y.; Bordner, J.; Leonard, J.; Medek, A.; Trask, A.V. Solid-State Acid−Base Interactions in Complexes of Heterocyclic Bases with Dicarboxylic Acids: Crystallography, Hydrogen Bond Analysis, and 15N NMR Spectroscopy. J. Am. Chem. Soc. 2006, 128, 8199–8210. [Google Scholar] [CrossRef] [PubMed]
- Gorobets, N.; Yermolayev, S.A.; Gurley, T.; Gurinov, A.A.; Tolstoy, P.M.; Shenderovich, I.G.; Leadbeater, N.E. Difference between 1H NMR signals of primary amide protons as a simple spectral index of the amide intramolecular hydrogen bond strength. J. Phys. Org. Chem. 2012, 25, 287–295. [Google Scholar] [CrossRef]
- Hartman, J.D.; Harper, J.K. Improving the accuracy of GIPAW chemical shielding calculations with cluster and fragment corrections. Solid State Nucl. Magn. Reson. 2022, 122, 101832. [Google Scholar] [CrossRef]
- Stevens, J.S.; Byard, S.J.; Seaton, C.C.; Sadiq, G.; Daveya, R.J.; Schroeder, S.L.M. Proton transfer and hydrogen bonding in the organic solid state: A combined XRD/XPS/ssNMR study of 17 organic acid–base complexes. Phys. Chem. Chem. Phys. 2014, 16, 1150–1160. [Google Scholar] [CrossRef]
- Tatton, A.S.; Blade, H.; Brown, S.P.; Hodgkinson, P.; Hughes, L.P.; Lill, S.O.N.; Yates, J.R. Improving Confidence in Crystal Structure Solutions Using NMR Crystallography: The Case of β-Piroxicam. Cryst. Growth Des. 2018, 18, 3339–3351. [Google Scholar] [CrossRef]
- Chernyshov, I.Y.; Vener, M.V.; Shenderovich, I.G. Local-structure effects on 31P NMR chemical shift tensors in solid state. J. Chem. Phys. 2019, 150, 144706. [Google Scholar] [CrossRef] [PubMed]
- Hartman, J.D.; Kudla, R.A.; Day, G.M.; Mueller, L.J.; Beran, G.J.O. Benchmark fragment-based 1H, 13C, 15N and 17O chemical shift predictions in molecular crystals. Phys. Chem. Chem. Phys. 2016, 18, 21686–21709. [Google Scholar] [CrossRef] [PubMed]
- Kleemiss, F.; Dolomanov, O.V.; Bodensteiner, M.; Peyerimhoff, N.; Midgley, L.; Bourhis, L.J.; Genoni, A.; Malaspina, L.A.; Jayatilaka, D.; Spencer, J.L.; et al. Accurate crystal structures and chemical properties from NoSpherA2. Chem. Sci. 2021, 12, 1675–1692. [Google Scholar] [CrossRef]
- Ludwig, M.; Himmel, D.; Hillebrecht, H. GIAO versus GIPAW: Comparison of Methods To Calculate 11B NMR Shifts of Icosahedral Closo-Heteroboranes toward Boron-Rich Borides. J. Phys. Chem. A 2020, 124, 2173–2185. [Google Scholar] [CrossRef]
- Shenderovich, I.G. Qualitative Analysis of the Geometry of the Hydrogen Bond in the Homoconjugated Pyridine Ion. Russ. J. Gen. Chem. 2007, 77, 620–625. [Google Scholar] [CrossRef]
- Shenderovich, I.G. Experimentally Established Benchmark Calculations of 31P NMR Quantities. Chem.—Methods 2021, 1, 61–70. [Google Scholar] [CrossRef]
- Light, M.E.; Murphy, B. The Cambridge Structural Database Communication ID ZUTDAT01; University of Southampton: Southampton, UK, 2018. [Google Scholar]
- Gurinov, A.A.; Lesnichin, S.B.; Limbach, H.-H.; Shenderovich, I.G. How short is the Strongest Hydrogen Bond in the Proton-Bound Homodimers of Pyridine Derivatives? J. Phys. Chem. A 2014, 118, 10804–10812. [Google Scholar] [CrossRef] [PubMed]
- Kong, S.; Borissova, A.O.; Lesnichin, S.B.; Hartl, M.; Daemen, L.L.; Eckert, J.; Antipin, M.Y.; Shenderovich, I.G. Geometry and Spectral Properties of the Protonated Homodimer of Pyridine in the Liquid and Solid States. A Combined NMR, X-ray Diffraction and Inelastic Neutron Scattering Study. J. Phys. Chem. A 2011, 115, 8041–8048. [Google Scholar] [CrossRef] [PubMed]
- Chan, B.; Del Bene, J.E.; Radom, L. What factors determine whether a proton-bound homodimer has a symmetric or an asymmetric hydrogen bond? Mol. Phys. 2009, 107, 1095–1105. [Google Scholar] [CrossRef]
- Mori, Y.; Takano, K. Location of protons in N–H⋯N hydrogen-bonded systems: A theoretical study on intramolecular pyridine–dihydropyridine and pyridine–pyridinium pairs. Phys. Chem. Chem. Phys. 2012, 14, 11090–11098. [Google Scholar] [CrossRef]
- Melikova, S.M.; Rutkowski, K.S.; Gurinov, A.A.; Denisov, G.S.; Rospenk, M.; Shenderovich, I.G. FTIR study of the hydrogen bond symmetry in protonated homodimers of pyridine and collidine in solution. J. Mol. Struct. 2012, 1018, 39–44. [Google Scholar] [CrossRef]
- Hakkert, S.B.; Erdėlyi, M. Halogen bond symmetry: The N-X-N bond. J. Phys. Org. Chem. 2015, 28, 226–233. [Google Scholar] [CrossRef]
- Mori, Y.; Takano, K. Effect of solvent on proton location and dynamic behavior in short intramolecular hydrogen bonds studied by molecular dynamics simulations and NMR experiments. Chem. Phys. 2015, 458, 18–29. [Google Scholar] [CrossRef]
- Gurinov, A.A.; Denisov, G.S.; Borissova, A.O.; Goloveshkin, A.S.; Greindl, J.; Limbach, H.-H.; Shenderovich, I.G. NMR Study of Solvation Effect on the Geometry of Proton-Bound Homodimers of Increasing Size. J. Phys. Chem. A 2017, 121, 8697–8705. [Google Scholar] [CrossRef]
- Reiersølmoen, A.C.; Battaglia, S.; Øien-Ødegaard, S.; Gupta, A.K.; Fiksdahl, A.; Lindh, R.; Erdėlyi, M. Symmetry of three-center, four-electron bonds. Chem. Sci. 2020, 11, 7979–7990. [Google Scholar] [CrossRef]
- Grabowski, S.J. Hydrogen Bond and Other Lewis Acid-Lewis Base Interactions as Preliminary Stages of Chemical Reactions. Molecules 2020, 25, 4668. [Google Scholar] [CrossRef] [PubMed]
- Shenderovich, I.G.; Denisov, G.S. Adduct under Field—A Qualitative Approach to Account for Solvent Effect on Hydrogen Bonding. Molecules 2020, 25, 436. [Google Scholar] [CrossRef] [PubMed]
- Shenderovich, I.G. Actual Symmetry of Symmetric Molecular Adducts in the Gas Phase, Solution and in the Solid State. Symmetry 2021, 13, 756. [Google Scholar] [CrossRef]
- Steiner, T. Lengthening of the Covalent X-H Bond in Heteronuclear Hydrogen Bonds Quantified from Organic and Organometallic Neutron Crystal Structures. J. Phys. Chem. A 1998, 102, 7041–7052. [Google Scholar] [CrossRef]
- Steiner, T. The Hydrogen Bond in the Solid State. Angew. Chem. Int. Ed. 2002, 41, 48–76. [Google Scholar] [CrossRef]
- Limbach, H.-H.; Tolstoy, P.M.; Pérez-Hernández, N.; Guo, J.; Shenderovich, I.G.; Denisov, G.S. OHO Hydrogen Bond Geometries and NMR Chemical Shifts: From Equilibrium Structures to Geometric H/D Isotope Effects, with Applications for Water, Protonated Water, and Compressed Ice. Israel J. Chem. 2009, 49, 199–216. [Google Scholar] [CrossRef]
- Shibl, M.F.; Pietrzak, M.; Limbach, H.-H.; Kühn, O. Geometric H/D isotope effects and cooperativity of the hydrogen bonds in porphycene. ChemPhysChem 2007, 8, 315–321. [Google Scholar] [CrossRef]
- Yamamoto, K.; Kanematsu, Y.; Nagashima, U.; Ueda, A.; Mori, H.; Tachikawa, M. Theoretical study of the H/D isotope effect on phase transition of hydrogen-bonded organic conductor κ-H3(Cat-EDT-TTF)2. Phys. Chem. Chem. Phys. 2016, 18, 29673–29680. [Google Scholar] [CrossRef]
- Golubev, N.S.; Melikova, S.M.; Shchepkin, D.N.; Shenderovich, I.G.; Tolstoy, P.M.; Denisov, G.S. Interpretation of H/D Isotope Effects on NMR Chemical Shifts of [FHF]− Ion Based on Calculations of Nuclear Magnetic Shielding Tensor Surface. Z. Phys. Chem. 2003, 217, 1549–1563. [Google Scholar] [CrossRef]
- Harris, R.K.; Becker, E.D.; Cabral De Menezes, S.M.; Granger, P.; Hoffman, R.E.; Zilm, K.W. Further conventions for NMR shielding and chemical shifts IUPAC recommendations 2008. Solid State Nucl. Magn. Reson. 2008, 33, 41–56. [Google Scholar] [CrossRef]
- Bertani, P.; Raya, J.; Bechinger, B. 15N chemical shift referencing in solid state NMR. Solid State Nucl. Magn. Reson. 2014, 61–62, 15–18. [Google Scholar] [CrossRef] [PubMed]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian 09; Revision D.01; Gaussian, Inc.: Wallingford, CT, USA, 2013. [Google Scholar]
- Staroverov, V.N.; Scuseria, G.E.; Tao, J.; Perdew, J.P. Comparative assessment of a new nonempirical density functional: Molecules and hydrogen-bonded complexes. J. Chem. Phys. 2003, 119, 12129. [Google Scholar] [CrossRef]
- Chai, J.-D.; Head-Gordon, M. Long-range corrected hybrid density functionals with damped atom–atom dispersion corrections. Phys. Chem. Chem. Phys. 2008, 10, 6615–6620. [Google Scholar] [CrossRef] [PubMed]
- Weigend, F.; Ahlrichs, R. Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for H to Rn: Design and assessment of accuracy. Phys. Chem. Chem. Phys. 2005, 7, 3297–3305. [Google Scholar] [CrossRef] [PubMed]
- Jensen, F. Segmented Contracted Basis Sets Optimized for Nuclear Magnetic Shielding. J. Chem. Theory Comput. 2015, 11, 132–138. [Google Scholar] [CrossRef]
- Pritchard, B.P.; Altarawy, D.; Didier, B.; Gibson, T.D.; Windus, T.L. New Basis Set Exchange: An Open, Up-to-Date Resource for the Molecular Sciences Community. J. Chem. Inf. Model. 2019, 59, 4814–4820. [Google Scholar] [CrossRef]
- Tomasi, J.; Mennucci, B.; Cammi, R. Quantum mechanical continuum solvation models. Chem. Rev. 2005, 105, 2999–3093. [Google Scholar] [CrossRef]
- Shenderovich, I.G. Simplified Calculation Approaches Designed to Reproduce the Geometry of Hydrogen Bonds in Molecular Complexes in Aprotic Solvents. J. Chem. Phys. 2018, 148, 124313. [Google Scholar] [CrossRef]
- Bryce, D.L.; Bernard, G.M.; Gee, M.; Lumsden, M.D.; Eichele, K.; Wasylishen, R.E. Practical Aspects of Modern Routine Solid-State Multinuclear Magnetic Resonance Spectroscopy: One-Dimensional Experiments. Can. J. Anal. Sci. Spectrosc. 2001, 46, 46–82. Available online: http://anorganik.uni-tuebingen.de/klaus/nmr/practical/practical.pdf (accessed on 4 June 2023). [CrossRef]
- Shenderovich, I.G.; Limbach, H.-H. Solid State NMR for Nonexperts: An Overview of Simple but General Practical Methods. Solids 2021, 2, 139–154. [Google Scholar] [CrossRef]
- Shenderovich, I.G. An Experimentally Established 15N NMR Absolute Shielding Scale for Theoretical Calculations. J. Phys. Chem. A 2023. [Google Scholar] [CrossRef]
- Shenderovich, I.G. 1,3,5-Triaza-7-Phosphaadamantane (PTA) as a 31P NMR Probe for Organometallic Transition Metal Complexes in Solution. Molecules 2021, 26, 1390. [Google Scholar] [CrossRef]
- Shenderovich, I.G. Electric field effect on 31P NMR magnetic shielding. J. Chem. Phys. 2020, 153, 184501. [Google Scholar] [CrossRef]
- Sheldrick, G.M. ShelXT-Integrated space-group and crystal-structure determination. Acta Crystallogr. Sect. A Found. Adv. 2015, A71, 3–8. [Google Scholar] [CrossRef] [PubMed]
- Dolomanov, O.V.; Bourhis, L.J.; Gildea, R.J.; Howard, J.A.K.; Puschmann, H. Olex2: A complete structure solution, refinement and analysis program. J. Appl. Cryst. 2009, 42, 339–341. [Google Scholar] [CrossRef]
- Bourhis, L.J.; Dolomanov, O.V.; Gildea, R.J.; Howard, J.A.K.; Puschmann, H. The Anatomy of a Comprehensive Constrained, Restrained, Refinement Program for the Modern Computing Environment—Olex2 Disected. Acta Crystallogr. Sect. A Found. Adv. 2015, A71, 59–71. [Google Scholar] [CrossRef]
- Ananyev, I.V.; Lyssenko, K.A. Conjugation effects in a para-nitroaniline molecule and its structural non-rigidity. Russ. Chem. Bull. 2014, 63, 1270–1282. [Google Scholar] [CrossRef]
- Borissova, A.O.; Lyssenko, K.A.; Gurinov, A.A.; Shenderovich, I.G. Energy Analysis of Competing Non-Covalent Interaction in 1:1 and 1:2 Adducts of Collidine with Benzoic Acids by Means of X-Ray Diffraction. Z. Phys. Chem. 2013, 227, 775–790. [Google Scholar] [CrossRef]
- Vologzhanina, A.V.; Lyssenko, K.A. Interatomic interactions in the crystal of (C4H11N2)2(C4H12N2)[Mo(CN)8]: Comparison of two approaches. Russ. Chem. Bull. 2013, 64, 1786–1792. [Google Scholar] [CrossRef]
- Nelyubina, Y.V.; Glukhov, I.V.; Antipin, M.Y.; Lyssenko, K.A. Higher density does not mean higher stability” mystery of paracetamol finally unraveled. Chem. Commun. 2010, 46, 3469–3471. [Google Scholar] [CrossRef]
- Nelyubina, Y.V.; Antipin, M.Y.; Lyssenko, K.A. Hydrogen Bonds between Zwitterions: Intermediate between Classical and Charge-Assisted Ones. A Case Study. J. Phys. Chem. A 2009, 113, 3615–3620. [Google Scholar] [CrossRef] [PubMed]
- Shenderovich, I.G.; Denisov, G.S. Modeling of the Response of Hydrogen Bond Properties on an External Electric Field: Geometry, NMR Chemical Shift, Spin-Spin Scalar Coupling. Molecules 2021, 26, 4967. [Google Scholar] [CrossRef] [PubMed]
- Shenderovich, I.G.; Denisov, G.S. Modeling of Solute-Solvent Interactions Using an External Electric Field—From Tautomeric Equilibrium in Nonpolar Solvents to the Dissociation of Alkali Metal Halides. Molecules 2021, 26, 1283. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).