Abstract
The calculation of the isobaric heat capacities of the liquid and solid phase of molecules at 298.15 K is presented, applying a universal computer algorithm based on the atom-groups additivity method, using refined atom groups. The atom groups are defined as the molecules’ constituting atoms and their immediate neighbourhood. In addition, the hydroxy group of alcohols are further subdivided to take account of the different intermolecular interactions of primary, secondary, and tertiary alcohols. The evaluation of the groups’ contributions has been carried out by solving a matrix of simultaneous linear equations by means of the iterative Gauss–Seidel balancing calculus using experimental data from literature. Plausibility has been tested immediately after each fitting calculation using a 10-fold cross-validation procedure. For the heat capacity of liquids, the respective goodness of fit of the direct (r2) and the cross-validation calculations (q2) of 0.998 and 0.9975, and the respective standard deviations of 8.24 and 9.19 J/mol/K, together with a mean absolute percentage deviation (MAPD) of 2.66%, based on the experimental data of 1111 compounds, proves the excellent predictive applicability of the present method. The statistical values for the heat capacity of solids are only slightly inferior: for r2 and q2, the respective values are 0.9915 and 0.9874, the respective standard deviations are 12.21 and 14.23 J/mol/K, and the MAPD is 4.74%, based on 734 solids. The predicted heat capacities for a series of liquid and solid compounds have been directly compared to those received by a complementary method based on the "true" molecular volume and their deviations have been elucidated.
1. Introduction
Most experimental measurements of thermodynamic properties, such as vaporization, sublimation, solvation, or fusion enthalpies, are usually carried out at temperatures that differ from the standard temperature, which has generally been accepted as being 298.15 K. These temperature differences lead to experimental values for the temperature-dependent properties that prevent a direct comparison of the results between various compounds or between scientific teams examining the same molecule, a deficiency which, however, can be corrected, provided that the heat capacity of the molecules under examination is known. Instead of measuring this property for a specific molecule, the large amount of experimental heat-capacity data for all kinds of compounds, such as inorganic and organic salts, liquid crystals, or ionic liquids, enabled its prediction by means of a large number of mathematical methods, a comprehensive overview of which has been given in a recent publication by the present author [1]. The majority of these prediction methods are based on the group-additivity (GA) approach, whereby the group notations vary from complete polyatomic ions as, e.g., applied by Gardas and Coutinho [2] to single atoms and their immediate neighbour atoms and ligands, as described by Benson and Buss [3]. Generally, the GA methods’ range of applicability for the prediction of any kind of descriptors varies over a large scope of molecular structures, depending on the complexity and number of the group notations as well as the number of experimental data upon which the group parameters are based. Similarly, the reliability of the predictions is highly dependent on the range of application. Zàbransky and Ruzicka [4], e.g., defined 130 functional groups including cis, trans, as well as ortho and meta corrections in the parametrization of their second-order polynomial GA model for the prediction of the liquid heat capacity and its temperature dependence, based on more than 1800 experimental data points. For the majority of compounds they reported an average deviation of below 2%. For alkanols, acids and aldehydes, however, the error was larger than 3% and rose with increasing temperature. A further limit to the use of their model was the observation that the prediction accuracy deteriorated further if the compounds contained functional groups from different families, such as N,N’-diethanolamine or 1-chloro-2-propanol. Another example of a GA method, provided by Chickos et al. [5], used 47 functional groups for the prediction calculation of the heat capacity of 810 liquids and 446 solids, reporting standard errors of 19.5 J/molK for the liquids and 26.9 J/mol/K for the solids. The authors compared these errors with the experimental uncertainties of 8.12 and 23.4 J/mol/K, respectively, which they estimated from the experimental data variations for each of 219 liquids and 102 solids published by independent sources.
A common deficiency of the GA and all the other approaches cited in [1] is that none of them enables the prediction of any specific descriptor for each and any molecular structure in the chemical realm. In the case of the heat capacities of the solid and liquid phase of molecules, however, this deficiency has been overcome in that their prediction values are determined via the "true" molecular volume (Vm) outlined in detail in [1]. Nevertheless, this approach has encountered several other shortcomings which could not all be addressed specifically, as it is based on one single number, the molecular volume. The three most important deficiencies are 1) the general influence of the hydroxy group of alcohols and carboxylic acids, 2) the specific effects of primary, secondary, and tertiary alcohols and 3) the impact of saturated cyclic rings vs. open-chained systems on the heat capacities. Accordingly, a first attempt of a linear correlation calculation in [1], which included the molecular volume and the experimental liquid heat capacity Cp(liq) of the complete set of compounds, for which both data were available, and which neglected the mentioned shortcomings, yielded a rather large standard deviation of 27.84 J/mol/K and a mean absolute percentage deviation (MAPD) of 8.23%. The neglect of the hydroxy-group effect on Cp(liq) was immediately manifest in that the predicted values for all those compounds carrying at least one OH group were systematically well below the experimental ones by up to ca. 130 J/mol/K. This general deviation, obviously caused by the formation of intermolecular hydrogen bridges between the OH groups, has been considered in subsequent calculations in that the complete set of compounds was separated by means of a few simple steps in the computer algorithm into three subsets, i.e., one encompassing all molecules lacking any OH group, a second one consisting of those carrying one OH group and a third one comprising those having more than one OH group. For each of these subsets, a separate linear correlation calculation had to be carried out yielding three sets of linear parameters for the prediction of the liquid and three for that of the solid heat capacities. In this way, the first one of the mentioned shortcomings has been eliminated, which correspondingly resulted in significantly better compliance of the predictions with the experimental data. The corresponding statistical results will be discussed and used for comparison in a later section. The remaining two deficiencies concerning the various alcohol classes as well as that of cyclic vs. open-chained structures in a saturated system, which exhibit a minor but still systematically negative influence on the prediction quality, has been plausibly explained, but a reasonably straightforward treatment within the context of the Vm method was not feasible.
Therefore, the question arose as to whether and how well a GA approach would overcome the remaining shortcomings of the Vm method and enable a more accurate and reliable prediction of the heat capacities of molecules in their liquid and solid phase at the standard temperature, in awareness of the disadvantage that it would not be able to cover each and every possible compound. A particularly versatile GA method, outlined in [6], enabling in a single sweep the calculation of 14 thermodynamic [6,7], solubility- [6,7,8], optics- [6], charge- [6], environment-related [6], and physical [8,9] properties of a nearly unlimited scope and size of molecular structures should best serve this purpose, all the more so as in most cases it in principle also opened a simple means for their reliable calculation on a sheet of paper. Accordingly, the present work puts a special focus on the effects of the hydroxy groups and the cyclization of saturated molecular parts on the heat capacities and how to deal with them. The statistical results of the present GA method will be put in relation to those of the Vm method but also to those of the GA approach of Chickos et al. [5], as this approach can be viewed as most closely related to the present one.
2. Method
The present study is founded on a project-owned and regularly updated, object-oriented database of more than 32000 molecules encompassing pharmaceuticals, plant protection, dyes, ionic liquids, liquid crystals, metal-organics, lab intermediates, and many more, all of which are stored as geometry-optimized 3-dimensional structures, including—besides several further descriptors—a set of 1176 experimental heat capacities of liquids and a corresponding set of 802 heat capacities of solids.
The details of the present atom-group additivity method and the evaluation of its group contributions have been outlined in an earlier paper [6]. Accordingly, its group notations have the same meaning as that exemplified in Table 1 of [6]. However, in order to include ionic liquids for which the experimental heat capacities are known, the list of group notations has been extended by ionic atom groups representing their charged fragments, as listed in the present Table 1. These special atom groups have already successfully been utilized in the calculation of the molecules’ viscosity [8] and surface tension [9], applied in the same way as the remaining groups. For the interpretation of the ionic atom groups of Table 1, the reader is invited to read section 2 of papers [8] and [9].

Table 1.
Atom-group examples for ionic liquids and their meaning.
In the course of the first preliminary group-contribution calculations, whereby tentatively certain “standard” atom groups have been replaced by refined ones and special groups, which will be described in the following, have been added or omitted, their statistical results quickly revealed significant improvement of the predictive quality if the groups listed in Table 2 are included in the prediction of both the liquid and solid heat capacities.

Table 2.
Refined atom and special groups and their meaning.
In the discussion of the shortcomings of the molecular volume-based calculations of the heat capacities outlined in the introductory section, the hydroxy group appeared to be the most accountable group for large deviations between experimental and predicted heat-capacity values, even within the restricted set of OH-containing compounds, i.e., after their separation from the remaining ones. It turned out that the definition of the OH group on saturated carbon as in ordinary alcohols by the simple atom type “O” and its neighbours “HC” was inadequate for heat-capacity calculations, in contrast to the calculations of all the other descriptors mentioned in our earlier papers [6,7,8,9]. As a consequence, an additional procedure had to be integrated in the general GA algorithm outlined in [1], which redefined the atom type “O” into “O(prim)”, “O(sec)”, or “O(tert)”, depending on the number of carbon atoms attached to the C atom neighbouring the O atom, according to the definition of primary, secondary, and tertiary alcohols, as shown in Table 2. (Consequently, the definition of their neighbourhood “HC” was no longer relevant and was thus not examined.) This redefinition procedure is only invoked if the redefined atom types appear in the group-parameters table, as a consequence of the algorithmic procedure determining that it is the content of the group-parameter tables that defines which group parameters are to be evaluated for the corresponding descriptors calculations (as explained in subsection 2.2 of [1]), and since none of the other descriptors in [6,7,8,9] requires this redefinition, this procedure is only called up for the evaluation of the group parameters of present Table 3 and Table 7 and the subsequent heat-capacity predictions. The remaining hydroxy groups attached to unsaturated carbon found in carboxylic acids and phenols are notated separately by the atom type “O” and the neighbourhood “HC(pi)”, as defined in [6].

Table 3.
Atom groups and their contributions for the heat-capacity calculation of liquids.
Another point of weakness discussed in the introductory section rested in the observation that the Vm approach systematically scored badly in the prediction of the heat capacities of molecules with cyclic saturated moieties. This deficiency has been resolved in the present GA method in that the endocyclic single bonds in a molecule are counted and their sum multiplied by the contribution value of the special group “Endocyclic bonds” to yield the effect of the cyclic moieties in a molecule on its heat capacity. The groups “Angle60”, “Angle90”, and “Angle102” serve as corrective elements for small rings. Not surprisingly, these special groups, which take account of an effect influencing the freedom of intramolecular motion, have also successfully been applied in the prediction of the entropy of fusion [7].
The special group “(COH)n” had to be introduced in the Cp calculations in order to compensate for deviations found for polyols and polyacids. This special group has played its useful part already in the calculation of the surface tension [9]. The test calculations also revealed a very strong influence of intramolecular hydrogen bonds on the liquid heat capacity, which had to be taken into account by the introduction of the special group “H/H Acceptor”, a group that has also been used successfully used in the prediction of the toxicity [6], the heats of solvation, and the sublimation, vaporization, and entropy of fusion [7].
The procedure for the evaluation of the atom-group contributions, as explained in [6], is identical for the two group-parameter sets for the prediction of the heat capacities of both the liquid and solid phases and may be summarized as follows: in a first step, a list of all the compounds, for which the experimental Cp values are known, is extracted from the database. In the next step, each “backbone” atom (i.e., each atom bound to at least two immediate neighbours) within each molecule has an atom type and its neighbourhood assigned to by means of two character strings defining an atom group, following the rules defined in [6] (e.g., “C sp3” and “H2CO” for the C1 atom in ethanol) and then this group’s occurrence in the molecule is counted. The list of M molecules and their N atom groups plus their experimental values are then entered into an M × (N + 1) matrix, wherein each matrix element (i,j) receives the number of occurrences of the jth atomic or special group in the ith molecule. The normalization of this matrix into an Ax = B matrix and its balancing by means of the Gauss–Seidel calculus, e.g., according to E. Hardtwig [10], yields the atom-group contributions. This mathematical approach is based on the assumption that the prediction value of a molecule’s descriptor in question can be evaluated by simply summing up all the group contributions in the molecule. For the evaluation of the heat capacities in this study, Equation 1 has been adopted, wherein Cp is the heat capacity at 298.15 K, ai and bj are the group contributions, Ai is the number of occurrences of the ith atom group, and Bj is the number of occurrences of the jth special group.
The reliance of this procedure is immediately examined by a subsequent 10-fold cross-validation plausibility test, carried out in a way to ensure that each compound has been entered into the calculation as a test as well as a training sample. All the group contribution values and the statistical results of both the direct equalization and the cross-validation calculation of the liquid heat capacity Cp(liq,298) are then collected in Table 3 and for the solid heat capacity Cp(sol,298) in Table 7. However, for the evaluation of the statistical results, only those group contributions are considered as valid for use that have been represented by at least three independent molecules in the equalization calculation. The number of molecules responsible for the respective group contribution is listed in the rightmost column of Table 3 and Table 7. Evidently, for several atom groups, this number falls short of the validity requirement. Nevertheless, as this work is part of a continuous project, these groups have deliberately remained in the parameters’ tables for future use. They might also motivate readers working in this area to contribute corresponding experimental data. In order to achieve reliable contribution values for the atom and special groups, it was necessary to filter out compounds with Cp values that deviated too far from the predicted results. In the present work, the limit was defined as three times the cross-validated standard deviation q2. The corresponding outliers have been excluded from the parameters’ calculations and are collected in an outliers list. The present calculations are generally restricted to molecules containing the elements H, B, C, N, O, P, S, Si, and/or halogen.
3. Sources of Heat-Capacity Data
The present work is essentially based on the comprehensive list of experimental heat-capacities collected in [1], used to substantiate the feasibility of the Vm approach. However, a recent scan of the literature brought forth a number of further publications, which either confirmed previous data or even improved the conformance with prediction, but also enabled an extension of the applicability of the present GA approach. A number of new experimental Cp data have been published for saturated and unsaturated hydrocarbons, especially for bicyclo[2.2.2]octane and bicyclo[2.2.2]octene [11], 1-octyne and 4-octyne [12], biphenyl [13], benzo[b]fluoranthene, benzo[k]fluoranthene, indeno[1,2,3-cd]pyrene [14], and adamantane [15]. In addition, further Cp values have been found for the amines hexamethylenetetramine [15], tetra-N-phenylbenzidine and 4,4′-bis (N-carbazolyl)-1,1′-biphenyl [16], 1,3,5-triazine [17], the ethers 1,3,5-trioxane [17], diethylene glycol n-pentyl ether [18], triethylene glycol monopentyl ether [19] and diphenyl ether [20], several alcohols and aldehydes [21], derivatives of glycidol [22], carboxylic acids [23,24], aliphatic esters [24,25,26,27], benzoates [28], haloalkanes [29,30], haloaromatics [31,32], thio ethers, sulfones and sulfoxides [33,34], alkanolamines, [35,36,37] and nitriles [38] For several compounds, more recent publications have been found the following: 4-ethylmorpholine [39], methionine [40], theophylline, and caffeine [41], as well as for (-)-menthone, (+)-pulegone, and (-)-isopulegol [42]. Beyond these, experimental Cp values of a number of new compounds have been published: namely 3-amino-4-amidoximinofurazan [43], 3-fluoro-5-(3-pyridinyloxy)- benzenamine and N-[3-fluoro-5-(3-pyridinyloxy)phenyl]-N’-3-pyridinyl urea [44], 7-Methyl-1,5,7-triazabicyclo[4.4.0]dec-5-ene [45], 2-[(4-nitro-benzoyl)-hydrazone]-propionic acid [46], eugenol and (+)-carvone [47], indapamide [48], and the explosives EDNH and DNTA [49]. For some silicon-containing compounds, new Cp data have been found in [50]. Finally, a few further heat capacities data of ionic liquids [51,52,53] have been included in the present dataset.
4. Results
4.1. General Remarks
- In the subsequent figures, the results of the cross-validation calculations have been superimposed in red over the training data drawn in black.
- The complete lists of compounds with known heat capacities used in this study are available as SDF files in the Supplementary Materials, downloadable by external chemistry software. In addition, the Supplementary Materials provides the results lists containing the molecules’ names and experimental, training, and cross-validation data. Beyond this, the lists of outliers of both heat-capacity calculations are also available in the Supplementary Materials.
4.2. Heat Capacity of Liquids
In Table 3, the atom groups and their contribution for the prediction of the heat capacity of liquids are collected, together with the number of molecules and occurrences upon which each of them is based.
In rows A to H, at the bottom of the table, the statistical data of this table have been gathered. As shown in row A, the group contributions have been evaluated on the basis of 1176 compounds yielding the data for 211 atom groups, of which, however, only 134 are considered as valid, i.e., that are supported by at least three compounds. Accordingly, since only valid groups have been used for the statistical evaluations, the numbers of compounds entered in the calculations of the trained and cross-validated correlation coefficients (“goodness of fit”) r2 and q2 (rows B and F) are lower with 1111 and 1060, respectively. Both the standard deviations of the complete data set (row D) as well as that of the combined cross-validation sets (row H) reveal excellently low values (in J/mol/K), not only in relation to the large range of experimental values of between 81.92 (methanol) and 1849 J/mol/K (trimethylpropane trioleate), but particularly also in comparison with the standard error of 19.5 J/mol/K reported by Chickos et al. [5] for 810 liquids. The result is a very low scatter along the correlation line, as is shown in Figure 1. Accordingly, the error distributions of both the training and the cross-validated sets fairly well follow the Gaussian distribution function, as demonstrated in the histogram (Figure 2). The MAPD for the complete set of 1111 liquid compounds was 2.66%, clearly by far better than the 8.23% for the entire set of 1303 liquids resulting from the Vm method [1], and still much better in comparison with the 6.51% for the OH-free subset of 1102 liquids reported in Figure 2 of [1].
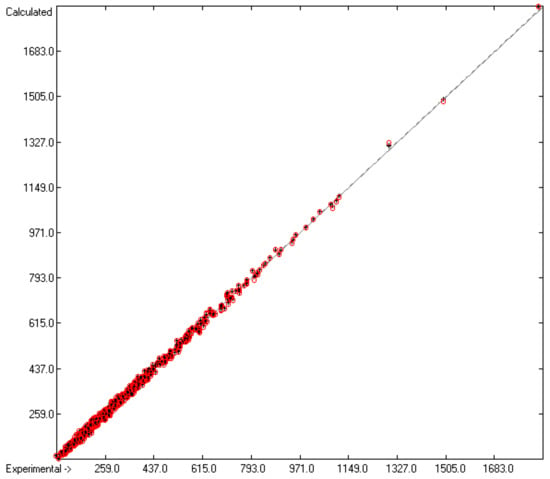
Figure 1.
Correlation diagram of the Cp(liq,298) data (in J/mol/K). The cross-validation data are superimposed as red circles. (n = 1111; r2 = 0.998; q2 = 0.9975; regression line: intercept = 0.7993; slope = 0.9977).
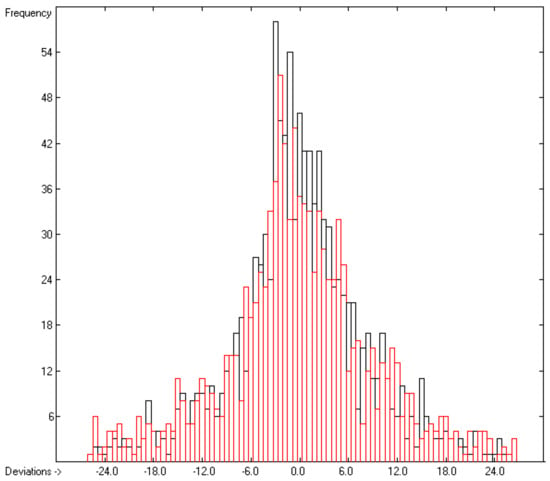
Figure 2.
Histogram of the liquid heat-capacity data. The deviations are in J/mol/K. The cross-validation data are superimposed as red bars. (S = ± 9.19; Experimental value range: 81.92–1849 J/molK).
The distinctly better conformance of the predicted with the experimental Cp(liq) values in comparison with earlier literature references is essentially based on three primary reasons. The first one is the refinement of the molecules’ description itself by the most detailed classification of group notations, which is precluded on principal to the Vm method [1], but requires a large number of atom groups and consequently a large amount of experimental data for their parametrization. The second reason originated from an observation made in [1], namely that the heat capacities of primary, and less so, of secondary alcohols have notoriously been overestimated by the Vm approach. These systematic deviations can be seen in Table 4, where the experimental Cp(liq,298) data and the predicted values of both the present GA and Vm method of the corresponding alkanols, encompassing saturated alkyl mono-, di- and polyols, are compiled for comparison. In order to overcome this deficiency, the alcohols have therefore been subdivided as described in Section 2 into the three subclasses primary, secondary, and tertiary alcohols. This additional separation indeed had a dramatically positive effect on the entire alcohols class, demonstrated by the comparison of the correlation diagrams of Figure 3. The MAPD values shown at the bottom of Table 4 confirm that the GA method on average produces distinctly lower deviations from experimental values than the Vm approach.

Table 4.
Experimental Cp(liq,298) data of 66 alkanols, compared with prediction values calculated by the present the group-additivity (GA) and the Vm [1] method (in J/mol/K).
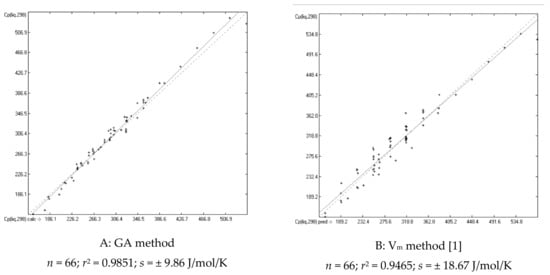
Figure 3.
Correlation diagrams of the calculated vs. experimental Cp(liq,298) data of saturated alcohols (in J/mol/K) based on A: the present GA; B: the Vm method.
A quick review of the contributions of the corresponding atom groups representing the primary, secondary, and tertiary alcohols (group numbers 166 to 168) in Table 3 reveals the large influence of the immediate neighbourhood of the OH group. Evidently, with its growing bulkiness, the contribution to the heat capacity of the OH group increases due to its progressively hampered accessibility to build a hydrogen bridge. This effect has been plausibly explained by Huelsekopf and Ludwig [54], who discovered, upon applying theoretical calculations based on the quantum cluster equilibrium theory (QCE) on two primary (ethanol and benzyl alcohol) and a tertiary alcohol (2,2-dimethyl-3-ethyl-3-pentanol), that primary alcohols on principle form cyclic tetramers and pentamers in the liquid phase, while tertiary alcohols under the same conditions only consist of monomers and dimers. Following this reasoning, the higher liquid heat capacity of secondary and tertiary alcohols over that of their primary counterparts having the same molecular formula is the result of their formation of smaller clusters, which inherently exhibit a higher number of rotational and translational degrees of freedom.
The third reason for the good compliance of the present Cp predictions with experimental values is the consideration of the cyclization effect in the present GA method. Table 5 presents a selection of some linear alkanes and their closely related cycloalkanes and compares their experimental Cp(liq) values with predicted data calculated by means of the present GA method and the Vm [1] approach. Scanning the table’s fifth column immediately reveals that the Vm approach systematically overestimates the liquid heat capacity of the cycloalkanes, whereas those of the linear alkanes are excellently well predicted. The reason is obvious: cyclization reduces the number of rotational degrees of freedom, an effect which is categorically excluded from consideration by the Vm method. The present GA method, however, includes this effect in that the number of endocyclic single bonds is counted and their count is multiplied by the assigned special group contribution, in this case by the value of −3.92 J/mol/K of group 212 in Table 3. The result of this inclusion is evident in column 3 of Table 5, proving that the overestimation of the Cp(liq) values of the cycloalkanes on average is completely lifted.

Table 5.
Experimental Cp(liq,298) data of four linear alkanes and four related cycloalkanes, compared with the prediction values calculated by the present GA and the Vm [1] method (in J/mol/K).
An exemplary implementation of these findings may be provided in the calculation according to Equation 1 of the Cp(liq,298) value of a cyclic alcohol, such as cyclohexanemethanol:
5 x [C sp3/H2C2] + [C sp3/HC3] + [C sp3/H2CO] + [O(prim)/HC] + 6 × [endocyclic bonds] = 5 × 30.06 + 21.11 + 73.79 + 14.41 + 6 × (−3.92) = 236.09 J/mol/K (experiment: 236.5 J/mol/K).
In this context, it is worth mentioning that Chickos et al. [5] took great care about the parametrization of the "cyclic tertiary sp3 carbons" (as they called them) and their neighbourhood, but only reserved a single atom group for all the alcohol classes including phenols.
Since, in recent years, the class of ionic liquids (IL) has received increasing interest as a group of new polar solvents, their heat capacity as an important property has come into focus. It was therefore interesting to examine how well the present GA method would cope in comparison with the Vm method of [1]. In Table 6, the experimental Cp(liq,298) data of 122 ILs have been collected and compared to the prediction data calculated by the present GA method and by the Vm method. A comparison of the MAPD values at the bottom of the table clearly demonstrate a substantial improvement of the present GA approach over the Vm method.

Table 6.
Experimental Cp(liq,298) data of 122 ionic liquids, compared with prediction values calculated by the present GA and the Vm [1] method (in J/mol/K).
The present calculation of the atom-group parameters for the prediction of Cp(liq,298) revealed ca. 170 compounds with experimental values exceeding the deviation limit, as defined in Section 2, which have been removed from parameters calculations and are collected in an outliers list. A comparison of this list with that resulting from calculations by means of the Vm method [1] showed very high overlap, indicating that the exclusion of these compounds was indeed justified. After the removal of these outliers, a limited number of 1202 compounds with usable experimental data remained, supporting the contributions of 134 atom and special groups valid for prediction calculations, as is shown in row A of Table 3. Despite this fairly low number of atom groups, the range of applicability of the present GA method is considerably high: for nearly 62% of ChemBrain’s database of the more than 32000 compounds, the liquid heat capacity has been evaluable.
4.3. Heat Capacity of Solids
While the measurement of the heat capacity of liquids principally implies a consistent isotropic phase, the corresponding examination of solids very often faces the question as to what type of association the particular compound has adopted in its solid phase. Many compounds precipitate in various crystalline forms, depending on the precipitation conditions, each of them having a different heat capacity, and many of these can change from one into another crystalline structure upon measurement, perhaps even switching from one tautomeric form into another one. In some cases, the apparent solid is merely a supercooled melt. The uncertainty of the actual structure of the solids appears to be the main cause of the larger scatter of the heat capacities of solids Cp(sol,298) as compared to that of the liquids, not only over the complete range of available compounds but also over particular compounds examined by several independent sources, as has been observed by Chickos et al. [5]. These uncertainties are expressed in the statistics data at the bottom of Table 7, which presents the list of atom and special groups and their contribution for the prediction of the heat capacity of solids. Based on the Cp data of 804 solids, the Gauss–Seidel calculus yielded 126 atom and special groups (row A in Table 7) valid for prediction calculations and a cross-validation standard deviation Q2 of 14.23 J/mol/K (row H). This standard deviation is clearly higher than that for the calculation of the liquid heat capacities, but much lower than the 26.9 J/mol/K of Chickos’ method [5] and even lower than the experimental variation of 23.4 J/mol/K for each of the 102 solids originating from independent sources [5]. The MAPD value for the complete set of solids was calculated to 4.74%, which is better than that of each of the subsets of compounds calculated by means of the Vm method [1]. Nevertheless, as is demonstrated in the corresponding diagram (Figure 4), the scatter around the correlation line is significantly larger compared to the one of Figure 1 for the liquid heat capacity. Analogously, the histogram (Figure 5) shows a wider "waist" than that of Figure 2.

Table 7.
Atom groups and their contributions for the heat-capacity calculation of solids.
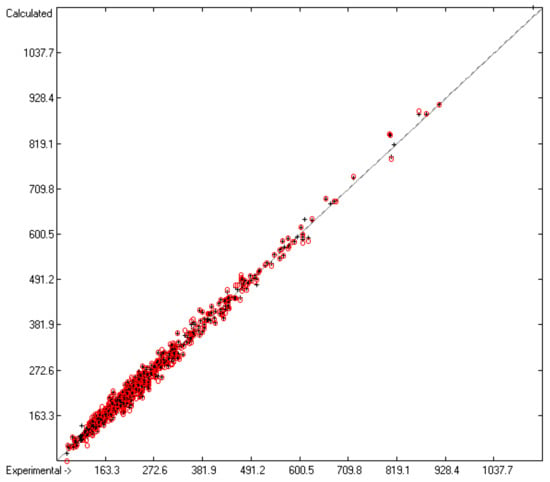
Figure 4.
Correlation diagram of the Cp(sol,298) data (in J/mol/K). The cross-validation data are superimposed as red circles. (n = 734; r2 = 0.9915; q2 = 0.9874; regression line: intercept = −0.0999; slope = 0.9984).
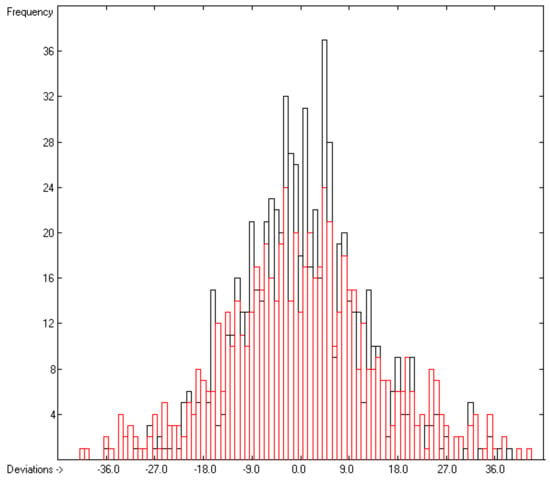
Figure 5.
Histogram of the solid heat-capacity data. The deviations are in J/mol/K. The cross-validation data are superimposed as red bars. (s = ±14.23; Experimental value range: 78.7–1129 J/molK).
Hydrogen bridges are known to play a crucial role in the formation of the crystalline structure of solids (think of snowflakes or water ice). Since the Vm approach of [1] is not able to include this effect directly, compounds containing OH groups were treated separately from the OH-free molecules. In analogy to the observation made with the liquid alcohols one would then have expected that the Vm approach again exhibited an unresolvable deficiency as concerning the deviations between experimental and predicted solid heat capacities of primary, secondary, and tertiary alcohols. Unfortunately, however, the enhanced extent of the scatter of the experimental Cp(sol) values in this compound’s class concealed these suspected deviations. The present GA method on the other hand provided an indirect proof of the influence of the immediate neighbourhood of the OH group in the alcohol subclasses: a comparison of the contributions of the atom groups 157, 158, and 159 in Table 7 (−23.36, −16.25 and −3.34 J/molK, respectively), assigned to the primary, secondary, and tertiary OH groups, immediately reveals that the primary alcohols exhibit the strongest hydrogen bridge effect, leading to the correspondingly largest decrease in the heat capacity due to the additional loss of freedoms of motion, followed by the secondary and the tertiary alcohols. The reason for this differentiation is the same as explained for that of the liquid alcohols in the prior section: the increase in the bulkiness around the OH group increasingly prevents hydrogen-bridge building. The separation of the alcohol subclasses in the present GA method also improved the reliability of the predicted Cp(sol,298) values. In Table 8, the results of the GA and the Vm method for 31 alkanols have been collected and compared with their experimental data. It is interesting to see that the largest deviations of the GA method coincide with large ones of the Vm method (i.e. for 2,2-dimethyl-1,3-propanediol and 1,15-pentadecanediol), indicating that their experimental values are probably incorrect. General experience suggests that, in cases where the Vm method exhibits a large deviation, it is the GA method that is more trustworthy.

Table 8.
Experimental Cp(sol,298) data of 31 alkanols, compared with prediction values calculated by the present GA and the Vm [1] method (in J/mol/K).
While the intermolecular interactions of OH groups exhibit a large influence on the heat capacity of solids, a similar effect of saturated cyclic structures over non-cyclic ones should not be expected as their interactions merely result from the weak dispersive forces. Beyond this—and in contrast to the conditions in the liquid phase—in a solid crystal not only the translational but also the intramolecular freedoms of motion are largely restricted independent of cyclic or non-cylic molecular moieties. This seems to be confirmed by the smaller contribution of the saturated endocyclic bonds (special group 194 in Table 7) of −1.44 J/mol/K compared to that for the calculation of the liquid Cp of −3.92 J/mol/K. However, as has been demonstrated by the comparison of some structurally closely related examples in [1], e.g., o-, m-, and p-quinquephenyl, anthracene, phenanthrene, and various dimethylnaphthalenes, although aromatics, the chemical structure of a molecule itself has a very dominant effect on the crystalline structure, which again affects the experimental value of the solid heat capacity. In Table 9, a selection of saturated alkanes and cycloalkanes has been listed and their experimental solid heat capacities compared with the prediction values calculated by means of the present GA and the Vm method [1].

Table 9.
Experimental Cp(sol,298) data of 18 alkanes and cycloalkanes, compared with prediction values calculated by the present GA and the Vm [1] method (in J/mol/K).
A quick scan of the deviations of the Vm-calculated Cp(sol,298) values (column 5 in Table 9) immediately shows that the Vm method systematically overestimates the solid heat capacity of the cycloalkanes (norbornane and the dicyclohexyldodecanes being exceptions), whereas that of the ring-free alkanes is systematically underestimated. Although the overestimation in the case of the cycloalkanes resembles the one found in the estimation of their liquid heat capacity, as demonstrated in Table 5, it does not seem far-fetched to assume that at least part of its extent lies in potentially more clearly defined crystalline structures as compared to the probably waxy consistence of the linear counterparts. The predicted Cp(sol,298) values resulting from the present GA method, on the other hand, yield excellent conformation with the experimental data. The largest deviations are interestingly found for norbornane, one of the exceptions in the Vm calculations, and bicyclo[3.3.3]undecane. For norbornane, the experimental value published by Steele [55] should be higher by ca. 8% to fit the respective deviations into the general picture of both prediction methods. For bicyclo[3.3.3]undecane, both prediction methods suggest a ca. 10% higher Cp(sol,298) value than reported by Parker et al. [56].
In conformance with the findings of the logP analysis in an earlier paper [6], the amino acids are assumed to exist in a zwitterionic form as solids (phenylglycine being an exception, as shown in Table 9 of [6], due to the lower basicity of the nitrogen atom conjugated to the phenyl ring). Accordingly, in Table 4, their carboxylate group is represented by entry 74, their alkyl- and dialkyl-ammonium functions by entries 148 and 149, respectively, and their immediate neighbours, the methyl and methylene groups, by the respective entries 4 and 11. Test calculations based on their non-ionic forms resulted in systematically and significantly overestimating the Cp(sol,298) values, indicating that their corresponding atom groups in Table 4, (i.e., entry 73, representing the carboxylic acid, and entries 122 and 125, representing the alkyl- and dialkyl-amino groups, respectively) are not applicable in the heat-capacity evaluation of amino acids. These results, however, should not be interpreted as a confirmation of the zwitterionic form of the amino acids as solids, because the basis for the parameters representing the neutral alkyl- and dialkyl-amino groups is at present too small, and a recalibration of the group parameters of Table 4 by applying the non-ionic instead of the zwitter-ionic forms could well lead to better-conforming GA-based results of the non-ionic forms with the experimental data.
In contrast, analogous comparative calculations based on the Vm method [1] revealed only minor prediction differences between the ionic and the non-ionic forms, which was to be expected as the "true" molecular volumes of both the prototropic forms are very similar. Typical examples listed in Table 10 demonstrate these observations. The MAPD between the experimental data and those calculated for the zwitterionic forms in Table 10 was 3.36 J/mol/K on applying the GA method and 4.02 J/mol/K when using the Vm approach.

Table 10.
Comparison of the Cp(sol,298) data of the ionic and the non-ionic forms of amino acids calculated by the present GA and the Vm [1] method (in J/mol/K).
As a consequence, and despite their excellent predictive quality, both the GA- and the Vm-based methods are not suitable to answer the question as to which form the amino acids exist as solids.
In the optimization process for the evaluation of the atom and special group contributions of Table 7, it turned out that 51 compounds had to be eliminated as outliers and have been collected in a separate list, available in the Supplementary Materials. This list again largely corresponded to the one resulting from the Vm optimization procedure. The remaining 800 compounds finally supported 126 atom and special groups valid for Cp(sol,298) predictions (row A in Table 7). Despite the smaller number of valid groups as compared to that of Table 3 for the liquid heat capacities, with 65% they cover an even slightly larger percentage of ChemBrain’s representative database.
5. Conclusions
The present paper is extending the series of publications [6,7,8,9] about the direct and indirect calculation of 14 molecular properties (enthalpy of combustion, formation, vaporization, sublimation and solvation, entropy of fusion, logPo/w, logS, logγinf, refractivity, polarizability, toxicity, liquid viscosity, and surface tension) by means of a single computer algorithm, adding two further molecular properties, the heat capacity for the liquid and solid phase of molecules. A comparison of the prediction quality of the present GA method for the heat capacities with that based on the "true" molecular volume [1] published recently proved a significantly higher accuracy over the latter. This was accomplished by directly addressing the deficiencies of the molecular volume approach, particularly its inevitable neglect of the intermolecular formation of hydrogen bridges of the OH groups as well as its non-consideration of the cyclization effect of saturated rings over ring-open forms on the heat capacity of both the liquid and solid phases. However, since the group additivity method in principle lacks the comprehensive range of the molecular volume approach, both prediction methods are beneficial in their own right—and they complement each other all the more, as in most cases they confirm each other’s result within explicable deviations. Therefore, in the present ongoing project ChemBrain IXL, version 5.9, available from Neuronix Software (www.neuronix.ch, Rudolf Naef, Lupsingen, Switzerland), the results of both methods are added to the database, the group-additivity result carrying the suffix "calc" and the volume-derived one the suffix "pred".
Supplementary Materials
Supplementary materials can be accessed at https://www.mdpi.com/1420-3049/25/5/1147/s1. The lists of 3D structures of the compounds and their experimental values used for the liquid and solid heat-capacities calculations are available online as standard SDF files under the names names “S01. Compounds List for Cp(liq,298) calculations.sdf” and “S02. Compounds List for Cp(sol,298) calculations.sdf”, respectively. The lists of compounds and their experimental and calculated Cp values are available as doc files under the names " S03. Experimental vs. calculated Cp(liq,298) Data Table.doc" and " S04. Experimental vs. calculated Cp(sol,298) Data Table.doc". The lists of outliers are available as excel files under the names "S05. Outliers of Cp(liq,298) by GA approach.xls" and " S06. Outliers of Cp(sol,298) by GA approach.xls". The figures are available as tif files and the tables as doc files under the names given in the text.
Funding
This research received no funding.
Acknowledgments
R. Naef is indebted to W.E. Acree of the University of North Texas for his support in the collection of literature references and for valuable discussions. He is also indebted to the library of the University of Basel for enabling full and free access to its electronic literature database.
Conflicts of Interest
The author declares no conflict of interest.
Abbreviations
- GA: atom-group additivity
- Vm: "true" molecular volume
References
- Naef, R. Calculation of the isobaric heat capacities of the liquid and solid phase of organic compounds at and around 298.15 K based on their “True” molecular volume. Molecules 2019, 24, 1626. [Google Scholar] [CrossRef] [PubMed]
- Gardas, R.L.; Coutinho, J.A.P. A group contribution method for heat capacity estimation of ionic liquids. Ind. Eng. Chem. Res. 2008, 47, 5751–5757. [Google Scholar] [CrossRef]
- Benson, S.W.; Buss, J.H. Additivity rules for the estimation of molecular properties. Thermodynamic properties. J. Chem. Phys. 1958, 29, 546–572. [Google Scholar] [CrossRef]
- Zàbransky, M.; Ruzicka, V. Estimation of the heat capacities of organic liquids as a function of temperature using group additivity: An amendment. J. Phys. Chem. Ref. Data 2004, 33, 1071–1081. [Google Scholar]
- Chickos, J.S.; Hesse, D.G.; Liebman, J.F. A group additivity approach for the estimation of heat capacities of organic liquids and solids at 298 K. Struct. Chem. 1993, 4, 261–269. [Google Scholar] [CrossRef]
- Naef, R. A generally applicable computer algorithm based on the group additivity method for the calculation of seven molecular descriptors: Heat of combustion, LogPO/W, LogS, refractivity, polarizability, toxicity and LogBB of organic compounds; scope and limits of applicability. Molecules 2015, 20, 18279–18351. [Google Scholar] [CrossRef]
- Naef, R.; Acree, W.E. Calculation of five thermodynamic molecular descriptors by means of a general computer algorithm based on the group-additivity method: Standard enthalpies of vaporization, sublimation and solvation, and entropy of fusion of ordinary organic molecules and total phase-change entropy of liquid crystals. Molecules 2017, 22, 1059. [Google Scholar] [CrossRef]
- Naef, R.; Acree, W.E. Application of a general computer algorithm based on the group-additivity method for the calculation of two molecular descriptors at both ends of dilution: Liquid viscosity and activity coefficient in water at infinite dilution. Molecules 2018, 23, 5. [Google Scholar] [CrossRef]
- Naef, R.; Acree, W.E., Jr. Calculation of the surface tension of ordinary organic and ionic liquids by means of a generally applicable computer algorithm based on the group-additivity method. Molecules 2018, 23, 1224. [Google Scholar] [CrossRef]
- Hardtwig, E. Fehler-und Ausgleichsrechnung. Hochschultaschenbücher 262/262a; Bibliographisches Institut AG: Mannheim, Germany, 1968. [Google Scholar]
- Wong, W.-K.; Westrum, E.F., Jr. Thermodynamics of globular molecules. XVII. Heat capacities and transition behavior of bicyclo[2.2.2]octane and bicyclo[2.2.2]octene. J. Phys. Chem. 1970, 74, 1303–1308. [Google Scholar] [CrossRef]
- Figueroa-Gerstenmaier, S.; Cabanas, A.; Costas, M. Self-association and complex formation in alcohol-unsaturated hydrocarbon systems. Heat capacities of linear alcohols mixed with alkenes and alkynes. Phys. Chem. Chem. Phys. 1999, 1, 665–674. [Google Scholar] [CrossRef]
- Zaitsau, D.H.; Emel’yanenko, V.N.; Pimerzin, A.A.; Verevkin, S.P. Benchmark properties of biphenyl as a liquid organic hydrogen carrier: Evaluation of thermochemical data with complementary experimental and computational methods. J. Chem. Thermodyn. 2018, 122, 1–12. [Google Scholar] [CrossRef]
- Mahnel, T.; Pokorny, V.; Fulem, M.; Sedmidubskym, D.; Ruzicka, K. Measurement of low-temperature heat capacity by relaxation technique: Calorimeter performance testing and heat capacity of benzo[b]fluoranthene, benzo[k]fluoranthene, and indeno[1,2,3-cd]pyrene. J. Chem. Thermodyn. 2020, 142, 105964. [Google Scholar] [CrossRef]
- Chang, S.-S.; Westrum, E.F., Jr. Heat Capacities and Thermodynamic Properties of Globular Molecules. I. Adamantane and Hexamethylenetetramine. J. Phys. Chem. 1960, 64, 1547–1551. [Google Scholar] [CrossRef]
- Mendoza-Ruiz, E.A.; Mentado-Morales, J.; Flores-Segura, H. Standard molar enthalpies of formation and phase changes of Tetra-N-phenylbenzidine and 4,4′-Bis (N-carbazolyl)-1,1′-biphenyl. J. Therm. Anal. Calor. 2019, 135, 2337–2345. [Google Scholar] [CrossRef]
- Van Bommel, M.J.; Van Miltenburg, J.C.; Schuijff, A. Heat-capacity measurements and thermodynamic functions of 1,3,5-triazine and 1,3,5-trioxane. J. Chem. Thermodyn. 1988, 20, 397–403. [Google Scholar] [CrossRef]
- Piekarski, H.; Tkaczyk, M.; Tyczynska, M. Heat capacity and phase behavior of aqueous diethylene glycol n-pentyl ether by DSC. Thermochim. Acta 2012, 550, 19–26. [Google Scholar] [CrossRef]
- Wasiak, M.; Tkaczyk, M.; Piekarski, H. Heat capacity and phase behaviour of aqueous solutions of triethylene glycol monopentyl ether. Two point scaling analysis. Fluid Phase Equil. 2017, 431, 16–23. [Google Scholar] [CrossRef]
- Emel’yanenko, V.N.; Zaitsau, D.H.; Pimerzin, A.A.; Verevkin, S.P. Benchmark properties of diphenyl oxide as a potential liquid organic hydrogen carrier: Evaluation of thermochemical data with complementary experimental and computational methods. J. Chem. Thermodyn. 2018, 125, 149–158. [Google Scholar] [CrossRef]
- Ashrafi, F.; Saadati, R.; Behboodi, A. Modeling and theoretical calculation of liquid heat capacity of alcohols and aldehydes using QSPR. African J. Pure Appl. Chem. 2008, 2, 116–120. [Google Scholar]
- Campos, J.B.; Martinez-Gomez, A.J.; Orozco-Guareno, E. Design and building of an isoperibolic calorimeter: Measurements of enthalpy of formation for derivatives of glycidol. Meas. Sci. Technol. 2019, 30, 035902. [Google Scholar] [CrossRef]
- Buchholz, H.; Hylton, R.K.; Brandenburg, J.G.; Seidel-Morgenstern, A.; Lorenz, H.; Stein, M.; Price, S.L. The thermochemistry of racemic and enantiopure molecular crystals for predicting enantiomer separation. Cryst. Growth Des. 2017, 17, 4676–4686. [Google Scholar] [CrossRef]
- Nikitin, E.D.; Popov, A.P.; Bogatishcheva, N.S.; Faizullin, M.Z. Critical temperatures and pressures, heat capacities, and thermal diffusivities of levulinic acid and four n-alkyl levulinates. J. Chem. Thermodyn. 2019, 135, 233–240. [Google Scholar] [CrossRef]
- Su, C.; Zhu, C.; Ye, F.Y.Z.; Liu, X.; He, M. Isobaric molar heat capacity of ethyl octanoate and ethyl decanoate at pressures up to 24 Mpa. Chem. Eng. Data 2018, 63, 2252–2256. [Google Scholar] [CrossRef]
- Van Bommel, M.J.; Oonk, H.A.J.; Van Miltenburg, J.C. Heat Capacity measurements of 13 methyl esters of n-carboxylic acids from methyl octanoate to methyl eicosanoate between 5 K and 350 K. J. Chem. Eng. Data 2004, 49, 1036–1042. [Google Scholar] [CrossRef]
- Xu, J.; Li, S.; Zeng, Z.; Xue, W. Heat capacity, density, vapor pressure, and enthalpy of vaporization of isoamyl DL-lactate. J. Chem. Eng. Data 2019, 64, 3793–3798. [Google Scholar] [CrossRef]
- Neau, S.H.; Flynn, G.L. Solid and liquid heat capacities of n-alkyl para-aminobenzoates near the melting point. Pharmaceut. Res. 1990, 7, 1157–1162. [Google Scholar] [CrossRef]
- Chorazewski, M.; Goralski, P.; Tkaczyk, M. Heat capacities of 1-chloroalkanes and 1-bromoalkanes within the temperature range from 284.15 K to 353.15 K. A group additivity and molecular connectivity analysis. J. Chem. Eng. Data 2005, 50, 619–624. [Google Scholar] [CrossRef]
- Goralski, P.; Tkaczyk, M.; Chorazewski, M. Heat capacities of α,ω-dichloroalkanes at temperatures from 284.15 K to 353.15 K and a group additivity analysis. J. Chem. Eng. Data 2003, 48, 492–496. [Google Scholar] [CrossRef]
- Lipovska, M.; Schmidt, H.-G.; Rohac, V.; Ruzicka, V.; Wolf, G.; Zabransky, M. Heat capacities of three isomeric chlorobenzenes and of three isomeric chlorophenols. J. Therm. Anal. Calor. 2002, 68, 753–766. [Google Scholar] [CrossRef]
- Goralski, P.; Piekarski, H. Heat capacities and densities of some liquid chloro-, bromo-, and bromochloro-substituted benzenes. J. Chem. Eng. Data 2007, 52, 655–659. [Google Scholar] [CrossRef]
- Michalski, D.; Perry, R.T.; White, M.A. Additivity of guest and host properties in clathrates: A thermodynamic and Raman spectroscopic investigation of HPTB-based solids. J. Phys.: Condens. M. 1996, 8, 1647–1661. [Google Scholar] [CrossRef]
- Roux, M.V.; Temprado, M.; Jimenez, P.; Guzman-Mejia, R.; Juaristi, E.; Chickos, J.S. Heat capacities of thiane sulfones and thiane sulfoxide Refining of Cp group values for organosulfur compounds and their oxides. Thermochim. Acta 2003, 406, 9–16. [Google Scholar] [CrossRef]
- Zhang, Z.Y.; Yang, M.L. Heat capacity and phase transition of 2-amino-2-methyl-1,3-propanediol from 280K to the melting point. Thermochim. Acta 1990, 169, 263–269. [Google Scholar] [CrossRef]
- Chiu, L.-F.; Liu, H.-F.; Li, M.-H. Heat capacity of alkanolamines by differential scanning calorimetry. J. Chem. Eng. Data 1999, 44, 631–636. [Google Scholar] [CrossRef]
- Soares, B.P.; Stejfa, V.; Ferreira, O.; Pinho, S.P.; Ruzicka, K.; Fulem, M. Vapor pressures and thermophysical properties of selected ethanolamines. Fluid Phase Equil. 2018, 473, 245–254. [Google Scholar] [CrossRef]
- Perisanu, S.; Contineanu, I.; Neacsu, A.; Notario, R.; Roux, M.V.; Liebman, J.F.; Dodson, B.J. Thermochemistry and quantum chemical calculations of two dibenzocycloalkane nitriles. Struct. Chem. 2011, 22, 89–94. [Google Scholar] [CrossRef]
- Stejfa, V.; Fulem, M.; Ruzicka, K. Vapor pressure of 4-ethylmorpholine revisited: Thermodynamically consistent vapor pressure equation. J. Chem. Eng. Data 2019, 644, 1605–1610. [Google Scholar] [CrossRef]
- Tyunina, V.V.; Krasnov, A.V.; Tyunina, E.Y.; Badelin, V.G.; Rybkin, V.V. Enthalpies of sublimation of L-methionine and DL-methionine: Knudsen’s effusion mass spectrometric study. J. Chem. Thermodyn. 2019, 135, 287–295. [Google Scholar] [CrossRef]
- Abdelaziz, A.; Zaitsau, D.H.; Buzyurov, A.; Minakov, A.A.; Verevkin, S.P.; Schick, C. Fast scanning calorimetry: Sublimation thermodynamics of low volatile and thermally unstable compounds. Thermochim. Acta 2019, 676, 249–262. [Google Scholar] [CrossRef]
- Stejfa, V.; Fulem, M.; Ruzicka, K. Thermodynamic study of selected monoterpenes IV. J. Chem. Thermodyn. 2019. [Google Scholar] [CrossRef]
- Zhang, G.-Y.; Jin, S.-H.; Li, L.-J.; Li, Z.-H.; Shu, Q.-H.; Wang, D.-Q.; Zhang, B.; Li, Y.-K. Evaluation of thermal hazards and thermokinetic parameters of 3-amino-4-amidoximinofurazan by ARC and TG. J. Therm. Anal. Calor. 2016, 126, 1223–1230. [Google Scholar] [CrossRef]
- Li, R.; Hua, Y.; Tan, Z.; Shi, Q. Low temperature calorimetry of 3-fluoro-5-(3-pyridinyloxy) benzenamine and N-[3-fluoro-5-(3-Pyridinyloxy)phenyl]-N’-3-pyridinyl urea. Intern. J. Thermodyn. 2017, 20, 153–157. [Google Scholar] [CrossRef]
- Baird, Z.S.; Dahlberg, A.; Uusi-Kyyny, P.; Osmanbegovic, N.; Witos, J.; Helminen, J.; Cederkrantz, D.; Hyväri, P.; Alopaeus, V.; Kilpeläinen, I.; et al. Physical properties of 7-methyl-1,5,7-triazabicyclo[4.4.0]dec-5-ene (mTBD). Intern. J. Thermophys. 2019, 40, 71. [Google Scholar] [CrossRef]
- Liu, Y.; Di, Y.; Di, Y.; Qiao, C.; Che, F.; Yuan, F.; Yue, K.; Zhou, C. The studies of structure, thermodynamic properties and theoretical analyses of 2-[(4-nitro-benzoyl)-hydrazone]-propionic acid. J. Mol. Struct. 2019, 1184, 532–537. [Google Scholar] [CrossRef]
- Vilas-Boas, S.M.; Pokorny, V.; Stejfa, V.; Ferreira, O.; Pinho, S.P.; Ruzicka, K.; Fulem, M. Vapor pressure and thermophysical properties of eugenol and (+)-carvone. Fluid Phase Equil. 2019, 499, 112248. [Google Scholar] [CrossRef]
- Skotnicki, M.; Drogon, A.; Calvin, J.J.; Rosen, P.F.; Woodfield, B.F.; Pyda, M. Heat capacity and enthalpy of indapamide. Thermochim. Acta 2019, 674, 36–43. [Google Scholar] [CrossRef]
- Cai, M.; Zhou, T.-H.; Li, Y.-N.; Xu, K.-Z. Two interesting derivatives of 1-amino-1-hydrazino-2,2-dinitroethylene (AHDNE): Synthesis and thermal properties. J. Therm. Anal. Calor. 2019. [Google Scholar] [CrossRef]
- Doncaster, A.M.; Walsh, R. Thermochemistry of silicon-containing compounds. J. Chem. Soc. Faraday Trans. 1986, 82, 707–717. [Google Scholar] [CrossRef]
- Waliszewski, D.; Stepniak, I.; Piekarski, H.; Lewandowski, A. Heat capacities of ionic liquids and their heats of solution in molecular liquids. Thermochim. Acta 2005, 433, 149–152. [Google Scholar] [CrossRef]
- Lopez-Bueno, C.; Bugallo, D.; Leboran, V.; Rivadulla, F. Sub-μL measurements of the thermal conductivity and heat capacity of liquids. Phys.Chem.Chem.Phys. 2018, 20, 7277. [Google Scholar] [CrossRef] [PubMed]
- Zaitsau, D.H.; Schmitz, A.; Janiak, C.; Verevkin, S.P. Heat capacities of ionic liquids based on tetrahydrothiophenium cation and NTf2 anion. Thermochim. Acta 2020, 686, 178547. [Google Scholar] [CrossRef]
- Huelsekopf, M.; Ludwig, R. Temperature dependence of hydrogen bonding. J. Mol. Liq. 2000, 85, 105–125. [Google Scholar] [CrossRef]
- Steele, W.V. The standard enthalpies of formation of a series of C7 bridged-ring hydrocarbons: Norbornane, norbornene, nortricyclene, norbornadiene, and quadricyclane. J. Chem. Thermodyn. 1978, 10, 919–927. [Google Scholar] [CrossRef]
- Parker, W.; Steele, W.V.; Watt, I. A high-precision aneroid static-bomb combustion calorimeter for samples of about 20 mg. The standard enthalpy of formation of bicyclo[3.3.3]undecane. J. Chem. Thermodyn. 1975, 7, 795–802. [Google Scholar] [CrossRef]
Sample Availability: Samples of the compounds are not available. |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).