Abstract
Recently, the author suggested a simple and composite equation of state by incorporating fundamental thermodynamic properties like heat capacities into her earlier concise equation of state for gases based on free volume and molecular association / dissociation. This work brings new results for aqueous solutions, based on the analogy of the equation of state for gases and solutions over wide ranges of pressures (for gases) and concentrations (for solutions). The definitions of entropy and heat energy through the equation of state for gases also hold for solutions.
1. Concise equation of state for aqueous solutions
The recent paper [1] on a concise equation of state for gases incorporating thermodynamic laws and entropy, was based on van’t Hoff’s ideal law analogy found valid [2] for higher pressures (for gases) and concentrations (for solutions). For aqueous solutions, the following concise equation of state was established for strong electrolytes like NaCl(aq) for all concentrations [2],
where π and VA are the osmotic pressure and total volume of water (A) respectively of a solution containing one mole (consisting of one molecular weight) of solute at temperature T, R is the molar gas constant, Vh is the volume of water held as hydration by one mole of solute, i [= 1 + (ν - 1) α] is the van't Hoff factor representing the actual number of moles of solute due to partial dissociation of one mole of the electrolyte into να ions and (1 - α) ion pairs, α is the degree of dissociation, ν is the number of moles into which one mole of solute dissociates at infinite dilution and Vf is the free (subscript f) volume of solvent per mole of solute. For a non-electrolyte like sucrose in water, i = 1. The values of π, Vh and i can be evaluated from the available data on osmotic coefficients as described in [2].
π(VA - Vh)/i = πVf = RT
Note that equation (1) is not the ideal law, πV = RT (although similar in mathematical form) but with Vf in place of V, the total volume of solution. As π → 0, i → ν and πVf → RT (ideal law). The equations presented earlier for gases [1], also hold for solutions (with subscript s, and with osmotic pressure π in place of pressure P for gases). For an easier comparison with the equations established for gases [1], this paper is written in a similar way.
2. Equation of state incorporating heat capacities
The above equation (1) can be combined with the heat capacity at constant osmotic pressure 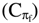 and constant volume (CVf) respectively, defined here on the free volume per mole basis. The ideal heat capacity difference is equal to the gas constant. Since the ideal law and equation (1) here are of the same form with Vf in place of V, the heat capacity difference is substituted here for R in equation (1) to obtain a new composite equation of state based on π, V, T and thermodynamic quantities,
and constant volume (CVf) respectively, defined here on the free volume per mole basis. The ideal heat capacity difference is equal to the gas constant. Since the ideal law and equation (1) here are of the same form with Vf in place of V, the heat capacity difference is substituted here for R in equation (1) to obtain a new composite equation of state based on π, V, T and thermodynamic quantities,
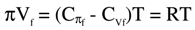 Small changes dπ, dVf and dT of π, Vf and T in equation (2) are related by,
Small changes dπ, dVf and dT of π, Vf and T in equation (2) are related by,
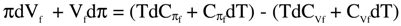
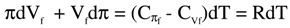 where
where 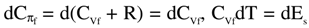 is the change in internal energy (Es) of the solution, πdVf = -dAs = RTdlnVf is the work of expansion (dilution, for solution), denoted as change in Helmholtz free energy (As) for the solution,
is the change in internal energy (Es) of the solution, πdVf = -dAs = RTdlnVf is the work of expansion (dilution, for solution), denoted as change in Helmholtz free energy (As) for the solution, 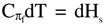 is the change in enthalpy (Hs), and -Vfdπ= -dGs = - RTdlnπ is the work of compression, denoted as the change in Gibbs free energy (Gs). Thus,
is the change in enthalpy (Hs), and -Vfdπ= -dGs = - RTdlnπ is the work of compression, denoted as the change in Gibbs free energy (Gs). Thus,
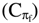 and constant volume (CVf) respectively, defined here on the free volume per mole basis. The ideal heat capacity difference is equal to the gas constant. Since the ideal law and equation (1) here are of the same form with Vf in place of V, the heat capacity difference is substituted here for R in equation (1) to obtain a new composite equation of state based on π, V, T and thermodynamic quantities,
and constant volume (CVf) respectively, defined here on the free volume per mole basis. The ideal heat capacity difference is equal to the gas constant. Since the ideal law and equation (1) here are of the same form with Vf in place of V, the heat capacity difference is substituted here for R in equation (1) to obtain a new composite equation of state based on π, V, T and thermodynamic quantities,
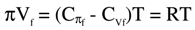
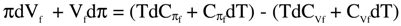
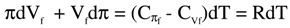
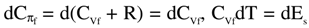 is the change in internal energy (Es) of the solution, πdVf = -dAs = RTdlnVf is the work of expansion (dilution, for solution), denoted as change in Helmholtz free energy (As) for the solution,
is the change in internal energy (Es) of the solution, πdVf = -dAs = RTdlnVf is the work of expansion (dilution, for solution), denoted as change in Helmholtz free energy (As) for the solution, 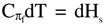 is the change in enthalpy (Hs), and -Vfdπ= -dGs = - RTdlnπ is the work of compression, denoted as the change in Gibbs free energy (Gs). Thus,
is the change in enthalpy (Hs), and -Vfdπ= -dGs = - RTdlnπ is the work of compression, denoted as the change in Gibbs free energy (Gs). Thus,
-dAs + dGs = dHs - dEs = RdT
3. Equation of state, heat, entropy and partition function
On rearranging the terms in equations (3), one finds that
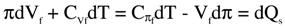 where dQs, the amount of heat energy absorbed by the solution, causes a temperature change dT and volume change dVf at osmotic pressure π, or osmotic pressure change dπ at volume Vf, as per Helmholtz’s definition, Es - As = TS, where S is the entropy. Thus, equations (5) are the energy conservation laws in accordance with the 1st law of thermodynamics.
where dQs, the amount of heat energy absorbed by the solution, causes a temperature change dT and volume change dVf at osmotic pressure π, or osmotic pressure change dπ at volume Vf, as per Helmholtz’s definition, Es - As = TS, where S is the entropy. Thus, equations (5) are the energy conservation laws in accordance with the 1st law of thermodynamics.
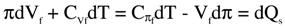
-dAs + dEs = dHs - dGs = d(TS) = dQs
From the relation between partition function (f) and molar entropy [3],
where W is the maximum probablitity of existence at the given π, V, T and the last term comes from the Helmholtz relation. Note that Es = RT2(dlnf/dT)V and dEs = CVfdT from equations (5), -As = RTlnf and -dAs = RTdlnf = RTdlnVf. The partition function is [1]
where VdB = (ΛdB)3, ΛdB = (h/p) is the de Broglie wavelength [4], h is the Planck constant and p is the linear momentum of the solute.
S = RlnW = Es/T + Rlnf = (Es - As)/T
f = Vf/VdB = RT/πVdB
Thus, from equations (5), Qs, the heat energy, can be defined as in the case of gases [1] (for the first time) as,
Qs = Es - As = Hs - Gs = TS = RTlnW = πVflnW
This shows that the solution at any given π, V, T has a heat energy, Qs and it is related to the internal energy Es, enthalpy Hs, the free energies As and Gs and entropy S as shown by equation (8). At T = 0, Q = 0 (and S is chosen as zero at T = 0, as per the 3rd law). Since the above quantities have standard values (Eo, Ho, Ao, Go and So) at STP, the standard value of Qo = Eo – Ao = Ho – Go = ToSo at STP. In the case of NaCl(aq), So = 115.48 J.mol-1K-1 at 25 oC as per the data in [5]. This allows one to obtain Qo as ToSo = 34.43 kJ.mol-1. The difference in Qs in any two states, ΔQs = Q - Qo = ΔE - ΔA = ΔH - ΔG = Δ(TS).
4. Equation of state, entropy and reversibility
In a reversible process consisting of isothermal expansion (dVf) at temperature T1 accompanied by a heat change dQπ = πd(VflnW) = T1dS (see equation (8)) followed by isothermal compression (dπ) at T2 accompanied by a heat change dQVf = Vfd(πlnW) = T2dS, (as in a Carnot cycle), the net change dQπ - dQVf• 0, but
Thus the ratio dQ/T is of significance for a reversible process [and it gave rise to the notion of entropy as dQ/T = S (instead of dS!) and that S – S = 0 for a reversible process (2nd law of thermodynamics). Note the inconsistency that S is also sometimes defined as δQ/T or qrev/T].
dQπ/T1 - dQVf/T2 = dS - dS = 0
It is to be noted that dQ is the sum of two terms:
The free energy terms in equations (5) depend on dS and dT as follows:
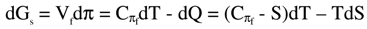 For an isothermal process, dT = 0 and dAT = dGT = -TdS = dQT.
For an isothermal process, dT = 0 and dAT = dGT = -TdS = dQT.
dQ = TdS + SdT
-dAs = πdVf = dQ - CVfdT = TdS + (S - CVf)dT
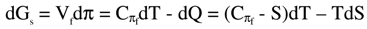
Thus, entropy, heat capacities and the thermodynamic laws are integral parts of the new equation of state, equation (2).
Acknowledgment
This work was supported by Grant No. 101/02/U111/CZ.
References
- Heyrovská, R. A new concise equation of state for gases incorporating thermodynamic laws, entropy and partition function. In Quantum Limits to the Second Law, First International Conference; AIP Conference Proceedings No. 643; Sheehan, D.P., Ed.; San Diego, California, 2002; pp. 157–162, and the literature therein. [Google Scholar]
- Heyrovská, R. Physical electrochemistry of solutions of strong electrolytes. Chemické Listy 1998, 92, 157–166. (in English), and the literature therein. [Google Scholar]
- Moelwyn-Hughes, E.A. Physical Chemistry; Pergamon: London, 1967. [Google Scholar]
- Hill, T.L. Statistical Mechanics; Dover: New York, 1987. [Google Scholar]
- Bard, A.J.; Parsons, R.; Jordan, J. Standard Potentials in Aqueous Solution; Marcel Dekker, Inc.: New York, 1985. [Google Scholar]
© 2004 by MDPI (http://www.mdpi.org). Reproduction for noncommercial purposes permitted.