Abstract
The nature of the thermodynamic behavior of Type I superconductor particles, having a cross section less than the Ginzburg-Landau temperature dependent coherence length, ξ(T), is discussed for magnetic field induced adiabatic phase transitions from the superconductive state to the normal state. Argument is advanced supporting the view that when the adiabatic magneto-caloric process is applied to particles, the phase transition is characterized by a decrease in entropy in violation of traditional formulations of the Second Law, evidenced by attainment of a final process temperature below that which would result from an adiabatic magneto-caloric process applied to bulk dimensioned specimens.
INTRODUCTION
The adiabatic phase transition of bulk dimensioned Type I superconductors has been studied extensively both theoretically and experimentally [1,2,3,4,5,6,7,8,9]. This paper investigates Second Law implications of relaxation phenomena in the adiabatic phase transition of particles of dimension on the order of the Ginzburg-Landau temperature dependent coherence length, ξ(T), typically 10−4 to 10−5 centimeters.
The Discussion begins with a summary description of the adiabatic phase transition (adiabatic magneto-caloric effect) of bulk Type I superconductors, which is used in the latter parts of the Discussion for comparative reference to the particle dimensioned transition description. The Ginzburg-Landau Theory will provide the basis for discussion of the particle dimensioned transition process. The major object of this paper is to provide a direction for experimental investigations in this area.
DISCUSSION
A. Description of the Adiabatic Phase Transition of Bulk Dimensioned Specimens
If a thermally isolated superconductor specimen of bulk dimension having a cross-section, d, defined by d >> ξ(T), is driven normal at finite temperature by application of a magnetic field, self-cooling will occur because of the difference in entropy between the superconductive and normal phases [9]. The final temperature attained is easily calculated by considering the process as a series of infinitesimal volume phase transitions as the magnetic field is slowly increased [7], taking account of the latent heat evolution as the relative proportion of phase which is superconductive becomes normally conductive, and the volume specific heats of the normal and superconductive phase regions which supply the evolving latent heat energy. The transition of an infinitesimal volume, ΔV, from the superconductive to the normal phase is described by:
where Cn and Cs are, respectively, the normal and superconductive specific heats, Vn and Vs are, respectively, the instantaneous normal and superconductive phase volumes, T1, and T2 are, respectively, the starting and ending temperatures of the transition process of the elemental volume, ΔV, and Sn and Ss are, respectively, the normal and superconductive phase entropies at T1.
The process under which this occurs, the adiabatic magneto-caloric effect, leads to an isentropic phase transition [6] involving the appearance of a mixture of superconductive and normal phases. Since the transition is the result of a series of infinitesimal increases in the external magnetic field, H, an increase in specimen free energy is expected [7] as magnetic work is done against the remaining diamagnetic regions of the specimen, given by:
where ΔF is the change in the Gibbs free energy of the specimen, H1 and H2 are, respectively, the critical magnetic fields at the initial temperature, T1, and the final temperature, Tf, attained by the transition of the entire specimen volume, and where M is the specimen magnetization and is related to H by the expression:
where the instantaneous value of VS is defined from equation (1) and the parabolic relation (Tuyn Curve) for the thermodynamic critical field:
where H2 is the critical field at T2, H0 is the critical field at absolute zero, Tc is the critical temperature in zero field, and T2 is defined by equation (1).
M = −H/4πVS
H2 = H0(1 − (T2/Tc)2)
Utilizing the foregoing equations, the adiabatic magneto-caloric effect phase transition process has been calculated for a bulk dimensioned tin specimen using the specific heat data of Bryant and Keesom, [10] with a finite starting temperature selected for exemplary purposes of .65Tc. The result, showing the change in proportion of the specimen in the superconductive phase versus reduced temperature of the specimen, is summarized in Figure 1. Comparison with the experimental results of Yaqub [9] shows good agreement.
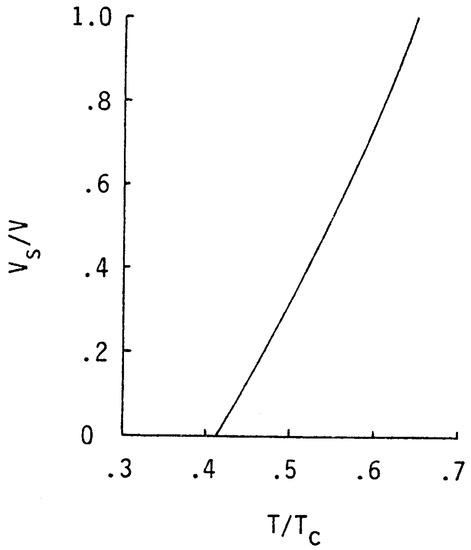
Figure 1.
The thermodynamic state of a bulk dimensioned tin specimen during an adiabatic phase transition is illustrated using equations developed in part A of the Discussion, where the starting temperature is .65TC. Shown is the variation in superconductive phase volume as a function of reduced temperature during a bulk size specimen adiabatic magneto-caloric process starting in the superconductive phase and ending in the normal phase. The final temperature achieved is 0.416TC.
As the latent heat is evolved due to infinitesimal phase volume changes, the temperature falls, while concomitantly the free energy increases as magnetic work is done against remaining superconductive regions of the specimen. The specimen entropy is constant, given by:
The reversibility of the adiabatic magneto-caloric effect has been experimentally verified: a normal to superconductive phase transition results in a heating accompanied by a decrease in specimen free energy [1].
B. Description of the Adiabatic Phase Transition of Particle Dimensioned Specimens
Attention shall now be directed to the magneto-caloric effect phase transition applied to a single superconductive particle of cross section d < ξ(T), or alternatively, an ensemble of such particles sufficiently insulated both electrically and thermally such as to be considered mutually non-coupled as well as environmentally non-interactive.
When the cross-section of a Type I superconductor particle becomes less than the Ginzburg-Landau temperature dependent coherence length, ξ(T), it is not energetically favorable for the specimen to be in a state of mixed phase [11,12]. This can be understood as follows. The spatial parameter ξ(T) defines the large finite spatial distance required for the Ginzburg- Landau order parameter, Ψ, of the superconductive electrons to go to zero, while simultaneously the spatial parameter λ(T) defines the relatively short spatial distance required for the applied magnetic field at the surface to go to zero interiorly. These spatial parameters collectively result in an appreciable positive interphase boundary surface energy in the presence of an external magnetic field when the diamagnetic and condensation energy potentials are accounted at the interface [11,13]. Hence, the free energy for a particle where λ(T)/ξ(T) << 1 is minimized when the particle is all superconducting or all normal in phase, a result first posited by Pippard in 1952 [11]. An experiment conducted on tin whiskers by Lutes and Maxwell [14] provides support for this view. The whiskers had a demagnetizing coefficient of one-half, meaning the intermediate state should exhibit during the phase transition process in the presence of an increasing transverse magnetic field at finite temperature. However, Lutes and Maxwell observed an abrupt transition from the superconductive to the normal phase without the appearance of the intermediate state.
Performing an adiabatic magneto-caloric process upon such a particle dimensioned specimen, therefore, cannot proceed in the familiar way of a bulk dimensioned specimen as was detailed above, since a mixture of phase state is not permissible for a particle. The transition, consequently, is characterized by an abrupt variation in magnetization, the time for which is limited by the rate of flux movement out of the particle [2], accompanied by thermal relaxation. Since the change in magnetization occurs homogeneously upon attainment of the critical field, work will not be invested in raising the applied magnetic field further, since the particle is entirely non-magnetic. Thus, the free energy will remain unchanged during the phase transition.
Under ideal conditions, during which the latent heat evolution follows completely the magnetization variation, the cooling expected, as defined by Tf, is found from the expression:
since the entropy variance is defined uniquely at the transition temperature, T1, and involves the entire volume, rather than a series of temperatures and infinitesimal volumes as occurs in the bulk dimensioned adiabatic magneto-caloric process. Notice that this expression is similar to equation (1) except here the entire volume undergoes simultaneous phase transition. Accordingly, the process is not isentropic, as is the case for a bulk dimensioned specimen, but rather, the end point entropy at Tf is less than the beginning point entropy at T1, in clear circumvention of the Second Law. This net lowering of entropy is explained by an absence of external energy contributions to the (particle sized) specimen during the transition in the form of magnetodynamic work performed against remaining diamagnetic regions (as would occur in bulk specimens) as the field is increased. More particularly, the difference in entropy of phase for a superconductor is given by the relation:
Hence, a comparison of the final entropies for the bulk and particle dimensioned specimens, as a result of an adiabatic magneto-caloric process with the same initial thermodynamic coordinates, would yield an entropy difference given by:
where M is defined by equation (3). The final process temperature attained for a particle dimensioned specimen will, therefore, be lower than that observed for bulk dimensioned specimens according to the relation:
where the subscript f defines final process values and where Tb is the final temperature achieved for a magneto-caloric process performed on a bulk dimensioned specimen.
Sn − Ss = −(1/4)πHcdHc/dT
C. Factors Affecting the Transition of Particle Dimensioned Specimens
When the specimen cross-section becomes on the order of ξ(T), an effect noted frequently in thin film experiments can become evident. This has to do with variation in the Ginzburg-Landau order parameter, Ψ, with applied magnetic field in very small dimensioned specimens. For particles of size d < √5λ(T), the Ginzburg-Landau Theory predicts [15] that when the critical magnetic field is applied, the order parameter will have gone smoothly to zero, meaning that a second order phase transition will occur, with no accompanying latent heat. Douglass [16] has calculated the effect of decreasing film thickness upon the BCS energy gap, Δ(T). Recognizing the order parameter is proportional to the energy gap, Douglass considers the case of a thin film in a parallel magnetic field under the assumption that the energy gap is independent of position; and in solving the Ginzburg-Landau equations, Douglass defines a ratio, Φ, where Φ = Δ(H)/Δ(H0) = Ψ(H)/Ψ(H0)), and a special case thereof, Φc, where Φc = Ψ(Hc)/Ψ(H0). Finally, Douglass predicts Φc as a function of specimen cross-section.
Because the order parameter is reduced by application of Hc for cross-sections less than 10λ(T), the latent heat evolution will be reduced likewise. Thus, for particles having dimension of √5λ(T) < d, no adiabatic magneto-caloric effect can occur; for particles having dimension of √5λ(T) < d < 10λ(T), a first order phase transition will occur, but the observed adiabatic magneto-caloric effect will be reduced dependent on the affect of Φc on the magnitude of the latent heat evolution at T1; and for particles having dimension of d > 10λ(T), no diminution in the adiabatic magneto-caloric effect will be observed due to size effects, the process being defined by equation (6).
When the cross-section of a particle dimensioned specimen exceeds ξ(T), a less pronounced abruptness in the variation of the magnetization is expected. For particle dimensions where ξ(T) < d < 10ξ(T), at least some measurable degree of abruptness in the transition should be observed. For the case where d > ξ(T), the transition can be visualized as a continuous phase variation process, not unlike that involved in the bulk dimensioned case, with the last nucleus of superconducting phase having a cross section of d = ξ(T) undergoing an abrupt transition in magnetization. Support for this view is found in the phase transition experiments of Faber [17], who found nucleation sites to be of a cross-section on the order of ξ(T). Thus, by assigning a bulk adiabatic magneto-caloric process to the specimen volume exceeding a nucleus of d = ξ(T) as described by equation (1), and then utilizing equation (6) to describe the transition of the nucleus, the effect of increasing cross-sectional diameter is determinable.
The effect of particle size on the adiabatic phase transition can be predicted by modification of the process defining equation (6) to include the above defined ratio Φc for reduction in the order parameter at Hc, as follows:
Figure 2 illustrates the effect of size on the adiabatic magneto-caloric effect phase transition of aluminum from the superconductive phase to the normal phase utilizing the techniques outlined above and published specific heat data [10,18] for particle cross-sections ranging from √5λ(T) < d < 5ξ(T). The starting temperature, T1, is arbitrarily .65Tc.
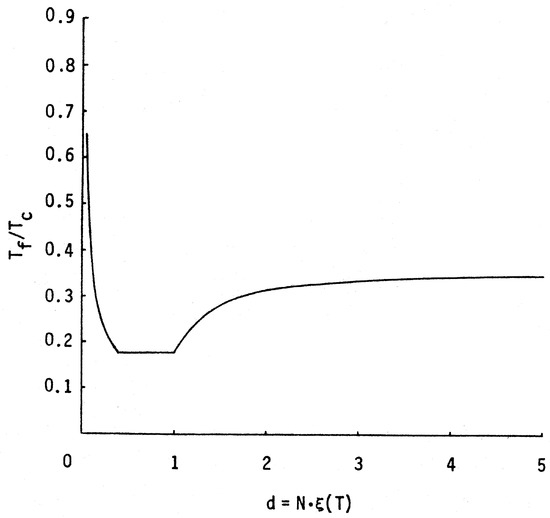
Figure 2.
The adiabatic magneto-caloric effect phase transition dependency on specimen cross-section is indicated by plotting the variation in the process reduced final temperature, Tf, as a function of specimen thickness in units of ξ(T). For reference, the final temperature for a bulk dimensioned specimen adiabatic magneto-caloric effect is 0.348Tc, and the lowest Tf plotted is 0.174Tc. For all Tf lower than 0.348Tc, the Second Law is violated.
It must be noted, however, that these calculations are not rigorous, as they are based on the Ginzburg-Landau Theory which applies more aptly to situations where T1 is very close to Tc. Douglass [19] has experimentally measured the energy gap at Hc for aluminum, where ξ(T)/λ(T) = 32, as a function of film thickness, and found that for d > 5λ(T), the order parameter remains essentially unchanged at Hc. Thus, Type I superconductors should have Φc behaviors less sensitive to cross-section than the Ginzburg-Landau Theory would predict. As such, the range of specimen cross-section over which Tf is below that for the bulk dimensioned specimen is probably more pronounced than the range shown in Figure 2.
The discussion thus far has assumed near perfect isolation of the particles, thereby precluding both mutual coupling and external connection heat transfer modes. Heat transfer to the environment will clearly limit the cooling effect of the latent heat evolution at T1 on the specimen temperature, causing Tf to be closer to T1 than Figure 2 would predict. Coupling between particles in an ensemble would have a similar effect on Tf due to adjacent particle heat exchange, which, in effect, would suggest a macroscopic magneto-caloric effect behavior for the ensemble, not unlike that of a bulk dimensioned specimen. This view is based on the fact that at any one time a minimum of ensemble free energy can be attained during an adiabatic magneto-caloric process if some of the particles become normal while others remain superconductive as the external field is slowly increased - essentially the situation in the bulk dimensioned specimen adiabatic magneto-caloric effect phase transition. Particle isolation, therefore, is a prerequisite to observing the effects predicted in Figure 2.
Another factor affecting the transition has to do with hysteresis in the critical magnetic field, which, if present, will generate Joule heating in the particle upon phase variation. Joule heating will cause an increase in the value of Tf predicted in Figure 2, since the diamagnetic energy will exceed the reversible Meissner effect energy, (Hcb)2/8π. Also of note is that the value of the critical field will be lower in the event the particle has a non-zero demagnetizing coefficient. This would follow from the above reported experiments by Lutes and Maxwell on tin whiskers. Since the exhibition of hysteresis is a maximum at absolute zero [20], where no latent heat is associated with the phase transition, any potential barriers inhibiting the particle phase variation can be predicted from isothermal transition models, as well as means to modify those expectancies [11,17,20,21,22,23].
Finally, the effect of particle size on the specific heat function will be considered. Experiments performed on tin particles by Tsuboi and Suzuki [24] and also Rao, Garland and Tanner [25] suggest that for specimen diameters of about one-quarter the Ginzburg-Landau temperature dependent coherence length at absolute zero, ξ(0), values for the superconductive specific heat are essentially the same as that observed for bulk dimensioned specimens. Thus, for specimens greater in cross section than about d = (1/4)ξ(T), transition models may employ bulk values for the specific heat calculation with confidence.
CONCLUSION
This paper describes an adiabatic magneto-caloric effect phase transition from the superconductive phase to the normal phase in which the Second Law is shown to be violated, provided the particle is a Type I superconductor having a cross-section, d, defined by 5λ(T) < d < ξ(T). Process cycles based on the adiabatic magneto-caloric effect phase transition applied to Type I superconductor particles having 5λ(T) < d < ξ(T) which extract work directly from ambient heat are possible [26,27].
REFERENCES
- Keesom, W.; Kok, J. Further Calorimetric Experiments on Thallium. Physica 1934, I, 595–608. [Google Scholar] [CrossRef]
- Keesom, W.; Van Laer, P. Relaxation Phenomena in the Transition from the Supraconductive to the Non-Supraconductive State. Physica 1936, III, 173–181. [Google Scholar] [CrossRef]
- Keesom, W.; Van Laer, P. Measurements of the Latent Heat of Tin passing from the Supraconductive to the Non-Supraconductive State. Physica 1936, III, 371–384. [Google Scholar] [CrossRef]
- Keesom, W.; Van Laer, P. Measurements of the Latent Heat of Tin While Passing from the Superconductive tto the Non-Superconductive State at Constant Temperature. Physica 1937, IV, 487–493. [Google Scholar] [CrossRef]
- Keesom, W.; Van Laer, P. Relaxation Phenomena in Superconductivity. Physica 1937, IV, 499–502. [Google Scholar] [CrossRef]
- Dolecek, R.L. Adiabatic Magnetization of a Superconductor. Phys. Rev. 1951, 82, 102. [Google Scholar] [CrossRef]
- Shoenberg, D. Superconductivity; Cambridge Univ. Press: London, 1952. [Google Scholar]
- Dolecek, R.L. Adiabatic Magnetization of a Superconducting Sphere. Phys. Rev. 1954, 96, 25–28. [Google Scholar] [CrossRef]
- Yaqub, M. Cooling By Adiabatic Magnetization of Superconductors. Cryogenics 1960, 1, 101–107. [Google Scholar] [CrossRef]
- Bryant, C.; Keesom, P. Low-Temperature Specific Heat of Indium and Tin. Phys. Rev. 1961, 123, 491–499. [Google Scholar] [CrossRef]
- Pippard, A.B. Magnetic Hysteresis in Superconducting Colloids. Phil. Mag. 1952, 43, 273–284. [Google Scholar] [CrossRef]
- Whitehead, C.S. The Magnetic Properties of Some Superconducting Mercury Colloids. Proc. Roy. Soc. 1956, A238, 175–193. [Google Scholar] [CrossRef]
- Pippard, A.B. The Surface Energies of Superconductors, Proc. Camb. Phil. Soc. 1951, 47, 617–625. [Google Scholar]
- Lutes, O.; Maxwell, E. Superconducting Transitions in Tin Whiskers. Phys. Rev. 1955, 97, 1718–1720. [Google Scholar] [CrossRef]
- Shigi, T.; Uchiho, K.; Nakaya, S. Dependence of the Energy Gap in Tin Films on Magnetic Field and Film Thickness by Electron Tunnelling. J. Phys. Soc. of Jap. 1968, 24, 82–91. [Google Scholar] [CrossRef]
- Douglass, D.H., Jr. Magnetic Field Dependence of the Superconducting Energy Gap. Phys. Rev. Lett. 1961, 6, 346–348. [Google Scholar] [CrossRef]
- Faber, T.E. The Phase Transition in Superconductors. Proc. Roy. Soc. 1952, A214, 392–412. [Google Scholar] [CrossRef]
- Dixon, M.; Hoare, F.E.; Holden, T.M.; Moody, O.E. The Low Temperature Specific Heats of Some Pure Metals (Cu, Ag, Pt, Al, Ni, Fe, Co). Proc. Roy. Soc. 1965, A285, 561–580. [Google Scholar] [CrossRef]
- Douglass, D.H., Jr. Direct Experimental Measurement of the Magnetic Field Dependence of the Superconducting Energy Gap of Aluminum. Phys. Rev. Lett. 1961, 7, 14–16. [Google Scholar] [CrossRef]
- Baldwin, J.P. Hysteresis in Superconducting Phase Transitions in Tin Films. Phys. Lett. 1963, 3, 223–226. [Google Scholar] [CrossRef]
- Pippard, A.B. Trapped Flux in Superconductors. Phil. Trans. Roy. Soc. 1955, A248, 97–125. [Google Scholar] [CrossRef]
- Caswell, H. Magnetic Hysteresis in Superconducting Thin Films. J. of Appl. Phys. 1965, 36, 80–84. [Google Scholar] [CrossRef]
- Feder, J.; McLachlan, D.S. Superheating and Supercooling in Single Spheres of Tin, Indium, and Gold-Plated Indium. Phys. Rev. 1969, 177, 763–776. [Google Scholar] [CrossRef]
- Tsuboi, T.; Suzuki, T. Specific Heat of Superconducting Fine Particles of Tin. I. Fluctuations in Zero Magnetic Field. J. Phys. Soc. of Jap. 1977, 42, 437–444. [Google Scholar] [CrossRef]
- Rao, N.A.H.K.; Garland, J.C.; Tanner, D.B. Thermodynamic Transition of Small Superconducting Particles. Phys. Rev. B1 1984, 29, 1214–1217. [Google Scholar] [CrossRef]
- Keefe, P.D. Coherent Magneto-Caloric Effect Superconductive Heat Engine Process Cycle. United States Patent 4,638,194, 1987. [Google Scholar] [CrossRef]
- Keefe, P.D. Coherent Magneto-Caloric Effect Heat Engine Process Cycle, Quantum Limits to the Second Law: First International Conference. AIP Proceedings CP643 2002, CP643, 213–218. [Google Scholar]
© 2004 by MDPI (http://www.mdpi.org). Reproduction for noncommercial purposes permitted.