Sum Capacity for Single-Cell Multi-User Systems with M-Ary Inputs
Abstract
:1. Introduction
2. System Model
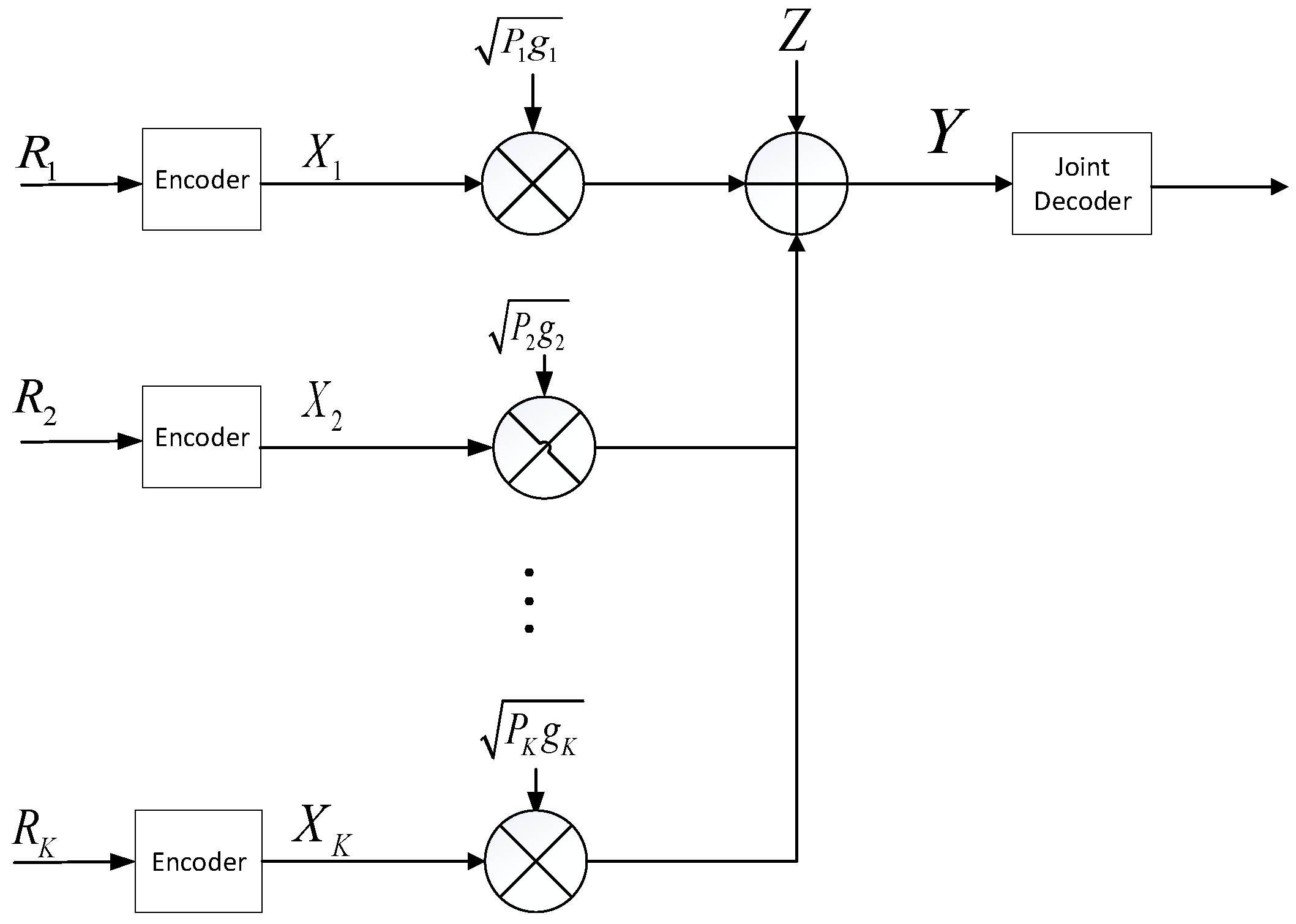
2.1. Multiple Assess Channel
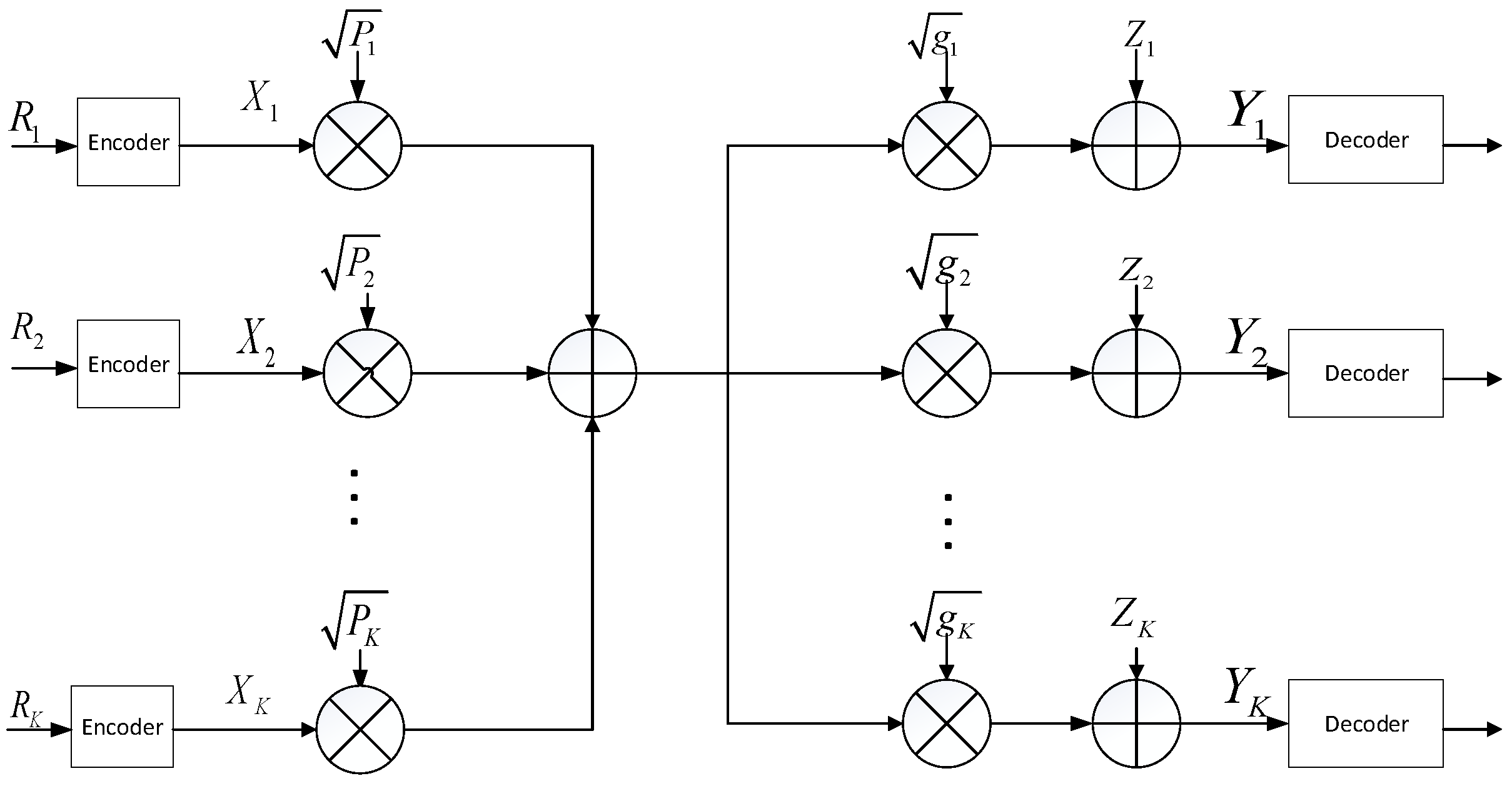
2.2. Broadcast Channel
3. Entropy Power and the Parallelization of MAC and BC
3.1. Entropy Power
3.2. Parallelization for MAC
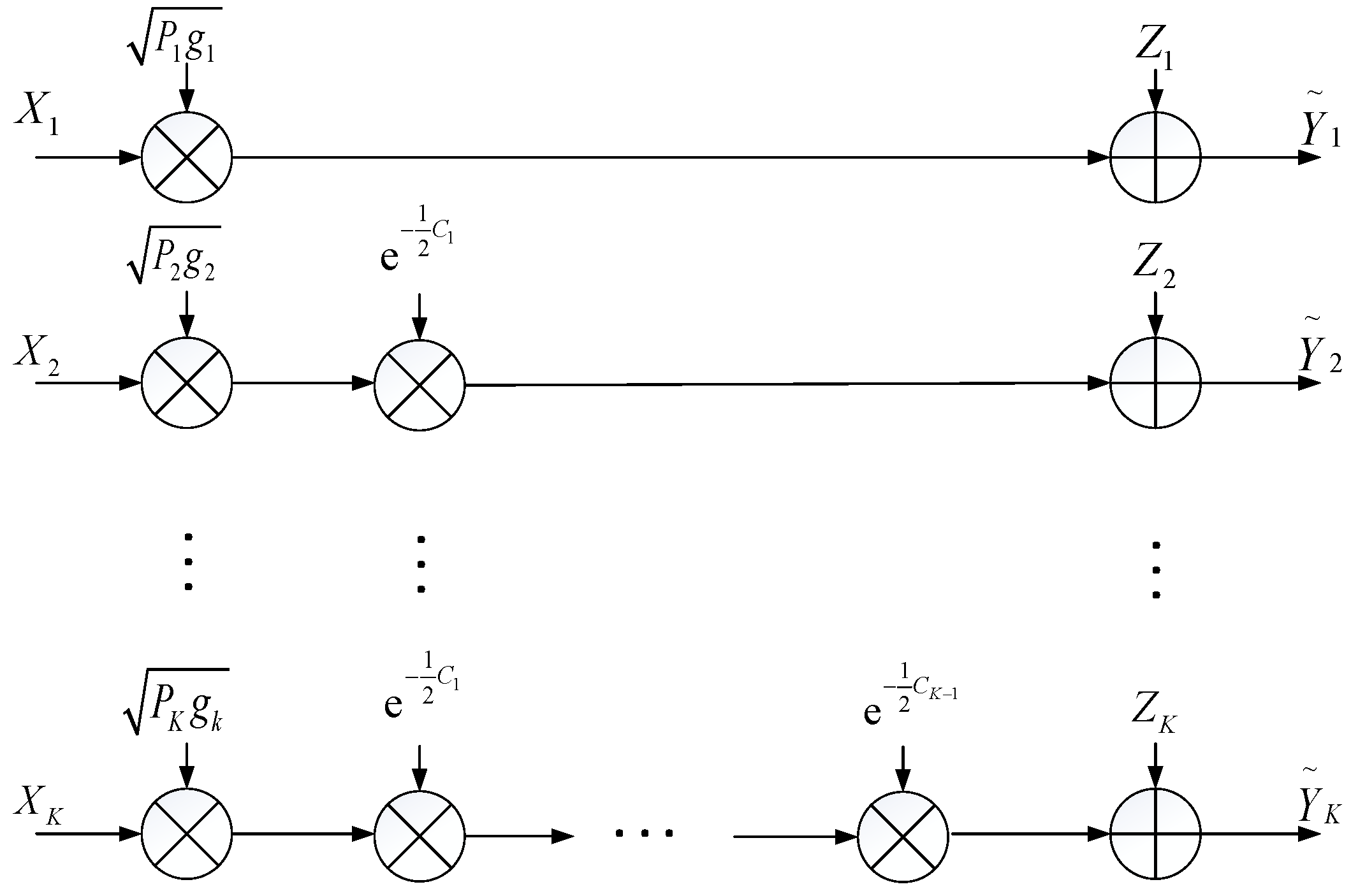
3.3. Parallelization for BC
4. Sum Capacity for MAC with Different Power Allocation Strategies
4.1. Equal Power Distribution
4.2. Power Allocation for Equal Capacity
4.3. Optimal Power Allocation for Maximum Sum Capacity
| Algorithm 1 Optimal Power Allocation Algorithm. |
| Step 1: initialize: set , set . |
| Step 2: Calculate . |
| Step 3: Let and be the maximum and minimum values of . |
| Step 4: and . |
| Step 5: Goto Step 2 if the incremental of is large than a threshold. |
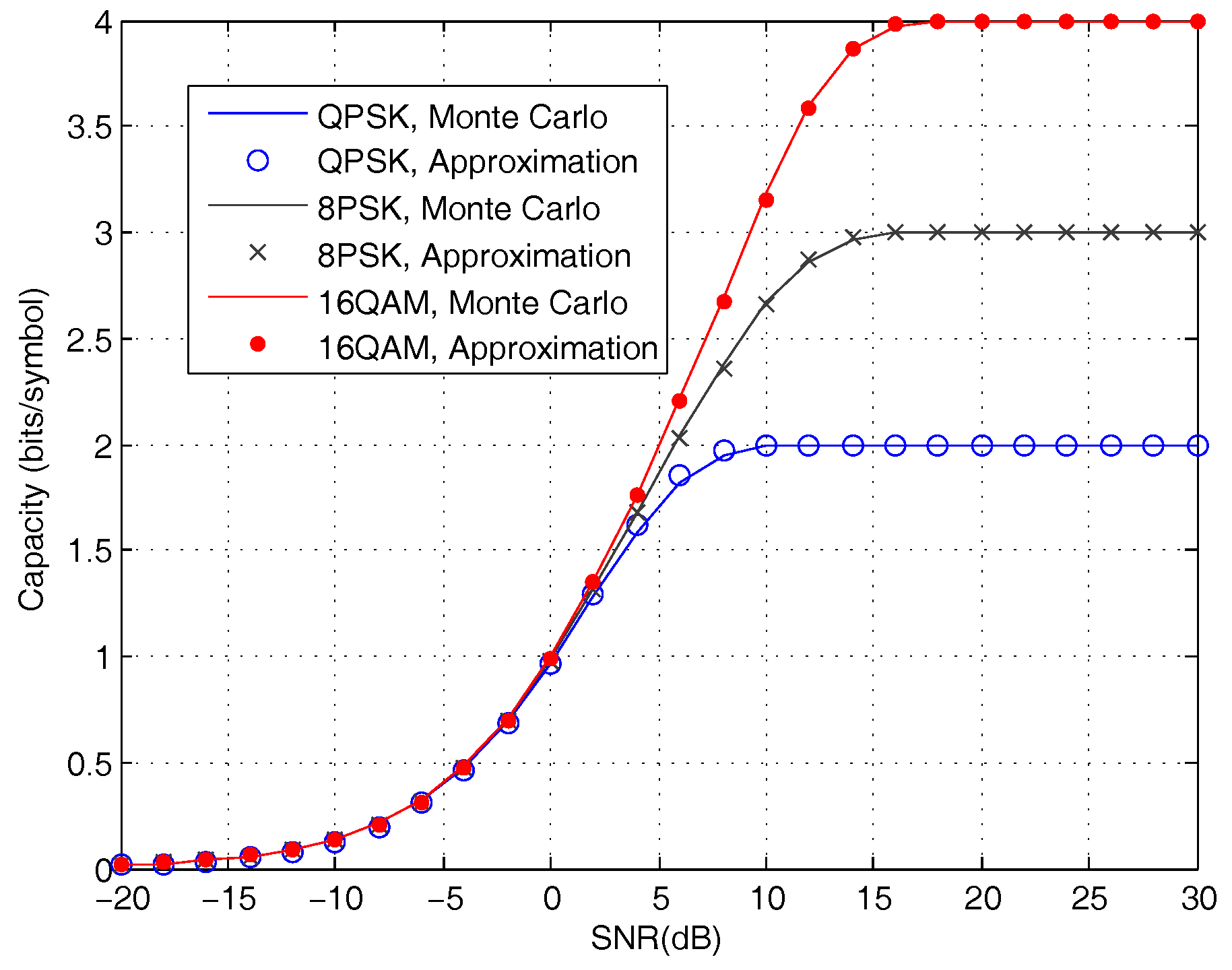
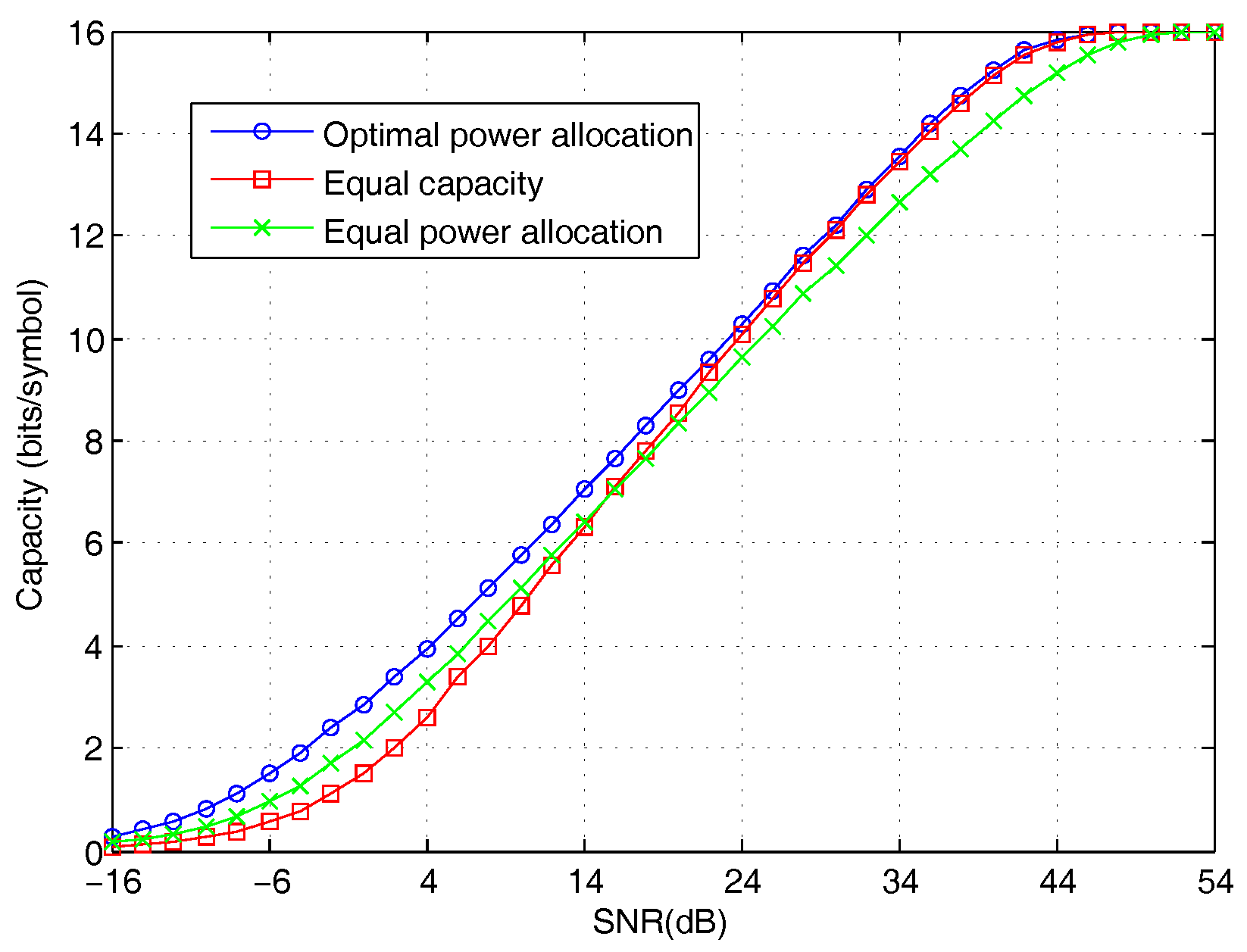
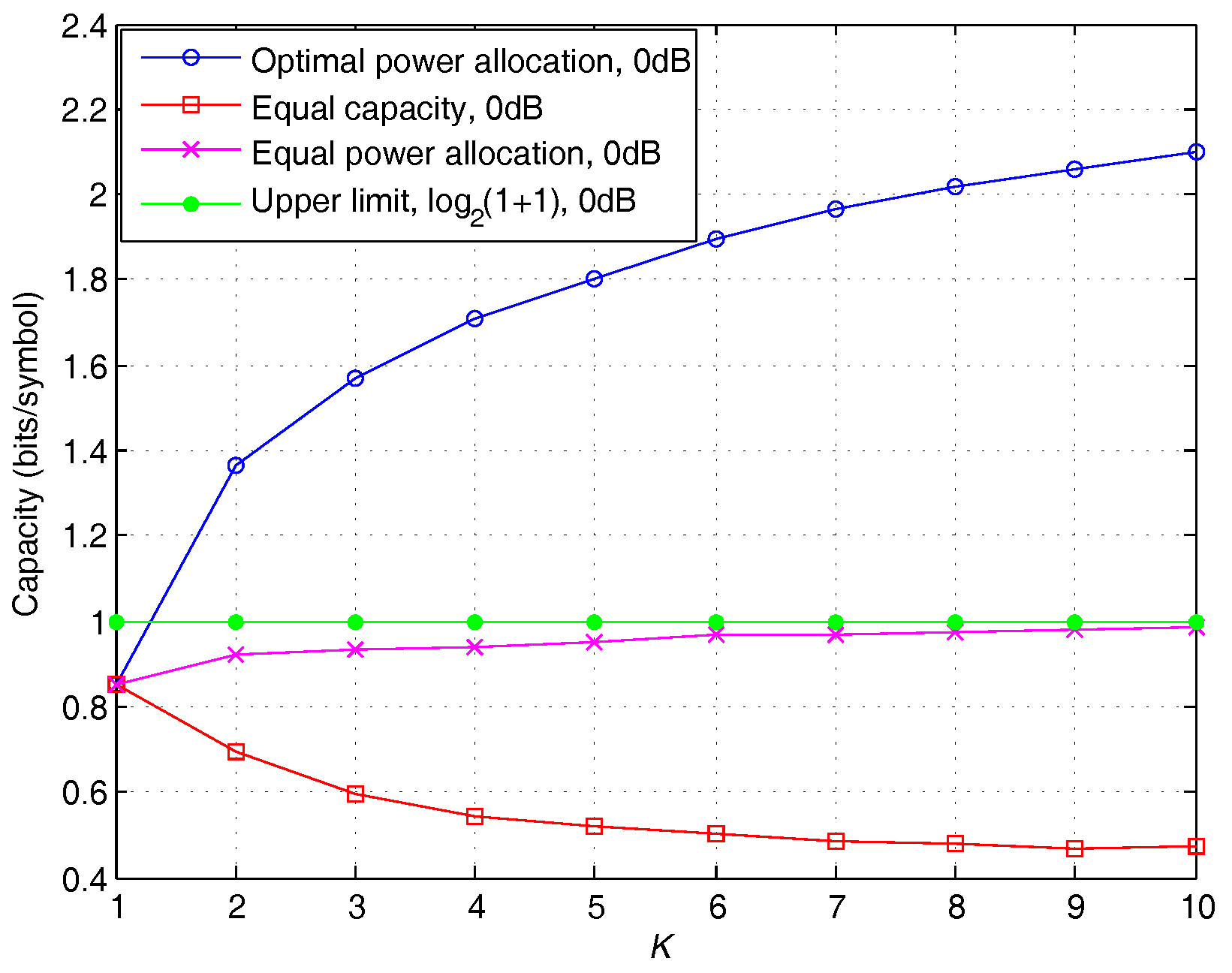
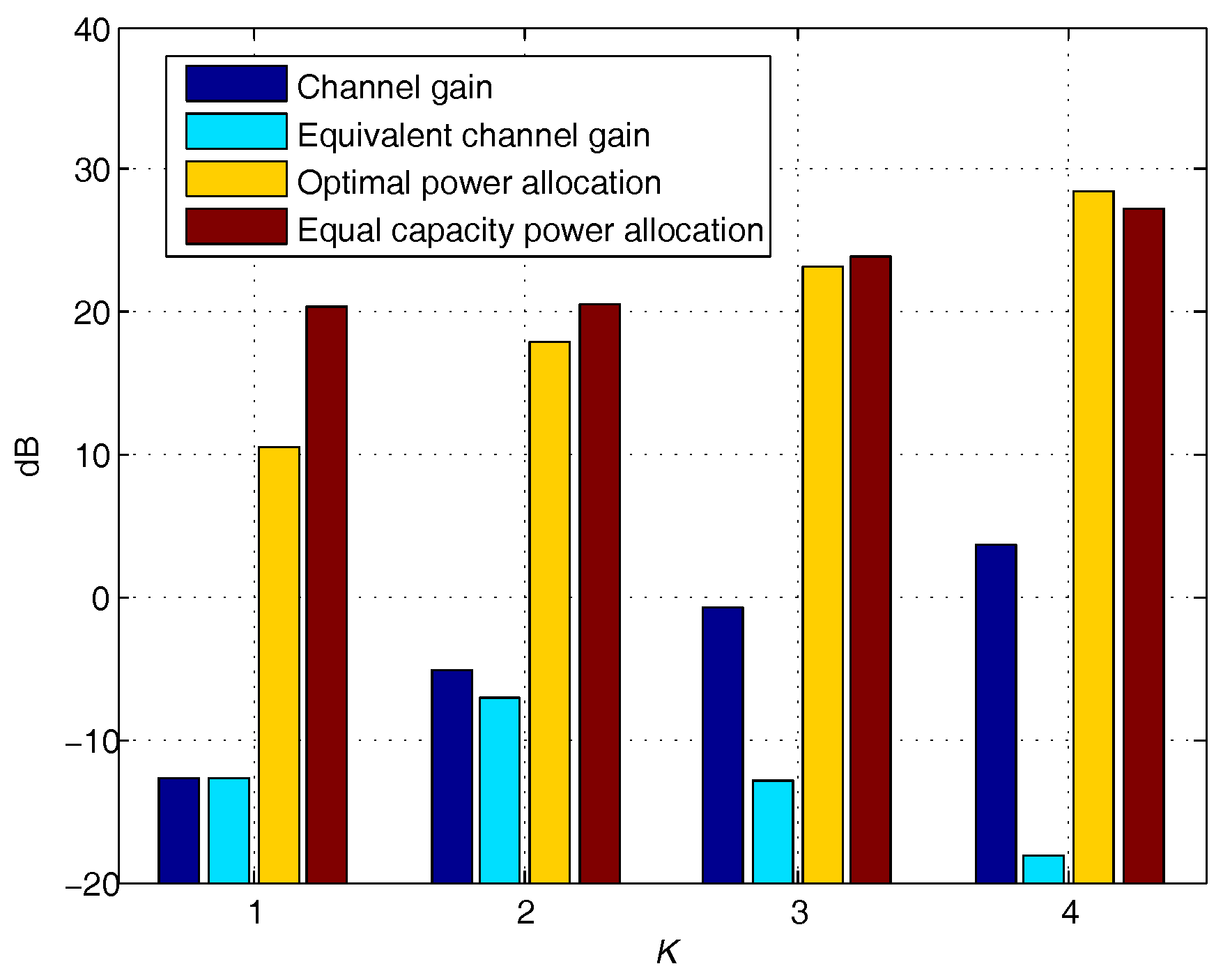
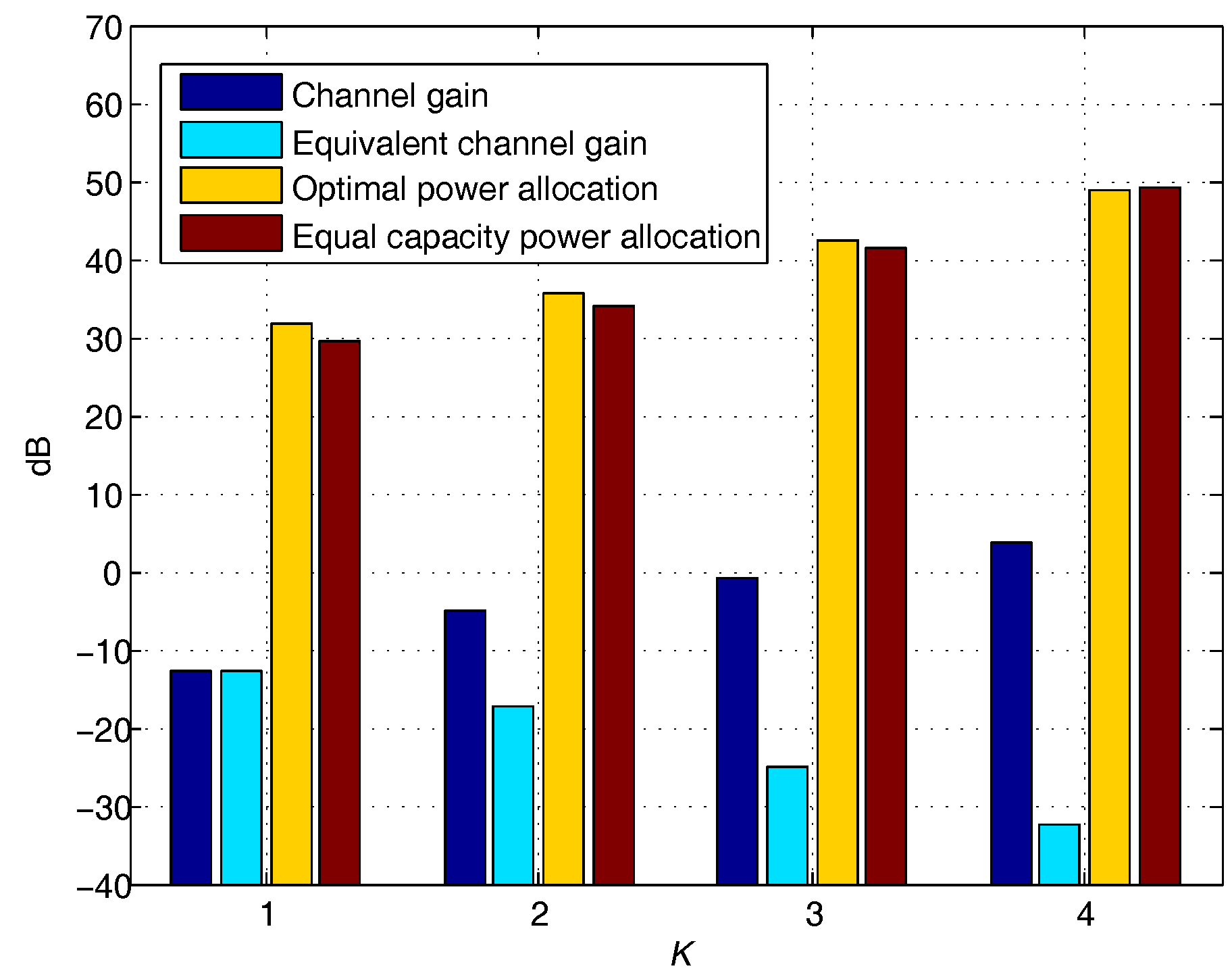
5. Numerical Results
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Jindal, N.; Vishwanath, S.; Goldsmith, A. On the duality of Gaussian multiple-access and broadcast channels. IEEE Trans. Inf. Theory 2004, 50, 768–783. [Google Scholar] [CrossRef]
- Goldsmith, A. Multiuser systems. In Wireless Communications; Cambridge University Press: Cambridge, UK, 2005; pp. 297–314. [Google Scholar]
- Tse, D.; Viswanath, P. Multiuser capacity and opportunistic communication. In Fundamentals of Wireless Communication; Cambridge University Press: Cambridge, UK, 2005; pp. 228–278. [Google Scholar]
- Cover, T.M.; Thomas, J.A. Multiuser Information Theory. In Elements of Information Theory; Wiley: New York, NY, USA, 2012; pp. 509–609. [Google Scholar]
- Benfarah, A.; Tomasin, S.; Laurenti, N. Power Allocation in Multiuser Parallel Gaussian Broadcast Channels With Common and Confidential Messages. IEEE Trans. Commun. 2016, 64, 2326–2339. [Google Scholar] [CrossRef]
- Yang, S.; Jiang, T. Closed-Form Optimal Power Allocation for Weighted Rate Sum Maximization in Gaussian Broadcast Channel. IEEE Trans. Commun. 2012, 60, 1782–1787. [Google Scholar] [CrossRef]
- Jiang, W.; Cui, Y. Comments on “Closed-Form Optimal Power Allocation for Weighted Rate Sum Maximization in Gaussian Broadcast Channel”. IEEE Trans. Commun. 2014, 62, 316–319. [Google Scholar] [CrossRef]
- He, P.; Zhao, L. Optimal Power Allocation for Maximum Throughput of General MU-MIMO Multiple Access Channels with Mixed Constraints. IEEE Trans. Commun. 2016, 64, 1042–1054. [Google Scholar] [CrossRef]
- Liang, J.; Wang, X.; Zhang, W. Capacity Theorem and Optimal Power Allocation for Frequency Division Multiple-Access Relay Channels. In Proceedings of the IEEE Global Telecommunications Conference (GLOBECOM), Kathmandu, Nepal, 5–9 December 2011. [Google Scholar]
- Kang, X. Optimal Power Allocation for Fading Cognitive Multiple Access Channels: A Two-User Case. IEEE Wirel. Commun. Lett. 2013, 6, 683–686. [Google Scholar] [CrossRef]
- Fong, S.L.; Tan, V.Y.F. A Proof of the Strong Converse Theorem for Gaussian Multiple Access Channels. IEEE Trans. Inf. Theory 2016, 62, 4376–4394. [Google Scholar] [CrossRef]
- Romero, H.P.; Varanasi, M.K. The K-User Vector Gaussian Multiple-Access Channel With General Messages Sets: Capacity, Polymatroidal Structure, and Efficient Computation. IEEE Trans. Inf. Theory 2017, 63, 3875–3893. [Google Scholar]
- Lin, L.; Ma, X.; Liang, C.; Huang, X.; Bai, B. An Information-Spectrum Approach to the Capacity Region of the Interference Channel. Entropy 2017, 19, 270. [Google Scholar] [CrossRef]
- Baccarelli, E. Asymptotically tight bounds on the capacity and outage probability for QAM transmissions over Rayleigh-faded data channels with CSI. IEEE Trans. Commun. 1999, 47, 1273–1277. [Google Scholar] [CrossRef]
- Slimane, S.B. Approximation to the symmetric capacity of Rayleigh fading channels with multi-level signals. IEEE Commun. Lett. 2006, 10, 129–131. [Google Scholar] [CrossRef]
- Yang, P.; Wu, Y.; Yang, H. Capacity of Nakagami-m Fading Channel With BPSK/QPSK Modulations. IEEE Commun. Lett. 2017, 21, 564–567. [Google Scholar] [CrossRef]
- Yang, P.; Jin, L.; Yang, H. An improved approximation formula for the symmetric capacity of 2-dimentional constellations under AWGN channel. In Proceedings of the 2016 International Conference on Computer Science, Technology and Application (CSTA2016), Changsha, China, 2016; World Scientific: Singapore, 2016. [Google Scholar]
- Ungerboeck, G. Channel coding with multilevel/phase signals. IEEE Trans. Inf. Theory 1982, 28, 55–67. [Google Scholar] [CrossRef]
- Rioul, O. Information theoretic proofs of entropy power inequalities. IEEE Trans. Inf. Theory 2011, 57, 33–55. [Google Scholar] [CrossRef]
- Verdú, S.; Guo, D. A simple proof of the entropy-power inequality. IEEE Trans. Inf. Theory 2006, 52, 2165–2166. [Google Scholar]
- Shannon, C.E.; Weaver, W. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Lozano, A.; Tulino, A.M.; Verdú, S. Optimum power allocation for parallel Gaussian channels with arbitrary input distributions. IEEE Trans. Inf. Theory 2006, 52, 3033–3051. [Google Scholar] [CrossRef]
- Fletcher, R. The Theory of Constrained Optimization. In Practical Methods of Optimization; Wiley: New York, NY, USA, 1987; pp. 195–224. [Google Scholar]





| Modulation | a | b | N |
|---|---|---|---|
| QPSK | 1 | 0.6507 | 1 |
| 8PSK | 0.6130 | 0.1681 | 2 |
| 0.3855 | 0.8992 | ||
| 16QAM | 0.7177 | 0.1225 | 2 |
| 0.2804 | 0.8702 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, P.; Wu, Y.; Jin, L.; Yang, H. Sum Capacity for Single-Cell Multi-User Systems with M-Ary Inputs. Entropy 2017, 19, 497. https://doi.org/10.3390/e19090497
Yang P, Wu Y, Jin L, Yang H. Sum Capacity for Single-Cell Multi-User Systems with M-Ary Inputs. Entropy. 2017; 19(9):497. https://doi.org/10.3390/e19090497
Chicago/Turabian StyleYang, Pei, Yue Wu, Liqiang Jin, and Hongwen Yang. 2017. "Sum Capacity for Single-Cell Multi-User Systems with M-Ary Inputs" Entropy 19, no. 9: 497. https://doi.org/10.3390/e19090497
APA StyleYang, P., Wu, Y., Jin, L., & Yang, H. (2017). Sum Capacity for Single-Cell Multi-User Systems with M-Ary Inputs. Entropy, 19(9), 497. https://doi.org/10.3390/e19090497





