Abstract
The Stock Exchange is basically ruled by the extreme market sentiments of euphoria and fear. The type of sentiment is given by the color of the candlestick (white = bullish sentiments, black = bearish sentiments), meanwhile the intensity of the sentiment is given by the size of it. In this paper you will see that the intensity of any sentiment is astonishingly distributed in a robust, systematic and universal way, according to a law of exponential decay, the conclusion of which is supported by the analysis of the Lyapunov exponent, the information entropy and the frequency distribution of candlestick size.
1. Introduction
As it is known, Japanese candlesticks allow the identification of the open-high-low-close chart (OHLC) prices and the trend (black or bearish vs. white or bullish) [1,2,3]. The hypothesis guiding this work is: “The intensity of emotions (bearish, bullish or both) is distributed as a universal manner according to a law of exponential decay”. To understand the concepts underlying the hypothesis, the following situations must be considered:
Case A: Imagine that in D1 view the Japanese candlesticks show a decline in the gold price at a rate of USD 1 per day (i.e., black candlesticks will be observed where Open − Close = 1).
Case B: Imagine that in the same D1 view is observed a decline in the gold price at a rate of USD 50 per day (i.e., black candlesticks will be observed where Open − Close = 50).
It is evident that the fear that the gold holders feel in the case B will be much higher than the fear that the gold holders feel in the case A feel. In this paper we assume as true the following approximation that is derived from the Japanese Candlesticks Patterns Analysis: the intensity of emotions (bullish or bearish) is directly proportional to the size of the candlestick [4]. On the other hand, continuing with the cases A and B, it is evident that in a specified period of observation (e.g., one year), the case A will occur at a higher frequency than the case B, which shows that the frequency that traders experience great emotions decreases with increasing intensity of emotion (or the size of the candlestick).
This paper focuses on providing evidence supporting the possibility that the intensity of emotions is distributed according to an invariant formula whose expression is:
where x is the size of the candlestick, λ is a constant and N is the number of candlesticks in the range whose class mark is x.
N = No·exp(−λx)
2. Literature Review
While there are various graphical ways to represent the evolution of the market (candlesticks, lines, point and figures, etc.) [4,5,6,7], it is usually considered that the view that provides more information is known as the “Japanese candlesticks chart” [8,9,10]. The trading techniques based on Japanese candlesticks are based on thorough research conducted at the Rice Market in Osaka by the trader Munehisa Homma during the eighteenth century, who recorded his rules in 1755 in the book entitled “The Fountain of Gold—The Three Monkey Record of Money” [11,12]. These techniques were unknown in the West until Steve Nison wrote about them in 1991 when he published the book “Japanese Candlestick Charting Techniques: A Contemporary Guide to the Ancient Investment Techniques of the Far East” [4].
This paper is based on the counting and classification of the candlesticks according to their length, because this is related to the use of technical indicators such as: Mass Index of Donald Dorsey (considering the length High–Low), Bollinger Bands (based on the standard deviation or length |Close-Moving Average|), Vortex index of Etienne Botes and Douglas Siepman (using High–Low distances outdated over time), etc. [13,14,15,16]. The preprocessing of the OHLC prices is meant to determine what type of format gives more information. This is the reason why the largest Lyapunov exponent base 2 (bits) and the information entropy base e were applied in various ways to express the price. To calculate the largest Lyapunov exponent, the Wolf et al. [17] algorithm was used along with the support of the paper of Zhou et al. [18]. To calculate the information entropy, the Grassberger and Proccaccia algorithm was used, along with the analysis that can be found in Shanon and He et al. [19,20,21].
3. Methodology
A mathematical way of expressing the working hypothesis is as follows:
- Let x be the size of a candlestick
- Let I be an interval of width equal to x centered x, which is calculated as follows:I = [x − Δx/2, x + Δx/2]
- Let N be the number of candlesticks found in the interval I
- Then, we affirm that: N = No·exp(−λx)
Corollary: “The most intense sentiments occur less frequently than the least intense sentiments”.
The preprocessing of the original data (OHLC prices for every trading day) is required to determine what type of format gives more information (for instance, the price or the derivative of price). After analyzing different alternatives, in this paper, the relevant results are presented and these correspond to those related to the calculation of the information entropy and the largest Lyapunov exponent of the median price and the extension of the candlestick (peak to peak amplitude, similar value to the rate of change of the price).
Median price P is defined as:
while the extension E of the candlestick is:
P = (High + Low)/2
E = High − Low
4. Data Preprocessing
The analyzed financial instruments in this paper were USA30, GBPUSD, IBM and Copper and the data were the OHLC prices of every available day in the History Center of the trading account of the researcher. It is evident that the data must be transformed to a value representing the situation every day, which is the reason why many combinations were tested, to obtain the median price and the candlestick length (2 and 3 equalities). After that we analyzed which of the two formats provided more information, which is the reason why the largest Lyapunov exponent base 2 and the information entropy were calculated; the latter is understood as the sum of the positive Lyapunov exponents (base e).
Forth the largest Lyapunov exponent (LLE) the Wolf et al. algorithm was used [14]. According to Table 1 it can be observed that the LLE values are of the order of 0.3 for the median price, and the order of 0.6–0.7 for the extension or peak to peak amplitude. This means that, using the criteria, for the largest Lyapunov exponent, the variable “extension” shows greater chaos than the median price. At this point it is important to mention that Zhou et al. [18], states the following with respect to the Lyapunov exponent base e:
“When the maximum Lyapunov exponent exceeds zero, the system exhibits chaos. If it is greater than one, the predictable limit is less than the sampling frequency. Thus, the chaotic time series predictions are only of practical use when the chaotic system with the maximum Lyapunov exponent is between zero and one. If the positive exponent approaches zero, long-term predictions are possible.”

Table 1.
Largest Lyapunov Exponent (LLE) according Wolf et al. algorithm.
Therefore, Table 1 allows us to conclude that the E length of the candlesticks shows greater chaos than the median price. In addition, both series exhibit greater predictability horizon than the sampling interval (daily), which is either considered with base e or base 2.
Then the entropy or amount of information of each series was studied. Table 2 indicates that the extension of candlesticks contains higher entropy than the median price. Note that it may be considered that the reciprocal of the entropy is roughly the predictability horizon according to Sprott and Rowlands [22].

Table 2.
Information Entropy base e according to Grassberger and Procaccia algorithm.
Considering the results presented in Table 1 and Table 2, it is clear that the E length of the candlestick has on average twice as much information as the median price.
This implies that the trading rules must be based mainly on the peak to peak amplitude instead of the price of the financial instrument, a proof that supports the Japanese candlesticks theory. This is the reason why, in this paper, the parameter E is studied in the following sections. It is important to mention that the proportion between the E length and the size of the real body of the candlestick in certain occasions can provide information about important processes that happen in the Stock Market. If we call u to E/(size of the real body), then a Marubozu candlestick will have u = 1, while a Doji candlestick will have u >> 1 (or also u = a/0 or 0/0). The fact of watching a Marubozu candlestick indicate a process where the inertia of the Market is high (sustained bearish or bullish trend), while a Doji candlestick indicates that the Market is experiencing indecision (a tie between bulls and bears) [23,24,25].
5. Results
The working hypothesis states that the intensity of sentiments is distributed according to an exponential decay law. We also know that the intensity of sentiments can be measured from the size of candlesticks (in this case, E length).
For the first statistic, we will use the financial instrument known as USA30 with data ranging from 1 April 2010 to 12 February 2016. Table 3 shows the E lengths distribution of USA30, which can be seen in Figure 1a. The fitting of the curve was found to be:
The R2 value was equal to 0.9980.
N = 2175exp(−0.010E)

Table 3.
Candlesticks distribution for USA30 with E length.
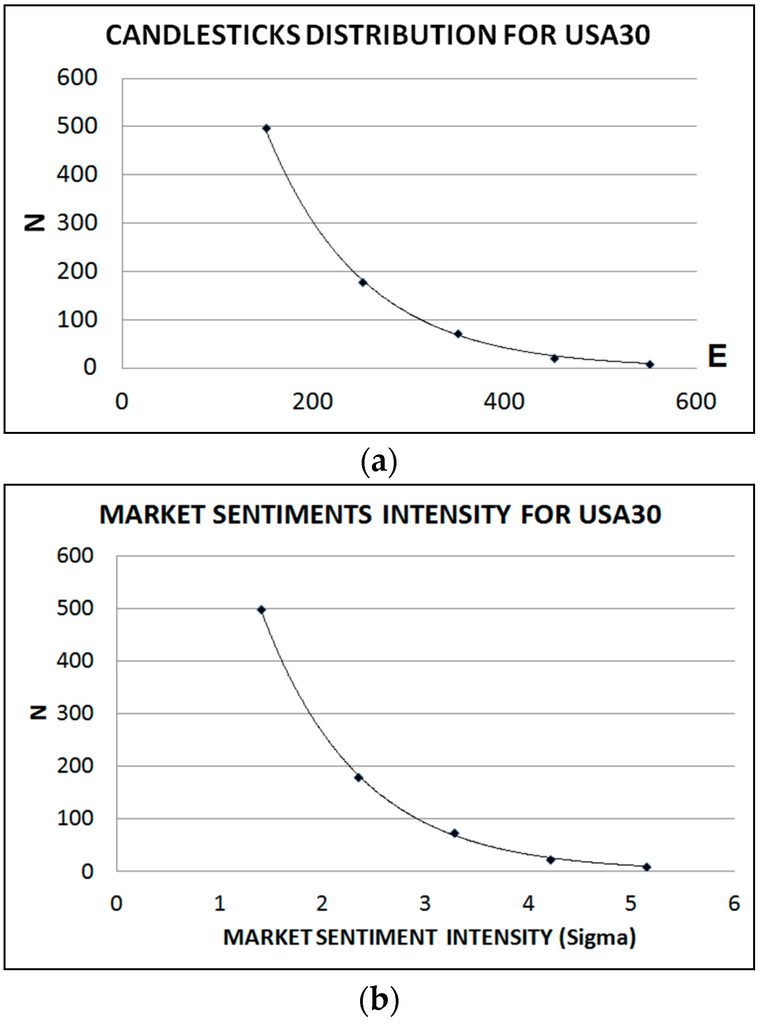
Figure 1.
(a) Candlesticks distribution for USA30 with E length; (b) Market sentiments intensity for USA30 in σ units (σ = 107).
Note that, according to our main argument, it is permissible to label the X axis (E length or peak to peak amplitude) as “Market sentiment intensity” and measure this new variable in standard deviation units, which has been made and shown in Figure 1b.
Later, the hypothesis was tested using the IBM shares with data ranging from 2 January 2008 to 12 February 2016. Table 4 shows the E lengths distribution of IBM shares, which can be seen in Figure 2. The fitting of the curve is:
The R2 value was equal to 0.9775.
N = 11623exp(−0.886E)

Table 4.
Candlesticks distribution for IBM shares with E length.
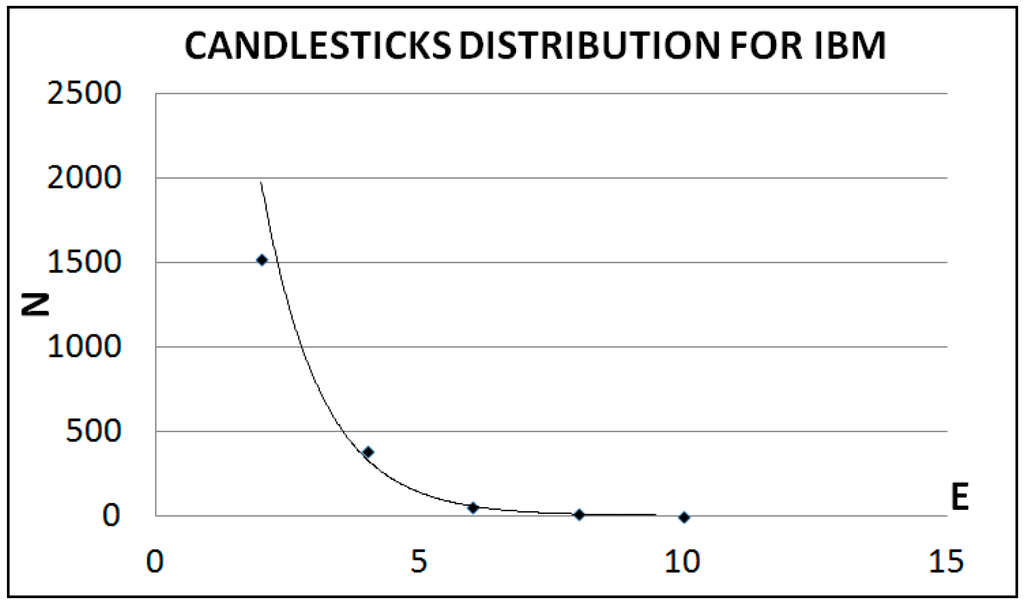
Figure 2.
Candlesticks distribution for IBM shares with E length.
Afterwards, the GBP/USD pair was used with the E length measured in cents, during the period 1 July 2009 to 12 February 2016. The Table 5 shows the results and you can see the chart in Figure 3. The fitting of the curve is:
And the R2 value was equal to 0.9712.
N = 8706exp(−1.744E)

Table 5.
Candlesticks distribution for GBP/USD with E length.
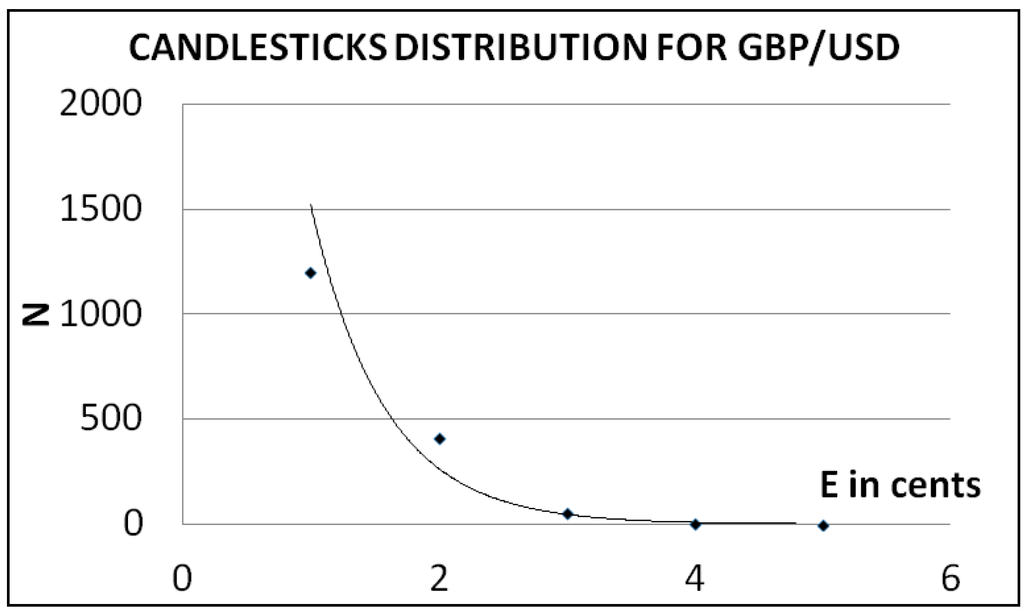
Figure 3.
Candlesticks distribution for GBP/USD with E length in cents.
Finally, we repeated the test with the price of Copper with the E length in cents, during the period 1 October 2013 to 12 February 2016. Table 6 shows the results and you can see the chart in Figure 4. The fitting of the curve is:
The R2 value was equal to 0.9357.
N = 1420exp(−0.329E)

Table 6.
Candlesticks distribution for Copper with E length in cents.
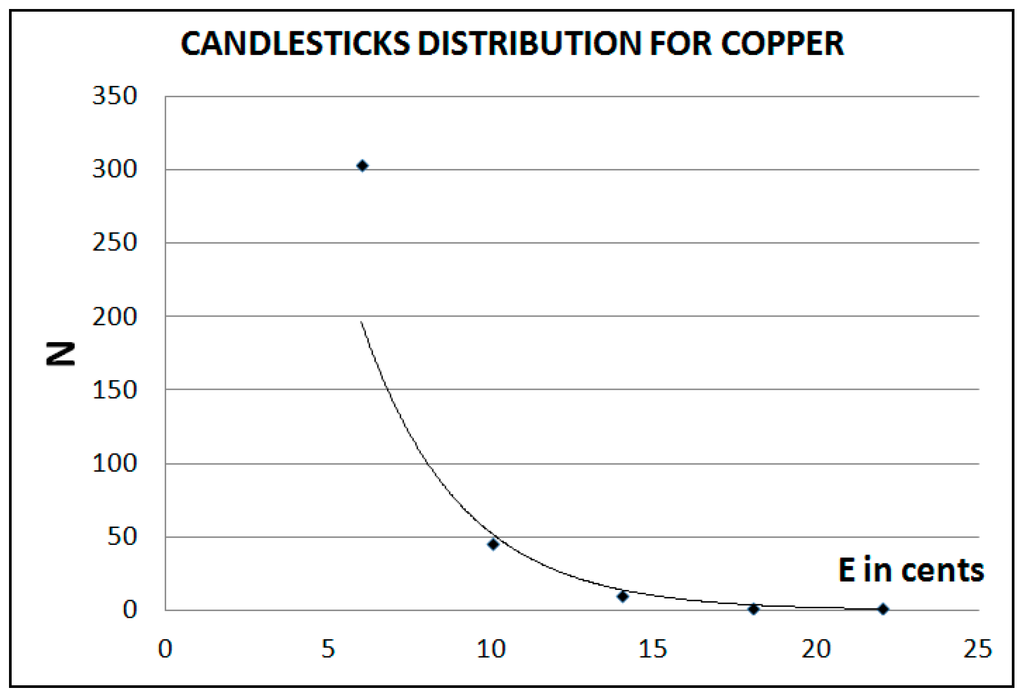
Figure 4.
Candlesticks distribution for Copper with E length in cents.
It is important to note that in all cases the negative exponential function satisfactorily fits the lengths distribution.
6. Discussion
The working hypothesis is: “The intensity of the sentiments is distributed according to an exponential decay law” where we do the following basic equivalences [4,26]:
- (i)
- Black candlestick is equal to bearish sentiments.
- (ii)
- White candlestick is equal to bullish sentiments.
- (iii)
- The intensity of the sentiment is measured by the length of the candlestick. That is, the greater the length of the candlestick, the greater the intensity of the sentiment because each candlestick is observed in the same time unit (“day”, in our case).
We have provided the following evidences:
- (i)
- Section 4 shows that the extension or peak to peak amplitude has more information than the price of the studied financial instrument
- (ii)
- It proved to be lawful to measure the market sentiments intensity in standard deviation units of E length.
- (iii)
- Section 5 shows that the working hypothesis is supported by the coefficient of correlation whose values fluctuate between 0.9357 and 0.9980.
According to Newton’s First Law, an isolated body cannot change its speed by itself. That is, to achieve this, the required action of an external agent is necessary. Using this statement as a basis for an analogy or conjecture, we think that, to see a radical change in the λ value (the exponent of the function N(x)) of a specific financial instrument, it is necessary that the price evolution ceases to be “natural”. That is, a radical change in λ value may indicate collusion, transmission of privileged information, unforeseen disasters, etc. A possible way to detect these phenomena can be constructing Bollinger Bands for lambda value calculated with the last 30 prices. In this way, the anomaly will be detected when the lambda value exceeds a band.
7. Conclusions
In this paper we have provided evidence to support our working hypothesis which states that the peak to peak amplitude of the candlesticks are universally distributed according to a law of exponential decay. Having in mind that the basic sentiments that govern the evolution of the Stock Market can be included in two big groups (fear vs. euphoria or bearish vs. bullish) and since the intensities are proportional to the size of the candlesticks (and the type is identified by color), we can also say that the sentiments are naturally distributed according to a law of exponential decay, which may mean that any radical deviation from this law may indicate the presence of artificial forces such as collusion, transmission of privileged information, unforeseen disasters, etc. In addition, we have seen that this law can be expressed with the intensity of the market sentiments measured in standard deviation units of the E length. Our findings are supported by R2 values ranging between 0.9354 and 0.9981.
Acknowledgments
The author wishes to thank to NT2 Labs scientists, to Rodrigo Aguayo and Alberto Abudinen for supporting this research through grants number 2721 and 2722.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Cheung, Y.W. An empirical model of daily highs and lows. Int. J. Finance Econ. 2007, 12, 1–20. [Google Scholar] [CrossRef]
- Balasubramani, S.; Suganthi, M.; Suresh, P. Study and Analysis of Causal Relationship of Various Macroeconomic Variables on Stock Market Index in India for the Year 2001 to 2003 by Candlestick Chart—A Review. Available online: http://www.icmrr.org/October_2013/IJFRR/10132001.pdf (accessed on 1 September 2016).
- Lu, T.H.; Shiu, Y.M. Pinpoint and Synergistic Trading Strategies of Candlesticks. Int. J. Econ. Finance 2011, 3. [Google Scholar] [CrossRef]
- Nison, S. Japanese Candlestick Charting Techniques: A Contemporary Guide to the Ancient Investment Techniques of the Far East; Simon & Schuster: New York, NY, USA, 2001. [Google Scholar]
- Cofnas, A. The Forex Trading Course: A Self-Study Guide to Becoming a Successful Currency Trader, 2nd ed.; Wiley: Hoboken, NJ, USA, 2015. [Google Scholar]
- Du Plessis, J. The Definitive Guide to Point and Figure: A Comprehensive Guide to the Theory and Practical Use of the Point and Figure Charting Method; Harriman House: Petersfield, UK, 2012. [Google Scholar]
- Lee, K.H.; Jo, G.S. Expert system for predicting stock market timing using a candlestick chart. Expert Syst. Appl. 1999, 16, 357–364. [Google Scholar] [CrossRef]
- Chmielewski, L.; Janowicz, M.; Orlowski, A. Prediction of Trend Reversals in Stock Market by Classification of Japanese Candlesticks. In Proceedings of the 9th International Conference on Computer Recognition Systems CORES, Wroclow, Poland, 25–27 May 2015; pp. 641–647.
- Xie, H.; Fan, K.; Wang, S. The role of Japanese Candlestick in DVAR model. J. Syst. Sci. Complex. 2015, 28, 1177–1193. [Google Scholar] [CrossRef]
- Roy, P. A novel fuzzy document-based information retrieval scheme (FDIRS). Appl. Inf. 2016, 3. [Google Scholar] [CrossRef]
- Hyongdo, L. The God of Trading, Honma: The Creator of Japanese Candle Charts, Honma’s Secret Methods of Investment. Available online: https://www.amazon.com/God-Trading-Honma-Japanese-Investment-ebook/dp/B00J24NXJK (accessed on 1 September 2016).
- Marshall, B.R.; Young, M.R.; Rose, L.C. Candlestick technical trading strategies: Can they create value for investors? J. Bank. Finance 2006, 30, 2303–2323. [Google Scholar] [CrossRef]
- Dorsey, D. The Mass Index. Tech. Anal. Stock. Commod. 1992, 10, 265–267. [Google Scholar]
- Bollinger, J.A. Bollinger on Bollinger Bands; McGraw Hill: New York, NY, USA, 2002. [Google Scholar]
- Botes, E.; Siepman, D. The Vortex Indicator. Tech. Anal. Stock. Commod. 2010, 28, 20–30. [Google Scholar]
- Eric, D.; Andjelic, G.B.; Redzepagic, S. Application of MACD and RVI Indicators as Functions of Investment Strategy Optimization on the Financial Market. J. Econ. Bus. 2009, 27, 171–196. [Google Scholar]
- Wolf, A.; Swift, J.B.; Swinney, H.L.; Vastano, J.A. Determining Lyapunov exponents from a time series. Physica D 1985, 16, 285–317. [Google Scholar] [CrossRef]
- Zhou, T.; Gao, S.; Wang, J.; Chu, C.; Todo, Y.; Tang, Z. Financial time series prediction using a dendritic neuron model. Knowl. Based Syst. 2016, 105, 214–224. [Google Scholar] [CrossRef]
- Grassberger, P.; Procaccia, I. Estimation of the Kolmogorov entropy from a chaotic signal. Phys. Rev. A 1983, 28. [Google Scholar] [CrossRef]
- Shannon, C.E. A Mathematical Theory of Communication. Bell Syst. Tech. J. 1948, 27, 623–656. [Google Scholar] [CrossRef]
- He, S.; Sun, K.; Wang, H. Multivariate permutation entropy and its application for complexity analysis of chaotic systems. Physica A 2016, 461, 812–823. [Google Scholar] [CrossRef]
- Sprott, J.C. Chaos Data Analizer. Available online: http://sprott.physics.wisc.edu/cda.htm (accessed on 1 September 2016).
- Bitvai, Z.; Cohn, T. Day trading profit maximization with multi-task learning and technical analysis. Mach. Learn. 2015, 101, 187–209. [Google Scholar] [CrossRef]
- Di Lorenzo, R. Basic Technical Analysis of Financial Markets; Springer: Milan, Italy, 2013; pp. 135–142. [Google Scholar]
- Hussein, A.S.; Hamed, I.M.; Tolba, M.F. An Efficient System for Stock Market Prediction. In Proceedings of the 7th IEEE International Conference Intelligent Systems, Warsaw, Poland, 24–26 September 2014; pp. 871–882.
- Lu, T.H.; Shiu, Y.M.; Liu, T.C. Profitable candlestick trading strategies—The evidence from a new perspective. Rev. Financ. Econ. 2012, 21, 63–68. [Google Scholar] [CrossRef]
© 2016 by the author; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).