Mechanothermodynamic Entropy and Analysis of Damage State of Complex Systems

Abstract

Mechanics from its side and thermodynamics from its side consider evolution of complex systems, including the Universe. Created classical thermodynamic theory of evolution has one important drawback since it predicts an inevitable heat death of the Universe which is unlikely to take place according to the modern perceptions. The attempts to create a generalized theory of evolution in mechanics were unsuccessful since mechanical equations do not discriminate between future and past. It is natural that the union of mechanics and thermodynamics was difficult to realize since they are based on different methodology. We make an attempt to propose a generalized theory of evolution which is based on the concept of tribo-fatigue entropy. Essence of the proposed approach is that tribo-fatigue entropy is determined by the processes of damageability conditioned by thermodynamic and mechanical effects causing to the change of states of any systems. Law of entropy increase is formulated analytically in the general form. Mechanothermodynamical function is constructed for specific case of fatigue damage of materials due to variation of temperature from 3 K to 0.8 of melting temperature basing on the analysis of 136 experimental results.

1. Introduction

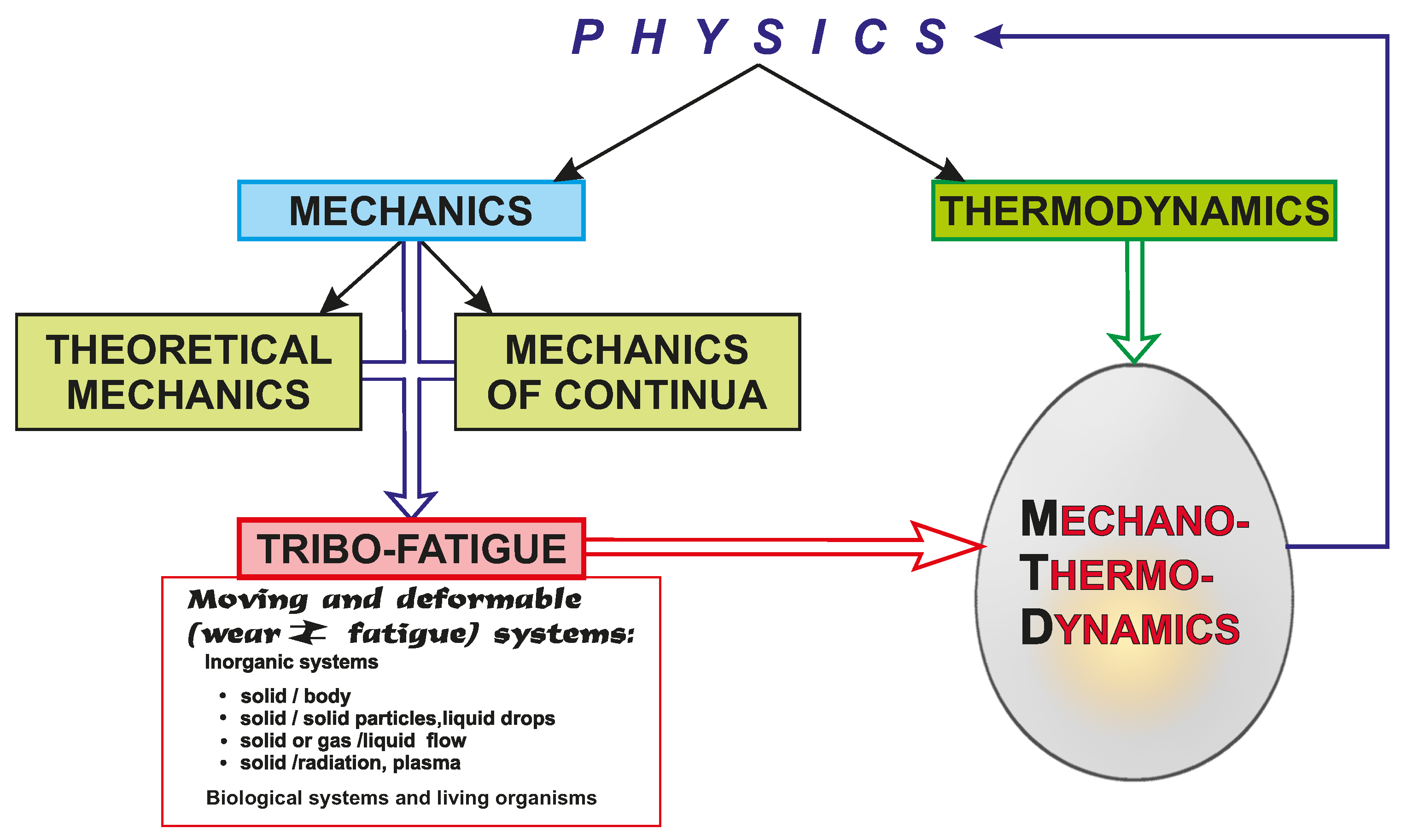
As is known, any scientific discipline serves and aims at understanding and describing these or those regularities and features of certain phenomena, situations, events caused by the existence of some real or thinkable objects that manifest themselves their specific properties [1,2]. Based on the considerations that the study of a new object, as a rule, generates a new scientific discipline as applied to Mechanics, the hierarchy of objects can be built. Successive complexity of objects studied by mechanics is shown in works [1,2,3,4]. The next new object is multiphase—mechanothermodynamics system. Methods of mechanics alone are insufficient for its study as well as methods of thermodynamics alone.

These methods and models addressing coupled problems of both stress-strain states and energy states of the complex systems working under mechanical and thermodynamic loading are discussed in well-known monographs [5,6,7,8,9,10,11]. The concepts of entropy and damage are important in order to construct models of the mechanothermodynamical system.

Basic ideas about mechanical behavior of materials under the fracture process are discussed in [9]. The work [12] addresses the main aspects of Damage Mechanics as the branch of Fracture Mechanics and some of its applications. Fundamentals of Physical Mesomechanics of heterogeneous media that develops at the boundary of Continuum Mechanics, Physics of Plasticity and Strength of Materials and studies the stressed and damaged material at linked micro-, meso- and macro levels are given in [13].

Constitutive relations for strain-induced damage in terms of thermodynamic consistency and also applications of Continuum Damage Mechanics to failures of mechanical and civil engineering components in ductile, creep, fatigue and brittle conditions due to thermomechanical loading are considered in [14,15]. The related problems of constructing theories of vibration and plasticity for steady-state vibrations in elastoplastic bodies are discussed in [16].

The works [17,18] contain a concise review of basic continuum damage models, micromechanics of damage, kinetics of damage evolution and discuss the areas of further research. A general framework for the development of continuum damage models defined by yield and damage surfaces in stress space with consideration of the damage mechanisms (isotropic damage, cracking, etc.) which degrade the stiffness of the material is proposed in [19]. A detailed experimental and theoretical study on the stress-based forming limit criterion during linear and complex strain paths is given in [20]. A thermodynamic framework intended for modelling both friction and non-associated flow for geotechnical materials is presented [21]. The papers [22,23] are dedicated to modelling of the large strain elastic–plastic deformation behavior of anisotropically damaged ductile metals. The formulation of the elasto-plastic-damage behavior of materials is introduced in [24] within a thermodynamically consistent framework that uses functional forms of hardening internal state variables in both damage and plasticity. Paper [25] proposes a damage theory in terms of kinematic, thermodynamic and kinetic coupling for polycrystalline material.

A microscopic damage model considering an ellipsoidal void that is able to change its shape is considered in [26] for mixed-hardening materials. Results of experimental analysis of voids behavior in model materials using X-ray tomography are discussed in [27,28]. Analytical and scanning electron microscopy based study of void growth and change of shape under large plastic deformation is presented in [29]. Phenomenological representation of anisotropic damage progression for porous ductile metals with second phases is described through mechanisms of void nucleation, growth and coalescence in [30]. An analytical and computational mesoscopic models for the nucleation and interaction of microcracks near a macrocrack tip based on both the theory of elasticity and the theory of dislocations are presented in [31]. The framework allowing the combination of plasticity and damage models of inelastic behaviour is proposed in [32].

A damage evolution model based on thermodynamic theory is developed in works [33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60]. According to this model irreversible entropy production rate under loadings of different nature is considered as a single universal damage term—damage metric. In particular this model was used to predict damage evolution and viscoplastic behavior in polymer composites with imperfect interfacial bonds. A corresponding viscoplastic constitutive model was used to describe thermomechanical response of amorphous polymers below and above glass transition temperature. Method of numerical study of voids migration due to action of pulse electric current and thermal gradient solder joints was developed using entropy based damage criteria in order to characterize the mass transportation mechanism.

Recent advances in Tribology involve the use of the fundamental concepts of thermodynamic entropy. Significant accomplishments are reported in the works [61,62,63] aimed at developing a unifying theory for friction and wear. The motivation of this study was a series of experimental investigation that appeared in an article [63] and a pioneering theory on the science of degradation [62]. Development of the thermodynamics of fatigue fracture as well as thermodynamically-based damage mechanics are reported in [64,65,66].

In [1,67,68,69], the fundamentals of Mechanothermodynamics are given and two of its principles are formulated: (1) damage of all things has no conceivable boundaries; (2) effective energy fluxes (entropy) that are caused by loads of different nature during irreversible changes in the MTD system have no additivity—they interact dialectically. In [1], the analysis is made according to the main principles of Tribo-Fatigue [2,3,4] and Thermodynamics [5] and is based on the concept of entropy. In this paper, the similar analysis is made on the basis of the energy representations of mechanics, tribo-fatigue, and thermodynamics. This has made it possible to reveal and investigate new regularities of the behavior and evolution of the mechanothermodynamical system.

2. Thermomechanical Statement

Consider the statement of thermomechanical problem [5,6,7,8] needed for further development of models of energy and entropy states of mechanothermodynamical systems.

Energy and entropy descriptions of continuum state of elementary volume dV are of the following form [6,7]:

$${\mathsf{\sigma }}_{ij,j}+\mathsf{\rho }{f}_i=\mathsf{\rho }{\dot{v}}_i,i=1,2,3$$

(1)

where σ_ij are stresses; $\mathsf{\rho }$ is density; f_i are volumetric forces; $v_i$ are velocities.

The law of conservation of mechanical energy for the continuum of the volume V, with regard to the repeated index summation rule is obtained by multiplying scalar Equation (1) by the velocity vector $v_i$:

$${\displaystyle \underset{V}{\int }{v}_i{\mathsf{\sigma }}_{ij,j}}dV+{\displaystyle \underset{V}{\int }\mathsf{\rho }{v}_i{f}_i}dV={\displaystyle \underset{V}{\int }\mathsf{\rho }{v}_i{\dot{v}}_i}dV.$$

(2)

The right hand-side of Equation (2) is the change in the kinetic energy K of the continuum of volume V:

$${\displaystyle \underset{V}{\int }\mathsf{\rho }{v}_i{\dot{v}}_i}dV=\frac{d}{dt}{\displaystyle \underset{V}{\int }\mathsf{\rho }\frac{v_i{v}_i}{2}dV=\frac{d}{dt}}{\displaystyle \underset{V}{\int }\mathsf{\rho }\frac{v^2}{2}}dV=\frac{dK}{dt}.$$

(3)

The equation for mechnical energy of continuum [6] is derived basing on the known transformations with regard to Gauss—Ostrogradsky’s theorem:

$$\frac{dK}{dt}+{\displaystyle \underset{V}{\int }{\mathsf{\sigma }}_{ij}}{\dot{\mathsf{\epsilon }}}_{ij}dV={\displaystyle \underset{\mathsf{\Pi }}{\int }{\mathsf{\sigma }}_{ij}}{l}_{j}d\mathsf{\Pi }+{\displaystyle \underset{V}{\int }\mathsf{\rho }{v}_i{f}_i}dV,$$

(4)

or:

$$\frac{dK}{dt}+\frac{\mathsf{\delta }U}{dt}=\frac{\mathsf{\delta }A}{dt},$$

where ε_ij is the strain rate; Π is the continuum surface; the l are the direction cosines at the continuum surface; δU/dt is the power of internal forces; δA/dt is the power of internal surfaces and volumetric forces.

The symbol δ in expression (4) is used to underline that the increment in the general case cannot be an accurate differential.

In the thermomechanical statement the rate of change in internal energy U [6] is usually given by the integral:

$$\frac{dU}{dt}=\frac{d}{dt}{\displaystyle \underset{V}{\int }\mathsf{\rho }u}dV={\displaystyle \underset{V}{\int }\mathsf{\rho }\dot{u}}dV,$$

(5)

where $u=\underset{\mathsf{\Delta }m\to 0}{\lim }\frac{u(\mathsf{\Delta }m)}{\mathsf{\Delta }m}$ is the specific internal energy (internal energy density) of the elementary volume of the mass Δm.

The rate of heat transfer to the continuum is expressed as follows:

$$\frac{\mathsf{\delta }Q}{dt}=-{\displaystyle \underset{\mathsf{\Pi }}{\int }{c}_i{l}_i}d\mathsf{\Pi }+{\displaystyle \underset{V}{\int }\mathsf{\rho }z}dV,$$

(6)

where c_i is the characteristic of the heat flux per unit area of continuum surface per unit time due to heat conduction; z is the constant of heat radiation per unit mass per unit time.

The law of change in the energy of thermomechanical continuum then assumes the form:

$$\frac{dK}{dt}+\frac{dU}{dt}=\frac{\mathsf{\delta }A}{dt}+\frac{\mathsf{\delta }Q}{dt}.$$

(7)

In (7), the transformation of surface integrals into volume integrals allows the local form of the energy equation to be obtained:

$$\frac{d}{dt}\left(\frac{v^2}{2}+u\right)=\frac{1}{\mathsf{\rho }}{\left({\mathsf{\sigma }}_{ij}{v}_i\right)}_{,j}+f_i{v}_i-\frac{1}{\mathsf{\rho }}{c}_{i,i}+z.$$

(8)

If the scalar product of Equation (1) and the velocity vector $v_i$ is subtracted from Equation (8), then the following form of the local energy equation is obtained:

$$\frac{du}{dt}=\frac{1}{\mathsf{\rho }}{\mathsf{\sigma }}_{ij}{\dot{\mathsf{\epsilon }}}_{ij}-\frac{1}{\mathsf{\rho }}{c}_{i,i}+z=\frac{1}{\mathsf{\rho }}{\mathsf{\sigma }}_{ij}{\dot{\mathsf{\epsilon }}}_{ij}+\frac{dq}{dt},$$

(9)

where $dq$ is the heat flux per unit mass.

According to expression (9), the rate of change in the internal energy is equal to the sum of the stress power and the heat flux to the continuum.

As applied to the thermodynamic system, two characteristic functions of its state are defined: absolute temperature T and entropy S that can be interpreted as the characteristic of ordering (or chaotic state) of the thermodynamic system. Usually it is assumed that the entropy possesses the property of additivity, i.e.,:

$$S={\displaystyle \sum _i{S}_i}.$$

(10)

In continuum mechanics [6,7], the specific entropy per unit mass is considered:

$$S={\displaystyle \underset{V}{\int }\mathsf{\rho }sdV}.$$

(11)

The specific entropy increment ds can be due to the interaction with the environment (the increment ds^(e)) or inside the system itself (the increment ds⁽ⁱ⁾) [6,7]:

$$ds=d{s}^{(e)}+d{s}^{(i)}.$$

(12)

The increment ds⁽ⁱ⁾ is equal to zero in reversible processes and is greater than zero in irreversible processes.

If the heat flux per unit mass is expressed through $dq$, then for reversible processes the increment will be:

$$Tds=dq.$$

(13)

According to the second law of thermodynamics, the rate of change in the total entropy S of the continuum of the volume V cannot be smaller than the sum of the heat flux through the volume boundary and the entropy produced inside the volume by external sources (Clausius–Duhem’s inequality) [6,7]:

$$\frac{d}{dt}{\displaystyle \underset{V}{\int }\mathsf{\rho }sdV}\ge {\displaystyle \underset{V}{\int }\mathsf{\rho }edV}-{\displaystyle \underset{\mathsf{\Pi }}{\int }\frac{c_i{l}_i}{T}d\mathsf{\Pi }},$$

(14)

where e is the power of local external entropy sources per unit mass. The equality in Formula (14) is valid for reversible processes and the inequality—for irreversible processes.

Transforming the surface integral into the volume integral in expression (14) can yield the relation for the rate of the internal entropy production per unit mass:

$$\mathsf{\gamma }\equiv \frac{ds}{dt}-e-\frac{1}{\mathsf{\rho }}{\left(\frac{c_i}{T}\right)}_j\ge 0.$$

(15)

In continuum mechanics, it is assumed that the stress tensor can be decomposed into two parts: the conservative part ${\mathsf{\sigma }}_{ij}^{(C)}$ for reversible processes (elastic deformation, liquid pressure) and the dissipative part ${\mathsf{\sigma }}_{ij}^{(D)}$ for irreversible processes (plastic deformation, liquid viscous stresses):

$${\mathsf{\sigma }}_{ij}={\mathsf{\sigma }}_{ij}^{(C)}+{\mathsf{\sigma }}_{ij}^{(D)}.$$

(16)

The expression for the rate of change in energy (9) can then be presented in the following form:

$$\frac{du}{dt}=\frac{1}{\mathsf{\rho }}{\mathsf{\sigma }}_{ij}{\dot{\mathsf{\epsilon }}}_{ij}+\frac{dq}{dt}=\frac{1}{\mathsf{\rho }}{\mathsf{\sigma }}_{ij}^{(C)}{\dot{\mathsf{\epsilon }}}_{ij}+\frac{1}{\mathsf{\rho }}{\mathsf{\sigma }}_{ij}^{(D)}{\dot{\mathsf{\epsilon }}}_{ij}+\frac{dq}{dt}.$$

(17)

If it is assumed that relation (13) is valid for irreversible processes, then the rate of the total entropy production is:

$$\frac{ds}{dt}=\frac{1}{\mathsf{\rho }T}{\mathsf{\sigma }}_{ij}^{(C)}{\dot{\mathsf{\epsilon }}}_{ij}+\frac{1}{\mathsf{\rho }T}{\mathsf{\sigma }}_{ij}^{(D)}{\dot{\mathsf{\epsilon }}}_{ij}+\frac{1}{T}\frac{dq}{dt},$$

(18)

or:

$$\frac{ds}{dt}=\frac{1}{\mathsf{\rho }T}\left(\frac{d{u}_M}{dt}+\frac{d{u}_T}{dt}\right)=\frac{1}{\mathsf{\rho }T}\left(\frac{d{u}_M^{(C)}}{dt}+\frac{d{u}_M^{(D)}}{dt}+\frac{d{u}_T}{dt}\right).$$

Expression (18) for the rate of a total change of local entropy in the elementary volume of the continuum can be very convenient in practice.

In view of assumption (10) on the entropy additivity the sum in (18) can be supplemented by other terms considering the internal entropy production in the liquid (gas) volume due to different mechanisms. Similarly, for the continuum volume dV, for example, internal chemical processes can be considered [5]:

$$dU=dQ+dA+d{U}_{sub}=TdS-pdV+{\displaystyle \sum _1^n{\mathsf{\mu }}_{k}d{N}_k},$$

(19)

$$dS=\frac{dU+pdV}{T}-\frac{1}{T}{\displaystyle \sum _1^n{\mathsf{\mu }}_{k}d{N}_k}.$$

(20)

If dV is considered not as a finite volume but as an elementary volume of continuum, then changes in its specific energy and entropy based on Equation (17), Equations (19) and (20) can be written in the following differential form:

$$du=\frac{1}{\mathsf{\rho }}{\mathsf{\sigma }}_{ij}d{\mathsf{\epsilon }}_{ij}+dq+{\displaystyle \sum _k{\mathsf{\mu }}_{k}d{n}_k},$$

(21)

$$ds=\frac{1}{\mathsf{\rho }T}{\mathsf{\sigma }}_{ij}d{\mathsf{\epsilon }}_{ij}+\frac{1}{T}dq+\frac{1}{T}{\displaystyle \sum _k{\mathsf{\mu }}_{k}d{n}_k},$$

(22)

where n_k is the number of mols per unit mass.

For the continuum of the volume V, expressions (21) and (22) on the basis of relations (5) and (11) will assume the form:

$$dU={\displaystyle \underset{V}{\int }\mathsf{\rho }du}dV={\displaystyle \underset{V}{\int }{\mathsf{\sigma }}_{ij}d{\mathsf{\epsilon }}_{ij}}dV+{\displaystyle \underset{V}{\int }\mathsf{\rho }dq}dV+{\displaystyle \underset{V}{\int }\mathsf{\rho }{\displaystyle \sum _k{\mathsf{\mu }}_{k}d{n}_k}}dV,$$

(23)

$$dS={\displaystyle \underset{V}{\int }\mathsf{\rho }ds}dV=\frac{1}{T}{\displaystyle \underset{V}{\int }{\mathsf{\sigma }}_{ij}d{\mathsf{\epsilon }}_{ij}}dV+\frac{1}{T}{\displaystyle \underset{V}{\int }\mathsf{\rho }dq}dV+\frac{1}{T}{\displaystyle \underset{V}{\int }\mathsf{\rho }{\displaystyle \sum _k{\mathsf{\mu }}_{k}d{n}_k}}dV.$$

(24)

The introduction of the chemical entropy component (the last terms in (21)–(23)) allowed one not only to obtain a more complete picture of the continuum state, but also to describe self-organization processes that result in initiating stable structures when the heat flux to the continuum is increased.

The above-presented known models of energy and entropy states of continuum (17)–(24), being rather general, do not nevertheless permit one to satisfactorily describe some processes occurring in such a continuum as a deformable solid. Convenient representation of the additivity of energy and entropy components (11) used, for example, for modeling elastic deformation is not suitable for the description of non-linear processes. The available models do not also allow for the entropy growth due to damageability of solids as a specific characteristic of changes in the structural organization. According to the tribo-fatigue concepts [1,2,3,4,67,68,69], the damageability is interpreted as any irreversible change in structure, continuity, shape, etc. of a deformable solid that leads to its limiting state (separation into pieces under mechanical fatigue, occurrence of the pitting of critical density or sizes under contact fatigue, limiting wear under sliding fatigue). Although, for example, the elasticity limit is implicitly taken into account during plasticity modeling, the damageability, for example, during mechanical or contact fatigue occurs in the conditions of linear elastic deformation and requires a particular approach for its description with regard to limiting fatigue characteristics of material. The above drawbacks are overcome in the approach below.

3. Main Principles

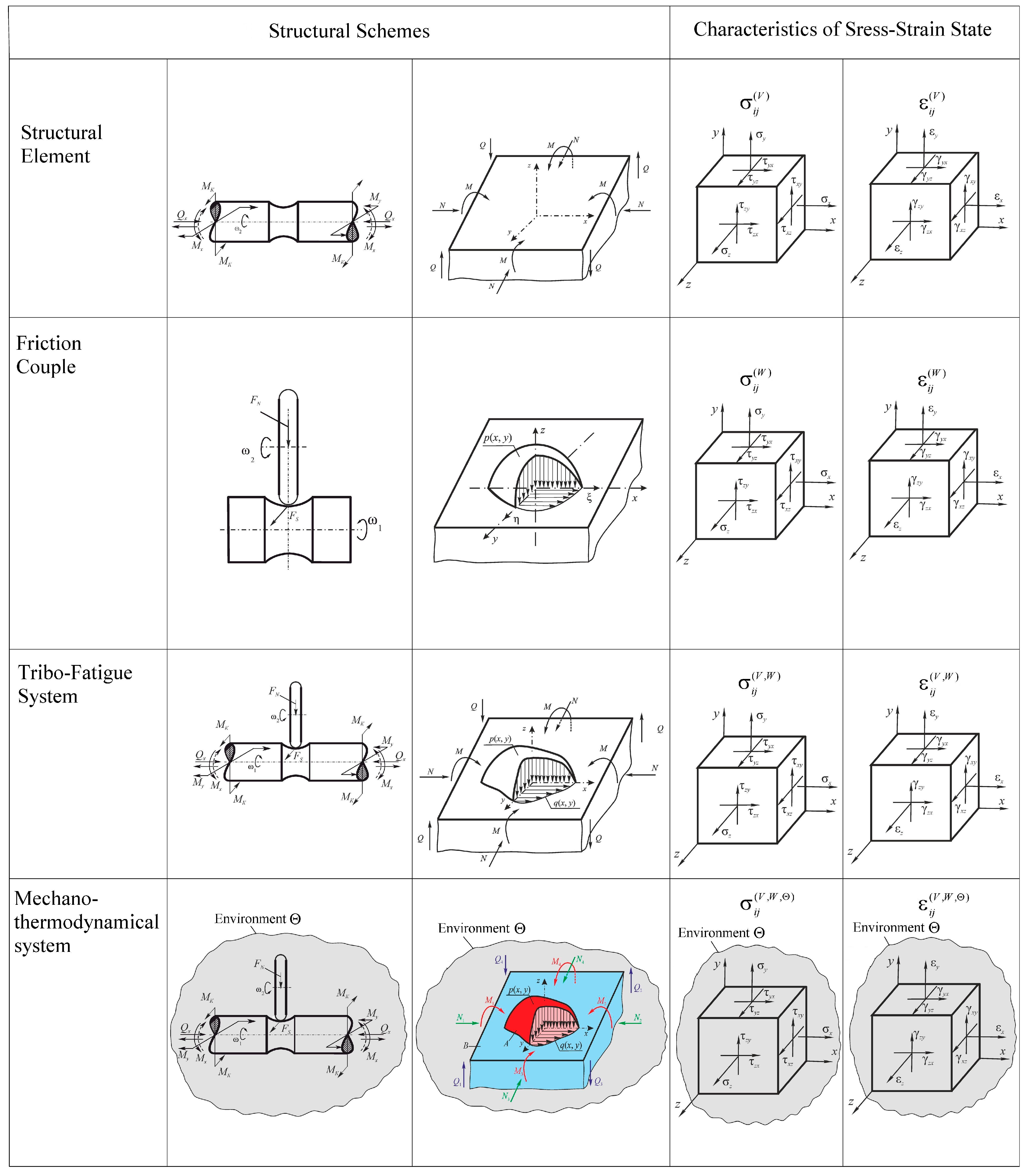
According to [2,4,67], the mechanothermodynamical (MTD) system in the general case represents the thermodynamic continuum with solids distributed (scattered) within it, interacting with each other and with the continuum. Consider its fragment of limited size $\mathsf{\Omega }(X,Y,Z)$ shown in Figure 1.

The continuum has a temperature θ and a chemical composition Ch. Here are two interacting solid elements (A and B) that can move relatively to each other at the contact zone S(x, y, z). Arbitrary mechanical loads applied to one of them (for example, to element A) in x, y, z coordinate system are transformed into the internal transverse forces Q_x, Q_y, Q_z, longitudinal forces N_x, N_y, N_z and also into the bending moments M_x, M_y, M_z. Element B is pressed to element A by the loads that are transformed into the distributed normal pressure p(x, y) and the tangential tractions q(x, y). The origin of the coordinates is placed at the point of original contact O of the two elements (prior to deformation). It is easy to see that the elements A and B together form the Tribo-Fatigue system [4] which could be reduced to the friction pair [2] in the absence of internal forces ($N_i=0$, $Q_i=0$, $M_i=0$, i = x, y, z). Thus, the Tribo-Fatigue system is the friction pair in which at least one of the elements perceives non-contact loads and, consequently, undergoes volumetric deformation. This representation of the MTD system has an advantage that the analysis of the states of a solid and the components of a system can adopt the appropriate solutions known in mechanics of deformable solid, in contact mechanics, in mechanics of tribo-fatigue systems (tribo-fatigue) and in tribology.

Our main task is to describe the energy state of the MTD system under the action of mechanical and thermodynamic loads with regard to the environmental influence.

The energy state of any system is very interesting in itself. However, as applied to the MTD system it is very important to study its damage and, as a result, to study the conditions of reaching the limiting state (fatigue fracture, wear etc.). Of special interest is the analysis of translimiting or supercritical conditions [2].

The main ideas, which are the fundamentals of the given theory, can be formulated with regard to [2,3,4] as follows:

I. Due to the fact that the elements of the MTD system are subject to the loads of different nature—mechanical, thermal and electrochemical, the traditional analysis of their damage and limiting state under the action only of mechanical stresses or strains [70,71,72,73,74,75,76,77,78] etc. can be the basis for research. However it appears insufficient and, as a result, is ineffective. This means that there is a need to analyze MTD system states using more general energy concepts.

II. Considering that the damage of MTD system solids is determined by mechanical, thermodynamic [79,80,81,82,83] etc. and electrochemical loads, it is needed to introduce the generalized representation of its complex damage that is caused by these loads acting at a time. Call such damage any irreversible changes in shape, size, volume, mass, composition, structure, continuity and, as a result, physical and mechanical properties of the system elements. This means the corresponding changes in the functions of the system as the integrity.

III. The onset and development of complex damage is mainly determined by means of four particular phenomena: mechanical fatigue, friction, wear, thermodynamic and electrochemical processes. These phenomena are called particular in the sense that each of them can be realized as independent and separate. This leads to the corresponding energy state and damage in terms of particular (separate) criteria.

IV. In the general case, all these particular phenomena and processes in the MTD system appear simultaneously and within one area. The states of such a system are then caused not by one of any mentioned phenomena but by their joint (collective) development and, consequently, by their interaction.

V. If the physical state of the MTD system is described by means of all input energy $u_{\sum }$, then its damage condition is determined only by the effective (dangerous) part $u_{\sum }^{eff}<<u_{\sum }$ that is spent for generation, motion, and interaction of irreversible damages.

VI. The effective energy $u_{\sum }^{eff}$ at the volume strain of solids can be represented by the function of three energy components: thermal $u_T^{eff}$, force $u_n^{eff}$, and frictional $u_{\mathsf{\tau }}^{eff}$:

$$u_{\sum }^{eff}=F_{\mathsf{\Lambda }}\left(u_T^{eff},u_n^{eff},u_{\mathsf{\tau }}^{eff}\right),$$

(25)

where F_Λ takes into account the irreversible kinetic interaction of particular damage phenomena. The components $u_T^{eff},u_n^{eff},u_{\mathsf{\tau }}^{eff}$ of the effective energy $u_{\sum }^{eff}$ have no property of additivity.

VII. The processes of electrochemical (in particular, corrosion) damage of solids can be taken into consideration by introducing the parameter 0 ≤ D_ch ≤ 1 and can be studied, for example, as electrochemical damage under the influence of temperature (D_T(ch)), stress (D_σ(ch)), and friction corrosion (D_τ(ch)). So function (25) takes the form:

$$u_{\sum }^{eff}=F_{\mathsf{\Lambda }}\left(u_{T(ch)}^{eff},u_{n(ch)}^{eff},u_{\mathsf{\tau }(ch)}^{eff}\right).$$

(26)

VIII. The generalized criteria of the limiting (critical) state is represented by the condition when the effective energy $u_{\sum }^{eff}$ reaches its limiting value—critical quantity u₀ in some area of limited size—in the dangerous volume of the MTD system.

IX. The energy u₀ is considered to be a fundamental constant for a given material. It shouldn’t depend on testing conditions, input energy types, damage mechanisms.

X. Dangerous volume is the 3D area $V_{ij}\subset V_0$ of the deformable solid ($V_0$ is its working volume) with the critical state of material at all its points, of which it consists.

XI. In the general case, the limiting (critical) state of the MDT system is reached not due to a simple growth of effective energy components and, hence, due to the accumulation of irreversible damages that are caused by separate actions (loads of different nature), but as a result of their dialectical interaction, whose direction is characterized by the development of spontaneous phenomena of hardening-softening of materials in the given operating or testing conditions. In such a way, taking into consideration function (26), the hypothesis of the limiting (critical) state of the MTD system can be represented in the following general form:

$$\mathsf{\Phi }(u_{\mathsf{\sigma }(ch)}^{eff},u_{\mathsf{\tau }(ch)}^{eff},u_{T(ch)}^{eff},{\mathsf{\Lambda }}_{n\backslash k\backslash l},m_k,u_0)=0,$$

(27)

where m_k, k = 1, 2, …, are some characteristic properties (hardening-softening) of contacting materials, ${\mathsf{\Lambda }}_{k\backslash l\backslash n}$ ⋛ 1 are the functions (parameters) of dialectic interactions of effective energies (irreversible damages) that are caused by loads of different nature. This means that at Λ_k > 1, the damage increase is realized, at Λ_l < 1—its decrease, and at Λ_n = 1—its stable development.

XII. Taking into consideration Item III, from the physical viewpoint, hypothesis (27) should be multi-criterion, i.e., it should describe not only the states of the system as the integrity but its separate elements in terms of different criteria of performance loss (wear, fatigue damage, pitting, corrosion damage, thermal damage, etc.). In particular cases, it is possible to reach the corresponding limiting (critical) states in terms of one or two, three or several criteria at a time.

XIII. Reaching the limiting state:

$$u_{\mathsf{\Sigma }}^{eff}=u_0,$$

(28)

means the full loss of the integrity of the MTD system, i.e., of all its functions. At the same time damageability of its elements:

$$0<{\mathsf{\psi }}_u^{eff}=u_{\mathsf{\Sigma }}^{eff}/u_0,$$

(29)

reach the critical value:

$${\mathsf{\psi }}_u^{eff}\left({\mathsf{\psi }}_{\mathsf{\sigma }(ch)},{\mathsf{\psi }}_{\mathsf{\tau }(ch)},{\mathsf{\psi }}_{T(ch)},{\mathsf{\Lambda }}_{k\backslash l\backslash n},m_k\right)=1.$$

(30)

XIV. If t = t₀ is the time of origination of the system and $T_{\oplus }$ is the time of reaching the limiting state, then the failure time of its functions corresponds to the relative lifetime (longevity) $t/T_{\oplus }=1$. But the system lifetime $T_{*}$ as the material object is longer than its lifetime as the functional integrity ($T_{*}>>T_{\oplus }$) since at the time moment $t>T_{\oplus }$ the process of degradation—disintegration is realized by forming a great number of remains, pieces, fragments, etc. This process develops under the influence of not only possible mechanical loads but mainly of the environment—up to the system death as the material object at the time moment t = $T_{*}$. The system death means its complete disintegration into an infinitely large number of ultimately small particles (for example, atoms). The translimiting existence of the system as a gradually disintegrating material object can then be described by the following conditions:

$${\mathsf{\psi }}_u^{eff}\to \infty ,$$

(31)

$$d_{\mathsf{\psi }}\to 0,$$

(32)

where $d_{\mathsf{\psi }}$ is the average size of disintegrating particles and the natural relation ${\mathsf{\psi }}_u^{eff}(d_{\mathsf{\psi }})$ should exist between ${\mathsf{\psi }}_{\mathsf{\Sigma }}$ and $d_{\mathsf{\psi }}$. Then the condition for the system death is:

$$t/T_{*}=1.$$

(33)

XV. The particles of the “old system” disintegration are not destructed but are spent for the formation and growth of a number of “new systems”. This is the essence of the MTD system evolution hysteresis.

Finally it should be noted that not irreversible but effective energy causing damages production is considered in the present work. Determination of parameters denoting effective (damaging) part of energies of different nature (due to stresses, friction, temperature) is explained in Section 4 “Energy Theory of Damage and Limiting States”.

Our idea is that failure depends on fundamental physical property of the material—critical energy u₀ which is independent of the conditions of deformation, shapes and sizes of objects. Limiting energy u₀ is considered as the initial activation energy of the disintegration process (critical energy) which approximately corresponds both to the sublimation heat for metals and crystals with ionic bonds and to the activation energy of thermal destruction for polymers. It is independent of conditions and ways of reaching the limiting state. Longevity of a gear or a shaft in the given conditions of operation would be different but determined by fundamental parameter u₀.

On the other hand effective energy is of course dependent on all these conditions and external loads and corresponding stress-strain state. Limiting state occurs when effective energy reaches u₀. In cases of different sizes, shapes, number of cycles and stress concentrators effective energy is different. Therefore it may need different conditions and time for effective energy to reach fundamental material constant u₀.

In our case entropy is defined as the ratio between the effective energy and critical energy u₀ (see Section 5 “Mechanothermodynamical states”). Therefore the proposed formulation of entropy simultaneously contains acting and critical energy. The limiting state occurs when this ratio is equal to 1. Latter studies could show effectiveness of this in certain cases.

4. Energy Theory of Damage and Limiting States

Let us specify function (25). To determine the effective energy, consider the work of internal forces in the elementary volume dV of tribo-fatigue systems (in Figure 1). In the general case, the differential of the work of the internal forces and the temperature dT_∑ can be written with regard to the rule of disclosing the biscalar product of the stress and strain tensors σ and ε:

$$\begin{array}{c}du={\mathsf{\sigma }}_{ij}\cdot \cdot d{\mathsf{\epsilon }}_{ij}+kd{T}_{\mathsf{\Sigma }}=\left(\begin{array}{ccc}{\mathsf{\sigma }}_{xx}& {\mathsf{\sigma }}_{xy}& {\mathsf{\sigma }}_{xz}\\ {\mathsf{\sigma }}_{yx}& {\mathsf{\sigma }}_{yy}& {\mathsf{\sigma }}_{yz}\\ {\mathsf{\sigma }}_{zx}& {\mathsf{\sigma }}_{zy}& {\mathsf{\sigma }}_{zz}\end{array}\right)\cdot \cdot \left(\begin{array}{ccc}d{\mathsf{\epsilon }}_{xx}& d{\mathsf{\epsilon }}_{xy}& d{\mathsf{\epsilon }}_{xz}\\ d{\mathsf{\epsilon }}_{yx}& d{\mathsf{\epsilon }}_{yy}& d{\mathsf{\epsilon }}_{yz}\\ d{\mathsf{\epsilon }}_{zx}& d{\mathsf{\gamma }}_{zy}& d{\mathsf{\epsilon }}_{zz}\end{array}\right)+kd{T}_{\mathsf{\Sigma }}=\\ ={\mathsf{\sigma }}_{xx}d{\mathsf{\epsilon }}_{xx}+{\mathsf{\sigma }}_{yy}d{\mathsf{\epsilon }}_{yy}+{\mathsf{\sigma }}_{zz}d{\mathsf{\epsilon }}_{zz}+{\mathsf{\sigma }}_{xy}d{\mathsf{\epsilon }}_{xy}+{\mathsf{\sigma }}_{xz}d{\mathsf{\epsilon }}_{xz}+{\mathsf{\sigma }}_{yz}d{\mathsf{\epsilon }}_{yz}+kd{T}_{\mathsf{\Sigma }};\end{array}$$

(34)

here k is the Boltzmann constant.

We proceed from the idea that in the general case, according to [2,4], the main role in forming wear-fatigue damage is played by the normal and shear stresses that cause the processes of shear (due to friction) and tear (due to tension-compression).

In this case, it is reasonable to divide the tensor σ into two parts: σ_τ is the tensor of friction-shear stresses, or, briefly, the shear tensor and σ_n is the tensor of normal stresses (tension-compression), or, briefly, the tear tensor. So in (28), the tear part σ_n and shear part σ_τ of the tensor σ will be set as:

$$du={\mathsf{\sigma }}_{ij}\cdot \cdot d{\mathsf{\epsilon }}_{ij}+kd{T}_{\mathsf{\Sigma }}=\left({\mathsf{\sigma }}_n+{\mathsf{\sigma }}_{\mathsf{\tau }}\right)\cdot \cdot d{\mathsf{\epsilon }}_{ij}+kd{T}_{\mathsf{\Sigma }}={\mathsf{\sigma }}_n\cdot \cdot d{\mathsf{\epsilon }}_{ij}+{\mathsf{\sigma }}_{\mathsf{\tau }}\cdot \cdot d{\mathsf{\epsilon }}_{ij}+kd{T}_{\mathsf{\Sigma }}.=d{u}_n+d{u}_{\mathsf{\tau }}+d{u}_T.$$

(35)

According to items III and IV, the tensors σ and ε should be represented as follows:

$$\begin{array}{l}{\mathsf{\sigma }}_{ij}={\mathsf{\sigma }}_{ij}^{\left(V,W\right)}={\mathsf{\sigma }}_{ij}\left({\mathsf{\sigma }}_{ij}^{\left(V\right)},{\mathsf{\sigma }}_{ij}^{\left(W\right)}\right),\\ {\mathsf{\epsilon }}_{ij}={\mathsf{\epsilon }}_{ij}^{\left(V,W\right)}={\mathsf{\epsilon }}_{ij}\left({\mathsf{\epsilon }}_{ij}^{\left(V\right)},{\mathsf{\epsilon }}_{ij}^{\left(W\right)}\right).\end{array}$$

(36)

Here the stress and strain tensors with the superscript V are caused by the action of volume loads (the general cases of 3D bending, torsion, tension-compression) and those with the superscript W—by the contact interaction of the system elements. Expression (35) with regard to (36) can be given as follows:

$$\begin{array}{c}du={\mathsf{\sigma }}_{ij}^{\left(V,W\right)}\cdot \cdot d{\mathsf{\epsilon }}_{ij}^{\left(V,W\right)}+kd{T}_{\mathsf{\Sigma }}=\left({{\mathsf{\sigma }}_n}^{\left(V,W\right)}+{{\mathsf{\sigma }}_{\mathsf{\tau }}}^{\left(V,W\right)}\right)\cdot \cdot d{\mathsf{\epsilon }}_{ij}^{\left(V,W\right)}+kd{T}_{\mathsf{\Sigma }}=\\ ={{\mathsf{\sigma }}_n}^{\left(V,W\right)}\cdot \cdot d{\mathsf{\epsilon }}_{ij}^{\left(V,W\right)}+{{\mathsf{\sigma }}_{\mathsf{\tau }}}^{\left(V,W\right)}\cdot \cdot d{\mathsf{\epsilon }}_{ij}^{\left(V,W\right)}+kd{T}_{\mathsf{\Sigma }}\cdot =d{u}_n+d{u}_{\mathsf{\tau }}+d{u}_T.\end{array}$$

(37)

In the case of the linear relationship between the stresses and strains, expression (36) will assume the form:

$${\mathsf{\sigma }}_{ij}={\mathsf{\sigma }}_{ij}^{\left(V,W\right)}={\mathsf{\sigma }}_{ij}^{\left(V\right)}+{\mathsf{\sigma }}_{ij}^{\left(W\right)}=\left(\begin{array}{ccc}{\mathsf{\sigma }}_{xx}^{\left(V\right)}+{\mathsf{\sigma }}_{xx}^{\left(W\right)}& {\mathsf{\sigma }}_{xy}^{\left(V\right)}+{\mathsf{\sigma }}_{xy}^{\left(W\right)}& {\mathsf{\sigma }}_{xz}^{\left(V\right)}+{\mathsf{\sigma }}_{xz}^{\left(W\right)}\\ {\mathsf{\sigma }}_{yx}^{\left(V\right)}+{\mathsf{\sigma }}_{yx}^{\left(W\right)}& {\mathsf{\sigma }}_{yy}^{\left(V\right)}+{\mathsf{\sigma }}_{yy}^{\left(W\right)}& {\mathsf{\sigma }}_{yz}^{\left(V\right)}+{\mathsf{\sigma }}_{yz}^{\left(W\right)}\\ {\mathsf{\sigma }}_{zx}^{\left(V\right)}+{\mathsf{\sigma }}_{zx}^{\left(W\right)}& {\mathsf{\sigma }}_{zy}^{\left(V\right)}+{\mathsf{\sigma }}_{zy}^{\left(W\right)}& {\mathsf{\sigma }}_{zz}^{\left(V\right)}+{\mathsf{\sigma }}_{zz}^{\left(W\right)}\end{array}\right),$$

(38)

$${\mathsf{\epsilon }}_{ij}={\mathsf{\epsilon }}_{ij}^{\left(V,W\right)}={\mathsf{\epsilon }}_{ij}^{\left(V\right)}+{\mathsf{\epsilon }}_{ij}^{\left(W\right)}=\left(\begin{array}{ccc}{\mathsf{\epsilon }}_{xx}^{\left(V\right)}+{\mathsf{\epsilon }}_{xx}^{\left(W\right)}& {\mathsf{\epsilon }}_{xy}^{\left(V\right)}+{\mathsf{\epsilon }}_{xy}^{\left(W\right)}& {\mathsf{\epsilon }}_{xz}^{\left(V\right)}+{\mathsf{\epsilon }}_{xz}^{\left(W\right)}\\ {\mathsf{\epsilon }}_{yx}^{\left(V\right)}+{\mathsf{\epsilon }}_{yx}^{\left(W\right)}& {\mathsf{\epsilon }}_{yy}^{\left(V\right)}+{\mathsf{\epsilon }}_{yy}^{\left(W\right)}& {\mathsf{\epsilon }}_{yz}^{\left(V\right)}+{\mathsf{\epsilon }}_{yz}^{\left(W\right)}\\ {\mathsf{\epsilon }}_{zx}^{\left(V\right)}+{\mathsf{\epsilon }}_{zx}^{\left(W\right)}& {\mathsf{\epsilon }}_{zy}^{\left(V\right)}+{\mathsf{\epsilon }}_{zy}^{\left(W\right)}& {\mathsf{\epsilon }}_{zz}^{\left(V\right)}+{\mathsf{\epsilon }}_{zz}^{\left(W\right)}\end{array}\right),$$

(39)

and (37) will be as follows:

$$\begin{array}{c}du=u=\frac{1}{2}{\mathsf{\sigma }}_{ij}\cdot \cdot {\mathsf{\epsilon }}_{ij}+k{T}_{\mathsf{\Sigma }}=\frac{1}{2}\left({\mathsf{\sigma }}_{ij}^{\left(V\right)}+{\mathsf{\sigma }}_{ij}^{\left(W\right)}\right)\cdot \cdot \left({\mathsf{\epsilon }}_{ij}^{\left(V\right)}+{\mathsf{\epsilon }}_{ij}^{\left(W\right)}\right)+k{T}_{\mathsf{\Sigma }}=\\ =\frac{1}{2}\left[\left({\mathsf{\sigma }}_n^{\left(V\right)}+{\mathsf{\sigma }}_n^{\left(W\right)}\right)+\left({\mathsf{\sigma }}_{\mathsf{\tau }}^{\left(V\right)}+{\mathsf{\sigma }}_{\mathsf{\tau }}^{\left(W\right)}\right)\right]\cdot \cdot \left({\mathsf{\epsilon }}_{ij}^{\left(V\right)}+{\mathsf{\epsilon }}_{ij}^{\left(W\right)}\right)+k{T}_{\mathsf{\Sigma }}=\\ =\frac{1}{2}\left[\left(\begin{array}{ccc}{\mathsf{\sigma }}_{xx}^{\left(V\right)}+{\mathsf{\sigma }}_{xx}^{\left(W\right)}& 0& 0\\ 0& {\mathsf{\sigma }}_{yy}^{\left(V\right)}+{\mathsf{\sigma }}_{yy}^{\left(W\right)}& 0\\ 0& 0& {\mathsf{\sigma }}_{zz}^{\left(V\right)}+{\mathsf{\sigma }}_{zz}^{\left(W\right)}\end{array}\right)+\left(\begin{array}{ccc}0& {\mathsf{\sigma }}_{xy}^{\left(V\right)}+{\mathsf{\sigma }}_{xy}^{\left(W\right)}& {\mathsf{\sigma }}_{xz}^{\left(V\right)}+{\mathsf{\sigma }}_{xz}^{\left(W\right)}\\ {\mathsf{\sigma }}_{yx}^{\left(V\right)}+{\mathsf{\sigma }}_{yx}^{\left(W\right)}& 0& {\mathsf{\sigma }}_{yz}^{\left(V\right)}+{\mathsf{\sigma }}_{yz}^{\left(W\right)}\\ {\mathsf{\sigma }}_{zx}^{\left(V\right)}+{\mathsf{\sigma }}_{zx}^{\left(W\right)}& {\mathsf{\sigma }}_{zy}^{\left(V\right)}+{\mathsf{\sigma }}_{zy}^{\left(W\right)}& 0\end{array}\right)\right]\cdot \cdot \\ \cdot \cdot \left(\begin{array}{ccc}{\mathsf{\epsilon }}_{xx}^{\left(V\right)}+{\mathsf{\epsilon }}_{xx}^{\left(W\right)}& {\mathsf{\epsilon }}_{xy}^{\left(V\right)}+{\mathsf{\epsilon }}_{xy}^{\left(W\right)}& {\mathsf{\epsilon }}_{xz}^{\left(V\right)}+{\mathsf{\epsilon }}_{xz}^{\left(W\right)}\\ {\mathsf{\epsilon }}_{yx}^{\left(V\right)}+{\mathsf{\epsilon }}_{yx}^{\left(W\right)}& {\mathsf{\epsilon }}_{yy}^{\left(V\right)}+{\mathsf{\epsilon }}_{yy}^{\left(W\right)}& {\mathsf{\epsilon }}_{yz}^{\left(V\right)}+{\mathsf{\epsilon }}_{yz}^{\left(W\right)}\\ {\mathsf{\epsilon }}_{zx}^{\left(V\right)}+{\mathsf{\epsilon }}_{zx}^{\left(W\right)}& {\mathsf{\epsilon }}_{zy}^{\left(V\right)}+{\mathsf{\epsilon }}_{zy}^{\left(W\right)}& {\mathsf{\epsilon }}_{zz}^{\left(V\right)}+{\mathsf{\epsilon }}_{zz}^{\left(W\right)}\end{array}\right)+k{T}_{\mathsf{\Sigma }}.\end{array}$$

(40)

From (40) it is seen that the tear part σ_n of the tensor σ is the sum of the tear parts of the tensors at the volume strain ${\mathsf{\sigma }}_n^{\left(V\right)}$ and the surface load (friction) ${\mathsf{\sigma }}_n^{\left(W\right)}$, whereas the shear part σ_τ is the sum of the shear parts ${\mathsf{\sigma }}_{\mathsf{\tau }}^{\left(V\right)}$ and ${\mathsf{\sigma }}_{\mathsf{\tau }}^{\left(W\right)}$. This means the vital difference of the generalized approach to the construction of the criterion for the limiting state of the MTD system.

From total energy (40), its effective part is separated according to Items V and VIII with regard to [2,3]. To do this, introduce the coefficients of appropriate dimensions A_n(V), A_τ(V) and A_T(V) that determine the fraction of the absorbed energy:

$$d{u}_{\mathsf{\Sigma }}^{eff}={\mathsf{\Lambda }}_{M\backslash T}\left(V\right)\left\{{\mathsf{\Lambda }}_{\mathsf{\tau }\backslash n}\left(V\right)\left[A_n\left(V\right){\mathsf{\sigma }}_n\cdot \cdot d{\mathsf{\epsilon }}_{ij}+A_{\mathsf{\tau }}\left(V\right){\mathsf{\sigma }}_{\mathsf{\tau }}\cdot \cdot d{\mathsf{\epsilon }}_{ij}\right]+A_T\left(V\right)kd{T}_{\mathsf{\Sigma }}\right\}$$

(41)

or:

$$d{u}_{\mathsf{\Sigma }}^{eff}={\mathsf{\Lambda }}_{M\backslash T}\left(V\right)\left\{{\mathsf{\Lambda }}_{\mathsf{\tau }\backslash n}\left(V\right)\left[A_n\left(V\right)d{u}_n^{}+A_{\mathsf{\tau }}\left(V\right)d{u}_{\mathsf{\tau }}^{}\right]+A_T\left(V\right)d{u}_T^{}\right\}$$

(42)

where Λ_M\T(V) and Λ_τ\n(V) are the functions of interaction between energies of different nature. The subscript τ\n means that the function Λ describes the interaction between the shear (τ) and tear (σ) components of the effective energy, and the subscript М\T means that the function Λ describes the interaction between the mechanical (M) and thermal (T) parts of the effective energy. That fact that the coefficients A can be, generally speaking, different for different points of the volume V, enables one to take into account the inhomogeneity of environment.

Taking into consideration (42), criteria (27) can be specified with no regard to the environmental influence:

$${\mathsf{\Lambda }}_{M\backslash T}\left(V\right)\left\{{\mathsf{\Lambda }}_{\mathsf{\tau }\backslash n}\left(V\right)\left[d{u}_n^{eff}+d{u}_{\mathsf{\tau }}^{eff}\right]+d{u}_T^{eff}\right\}=u_0.$$

(43)

In the case of the linear relationship between the stresses and strains, expressions (41) and (42) will be as follows:

$$u_{\mathsf{\Sigma }}^{eff}={\mathsf{\Lambda }}_{M\backslash T}\left(V\right)\{{\mathsf{\Lambda }}_{\mathsf{\tau }\backslash n}\left(V\right)[\frac{1}{2}{A}_n\left(V\right){\mathsf{\sigma }}_n\cdot \cdot {\mathsf{\epsilon }}_{ij}+\frac{1}{2}{A}_{\mathsf{\tau }}\left(V\right){\mathsf{\sigma }}_{\mathsf{\tau }}\cdot \cdot {\mathsf{\epsilon }}_{ij}]+A_T\left(V\right)k{T}_{\mathsf{\Sigma }}\},$$

(44)

or:

$$\begin{array}{c}{u}_{\mathsf{\Sigma }}^{eff}={\mathsf{\Lambda }}_{M\backslash T}\left(V\right)\left\{{\mathsf{\Lambda }}_{\mathsf{\tau }\backslash n}\left(V\right)\left[A_n\left(V\right)u_n^{}\left(V\right)+A_{\mathsf{\tau }}\left(V\right)u_{\mathsf{\tau }}^{}\left(V\right)\right]+A_T\left(V\right)u_n^{}(V)\right\}=\\ ={\mathsf{\Lambda }}_{M\backslash T}\left(V\right)\left\{{\mathsf{\Lambda }}_{\mathsf{\tau }\backslash n}\left(V\right)\left[u_n^{eff}\left(V\right)+u_{\mathsf{\tau }}^{eff}\left(V\right)\right]+u_T^{eff}(V)\right\}.\end{array}$$

(45)

With regard to expression (36), criterion (43) can be represented as follows:

$$u_{\mathsf{\Sigma }}^{eff}=\{\left[u_n^{eff}({{\mathsf{\sigma }}_n}^{(V,W)},{{\mathsf{\epsilon }}_n}^{(V,W)})+u_{\mathsf{\tau }}^{eff}({{\mathsf{\sigma }}_{\mathsf{\tau }}}^{(V,W)},{{\mathsf{\epsilon }}_{\mathsf{\tau }}}^{(V,W)})\right]{\mathsf{\Lambda }}_{\mathsf{\tau }\backslash n}+u_T^{eff}\}{\mathsf{\Lambda }}_{T\backslash M}=u_0.$$

(46)

When the time effects should be taken into consideration, criterion (46) will assume the form:

$$u_{\mathsf{\Sigma }t}^{eff}={\displaystyle \underset{0}{\overset{t}{\int }}\{\left[u_n^{eff}({{\mathsf{\sigma }}_n}^{(V,W)},{{\mathsf{\epsilon }}_n}^{(V,W)},t)+u_{\mathsf{\tau }}^{eff}({{\mathsf{\sigma }}_{\mathsf{\tau }}}^{(V,W)},{{\mathsf{\epsilon }}_{\mathsf{\tau }}}^{(V,W)},t)\right]{\mathsf{\Lambda }}_{\mathsf{\tau }\backslash n}(t)}+u_T^{eff}(t)\}{\mathsf{\Lambda }}_{T\backslash M}(t)dt=u_0.$$

(47)

Thus, expression (45) is the concretization of function (25) and formula (46) is the concretization of criterion (27) for that case when the environmental influence is not taken into account.

Criterion (27) in the form of (46) and (47) says: when the sum of interacting effective energy components caused by the action of force, frictional, and thermal (thermodynamic) loads reach the critical (limiting) quantity u₀, the limiting (or critical) state of the MTD system (of both separate elements of the system and the system as the integrity) is realized. Physically, this state is determined by many and different damages.

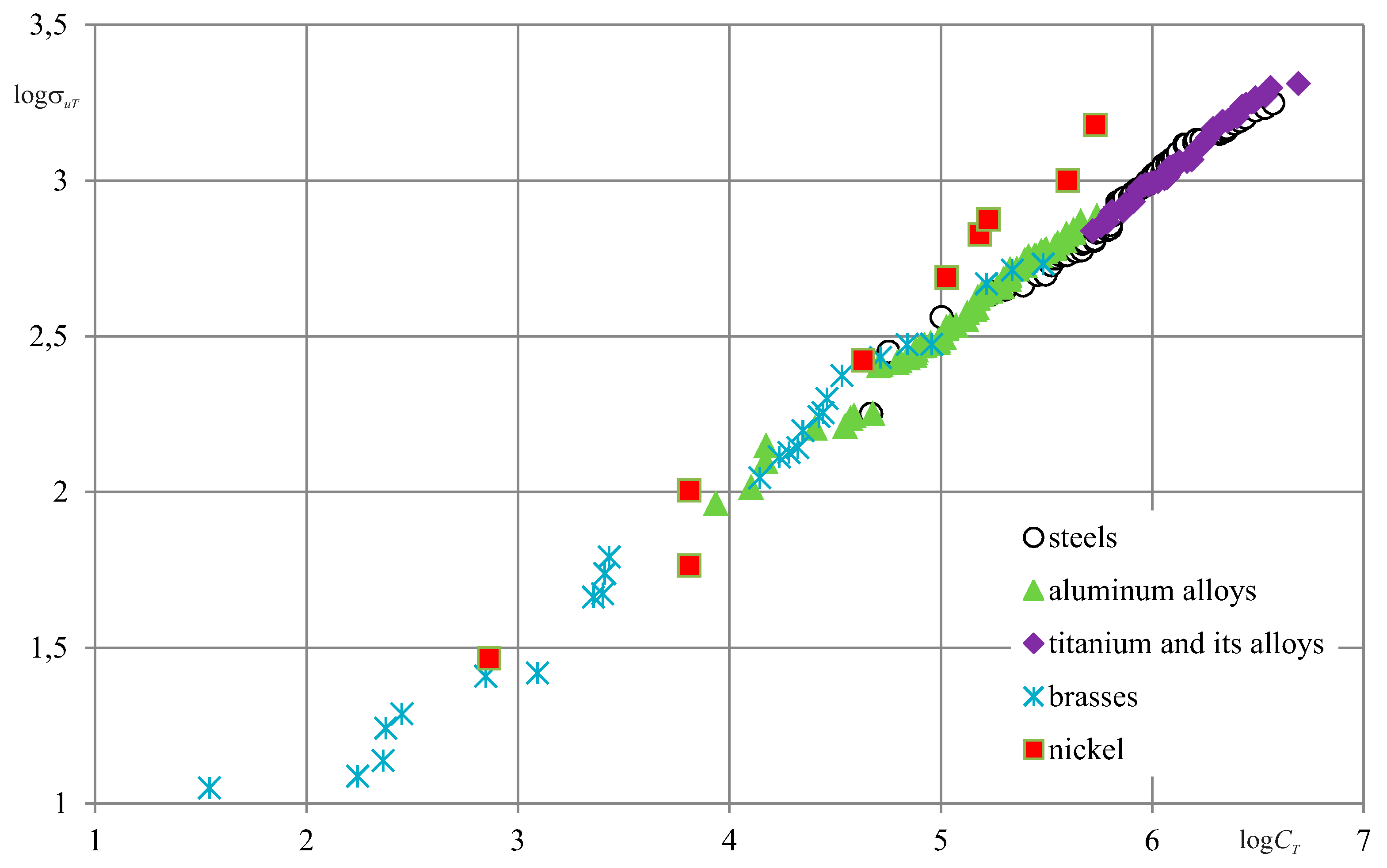
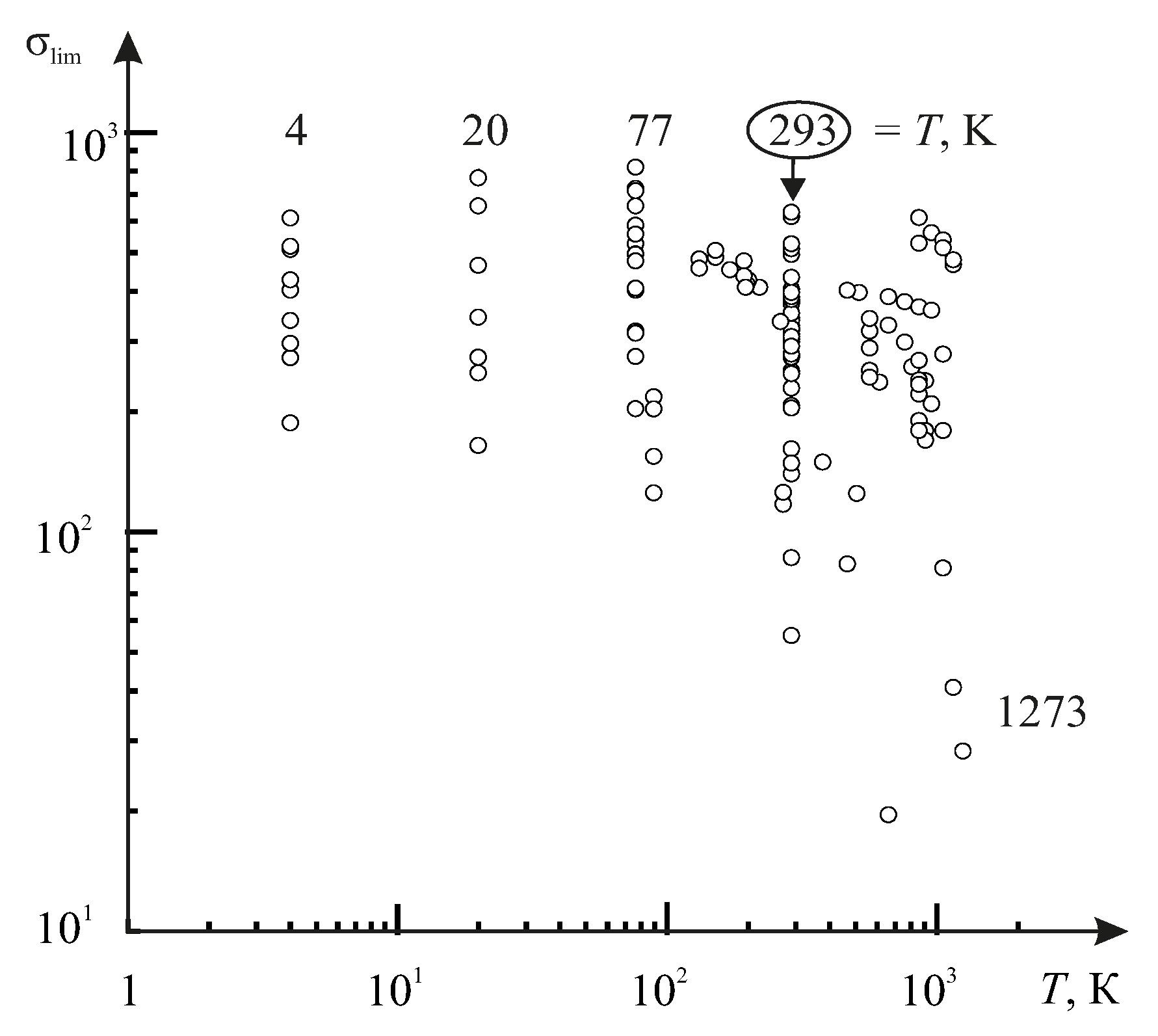
The fundamental character of the parameter u₀ has been mentioned above. According to [82,83,84,85,86,87,88,89,90,91,92,93,94,95], the parameter u₀ will be interpreted as the initial activation energy of the disintegration process. It is shown that the quantity u₀ approximately corresponds both to the sublimation heat for metals and crystals with ionic bonds and to the activation energy of thermal destruction for polymers:

$$u_0\approx u_T.$$

On the other hand, the quantity u₀ is determined as the activation energy for mechanical fracture:

$$u_0\approx u_M.$$

In such a way, the energy U₀ can be considered to be the material constant:

$$u_0\approx u_M\approx u_T=\text{const}.$$

(48)

Taking into consideration the physical-mechanical and thermodynamic representations of the processes of damage and fracture [84,85,87], write down (48) in the following form:

$$u_M=s_k\frac{{\mathsf{\sigma }}_{th}}{E}\frac{C_a}{{\mathsf{\alpha }}_V}=u_0=k{T}_S\ln \frac{k{\mathsf{\theta }}_D}{h}=u_T,$$

(49)

where s_k is the reduction coefficient, σ_th is the theoretical strength, E is the elasticity modulus, C_a is the atom heat capacity, α_V is the thermal expansion of the volume, k is the Boltzmann constant, T_S is the melting point, θ_D is the Debye temperature, h is the Planck constant. According to (49), it can be taken approximately [84]:

$$u_0\approx {\mathsf{\epsilon }}_{*}\frac{C_a}{{\mathsf{\alpha }}_V},$$

(50)

where ${\mathsf{\epsilon }}_{*}$ ≈ 0.6 is the limiting strain of the interatomic bond. Calculations according to (50) are not difficult. Methods of experimental determination of the quantity u₀ have also been developed [85].

From equality (49) it follows that u₀ is the activation energy of a given material, which is by the order of magnitude equal to 1–10 eV per one particle or molecule (~10²–10³ kJ/mol), i.e., the value that is close to the energy of interatomic bond rupture in the solid [88]. Its level doesn’t depend on how the rupture is —mechanically, thermally or by their simultaneous action. In [85], it is possible to find the tables containing the u₀ values for different materials.

From (49) it is possible to find the thermomechanical constant of the material [2]:

$$\frac{{\mathsf{\sigma }}_{th}}{T_S}=E\frac{{\mathsf{\alpha }}_{V}k}{C_a}\ln \frac{k{\mathsf{\theta }}_D}{h}={\mathsf{\theta }}_{\mathsf{\sigma }}.$$

(51)

The constant θ_σ characterizes the strength loss per 1 К.

Criterion (46) is written in the absolute values of physical parameters—the values of the effective and critical energy components. This criterion can be easily made dimensionless by diving it by the quantity $u_0$. Then it can be represented in terms of irreversible (effective) damage:

$${\mathsf{\psi }}_u^{eff}=\frac{u_{\mathsf{\Sigma }}^{eff}}{u_0}=1.$$

(52)

It is clear that the local (at the point) energy measure of damage ${\mathsf{\psi }}_u^{eff}$ is within the range:

$$0\le {\mathsf{\psi }}_u^{eff}\le 1,$$

(53)

or in detailed form:

$$0\le {\mathsf{\psi }}_u^{eff}=\frac{{\mathsf{\Lambda }}_{T\backslash M}}{u_0}\{\left[u_n^{eff}({\mathsf{\sigma }}_n{}^{(V,W)},{\mathsf{\epsilon }}_n{}^{(V,W)})+u_{\mathsf{\tau }}^{eff}({\mathsf{\sigma }}_{\mathsf{\tau }}{}^{(V,W)},{\mathsf{\epsilon }}_{\mathsf{\tau }}{}^{(V,W)})\right]{\mathsf{\Lambda }}_{n\backslash \mathsf{\tau }}+u_T^{eff}\}\le 1.$$

(54)

According to (54), it is also possible to determine particular energy measures of damage:

$$0\le {\mathsf{\psi }}_n^{eff}=\frac{u_n^{eff}\left({\mathsf{\sigma }}_n^{(V,W)},{\mathsf{\epsilon }}_n^{(V,W)}\right)}{u_0}\le 1,$$

(55)

$$0\le {\mathsf{\psi }}_{\mathsf{\tau }}^{eff}=\frac{u_{\mathsf{\tau }}^{eff}\left({\mathsf{\sigma }}_{\mathsf{\tau }}^{(V,W)},{\mathsf{\epsilon }}_{\mathsf{\tau }}^{(V,W)}\right)}{u_0}\le 1,$$

(56)

$$0\le {\mathsf{\psi }}_T^{eff}=\frac{u_T^{eff}}{u_0}\le 1,$$

(57)

due to the effective energies of different nature that are determined by the force (the subscript n), frictional (the subscript τ), and thermodynamic (the subscript T) loads, respectively. Now criterion (52) can be written in dimensionless form:

$${\mathsf{\psi }}_u^{eff}=\left[\left({\mathsf{\psi }}_n^{eff}+{\mathsf{\psi }}_{\mathsf{\tau }}^{eff}\right){\mathsf{\Lambda }}_{n\backslash \mathsf{\tau }}+{\mathsf{\psi }}_T^{eff}\right]{\mathsf{\Lambda }}_{М\backslash Т}=1.$$

(58)

According to (58), the limiting state of the MTD system is reached when the sum of interacting damages (0 < ψ < 1) at mechanical and thermodynamic loads is equal to 1. Criterion (46) in form (58) is convenient because all damage measures are dimensionless and are within the same range 0 ≤ ψ ≤ 1.

Since numerous and infinite actions, as well as the interaction effects of physical damages of many types (dislocations, vacancies, non-elastic deformations, etc.) cannot be described and predicted exactly, when analyzing the MTD system, one introduces the concept of the interaction of dangerous volumes [2] that contain a real complex of damages (defects generated by the action of the corresponding fields of stresses (strains)). According to the statistical model of the deformable solid with the dangerous volume [88], such a volume should depend on the geometric parameters of the solid responsible for its working volume V₀, on the distribution function parameters p(σ₋₁) and p(σ) of the durability limit σ₋₁ and the effective stresses σ considering both the effective stress probabilities P and γ₀ and gradients G_σ:

$$V_{P\mathsf{\gamma }}=F_V\left[p({\mathsf{\sigma }}_{-1}),p(\mathsf{\sigma }),G_{\mathsf{\sigma }},V_0,P,{\mathsf{\gamma }}_0,{\mathsf{\vartheta }}_V\right].$$

(59)

Here ${\mathsf{\vartheta }}_V$ describes how the limiting durability is influenced by the body shape and the scheme of body loading during fatigue tests.

Thus, the dangerous volume can serve as the equivalent of the complex of damages, as its value is proportional, in particular to the level of effective stresses and, hence, to the number (concentration) of defects (damages).

The boundary between the volumes of dangerous and safe, as it follows from expression (59), is generally blurred and probabilistic in nature. As the damage probability P of the solid increases, the dangerous volume $V_{P\gamma }$ is growing. At a given value of P the volume can vary depending on the confidence probability ${\mathsf{\gamma }}_0$. It means that at P = const:

$$V_{P_{\mathsf{\gamma }\min }}\le V_{P_{\mathsf{\gamma }}}\le V_{P_{\mathsf{\gamma }\max }},$$

(60)

if ${\mathsf{\gamma }}_{\min }\le {\mathsf{\gamma }}_0\le {\mathsf{\gamma }}_{\max }$. Here ${\mathsf{\gamma }}_{\min },{\mathsf{\gamma }}_{\max }$ form the permissible range. If it is accepted that ${\mathsf{\gamma }}_0$ = const, then the dangerous volume will have a single value associated with the damage probability P.

Scattered damage within the dangerous volume is characteristic not only for the so-called smooth bodies but also for the elements with the structural stress concentrators [88].

Thus, if in the uniaxial stress state, the stress distribution $\mathsf{\sigma }$ (x, y, z) in x, y, z coordinates is known, then the dangerous volume should be calculated by the formula:

$$V_{P\mathsf{\gamma }}={\displaystyle \underset{\mathsf{\sigma }(x,y,z)>{\mathsf{\sigma }}_{-1\min }}{\iiint }dxdydz},$$

(61)

where ${\mathsf{\sigma }}_{-1\min }$ being the lower boundary of the range of the durability limit ${\mathsf{\sigma }}_{-1}$ statistical distribution is such that if ${\mathsf{\sigma }}_{-1}<{\mathsf{\sigma }}_{-1\text{min}}$, then P = 0.

From expression (61) it follows that the generalized condition for fatigue fracture is of the form:

$$V_{P\mathsf{\gamma }}>0$$

(62)

with some probability P under the confidence probability ${\mathsf{\gamma }}_0$.

If:

$$V_{P\mathsf{\gamma }}=0,$$

(63)

then the fatigue damage cannot occur physically (because in this case, $\mathsf{\sigma }<{\mathsf{\sigma }}_{-1\min }$); hence, (63) is the generalized condition of non-fracture.

The methods for calculation of dangerous volumes $V_{ij}$ for friction pairs and tribo-fatigue systems are developed similar to (59):

$$V_{ij}=V_{ij}\left({\mathsf{\sigma }}_n^{(V,W)},{\mathsf{\sigma }}_{\mathsf{\tau }}^{(V,W)},{\mathsf{\sigma }}_{\text{lim}}^{(V,W)},G_{{\mathsf{\sigma }}_{ij}},V_0,P,{\mathsf{\gamma }}_0\right)$$

(64)

and outlined in [4,90,91,92]. Here ${\mathsf{\sigma }}_{\text{lim}}^{(V,W)}$ is the limiting stress based on the assigned criterion of damage and fracture.

Further, the following dimensionless characteristics of damage can be introduced: integral energy damage within the dangerous volume:

$${\mathsf{\Psi }}_u^{eff}\left(V\right)={\displaystyle \underset{{\mathsf{\psi }}_u^{eff}\left(dV\right)\ge 1}{\iiint }\frac{u_{\mathsf{\Sigma }}^{eff}}{u_0}dV}$$

(65)

and the average energy damage (at each point of the dangerous volume):

$${\overline{\mathsf{\Psi }}}_u^{eff}\left(V\right)=\frac{1}{V_u}{\displaystyle \underset{{\mathsf{\psi }}_u^{eff}\left(dV\right)\ge 1}{\iiint }\frac{u_{\mathsf{\Sigma }}^{eff}}{u_0}dV}.$$

(66)

The accumulation of energy damage in time within the dangerous volume is described by the formulas:

$${\mathsf{\Psi }}_u^{eff}\left(V,t\right)={\displaystyle \underset{t}{\int }{\displaystyle \underset{{\mathsf{\psi }}_u^{eff}\left(dV\right)\ge 1}{\iiint }\frac{u_{\mathsf{\Sigma }}^{eff}}{u_0}dV}}dt$$

(67)

$${\overline{\mathsf{\Psi }}}_u^{eff}\left(V,t\right)={\displaystyle \underset{t}{\int }\frac{1}{V_u}{\displaystyle \underset{{\mathsf{\psi }}_u^{eff}\left(dV\right)\ge 1}{\iiint }\frac{u_{\mathsf{\Sigma }}^{eff}}{u_0}dV}}dt.$$

(68)

Having used (63)–(68), the MTD system damage can be described and analyzed using the most general representations—the energy concepts with regard to the influence of numerous and different factors taken into account by (59), including the scale effect, i.e., the changes in the size and shape (mass) of system elements.

According to [2,95], the function Λ_k\l\n for damage interactions in the MTD system is determined by the parameters ρ of the effective energy ratio (Λ_k\l\n):

$${\mathsf{\Lambda }}_{n\backslash k\backslash l}={\mathsf{\Lambda }}_{n\backslash k\backslash l}\left({\mathsf{\rho }}_{M\backslash T},{\mathsf{\rho }}_{n\backslash \mathsf{\tau }}\right)⋛1,$$

(69)

$${\mathsf{\rho }}_{n\backslash \mathsf{\tau }}=u_{\mathsf{\tau }}^{eff}/u_n^{eff},{\mathsf{\rho }}_{M\backslash T}=u_M^{eff}/u_T^{eff}.$$

(70)

The quantities Λ calculated by (69) describe the influence of the load parameter ratio on the character and direction of interaction of irreversible damages [2,3,4]. If Λ > 1, then the system is self-softening because at the balance of hardening-softening phenomena, softening processes are dominant. If Λ < 1, the system is self-hardening, because at the balance of hardening-softening phenomena, hardening processes are dominant. At Λ = 1, the system is stable—the spontaneous hardening-softening phenomena are at balance in it. The general analysis of damage interactions in the MTD systems will be given on account of its fundamental importance in a separate paper.

After criterion (27) has been basically formalized, the action of electrochemical loads (damages) should be taken into consideration according to Item VII. It should be said at once that it is difficult to do in the strict mechanothermodynamical statement: electrochemical reactions are very diverse and complex, when the environment interacts with a deformable solid body, and are insufficiently studied. That’s why, the approach proposed in [2,3] is adopted: the simplification is introduced, according to which the damage of solids in the environment is determined by corrosion-electrochemical processes. In addition, the hypothesis is put forward, following to which the effective energy of corrosion-electrochemical damage is proportional to the square of the corrosion speed, i.e.,:

$$u_{ch}^{eff}~v_{ch}^2.$$

(71)

If according to Item VII, 0 ≤ D_ch ≤ 1 is the parameter of corrosion-electrochemical damage of the body, then based on [2,4,92], criterion (26) with regard to its shape will be as follows:

$${\mathsf{\Lambda }}_{M\backslash T}\left[\left(\frac{u_n^{eff}\left({\mathsf{\sigma }}_n^{(V,W)},{\mathsf{\epsilon }}_n^{(V,W)}\right)}{u_0\left(1-D_n\right)}+\frac{u_{\mathsf{\tau }}^{eff}\left({\mathsf{\sigma }}_{\mathsf{\tau }}^{(V,W)},{\mathsf{\epsilon }}_{\mathsf{\tau }}^{(V,W)}\right)}{u_0\left(1-D_{\mathsf{\tau }}\right)}\right){\mathsf{\Lambda }}_{\mathsf{\tau }\backslash n}+\frac{u_T^{eff}}{u_0\left(1-D_T\right)}\right]=1,\hspace{1em}\mathsf{\Lambda }⋛1,$$

(72)

where:

$$0\le \frac{u_n^{eff}\left({\mathsf{\sigma }}_n^{(V,W)},{\mathsf{\epsilon }}_n^{(V,W)}\right)}{u_0\left(1-D_n\right)}={\mathsf{\psi }}_{n(ch)}^{eff}\le 1,$$

(73)

$$0\le \frac{u_{\mathsf{\tau }}^{eff}\left({\mathsf{\sigma }}_{\mathsf{\tau }}^{(V,W)},{\mathsf{\epsilon }}_{\mathsf{\tau }}^{(V,W)}\right)}{u_0\left(1-D_{\mathsf{\tau }}\right)}={\mathsf{\psi }}_{\mathsf{\tau }(ch)}^{eff}\le 1,$$

(74)

$$0\le \frac{u_T^{eff}}{u_0\left(1-D_T\right)}={\mathsf{\psi }}_{T(ch)}^{eff}\le 1,$$

(75)

$$1-D_T=b_{e(T)}{\left(\frac{v_{ch}}{v_{ch(T)}}\right)}^{m_{v(T)}}, 1-D_n=b_{e(n)}{\left(\frac{v_{ch}}{v_{ch(n)}}\right)}^{m_{v(n)}}.$$

(76)

Here $v_{ch}$ is the corrosion speed in this environment, $v_{ch(T)}$, $v_{ch(\mathsf{\sigma })}$, $v_{ch(\mathsf{\tau })}$ is the corrosion speed in the same environment under thermal, force, and friction actions, respectively; b_e are the coefficients responsible for corrosive erosion processes; m_V(•) are the parameters responsible for the electrochemical activity of materials at force (the subscript σ), friction (the subscript τ), and thermodynamic (the subscript T) loads, wherein m_V(•) = 2/A_ch and the parameter A_ch ⋛ 1.

In [95], other methods for assessment of the parameter D_ch can be found. As seen, Equation (72) is the specification of criterion (27). According to this criterion, the limiting state of the MTD system is reached when the sum of dialectically interacting irreversible damages at force, friction, and thermodynamic loads (including electrochemical damage when acted upon by stress, friction, temperature) becomes equal to unity.

Further, consider the particular case when in (46) it is assumed that A_σ(V) = A_σ = const, A_τ(V) = A_τ = const, A_T(V) = A_T = const, ${\mathsf{\Lambda }}_{\mathsf{\tau }\backslash n}$ (V) = ${\mathsf{\Lambda }}_{\mathsf{\tau }\backslash n}$ = const, ${\mathsf{\Lambda }}_{M\backslash T}$ (V) = ${\mathsf{\Lambda }}_{M\backslash T}$ = const.

Firstly, the stress state is caused by volume deformation, for which all components of the stress tensor, except for one component σ (one-dimensional tension-compression, pure bending), can be neglected. Secondly, the stress state is caused by surface friction, for which all components of the stress tensor, except for one component τ_w, can be neglected. Then (40) assumes the following form:

$${\mathsf{\Lambda }}_{M\backslash T}\left[{\mathsf{\Lambda }}_{\mathsf{\tau }\backslash n}\left(A_{\mathsf{\sigma }}{\mathsf{\sigma }}^2+A_{\mathsf{\tau }}{\mathsf{\tau }}^2\right)+A_T{T}_{\mathsf{\Sigma }}\right]=u_0,$$

or in accordance with (72):

$${\mathsf{\Lambda }}_{M\backslash T}\left[\frac{a_T}{1-D_T}{T}_{\mathsf{\Sigma }}+{\mathsf{\Lambda }}_{\mathsf{\sigma }\backslash \mathsf{\tau }}\left(\frac{a_{\mathsf{\sigma }}}{1-D_{\mathsf{\sigma }}}{\mathsf{\sigma }}^2+\frac{a_{\mathsf{\tau }}}{1-D_{\mathsf{\tau }}}{\mathsf{\tau }}_w^2\right)\right]=u_0,\hspace{1em}\mathsf{\Lambda }⋛1,$$

(77)

where $\frac{a_{\mathsf{\sigma }}}{1-D_{\mathsf{\sigma }}}=A_{\mathsf{\sigma }}$, $\frac{a_{\mathsf{\tau }}}{1-D_{\mathsf{\tau }}}=A_{\mathsf{\tau }}$, $\frac{a_T}{1-D_T}=A_n$.

Thus, Equation (77) is the simplest form of the energy criterion of the limiting state that is nevertheless of great practical importance [2].

If there is no electrochemical influence of the environment ($D_{ch}$ = 0), then:

$$u_{\mathsf{\Sigma }}^{eff}={\mathsf{\Lambda }}_{M\backslash T}\left[a_T{T}_{\mathsf{\Sigma }}+{\mathsf{\Lambda }}_{\mathsf{\tau }\backslash n}\left(a_{\mathsf{\sigma }}{\mathsf{\sigma }}^2+a_{\mathsf{\tau }}{\mathsf{\tau }}_w^2\right)\right]=u_0,\hspace{1em}\mathsf{\Lambda }⋛1.$$

(78)

Equation (78) is the simplest form of the energy criterion of the limiting state, which, nevertheless, is of great practical importance [2,92,95]. It serves particularly for the development of methods of assessing the parameters $a_T,a_{\mathsf{\sigma }},a_{\mathsf{\tau }}$. In fact, at ${\mathsf{\Lambda }}_{M\backslash T}={\mathsf{\Lambda }}_{\mathsf{\tau }\backslash n}=1$, the boundary conditions are the following:

$$\begin{array}{l}{T}_{\mathsf{\Sigma }}=0,{\mathsf{\tau }}_w=0:a_n{\mathsf{\sigma }}_d^2=u_0,a_n=u_0/{\mathsf{\sigma }}_d^2;\\ T_{\mathsf{\Sigma }}=0,\mathsf{\sigma }=0:a_{\mathsf{\tau }}{\mathsf{\tau }}_d^2=u_0,a_{\mathsf{\tau }}=u_0/{\mathsf{\tau }}_d^2;\\ \mathsf{\sigma }=0,{\mathsf{\tau }}_w=0:a_{Т}{\mathsf{\sigma }}_d=u_0,a_{Т}=u_0/T_d,\end{array}\},$$

(79)

where σ_d, τ_d are the force and friction limiting stresses as T → 0. These are called the limits of (mechanical) destruction, T_d is the destruction temperature (when σ = 0, τ_w = 0) or the thermal destruction limit.

The effective (“dangerous”) part of total energy of strain can also be determined from the following physical considerations. It shall be assumed that the strain energy flux U generated in the material sample during its cyclic strain ($\mathsf{\epsilon }={\mathsf{\epsilon }}_{\max }\sin \mathsf{\omega }t$) in the homogeneous (linear) stress state is to a certain extent similar to the light flux. In fact, it is continuously excited when the loading cycle is repeated with the speed $\mathsf{\omega }=1/\mathsf{\lambda }$. This enables one to consider it as a wave (with the length λ). Some part of the energy u generated in such a way can be absorbed by material atoms and structural formations, followed by damage of material. Denote the absorbed part of the energy by u^eff. Then the generated energy u is equal to:

$$u=u^{eff}+u_{cons},$$

(80)

where u_cons is the non-absorbed part (it is called the conservative part) of the generated energy u.

If the analogy of light and energy strain is justified, then the strain absorption law may be similar to Bouguer’s light absorption law. Consequently, the equation relating the energy u_cons passed through the material strain volume V and the generated energy u is of the form:

$$u_{cons}=u\exp \left(-{\mathsf{\chi }}_{\mathsf{\epsilon }}V\right),$$

(81)

or, in accordance with Lambert, in differential form:

$$\frac{du}{u}=-{\mathsf{\chi }}_{\mathsf{\epsilon }}V.$$

(82)

Here as in Bourguer—Lambert’s equation, the coefficient χ_ε independent of u is the energy absorption parameter.

Taking into account (81) into (80), the strain energy absorption law is obtained:

$$u^{eff}=u\left[1-\exp \left(-{\mathsf{\chi }}_{\mathsf{\epsilon }}V\right)\right],$$

(83)

and hence if u = 0 or V = 0 then u^eff = 0. If V → ∞ it appears that according to (81) u_cons = u, i.e., all input energy is dissipated within such a volume.

From the physical point of view, the strain energy absorption process is caused by many phenomena:

• transition of electrons in absorbing atoms from lower to higher energy levels (quantum theory);
• generation and development of dislocation structures (dislocation theory);
• emergence of II and III order residual strains (stresses) (elasticity theory);
• formation and development of any imperfections (defects) of material composition and structure—point, planar and spatial (physical materials science);
• hardening-softening phenomena (including strain aging) developing in time (fatigue theory);
• changes in (internal) Tribo-Fatigue entropy (wear-fatigue damage mechanics [2]).

It should be noted that approach (83) can also be extended to the case of friction, since any indenter drives a strain wave upstream in the thin surface layer of the solid to which indenter is pressed to. Energy absorption parameter in this case will be χ_γ where the subscript γ denotes the shear strain. Similarly, heat absorption in the deformable solid body can also be considered. Finally, the problem of strain energy absorption in the non-uniform (including complex) stress state can be easily solved by putting the dangerous volume $V=V_{P\mathsf{\gamma }}$ into (81)–(83).

It should be noted that although criterion (78) is special, it is fundamental and general in nature. Its general nature is caused by the fact that in this case, all four particular phenomena responsible for the MTD system state (in the statement simplified in terms of the stress-strain state) are taken into account (in accordance with Item III). Its fundamental nature is that here, as in complete solution (46), Λ_n\τ takes into account the interaction of effective mechanical energy components caused by friction τ_w and normal σ stresses, whereas Λ_M\T takes into account the interaction of the thermal and mechanical components of the effective energy. The effective energy thermal component is determined by the variations of the total temperature T_∑ = T₂ − T₁ in the bodies contact zone caused by all heat sources, including the heat released during mechanical (spatial and surface) strain, structural changes, etc.

5. Mechanothermodynamical States

Within the framework of mechanothermodynamics a special approach is being developed to assess the entropy in terms of a generalized energy state. Following this approach and formula (77), out of the total energy (specific) due to some particular loads (force, temperature, etc.), its effective part directly spent for the damage production is defined by the experimentally found coefficients A_l in formulas (41), (42), (77) [2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68]:

$$u_l^{eff}=A_l{u}_l,$$

(84)

where the u_l are the specific internal energies at tear (u_n), shear (u_τ), thermal action (u_T).

The total specific energy of an elementary volume and a rate of its change are then given as:

$$u={\displaystyle \sum _l\left[\left(1-A_l\right)u_l+u_l^{eff}\right]},$$

(85)

$$\frac{du}{dt}={\displaystyle \sum _l\left[\left(1-A_l\right)\frac{d{u}_l}{dt}+\frac{d{u}_l^{eff}}{dt}\right]}.$$

(86)

Moreover, the Λ-functions are used to take into consideration a complex (nonadditive) character of interactions between effective energies of different nature expressed by formula (42). This allows the total effective energy of the system to be assessed:

$$u_{\mathsf{\Sigma }}^{eff}={\mathsf{\Lambda }}_{\mathsf{\alpha }}\left(u_l^{eff}\right)={\mathsf{\Lambda }}_{M\backslash T}\left({\mathsf{\Lambda }}_{\mathsf{\tau }\backslash n},A_l{u}_l^{}\right)={\mathsf{\Lambda }}_{M\backslash T}\left\{{\mathsf{\Lambda }}_{\mathsf{\tau }\backslash n}\left[A_n{u}_n^{}+A_{\mathsf{\tau }}{u}_{\mathsf{\tau }}^{}\right]+A_T{u}_T^{}\right\}.$$

(87)

where the Λ_α are the possible combinations of interaction of effective energies (irreversible damages).

The specific feature of Λ-functions is such that:

$$u_{\mathsf{\Sigma }}^{eff}⋛u_l^{eff},$$

(88)

and hence:

$$u_{\mathsf{\Sigma }}^{eff}⋛{\displaystyle \sum u}.$$

(89)

Thus, using coefficients A_l and Λ-functions it is possible to assess energy interaction due to different-nature loads. Such interaction can cause both a sharp growth and a substantial decrease of effective energy, resulting in damages and limiting states, as compared to the one calculated by the ordinary additivity model of type (17):

$$u_{\mathsf{\Sigma }}={\displaystyle \sum A_l{u}_l}.$$

(90)

The total effective energy of volume V and its accumulation in time with regard to formula (87) are of the form:

$$U_{\mathsf{\Sigma }}^{eff}={\displaystyle \underset{V}{\int }\mathsf{\rho }{u}_{\mathsf{\Sigma }}^{eff}\left(V\right)dV}$$

(91)

and:

$$U_{\mathsf{\Sigma }}^{eff}\left(t\right)={\displaystyle \underset{t}{\int }{\displaystyle \underset{V}{\int }\mathsf{\rho }{u}_{\mathsf{\Sigma }}^{eff}\left(V,t\right)dV}}dt.$$

(92)

The principal moment of the mechanothermodynamical model is the account of the limiting state (limits of plasticity, strength, fatigue, etc.) according to Item XIII:

$$u_{\mathsf{\Sigma }}^{eff}=u_0,$$

(93)

where u₀ is the limiting density of the internal energy interpreted as the initial activation energy of the disintegration process.

A relationship between the current state (mechanical, thermomechanical, energy) of an elementary volume of a solid (medium) and its limiting state enables one to construct the parameter of local energy damageability: dimensionless:

$${\mathsf{\psi }}_u^{eff}=\frac{u_{\mathsf{\Sigma }}^{eff}}{u_0}$$

(94)

or dimensional:

$${\mathsf{\psi }}_{u*}^{eff}=u_{\mathsf{\Sigma }}^{eff}-u_0.$$

(95)

Local energy damageability (94) or (95) is most general out of the damageability parameters constructed in terms of different mechanical (thermomechanical) states φ [2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68]:

$${\mathsf{\psi }}_q={\mathsf{\varphi }}_q/{\mathsf{\varphi }}_q^{(*\text{lim})},$$

(96)

where φ = σ, ε, u; the σ are the stresses; the ε are the strains; u is the density of internal energy; the ${\mathsf{\varphi }}_q^{(*\text{lim})}$ are the limiting values of the state φ $q\in \{eqv,ij,i,S,{}_{ij}^D,n,\mathsf{\tau },\text{int},$ $u,{}_u^n,{}_u^{\mathsf{\tau }},{}_u^{eff}\}$; eqv is the equivalent mechanical state; the ij are the components of the tensor φ; the i are the main components of the tensor φ; S and ${}_{ij}^D$ and the sphere and deviator parts of the tensor φ; n and τ are the normal and tangential components of the tensor φ; int is the intensity φ; u is the specific potential strain energy (internal energy density); the indices at u mean: ${}_u^n$ and ${}_u^{\mathsf{\tau }}$ are the specific potential strain energy at tension-compression and shear; ${}_u^{eff}$ is the effective specific potential strain energy.

Integral damageability measures can be built on the basis of local measures (96) with the use of the model of a deformable solid with a dangerous volume (64)–(68) [89].

By the dangerous volume is understood the spatial region of a loaded solid, at each point of which the value of local damageability is smaller than the limiting one [2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68]:

$$V_q=\left\{dV/{\mathsf{\phi }}_q\ge {\mathsf{\phi }}_q^{(*\lim )},dV\subset V_k\right\},$$

(97)

or:

$$V_q=\left\{dV/{\mathsf{\psi }}_q\ge 1,dV\subset V_k\right\}.$$

Dangeous volumes are calculated by the following general formula:

$$V_q={\displaystyle \underset{{\mathsf{\psi }}_q\left(V\right)\ge 1}{\iiint }dV}.$$

(98)

The integral condition of damageability of a solid or a system can be written in the form:

$$0<{\mathsf{\omega }}_q=\frac{V_q}{V_0}<1,$$

(99)

where V₀ is the working volume of the solid.

To analyze at a time dangerous volumes local damageability distributed within them, the function of damageability of unit volume is introduced:

$$d{\mathsf{\Psi }}_q={\mathsf{\psi }}_q\left(V\right)dV.$$

(100)

The function of damageability of the entire volume V will then be as:

$${\mathsf{\Psi }}_q={\displaystyle \underset{{\mathsf{\psi }}_q\ge 1}{\int }{\mathsf{\psi }}_q\left(V\right)dV}.$$

(101)

The simplest functions of damageability accumulation in time for unit volume and the enrire volume will be of the following form, respectively:

$$d{\mathsf{\Psi }}_q^{(t)}={\displaystyle \underset{t}{\int }{\mathsf{\psi }}_q}\left(t\right)dt,$$

(102)

$${\mathsf{\Psi }}_q^{(t)}={\displaystyle \underset{{\mathsf{\psi }}_q\ge 1}{\int }{\displaystyle \underset{t}{\int }{\mathsf{\psi }}_q\left(V,t\right)}dtdV}.$$

(103)

The indices of volume-mean damageability:

$${\overline{\mathsf{\Psi }}}_q^{(V)}=\frac{1}{V_q}{\displaystyle \underset{{\mathsf{\psi }}_q\ge 1}{\int }{\mathsf{\psi }}_q\left(V\right)dV}$$

(104)

and its accumulation in time can be used:

$${\overline{\mathsf{\Psi }}}_q^{(V,t)}=\frac{1}{V_q}{\displaystyle \underset{t}{\int }{\displaystyle \underset{{\mathsf{\psi }}_q\ge 1}{\int }{\mathsf{\psi }}_q\left(V,t\right)}dVdt}.$$

(105)

The analysis of formulas (94), (100), (102) comes to the conclusion that conceptually, they are related to the concept of entropy as a difference (or relations) between two states (configurations) of a system, the degree of its organization (chaotic state). As applied to damageability, such states are current and limiting.

Now using local energy damageability (94), construct specific (per unit mass) tribo-fatigue entropy (up to a constant):

$$s_{TF}={\mathsf{\psi }}_u^{eff}\left({\mathsf{\Lambda }}_{\mathsf{\alpha }},A_l,{\mathsf{\sigma }}_{ij},T\right)=\underset{\mathsf{\Delta }m->0}{\lim }{A}_{\mathsf{\psi }}\frac{u_{\mathsf{\Sigma }}^{eff}(\mathsf{\Delta }m)}{u_0\mathsf{\Delta }m},$$

(106)

or:

$$s_{TF}=s_{TF*}=\frac{{\mathsf{\psi }}_{u*}^{eff}\left({\mathsf{\Lambda }}_{\mathsf{\alpha }},A_l,{\mathsf{\sigma }}_{ij},T\right)}{T}=\frac{u_{\mathsf{\Sigma }}^{eff}-u_0}{T}.$$

(107)

where $A_{\mathsf{\psi }}$ is the dimensional parameter (J·mol⁻¹·K⁻¹).

On the basis of the expressions for entropy (18), аs well as of formulas (85), (86) the local entropy and the rate of its change within an elementary volume will be:

$$s=\frac{1}{T}{\displaystyle \sum _l\left[\left(1-A_l\right)u_l\right]}+s_{TF}$$

(108)

and:

$$\frac{ds}{dt}=\frac{1}{T}{\displaystyle \sum _l\left[\left(1-A_l\right)\frac{d{u}_l}{dt}\right]}+\frac{d{s}_{TF}}{dt}.$$

(109)

From formulas (108) and (109), it is seen that unlike the thermomechanical model, the state indices of the mechanothermodynamical system u and s are not equivalent. This is due to the fact that the calculation of the specific tribo-fatigue entropy $s_{TF}$ by formula (106) is supplemented by the limiting state in the form of the limiting density of the internal energy u₀.

The tribo-fatigue entropy $S_{TF}$ is calculated not within the entire volume V, but only within its damageable part, i.e., within the energy effective dangerous volume $V_u^{eff}$:

$$V_u^{eff}=\left\{dV/u_{\mathsf{\Sigma }}^{eff}\ge u_0,dV\subset V_k\right\}.$$

(110)

On the basis of formulas (11), (106) and (110), the tribo-fatigue entropy of volume V will be:

$$S_{TF}={\displaystyle \underset{u_{\mathsf{\Sigma }}^{eff}(V)\ge u_0}{\int }\mathsf{\rho }{s}_{TF}\left(V\right)dV}={\displaystyle \underset{u_{\mathsf{\Sigma }}^{eff}(V)\ge u_0}{\int }\mathsf{\rho }{\mathsf{\psi }}_u^{eff}\left(V\right)dV},$$

(111)

where:

$${\mathsf{\psi }}_u^{eff}(V)=\frac{u_{\mathsf{\Sigma }}^{eff}(V)}{u_0},$$

or:

$${\mathsf{\psi }}_u^{eff}(V)=\frac{{\mathsf{\psi }}_{u*}^{eff}(V)}{T}=\frac{u_{\mathsf{\Sigma }}^{eff}(V)-u_0}{T(V)},$$

(112)

and its accumulation will be:

$$S_{TF}\left(t\right)={\displaystyle \underset{t}{\int }{\displaystyle \underset{u_{\mathsf{\Sigma }}^{eff}(V,t)\ge u_0}{\int }\mathsf{\rho }{s}_{TF}\left(V,t\right)dV}}dt={\displaystyle \underset{t}{\int }{\displaystyle \underset{u_{\mathsf{\Sigma }}^{eff}(V,t)\ge u_0}{\int }\mathsf{\rho }{\mathsf{\psi }}_u^{eff}\left(V,t\right)dV}}dt,$$

(113)

where:

$${\mathsf{\psi }}_u^{eff}(V,t)=\frac{u_{\mathsf{\Sigma }}^{eff}(V,t)}{u_0},$$

or:

$${\mathsf{\psi }}_u^{eff}(V,t)=\frac{{\mathsf{\psi }}_{u*}^{eff}(V,t)}{T(V,t)}=\frac{u_{\mathsf{\Sigma }}^{eff}(V,t)-u_0}{T(V,t)}.$$

(114)

The principal feature of tribo-fatigue total $S_{TF}$ and specific $s_{TF}$ entropies should be emphasized. They allow the difference between two states to be assesses not only quantitatively (as thermomechanical entropy), but also qualitatively, as the value of the limiting density of the internal energy u₀ is explicitly introduced into the calculation of the specific entropy $s_{TF}$. Thus, $s_{TF}$ and $S_{TF}$ allow one to answer the question how much the current state of a solid or a system is dangerous in comparison with limiting states.

The total entropy and the rate of its change for a solid of a system with regard to (111) and (113) assume the form:

$$S={\displaystyle \underset{V}{\int }\frac{1}{T(V)}{\displaystyle \sum _l\mathsf{\rho }\left[\left(1-A_l(V)\right)u_l(V)\right]}}dV+S_{TF}$$

(115)

and:

$$\frac{dS}{dt}={\displaystyle \underset{V}{\int }\frac{1}{T(V)}{\displaystyle \sum _l\mathsf{\rho }\left[\left(1-A_l(V)\right)\frac{d{u}_l(V)}{dt}\right]}}dV+\frac{d{S}_{TF}}{dt}.$$

(116)

Based on formulas (106)–(116), the function of accumulation of total entropy in time can be built:

$$\begin{array}{c}S\left(t\right)={\displaystyle \underset{t}{\int }{\displaystyle \underset{V}{\int }{\displaystyle \sum _l\mathsf{\rho }{s}_l}}(V,t)dV}dt+{\displaystyle \underset{t}{\int }{\displaystyle \underset{u_{\mathsf{\Sigma }}^{eff}(V,t)\ge u_0}{\int }\mathsf{\rho }{s}_{TF}}(V,t)dV}dt=\\ ={\displaystyle \underset{t}{\int }{\displaystyle \underset{V}{\int }\frac{1}{T(V,t)}{\displaystyle \sum _l\mathsf{\rho }\left[\left(1-A_l(V,t)\right)\frac{d{u}_l(V,t)}{dt}\right]}}dV}dt+{\displaystyle \underset{t}{\int }{\displaystyle \underset{u_{\mathsf{\Sigma }}^{eff}(V,t)\ge u_0}{\int }\mathsf{\rho }{\mathsf{\psi }}_u^{eff}(V,t)dV}}dt\end{array}.$$

(117)

In this respect, bearing in mind the limiting states of a solid or a system, models (115)–(117) permit one to answer the question whether the current state is the point of a qualitative jump in the system, i.e., whether the current state is close to the limiting one. A similar (dialectical as a matter of fact) qualitative transition differs, for example, from the bifurcation point having the uncertainty in a further development of events and the possibility to predict the system behavior after a transition on the basis of the analysis of $s_{TF}$ and $S_{TF}$. Particular limiting states (limit of strength, mechanical or contact fatigue, etc.) enable one to predict the situation after transition the given point: principal changes in the system properties and behavior or the formation of a new system based on the previous one.

As an example, there can be non-linear deformation or generation of microcracks in the solid (or the system) that cause the changes in its strength and fatigue properties, and, hence, to its response to loads. In turn, formed macrocracks lead to local continuum violation—formation of new free surfaces (possibly, of new solids—destruction products), i.e., a new system.

It should be noted that models (115)–(117) were built using a traditional concept of entropy additivity (10) although with regard to substational improvements. These models also contain reversible processes described by the entropy components s_l not yielding primary damages and, hence, the limiting states—the points of a qualitative change of the system.

It is therefore more advisable for a qualitative and quantitative analysis of evolution of systems (whose states are traditionally defined as bifurcation branches) that the entropy state should be determined using the mechanothermodynamical model of the solid using only tribo-fatigue entropy. In this case, formulas (111)–(113) for entropy and its accumulation will be of the form:

$$S=S_{TF}={\displaystyle \underset{u_{\mathsf{\Sigma }}^{eff}(V,t)\ge u_0}{\int }\mathsf{\rho }{s}_{TF}\left(V\right)dV}={\displaystyle \underset{u_{\mathsf{\Sigma }}^{eff}(V,t)\ge u_0}{\int }\mathsf{\rho }{\mathsf{\psi }}_u^{eff}\left(V\right)dV},$$

(118)

and:

$$\begin{array}{l}S\left(t\right)=S_{TF}\left(t\right)={\displaystyle \underset{t}{\int }{\displaystyle \underset{u_{\mathsf{\Sigma }}^{eff}(V,t)\ge u_0}{\int }\mathsf{\rho }{s}_{TF}\left(V\right)dV}}dt=\\ ={\displaystyle \underset{t}{\int }{\displaystyle \underset{u_{\mathsf{\Sigma }}^{eff}(V,t)\ge u_0}{\int }\mathsf{\rho }{\mathsf{\psi }}_u^{eff}(V,t)dV}}dt.\end{array}$$

(119)

To identify the points of qualitative change in the limiting states of solids (systems), the indices of relative integral entropy and its accumulation built on the basis of the concept of integral condition of damageability of a solid (99) can be used:

$${\mathsf{\omega }}_S=\frac{S_{TF}}{V_0}=\frac{1}{V_0}{\displaystyle \underset{u_{\mathsf{\Sigma }}^{eff}(V,t)\ge u_0}{\int }\mathsf{\rho }{s}_{TF}\left(V\right)dV};$$

(120)

$${\mathsf{\omega }}_S\left(t\right)=\frac{S_{TF}\left(t\right)}{V_0}=\frac{1}{V_0}{\displaystyle \underset{t}{\int }{\displaystyle \underset{u_{\mathsf{\Sigma }}^{eff}(V,t)\ge u_0}{\int }\mathsf{\rho }{s}_{TF}\left(V\right)dV}}dt.$$

(121)

The indices $S_{TF}$, $S_{TF}\left(t\right)$, ${\mathsf{\omega }}_S$, ω_S, ${\mathsf{\omega }}_S\left(t\right)$ can grow infinitely, allowing not only the limiting states of type (93), but also different transmitting states to be described; in essence, they “provide” a quantitative description of the law of increase of entropy.

Now based on formulas (24), (115), (117) and (119) let us construct generalized expresssions for entropy, a rate of its change аs well as its accumulation in the mechanothermodynamical system consisting of a liquid (gas) medium of volume V and a solid of volume V_ψ:

$$\begin{array}{c}S={\displaystyle \underset{V}{\int }\mathsf{\rho }{s}_T}dV+{\displaystyle \underset{V_{\mathsf{\psi }}}{\int }{\displaystyle \sum _l\mathsf{\rho }{s}_l}}d{V}_{\mathsf{\psi }}+{\displaystyle \underset{u_{\mathsf{\Sigma }}^{eff}\ge u_0}{\int }\mathsf{\rho }{s}_{TF}}d{V}_{\mathsf{\psi }}=\\ ={\displaystyle \underset{V}{\int }\frac{1}{T}{\mathsf{\sigma }}_{ij}{\mathsf{\epsilon }}_{ij}}dV+{\displaystyle \underset{V}{\int }\frac{1}{T}\mathsf{\rho }q}dV+{\displaystyle \underset{V}{\int }\frac{1}{T}\mathsf{\rho }{\displaystyle \sum _k{\mathsf{\mu }}_k{n}_k}}dV+{\displaystyle \underset{V_{\mathsf{\psi }}}{\int }\frac{1}{T}{\displaystyle \sum _k\mathsf{\rho }\left[\left(1-a_k\right)u_k\right]}}d{V}_{\mathsf{\psi }}+{\displaystyle \underset{u_{\mathsf{\Sigma }}^{eff}\ge u_0}{\int }\mathsf{\rho }{\mathsf{\psi }}_u^{eff}d{V}_{\mathsf{\psi }}}\end{array},$$

(122)

$$\begin{array}{c}\frac{dS}{dt}={\displaystyle \underset{V}{\int }\mathsf{\rho }\frac{d{s}_T}{dt}}dV+{\displaystyle \underset{V_{\mathsf{\psi }}}{\int }{\displaystyle \sum _l\mathsf{\rho }\frac{d{s}_l}{dt}}}d{V}_{\mathsf{\psi }}+{\displaystyle \underset{V_{\mathsf{\psi }}}{\int }\mathsf{\rho }\frac{d{s}_{TF}}{dt}}d{V}_{\mathsf{\psi }}=\\ ={\displaystyle \underset{V}{\int }\frac{1}{T}{\mathsf{\sigma }}_{ij}\frac{d{\mathsf{\epsilon }}_{ij}}{dt}}dV+{\displaystyle \underset{V}{\int }\frac{1}{T}\mathsf{\rho }\frac{dq}{dt}}dV+{\displaystyle \underset{V}{\int }\frac{1}{T}\mathsf{\rho }{\displaystyle \sum _k{\mathsf{\mu }}_k\frac{d{n}_k}{dt}}}dV+{\displaystyle \underset{V_{\mathsf{\psi }}}{\int }\frac{1}{T}{\displaystyle \sum _k\mathsf{\rho }\left[\left(1-a_k\right)\frac{d{u}_k}{dt}\right]}}d{V}_{\mathsf{\psi }}+{\displaystyle \underset{u_{\mathsf{\Sigma }}^{eff}\ge u_0}{\int }\mathsf{\rho }\frac{d{\mathsf{\psi }}_u^{eff}}{dt}d{V}_{\mathsf{\psi }}}\end{array},$$

(123)

$$\begin{array}{c}S\left(t\right)={\displaystyle \underset{t}{\int }{\displaystyle \underset{V}{\int }\mathsf{\rho }{s}_T}dV}dt+{\displaystyle \underset{t}{\int }{\displaystyle \underset{V_{\mathsf{\psi }}}{\int }{\displaystyle \sum _l\mathsf{\rho }{s}_l}}d{V}_{\mathsf{\psi }}}dt+{\displaystyle \underset{t}{\int }{\displaystyle \underset{u_{\mathsf{\Sigma }}^{eff}\ge u_0}{\int }\mathsf{\rho }{s}_{TF}}d{V}_{\mathsf{\psi }}}dt=\\ ={\displaystyle \underset{t}{\int }{\displaystyle \underset{V}{\int }\frac{1}{T}{\mathsf{\sigma }}_{ij}{\mathsf{\epsilon }}_{ij}}dV}dt+{\displaystyle \underset{t}{\int }{\displaystyle \underset{V}{\int }\frac{1}{T}\mathsf{\rho }q}dVdt}+{\displaystyle \underset{t}{\int }{\displaystyle \underset{V}{\int }\frac{1}{T}\mathsf{\rho }{\displaystyle \sum _k{\mathsf{\mu }}_k{n}_k}}dV}dt+{\displaystyle \underset{t}{\int }{\displaystyle \underset{V_{\mathsf{\psi }}}{\int }\frac{1}{T}{\displaystyle \sum _l\mathsf{\rho }\left[\left(1-a_l\right)u_l\right]}}d{V}_{\mathsf{\psi }}}dt+{\displaystyle \underset{t}{\int }{\displaystyle \underset{u_{\mathsf{\Sigma }}^{eff}\ge u_0}{\int }\mathsf{\rho }{\mathsf{\psi }}_u^{eff}d{V}_{\mathsf{\psi }}}}dt\end{array}.$$

(124)

Entropy state indices can be built similarly for a system composed of many media.

It should be noted that the interaction (contact) of two media in formulas (122)–(125), which can be complex in nature, is taken into account only implicitly in terms of medium state parameters (stresses, strains, temperature). It is obvious that this is only the first step to a comprehensive (generalized) solution of the problem stated.

The simplified writing of expression (123) for the entropy increment of the mechanothermodynamical system composed of finite volumes dV and dV_ψ given in [68] can be re-written in the following form:

$$dS={\left(dS\right)}_T+{\left(d_{i}S\right)}_{TF}=\frac{dU+\mathsf{\Delta }pdV}{T}-\frac{1}{T}{\displaystyle \sum _k{\mathsf{\mu }}_{k}d{N}_k+{\mathsf{\Psi }}_u^{eff}d{V}_{\mathsf{\psi }}}.$$

(125)

Expression (125) can also be represented in terms of specific quantities as:

$$dS={\displaystyle \underset{V}{\int }\frac{\mathsf{\rho }du+\mathsf{\rho }dp}{T}}dV-{\displaystyle \underset{V}{\int }\frac{1}{T}\mathsf{\rho }{\displaystyle \sum _k{\mathsf{\mu }}_{k}d{n}_k}}dV+{\displaystyle \underset{u_{\mathsf{\Sigma }}^{eff}\ge u_0}{\int }\mathsf{\rho }d{\mathsf{\psi }}_u^{eff}d{V}_{\mathsf{\psi }}},$$

(126)

or on the basis of (123) as:

$$\frac{dS}{dt}={\displaystyle \underset{V}{\int }\frac{{\mathsf{\sigma }}_{ij}d{\mathsf{\epsilon }}_{ij}+\mathsf{\rho }dq}{Tdt}}dV-{\displaystyle \underset{V}{\int }\frac{1}{T}\mathsf{\rho }{\displaystyle \sum _k{\mathsf{\mu }}_k\frac{d{n}_k}{dt}}}dV+{\displaystyle \underset{u_{\mathsf{\Sigma }}^{eff}\ge u_0}{\int }\mathsf{\rho }\frac{d{\mathsf{\psi }}_u^{eff}}{dt}d{V}_{\mathsf{\psi }}}.$$

(127)

In formulas (111)–(113) for calculation of the tribo-fatigue entropy $S_{TF}$ and its accumulation $S_{TF}\left(t\right)$, the specific entropy $s_{TF}$ is assumed to be integrated in terms only of the damageable part of the solid—the dangerous volume. However the influence of undamagable regions can also be allowed for by integrating $S_{TF}$ over the entire volume:

$$S_{TF}={\displaystyle \underset{V}{\int }\mathsf{\rho }{s}_{TF}\left(V\right)dV}={\displaystyle \underset{V}{\int }\mathsf{\rho }{\mathsf{\psi }}_u^{eff}\left(V\right)dV};$$

(128)

$$S_{TF}\left(t\right)={\displaystyle \underset{t}{\int }{\displaystyle \underset{V}{\int }\mathsf{\rho }{s}_{TF}\left(V,t\right)dV}}dt={\displaystyle \underset{t}{\int }{\displaystyle \underset{V}{\int }\mathsf{\rho }{\mathsf{\psi }}_u^{eff}\left(V,t\right)dV}}dt,$$

(129)

where:

$${\mathsf{\psi }}_u^{eff}=\{\begin{array}{l}\frac{u_{\mathsf{\Sigma }}^{eff}\left(V,t\right)}{u_0}\ge 1,\text{\hspace{1em}if\hspace{1em}}{u}_{\mathsf{\Sigma }}^{eff}\ge u_0;\\ \frac{u_{\mathsf{\Sigma }}^{eff}\left(V,t\right)}{u_0}<1,\text{\hspace{1em}if\hspace{1em}}{u}_{\mathsf{\Sigma }}^{eff}<u_0,\end{array}$$

(130)

or:

$${\mathsf{\psi }}_u^{eff}=\frac{{\mathsf{\psi }}_{u*}^{eff}\left(V,t\right)}{T\left(V,t\right)}=\{\begin{array}{l}\frac{u_{\mathsf{\Sigma }}^{eff}\left(V,t\right)-u_0}{T\left(V,t\right)}\ge 0,\text{\hspace{1em}if\hspace{1em}}{u}_{\mathsf{\Sigma }}^{eff}\ge u_0;\\ \frac{u_{\mathsf{\Sigma }}^{eff}\left(V,t\right)-u_0}{T\left(V,t\right)}<0,\text{\hspace{1em}if\hspace{1em}}{u}_{\mathsf{\Sigma }}^{eff}<u_0.\end{array}$$

(131)

From expression (131), it is seen that ${\mathsf{\psi }}_u^{eff}$ < 0 is observed outside the dangerous volume (at $u_{\mathsf{\Sigma }}^{eff}<u_0$). This means that the specific tribo-fatigue entropy $s_{TF}$ also appears to be negative (or less than unity for its alternative definition) outside the dangerous volume where the limiting state is not reached. Negative values of ${\mathsf{\psi }}_u^{eff}$ and $s_{TF}$ can then be interpreted as the absence of damageability or in other words as the retention of structure and/or properties of the solid.

As follows from the above-stated, the assumption on the entropy additivity is wrong in the general case for a system composed of both a solid and a liquid (gas) where chemical reactions can occur. By analogy with Λ-functions, interaction functions of different-nature energy (179) it is necessary to introduce interaction functions of different-nature entropy by adding them to expression (125) in effort to determine total effective entropy:

$$\begin{array}{c}d{S}_{total}^{eff}={\mathsf{\Lambda }}_{T\backslash TF}^{\left(S\right)}\left(d{S}_T+d_i{S}_{TF}\right)={\mathsf{\Lambda }}_{T\backslash TF}^{\left(S\right)}\left[{\mathsf{\Lambda }}_{Q\backslash Ch}^{\left(S\right)}\left(d{S}_T^Q+d{S}_{Ch}^Q\right)+d_i{S}_{TF}\right]=\\ ={\mathsf{\Lambda }}_{T\backslash TF}^{\left(S\right)}\left[{\mathsf{\Lambda }}_{Q\backslash Ch}^{\left(S\right)}\left(\frac{dU+\mathsf{\Delta }pdV}{T}-\frac{1}{T}{\displaystyle \sum _k^{}{\mathsf{\mu }}_{k}d{N}_k}\right)+{\mathsf{\Psi }}_u^{eff}d{V}_{\mathsf{\psi }}\right],\end{array}$$

(132)

or:

$$d{S}_{total}^{eff}={\mathsf{\Lambda }}_{T\backslash TF\backslash Ch}^{\left(S\right)}\left(d{S}_T+d_i{S}_{TF}\right)={\mathsf{\Lambda }}_{T\backslash TF\backslash Ch}^{\left(S\right)}\left[\frac{dU+\mathsf{\Delta }pdV}{T}-\frac{1}{T}{\displaystyle \sum _k^{}{\mathsf{\mu }}_{k}d{N}_k}+{\mathsf{\Psi }}_u^{eff}d{V}_{\mathsf{\psi }}\right],$$

(133)

where the subscripts Q and Ch denote the thermodynamic and chemical entropy components.

Formulas (132)–(133) are supplemented by the generalized interaction functions ${\mathsf{\Lambda }}_{T\backslash TF}^{\left(S\right)}$, ${\mathsf{\Lambda }}_{Q\backslash Ch}^{\left(S\right)}$, ${\mathsf{\Lambda }}_{T\backslash TF\backslash Ch}^{\left(S\right)}$ in mechanothermodynamical systems. This means that the hypothesis on the additivity of thermodynamic and tribo-fatigue entropy is not accepted. The appropriate Λ-functions of interactions should then be specified and introduced into Equations (132)–(133).

6. Laws of Mechanothermodynamics

From the above-stated three main conclusions follow:

• Damages are the fundamental physical property (and the functional duty) of any system and all of its elements.
• Damage of each object (any existing one) inevitably grows up to its breakdown—decomposition (disintegration) into a set of particles of arbitrarily small size, i.e., it is the unidirectional process of time.
• Not only the unity and struggle of opposites but also the directivity of various and complex physical processes of hardening-softening (depending on the level of loads and time) are typical of the evolution of the system by damage. It means that the Λ-function of damage interactions (of all kinds) can take three classes of values: (a) Λ < 1 when the hardening process is dominant; (b) Λ > 1 when the softening process is dominant; (c) Λ = 1 when a stable hardening to softening process ratio is found.

Thus, the First Law of Mechanothermodynamics (see Figure 2) states that for evolution of any system the unidirectional process of its damage and disintegration, finally, into an infinitely large number of small components (fragments, atoms, elementary particles, etc.) is inevitable. In fact, it is equivalent to the recognition of the thesis on the unending of evolution if it is taken into account that disintegration products of any system become a construction material for new systems. Thus, the evolution hysteresis is formed. Generalizing, it may be said that our Universe is indestructible as it evolves by damage. This corresponds to the philosophical concept that matter and motion are eternal, and damage is the fundamental property (and a duty) of all systems, including living and intelligent ones [1,67,96,97].

The Second Law of Mechanothermodynamics states Figure 3): Λ-functions of interactions must take three classes of values (Λ ⋛ 1) to describe not only the unity and struggle, but also the directivity of physical hardening-softening processes in the system, i.e., the system evolution by damage [1,67].

It can be seen that the state of a system can be equivalently described in terms of either energy or entropy. The main drawback of such descriptions is the known unreality of energy and, hence, of entropy: physical energy carriers are not detected and, apparently, do not exist. As Feynman [98] said figuratively, they cannot be touched. Damages are quite a different matter: they are physically real, can be touched, actually define any of the conceivable states of material bodies and systems. Kinetic process of their accumulation, as well as the time stream is inevitable and unidirectional. If Mechanothermodynamics considers the damage of a system as its fundamental physical property (and duty), one can hope that based on it, the consistent general theory of evolution of any systems, including living and intelligent, can be created. For instance, the idea of life as of a special method of damage accumulation (biological, mechanical, intellectual, etc.) is being developed in [68,97,99].

Thus, the attempt was made above to formulate the basic provisions of a new (or, better to say, integrated) physical discipline—Mechanothermodynamics with the use of the energy principles. This discipline combines two branches of Physics in effort not to argue or not to compete with each other, but to take a fresh look at the MTD system evolution (Figure 4).

From Figure 5 it follows that the principles of Mechanothermodynamics can be formulated in two ways: (1) Mechanics → Tribo-Fatigue → Mechanothermodynamics and (2) Thermodynamics → Tribo-Fatigue → Mechanothermodynamics.

Thus, Tribo-Fatigue has become a bridge for transition from Mechanics and Thermodynamics to Mechanothermodynamics. The fact that the both ways are leading to one purpose and, finally, yield the same (unified) result, means that the above-mentioned two methodologies of analysis are valid, correct and do not contradict each other. From Figure 1 it is clear that the MTD system should be followed by an object that is somewhat more complex (however simpler) than the real system, for example, the MTD system with some “elements of intelligence”. The first works in this area of research are already available [100,101,102].

7. Analysis of Experimental Data

Experimental verification of generalized criterion (72) of the limiting state of a MTD system is extremely difficult because of the absence of relevant experimental data. Their acquisition is though very relevant but at the same time is very difficult and expensive. Therefore, in this paper, the analysis of the particular solution of criterion (77) in form of (78) is given.

From (78) it is easy to obtain a number of formulas important for application. So, the conditions of purely thermal (or thermodynamic) damage (when σ = 0 and τ_w = 0) or purely mechanical damage [when T_∑ → 0)] will be as follows:

$$a_T{T}_{\mathsf{\Sigma }}=u_0,$$

(134)

$${\mathsf{\Lambda }}_{n\backslash \mathsf{\tau }}\left(a_n{\mathsf{\sigma }}^2+a_{\mathsf{\tau }}{\mathsf{\tau }}_w^2\right)=u_0.$$

(135)

For isothermal mechanical fatigue (when τ_w = 0) we have:

$${\mathsf{\Lambda }}_{M\backslash T}\left(a_T{T}_{\mathsf{\Sigma }}+a_n{\mathsf{\sigma }}^2\right)=u_0,$$

(136)

and for isothermal frictional fatigue (when σ = 0) we obtain:

$${\mathsf{\Lambda }}_{M\backslash T}\left(a_T{T}_{\mathsf{\Sigma }}+a_{\mathsf{\tau }}{\mathsf{\tau }}_w^2\right)=u_0.$$

(137)

The general analysis of the above-described partial criteria allows three main conclusions to be reached:

• The growth of loading parameters (σ, τ_w, T_∑, D) results in the corresponding acceleration of reaching the limiting state (u₀).
• The limiting state of the system can also be reached by increasing only one (any) of the loading parameters (when maintaining the same values of other parameters).
• If $\mathsf{\Lambda }$ > 1, the damageability of the system accordingly enhances (i.e., the processes of its softening are dominant), and if $\mathsf{\Lambda }$ < 1 it slows down (i.e., the processes of its hardening appear to be preferable) in comparison with the damage due to the joint action of loading parameters alone (with no regard to the dialectic interaction of irreversible damages).

The last conclusion is also the result of a fundamentally new approach to the construction of the criterion of the limiting state of MTD systems [102]. According to this approach, not the mutual influence of the factors, but the interaction ($\mathsf{\Lambda }$ ⋛ 1) of phenomena determines the damage processes in the MTD system [1,67,68,69,102]. In this regard, the paper synthesized the results of more than 600 diverse experimental data. This permitted the generalized MTD function of critical by damage states to be revealed.

Refer to one of the special cases of criterion (78)—isothermal mechanical fatigue. From (136) it follows that:

$$\text{log}{\mathsf{\sigma }}_{-1T}=\frac{1}{2}\log C_T;C_T=\left[u_0/{\mathsf{\Lambda }}_{M\backslash T}-a_T{T}_{\mathsf{\Sigma }}\right]\cdot \frac{1}{a_n}.$$

(138)

According to (138), the dependence of limiting stresses on the parameter of thermomechanic resistance C_T in the double logarithmic coordinates is to be a straight line with the angular coefficient (1/2). The general regularity is as follows: the higher the value of the parameter C_T, the greater is the quantity ${\mathsf{\sigma }}_{-1T}$. Figure 6 shows a satisfactory evidence of this dependence for numerous different-grade steels tested for fatigue in different conditions [93,95,103,104,105]. It is seen that the C_T value varied by more than two orders, i.e., by a factor of 100 or more, and the values of the endurance limit ${\mathsf{\sigma }}_{-1T}$—by more than two orders, i.e., by a factor of 10 or more, thus the testing temperature varied in the range from the helium temperature to 0.8 T_s ($T_S$ is the temperature of melting). As shown in Figure 6, Equation (138) adequately describes the results of 136 experiments.

In Figure 7, the similar analysis is made on the basis of the test results for tension at different temperatures (σ_иT is the stress limit). In this case, it is taken that σ_–1 = σ_иT in Equation (138). It is obvious: the correlation coefficient is very high—not less than r = 0.722 (very occasionally), but in the most cases it exceeds r = 0.9; the analysis includes more than 300 test results. Works [103,104] and may others contain other examples of successful experimental approbation of criterion (138). This allows us to hope that even more general criteria (for example, Equations (77) and (78)) will appear to be practically acceptable. In our opinion, further studies should confirm our hope.

Note that the attempts to construct the explicit temperature dependence of limiting stresses in uniform, semilogarithmic and logarithmic coordinates for different materials and different testing conditions are quite ineffective (Figure 8).

8. Conclusions

It is shown, that the creation of Mechanothermodynamics—a generalized physical discipline is possible by constructing two bridges. The first is tribo-fatigue entropy which paved the way from Thermodynamics to Mechanics. The second is a fundamental understanding in Tribo-Fatigue of irreversible damage of everything that exists which paved the way from Mechanics to Thermodynamics (Figure 4 and Figure 5). The first and the second principles of Mechanothermodynamics are presented and discussed.

Main provisions (I-XV) which constitute the foundation of the general theory of evolution of mechanothermodynamical systems are formulated.

The following theories and models are developed:

• energy theory of limiting states,
• energy theory of damage,
• foundations of the theory of electrochemical damage.

Methods and procedures for calculating effective (dangerous) energy which is spent on generation, motion and accumulation of irreversible damages are developed (see formulas (79)–(83) and corresponding text).

Fundamentals of the theory of Λ-interaction between damages caused by loads of different nature (mechanical, thermodynamic, etc.; see formulas (69), (70), (136) and corresponding text) are given. This theory allows considering the influence of the spontaneous processes of hardening-softening on the state of damage of mechanothermodynamical systems.

In practical terms, a single MTD function of critical by damage (limiting) states of metal and polymer materials operating in different conditions (formula (138)) is obtained in this work. The analysis of 136 experimental results (Figure 6) showed that this function is fundamental: it is valid for low-, average- and high-strength states of pure metals, alloys, and polymers over a wide range of temperatures of medium (from helium temperature to 0.8 T_S, where T_S is the material melting temperature) and mechanical stresses (up to the strength limit for single static loading) while the fatigue life was of the order of 10⁶–10⁸ cycles.

Finally, it should be noted that the research in Mechanothermodynamics is just beginning. The deepening and broadening of the scope of works in this new and promising area of knowledge are expected in the near future. In the authors’ opinion, the utility of works is so great that it is difficult to foresee their results.