Complex Dynamics of a Continuous Bertrand Duopoly Game Model with Two-Stage Delay
Abstract
:1. Introduction
2. The Model
3. Equilibrium Points and Local Stability
3.1. Case 1. ,
3.2. Case 2. ,
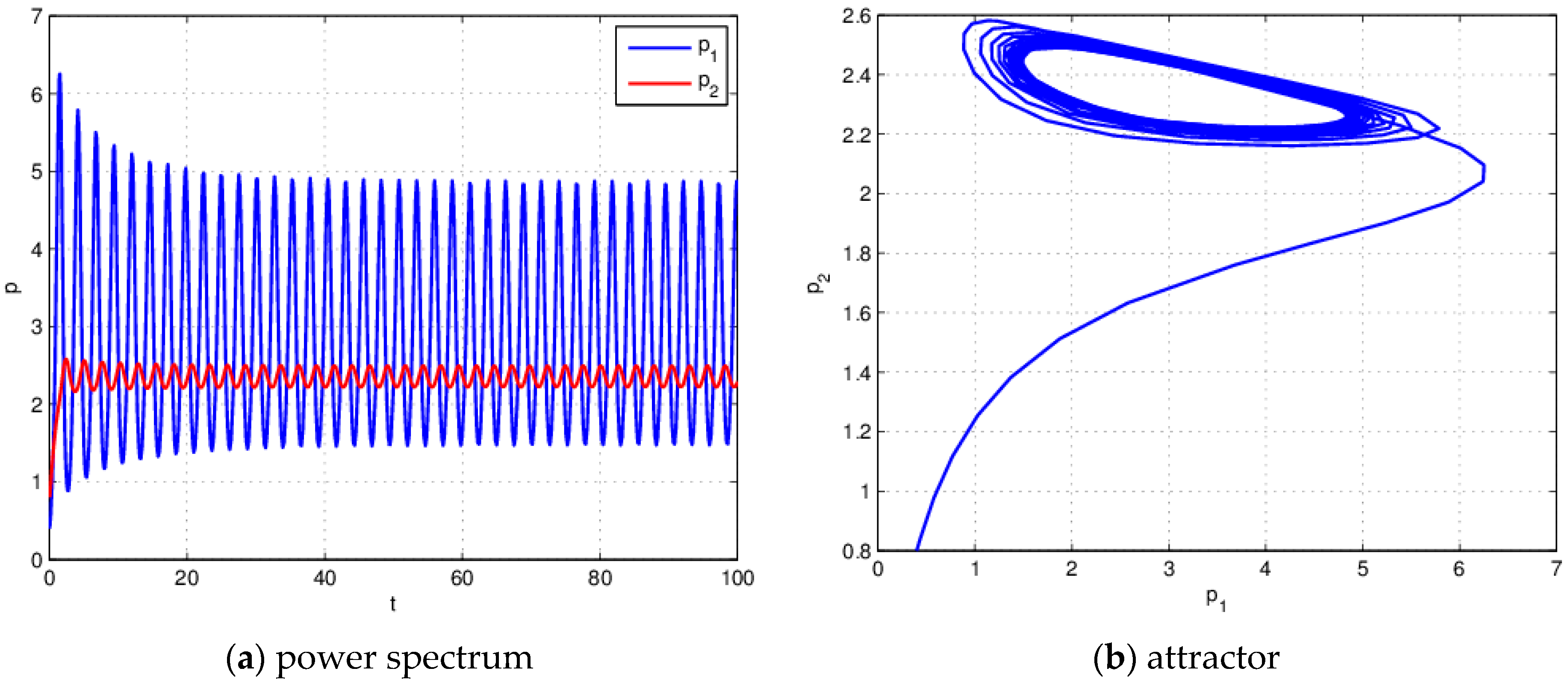
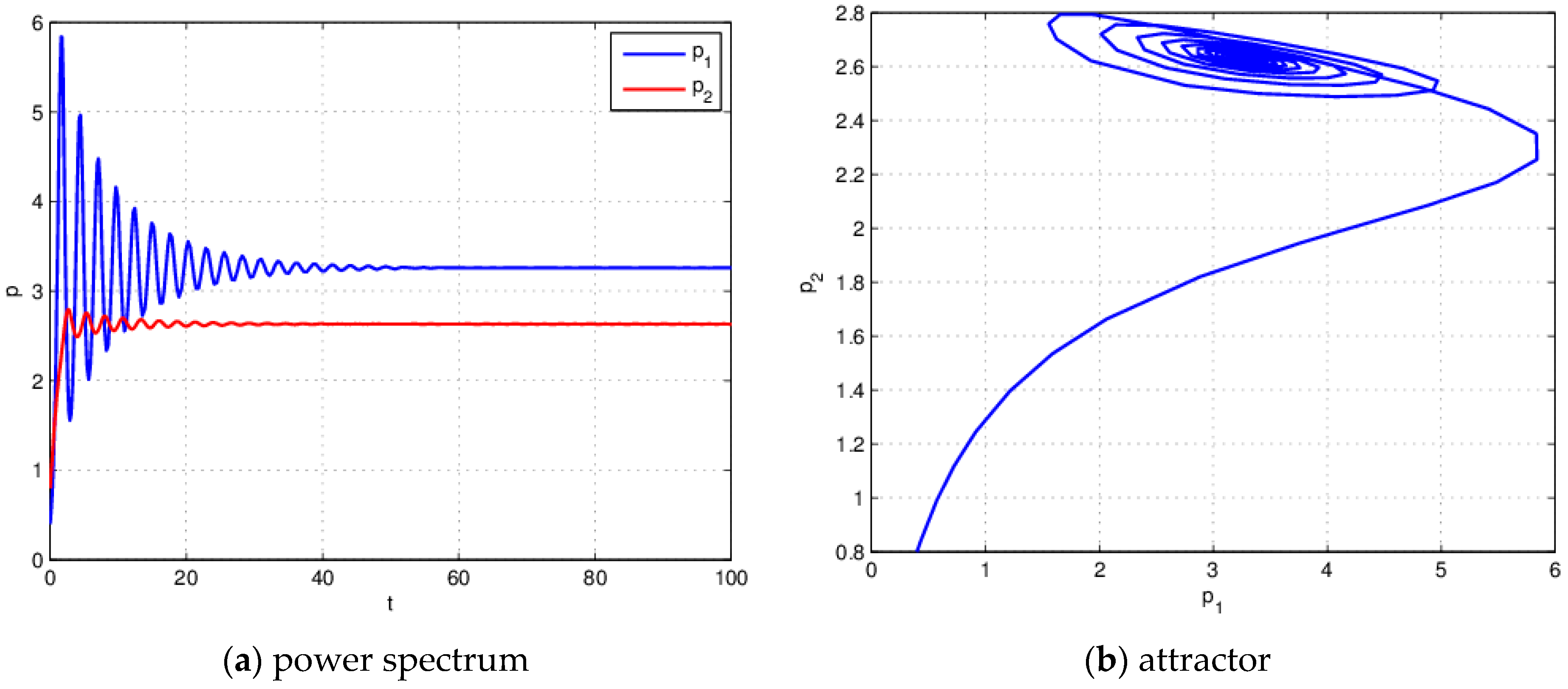
4. Numerical Simulations
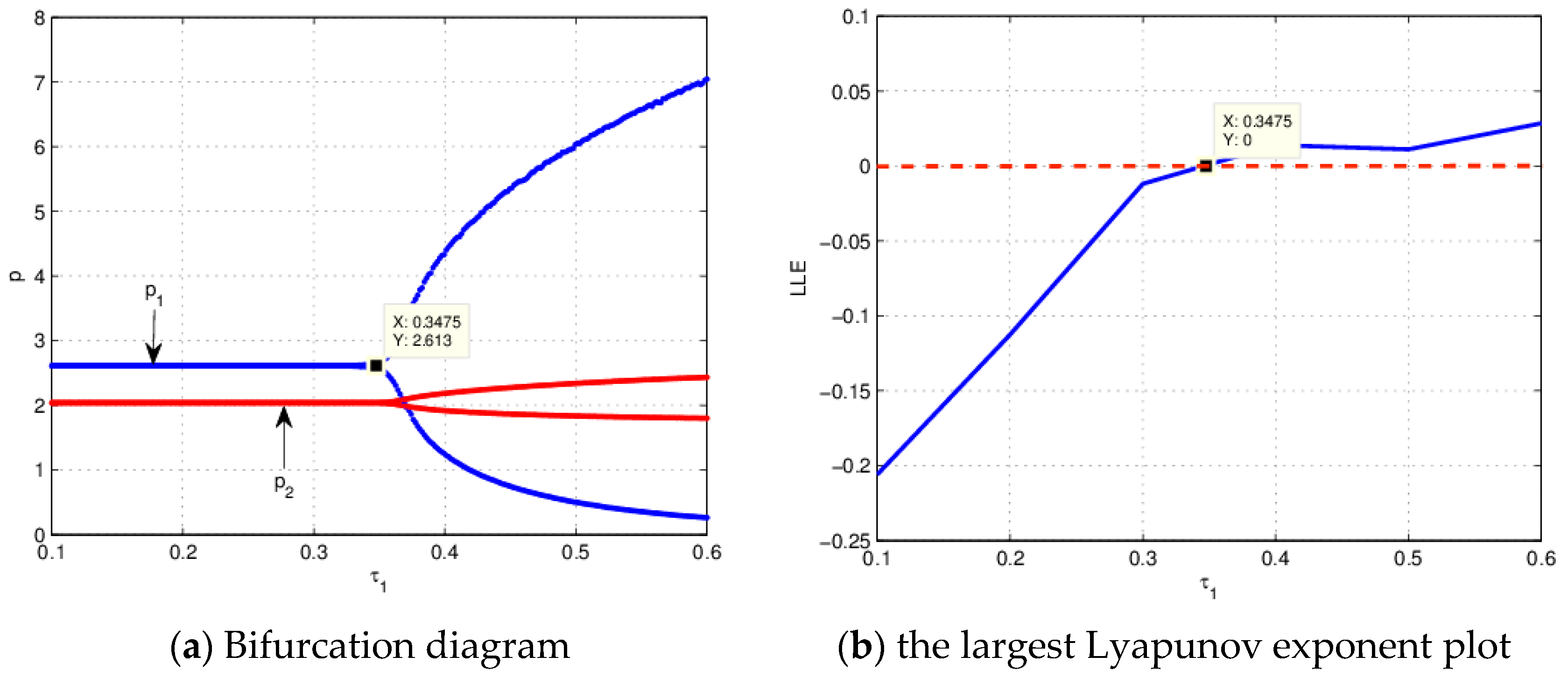
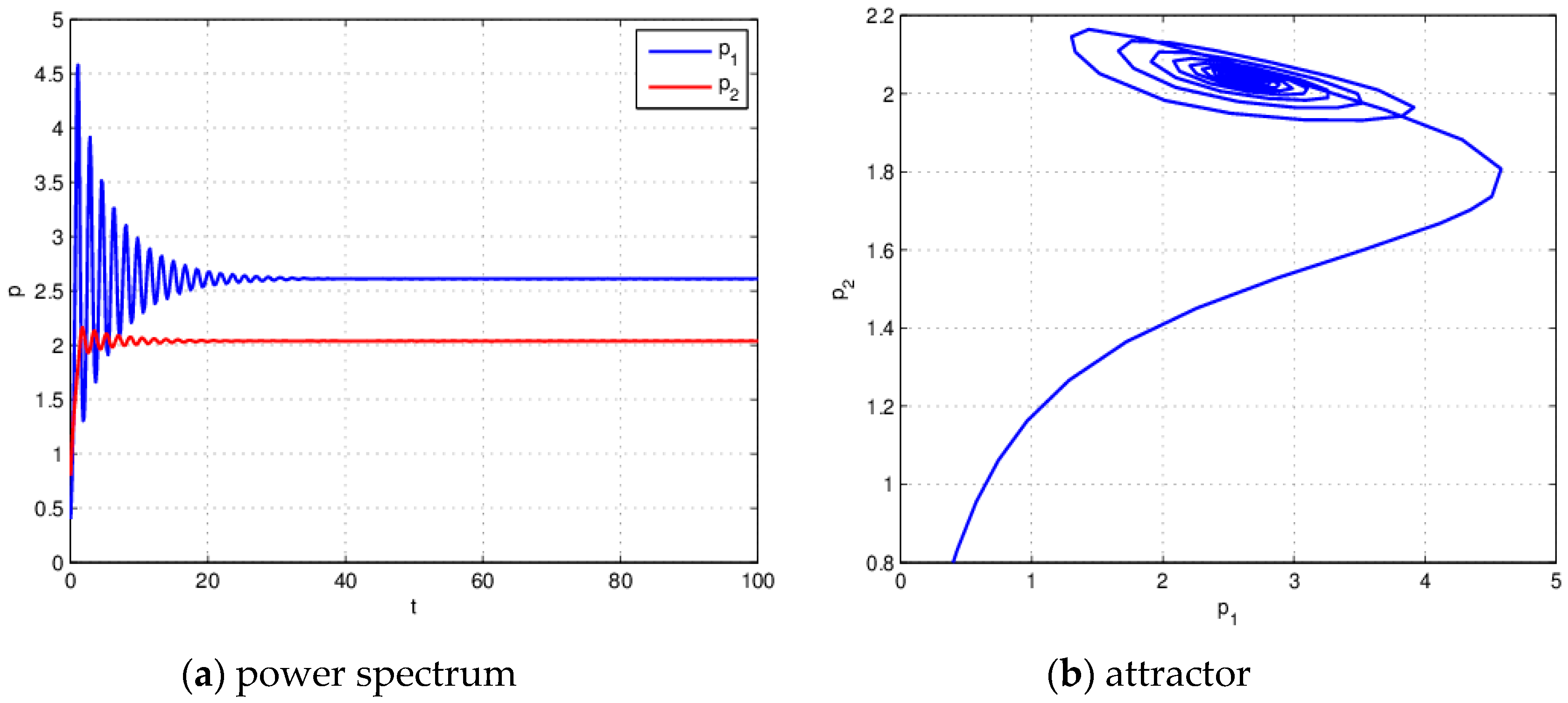
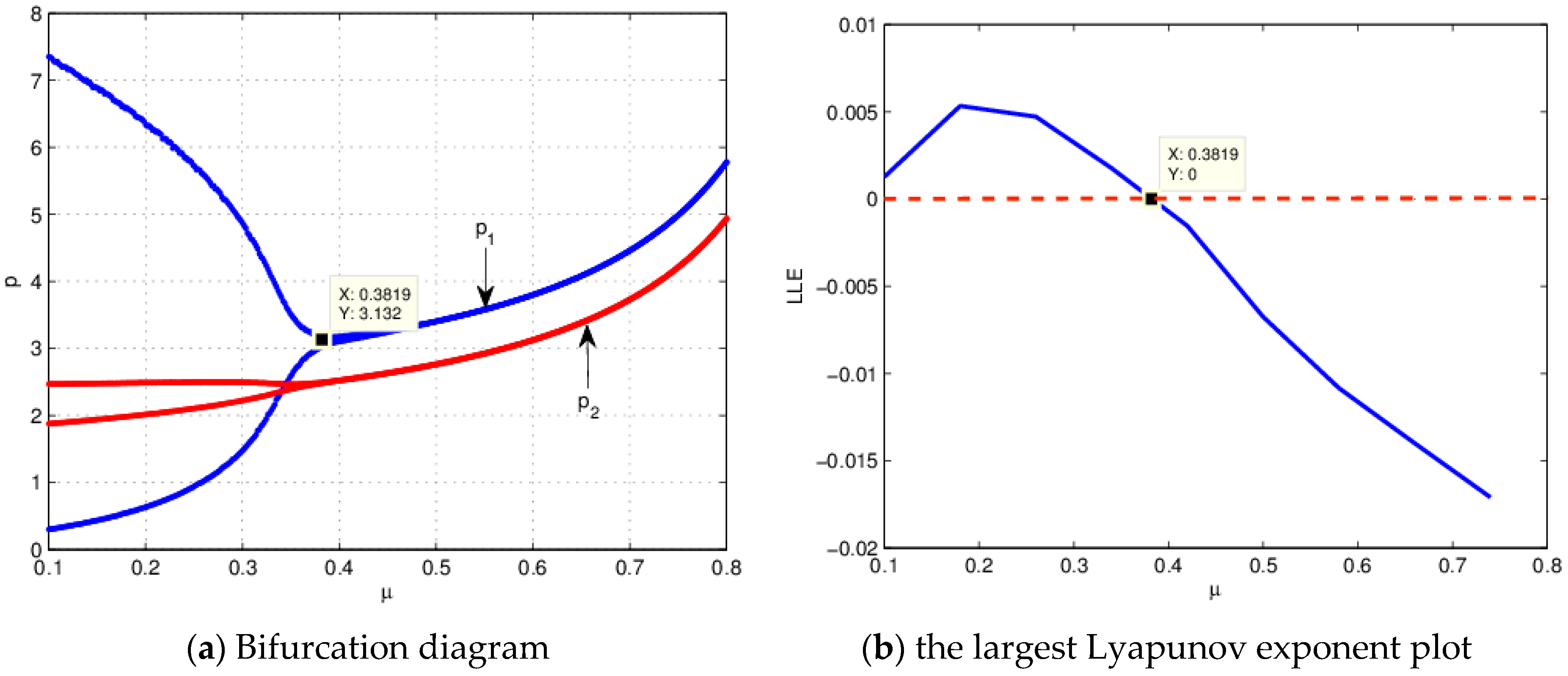
4.1. The Influence of on the Stability of the System (21) When
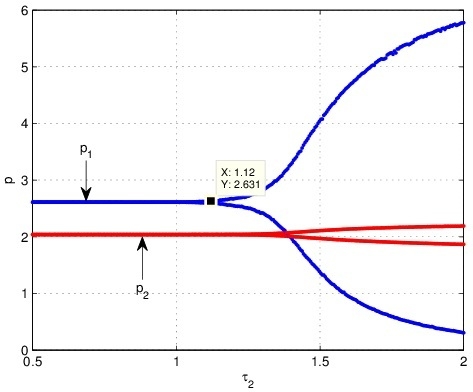
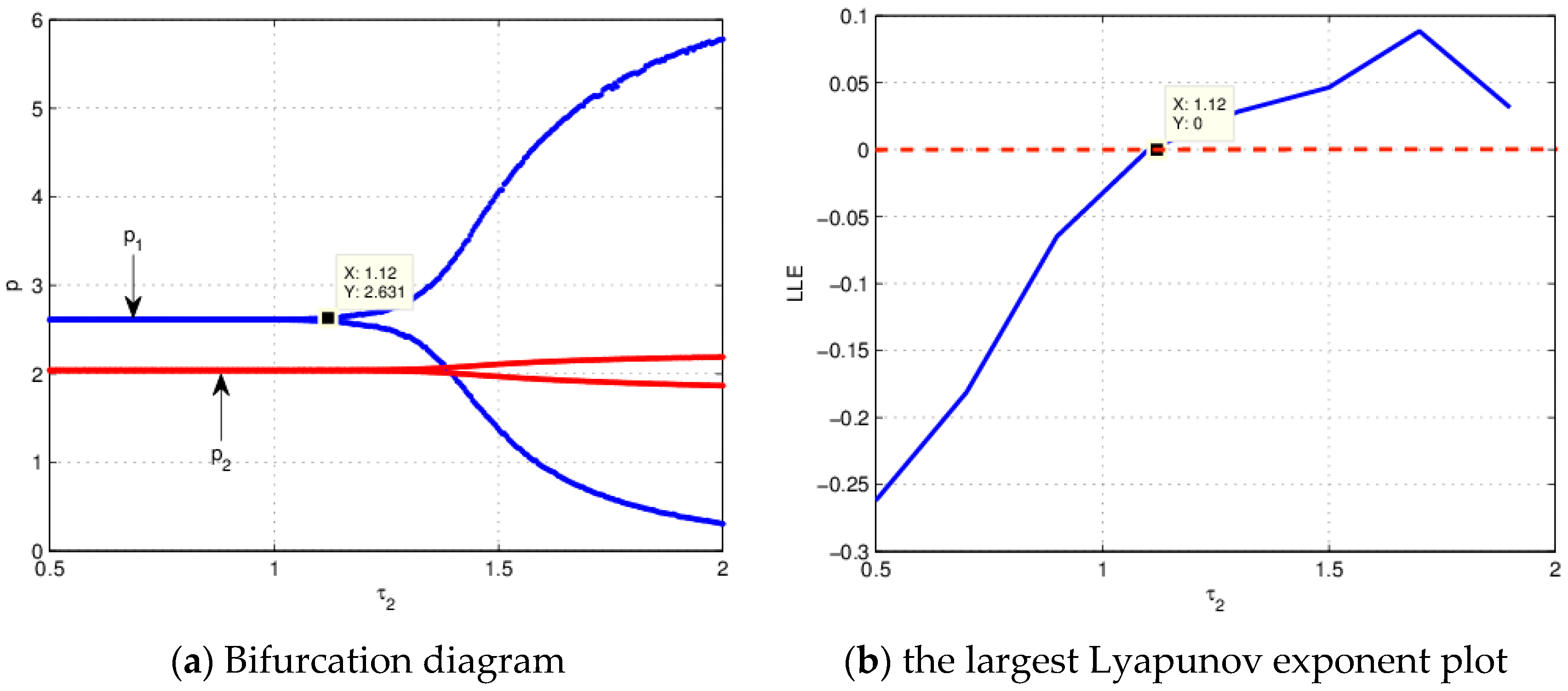
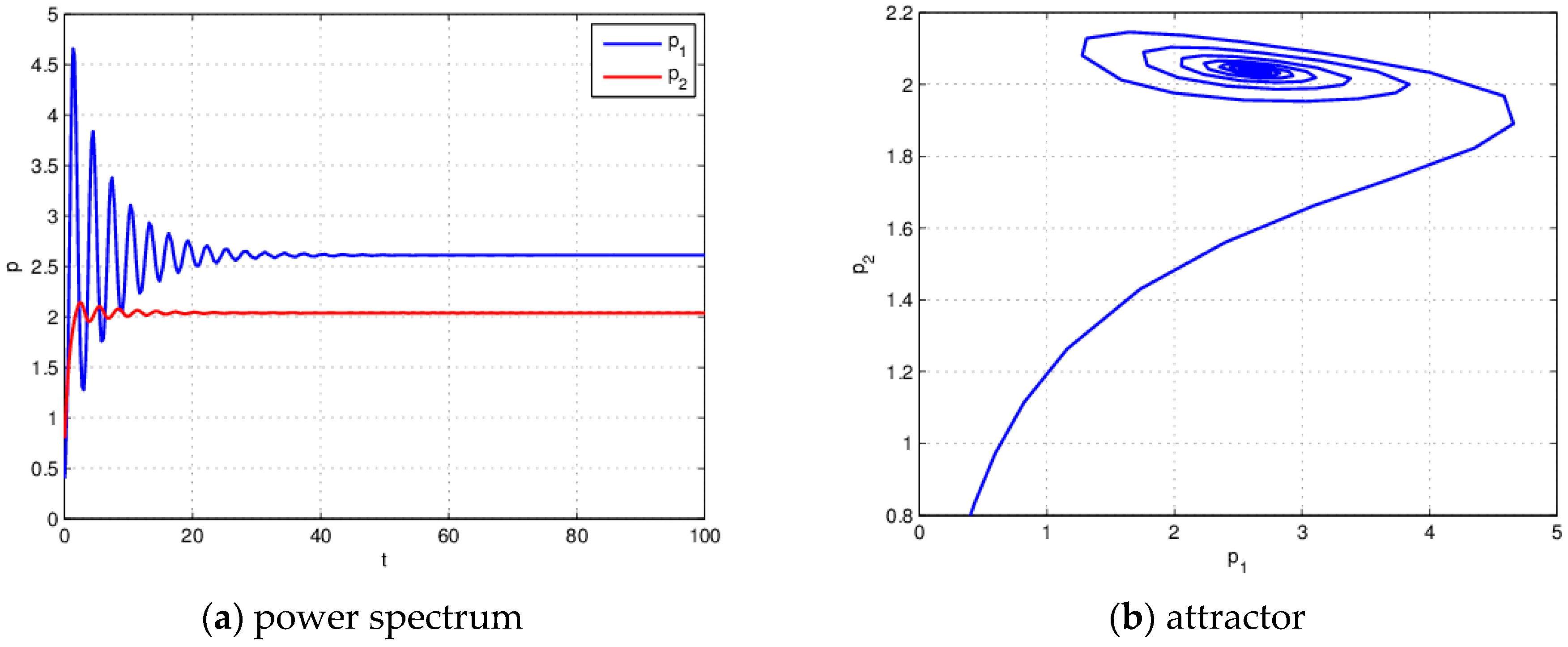
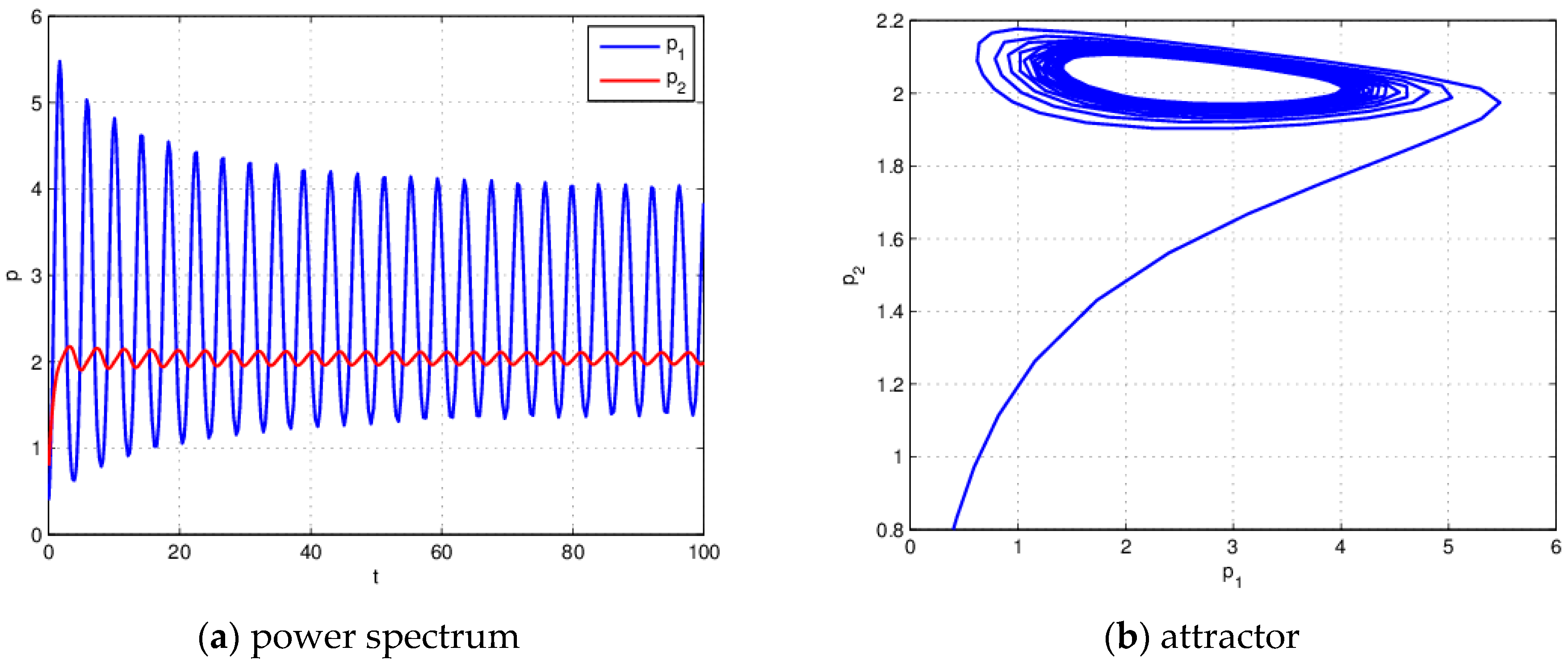
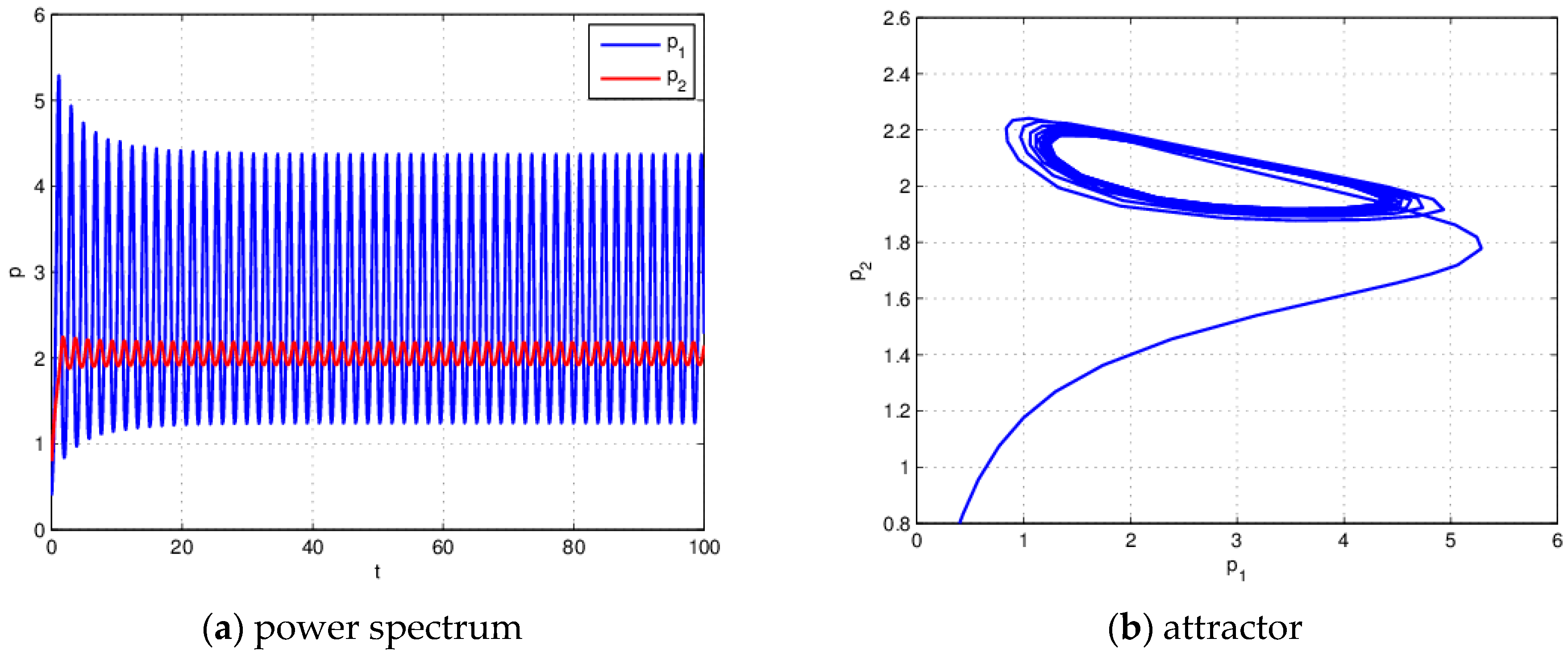
4.2. The Influence of on the Stability of the System (21) When
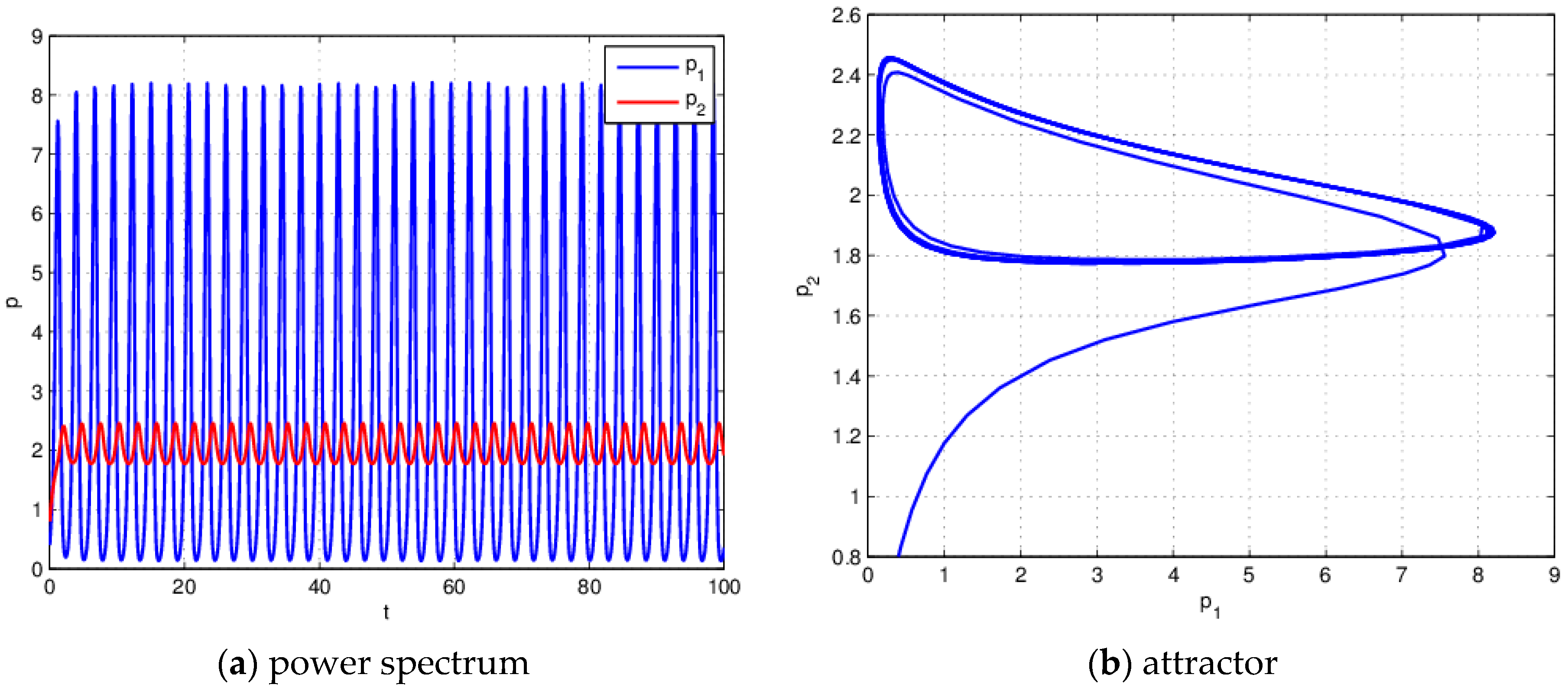
4.3. Initial Value Sensitivity
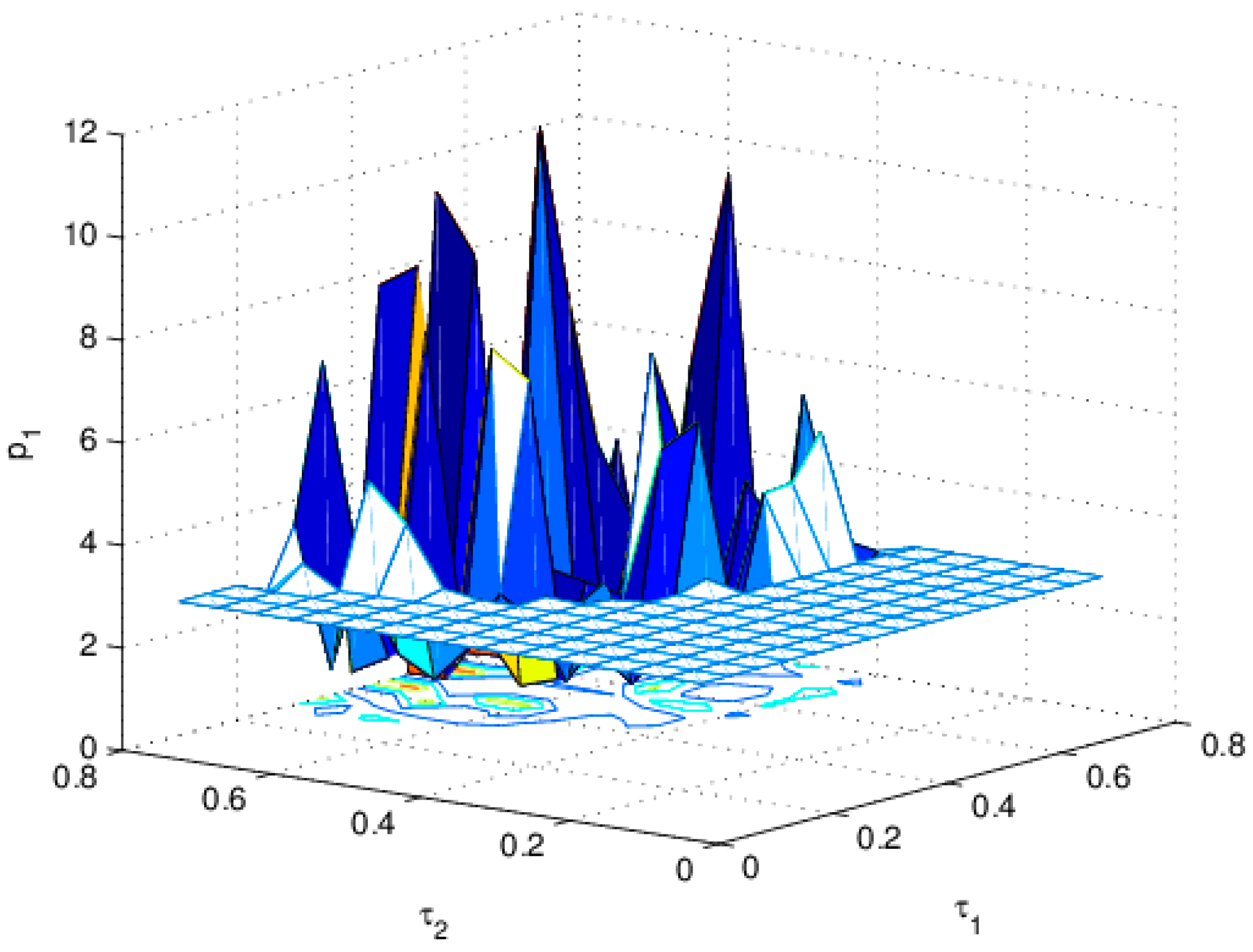
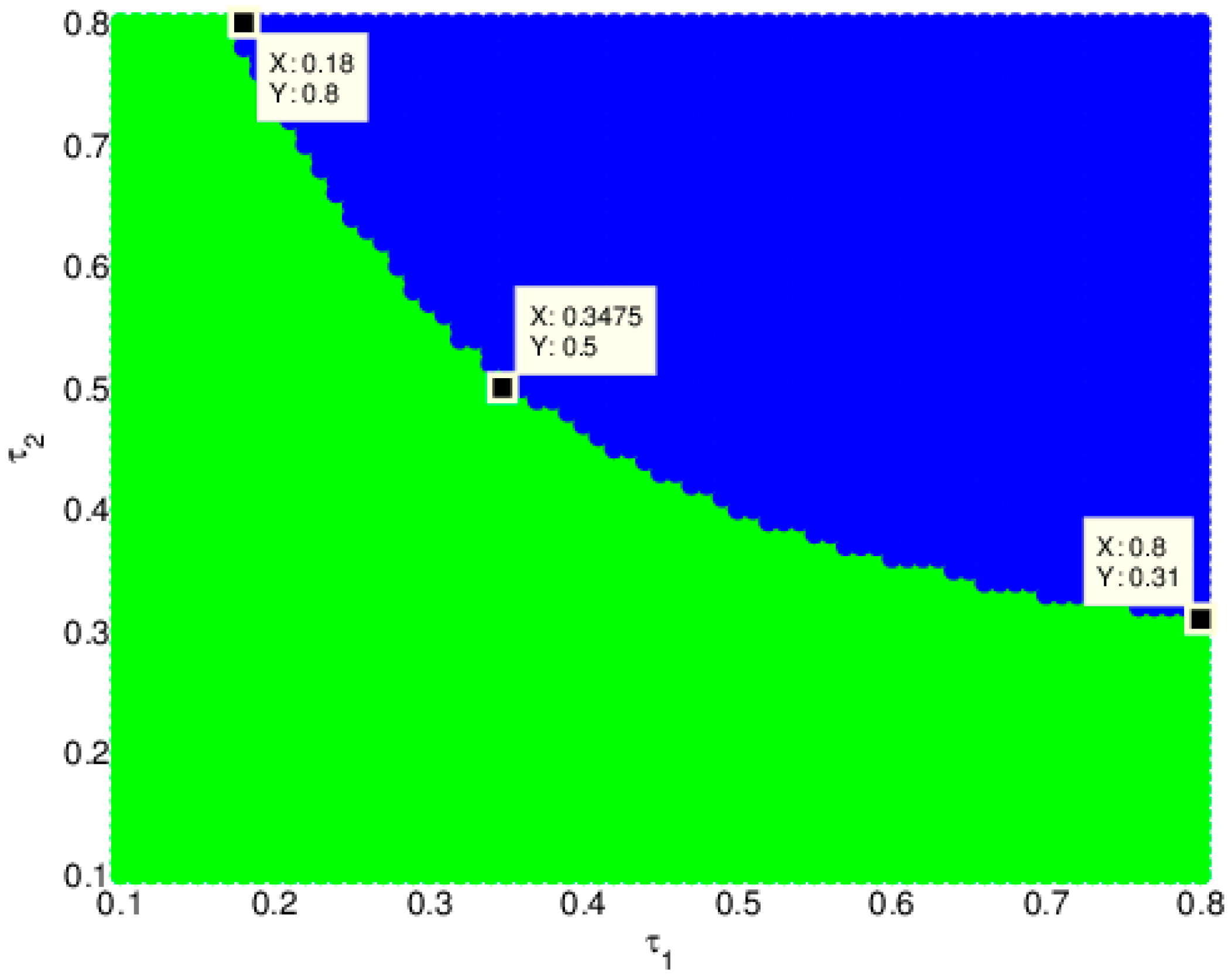
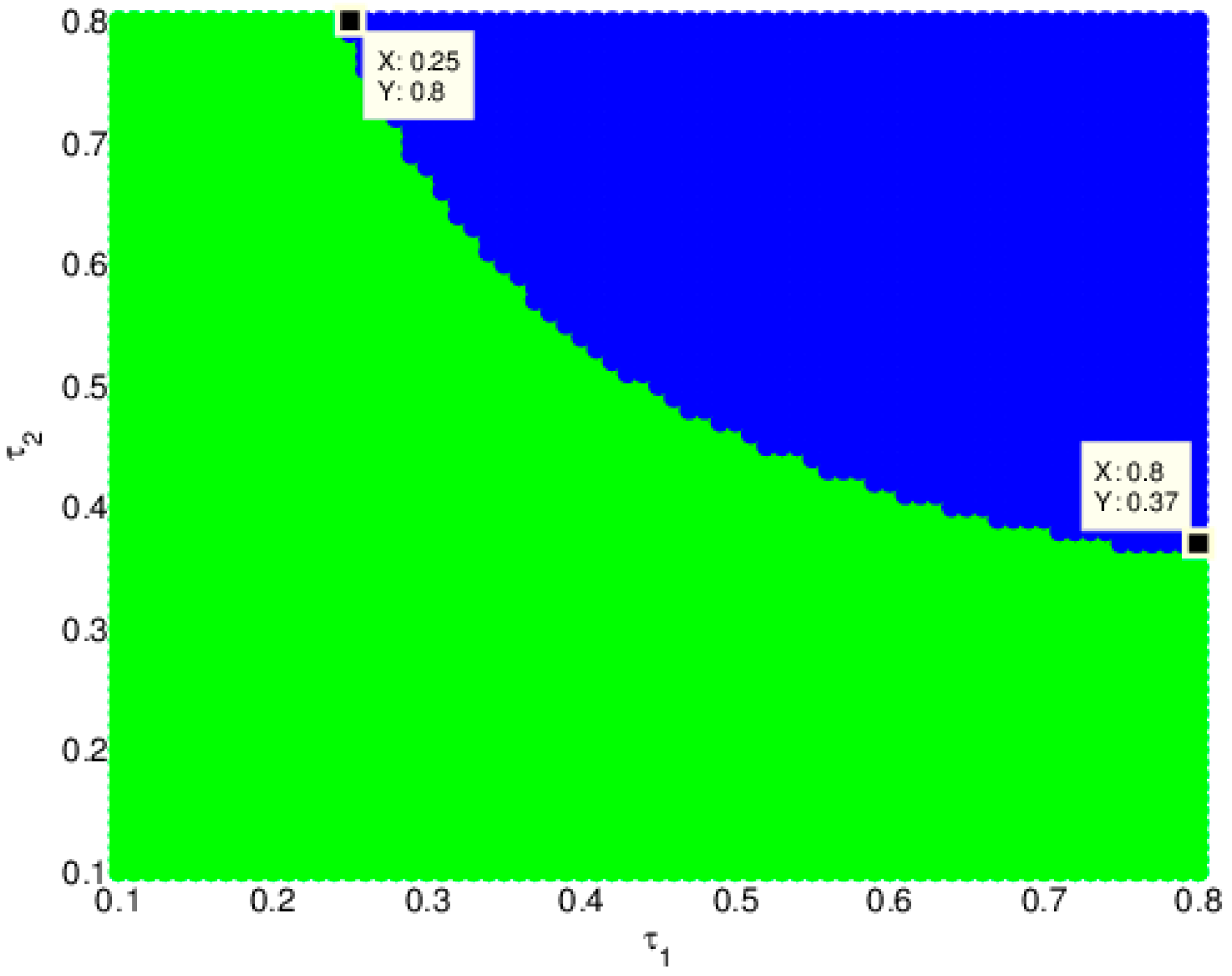
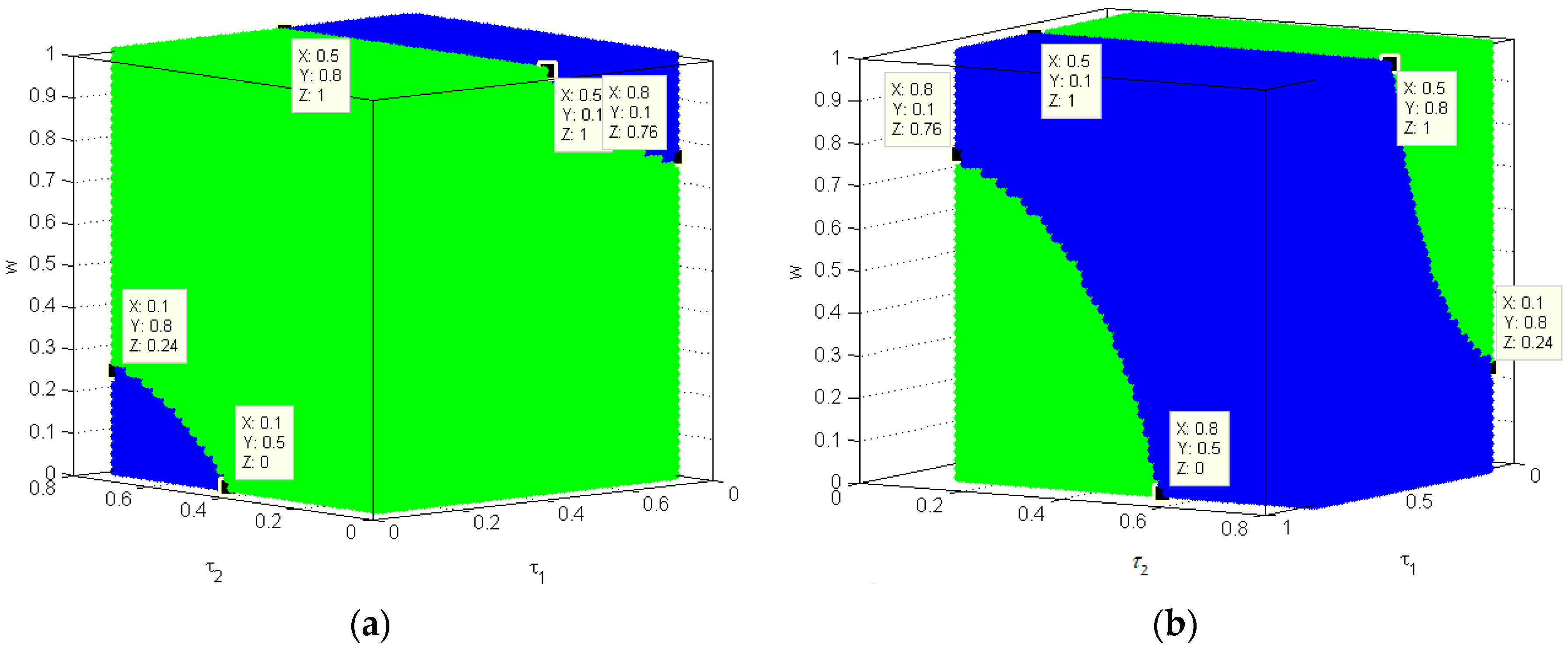
4.4. The Influence of and on the Stability of the Price
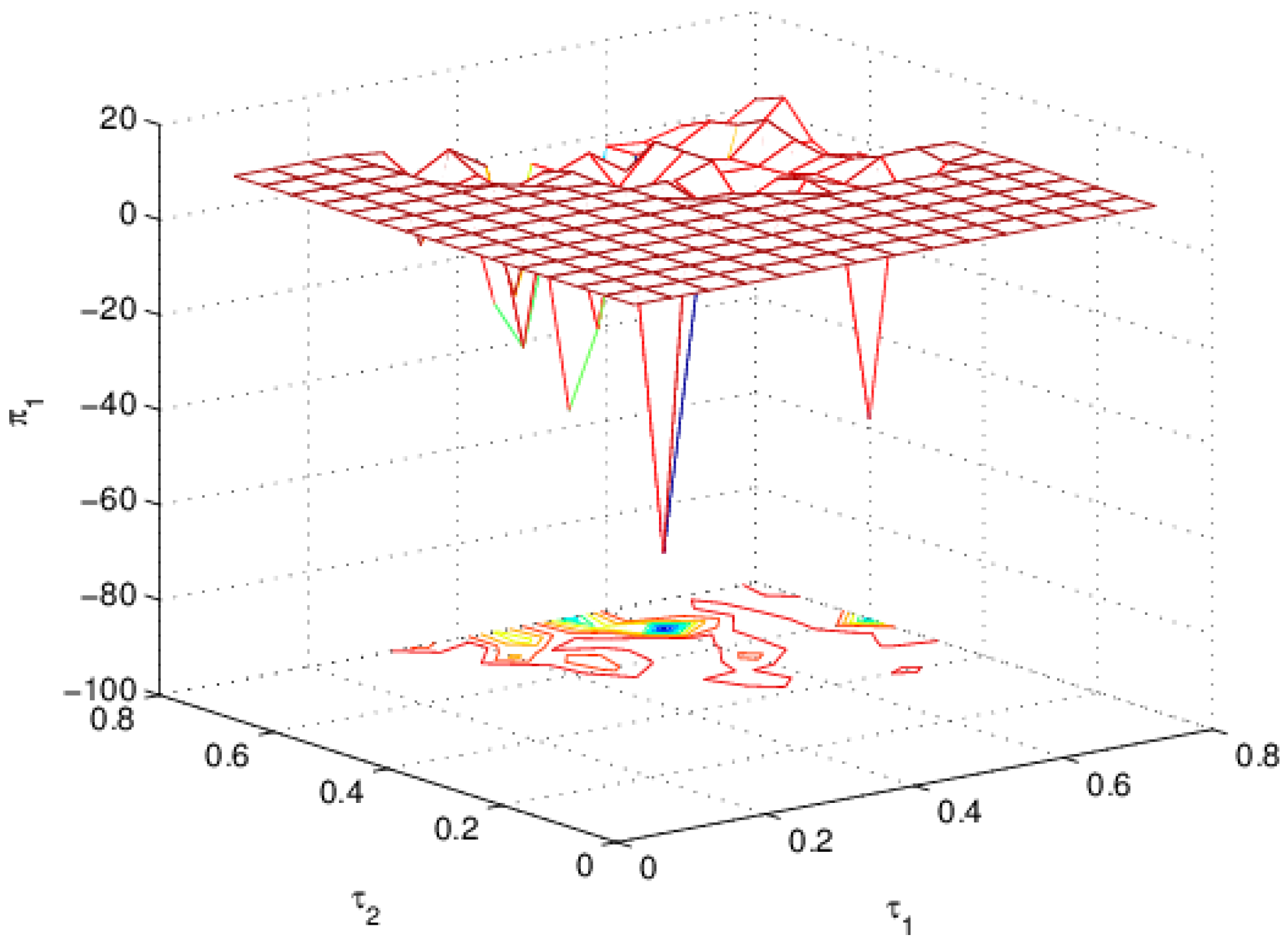
4.5. The Influence of and on the Profit
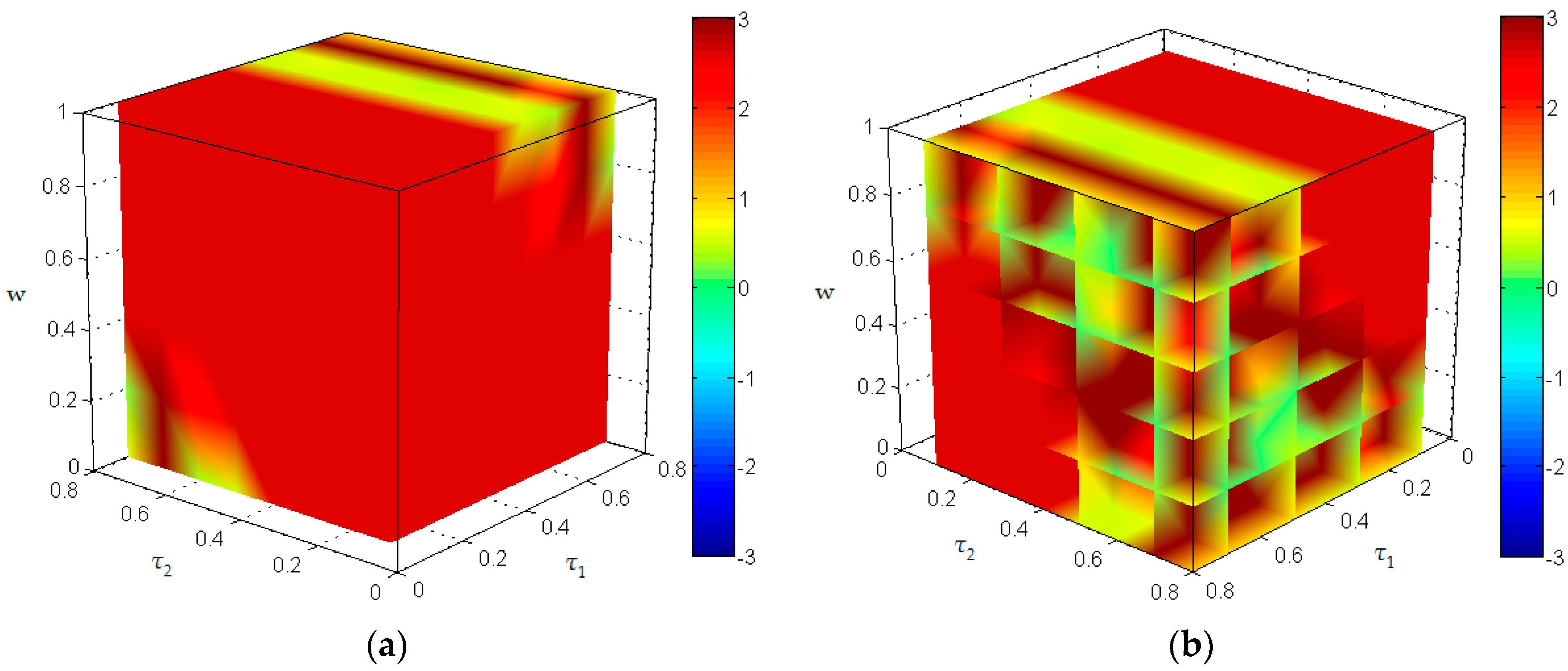
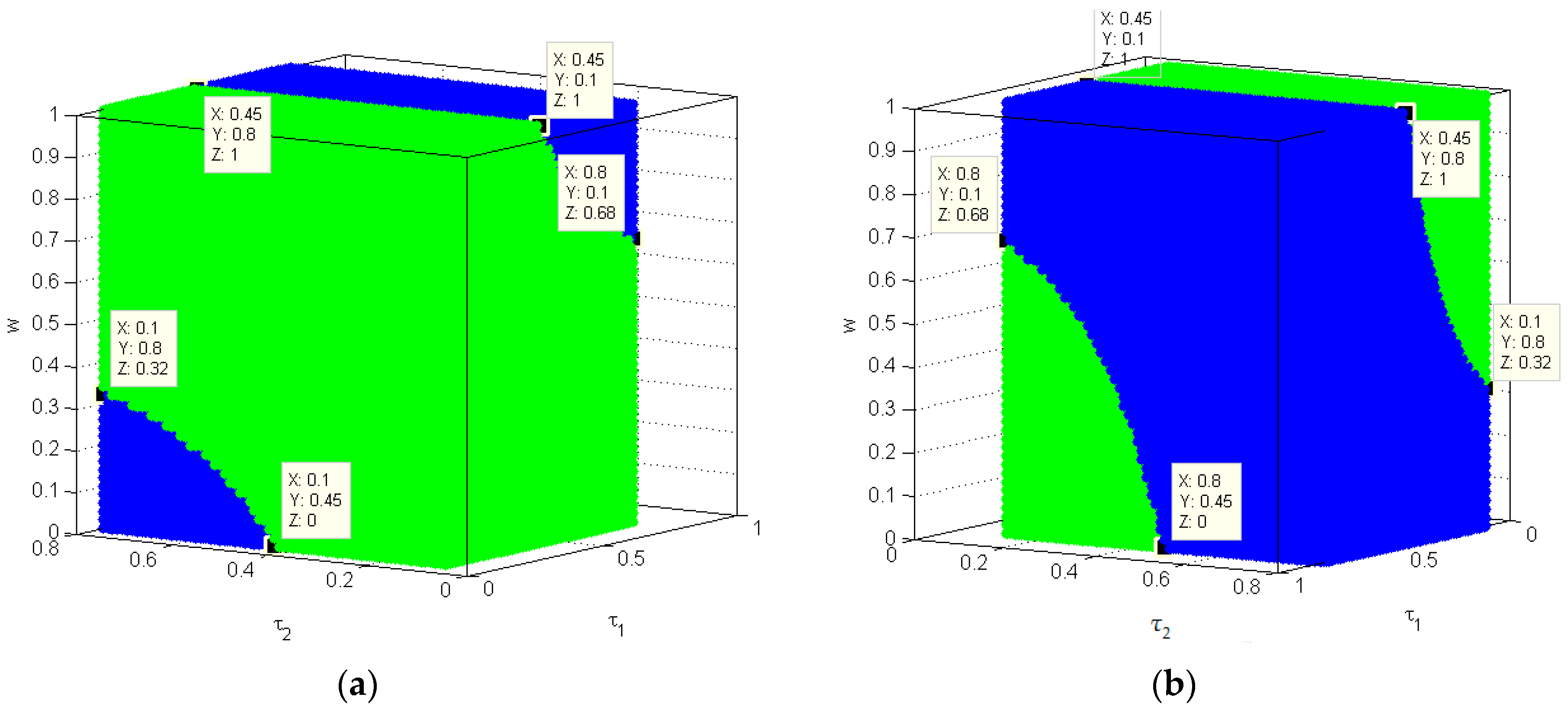
4.6. The Influence of , and on the Stability of the Price
4.7. The Influence of , and on the Profit
5. Chaos Control
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Brianzoni, S.; Luca, G.B.; Michetti, E. Dynamics of a Bertrand duopoly with differentiated products and nonlinear costs: Analysis, comparisons and new evidences. Chaos Solitons Fractals 2015, 79, 191–203. [Google Scholar] [CrossRef]
- Ahmed, E.; Elsadany, A.A.; Tonu, P. On Bertrand duopoly game with differentiated goods. Appl. Math. Comput. 2015, 251, 169–179. [Google Scholar] [CrossRef]
- Zhao, L.; Zhang, J. Analysis of a duopoly game with heterogeneous players participating in carbon emission trading. Nonlinear Anal. Model. Control 2014, 19, 118–131. [Google Scholar]
- Ma, J.; Guo, Z. The influence of information on the stability of a dynamic Bertrand game. Commun. Nonlinear Sci. Numer. Simul. 2016, 30, 32–44. [Google Scholar] [CrossRef]
- Fanti, L.; Gori, L.; Mammana, C.; Michetti, E. Local and global dynamics in a duopoly with price competition and market share delegation. Chaos Solitons Fractals 2014, 69, 253–270. [Google Scholar] [CrossRef]
- Yi, Q.G.; Zeng, X.J. Complex dynamics and chaos control of duopoly Bertrand model in Chinese air-conditioning market. Chaos Solitons Fractals 2015, 76, 231–237. [Google Scholar] [CrossRef]
- Ma, J.; Xie, L. Study on the complexity pricing game and coordination of the duopoly air conditioner market with disturbance demand. Commun. Nonlinear Sci. Numer. Simul. 2016, 32, 99–113. [Google Scholar] [CrossRef]
- Agiza, H.N.; Hegazi, A.S.; Elsadany, A.A. Complex dynamics and synchronization of duopoly game with bounded rationality. Math. Comput. Simul. 2002, 58, 133–146. [Google Scholar] [CrossRef]
- Yali, L. Dynamics of a delayed Duopoly game with increasing marginal costs and bounded rationality strategy. Procedia Eng. 2011, 15, 4392–4396. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, G. Complex Dynamics of Bertrand duopoly games with bounded rationality. World Acad. Sci. Eng. Technol. 2013, 79, 106–110. [Google Scholar]
- Li, T.; Ma, J. Complexity analysis of the dual-channel supply chain model with delay decision. Nonlinear Dyn. 2014, 78, 2617–2626. [Google Scholar] [CrossRef]
- Ma, J.; Guo, Z. The parameter basin and complex of dynamic game with estimation and two-stage consideration. Appl. Math. Comput. 2014, 248, 131–142. [Google Scholar] [CrossRef]
- Elabbasy, E.M.; Agiza, H.N.; Elsadany, A.A. Analysis of nonlinear triopoly game with heterogeneous players. Comput. Math. Appl. 2009, 57, 488–499. [Google Scholar] [CrossRef]
- Peng, J.; Miao, Z.H.; Peng, F. Study on a 3-dimensional game model with delayed bounded rationality. Appl. Math. Comput. 2011, 218, 1568–1576. [Google Scholar] [CrossRef]
- Agiza, H.N.; Elsadany, A.A.; El-Dessoky, M.M. On a new Cournot duopoly game. J. Chaos 2013, 2013, 487803. [Google Scholar] [CrossRef]
- Li, Q.; Ma, J. Research on price Stackelberg game model with probabilistic selling based on complex system theory. Commun. Nonlinear Sci. Numer. Simul. 2016, 30, 387–400. [Google Scholar] [CrossRef]
- Zhang, J.-F. Bifurcation analysis of a modified Holling–Tanner predator–prey model with time delay. Appl. Math. Model. 2012, 36, 1219–1231. [Google Scholar] [CrossRef]
- Hale, J.K. Theory of Functional Differential Equations; Springer: New York, NY, USA, 1977. [Google Scholar]
- Gori, L.; Guerrini, L.; Sodini, M. Hopf bifurcation and stability crossing curves in a cobweb model with heterogeneous producers and time delays. Nonlinear Anal. Hybrid Syst. 2015, 18, 117–133. [Google Scholar] [CrossRef]
- Agiza, H.N. On the Analysis of stability, Bifurcations, Chaos and Chaos Control of Kopel Map. Chaos Solitons Fractals 1999, 10, 1909–1916. [Google Scholar] [CrossRef]
- Du, J.; Huang, T.; Sheng, Z. Analysis of decision-making in economic chaos control. Nonlinear Anal. Real World Appl. 2009, 10, 2493–2501. [Google Scholar] [CrossRef]
- Holyst, J.; Urbanowicz, K. Chaos control in economic model by time-delayed feedback method. Phys. A Stat. Mech. Appl. 2000, 287, 587–598. [Google Scholar] [CrossRef]
- Matsumoto, A. Controlling the Cournot–Nash chaos. J. Optim. Theory Appl. 2006, 128, 379–392. [Google Scholar] [CrossRef]
- Luo, X.S.; Chen, G.R.; Wang, B.H.; Fang, J.Q.; Zou, Y.L.; Quan, H.J. Control of period-doubling bifurcation and chaos in a discrete nonlinear system by the feedbackof states and parameter adjustment. Acta Phys. Sin. 2003, 52, 790–794. [Google Scholar]


© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, J.; Si, F. Complex Dynamics of a Continuous Bertrand Duopoly Game Model with Two-Stage Delay. Entropy 2016, 18, 266. https://doi.org/10.3390/e18070266
Ma J, Si F. Complex Dynamics of a Continuous Bertrand Duopoly Game Model with Two-Stage Delay. Entropy. 2016; 18(7):266. https://doi.org/10.3390/e18070266
Chicago/Turabian StyleMa, Junhai, and Fengshan Si. 2016. "Complex Dynamics of a Continuous Bertrand Duopoly Game Model with Two-Stage Delay" Entropy 18, no. 7: 266. https://doi.org/10.3390/e18070266
APA StyleMa, J., & Si, F. (2016). Complex Dynamics of a Continuous Bertrand Duopoly Game Model with Two-Stage Delay. Entropy, 18(7), 266. https://doi.org/10.3390/e18070266