Abstract
We review a coherent mesoscopic presentation of thermodynamics and fluctuations far from and near equilibrium, applicable to chemical reactions, energy transfer and transport processes, and electrochemical systems. Both uniform and spatially dependent systems are considered. The focus is on processes leading to and in non‑equilibrium stationary states; on systems with multiple stationary states; and on issues of relative stability of such states. We establish thermodynamic state functions, dependent on the irreversible processes, with simple physical interpretations that yield the work available from these processes and the fluctuations. A variety of experiments are cited that substantiate the theory. The following topics are included: one-variable systems, linear and nonlinear; connection of thermodynamic theory with stochastic theory; multivariable systems; relative stability of different phases; coupled transport processes; experimental determination of thermodynamic and stochastic potentials; dissipation in irreversible processes and nonexistence of extremum theorems; efficiency of oscillatory reactions, including biochemical systems; and fluctuation-dissipation relations.
Keywords:
nonequilibrium thermodynamics; irreversible thermodynamics; stochastic processes; diffusion in chemical reaction kinetics; chemical reactions PACS Codes:
05.70.Ln Nonequilibrium and irreversible thermodynamics; 05.40.-a Fluctuation phenomena, random processes, noise, and Brownian motion; 82.40.Ck Pattern formation in reactions with diffusion, flow and heat transfer; 82.20.-w Chemical kinetics and dynamics
1. Introduction
In the last twenty years we have developed a mesoscopic formulation of thermodynamics and fluctuations both far from, and near to, equilibrium []. We briefly review some of this work here. The word mesoscopic denotes an approach based on the master equation for probability distributions []. This is not as detailed as a statistical mechanical analysis based on averages over mechanical motions, but is related to probability distributions and macroscopic chemical rate, and transport, coefficients. We treat primarily chemical reaction systems, but also transport processes and electrochemical kinetic systems.
We establish thermodynamic state functions, dependent on the irreversible processes, that provide necessary and sufficient conditions for stability and instability of systems and provide the fluctuations in the system; these state functions can be measured and have simple relations to the concept of work. For systems with multiple stable stationary states the thermodynamic functions provide measures of relative stability and equistability. A number of experiments are cited and discussed which substantiate the theory. The review consists of chosen selections, shortened and edited, from the book Thermodynamics and Fluctuations far from Equilibrium by John Ross [].
2. One-variable Systems
We begin this section with the presentation of the linear one-variable case, for which a thermodynamic state function is obtained in 2.1, and proceed to the more general nonlinear case in 2.2. These first two subsections deal with establishing reference states. We then discuss dissipation in section 2.3; connect the thermodynamic theory with stochastic theory in 2.4, and finally comment on the relative stability of multiple stationary stable states in 2.5.
2.1. Linear One-variable Systems
Consider the reaction sequence:
with rate coefficients k1 and k2 for the forward and reverse reaction of the first reaction () and k3 and k4 the corresponding rates for the second reaction. In this sequence A is the reactant, X the intermediate, and B the product. Let the reactions occur in the schematic apparatus of Figure 1 at constant temperature.
Let us assume ideal gases and mass action kinetics; in that case the deterministic rate equation is:
Hence at a stationary state the pressure of X is
. We denote the first term on the RHS (right-hand side) of (2) by
and the second term by
[]. At the stationary state,
is constant, and the pressure pX is given by:
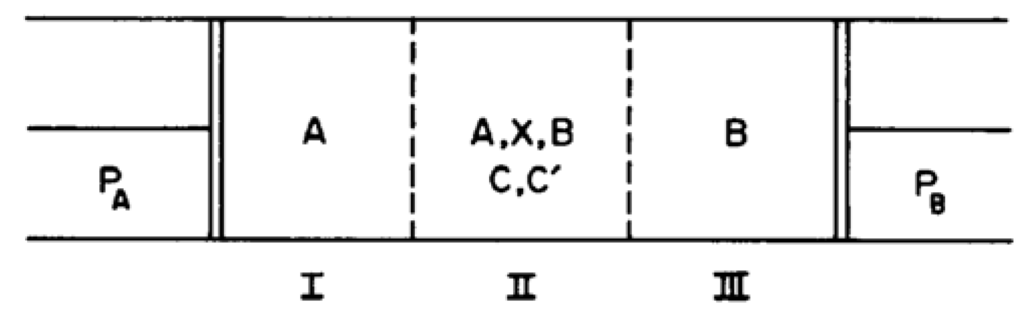
Figure 1.
Two piston model. The reaction compartment (II) is separated from a reservoir of species A (I) by a membrane permeable only to A and from a reservoir of species B (III) by a membrane permeable only to B. The pressures of A and B are held fixed by constant external forces on the pistons. Catalysts C and C’ are required for the reactions to occur at appreciable rates and are contained only in region II.
We use the hypothesis of local equilibrium: it is assumed that at each time there exists a temperature, a pressure, and a chemical potential for each chemical species. These quantities change on shorter time scales than the changes in pressure or concentration of chemical species due to chemical reaction. Thus the chemical potential is
, where
is the chemical potential in the standard state. Hence we have:
We define a thermodynamic state function []:
where VII is a volume shown in Figure 1. This function has many important properties. At the stationary state of this system, is zero. If we start at the stationary state and increase pX then dpX ≥ 0 and the integrand is larger than zero; hence is positive. Similarly, if we start at the stationary state and decrease pX, then dpX and the integrand are both negative and is positive. Hence is an extremum at the stable stationary state, a minimum.
2.2. Nonlinear One-variable Systems
Let us consider now a nonlinear model of a stoichiometric equation, also occurring in the apparatus of Figure 1, as follows:
Since this isothermal system has chambers I and III at constant pressure and chamber II at constant volume, the proper thermodynamic function for the entire system is a linear sum of Gibbs free energies for I and III and the Helmholtz free energy for II. If in (6) we set r = 3 and s = 1 then we have the Schlögl model []:
with the rate coefficients k1 and k2 for the forward and reverse reaction in (7), and k3 and k4 in (8). For this system there exists the possibility of multiple stationary states for given constraints of the pressures pA and pB . The kinetic equation for pX is:
which is cubic in pX and hence may have three stationary states (RHS of (9) equals zero), as shown in Figure 2.
A + 2X ⇔ 3X
X ⇔ B
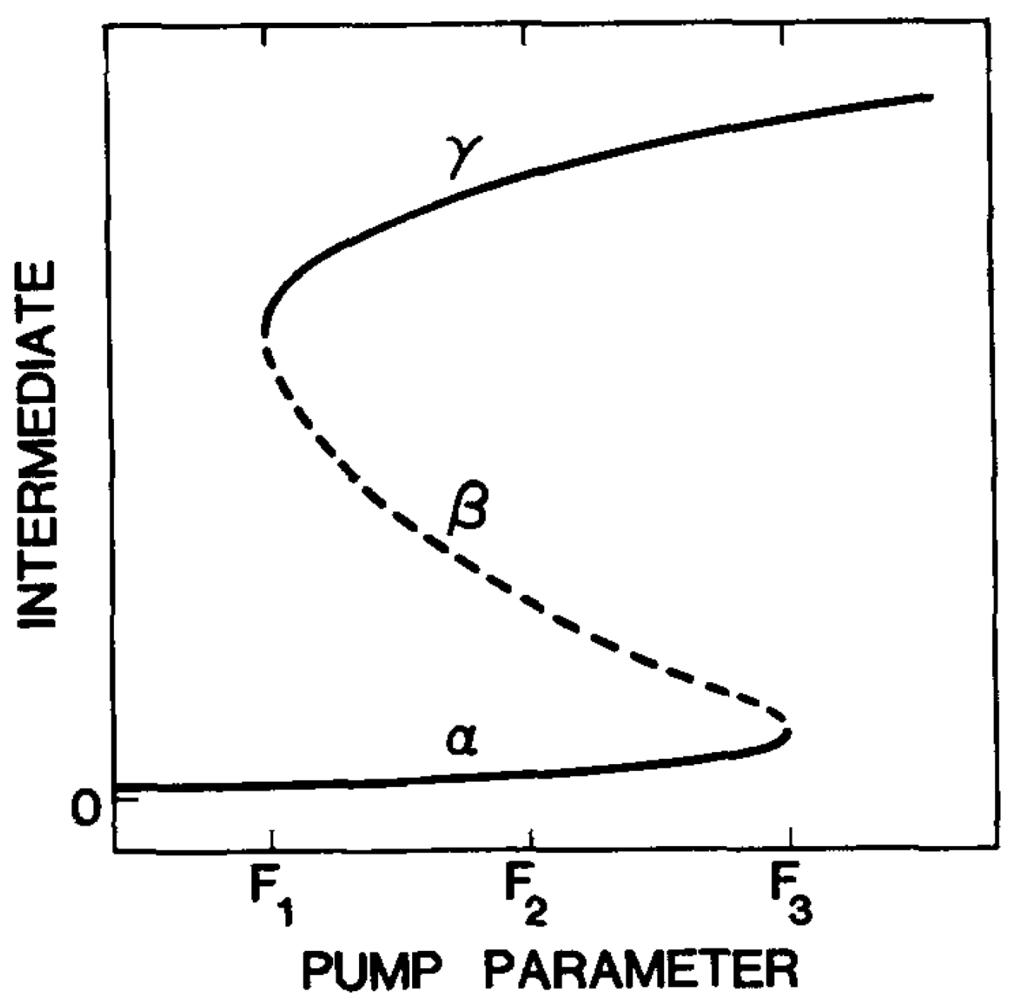
Figure 2.
Stationary states of the Schlögl model with fixed reactants and products pressures. Plot of the pressure of the intermediate pX vs. the pump parameter (pA/pB). The branches of stable stationary states are labeled α and γ and the branch of unstable stationary states is labeled β. The marginal stability points are at F1 and F3 and the system has two stable stationary states between these limits. The equistability point of the two stable stationary states is at F2.
The deterministic kinetic equation for the Schlögl model is:
The first two positive terms on the RHS of (10) are again given the symbol
and the two negative terms the symbol
; their ratio is:
which we use to define the quantity
, the pressure in a reference state for which the following holds:
Thus is:
It is useful to compare the linear model with the Schlögl model in the following way: assign to each model the same values of pA, pB, T, VI, VII, VIII, and equilibrium constants for the A⇔X and B⇔X reactions. Then the two model systems are instantaneously thermodynamically equivalent. If furthermore
and
have the same values in the two systems at each point in time, the two systems are instantaneously kinetically indistinguishable. If we define
as the pressure of X in the instantaneously indistinguishable linear system at stationary state, we may write from (4) and (5):
This equation relates the chemical driving force towards a stable stationary state (LHS) to the ratio of sums of fluxes of X (RHS). We write the analog of (5) for our chosen thermodynamic function:
where the integrand is a species specific activity which plays a crucial role. The function in (5) is an excess work: the work of moving the system from a stable stationary state to an arbitrary value pX compared to the work of moving the system from the stationary state of the instantaneous indistinguishable linear system to pX. If A and B in (6) are chosen such that the ratio of their pressures equals the equilibrium constant, then = ΔG and
.
With the species specific activity and the thermodynamic state function
* we can state the following conditions:
at each stationary state,
at each stable stationary state, with the equality sign holding at marginal stability,
at each unstable stationary state, with the equality sign holding at marginal stability.
Equations (16,17) are necessary and sufficient conditions for the existence and stability of non‑equilibrium stationary states.
2.3. Dissipation
For a spontaneously occurring chemical reaction at constant pressure, p, and temperature, T, the Gibbs free energy change gives the maximum work, other than p·V work, that can be obtained from the reaction. For systems at constant V,T it is the Helmholtz free energy change that yields that measure. If no work is done by the reaction then the respective free energy changes are dissipated, lost. For reactions of ideal gases run in the apparatus in Figure 1, we can define a hybrid free energy, M:
The time rate of change of M is:
if there is no depletion of the reservoirs I and III. According to conservation of mass we have:
and therefore we may write:
Hence we write for the dissipation D:
where the first term on the RHS is the dissipation due to the conversion of A to X at the pressure
and at the rate
and the conversion of X to B at the same pressure of X and the rate
. The second term on the RHS of (23) is a species-specific dissipation, DX:
From this last equation it is clear that
for all pX, regardless of the reaction mechanism; the equality holds only at the stationary state.
As we shall discuss later, the total dissipation D is not an extremum at stationary states in general, but there may be exceptions. DX is such an extremum and the integral:
is a Lyapunov function in the domain of attraction of each stable stationary state.
The dissipation in a reaction can range from zero, for a reversible reaction, to its maximum of ΔG when no work is done in the surroundings. Hence the dissipation can be taken to be a measure of the efficiency of a reaction in regard to doing work. There is more on this subject in Section 7.
2.4. Connection of the Thermodynamic Theory with Stochastic Theory
The deterministic theory of chemical kinetics is formulated in terms of pressures, for gases, or concentrations of species for gases and solutions. These quantities are macroscopic variables and fluctuations of theses variables are neglected in this approach. In stochastic theory, however, one assumes that fluctuations do occur, say in the number of particles of a given species X, that there is a probability distribution P(X,t) for that number of particles at a given time, and that changes in this distribution occur due to chemical reactions. The transition probabilities of such changes are assumed to be given by macroscopic kinetics. We shall show that the non-equilibrium thermodynamic functions (for linear systems), (for nonlinear systems), the excess work, determines the stationary, time‑independent, probability distribution, which leads to a physical interpretation of the connection of the thermodynamic and stochastic theory. At equilibrium the probability distribution of fluctuations is determined by the Gibbs free energy change at constant T,p, which is the work other than p·V work. We restrict the analysis at first to reaction mechanisms for which the number of molecules of species X changes by ±1 in each elementary step. We take the probability distribution to obey the master equation. For the cubic Schlögl model ((6) with r = 3, s = 1) the master equation is [,]:
The first two terms on the RHS yield an increase in X, the last two terms a decrease in X. The fluxes in this equation are:
with the parameters ci related to the rate coefficients ki by
for , where mi is the molecularity of the ith step and ni the molecularity in X.
From the master equation we can derive the result that the average concentration, the average number of X in a volume V, obeys the deterministic rate equation in the limit of large numbers of molecules.
The time-independent solution of the master equation is:
which by retention of only the leading term in the Euler-MacLaurin summation formula reduces to
and N is a normalization constant. The connection between the thermodynamic and stochastic theory is established with the use of (14) to give:
The Lyapunov function (15) is both the thermodynamic driving force towards a stable stationary state and determines the stationary probability distribution of the master equation. The stationary distributions (29,30) are non-equilibrium analogs of the Einstein relations at equilibrium, which give fluctuations around equilibrium.
There is another interesting connection []. We define
to be the probability density of observing X1 molecules in V at time t1 given that there are X0 molecules at t0. This function is the solution of the master equation (26) for the initial condition
. The probability density can be factored into two terms []:
in which the first term on the RHS is independent of the path from X0 to X1 and independent of the time interval (t1–t0). To the same approximation with which we obtained (29) we can reduce the first term to:
and find it to be of the same form as the probability distribution (29). It contains the irreversible part of the probability density (31).
2.5. Relative Stability of Multiple Stationary Stable States
For systems with multiple stable stationary states there arises the issue of relative stability of such states. We treat systems with a single intermediate and stoichiometric changes in X are limited to ±1.
In regions of multistability the stationary probability distribution is bimodal and is shown in Figure 3 for the cubic Schlögl model. Stable stationary states are located at maxima, labeled 1 and 3, and unstable stationary states at minima, labeled 2.
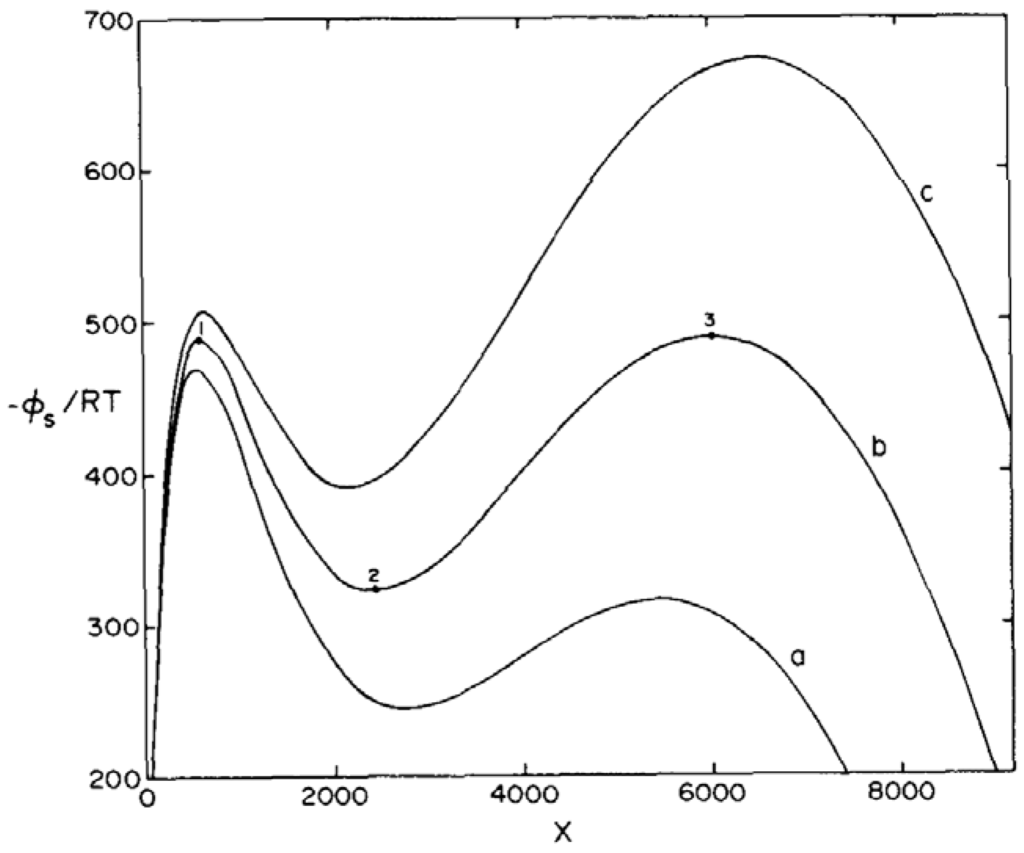
Figure 3.
Plot of the integral in (30), marked vs. X for the Schlögl model with parameters: c1 = 3.10−10 s−1; c2 = 1.10−7 s−1; c3 = 0.33 s−1; c4 = 1.5.10−4 s−1; and A = B. For curve (a) B = 9.8.106; for curve (b) B = 1.01.106; curve (c) B = 1.04.106. Curve (b) lies close to the equistability of the stable stationary states 1 and 3; 2 marks the unstable stationary state.
Consider now the ratio of the probability density (31), for a given transition from X1 to X2 to that of the reverse transition:
Equistability of two stable stationary states, labeled now 1 and 3 to correspond to Figure 3, is defined by:
which with the use of (24) we may also express as:
The integral of the species-specific dissipation from the unstable stationary state 2 to the stable stationary state 3 equals, at equistability, to the integral of the dissipation from the unstable stationary state 2 to the stable stationary state 1. Whereas the integral of the total dissipation for the limits in (35) goes to infinity, that of the species specific dissipation is finite. We can restate (35) in terms of the excess work:
These results constitute a fluctuation-dissipation relation, rediscovered in a statistical mechanical approach by Evans and coworkers (see [] and references therein). At equistability the integral of the excess work from 2 to 3 equals the integral of the excess work from 2 to 1. Equations (34–36) provide necessary and sufficient conditions of equistability of stable stationary states.
The master equation has been investigated for a sequence of unimolecular (non-autocatalytic) reactions based on moment generating functions []; these yield Poissonian stationary distribution for single intermediate systems in terms of the number of particles X of species X, with Xss that number in the stationary state,
. Our results are consistent with (36), as can be seen from the use of (15) and (30), a change of variables to particle numbers X, and the use of Stirling’s approximation:
Here
is the normalization constant exp(−Xss). The formulation given in this section has the advantage of the physical interpretation in terms of species-specific thermodynamic driving forces and in terms of Lyapunov functions; further our formulation is generalizable to autocatalytic systems and many variable systems.
3. Thermodynamic State Function for Multivariable Systems
In the previous section we have obtained thermodynamic state functions for single variable systems, both linear (5) and nonlinear (15). In this section we obtain a thermodynamic state function for multivariable systems. To this end we need to consider fluctuations []. We start with the master equation []:
in which PX is the probability distribution of finding X particles (molecules) in a given volume, and W(X,r) is the transition probability due to reaction from X to X+r particles. Now we do a Taylor expansion of the term
around X:
and introduce the concentration vector
; then we have the reduced relations:
where V is the volume of the system. We substitute these relations into (39) and obtain:
Next we introduce the momentum operator,
, with which we can write:
The master equation becomes:
where we have defined the Hamiltonian operator [,]:
Thus we have formally, and exactly, converted the master equation to a Schrödinger equation. This has the substantial advantage that we can apply well-known approximations in quantum mechanics to obtain solutions to the master equation. In particular we refer to the W.K.B. approximation valid for semi-classical cases, those for which Planck’s constant formally approaches zero. The equivalent limit for (43) is that of large volumes (large numbers of particles). Hence we seek a stationary solution of (43), that is the time derivative of PX(X,t) is set to zero, of the form:
where Sn will be shown to be the classical action of a fluctuational trajectory accessible from the nth stable stationary state. We substitute (45) into the stationary part of (43) and obtain:
the equation satisfied by Sn(X) with the Hamiltonian function ( not operator):
and the boundary condition:
These equations show that it is the classical action Sn that satisfies the Hamiltonian-Jacoby equation (46) with coordinate x, momentum
, and Hamiltonian equal to zero (stationary condition). The Hamiltonian equations of motion for the system are:
and:
From these relations we determine the action:
for the fluctuational trajectory starting at the nth stable stationary state xns with p = 0 at t = − and ending at x at t = 0.
3.1. Linear Multi-variable Systems
Let us consider the following linear reaction system []:
run in an apparatus as in Figure 1, where the pressures of A and B are held constant. The action is:
where Xs, Ys are stable stationary state concentrations. We see that the integrand is an exact differential and hence the action is independent of the path of integration in concentration space. The action is a state function [,].
The physical interpretation of the action comes from consideration of the free energy M for the three compartments in Figure 1 (19):
For differential changes in A,X,Y,B the differential change in M is:
The differential excess free energy change
is the difference between dM, the system with arbitrary concentrations of X and Y, and dMs, the system in the stationary state. Hence we have:
When we compare Equation (56) with (53) we see that:
This important physical result was first given in []: the mathematical concept of the action can be identified with the thermodynamic excess work.
On a fluctuational trajectory the differential excess free energy is positive and zero at a stable stationary state. We show this by considering the differential action:
The transition probabilities
(x,r) are all positive and the square bracket is larger than zero except for p = 0, that is at the stable stationary state. Therefore we have:
and hence the excess differential free energy dϕ is positive in general and zero at stationary states.
Suppose we prepare this system at a given (x,y) and let it proceed along the deterministic trajectory back to the stationary state. Along this path dϕ is negative which follows from the deterministic variation of the action in time:
which holds since the Hamiltonian is zero. For all real values of r·p the square bracket in (60) is negative unless p = 0. And therefore:
with the equality holding only at a stationary state. Hence an excess work is required to move a system from a stable stationary state, and excess work can be done by a system relaxing towards a stable stationary state. The action and the excess work are both Lyapunov functions; they serve for non‑equilibrium systems the role the Gibbs free energy serves for systems going to equilibrium .
We note here that (59) and (61) hold for nonlinear multi-variable systems as well; no assumption of a linear reaction mechanism was made in their derivation.
3.2. Nonlinear Multi-variable Systems
Let us consider now a non-linear multi-variable system such as the following example:
The stationary distribution is given by (45) and (51), with p and dx/dt obtained from solutions of Hamilton’s equations. We now choose our reference by using the equations:
Equation (62) yields unique values of (X0,Y0) in the absence of certain crossings of fluctuational trajectories in the (X,Y) space, called ‘caustics’, see []. There may be more than one fluctuational trajectory which starts at p = 0 at a stable stationary state and passes through a given (X,Y). These trajectories will have different values of p and the one with the lowest value of p will determine the action in the thermodynamic limit, the contributions from other trajectories vanishing in that limit.
Hence we find for the action the expressions:
where the reference state used here (X0,Y0) replaces the starred reference state of section 2, see Equation (13). The important point is that the action and the excess work in (64) are state functions for single and multi-variable systems. Both X0 and Y0 are functions of X and Y in general, but the integrand in (64) is an exact differential, because p is the gradient of the action, (51). For the starred reference state the excess work is a state function only for single variable systems.
The fluctuational trajectory away from a stationary state to a given point in concentration space (X,Y) in general differs from the deterministic path from that point back to the stationary state for systems without detailed balance. We show this in some calculations for the Selkov model []; in (62) we take m = n = r = 1, s = 3; other parameters are given in [], p. 4555. Figure 4 gives some results of these calculations.
For one-variable systems the fluctuational trajectory away from the stationary state is the same as the deterministic trajectory back to the stationary state. Therefore for such systems ∗ equals 0 (64). In summary, we define the state function 0 with the use of (64):
and list the following results (compare with the results listed in section 2 for single variable systems).
0 is a thermodynamic state function. It is a potential for the stationary probability distribution of the master equation, and is a Lyapunov function in the domain of each stable stationary state. See also [,,,,,,,]. It is directly related to the excess work necessary to remove a system from a stable stationary state, and the work obtainable from a system in its return to such a state. It is an extremum at stationary states; a minimum (zero) at stable stationary states, a maximum at unstable stationary states (59). For a fluctuational trajectory 0 increases away from the stable stationary state (59); for a deterministic trajectory towards a stable stationary state it decreases, (60). The first derivative of 0 is larger than zero at each stable stationary state, smaller than zero at each unstable stationary state. The function provides necessary and sufficient criteria for the existence and stability of stationary states. 0 serves to determine relative stability of multi-variable homogeneous systems in exactly the same way as shown in (33) for single variable systems. Comparison with experiments on relative stability requires consideration of space-dependent (inhomogeneous) systems and that subject is discussed in the next section.
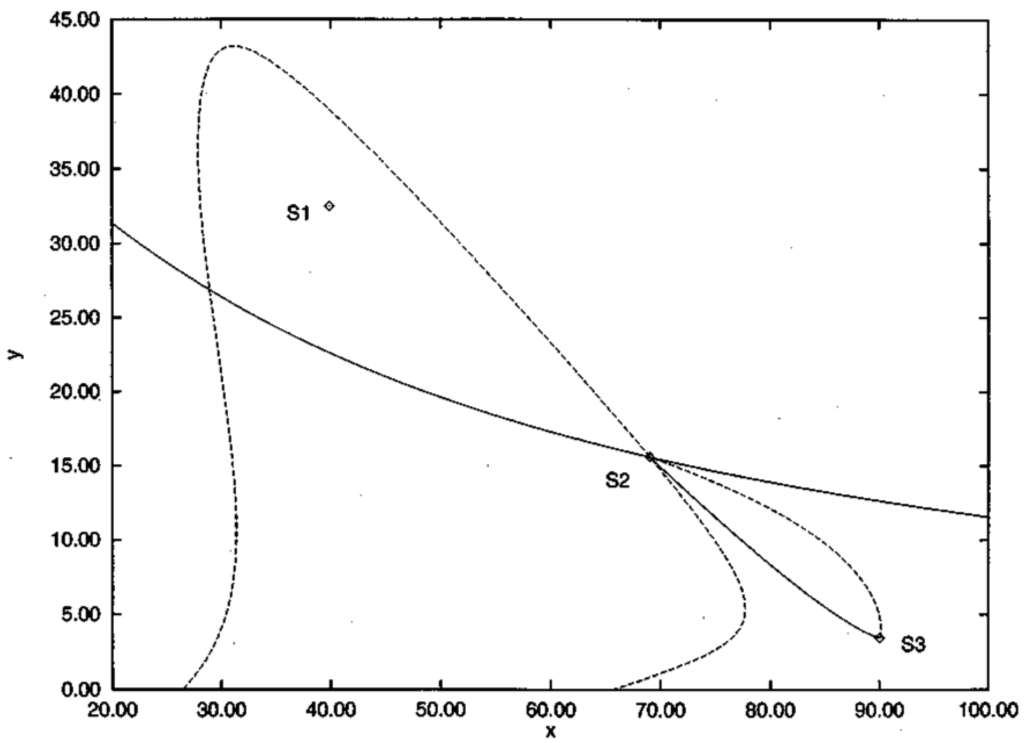
Figure 4.
From []. S1 and S3 are stable stationary states (stable foci); S2 denotes an unstable stationary state. The solid line from S2 to S3 indicates the deterministic trajectory. The other solid line through S2 is the deterministic separatrix, that is the line that separates deterministic trajectories, on one side going towards S2 and on the other side going towards S3. The dotted lines are fluctuational trajectories: one from S3 to S2 and the others proceeding from S2 in two different directions. The fluctuational trajectory need not differ so much from the reverse of the deterministic trajectory.
The specification of the reference state X0, Y0 requires solution of the master equation for a particular reaction mechanism. This in general demands numerical solutions, which can be lengthy. However, if we do not need to obtain a thermodynamic function, this is not necessary and the deterministic approach of section 2 may be used instead.
The state function 0 can be determined from macroscopic electrochemical measurements, as well as other measurements, see section 6.3.
4. Thermodynamic and Stochastic Theory of Reaction-diffusion Systems
In the previous sections we have studied only homogeneous reaction systems. In the more general, inhomogeneous case, concentrations are not only function of time but also of space. Hence there may be concentration gradients in space and diffusion will occur. In this section we formulate a thermodynamic and stochastic theory for such systems []. First we analyze one-variable systems and then multi-variable systems with multiple stable stationary states; then we apply the theory to study relative stability of these multiple stationary states.
4.1. Systems with One Intermediate
We begin with a one-variable system such as the Schlögl model, which is described by (7,8). If the system is homogeneous its deterministic kinetics is:
where t+, t− are kinetic fluxes. If the system is inhomogeneous, the concentrations are functions of time and spatial coordinates. Let us consider a one-dimensional system with spatial coordinate z and discretize the space into many boxes labeled with …i−1, i, i+1, as in Figure 5. The change in the number of particles Xi is due to reaction and diffusion into and out of box i and can be written:
where the fluxes of diffusion can be expressed as a function of a constant diffusion coefficient, d:
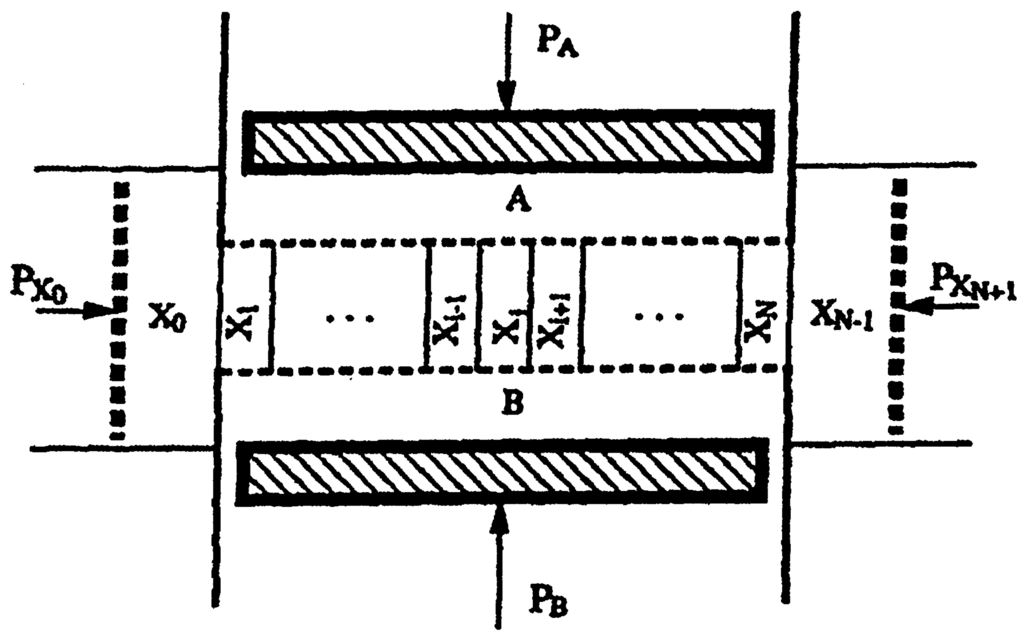
Figure 5.
Schematic apparatus for reaction-diffusion system in one spatial dimension. The boxes 1 to N are separated from a constant-pressure reservoir of A by a membrane permeable only to A, and similarly for the reservoir of B [].
Let us write the diffusivity of the system as D = l2d, where l is the length of a box. Then in the continuous limit we have:
Since changes in A and B take place at constant temperature and pressure, and in X at constant temperature and volume, the differential free energy for a box i, dMi, is:
A linear system thermodynamically and kinetically equivalent to (67) is:
where the superscript L stands for linear. For the instantaneous equivalencies we require
and
. The stationary solution is:
The excess work for a box i of the equivalent linear system is the difference between the free energy change dM at an arbitrary state
and that at the stationary state
:
where the notation indicates inexact differential. The driving force towards the stationary state is
In a nonlinear system the driving force is the potential difference between state
and a reference state
, which is the stationary state of the equivalent linear system at the specified value of
. Thus the reference state is:
The excess work for a box i of the nonlinear system is:
and the total excess work of all the boxes is:
Since is not a state function, a path of integration must be specified in order to evaluate it. We can easily check two limiting cases: the homogeneous limit (no diffusion) and the limit of no reaction (diffusion only). In the homogeneous limit there is only one box for which
, so:
which agrees with (14,15). In the limit of no reaction we have
, and hence
If the spatial variable z is continuous and S is the area perpendicular to the z axis, (77) becomes:
Since the number of X molecules in each box, Xi, is an independent variable, a reaction-diffusion system is isomorphic to a multivariable homogeneous reaction system, which can be linearized around a stable stationary state. At that state we have
, where ‘det’ means that the deterministic path is the path of integration. The time derivative of satisfies
. is a minimum at stable stationary states and a Lyapunov function in their vicinity.
4.2. Systems with Two Intermediates
Now we extend this approach to systems with two intermediates and multiple stationary states. Let us consider first a linear system such as the one in (52). By carrying out the same calculations as in the previous subsection, we obtain the following expression for the total excess work:
which is a state function for linear systems, since the integral is path-independent. It can be seen that the derivative of with respect to time is negative semidefinite, so the system tends towards the minimum of , that is towards the stable stationary state. Hence, is a Lyapunov function. Further, satisfies the stationary solution of the master equation in the thermodynamic limit. These properties assure that provides necessary and sufficient conditions for the existence and stability of stationary states.
Let us consider now nonlinear systems such as the reaction mechanism of (62). For each set of (Xi, Yi) we can uniquely map the non-linear system to a thermodynamically and kinetically equivalent linear system. In this case the total excess work is:
which depends on the path of integration. is zero at the stationary state and so are its first derivatives. Since the nonlinear system is indistinguishable from the instantaneously equivalent linear system, their time derivatives are equal. It can be seen that
, with the equality holding only at the stationary state (which is a minimum). Hence is a Lyapunov function and it provides necessary and sufficient conditions for the existence and stability of stationary states.
4.3. Relative Stability of Stable Stationary States
Let us consider a reaction-diffusion system with two phases numbered 1 and 3, each at a different stable stationary state. If both phases are placed in contact under the same external constraints, reaction and diffusion will occur and a reaction diffusion front may be formed in an interphase region. This front will travel into the less stable state, and the more stable state will displace the less stable one.
For systems at equilibrium the Gibbs free energy serves as a criterion of equistability; for systems far from equilibrium it is the excess work which serves that purpose. If the excess work required to form the reaction diffusion front from phase 1 is less than that necessary to form the front from phase 3, then phase 1 is more stable than phase 3. If both excess works are equal then we may expect equistability.
The excess work can be calculated as follows. We divide the interphase region into N boxes and integrate numerically the 2N ordinary differential equations:
From (82), the excess work as a function of the reference states () is:
which may be written as:
where “St.Fr.” stands for stationary front. The direction of propagation of the interface is predicted by the theory as a function of the sign of ∆. If we have
, then the more stable phase is 3 and the interface region moves in the direction which annihilates phase 1. If in the previous expression we have < instead of >, the case is the opposite. If both sides of the expression are equal (=), we have equistability and the interface does not move.
This can be illustrated with an example taken from []: the Selkov model, which is obtained from (62) with m = n = r = 1, s = 3. Figure 6 shows an example of the solutions of the reaction diffusion equations for a certain selection of parameter values.
For a different selection of values a stationary front can be obtained and the interface propagates with zero velocity. This is shown in Figure 7, which plots the curve of zero velocity as a function of two parameters: k6, which is the rate coefficient corresponding to the transformation from B to Y, and the ratio of diffusivities of X and Y, δ = Dy /Dx.
Finally, we compare the predictions of the theory with the numerical results in Figure 8. The theoretical results approach the numerical ones as the length of the interface region is increased.
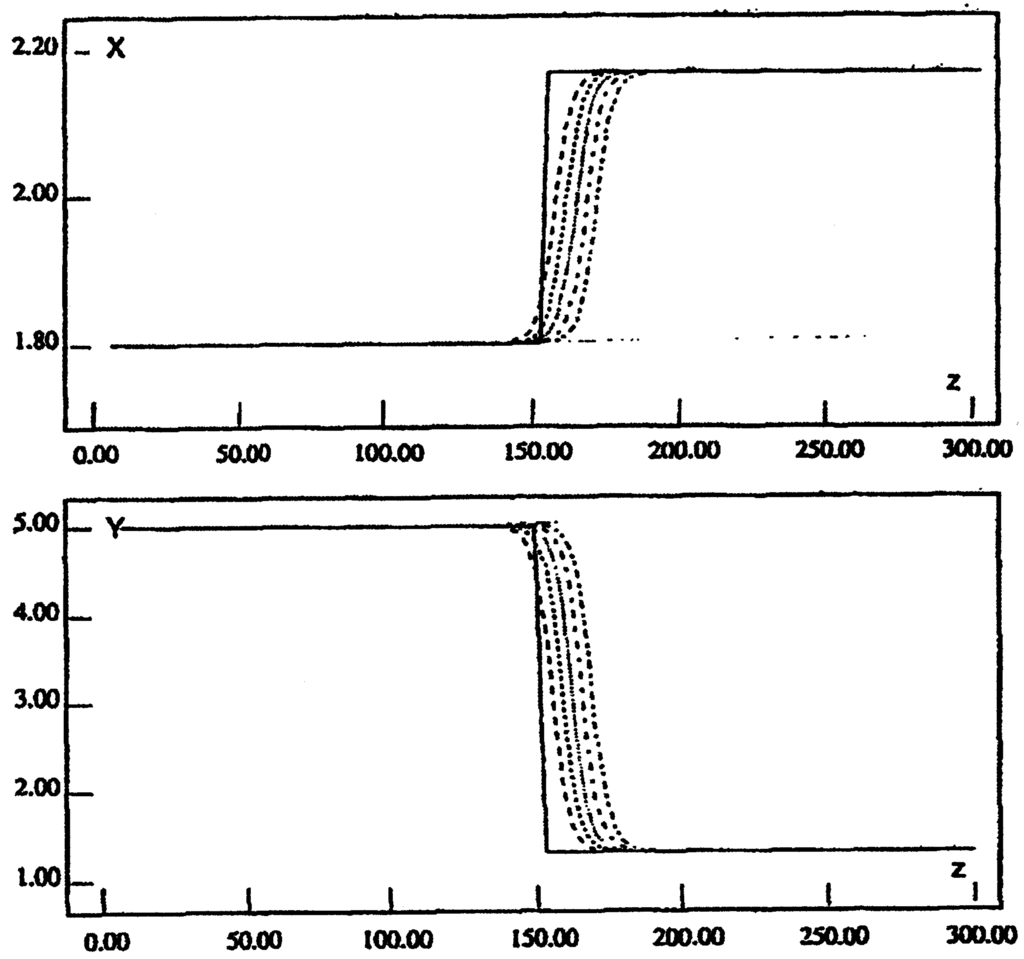
Figure 6.
Plots of concentration profiles of X and Y vs. distance z during the front propagation in the Selkov model. The solid line is the initial concentration profile; the dotted lines are the concentration profiles with uniform time spacing.
Figure 7.
Selkov model: the solid line is a plot of zero velocity of the interface between phase 1 and 3. Above the solid line the interface moves to the right, below it to the left.
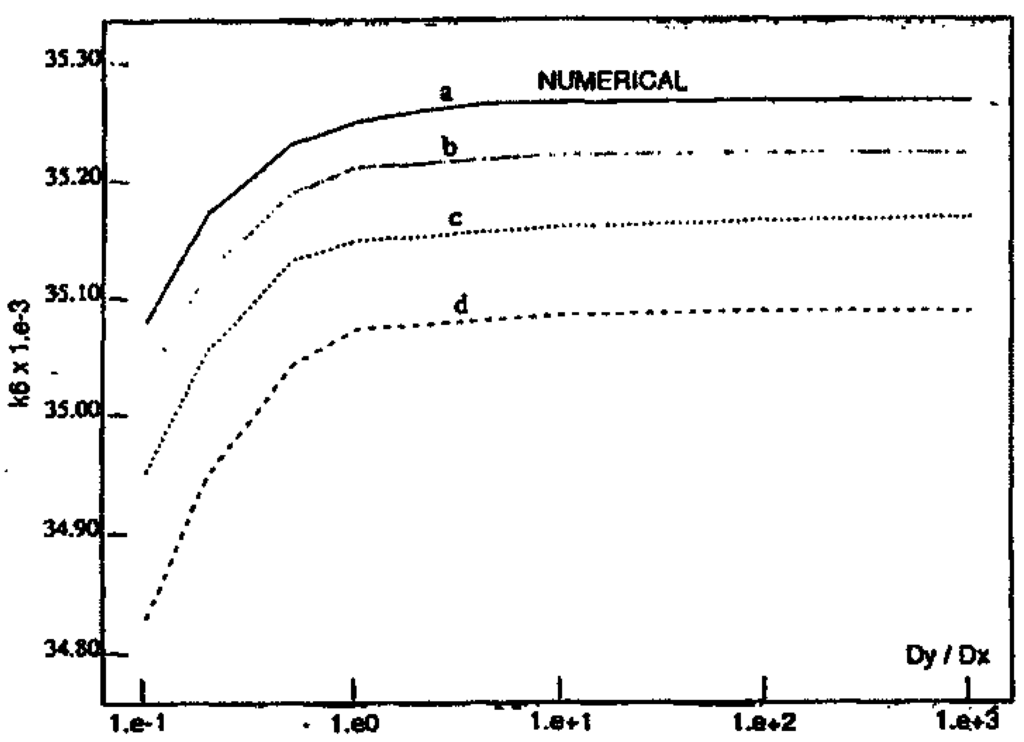
Figure 8.
Comparison of predictions of equistability from the thermodynamic theory (b, c, d) with the numerical solution (a) repeated from Figure 7. The theoretical solutions correspond to different lengths of the interface region L: (b) 6L, (c) 2L, (d) L. The theoretical curves approach the numerical calculations as the length of the interface region, and the number of boxes, are increased.
4.4. Stability and Relative Stability of Reaction-diffusion Systems Related to Fluctuations
In Section 4 we have discussed the thermodynamics of reaction-diffusion systems by means of deterministic kinetic equations. This can also be carried out on the basis of consideration of fluctuations, as was done in section 3 for the homogeneous systems previously discussed in section 2. In this subsection we follow again this approach. In parallel with section 3, we connect the stationary solution of the master equation and the thermodynamic excess work, a state function, 0. This presentation is based on the results in [,]. For a system with two intermediates (x,y) we can write:
where (x0,y0) refer to a reference state given by
which hold for an equivalent linear system. The displacements on the RHS of (86) are along the most probable fluctuational path. The momentum p is the gradient of the action, and therefore ds and d0 are exact differentials. Let us divide the interphase region into N boxes; then the state function of the total excess work is the sum of that in each box:
The reference state is determined as for the homogeneous case, but now in the full 2N dimensional case. Figure 9 shows the developed interface region, the dotted line. At equistability this line does not move, and translation of the dotted line does not change 0. If the stationary state 1 (SS1) is slightly more stable than the stationary state 3 (SS3) then the deterministic motion of the front is a translation to the right. Since 0 is a Lyapunov function Δ0 for this process must be negative. Similarly for the opposite case, 3 slightly more stable than 1, Δ0 is also negative. Hence at equistability the limiting value of Δ0 for a translation along the position z must be zero.
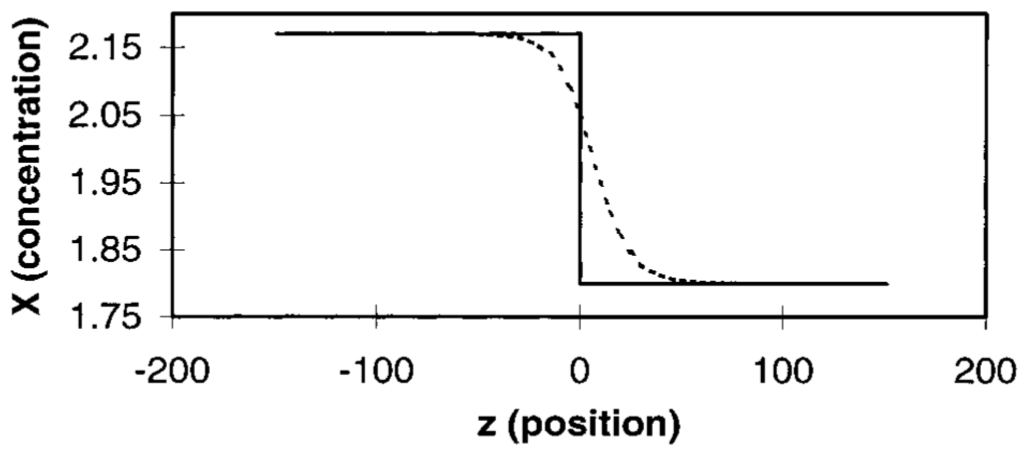
Figure 9.
Concentration (X) versus position (z) for the Selkov model. The initial concentration profile is shown by the solid line; the space with negative z is filled initially with stationary state 1, the space with positive z is filled initially with stationary state 3. The dotted line denotes the interphase region.
The change in the excess work for establishing the stable front (SF) from SS1 equals at equistability the change in excess work of establishing the stable front from SS3:
Thus the stationary probability distribution of the master equation in the eikonal approximation [] is a Lyapunov function which gives necessary and sufficient conditions of the existence and stability of non-equilibrium stationary states and provides a measure of relative stability on the basis of inhomogeneous fluctuations (88).
4.5. An Experiment on Relative Stability of Multiple Stationary States
In order to put to test the theory presented in this section we consider a multi-variable system, the bromate oxidation of ferroin, which exhibits bistability. We assume the NFT reaction mechanism considered in [] and discuss the experimental results reported in [].
In the experimental setup, two solution mixtures in different stable stationary states are pumped through a laminar flow reactor. They are brought in contact with each other on one edge of each solution; there is hardly any mixing due to the flow. When the flows are stopped diffusion occurs. The goal of the experiment is to measure the front propagation of one stable state to the other. The experimental results shown on Figure 10 yield an average value of (6.1 ± 0.6) × 10−3 s−1 for the flow rate coefficient at zero velocity of propagation. This experimental result was compared with a calculation based on a further simplification of the NFT mechanism to a two-variable system []. Numerical solution of the corresponding deterministic reaction-diffusion equations yields the value of 12.2 × 10−3 s−1, while the thermodynamic theory of section 4.3 predicts a value of 12.45 × 10−3 s−1. In view of the limited precision of the experiments and the use of a very simple model of the reaction mechanism, the agreement of the experiment with the theory and the calculations is satisfactory.
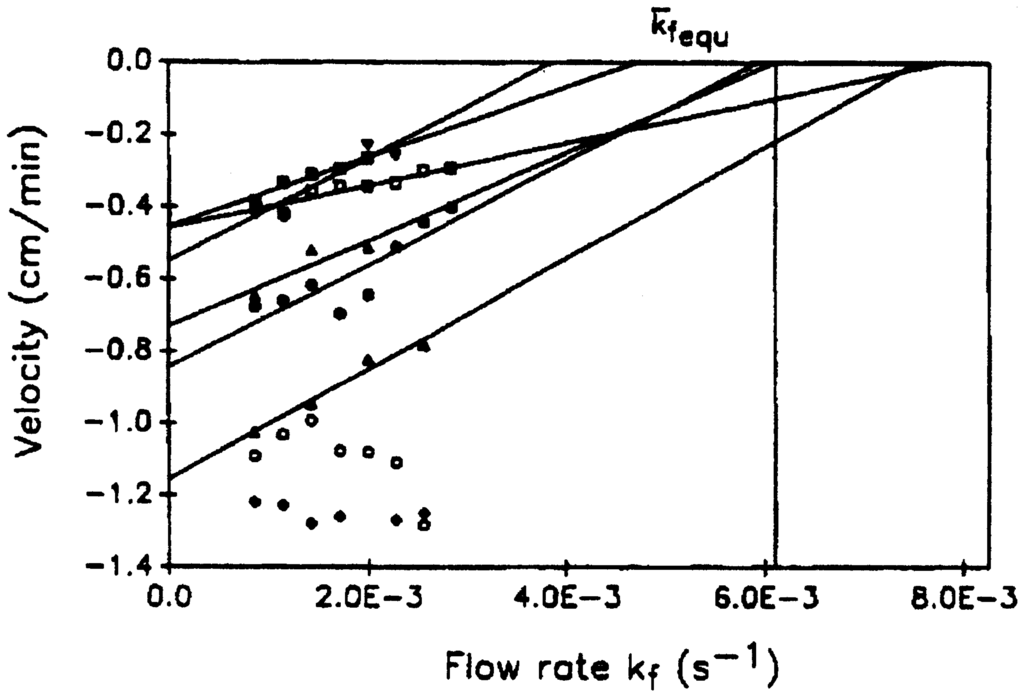
Figure 10.
Plots of the measured dependency of the velocity of front propagation of one stationary state into the other on the flow rate, kf. The eight different symbols correspond to eight experiments. Two of the plots are shifted from their original positions for the purpose of better display: circles by −0.6 cm/min in V; diamonds by −0.7 cm/min in V. Lines are fitted to each set of points for purpose of extrapolation to zero velocity of front propagation. The precision of the points at the largest velocities is insufficient to permit extrapolation.
5. Thermodynamic and Stochastic Theory of Transport Processes
We present a brief description of the thermodynamic and stochastic theory of simple transport processes, linear and non-linear: diffusion, thermal conduction, and viscous flow. We select thermal conduction as a specific example, and indicate some advanced work on hydrodynamic equations and some interesting experiments.
5.1. Linear Thermal Conduction
We consider a simple schematic of the apparatus depicted in Figure 11. It consists of two heat reservoirs, each of infinite heat capacity, one at temperature T1 and the other at T3, with T1 > T3. Volume 2 is between the two thermal reservoirs and is of small width so that its temperature T is uniform within it. The flow of heat occurs with conservation of energy and no work done.
Figure 11.
Schematic apparatus for study of thermal conduction.
We write the ‘mixed’ thermodynamic function M as a function of the entropies S:
or equivalently, . At the stationary state we have
; hence the driving force towards the stationary state is:
for the same changes dQ1, dQ, dQ3. The integral of d is:
This is an excess work as seen from the last two equations.
The macroscopic transport equation for this thermal conduction process is:
where k1 and k3 are proportional to thermal conduction coefficients for the interface of the system with the heat reservoirs 1 and 3, respectively. The temperature of the stationary state is
, and hence we may write
. If we divide by dt in (90) and use
, we obtain for the time derivative of :
Since (T) ≥ 0 and lower-bounded it is a Lyapunov function. Its first derivative with respect to T is:
and the second derivative with respect to T is:
so that is a minimum at the stationary state TS.
The total dissipation is the sum of the dissipation of the reservoirs in the stationary state, and
. Next we seek a stochastic equation for the distribution of fluctuations of the macroscopic temperature T for which the excess work (91) is its stationary distribution. This is a Fokker-Planck type equation:
in which the probability diffusion coefficient f(T) is cT with
, which is constant. The stationary solution of the stochastic equation is:
We rescale the temperature
and use Stirling’s approximation for
and obtain for the stationary distribution:
where Γ is the gamma function. If we expand this solution around TS we arrive at the expected quadratic form:
and the Gaussian stationary distribution:
This is exactly the same form as the equilibrium probability distribution for the fluctuations in temperature 2 at the equilibrium temperature TS = Tequ. For an ideal gas we have E = CVT and the fluctuations are in the Gaussian form in energy:
The generalization to a system with a discreet distribution of temperature follows closely the development for diffusion.
In the next subsection we present an experimental test of the theory for thermal conduction.
5.2. An Experiment on Optical Bistability
Here we discuss measurements of the relative stability of two stable stationary states in a bistable system, that of an optically bistable ZnSe interference filter. A thin ZnSe rectangle is illuminated with an argon laser (514 nm) and bounded by nonilluminated regions at room temperature. This produces optical bistability in certain ranges of power of the irradiating light. Part of the incoming light is absorbed by the filter and turned into heat, resulting in an increase in temperature. Two possible temperature profiles [] are shown on Figure 12, where temperature T is plotted against distance z.
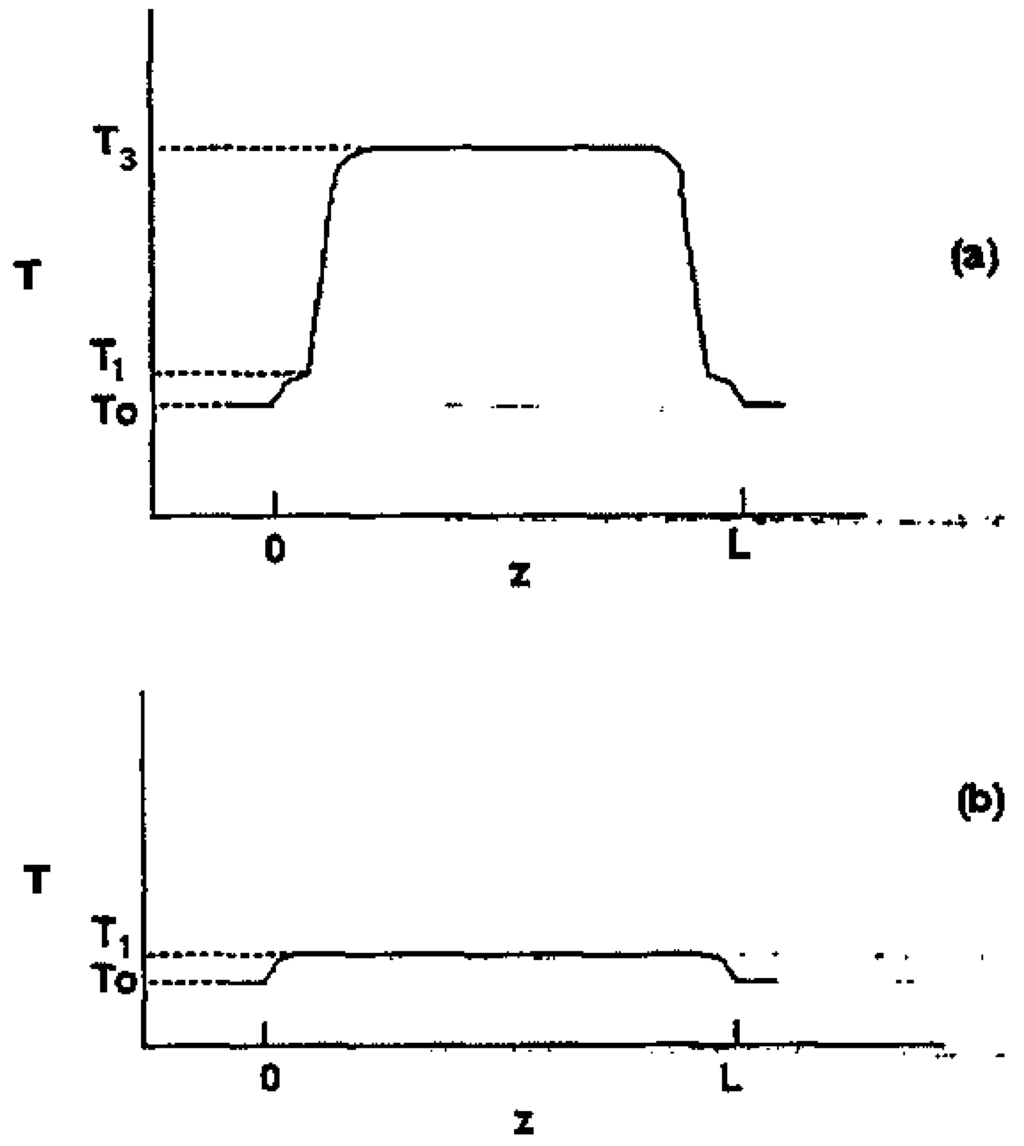
Figure 12.
Two possible stable stationary states of an optically bistable interference filter. The region of irradiation is the length L; the ambient, lower, and upper temperatures are T0, T1, and T3.
The upper and lower stable stationary states decay differently on stopping the irradiation. The upper state is annihilated by fronts moving inward from the boundaries; the lower state by the simultaneous decay of all regions at T3 toward T0. Calculations are shown on the left side of Figure 13 []; they are confirmed by the experimental measurements on the right side. The reaction-diffusion theory is amended for a problem in thermal conduction [], yielding a calculation of the irradiation power at equistability can of 1.375 mW. This shows a very good agreement with the experimental measurement, which was 1.395 ± 0.015 mW.
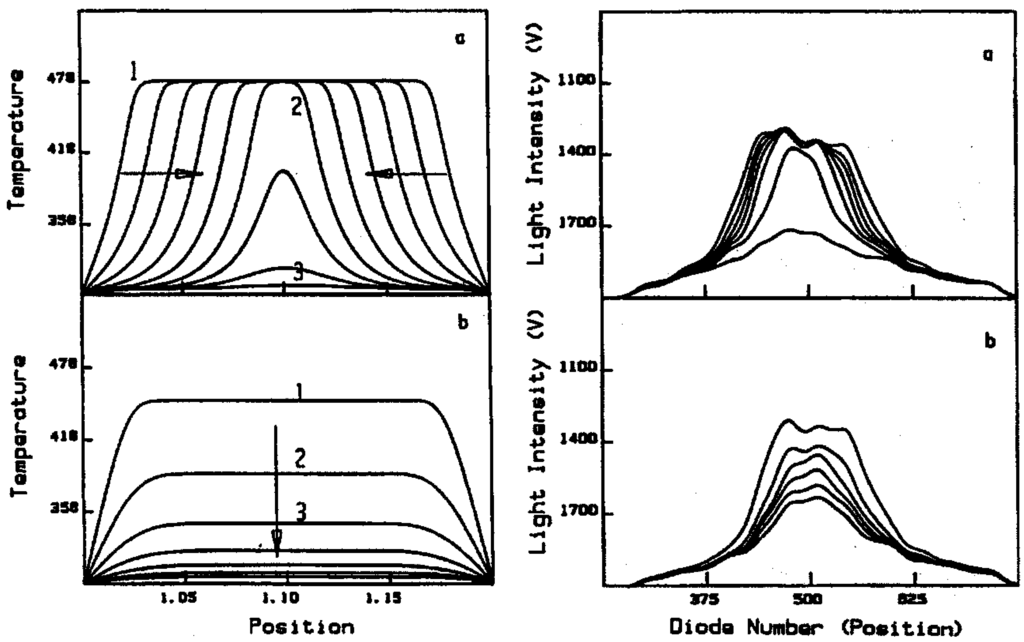
Figure 13.
Calculated (left) and measured (right) plots of the decay of temperature profiles on stoppage of irradiation of the upper stationary state (a) and the lower stationary state (b).
5.3. Coupled Transport Processes: An Approach to Thermodynamics and Fluctuations in Hydrodynamics
5.3.1. Lorenz Equations and an Interesting Experiment
Coupled transport processes are described macroscopically by hydrodynamic equations, the Navier‑Stokes equations []. These are difficult, highly nonlinear coupled partial differential equations; they are frequently approximated. One such approximation consists of the Lorenz equations [,], which are obtained from the Navier-Stokes equations by Fourier transform of the spatial variables in those equations, retention of first order Fourier modes, and restriction to small deviations from a bifurcation of an homogeneous motionless stationary state (a conductive state) to an inhomogeneous convective state in Rayleigh-Benard convection []. The Lorenz equations have been applied successfully in various fields ranging from meteorology to laser physics.
The aims of a theory of thermodynamics for hydrodynamics are the establishment of evolution criteria (Lyapunov functions) with physical significance, such as the excess work; the work and power available from a transient decay to a stationary state; macroscopic necessary and sufficient criteria of stability of stationary states; thermodynamic criteria for bifurcations from one type of stationary state to another type; thermodynamic criteria of relative stability, that is thermodynamic criteria of state selection; and a connection of the thermodynamic theory to fluctuations.
Attempts in these directions have a long history going back to Helmholtz, Korteweg, and Rayleigh, which we shall not review here; for a comprehensive account see Lamb’s classical treatise []. The emphasis was on the total dissipation, which however does not provide thermodynamic evolution criteria far from equilibrium. Glansdorff and Prigogine [,] considered the second variation of the entropy as a criterion for evolution and stability. Their approach is limited to small deviations from a stationary state, provides only sufficient not necessary conditions, and has no connections with work or excess work, nor with fluctuations (master equation). Keizer formulated a stochastic approach for the relaxation to stationary states and fluctuations around a single stationary state []; he assumed Gaussian fluctuations, limited to small fluctuations related to linearized kinetics (for chemical kinetics). There are several approaches to the statistical mechanics of stationary states and fluctuating hydrodynamics (see [] and references therein); some consist of the addition of Gaussian fluctuations to the linearized Navier-Stokes equations [,]. Here the thermodynamics may be sufficient for systems approaching equilibrium but not for stationary states far from equilibrium. In most of these studies no connections are made to work or power, nor to Lyapunov functions, nor to issues of relative stability when several states are available.
We developed our thermodynamic theory for the Lorenz equations, obtained with approximations from the Navier-Stokes equations (we present almost no mathematics here; that is given in detail in []). The Lorenz equations are:
where X represents the amplitude of the stream function of the macroscopic velocity of the fluid; Y the reduced temperature mode of the thermal conduction; and Z the reduced temperature mode related to the vertical flow in the liquid layer. P is the Prandtl number (the kinematic viscosity divided by the thermal conductivity). The parameters r and b are
, where R is the Rayleigh number,
, and ρ the density, α the thermal expansion coefficient, g the gravitational constant, h the height of the fluid layer, ΔT the temperature difference across the layer of liquid, η is the viscosity, and κ the thermal conductivity. These are the variables and parameters of this system.
One solution of the Lorenz equations is (X,Y,Z) = (0,0,0). When the control parameter r is less than unity, that is the Rayleigh number is less than its critical value Rc, then the zero solution is unique and stable, and it corresponds to the motionless conductive state of the fluid. At the bifurcation point r = 1 this solution becomes unstable, and a new solution becomes stable corresponding to convective modes. These solutions can be used to construct an excess work function, just as we did for single transport properties.
Now we return to a fascinating experiment in alignment with our theory. Zamora and Ray de Luna [] carried out Rayleigh-Benard experiments in an apparatus that could be inverted 180° in the gravitational field. In their experimental arrangement the bottom and top sides of the fluid are connected to heat reservoirs at different temperatures. Suppose a stationary state is homogeneous and conductive, achieved by setting the low temperature reservoir below the one at high temperature in the gravitational field. Next the entire apparatus is turned in the gravitational field; then the conductive state becomes unstable and a stable convective state appears. Throughout the experiment the reservoir temperatures are held fixed and the average temperature of the fluid is nearly constant. They measured the heat fluxes into and out from the reservoirs during all transients, that is the relaxations from a conductive to a convective state, and the reverse. For example, say the fluid is in a convective state; invert the apparatus; the convective state is unstable and a transient change to a conductive state takes place. Measure the heat fluxes in and out of the reservoirs. The integration of the differences of the heat fluxes in and out during this transient process is the total energy change accompanying the destruction of the convective rolls. Similarly they measured the total energy change accompanying the formation of the convective rolls. The results show that the heat releases for both the destruction and formation of convective structures are positive, which means that the system always releases energy in the form of heat when it approaches a stable stationary state, either the convective state or the motionless conductive state. In an auxiliary experiment they found that the change in average temperature of the system is very small; the change in internal energy due to this small temperature is less than 10% of the heat release during the relaxation processes, so this can not be the reason for the experimental observations. Moreover, the change in internal energy cannot explain the observed heat release in both the destruction and the formation of a convective structure.
Our theory based on the concept of excess work accounts for these experiments, at least qualitatively. According to our theory, when the system approaches a stable stationary state, either convective or conductive, there is a decrease in , the excess work, and a positive excess work is released, which will be dissipated and released as heat. This is shown in a calculation from the theory in Figure 14, from []. Figure 14a is for the transition from a conductive to a convective state, and Figure 14b for the reverse transition. In each case the integral of d / dt over time is negative, that is excess work is dissipated and heat is generated. Further we note that the entropy production in the convective state is always larger than that in the conductive state, and no explanation of heat release in the transition from one state to the other can thereby be derived.
The theoretical results, based on the Lorenz model, agree with experiments qualitatively in that the total excess work change is of the same order of magnitude as the heat release measured in the experiments, and this is a major confirmation of our theory.
5.3.2. Rayleigh Scattering in a Fluid in a Temperature Gradient
In a simple fluid, in an imposed temperature gradient, light is scattered due to fluctuations in temperature and due to fluctuations in the transverse hydrodynamic velocity. Excellent experiments have been made on the measurement of this light scattering. The problem has been studied theoretically as well, by means of fluctuating hydrodynamics [,], valid for small fluctuations around a conductive state with a constant temperature gradient, which can be close to or far from equilibrium. Theory and experiment are in very good agreement [,,,].
In [] we developed the relation of our studies on the thermodynamic and stochastic theory of transport properties to the reported research on this topic. There we showed that the deterministic excess work, as formulated in Section 2 for reactions and in this section for transport processes, provides a thermodynamic interpretation of fluctuations around a stationary state, either close to or far from equilibrium, for the case of Raleigh scattering from fluctuations in a fluid with an imposed temperature gradient. The stationary probability distribution is determined by a quantity proportional to the excess deterministic work. From the probability distribution we obtain, in the Gaussian approximation for small fluctuations, the matrix of correlations derived from fluctuating hydrodynamics, Equation (51) in []. Thus in this limit of small fluctuations there is agreement between the theory of fluctuating hydrodynamics and our theory of the thermodynamics and fluctuations in transport properties.
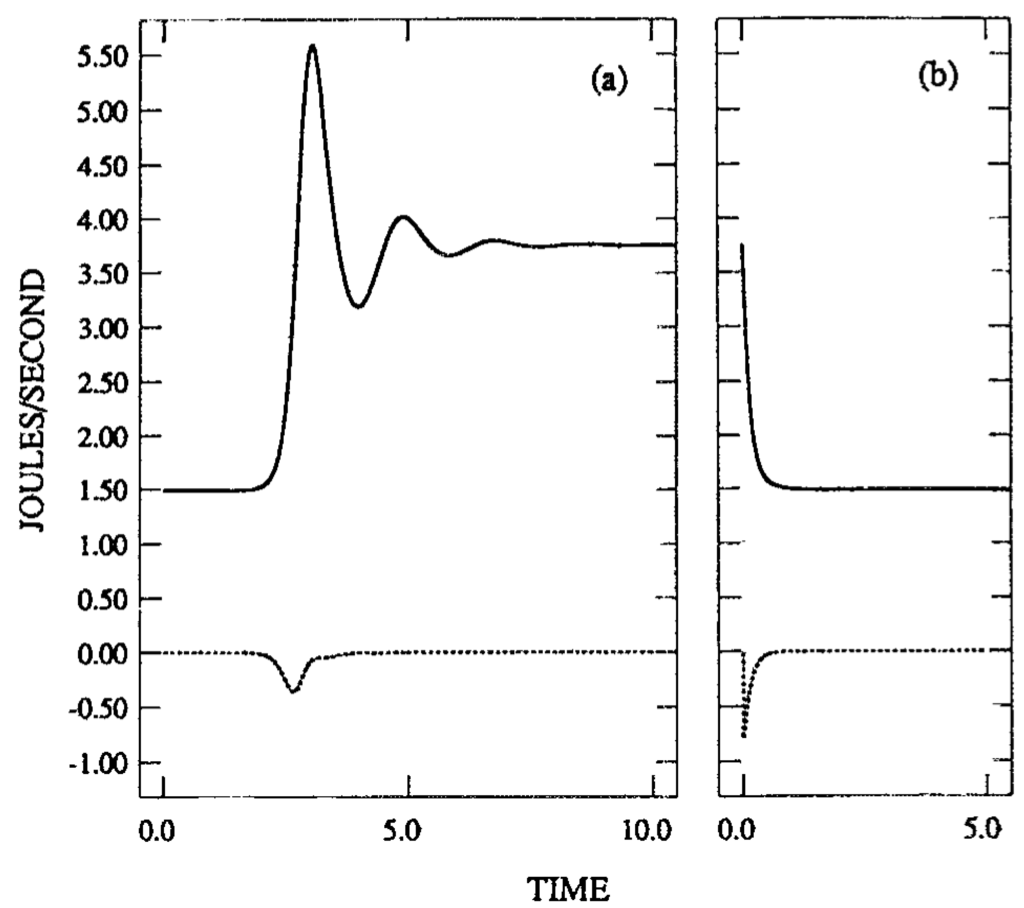
Figure 14.
The product of the total rate of dissipation times temperature (solid line) in J/s and the time derivative of excess work (dashed line) vs. time in the following processes for the Lorenz model: (a) Gravity is initially set in the direction along which the temperature decreases, and the system is at a stable motionless conductive stationary state; at t = 0, invert the direction of gravity; the motionless conductive state becomes unstable and the system approaches the convective stationary state. (b) The reverse process. The temperature difference is
in both cases.
It should be noted that the presentations in the prior sections have been limited to ideal systems, either gases or solutions. The thermodynamic and stochastic theory can be extended for non-ideal systems; the interested reader is referred to [].
6. Electrochemical Experiments in Systems Far from Equilibrium
In chemical systems at equilibrium, Gibbs free energy changes and other thermodynamic quantities can be determined from electrochemical experiments []. At equilibrium the Nernst equation relates the Gibbs free energy change of a chemical reaction, ΔG, to the voltage (the electrochemical potential E) generated by that reaction run in an electrochemical cell:
where n is the number of equivalents of electrons transferred from one electrode to the other.
In the preceding sections we have presented a thermodynamic and stochastic theory of chemical reactions and transport processes in non-equilibrium stationary and transient states approaching non‑equilibrium stationary states. We established a state function , which for systems approaching equilibrium reduces to ΔG. Since Gibbs free energy changes can be determined by macroscopic electrochemical measurements, we seek a parallel development for the determination of by macroscopic electrochemical and other measurements. We discuss two kinds of experiments in Section 6.1 and Section 6.2; then in Section 6.3 we turn to the development of the thermodynamic and stochastic theory to connect with these experiments.
6.1. Measurement of Electrochemical Potentials in Non-equilibrium Stationary States
When chemical species come into equilibrium with an electrode in an open circuit, the potential between the electrode and a reference electrode is related to the potential difference of the half reaction occurring at the electrode. If no other reactions are occurring then this potential is related to the Gibbs free energy difference of the half reaction at the electrode. If there are other reactions occurring then the species may be in non-equilibrium states, even though they are in equilibrium with the electrode, and the potential is that of a non-equilibrium stationary state. If local equilibrium holds then the potential is the Gibbs free energy difference; if it does not hold, in that there are degrees of freedom, such as the reactions, which are explicitly held away from equilibrium, then deviations from the Gibbs free energy difference may occur. We shall speak of Nernstian (103) and non-Nernstian contributions to the electrochemical potential. There is one prior measurement of the type to be described and that is by Keizer and Chang [] following a suggestion by Keizer [,,] that there should be a non‑Nernstian contribution to the electrochemical potential in nonlinear reaction systems approaching to, or in, stationary states far from equilibrium. They reported a very small non-Nernstian contribution in a Fe(II)/Fe(III) reaction system in a non-equilibrium stationary state.
We studied the autocatalytic minimal bromate reaction, which can be oscillatory, but was studied in a bistable regime. A mechanism for this reaction was proposed in []. The net reaction is the oxidation of Ce(III) to Ce(IV) by bromate. In the bistable regime there is a state, where essentially no reaction occurs, which coexists with a state in which a percentage of Ce(III) is oxidized to Ce(IV). In this system we measured [] at the same time the optical density which gives concentrations of Ce(IV) by Beer’s law, and hence also the concentration of Ce(III) by conservation, and the emf of a Pt electrode which at equilibrium follows the Nernst equation (103). The experiment consisted of the measurement of the emf of the Ce(III)/Ce(IV) half reaction at a redox (Pt-Ag/AgCl) electrode under equilibrium and stationary non-equilibrium conditions. From these measurements we determined that there exists a non-Nernstian contribution in a non-equilibrium stationary state as shown in Table 1. The concentration of [Ce(III)]ss in the stationary state is obtained from the absorption measurement. The local equilibrium emf, the third column in Table 1 is calculated from the ratio Ce(III)/Ce(IV) and the Nernst equation. The measured emf in the fourth column of the table is that measured by the Pt electrode. The difference is small, about 1% of the emf at the largest inflow concentration of Ce(III)0 and decreases for smaller inflow concentrations.

Table 1.
Results from the Minimal Bromate Experiment with Various Concentrations of Ce(III) in the combined feedstreams into the Reactor, [Ce(III)]0. From [].
| [Ce(III)]0 (M) | [Ce(III)]ss | IE emf (mV) | M emf (mV) |
|---|---|---|---|
| 1.500 × 10−3 | 1.393 × 10−3 | 1167.0 | 1180.2 |
| 1.397 × 10−3 | 1.361 × 10−3 | 1176.0 | 1183.0 |
| 1.297 × 10−3 | 1.277 × 10−3 | 1187.5 | 1189.7 |
| 8.333 × 10−4 | 8.700 × 10−4 | 1223.7 | 1223.8 |
6.2. Kinetic and Thermodynamic Information Derived from Electrochemical Measurements
We study now the electrochemical displacement of a non-linear chemical system from non‑equilibrium stationary states and from equilibrium. Then in Section 6.3 we shall relate such measurements to the thermodynamic and stochastic theory of potentials governing fluctuations in electrochemical systems in stationary states far from, near to, and at equilibrium.
We study again the minimal bromate reaction, where we measure the Ce(III)/Ce(IV) potential (for further details about the experimental setup see []). The contents of three reservoirs are pumped separately into a CSTR; the three reservoirs contain 0.00450 M CeIII, 0.0100 M BrO2−, and 1.00 × 10−6 M Br−, and each reservoir contains also 0.72 M H2SO4. To run the reaction at equilibrium the three solutions are mixed and allowed to react for a day prior to being pumped into the CSTR. First we measure the Ce(III)/Ce(IV) potential with zero imposed current from an external current source; then we impose various currents and displace the equilibrium mixture in the CSTR from equilibrium. A non-equilibrium stationary state is achieved by flowing the reacting solutions into the CSTR at given flow rates, that is given residence times in the reactor. For a residence time of 175 seconds, Figure 15 shows the measured voltages plotted against the imposed current, as well as the Ce(IV) concentration, and the product of the measured voltage minus the stationary state voltage multiplied by the imposed current. The left hand part of Figure 15 shows results for an equilibrium mixture, while the right hand part shows displacements from a non-equilibrium stationary state.
It is interesting to compare the equilibrium displacement plot with the plot of displacements from non‑equilibrium stationary states. To achieve a given displacement, either in Ce(IV) concentration or in the potential from its stationary value at zero current, a larger imposed current is necessary in the non‑equilibrium case than in the equilibrium case. We further note that the plot of (V − Vss) × I in the equilibrium case is nearly symmetric, but that for the non-equilibrium cases it is not.
The plots of power input vs. imposed current can be obtained by a simple, nearly dimensional argument from our theory. For a one-variable linear system the excess work is, as seen in section 2,
; hence
and
; so that with Nernst’s equation we have:
The time derivative of the excess work, which is that part of the dissipation due to the variation in X, equals the power input necessary to maintain the system away from its stationary state. In the next subsection we outline the theory in more detail.
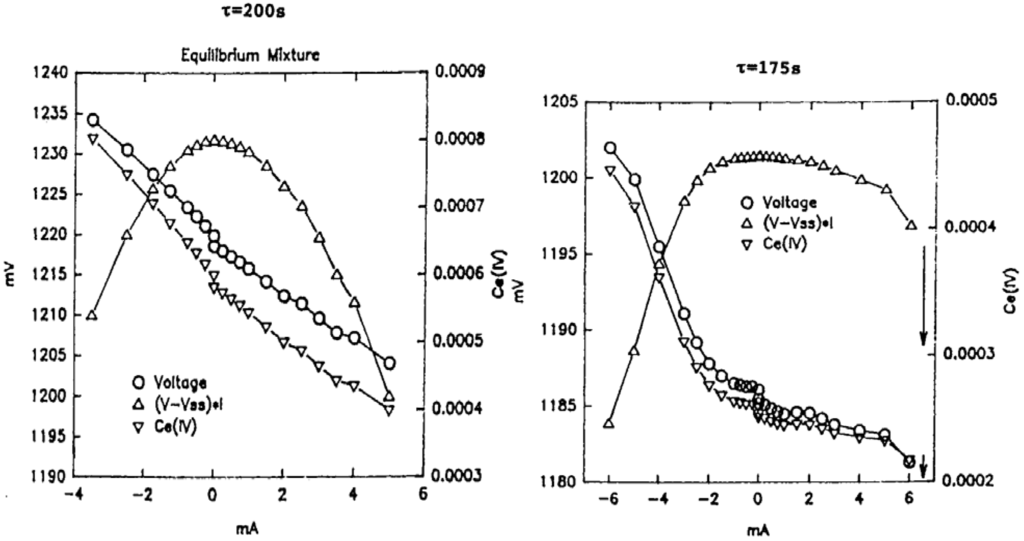
Figure 15.
Plot of voltage V, the power input (V − Vss) × I, and the Ce(IV) concentration versus the imposed current I. Vss is the measured voltage at a non-equilibrium stationary state at zero imposed current. The plot on the left corresponds to an equilibrium stationary state; the residence time in the CSTR is 200 seconds. The plot on the right hand corresponds to a non-equilibrium stationary state at zero imposed current and displacements from that state with imposed currents; the residence time is 175 s. The arrows indicate transitions to other stationary states. From [].
6.3. Theory of Determination of Thermodynamic and Stochastic Potentials from Macroscopic Measurements
First we present an outline to an approach to the determination of thermodynamic and stochastic potentials, , for non-equilibrium systems from electrochemical measurements; and second, a parallel development for neutral (not ionic) systems in general. We conclude with some suggestions for testing the consistency of the master equation with measurements.
For the first purpose we choose a chemical reaction system with some ionic species, as for example the minimal bromate reaction, for which we presented some experiments in chapter X. We consider a simple representation of a reaction:
where the signs + or − indicate ionic species and the other species are neutral.
The reactions system may be in equilibrium or in a non-equilibrium stationary state. An ion selective electrode is inserted into the chemical system and connected to a reference electrode. The imposition of a current flow through the electrode connection drives the chemical system (CS), written above, away from its initial stationary state to a new stationary state of the combined chemical and electrochemical system (CCECS), analogous to driving the CS away from equilibrium in the same manner. A potential difference is generated by the imposed current, which consists of a Nernstian term dependent on concentrations only, and a non-Nernstian term dependent on the kinetics. We shall relate the potential difference to the stochastic potential; for this we need to know the ionic species present and their concentrations, but we do not need to know the reaction mechanism of the chemical system, nor rate coefficients.
The differential of the stochastic potential for the chemical system in one of its stationary states, dc, is (see Section 3):
with the index i extending over A1, B1, taken to be neutral, and the species A2, B2 taken to be negatively charged. The differential dc is exact and any path of integration suffices to obtain . The exponential of the integral in (106) is a formal representation of the eikonal approximation for the stationary solution of the master equation of the chemical system.
We choose the same variables for the chemical as for the electrochemical system. The reactions at the electrodes are sufficiently fast that the measured potential is the equilibrium potential; fluctuations in that potential and in the imposed current are neglected. This is analogous to neglecting fluctuations in concentrations of species in equilibrium with mass reservoirs. For systems for which equilibrium is the only stable attractor, the chemical potential of each chemical species, say that of A2, is
where EA2 is the potential for a given imposed current, N is the number of equivalents in the half-cell reaction for A2, and F is the Faraday constant. We postulate that we may write dE for the combined chemical and electrochemical system in a parallel way:
where the first line is for the neutral species and the next two line for the ionic species. The fourth line gives the relation of the stochastic potential of the combined systems to that of the chemical system.
This postulate is consistent to given approximations with an expansion of the master equation or an equivalent Hamilton-Jacobi equation. The derivation is given in Appendix A and B of []; the mathematics is complex and specialized. The study of stochastic equations of electrochemical systems is in its infancy; we know of no prior work on this subject. Further intensive studies will be necessary to fully substantiate the postulate of (107).
At a stationary state of the combined system the differential dE = 0 and therefore we have for dc the result:
where we added and subtracted the potentials EA2(s) of A and EB2(s) of B in the stationary state of the system of the chemical system. The first term in each square bracket depends on concentrations only and thus is the Nernstian contribution to the measured electrochemical potential. The second term in each square bracket depends on the kinetics of the chemical system and thus is the non-Nernstian contribution the electrochemical potential. Measurements of this potential, say with ion-specific electrodes, yield the slopes
and
; thus with measurements of the macroscopic concentrations of A1, A2, B1, and B2 at a sufficient number of displacements from the stationary state of the chemical system we can determine the stochastic potential of that system from macroscopic measurements. To obtain these results no direct use of any master equation has been made and no model of the reaction mechanism was necessary.
6.3.1. Determination of the Stochastic Potential in Chemical Systems with Imposed Fluxes
Consider the chemical system in (105) with the species being either ions or neutrals; the system is in a reaction chamber in a non-equilibrium stationary state. We impose a flux of species A1, J = k’A1’, into the reaction chamber with Q+ and Q− held constant and thereby move the chemical system to a different non-equilibrium stationary state with different concentrations of the reacting species A1, B1, A2, B2. This procedure allows the sampling of different combinations of the reacting species by means of the imposition of different fluxes of these reactants. These combinations represent different non‑stationary states in the absence of imposed fluxes, but with the imposed fluxes they are stationary states and hence measurements may be made without constraints of time. If we would attempt to measure concentrations in non-stationary states then the measurement technique would have to be fast compared to the time scale of change of the concentrations due to chemical reactions.
Now we impose a flux of a chemical species present in the system and inquire on the effect of that imposition on the stochastic potential of the system. For that we need to go from the deterministic kinetic equations to a stochastic equation, say the lowest order eikonal approximation to the chemical master equation. The response measurements to the imposed flux provide an indirect determination of the stochastic potential, one that depends on the use of the master equation, an assumed reaction mechanism, and assumed rate coefficients.
This procedure is easy for a one-variable system because we know the solution of the stationary master equation to this approximation. For example, for the one variable Schlögl model we have the elementary reaction steps:
with the concentrations of A and B held constant. The kinetic equation without the imposed flux is:
Let the imposed flux be J = k’X’. The stationary solution of the lowest order eikonal approximation of the master equation for the system Equation (15) with the imposed flux is
where:
In the absence of an imposed flux the solution reduces to
At a stationary state of the system with imposed flux we have
and hence from (111) we obtain:
Thus from measurements with imposed flux we obtain the derivative of the stochastic potential for the system without imposed flux, but we need kinetic information, the rate coefficients in t−, as well. For multivariable systems this approach is more difficult; the determination of the stochastic potential requires sufficient measurements to determine rate coefficients and then the numerical solution of the stationary form of the master equation. Details of this procedure are described in Appendix A of [].
6.3.2. Suggestions for Experimental Tests of the Master Equation
A direct test of the master equation for systems in non-equilibrium stationary states comes from the measurements of concentration fluctuations; there have been a few of such measurements. Some other tests of the master equation are possible based on the earlier sections in this chapter, where we can compare measurements of the stochastic potential with numerical solutions of the master equation (which requires knowledge of rate coefficients and the reaction mechanism of the system).
There are other indirect methods. Consider a one-variable system (or an effectively one variable). Let the system have multiple stationary states and in Figure 16, taken from [], we show a schematic diagram of the hysteresis loop in such systems.
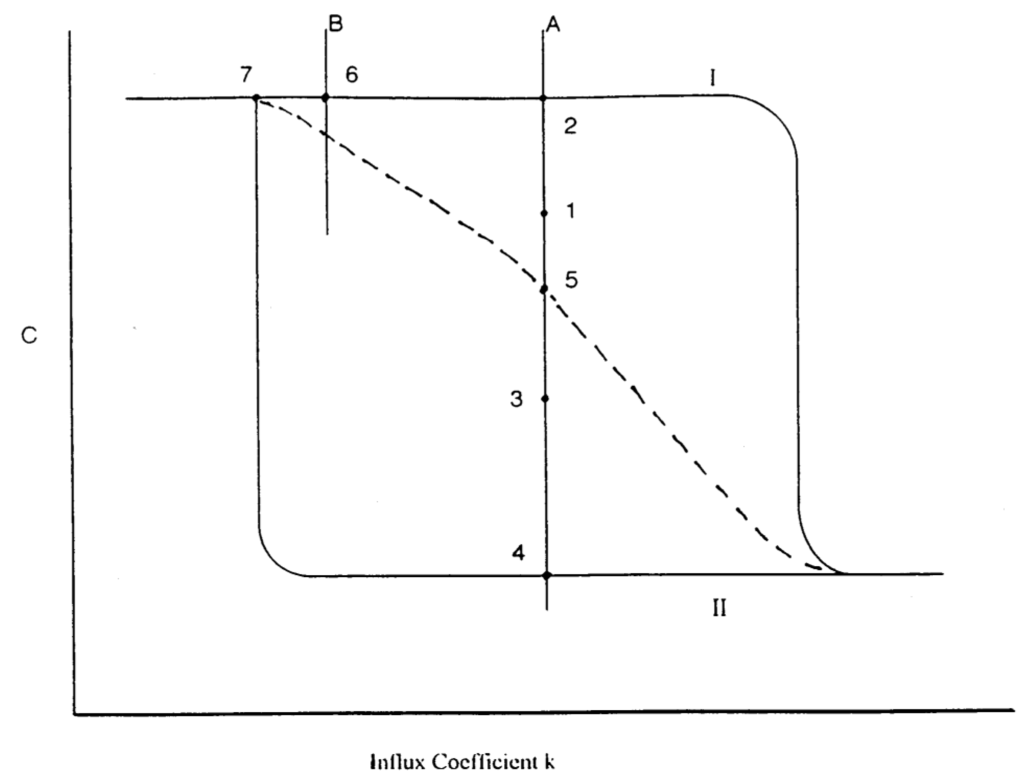
Figure 16.
Typical hysteresis loop for a one-variable system with a cubic kinetic equation: plot of concentration c vs. influx coefficient. Solid lines, stable stationary states (nodes); broken line, unstable stationary state. For a discussion of lines A and B and numbers, see text.
Several experiments can be suggested to test aspects of the predictions of the master equation. To construct a diagram as in Figure 16 from the master equation we need to know or guess rate coefficients and the reaction mechanism of the system. For the experiments we need to measure the concentration c of a given species as the influx coefficient is varied. Thus we establish the solid lines by experiment. If we can form a combined chemical and electrochemical system, as discussed in subsection 6.3, then we can locate the combined system at point 1 on line A by imposing a given current flow. This point is a stable stationary state of the combined system. If the imposed current is stopped (the electrochemical system is disconnected) then the chemical system will return deterministically to the nearest stable stationary state of the chemical system, that is point 2 on line A and on the stable branch I. We can repeat this experiment by locating the combined chemical and electrochemical system, say on point 3 on line A; then on stopping the imposed current the chemical system will return to point 4 on line A and on the stable branch II. By means of such experiments we can locate the branch of unstable stationary states, the separatrix, the dotted line in Figure 16, and compare it with predictions of the master equation. The same approach works for the displacement of a system by imposition of an influx of a given species.
Equistability of a homogeneous stable stationary state on the upper branch of the hysteresis loop, labeled I in Figure 16, with a homogeneous stable stationary state on the lower branch, labeled II, occurs at one value of the influx coefficient k within the loop. Say that point occurs at the location of line A. The predictions of the stationary solution of the stochastic master equation are: (a) the minimum of the bimodal stationary probability distribution is located on the separatrix, and (b) at equistability the probability of fluctuations P(c) obeys the condition:
Approximately, at equistability the height of the probability peak at point 2 equals that at point 4. To either side of the value of k at equistability, the peak of the more stable stationary state is higher than the other peak.
A comparison of deterministic and stochastic calculations (not experiments) has been discussed in a different context, that of viewing the stochastic potential as an excess work [,]. A point at the end of a hysteresis loop, such as point 7 in Figure 16, is called a marginal stability point. Near such points, such as 6, critical slowing occurs. After a perturbation of the system in the stable stationary state at 6 the system returns to 6, but increasingly more slowly for values of the influx coefficient to the left of 6 but to the right of 7, and increasingly faster to the right of 6. This effect has been observed experimentally in several systems []. Critical slowing down manifests itself in the stationary solution of the master equation near marginal stability points. Hence a quantitative comparison of experiment and theoretical predictions leads to a test of the master equation and the assumed parameters.
7. Dissipation in Irreversible Processes
The entropy production rate is a measure of the dissipation in an irreversible process. A popular ‘principle’ in the literature states that, if a stationary state is close enough to equilibrium, then the entropy production rate has an extremum at the steady state []. This is known as the principle of minimum entropy production. In this section we show that neither this principle nor the principle of maximum entropy production is valid. To this end we follow [] and begin with the exact solution for thermal conduction.
7.1. Exact Solution for Thermal Conduction
We consider an example of thermal conduction, which we shall analyze exactly, without approximations. Consider a macroscopic, homogeneous system with cylindrical shape of length l and cross-sectional area A; and time-dependent temperature T. Heat is transported across the boundary of the cylinder at each end in contact with two thermal baths with temperature T1 and T2; we assume T1 > T2. We take the conduction of heat to be given by Newton’s equations:
where k is the thermal conductivity, ρ the density of the system taken to be constant, and c the mass specific heat capacity, also taken to be constant. The solution of this equation is:
where the relaxation rate is
and the stationary state temperature is
. The rate of entropy production is the product of the heat flux times the conjugated force:
and is always positive. Note that the flux is not proportional to the force. The derivative of the entropy production with respect to temperature is:
and at the stationary state we have:
Since the derivative is always positive the rate of entropy production is never an extremum at a stationary state, whether close to or far from equilibrium, except at equilibrium. At equilibrium (), the entropy production rate has an extremum which is a minimum.
7.2. Invalidity of the Principles of Minimum and Maximum Entropy Production
Glansdorff and Prigogine [] stated the Minimum Entropy Production principle as follows: “… if the steady states occur sufficiently close to equilibrium states they may be characterized by an extremum principle according to which the entropy production has its minimum value at the steady state compatible with the prescribed conditions (constraints).” Since then it has been frequently presented as a fundamental law of nature with a deep meaning.
We have shown by a counterexample that the entropy production rate does not have an extremum for a steady state, not even in the vicinity of thermodynamic equilibrium. Two additional counterexamples are given in [], for Fourier’s law of heat conduction and for a chemical reaction network with mass-action kinetics. In fact, the entropy production rate has a minimum at the steady state only if the flux of the transport process is strictly proportional to the force. The common error of accepting the Minimum Entropy Production principle is caused by ignoring the noncommutativity of two different operations: (1) the truncation of a Taylor series for the entropy production rate in terms of a set of parameters which express the distance from equilibrium, and (2) the differentiation of entropy production rate with respect to temperature.
A related albeit less known theorem is the Maximum Entropy Production principle [], which states that irreversible processes proceed in a direction which produces maximum entropy production. If there is a choice then the path with the highest entropy production has the fastest rate. For chemistry this principle is generally invalid; the rates of reactions are governed by the Gibbs free energy of activation, not by the rate of entropy production.
8. Efficiency of Oscillatory Reactions
State variables, such as concentrations of chemical species, are constant in a stationary state, whether at equilibrium or nonequilibrium; or they may be oscillatory in a non-equilibrium state, such as a limit cycle. In an oscillatory chemical reaction system the Gibbs free energy change of the reaction (ΔG) is oscillatory (usually not sinusoidally) and the rate of the overall reaction is oscillatory. The dissipation of the system is the product of ΔG and the rate of the reaction if no external work is done by the reaction.
There now appears a new quantity, the phase relation of the oscillations of ΔG to the oscillations of the rate. As in electric alternating current systems the phase between the current (rate) and the voltage (ΔG) determines the power output of the system. We illustrate this point with experiments on the oscillatory horse radish peroxidase (HRP) reaction:
In Figure 17 we plot ΔG, calculated from measurements of concentrations, and the rate vs. time for constant influx of oxygen, the flat part of the top line, and oscillatory influx of oxygen, the oscillatory part of the top line. The phase between the oscillation of ΔG and the rate is changed from the constant input of oxygen and the oscillatory input, as show in greater detail in Figure 18.
This change in phase changes the dissipation, or the power output, and we see that we can affect, control, these important quantities by controlling external inputs (influxes).
In [] other examples are discussed: an oscillatory reaction with constant influx of reactants; the efficiency of pumped chemical reactions; and the efficiency of a proton pump.
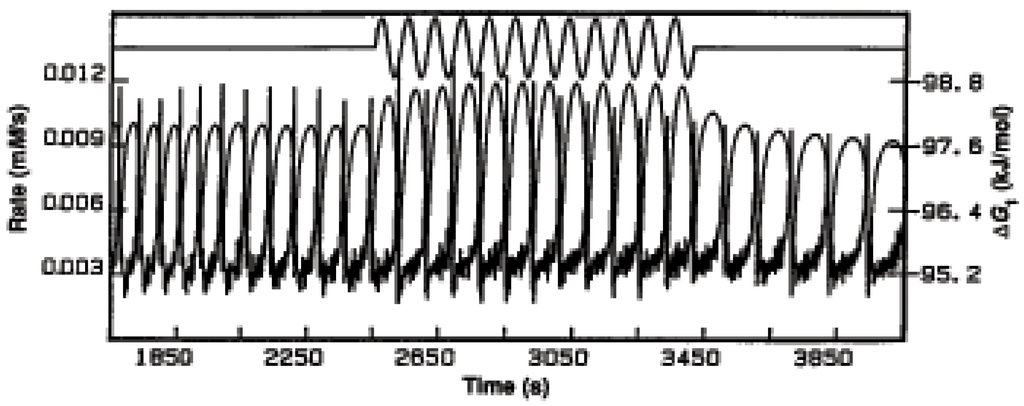
Figure 17.
Plot of ΔG and the rate of the HRP reaction vs. time. See text for further explanation. From [].
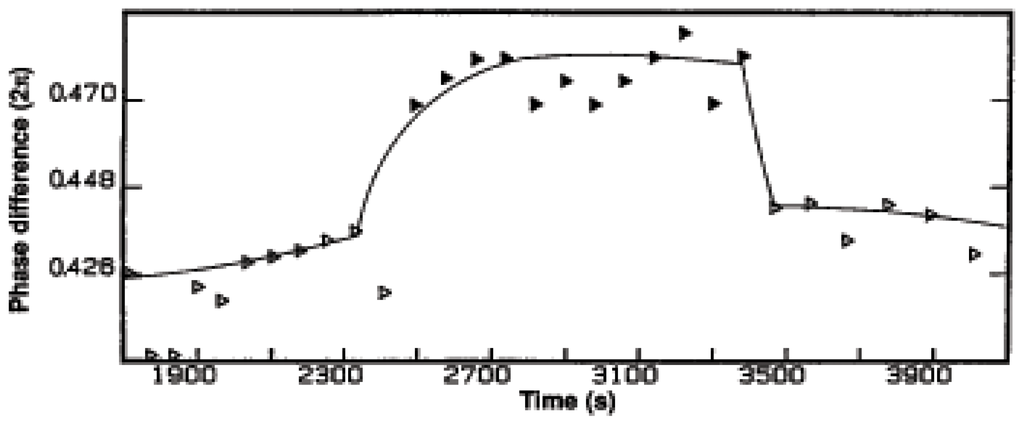
Figure 18.
Plot of the phase difference between the Gibbs free energy change and the rate of the HRP reaction in units of 2π. From [].
9. Fluctuation-Dissipation Relations
We discuss briefly the relations between dissipative, deterministic kinetics and fluctuations for the purpose of an introduction to the interesting topic of fluctuation-dissipation relations. This subject has a long history, more than 100 years [,,,,]; [,,] are a classical review with many references to fundamental earlier work. A brief reminder of one of the early examples, that of Brownian motion, may be helpful.
The dynamics of a Brownian particle of mass m velocity v is described by a Langevin equation []:
where the first term is the force due to acceleration of the particle, the second term the frictional force on the particle, and F(t) is a delta correlated Gaussian random force for which the first two moments are:
in which λ is a parameter that gives the strength of the fluctuations that affect the Brownian particle. In a derivation due to Langevin, given in [], it is shown that the friction coefficient γ in (120), which characterizes the dissipative process, and λ, which characterizes the fluctuations, are related by:
Equation (122) is a fluctuation-dissipation relation.
Now consider a one-variable open chemical system, either linear:
or non-linear:
We need two definitions, one for the net rate of the reaction:
and the other for the total rates in the forward and reverse reaction:
t(x) = t+(x) − t−(x)
D(x) = [t+(x) + t−(x)]/ 2.
With that we write a fluctuation–dissipation relation:
with the species specific affinity A(x):
for the linear case, and:
for the nonlinear case. By substituting (125,126) into (127) and writing out the tanh term,
you obtain consistently the derivative of (5) for the linear reaction mechanism, and (15) for the non-linear reaction mechanism.
In (127) the macroscopic kinetics (dissipation) is connected to the thermodynamic potential which yields the fluctuations. What are the advantages of this formulation? The term t(x) is the net flux of the deterministic kinetics, (125), and the derivative of the state function is the species specific affinity, (μx − μsx ) for the linear case or (μx − μ*x) for the non-linear case, the driving force for the reaction towards a stationary state. Thus we have a flux–driving force relation. Secondly, the formulation is symmetric with respect to t+(x) and t−(x), which is not the case with other formulations. Third, the state function determines the probability distribution of fluctuations in x from its value at the stationary state, see (30). Further, as we shall show shortly, the term D(x) is a measure of the strength of the fluctuations of the total number of reaction events (total in the forward and reverse reaction). We emphasize that (127) is non-linear and holds for arbitrarily large fluctuations. Expressions for different regimes of affinity and dissipation can be easily obtained [,,].
We return to the interpretation of the quantity D(x) in the fluctuation-dissipation relation, (127). Consider the concept of “reaction event” [,,], that is a generation or consumption of X in reactions (123) or (124). Let the total number of reaction events be labeled q(t) which occur in the time interval (0,t). Further we take q(t) to be a nondecreasing random function of time even at a stationary state and at equilibrium. The variable q is a discreet time scale; the chemical reaction is a clock, the time being measured by the number of reaction events. Since the reaction events are independent the distribution of reaction events obeys Poisson statistics []. The first and second moments of the Poisson distribution are:
The second of the equations (131) is similar to the Einstein equation for the mean square displacement of a Brownian particle in one dimension:
Here X is the displacement, in one variable, and D is the diffusion coefficient of the Brownian particles. Hence we can identify D(x) in (131) as a probability diffusion coefficient in concentration space. The dispersion of q, the second equation in (131), is proportional to D(x) and hence D(x) is a measure of the strength of the fluctuations of q at a stationary state. For further analysis of this subject see [].
Acknowledgements
A.F.V. acknowledges financial support from Spanish Ministry of Research and Innovation (MICINN) Grant MultiSysBio DPI2008-06880-C03-02. J.R. is grateful for partial support of this work by the National Science Foundation.
Appendix: Elementary Thermodynamics and Kinetics
Let us consider J coupled chemical reactions with L species, and let the stoichiometry of the jth reaction () be
. The stoichiometric coefficient
is negative for a reactant, zero for a catalyst, and positive for a product. We introduce progress variables ξj for each of the j reactions:
where ni denotes number of moles of species i, and the affinities Aj []:
expressed in terms of the chemical potentials
. The introduction of chemical potentials in chemical kinetics requires the assumption of local equilibrium, as explained in the previous subsection. With (A.2) we write the differential change in Gibbs free energy for the reactions:
For the jth reaction the kinetics can be written as
, where
are the reaction fluxes for this reaction step in the forward and reverse direction, respectively. Hence the affinities may be rewritten as
, which is easily obtained for any elementary reaction by writing out the
in terms of concentrations and the introduction of chemical potentials. The time rate of change of the Gibbs free energy is:
in which each term on the RHS is a product of the affinity of a given reaction times the rate of that reaction. The rate of change of ΔG is negative for every term until equilibrium is reached when ΔG of the reaction is zero. Hence ΔG is a Lyapunov function and provides an evolution criterion for the kinetics of the system in its approach to equilibrium. The form of (A.4) is the same as that of Boltzmann’s H theorem for the increase in entropy during an irreversible process in an isolated system []. For an isothermal system we have:
and hence
. At constant concentration (chemical potential), and hence pressure for each of the reservoirs we have the relation:
where
is the differential change in entropy of the surroundings due to (reversible) passage of heat from the system to the surroundings. Hence we may write:
that is the dissipation equals the product of T and the total rate of entropy production in the universe.
References and Notes
- Ross, J. Thermodynamics and Fluctuations Far from Equilibrium; Springer: Berlin, Germany, 2008. [Google Scholar]
- Van KampenN.G.Stochastic Processes in Physics and Chemistry; North-Holland: Amsterdam, The Netherlands, 1981.
- Ross, J.; Hunt, K.L.C.; Hunt, P.M. Thermodynamics far from equilibrium: Reactions with multiple stationary states. J. Chem. Phys. 1988, 88, 2719–2729. [Google Scholar] [CrossRef]
- Schlögl, F. On thermodynamics near a steady state. Z. Phys. 1971, 248, 446–458. [Google Scholar] [CrossRef]
- Evans, D.J.; Searles, D.J.; Williams, S.R. On the fluctuation theorem for the dissipation function and its connection with response theory. J. Chem. Phys. 2008, 128, 014504. [Google Scholar] [CrossRef] [PubMed]
- Glansdorff, P.; Nicolis, G.; Prigogine, I. The thermodynamic stability theory of non-equilibrium states. Proc. Natl. Acad. Sci. U. S. A. 1974, 71, 197–199. [Google Scholar] [CrossRef] [PubMed]
- Peng, B.; Hunt, K.L.C.; Hunt, P.M.; Suárez, A.; Ross, J. Thermodynamic and stochastic theory of nonequilibrium systems: Fluctuation probabilities and excess work. J. Chem. Phys. 1995, 102, 4548–4562. [Google Scholar] [CrossRef]
- Oppenheim, I.; Shuler, K.E.; Weiss, G.H. Stochastic Processes in Chemical Physics: The Master Equation; MIT: Cambridge, MA, USA, 1977. [Google Scholar]
- Gardiner, C.W. Handbook of Stochastic Methods; Springer: New York, NY, USA, 1990. [Google Scholar]
- Nicolis, G.; Babloyantz, A. Fluctuations in open systems. J. Chem. Phys. 1969, 51, 2632–2637. [Google Scholar] [CrossRef]
- Selkov, E.E. Self-oscillations in glycolysis. J. Biochem. 1968, 4, 79–86. [Google Scholar]
- Graham, R.; Tél, T. Nonequilibrium potential for coexisting attractors. Phys. Rev. A 1986, 33, 1322–1337. [Google Scholar]
- Maier, R.S.; Stein, D.L. Transition-rate theory for nongradient drift fields. Phys. Rev. Lett. 1992, 69, 3691–3695. [Google Scholar] [CrossRef] [PubMed]
- Crandall, M.G; Evans, L.C.; Lions, P.L. Some Properties of Viscosity Solutions of Hamilton‑Jacobi Equations. Trans. AMS 1984, 282, 487–502. [Google Scholar]
- Jauslin, H.R. Nondifferentiable potentials for nonequilibrium steady states. Physica A 1987, 144, 179–191. [Google Scholar] [CrossRef]
- Jauslin, H.R. Melnikov's criterion for nondifferentiable weak-noise potentials. J. Stat. Phys. 1986, 42, 573–585. [Google Scholar] [CrossRef]
- Freidlin, M.I.; Wentzell, A.D. Random Perturbations of Mechanical Systems; Springer: Berlin, Germany, 1984. [Google Scholar]
- Chu, X.; Ross, J.; Hunt, P.M.; Hunt, K.L.C. Thermodynamic and stochastic theory of reaction‑diffusion systems with multiple stationary status. J. Chem. Phys. 1993, 99, 3444–3454. [Google Scholar] [CrossRef]
- Hansen, N.F.; Ross, J. Lyapunov functions and relative stability in reaction-diffusion systems with multiple stationary states. J. Phys. Chem. 1996, 100, 8040–8043. [Google Scholar] [CrossRef]
- Hansen, N.F.; Ross, J. Relative stability of multiple stationary states related to fluctuations. J. Phys. Chem. 1998, 102, 7123–7126. [Google Scholar] [CrossRef]
- Glauber, R.J. Lectures in Theoretical Physics; Interscience Publishing: New York, NY, USA, 1959. [Google Scholar]
- Noyes, R.M.; Field, R.J.; Thompson, R.C. Mechanism of reaction of bromine (V) with weak one‑electron reducing agents. J. Am. Chem. Soc. 1971, 93, 7315–7316. [Google Scholar] [CrossRef]
- Foerster, Y.-X.; Zhang, J.; Ross, J. Experiments on relative stability in the bistable multivariable bromate-ferroin reaction. J. Phys. Chem. 1993, 97, 4708–4713. [Google Scholar] [CrossRef]
- Bar-Eli, K; Geiseler, W. Mixing and relative stabilities of pumped stationary states. J. Phys. Chem. 1981, 85, 3461–3468. [Google Scholar]
- Wolff, A.N.; Hjelmfelt, A.; Ross, J.; Hunt, P.M. Tests of thermodynamic theory of relative stability in one-variable systems. J. Chem. Phys. 1993, 99, 3455–3460. [Google Scholar] [CrossRef]
- Harding, R.H.; Ross, J. Experimental measurement of the relative stability of two stationary states in optically bistable ZnSe interference filters. J. Chem. Phys. 1990, 92, 1936–1946. [Google Scholar] [CrossRef]
- Lamb, H. Hydrodynamics, 6th ed.; Dover Publications: New York, NY, USA, 1945. [Google Scholar]
- Saltzman, B. Finite amplitude free convection as an initial value problem-I. J. Atmos. Sci. 1962, 19, 329–341. [Google Scholar] [CrossRef]
- Lorenz, E.N. Deterministic nonperiodic flow. J. Atmos. Sci. 1963, 20, 130–141. [Google Scholar] [CrossRef]
- Getling, A.V. Rayleigh-Bénard Convection. Structure and Dynamics; World Scientific Pub. Co.: London, UK, 1997. [Google Scholar]
- Glansdorff, P.; Prigogine, I. Thermodynamic Theory of Structure, Stability, and Fluctuations; Wiley: New York, NY, USA, 1971. [Google Scholar]
- Keizer, J. Statistical Thermodynamics of Nonequilibrium Processes; Springer-Verlag: New York, NY, USA, 1987. [Google Scholar]
- Attard, P. The second entropy: A general theory for non-equilibrium thermodynamics and statistical mechanics. Annu. Rep. Prog. Chem. Sect. C Phys. Chem. 2009, 105, 63–173. [Google Scholar] [CrossRef]
- Ronis, D.; Procaccia, I. Nonlinear resonant coupling between shear and heat fluctuations in fluids far from equilibrium. Phys. Rev. A 1982, 26, 1812–1815. [Google Scholar] [CrossRef]
- Fox, R.F. Gaussian stochastic processes in physics. Phys. Rep. 1978, 48, 179–283. [Google Scholar] [CrossRef]
- Velarde, M.G.; Chu, X.-L.; Ross, J. Toward a thermodynamic theory of hydrodynamics: The Lorenz equations. Phys. Fluids. 1994, 6, 550–563. [Google Scholar] [CrossRef]
- Zamora, M.; Rey de Luna, A. Energy of a system formed by a convective fluid and its container. J. Fluid Mech. 1986, 167, 427–437. [Google Scholar] [CrossRef]
- Law, B.M.; Sengers, J.V. Fluctuations in fluids out of thermal equilibrium. J. Stat. Phys. 1989, 57, 531–547. [Google Scholar] [CrossRef]
- Law, B.M.; Segrè, P.N.; Gammon, R.W.; Sengers, J.V. Light-scattering measurements of entropy and viscous fluctuations in a liquid far from thermal equilibrium. Phys. Rev. A 1990, 41, 816–824. [Google Scholar] [CrossRef] [PubMed]
- Segrè, P.N.; Gammon, R.W.; Sengers, J.V.; Law, B.M. Rayleigh scattering in a liquid far from thermal equilibrium. Phys. Rev. A 1992, 45, 714–724. [Google Scholar] [CrossRef] [PubMed]
- Li, W.B.; Segrè, P.N.; Gammon, R.W.; Sengers, J.V. Small-angle Rayleigh scattering from nonequilibrium fluctuations in liquids and liquid mixtures. Physica A 1994, 204, 399–435. [Google Scholar] [CrossRef]
- Suárez, A.; Ross, J. Thermodynamic and stochastic theory of coupled transport processes: Rayleigh scattering in a fluid in a temperature gradient. J. Phys. Chem. 1995, 99, 14854–14863. [Google Scholar] [CrossRef]
- Ross, J.; Chu, X.-L. Thermodynamic and stochastic theory for nonideal systems far from equilibrium. J. Chem. Phys. 1993, 98, 9765–9770. [Google Scholar] [CrossRef]
- Berry, R.S.; Rice, S.A.; Ross, J. Physical Chemistry, 2nd ed.; Oxford University Press: New York, NY, USA, 2000. [Google Scholar]
- Keizer, J.; Chang, O.-K. The nonequilibrium electromotive force. I. Measurements in a continuously stirred tank reactor. J. Chem. Phys. 1987, 87, 4064–4073. [Google Scholar]
- Keizer, J. The nonequilibrium electromotive force. II. Theory for a continuously stirred tank reactor. J. Chem. Phys. 1987, 87, 4074–4087. [Google Scholar]
- Keizer, J. Thermodynamics at isothermal, isobaric steady states: vapor pressure, colligative properties, and the electromotive force. J. Phys. Chem. 1989, 93, 6939–6943. [Google Scholar] [CrossRef]
- Keizer, J. Heat, work, and the thermodynamic temperature at non‑equilibrium steady states. J. Chem. Phys. 1985, 82, 2751–2771. [Google Scholar] [CrossRef]
- Field, R.J.; Burger, M. Oscillations and Traveling Waves in Chemical Systems; Wiley: New York, NY, USA, 1985. [Google Scholar]
- Hjelmfelt, A.; Ross, J. Electrochemical experiments on thermodynamics at nonequilibrium steady states. J. Phys. Chem. 1994, 98, 9900–9902. [Google Scholar] [CrossRef]
- Hjelmfelt, A.; Ross, J. Kinetic and thermodynamic information derived from electrochemical measurements on stationary states. J. Phys. Chem. B 1998, 102, 3441–3444. [Google Scholar] [CrossRef]
- Ross, J.; Hunt, K.L.C.; Vlad, M.O. Determination of thermodynamic and stochastic potentials in non-equilibrium system from macroscopic measurements. J. Phys. Chem. A 2002, 106, 10951–10960. [Google Scholar] [CrossRef]
- Ross, J.; Hunt, K.L.C.; Hunt, P. Thermodynamics and stochastic theory for non-equilibrium systems with multiple reactive intermediates: The concept and role of excess work. J. Chem. Phys. 2002, 96, 618–629. [Google Scholar] [CrossRef]
- Kramer, J.; Ross, J. Stabilization of unstable states, relaxation, and critical slowing down in a bistable system. J. Chem. Phys. 1985, 83, 6234–6241. [Google Scholar] [CrossRef]
- Prigogine, I. Moderation et transformations irreversibles des systemes ouverts. Bull. Cl. Sci., Acad. R. Belg. 1945, 31, 600–606. [Google Scholar]
- Ross, J.; Vlad, M.O. Exact solutions for the entropy production rate of several irreversible processes. J. Phys. Chem. A 2005, 109, 10607–10612. [Google Scholar] [CrossRef] [PubMed]
- Martyushev, L.M.; Seleznev, V.D. Maximum entropy production principle in physics, chemistry, and biology. Phys. Rep. 2006, 426, 1–45. [Google Scholar]
- Lazar, J.G.; Ross, J. Changes in mean concentration, phase shifts, and dissipation in a forced oscillatory reaction. Science 1990, 247, 189–192. [Google Scholar] [CrossRef] [PubMed]
- Lax, M. Fluctuations in a nonequilibrium stable state. Rev. Mod. Phys. 1960, 32, 25–64. [Google Scholar] [CrossRef]
- Lax, M. Classical noise III: Nonlinear markoff processes. Rev. Mod. Phys. 1966, 38, 359–379. [Google Scholar] [CrossRef]
- Lax, M. Classical noise IV: Langevin methods. Rev. Mod. Phys. 1966, 38, 541–566. [Google Scholar] [CrossRef]
- Reif, F. Fundamentals of Statistical and Thermal Physics; McGraw-Hill: New York, NY, USA, 1965; Chapters 1, 15. [Google Scholar]
- Chandrasekhar, S. Stochastic Problems in Physics and Astronomy. Rev. Mod. Phys. 1943, 15, 1–89. [Google Scholar] [CrossRef]
- Vlad, M.O.; Ross, J. Fluctuation-dissipation relations for chemical systems far from equilibrium. J. Chem. Phys. 1994, 100, 7268–7278. [Google Scholar] [CrossRef]
- Vlad, M.O.; Ross, J. Random paths and fluctuation-dissipation dynamics for one-variable chemical systems far from equilibrium. J. Chem. Phys. 1994, 100, 7279–7294. [Google Scholar] [CrossRef]
- Vlad, M.O.; Ross, J. Thermodynamic approach to nonequilibrium chemical fluctuations. J. Chem. Phys. 1994, 100, 7295–7309. [Google Scholar] [CrossRef]
- Nicolis, G.; Prigogine, I. Self-organization in Nonequilibrium Systems; Wiley: New York, NY, USA, 1977. [Google Scholar]
- Tolman, R.C. The Principles of Statistical Mechanics; Oxford University Press: London, UK, 1938. [Google Scholar]
© 2010 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).