Abstract
The dark energy issue is attracting the attention of an increasing number of physicists all over the world. Among the possible alternatives to explain what as been named the “Mystery of the Millennium” are the so-called Modified Theories of Gravity. A crucial test for such models is represented by the existence and (if this is the case) the properties of their black hole solutions. Nowadays, to our knowledge, only two non-trivial, static, spherically symmetric, solutions with vanishing cosmological constant are known by Barrow & Clifton (2005) and Deser, Sarioglu & Tekin (2008). The aim of the paper is to discuss some features of such solutions, with emphasis on their thermodynamic properties such as entropy and temperature.
1. Introduction
Since the discovery by Riess and Perlmutter and respective collaborators [1,2] that the universe is—against any previous belief—in an accelerating epoch, the dark energy issue has become the “Mystery of the Millennium” [3]. Today, dark energy is probably the most ambitious and tantalizing field of research because of its implications in fundamental physics. That the dark energy fluid has an equation of state index w very close to minus one represents an important point in favour of those who propose to explain dark energy in terms of a cosmological constant, Λ. Still, a non-vanishing cosmological constant does not exhaust the range of models that have been proposed so far in order to solve the aforementioned issue. This is justified, in part, by the whole sort of well-known problems raised by the existence of a strictly positive cosmological constant.
On the other hand, it is well accepted the idea according to which general relativity is not the ultimate theory of gravity, but an extremely good approximation valid in the present day range of detection. It basically comes from this viewpoint the input to so-called modified theories of gravity which nowadays enjoy great popularity (cf. [4,5,6,7,8,9,10] for a review). Without any claim for unification, such models propose to change the Einstein–Hilbert Lagrangian to a more general form able to reproduce the same general relativity tests on solar distance scales and further justify both inflationary and current acceleration of the universe.
The original idea of introducing a correction to the Einstein–Hilbert action in the form of was proposed long time ago by Starobinsky [11] in order to solve many of the problems left open by the so-called hot universe scenario. This, in turn, had the consequence of introducing an accelerating expansion in the primordial universe, so that the Starobinsky model can be considered as the first inflationary model. The recent interest in models of modified gravity instead, grew up in cosmology with the appearance of [12,13,14].
The mathematical structure of -theories of gravity and their physical properties (e.g., asymptotic flatness, renormalizability, unitarity) have been an exciting field of research over the last four decades; a small but significant trace of which is represented by [15,16,17,18,19,20,21].
The arena of models is in principle infinite while departures from Einstein’s theory are most of the times all but minimal. Of crucial interest is, of course, the existence and, if this is the case, the properties of black holes in modified gravities. It is quite easy to find the conditions allowing the existence of de Sitter-Schwarzschild black holes (see, for example [22] for modified gravity, [23] for Gauss-Bonnet modified gravity, and [24,25,26,27] for related topics).
Here, we are interested in non-trivial and static black holes solutions. However, the number of exact non-trivial static black hole solutions so far known in modified theories of gravity is extremely small: just two, both spherically symmetric. They have been obtained by Barrow & Clifton (2005) in a modified theory of the type with δ a small real parameter; and by Deser, Sarioglu & Tekin (2008) by adding to Einstein–Hilbert Lagrangian a non-polynomial contribution of the type , with being the Weyl tensor.
These black hole solutions are not expected to share the same laws of their Einsteinian counterparts: for this reason, following [31], we shall refer to them as dirty black holes. Some of the physical quantities one would like to address to dirty black holes are their mass, the horizon entropy, their temperature and so on. Thanks to the large amount of work carried over in the last decade, we can firmly say that the issue of entropy and temperature of dirty black holes represents a well posed problem [30]; a nice and recent review on the entropy issue associated with gravity models is [32], where a complete list of references can be found. Here, we only mention [22,23,33]. However, with regard to the mass issue, all considerations still lay on a much more precise ground.
In the present paper we shall work in units of . The organization is as follows: in Section 2 we review the Deser-Sarioglu-Tekin solution and compute entropy and temperature for such black hole; in Section 3 we do the same for the Clifton-Barrow solution. In the Conclusions we address the difficulties faced trying to define meaningfully the concept of mass for dirty black holes.
2. The Deser-Sarioglu-Tekin Solution
Let us start by recapitulating the Deser-Sarioglu-Tekin solution [28]. The authors start from the action
where σ is a real parameter and is the trace of the Weyl tensor squared. Looking for static, spherically symmetric solutions of the type,
the action (1) becomes
Imposing the stationarity condition gives the equations of motion for the unknown functions and .
According to σ, the space of solutions of (4) can be different, in particular:
- corresponds to Einstein-Hilbert action. In fact, and and for positive constants, the Schwarzschild solution of general relativity is recovered;
- : only the trivial, physically unacceptable, solution exists;
- : then, for some positive constants and :
- In all other cases, the general solution to (4) turns out to befor some positive constants .
In order to treat (6), let us introduce the parameter so that the metric becomes
For , or , for all r, that is, the parameter region needs to be excluded to preserve the metric signature. As regard the asymptotic behaviour of (7), we see that:
- for or , we have that and as ;
- for or , we have that and as .
Looking at the solution (7), we see that the hypersurface defined by the condition behaves as a Killing horizon with respect to the timelike Killing vector field . To prove this, let us define a complex null tetrad for the metric (7) according to the following rules [35]:
satisfy the list of conditions to form a complex null tetrad. As a consequence, for example, the metric can be re-written as . The null expansions are, by definition,
Thus, in-going light rays always converge ( for all ); out-going light rays, instead, focus inside the horizon ( as ), diverge outside it ( as ) and run in parallel at the horizon (). When they are slightly perturbed in the in-direction (that is, along n), the out-going null ray is absorbed inside the horizon as it is confirmed by the fact that the in-going Lie derivative is everywhere negative. Computing the convergence () and the shear () of the null congruences at the horizon we can immediately check they vanish, as expected for any Killing horizon. The Killing surface gravity
turns out to depend by the normalization of the Killing vector . In order to fix λ, we may implement the conical singularity method. To this aim, let us start by the Euclidean metric
where we suppose that both and have a structure like
with regular for . may be identified with some type of horizon close to which we are interested in the behaviour of the metric.
with ζ a constant we are going to fix very soon.
Let us choose , the Euclidean metric takes the form
Equation (17) shows that close to the horizon ( or ) the metric factorizes into : being the metric of flat two-dimensional metric on behalf of identifying x with the polar distance and τ with the angular coordinate. However, is regular if and only if
or, in other words,
β representing the (unique) τ-period which allows to impose a smooth flat metric on .
- is s.t. on the horizon
- The normalization conditions hold
- All the other scalar products vanishes.
In Quantum Field Theory, the KMS propagator exhibits a periodicity in time when the system is at finite temperature. The period of the compactified time, β, is directly related to the temperature of the system in Lorentzian signature, through ()
If we assume the standard Hawking temperature formula, , the period β in (19) can be re-written according to
which for the metric (2) reads . Comparison between the latter and (12) fixes the normalization of the Killing vector to be . What is most important to us is that , so that we may conclude that the Killing horizon is of the bifurcate type. We may anticipate that this is not the unique surface gravity which can defined for a generic spherically symmetric static black hole. For the sake of simplicity, we shall postpone this discussion to the Conclusion an alternative definition.
Given these preliminary remarks, we are now in the position to apply Wald’s argument [30] to derive the black hole entropy associated to the Killing horizon of the solution (7).
Following [30,31,34], the explicit calculation of the black hole entropy of the horizon is provided by the formula
where is the Lagrangian density of any general theory of gravity, in the specific case,
The hatted variable, , is the binormal vector to the (bifurcate) horizon: it is antisymmetyric under the exchange of and normalized so that . For the metric (2), the binormal turns out to be
The induced volume form on the bifurcate surface , constant is represented by , where, for any spherically symmetric metric, and the angular variables run over the intervals , , respectively.
Finally, the superscript indicates that the partial derivative is evaluated on shell. The variation of the Lagrangian density with respect to is performed as if and the metric are independent.
In the specific case, Equation (22) becomes
with the area of the black hole horizon. Let us compute the Lagrangian variation,
Using the fact that , we get,
In the specific,
Since in general, tr , for and
for the metric (2), we may write
Taking together (25), (28) and (30), for both the solutions (5) and (7), we finally have that the horizon entropy for the Deser et al. black hole is
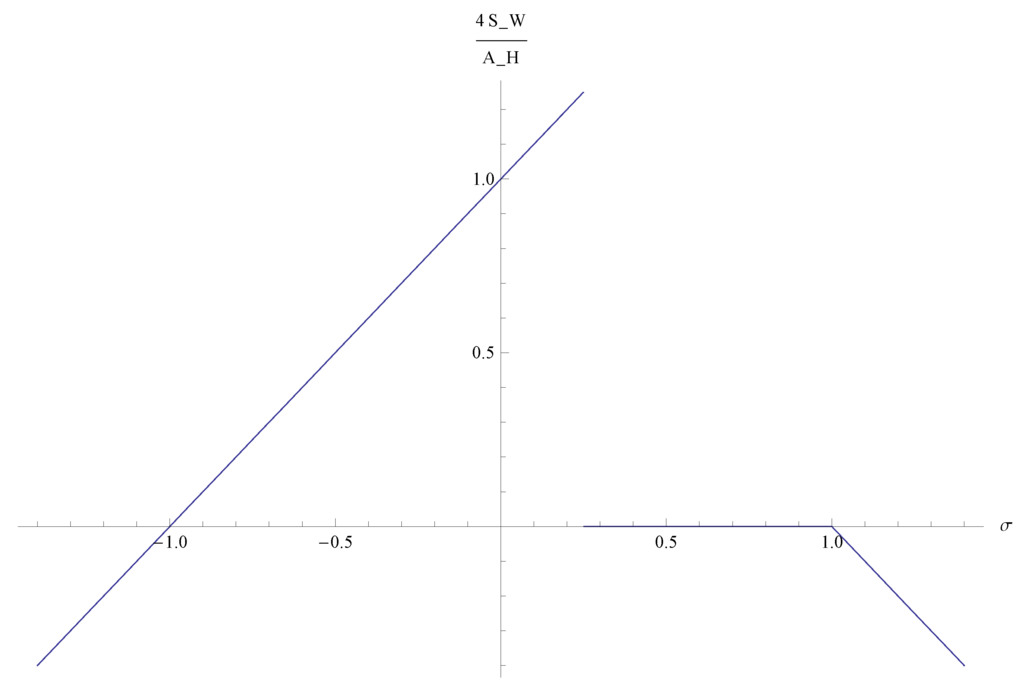
Figure 1.
Wald’s entropy in units of versus σ parameter for the Deser et al. black hole.
According to (31) the entropy predicted by Wald’s formula restricts considerably the space of the σ parameter with respect to our previous considerations. In fact, as shown by Figure 1, the entropy of the black hole is positive only as far as . For , the entropy vanishes suggesting (but we leave this to the level of a speculation) that, for this value of σ, the number of microscopic configurations realizing the black hole is only one. For , the entropy of Deser’s black hole is always smaller than its value in general relativity. Notice also that for , the entropy function is continuous even if the black hole metric changes. However, as pointed out above, such solution is not physical because of its pathological asymptotic behaviour.
En passant, we notice how Wald’s entropy could be computed equally well following [34]. Introducing a new radial co-ordinate ρ such that
the metric (7) transforms to
with
This time, Wald’s entropy (31) will follow from
3. The Clifton-Barrow Solution
The Clifton-Barrow solution starts from the following modified-gravity action (evaluated in the vacuum space):
Here, δ is a constant and χ is a dimensional parameter. We can choose . When , we recover the Hilbert-Einstein action of General Relativity.
Taking the variation of the action with respect to the metric , we obtain:
Looking for static, spherically symmetric metric of the type,
we find the Clifton-Barrow solution of Equation (37):
C and are dimensional constants.
In a similar way with respect to the previous section, we can see that the hypersurface , for which and , determines an event horizon, and, since , the Clifton-Barrow metric is a Black Hole solution.
According to Equation (21), we recover the Killing-horizon surface gravity
which can be used to find the Hawking temperature .
As a last remark, we are able to derive the Black Hole entropy associated to the event horizon of the Clifton-Barrow solution. For modified gravity -theories (where the gravity lagrangian is a function of the Ricci scalar only), it is easy to see that the Wald formula in Equation (22) is simplified as
In our case, , so we find:
proved by the fact that on the Clifton-Barrow solution .
In order to have the positive sign of entropy, we must require . The solutions with are unphysical, whereas for we find the result of General Relativity.
4. Conclusions
Despite the great success enjoyed by modified theories of gravity, we have seen that only two non-trivial, static, spherically symmetric, vacuum black-hole solutions are known so far. Their thermodynamic properties have been taken into considerations. We have shown that the solutions we considered in Section 2 and Section 3 possess a Killing horizon with a Killing vector associated which cannot be defined unambiguously due to the fact that the spacetimes are not asymptotically flat. What is most important, however, is that we have been able to deduce a non-vanishing Killing temperature for such horizons. Of course, this is not the only temperature we can define for such horizons. As shown in [36], in spherically symmetric spacetimes always exists a Kodama vector field K whose defining property is that . The Kodama vector turns out to be time/light/space-like in untrapped/marginal/trapped spacetime regions; it gives a preferred flow of time generalizing the Killing time flow familiar to static cases; it makes possible to define an invariant particle energy even in non-stationary spacetimes and it associates a Kodama-Hayward surface gravity to any future outer trapping horizon [37]. In static, asymptotically flat spacetimes, both the Killing and Kodama vectors coincide, so that they give rise to the same concepts of energy and temperature. In static, non-asymptotically flat spaces, they are both ambiguous and can differ by normalizations, but nonetheless the ratio “energy/surface gravity” remains fixed [38,39,40]. This means that as far as the Killing temperature associated with the black holes mentioned here is non-vanishing, also their Kodama-Hayward temperature will be so. On the other hand, that the horizons we are concerned are of the bifurcate type means we are in Wald’s hypothesis in order to compute their entropy. In this sense, equations (31–43) and Figure 1 represent our main results.
To complete the picture of thermodynamic features of black holes in modified theories of gravity, it would be necessary to formulate a consistent definition of their mass. As it is well known, in modified theories of gravity the first law of thermodynamics generally requires a work term even in vacuum solutions something which makes the first law useless in the situations at hand. Quite recently some attempts have been put forward in order to answer the question, but only for asymptotically flat spacetimes, cf. [41,42].
In principle, a powerful tool to evaluate the black hole mass in a theory of the type is represented by the so-called Brown-York quasi-local mass [43,44,45]. In static, spherically symmetric spacetimes where the metric can be put in the form (2) the BY mass reads
with an arbitrary function which determines the zero of the energy for a background spacetime and r is the radius of the spacelike hypersurface boundary. When the spacetime is asymptotically flat, the ADM mass M is the determined in (44) in the limit . If no cosmological horizon is present, the large r limit of (44) is used to determine the mass. However, this approach is known to fail whenever the matter action (i.e., what we have represented with few line above) contains derivatives of the metric as it is the case of the Deser et al. action, (1).
Another quasi-local energy definition well known in general relativity and fully employed in spherical symmetry is the so-called Misner-Sharp energy [46] which can be proved to be the conserved charge generated by the Kodama vector K [47,48]. In the last few years, different authors have tried to generalize the Misner-Sharp energy definition to wider classes of gravity theories [49,50]. But even if Cai et al. provide a general formula for the generalized MS energy in gravity, this does not produce any explicit, useful, result for the Clifton-Barrow black hole.
In conclusion, we have succeeded in computing two of three most relevant thermodynamic parameters (entropy and temperature) of the known black hole solutions in modified theories of gravity; the mass resisting up to now to any attack led by conventional methods.
Acknowledgements
E.B. thanks the members of the Group of Theory of Gravity in the Department of Physics of the University of Trento where most of this work has been done.
References
- Riess, A.G.; Filippenko, A.V.; Challis, P.; Clocchiatti, A.; Diercks, A.; Garnavich, P.M.; Gilliland, R.L.; Hogan, C.J.; Jha, S.; Kirshner, R.P.; Leibundgut, B.; Phillips, M.M.; Reiss, D.; Schmidt, B.P.; Schommer, R.A.; Smith, R.S.; Spyromilio, J.; Stubbs, C.; Suntzeff, N.b.; Tonry, J. Observational evidence from supernovae for an accelerating universe and a cosmological constant. Astron. J. 1998, 116, 1009. [Google Scholar] [CrossRef]
- Perlmutter, S.; Aldering, G.; Goldhaber, G.; Knop, R.A.; Nugent, P.; Castro, P.G.; Deustua, S.; Fabbro, S.; Goobar, A.; Groom, D.E.; Hook, I.M.; Kim, A.G.; Kim, M.Y.; Lee, J.C.; Nunes, N.J.; Pain, R.; Pennypacker, C.R.; Quimby, R.; Lidman, C.; Ellis, R.S.; Irwin, M.; McMahon, R.G.; Ruiz-Lapuente, P.; Walton, N.; Schaefer, B.; Boyle, B.J.; Filippenko, A.V.; Matheson, T.; Fruchter, A.S.; Panagia, N.; Newberg, H.J.M.; Couch, W.J. Measurements of Ω and Λ from 42 high-redshift supernovae. Astrophys. J. 1999, 517, 565. [Google Scholar] [CrossRef]
- Padmanabhan, T. Dark energy: Mystery of the millennium. AIP Conf. Proc. 2006, 861, 179. [Google Scholar]
- Sahni, V.; Starobinsky, A.A. The Case for a positive cosmological Lambda term. Int. J. Mod. Phys. 2000, D9, 373. [Google Scholar] [CrossRef]
- Carroll, S.M. The Cosmological constant. Living Rev. Rel. 2001, 4, 1. [Google Scholar] [CrossRef]
- Peebles, P.J.E.; Ratra, B. The cosmological constant and dark energy. Rev. Mod. Phys. 2003, 75, 559. [Google Scholar] [CrossRef]
- Padmanabhan, T. Cosmological constantthe weight of the vacuum. Phys. Rept. 2003, 380, 235. [Google Scholar] [CrossRef]
- Copeland, E.; Sami, M.; Tsujikawa, S. Dynamics of dark energy. Int. J. Mod. Phys. 2006, D15, 1753. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D. Introduction to modified gravity and gravitational alternative for dark energy. Int. J. Geom. Meth. Mod. Phys. 2007, 4, 115. [Google Scholar] [CrossRef]
- Sotiriou, T.P.; Faraoni, V. f(R) Theories Of gravity. Rev. Mod. Phys. 2010, 82, 451. [Google Scholar] [CrossRef]
- Starobinsky, A.A. A new type of isotropic cosmological models without singularity. Phys. Lett. 1980, B91, 99. [Google Scholar] [CrossRef]
- Carroll, S.M.; Duvvuri, V.; Trodden, M.; Turner, M.S. Is cosmic speed-up due to new gravitational physics? Phys. Rev. 2004, D70, 043528. [Google Scholar] [CrossRef]
- Capozziello, S.; Carloni, S.; Troisi, A. Quintessence without scalar fields. arXiv astro-ph/0303041.
- Capozziello, S.; Cardone, V.F.; Troisi, A. Reconciling dark energy models with f(R) theories. Phys. Rev. 2005, D71, 043503. [Google Scholar]
- Utiyama, R.; DeWitt, B.S. Renormalization of a classical gravitational field interacting with quantized matter fields. J. Math. Phys. 1962, 3, 608. [Google Scholar] [CrossRef]
- Fradkin, E.S.; Vilkovisky, G.A. S Matrix for Gravitational Field. II. Local measure; General relations; Elements of renormalization theory. Phys. Rev. 1973, D8, 4241. [Google Scholar]
- Fradkin, E.S.; Tseytlin, A.A. Renormalizable asymptotically free quantum theory of gravity. Nucl. Phys. 1982, B201, 469. [Google Scholar] [CrossRef]
- Stelle, K.S. Renormalization of higher-derivative quantum gravity. Phys. Rev. 1977, D 16, 953. [Google Scholar] [CrossRef]
- Avramidi, I.G.; Barvinsky, A.O. Asymptotic freedom in higher derivative quantum gravity. Phys. Lett. 1985, B159, 269. [Google Scholar] [CrossRef]
- Avramidi, I.G. Asymptotic behavior of the quantum theory of gravity with higher order derivatives. Yad. Fiz. 1986, 44, 255. [Google Scholar]
- Hawking, S.W.; Hertog, T. Living with ghosts. Phys. Rev. 2002, D65, 103515. [Google Scholar] [CrossRef]
- Cognola, G.; Elizalde, E.; Nojiri, S.; Odintsov, S.D.; Zerbini, S. One-loop f(R) gravity in de Sitter universe. JCAP 2005, 0502, 010. [Google Scholar] [CrossRef]
- Cognola, G.; Elizalde, E.; Nojiri, S.; Odintsov, S.D.; Zerbini, S. Dark energy in modified Gauss-Bonnet gravity: Late-time acceleration and the hierarchy problem. Phys. Rev. 2006, D73, 084007. [Google Scholar] [CrossRef]
- Oliva, J.; Ray, S. A new cubic theory of gravity in five dimensions: Black hole, Birkhoff’s theorem and C-function. arXiv 1003.4773. [CrossRef]
- Oliva, J.; Ray, S. A classification of six derivative lagrangians of gravity and static spherically symmetric solutions. [CrossRef]
- Cai, Y.F.; Easson, D.A. Black holes in an asymptotically safe gravity theory with higher derivatives. JCAP 2010, 1009, 002. [Google Scholar] [CrossRef]
- Berezhiani, Z.; Comelli, D.; Nesti, F.; Pilo, L. Exact spherically symmetric solutions in massive gravity. JHEP 2008, 0807, 130. [Google Scholar] [CrossRef]
- Deser, S.; Sarioglu, O.; Tekin, B. Spherically symmetric solutions of Einstein + non-polynomial gravities. Gen. Rel. Grav. 2008, 40, 1. [Google Scholar] [CrossRef]
- Clifton, T.; Barrow, J.D. The power of general relativity. Phys. Rev. 2005, D72, 103005. [Google Scholar] [CrossRef]
- Wald, R.M. Black hole entropy is the Noether charge. Phys. Rev. 1993, D48, 3427. [Google Scholar] [CrossRef]
- Visser, M. Dirty black holes: Entropy as a surface term. Phys. Rev. 1993, D48, 5697. [Google Scholar] [CrossRef]
- Faraoni, V. Black hole entropy in scalar-tensor and f(R) gravity: An overview. Entropy 2010, 12, 1246. [Google Scholar] [CrossRef]
- Brevik, I.H.; Nojiri, S.; Odintsov, S.D.; Vanzo, L. Entropy and universality of Cardy-Verlinde formula in dark energy universe. Phys. Rev. 2004, D70, 043520. [Google Scholar] [CrossRef]
- Brustein, R.; Gorbonos, D.; Hadad, M. Wald’s entropy is equal to a quarter of the horizon area in units of the effective gravitational coupling. Phys. Rev. 2009, D79, 044025. [Google Scholar] [CrossRef]
- Frolov, V.P.; Novikov, I.D. Black hole physics: Basic concepts and new developments; Kluwer Academic: Dordrecht, Netherlands, 1998. [Google Scholar]
- Kodama, H. Conserved energy flux for the spherically symmetric system and the back reaction problem in the black hole evaporation. Prog. Theor. Phys. 1980, 63, 1217. [Google Scholar] [CrossRef]
- Hayward, S.A. Unified first law of black-hole dynamics and relativistic thermodynamics. Class. Quant. Grav. 1998, 15, 3147. [Google Scholar] [CrossRef]
- Di Criscienzo, R.; Nadalini, M.; Vanzo, L.; Zerbini, S.; Zoccatelli, G. On the Hawking radiation as tunnellingfor a class of dynamical black holes. Phys. Lett. 2007, B657, 107. [Google Scholar] [CrossRef]
- Hayward, S.A.; Di Criscienzo, R.; Vanzo, L.; Nadalini, M.; Zerbini, S. Local Hawking temperature for dynamical black holes. Class. Quant. Grav. 2009, 26, 062001. [Google Scholar] [CrossRef]
- Di Criscienzo, R.; Hayward, S.A.; Nadalini, M.; Vanzo, L.; Zerbini, S. Hamilton–Jacobi tunneling method for dynamical horizons in different coordinate gauges. Class. Quant. Grav. 2010, 27, 015006. [Google Scholar] [CrossRef]
- Deser, S.; Tekin, B. New energy definition for higher curvature gravities. Phys. Rev. 2007, D75, 084032. [Google Scholar] [CrossRef]
- Abreu, G.; Visser, M. Tolman mass, generalized surface gravity, and entropy bounds. Phys. Rev. Lett. 2010, 105, 041302. [Google Scholar] [CrossRef] [PubMed]
- Brown, J.D.; York, J.W. Quasilocal energy and conserved charges derived from the gravitational action. Phys. Rev. 1993, D47, 1407. [Google Scholar]
- Brown, J.D.; Creighton, J.; Mann, R.B. Temperature, energy and heat capacity of asymptotically anti-de Sitter black holes. Phys. Rev. 1994, D50, 6394. [Google Scholar] [CrossRef]
- Chan, K.C.K.; Horne, J.H.; Mann, R.B. Charged dilaton black holes with unusual asymptotics. Nucl. Phys. 1995, B447, 441. [Google Scholar] [CrossRef]
- Misner, C.W.; Sharp, D.H. Relativistic equations for adiabatic, spherically symmetric gravitational collapse. Phys. Rev 1964, 136, B571. [Google Scholar] [CrossRef]
- Hayward, S.A. Quasilocal gravitational energy. Phys. Rev. 1994, D49, 831. [Google Scholar] [CrossRef]
- Hayward, S. A. Gravitational energy in spherical symmetry. Phys. Rev. 1996, D53, 1938. [Google Scholar] [CrossRef]
- Maeda, H.; Nozawa, M. Generalized Misner-Sharp quasi-local mass in Einstein-Gauss-Bonnet gravity. Phys. Rev. 2008, D77, 064031. [Google Scholar]
- Cai, R.G.; Cao, L.M.; Hu, Y.P.; Ohta, N. Generalized Misner-Sharp energy in f(R) gravity. Phys. Rev. 2009, D80, 104016. [Google Scholar] [CrossRef]
© 2010 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/.)