There are several arguments indicating that our derivation of the EE of 2D AdS black holes could be extended to black holes in 3D AdS spacetime,
i.e. to the BTZ black hole. Pure gravity in three spacetime dimensions has the same degrees of freedom (DOF) of 2D dilaton gravity, that is only global DOFs and no propagating gravitons. Moreover, 2D AdS dilaton gravity can be considered as a circular symmetric dimensional reduction of 3D AdS gravity with the dilaton parametrizing the radius of the transverse circle. The 2D AdS black hole discussed in
Section 3 of this paper can be obtained as dimensional reduction of the BTZ black hole with vanishing angular momentum
J. The thermodynamic parameters (mass, temperature and entropy) characterizing the
BTZ black hole match exactly those pertinent to the 2D AdS black hole, given by Equation (
10), once one expresses the 3D Newton constant
in terms of the 2D Newton constant
and of the de Sitter length
ℓ.
In the case of 2D AdS gravity, the dual theory has the form of a chiral CFT, whereas in the 3D case, owing to different boundary conditions, the dual theory is a 2D CFT with both left and right movers.
In this section of the paper we investigate quantum entanglement in the context of 3D AdS gravity, in particular the Bañados-Teitelboim-Zanelli (BTZ) black hole, using the AdS/CFT correspondence. We will tackle the problem using a standard method for studying correlations in QFT: we introduce in the boundary 2D CFT two external length-scales, a thermal wavelength (with T temperature of the CFT) and a spatial length γ, which is the measure of the observable spatial region of our 2D universe. Varying β we can probe thermal correlations of the CFT at different energy scales, whereas varying γ we can probe the spatial correlations at different length scales. The EE of a QFT gives information about the spatial correlations of the theory. It follows that the EE of a 2D CFT, which is the holographic dual of 3D gravity, should contain information about bulk quantum gravity correlations.
We will show that the AdS/CFT correspondence, and in particular the UV/IR relation, allows us to identify in a natural way
β and
γ in terms of the two fundamental bulk length-scales, the horizon of the BTZ black hole
and the AdS length
ℓ. This enables us, using the expression (
5), (
6), (
7) for the EE of 2D CFTs and modular symmetry, to associate a “holographic” EE to regularized 3D AdS, to the BTZ black hole and to 3D AdS with conical singularities.
4.1. AdS Gravity and Dual CFT
Classical, pure AdS
gravity is described by the action
where
ℓ is the de Sitter length and
is the 3D Newton constant. The exact form of the 2D CFT dual to 3D AdS gravity still remains a controversial point [
55,
56,
57]. However, in the large
N regime (central charge
),
i.e. in the region of validity of the gravity description, we know that the dual CFT has central charges [
58]
AdS
classical gravity allows for three kinds of spacetime configurations. These are solutions of the action (
17) and can be classified in terms of orbits (elliptic, hyperbolic, parabolic) of the SL
group manifold [
55,
59,
60]. The solutions corresponding to elliptic orbits can be written as
where
,
,
and
is a constant. The corresponding 3D Euclidean space has a contractible cycle in the spatial
ϕ-direction. For generic values of
we have therefore a conical singularity in this direction. Only for
the conical singularity disappears and the manifold becomes a nonsingular 3D AdS space at finite temperature
. The conformal boundary of the 3D spacetime is a torus with cycles of length
β and
. Correspondingly, the dual CFT will live in the torus
. The CFT on the cylinder
discussed in
Section 2.2 can be obtained in the limit
. This corresponds to consider
and
.
The classical solutions of 3D gravity corresponding to hyperbolic orbits of SL
are
Now the 3D Euclidean manifold has a contractible cycle in the
t-direction. For generic values of
β and
we have therefore a conical singularity in this direction. Only for
, where
is the inverse Hawking temperature
the conical singularity can be removed and the space describes the Euclidean BTZ black hole. The black hole has horizon radius
, and mass and Bekenstein-Hawking entropy given by
Also in this case the conformal boundary of the 3D spacetime is the torus with cycles of length
and
, and the dual CFT will live on
. The CFT on the cylinder
C discussed in
Section 2.2 can be obtained in the limit
. This corresponds to consider a CFT at finite temperature,
, with noncompact spacelike dimension
. In terms ofthe 3D bulk theory this corresponds to a macroscopic black hole with
.
The separating element between the two classes of solutions discussed above corresponds to parabolic orbits of SL
,
The solution can be seen as the
ground state of the BTZ black hole,
i.e. the
solution.
For
the solution (
19) has a conical singularity not shielded by an event horizon [
59,
60]. The conical singularity can also be thought of as originated by a pointlike source of mass
m. In the spectrum of AdS
gravity these solutions are located between the NS vacuum,
, and the RR vacuum,
. Therefore we will consistently take
.
If we rescale the coordinates in Equation (
19),
the metric becomes
The previous expression describes thermal AdS
in global coordinates but, owing to the rescaling of the coordinates, we have now
, with
. The spacetime has a conical singularity originated by a deficit angle
, where we have introduced
is the analogous of the inverse Hawking temperature
and characterizes the conical singularity. In the case of solution (
20), setting
eliminates the conical singularity, whereas for solution (
19) we get a regular manifold (AdS
at finite temperature) for
.
In order to find the holographic EE of the solution (
19), (
20) and (
23), we have to discuss first the modular symmetry of the 2D CFT dual to 3D AdS gravity.
4.2. Modular Invariance
It is well known that the partition function of a 2D CFT on the complex has to be invariant for transformation of the modular group PSL
where
are integers satisfying
,
is the modular parameter of the torus and
are the periods of the torus. For simplicity we will take
real and
purely imaginary. We are mainly interested in the modular transformation of the torus
3D spaces which are asymptotically AdS are locally equivalent. The asymptotic form of the coordinate transformations mapping the various spaces can be used to map one into the other the tori describing the associated conformal boundaries. For our discussion the relevant elements are the Euclidean BTZ black hole at Hawking temperature
, AdS
space with deficit angle
and AdS
at finite temperature
. It will turn out that the boundary tori associated with these three spaces are related by modular transformations of the torus.
Let us briefly review the well-known duality between the BTZ black hole and AdS
at finite temperature [
34,
61]. To this purpose, we use the fact that the Euclidean BTZ solution (
20) with periodicity
can be mapped by a diffeomorphism into AdS
in Poincaré coordinates
where
z is a complex coordinate.
In the asymptotic
(
) region the map between the BTZ black hole and AdS
in Poincaré coordinates is
In order to have a natural periodicity, we introduce a new complex variable
wso that
. One can now easily realize that the asymptotic conformal boundary of the BTZ black hole is a complex torus with metric
. The periodicity of the imaginary (
) and real (
) part of
w are determined by the periodicity of
:
. The modular parameter
of the torus is therefore
Consider now Euclidean AdS
at finite temperature, described by the metric (
25) with periodicity
and
. The
asymptotic form of the map between AdS
at finite temperature and AdS
in Poincaré coordinates is
whereas the coordinate
w in Equation (
31) is now
. The complex coordinate
w has now periodicity
. The boundary of thermal AdS
is a torus with modular parameter
Hence the boundary torus of the BTZ black hole and that of thermal AdS
are related by the modular transformation
Passing to consider the Euclidean solution with the conical singularity (
19), we note that it is related to AdS
just by the rescaling (
24). This changes the periodicity of the coordinates, which becomes
,
. Because the coordinate transformation mapping the boundary torus of the conical singularity space into the boundary torus of AdS
has the same form given by Equation (
33), it follows that the periodicity of the coordinate
w is now
. If we set
, the periodicities of the two tori are related by
The boundary torus of Euclidean AdS
with conical singularity characterized by the deficit angle
has the same modular parameter as that of AdS
at temperature
. Notice that, although the two manifolds have the same topology and the same boundary torus, they describe different three-geometries. The first is a singular one, whereas the latter is a perfectly well-behaved geometry. For this reason, one usually does not include AdS
with conical singularities in the physical spectrum of the theory.
Because
, from Equation (
35) it follows immediately that the boundary tori of AdS
with conical defect
and that of the BTZ black hole at inverse temperature
are related by the modular transformation
4.3. EE and the UV/IR Relation
As a consequence of the AdS/CFT correspondence, the EE expressed in Equations (
5), (
6) and (
7) should give information about bulk correlators. More precisely, one would expect the EE in Equation (
5) to describe quantum correlations in the presence of conical singularity (
19) and the EE in Equation (
7) of the thermal CFT to describe the interplay between thermal and quantum correlations in the black hole background (
20). The main obstacle to make the above relation precise is due to the holographic nature of the AdS/CFT correspondence. Spatial correlations in the bulk gravity theory are codified in the boundary CFT in a highly nonlocal way. Whereas the inverse temperature
β appearing in Equation (
7) can be naturally identified as the inverse of the black hole temperature (
21), the same is not true for the parameters
γ and
ε in Equations (
5), (
6) and (
7).
Owing to the holographic nature of the correspondence, the bulk interpretation of these parameters requires careful investigation. As discussed in
Section 2.3, the AdS
/CFT
correspondence indicates a way to relate length scales on the boundary with length scales on the bulk, this is the UV/IR connection [
27,
28]. Infrared effects in bulk AdS
gravity correspond to ultraviolet effects in the boundary CFT
, and
vice versa.
The UV/IR connection allows to identify the UV cut-off
ε in Equation (
6) as an IR regulator of AdS
gravity [
27,
28]. This can be done in the usual way by using the dilatation isometry of the metric (
23):
,
,
. Equivalently, one can introduce “cavity coordinates” on AdS
and show that
ε acts as an infrared regulator of the “area” of the
boundary sphere [
27]. In fact, the regularized radius of the
is
. The same is true in terms of the coordinate
r parametrizing AdS
in the modified Poincaré form (
23): cutting off the 2D CFT at length scale less than
ε implies an infrared cut-off on the radial coordinate of AdS
,
, where
The length-scales
γ and
ε are defined up to a dimensionless multiplicative constant of
. In the following we will set this multiplicative constant equal to
.
The bulk interpretation of the parameter
γ in Equation (
6) is not as straightforward as that of
ε.
γ is not a simple external length scale we are using to cut off excitations of energy less than
. It is the length of a
localized spacelike slice of the 2D space on which the CFT lives. On the other hand, owing to the holographic, nonlocal nature of the bulk/boundary correspondence, we expect that any localization of DOFs on the boundary will be lost by the correspondence with DOFs in the bulk. If any localization property of the observable slice
Q is lost in the boundary/bulk duality,
γ can only play the role of an upper bound above which spatial correlations for the boundary CFT are traced out. Because of the UV/IR connection, in AdS
this will correspond to tracing out the bulk DOFs at small values of the radial coordinate
r,
i.e. for
, where
It is important to stress that the bulk parameter
ω has not the same physical meaning of the boundary parameter
γ. Whereas
γ is the length of a spacelike slice, which is sharply separated from the observable region (hence it needs a UV regulator),
ω has the much weaker meaning of a length scale below which spatial correlations are traced out. In particular in the AdS
bulk there is no sharp boundary separating observable and unobservable regions. The bulk interpretation of
γ, given Equation (
39) is highly nontrivial and has the status of a conjecture, which is supported by the UV/IR relation. On the other hand, once one accepts the validity of Equation (
39) from the UV/IR relation it follows immediately that tracing in the boundary for distances greater than
γ corresponds to tracing in the bulk for
. We can use this meaning of
γ and
ω to interpret the EE (
5), (
6) and (
7) as holographic entanglement entropies of gravitational configurations.
The AdS/CFT correspondence and the IR/UV connection allow us to give to the EE (
6) a simple bulk interpretation: it is the EE of the regularized AdS
spacetime (
23),
i.e. it gives a measure of the von Neumann entropy that arises when an IR cut-off Σ is introduced and correlations are traced over for
. Substituting Eqs. (
38) and (
39) into Equation (
6), we find
(we have used
). The natural length scale for cutting off quantum bulk correlations is given by the AdS length
ℓ:
. This means that we are considering curvature effects much smaller than
. Using Equation (
39), this allows the identification of the boundary parameter in terms of the AdS length
ℓThe holographic EE of the regularized AdS
spacetime
has a simple geometric interpretation. Apart from a proportionality factor, it is the (regularized) proper length of the spacelike curve
,
. This can be easily shown integrating Equation (
23) for
.
It is interesting to notice that the identification can be obtained without using the UV/IR connection, just assuming that in the large N limit the mass/temperature relationship for the BTZ black hole exactly reproduces that of a thermal 2D CFT.
From Equations (
21) and (
22) one easily finds the mass/temperature relationship for the BTZ black hole,
On the other hand, in the large temperature limit
the EE (
7) reduces to the classical, extensive thermal entropy for an isolated system of length
γ. The energy/temperature relationship for such a 2D CFT is given by
where
is the energy of the vacuum and
,
are the temperatures for the right and left oscillators. Identifying the black hole mass
M with
and the temperature
of the CFT thermal state with the Hawking temperature of the black hole, we easily find, comparing Equation (
43) with Equation (
42) and using Equation (
18),
.
4.4. Holographic EE of Conical Singularities
Let us now consider the classical solution of 3D AdS gravity given by Equation (
19), which describes 3D AdS spacetime with conical singularities. As explained in
Section 4.2, solution (
19) can be locally obtained applying a diffeomorphism to the AdS spacetime (
23). This transformation is the “spacelike” counterpart of the “thermalization” mapping the metric (
23) into the BTZ black hole. On the 2D conformal boundary of the 3D AdS spacetime this transformation is described by the map
β is easily determined by first applying the transformation (
33) mapping full AdS
into (
23) and then using the rescaling (
24):
, where
is given by (
26). In the limit
(
i.e. ) the map (
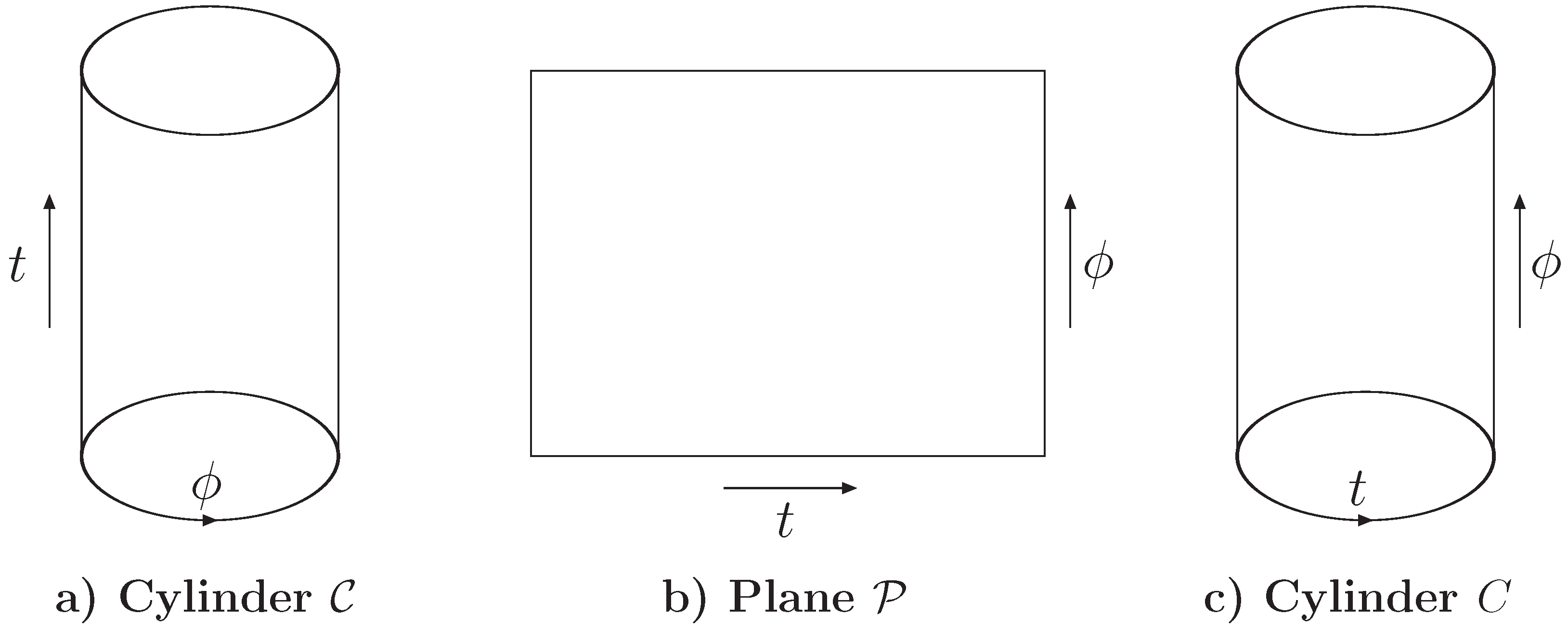
44) corresponds to a plane/cylinder transformation that maps the CFT on the plane
into the CFT on the cylinder
. Thus, this conformal transformation maps the EE of a CFT on the plane
into the EE of a CFT in the cylinder
[
21],
i.e. the EE of a CFT at zero temperature and noncompact spacelike dimension given by Equation (
6) into the EE of a CFT at zero temperature with a compact spacelike dimension given by Equation (
5). Correspondingly, the holographic EE of the regularized AdS spacetime becomes the holographic EE associated to AdS
with a conical singularity:
Equation (
45) can be considered as the analytic continuation
of Equation (
46) in the next section. The holographic EE of a conical singularity described by a deficit angle
is the analytic continuation of the holographic EE for the BTZ black hole with inverse temperature
. The analytic continuation corresponds to the exchange of the (compact) timelike with the spacelike direction. This result is a consequence of the modular symmetry (
37) of the boundary CFT on the torus relating the BTZ solution and the conical singularity spacetime. In the limit
the boundary torus corresponding to the BTZ black hole can be approximated by the infinitely long (along the spacelike direction) cylinder
C. The modular transformation (
37) maps the cylinder
C into the cylinder
, which has infinitely long direction along the timelike direction and approximates the torus for
. Correspondingly, the EE for the BTZ black hole (
46) is transformed into the EE for the conical singularity (
45).
An important point, which we have only partially addressed, concerns the role played by the classical solutions of 3D AdS gravity describing conical singularities of the spacetime. Since they represent singular geometries, they cannot be part of the physical spectrum of pure 3D AdS gravity (although they may play a role for gravity interacting with pointlike matter). On the other hand, they are related with the BTZ black hole solutions by modular transformations, and one can associate an EE to them. All this could be very useful for shedding light on the phase transition (analogue to the Hawking-Page transition of four-dimensional gravity [
53,
54]), which is expected to take place at
.
4.5. Holographic Entanglement Entropy of the BTZ Black Hole
The spinless BTZ black hole (
20) can be considered as the thermalization at temperature
of the AdS spacetime (
23). On the 2D boundary of the AdS spacetime, and in the above discussed large temperature limit
, this thermalization corresponds to a plane/cylinder transformation that maps the CFT on the plane
into the CFT on the cylinder
C. The conformal map plane/cylinder has the (Euclidean) form given in Equation (
30). One can easily check that the above transformation is the asymptotic form of the map between the BTZ black hole and AdS
in Poincaré coordinates. The conformal transformation (
30) maps the EE of a CFT on the plane
into the EE of a CFT in the cylinder
C [
21],
i.e. the EE of a CFT at zero temperature in a spacetime with noncompact spacelike dimension into the EE of a CFT at finite temperature. As a result, Equation (
6) is transformed into Equation (
7) with
. Correspondingly, the holographic EE of the regularized AdS spacetime becomes the holographic EE of the BTZ black hole
The EE (
46) still depends on the UV cut-off
ε. A renormalized entropy
can be defined by subtracting the contribution of the vacuum (the zero mass, zero temperature BTZ black hole solution). In terms of the dual CFT, we have to subtract the EE of the zero-temperature vacuum state, which is given by Equation (
6) with
The renormalized EE is therefore given by
As expected, the renormalized EE vanishes for
(the BTZ black hole ground state).
The holographic EE (
47) for the BTZ black hole coincides exactly with the previously derived entropy for the 2D AdS black hole. The 2D AdS black hole is the dimensional reduction of the spinless BTZ black hole. Using the relationship between 2D and 3D Newton constant
, Equation (
47) reproduces exactly the result (
14).
Macroscopic,
i.e. large temperature, black holes (with
) correspond, in terms of the 2D CFT, to a thermal wavelength
much smaller than the length
. The expansion of Equation (
47) for
gives
The leading term in EE is exactly the Bekenstein-Hawking entropy. This leading term describes the extreme situation in which thermal fluctuations dominate completely. In this limit the EE is just a measure of thermodynamic entropy. The EE (the von Neumann entropy) for the CFT becomes extensive and it agrees with the Gibbs entropy of an isolated system of length
. The subleading term behaves as
and describes the first corrections due to quantum entanglement.
The logarithmic correction in Equation (
48) matches exactly the short scale correction for the quantum entropy of a scalar field in the BTZ Euclidean background found in [
62] by Mann and Solodukhin. Notice that the authors of [
62] consider the case of a single scalar field, therefore we can reproduce their result by using for the central charge
. The fact that a 3D bulk calculation of the quantum entropy gives the same result of a boundary CFT calculation is not only a nontrivial check of their correctness, but also a highly nontrivial check of the AdS
/CFT
correspondence.
In principle, one could also consider the regime
in which the full quantum nature of the EE should be evident. However, this regime is singular from the black hole point of view: it corresponds to the 3D analogous of the Hawking-Page phase transition [
53,
54].
The derivation of the EE for the spinless BTZ black hole can be easily extended to the rotating BTZ solution, obtaining (see [
19] for details):
where
are the positions of the outer and inner horizons. Expanding the previous expression for
and
, we get the same result given in (
48).
Let us now briefly comment on the relationship between our approach and that of [
5,
6,
7,
35,
36,
37], where the EE of the 2D CFT is computed in terms of 3D bulk geometric quantities (minimal area surfaces). Conversely, in our approach we assume the validity of the EE formulas for the 2D CFT and use them (by means of the AdS/CFT correspondence) for giving a holographic interpretation to the EE of gravitational configurations. The two approaches are complementary in the sense that in [
5,
6,
7,
35,
36,
37] bulk gravitational quantities are used to reproduce the EE of the boundary CFT, whereas we use the EE of the CFT to reproduce the EE of bulk gravitational configurations.
4.6. Entanglement Entropy vs. Thermal Entropy
In this section we show that the leading term of the holographic EE for the BTZ black hole can be obtained from the large temperature expansion of the partition function of a broad class of 2D CFTs on the torus [
19]. This result indicates that black hole EE emerges when the semiclassical notion of spacetime geometry is used to describe the black hole.
In the previous section we have discussed the holographic EE of gravitational configurations in 3D AdS spacetime. In our approach the EE of the boundary CFT, , is used to probe thermal correlations at scales set by β and spatial correlations at scales set by γ. The bulk description depends crucially on the regime of the AdS/CFT correspondence we want to investigate.
First of all, we work in the region of validity of the gravity description of the AdS/CFT correspondence, when the AdS length
ℓ is much larger than the Planck length, which coincides in our units with the 3D Newton constant
:
This is the so-called “large
N approximation”.
Moreover, considering curvature effects much smaller than the curvature
of the AdS spacetime allows the identification of the external parameter
γ in terms of
ℓ. On the other hand, the thermal scale
β can be easily identified when a black hole is present in the bulk:
. The semiclassical description for black holes holds when the horizon radius
is much larger than the Planck length,
, whereas the holographic EE formula (
47) holds for
. We are in the regime where we are allowed to approximate the boundary torus with the cylinder
C. The path integral of Euclidean quantum gravity on AdS
is dominated by the contribution coming from the BTZ black hole at
. The leading term in the EE (
48) describes the main (thermal) contribution of the BTZ geometry and corresponds to the EE for the CFT dominated completely by thermal correlations. When we increase the energy scale, we reach a regime for which contributions coming from geometries different from the BTZ instanton cannot be neglected. Quantum entanglement and the subleading term in Equation (
48) become relevant.
The other regime we have investigated so far is
, which is related to the previous one by the modular transformation (
37). The Euclidean quantum gravity partition function for 3D AdS gravity is now dominated by AdS
at temperature
. Although the solutions (
19) describe singular geometries with conical singularities—therefore they cannot be part of the physical spectrum of the theory—the modular symmetry strongly indicates that they can be used to probe quantum entanglement. In this regime the boundary torus can be described by the cylinder
and the EE is given by Equation (
45).
One may now wonder about the regime
. In this parameter region we cannot approximate the torus with an infinitely long cylinder.
is the fixed point of the modular transformations (
35), (
37) and we have a “large
N phase transition”, which is the 3D analogue of the Hawking-Page transition [
53,
54]. Since now the dual boundary CFT lives on the torus
, our calculations of the EE on the cylinder lose their validity. Furthermore, it is not a priori evident that the very notion of EE would maintain a sensible physical meaning in a regime where the semiclassical description of gravity is expected to fail.
The most direct way to learn something about the relationship between the two regimes
and
is to compare the
asymptotic behavior of the thermal entropy
, derived from the partition function of the dual CFT on the torus, with the EE given by Equation (
47). Unfortunately, whereas the EE for a 2D CFT on a cylinder has an universal form, the thermal entropy
for the CFT on the torus takes different form depending on the details of the CFT we are dealing with. Let us notice that, despite the intense activity on the subject in the last decade, the exact form of the 2D CFT dual to pure 3D AdS gravity remains still a controversial point [
55,
56,
57].
Here we will use a simple, albeit not completely general, approach to this problem. We will show that, for the most common 2D CFTs (free bosons, free fermions, minimal models and Wess-Zumino-Witten models), the asymptotic, large temperature
behavior of
calculated from the partition function of the CFT on the torus reproduces exactly the leading term of the EE (
47) for the BTZ black hole.
The partition function of the CFT on the torus,
, is a function of the modular parameter
. Moreover, we will make use of the modular invariance of the partition function under the modular transformation (
28) to write
. From the partition function one can easily compute the thermal entropy
We are interested in the asymptotic expansion of
in terms of the variable
when
. The asymptotic form of
is determined writing
Z as a function of the usual variable
. After making use of the modular invariance of the partition function under the modular transformation (
28), we then introduce the new variable
and determine the
asymptotic expansion of
. Finally, we determine
by making use of the
asymptotic expansion
For free bosons on the torus the asymptotic expansion of the entropy is
For free fermions on the torus, as well as for minimal models and for Wess-Zumino-Witten models, the entropy has the asymptotic form
The leading term in the large temperature expansion of the thermal entropy for the four CFT classes on the torus considered in this section is
reproduces, for
, the leading term of the holographic EE for the BTZ black hole given by Equation (
47). This result sheds light on the meaning of the holographic EE for the BTZ black hole in particular and, more in general, on the very meaning of entanglement for black holes. In fact, our result indicates that the EE of a black hole is a semiclassical concept, which has a meaning only for macroscopic black holes in the regime
. Thus, entanglement seems to arise from a purely thermal description of the underlying quantum theory of gravity, which is assumed to describe 3D quantum gravity in the region
. This fact supports the point of view that the microscopic theory describing the BTZ black hole at short scales is unitary. EE is an emergent concept, which comes out when the semiclassical notion of spacetime geometry is used to describe the black hole. The agreement between thermal entropy for the CFT on the torus and holographic EE for the BTZ black hole is limited to the leading term in the large temperature expansion. The subleading terms are not of the same order for the different CFTs we have considered: they behave as
for free bosons on the torus, whereas they are
for the other three cases. Therefore, the subleading terms seem not to be universal (see [
63]), but they depend on the actual CFT we are dealing with.