Abstract
Sarcopenia can cause various senile diseases and is a major factor associated with the quality of life in old age. To diagnose, assess, and monitor muscle loss in daily life, 10 sarcopenia and 10 normal subjects were selected using lean mass index and grip strength, and their gait signals obtained from inertial sensor-based gait devices were analyzed. Given that the inertial sensor can measure the acceleration and angular velocity, it is highly useful in the kinematic analysis of walking. This study detected spatial-temporal parameters used in clinical practice and descriptive statistical parameters for all seven gait phases for detailed analyses. To increase the accuracy of sarcopenia identification, we used Shapley Additive explanations to select important parameters that facilitated high classification accuracy. Support vector machines (SVM), random forest, and multilayer perceptron are classification methods that require traditional feature extraction, whereas deep learning methods use raw data as input to identify sarcopenia. As a result, the input that used the descriptive statistical parameters for the seven gait phases obtained higher accuracy. The knowledge-based gait parameter detection was more accurate in identifying sarcopenia than automatic feature selection using deep learning. The highest accuracy of 95% was achieved using an SVM model with 20 descriptive statistical parameters. Our results indicate that sarcopenia can be monitored with a wearable device in daily life.
1. Introduction
The interest in maintaining the daily abilities for a healthy retirement life is increasing owing to the increase of the elderly population and the extended life expectancy. Elderly people are susceptible to sarcopenia that is characterized by decreased muscle mass and muscle function owing to nutritional deficiencies and decreased physical activity. Sarcopenia is the cause of numerous senile decays, such as falls, fractures, physical disabilities, depression, poor quality of life, nursing home admission, and even death [1].
Dual energy X-ray absorptiometry (DEXA) and bioelectrical impedance analysis (BIA) are primarily used as tools for diagnosing patients with sarcopenia. The European working group on sarcopenia in older people (EWGSOP) uses the grip strength and walking speed as additional variables to determine the level of sarcopenia [2]. Existing screening methods cannot be applied without expert help. Therefore, a screening study that can be easily conducted in nonhospital settings is required. Studies on muscle reduction and walking speed are actively being conducted. Interestingly, walking speed has allowed independent predictions of mortality [3]. Therefore, gait analysis can be a useful tool to determine muscle loss [4]. Cameras and force plates are gold-standard tools for clinical gait evaluations. Camera-based gait analyses are used in large institutions and university hospitals. In order to accurately analyze gait, it is necessary to capture three-dimensional (3D) motion. Since two-dimensional (2D) cameras cannot detect 3D motion, 2D camera recordings from various angles are needed to visualize and quantify gait [5]. Recently, spatial issues have been solved because 3D data have been easily obtained owing to the development of depth cameras [6]. However, expensive high-speed cameras are required to accurately analyze human gait. Force-plate-based methods [7] are very good tools used to measure the reaction force of gait, and to detect step lengths and widths. However, they have the disadvantage of not acquiring kinematic information.
Inertial measurement units (IMUs) are attracting increased scientific attention as gait analysis tools because the gold-standard tools are difficult to use to conduct gait monitoring at home or outdoors [8,9].
The gait parameters are detected to determine the effective gait condition. The parameters used in clinical analysis are (a) spatial-temporal parameters (e.g., step length, stance phase, swing phase, single support, double support, step time, cadence, and speed) and (b) kinematic parameters (the rotational angles of the sagittal, coronal, and transverse sections of the pelvis, hip, knee, and ankle) [10].
The inertial sensor-based gait parameter detection method derives spatial-temporal parameters from the values of acceleration and angular velocity signals measured by the inertial sensor, and extracts features of descriptive statistics (maximum, mean, standard deviation, etc.) of the acceleration and angular velocity signal. Segmentation of the gait phase is necessary to classify daily activities or to assess pathological gait.
Machine learning algorithms are used as a method for screening various diseases using gait. As a method of detecting gait features, support vector machines (SVM) and random forest (RF) obtained the best results, and high-screening results were obtained using deep learning technology that does not extract features [11]. In the field of gait analysis, domain knowledge to detect gait parameters remains important for designing the inputs of the model. The explainable artificial intelligence (XAI) method is receiving increased attention as a method used to obtain domain knowledge based on machine learning [12].
The aim of this study is to detect parameters from the gait signal measured in the inertial sensors as a screening method for the sarcopenia group and identify the optimal classification method. The highlights and contributions of our work can be summarized as follows: DEXA and grip strength were measured to classify 10 sarcopenia patients and 10 normal volunteers, and inertial gait data were obtained from each participant. Gait parameters effective for identifying sarcopenia were detected using the XAI technique. The optimum classification method was achieved with the use of the various parameters as input.
For gait parameters, the criteria for data analysis were selected to be right because 13 subjects were right-leg dominant and 7 were left-leg dominant. Owing to insufficient data, the effect of the dominant leg could not be analyzed and was, therefore, not considered. Further, the proportion of dominant leg per group (control = 7, sarcopenia = 6) was similar.
The remainder of this paper is organized as follows. Section 2 introduces related studies on detecting gait parameters and classifying diseases. Section 3 presents detailed screening methods for sarcopenia groups, sensor devices, and proposed algorithms. Section 4 presents the results for detection of gait parameters and identification of sarcopenia. Section 5 presents the discussion. Conclusions are listed in Section 6.
2. Related Work
2.1. Gait Phases
Gait describes human walking that exhibits periodic patterns termed as gait cycles. For gait analysis, it is important to detect various gait parameters. The gait parameters are detected based on the gait cycle, and the gait phase is clinically divided into 2–7 phases [13]. Gait is divided into the stance and swing phases; the stance phase refers to the case in which the foot is attached to the ground, and the swing phase refers to the case in which the foot is separated from the ground. The stance and the swing phases are further divided into 2–4 subphases. Whittle et al. [14] divided gait into seven phases. The stance phase was classified into the loading response, mid stance, terminal stance, and preswing phases, and the swing stage was classified into the initial swing, mid swing, and terminal swing phases, as shown in Figure 1.
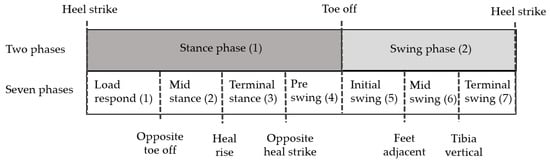
Figure 1.
Two and seven gait phases.
Heel strike (HS) and toe-off (TO) detection is required to separate the stance and swing phases. Spatial-temporal parameters, such as cadence, stance phase (time), swing phase (time), single-support phase (time), double-support phase (time), step time, and stride time can be detected by mathematical calculations with HS, TO, opposite HS, and opposite TO. Therefore, detection of HS and TO is very important for detecting gait parameters.
Misu et al. [15] detected HS as an acceleration signal and TO based on angular velocity signals. Mo and Chow [16] detected HS and TO based only on residual acceleration. HS yielded the highest acceleration peak, and TO was selected as the phase associated with 2 g or more. Khandelwal et al. [17] detected HS and TO using complex acceleration signals according to continuous wavelet transform (CWT)-based frequency analysis. We obtained very good accuracy by detecting acceleration along the x-axis for HS and acceleration along the z-axis for TO instead of complex acceleration signals through CWT [18]. Based on IMUs attached on the foot, existing work involve 3–4 phases, including HS and TO. More studies have been conducted on the classification of stance rather than the swing phase. The front and rear of the flat foot where the foot touched the ground were classified, and an algorithm was proposed based on the rule and hidden Markov models (HMM). The existing gait phase studies are frequently divided into the HS-FF (TS)-HO-TO phases, as shown in Table 1. The abbreviations for each phase or event are as follows: ST: Stance, SW: Swing, MSw: Mid swing, MSt: Mid stance, HO: Heel off, TS: Toe strike, FF: Flat foot, oHS: Opposite heal strike, oTO: Opposite toe off, HR: Heel rise, FA: Feet adjacent, and TV: Tibia vertical. These are mainly detected using gyroscope data, and the position of the sensor changes from forefoot to hindfoot. Pérez-Ibarra et al. [19] identified HS as the zero-crossing of sagittal angular velocity during the swing phase. TO was determined by the zero-crossing of sagittal angular velocity during negative to positive changes before HS. MSt (from TS to HO) was detected when the resultant angular velocity was below the threshold. Zhao et al. [20] detected HS-FF-HO-TO using inertial sensors and multisensor fusion. MSw and MSt events were detected as the events associated with the minimum magnitudes of specific forces compared with Vicon data. FF and HO were detected when the sagittal angular velocity was almost zero. HS was detected as the zero crossing in the same manner as Pérez-Ibarra’s method, and TO was detected as the maximum value of the sagittal angular velocity. Two negative peaks occurred after the positive signal of the sagittal angular velocity and are related to TO and HS events. The gait phase detection methods in the studies [21,22,23,24,25,26,27,28] listed in Table 1 have been reported by Pérez-Ibarra et al. [19] and Zhao et al. [20].

Table 1.
Existing studies on gait phase detection.
2.2. Patient Identification Using IMU
Studies conducted to identify patients based on inertial sensors include Faller, Parkinson’s disease (PD), and total hip arthroplasty (TPA). Moreover, algorithms such as naive Bayes (NB), SVM, RF, decision tree (DT), k-nearest neighbor (kNN), and deep learning (DL), were applied as classification methods. The spatial-temporal and descriptive statistical parameters derived from the acceleration and angular velocity signals were used as input to the algorithm. Existing studies include the spatial-temporal, descriptive statistics, and frequency parameters. Spatial-temporal parameters are cadence, stride time, stride length, speed, stance, swing, and double and single support. Descriptive statistical parameters include range of motions (ROM), maximum, mean, and standard deviation. Frequency parameters, such as the spectral entropy, median frequency, and fast Fourier transform were used.
Teufl et al. [29] classified TPA patients using stride length, stride time, cadence, speed, hip, and pelvis ROM as features of the SVM, and obtained an accuracy of 97%. Caramia et al. [30] classified PD using the linear discriminant analysis (LDA), NB, k-NN, SVM, SVM radial basis function (RBF), DT, and the majority of votes. The performance of the machine learning technique—the SVM with nonlinear kernel basis—was the best. Howcroft et al. [31] predicted the risk of falls using accelerometer data and used temporal (cadence and stride time) and descriptive statistics (maximum, mean, and standard deviation of acceleration). NB, SVM, and artificial neural networks (ANN) were used as classification methods, and the best single-sensor model was the neural network. Deep learning is currently receiving tremendous attention as a classification algorithm. Additionally, Eskofier et al. [32] classified PD based on the application of AdaBoost, PART, kNN, SVM, and convolutional neural networks (CNN), and CNN yielded the highest accuracy. Deep learning has an advantage in that it can detect features within the algorithm from the raw signal, but Tunca et al. [33] achieved a higher accuracy in long short-term memory (LSTM) when parameters (e.g., speed, stride length, cycle time, stance time, swing time, clearance, stance ratio, and cadence) were used as input compared with raw signals. Zhou et al. [34] classified age groups by dynamic gait outcomes with SVM, RF, and ANN. Gait outcomes that significantly contributed to classification included the root-mean square, cross entropy, Lyapunov exponent, step regularity, and gait speed. In recent years, interest in XAI has been increasing owing to its classification accuracy and to features that significantly contributed to classification. Dindorf et al. [12] used the local interpretable model-agnostic explanations (LIME) to understand the features for identifying total hip arthroplasty (THA), and found that the sagittal movement of the hip, knee, and pelvis as well as transversal movement of the ankle were especially important for this specific classification task, as shown in Table 2.

Table 2.
Existing studies on disease identification using gait parameters.
3. Methods
In this section, we present detailed screening methods for sarcopenia groups, sensor devices, and proposed algorithms.
3.1. Subject, Equipment, and Data Collection
Ethical approval was obtained from the Chungnam National University Hospital Institutional Review Boards before the study was conducted (File No: CNUH 2019-06-042). We collected gait data from 10 elderly women with sarcopenia and 10 normal women with non-sarcopenia. The diagnosis of the sarcopenia group was selected as the lean mass index (appendicular skeletal muscle mass in kg/height in m2) of less than 5.4 kg/m2 as a result of DEXA, while the grasp power was less than 18 kg. Population statistics can be found in Table 3. The walking data of the 20 subjects were obtained with a sensor that was attached to their insoles over four walking cycles at the speed of their choice through a straight corridor of 27 m. A total of 80 walking cycles were acquired. The sampling rate of the inertial sensor was measured at 100 Hz.

Table 3.
Population statistics for normal and sarcopenia groups.
The proposed insole system obtained Pearson’s correlation, r > 0.9, for HS, TO, opposite HS, and opposite TO, compared to the camera- and force-plate-based clinical standard system. An intraclass correlation >0.9 was obtained based on four measurements. The results achieved the same high validity and reliability as existing inertial system [35,36,37].
The clinical system consisted of 10 cameras (Vicon, Oxford Metrics, Oxford, UK) and four force plates (ATMI, Advanced Mechanical Technology, Watertown, MA, USA). Data analysis was performed with Vicon Polygon 3.5.2 (3.5.2, Oxford Metrics, Oxford, UK).
The size of inertial insole device was 17 × 25 × 3 mm; the processor was a Nordic nRF52840 (ARM Cortex-M4 32-bit processor with FPU, 64 MHz, Cambridge, UK), the inertial sensor was an Invensense MPU-9250 with 16-bit ADCs, the flash was 512 Mbits, memory was 1 MB flash and 256 kB RAM, and the device supported Bluetooth low energy (BLE) mode.
3.2. Extraction of Gait Parameters
The 3-axis acceleration and angular velocity signals of the right foot and the left foot were obtained from the inertial sensor, and spatial-temporal and descriptive statistics parameters were obtained from the signals. The definitions of the gait parameters used in this study are shown in Table 4. The value of the descriptive statistics is the 3-axis inertial signal divided by the gait phases given in Table 4.

Table 4.
Definition of gait parameters.
To detect the spatial-temporal parameters, the HS, TO, opposite HS, and opposite TO were detected. Acceleration increased rapidly when the swing phase was changed in the stance phase but decreased gradually during the swing phase, and the acceleration value was suddenly zero at HS. The time to return to zero near the minimum value of acceleration ranged from 0.01–0.02 s and was detected at the HS. Given that the x-axis acceleration signal has a minimum value before the stance phase, the minimum value of the acceleration is detected within the interval, and the highest value of the derivative x-axis acceleration (change in acceleration) is then selected as the HS within 10 samples (the minimum value of the acceleration along the x-axis).
TO detection occurred when a rapid rotational force about the y-axis was generated so that the foot came off the ground during gait phases. This constituted a change associated with the swing phase from the stance phase. The gyro sensor in the insole detected an increase when the heel came off the ground and had the highest torque because the greatest force was applied to the foot at TO. Therefore, the maximum value of the gyro y-axis signal was used to identify TO.
To extract the stride and step lengths, we applied a distance estimation algorithm based on zero velocity detection (zero-velocity update) with an extended Kalman filter [38,39].
3.3. Extraction of Gait Phase
To divide the gait into seven phases, heel rise (HR), feet adjacent (FA), and tibia vertical (TV) were also detected.
The HR distinguishes the transition from the mid stance to the terminal stance and depends on the individual and walking speed. In the mid stance phase, the angular velocity of the gyro y-axis (pitch) is close to zero, and then increases to a value (in the counterclockwise direction) as the heel falls off the floor. The mid stance appears at 32% of the walking cycle, and the position where the y-axis angular velocity changes to 0.25 or more was selected as the HR.
The FA values are in positions that separate the initial swing and the mid swing when both feet cross the stance leg on the opposite side of the swing leg in the sagittal plane. The FA occurs in 77% of the gait cycle. When both feet are adjacent, the body is in the highest position and the toes are located closest to the ground [14]. In the case of the inertial sensor attached to the insole, it is difficult to detect the exact point adjacent to the feet. However, assuming that the foot moves the pendulum, the acceleration has a value of zero at the lowest point. Therefore, the FA was detected as the point where the x-axis acceleration became zero.
The TV corresponds to 86% of the gait cycle based on the division of the mid swing and the terminal swing. The TV is a position between the dorsiflexion and the plantarflexion before the subsequent HS [14]. Given that the joint angle is located immediately at zero, the point where the joint angle is zero is defined as the TV. The joint angle is calculated by integrating the angular velocity along the y-axis. However, the error is minimized by using the minimum integration because the cumulative error occurs in obtaining the angle based on integration. At the point at which the joint angle is zero, the x-axis speed is close to zero. In the case of the detection method, when the foot rises to the maximum point after TO in the swing phase, the x-axis speed becomes zero, and the angular rotation speed along the y-axis also has a value of zero. The x-axis acceleration is integrated to obtain the velocity from the point at which the y-axis angular velocity is zero. Accordingly, the point at which the velocity becomes zero is detected by the TV.
3.4. Feature Selection
The detected gait parameters differ in their capacity to identify sarcopenia. Applying many dimensional parameters to the classifier can yield poor results. Therefore, it is necessary to reduce the dimensions or select features and apply them to the classifier. In recent years, XAI technology has been attracting attention as a method used to help understand the classification result rather than simply reduce the dimension. XAI presents predictive results for machine learning in a way that humans can understand [40]. Machine learning models based on trees are the most popular nonlinear models in use today [41]. Extreme gradient boosting (Xgboost) proposed by Chen and Guestrin [42] is one of the decision tree ensemble models. Xgboost is an algorithm that improves the performance of the gradient boosting machine (GBM) in terms of speed. The boosting model has a low-overfitting risk because it generates a powerful classifier by updating the parameters of the former classifier iteratively to decrease the gradient of the loss function [43]. By focusing on the model performance, Xgboost has become more complex and lost its interpretability. These models provide an inconsistent measure depending on the tree structure. It only shows the overall importance and not the effect of independent variables. Shapley Additive explanation (SHAP) values are utilized with the intention to improve these problems. The SHAP is a method used to interpret results from tree-based models. The values are based on Shapley values from game theory. The main advantages of the SHAP method are the local explanation and consistency in global model structure. The SHAP value is a numerical expression of how much each feature contributed to creating the total outcome. The contribution of each feature can be expressed as the degree of change in the total outcome when the contribution of that feature is excluded. Equation (1) represents the SHAP value, where is the SHAP value for the data, n is the number of feature, N is the set all n features, S is all features except the i-th feature, is the contribution to the result without the i-th feature, and is the contribution of all features including the i-th feature. The degree of contribution of the i-th feature is the value obtained by subtracting the sum of the contributions excluding the i-th feature from the total contribution.
Analysis of summary plot obtained by SHAP can provide the distribution of the impact of each feature. The summary plot superimposes feature importance and feature effects. Each point in the summary plot representsthe SHAP value and observation value for the feature (gait parameters), where the x-axis represents the SHAP value from the scale of negative factors to the scale of positive factors for sarcopenia identification, and the y-axis represents the feature. The features are ordered according to their importance. The color represents the feature value from low (yellow) to high (purple). Therefore, the summary plot shows the magnitude of the positive or negative impact of the feature on the identification of sarcopenia when the value of each parameters is high or low. The SHAP summary plot can be seen in Figure 2 The parameter settings for the SHAP for Xgboost are as follows: Objective: Binary logistic, nroonds: 20, max_depth: 15, gamma: 0.009, and subsample: 0.98. The SHAP for Xgboost are implemented as an R package and is available from Comprehensive R Archive Network (CRAN).
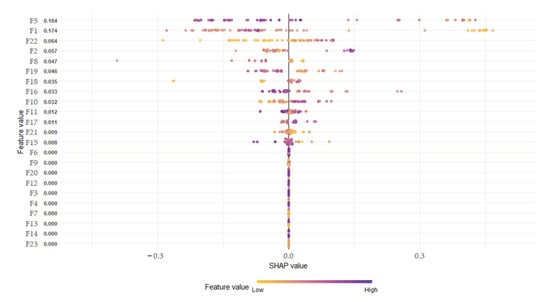
Figure 2.
Summary plot of spatial-temporal parameters.
3.5. Machine Learning
We explored the most suitable method for identifying sarcopenia using inertial signals and gait parameters. RF, SVM, and multilayer perceptron (MLP) are the most popular machine learning methods in gait analysis and use feature parameters as input. Deep learning models that do not require feature extraction, such as the CNN and LSTM, have yielded the best results in various fields. RF is a decision tree ensemble classifier that combines multiple single classifiers to finalize the results from each classification model through a majority vote or a weighted average. The RF was constructed based on the decision tree so it can classify various categories. It has a fast learning speed and big data processing ability [44]. The number of RF trees was 50, and the number of features was selected to be the square root of the gait parameter; the max depth of trees was 30, and the minimum leaf size of the sample was 1.
SVM is a binary classifier that aims to find the optimal separation hyperplane that maximizes the margin between the two classes. Kernel functions are used to map data to a higher dimensional space, so SVM can compute nonlinear decision boundaries [45]. We explored the linear and RBF kernels, and the parameters were gamma = 1.0 and C = 5.0.
The MLP [46] is a feed-forward neural network with input, hidden, and output layers. The hidden layer employs activation functions to be able to capture nonlinear associations. This model is used for the classification based on feature inputs, unlike the deep learning method. The hyperbolic tangent sigmoidal function (tanh) is used as the activation function in the hidden unit. The scaled conjugate gradient backpropagation algorithm is used to train the network. We chose to use the MLP with two hidden layers that contained 20 hidden units and 70 epochs.
The CNN [47] is composed of one or more convolutional, pooling, and fully connected (FC) layers. In the convolutional layer, the kernel extracts features while traversing the input data at regular intervals. The output of this layer is the feature map. Distinct from the standard ANN, CNN just needs to train the kernels of each convolutional layer. The convolutional operation acts as a feature extractor by learning from the diverse input signals. The extracted features can be used for classification in subsequent layers. In the pooling layer, this is a down-sampling layer. The samples of the most representative features are extracted from the convolutional layer. The sampling method includes the max and average pooling, which is performed by extracting the maximum or the average value of each interval.
In the case of CNN, the raw data of the acceleration and angular velocity are used as input data, and the length of the data is selected to include 100 samples. The CNN architecture was initially implemented with a one-dimensional (1D) convolutional layer with 64 filters, 1 stride, and a kernel size equal to 8. The next layer was a max-pooling layer with a pooling size of 4 and with 4 strides. The third layer was the FC layer with CNN feature inputs and 2014 neuronal outputs. The last layer was another FC layer with neuronal outputs classes and a softmax function.
The recurrent neural network (RNN) [48] architecture was a highly preferred architecture for sequential data. This architecture has been successfully applied to many problems, such as natural language processing, speech recognition, prediction of stock market, and machine translation. Unlike a traditional neural network, the RNN has a learning structure in which all inputs and outputs are connected to each other, so it can memorize previous data and be recursively used as input in the current state. This recurrent connection structure was developed in 1982 by Hopfield [49]. The LSTM network by Hochreiter and Schmidhuber [50] emerged in sequential data analysis as the most extensively used type of RNN architecture. The LSTM has the disadvantage that the input is heavily influenced by the previous input because the input value is time dependent. To eliminate this disadvantage, Bidirectional LSTM (BiLSTM) [51] has been proposed. BiLSTM have forward and backward hidden layers, which are not connected to each other. Thus, they can learn both the prior and subsequent information. The BiLSTM architecture started with two BiLSTM layers with 64 and 32 filters. The layers after BiLSTM were the same as the CNN architectures. The learning rate was 0.0005, and the dropout was 0.2.
The parameters of SVM, RF, MLP, CNN, and BiLSTM were obtained by grid search. Optimal parameters were obtained for various input features; spatial temporal parameters, descriptive statistical parameters for two phases and seven phases, and the parameters that did not affect the results and classification accuracy were selected.
3.6. Proposed Data Pipeline
The acceleration and angular velocity walking signals (12-axis) of 20 subjects were detected by using the inertial sensors of both feet. HS, TO, opposite HS, and opposite TO were detected from the inertial signals. Spatial-temporal parameters (23) were calculated using the detected HS and TO of both feet, and HR, FA, and TA were additionally detected. The gait phases were classified into either two or seven phases. The two phases were classified into HS and TO, and the seven phases were classified into HS, opposite TO, HR, opposite HS, TO, FA, and TA. Descriptive statistical parameters (10) were detected for each inertial signal that was divided into two and seven phases. For descriptive statistical parameters, 240 (12 × 2 × 10) parameters and 840 (12 × 7 × 10) parameters were detected for the two and seven phases, respectively, as shown in Figure 3. Of the detected parameters, only 50 were applied to the SHAP in the order of the lowest p-value resulting from the independent t-test because the descriptive statistical parameters had too many features compared with the data used to apply the SHAP. The 50 parameters were determined using a grid search and the designer’s intuition, and this number did not generate big errors in the results. Parameters 1–20, were used as inputs to RF, SVM, MLP, CNN, and BiLSTM because the SHAP values were 0.002 or more within the top 20. Raw inertial signals from the current to the next HS (one stride) were transformed into 100 samples by spline interpolation because the number of samples for each stride was different, and the samples were used as input for deep learning. For evaluation, nine subjects in each group were used as training data, and one subject in each group was used as test data. Evaluation results averaged the accuracy of 10 evaluations.
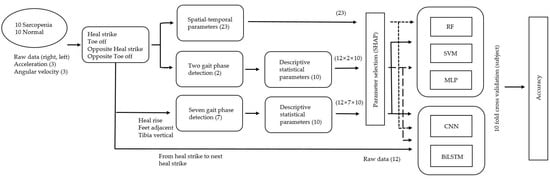
Figure 3.
Data processing pipeline for the identification of sarcopenia.
4. Results
4.1. Gait Parameters
The detected spatial-temporal parameters and descriptive statistics parameters for two and seven phases are outlined in the Appendix A. Since the proposed parameter accuracy is calculated based on HS, opposite TO, HR, opposite HS, TO, FA, and TA, these seven events should be accurately detected. HS and TO from the inertial sensor were detected with an error of less than 0.03 s (3 samples) compared to the standard system. HR, FA, and TA were calculated according to the proposed method from the detected HS and TO, and all were detected without error. The results of the application of the SHAP with Xgboost to the spatial-temporal and descriptive statistical parameters for two and seven phases are as follows:
- Spatial-temporal parameter (top 20): 5, 1, 22, 2, 8, 19, 18, 16, 10, 11, 17, 21, 15, 6, 9, 20, 12, 3, 4, and 7.
- Descriptive statistical parameters for two phases (top 20): 52, 126, 37, 97, 8, 51, 144, 211, 24, 3, 232, 115, 116, 31, 57, 50, 109, 43, 100, and 4.
- Descriptive statistical parameters for seven phases (top 20): 196, 524, 504, 97, 3, 231, 526, 507, 430, 187, 380, 8, 130, 57, 51, 200, 828, 283, 523, and 9.
Regarding the spatial-temporal parameters, the parameter for phase (%) was detected as the most important parameter, and time dRL representing the balance of both sides obtained high importance.
In the case of descriptive statistical parameters for two phases, the stance parameters gained higher importance with 13 stance parameters and 7 swing parameters among the top 20 important parameters. Regarding the parameter importance according to the sensor type, the parameters of the gyro sensor were more important with 14 gyroscope sensors and 6 acceleration sensors. The high importance parameters for seven phases included 17 stance parameters and 3 swing parameters, and the stance parameters had the same high importance as those of the two-phase case. In the stance phases, seven mid stance parameters and six loading response parameters gained high importance. In the case of the sensor type, the acceleration x-axis was six parameters, the gyroscope y-axis was five parameters, and the parameter for the direction of the walking was highly important.
4.2. Identification of Sarcopenia
Twenty-three spatial-temporal parameters, 240 two-phase descriptive statistical parameters, and 840 seven-phase descriptive statistical parameters were applied as input to the SVM, RF, MLP, CNN, and BiLSTM. In addition, the important parameters of the top 20 of the two- and seven-phase descriptive statistical parameters were applied to each classification algorithm, as shown in Table 5 and Table 6. The application of the spatial-temporal parameters yielded the best results in the MLP. When descriptive statistics were used, sevens phases, which had more information than two phases, yielded outcomes with good accuracy. The highest accuracy was obtained when the parameters detected by the SHAP with the highest importance (ranked from 1 to 20) were used in conjunction with the SVM. The results of using the raw signal, spatial-temporal parameters, and descriptive statistics parameters for the top 20 importance parameters as inputs for deep learning were better when gait parameters were used than when the raw signal was used.

Table 5.
Evaluation result of support vector machines (SVM), random forest (RF), and multilayer perceptron (MLP) (accuracy (standard deviation), %).

Table 6.
Evaluation result of deep learning models (accuracy (standard deviation), %).
5. Discussion
To identify sarcopenia, existing studies involving the sarcopenia and normal groups reported a decrease in walking speed [2,4] and a poor body balance [52]. In gait analysis using inertial sensors, spatial-temporal parameters have traditionally been used as features to conveniently identify diseases such as Faller, PD, and TPA in daily life. In this study, 23 spatial-temporal parameters used in existing disease recognition were detected to identify sarcopenia patients. As a result of detecting the importance of 23 parameters, the top five were found to be single support phase right, stance phase right, stance time dRL, stance phase left, and stance time right. As shown in Figure 2, the SHAP summary plot of spatial-temporal parameters, the single support phase right decreased in the sarcopenia group compared with the normal group and the negative effect (decreased probability of classification as sarcopenia) increased when the single support phase increased. The decrease in the stance phase right and increase in the stance phase left increased the positive effect of the SHAP value. The mean value of sarcopenia group was higher than that of the normal group, but the opposite result of the two legs in the SHAP influence indicated the imbalance of the two leg abilities in sarcopenia patients. When the speed decreased, the single support phase decreased. Therefore, the same results were obtained as the results of previous studies, i.e., muscle reduction decreased the walking speed. The stance time dRL is the difference between the stance time of both feet and has a high value when there is a large difference, indicating poor body balance. When the stance time dRL increased, the effect of SHAP value also increased. The spatial-temporal parameters are good for understanding the gait characteristics of sarcopenia; however, they do not yield sufficient accuracy when used to identify sarcopenia. Therefore, to detect the acceleration and gyroscope 3-axis signal characteristics obtained from the inertial sensor, descriptive statistical parameters of the signal were extracted and used as inputs of the classifier. The gait signal contained unique characteristics for each gait phase. As a result of subdividing the gait phases, detecting descriptive statistical parameters, and applying them to a classifier, a better identification result was obtained in seven phases compared with two phases. There were 12 gait signals from the three-axis acceleration and gyroscope sensor of both feet, and 10 descriptive statistical parameters of each signal were detected. Increasing gait phases also created many parameters that are meaningless in identifying sarcopenia. Among the detected parameters, high accuracy was obtained by detecting an important parameter using the SHAP for identifying sarcopenia. The highest recognition accuracy was obtained when the seven-phase descriptive statistical parameters were used as input to the SVM, RF, and MLP, which were used as inputs for feature selection using domain knowledge. When the top 20 parameters were used, the highest result was obtained in SVM, which yielded the highest performance in binary classification. This can explain why SVM was frequently used in other disease classifications.
Additionally, raw gait signals and gait parameters were used as inputs for the CNN and BiLSTM; however, the accuracy of the identification of sarcopenia and normal group was lower than that of conventional classification methods. To compare the performance of the model, we applied the identification of 20 subjects and obtained an accuracy of 97% in the CNN. There are studies that have shown good performances using deep learning, but exhibited better performances when parameters were used as inputs compared with raw signals. We confirmed that better performance can be obtained when important parameters are used for sarcopenia recognition using XAI rather than traditional deep learning models.
6. Conclusions
Based on various classification algorithms, sarcopenia patients were identified by inputting signals from inertial sensors and gait parameters. The spatial-temporal parameters used in the existing clinical evaluation and diagnosis represent a good tool for understanding gait. However, this does not include the features of kinematic signals during the gait cycle. Therefore, the use of descriptive statistical parameters for each gait phase can yield higher accuracy. High performance can be obtained by selecting important descriptive statistical parameters because the use of many parameters as inputs leads to overfitting or to an excessive learning time. Recently, the SHAP received tremendous attention as a feature selection method. Unlike the conventional feature selection method, which selects features with high accuracy, the SHAP has the advantage of lowering the importance of parameters if similar features exist among parameters with high importance. The input that applied the SHAP to the descriptive statistical parameters of sevens phases yielded the best performance. Specifically, it was shown that the signal of the inertial sensor contained abundant information on gait. Therefore, it is possible to diagnose and manage sarcopenia in daily life with a smart insole and not with an expensive clinical tool. Deep learning did not extract effective features from inertial signals. However, large amounts of data and the selection of different deep learning models and parameters can yield good results. Therefore, additional research on deep learning methods used for the identification of sarcopenia using inertial sensors is needed. We will apply various deep learning techniques and deep learning-based XAI techniques in future research to understand the inertial signals of sarcopenia patients. Further, analysis using deep learning requires a large amount of data; therefore, additional clinical evaluations will be conducted to obtain and analyze data of sarcopenia patients by age and dominant leg.
Author Contributions
Conceptualization, J.-K.K. and M.-N.B.; formal analysis, J.-K.K.; funding acquisition, M.-N.B., K.B.L., and S.G.H.; methodology, J.-K.K., M.-N.B., and S.G.H.; project administration, M.-N.B. and K.B.L.; software, J.-K.K.; supervision, K.B.L.; validation, J.-K.K. and S.G.H.; visualization, J.-K.K.; writing—original draft, J.-K.K.; writing—review and editing, S.G.H. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by a grant (21DRMS-B146826-04) from Development of Customized Contents Provision Technology for Realistic Disaster Management Based on Spatial Information Program funded by Ministry of the Interior and Safety of Korean government.
Institutional Review Board Statement
The study was conducted according to the guidelines of the Declaration of Helsinki and approved by the Institutional Review Board of Chungnam National University Hospital Institutional (File No: CNUH 2019-06-042).
Informed Consent Statement
Informed consent was obtained from all subjects involved in the study.
Data Availability Statement
The data are not publicly available due to company security policy and personal protection of subjects. Data are available from the authors upon reasonable request.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A

Table A1.
Spatial-temporal parameters.
Table A1.
Spatial-temporal parameters.
| Number | Subject | Normal | Sarcopenia | Normal | Sarcopenia | T-Test (Mean) | |
|---|---|---|---|---|---|---|---|
| Parameter | Mean | Mean | STD | STD | p-Value | Statistic | |
| 1 | Stance phase_right (%) | 60.263 | 60.432 | 0.683 | 0.925 | 0.697 | −0.358 |
| 2 | Stance phase_left (%) | 59.870 | 60.808 | 0.772 | 1.042 | 0.014 | −2.250 |
| 3 | Swing phase_right (%) | 39.736 | 39.567 | 0.683 | 0.925 | 0.697 | 0.358 |
| 4 | Swing phase_left (%) | 40.129 | 39.191 | 0.772 | 1.042 | 0.014 | 2.250 |
| 5 | Single support phase_right (%) | 40.182 | 39.141 | 0.926 | 1.202 | 0.006 | 2.486 |
| 6 | Single support phase_left (%) | 39.826 | 39.633 | 0.901 | 1.169 | 0.657 | 0.439 |
| 7 | Double support phase (%) | 19.975 | 21.101 | 2.149 | 4.038 | 0.142 | −1.347 |
| 8 | Stance time_right (s) | 0.604 | 0.615 | 0.013 | 0.017 | 0.323 | −0.615 |
| 9 | Stance time_left (s) | 0.600 | 0.618 | 0.013 | 0.017 | 0.091 | −1.250 |
| 10 | Swing time_right (s) (stride time) | 0.415 | 0.417 | 0.009 | 0.012 | 0.588 | 0.180 |
| 11 | Swing time_left (s) | 0.418 | 0.414 | 0.009 | 0.012 | 0.250 | 1.713 |
| 12 | Single support_left (s) | 0.401 | 0.391 | 0.006 | 0.008 | 0.013 | 2.300 |
| 13 | Double support (s) | 0.200 | 0.210 | 0.018 | 0.034 | 0.186 | −1.216 |
| 14 | Single support_right (s) | 0.397 | 0.395 | 0.006 | 0.007 | 0.642 | 0.459 |
| 15 | Stride length (m) | 0.954 | 0.915 | 0.132 | 0.148 | 0.149 | 1.297 |
| 16 | Step length_right (m) | 0.483 | 0.467 | 0.141 | 0.147 | 0.226 | 1.050 |
| 17 | Step length_left (m) | 0.471 | 0.448 | 0.123 | 0.148 | 0.107 | 1.482 |
| 18 | Step time_right (s) | 0.515 | 0.523 | 0.009 | 0.011 | 0.262 | −0.697 |
| 19 | Step time_left (s) | 0.501 | 0.506 | 0.009 | 0.011 | 0.531 | −0.114 |
| 20 | Cadence (steps/min) | 123.331 | 121.978 | 0 | 0 | 0.399 | 0.251 |
| 21 | Stance phase dRL | 1.224 | 1.812 | 0.007 | 0.011 | <0.001 | −3.973 |
| 22 | Stance time dRL | 0.014 | 0.021 | 1.025 | 1.405 | <0.001 | −3.846 |
| 23 | Swing time dRL | 0.012 | 0.019 | 0.901 | 1.319 | <0.001 | −4.032 |

Table A2.
Two phase descriptive statistical parameters.
Table A2.
Two phase descriptive statistical parameters.
| Right | Left | ||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Parameter | Max | Min | STD | AbSum | RMS | Ku | Ske | MMgr | DMM | Mdif | Max | Min | STD | AbSum | RMS | Ku | Ske | MMgr | DMM | Mdif | |
| Stance phase | AccX | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 121 | 122 | 123 | 124 | 125 | 126 | 127 | 128 | 129 | 130 |
| AccY | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 131 | 132 | 133 | 134 | 135 | 136 | 137 | 138 | 139 | 140 | |
| AccZ | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 141 | 142 | 143 | 144 | 145 | 146 | 147 | 148 | 149 | 150 | |
| GyroX | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 151 | 152 | 153 | 154 | 155 | 156 | 157 | 158 | 159 | 160 | |
| GyroY | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 | 161 | 162 | 163 | 164 | 165 | 166 | 167 | 168 | 169 | 170 | |
| GyroZ | 51 | 52 | 53 | 54 | 55 | 56 | 57 | 58 | 59 | 60 | 171 | 172 | 173 | 174 | 175 | 176 | 177 | 178 | 179 | 180 | |
| Swing phase | AccX | 61 | 62 | 63 | 64 | 65 | 66 | 67 | 68 | 69 | 70 | 181 | 182 | 183 | 184 | 185 | 186 | 187 | 188 | 189 | 190 |
| AccY | 71 | 72 | 73 | 74 | 75 | 76 | 77 | 78 | 79 | 80 | 191 | 192 | 193 | 194 | 195 | 196 | 197 | 198 | 199 | 200 | |
| AccZ | 81 | 82 | 83 | 84 | 85 | 86 | 87 | 88 | 89 | 90 | 201 | 202 | 203 | 204 | 205 | 206 | 207 | 208 | 209 | 210 | |
| GyroX | 91 | 92 | 93 | 94 | 95 | 96 | 97 | 98 | 99 | 100 | 211 | 212 | 213 | 214 | 215 | 216 | 217 | 218 | 219 | 220 | |
| GyroY | 101 | 102 | 103 | 104 | 105 | 106 | 107 | 108 | 109 | 110 | 221 | 222 | 223 | 224 | 225 | 226 | 227 | 228 | 229 | 230 | |
| GyroZ | 111 | 112 | 113 | 114 | 115 | 116 | 117 | 118 | 119 | 120 | 231 | 232 | 233 | 234 | 235 | 236 | 237 | 238 | 239 | 240 | |

Table A3.
Seven phase descriptive statistical parameters.
Table A3.
Seven phase descriptive statistical parameters.
| Right | Left | ||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Parameter | Max | Min | STD | AbSum | RMS | Ku | Ske | MMgr | DMM | Mdif | Max | Min | STD | AbSum | RMS | Ku | Ske | MMgr | DMM | Mdif | |
| Loading response | AccX | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 421 | 422 | 423 | 424 | 425 | 426 | 427 | 428 | 429 | 430 |
| AccY | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 431 | 432 | 433 | 434 | 435 | 436 | 437 | 438 | 439 | 440 | |
| AccZ | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 441 | 442 | 443 | 444 | 445 | 446 | 447 | 448 | 449 | 450 | |
| GyroX | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 451 | 452 | 453 | 454 | 455 | 456 | 457 | 458 | 459 | 460 | |
| GyroY | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 | 461 | 462 | 463 | 464 | 465 | 466 | 467 | 468 | 469 | 470 | |
| GyroZ | 51 | 52 | 53 | 54 | 55 | 56 | 57 | 58 | 59 | 60 | 471 | 472 | 473 | 474 | 475 | 476 | 477 | 478 | 479 | 480 | |
| Mid stance | AccX | 61 | 62 | 63 | 64 | 65 | 66 | 67 | 68 | 69 | 70 | 481 | 482 | 483 | 484 | 485 | 486 | 487 | 488 | 489 | 490 |
| AccY | 71 | 72 | 73 | 74 | 75 | 76 | 77 | 78 | 79 | 80 | 491 | 492 | 493 | 494 | 495 | 496 | 497 | 498 | 499 | 500 | |
| AccZ | 81 | 82 | 83 | 84 | 85 | 86 | 87 | 88 | 89 | 90 | 501 | 502 | 503 | 504 | 505 | 506 | 507 | 508 | 509 | 510 | |
| GyroX | 91 | 92 | 93 | 94 | 95 | 96 | 97 | 98 | 99 | 100 | 511 | 512 | 513 | 514 | 515 | 516 | 517 | 518 | 519 | 520 | |
| GyroY | 101 | 102 | 103 | 104 | 105 | 106 | 107 | 108 | 109 | 110 | 521 | 522 | 523 | 524 | 525 | 526 | 527 | 528 | 529 | 530 | |
| GyroZ | 111 | 112 | 113 | 114 | 115 | 116 | 117 | 118 | 119 | 120 | 531 | 532 | 533 | 534 | 535 | 536 | 537 | 538 | 539 | 540 | |
| Terminal stance | AccX | 121 | 122 | 123 | 124 | 125 | 126 | 127 | 128 | 129 | 130 | 541 | 542 | 543 | 544 | 545 | 546 | 547 | 548 | 549 | 550 |
| AccY | 131 | 132 | 133 | 134 | 135 | 136 | 137 | 138 | 139 | 140 | 551 | 552 | 553 | 554 | 555 | 556 | 557 | 558 | 559 | 560 | |
| AccZ | 141 | 142 | 143 | 144 | 145 | 146 | 147 | 148 | 149 | 150 | 561 | 562 | 563 | 564 | 565 | 566 | 567 | 568 | 569 | 570 | |
| GyroX | 151 | 152 | 153 | 154 | 155 | 156 | 157 | 158 | 159 | 160 | 571 | 572 | 573 | 574 | 575 | 576 | 577 | 578 | 579 | 580 | |
| GyroY | 161 | 162 | 163 | 164 | 165 | 166 | 167 | 168 | 169 | 170 | 581 | 582 | 583 | 584 | 585 | 586 | 587 | 588 | 589 | 590 | |
| GyroZ | 171 | 172 | 173 | 174 | 175 | 176 | 177 | 178 | 179 | 180 | 591 | 592 | 593 | 594 | 595 | 596 | 597 | 598 | 599 | 600 | |
| Pre swing | AccX | 181 | 182 | 183 | 184 | 185 | 186 | 187 | 188 | 189 | 190 | 601 | 602 | 603 | 604 | 605 | 606 | 607 | 608 | 609 | 610 |
| AccY | 191 | 192 | 193 | 194 | 195 | 196 | 197 | 198 | 199 | 200 | 611 | 612 | 613 | 614 | 615 | 616 | 617 | 618 | 619 | 620 | |
| AccZ | 201 | 202 | 203 | 204 | 205 | 206 | 207 | 208 | 209 | 210 | 621 | 622 | 623 | 624 | 625 | 626 | 627 | 628 | 629 | 630 | |
| GyroX | 211 | 212 | 213 | 214 | 215 | 216 | 217 | 218 | 219 | 220 | 631 | 632 | 633 | 634 | 635 | 636 | 637 | 638 | 639 | 640 | |
| GyroY | 221 | 222 | 223 | 224 | 225 | 226 | 227 | 228 | 229 | 230 | 641 | 642 | 643 | 644 | 645 | 646 | 647 | 648 | 649 | 650 | |
| GyroZ | 231 | 232 | 233 | 234 | 235 | 236 | 237 | 238 | 239 | 240 | 651 | 652 | 653 | 654 | 655 | 656 | 657 | 658 | 659 | 660 | |
| Initial swing | AccX | 241 | 242 | 243 | 244 | 245 | 246 | 247 | 248 | 249 | 250 | 661 | 662 | 663 | 664 | 665 | 666 | 667 | 668 | 669 | 670 |
| AccY | 251 | 252 | 253 | 254 | 255 | 256 | 257 | 258 | 259 | 260 | 671 | 672 | 673 | 674 | 675 | 676 | 677 | 678 | 679 | 680 | |
| AccZ | 261 | 262 | 263 | 264 | 265 | 266 | 267 | 268 | 269 | 270 | 681 | 682 | 683 | 684 | 685 | 686 | 687 | 688 | 689 | 690 | |
| GyroX | 271 | 272 | 273 | 274 | 275 | 276 | 277 | 278 | 279 | 280 | 691 | 692 | 693 | 694 | 695 | 696 | 697 | 698 | 699 | 700 | |
| GyroY | 281 | 282 | 283 | 284 | 285 | 286 | 287 | 288 | 289 | 290 | 701 | 702 | 703 | 704 | 705 | 706 | 707 | 708 | 709 | 710 | |
| GyroZ | 291 | 292 | 293 | 294 | 295 | 296 | 297 | 298 | 299 | 300 | 711 | 712 | 713 | 714 | 715 | 716 | 717 | 718 | 719 | 720 | |
| Mid swing | AccX | 301 | 30 | 303 | 304 | 305 | 306 | 307 | 308 | 309 | 310 | 721 | 722 | 723 | 724 | 725 | 726 | 727 | 728 | 729 | 730 |
| AccY | 311 | 312 | 313 | 314 | 315 | 316 | 317 | 318 | 319 | 320 | 731 | 732 | 733 | 734 | 735 | 736 | 737 | 738 | 739 | 740 | |
| AccZ | 321 | 322 | 323 | 324 | 325 | 326 | 327 | 328 | 329 | 330 | 741 | 742 | 743 | 744 | 745 | 746 | 747 | 748 | 749 | 750 | |
| GyroX | 331 | 332 | 333 | 334 | 335 | 336 | 337 | 338 | 339 | 340 | 751 | 752 | 753 | 754 | 755 | 756 | 757 | 758 | 759 | 760 | |
| GyroY | 341 | 342 | 343 | 344 | 345 | 346 | 347 | 348 | 349 | 350 | 761 | 762 | 763 | 764 | 765 | 766 | 767 | 768 | 769 | 770 | |
| GyroZ | 351 | 352 | 353 | 354 | 355 | 356 | 357 | 358 | 359 | 360 | 771 | 772 | 773 | 774 | 775 | 776 | 777 | 778 | 779 | 780 | |
| Terminal swing | AccX | 361 | 362 | 363 | 364 | 365 | 366 | 367 | 368 | 369 | 370 | 781 | 782 | 783 | 784 | 785 | 786 | 787 | 788 | 789 | 790 |
| AccY | 371 | 372 | 373 | 374 | 375 | 376 | 377 | 378 | 379 | 380 | 791 | 792 | 793 | 794 | 795 | 796 | 797 | 798 | 799 | 800 | |
| AccZ | 381 | 382 | 383 | 384 | 385 | 386 | 387 | 388 | 389 | 390 | 801 | 802 | 803 | 804 | 805 | 806 | 807 | 808 | 809 | 810 | |
| GyroX | 391 | 392 | 393 | 394 | 395 | 396 | 397 | 398 | 399 | 400 | 811 | 812 | 813 | 814 | 815 | 816 | 817 | 818 | 819 | 820 | |
| GyroY | 401 | 402 | 403 | 404 | 405 | 406 | 407 | 408 | 409 | 410 | 821 | 822 | 823 | 824 | 825 | 826 | 827 | 828 | 829 | 830 | |
| GyroZ | 411 | 412 | 413 | 414 | 415 | 416 | 417 | 418 | 419 | 420 | 831 | 832 | 833 | 834 | 835 | 836 | 837 | 838 | 839 | 840 | |
References
- Cruz-Jentoft, A.J.; Baeyens, J.P.; Bauer, J.M.; Boirie, Y.; Cederholm, T.; Landi, F.; Martin, F.C.; Michel, J.-P.; Rolland, Y.; Schneider, S.M.; et al. Sarcopenia: European consensus on definition and diagnosis: Report of the European Working Group on Sarcopenia in Older People. Age Ageing 2010, 39, 412–423. [Google Scholar] [CrossRef]
- Bahat, G.; Tufan, A.; Tufan, F.; Kilic, C.; Akpinar, T.S.; Kose, M.; Erten, N.; Karan, M.A.; Cruz-Jentoft, A.J. Cut-off points to identify sarcopenia according to European Working Group on Sarcopenia in Older People (EWGSOP) definition. Clin. Nutr. 2016, 35, 1557–1563. [Google Scholar] [CrossRef]
- Larsson, L.; Degens, H.; Li, M.; Salviati, L.; Lee, Y.I.; Thompson, W.; Kirkland, J.L.; Sandri, M. Sarcopenia: Aging-Related Loss of Muscle Mass and Function. Physiol. Rev. 2019, 99, 427–511. [Google Scholar] [CrossRef]
- Perez-Sousa, M.A.; Venegas-Sanabria, L.C.; Chavarro-Carvajal, D.A.; Cano-Gutierrez, C.A.; Izquierdo, M.; Correa-Bautista, J.E.; Ramírez-Vélez, R. Gait speed as a mediator of the effect of sarcopenia on dependency in activities of daily living. J. Cachexia Sarcopenia Muscle 2019, 10, 1009–1015. [Google Scholar] [CrossRef]
- De Miguel, K.; Brunete, A.; Hernando, M.; Gambao, E. Home Camera-Based Fall Detection System for the Elderly. Sensors 2017, 17, 2864. [Google Scholar] [CrossRef]
- Zhao, G.; Liu, G.; Li, H.; Pietikainen, M. 3D Gait Recognition Using Multiple Cameras. In Proceedings of the 7th International Conference on Automatic Face and Gesture Recognition (FGR06), Southampton, UK, 10–12 April 2006; pp. 529–534. [Google Scholar]
- Rashid, U.; Kumari, N.; Taylor, D.; David, T.; Signal, N. Gait Event Anomaly Detection and Correction During a Split-Belt Treadmill Task. IEEE Access 2019, 7, 68469–68478. [Google Scholar] [CrossRef]
- Seel, T.; Raisch, J.; Schauer, T. IMU-Based Joint Angle Measurement for Gait Analysis. Sensors 2014, 14, 6891–6909. [Google Scholar] [CrossRef]
- Panahandeh, G.; Mohammadiha, N.; Leijon, A.; Händel, P. Continuous Hidden Markov Model for Pedestrian Activity Clas-sification and Gait Analysis. IEEE Trans. Instrum. Meas. 2013, 62, 1073–1083. [Google Scholar] [CrossRef]
- Wang, Z.; Ji, R. Estimate spatial-temporal parameters of human gait using inertial sensors. In Proceedings of the 2015 IEEE International Conference on Cyber Technology in Automation, Control, and Intelligent Systems (CYBER), Shenyang, China, 8–12 June 2015; pp. 1883–1888. [Google Scholar]
- Kyritsis, K.; Tatli, C.L.; Diou, C.; Delopoulos, A. Automated analysis of in meal eating behavior using a commercial wristband IMU sensor. In Proceedings of the 2017 39th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Jeju, Korea, 11–15 July 2017; pp. 2843–2846. [Google Scholar]
- Dindorf, C.; Teufl, W.; Taetz, B.; Bleser, G.; Fröhlich, M. Interpretability of Input Representations for Gait Classification in Patients after Total Hip Arthroplasty. Sensors 2020, 20, 4385. [Google Scholar] [CrossRef]
- Taborri, J.; Palermo, E.; Rossi, S.; Cappa, P. Gait Partitioning Methods: A Systematic Review. Sensors 2016, 16, 66. [Google Scholar] [CrossRef]
- Levine, D.; Richards, J.; Whittle, M.W. Whittle’s Gait Analysis-E-Book, 5th ed.; Churchill Livingstone: London, UK, 2012. [Google Scholar]
- Misu, S.; Asai, T.; Ono, R.; Sawa, R.; Tsutsumimoto, K.; Ando, H.; Doi, T. Development and validity of methods for the esti-mation of temporal gait parameters from heel-attached inertial sensors in younger and older adults. Gait Posture 2017, 57, 295–298. [Google Scholar] [CrossRef]
- Mo, S.; Chow, D.H. Accuracy of three methods in gait event detection during overground running. Gait Posture 2018, 59, 93–98. [Google Scholar] [CrossRef]
- Khandelwal, S.; Wickström, N. Gait event detection in real-world environment for long-term applications: Incorporating domain knowledge into time-frequency analysis. IEEE Trans. Neural Syst. Rehabil. Eng. 2016, 24, 1363–1372. [Google Scholar] [CrossRef]
- Kim, J.; Bae, M.-N.; Lee, K.B.; Hong, S.G. Gait event detection algorithm based on smart insoles. ETRI J. 2019, 42, 46–53. [Google Scholar] [CrossRef]
- Perez-Ibarra, J.C.; Siqueira, A.A.G.; Krebs, H.I. Real-Time Identification of Gait Events in Impaired Subjects Using a Single-IMU Foot-Mounted Device. IEEE Sens. J. 2019, 20, 2616–2624. [Google Scholar] [CrossRef]
- Zhao, H.; Wang, Z.; Qiu, S.; Wang, J.; Xu, F.; Wang, Z.; Shen, Y. Adaptive gait detection based on foot-mounted inertial sensors and multi-sensor fusion. Inf. Fusion 2019, 52, 157–166. [Google Scholar] [CrossRef]
- Seel, T.; Werner, C.; Raisch, J.; Schauer, T. Iterative learning control of a drop foot neuroprosthesis—Generating physiological foot motion in paretic gait by automatic feedback control. Control Eng. Pract. 2016, 48, 87–97. [Google Scholar] [CrossRef]
- Gouwanda, D.; Gopalai, A.A.; Khoo, B.H. A Low Cost Alternative to Monitor Human Gait Temporal Parameters–Wearable Wireless Gyroscope. IEEE Sens. J. 2016, 16, 9029–9035. [Google Scholar] [CrossRef]
- Rueterbories, J.; Spaich, E.G.; Andersen, O.K. Gait event detection for use in FES rehabilitation by radial and tangential foot accelerations. Med. Eng. Phys. 2014, 36, 502–508. [Google Scholar] [CrossRef]
- Mariani, B.; Rouhani, H.; Crevoisier, X.; Aminian, K. Quantitative estimation of foot-flat and stance phase of gait using foot-worn inertial sensors. Gait Posture 2013, 37, 229–234. [Google Scholar] [CrossRef]
- Sabatini, A.M.; Martelloni, C.; Scapellato, S.; Cavallo, F. Assessment of Walking Features from Foot Inertial Sensing. IEEE Trans. Biomed. Eng. 2005, 52, 486–494. [Google Scholar] [CrossRef]
- Kang, D.W.; Choi, J.S.; Kim, H.S.; Oh, H.S.; Seo, J.W.; Lee, J.W.; Tack, G.R. Wireless gait event detection system based on single gyroscope. In Proceedings of the 6th International Conference on Ubiquitous Information Management and Communication, Kuala Lumpur, Malaysia, 20–22 February 2012; p. 88. [Google Scholar]
- Mannini, A.; Genovese, V.; Sabatini, A.M. Online Decoding of Hidden Markov Models for Gait Event Detection Using Foot-Mounted Gyroscopes. IEEE J. Biomed. Health Inform. 2013, 18, 1122–1130. [Google Scholar] [CrossRef]
- Abaid, N.; Cappa, P.; Palermo, E.; Petrarca, M.; Porfiri, M. Gait detection in children with and without hemiplegia using sin-gle-axis wearable gyroscopes. PLoS ONE 2013, 8, e73152. [Google Scholar] [CrossRef]
- Teufl, W.; Taetz, B.; Miezal, M.; Lorenz, M.; Pietschmann, J.; Jöllenbeck, T.; Fröhlich, M.; Bleser, G. Towards an Inertial Sen-sor-Based Wearable Feedback System for Patients after Total Hip Arthroplasty: Validity and Applicability for Gait Classification with Gait Kinematics-Based Features. Sensors 2019, 19, 5006. [Google Scholar] [CrossRef]
- Caramia, C.; Torricelli, D.; Schmid, M.; Muñoz-Gonzalez, A.; Gonzalez-Vargas, J.; Grandas, F.; Pons, J.L. IMU-based classi-fication of Parkinson’s disease from gait: A sensitivity analysis on sensor location and feature selection. IEEE J. Biomed. Health Inform. 2018, 22, 1765–1774. [Google Scholar] [CrossRef]
- Howcroft, J.; Kofman, J.; Lemaire, E.D. Prospective Fall-Risk Prediction Models for Older Adults Based on Wearable Sensors. IEEE Trans. Neural Syst. Rehabil. Eng. 2017, 25, 1812–1820. [Google Scholar] [CrossRef]
- Eskofier, B.M.; Lee, S.I.; Daneault, J.-F.; Golabchi, F.N.; Ferreira-Carvalho, G.; Vergara-Diaz, G.; Sapienza, S.; Costante, G.; Klucken, J.; Kautz, T.; et al. Recent machine learning advancements in sensor-based mobility analysis: Deep learning for Parkinson’s disease assessment. In Proceedings of the 2016 38th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Orlando, FL, USA, 16–20 August 2016; pp. 655–658. [Google Scholar]
- Tunca, C.; Salur, G.; Ersoy, C. Deep learning for fall risk assessment with inertial sensors: Utilizing domain knowledge in spa-tio-temporal gait parameters. IEEE J. Biomed. Health Inform. 2019, 24, 1994–2005. [Google Scholar] [CrossRef] [PubMed]
- Zhou, Y.; Romijnders, R.; Hansen, C.; Van Campen, J.; Maetzler, W.; Hortobágyi, T.; Lamoth, C.J.C. The detection of age groups by dynamic gait outcomes using machine learning approaches. Sci. Rep. 2020, 10, 1–12. [Google Scholar] [CrossRef] [PubMed]
- Rantalainen, T.; Pirkola, H.; Karavirta, L.; Rantanen, T.; Linnamo, V. Reliability and concurrent validity of spatiotemporal stride characteristics measured with an ankle-worn sensor among older individuals. Gait Posture 2019, 74, 33–39. [Google Scholar] [CrossRef]
- Cho, Y.-S.; Jang, S.-H.; Cho, J.-S.; Kim, M.-J.; Lee, H.D.; Lee, S.Y.; Moon, S.-B. Evaluation of Validity and Reliability of Inertial Measurement Unit-Based Gait Analysis Systems. Ann. Rehabil. Med. 2018, 42, 872–883. [Google Scholar] [CrossRef] [PubMed]
- Washabaugh, E.P.; Kalyanaraman, T.; Adamczyk, P.G.; Claflin, E.S.; Krishnan, C. Validity and repeatability of inertial measurement units for measuring gait parameters. Gait Posture 2017, 55, 87–93. [Google Scholar] [CrossRef]
- Nilsson, J.-O.; Gupta, A.K.; Handel, P. Foot-mounted inertial navigation made easy. In Proceedings of the 2014 International Conference on Indoor Positioning and Indoor Navigation (IPIN), Busan, Korea, 27–30 October 2014; pp. 24–29. [Google Scholar]
- Skog, I.; Nilsson, J.-O.; Handel, P. Pedestrian tracking using an IMU array. In Proceedings of the 2014 IEEE International Conference on Electronics, Computing and Communication Technologies (CONECCT), Bangalore, India, 6–7 January 2014; pp. 1–4. [Google Scholar]
- Adadi, A.; Berrada, M. Peeking Inside the Black-Box: A Survey on Explainable Artificial Intelligence (XAI). IEEE Access 2018, 6, 52138–52160. [Google Scholar] [CrossRef]
- Lundberg, S.M.; Erion, G.; Chen, H.; DeGrave, A.; Prutkin, J.M.; Nair, B.; Katz, R.; Himmelfarb, J.; Bansal, N.; Lee, S.I. Ex-plainable AI for trees: From local explanations to global understanding. arXiv 2019, arXiv:1905.04610. [Google Scholar]
- Chen, T.; Guestrin, C. Xgboost: A scalable tree boosting system. In Proceedings of the 22nd acm sigkdd international conference on knowledge discovery and data mining, San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar]
- Friedman, J.H. Greedy function approximation: A gradient boosting machine. Ann. Stat. 2001, 29, 1189–1232. [Google Scholar] [CrossRef]
- Chen, C.; Liaw, A.; Breiman, L. Using Random Forest to Learn Imbalanced Data. University of California, Berkeley. 2004. Available online: https://statistics.berkeley.edu/sites/default/files/tech-reports/666.pdf (accessed on 3 March 2021).
- Suykens, J.A.K.; Vandewalle, J. Least Squares Support Vector Machine Classifiers. Neural Process. Lett. 1999, 9, 293–300. [Google Scholar] [CrossRef]
- Gardner, M.W.; Dorling, S.R. Artificial neural networks (the multilayer perceptron)—A review of applications in the atmos-pheric sciences. Atmos. Environ. 1998, 32, 2627–2636. [Google Scholar] [CrossRef]
- Kalchbrenner, N.; Grefenstette, E.; Blunsom, P. A Convolutional Neural Network for Modelling Sentences. In Proceedings of the 52nd Annual Meeting of the Association for Computational Linguistics (Volume 1: Long Papers), Baltimore, MD, USA, 22–27 June 2014; pp. 655–665. [Google Scholar]
- Zaremba, W.; Sutskever, I.; Vinyals, O. Recurrent neural network regularization. arXiv 2014, arXiv:1409.2329. [Google Scholar]
- Hopfield, J.J. Hopfield network. Scholarpedia 2007, 2. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long Short-Term Memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Chen, T.; Xu, R.; He, Y.; Wang, X. Improving sentiment analysis via sentence type classification using BiLSTM-CRF and CNN. Expert Syst. Appl. 2017, 72, 221–230. [Google Scholar] [CrossRef]
- Hida, T.; Harada, A. Fall risk and fracture. Diagnosing sarcopenia and sarcopenic leg to prevent fall and fracture: Its difficulty and pit falls. Clin. Calcium 2013, 23, 707–712. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).