Spaces of Polynomials as Grassmanians for Immersions and Embeddings

Abstract

Let Y be a smooth compact n-manifold. We studied smooth embeddings and immersions $\beta :M\to \mathbb{R}\times Y$ of compact n-manifolds M such that $\beta \left(M\right)$ avoids some priory chosen closed poset $\mathrm{\Theta }$ of tangent patterns to the fibers of the obvious projection $\pi :\mathbb{R}\times Y\to Y$. Then, for a fixed Y, we introduced an equivalence relation between such $\beta$’s; creating a crossover between pseudo-isotopies and bordisms. We called this relation quasitopy. In the presented study of quasitopies, the spaces ${\mathcal{P}}_d^{\mathbf{c}\mathrm{\Theta }}$ of real univariate polynomials of degree d with real divisors, whose combinatorial patterns avoid a given closed poset $\mathrm{\Theta }$, play the classical role of Grassmanians. We computed the quasitopy classes ${\mathcal{Q}}_d^{\mathsf{emb}}(Y,\mathbf{c}\mathrm{\Theta })$ of $\mathrm{\Theta }$-constrained embeddings $\beta$ in terms of homotopy/homology theory of spaces Y and ${\mathcal{P}}_d^{\mathbf{c}\mathrm{\Theta }}$. We proved also that the quasitopies of embeddings stabilize, as $d\to \infty$.

1. Introduction

This paper is the first in a series, inspired by the pioneering works of Arnold [1,2,3], and Vassiliev [4]. It is based heavily on computations from [5,6].

The research of Ekholm, Szücs, and Terpai [7,8,9,10,11,12] deals with bordisms of smooth maps whose singularity types are controlled locally. Philosophically, our work is closely related to the investigations in these papers, especially to the work of Lippner [13]. On the one hand, by dealing with immersions of manifolds of a variety of dimensions, the papers [8,9,10,11,12,13] contain more general results, while we are concerned here only with immersions of n-dimensional manifolds into $(n+1)$-dimensional targets. On the other hand, this selectivity, forces us to deal with a more complex combinatorics than the one exhibited by the general Morin-type singularities.

The main difference between the forth mentioned research and our efforts here is that we deal with bordisms of smooth maps with not locally controlled singularity types, but with bordisms of maps whose singularity types are controlled semi-locally, i.e., we impose restrictions on the types of singularities and on their order along the one-dimensional oriented fibers of smooth maps.

In this paper, the singularity type of a map is represented by a sequence $\omega$ of natural numbers. For example, $\omega =\left(12421\right)$. The sets of such sequences $\omega$ admit a particular partial order “≻”, mimicking the behavior of real roots of real polynomials in one variable under deformations. Section 2 is devoted to describing the nature of this partial order. For example, $\left(12421\right)\succ \left(1621\right)$, the result of merging two adjacent roots of multiplicity 2 and 4.

In the case of [14], we applied and extended the results of this article to a study of the traversing, smooth vector flows on manifolds X with boundaries (these flows admit Lyapunov functions). There is a poset $\mathbf{c}\mathrm{\Theta }$ that controls the combinatorial patterns $\omega$ of tangency of the flow trajectories to the boundary $\mathit{\partial }X$, and $\mathrm{\Theta }$ stands for the corresponding “forbidden” closed poset.

For example, we may ask whether a given manifold X admits a traversing flow whose trajectories have an order of tangency to $\mathit{\partial }X$ that does not exceed a given number k, or, say, have trajectories that are simply tangent to $\mathit{\partial }X$ at less than k points.

In particular, applications of this paper to the traversing vector flows on manifolds with boundaries and their convex envelops (see [14] for the relevant definitions) lead to new characteristic classes of such flows. They represent obstructions to finding a traversing flow on a given manifold X, whose trajectories avoid a priori given patterns $\omega \in \mathrm{\Theta }$ of tangency to the boundary $\mathit{\partial }X$. Bridging between algebraic topology of polynomial spaces and characteristic classes of traversing flows seems to an interesting endeavor.

Now, let us describe our results informally, in a manner that clarifies their nature, but does not involve their most general forms (which carry the burden of combinatorial decorations).

We studied immersions and embeddings $\beta :M\to \mathbb{R}\times Y$ of compact smooth n-manifolds M into products $\mathbb{R}\times Y$, where Y is a given compact smooth n-manifold. We denote $\mathcal{L}$ as the oriented one-dimensional foliation on $\mathbb{R}\times Y$, formed by the fibers of the obvious projection $\pi :\mathbb{R}\times Y\to Y$. We are interested in the ways the hypersurface $\beta \left(M\right)$ may be tangent to the fibers of $\mathcal{L}$. More precisely, we impose a set of restrictions $\mathrm{\Theta }$ on the combinatorial patterns $\omega$ of such tangencies. As before, each pattern $\omega$ is an ordered sequence of natural numbers, each of which represents the tangency order between an oriented $\pi$-fiber ${\mathcal{L}}_y$ and the hypersurface $\beta \left(M\right)\subset \mathbb{R}\times Y$.

Ref. [15] contains a similar investigation of immersions (“doodles”) of one-dimensional manifolds M in the ruled products $\mathbb{R}\times S^1$ and $\mathbb{R}\times [0,1]$.

Next, we organize immersions $\{\beta :M\to \mathbb{R}\times Y\}$ that do not violate restrictions from a partially ordered set $\mathrm{\Theta }$ into a set $\mathcal{Q}(Y,\mathbf{c}\mathrm{\Theta })$ of equivalence classes; we call equivalent $\beta$’s “quasitopic” (see Definition 9). The quasitopies is a hybrid between classical notions of pseudo-isotopies and bordisms (see Figure 2). In this paper, we deal with various brands of quasitopies, richly decorated by combinatorial data. However, in this introduction, to simplify the description of our results by omitting the decorations. In particular, we may insist that the cardinality of the fiber of $\pi \circ \beta$ is less than or equal to a given natural number d. In such a case, we are dealing with the quasitopies ${\mathcal{Q}}_d(Y,\mathbf{c}\mathrm{\Theta })$.

Our main observation is that spaces ${\mathcal{P}}_d^{\mathbf{c}\mathrm{\Theta }}$ of real degree d monic polynomials in one variable, whose real divisors do not belong to the forbidden closed poset $\mathrm{\Theta }$, play a role of Grassmanians for immersions/embeddings $\beta$ as above. This is reminiscent to the role played by the Stiefel manifolds of k-frames in ${\mathbb{R}}^m$ in the Smale theory of immersions [16].

At least for embeddings, we are able to compute ${\mathcal{Q}}_d^{\mathsf{emb}}(Y,\mathbf{c}\mathrm{\Theta })$ in terms of the homotopy theory of ${\mathcal{P}}_d^{\mathbf{c}\mathrm{\Theta }}$ and Y. Our computation is heavily based on the results from [5,6] about homotopy and homology types of ${\mathcal{P}}_d^{\mathbf{c}\mathrm{\Theta }}$ for many specific $\mathrm{\Theta }$’s. This information allows us to describe new cohomological invariants of ${\mathcal{Q}}_d^{\mathsf{emb}}(Y,\mathbf{c}\mathrm{\Theta })$ and ${\mathcal{Q}}_d^{\mathsf{imm}}(Y,\mathbf{c}\mathrm{\Theta })$ (characteristic classes of quasitopies) in purely combinatorial terms, related to $\mathrm{\Theta }$. Here, the superscript “$\mathsf{imm}$” stands for immersions. In many special cases, we see subtle connections between ${\mathcal{Q}}_d^{\mathsf{emb}}(Y,\mathbf{c}\mathrm{\Theta })$ and homotopy groups of spheres. Implicitly, this connection goes back to [1,2,4].

Let $D^n$ denote the standard n-ball. We notice that the sets ${\mathcal{Q}}_d^{\mathsf{emb}}(D^n,\mathbf{c}\mathrm{\Theta })$ and ${\mathcal{Q}}_d^{\mathsf{imm}}(D^n,\mathbf{c}\mathrm{\Theta })$ have a group structure (abelian for $n>1$). We denote these groups by ${\mathsf{G}}_d^{\mathsf{emb}}(n;\mathbf{c}\mathrm{\Theta })$ and ${\mathsf{G}}_d^{\mathsf{imm}}(n;\mathbf{c}\mathrm{\Theta })$ and prove that ${\mathsf{G}}_d^{\mathsf{imm}}(n;\mathbf{c}\mathrm{\Theta })$ is a split extension of ${\mathsf{G}}_d^{\mathsf{emb}}(n;\mathbf{c}\mathrm{\Theta })$. Then, we are able to validate a group isomorphism ${\mathsf{G}}_d^{\mathsf{emb}}(n;\mathbf{c}\mathrm{\Theta })\approx {\pi }_n({\mathcal{P}}_d^{\mathbf{c}\mathrm{\Theta }},pt)$.

With the help of the boundary connected sum operation, the groups ${\mathsf{G}}_d^{\mathsf{emb}}(n;\mathbf{c}\mathrm{\Theta })$ and ${\mathsf{G}}_d^{\mathsf{imm}}(n;\mathbf{c}\mathrm{\Theta })$ act naturally on the sets ${\mathcal{Q}}_d^{\mathsf{emb}}(Y,\mathbf{c}\mathrm{\Theta })$ and ${\mathcal{Q}}_d^{\mathsf{imm}}(Y,\mathbf{c}\mathrm{\Theta })$, respectively.

For two pairs $A\supset B$, $C\supset D$ of topological spaces, let $\left[\right(A,B),(C,D\left)\right]$ denote the homotopy classes of continuous maps $f:(A,B)\to (C,D)$, where $f\left(B\right)\subset D$.

We prove that the classifying map

$${\mathrm{\Phi }}^{\mathsf{emb}}:{\mathcal{Q}}_d^{\mathsf{emb}}(Y,\mathbf{c}\mathrm{\Theta })\to [(Y,\mathit{\partial }Y),({\mathcal{P}}_d^{\mathbf{c}\mathrm{\Theta }},pt)]$$

is a bijection, and the classifying map

$${\mathrm{\Phi }}^{\mathsf{imm}}:{\mathcal{Q}}_d^{\mathsf{imm}}(Y,\mathbf{c}\mathrm{\Theta })\to [(Y,\mathit{\partial }Y),({\mathcal{P}}_d^{\mathbf{c}\mathrm{\Theta }},pt)]$$

is a surjection. Moreover, these maps are equivariant with respect to the ${\mathsf{G}}_d^{\mathsf{emb}}(n;\mathbf{c}\mathrm{\Theta })$- or ${\mathsf{G}}_d^{\mathsf{imm}}(n;\mathbf{c}\mathrm{\Theta })$-actions on the quasitopies (on the sources of the classifying maps ${\mathrm{\Phi }}^{\mathsf{emb}/\mathsf{imm}}$) and the corresponding action of the homotopy groups ${\pi }_n({\mathcal{P}}_d^{\mathbf{c}\mathrm{\Theta }},pt)$ on the sets $[(Y,\mathit{\partial }Y),({\mathcal{P}}_d^{\mathbf{c}\mathrm{\Theta }},pt)]$ (on the targets of the maps ${\mathrm{\Phi }}^{\mathsf{emb}/\mathsf{imm}}$).

We present also a variety of results (for example, see Proposition 14) about the stabilization of ${\mathcal{Q}}_d^{\mathsf{emb}}(Y,\mathbf{c}\mathrm{\Theta })$ as $d\to \infty$.

See [15] for similar computations of quasitopies of immersions/embeddings of one-dimensional manifolds M into ruled cylinders $\mathbb{R}\times S^1$ or ruled strips $\mathbb{R}\times [0,1]$, subject to a very special and much simpler combinatorics $\mathbf{c}\mathrm{\Theta }$.

We conclude this introduction with a few examples of computations, performed in this paper. There is nothing exceptional about these examples, they are exhibited here just to illustrate the intricate flavor of meta-theorems in this article. On a positive note, the next four propositions are formulated in terms which do not require familiarity with the notations introduced later. The notion of quasitopies is implicit in these examples.

Consider the space ${\mathbb{R}}^n$ with the coordinates $u,x_1,\dots ,x_{n-1}$ and the projections

$${\pi }_n:(u,x_1,\dots ,x_{n-1})\to (x_1,\dots ,x_{n-1})$$

where we denote by ${\mathbb{R}}_{+}^n\subset {\mathbb{R}}^n$ the half space $\{x_{n-1}\ge 0\}$.

For any subset $A\subset {\mathbb{R}}^n$ whose $x_1$-coordinates belong to an interval $(0,1)$, we denote by $kA$ the disjoint union of k copies of A, obtained from A by applying $(k-1)$ times the parallel shift

$$\{Sh:(u,x_1,\dots ,x_{n-1})\to (u,x_1+1,\dots ,x_{n-1})\}.$$

In the following four proposition examples, we assume that all the submanifolds are in general position with respect to the projections ${\left\{{\pi }_n\right\}}_n$, i.e., the restrictions of the projections to submanifolds locally are Morin maps [17].

Proposition 1. 

There exists a regularly embedded closed oriented three-fold $M^3\subset {\mathbb{R}}^4$ such that

• The fibers of the projection ${\pi }_4|:M^3\to {\mathbb{R}}^3$ have cardinalities $\le 9$;
• Every ${\pi }_4$-fiber is tangent to $M^3$ with order of tangency $\le \mathbf{3}$;
• $M^3$ is the boundary of an oriented compact smooth 4-manifold $N^4\subset {\mathbb{R}}_{+}^5$;
• Any such $N^4$ must be tangent to some ${\pi }_5$-fiber with the order of tangency $\ge \mathbf{4}$, provided that the fibers of the projection ${\pi }_5|:N^4\to {\mathbb{R}}^4$ have cardinalities $\le 9$;
• Moreover, for any natural k, the disjoint union $k{M}^3\subset {\mathbb{R}}^4$ of k copies of $M^3$, has the same properties as $M^3$.

Proposition 2. 

There exists a regularly embedded closed oriented 14-dimensional manifold $M^{14}\subset {\mathbb{R}}^{15}$ such that

• The fibers of the projection ${\pi }_{15}:M^{14}\to {\mathbb{R}}^{14}$ have cardinalities $\le 9$;
• Every ${\pi }_{15}$-fiber is tangent to $M^{14}$ with order of tangency $\le \mathbf{3}$;
• $M^{14}$ is a boundary of a compact smooth 15-manifold $N^{15}\subset {\mathbb{R}}_{+}^{16}$;
• Any such $N^{15}$ must be tangent to some ${\pi }_{16}$-fiber with the order of tangency $\ge \mathbf{4}$, provided that the fibers of the projection ${\pi }_{16}:N^{15}\to {\mathbb{R}}_{+}^{15}$ have cardinalities $\le 9$;
• Moreover, 84 disjoint copies of $M^{14}$ form the boundary of some 15-dimensional ${\tilde{N}}^{15}\subset {\mathbb{R}}_{+}^{16}$, tangent to all ${\pi }_{16}$-fibers with the order of tangency $\le \mathbf{3}$, provided that the fibers of the projection ${\pi }_{16}:N^{15}\to {\mathbb{R}}_{+}^{15}$ have cardinalities $\le 9$; less than $\mathbf{84}$ copies of $M^{14}$ do not bound such $N^{15}$.

Proposition 3. 

There exists a regularly embedded closed oriented seven-dimensional manifold $M^7\subset {\mathbb{R}}^8$ such that

• The fibers of the projection ${\pi }_8:M^7\to {\mathbb{R}}^7$ have cardinalities $\le 8$;
• Every ${\pi }_8$-fiber is tangent to $M^7$ with order of tangency $\le \mathbf{3}$;
• $M^7$ is a boundary of a compact orientable smooth eight-manifold $N^8\subset {\mathbb{R}}_{+}^9$;
• Any such $N^8$ must be tangent to some ${\pi }_8$-fiber with the order of tangency $\ge \mathbf{4}$, provided that the fibers of the projection ${\pi }_9:N^8\to {\mathbb{R}}_{+}^8$ have cardinalities that do not exceed eight;
• Moreover, $\mathbf{12}$ disjoint copies of $M^7$ form the boundary of some eight-dimensional ${\tilde{N}}^8\subset {\mathbb{R}}_{+}^9$, tangent to all ${\pi }_9$-fibers with the order of tangency $\le \mathbf{3}$, provided that the fibers of the projection ${\pi }_9:N^8\to {\mathbb{R}}_{+}^8$ have cardinalities that do not exceed eight; less than 12 copies of $M^7$ do not bound such ${\tilde{N}}^8$.

Based on Example 4, the number of copies of M in these assertions reflect the computations of the homotopy groups ${\pi }_n\left(S^2\right)$ for $n=3$ and $n=14$ in case of the first two propositions, and of the homotopy group ${\pi }_7\left(S^4\right)$ in case of the last one.

Evidently, all three propositions depend very much on the delicate interplay between the maximal cardinalities d of fibers of the generic smooth maps ${\pi }_n:M^{n-1}=\mathit{\partial }{N}^n\to {\mathbb{R}}^{n-1}$ and ${\pi }_{n+1}:N^n\to {\mathbb{R}}_{+}^n$ and the permissible orders k of tangency of these submanilolds to the fibers. For fixed k’s, as d increases, these assertions may fail.

In contrast, the next proposition, based on Example 8, exhibits a stabilization of the cardinalities of the $({\pi }_{n+1}:N^n\to {\mathbb{R}}_{+}^n)$ fibers for the fixed boundary $M=\mathit{\partial }{N}^n\subset {\mathbb{R}}^n$ and the fixed “forbidden” closed poset $\mathrm{\Theta }=⟨\left(4\right),\left(33\right)⟩$. The poset is generated by two tangency patterns, $\left(4\right)$ and $\left(33\right)$ (see Section 2 for the exact definition of the poset $⟨\left(4\right),\left(33\right)⟩$).

Proposition 4. 

as followed.

• Let $M^{n-1}\subset {\mathbb{R}}^n$ be a smooth closed submanifold such that the fibers of the map ${\pi }_n:M^{n-1}\subset {\mathbb{R}}^{n-1}$ avoid the tangency patterns from the poset $⟨\left(4\right),\left(33\right)⟩$ and are of the maximal cardinality $\le 2n-6$.
  If no smooth compact submanifold $(N^n,\mathit{\partial }{N}^n)\subset ({\mathbb{R}}_{+}^{n+1},{\mathbb{R}}^n)$, subject to the following three properties:
  (1) The boundary $\mathit{\partial }{N}^n=M^{n-1}$;
  (2) The fibers of ${\pi }_{n+1}:N^n\to {\mathbb{R}}_{+}^n$ avoid the tangency patterns from the poset $⟨\left(4\right),\left(33\right)⟩$;
  (3) The maximal cardinality of the of ${\pi }_{n+1}$-fibers does not exceed $2n-4$;exists, then no such $N^n$, possessing only properties (1) and (2), exists as well.
• Let $(N^n,\mathit{\partial }{N}^n)\subset ({\mathbb{R}}_{+}^{n+1},{\mathbb{R}}^n)$ be a smooth compact submanifold whose ${\pi }_{n+1}$-fibers avoid tangency patterns from the poset $⟨\left(4\right),\left(33\right)⟩$. Assume that the fibers of the map ${\pi }_{n+1}|:\mathit{\partial }{N}^n\to {\mathbb{R}}^n$ have the maximal cardinality $\le 2n-6$.
  Then, there exists another smooth compact submanifold manifold $({\tilde{N}}^n,\mathit{\partial }{\tilde{N}}^n)\subset ({\mathbb{R}}_{+}^{n+1},{\mathbb{R}}^n)$ such that
  (1) $\mathit{\partial }{\tilde{N}}^n=\mathit{\partial }{N}^n$;
  (2) The tangency patterns to the fibers ${\pi }_{n+1}:{\tilde{N}}^n\to {\mathbb{R}}_{+}^n$ still avoid $⟨\left(4\right),\left(33\right)⟩$;
  (3) The cardinality of the fibers of the map ${\pi }_{n+1}|:{\tilde{N}}^n\to {\mathbb{R}}^n$ is $\le 2n-4$.

2. Spaces of Real Polynomials with Constrained Real Divisors

For readers’ convenience, in this section, we state a number of results from [5,6] about the algebraic topology of spaces of real monic univariate polynomials with constrained real divisors. These results will be crucial for the applications to follow.

Let ${\mathcal{P}}_d$ denote the space of real monic univariate polynomials of degree d. Given a polynomial $P\left(u\right)=u^d+a_{d-1}{u}^{d-1}+\cdots +a_0$ with real coefficients, we consider its real divisor $D_{\mathbb{R}}\left(P\right)$.

Let ${\omega }_i$ denotes the multiplicity of the i-th real root of P, the roots being ordered by their magnitude in $\mathbb{R}$. The ordered ℓ-tuple $\omega =({\omega }_1,\dots ,{\omega }_{\mathit{\ell }})$ is called the real root multiplicity pattern of $P\left(x\right)$, or the multiplicity pattern for short.

Such sequences $\omega$ form a universal poset $(\mathbf{\Omega },\succ )$. The partial order “≻” in $\mathbf{\Omega }$ is defined in terms of two types of elementary operations: merges ${\left\{{\mathsf{M}}_i\right\}}_i$ and inserts ${\left\{{\mathsf{I}}_i\right\}}_i$.

The operation ${\mathsf{M}}_i$ merges a pair of adjacent entries ${\omega }_i,{\omega }_{i+1}$ of $\omega =({\omega }_1,\dots ,{\omega }_i,{\omega }_{i+1},\dots ,{\omega }_q)$ into a single component ${\tilde{\omega }}_i={\omega }_i+{\omega }_{i+1}$, thus forming a new shorter sequence ${\mathsf{M}}_i\left(\omega \right)=({\omega }_1,\dots ,{\tilde{\omega }}_i,\dots ,{\omega }_q)$. The operation ${\mathsf{I}}_i$ either insert 2 in-between ${\omega }_i$ and ${\omega }_{i+1}$, thus forming a new longer sequence ${\mathsf{I}}_i\left(\omega \right)=(\dots ,{\omega }_i,2,{\omega }_{i+1},\dots )$, or, in the case of ${\mathsf{I}}_0$, appends 2 before the sequence $\omega$, or, in the case ${\mathsf{I}}_q$, appends 2 after the sequence $\omega$.

So the merge operation ${\mathsf{M}}_j:\mathbf{\Omega }\to \mathbf{\Omega }$ sends $\omega =({\omega }_1,\dots ,{\omega }_{\ell })$ to the composition

$${\mathsf{M}}_j\left(\omega \right)=(M_j{\left(\omega \right)}_1,\dots ,M_j{\left(\omega \right)}_{\ell -1}),$$

where, for any $j\ge \ell$, one gets ${\mathsf{M}}_j\left(\omega \right)=\omega$, and for $1\le j<\ell$, one gets

$$\begin{array}{c}\hfill \left\{\begin{array}{ccc}{\mathsf{M}}_j{\left(\omega \right)}_i\hfill & =\hfill & {\omega }_i\mathrm{if}i<j,\hfill \\ {\mathsf{M}}_j{\left(\omega \right)}_j\hfill & =\hfill & {\omega }_j+{\omega }_{j+1},\hfill \\ {\mathsf{M}}_j{\left(\omega \right)}_i\hfill & =\hfill & {\omega }_{i+1}\mathrm{if}i+1<j\le \ell -1.\hfill \end{array}\right.\end{array}$$

(1)

Similarly, we introduce the insert operation ${\mathsf{I}}_j:\mathbf{\Omega }\to \mathbf{\Omega }$ that sends $\omega =({\omega }_1,\dots ,{\omega }_{\ell })$ to the composition ${\mathsf{I}}_j\left(\omega \right)=(I_j{\left(\omega \right)}_1,\dots ,I_j{\left(\omega \right)}_{\ell +1})$, where for any $j>\ell +1$, one gets ${\mathsf{I}}_j\left(\omega \right)=\omega$, and for $1\le j\le \ell +1$, one gets

$$\begin{array}{c}\hfill \left\{\begin{array}{ccc}{\mathsf{I}}_j{\left(\omega \right)}_i\hfill & =\hfill & {\omega }_i\mathrm{if}i<j,\hfill \\ {\mathsf{I}}_j{\left(\omega \right)}_j\hfill & =\hfill & 2,\hfill \\ {\mathsf{I}}_j{\left(\omega \right)}_i\hfill & =\hfill & {\omega }_{i-1}\mathrm{if}j\le i\le \ell +1.\hfill \end{array}\right.\end{array}$$

(2)

Definition 1. 

For $\omega ,{\omega }^{\prime }\in \mathbf{\Omega }$, we define the order relation $\omega \succ {\omega }^{\prime }$ if one can produce ${\omega }^{\prime }$ from ω by applying a sequence of the elementary operations in (1) and (2). □

For a sequence $\omega =({\omega }_1,{\omega }_2,\dots ,{\omega }_q)\in \mathbf{\Omega }$, we introduce the norm and the reduced norm of $\omega$ by the following formulas:

$$\begin{array}{c}\hfill \left|\omega \right|{=}_{\mathsf{def}}\sum _i{\omega }_i\mathrm{and}{\left|\omega \right|}^{\prime }{=}_{\mathsf{def}}\sum _i({\omega }_i-1).\end{array}$$

(3)

Note that q, the cardinality of the support of $\omega$, is equal to $\left|\omega \right|-{\left|\omega \right|}^{\prime }$.

Let ${\mathring{\mathsf{R}}}_d^{\omega }$ be of the set of all polynomials with real root multiplicity pattern $\omega$, and let ${\mathsf{R}}_d^{\omega }$ be its closure in ${\mathcal{P}}_d$.

For a given collection $\mathrm{\Theta }$ of multiplicity patterns $\left\{\omega \right\}$ which share the parity of their norms $\left\{\right|\omega \left|\right\}$ and is closed under the merge and insert operations, we consider the union ${\mathcal{P}}_d^{\mathrm{\Theta }}$ of the subspaces ${\left\{{\mathsf{R}}_d^{\omega }\right\}}_{\omega }$, taken over all $\omega \in \mathrm{\Theta }$ such that $\left|\omega \right|\le d$ and $\left|\omega \right|\equiv dmod2$. We denote by ${\mathcal{P}}_d^{\mathbf{c}\mathrm{\Theta }}$ its complement ${\mathcal{P}}_d\setminus {\mathcal{P}}_d^{\mathrm{\Theta }}$.

Since ${\mathcal{P}}_d^{\mathrm{\Theta }}$ is contractible, it makes more sense to consider its one-point compactification ${\overline{\mathcal{P}}}_d^{\mathrm{\Theta }}$ (which is the union of the one-point compactifications ${\overline{\mathsf{R}}}_d^{\omega }$ for $\omega \in \mathrm{\Theta }$ with all the points at infinity being identified). If the set ${\overline{\mathcal{P}}}_d^{\mathrm{\Theta }}$ is closed in ${\overline{\mathcal{P}}}_d$, by the Alexander duality on the sphere ${\overline{\mathcal{P}}}_d\cong S^d$, we get

$$H^j({\mathcal{P}}_d^{\mathbf{c}\mathrm{\Theta }};\mathbb{Z})\approx H_{d-j-1}({\overline{\mathcal{P}}}_d^{\mathrm{\Theta }};\mathbb{Z}).$$

This implies that the spaces ${\mathcal{P}}_d^{\mathbf{c}\mathrm{\Theta }}$ and ${\overline{\mathcal{P}}}_d^{\mathrm{\Theta }}$ carry the same (co)homological information. Let us describe it in pure combinatorial terms.

For a subposet $\mathrm{\Theta }\subset \mathbf{\Omega }$ and natural numbers $d,k$, we introduce the following notations:

$$\begin{array}{cc}\hfill {\mathrm{\Theta }}_{\left[d\right]}{=}_{\mathsf{def}}& \{\omega \in \mathrm{\Theta }:|\omega |=d\},{\mathrm{\Theta }}_{⟨d]}{=}_{\mathsf{def}}\{\omega \in \mathrm{\Theta }:|\omega |\le d\},\\ \hfill {\mathrm{\Theta }}_{{|\sim |}^{\prime }=k}{=}_{\mathsf{def}}& {\{\omega \in \mathrm{\Theta }:|\omega |}^{\prime }=k\},{\mathrm{\Theta }}_{{|\sim |}^{\prime }\ge k}{=}_{\mathsf{def}}{\{\omega \in \mathrm{\Theta }:|\omega |}^{\prime }\ge k\}.\end{array}$$

(4)

Assuming that $\mathrm{\Theta }\subset \mathbf{\Omega }$ is a closed sub-poset, let

$$\mathbf{c}\mathrm{\Theta }{=}_{\mathsf{def}}\mathbf{\Omega }\setminus \mathrm{\Theta }\mathrm{and}\mathbf{c}{\mathrm{\Theta }}_{⟨d]}{=}_{\mathsf{def}}{\mathbf{\Omega }}_{⟨d]}\setminus {\mathrm{\Theta }}_{⟨d]}.$$

We denote by $\mathbb{Z}\left[{\mathbf{\Omega }}_{⟨d]}\right]$ the free $\mathbb{Z}$-module, generated by the elements of ${\mathbf{\Omega }}_{⟨d]}$. Using the merge operators ${\mathsf{M}}_k$ and the insert operators ${\mathsf{I}}_k$ on ${\mathbf{\Omega }}_{⟨d]}$, we define two homomorphisms of $\mathbb{Z}\left[{\mathbf{\Omega }}_{⟨d]}\right]$:

$${\mathit{\partial }}_{\mathsf{M}}\left(\omega \right){=}_{\mathsf{def}}-\sum _{k=1}^{s_{\omega }-1}{(-1)}^k{\mathsf{M}}_k\left(\omega \right)\mathrm{and}{\mathit{\partial }}_{\mathsf{I}}\left(\omega \right){=}_{\mathsf{def}}\sum _{k=0}^{s_{\omega }}{(-1)}^k{\mathsf{I}}_k\left(\omega \right),$$

where $s_{\omega }{=}_{\mathsf{def}}\left|\omega \right|-{\left|\omega \right|}^{\prime }$ is the cardinality of the support of $\omega$. The homomorphisms ${\mathit{\partial }}_{\mathsf{M}}$ and ${\mathit{\partial }}_{\mathsf{I}}$ are anti-commuting differentials.

Next, we introduce the homomorphism

$$\mathit{\partial }{=}_{\mathsf{def}}{\mathit{\partial }}_{\mathsf{M}}+{\mathit{\partial }}_{\mathsf{I}}:\mathbb{Z}\left[{\mathbf{\Omega }}_{⟨d]}\right]\to \mathbb{Z}\left[{\mathbf{\Omega }}_{⟨d]}\right]$$

by the formula

$$\begin{array}{c}\hfill \mathit{\partial }\left(\omega \right){=}_{\mathsf{def}}\left\{\begin{array}{c}-\sum _{k=1}^{s_{\omega }-1}{(-1)}^k{\mathsf{M}}_k\left(\omega \right)+\sum _{k=0}^{s_{\omega }}{(-1)}^k{\mathsf{I}}_k\left(\omega \right),\mathrm{for}\left|\omega \right|<d,\hfill \\ \\ -\sum _{k=1}^{s_{\omega }-1}{(-1)}^k{\mathsf{M}}_k\left(\omega \right),\mathrm{for}\left|\omega \right|=d.\hfill \end{array}\right.\end{array}$$

(5)

It is easy to see that for a closed poset ${\mathrm{\Theta }}_{⟨d]}\subset {\mathbf{\Omega }}_{⟨d]}$, the restrictions of the differentials $\mathit{\partial },{\mathit{\partial }}_{\mathsf{M}}$, and ${\mathit{\partial }}_{\mathsf{I}}$ to the free $\mathbb{Z}$-module $\mathbb{Z}\left[{\mathrm{\Theta }}_{⟨d]}\right]$ are well-defined. Thus, for any closed sub-poset ${\mathrm{\Theta }}_{⟨d]}\subset {\mathbf{\Omega }}_{⟨d]}$, we may consider the differential complex $\mathit{\partial }:\mathbb{Z}\left[{\mathrm{\Theta }}_{⟨d]}\right]\to \mathbb{Z}\left[{\mathrm{\Theta }}_{⟨d]}\right]$, whose $(d-j)$-grading is defined by the module $\mathbb{Z}\left[{\mathrm{\Theta }}_{{⟨d],|\sim |}^{\prime }=j}\right]$. We denote by ${\mathit{\partial }}^{*}:\mathbb{Z}{\left[{\mathrm{\Theta }}_{⟨d]}\right]}^{*}\to \mathbb{Z}{\left[{\mathrm{\Theta }}_{⟨d]}\right]}^{*}$ its dual, where $\mathbb{Z}{\left[{\mathrm{\Theta }}_{⟨d]}\right]}^{*}:=\mathsf{Hom}(\mathbb{Z}\left[{\mathrm{\Theta }}_{⟨d]}\right],\mathbb{Z})$ and the operator ${\mathit{\partial }}^{*}$ is the dual of the boundary operator ∂.

Then, we consider the quotient set ${\mathrm{\Theta }}_{⟨d]}^{\#}:={\mathbf{\Omega }}_{⟨d]}/{\mathrm{\Theta }}_{⟨d]}$. For the closed subposet ${\mathrm{\Theta }}_{⟨d]}$, the partial order in ${\mathbf{\Omega }}_{⟨d]}$ induces a partial order in the quotient ${\mathrm{\Theta }}_{⟨d]}^{\#}$.

Next, we introduce a new differential complex $(\mathbb{Z}[{\mathrm{\Theta }}_{⟨d]}^{\#}],{\mathit{\partial }}^{\#})$ by including it in the short exact sequence of differential complexes:

$$\begin{array}{c}\hfill 0\to (\mathbb{Z}\left[{\mathrm{\Theta }}_{⟨d]}\right],\mathit{\partial })\to (\mathbb{Z}\left[{\mathbf{\Omega }}_{⟨d]}\right],\mathit{\partial })\to (\mathbb{Z}\left[{\mathrm{\Theta }}_{⟨d]}^{\#}\right],{\mathit{\partial }}^{\#})\to 0.\end{array}$$

(6)

We will rely on the following result from [6], which reduces the computation of the (reduced) cohomology ${\tilde{H}}^{*}({\mathcal{P}}_d^{\mathbf{c}\mathrm{\Theta }};\mathbb{Z})$ to Algebra and Combinatorics.

Theorem 1 

([6]). Let $\mathrm{\Theta }\subset {\mathbf{\Omega }}_{⟨d]}$ be a closed subposet. Then, for any $j\in [0,d]$, there are group isomorphisms

$$\begin{array}{c}\hfill {\tilde{H}}^j({\mathcal{P}}_d^{\mathbf{c}\mathrm{\Theta }};\mathbb{Z})\stackrel{\mathcal{D}}{\approx }{H}_{d-j}({\overline{\mathcal{P}}}_d,{\overline{\mathcal{P}}}_d^{\mathrm{\Theta }};\mathbb{Z})\approx H_{d-j}\left({\mathit{\partial }}^{\#}:\mathbb{Z}\left[{\mathrm{\Theta }}^{\#}\right]\to \mathbb{Z}\left[{\mathrm{\Theta }}^{\#}\right]\right),\\ \hfill {\tilde{H}}_j({\mathcal{P}}_d^{\mathbf{c}\mathrm{\Theta }};\mathbb{Z})\stackrel{\mathcal{D}}{\approx }{H}^{d-j}({\overline{\mathcal{P}}}_d,{\overline{\mathcal{P}}}_d^{\mathrm{\Theta }};\mathbb{Z})\approx H_{d-j}\left({\left({\mathit{\partial }}^{\#}\right)}^{*}:{\left(\mathbb{Z}\left[{\mathrm{\Theta }}^{\#}\right]\right)}^{*}\to {\left(\mathbb{Z}\left[{\mathrm{\Theta }}^{\#}\right]\right)}^{*}\right),\end{array}$$

(7)

where $\mathcal{D}$ denote the Poincaré duality isomorphisms.

For $d^{\prime }\ge d$, $d^{\prime }\equiv dmod2$, we consider an embedding ${ϵ}_{d,d^{\prime }}:{\mathcal{P}}_d\to {\mathcal{P}}_{d^{\prime }}$, defined by

$$\begin{array}{c}\hfill {ϵ}_{d,d^{\prime }}\left(P\right)\left(u\right){=}_{\mathsf{def}}{(u^2+1)}^{{\displaystyle \frac{d^{\prime }-d}{2}}}·P\left(u\right).\end{array}$$

(8)

It preserves the $\mathbf{\Omega }$-stratifications of the two spaces by the combinatorial types $\omega$ of real divisors.

Definition 2. 

We call a closed poset $\mathrm{\Theta }\subseteq \mathbf{\Omega }$ profinite if, for all integers $q\ge 0$, there exist only finitely many elements $\omega \in \mathrm{\Theta }$ such that their reduced norm ${\left|\omega \right|}^{\prime }\le q$.

Note that any finitely generated (i.e., having a finite set of maximal elements) closed $\mathrm{\Theta }$ is profinite.

For a profinite $\mathrm{\Theta }$, the embedding ${ϵ}_{d,d^{\prime }}$ makes it possible to talk about stabilization of the homology/cohomology of spaces ${\overline{\mathcal{P}}}_d^{\mathrm{\Theta }}$ and ${\mathcal{P}}_d^{\mathbf{c}\mathrm{\Theta }}$, as $d\to \infty$.

For a closed poset $\mathrm{\Theta }\subset \mathbf{\Omega }$, consider the closed finite poset ${\mathrm{\Theta }}_{⟨d]}={\mathbf{\Omega }}_{⟨d]}\cap \mathrm{\Theta }$. It is generated by some maximal elements ${\omega }_{★}^{\left(1\right)},\dots ,{\omega }_{★}^{(\ell )}$, $\ell =\ell \left(d\right)$. We introduce two useful quantities:

$$\begin{array}{ccc}\hfill {\eta }_{\mathrm{\Theta }}\left(d\right)& {=}_{\mathsf{def}}& \underset{i\in [1,\ell (d\left)\right]}{max}\left\{\left(|{\omega }_{★}^{\left(i\right)}|-2|{\omega }_{★}^{\left(i\right)}{|}^{\prime }\right)\right\},\hfill \end{array}$$

(9)

$$\begin{array}{ccc}\hfill {\psi }_{\mathrm{\Theta }}\left(d\right)& {=}_{\mathsf{def}}& {\displaystyle \frac{1}{2}}\left(d+{\eta }_{\mathrm{\Theta }}\left(d\right)\right).\hfill \end{array}$$

(10)

Note that

$${\psi }_{\mathrm{\Theta }}\left(d\right)={\displaystyle \frac{1}{2}}\underset{i\in [1,\ell (d\left)\right]}{min}\left\{(d-|{\omega }_{★}^{\left(i\right)}{|}^{\prime })+(|{\omega }_{★}^{\left(i\right)}|-|{\omega }_{★}^{\left(i\right)}{|}^{\prime })\right\}<d,$$

where both summands, the “codimension” $(d-|{\omega }_{★}^{\left(i\right)}{|}^{\prime })$ and the “support” $\left(\right|{\omega }_{★}^{\left(i\right)}|-|{\omega }_{★}^{\left(i\right)}{|}^{\prime })$, are positive and each one does not exceed d. At the same time, ${\eta }_{\mathrm{\Theta }}\left(d\right)$ may be negative.

The quantity ${\psi }_{\mathrm{\Theta }}(d+2)$ is employed on many occasions. It plays a key role in describing the stabilization in the homology $H_{*}({\mathcal{P}}_d^{\mathbf{c}\mathrm{\Theta }};\mathbb{Z})$.

Now we can state one of the main stabilization results from [6]:

Theorem 2 (short stabilization: $\{\mathbf{d}\Rightarrow \mathbf{d}+\mathbf{2}\}$). 

Let Θ be a closed subposet of Ω. Let the embedding ${ϵ}_{d,d+2}:{\mathcal{P}}_d\subset {\mathcal{P}}_{d+2}$ be as in (8).

• Then, for all $j+2>{\psi }_{\mathrm{\Theta }}(d+2)$, we get a homological isomorphism

  $${\left({ϵ}_{d,d+2}\right)}_{*}:H_j({\overline{\mathcal{P}}}_d^{\mathrm{\Theta }};\mathbb{Z})\approx H_{j+2}({\overline{\mathcal{P}}}_{d+2}^{\mathrm{\Theta }};\mathbb{Z});$$
• For all $j\le d+2-{\psi }_{\mathrm{\Theta }}(d+2)$, a homological isomorphism

  $${\left({ϵ}_{d,d+2}\right)}_{*}:H_j({\mathcal{P}}_d^{\mathbf{c}\mathrm{\Theta }};\mathbb{Z})\approx H_j({\mathcal{P}}_{d+2}^{\mathbf{c}\mathrm{\Theta }};\mathbb{Z}).$$

Example 1. 

Let the closed poset Θ be generated by two elements: $\left(4\right)$ and $\left(33\right)$. Then, ${\eta }_{\mathrm{\Theta }}\left(d\right)=-2,{\psi }_{\mathrm{\Theta }}\left(d\right)={\displaystyle \frac{1}{2}}(d-2)$. Applying Theorem 2 to this Θ, we get isomorphisms

$${\left({ϵ}_{d,d+2}\right)}_{*}:H_j({\mathcal{P}}_d^{\mathbf{c}\mathrm{\Theta }};\mathbb{Z})\approx H_j({\mathcal{P}}_{d+2}^{\mathbf{c}\mathrm{\Theta }};\mathbb{Z})$$

for all $j\le {\displaystyle \frac{1}{2}}d+2$. Moreover, since ${\overline{\mathcal{P}}}_d^{\mathrm{\Theta }}$ is of codimension 3 in ${\overline{\mathcal{P}}}_d\approx S^d$, we get ${\pi }_1\left({\mathcal{P}}_d^{\mathbf{c}\mathrm{\Theta }}\right)=1$ for all $d\ge 6$. Therefore, we get the homotopy groups isomorpisms

$${\left({ϵ}_{d,d+2}\right)}_{*}:{\pi }_j\left({\mathcal{P}}_d^{\mathbf{c}\mathrm{\Theta }}\right)\approx {\pi }_j\left({\mathcal{P}}_{d+2}^{\mathbf{c}\mathrm{\Theta }}\right)$$

for all $j\le {\displaystyle \frac{1}{2}}d+2$, where $d\ge 6$.

Corollary 1 (long stabilization: $\{\mathbf{d}\Rightarrow \infty \}$). 

If $\mathrm{\Theta }\subset \mathbf{\Omega }$ is a closed profinite subposet, then for each j, the homomorphism

$${\left({ϵ}_{d,d^{\prime }}\right)}_{*}:H_j({\mathcal{P}}_d^{\mathbf{c}\mathrm{\Theta }};\mathbb{Z})\approx H_j({\mathcal{P}}_{d^{\prime }}^{\mathbf{c}\mathrm{\Theta }};\mathbb{Z})$$

is an isomorphism for all sufficiently big $d\le d^{\prime }$, $d\equiv d^{\prime }mod2$.

As a result, for such profinite posets Θ’s, we may talk about the stable homology $H_j({\mathcal{P}}_{\infty }^{\mathbf{c}\mathrm{\Theta }};\mathbb{Z})$, the direct limit ${lim}_{d\to \infty }{H}_j({\mathcal{P}}_d^{\mathbf{c}\mathrm{\Theta }};\mathbb{Z})$.

Let us describe a few special cases of posets $\mathrm{\Theta }$ from [6]. For $k\ge 1$, $q\in [0,d]$, and $q\equiv dmod2$, let us consider the closed poset

$$\begin{array}{c}\hfill {\mathbf{\Omega }}_{{|\sim |}^{\prime }\ge k}^{\left(q\right)}{=}_{\mathsf{def}}\left\{\omega \in {\mathbf{\Omega }}_{⟨d]}{\mathrm{such}\mathrm{that}\left|\omega \right|}^{\prime }\ge k\mathrm{and}\left|\omega \right|\ge q\right\}.\end{array}$$

(11)

Note that, for $\mathrm{\Theta }={\mathbf{\Omega }}_{{|\sim |}^{\prime }\ge k}^{\left(0\right)}:={\mathbf{\Omega }}_{{|\sim |}^{\prime }\ge k}$, the space ${\overline{\mathcal{P}}}_d^{\mathrm{\Theta }}$ is the entire $(d-k)$-skeleton of ${\overline{\mathcal{P}}}_d$.

$$\begin{array}{c}\hfill \mathrm{Let}A(d,k,q){=}_{\mathsf{def}}\left|\chi \left((\mathbb{Z}\left[{\mathbf{\Omega }}_{{|\sim |}^{\prime }\ge k}^{\left(q\right)}\right],\mathit{\partial })\right)\right|,\end{array}$$

(12)

the absolute value of the Euler number of the differential complex $\left(\mathbb{Z}\left[{\mathbf{\Omega }}_{{|\sim |}^{\prime }\ge k}^{\left(q\right)}\right],\mathit{\partial }\right)$.

Proposition 5 

([6]). Fix $k\in [1,d)$ and $q\ge 0$ such that $q\equiv dmod2$, and set $\mathrm{\Theta }={\mathbf{\Omega }}_{{|\sim |}^{\prime }\ge k}^{\left(q\right)}$.

Then, ${\mathcal{P}}_d^{\mathbf{c}\mathrm{\Theta }}$ has the homotopy type of a bouquet of $(k-1)$-dimensional spheres. The number of spheres in the bouquet equals $A(d,k,q)$.

Proposition 6 

([5]). Let $\mathrm{\Theta }\subseteq {\mathbf{\Omega }}_{{⟨d],|\sim |}^{\prime }\ge 2}$ be a closed poset. For $d^{\prime }\ge d+2$ such that $d^{\prime }\equiv dmod2$, let ${\widehat{\mathrm{\Theta }}}_{\left\{d^{\prime }\right\}}$ be the smallest closed poset in ${\mathbf{\Omega }}_{⟨d^{\prime }]}$ containing Θ.

Then, for $d^{\prime }\ge d+2$, we have an isomorphism ${\pi }_1\left({\mathcal{P}}_{d^{\prime }}^{\mathbf{c}{\widehat{\mathrm{\Theta }}}_{\left\{d^{\prime }\right\}}}\right)\cong {\pi }_1\left({\mathcal{P}}_{d+2}^{\mathbf{c}{\mathrm{\Theta }}_{\{d+2\}}}\right)$ of the fundamental groups.

3. Immersions and Embeddings with Restricted Tangency Patterns to the Product 1-Foliations

3.1. On Immersions $\{\beta :M^n\to \mathbb{R}\times Y^n\}$ and Their Self-Intersections Loci

We adopt the following definition of a proper immersion.

Definition 3. 

Let M be a compact smooth n-manifold and W a compact smooth $(n+1)$-manifold. We call an immersion $\beta :M\to W$ proper if

• $\beta (\mathit{\partial }M)\subset \mathit{\partial }W$;
• β is transversal to $\mathit{\partial }W$ (thus the kernel of $D\left(\beta {|}_{\mathit{\partial }M}\right)$ is also trivial).

When M is closed, requirements (1) and (2) are vacuous. When Y is closed, then M must be closed as well.

Remark 1.

In this paper, for a given compact smooth n-manifold Y, we are only interested in proper immersions/embeddings β of compact smooth n-manifolds M into the product $\mathbb{R}\times Y$. The existence of such β puts substantial restrictions on the topological nature of M. For example, the tangent n-bundle ${\tau }_M$ must be a subbundle of the $(n+1)$-bundle ${\beta }^{*}\left({\tau }_Y\right)\oplus \underline{\mathbb{R}}$. By the classical Hirsch Theorem [18], the existence of such an immersion β in the homotopy class of a given map $\tilde{\beta }:M\to \mathbb{R}\times Y$ is equivalent to the property of the stable bundle ${\tilde{\beta }}^{*}\left({\tau }_{\mathbb{R}\times Y}\right)\oplus {\nu }_M$ to be of geometric dimension $\le 1$. Here, ${\nu }_M$ is the stable normal bundle of M. The geometric dimension of a stable bundle η is defined to be the minimal dimension of a bundle ${\eta }^{♯}$ in the stable equivalence class of η.

Definition 4 below requires the introduction of the following notion. Let $G,H$ be two smooth hypersurfaces in a smooth manifold X. We fix a point $a\in G\cap H$ and consider its neighborhood $U_a\subset X$. Let $g:U_a\to \mathbb{R}$, $h:U_a\to \mathbb{R}$ be two smooth functions such that 0 is a regular value for both, and $G=g^{-1}\left(0\right),H=h^{-1}\left(0\right)$.

Let q be a natural number. We say that two hypersurfaces $G,H$ are q-jet equivalent at $a\in G\cap H$, if there exists smooth functions $\varphi ,\chi :U_a\to \mathbb{R}$ such that $\varphi \left(a\right)\ne 0,\chi \left(a\right)\ne 0$ and the q-jet $je{t}_a^q(\chi ·g)=je{t}_a^q(\varphi ·h)$. In other words, $je{t}_a^q\left(\chi \right)·je{t}_a^q\left(g\right)=je{t}_a^q\left(\varphi \right)·je{t}_a^q\left(h\right)$ modulo the ${(q+1)}^{st}$ power of the maximal ideal ${\mathsf{m}}_0$ in the polynomial ring in $dimX$ variables.

We denote by ${\mathsf{j}}_a^q\left(H\right)$ the q-jet equivalence class of $H\subset X$ at a, and by ${\mathsf{J}}_a^q$ the set of all such q-jet equivalence classes of hypersurfaces through a. The space ${\mathsf{J}}_a^q$ depends on finitely many parameters, the number of which is a function of $dimX$ and q. Since ${\mathsf{J}}_a^1$ is the Grassmanian of hyperplanes, we view ${\mathsf{J}}_a^q$ as a generalized Grassmanian. We denote by ${\mathsf{J}}^q\left(X\right)\to X$ the fibration over X, whose fiber is ${\mathsf{J}}_a^q$.

Definition 4. 

We call an immersion $\beta :M\to X$ of a smooth compact n-manifold M into a smooth compact $(n+1)$-manifold Xq-separable if

• For any point $a\in \beta \left(M\right)$, the set ${\beta }^{-1}\left(a\right)$ is finite;
• There is a natural number q such that, for any point $a\in \beta \left(M\right)$, the q-jet equivalence classes of the local branches of $\beta \left(M\right)$, labeled by points ${\beta }^{-1}\left(a\right)$, are all distinct.

For the rest of the section, we fix a compact connected smooth n-manifold Y and consider proper immersions $\beta :M\to \mathbb{R}\times Y$ of compact smooth n-manifolds M. By a small perturbation, we may assume that different local branches of $\beta \left(M\right)$ are in general position at their mutual intersections (see [19], Theorem 4.13). In particular, we may assume that $\beta$ is 1-separable in the sense of Definition 4.

Recall the following definition from [20,21], adjusted for our setting.

Definition 5. 

A smooth proper immersion $\beta :M\to \mathbb{R}\times Y$ is called k-normal if, for each k-tuple of distinct points $x_1,\dots ,x_k\in M$ with $\beta \left(x_1\right)=\dots =\beta \left(x_k\right)$, the images of the tangent spaces $T_{x_1}M,\dots ,T_{x_k}M$ under the differential $D\beta$ are, in general, positioned in the tangent space $T_y(\mathbb{R}\times Y)$, where $y=\beta \left(x_i\right)$. Also, for such a k-tuple, the images of the tangent spaces $T_{x_1}(\mathit{\partial }M),\dots ,T_{x_k}(\mathit{\partial }M)$ under the differential $D\left(\beta {|}_{\mathit{\partial }M}\right)$ are, in general, positioned in the tangent space $T_y(\mathbb{R}\times \mathit{\partial }Y)$.

For a given proper immersion $\beta :(M,\mathit{\partial }M)\to (\mathbb{R}\times Y,\mathbb{R}\times \mathit{\partial }Y)$, we consider the k-fold product map ${\left(\beta \right)}^k:{\left(M\right)}^k\to {(\mathbb{R}\times Y)}^k$. Let ${\mathrm{\Sigma }}_k$ be the preimage of the diagonal $\mathrm{\Delta }\subset {(\mathbb{R}\times Y)}^k$ under the map ${\left(\beta \right)}^k$. For a k-normal $\beta$, ${\mathrm{\Sigma }}_k$ is a smooth manifold of dimension $n-k+1$ [20]. Following [20], we call ${\mathrm{\Sigma }}_k$ the k self-intersection manifold of $\beta$. Note that the same construction applies to $\beta |:\mathit{\partial }M\to \mathbb{R}\times \mathit{\partial }Y$, producing the boundary $\mathit{\partial }{\mathrm{\Sigma }}_k$.

Let $p_1:{\left(M\right)}^k\to M$ be the obvious projection on the first factor of the product. Then, $p_1:{\mathrm{\Sigma }}_k\to M$ is an immersion [20]. Its image $p_1\left({\mathrm{\Sigma }}_k\right)$ is the set of points $x_1\in M$ such that there exist distinct $x_2,\dots ,x_k\in M$ with the property $\beta \left(x_2\right)=\beta \left(x_1\right),\dots ,\beta \left(x_k\right)=\beta \left(x_1\right)$.

If both M and Y are orientable, then so is ${\mathrm{\Sigma }}_k$. In such a case, we denote by ${\left[{\mathrm{\Sigma }}_k\right]}_{★}^{\beta }\in H_{n-k+1}(Y,\mathit{\partial }Y;\mathbb{Z})$ the image of the relative fundamental class $\left[{\mathrm{\Sigma }}_k\right]$ under the composition $\pi \circ \beta \circ p_1$, where $\pi :\mathbb{R}\times Y\to Y$ is the obvious projection. Without orientability assumptions, only the classes ${\left[{\mathrm{\Sigma }}_k\right]}_{★}^{\beta }\in H_{n-k+1}(Y,\mathit{\partial }Y;{\mathbb{Z}}_2)$ are available.

Let ${\mathcal{D}}_M:H_{*}(M,\mathit{\partial }M)\to H^{n-*}\left(M\right)$ be the Poincaré duality isomorphism. (Here, depending on the orientability of M, the coefficients are $\mathbb{Z}$ or ${\mathbb{Z}}_2$.) Also, we have the Poincaré duality isomorphism ${\mathcal{D}}_{\mathbb{R}\times Y}:H_{*}(\mathbb{R}\times Y,\mathbb{R}\times \mathit{\partial }Y)\to H_c^{n+1-*}(\mathbb{R}\times Y)$, where the subscript c indicates the cohomology with compact support and the choice of coefficients $\mathbb{Z}$ or $\mathbb{Z}/2\mathbb{Z}$ depends on the orientability of Y.

Let ${\nu }_{\beta }:={\beta }^{*}\left({\tau }_{\mathbb{R}\times Y}\right)/{\tau }_M$ be the 1-bundle over M, normal to $\beta \left(M\right)$, and let $W^1\left({\nu }_{\beta }\right)$ denote its first Stiefel–Whitney characteristic class. Put ${\tilde{\mathrm{\Sigma }}}_k:=p_1\left({\mathrm{\Sigma }}_k\right)\subset M$. Then, applying the main result of [20] to our setting, for $k>1$, we get a pleasing formula

$$\begin{array}{c}\hfill {\mathcal{D}}_M\left(\left[{\tilde{\mathrm{\Sigma }}}_k\right]\right)=\pm {\left({\beta }^{*}\circ {\mathcal{D}}_{\mathbb{R}\times Y}\circ {\beta }_{*}\left(\left[{\tilde{\mathrm{\Sigma }}}_k\right]\right)-W^1\left({\nu }_{\beta }\right)\right)}^{k-1}.\end{array}$$

(13)

Applying $\pi \circ \beta \circ p_1$ to ${\mathrm{\Sigma }}_k$, these constructions have the following direct implication.

Lemma 1. 

For compact oriented n-manifolds M and Y and $k\in [2,n+1]$, a proper k-normal immersion $\beta :M\to \mathbb{R}\times Y$ generates the homology class ${\left[{\mathrm{\Sigma }}_k\right]}_{★}^{\beta }\in H_{n-k+1}(Y,\mathit{\partial }Y;\mathbb{Z})$ and its Poincaré dual ${\left[{\mathrm{\Sigma }}_k\right]}_{\beta }^{★}\in H^{k-1}(Y;\mathbb{Z})$. For non-orientable M or Y, a proper k-normal immersion β produces similar classes ${\left[{\mathrm{\Sigma }}_k\right]}_{★}^{\beta }$ and ${\left[{\mathrm{\Sigma }}_k\right]}_{\beta }^{★}$ in the homology/cohomology with coefficients in ${\mathbb{Z}}_2$.

Lemma 2. 

Let two proper k-normal immersions

$${\beta }_0:(M_0,\mathit{\partial }{M}_0)\to (\mathbb{R}\times Y\times \left\{0\right\},\mathbb{R}\times \mathit{\partial }Y\times \left\{0\right\})$$

$${\beta }_1:(M_1,\mathit{\partial }{M}_1)\to (\mathbb{R}\times Y\times \left\{1\right\},\mathbb{R}\times \mathit{\partial }Y\times \left\{1\right\})$$

be cobordant with the help of a proper k-normal immersion

$$B:(N,\delta N)\to (\mathbb{R}\times Y\times [0,1],\mathbb{R}\times \mathit{\partial }Y\times [0,1\left]\right),$$

where the boundary $\mathit{\partial }N=(M_0\bigsqcup -M_1){\cup }_{(\mathit{\partial }{M}_0\bigsqcup -\mathit{\partial }{M}_1)}\delta N$, ${B|}_{M_0}={\beta }_0$, ${B|}_{M_1}={\beta }_1$, and $B\left(\delta N\right)\subset \mathbb{R}\times \mathit{\partial }Y\times [0,1]$.

Then, the k-intersection manifolds

$${\beta }_0\circ {\left(p_0\right)}_1:({\mathrm{\Sigma }}_k^{{\beta }_0},{\mathrm{\Sigma }}_k^{{\beta }_0^{\mathit{\partial }}})\to (\mathbb{R}\times Y\times \left\{0\right\},\mathbb{R}\times \mathit{\partial }Y\times \left\{0\right\}),$$

$${\beta }_1\circ {\left(p_1\right)}_1:({\mathrm{\Sigma }}_k^{{\beta }_1},{\mathrm{\Sigma }}_k^{{\beta }_1^{\mathit{\partial }}})\to (\mathbb{R}\times Y\times \left\{1\right\},\mathbb{R}\times \mathit{\partial }Y\times \left\{1\right\})$$

are cobordant with the help of the map

$$B\circ P_1:({\mathrm{\Sigma }}_k^B,{\mathrm{\Sigma }}_k^{B^{\delta }})\to (\mathbb{R}\times Y\times [0,1],\mathbb{R}\times \mathit{\partial }Y\times [0,1]).$$

Here, ${\left(p_0\right)}_1:{\mathrm{\Sigma }}_k^{{\beta }_0}\to M_0$, ${\left(p_1\right)}_1:{\mathrm{\Sigma }}_k^{{\beta }_1}\to M_0$, and $P_1:{\mathrm{\Sigma }}_k^B\to N$ denote the projections on the first factors of the k-th powers ${\left(M_0\right)}^k$, ${\left(M_1\right)}^k$, and ${\left(N\right)}^k$, respectively. The maps, ${\left(p_0\right)}_1$, ${\left(p_1\right)}_1$, and $P_1$, are immersions.

If the manifolds $M_0,M_1,N$, and Y are orientable, then so are the manifods ${\mathrm{\Sigma }}_k^{{\beta }_0}$, ${\mathrm{\Sigma }}_k^{{\beta }_1}$, and ${\mathrm{\Sigma }}_k^B$.

Proof. 

By the definition of k-normality, the k-th power $B^k$ of B is transversal to the diagonal $\tilde{\mathrm{\Delta }}\subset {(\mathbb{R}\times Y\times [0,1])}^k$, a manifold with corners $\mathit{\partial }Y\times \mathit{\partial }[0,1]$. Thus, ${\mathrm{\Xi }}_k^B:={\left(B^k\right)}^{-1}\left(\tilde{\mathrm{\Delta }}\right)\subset {\left(N\right)}^k$ will be a compact smooth manifold of dimension $n-k+2$. Its projection $P:{\left(N\right)}^k\to N$ on the first factor N is an immersion [20]. So the composition of $B\circ P:{\mathrm{\Xi }}_k\to \mathbb{R}\times Y\times [0,1]$ delivers a cobordism between the pair of maps

$${\beta }_0\circ {\left(p_0\right)}_1:({\mathrm{\Sigma }}_k\left({\beta }_0\right),\mathit{\partial }{\mathrm{\Sigma }}_k\left({\beta }_0\right))\to (\mathbb{R}\times Y\times \left\{0\right\},\mathbb{R}\times \mathit{\partial }Y\times \left\{0\right\})$$

$${\beta }_1\circ {\left(p_1\right)}_1:({\mathrm{\Sigma }}_k\left({\beta }_1\right),\mathit{\partial }{\mathrm{\Sigma }}_k\left({\beta }_1\right))\to (\mathbb{R}\times Y\times \left\{1\right\},\mathbb{R}\times \mathit{\partial }Y\times \left\{1\right\}).$$

By [20], if $M_0,M_1,N$, and Y are orientable, then so are ${\mathrm{\Sigma }}_k^{{\beta }_0}$, ${\mathrm{\Sigma }}_k^{{\beta }_1}$, and ${\Xi }_k^B$. □

Corollary 2. 

Let $\pi :\mathbb{R}\times Y\to Y$ be the obvious projection. Let proper k-normal immersions ${\beta }_0:(M_0,\mathit{\partial }{M}_0)\to (\mathbb{R}\times Y,\mathbb{R}\times \mathit{\partial }Y)$ and ${\beta }_1:(M_1,\mathit{\partial }{M}_1)\to (\mathbb{R}\times Y,\mathbb{R}\times \mathit{\partial }Y)$ be cobordant with the help of a proper immersion (not necessary k-normal!) $B:(N,\delta N)\to (\mathbb{R}\times Y\times [0,1],\mathbb{R}\times \mathit{\partial }Y\times [0,1\left]\right)$, as in Lemma 1. Then, both maps

$$\pi \circ {\beta }_0\circ {\left(p_0\right)}_1:({\mathrm{\Sigma }}_k^{{\beta }_0},{\mathrm{\Sigma }}_k^{{\beta }_0^{\mathit{\partial }}})\to (Y,\mathit{\partial }Y)\mathrm{and}\pi \circ {\beta }_1\circ {\left(p_1\right)}_1:({\mathrm{\Sigma }}_k^{{\beta }_1},{\mathrm{\Sigma }}_k^{{\beta }_1^{\mathit{\partial }}})\to (Y,\mathit{\partial }Y)$$

define the same element $[({\mathrm{\Sigma }}_k^{\beta },\mathit{\partial }{\mathrm{\Sigma }}_k^{\beta })\to (Y,\mathit{\partial }Y)]$ of the relative bordism group ${\mathbf{B}}_{n+1-k}(Y,\mathit{\partial }Y)$.

If $M_0,M_1,N$, and Y are orientable, then the two immersions ${\beta }_0,{\beta }_1$ define the same element of the oriented bordism group ${\mathbf{OB}}_{n+1-k}(Y,\mathit{\partial }Y)$.

Proof. 

By the Thom Multijet Transversality Theorem [22], we may smoothly perturb the cobordism map B within the space of immersions, without changing it on $\mathit{\partial }N\setminus \delta N=M_0\bigsqcup M_1$, so that its k-th power $B^k$ will become transversal to the diagonal $\tilde{\mathrm{\Delta }}\subset {(\mathbb{R}\times Y\times [0,1])}^k$. For such a perturbation, B becomes k-normal, and ${\mathrm{\Xi }}_k:={\left(B^k\right)}^{-1}\left(\tilde{\mathrm{\Delta }}\right)\subset {\left(N\right)}^k$ is a compact manifold of dimension $n-k+2$. Now the claim follows from Lemma 2. □

3.2. Constrained Patterns of Tangency to the Foliation $\mathcal{L}$ and the Classifying Maps to the Spaces ${\mathcal{P}}_d^{\mathbf{c}\mathrm{\Theta }}$

Let X be a compact topological space. We denote by $C\left(X\right)$ the algebra of real continuous functions on X. Let

$$\{P\left(u\right)=u^d+a_{d-1}{u}^{d-1}+\dots +a_{1}u+a_0\}$$

be a family of real monic polynomials on X, where the functional coefficients $a_i\in C\left(X\right)$. We fix a closed subposet $\mathrm{\Theta }\subset {\mathbf{\Omega }}_{\le d}$ and assume that, for each point $x\in X$, the polynomial

$$P(u,x)=u^d+a_{d-1}\left(x\right)u^{d-1}+\dots +a_1\left(x\right)u+a_0\left(x\right)$$

has a real zero divisor whose combinatorial pattern $\omega \left(x\right)\in \mathbf{c}\mathrm{\Theta }:=\mathbf{\Omega }\setminus \mathrm{\Theta }$.

Evidently, such polynomial family $P\left(u\right)$ gives rise to a continuous map ${\mathrm{\Phi }}_P:X\to {\mathcal{P}}_d^{\mathbf{c}\mathrm{\Theta }}$, defined by the formula $x\to P(\sim ,x)$, where the target space ${\mathcal{P}}_d^{\mathbf{c}\mathrm{\Theta }}$ is an open subset of ${\mathcal{P}}_d\approx {\mathbb{R}}^d$. The preimage of $\mathbf{c}\mathrm{\Theta }$-stratification of ${\mathcal{P}}_d^{\mathbf{c}\mathrm{\Theta }}$ under ${\mathrm{\Phi }}_P$ produces an interesting stratification $\mathcal{S}(X,P)$ of the space X.

When X is a smooth compact manifold, it is possible to perturb the coefficients of P to form a new family $\tilde{P}$ so that the perturbed map ${\mathrm{\Phi }}_{\tilde{P}}$ will be transversal to each pure stratum ${\left\{{\mathcal{P}}_d^{\omega }\right\}}_{\omega \in \mathbf{c}\mathrm{\Theta }}$. If X has a boundary $\mathit{\partial }X$, then we may assume also that ${\mathrm{\Phi }}_{\tilde{P}}{|}_{\mathit{\partial }X}$ is transversal to each pure stratum ${\mathcal{P}}_d^{\omega }\subset {\mathcal{P}}_d^{\mathbf{c}\mathrm{\Theta }}$.

For such a polynomial family ${\left\{\tilde{P}(u,x)\right\}}_{x\in X}$, the stratification $\mathcal{S}(X,\tilde{P})$ of X mimics the geometry of the $\mathbf{c}\mathrm{\Theta }$-stratification of the target space ${\mathcal{P}}_d^{\mathbf{c}\mathrm{\Theta }}$ and gives rise to a variety of topological invariants of X, generated by the polynomial family.

The polynomial family $P={\left\{P(u,x)\right\}}_{x\in X}$ as above generates loci

$$\begin{array}{c}\hfill \mathit{\partial }{\mathcal{E}}_P{=}_{\mathsf{def}}\left\{(u,x)\right|P(u,x)=0\}\subset \mathbb{R}\times X,\\ \hfill {\mathcal{E}}_P{=}_{\mathsf{def}}\left\{(u,x)\right|P(u,x)\le 0\}\subset \mathbb{R}\times X,\end{array}$$

(14)

which are mapped on X by the obvious projection $\pi :\mathbb{R}\times X\to X$. The fiber over $x\in X$ of the projection ${\pi }^{\mathit{\partial }}:\mathit{\partial }{\mathcal{E}}_P\to X$ is the support of a real zero divisor $D_{\mathbb{R}}\left(x\right)$ of $P(u,x)$ of a degree $\le d$. For some $x\in X$, the x-fiber may be empty; then the divisor $D_{\mathbb{R}}\left(x\right)$ is equal to zero.

This setting leads to a natural question: “What are the maximal sets ${\{U_{\alpha }\subset X\}}_{\alpha }$ (open, closed, any …) which admit a continuous section ${\sigma }_{\alpha }:U_{\alpha }\to \mathit{\partial }{\mathcal{E}}_P$ of the projection ${\pi }^{\mathit{\partial }}:\mathit{\partial }{\mathcal{E}}_P\to X$?” In other words, given a particular root $u_{★}$ of $P(u,x_{★})$, what is the maximal set $U_{u_{★},x_{★}}\subset X$ over which a global solution of the equation $\left\{P\right(u,x)=0\}$, which extends $u_{★}$, exists? The question resembles the question about the maximal domain of an analytic continuation of a given analytic function f (leading to the Riemannian surface associated with f). Perhaps, tackling this question deserves a separate study, dealing with the interplay between the fundamental groups ${\pi }_1\left(X\right)$ and ${\pi }_1\left({\mathcal{P}}_d^{\mathbf{c}\mathrm{\Theta }}\right)$…

Let $C^k(\sim )$ denote the space of k times continuously differentiable functions. When X is a $C^k$-differentiable manifold and all the coefficients of polynomials $a_i\in C^k\left(X\right)$, then $\mathit{\partial }{\mathcal{E}}_P$ is a $C^k$-differentiable hypersurface in $\mathbb{R}\times X$, since $\mathit{\partial }{\mathcal{E}}_P$ admits the $C^k$-differentiable parametrization $(u,a_{d-1},\dots ,a_1)\to (u,a_{d-1},\dots ,a_1,P\left(u\right)-P\left(0\right))$.

Now, given an appropriate hypersurface $\mathit{\partial }\mathcal{E}\subset \mathbb{R}\times X$, we aim to reverse the correspondence $P⇝({\mathcal{E}}_P,\mathit{\partial }{\mathcal{E}}_P)$ by constructing a polynomial family $P=P(\mathit{\partial }\mathcal{E})$ on X that generates $\mathit{\partial }\mathcal{E}$.

For a given d, let us consider the crucial for us $(d+1)$-dimensional domain

$$\begin{array}{ccc}\hfill {\mathcal{E}}_d& {=}_{\mathsf{def}}& \left\{(u,P)\in \mathbb{R}\times {\mathcal{P}}_d|P\left(u\right)\le 0\right\}\mathrm{and}\mathrm{its}\mathrm{boundary}\hfill \\ \hfill \mathit{\partial }{\mathcal{E}}_d& {=}_{\mathsf{def}}& \left\{(u,P)\in \mathbb{R}\times {\mathcal{P}}_d|P\left(u\right)=0\right\}.\hfill \end{array}$$

(15)

Since $\mathit{\partial }{\mathcal{E}}_d$ is a graph of the map $(u,a_1,\dots ,a_{d-1})⟶a_0=-{\sum }_{i=1}^{d-1}{a}_i{u}^i$, it follows that ${\mathcal{E}}_d$ is diffeomorphic to the half-space ${\mathbb{R}}_{+}^{d+1}$, and $\mathit{\partial }{\mathcal{E}}_d$ to the space ${\mathbb{R}}^d$.

We denote by ${\pi }_d:{\mathcal{E}}_d\to {\mathcal{P}}_d$ the obvious projection map. For $d\equiv 0mod2$, its fibers are compact (are finite unions of closed intervals and singletons).

Let Y be a smooth compact manifold, and $\beta :(M,\mathit{\partial }M)\to (\mathbb{R}\times Y,\mathbb{R}\times \mathit{\partial }Y)$ an immersion. We denote by $\mathcal{L}$ the one-dimensional oriented foliation, defined by the fibers of the projection map $\pi :\mathbb{R}\times Y\to Y$, and by ${\mathcal{L}}_y$ the fiber ${\pi }^{-1}\left(y\right)$.

If $\mathit{\partial }Y\ne \varnothing$, we add a collar to Y and denote the resulting manifold by $\widehat{Y}$. Similarly, if $\mathit{\partial }M\ne \varnothing$, we add a collar to M, which results in a new manifold $\widehat{M}$. We still assume that $\beta (\mathit{\partial }M)\subset \mathbb{R}\times \mathit{\partial }Y$ and that $\widehat{\beta }(\widehat{M}\setminus M)\subset \mathbb{R}\times (\widehat{Y}\setminus Y)$. Using that $\beta$ is transversal to $\mathbb{R}\times \mathit{\partial }Y$, so we may assume that $\beta :M\to \mathbb{R}\times Y$ extends to an immersion $\widehat{\beta }:\widehat{M}\to \mathbb{R}\times \widehat{Y}$.

Next, for each point $b\in M$, we introduce a natural number ${\mu }^{\beta }\left(b\right)$, the multiplicity of tangency between the b-labeled local branch of $\widehat{\beta }\left(\widehat{M}\right)$ and the leaf of $\mathcal{L}$ through the point $a:=\beta \left(b\right)$. If a local branch $\tilde{M}$ of $\widehat{\beta }\left(\widehat{M}\right)$ is given as the zero set of a locally defined smooth function $z:\mathbb{R}\times \widehat{Y}\to \mathbb{R}$ which has 0 as its regular value, then the multiplicity/order of tangency of the $\pi$-fiber ${\mathcal{L}}_y$ with $\tilde{M}$ at a point $a=(u,y)\in \tilde{M}\cap {\mathcal{L}}_y$ is defined as the natural number $\mu :={\mu }^{\beta }\left(b\right)$ such that the jet ${\mathsf{jet}}_a^{\mu -1}\left(z{|}_{{\mathcal{L}}_y}\right)=0$, but ${\mathsf{jet}}_a^{\mu }\left(z{|}_{{\mathcal{L}}_y}\right)\ne 0$. In particular, if the branch is transversal to the leaf, then ${\mu }^{\beta }\left(b\right)=1$.

We fix a natural number d and assume that an immersion $\beta :M\to \mathbb{R}\times Y$ is such that each leaf ${\left\{{\mathcal{L}}_y\right\}}_{y\in Y}$ hits the image $\beta \left(M\right)$ so that

$$\begin{array}{c}\hfill {\mu }^{\beta }\left(y\right){=}_{\mathsf{def}}\sum _{\{a\in {\mathcal{L}}_y\cap \beta \left(M\right)\}}\left(\sum _{\{b\in {\beta }^{-1}\left(a\right)\}}{\mu }^{\beta }\left(b\right)\right)\le d.\end{array}$$

(16)

Note that this assumption rules out the infinite multiplicity tangencies ${\mu }^{\beta }\left(y\right)$.

We ordered the points $\left\{a_i\right\}$ of ${\mathcal{L}}_y\cap \beta \left(M\right)$ by the values of their projections on $\mathbb{R}$ and introduce the combinatorial pattern ${\omega }^{\beta }\left(y\right)$ of $y\in Y$ as the ordered sequence of multiplicities

$${\{}_{{\omega }_i^{\beta }\left(y\right){=}_{\mathsf{def}}\sum _{\{b\in {\beta }^{-1}\left(a_i\right)\}}{\mu }^{\beta }\left(b\right)\}i}.$$

We denote by $D^{\beta }\left(y\right)$ the real divisor on ${\mathcal{L}}_y$, whose support is ${\mathcal{L}}_y\cap \beta \left(M\right)$ and whose multiplicities are the ${\left\{{\omega }_i^{\beta }\left(y\right)\right\}}_i$.

In particular, the combinatorial type of $D^{\beta }\left(y\right)$ is sensitive to the points $y\in Y$ over which the multiple self-intersections of $\beta$ reside. Note also that the definition of the divisor $D^{\beta }\left(y\right)$ depends only on the image $\beta \left(M\right)\subset \mathbb{R}\times Y$ of M.

A special case of the following theorem may be found in [5], Proposition 3.

Theorem 3. 

Let M and Y be smooth compact n-manifolds. For any proper (in the sense of Definition 3) immersion $\beta :(M,\mathit{\partial }M)\to (\mathbb{R}\times Y,\mathbb{R}\times \mathit{\partial }Y)$ which satisfies inequality (16) and the parity condition ${\mu }^{\beta }\left(y\right)\equiv dmod2$, there exists a smooth map ${\mathrm{\Phi }}^{\beta }:Y\to {\mathcal{P}}_d$ such that the locus

$$\left\{(u,y)\in \mathbb{R}\times Y|{\mathrm{\Phi }}^{\beta }\left(y\right)\left(u\right)=0\right\}=\beta (\mathit{\partial }X).$$

If, for a given pair of closed posets $\mathrm{\Theta }\subset \mathrm{\Lambda }\subset {\mathbf{\Omega }}_{⟨d]}$, the immersion β is such that no ${\omega }^{\beta }\left(y\right)$ belongs to Θ and, for $y\in \mathit{\partial }Y$, no ${\omega }^{\beta }\left(y\right)$ belongs to Λ, then ${\mathrm{\Phi }}^{\beta }$ maps Y to the open subset ${\mathcal{P}}_d^{\mathbf{c}\mathrm{\Theta }}\subset {\mathcal{P}}_d$ and $\mathit{\partial }Y$ to the open subset ${\mathcal{P}}_d^{\mathbf{c}\mathrm{\Lambda }}\subset {\mathcal{P}}_d$. Moreover, any two such maps ${\mathrm{\Phi }}_0^{\beta },{\mathrm{\Phi }}_1^{\beta }:(Y,\mathit{\partial }Y)\to ({\mathcal{P}}_d^{\mathbf{c}\mathrm{\Theta }},{\mathcal{P}}_d^{\mathbf{c}\mathrm{\Lambda }})$ are homotopic as maps of pairs.

Proof. 

Let us denote by ${\widehat{M}}^{\circ }$ the interior of $\widehat{M}$ and by ${\widehat{Y}}^{\circ }$ the interior of $\widehat{Y}$.

We claim that the set $\widehat{\beta }\left({\widehat{M}}^{\circ }\right)$ may be viewed as the solution set of the equations

$${\left\{u^d+\sum _{j=0}^{d-1}{a}_j\left(y\right)u^j=0\right\}}_{y\in {\widehat{Y}}^{\circ }},$$

where ${\{a_j:{\widehat{Y}}^{\circ }\to \mathbb{R}\}}_j$ are some smooth functions.

Let us justify this claim. By Lemma 4.1 from [23] and Morin’s Theorem [17] (both based on the Malgrange Preparation Lemma), if a particular branch $\widehat{\beta }{\left({\widehat{M}}^{\circ }\right)}_{\kappa }$ of $\widehat{\beta }\left({\widehat{M}}^{\circ }\right)$ is tangent to the leaf ${\mathcal{L}}_{y_{★}}$ at a point $a_{★}=(\alpha ,y_{★})$ with the order of tangency $j=j(a_{★},\kappa )$, then there is a system of local coordinates $(\tilde{u},\tilde{x},\tilde{z})$ in the vicinity of $a\in \mathbb{R}\times {\widehat{Y}}^{\circ }$ such that

(1)

$\widehat{\beta }{\left({\widehat{M}}^{\circ }\right)}_{\kappa }$ is given by the equation $\left\{{\tilde{u}}^j+{\sum }_{k=0}^{j-1}{\tilde{x}}_k{\tilde{u}}^k=0\right\}$, where ${\tilde{x}}_k\left(y_{★}\right)=0$ and $\tilde{u}\left(\alpha \right)=0$;

(2)

Each nearby leaf ${\mathcal{L}}_y$ is given by the equations $\{\tilde{x}=\overrightarrow{const},\tilde{z}=\overrightarrow{cons{t}^{\prime }}\}$.

Letting $\tilde{u}=u-\alpha$ and writing ${\tilde{x}}_k$’s as smooth functions of $y\in {\widehat{Y}}^{\circ }$, the same locus $\widehat{\beta }{\left({\widehat{M}}^{\circ }\right)}_{\kappa }$ can be given by the following equation:

$$\begin{array}{c}\hfill \{P_{\alpha ,\kappa }(u,y):={(u-\alpha )}^j+\sum _{j=0}^{j-1}{a}_{\kappa ,k}\left(y\right){(u-\alpha )}^k=0\},\end{array}$$

(17)

where $a_{\kappa ,k}:{\widehat{Y}}^{\circ }\to \mathbb{R}$ are smooth functions, vanishing at $y_{★}$. Therefore, there exists an open neighborhood $U_{y_{★}}$ of $y_{★}$ in ${\widehat{Y}}^{\circ }$ such that, in $\mathbb{R}\times U_{y_{★}}$, the locus $\widehat{\beta }\left({\widehat{M}}^{\circ }\right)$ is given by the following monic polynomial equation:

$$\begin{array}{c}\hfill \left\{P_{y_{★}}(u,y):=\prod _{(\alpha ,y_{★})\in {\mathcal{L}}_{y_{★}}\cap \widehat{\beta }\left({\widehat{M}}^{\circ }\right)}\left(\prod _{\kappa \in A_{\alpha }}{P}_{\alpha ,\kappa }(u,y)\right)=0\right\},\end{array}$$

(18)

of degree ${\mu }^{\beta }\left(y_{★}\right)\le d$ in u. Here, the finite set $A_{\alpha }$ labels the local branches of $\beta \left(M\right)$ that contain the point $(\alpha ,y_{★})\in {\mathcal{L}}_{y_{★}}\cap \beta \left(M\right)$.

By multiplying $P_{y_{★}}(u,y)$ with ${(u^2+1)}^{{\displaystyle \frac{d-{\mu }^{\beta }\left(y_{★}\right)}{2}}}$, we get a polynomial ${\tilde{P}}_{y_{★}}(u,y)$ of degree d. For each $y\in U_{y_{★}}$, ${\tilde{P}}_{y_{★}}(u,y)$ shares with $P_{y_{★}}(u,y)$ the zero set $\widehat{\beta }\left({\widehat{M}}^{\circ }\right)\cap (\mathbb{R}\times U_{y_{★}})$, as well as the divisors $D^{\widehat{\beta }}\left(y\right)$.

For each $y\in {\widehat{Y}}^{\circ }$, we consider the space ${\mathcal{X}}_{\widehat{\beta }}\left(y\right)$ of monic polynomials $\tilde{P}\left(u\right)$ of degree d such that their real divisors coincide with the $\widehat{\beta }$-induced divisor $D^{\widehat{\beta }}\left(y\right)$. We view ${\mathcal{X}}_{\widehat{\beta }}{=}_{\mathsf{def}}{\coprod }_{y\in {\widehat{Y}}^{\circ }}{\mathcal{X}}_{\widehat{\beta }}\left(y\right)$ as a subspace of ${\widehat{Y}}^{\circ }\times {\mathcal{P}}_d$. It is equipped with the obvious projection $p:{\mathcal{X}}_{\widehat{\beta }}\to {\widehat{Y}}^{\circ }$. The smooth sections of the map p are exactly the smooth functions $\tilde{P}(u,y)$ that interest us. By the previous argument, p admits a local smooth section over the vicinity of each $y_{★}\in {\widehat{Y}}^{\circ }$.

Evidently, each p-fiber ${\mathcal{X}}_{\widehat{\beta }}\left(y\right)$ is a convex set. Thus, given finitely many smooth sections ${\left\{{\sigma }_i\right\}}_i$ of p, we conclude that ${\sum }_i{\varphi }_i·{\sigma }_i$ is again a section of p, provided that the smooth functions ${\varphi }_i:Y\to [0,1]$ have the property ${\sum }_i{\varphi }_i\equiv \mathbf{1}$. Note that an individual term ${\varphi }_i·{\sigma }_i$ may not belong to ${\mathcal{P}}_d$ due to the failure of the polynomials to be monic.

Since Y is compact, it admits a finite cover by the open sets ${\{U_{y_i}\subset {\widehat{Y}}^{\circ }\}}_i$ as above (see Formulas (17) and (18)). Let ${\{{\varphi }_i:Y\to [0,1]\}}_i$ be a smooth partition of unity, subordinated to this finite cover. Then, the monic u-polynomial

$$\tilde{P}(u,y):=\sum _i{\varphi }_i\left(y\right)·{\tilde{P}}_{y_i}(u,y)$$

of degree d has the desired properties. In particular, its divisor ${\tilde{D}}^{\beta }\left(y\right)=D^{\beta }\left(y\right)$ for each $y\in Y$. Thus, using $\tilde{P}(u,y)$, any immersion $\beta :(M,\mathit{\partial }M)\to (\mathbb{R}\times Y,\mathbb{R}\times \mathit{\partial }Y)$, such that

(i)

$\beta$ is transversal to $\mathbb{R}\times \mathit{\partial }Y$;

(ii)

no ${\omega }^{\beta }\left(y\right)$ belongs to $\mathrm{\Theta }$;

(iii)

for $y\in \mathit{\partial }Y$, no ${\omega }^{\beta }\left(y\right)$ belongs to $\mathrm{\Lambda }$,

is realized by a smooth map ${\mathrm{\Phi }}^{\beta }:(Y,\mathit{\partial }Y)\to ({\mathcal{P}}_d^{\mathbf{c}\mathrm{\Theta }},{\mathcal{P}}_d^{\mathbf{c}\mathrm{\Lambda }})$ for which $\beta \left(M\right)=\{{\mathrm{\Phi }}^{\beta }\left(y\right)\left(u\right)=0\}$.

If two such maps ${\mathrm{\Phi }}_0^{\beta },{\mathrm{\Phi }}_1^{\beta }:(Y,\mathit{\partial }Y)\to ({\mathcal{P}}_d^{\mathbf{c}\mathrm{\Theta }},{\mathcal{P}}_d^{\mathbf{c}\mathrm{\Lambda }})$ share the same divisor $D^{\beta }\left(y\right)$ for each $y\in Y$, then the quotients ${\mathrm{\Phi }}_0^{\beta }\left(y\right)/{\mathrm{\Phi }}_1^{\beta }\left(y\right)$ and ${\mathrm{\Phi }}_1^{\beta }\left(y\right)/{\mathrm{\Phi }}_0^{\beta }\left(y\right)$ are strictly positive rational functions and their numerators and denominators are monic non-vanishing polynomials of degree d. Such rational functions form a convex set ${\mathcal{Q}}_{+}\left(d\right)$ that retracts to the point-function $\mathbf{1}$. Therefore ${\mathrm{\Phi }}_0^{\beta },{\mathrm{\Phi }}_1^{\beta }$ produce a continuous map ${\mathrm{\Phi }}_0^{\beta }/{\mathrm{\Phi }}_1^{\beta }$ into a contractible space ${\mathcal{Q}}_{+}\left(d\right)$. As a result, by the linear homotopy ${\{(1-t){\mathrm{\Phi }}_0^{\beta }+t{\mathrm{\Phi }}_1^{\beta }\}}_{t\in [0,1]}$, ${\mathrm{\Phi }}_0^{\beta },{\mathrm{\Phi }}_1^{\beta }$ are homotopic maps. □

Definition 6. 

Let Y be a smooth compact n-manifold and the domain ${\mathcal{E}}_d\subset \mathbb{R}\times {\mathcal{P}}_d$ be as in (15). A smooth map $\mathrm{\Phi }:Y\to {\mathcal{P}}_d$ is called $(\mathit{\partial }{\mathcal{E}}_d)$-regular if the maps $\mathbb{R}\times Y\stackrel{\mathsf{id}\times \mathrm{\Phi }}{⟶}\mathbb{R}\times {\mathcal{P}}_d$ and $\mathbb{R}\times \mathit{\partial }Y\stackrel{\mathsf{id}\times {\mathrm{\Phi }}^{\mathit{\partial }}}{⟶}\mathbb{R}\times {\mathcal{P}}_d$ are transversal to the hypersurface $\mathit{\partial }{\mathcal{E}}_d$.

Thus, for a $(\mathit{\partial }{\mathcal{E}}_d)$-regular $\mathrm{\Phi }$, the preimage ${(\mathsf{id}\times \mathrm{\Phi })}^{-1}(\mathit{\partial }{\mathcal{E}}_d)$ is a compact smooth n-manifold $(M,\mathit{\partial }M)\subset (\mathbb{R}\times Y,\mathbb{R}\times \mathit{\partial }Y)$. Of course, if $\beta :(M,\mathit{\partial }M)\to (\mathbb{R}\times Y,\mathbb{R}\times \mathit{\partial }Y)$ is an immersion, but not an embedding, then any associated map ${\mathrm{\Phi }}^{\beta }:(Y,\mathit{\partial }Y)\to ({\mathcal{P}}_d^{\mathbf{c}\mathrm{\Theta }},{\mathcal{P}}_d^{\mathbf{c}\mathrm{\Lambda }})$ is not $\mathit{\partial }{\mathcal{E}}_d$-regular.

Figure 1, which illustrates the construction of the classifying map ${\mathrm{\Phi }}^{\beta }$, reveals an interesting duality: if $(u_{★},y_{★})\in \mathbb{R}\times Y$ is the point of transversal self-intersection of $\beta \left(M\right)=``{\infty }^{\prime \prime }$, then $y_{★}$ is mapped by ${\mathrm{\Phi }}^{\beta }$ to a point where the curve ${\mathrm{\Phi }}^{\beta }\left(Y\right)$ is tangent to the discriminant variety ${\mathcal{D}}_2$; in contrast, if $(u_{*},y_{*})\in \mathbb{R}\times Y$ is the point of tangency of $\beta \left(M\right)$ to $\mathcal{L}$, then $y_{*}$ is mapped by ${\mathrm{\Phi }}^{\beta }$ to a point where ${\mathrm{\Phi }}^{\beta }\left(Y\right)$ is transversal to ${\mathcal{D}}_2$. Since the presence of self-intersection point of $\beta \left(M\right)=``{\infty }^{\prime \prime }$ is a stable phenomenon with respect to perturbations of $\beta$ within immersions, the tangency of $\beta \left(M\right)$ to ${\mathcal{D}}_2$ must be stable, despite the fact that a perturbation of the loop ${\mathrm{\Phi }}^{\beta }\left(Y\right)$ can eliminate its tangency to ${\mathcal{D}}_2$.

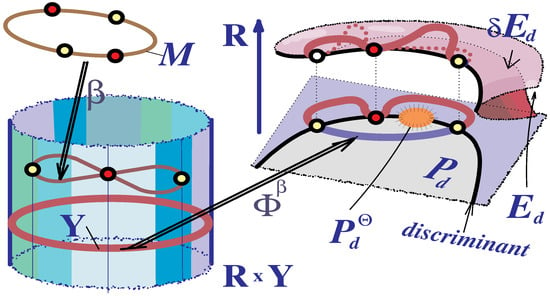
Figure 1. An immersion $\beta :M\to \mathbb{R}\times Y$ (the circle M being immersed as the figure ∞ in the cylinder $\mathbb{R}\times S^1$), and the classifying map ${\mathrm{\Phi }}^{\beta }:Y\to {\mathcal{P}}_d^{\mathbf{c}\mathrm{\Theta }}$ (where $Y=S^1$) that $\beta$ generates (see Theorem 3). To obtain a figure realistic in $3D$, we have chosen the simplest possible case: $d=2$, $\mathrm{\Theta }=\varnothing$. The loop ${\mathrm{\Phi }}^{\beta }\left(S^1\right)$ crosses transversally the discriminant curve (a parabola) at two points and is tangent to it at a single point. Note that $\beta \left(M\right)={(\mathsf{id}\times {\mathrm{\Phi }}^{\beta })}^{-1}\left((\mathbb{R}\times {\mathrm{\Phi }}^{\beta }\left(Y\right))\cap \mathit{\partial }{\mathcal{E}}_d\right)$, where the surface $\mathit{\partial }{\mathcal{E}}_d$ is introduced in (15).

Note that, in Figure 1, we can perturb the map ${\mathrm{\Phi }}^{\beta }:Y\to {\mathcal{P}}_d$ so that it will become transversal to the discriminant variety. Such a perturbation ${\tilde{\mathrm{\Phi }}}^{\beta }$ may be assumed to be $(\mathit{\partial }{\mathcal{E}}_d)$-regular. It will resolve the image $\beta \left(M\right)$ into a nonsingular manifold $N\subset \mathbb{R}\times Y$. In general, N may be topologically different from the original M. These observations are generalized in the next couple lemmas.

Lemma 3. 

For a compact smooth manifold Y, the $(\mathit{\partial }{\mathcal{E}}_d)$-regular maps $\{\mathrm{\Phi }:Y\to {\mathcal{P}}_d\}$ form an open and dense set in the space $C^{\infty }(Y,{\mathcal{P}}_d)$ of all smooth maps.

Proof. 

A smooth map $\mathrm{\Phi }:Y\to {\mathcal{P}}_d$, given by d functions coefficients $x_{d-1}\left(y\right),\dots ,x_1\left(y\right),x_0\left(y\right)$ on Y, is $(\mathit{\partial }{\mathcal{E}}_d)$-regular if and only if, in any local coordinate system $\overrightarrow{y}=\{y_1,\dots y_n\}$ on Y, the system

$$\begin{array}{ccc}\hfill u^d+x_{d-1}{u}^{d-1}+\dots x_{1}u+x_0& =& 0\hfill \\ \hfill d{u}^{d-1}+(d-1)x_{d-1}{u}^{d-2}+\dots +x_1& =& 0\hfill \\ \hfill \{{\displaystyle \frac{\mathit{\partial }{x}_{d-1}}{\mathit{\partial }{y}_j}}{u}^{d-1}+\dots {\displaystyle \frac{\mathit{\partial }{x}_1}{\mathit{\partial }{y}_j}}u+{\displaystyle \frac{\mathit{\partial }{x}_0}{\mathit{\partial }{y}_j}}& =& 0{\}}_{j\in [1,n]}\hfill \end{array}$$

(19)

of $(n+2)$ equations has no solutions in $\overrightarrow{y}$ for all u, and a similar property holds for $\mathit{\partial }Y$. Indeed, $\mathit{\partial }{\mathcal{E}}_d$ is given by the equation $\wp (u,\overrightarrow{x}):=u^d+x_{d-1}{u}^{d-1}+\dots x_{1}u+x_0=0$. The pull-back ${\Psi }^{*}(\wp )$ of ℘ under the map $\Psi =(\mathsf{id},\mathrm{\Phi }):\mathbb{R}\times Y\to \mathbb{R}\times {\mathcal{P}}_d$ is the function

$$u^d+x_{d-1}\left(y\right)u^{d-1}+\dots x_1\left(y\right)u+x_0\left(y\right)$$

on $\mathbb{R}\times Y$. So the first equation in (19) defines the preimage of $\mathit{\partial }\mathcal{E}$ under $\Psi$. The transversality of $\Psi$ to $\mathit{\partial }{\mathcal{E}}_d$ can be expressed as the non-vanishing of the one-jet of ${\Psi }^{*}(\wp )$ along the locus $\{{\Psi }^{*}(\wp )=0\}$. In local coordinates on $\mathbb{R}\times Y$, the vanishing of ${\mathsf{jet}}^1\left({\Psi }^{*}(\wp )\right)$ is exactly the constraints imposed by (19).

Note that, for each $u\in \mathbb{R}$, the system (19) imposes $(n+2)$affine constraints on the functions ${\{x_k:Y\to \mathbb{R}\}}_{k\in [1,d]}$ and their first derivatives $\left\{{\displaystyle \frac{\mathit{\partial }{x}_k}{\mathit{\partial }{y}_j}}\right\}$. Thus for any u, (19) defines an affine subbundle $\mathcal{W}\left(u\right)$ of the jet bundle $\{{\mathsf{J}}^1(Y,{\mathcal{P}}_d)\to Y\}$. The union $\mathcal{W}={\bigcup }_{u\in \mathbb{R}}\mathcal{W}\left(u\right)$ is a ruled variety, residing in ${\mathsf{J}}^1(Y,{\mathcal{P}}_d)$. Since $\mathrm{codim}\left(\mathcal{W}\right(u\left)\right)=n+2$, the codimension of $\mathcal{W}$ in ${\mathsf{J}}^1(Y,{\mathcal{P}}_d)$ is $n+1$.

Consider the jet map ${\mathsf{jet}}^1\left(\mathrm{\Phi }\right):Y\to {\mathsf{J}}^1(Y,{\mathcal{P}}_d)$. By the Thom Transversality Theorem (see [19], Theorem 4.13), the space of $\mathrm{\Phi }$ for which ${\mathsf{jet}}^1\left(\mathrm{\Phi }\right)$ is transversal to the subvariety $\mathcal{W}$ is open and dense (recall that Y is compact). Since Y is n-dimensional, this transversality implies that $\left({\mathsf{jet}}^1\left(\mathrm{\Phi }\right)\right)\left(Y\right)\cap \mathcal{W}=\varnothing$ for an open and dense set of maps $\mathrm{\Phi }$.

Similar arguments apply to the smooth maps ${\mathrm{\Phi }}^{\mathit{\partial }}:\mathit{\partial }Y\to {\mathcal{P}}_d$. Thus we may perturb first any given $\mathrm{\Phi }:Y\to {\mathcal{P}}_d$ to insure the $(\mathit{\partial }{\mathcal{E}}_d)$-regularity of ${\mathrm{\Phi }}^{\mathit{\partial }}{=\mathrm{\Phi }|}_{\mathit{\partial }Y}$ and then perturb $\mathrm{\Phi }$ to insure its $(\mathit{\partial }{\mathcal{E}}_d)$-regularity, while keeping the regularity of ${\mathrm{\Phi }}^{\mathit{\partial }}$.

Therefore, the set of $(\mathit{\partial }{\mathcal{E}}_d)$-regular maps $\mathrm{\Phi }$ is open and dense in $C^{\infty }(Y,{\mathcal{P}}_d)$. □

Corollary 3. 

Let $\mathrm{\Theta }\subset \mathrm{\Lambda }\subset {\mathbf{\Omega }}_{⟨d]}$ be closed subposets. For a compact smooth manifold Y, the $(\mathit{\partial }{\mathcal{E}}_d)$-regular maps $\{\mathrm{\Phi }:(Y,\mathit{\partial }Y)\to (P_d^{\mathbf{c}\mathrm{\Theta }},P_d^{\mathbf{c}\mathrm{\Lambda }})\}$ form an open and dense set in the space of all smooth maps $C^{\infty }\left((Y,\mathit{\partial }Y),(P_d^{\mathbf{c}\mathrm{\Theta }},P_d^{\mathbf{c}\mathrm{\Lambda }})\right)$.

Proof. 

Since Y is compact and the posets $\mathrm{\Theta },\mathrm{\Lambda }$ are closed, the target spaces ${\mathcal{P}}_d^{\mathbf{c}\mathrm{\Theta }}\supset {\mathcal{P}}_d^{\mathbf{c}\mathrm{\Lambda }}$ are both open in ${\mathcal{P}}_d$. Therefore the claim follows from Lemma 3. □

Lemma 4. 

For a compact n-dimensional Y, any $\mathit{\partial }{\mathcal{E}}_d$-regular smooth map $h:Y\to {\mathcal{P}}_d^{\mathbf{c}\mathrm{\Theta }}$ is realized by an embedding ${\beta }_h:(M,\mathit{\partial }M)\hookrightarrow (\mathbb{R}\times Y,\mathbb{R}\times \mathit{\partial }Y)$, where the smooth manifold M is n-dimensional and $\mathsf{rk}\left(D{\beta }_h\right)=n$. The manifold M is orientable if Y is orientable.

If $\mathit{\partial }Y=\varnothing$ and $d\equiv 0mod2$, then M is a boundary of a compact (orientable, if Y is orientable) $(n+1)$-manifold $L\subset \mathbb{R}\times Y$.

Proof. 

A $\mathit{\partial }{\mathcal{E}}_d$-regular smooth map $h:Y\to {\mathcal{P}}_d^{\mathbf{c}\mathrm{\Theta }}$ produces the locus $M={(\mathsf{id}\times h)}^{-1}(\mathit{\partial }{\mathcal{E}}_d)$ which is a smooth manifold by the transversality of $\mathsf{id}\times h$ to $\mathit{\partial }{\mathcal{E}}_d$. If Y is orientable, so is $\mathbb{R}\times Y$. Thus, the pull-back of the normal vector field to $\mathit{\partial }{\mathcal{E}}_d$ in ${\mathcal{E}}_d$ helps to orient the tangent bundle of M.

Given an embedding $\beta :M\hookrightarrow \mathbb{R}\times Y$, $dimM=n$, whose tangent patterns belong to $\mathbf{c}\mathrm{\Theta }$ and using that $d\equiv 0mod2$, we conclude that when Y is closed, then $\beta \left(M\right)$ bounds a compact $(n+1)$-manifold $X\subset \mathbb{R}\times Y$. Indeed, for each $y\in Y$, we consider the even degree d real monic polynomial $P_y\left(u\right)$ whose real divisor is ${\mathcal{L}}_y\cap \beta \left(M\right)$, counted with the multiplicities. Then, we define $L\cap {\mathcal{L}}_y$ as the compact set of $u\in \mathbb{R}$ that satisfies $\{P_y\left(u\right)\le 0\}$. The Y-family of such inequalities determines L. □

As a result, any closed n-manifold M, which is not (orientably, if Y is orientable) cobordant to ∅, does not arise via $\mathit{\partial }{\mathcal{E}}_d$-regular maps $h:Y\to {\mathcal{P}}_d$ for any closed Y and $d\equiv 0mod2$.

Consider the tautological function $\wp :\mathbb{R}\times {\mathcal{P}}_d\to \mathbb{R}$ whose value at the point $(u,P)$ is $P\left(u\right)$.

Definition 7. 

Let Y be a smooth compact n-manifold. Let $k\le d+1$.

We call a smooth map $\mathrm{\Phi }:Y\to {\mathcal{P}}_d$$(\mathit{\partial }{\mathcal{E}}_d,k)$-regular if the map $\mathbb{R}\times Y\stackrel{\mathsf{id}\times \mathrm{\Phi }}{⟶}\mathbb{R}\times {\mathcal{P}}_d$ has the following properties:

• The pull-back ${(\mathsf{id}\times \mathrm{\Phi })}^{*}(\wp )$ of the function ℘ in the vicinity $U_a$ of every point

  $$a=(u,y)\in {\mathcal{M}}_{\mathrm{\Phi }}:=\{{(\mathsf{id}\times \mathrm{\Phi })}^{*}(\wp )=0\}$$

  is locally a product of at most $\ell \le k$ smooth functions ${\{z_i:U_a\to \mathbb{R}\}}_{i\in [1,\ell ]}$ for each of which 0 is a regular value;
• There is a natural number q such that the q-jet equivalence classes of the local branches ${\{z_i=0\}}_i$ of ${\mathcal{M}}_{\mathrm{\Phi }}$ at a are distinct for all points a, (the branches are q-separable in the sense of Definition 4);
• If $y\in \mathit{\partial }Y$, the restrictions ${\left\{z_i{|}_{\mathbb{R}\times \mathit{\partial }Y}\right\}}_i$ have 0 as a regular value, and the q-jet equivalence classes of local branches ${\{z_i{|}_{\mathbb{R}\times \mathit{\partial }Y}=0\}}_i$ are distinct as well.

Evidently, $(\mathit{\partial }{\mathcal{E}}_d,1)$-regular map is $(\mathit{\partial }{\mathcal{E}}_d)$-regular.

Informally, we would like to think of $(\mathit{\partial }{\mathcal{E}}_d,k)$-regular maps $\mathrm{\Phi }$ as hypersurfaces that divide the space of $(\mathit{\partial }{\mathcal{E}}_d,k-1)$-regular maps into chambers. Presently, this interpretation is just wishful thinking. What is clear that, if a map $\mathrm{\Phi }:Y\to {\mathcal{P}}_d$ is $(\mathit{\partial }{\mathcal{E}}_d,k)$-regular, then there exists its open neighborhood in the space $C^{\infty }(Y,{\mathcal{P}}_d)$ that does not contain any $(\mathit{\partial }{\mathcal{E}}_d,l)$-maps, where $l>k$.

Lemma 5. 

If a map $\mathrm{\Phi }:Y\to {\mathcal{P}}_d$ is $(\mathit{\partial }{\mathcal{E}}_d,k)$-regular, then the locus

$${\mathcal{M}}_{\mathrm{\Phi }}{=}_{\mathsf{def}}\{{(\mathsf{id}\times \mathrm{\Phi })}^{*}(\wp )=0\}\subset \mathbb{R}\times Y$$

is a compact n-dimensional set with singularities of the local types $\{{\prod }_{i=1}^{\ell }{z}_i=0\}$, where $2\le \ell \le k\le d+1$, and each $z_i$ has 0 as its regular value.

Moreover, ${\mathcal{M}}_{\mathrm{\Phi }}$ is the image of a smooth compact n-manifold M under an immersion $\beta :M\to \mathbb{R}\times Y$.

Proof. 

The validation of the first claim is on the level of definitions.

Recall that we denote by ${\mathsf{J}}^q\left(X\right)\to X$ the fibration over a smooth manifold X, whose fiber over a point $x\in X$ is ${\mathsf{J}}_x^q$, the space of q-equivalence classes of germs of smooth hypersurfaces in X at x.

It remains to show that, if a map $\mathrm{\Phi }:Y\to {\mathcal{P}}_d$ is $(\mathit{\partial }{\mathcal{E}}_d,k)$-regular and, for some $q\ge 1$, the branches of the locus ${\mathcal{M}}_{\mathrm{\Phi }}\subset \mathbb{R}\times Y$ at their mutual intersections are q-separable, then ${\mathcal{M}}_{\mathrm{\Phi }}$ is the immersed image of some n-manifold M. In fact, there is an obvious canonical resolution$M\subset {\mathsf{J}}^{\mathsf{q}}(\mathbb{R}\times Y)$ of ${\mathcal{M}}_{\mathrm{\Phi }}$, so that the projection $\beta :M\subset {\mathsf{J}}^{\mathsf{q}}(\mathbb{R}\times Y)\stackrel{\pi }{⟶}\mathbb{R}\times Y$ is the desired immersion. We just associate with each point $a\in \{{\prod }_{i=1}^{\ell }{z}_i=0\}$ the (unordered) set of $\ell \le k$ distinct points ${\left\{{\mathsf{J}}_a^q\left(\{z_i=0\}\right)\right\}}_{i\in [1,\ell ]}\subset {\mathsf{J}}_a^q(\mathbb{R}\times Y)$. In this way, each local branch ${\mathcal{M}}_{\mathrm{\Phi },i}:=\{z_i=0\}$ of ${\mathcal{M}}_{\mathrm{\Phi }}$ defines a smooth section ${\sigma }_i:{\mathcal{M}}_{\mathrm{\Phi },i}\to {\mathsf{J}}^q{(\mathbb{R}\times Y)|}_{{\mathcal{M}}_{\mathrm{\Phi },i}}$. Over the vicinity of a, thanks to the q-separability, all the sections ${\left\{{\sigma }_i\right\}}_i$ are disjoint. Since $\pi \circ {\sigma }_i=\mathsf{id}$, we conclude that $\beta :M\to {\mathcal{M}}_{\mathrm{\Phi }}$ is an immersion. □

Definition 8. 

We say that an immersion $\beta :M\to \mathbb{R}\times Y$ is k-flat, if for all $y\in Y$, the reduced multiplicity

$$\begin{array}{c}\hfill {\left({\mu }^{\beta }\right)}^{\prime }\left(y\right){=}_{\mathsf{def}}\sum _{\{a\in {\mathcal{L}}_y\cap \beta \left(M\right)\}}\left(\sum _{\{b\in {\beta }^{-1}\left(a\right)\}}({\mu }^{\beta }\left(b\right)-1)\right)<k.\end{array}$$

(20)

In particular, if β is k-flat and k-normal, then the k-intersection manifold ${\mathrm{\Sigma }}_k^{\beta }=\varnothing$.

3.3. Quasitopies of Immersions and Embeddings with Constrained Tangencies Against the Background of 1-Foliations $\mathcal{L}$: The Case of General Combinatorics

We use the abbreviation “$\mathsf{imm}$” for immersions and “$\mathsf{emb}$” for regular embeddings. When the arguments work equally well for both types, we use the abbreviation “$\mathsf{i}/\mathsf{e}$”.

Fix two natural numbers $d\le d^{\prime }$, $d\equiv d^{\prime }mod2$ and consider the embedding ${ϵ}_{d,d^{\prime }}:{\mathcal{P}}_d\hookrightarrow {\mathcal{P}}_{d^{\prime }}$, defined by the Formula (8). Recall that it preserves the $\mathbf{\Omega }$-stratifications of the two spaces, ${\mathcal{P}}_d$ and ${\mathcal{P}}_{d^{\prime }}$, by the combinatorial types $\omega$ of real divisors $D_{\mathbb{R}}\left(P\right)$, $D_{\mathbb{R}}\left({ϵ}_{d,d^{\prime }}\left(P\right)\right)$.

For a closed profinite (see Definition 2) poset $\mathrm{\Theta }\subset \mathbf{\Omega }$, the embeddings ${ϵ}_{d,d^{\prime }}$ make it possible to talk about the stabilization in the homology of spaces ${\mathcal{P}}_d^{\mathbf{c}\mathrm{\Theta }}$, as $d\to \infty$. With the help of $\left\{{ϵ}_{d,d^{\prime }}\right\}$, it also makes sense to introduce the limit spaces ${\overline{\mathcal{P}}}_{\infty }^{\mathrm{\Theta }}$ and ${\mathcal{P}}_{\infty }^{\mathbf{c}\mathrm{\Theta }}$ [6].

For a smooth compact connected n-manifold Y, put $Z{=}_{\mathsf{def}}Y\times [0,1]$ and $Z^{\delta }{=}_{\mathsf{def}}\mathit{\partial }Y\times [0,1]$. We denote by ${\mathcal{L}}^{•}$ the 1-dimensional oriented foliation of $\mathbb{R}\times Z$, produced by the fibers of the obvious projection $\mathrm{\Pi }:\mathbb{R}\times Z\to Z$.

In Definition 9 below, central to our investigation, we start with a quite general set of combinatorial input data: $\{n,d,d^{\prime },\mathrm{\Theta },{\mathrm{\Theta }}^{\prime },\mathrm{\Lambda }\}$. We will gradually restrict them, as we develop the theory. Figure 2 may help the reader to follow our unfortunately cumbersome notations.

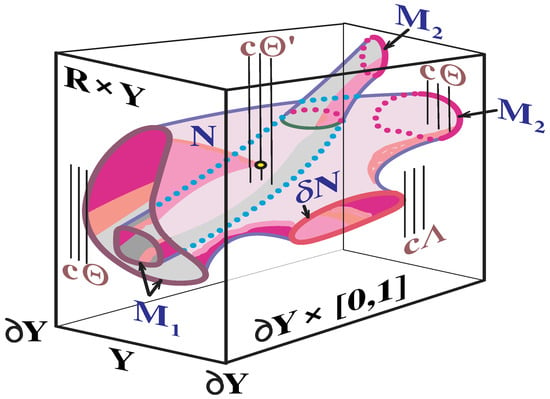
Figure 2. The ingredients of Definition 3.7, which illustrate the notion of quasitopy between immersions ${\beta }_1:M_1\to \mathbb{R}\times Y$ and ${\beta }_2:M_2\to \mathbb{R}\times Y$. The quasitopy is realized by an immersion-cobordism $B:N\to \mathbb{R}\times Y\times [0,1]$. The vertical lines are the fibers of the projection $p:\mathbb{R}\times Y\times [0,1]\to Y\times [0,1]$. Different combinatorial restrictions are imposed on different parts of $B\left(N\right)$: the combinatorial types of the fibers of the map $N\stackrel{B}{\to }\mathbb{R}\times Y\times [0,1]\stackrel{p}{\to }Y\times [0,1]$ avoid ${\mathrm{\Theta }}^{\prime }\subseteq \mathrm{\Theta }$, the combinatorial types of the fibers of the map $M_1\coprod M_2\stackrel{B|}{\to }\mathbb{R}\times Y\times (\left\{0\right\}\cup \left\{1\right\})\stackrel{p|}{\to }Y\times (\left\{0\right\}\cup \left\{1\right\})$ avoid $\mathrm{\Theta }$, while the fibers through $B\left(\delta \right(N)\subset \mathbb{R}\times \mathit{\partial }Y\times [0,1]$ avoid $\mathrm{\Lambda }\supset \mathrm{\Theta }$.

Definition 9. 

Let us fix natural numbers $d\le d^{\prime }$, $d\equiv d^{\prime }mod2$, and a triple of closed subposets ${\mathrm{\Theta }}^{\prime }\subset \mathrm{\Theta }\subset \mathrm{\Lambda }$ of the universal poset Ω. Let Y be a fixed smooth compact n-manifold and $M_0,M_1$ be two smooth compact n-manifolds.

We say that two proper immersions/embeddings,

$${\beta }_0:(M_0,\mathit{\partial }{M}_0)\to (\mathbb{R}\times Y,\mathbb{R}\times \mathit{\partial }Y)\mathrm{and}{\mathit{\beta }}_1:(M_1,\mathit{\partial }{M}_1)\to (\mathbb{R}\times Y,\mathbb{R}\times \mathit{\partial }Y),$$

are $(d,d^{\prime };\mathbf{c}\mathrm{\Theta },\mathbf{c}\mathrm{\Lambda };\mathbf{c}{\mathrm{\Theta }}^{\prime })$-quasitopic, if there exists a compact smooth $(n+1)$-manifold N with corners $\mathit{\partial }{M}_0\coprod \mathit{\partial }{M}_1$ and the boundary $\mathit{\partial }N=(M_0\coprod M_1)\cup \delta N$, ($\delta N$ is the closure of the complementary to $M_0\coprod M_1$ portion of $\mathit{\partial }N$). And a smooth proper immersion/embedding $B:N\to \mathbb{R}\times Z$ such that

• ${B|}_{M_0}={\beta }_0$, ${B|}_{M_1}={\beta }_1$, and $B\left(\delta N\right)\subset \mathbb{R}\times \mathit{\partial }Y\times [0,1]:=\mathbb{R}\times Z^{\delta }$;
• For each $z\in Z$, the total multiplicity $m_B\left(z\right)$ (see (16)) of $B\left(N\right)$ with respect to the fiber ${\mathcal{L}}_z^{•}$ is such that: $m_B\left(z\right)\le d^{\prime }$, $m_B\left(z\right)\equiv d^{\prime }mod2$, and the combinatorial tangency pattern ${\omega }^B\left(z\right)$ of $B\left(N\right)$ with respect to ${\mathcal{L}}_z^{•}$ belongs to the poset $\mathbf{c}{\mathrm{\Theta }}^{\prime }$;
• For each $z\in Y\times \mathit{\partial }[0,1]$, the total multiplicity of $B\left(N\right)$ with respect to ${\mathcal{L}}_z$ is such that: $m_B\left(z\right)\le d$, $m_B\left(z\right)\equiv dmod2$, and the combinatorial tangency pattern ${\omega }^B\left(z\right)$ of $B\left(N\right)$ with respect to ${\mathcal{L}}_z$ belongs to the poset $\mathbf{c}\mathrm{\Theta }$;
• For each $z\in Z^{\delta }$, the multiplicity of $B\left(N\right)$ with respect to ${\mathcal{L}}_z^{•}$ is such that: $m_B\left(z\right)\le d^{\prime }$, $m_B\left(z\right)\equiv d^{\prime }mod2$, and the combinatorial tangency pattern ${\omega }^B\left(z\right)$ of $B\left(\delta N\right)$ with respect to ${\mathcal{L}}_z^{•}$ belongs to the poset $\mathbf{c}\mathrm{\Lambda }$.

We denote by ${\mathcal{Q}}_{d,d^{\prime }}^{\mathsf{imm}}(Y,\mathit{\partial }Y;\mathbf{c}\mathrm{\Theta },\mathbf{c}\mathrm{\Lambda };\mathbf{c}{\mathrm{\Theta }}^{\prime })$ the set of quasitopy classes of such immersions $\beta :(M,\mathit{\partial }M)\to \mathbb{R}\times (Y,\mathit{\partial }Y)$.

We use the notation ${\mathcal{Q}}_{d,d^{\prime }}^{\mathsf{emb}}(Y,\mathit{\partial }Y;\mathbf{c}\mathrm{\Theta },\mathbf{c}\mathrm{\Lambda };\mathbf{c}{\mathrm{\Theta }}^{\prime })$ for the set of quasitopy classes of embeddings $\beta :(M,\mathit{\partial }M)\hookrightarrow \mathbb{R}\times (Y,\mathit{\partial }Y)$. Finally, we use the neutral notation ${\mathcal{Q}}_{d,d^{\prime }}^{\mathsf{i}/\mathsf{e}}(Y,\mathit{\partial }Y;\mathbf{c}\mathrm{\Theta },\mathbf{c}\mathrm{\Lambda };\mathbf{c}{\mathrm{\Theta }}^{\prime })$ for both.

It is possible to build a parallel notion of quasitopies for oriented M’s by insisting that the cobordism N is oriented as well. We use the notation ${\mathcal{OQ}}_{d,d^{\prime }}^{\mathsf{i}/\mathsf{e}}(Y,\mathit{\partial }Y;\mathbf{c}\mathrm{\Theta },\mathbf{c}\mathrm{\Lambda };\mathbf{c}{\mathrm{\Theta }}^{\prime })$ for these oriented quasitopy classes.

When Y is a closed manifold, we get ${\mathcal{Q}}_{d,d^{\prime }}^{\mathsf{i}/\mathsf{e}}(Y;\mathbf{c}\mathrm{\Theta };\mathbf{c}{\mathrm{\Theta }}^{\prime })$, a simplification of our settings. Also, when $\mathrm{\Theta }={\mathrm{\Theta }}^{\prime }$, we get another natural simplification: ${\mathcal{Q}}_{d,d^{\prime }}^{\mathsf{i}/\mathsf{e}}(Y,\mathit{\partial }Y;\mathbf{c}\mathrm{\Theta },\mathbf{c}\mathrm{\Lambda };\mathbf{c}\mathrm{\Theta })$. Both special cases, $d^{\prime }=d$ and $d^{\prime }=d+2$, have significant applications.

Remark 2.

If in Definition 9 we would require that the pair $(N,\delta N)$ is diffeomorphic to the pair $(M_0\times [0,1],\mathit{\partial }{M}_0\times [0,1])$, then a more recognizable definition of pseudo-isotopy would emerge. So the notion of quasitopy is more flexible than the one of pseudo-isotopy. It is closer to the notion of bordisms.

Remark 3.

The quasitopy ${\mathcal{Q}}_{d,d^{\prime }}^{\mathsf{i}/\mathsf{e}}(\sim ,\mathit{\partial }\sim ;\mathbf{c}\mathrm{\Theta },\mathbf{c}\mathrm{\Lambda };\mathbf{c}{\mathrm{\Theta }}^{\prime })$ is covarientely functorial under the regular embeddings $f:(Y,\mathit{\partial }Y)\hookrightarrow (Y^{\prime },\mathit{\partial }{Y}^{\prime })$ of equidimentional manifolds $Y,Y^{\prime }$. At the same time, ${\mathcal{Q}}_{d,d^{\prime }}^{\mathsf{i}/\mathsf{e}}(\sim ,\mathit{\partial }\sim ;\mathbf{c}\mathrm{\Theta },\mathbf{c}\mathrm{\Lambda };\mathbf{c}{\mathrm{\Theta }}^{\prime })$ is contravariantly functorial under submersions $g:(Y^{\prime },\mathit{\partial }{Y}^{\prime })\to (Y,\mathit{\partial }Y)$, provided that the fibers of g are closed manifolds. The contravariance is delivered via the pull back construction which involves ${\mathsf{id}}_{\mathbb{R}}\times g$ and $\beta :(M,\mathit{\partial }M)\to (\mathbb{R}\times Y,\mathbb{R}\times \mathit{\partial }Y)$.

Consider the group $\mathsf{Diff}\left(\mathcal{L}\right)$ of smooth diffeomorphisms of $\mathbb{R}\times Y$ that preserve the 1-foliation $\mathcal{L}$ and its orientation. We denote by ${\mathsf{Diff}}_0\left(\mathcal{L}\right)$ its subgroup, generated by the diffeomorphisms that are isotopic to the identity. Similar groups, $\mathsf{Diff}\left({\mathcal{L}}^{•}\right)$ and ${\mathsf{Diff}}_0\left({\mathcal{L}}^{•}\right)$ are available for the foliation ${\mathcal{L}}^{•}$ on $\mathbb{R}\times Y\times [0,1]$. Note that the group $\mathsf{Diff}\left(Y\right)$ is, in the obvious way, a subgroup of $\mathsf{Diff}\left(\mathcal{L}\right)$, and the group ${\mathsf{Diff}}_0\left(Y\right)$ is a subgroup of ${\mathsf{Diff}}_0\left(\mathcal{L}\right)$.

If $\beta :(M,\mathit{\partial }M)\to (\mathbb{R}\times Y,\mathbb{R}\times \mathit{\partial }Y)$ is a proper immersion/embedding as in Definition 9, then, for any $h\in {\mathsf{Diff}}_0\left(\mathcal{L}\right)$, the immersion/embedding $h\circ \beta$ is $(d,d^{\prime };\mathbf{c}\mathrm{\Theta },\mathbf{c}\mathrm{\Lambda };\mathbf{c}{\mathrm{\Theta }}^{\prime })$-quasitopic to $\beta$. In a similar way, ${\mathsf{Diff}}_0\left({\mathcal{L}}^{•}\right)$ acts on quasitopies of immersion/embedding. Therefore, in what follows, we may ignore the dependence of our constructions on the isotopies of the base manifold Y.

Definition 10. 

For a given closed poset ${\mathrm{\Theta }}_{⟨d]}\subset {\mathbf{\Omega }}_{⟨d]}$, we denote by $\widehat{m}\left(\mathbf{c}{\mathrm{\Theta }}_{⟨d]}\right)$ the maximum of entries ${\omega }_i$ for all $\omega =({\omega }_1,\dots ,{\omega }_i,\dots ,{\omega }_{\ell })\in \mathbf{c}{\mathrm{\Theta }}_{⟨d]}$.

Proposition 7. 

We adopt the notations of Corollary 2. Any proper immersion $\beta :(M,\mathit{\partial }M)\to (\mathbb{R}\times Y,\mathbb{R}\times \mathit{\partial }Y)$, as in Definition 9, which is k-normal for all k in the interval $[2,min\{n+1,\widehat{m}\left(\mathbf{c}{\mathrm{\Theta }}_{⟨d]}\right)\}]$, generates canonically smooth maps

$${\left\{\pi \circ \beta \circ p_1:({\mathrm{\Sigma }}_k^{\beta },{\mathrm{\Sigma }}_k^{{\beta }^{\mathit{\partial }}})\to (Y,\mathit{\partial }Y)\right\}}_k,$$

where ${\mathrm{\Sigma }}_k^{\beta }$ is the $k^{th}$ self-intersection manifold of β. The relative non-oriented bordism classes $\left[{\mathrm{\Sigma }}_k^{\beta }\right]\in {\mathbf{B}}_{n-k+1}(Y,\mathit{\partial }Y)$ of these maps $\pi \circ \beta \circ p_1$ are invariants of the $(d,d^{\prime };\mathbf{c}\mathrm{\Theta },\mathbf{c}\mathrm{\Lambda };\mathbf{c}{\mathrm{\Theta }}^{\prime })$-quasitopy class of β.

If $M,Y$ are oriented, then oriented bordism classes $\left[{\mathrm{\Sigma }}_k^{\beta }\right]\in {\mathbf{OB}}_{n-k+1}(Y,\mathit{\partial }Y)$ are invariants of the oriented $(d,d^{\prime };\mathbf{c}\mathrm{\Theta },\mathbf{c}\mathrm{\Lambda };\mathbf{c}{\mathrm{\Theta }}^{\prime })$-quasitopy class of β. In particular, if Y is closed, then the Pontryagin numbers of the manifold ${\mathrm{\Sigma }}_k^{\beta }$ are invariants of the quasitopy class of β.

Proof. 

If $\beta$ is an immersion as in Definition 9, then its sufficiently small perturbation still has combinatorial tangency patterns which belong to $\mathbf{c}\mathrm{\Theta }$, since $\mathrm{\Theta }$ is a closed poset in ${\mathbf{\Omega }}_{⟨d]}$. This claim is based on the behavior of real divisors of real polynomials under their perturbations [24]. Similarly, a sufficiently small perturbation of any cobordism B between such immersions, still will have combinatorial tangency patterns which belong to $\mathbf{c}{\mathrm{\Theta }}^{\prime }$, since ${\mathrm{\Theta }}^{\prime }$ is a closed poset in ${\mathbf{\Omega }}_{⟨d^{\prime }]}$. Therefore, according to [20], we may assume that $\beta$, within its $(d,d^{\prime };\mathbf{c}\mathrm{\Theta },\mathbf{c}\mathrm{\Lambda };\mathbf{c}{\mathrm{\Theta }}^{\prime })$-quasitopy class, is k-normal for all $k\le n+1$ and B is k-normal for all $k\le n+2$. Revisiting Definition 10, we notice that also $k\le \widehat{m}\left(\mathbf{c}{\mathrm{\Theta }}_{⟨d]}\right)$ by the very definition of quasitopies. Now the claim follows directly from Corollary 2. □

We are interested in two special cases of Definition 9 to be referred in what follows as the $\mathrm{\Lambda }$-condition:

$$\begin{array}{cc}\hfill \left(\mathbf{1}\right)& d^{\prime }\equiv d\equiv 0mod2\mathrm{and}\mathbf{c}\mathrm{\Lambda }=(\varnothing ),\\ \hfill \left(\mathbf{2}\right)& d^{\prime }\equiv d\equiv 1mod2\mathrm{and}\mathbf{c}\mathrm{\Lambda }=\left(1\right).\end{array}$$

(21)

Case (1) forces $\delta N=\varnothing$; so $M_0,M_1$ must be closed and $\mathit{\partial }N=M_0\coprod M_1$. This is evidently the case when $\mathit{\partial }Y=\varnothing$. Case (2) forces ${B|}_{\delta N}$ to be transversal to the foliation ${\mathcal{L}}^{•}{|}_{\mathbb{R}\times \mathit{\partial }Y\times [0,1]}$; so we get diffeomorphisms $B\left(\delta N\right)\approx \mathit{\partial }Y\times [0,1]$ and ${\beta }_i(\mathit{\partial }{M}_i)\approx \mathit{\partial }Y$.

Given two compact connected n-manifolds with boundaries, let $Y_1\#Y_2$ denote their connected sum and $Y_1{\#}_{\mathit{\partial }}{Y}_2$ their boundary connected sum. The 1-handle $H\approx D^{n-1}\times [0,1]$ that participates in the connected sum operation is attached to $Y_1\coprod Y_2$. In the special case $dim{Y}_1=dim{Y}_2=1$, the manifolds $Y_1,Y_2$ are closed segments and $Y_1{\#}_{\mathit{\partial }}{Y}_2$ is understood as a new segment, obtained by attaching one end of $Y_1$ to an end of $Y_2$.

If the boundaries of $Y_1$ and $Y_2$ are connected, the smooth topological type of $Y_1{\#}_{\mathit{\partial }}{Y}_2$ does not depend on how the 1-handle H is attached to $Y_1\coprod Y_2$ to form $Y_1{\#}_{\mathit{\partial }}{Y}_2$. In general, to avoid ambiguity of the operation ${\#}_{\mathit{\partial }}$, we pick some elements ${\kappa }_1\in {\pi }_0(\mathit{\partial }{Y}_1)$ and ${\kappa }_2\in {\pi }_0(\mathit{\partial }{Y}_2)$.

Definition 11. 

Under the $\mathrm{\Lambda }$-condition (21), we simplify our notations as follows:

$$\begin{array}{c}\hfill {\mathsf{Q}}_{d,d^{\prime }}^{\mathsf{i}/\mathsf{e}}(Y;\mathbf{c}\mathrm{\Theta };\mathbf{c}{\mathrm{\Theta }}^{\prime }){=}_{\mathsf{def}}{\mathcal{Q}}_{d,d^{\prime }}^{\mathsf{i}/\mathsf{e}}(Y,\mathit{\partial }Y;\mathbf{c}\mathrm{\Theta },(\varnothing );\mathbf{c}{\mathrm{\Theta }}^{\prime }),\mathrm{for}{d}^{\prime }\equiv d\equiv 0mod2,\end{array}$$

(22)

$$\begin{array}{c}\hfill {\mathsf{Q}}_{d,d^{\prime }}^{\mathsf{i}/\mathsf{e}}(Y;\mathbf{c}\mathrm{\Theta };\mathbf{c}{\mathrm{\Theta }}^{\prime }){=}_{\mathsf{def}}{\mathcal{Q}}_{d,d^{\prime }}^{\mathsf{i}/\mathsf{e}}(Y,\mathit{\partial }Y;\mathbf{c}\mathrm{\Theta },\left(1\right);\mathbf{c}{\mathrm{\Theta }}^{\prime }),\mathrm{for}{d}^{\prime }\equiv d\equiv 1mod2,\end{array}$$

(23)

$$\begin{array}{c}\hfill {\mathsf{G}}_{d,d^{\prime }}^{\mathsf{i}/\mathsf{e}}(n;\mathbf{c}\mathrm{\Theta };\mathbf{c}{\mathrm{\Theta }}^{\prime }){=}_{\mathsf{def}}{\mathcal{Q}}_{d,d^{\prime }}^{\mathsf{i}/\mathsf{e}}(D^n,\mathit{\partial }{D}^n;\mathbf{c}\mathrm{\Theta },(\varnothing );\mathbf{c}{\mathrm{\Theta }}^{\prime }),\mathrm{for}{d}^{\prime }\equiv d\equiv 0mod2,\end{array}$$

(24)

$$\begin{array}{c}\hfill {\mathsf{G}}_{d,d^{\prime }}^{\mathsf{i}/\mathsf{e}}(n;\mathbf{c}\mathrm{\Theta };\mathbf{c}{\mathrm{\Theta }}^{\prime }){=}_{\mathsf{def}}{\mathcal{Q}}_{d,d^{\prime }}^{\mathsf{i}/\mathsf{e}}(D^n,\mathit{\partial }{D}^n;\mathbf{c}\mathrm{\Theta },\left(1\right);\mathbf{c}{\mathrm{\Theta }}^{\prime }),\mathrm{for}{d}^{\prime }\equiv d\equiv 1mod2,\end{array}$$

(25)

where $D^n$ stands for the standard n-ball.

Assuming the $\mathrm{\Lambda }$-condition (21), for any the choice of ${\kappa }_1\in {\pi }_0(\mathit{\partial }{Y}_1)$ and ${\kappa }_2\in {\pi }_0(\mathit{\partial }{Y}_2)$, let us introduce an operation

$$\begin{array}{c}\hfill \uplus :{\mathsf{Q}}_{d,d^{\prime }}^{\mathsf{i}/\mathsf{e}}(Y_1;\mathbf{c}\mathrm{\Theta };\mathbf{c}{\mathrm{\Theta }}^{\prime })\times {\mathsf{Q}}_{d,d^{\prime }}^{\mathsf{i}/\mathsf{e}}(Y_2;\mathbf{c}\mathrm{\Theta };\mathbf{c}{\mathrm{\Theta }}^{\prime })\to {\mathsf{Q}}_{d,d^{\prime }}^{\mathsf{i}/\mathsf{e}}(Y_1{\#}_{\mathit{\partial }}{Y}_2;\mathbf{c}\mathrm{\Theta };\mathbf{c}{\mathrm{\Theta }}^{\prime }).\end{array}$$

(26)

Let $H\approx D^{n-1}\times D^1$ be a 1-handle attached to $Y_1\coprod Y_2$, to the preferred connected components ${\kappa }_1$ and ${\kappa }_2$ of $\mathit{\partial }{Y}_1$ and $\mathit{\partial }{Y}_2$. The result is the connected sum $Y_1{\#}_{\mathit{\partial }}{Y}_2$. From now on, we assume that the handles are attached so that the corners are smoothened and the resulting manifold has a smooth boundary. Different attachments of H produce diffeomorphic connected sums, provided that the disks $D^{n-1}\times \left\{0\right\}\subset H$ and $D^{n-1}\times \left\{1\right\}\subset H$ are placed in the same connected components ${(\mathit{\partial }{Y}_1)}_{{\kappa }_1}$ and ${(\mathit{\partial }{Y}_2)}_{{\kappa }_2}$ of the boundaries $\mathit{\partial }{Y}_1$ and $\mathit{\partial }{Y}_2$.

In case (1) from (21), $\mathbf{c}\mathrm{\Lambda }=(\varnothing )$, thus forcing the two immersions ${\beta }_i:M_i\to \mathbb{R}\times Y_i$ ($i=1,2$) to be immersions of closed manifolds. With ${(\mathit{\partial }{Y}_1)}_{{\kappa }_1}$ and ${(\mathit{\partial }{Y}_2)}_{{\kappa }_2}$ being fixed, the map ${\beta }_1\coprod {\beta }_2:M_1\coprod M_2\to \mathbb{R}\times \left(Y_1{\#}_{\mathit{\partial }}{Y}_2\right)$ is a well-defined immersion within its quasitopy class. Note that by (1) from (21), $({\beta }_1\coprod {\beta }_2)(M_1\coprod M_2)$ is disjoint from $\mathbb{R}\times \mathit{\partial }\left(Y_1{\#}_{\mathit{\partial }}{Y}_2\right)$. Thus we put ${\beta }_1\uplus {\beta }_2{=}_{\mathsf{def}}{\beta }_1\coprod {\beta }_2$.

In the case (2) from (21), $\mathbf{c}\mathrm{\Lambda }=\left(1\right)$, by an action of a diffeomorphism from ${\mathsf{Diff}}_0\left({\mathcal{L}}_i\right)$, we insure that ${\beta }_i(\mathit{\partial }{M}_i)=\left\{0\right\}\times \mathit{\partial }{Y}_i$, where $i=1,2$ and $\left\{0\right\}\in \mathbb{R}$. The ${\mathsf{Diff}}_0\left({\mathcal{L}}_i\right)$-action does not change the quasitopy classes of $\left\{{\beta }_i\right\}$.

As we attach a 1-handle H to $Y_1\coprod Y_2$ to form $Y_1{\#}_{\mathit{\partial }}{Y}_2$, we simultaneously attach the 1-handle $\tilde{H}=\left\{0\right\}\times H$ to $M_1\coprod M_2$ to form $M_1{\#}_{\mathit{\partial }}{M}_2$ and extend ${\beta }_1\coprod {\beta }_2$ across $\tilde{H}$ to a new map $\beta :M_1{\#}_{\mathit{\partial }}{M}_2\to \mathbb{R}\times \left(Y_1{\#}_{\mathit{\partial }}{Y}_2\right)$. On the handle $\tilde{H}$, the map $\beta$ is a regular embedding $\tilde{H}\hookrightarrow \mathbb{R}\times H$ and the obvious projection $\beta \left(\tilde{H}\right)\to H$ is an immersion.

The transversality of ${\beta }_i$ to $\mathbb{R}\times \mathit{\partial }{Y}_i$, together with the property (2) from (21), allows us to smoothen the immersed manifold $\beta \left(M_1{\#}_{\mathit{\partial }}{M}_2\right)={\beta }_1\left(M_1\right)\bigcup \beta \left(\tilde{H}\right)\bigcup {\beta }_2\left(M_2\right)$ in the neighborhood of $\tilde{H}$. This smoothing construction is again well-defined within the relative quasitopy classes of ${\beta }_1,{\beta }_2$. Thus, we put ${\beta }_1\uplus {\beta }_2{=}_{\mathsf{def}}\beta$.

However, in the case (2) from (21), when dealing with the oriented quasitopies, we face a problem. If $M_1$ and $M_2$ are oriented, the handle $\tilde{H}$ must be attached so that the preferred orientations extend across the handle. In “half” of the cases (when the orientations of ${\beta }_1\left(M_1\right)$ and ${\beta }_2\left(M_2\right)$) is “incoherent”), the obvious projection $\beta \left(\tilde{H}\right)\to H$ will fail to have tangency patterns of finite multiplicity, which violates our basic requirement in (16).

To summarize, the operation ⊎ is well-defined for the elements of the sets ${\mathcal{Q}}_d^{\mathsf{i}/\mathsf{e}}(Y,\mathit{\partial }Y;\mathbf{c}\mathrm{\Theta },(\varnothing );\mathbf{c}{\mathrm{\Theta }}^{\prime })$ and ${\mathcal{OQ}}_d^{\mathsf{i}/\mathsf{e}}(Y,\mathit{\partial }Y;\mathbf{c}\mathrm{\Theta },(\varnothing );\mathbf{c}{\mathrm{\Theta }}^{\prime })$, where $d\equiv 0mod2$, and for the elements of the set ${\mathcal{Q}}_d^{\mathsf{i}/\mathsf{e}}(Y,\mathit{\partial }Y;\mathbf{c}\mathrm{\Theta },\left(1\right);\mathbf{c}{\mathrm{\Theta }}^{\prime })$, where $d\equiv 1mod2$.

In particular, by fixing a diffeomorphism $\varphi :D^n{\#}_{\mathit{\partial }}{D}^n\approx D^n$, we get two interesting special cases of the operation ⊎:

$$\begin{array}{c}\hfill \uplus :{\mathsf{G}}_{d,d^{\prime }}^{\mathsf{i}/\mathsf{e}}(n;\mathbf{c}\mathrm{\Theta },\mathbf{c}{\mathrm{\Theta }}^{\prime })\times {\mathsf{G}}_{d,d^{\prime }}^{\mathsf{i}/\mathsf{e}}(n;\mathbf{c}\mathrm{\Theta },\mathbf{c}{\mathrm{\Theta }}^{\prime })\to {\mathsf{G}}_{d,d^{\prime }}^{\mathsf{i}/\mathsf{e}}(n;\mathbf{c}\mathrm{\Theta },\mathbf{c}{\mathrm{\Theta }}^{\prime }),\\ \hfill \uplus :{\mathsf{OG}}_{d,d^{\prime }}^{\mathsf{i}/\mathsf{e}}(n;\mathbf{c}\mathrm{\Theta },\mathbf{c}{\mathrm{\Theta }}^{\prime })\times {\mathsf{OG}}_{d,d^{\prime }}^{\mathsf{i}/\mathsf{e}}(n;\mathbf{c}\mathrm{\Theta },\mathbf{c}{\mathrm{\Theta }}^{\prime })\to {\mathsf{OG}}_{d,d^{\prime }}^{\mathsf{i}/\mathsf{e}}(n;\mathbf{c}\mathrm{\Theta },\mathbf{c}{\mathrm{\Theta }}^{\prime }),\end{array}$$

(27)

provided that, in the last formula, $d\equiv 0mod2$.

Proposition 8. 

Consider two closed subposets ${\mathrm{\Theta }}^{\prime }\subset \mathrm{\Theta }\subset \mathbf{\Omega }$, where $(\varnothing )\notin \mathrm{\Theta }$ for $d\equiv 0mod2$, and $\left(1\right)\notin \mathrm{\Theta }$ for $d\equiv 1mod2$.

For $d\equiv d^{\prime }\equiv 0mod2$, the operation ⊎ introduces a group structure to the sets ${\mathsf{G}}_{d,d^{\prime }}^{\mathsf{i}/\mathsf{e}}(n;\mathbf{c}\mathrm{\Theta },\mathbf{c}{\mathrm{\Theta }}^{\prime })$ and ${\mathsf{OG}}_{d,d^{\prime }}^{\mathsf{i}/\mathsf{e}}(n;\mathbf{c}\mathrm{\Theta },\mathbf{c}{\mathrm{\Theta }}^{\prime })$.

For $d\equiv d^{\prime }\equiv 1mod2$, the operation ⊎ introduces a group structure to the sets ${\mathsf{G}}_{d,d^{\prime }}^{\mathsf{i}/\mathsf{e}}(n;\mathbf{c}\mathrm{\Theta },\mathbf{c}{\mathrm{\Theta }}^{\prime })$.

For $n>1$, all these groups are abelian.

Proof. 

In this proof, for a given map $\alpha :X\to X$ of a topological space X, we denote by $\tilde{\alpha }$ the product map $\mathsf{id}\times \alpha :\mathbb{R}\times X\to \mathbb{R}\times X$.

In the case of $d\equiv d^{\prime }\equiv 0mod2$, the following arguments work equally well for ${\mathsf{OG}}_{d,d^{\prime }}^{\mathsf{i}/\mathsf{e}}(n;\mathbf{c}\mathrm{\Theta };\mathbf{c}{\mathrm{\Theta }}^{\prime })$ and for ${\mathsf{G}}_{d,d^{\prime }}^{\mathsf{i}/\mathsf{e}}(n;\mathbf{c}\mathrm{\Theta };\mathbf{c}{\mathrm{\Theta }}^{\prime })$, the oriented and non-oriented quasitopies over the n-ball $D^n$.

Let $B^n=D^n{\#}_{\mathit{\partial }}{D}^n$ be a n-ball, represented as a connected sum of two standard balls $D^n$. Let $H\approx D^{n-1}\times I$ be the 1-handle that participates in the construction of the ball $B^n$ as a connected sum: $B^n=D^n\cup H\cup D^n$. We fix a diffeomorphism $\chi :D^n\subset B^n$, which identifies the ball $D^n$ with the first ball in the connected sum $B^n$, and a diffeomorphism $\varphi :B^n\approx D^n$. Consider an isotopy ${\{{\psi }_t:B^n\to B^n\}}_{t\in [0,1]}$ that starts with the identity map and terminates with the diffeomorphism ${\psi }_1$ whose image is $\chi \left(D^n\right)\subset B^n$. With the help of ${\varphi }^{-1}$, we transfer the isotopy ${\psi }_t$ to an isotopy ${\{{\eta }_t:D^n\to D^n\}}_{t\in [0,1]}$. The isotopy ${\psi }_t$ lifts to the isotopy ${\tilde{\psi }}_t=\mathsf{id}\times {\psi }_t$ of $\mathbb{R}\times B^n$, and the isotopy ${\eta }_t$ lifts to the isotopy ${\tilde{\eta }}_t=\mathsf{id}\times {\eta }_t$ of $\mathbb{R}\times D^n$.

For $d\equiv 0mod2$, the neutral element ${\beta }_{★}$ is represented by ${\beta }_{★}:\varnothing \to \mathbb{R}\times D^n$ (by the “empty” cylinder). For $d\equiv 1mod2$, the neutral element ${\beta }_{★}$ is represented by the obvious embedding ${\beta }_{★}:D^n\to \left\{0\right\}\times D^n\subset \mathbb{R}\times D^n$.

We use ${\tilde{\eta }}_t$ to show that, for any immersion $\beta :M\to \mathbb{R}\times D^n$ and $d\equiv 0mod2$, the immersion $\tilde{\varphi }\circ (\beta \uplus {\beta }_{★}):M{\#}_{\mathit{\partial }}\varnothing \to \mathbb{R}\times D^n$ is isotopic (and thus quasitopic) to $\beta :M\to \mathbb{R}\times D^n$. We identify $M{\#}_{\mathit{\partial }}{D}^n$ with M with the help of a diffeomorphism $\rho$. For $d\equiv 1mod2$ and any immersion $\beta :M\to \mathbb{R}\times D^n$, with the help of ${\tilde{\eta }}_t$, the immersion $\tilde{\varphi }\circ (\beta \uplus {\beta }_{★})\circ {\rho }^{-1}:M\to \mathbb{R}\times D^n$ is isotopic to $\beta$. This validates the existence of the neutral element ${\beta }_{★}$ for the operation ⊎ within the $(d,d;\mathbf{c}\mathrm{\Theta },\mathbf{c}\mathrm{\Lambda };\mathbf{c}\mathrm{\Theta })$-quasitopy classes. Of course, any $(d,d;\mathbf{c}\mathrm{\Theta },\mathbf{c}\mathrm{\Lambda };\mathbf{c}\mathrm{\Theta })$-quasitopy is automatically a $(d,d^{\prime };\mathbf{c}\mathrm{\Theta },\mathbf{c}\mathrm{\Lambda };\mathbf{c}{\mathrm{\Theta }}^{\prime })$-quasitopy.

Consider an involution $\tau :B^n\to B^n$ that flips the two copies of $D^n$ in $B^n$ and has the ball $B^{n-1}$ in the middle of 1-handle $H\approx B^{n-1}\times I$ as its fixed point set. Then, for any immersion $\beta :M\to \mathbb{R}\times D^n$, the immersion $\tilde{\varphi }\circ \tilde{\tau }\circ \tilde{\chi }\circ \beta$ plays the role of the inverse ${\beta }^{-1}$ with respect to ⊎. Indeed, consider the unit half-disk $D_{+}^2$ and the unit half-cylinder $C_{+}^{n+1}:=D_{+}^2\times B^{n-1}$, inscribed in the cylinder $B^n\times [0,1+ϵ]$, $ϵ>0$. We will use the rotations $\tau \left(\theta \right)$ of $D^2\times B^{n-1}\supset C_{+}^{n+1}$ around the axis $B^{n-1}$ at the angles $\theta \in [0,\pi ]$, so that $\tau \left(\pi \right)=\tau$. Let $N=M\times [0,\pi ]$. In the case $d\equiv 0mod2$, we form an immersion

$$A:N\to \mathbb{R}\times C_{+}^{n+1}\subset \mathbb{R}\times B^n\times [0,1+ϵ],$$

defined by the formula $A(m,\theta )=\tilde{\tau }\left(\theta \right)\circ \beta \left(m\right)$.

Let $\left\{\underline{0}\right\}\in \mathbb{R}$ denote the origin. In the case $d\equiv 1mod2$, to satisfy Definition 9 for $\mathbf{c}\mathrm{\Lambda }=\left(1\right)$, we need to insure that

$$A\left(N\right)\cap \left\{\mathbb{R}\times \left(\mathit{\partial }(B^n\times [0,1+ϵ])\setminus (B^n\times \left\{0\right\})\right)\right\}=\left\{\underline{0}\right\}\times \left\{\mathit{\partial }(B^n\times [0,1+ϵ])\setminus (B^n\times \left\{0\right\})\right\}.$$

Therefore, we further isotop Aradially in each of the multipliers $D_{+}^2$ onto the rectangle $D^1\times [0,1+ϵ]$. The result is an isotopy of A inside the cylinder $\left\{\underline{0}\right\}\times B^n\times [0,1+ϵ]$.

Since $\left\{\tilde{\tau }\left(\theta \right)\right\}$ preserve the combinatorial $\mathcal{L}$-tangency patterns of $\beta \left(M\right)$ within to the ambient foliation ${\mathcal{L}}^{•}$ on $\mathbb{R}\times B^n\times [0,1+ϵ]$, we conclude that the cobordism $A:N\to \mathbb{R}\times B^n\times [0,1+ϵ]$ delivers $(d,d;\mathbf{c}\mathrm{\Theta },\mathbf{c}\mathrm{\Lambda };\mathbf{c}\mathrm{\Theta })$-quasitopy between $\beta \uplus {\beta }^{-1}$ and the neutral element ${\beta }_{★}$, provided that $\mathbf{c}\mathrm{\Lambda }$ is as in the hypotheses of the proposition.

Next, we need to verify the associativity of the operation ⊎. The argument is similar to the one that has validated that $\beta \uplus {\beta }_{★}$ is $(d,d;\mathbf{c}\mathrm{\Theta },\mathbf{c}\mathrm{\Lambda };\mathbf{c}\mathrm{\Theta })$-quasitopic to $\beta$. It uses diffeomorphisms ${\varphi }_{21}:D^n{\#}_{\mathit{\partial }}{D}^n\to D^n$ and ${\varphi }_{32}:D^n{\#}_{\mathit{\partial }}{D}^n{\#}_{\mathit{\partial }}{D}^n\to D^n{\#}_{\mathit{\partial }}{D}^n$, embeddings ${\chi }_1,{\chi }_2:D^n\to D^n{\#}_{\mathit{\partial }}{D}^n$ on the first and the second ball, and the embeddings ${\chi }_{12},{\chi }_{23}:D^n{\#}_{\mathit{\partial }}{D}^n\to D^n{\#}_{\mathit{\partial }}{D}^n{\#}_{\mathit{\partial }}{D}^n$ on the first and the second ball and on the second and third ball in $D^n{\#}_{\mathit{\partial }}{D}^n{\#}_{\mathit{\partial }}{D}^n$, respectively. We leave the rest of the argument to the reader.

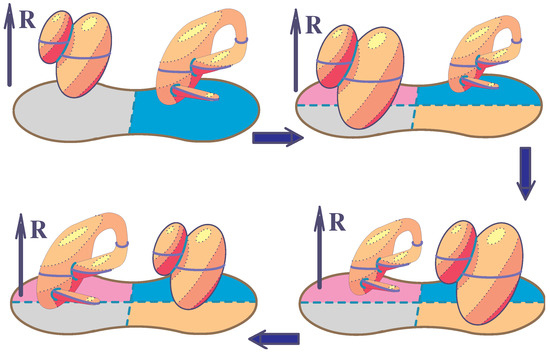
The validation of the fact that ⊎ is commutative for $n>1$ is a bit more involved and similar to the classical proof of the fact that the homotopy groups ${\pi }_n(\sim )$ of spaces are commutative for $n>1$ (see Figure 3). Let us sketch this validation.

Figure 3. Proving the commutativity of the operation ⊎ in the group ${\mathsf{G}}_{d,d^{\prime }}^{\mathsf{i}/\mathsf{e}}(n;\mathbf{c}\mathrm{\Theta };\mathbf{c}{\mathrm{\Theta }}^{\prime })$ for $n\ge 2$. The three bold arrows show the effects of isotopies in $\mathbb{R}\times B^n$.

As before, put $B^n=D_1^n\cup H\cup D_2^n$. We start with the case $d\equiv 0mod2$ and two immersions ${\beta }_i:M_i\to \mathbb{R}\times B^n$ ($i=1,2$) such that the image of ${\beta }_i$ belongs to the cylinder $\mathbb{R}\times D_i^n$. Consider an equatorial hyperplane $K^{n-1}\subset B^n$ (the horizontal punctured line in Figure 3), transversal to the ball $B^{n-1}\subset H$ and such that $K^{n-1}$ is the fixed point set of another involution $\lambda$ on $B^n$. So the pair of $(n-1)$-balls $K^{n-1}$ and $B^{n-1}$ divide $B^n$ in the four regions (“quadrants”): $B_I^n,B_{II}^n,B_{III}^n,B_{IV}^n$, ordered counterclockwise around the axle $K^{n-1}\cap B^{n-1}$. Each of these regions is homeomorphic to a n-ball.

First, we choose an isotopy ${\eta }_{III}^t$ to compress $D_1^n=B_{II}^n\cup B_{III}^n$ in the interior of the region $B_{III}^n$ and an isotopy ${\eta }_I^t$ to compress $D_2^n=B_I^n\cup B_{IV}^n$ in the interior of the region $B_I^n$. We may assume that these isotopies are smooth in the interior of the relevant regions. We lift ${\eta }_{III}^t$ to an isotopy ${\tilde{\eta }}_{III}^t$ and compose it with ${\beta }_1$. We lift ${\eta }_I^t$ to an isotopy ${\tilde{\eta }}_I^t$ and compose it with ${\beta }_2$. Let us denote these compositions by ${\beta }_{1,III}$ and ${\beta }_{2,I}$, respectively. Next, we choose an isotopy ${\zeta }_{II}^t$ to compress $B_I^n\cup B_{II}^n$ in the interior of $B_{II}^n$, and an isotopy ${\zeta }_{IV}^t$ to compress $B_{III}^n\cup B_{IV}^n$ in the interior of $B_{IV}^n$. The composition ${\tilde{\zeta }}_{II}^t\circ {\beta }_{2,I}$ places the image of $M_2$ over the quadrant $B_{II}^n$ and composition ${\tilde{\zeta }}_{IV}^t\circ {\beta }_{1,III}$ places the image $M_1$ over the quadrant $B_{IV}^n$. To complete the cycle that “switches” ${\beta }_1$ and ${\beta }_2$, it remains to expand the image ${\tilde{\zeta }}_{II}^t\circ {\beta }_{2,I}\left(M_2\right)\subset \mathbb{R}\times B_{II}^n$ into $\tilde{\tau }\left(M_2\right)$ and the image ${\tilde{\zeta }}_{IV}^t\circ {\beta }_{1,III}\left(M_1\right)\subset \mathbb{R}\times B_{IV}^n$ into $\tilde{\tau }\left(M_1\right)$.

In the case $d\equiv 1mod2$, more careful arguments are needed to insure that ${\beta }_1\uplus {\beta }_2$ is $(d,d;\mathbf{c}\mathrm{\Theta },(1);\mathbf{c}\mathrm{\Theta })$-quasitopic to $(\tilde{\tau }\circ {\beta }_2)\uplus (\tilde{\tau }\circ {\beta }_1)$. They are similar to the ones we used to prove that $\beta \uplus (\tilde{\tau }\circ \beta )$ is $(d,d;\mathbf{c}\mathrm{\Theta },(1);\mathbf{c}\mathrm{\Theta })$-quasitopic to the neutral element ${\beta }_{★}$. □

Remark 4.

We stress that the “1-dimensional” groups ${\mathsf{G}}_{d,d^{\prime }}^{\mathsf{i}/\mathsf{e}}(1;\mathbf{c}\mathrm{\Theta };\mathbf{c}{\mathrm{\Theta }}^{\prime })$ typically are not commutative. There are quite a few examples (see Corollary 13 and Figure 3) where, for ${\mathrm{\Theta }}^{\prime }=\mathrm{\Theta }$ and $d^{\prime }=d$, they are free groups with the number of free generators being bounded from above by some quadratic functions in d. In general, these groups form an interesting class, whose presentations are well-understood [5] and whose group theoretical properties deserve a study.

For a given group $\mathsf{G}$, we denote by ${\left(\mathsf{G}\right)}^r$ its r-fold direct product.

Corollary 4. 

Let ${\mathrm{\Theta }}^{\prime }\subset \mathrm{\Theta }\subset \mathbf{\Omega }$ be two closed subposets, where $(\varnothing )\notin \mathrm{\Theta }$ for $d\equiv 0mod2$ and $\left(1\right)\notin \mathrm{\Theta }$ for $d\equiv 1mod2$. Let $d\equiv d^{\prime }mod2$.

For any compact connected smooth n-dimensional manifold Y with boundaries that has r connected components, the group ${\left({\mathsf{G}}_{d,d^{\prime }}^{\mathsf{i}/\mathsf{e}}(n;\mathbf{c}\mathrm{\Theta },\mathbf{c}{\mathrm{\Theta }}^{\prime })\right)}^r$ acts, with the help of the operation ⊎, on the set ${\mathsf{Q}}_{d,d^{\prime }}^{\mathsf{i}/\mathsf{e}}(Y;\mathbf{c}\mathrm{\Theta },\mathbf{c}{\mathrm{\Theta }}^{\prime })$. Similarly, the group ${\left({\mathsf{OG}}_{d,d^{\prime }}^{\mathsf{i}/\mathsf{e}}(n;\mathbf{c}\mathrm{\Theta },\mathbf{c}{\mathrm{\Theta }}^{\prime })\right)}^r$ acts on ${\mathsf{OQ}}_{d,d^{\prime }}^{\mathsf{i}/\mathsf{e}}(Y;\mathbf{c}\mathrm{\Theta },\mathbf{c}{\mathrm{\Theta }}^{\prime })$, provided $d\equiv 0mod2$.

Proof. 

Let $\mathcal{G}:={\mathsf{G}}_{d,d^{\prime }}^{\mathsf{i}/\mathsf{e}}(n;\mathbf{c}\mathrm{\Theta };\mathbf{c}{\mathrm{\Theta }}^{\prime })$. By Proposition 8, $\mathcal{G}$ is a group with respect to the ⊎ operation. By the arguments that follow (26), for each choice of a connected component ${\mathit{\partial }}_{\kappa }Y$ of $\mathit{\partial }Y$, the group $\mathcal{G}$ acts via Formula (26) on the set ${\mathsf{Q}}_{d,d^{\prime }}^{\mathsf{i}/\mathsf{e}}(Y;\mathbf{c}\mathrm{\Theta };\mathbf{c}{\mathrm{\Theta }}^{\prime })$. In the case of an even d and $\mathbf{c}\mathrm{\Lambda }=(\varnothing )$, for a pair $\beta :M\to \mathbb{R}\times Y$, and ${\beta }^{\prime }:M^{\prime }\to \mathbb{R}\times D^n$, the action is defined by the formula $\beta \coprod {\beta }^{\prime }:M\coprod M^{\prime }\to \mathbb{R}\times \left(Y{\#}_{{\mathit{\partial }}_{\kappa }}{D}^n\right)\approx \mathbb{R}\times Y$, where ${\#}_{{\mathit{\partial }}_{\kappa }}$ is the boundary connected sum that employs the connected component ${\mathit{\partial }}_{\kappa }Y$. In the case of an odd d and $\mathbf{c}\mathrm{\Lambda }=\left(1\right)$, for a given pair $\beta :M\to \mathbb{R}\times Y$ and ${\beta }^{\prime }:M^{\prime }\to \mathbb{R}\times D^n$, the action is defined by the formula $\beta {\#}_{{\mathit{\partial }}_{\kappa }}{\beta }^{\prime }:M{\#}_{{\mathit{\partial }}_{\kappa }^{†}}{M}^{\prime }\to \mathbb{R}\times \left(Y{\#}_{{\mathit{\partial }}_{\kappa }}{D}^n\right)$, where ${\#}_{{\mathit{\partial }}_{\kappa }^{†}}$ is a boundary connected sum using the single component of $\mathit{\partial }M$, embedded by $\beta$ in $\mathbb{R}\times {\mathit{\partial }}_{\kappa }Y$, and the single component of $\mathit{\partial }{M}^{\prime }$, embedded by ${\beta }^{\prime }$ in $\mathbb{R}\times \mathit{\partial }{D}^n$.

For different choices of elements $\kappa \in {\pi }_0(\mathit{\partial }Y)$, these ${\mathcal{G}}_{\kappa }$-actions evidently commute. Thus ${\mathcal{G}}^r$ acts on ${\mathsf{Q}}_{d,d^{\prime }}^{\mathsf{i}/\mathsf{e}}(Y;\mathbf{c}\mathrm{\Theta };\mathbf{c}{\mathrm{\Theta }}^{\prime })$, where $r=\#\left({\pi }_0(\mathit{\partial }Y)\right)$. Similar arguments work for the oriented case, provided $d\equiv 0mod2$. □

Remark 5.

We will see soon that the group’s ${\mathsf{G}}_{d,d^{\prime }}^{\mathsf{i}/\mathsf{e}}(n;\mathbf{c}\mathrm{\Theta };\mathbf{c}{\mathrm{\Theta }}^{\prime })$ may have elements of infinite order, as well as some torsion, as complex as the torsion of the homotopy groups of spheres. As a result, the ${\mathsf{G}}_{d,d^{\prime }}^{\mathsf{i}/\mathsf{e}}(n;\mathbf{c}\mathrm{\Theta };\mathbf{c}{\mathrm{\Theta }}^{\prime })$-orbits in ${\mathsf{Q}}_{d,d^{\prime }}^{\mathsf{i}/\mathsf{e}}(Y;\mathbf{c}\mathrm{\Theta };\mathbf{c}{\mathrm{\Theta }}^{\prime })$ may have complex and diverse periods. We have a limited understanding of the orbit-space of this action; however, for embeddings, this problem is reduced to the homotopy theory of the spaces of real polynomials with constrained real divisors. In some cases (see Proposition 18 and Example 6), we can estimate the “size” of the orbit-space ${\mathsf{Q}}_{d,d^{\prime }}^{\mathsf{i}/\mathsf{e}}(Y;\mathbf{c}\mathrm{\Theta };\mathbf{c}{\mathrm{\Theta }}^{\prime })/{\mathsf{G}}_{d,d^{\prime }}^{\mathsf{i}/\mathsf{e}}(n;\mathbf{c}\mathrm{\Theta };\mathbf{c}{\mathrm{\Theta }}^{\prime })$.

Definition 12. 

as followed.

• Given two pairs of spaces $X_1\supset A_1$ and $X_2\supset A_2$, we denote by $[(X_1,A_1),(X_2,A_2)]$ the set of homotopy classes of continuous maps $g:X_1\to X_2$ such that $g\left(A_1\right)\subset A_2$.
• Given three pairs of spaces $X_1\supset A_1$, $X_2\supset A_2$, and $X_3\supset A_3$ and a fixed continuous map $ϵ:(X_2,A_2)\to (X_3,A_3)$, we denote by

  $$\begin{array}{c}\hfill \left[[(X_1,A_1),ϵ:(X_2,A_2)\to (X_3,A_3)]\right]\end{array}$$

  (28)

  the set of homotopy classes $\left[g\right]$ of continuous maps $g:(X_1,A_1)\to (X_2,A_2)$, modulo the following equivalence relation: $\left[g_0\right]\sim \left[g_1\right]$, where $g_0:(X_1,A_1)\to (X_2,A_2)$ and $g_1:(X_1,A_1)\to (X_2,A_2)$, if the compositions $ϵ\circ g_0$ and $ϵ\circ g_1$ are homotopic as maps from $(X_1,A_1)$ to $(X_3,A_3)$.

If all the spaces above are locally compact $CW$-complexes, then the set in (28) is countable or finite.

The next two propositions deliver new characteristic homotopy classes of immersions/embeddings against a fixed background of 1-foliations of the product type.

Proposition 9. 

Let ${\mathrm{\Theta }}^{\prime }\subset \mathrm{\Theta }\subset \mathrm{\Lambda }\subset \mathbf{\Omega }$ be closed subposets. Let M, Y be smooth compact n-manifolds.

• Any proper immersion/embedding $\beta :(M,\mathit{\partial }M)\to (\mathbb{R}\times Y,\mathbb{R}\times \mathit{\partial }Y)$, such that
  • $m^{\beta }\left(y\right)\le d$ (see (16)) and $m^{\beta }\left(y\right)\equiv dmod2$ for all $y\in Y$;
  • The combinatorial patterns ${\left\{{\omega }^{\beta }\left(y\right)\right\}}_{y\in Y}$ belong to $\mathbf{c}\mathrm{\Theta }$;
  • The combinatorial patterns ${\left\{{\omega }^{\beta }\left(y\right)\right\}}_{y\in \mathit{\partial }Y}$, belong to $\mathbf{c}\mathrm{\Lambda }$,
  generates a continuous map ${\mathrm{\Phi }}_d^{\beta }:(Y,\mathit{\partial }Y)\to ({\mathcal{P}}_d^{\mathbf{c}\mathrm{\Theta }},{\mathcal{P}}_d^{\mathbf{c}\mathrm{\Lambda }})$, whose homotopy class $\left[{\mathrm{\Phi }}^{\beta }\right]$ depends on β only.
• Moreover, any such pair

  $${\beta }_0:(M_0,\mathit{\partial }{M}_0)\to (\mathbb{R}\times Y,\mathbb{R}\times \mathit{\partial }Y)\mathrm{and}{\beta }_1:(M_1,\mathit{\partial }{M}_1)\to (\mathbb{R}\times Y,\mathbb{R}\times \mathit{\partial }Y)$$

  of $(d,d^{\prime };\mathbf{c}\mathrm{\Theta },\mathbf{c}\mathrm{\Lambda };\mathbf{c}{\mathrm{\Theta }}^{\prime })$-quasitopic immersions/embeddings generates homotopic composit maps

  $${ϵ}_{d,d^{\prime }}\circ {\mathrm{\Phi }}^{{\beta }_0}:(Y,\mathit{\partial }Y)\to ({\mathcal{P}}_{d^{\prime }}^{\mathbf{c}{\mathrm{\Theta }}^{\prime }},{\mathcal{P}}_{d^{\prime }}^{\mathbf{c}\mathrm{\Lambda }})\mathrm{and}{ϵ}_{d,d^{\prime }}\circ {\mathrm{\Phi }}^{{\beta }_1}:(Y,\mathit{\partial }Y)\to ({\mathcal{P}}_{d^{\prime }}^{\mathbf{c}{\mathrm{\Theta }}^{\prime }},{\mathcal{P}}_{d^{\prime }}^{\mathbf{c}\mathrm{\Lambda }}).$$
  Thus we get a well-defined surjective map

  $$\begin{array}{c}\hfill {\mathrm{\Phi }}_{d,d^{\prime }}(Y,\mathit{\partial }Y;\mathbf{c}\mathrm{\Theta },\mathbf{c}\mathrm{\Lambda };\mathbf{c}{\mathrm{\Theta }}^{\prime }):{\mathcal{Q}}_{d,d^{\prime }}^{\mathsf{i}/\mathsf{e}}(Y,\mathit{\partial }Y;\mathbf{c}\mathrm{\Theta },\mathbf{c}\mathrm{\Lambda };\mathbf{c}{\mathrm{\Theta }}^{\prime })\to \\ \hfill \to \left[[(Y,\mathit{\partial }Y),{ϵ}_{d,d^{\prime }}:({\mathcal{P}}_d^{\mathbf{c}\mathrm{\Theta }},{\mathcal{P}}_d^{\mathbf{c}\mathrm{\Lambda }})\to ({\mathcal{P}}_{d^{\prime }}^{\mathbf{c}{\mathrm{\Theta }}^{\prime }},{\mathcal{P}}_{d^{\prime }}^{\mathbf{c}\mathrm{\Lambda }})]\right],\end{array}$$

  (29)

  from the (oriented) quasitopies of immersions/embeddings to the homotopy classes of triples of spaces, as introduced in Definition 12.

Proof. 

The two claims follow from Theorem 3, being applied first to proper immersions ${\beta }_0:M_0\to \mathbb{R}\times Y$ and ${\beta }_1:{\beta }_1:M_1\to \mathbb{R}\times Y$, and then to the proper immersion $B:(N,\delta N)\to (\mathbb{R}\times Y\times [0,1],\mathbb{R}\times \mathit{\partial }Y\times [0,1\left]\right)$ of a relative cobordism N between $M_0$ and $M_1\cup \delta N$. There is only one technical wrinkle in this application: N is a compact manifold with corners $\mathit{\partial }{M}_0\coprod \mathit{\partial }{M}_1$; so Theorem 3 must be adjusted to such a situation. Note that B is transversal to both hypersurfaces, $\mathbb{R}\times Y\times \mathit{\partial }[0,1]$ and to $\mathbb{R}\times \mathit{\partial }Y\times [0,1]$. This fact allows to add a collar to $Y\times [0,1]$ and to extend the arguments of Theorem 3 to a new enlarged $(n+1)$-manifold $\widehat{Z}$ whose interior contains $Y\times [0,1]$.

Thus, the map ${\mathrm{\Phi }}^B:(Y\times [0,1],\mathit{\partial }Y\times [0,1])\to ({\mathcal{P}}_{d^{\prime }}^{\mathbf{c}{\mathrm{\Theta }}^{\prime }},{\mathcal{P}}_{d^{\prime }}^{\mathbf{c}\mathrm{\Lambda }})$ delivers a homotopy between the maps ${ϵ}_{d,d^{\prime }}\circ {\mathrm{\Phi }}^{{\beta }_0}$ and ${ϵ}_{d,d^{\prime }}\circ {\mathrm{\Phi }}^{{\beta }_1}$. Revisiting Definition 12, this implies that (29) is a well-defined map. In fact, similar map may be defined from the oriented quasitopies.

It will follow from Formula (37) below that the map in (29) is surjective. □

Corollary 5. 

Under the hypotheses of Proposition 9 and assuming the Λ-condition (21), we get a well-defined map

$$\begin{array}{c}\hfill {\mathrm{\Phi }}_{d,d^{\prime }}(Y;\mathbf{c}\mathrm{\Theta };\mathbf{c}{\mathrm{\Theta }}^{\prime }):{\mathsf{Q}}_{d,d^{\prime }}^{\mathsf{i}/\mathsf{e}}(Y;\mathbf{c}\mathrm{\Theta };\mathbf{c}{\mathrm{\Theta }}^{\prime })\to \\ \hfill \to \left[[(Y,\mathit{\partial }Y),{ϵ}_{d,d^{\prime }}:({\mathcal{P}}_d^{\mathbf{c}\mathrm{\Theta }},pt)\to ({\mathcal{P}}_{d^{\prime }}^{\mathbf{c}{\mathrm{\Theta }}^{\prime }},p{t}^{\prime })]\right],\end{array}$$

(30)

where the base point $pt\in {\mathcal{P}}_d^{\mathbf{c}\mathrm{\Lambda }}$ and $p{t}^{\prime }={ϵ}_{d,d^{\prime }}\left(pt\right)$. Similarly, a map from ${\mathsf{OQ}}_{d,d^{\prime }}^{\mathsf{i}/\mathsf{e}}(Y;\mathbf{c}\mathrm{\Theta };\mathbf{c}{\mathrm{\Theta }}^{\prime })$ to the same target is available.

Proof. 

If $\mathbf{c}\mathrm{\Lambda }=(\varnothing )$ or $\mathbf{c}\mathrm{\Lambda }=\left(1\right)$, then the spaces ${\mathcal{P}}_d^{\mathbf{c}\mathrm{\Lambda }}$ and ${\mathcal{P}}_{d^{\prime }}^{\mathbf{c}\mathrm{\Lambda }}$ are contractible. So the corollary follows from Proposition 9. □

Let Y be a connected n-dimensional manifold with boundary. Let us pick a preferred component $\mathit{\partial }{Y}_i$ of $\mathit{\partial }Y$. Then, the group ${\pi }_n({\mathcal{P}}_d^{\mathbf{c}\mathrm{\Theta }},pt)/ker\left({\left({ϵ}_{d,d^{\prime }}\right)}_{*}\right)$ acts naturally on the set $\left[[(Y,\mathit{\partial }Y),{ϵ}_{d,d^{\prime }}]\right]$ by forming the connected sum $g{\#}_{\mathit{\partial }{Y}_i}f$ of maps $f:(D^n,\mathit{\partial }{D}^n)\to ({\mathcal{P}}_d^{\mathbf{c}\mathrm{\Theta }},pt)$ and $g:(Y,\mathit{\partial }Y)\to ({\mathcal{P}}_d^{\mathbf{c}\mathrm{\Theta }},pt)$. As a result, we get an action of ${\left({\pi }_n({\mathcal{P}}_d^{\mathbf{c}\mathrm{\Theta }},pt)/ker\left({\left({ϵ}_{d,d^{\prime }}\right)}_{*}\right)\right)}^r$ on $\left[[(Y,\mathit{\partial }Y),{ϵ}_{d,d^{\prime }}]\right]$, where $r=\#\left({\pi }_0(\mathit{\partial }Y)\right)$. Let us denote this action by $h{\#}_{{\mathit{\partial }}_1}{f}_1{\#}_{{\mathit{\partial }}_2}\dots {\#}_{{\mathit{\partial }}_r}{f}_r$, where $h\in \left[[(Y,\mathit{\partial }Y),{ϵ}_{d,d^{\prime }}]\right]$, $f_i\in {\pi }_n({\mathcal{P}}_d^{\mathbf{c}\mathrm{\Theta }},pt)$, and ${\#}_{{\mathit{\partial }}_i}{f}_i$ stands for forming a boundary connected sum map $h{\#}_{\mathit{\partial }}{f}_i$ with h by using the $i^{th}$ component of $\mathit{\partial }Y$.

• Assuming the $\mathrm{\Lambda }$-condition (21), in what follows, we use the abbreviation

  $${\mathrm{\Phi }}_{d,d^{\prime }}(n;\mathbf{c}\mathrm{\Theta };\mathbf{c}{\mathrm{\Theta }}^{\prime }){=}_{\mathsf{def}}{\mathrm{\Phi }}_{d,d^{\prime }}(D^n,\mathit{\partial }{D}^n;\mathbf{c}\mathrm{\Theta },\mathbf{c}\mathrm{\Lambda };\mathbf{c}{\mathrm{\Theta }}^{\prime }).$$

Combining Proposition 8 with Proposition 9, leads to the following result.

Proposition 10. 

Under the Λ-condition (21),

• The map in (29) generates a group homomorphism

  $$\begin{array}{c}\hfill {\mathrm{\Phi }}_{d,d^{\prime }}(n;\mathbf{c}\mathrm{\Theta };\mathbf{c}{\mathrm{\Theta }}^{\prime }):{\mathsf{G}}_{d,d^{\prime }}^{\mathsf{i}/\mathsf{e}}(n;\mathbf{c}\mathrm{\Theta };\mathbf{c}{\mathrm{\Theta }}^{\prime })\to \\ \hfill \to {\pi }_n({\mathcal{P}}_d^{\mathbf{c}\mathrm{\Theta }},pt)/ker\left\{{\left({ϵ}_{d,d^{\prime }}\right)}_{*}:{\pi }_n({\mathcal{P}}_d^{\mathbf{c}\mathrm{\Theta }},pt)\to {\pi }_n({\mathcal{P}}_{d^{\prime }}^{\mathbf{c}{\mathrm{\Theta }}^{\prime }},p{t}^{\prime })\right\},\end{array}$$

  (31)

  where the group operation in ${\mathsf{G}}_{d,d^{\prime }}^{\mathsf{i}/\mathsf{e}}(n;\mathbf{c}\mathrm{\Theta };\mathbf{c}{\mathrm{\Theta }}^{\prime })$ is “ ⊎”. By Corollary 7, ${\mathrm{\Phi }}_{d,d^{\prime }}^{\mathsf{emb}}(n;\mathbf{c}\mathrm{\Theta };\mathbf{c}{\mathrm{\Theta }}^{\prime })$ is an isomorphism, and ${\mathrm{\Phi }}_{d,d^{\prime }}^{\mathsf{imm}}(n;\mathbf{c}\mathrm{\Theta };\mathbf{c}{\mathrm{\Theta }}^{\prime })$ is an epimorphism.
  For $d\equiv 0mod2$, the base points $pt\in {\mathcal{P}}_d^{\mathbf{c}\mathrm{\Theta }}$ resides in the chamber ${\mathsf{R}}_d^{(\varnothing )}$ of positive monic polynomials, and for $d\equiv 1mod2$, in the chamber ${\mathsf{R}}_d^{\left(1\right)}$ of monic polynomials with a single simple real root. Similar choices of the base point are made for $p{t}^{\prime }\in {\mathcal{P}}_{d^{\prime }}^{\mathbf{c}{\mathrm{\Theta }}^{\prime }}$.
• Let $r=\#\left({\pi }_0(\mathit{\partial }Y)\right)$. The $r^{th}$ power of the homomorphism ${\mathrm{\Phi }}_{d,d^{\prime }}(n;\mathbf{c}\mathrm{\Theta };\mathbf{c}{\mathrm{\Theta }}^{\prime })$ from (31) generates a representation of the group ${\left({\mathsf{G}}_{d,d^{\prime }}^{\mathsf{i}/\mathsf{e}}(n;\mathbf{c}\mathrm{\Theta };\mathbf{c}{\mathrm{\Theta }}^{\prime })\right)}^r$ in the group

  $${\left({\pi }_n\left({\mathcal{P}}_d^{\mathbf{c}\mathrm{\Theta }},pt\right)/ker\left\{{\left({ϵ}_{d,d^{\prime }}\right)}_{*}:{\pi }_n({\mathcal{P}}_d^{\mathbf{c}\mathrm{\Theta }},pt)\to {\pi }_n({\mathcal{P}}_{d^{\prime }}^{\mathbf{c}{\mathrm{\Theta }}^{\prime }},p{t}^{\prime })\right\}\right)}^r.$$
  With the help of this representation, the map in (29) is equivariant with respect to the ${\left({\mathsf{G}}_{d,d^{\prime }}^{\mathsf{i}/\mathsf{e}}(n;\mathbf{c}\mathrm{\Theta };\mathbf{c}{\mathrm{\Theta }}^{\prime })\right)}^r$-action on the set ${\mathsf{Q}}_{d,d^{\prime }}^{\mathsf{i}/\mathsf{e}}(Y;\mathbf{c}\mathrm{\Theta };\mathbf{c}{\mathrm{\Theta }}^{\prime })$ and with respect to the ${\left({\pi }_n({\mathcal{P}}_d^{\mathbf{c}\mathrm{\Theta }},pt)/ker\left\{{\left({ϵ}_{d,d^{\prime }}\right)}_{*}:{\pi }_n({\mathcal{P}}_d^{\mathbf{c}\mathrm{\Theta }},pt)\to {\pi }_n({\mathcal{P}}_{d^{\prime }}^{\mathbf{c}{\mathrm{\Theta }}^{\prime }},p{t}^{\prime })\right\}\right)}^r-\mathrm{action}$ on the set $\left[[(Y,\mathit{\partial }Y),{ϵ}_{d,d^{\prime }}:({\mathcal{P}}_d^{\mathbf{c}\mathrm{\Theta }},{\mathcal{P}}_d^{\mathbf{c}\mathrm{\Lambda }})\to ({\mathcal{P}}_{d^{\prime }}^{\mathbf{c}{\mathrm{\Theta }}^{\prime }},{\mathcal{P}}_{d^{\prime }}^{\mathbf{c}\mathrm{\Lambda }})]\right]$.
• Similar claims hold for the oriented quasitopies ${\mathsf{OQ}}_{d,d^{\prime }}^{\mathsf{i}/\mathsf{e}}(Y;\mathbf{c}\mathrm{\Theta };\mathbf{c}{\mathrm{\Theta }}^{\prime })$ and the ${\left({\mathsf{OG}}_{d,d^{\prime }}^{\mathsf{i}/\mathsf{e}}(n;\mathbf{c}\mathrm{\Theta };\mathbf{c}{\mathrm{\Theta }}^{\prime })\right)}^r$-action on them, provided $d\equiv d^{\prime }\equiv 0mod2$.

Proof. 

By Proposition 9, we get a group representation ${\mathrm{\Phi }}_{d,d^{\prime }}(n;\mathbf{c}\mathrm{\Theta },\mathbf{c}\mathrm{\Lambda };\mathbf{c}{\mathrm{\Theta }}^{\prime })$ from (31). By Corollary 4, the group ${\left({\mathsf{G}}_{d,d^{\prime }}^{\mathsf{i}/\mathsf{e}}(n;\mathbf{c}\mathrm{\Theta };\mathbf{c}{\mathrm{\Theta }}^{\prime })\right)}^r$ acts on ${\mathsf{Q}}_{d,d^{\prime }}^{\mathsf{i}/\mathsf{e}}(Y;\mathbf{c}\mathrm{\Theta };\mathbf{c}{\mathrm{\Theta }}^{\prime })$. Employing Corollary 5, we get a well-defined map $\mathrm{\Phi }\left(Y\right){=}_{\mathsf{def}}{\mathrm{\Phi }}_{d,d^{\prime }}(Y,\mathit{\partial }Y;\mathbf{c}\mathrm{\Theta },\mathbf{c}\mathrm{\Lambda };\mathbf{c}{\mathrm{\Theta }}^{\prime })$ from (29).

If a map $F:(Y,\mathit{\partial }Y)\to ({\mathcal{P}}_d^{\mathbf{c}\mathrm{\Theta }},pt)$, being composed with ${ϵ}_{d,d^{\prime }}$, becomes null-homotopic in $({\mathcal{P}}_d^{\mathbf{c}{\mathrm{\Theta }}^{\prime }},p{t}^{\prime })$, then for any map $G:(D^n,\mathit{\partial }{D}^n)\to ({\mathcal{P}}_d^{\mathbf{c}\mathrm{\Theta }},pt)$ such that ${ϵ}_{d,d^{\prime }}\circ G$ is null-homotopic in $({\mathcal{P}}_d^{\mathbf{c}{\mathrm{\Theta }}^{\prime }},p{t}^{\prime })$, the map ${ϵ}_{d,d^{\prime }}\circ \left(G{\#}_{\mathit{\partial }}F\right)$ is null-homotopic in $({\mathcal{P}}_d^{\mathbf{c}{\mathrm{\Theta }}^{\prime }},p{t}^{\prime })$ as well. Thus, the action of the group ${\pi }_n\left(({\mathcal{P}}_d^{\mathbf{c}\mathrm{\Theta }},pt)\right)/ker\left\{{ϵ}_{d,d^{\prime }}\right\}$ on the set $\left[[(Y,\mathit{\partial }Y),{ϵ}_{d,d^{\prime }}:({\mathcal{P}}_d^{\mathbf{c}\mathrm{\Theta }},{\mathcal{P}}_d^{\mathbf{c}\mathrm{\Lambda }})\to ({\mathcal{P}}_{d^{\prime }}^{\mathbf{c}{\mathrm{\Theta }}^{\prime }},{\mathcal{P}}_{d^{\prime }}^{\mathbf{c}\mathrm{\Lambda }})]\right]$ is well-defined. Now, thanks to Theorem 3, it is on the level of definitions to verify the equivariant property of $\mathrm{\Phi }\left(Y\right)$, namely, that

$$\mathrm{\Phi }\left(Y\right)(\beta {\uplus }_1{\gamma }_1{\uplus }_2{\gamma }_2\dots {\uplus }_r{\gamma }_r)=\mathrm{\Phi }\left(Y\right)\left(\beta \right){\#}_{{\mathit{\partial }}_1}\mathrm{\Phi }\left(D^n\right)\left({\gamma }_1\right)\dots {\#}_{{\mathit{\partial }}_r}\mathrm{\Phi }\left(D^n\right)\left({\gamma }_r\right),$$

where $\beta \in {\mathsf{Q}}_{d,d^{\prime }}^{\mathsf{i}/\mathsf{e}}(Y;\mathbf{c}\mathrm{\Theta };\mathbf{c}{\mathrm{\Theta }}^{\prime })$ and ${\gamma }_i\in {\mathsf{G}}_{d,d^{\prime }}^{\mathsf{i}/\mathsf{e}}(n;\mathbf{c}\mathrm{\Theta };\mathbf{c}{\mathrm{\Theta }}^{\prime })$, or $\beta \in {\mathsf{OQ}}_{d,d^{\prime }}^{\mathsf{i}/\mathsf{e}}(Y;\mathbf{c}\mathrm{\Theta };\mathbf{c}{\mathrm{\Theta }}^{\prime })$ and ${\gamma }_i\in {\mathsf{OG}}_{d,d^{\prime }}^{\mathsf{i}/\mathsf{e}}(n;\mathbf{c}\mathrm{\Theta };\mathbf{c}{\mathrm{\Theta }}^{\prime })$. □

Definition 13. 

Let ${\mathrm{\Theta }}^{\prime }\subset \mathrm{\Theta }\subset \mathrm{\Lambda }\subset \mathbf{\Omega }$ be closed subposets.

Consider the obvious map ${\mathcal{Q}}_{d,d^{\prime }}^{\mathsf{i}/\mathsf{e}}(Y,\mathit{\partial }Y;\mathbf{c}\mathrm{\Lambda },\mathbf{c}\mathrm{\Lambda };\mathbf{c}{\mathrm{\Theta }}^{\prime })\to {\mathcal{Q}}_{d,d^{\prime }}^{\mathsf{i}/\mathsf{e}}(Y,\mathit{\partial }Y;\mathbf{c}\mathrm{\Theta },\mathbf{c}\mathrm{\Lambda };\mathbf{c}{\mathrm{\Theta }}^{\prime })$.

We denote by ${}^{†}{\mathcal{Q}}_{d,d^{\prime }}^{\mathsf{i}/\mathsf{e}}(Y,\mathit{\partial }Y;\mathbf{c}\mathrm{\Theta },\mathbf{c}\mathrm{\Lambda };\mathbf{c}{\mathrm{\Theta }}^{\prime })$ its image. It is represented by immersions/embeddings $\beta :(M,\mathit{\partial }M)\to (\mathbb{R}\times Y,\mathbb{R}\times \mathit{\partial }Y)$, whose combinatorial tangency patterns to the foliation $\mathcal{L}$ belong to the open subposet $\mathbf{c}\mathrm{\Lambda }\subset \mathbf{c}\mathrm{\Theta }$. We call such elements combinatorially trivial.

Then, we introduce the quotient set by the formula:

$$\begin{array}{c}\hfill {\mathbf{Q}}_{d,d^{\prime }}^{\mathsf{i}/\mathsf{e}}(Y,\mathit{\partial }Y;\mathbf{c}\mathrm{\Theta },\mathbf{c}\mathrm{\Lambda };\mathbf{c}{\mathrm{\Theta }}^{\prime }){=}_{\mathsf{def}}\end{array}$$

(32)

$$\begin{array}{c}\hfill {\mathcal{Q}}_{d,d^{\prime }}^{\mathsf{i}/\mathsf{e}}(Y,\mathit{\partial }Y;\mathbf{c}\mathrm{\Theta },\mathbf{c}\mathrm{\Lambda };\mathbf{c}{\mathrm{\Theta }}^{\prime })/{}^{†}{\mathcal{Q}}_{d,d^{\prime }}^{\mathsf{i}/\mathsf{e}}(Y,\mathit{\partial }Y;\mathbf{c}\mathrm{\Lambda },\mathbf{c}\mathrm{\Lambda };\mathbf{c}{\mathrm{\Theta }}^{\prime }).\end{array}$$

(33)

Under the $\mathrm{\Lambda }$-condition (21), we get

$$\begin{array}{c}\hfill {\mathbf{Q}}_{d,d^{\prime }}^{\mathsf{i}/\mathsf{e}}(Y,\mathit{\partial }Y;\mathbf{c}\mathrm{\Theta },\mathbf{c}\mathrm{\Lambda };\mathbf{c}{\mathrm{\Theta }}^{\prime })=\\ \hfill ={\mathcal{Q}}_{d,d^{\prime }}^{\mathsf{i}/\mathsf{e}}(Y,\mathit{\partial }Y;\mathbf{c}\mathrm{\Theta },\mathbf{c}\mathrm{\Lambda };\mathbf{c}{\mathrm{\Theta }}^{\prime }){=}_{\mathsf{def}}{\mathsf{Q}}_{d,d^{\prime }}^{\mathsf{i}/\mathsf{e}}(Y;\mathbf{c}\mathrm{\Theta };\mathbf{c}{\mathrm{\Theta }}^{\prime }),\end{array}$$

(34)

since ${}^{†}{\mathcal{Q}}_{d,d^{\prime }}^{\mathsf{i}/\mathsf{e}}(Y,\mathit{\partial }Y;\mathbf{c}\mathrm{\Lambda },\mathbf{c}\mathrm{\Lambda };\mathbf{c}{\mathrm{\Theta }}^{\prime })$ is represented by a single element, an empty embedding or the embedding $\mathsf{id}:Y\to \left\{0\right\}\times Y\subset \mathbb{R}\times Y$. In particular, if $\mathit{\partial }Y=\varnothing$, then we get the bijection (34). When Y is orientable, similar definitions/constructions of ${\mathbf{OQ}}_{d,d^{\prime }}^{\mathsf{i}/\mathsf{e}}(Y,\mathit{\partial }Y;\mathbf{c}\mathrm{\Theta },\mathbf{c}\mathrm{\Lambda };\mathbf{c}{\mathrm{\Theta }}^{\prime })$ are available for the oriented quasitopies, provided $d\equiv 0mod2$.

Lemma 6. 

Let ${\mathrm{\Theta }}^{\prime }\subset \mathrm{\Theta }\subset \mathrm{\Lambda }\subset \mathbf{\Omega }$ be closed subposets, and let Y be a compact manifold. We pick a pair of natural numbers $d\le d^{\prime }$ of the same parity.

• Any smooth $(\mathit{\partial }{\mathcal{E}}_d)$-regular map $h:(Y,\mathit{\partial }Y)\to ({\mathcal{P}}_d^{\mathbf{c}\mathrm{\Theta }},{\mathcal{P}}_d^{\mathbf{c}\mathrm{\Lambda }})$ produces a proper regular embedding ${\beta }_h:(M,\mathit{\partial }M)\hookrightarrow (\mathbb{R}\times Y,\mathbb{R}\times \mathit{\partial }Y)$ of some compact n-manifold M. The combinatorial patterns of ${\beta }_h$, relative to the foliation $\mathcal{L}$, belong to $\mathbf{c}\mathrm{\Theta }$ and of its restriction to $\mathit{\partial }M$ belong to $\mathbf{c}\mathrm{\Lambda }$. Moreover, ${\mathrm{\Phi }}^{{\beta }_h}=h$.
• Any pair $h_0,h_1:(Y,\mathit{\partial }Y)\to ({\mathcal{P}}_d^{\mathbf{c}\mathrm{\Theta }},{\mathcal{P}}_d^{\mathbf{c}\mathrm{\Lambda }})$ of $(\mathit{\partial }{\mathcal{E}}_d)$-regular maps such that ${ϵ}_{d,d^{\prime }}\circ h_0$ and ${ϵ}_{d,d^{\prime }}\circ h_1$ are linked by a smooth $(\mathit{\partial }{\mathcal{E}}_{d^{\prime }})$-regular homotopy

  $$H:(Y\times [0,1],\mathit{\partial }Y\times [0,1])\to ({\mathcal{P}}_{d^{\prime }}^{\mathbf{c}{\mathrm{\Theta }}^{\prime }},{\mathcal{P}}_{d^{\prime }}^{\mathbf{c}\mathrm{\Lambda }})$$

  gives rise to a $(d,d^{\prime };\mathbf{c}\mathrm{\Theta },\mathbf{c}\mathrm{\Lambda };\mathbf{c}{\mathrm{\Theta }}^{\prime })$-quasitopy $B_H:N\hookrightarrow \mathbb{R}\times Y\times [0,1]$ between ${\beta }_{h_0}$ and ${\beta }_{h_1}$. Moreover, ${\mathrm{\Phi }}^{B_H}=H$.
• If Y is orientable, then so are M and N.

Proof. 

The first claim of the lemma follows from Definition 6, since for a $\mathit{\partial }{\mathcal{E}}_d$-regular map, the preimage of the hypersurface $\mathit{\partial }{\mathcal{E}}_d\subset \mathbb{R}\times {\mathcal{P}}_d$ under $\mathsf{id}\times h$ is a regularly embedded codimension 1 submanifold M of $\mathbb{R}\times Y$, and the preimage of $\mathit{\partial }{\mathcal{E}}_d$ under the map ${\mathsf{id}\times h|}_{\mathit{\partial }Y}$, where ${h|}_{\mathit{\partial }Y}$ is a $\mathit{\partial }{\mathcal{E}}_d$-regular map, is the boundary $\mathit{\partial }M$, regularly embedded in $\mathbb{R}\times \mathit{\partial }Y$. Recall that the map $\mathsf{id}\times h$ pulls back the universal function $\wp (u,x):\mathbb{R}\times {\mathbb{R}}^d\to \mathbb{R}$ to the function ${(\mathsf{id}\times h)}^{*}(\wp )$ on $\mathbb{R}\times Y$ for which 0 is a regular value. Using this function ${(\mathsf{id}\times h)}^{*}(\wp )$, the arguments from Theorem 3 imply that ${\mathrm{\Phi }}^{{\beta }_h}=h$.

Let us validate the second claim. Recall that ${ϵ}_{d,d^{\prime }}\left({\mathcal{P}}_d^{\mathbf{c}\mathrm{\Lambda }}\right)\subset {\mathcal{P}}_{d^{\prime }}^{\mathbf{c}\mathrm{\Lambda }}$, since ${ϵ}_{d,d^{\prime }}$ preserves the combinatorial types $\omega$ of real divisors of real polynomials.

By definition of ${ϵ}_{d,d^{\prime }}$, we get ${ϵ}_{d,d^{\prime }}^{*}\left({\wp }_{d^{\prime }}\right)={(u^2+1)}^{(d^{\prime }-d)/2}·{\wp }_d$. Thus

$${\left(\mathsf{id}\times ({ϵ}_{d,d^{\prime }}\circ h)\right)}^{*}\left({\wp }_{d^{\prime }}\right)={(\mathsf{id}\times h)}^{*}\left({\wp }_d\right)·Q,$$

where $Q:\mathbb{R}\times Y\to {\mathbb{R}}_{+}$ is a smooth positive function. So the zero loci

$$\{{\left(\mathsf{id}\times ({ϵ}_{d,d^{\prime }}\circ h)\right)}^{*}\left({\wp }_{d^{\prime }}\right)=0\}\mathrm{and}\{{\left(\mathsf{id}\times h\right)}^{*}\left({\wp }_d\right)=0\}$$

coincide. Moreover, using that $Q>0$, if the 1-jet of ${\left(\mathsf{id}\times h\right)}^{*}\left({\wp }_d\right)$ does not vanish along $\{{\left(\mathsf{id}\times h\right)}^{*}\left({\wp }_d\right)=0\}$, then the 1-jet of ${(\mathsf{id}\times h)}^{*}\left({\wp }_d\right)·Q$ does not vanish along the shared locus. Therefore, if ${(\mathsf{id}\times h)}^{*}\left({\wp }_d\right)$ has 0 is a regular value, then ${\left(\mathsf{id}\times ({ϵ}_{d,d^{\prime }}\circ h)\right)}^{*}\left({\wp }_{d^{\prime }}\right)$ has 0 as a regular value as well.

Now, given two $\mathit{\partial }{\mathcal{E}}_d$-regular maps $h_0,h_1:(Y,\mathit{\partial }Y)\to ({\mathcal{P}}_d^{\mathbf{c}\mathrm{\Theta }},{\mathcal{P}}_d^{\mathbf{c}\mathrm{\Lambda }})$ such that ${ϵ}_{d,d^{\prime }}\circ h_0$ and ${ϵ}_{d,d^{\prime }}\circ h_1$ are linked by a smooth $\mathit{\partial }{\mathcal{E}}_{d^{\prime }}$-regular homotopy

$$H:(Y\times [0,1],\mathit{\partial }Y\times [0,1])\to ({\mathcal{P}}_{d^{\prime }}^{\mathbf{c}{\mathrm{\Theta }}^{\prime }},{\mathcal{P}}_{d^{\prime }}^{\mathbf{c}\mathrm{\Lambda }}),$$

we conclude that the preimage of $\mathit{\partial }{\mathcal{E}}_{d^{\prime }}$ under $\mathsf{id}\times H$ is a regularly embedded codimension 1 submanifold $N\subset \mathbb{R}\times Y\times [0,1]$ with corners $\mathit{\partial }{M}_0\coprod \mathit{\partial }{M}_1$. Its boundary $\mathit{\partial }N=(\mathit{\partial }{M}_0\coprod \mathit{\partial }{M}_1)\bigcup \delta N$, where $\delta N=H^{-1}(\mathit{\partial }{\mathcal{E}}_{d^{\prime }})\cap (\mathbb{R}\times \mathit{\partial }Y\times [0,1])$. Moreover, for $i=0,1$, the transversality of $\mathsf{id}\times H$ to $\mathit{\partial }{\mathcal{E}}_{d^{\prime }}$ implies the transversality of

$${\beta }_i:M_i={({ϵ}_{d,d^{\prime }}\circ h_i)}^{-1}(\mathit{\partial }{\mathcal{E}}_{d^{\prime }})\hookrightarrow \mathbb{R}\times Y$$

to $\mathbb{R}\times \mathit{\partial }Y$, and the transversality of $B:N=H^{-1}(\mathit{\partial }{\mathcal{E}}_{d^{\prime }})\hookrightarrow \mathbb{R}\times Y\times [0,1]$ to $\mathbb{R}\times \mathit{\partial }Y\times [0,1]$. Using the pull-back ${(\mathsf{id}\times H)}^{*}\left({\wp }_{d^{\prime }}\right)$, again by the arguments from Theorem 3, we get that ${\mathrm{\Phi }}^{B_H}=H$.

Finally, if Y is oriented, then so are $\mathbb{R}\times Y$ and $\mathbb{R}\times Y\times [0,1]$. Then, the pull-backs under $\mathsf{id}\times h$ or $\mathsf{id}\times H$ of the normal fields $n(\mathit{\partial }{\mathcal{E}}_d,{\mathcal{E}}_d)$ or $n(\mathit{\partial }{\mathcal{E}}_{d^{\prime }},{\mathcal{E}}_{d^{\prime }})$ help to orient M or N. □

Lemma 7 below is a natural generalization of Lemma 6 from the case $k=1$ to the case of a general k. It is based on Lemma 5. We skip the proof of Lemma 7, since we will not rely on it. However, its formulation may give a bit wider perspective of our effort.

Lemma 7. 

Let ${\mathrm{\Theta }}^{\prime }\subset \mathrm{\Theta }\subset \mathrm{\Lambda }\subset \mathbf{\Omega }$ be closed sub-posets, and Y a compact manifold. Let $k\le d$, $k^{\prime }\le d^{\prime }$, $d\le d^{\prime }$, $k\le k^{\prime }$, and $d\equiv d^{\prime }mod2$.

• Any smooth $(\mathit{\partial }{\mathcal{E}}_d,k)$-regular map $h:(Y,\mathit{\partial }Y)\to ({\mathcal{P}}_d^{\mathbf{c}\mathrm{\Theta }},{\mathcal{P}}_d^{\mathbf{c}\mathrm{\Lambda }})$ produces a proper immersion ${\beta }_h:(M,\mathit{\partial }M)\hookrightarrow (\mathbb{R}\times Y,\mathbb{R}\times \mathit{\partial }Y)$ of some compact n-manifold M. The combinatorial patterns of ${\beta }_h$, relative to the foliation $\mathcal{L}$, belong to $\mathbf{c}\mathrm{\Theta }$ and of its restriction to $\mathit{\partial }M$ to $\mathbf{c}\mathrm{\Lambda }$. Moreover, ${\mathrm{\Phi }}^{{\beta }_h}=h$.
• Any pair $h_0,h_1:(Y,\mathit{\partial }Y)\to ({\mathcal{P}}_d^{\mathbf{c}\mathrm{\Theta }},{\mathcal{P}}_d^{\mathbf{c}\mathrm{\Lambda }})$ of $(\mathit{\partial }{\mathcal{E}}_d,k)$-regular maps such that ${ϵ}_{d,d^{\prime }}\circ h_0$ and ${ϵ}_{d,d^{\prime }}\circ h_1$ are linked by a smooth $(\mathit{\partial }{\mathcal{E}}_{d^{\prime }},k^{\prime })$-regular homotopy

  $$H:(Y\times [0,1],\mathit{\partial }Y\times [0,1])\to ({\mathcal{P}}_{d^{\prime }}^{\mathbf{c}{\mathrm{\Theta }}^{\prime }},{\mathcal{P}}_{d^{\prime }}^{\mathbf{c}\mathrm{\Lambda }}),$$

  where $k\le k^{\prime }\le d^{\prime }$, gives rise to a $(d,d^{\prime };\mathbf{c}\mathrm{\Theta },\mathbf{c}\mathrm{\Lambda };\mathbf{c}{\mathrm{\Theta }}^{\prime })$-quasitopy $B_H:N\to \mathbb{R}\times Y\times [0,1]$ between the immersions ${\beta }_{h_0}$ and ${\beta }_{h_1}$. Moreover, ${\mathrm{\Phi }}^{B_H}=H$.

The next theorem provides homotopy theoretical invariants of the quasitopy classes of immersions and embeddings into $\mathbb{R}\times Y$. For embeddings, they compute the quasitopies.

Theorem 4. 

Let ${\mathrm{\Theta }}^{\prime }\subset \mathrm{\Theta }\subset \mathrm{\Lambda }\subset \mathbf{\Omega }$ be closed subposets, and Y be a smooth compact manifold. Assume that $d^{\prime }\ge d$ and $d^{\prime }\equiv dmod2$.

• Then, there is a canonicalal bijection

$$\begin{array}{c}\hfill {\mathrm{\Phi }}^{\mathsf{emb}}:{\mathbf{Q}}_{d,d^{\prime }}^{\mathsf{emb}}(Y,\mathit{\partial }Y;\mathbf{c}\mathrm{\Theta },\mathbf{c}\mathrm{\Lambda };\mathbf{c}{\mathrm{\Theta }}^{\prime })\stackrel{\approx }{⟶}\\ \hfill \stackrel{\approx }{⟶}\left[\left[(Y,\mathit{\partial }Y),{ϵ}_{d,d^{\prime }}:({\mathcal{P}}_d^{\mathbf{c}\mathrm{\Theta }},{\mathcal{P}}_d^{\mathbf{c}\mathrm{\Lambda }})\to ({\mathcal{P}}_{d^{\prime }}^{\mathbf{c}{\mathrm{\Theta }}^{\prime }},{\mathcal{P}}_{d^{\prime }}^{\mathbf{c}\mathrm{\Lambda }})\right]\right].\end{array}$$

(35)

• Assuming the Λ-condition (21), we get a bijection

$$\begin{array}{c}\hfill {\mathrm{\Phi }}^{\mathsf{emb}}:{\mathsf{Q}}_{d,d^{\prime }}^{\mathsf{emb}}(Y;\mathbf{c}\mathrm{\Theta };\mathbf{c}{\mathrm{\Theta }}^{\prime })\stackrel{\approx }{⟶}\left[\left[(Y,\mathit{\partial }Y),{ϵ}_{d,d^{\prime }}:({\mathcal{P}}_d^{\mathbf{c}\mathrm{\Theta }},{\mathcal{P}}_d^{\mathbf{c}\mathrm{\Lambda }})\to ({\mathcal{P}}_{d^{\prime }}^{\mathbf{c}{\mathrm{\Theta }}^{\prime }},{\mathcal{P}}_{d^{\prime }}^{\mathbf{c}\mathrm{\Lambda }})\right]\right]\end{array}$$

(36)

and a surjection

$$\begin{array}{c}\hfill {\mathrm{\Phi }}^{\mathsf{imm}}:{\mathsf{Q}}_{d,d^{\prime }}^{\mathsf{imm}}(Y;\mathbf{c}\mathrm{\Theta };\mathbf{c}{\mathrm{\Theta }}^{\prime })⟶\left[\left[(Y,\mathit{\partial }Y),{ϵ}_{d,d^{\prime }}:({\mathcal{P}}_d^{\mathbf{c}\mathrm{\Theta }},{\mathcal{P}}_d^{\mathbf{c}\mathrm{\Lambda }})\to ({\mathcal{P}}_{d^{\prime }}^{\mathbf{c}{\mathrm{\Theta }}^{\prime }},{\mathcal{P}}_{d^{\prime }}^{\mathbf{c}\mathrm{\Lambda }})\right]\right].\end{array}$$

(37)

By Proposition 11 below, ${\mathrm{\Phi }}^{\mathsf{imm}}$ admits a right inverse.

• If Y is orientable, similar claims are valid for oriented quasitopies.

Proof. 

By Proposition 9, the map ${\mathrm{\Phi }}^{\mathsf{emb}}$ from (36) is well-defined.

First, we show that the map ${\mathrm{\Phi }}^{\mathsf{emb}}$ is surjective. Recall that ${\mathcal{P}}_d^{\mathbf{c}\mathrm{\Lambda }}\subset {\mathcal{P}}_d^{\mathbf{c}\mathrm{\Theta }}$ both are open subspaces of ${\mathcal{P}}_d\approx {\mathbb{R}}^d$, and ${\mathcal{P}}_{d^{\prime }}^{\mathbf{c}\mathrm{\Lambda }}\subset {\mathcal{P}}_{d^{\prime }}^{\mathbf{c}\mathrm{\Theta }}$ are open subspaces of ${\mathcal{P}}_{d^{\prime }}\approx {\mathbb{R}}^{d^{\prime }}$. Thus any continuous map $h:(Y,\mathit{\partial }Y)\to ({\mathcal{P}}_d^{\mathbf{c}\mathrm{\Theta }},{\mathcal{P}}_d^{\mathbf{c}\mathrm{\Lambda }})$ may be approximated by a smooth map $\tilde{h}$ in the relative homotopy class of h. Similarly, any continuous map $H:(Y\times [0,1],\mathit{\partial }Y\times [0,1])\to ({\mathcal{P}}_{d^{\prime }}^{\mathbf{c}{\mathrm{\Theta }}^{\prime }},{\mathcal{P}}_{d^{\prime }}^{\mathbf{c}\mathrm{\Lambda }})$ may be approximated by a smooth map $\tilde{H}$ which shares with H its relative homotopy class.

By Corollary 3, $\tilde{h}$ may be approximated further by a $(\mathit{\partial }{\mathcal{E}}_d)$-regular map $h^{†}$ which is in the relative homotopy class of h. By Lemma 6, $h^{†}$ is realized by a proper embedding of some compact n-manifold $\beta :(M,\mathit{\partial }M)\subset (\mathbb{R}\times Y,\mathbb{R}\times \mathit{\partial }Y)$ whose tangency to $\mathcal{L}$ patterns belong to $\mathbf{c}\mathrm{\Theta }$, while the tangency patterns of $\beta (\mathit{\partial }M)$ belong to $\mathbf{c}\mathrm{\Lambda }$. Since the target set of the map ${\mathrm{\Phi }}^{\mathsf{emb}}$ is a quotient of the set $[(Y,\mathit{\partial }Y),({\mathcal{P}}_d^{\mathbf{c}\mathrm{\Theta }},{\mathcal{P}}_d^{\mathbf{c}\mathrm{\Lambda }})]$ by an equivalence relation, we conclude that ${\mathrm{\Phi }}^{\mathsf{emb}}$ is surjective.

Now we show that the map ${\mathrm{\Phi }}^{\mathsf{emb}}$ from (35) is well-defined and injective. Consider some proper $(\mathit{\partial }{\mathcal{E}}_d)$-regular embedding ${\beta }_0:(M,\mathit{\partial }M)\subset (\mathbb{R}\times Y,\mathbb{R}\times \mathit{\partial }Y)$ such that the map ${\psi }_0{=}_{\mathsf{def}}{ϵ}_{d,d^{\prime }}\circ {\mathrm{\Phi }}^{\mathsf{emb}}\left({\beta }_0\right)$ is homotopic to a map ${\psi }_1:(Y,\mathit{\partial }Y)\to ({\mathcal{P}}_{d^{\prime }}^{\mathbf{c}{\mathrm{\Theta }}^{\prime }},{\mathcal{P}}_{d^{\prime }}^{\mathbf{c}\mathrm{\Lambda }})$ whose image is contained in ${\mathcal{P}}_{d^{\prime }}^{\mathbf{c}\mathrm{\Lambda }}$. Again, by Corollary 3, this homotopy $H:(Y,\mathit{\partial }Y)\times [0,1]\to ({\mathcal{P}}_{d^{\prime }}^{\mathbf{c}{\mathrm{\Theta }}^{\prime }},{\mathcal{P}}_{d^{\prime }}^{\mathbf{c}\mathrm{\Lambda }})$ can be approximated by a $(\mathit{\partial }{\mathcal{E}}_{d^{\prime }})$-regular homotopy $H^{†}$ which coincides with ${\psi }_0$ on $Y\times \left\{0\right\}$. Let $N={(\mathsf{id}\times H^{†})}^{-1}(\mathit{\partial }{\mathcal{E}}_{d^{\prime }})$. By Lemma 6, $H^{†}$ is produced by a cobordism

$$B:(N,\delta N)\subset (\mathbb{R}\times Y\times [0,1],\mathbb{R}\times \mathit{\partial }Y\times [0,1\left]\right)$$

whose other end ${\beta }_1:(M,\mathit{\partial }M)\subset (\mathbb{R}\times Y\times \left\{1\right\},\mathbb{R}\times \mathit{\partial }Y\times \left\{1\right\})$ has tangency patters (to the fibration ${\mathcal{L}}^{•}$) that belong $\mathbf{c}\mathrm{\Lambda }$. In other words, ${\beta }_0\in {}^{†}{\mathcal{Q}}_{d,d^{\prime }}^{\mathsf{emb}}(Y,\mathit{\partial }Y;\mathbf{c}\mathrm{\Lambda },\mathbf{c}\mathrm{\Lambda };\mathbf{c}{\mathrm{\Theta }}^{\prime })$, which represents the trivial element of the quotient ${\mathbf{Q}}_{d,d^{\prime }}^{\mathsf{emb}}(Y,\mathit{\partial }Y;\mathbf{c}\mathrm{\Theta },\mathbf{c}\mathrm{\Lambda };\mathbf{c}{\mathrm{\Theta }}^{\prime })$. Thus, we get the bijection (35).

When $\mathbf{c}\mathrm{\Lambda }=(\varnothing )\mathrm{or}\left(1\right)$, the set ${}^{†}{\mathcal{Q}}_{d,d^{\prime }}^{\mathsf{emb}}(Y,\mathit{\partial }Y;\mathbf{c}\mathrm{\Lambda },\mathbf{c}\mathrm{\Lambda };\mathbf{c}{\mathrm{\Theta }}^{\prime })$ consists of a single element. Hence, we get the bijection in (36).

Finally, by Proposition 9, the map ${\mathrm{\Phi }}^{\mathsf{imm}}$ in (37) is surjective, since the map ${\mathrm{\Phi }}^{\mathsf{emb}}$ factors through it.

Assuming that Y is oriented, the preimages of the loci $\mathit{\partial }{\mathcal{E}}_d$ and $\mathit{\partial }{\mathcal{E}}_{d^{\prime }}$ under regular maps are oriented manifolds. This remark validates the last claim. □

Corollary 6. 

Under the hypotheses of Theorem 4, including the Λ-condition (21), the quasitopy set ${\mathsf{Q}}_{d,d^{\prime }}^{\mathsf{emb}}(Y,\mathit{\partial }Y;\mathbf{c}\mathrm{\Theta },\mathbf{c}{\mathrm{\Theta }}^{\prime })$ depends only on the homotopy type of the pair $(Y,\mathit{\partial }Y)$.

If Y is orientable, then the orientation forgetting map

$${\mathsf{OQ}}_{d,d^{\prime }}^{\mathsf{emb}}(Y,\mathit{\partial }Y;\mathbf{c}\mathrm{\Theta },\mathbf{c}{\mathrm{\Theta }}^{\prime })\to {\mathsf{Q}}_{d,d^{\prime }}^{\mathsf{emb}}(Y,\mathit{\partial }Y;\mathbf{c}\mathrm{\Theta },\mathbf{c}{\mathrm{\Theta }}^{\prime })$$

is a surjection. In particular, ${\mathsf{OG}}_{d,d^{\prime }}^{\mathsf{emb}}(n;\mathbf{c}\mathrm{\Theta };\mathbf{c}{\mathrm{\Theta }}^{\prime })\to {\mathsf{G}}_{d,d^{\prime }}^{\mathsf{emb}}(n;\mathbf{c}\mathrm{\Theta };\mathbf{c}{\mathrm{\Theta }}^{\prime })$ is a group epimorphism.

Proof. 

The first claim of the corollary follows instantly from Formula (36) and its analog for the oriented quasitopies.

The rest of the claims can be derived from the following already familiar observation. Since any element $\beta \in {\mathsf{Q}}_{d,d^{\prime }}^{\mathsf{emb}}(Y;\mathbf{c}\mathrm{\Theta },\mathbf{c}{\mathrm{\Theta }}^{\prime })$ is represented by a map $\mathsf{id}\times {\mathrm{\Phi }}^{\beta }:\mathbb{R}\times (Y,\mathit{\partial }Y)\to \mathbb{R}\times ({\mathcal{P}}_d^{\mathbf{c}\mathrm{\Theta }},pt)$ which is transversal to $\mathit{\partial }{\mathcal{E}}_d$, the manifold $M:={(\mathsf{id}\times {\mathrm{\Phi }}^{\beta })}^{-1}(\mathit{\partial }{\mathcal{E}}_d)$ has a trivial normal bundle in $\mathbb{R}\times Y$. Thus, M is orientable, when Y is present. The same argument applies to the cobordisms that connect quasitopic $\beta$’s. Therefore, when Y is orientable, the orientation forgetful map from the second claim is onto. □

Remark 6.

The first claim of Corollary 6 is a bit surprising, since not any homotopy equivalence $h:(Y,\mathit{\partial }Y)\to (Y^{\prime },\mathit{\partial }{Y}^{\prime })$ of smooth n-dimensional pairs may be homotoped to a diffeomorphism. Thus it is not clear how to transfer directly a regular embedding $\beta :(M,\mathit{\partial }M)\to (\mathbb{R}\times Y,\mathbb{R}\times \mathit{\partial }Y)$ to a regular embedding ${\beta }^{\prime }:(M^{\prime },\mathit{\partial }{M}^{\prime })\to (\mathbb{R}\times Y^{\prime },\mathbb{R}\times \mathit{\partial }{Y}^{\prime })$ without using the bijection ${\mathrm{\Phi }}^{\mathsf{emb}}$. Similarly, it is unclear whether ${\mathsf{Q}}_{d,d^{\prime }}^{\mathsf{imm}}(Y;\mathbf{c}\mathrm{\Theta },\mathbf{c}{\mathrm{\Theta }}^{\prime })$ depends only on the homotopy type of the pair $(Y,\mathit{\partial }Y)$. Conjecturally, it does.

Corollary 7. 

Assume that $d^{\prime }\ge d$, $d^{\prime }\equiv dmod2$, and the Λ-condition (21) is in place.

Then, the group homomorphism in (31) is a group isomorphism for embeddings and a split epimorphism for the immersions.

With the help of this group isomorphism (and by Theorem 10), the map in (36) is equivariant, and so is the map in (37) with the help of the epimorhism of the corresponding groups.

Proof. 

By Theorem 4, the map in (36) is bijective and the map in (37) is split surjective for any Y; in particular, this is the case for $Y=D^n$. By Theorem 10, all these maps are group homomorphisms. By Proposition 11 below, the map in (37) is a split epimorphism. □

Letting $d^{\prime }=d$ and ${\mathrm{\Theta }}^{\prime }=\mathrm{\Theta }$ in Theorem 4, we obtain the following two corollaries.

Corollary 8. 

Let $\mathrm{\Theta }\subset \mathrm{\Lambda }\subset \mathbf{\Omega }$ be a pair of closed subposets, and Y be a compact manifold.

• Then, there is a canonical bijection

$$\begin{array}{c}\hfill {\mathrm{\Phi }}^{\mathsf{emb}}:{\mathbf{Q}}_{d,d}^{\mathsf{emb}}(Y,\mathit{\partial }Y;\mathbf{c}\mathrm{\Theta },\mathbf{c}\mathrm{\Lambda };\mathbf{c}\mathrm{\Theta })\stackrel{\approx }{⟶}[(Y,\mathit{\partial }Y),({\mathcal{P}}_d^{\mathbf{c}\mathrm{\Theta }},{\mathcal{P}}_d^{\mathbf{c}\mathrm{\Lambda }})].\end{array}$$

(38)

• Assuming the Λ-condition (21), we get a bijection

$$\begin{array}{c}\hfill {\mathrm{\Phi }}^{\mathsf{emb}}:{\mathsf{Q}}_{d,d}^{\mathsf{emb}}(Y;\mathbf{c}\mathrm{\Theta };\mathbf{c}\mathrm{\Theta })\stackrel{\approx }{⟶}[(Y,\mathit{\partial }Y),({\mathcal{P}}_d^{\mathbf{c}\mathrm{\Theta }},pt)]\end{array}$$

(39)

and a surjection

$$\begin{array}{c}\hfill {\mathrm{\Phi }}^{\mathsf{imm}}:{\mathsf{Q}}_{d,d}^{\mathsf{imm}}(Y;\mathbf{c}\mathrm{\Theta };\mathbf{c}\mathrm{\Theta })⟶[(Y,\mathit{\partial }Y),({\mathcal{P}}_d^{\mathbf{c}\mathrm{\Theta }},pt)].\end{array}$$

(40)

Corollary 9. 

Let $\mathrm{\Theta }\subset \mathrm{\Lambda }\subset {\mathbf{\Omega }}_{⟨d]}$ be a pair of closed sub-posets. There exists a group isomorphism (abelian for $n>1$)

$$\begin{array}{c}\hfill {\mathrm{\Phi }}^{\mathsf{emb}}:{\mathbf{Q}}_{d,d}^{\mathsf{emb}}(D^n,\mathit{\partial }{D}^n;\mathbf{c}\mathrm{\Theta },\mathbf{c}\mathrm{\Lambda };\mathbf{c}\mathrm{\Theta })\stackrel{\approx }{⟶}{\pi }_n({\mathcal{P}}_d^{\mathbf{c}\mathrm{\Theta }},{\mathcal{P}}_d^{\mathbf{c}\mathrm{\Lambda }}).\end{array}$$

(41)

Assuming the Λ-condition (21), we get a group epimorphism

$$\begin{array}{c}\hfill {\mathrm{\Phi }}^{\mathsf{emb}}:{\mathsf{OG}}_{d,d}^{\mathsf{emb}}(n;\mathbf{c}\mathrm{\Theta };\mathbf{c}\mathrm{\Theta })\to {\mathsf{G}}_{d,d}^{\mathsf{emb}}(n;\mathbf{c}\mathrm{\Theta };\mathbf{c}\mathrm{\Theta })\stackrel{\approx }{⟶}{\pi }_n({\mathcal{P}}_d^{\mathbf{c}\mathrm{\Theta }},pt).\end{array}$$

(42)

Proof. 

The claim follows instantly from Theorem 4 and Proposition 8. □

The next proposition is an attempt “to reverse the direction” of the maps in (29) and (31).

Proposition 11. 

Let ${\mathrm{\Theta }}^{\prime }\subset \mathrm{\Theta }\subset \mathrm{\Lambda }\subset \mathbf{\Omega }$ be closed subposets, and Y be a smooth compact manifold. Assume that $d^{\prime }\ge d$ and $d^{\prime }\equiv dmod2$.

Then, the obvious map

$$\begin{array}{c}\hfill \mathcal{A}:{\mathcal{Q}}_{d,d^{\prime }}^{\mathsf{emb}}(Y,\mathit{\partial }Y;\mathbf{c}\mathrm{\Theta },\mathbf{c}\mathrm{\Lambda };\mathbf{c}{\mathrm{\Theta }}^{\prime })\to {\mathcal{Q}}_{d,d^{\prime }}^{\mathsf{imm}}(Y,\mathit{\partial }Y;\mathbf{c}\mathrm{\Theta },\mathbf{c}\mathrm{\Lambda };\mathbf{c}{\mathrm{\Theta }}^{\prime })\end{array}$$

(43)

is injective. That is, if two embeddings ${\beta }_1:(M_1,\mathit{\partial }{M}_1)\hookrightarrow (\mathbb{R}\times Y,\mathbb{R}\times \mathit{\partial }Y)$ and ${\beta }_2:(M_2,\mathit{\partial }{M}_2)\hookrightarrow (\mathbb{R}\times Y,\mathbb{R}\times \mathit{\partial }Y)$ are quaitopic via immersions, then they are quaitopic via embeddings.

Moreover, there exists a surjective “resolution map”

$$\begin{array}{c}\hfill \mathcal{R}:{\mathcal{Q}}_{d,d^{\prime }}^{\mathsf{imm}}(Y,\mathit{\partial }Y;\mathbf{c}\mathrm{\Theta },\mathbf{c}\mathrm{\Lambda };\mathbf{c}{\mathrm{\Theta }}^{\prime })\to {\mathcal{Q}}_{d,d^{\prime }}^{\mathsf{emb}}(Y,\mathit{\partial }Y;\mathbf{c}\mathrm{\Theta },\mathbf{c}\mathrm{\Lambda };\mathbf{c}{\mathrm{\Theta }}^{\prime })\end{array}$$

(44)

that serves as the right inverse of $\mathcal{A}$. In other words, there exists a canonical resolution of any such immersion into an embedding, well-defined within the relevant quasitopy classes.

Proof. 

In the proof, to simplify the notations further, put

$${\mathcal{Q}}^{\mathsf{imm}}\left(Y\right){=}_{\mathsf{def}}{\mathcal{Q}}_{d,d^{\prime }}^{\mathsf{imm}}(Y,\mathit{\partial }Y;\mathbf{c}\mathrm{\Theta },\mathbf{c}\mathrm{\Lambda };\mathbf{c}{\mathrm{\Theta }}^{\prime }),{\mathcal{Q}}^{\mathsf{emb}}\left(Y\right){=}_{\mathsf{def}}{\mathcal{Q}}_{d,d^{\prime }}^{\mathsf{emb}}(Y,\mathit{\partial }Y;\mathbf{c}\mathrm{\Theta },\mathbf{c}\mathrm{\Lambda };\mathbf{c}{\mathrm{\Theta }}^{\prime }).$$

Using the map (29), we see that the map ${\mathrm{\Phi }}^{\mathsf{emb}}\left(Y\right)$ is a composition of the map $\mathcal{A}$ and the map

$${\mathrm{\Phi }}^{\mathsf{imm}}\left(Y\right):{\mathcal{Q}}^{\mathsf{imm}}\left(Y\right)\to \left[\left[(Y,\mathit{\partial }Y),{ϵ}_{d,d^{\prime }}:({\mathcal{P}}_d^{\mathbf{c}\mathrm{\Theta }},{\mathcal{P}}_d^{\mathbf{c}\mathrm{\Lambda }})\to ({\mathcal{P}}_{d^{\prime }}^{\mathbf{c}{\mathrm{\Theta }}^{\prime }},{\mathcal{P}}_{d^{\prime }}^{\mathbf{c}\mathrm{\Lambda }})\right]\right].$$

However, by Formula (36) from Theorem 4, we have a bijective map

$${\mathrm{\Phi }}^{\mathsf{emb}}\left(Y\right):{\mathcal{Q}}^{\mathsf{emb}}\left(Y\right)\approx \left[\left[(Y,\mathit{\partial }Y),{ϵ}_{d,d^{\prime }}:({\mathcal{P}}_d^{\mathbf{c}\mathrm{\Theta }},{\mathcal{P}}_d^{\mathbf{c}\mathrm{\Lambda }})\to ({\mathcal{P}}_{d^{\prime }}^{\mathbf{c}{\mathrm{\Theta }}^{\prime }},{\mathcal{P}}_{d^{\prime }}^{\mathbf{c}\mathrm{\Lambda }})\right]\right].$$

Hence, we define the desired surjective map $\mathcal{R}$ by the formula $\mathcal{R}={\mathrm{\Phi }}^{\mathsf{emb}}{\left(Y\right)}^{-1}\circ {\mathrm{\Phi }}^{\mathsf{imm}}\left(Y\right)$. It is on the level of definitions to check that $\mathcal{R}\circ \mathcal{A}=\mathsf{id}$. □

Remark 7.

Of course, applying the resolution $\mathcal{R}$ to an immersion $\beta :M\to \mathbb{R}\times Y$ produces an embedding ${\beta }^{\prime }:M^{\prime }\to \mathbb{R}\times Y$, where the topology of $M^{\prime }$ is quite different from the topology of M. However, the sets${\beta }^{\prime }\left(M^{\prime }\right)$ and $\beta \left(M\right)$ can be assumed to be arbitrary close in the Hausdorff distance in $\mathbb{R}\times Y$.

Corollary 10. 

Each fiber of the resolution map $\mathcal{R}$ consists of the elements that share the same ${\mathrm{\Phi }}^{\mathsf{imm}}$-value in $\left[[(Y,\mathit{\partial }Y),{ϵ}_{d,d^{\prime }}:({\mathcal{P}}_d^{\mathbf{c}\mathrm{\Theta }},{\mathcal{P}}_d^{\mathbf{c}\mathrm{\Lambda }})\to ({\mathcal{P}}_{d^{\prime }}^{\mathbf{c}{\mathrm{\Theta }}^{\prime }},{\mathcal{P}}_{d^{\prime }}^{\mathbf{c}\mathrm{\Lambda }})]\right]$.

In particular, for $Y=D^n$, we get a splittable groups’ extension

$$\begin{array}{c}\hfill 1\to \mathsf{K}\to {\mathsf{Q}}_{d,d^{\prime }}^{\mathsf{imm}}(n;\mathbf{c}\mathrm{\Theta };\mathbf{c}{\mathrm{\Theta }}^{\prime })\stackrel{\mathcal{R}}{\to }{\mathsf{Q}}_{d,d^{\prime }}^{\mathsf{emb}}(n;\mathbf{c}\mathrm{\Theta };\mathbf{c}{\mathrm{\Theta }}^{\prime })\to 1,\end{array}$$

(45)

whose kernel $\mathsf{K}\subset {\mathsf{Q}}_{d,d^{\prime }}^{\mathsf{imm}}(n;\mathbf{c}\mathrm{\Theta };\mathbf{c}{\mathrm{\Theta }}^{\prime })$ consists of quasitopies of immersions that belong to the kernel of the map in (30) with $Y=D^n$. Via the operation ⊎, the subgroup $\mathsf{K}$ acts on the fibers of the map $\mathcal{R}$ from (44).

Proof. 

We use the notations from the previous proof. By Proposition 11, each fiber of $\mathcal{R}$ consists of the elements that share the same ${\mathrm{\Phi }}^{\mathsf{imm}}$-value in $\left[[(Y,\mathit{\partial }Y),{ϵ}_{d,d^{\prime }}:({\mathcal{P}}_d^{\mathbf{c}\mathrm{\Theta }},{\mathcal{P}}_d^{\mathbf{c}\mathrm{\Lambda }})\to ({\mathcal{P}}_{d^{\prime }}^{\mathbf{c}{\mathrm{\Theta }}^{\prime }},{\mathcal{P}}_{d^{\prime }}^{\mathbf{c}\mathrm{\Lambda }})]\right]$. For $Y=D^n$, this implies that the group ${\mathcal{Q}}^{\mathsf{imm}}\left(D^n\right)$ is a semidirect product $\mathsf{K}\bowtie {\mathcal{Q}}^{\mathsf{emb}}\left(D^n\right)$ of the groups $\mathsf{K}$ and ${\mathcal{Q}}^{\mathsf{emb}}\left(D^n\right)$. Again, $\mathsf{K}$ is characterized by the property of having trivial ${\mathrm{\Phi }}^{\mathsf{imm}}$ values.

Since, for ${\beta }_1\in {\mathcal{Q}}^{\mathsf{imm}}\left(Y\right)$ and ${\beta }_2\in {\mathcal{Q}}^{\mathsf{imm}}\left(D^n\right)$, we have ${\mathrm{\Phi }}^{\mathsf{imm}}({\beta }_1\uplus {\beta }_2)={\mathrm{\Phi }}^{\mathsf{imm}}\left({\beta }_1\right)\uplus {\mathrm{\Phi }}^{\mathsf{imm}}\left({\beta }_2\right)$, we conclude that ${\mathrm{\Phi }}^{\mathsf{imm}}({\beta }_1\uplus \mathsf{K})={\mathrm{\Phi }}^{\mathsf{imm}}\left({\beta }_1\right)\uplus 0={\mathrm{\Phi }}^{\mathsf{imm}}\left({\beta }_1\right)$. Therefore $\mathsf{K}$ acts on fibers of the map $\mathcal{R}$. □

Since $\beta \in {\mathcal{Q}}_{d,d^{\prime }}^{\mathsf{imm}}(Y,\mathit{\partial }Y;\mathbf{c}\mathrm{\Theta },\mathbf{c}\mathrm{\Lambda };\mathbf{c}{\mathrm{\Theta }}^{\prime })$ and $\mathcal{R}\left(\beta \right)\in {\mathcal{Q}}_{d,d^{\prime }}^{\mathsf{emb}}(Y,\mathit{\partial }Y;\mathbf{c}\mathrm{\Theta },\mathbf{c}\mathrm{\Lambda };\mathbf{c}{\mathrm{\Theta }}^{\prime })$ share the same invariants ${\mathrm{\Phi }}^{\mathsf{imm}}\left(\beta \right)={\mathrm{\Phi }}^{\mathsf{emb}}\left(\mathcal{R}\left(\beta \right)\right)\in \left[\left[(Y,\mathit{\partial }Y),{ϵ}_{d,d^{\prime }}:({\mathcal{P}}_d^{\mathbf{c}\mathrm{\Theta }},{\mathcal{P}}_d^{\mathbf{c}\mathrm{\Lambda }})\to ({\mathcal{P}}_{d^{\prime }}^{\mathbf{c}{\mathrm{\Theta }}^{\prime }},{\mathcal{P}}_{d^{\prime }}^{\mathbf{c}\mathrm{\Lambda }})\right]\right]$, we should be looking for new invariants that distinguish between $\beta$ and $\mathcal{R}\left(\beta \right)$.

Relying on Proposition 7, we may use the bordism classes $\left[{\mathrm{\Sigma }}_k^{\beta }\right]\in {\mathbf{B}}_{n-k+1}(Y,\mathit{\partial }Y)$ (or $\left[{\mathrm{\Sigma }}_k^{\beta }\right]\in {\mathbf{OB}}_{n-k+1}(Y,\mathit{\partial }Y)$ when Y is oriented) of the k-self-intersection manifolds ${\left\{{\mathrm{\Sigma }}_k^{\beta }\right\}}_{k\ge 2}$ of $\beta$ to produce the desired distinguishing invariants. In a sense, these quasitopy invariants “ignore” the foliations $\mathcal{L},{\mathcal{L}}^{•}$. Evidently, they vanish on the set ${\mathcal{Q}}_{d,d^{\prime }}^{\mathsf{emb}}(Y,\mathit{\partial }Y;\mathbf{c}\mathrm{\Theta },\mathbf{c}\mathrm{\Lambda };\mathbf{c}{\mathrm{\Theta }}^{\prime })$.

Therefore, for $dim\left(Y\right)=n$, assuming that $min\{n+1,\widehat{m}\left(\mathbf{c}{\mathrm{\Theta }}_{⟨d]}\right)\}\ge 2$ (see Definition 10), the correspondence $\beta ⇝{\{\pi \circ \beta \circ p_1:({\mathrm{\Sigma }}_k^{\beta },\mathit{\partial }{\mathrm{\Sigma }}_k^{\beta })\to (Y,\mathit{\partial }Y)\}}_k$ produces a map

$$\begin{array}{c}\hfill \mathcal{BB}:{\mathcal{Q}}_{d,d^{\prime }}^{\mathsf{imm}}(Y,\mathit{\partial }Y;\mathbf{c}\mathrm{\Theta },\mathbf{c}\mathrm{\Lambda };\mathbf{c}{\mathrm{\Theta }}^{\prime })/{\mathcal{Q}}_{d,d^{\prime }}^{\mathsf{emb}}(Y,\mathit{\partial }Y;\mathbf{c}\mathrm{\Theta },\mathbf{c}\mathrm{\Lambda };\mathbf{c}{\mathrm{\Theta }}^{\prime })\to \\ \hfill \to \underset{k\in [2,min\{n+1,\widehat{m}\left(\mathbf{c}{\mathrm{\Theta }}_{⟨d]}\right)\}]}{⨁}{\mathbf{B}}_{n-k+1}(Y,\mathit{\partial }Y),\end{array}$$

(46)

which has a potential to discriminate between ${\mathcal{Q}}_{d,d^{\prime }}^{\mathsf{imm}}(Y,\mathit{\partial }Y;\mathbf{c}\mathrm{\Theta },\mathbf{c}\mathrm{\Lambda };\mathbf{c}{\mathrm{\Theta }}^{\prime })$ and ${\mathcal{Q}}_{d,d^{\prime }}^{\mathsf{emb}}(Y,\mathit{\partial }Y;\mathbf{c}\mathrm{\Theta },\mathbf{c}\mathrm{\Lambda };\mathbf{c}{\mathrm{\Theta }}^{\prime })$. Lemma 8 provides the simplest example where it does.

Next, we “mix” the tangency patterns of immersions $\beta$ to $\mathcal{L}$ with the self-intersections of $\beta$ (which also influence the $\mathcal{L}$-tangency patterns). For simplicity, we assume the $\mathrm{\Lambda }$-condition and that Y is oriented.

Let $\beta :(M,\mathit{\partial }M)\to (\mathbb{R}\times Y,\mathbb{R}\times \mathit{\partial }Y)$ be an immersion whose quasitopy class belongs to ${\mathcal{Q}}_{d,d^{\prime }}^{\mathsf{imm}}(Y,\mathit{\partial }Y;\mathbf{c}\mathrm{\Theta },\mathbf{c}{\mathrm{\Theta }}^{\prime })$. Let $\mathsf{A}$ be an abelian group. We pick a cohomology class $\theta \in H^{n-k+1}({\mathcal{P}}_d^{\mathbf{c}\mathrm{\Theta }},pt;\mathsf{A})$ and evaluate its pull-back ${({\mathrm{\Phi }}^{\beta }\circ \pi \circ \beta \circ p_1)}^{*}\left(\theta \right)$ on the relative fundamental class $[{\mathrm{\Sigma }}_k^{\beta },\mathit{\partial }{\mathrm{\Sigma }}_k^{\beta }]$. This construction leads to the following proposition.

Proposition 12. 

Let ${\mathrm{\Theta }}^{\prime }\subset \mathrm{\Theta }\subset \mathbf{\Omega }$ be closed posets. We assume the Λ-condition. Let Y be an oriented smooth compact manifold. Pick a positive integer $k\le min\{\widehat{m}(\mathbf{c}{\mathrm{\Theta }}_{⟨d]},n+1\}$.

For any cohomology class $\theta \in H^{n-k+1}({\mathcal{P}}_d^{\mathbf{c}\mathrm{\Theta }},pt;\mathsf{A})$, the evaluation

$${\chi }_k(\theta ,\beta ):=⟨{({\mathrm{\Phi }}^{\beta }\circ \pi \circ \beta \circ p_1)}^{*}\left(\theta \right),[{\mathrm{\Sigma }}_k^{\beta },\mathit{\partial }{\mathrm{\Sigma }}_k^{\beta }]⟩\in \mathsf{A}$$

is an invariant of the quasitopy class $\left[\beta \right]\in {\mathcal{Q}}_{d,d^{\prime }}^{\mathsf{imm}}(Y,\mathit{\partial }Y;\mathbf{c}\mathrm{\Theta },\mathbf{c}{\mathrm{\Theta }}^{\prime })$.

If β is an embedding, then ${\chi }_k(\theta ,\beta )=0$ for $k\ge 2$.

Proof. 

By Corollary 2, the bordism class of $\pi \circ \beta \circ p_1:({\mathrm{\Sigma }}_k^{\beta },\mathit{\partial }{\mathrm{\Sigma }}_k^{\beta })\to (Y,\mathit{\partial }Y)$ is invariant under a change of $\beta$ within its quasitopy class. By Theorem 3, the cocycle ${\left({\mathrm{\Phi }}^{\beta }\right)}^{*}\left(\theta \right)$ is an invariant of the quasitopy class of $\beta$. By the topological Stokes’ Theorem, the cocycle ${\left({\mathrm{\Phi }}^{\beta }\right)}^{*}\left(\theta \right)$, being evaluated on the cycle $(\pi \circ \beta \circ p_1)({\mathrm{\Sigma }}_k^{\beta },\mathit{\partial }{\mathrm{\Sigma }}_k^{\beta })$ is an invariant of $\left[\beta \right]\in {\mathcal{Q}}_{d,d^{\prime }}^{\mathsf{imm}}(Y,\mathit{\partial }Y;\mathbf{c}\mathrm{\Theta },\mathbf{c}{\mathrm{\Theta }}^{\prime })$. □

Here, is the simplest example of an invariant ${\rho }_{\beta }:={\displaystyle \frac{1}{n+1}}\left[(\pi \circ \beta \circ p_1):{\mathrm{\Sigma }}_{n+1}^{\beta }\to Y\right]$, delivered by $\mathcal{BB}$ from (46), which does discriminate between the quasitopies of embeddings and immersions.

Lemma 8. 

Let $dimM=n$ and let ${\rho }_{\beta }$ be the number of points in Y where exactly $n+1$ branches of $\beta \left(M\right)$ meet transversally in $\mathbb{R}\times Y$. If ${\rho }_{\beta }\equiv 1mod2$, then $\beta \in {\mathcal{Q}}_{d,d^{\prime }}^{\mathsf{imm}}(Y,\mathit{\partial }Y;\mathbf{c}\mathrm{\Theta },\mathbf{c}\mathrm{\Lambda };\mathbf{c}{\mathrm{\Theta }}^{\prime })$ is nontrivial, provided $\mathbf{c}\mathrm{\Lambda }=(\varnothing ),\left(1\right)$.

Proof. 

Let $F_{\beta }$ denote the finite set of points, where exactly $n+1$ branches of $\beta \left(M\right)$ meet transversally in $\mathbb{R}\times Y$. Assume that $\beta$ be quasitopic to trivial immersion with the help of a cobordism $B:N\to \mathbb{R}\times Y\times [0,1]$. Then, in general, $B\left(N\right)$ may have points where exactly $n+2$ branches of $B\left(N\right)$ meet transversally. Let $E_B$ denote their set and let ${\eta }_B:=\#\left(E_B\right)$. The points, where exactly $n+1$ branches of $B\left(N\right)$ meet transversally, form a graph ${\Gamma }_B\subset \mathbb{R}\times Y\times [0,1]$. If $\mathbf{c}\mathrm{\Lambda }=(\varnothing ),\left(1\right)$, then ${\Gamma }_B$ has ${\rho }_{\beta }$ univalent vertices and ${\eta }_B$ vertices of valency $n+2$. Every edge of ${\Gamma }_B$ that does not terminate at a valency one vertex from $F_{\beta }$ is attached to $E_B$. Thus counting the edges of ${\Gamma }_B$ we get $2(n+2){\eta }_B-{\rho }_{\beta }\equiv 0mod2$. Therefore, when ${\rho }_{\beta }\equiv 1mod2$, we get a contradiction with the assumption that $\beta$ is quasitopic to trivial immersion. As a result, any immersion $\beta$ with an odd number ${\rho }_{\beta }$ is nontrivial in ${\mathcal{Q}}_{d,d^{\prime }}^{\mathsf{imm}}(Y,\mathit{\partial }Y;\mathbf{c}\mathrm{\Theta },\mathbf{c}\mathrm{\Lambda };\mathbf{c}{\mathrm{\Theta }}^{\prime })$, provided $\mathbf{c}\mathrm{\Lambda }=(\varnothing ),\left(1\right)$. □

Example 2. 

Pick $n=1$, $d^{\prime }=d=6$. Let $\mathbf{c}{\mathrm{\Theta }}^{\prime }=\mathbf{c}\mathrm{\Theta }$ consist of $\omega \in {\mathbf{\Omega }}_{⟨6]}$ such that all their entries are 1’s and 2’s and a single 2 is present at most. Put $Y=D^1$. Then, ${\mathsf{Q}}_{6,6}^{\mathsf{emb}}(1;\mathbf{c}\mathrm{\Theta };\mathbf{c}\mathrm{\Theta })\approx {\pi }_1({\mathcal{P}}_6^{\mathbf{c}\mathrm{\Theta }},pt)$. By [5], Theorem 2.4, the latter group is a free group ${\mathsf{F}}_6$ in 6 generators (see Figure 4). The group extension in (45) reduces to

$$1\to \mathsf{K}\to {\mathsf{Q}}_{6,6}^{\mathsf{imm}}(1;\mathbf{c}\mathrm{\Theta };\mathbf{c}\mathrm{\Theta })\stackrel{\mathcal{R}}{\to }{\mathsf{F}}_6\to 1.$$

The figure ∞, placed “horizontally” in $\mathbb{R}\times D^1$ ($D^1$ being the horizontal direction) represents an immersion $\beta :S^1\to \mathbb{R}\times D^1$. We claim that β belongs to the kernel $\mathsf{K}$ from (45). Indeed, consider a flip $\tau :\mathbb{R}\times D^1\to \mathbb{R}\times D^1$ whose fixed point set is the vertical line through the singularity of figure ∞. Due to the symmetry of ∞ with respect to τ, the path ${\mathrm{\Phi }}^{\mathsf{imm}}(D^1,\mathit{\partial }{D}^1)\subset ({\mathcal{P}}_6^{\mathbf{c}\mathrm{\Theta }},pt)$ is relatively contractible. Thus, ∞ is indeed in the kernel $\mathsf{K}$. By Lemma 8, β is nontrivial in ${\mathsf{Q}}_{6,6}^{\mathsf{imm}}(1;\mathbf{c}\mathrm{\Theta };\mathbf{c}\mathrm{\Theta })$. By the same lemma, the quasitopy class of any collection of smooth curves with an odd number of crossings is nontrivial in ${\mathsf{Q}}_{6,6}^{\mathsf{imm}}(1;\mathbf{c}\mathrm{\Theta };\mathbf{c}\mathrm{\Theta })$. At the same time, the immersion $\infty \uplus \infty \subset \mathbb{R}\times D^1$ is trivial in ${\mathsf{Q}}_{6,6}^{\mathsf{imm}}(1;\mathbf{c}\mathrm{\Theta };\mathbf{c}\mathrm{\Theta })$ since it is the boundary of a horseshoe surface $N\approx \infty \times I\subset \mathbb{R}\times D^1\times [0,1]$ with the ${\mathcal{L}}^{•}$-tangency patterns that belong to $\mathbf{c}\mathrm{\Theta }$. So the immersion β, such that $\beta \left(S^1\right)=\infty$, is an element of order two in the kernel $\mathsf{K}$. However, if we orient $S^1$, then ∞ becomes an element of infinite order in $\mathsf{ker}({\mathsf{OQ}}_{6,6}^{\mathsf{imm}}(1;\mathbf{c}\mathrm{\Theta };\mathbf{c}\mathrm{\Theta })\to {\mathsf{OQ}}_{6,6}^{\mathsf{emb}}(1;\mathbf{c}\mathrm{\Theta };\mathbf{c}\mathrm{\Theta }))$.

In fact, any collection of curves $\beta \left(M\right)$ in $\mathbb{R}\times D^1$ with the tangency patterns in $\mathbf{c}\mathrm{\Theta }$, with an odd number of transversal crossings, and which is symmetric under an involution $\tau :\mathbb{R}\times D^1\to \mathbb{R}\times D^1$ which preserves the oriented foliation $\mathcal{L}$, belongs to $\mathsf{K}$ and has order 2 there. Based on a sparse evidence, we conjecture that $\mathsf{K}\approx {\mathbb{Z}}_2$. If this is true, then ${\mathsf{Q}}_{6,6}^{\mathsf{imm}}(1;\mathbf{c}\mathrm{\Theta };\mathbf{c}\mathrm{\Theta })$ is a semi-direct product ${\mathbb{Z}}_2\bowtie {\mathsf{F}}_6$.

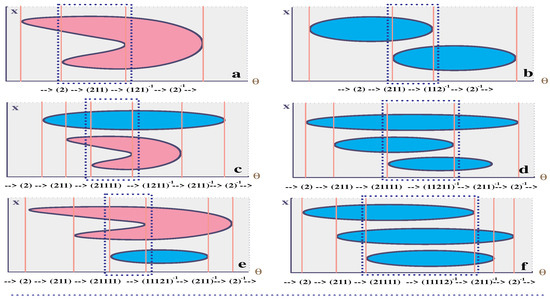
Figure 4. Six generators (a–f) of the free group ${\mathsf{Q}}_{6,6}^{\mathsf{emb}}(1;\mathbf{c}\mathrm{\Theta };\mathbf{c}\mathrm{\Theta })$, where $\mathrm{\Theta }\subset {\mathbf{\Omega }}_{⟨6]}$ is the closed poset generated by the elements $\omega$ with two 2’s or one 3. The vertical lines mark crossing the walls of the 6-dimensional chambers in ${\mathcal{P}}_6^{\mathbf{c}\mathrm{\Theta }}$.

The next theorem describes one very general mechanism for generating characteristic cohomology classes for immersions/embeddings $\beta :M\to \mathbb{R}\times Y$ with $\mathrm{\Theta }$-restricted tangency patterns to $\mathcal{L}$.

Theorem 5. 

For a compact manifold Y, $d^{\prime }=d$, and ${\mathrm{\Theta }}^{\prime }=\mathrm{\Theta }$, assuming the Λ-condition, any immersion/embedding $\beta :(M,\mathit{\partial }M)\to (\mathbb{R}\times Y,\mathbb{R}\times \mathit{\partial }Y)$ as in Proposition 9 induces a characteristic homomorphism ${\left({\mathrm{\Phi }}^{\beta }\right)}^{*}$ from the (co)homology of the differential complex $\{{\mathit{\partial }}^{\#}:\mathbb{Z}\left[{\mathrm{\Theta }}_{⟨d]}^{\#}\right]\to \mathbb{Z}\left[{\mathrm{\Theta }}_{⟨d]}^{\#}\right]\}$ in (6) to the cohomology $H^{*}(Y,\mathit{\partial }Y;\mathbb{Z})$.

Quasitopic immersions/embeddings induce the same characteristic homomorphisms.

Proof. 

For any closed poset $\mathrm{\Theta }\subset {\mathbf{\Omega }}_{⟨d]}$, by Corollary 2.6 and Theorem 2.2 ([6]), the homology of the differential complex in (6) is isomorphic to $H^{*}({\mathcal{P}}_d^{\mathbf{c}\mathrm{\Theta }},pt;\mathbb{Z})$. By Proposition 9, any immersion $\beta :(M,\mathit{\partial }M)\to (\mathbb{R}\times Y,\mathbb{R}\times \mathit{\partial }Y)$ whose tangency patterns belong to $\mathbf{c}\mathrm{\Theta }$ and the ones of ${\beta |}_{\mathit{\partial }M}$ to $\mathbf{c}\mathrm{\Lambda }=(\varnothing )\mathrm{or}\left(1\right)$, produces a map ${\mathrm{\Phi }}^{\beta }:(Y,\mathit{\partial }Y)\to ({\mathcal{P}}_d^{\mathbf{c}\mathrm{\Theta }},pt)$ whose homotopy class is determined by $\beta$. This $\beta$ induces a natural map ${\beta }^{*}:H^{*}({\mathcal{P}}_d^{\mathbf{c}\mathrm{\Theta }},pt;\mathbb{Z})\to H^{*}(Y,\mathit{\partial }Y;\mathbb{Z})$ in cohomology, and therefore, a characteristic homomorphism ${\left({\tilde{\mathrm{\Phi }}}^{\beta }\right)}^{*}:H^{*}(\mathbb{Z}\left[{\mathrm{\Theta }}^{\#}\right],{\mathit{\partial }}^{\#})\to H^{*}(Y,\mathit{\partial }Y;\mathbb{Z})$.

By Proposition 9, $(d,d;\mathbf{c}\mathrm{\Theta },(\varnothing );\mathbf{c}\mathrm{\Theta })$-quasitopic immersions/embeddings $\beta$ induce homotopic maps ${\tilde{\mathrm{\Phi }}}^{\beta }$ and hence the same characteristic homomorphisms ${\left({\tilde{\mathrm{\Phi }}}^{\beta }\right)}^{*}$. □

Thus various homomorphisms ${\left({\tilde{\mathrm{\Phi }}}^{\beta }\right)}^{*}$ may distinguish between different quasitopy classes of immersions $\beta$. We will soon exhibit multiple examples, where they do.

3.4. Quasitopies of Immersions/Embeddings with Special Forbidden Combinatorics $\mathrm{\Theta }$ and the Stabilization by d

In this subsection, we take advantage of a few results from [4,6], as formulated in Section 2, to advance computations of quasitopies of embeddings with special combinatorial patterns $\mathbf{c}\mathrm{\Theta }$ and $\mathbf{c}{\mathrm{\Theta }}^{\prime }$ of tangency to the foliations $\mathcal{L}$ and ${\mathcal{L}}^{•}$, respectively.

We start with the Arnold–Vassiliev case of real polynomials with, so called, moderate singularities [1,4]. Let ${\mathrm{\Theta }}_{max\ge k}\subset {\mathbf{\Omega }}_{⟨d]}$ be the closed poset consisting of $\omega$’s with the maximal entry $\ge k$. For $k\ge 3$, the cohomology $H^j({\mathcal{P}}^{\mathbf{c}{\mathrm{\Theta }}_{max\ge k}},pt;\mathbb{Z})$ is isomorphic to $\mathbb{Z}$ in each dimension j of the form $(k-2)m$, where the integer $m\le d/k$, and vanishes otherwise [1].

Based on Vassiliev’s computation of the cohomology ring $H^{*}({\mathcal{P}}^{\mathbf{c}{\mathrm{\Theta }}_{max\ge k}},pt;\mathbb{Z})$ (see [4], Theorem 1 on page 87), consider the graded ring $\mathcal{V}as{s}_{d,k}$, multiplicatively generated over $\mathbb{Z}$ by the elements ${\left\{e_m\right\}}_{m\le d/k}$ of the degrees $deg\left(e_m\right)=m(k-2)$, subject to the relations

$$\begin{array}{c}\hfill e_l·e_m={\displaystyle \frac{(l+m)!}{l!·m!}}{e}_{l+m}\mathrm{for}k\equiv 0mod2,\mathrm{and}\mathrm{the}\mathrm{relations}\end{array}$$

(47)

$$\begin{array}{c}\hfill e_1·e_1=0,e_1·e_{2m}=e_{2m+1},\end{array}$$

$$\begin{array}{c}\hfill e_{2l}·e_{2m}={\displaystyle \frac{(l+m)!}{l!·m!}}{e}_{2l+2m}\mathrm{for}k\equiv 1mod2.\end{array}$$

(48)

Guided by Theorem 5 and employing Theorem 3, we get the following claim.

Proposition 13. 

Let $k\ge 3$. Consider an immersion $\beta :(M,\mathit{\partial }M)\to (\mathbb{R}\times Y,\mathbb{R}\times \mathit{\partial }Y)$ whose tangency patterns to the foliation $\mathcal{L}$ belong to $\mathbf{c}{\mathrm{\Theta }}_{max\ge k}\subset {\mathbf{\Omega }}_{⟨d]}$ and the ones of ${\beta |}_{\mathit{\partial }M}$ either form an empty set $(\varnothing )$ when $d\equiv 0mod2$, or the set $\left(1\right)$ when $d\equiv 1mod2$.

Then, β generates a characteristic ring homomorphism ${\left({\mathrm{\Phi }}^{\beta }\right)}^{*}:\mathcal{V}as{s}_{d,k}\to H^{*}(Y,\mathit{\partial }Y;\mathbb{Z})$. The homomorphism ${\left({\mathrm{\Phi }}^{\beta }\right)}^{*}$ is an invariant of the quasitopy class of β. In other words, we get a map ${\mathrm{\Phi }}_{d,k}^{*}:{\mathsf{Q}}_{d,d}^{\mathsf{imm}}(Y;\mathbf{c}{\mathrm{\Theta }}_{max\ge k};\mathbf{c}{\mathrm{\Theta }}_{max\ge k})\to {\mathsf{Hom}}_{\mathsf{ring}}\left(\mathcal{V}as{s}_{d,k},H^{*}(Y,\mathit{\partial }Y;\mathbb{Z})\right).$

Remark 8.

Note that if some generator $e_{\ell }\in \mathcal{V}as{s}_{d,k}$ is mapped by ${\left({\mathrm{\Phi }}^{\beta }\right)}^{*}$ to zero in $H^{(k-2)\ell }(Y,\mathit{\partial }Y;\mathbb{Z})$, then the images of all $e_q$ with $q>\ell$ must be torsion elements. Thus some cohomology rings $H^{*}(Y,\mathit{\partial }Y;\mathbb{Z})$ may not be able to accommodate nontrivial images of the Vassiliev ring $\mathcal{V}as{s}_{d,k}$ in positive degrees.

In contrast, here is a case when the accommodation seems possible: take $Y=\mathbb{C}{\mathbb{P}}^3$, $k=4$, and $d=12$. Consider 9-dimensional variety ${\mathcal{P}}_{12}^{{\mathrm{\Theta }}_{max\ge 4}}$, its compliment ${\mathcal{P}}_{12}^{\mathbf{c}{\mathrm{\Theta }}_{max\ge 4}}$, and the cohomology ring $\mathcal{V}as{s}_{12,4}\approx H^{*}({\mathcal{P}}_{12}^{\mathbf{c}{\mathrm{\Theta }}_{max\ge 4}};\mathbb{Z})$. Then, the ring homomorphism ${\mathrm{\Phi }}^{*}:\mathcal{V}as{s}_{12,4}\to H^{*}(\mathbb{C}{\mathbb{P}}^3;\mathbb{Z})\approx \mathbb{Z}\left[a\right]/\{a^4=0\}$ that sends ${\mathrm{\Phi }}^{*}\left(e_1\right):=6a$, ${\mathrm{\Phi }}^{*}\left(e_2\right):=18a^2$, and ${\mathrm{\Phi }}^{*}\left(e_3\right):=36a^3$ embeds $\mathcal{V}as{s}_{12,4}$ as a subring of $\mathbb{Z}\left[a\right]/\{a^4=0\}$. We speculate that there is an embedding $\mathrm{\Phi }:\mathbb{C}{\mathbb{P}}^3\to {\mathcal{P}}_{12}^{\mathbf{c}{\mathrm{\Theta }}_{max\ge 4}}$ that induces that ${\mathrm{\Phi }}^{*}$.

Propositions 12 and 13 lead to the following corollary.

Corollary 11. 

Let $M,Y$ be compact oriented smooth n-manifolds. For any generator $e_{\ell }\in \mathcal{V}as{s}_{d,k}$ of degree $\ell (k-2)$ and an immersion $\beta :(M,\mathit{\partial }M)\to (\mathbb{R}\times Y,\mathbb{R}\times \mathit{\partial }Y)$ with k-moderate tangency patterns to $\mathcal{L}$, the integer

$${\chi }_k(e_{\ell },\beta )=⟨{({\mathrm{\Phi }}^{\beta }\circ \pi \circ \beta \circ p_1)}^{*}\left(e_{\ell }\right),[{\mathrm{\Sigma }}_{\ell (k-2)}^{\beta },\mathit{\partial }{\mathrm{\Sigma }}_{\ell (k-2)}^{\beta }]⟩$$

is an invariant of the quasitopy class $\left[\beta \right]\in {\mathcal{Q}}_{d,d^{\prime }}^{\mathsf{imm}}(Y,\mathit{\partial }Y;\mathbf{c}{\mathrm{\Theta }}_{max\ge k},\mathbf{c}{\mathrm{\Theta }}_{max\ge k})$. The invariant ${\chi }_k(e_{\ell },\beta )=0$ when β is an embedding and $k>1$, or when $H^{\ell (k-2)}(Y,\mathit{\partial }Y;\mathbb{Z})=0$.

The next proposition is a stabilization result by the increasing $d^{\prime }\ge d$ for the embeddings with moderate tangencies to the foliation $\mathcal{L}$ on $\mathbb{R}\times Y$.

Proposition 14. 

Let $k\ge 4$. If $dimY\le (k-2)(\lceil d/k\rceil +1)-2$, then the classifying map

$$\begin{array}{c}\hfill {\mathrm{\Phi }}^{\mathsf{emb}}:{\mathsf{Q}}_{d,d^{\prime }}^{\mathsf{emb}}(Y;\mathbf{c}{\mathrm{\Theta }}_{max\ge k};\mathbf{c}{\mathrm{\Theta }}_{max\ge k})\stackrel{\approx }{⟶}\left[(Y,\mathit{\partial }Y),({\mathcal{P}}_d^{\mathbf{c}{\mathrm{\Theta }}_{max\ge k}},pt)\right]\end{array}$$

(49)

is a bijection, and the classifying map

$$\begin{array}{c}\hfill {\mathrm{\Phi }}^{\mathsf{imm}}:{\mathsf{Q}}_{d,d^{\prime }}^{\mathsf{imm}}(Y;\mathbf{c}{\mathrm{\Theta }}_{max\ge k};\mathbf{c}{\mathrm{\Theta }}_{max\ge k})\stackrel{\approx }{⟶}\left[(Y,\mathit{\partial }Y),({\mathcal{P}}_d^{\mathbf{c}{\mathrm{\Theta }}_{max\ge k}},pt)\right]\end{array}$$

(50)

is a surjection for any $d^{\prime }\ge d$, $d^{\prime }\equiv dmod2$.

In particular, for a given Y, ${\mathsf{Q}}_{d,d^{\prime }}^{\mathsf{emb}}(Y;\mathbf{c}{\mathrm{\Theta }}_{max\ge k};\mathbf{c}{\mathrm{\Theta }}_{max\ge k})$ stabilizes for all $d^{\prime }\ge d\ge {\displaystyle \frac{k}{k-2}}(dimY+4-k)$, a linear function in $dimY$.

Proof. 

Let $q:=(k-2)(\lceil d/k\rceil +1)-2$. By [4], Theorem 3 on page 88, the ${ϵ}_{d,d^{\prime }}$-induced homomorhpism ${\left({ϵ}_{d,d^{\prime }}\right)}_{*}:{\pi }_i\left({\mathcal{P}}_d^{\mathbf{c}{\mathrm{\Theta }}_{max\ge k}}\right)\to {\pi }_i\left({\mathcal{P}}_{d^{\prime }}^{\mathbf{c}{\mathrm{\Theta }}_{max\ge k}}\right)$ of homotopy groups is an isomorphism for all $i\le q$. Thus the two spaces q-connected. Therefore, if $dimY\le q$, then no element of $\left[(Y,\mathit{\partial }Y),({\mathcal{P}}_d^{\mathbf{c}{\mathrm{\Theta }}_{max\ge k}},pt)\right]$ becomes, under the composition with ${ϵ}_{d,d^{\prime }}$, nill-homotopic. Hence,

$$\left[\left[(Y,\mathit{\partial }Y),{ϵ}_{d,d^{\prime }}:{\mathcal{P}}_d^{\mathbf{c}{\mathrm{\Theta }}_{max\ge k}}\to {\mathcal{P}}_{d^{\prime }}^{\mathbf{c}{\mathrm{\Theta }}_{max\ge k}}\right]\right]=\left[(Y,\mathit{\partial }Y),({\mathcal{P}}_d^{\mathbf{c}{\mathrm{\Theta }}_{max\ge k}},pt)\right].$$

In particular, if $dimY\le q$, then $\left[(Y,\mathit{\partial }Y),({\mathcal{P}}_d^{\mathbf{c}{\mathrm{\Theta }}_{max\ge k}},pt)\right]$ is stable in d, provided $d\ge {\displaystyle \frac{k}{k-2}}(dimY+4-k)$. Therefore, by Theorem 4, all the claims of the proposition are validated. □

Example 3. 

Let $k=4$. By Proposition 14 and Formula (49), for any compact connected surface Y, we get bijections:

$$\begin{array}{c}\hfill {\mathsf{Q}}_{4,4}^{\mathsf{emb}}(Y;\mathbf{c}{\mathrm{\Theta }}_{max\ge 4};\mathbf{c}{\mathrm{\Theta }}_{max\ge 4})\stackrel{\approx }{⟶}{\pi }^2(Y/\mathit{\partial }Y),\\ \hfill {\mathsf{Q}}_{4,6}^{\mathsf{emb}}(Y;\mathbf{c}{\mathrm{\Theta }}_{max\ge 4};\mathbf{c}{\mathrm{\Theta }}_{max\ge 4})\stackrel{\approx }{⟶}{\pi }^2(Y/\mathit{\partial }Y),\\ \hfill {\mathsf{Q}}_{6,6}^{\mathsf{emb}}(Y;\mathbf{c}{\mathrm{\Theta }}_{max\ge 4};\mathbf{c}{\mathrm{\Theta }}_{max\ge 4})\stackrel{\approx }{⟶}{\pi }^2(Y/\mathit{\partial }Y),\end{array}$$

whose target is the second cohomotopy group ${\pi }^2(Y/\mathit{\partial }Y)\approx \mathbb{Z}$, the latter isomorphism being generated by the degree of maps to $S^2$.

Let Z be a simply connected $CW$-complex whose cohomology ring, truncated in dimensions $\ge 5$, is isomorphic to $\mathbb{Z}[e_1,e_2]/\{e_1^2-2e_2\}$, where $deg{e}_1=2,deg{e}_2=4$. Then, by Proposition 14, for any compact smooth manifold Y of dimension $\le 4$, we get bijections:

$$\begin{array}{ccc}\hfill {\mathsf{Q}}_{8,8}^{\mathsf{emb}}(Y;\mathbf{c}{\mathrm{\Theta }}_{max\ge 4};\mathbf{c}{\mathrm{\Theta }}_{max\ge 4})& \stackrel{\approx }{⟶}& [Y/\mathit{\partial }Y,Z],\hfill \\ \hfill {\mathsf{Q}}_{8,10}^{\mathsf{emb}}(Y;\mathbf{c}{\mathrm{\Theta }}_{max\ge 4};\mathbf{c}{\mathrm{\Theta }}_{max\ge 4})& \stackrel{\approx }{⟶}& [Y/\mathit{\partial }Y,Z],\hfill \\ \hfill {\mathsf{Q}}_{10,10}^{\mathsf{emb}}(Y;\mathbf{c}{\mathrm{\Theta }}_{max\ge 4};\mathbf{c}{\mathrm{\Theta }}_{max\ge 4})& \stackrel{\approx }{⟶}& [Y/\mathit{\partial }Y,Z].\square \hfill \end{array}$$

Corollary 12. 

Let ${\mathrm{\Theta }}_{max\ge k}\subset {\mathbf{\Omega }}_{⟨d]}$ be the closed poset of ω’s with at least one entry $\ge k$. Assume that $k\le d\le 2k-1$.

Then, there is a group epimorphism

$${\mathsf{OG}}_{d,d}^{\mathsf{emb}}(n;\mathbf{c}{\mathrm{\Theta }}_{max\ge k};\mathbf{c}{\mathrm{\Theta }}_{max\ge k})\to {\mathsf{G}}_{d,d}^{\mathsf{emb}}(n;\mathbf{c}{\mathrm{\Theta }}_{max\ge k};\mathbf{c}{\mathrm{\Theta }}_{max\ge k})\approx {\pi }_n\left(S^{k-2}\right).$$

In other words, the quasitopy group of non-oriented embeddings $\beta :M\hookrightarrow \mathbb{R}\times D^n$ into the cylinder $\mathbb{R}\times D^n$ with no vertical tangencies of $\beta \left(M\right)$ to $\mathcal{L}$ of the order $\ge k$ and with the total multiplicities ${\{{\mu }_{\beta }\left(y\right)\le d\}}_{y\in D^n}$ is isomorphic to the group ${\pi }_n\left(S^{k-2}\right)$, provided that $d\in [k,2k-1]$.

As a result, in this range of d’s and for $n>1$, all the groups ${\mathsf{G}}_{d,d}^{\mathsf{emb}}(n;\mathbf{c}{\mathrm{\Theta }}_{max\ge k};\mathbf{c}{\mathrm{\Theta }}_{max\ge k})$ are finite abelian, except for $n=k-2$ and $n=2k-5$, where they are infinite of rank one.

Proof. 

According to Arnold’s theorem [1], for $d\in [k,2k+1]$, ${\pi }_n\left({\mathcal{P}}_d^{\mathbf{c}{\mathrm{\Theta }}_{max\ge k}}\right)\approx {\pi }_n\left(S^{k-2}\right)$. Applying Corollary 7, the claim follows by examining the tables of homotopy groups of spheres. □

Example 4. 

For $k=4$, $d\in [4,9]$, and all n, we get a group isomorphism

$${\mathsf{G}}_{d,d}^{\mathsf{emb}}(n;\mathbf{c}{\mathrm{\Theta }}_{max\ge 4};\mathbf{c}{\mathrm{\Theta }}_{max\ge 4})\approx {\pi }_n\left(S^2\right).$$

In particular, for $d\in [4,9]$, visiting the table of homotopy groups of spheres, we get:

$$\begin{array}{ccc}& {\mathsf{G}}_{d,d}^{\mathsf{emb}}(3;\mathbf{c}{\mathrm{\Theta }}_{max\ge 4};\mathbf{c}{\mathrm{\Theta }}_{max\ge 4})\approx \mathbb{Z},& {\mathsf{G}}_{d,d}^{\mathsf{emb}}(4;\mathbf{c}{\mathrm{\Theta }}_{max\ge 4};\mathbf{c}{\mathrm{\Theta }}_{max\ge 4})\approx {\mathbb{Z}}_2,\hfill \\ & {\mathsf{G}}_{d,d}^{\mathsf{emb}}(14;\mathbf{c}{\mathrm{\Theta }}_{max\ge 4};\mathbf{c}{\mathrm{\Theta }}_{max\ge 4})\approx {\mathbb{Z}}_{84}\times {\mathbb{Z}}_2^2.\end{array}$$

It would be very interesting to understand and describe, in the sprit of the Arnold’s “kidneys” in Figure 3 (see [1]), the shapes of embeddings $\beta :M\hookrightarrow \mathbb{R}\times D^n$ that produce such mysterious periods… In principle, Theorem 4 contains the instructions for such attempts. Perhaps, at least for $n=1,2$, one has a fighting chance…

Let $H,G$ be two groups, and $\mathsf{Hom}(H,G)$ their group of homomorphisms. Then, G acts on $\mathsf{Hom}(H,G)$ by the conjugation: for any $\varphi :H\to G$, $h\in H$, and $g\in G$, we define $\left(A{d}_g\varphi \right)\left(h\right)$ by the formula $g^{-1}\varphi \left(h\right)g$. We denote by ${\mathsf{Hom}}^{•}(H,G)$ the quotient $\mathsf{Hom}(H,G)/A{d}_G$.

The next corollary deals with special $\mathrm{\Theta }$’s for which ${\mathcal{P}}_d^{\mathbf{c}\mathrm{\Theta }}$ is a $K(\pi ,1)$-space [5].

Corollary 13. 

Let $\mathbf{c}\mathrm{\Theta }$ consist of all ω’s with entries 1 and 2 only and no more than a single entry 2. Put $\kappa \left(d\right):={\displaystyle \frac{d(d-2)}{4}}$ for $d\equiv 0mod2$, and $\kappa \left(d\right):={\displaystyle \frac{{(d-1)}^2}{4}}$ for $d\equiv 1mod2$. Let ${\mathsf{F}}_{\kappa \left(d\right)}$ be the free group in $\kappa \left(d\right)$ generators.

Assume that either Y is a closed manifold, or $\mathit{\partial }Y\ne \varnothing$ and the Λ-condition is in place.

If $\mathit{\partial }Y\ne \varnothing$, then there is a bijection

$${\mathrm{\Phi }}^{\mathsf{emb}}:{\mathsf{Q}}_{d,d}^{\mathsf{emb}}(Y;\mathbf{c}\mathrm{\Theta };\mathbf{c}\mathrm{\Theta })\stackrel{\approx }{⟶}\mathsf{Hom}({\pi }_1\left(Y\right),{\mathsf{F}}_{\kappa \left(d\right)})$$

and a surjection

$${\mathrm{\Phi }}^{\mathsf{imm}}:{\mathsf{Q}}_{d,d}^{\mathsf{imm}}(Y;\mathbf{c}\mathrm{\Theta };\mathbf{c}\mathrm{\Theta })⟶\mathsf{Hom}({\pi }_1\left(Y\right),{\mathsf{F}}_{\kappa \left(d\right)}).$$

When Y is closed, then similar claims hold with the targets of ${\mathrm{\Phi }}^{\mathsf{emb}}$ and ${\mathrm{\Phi }}^{\mathsf{imm}}$ being replaced by the set ${\mathsf{Hom}}^{•}({\pi }_1\left(Y\right),{\mathsf{F}}_{\kappa \left(d\right)})$.

In particular, ${\mathrm{\Phi }}^{\mathsf{emb}}:{\mathsf{Q}}_{d,d}^{\mathsf{emb}}(S^1;\mathbf{c}\mathrm{\Theta };\mathbf{c}\mathrm{\Theta })\stackrel{\approx }{⟶}{\mathsf{F}}_{\kappa \left(d\right)}/A{d}_{{\mathsf{F}}_{\kappa \left(d\right)}}$, the free group of cyclic words in $\kappa \left(d\right)$ letters (see Figure 3).

Thus, if ${\pi }_1\left(Y\right)$ has no nontrivial free images, then the group ${\mathsf{Q}}_{d,d}^{\mathsf{emb}}(Y;\mathbf{c}\mathrm{\Theta };\mathbf{c}\mathrm{\Theta })$ is trivial.

Proof. 

By Theorem 2.4, [5], for such a $\mathbf{c}\mathrm{\Theta }$, the space ${\mathcal{P}}_d^{\mathbf{c}\mathrm{\Theta }}$ is of the homotopy type of $K({\mathsf{F}}_{\kappa \left(d\right)},1)={\bigvee }_{\sigma =1}^{\kappa \left(d\right)}{S}_{\sigma }^1$. Thus, when Y is closed, by the obstruction theory, $[Y,{\bigvee }_{\sigma =1}^{\kappa \left(d\right)}{S}_{\sigma }^1]\approx {\mathsf{Hom}}^{•}({\pi }_1\left(Y\right),{\mathsf{F}}_{\kappa \left(d\right)})$ (see [25], Section VI, F). When $\mathit{\partial }Y\ne \varnothing$, the boundary of Y is mapped by ${\mathrm{\Phi }}^{\beta }$ to the preferred point $pt\in {\mathcal{P}}_d^{\mathbf{c}\mathrm{\Theta }}$. This makes it possible to consider the based loops in Y, the base point b being chosen in $\mathit{\partial }Y$, and the based loops in ${\bigvee }_{\sigma =1}^{\kappa \left(d\right)}{S}_{\sigma }^1$, the base point $pt$ being the apex ★ of the bouquet. Again, by the standard obstruction theory, we get $[(Y,\mathit{\partial }Y),({\bigvee }_{\sigma =1}^{\kappa \left(d\right)}{S}_{\sigma }^1,★)]\approx \mathsf{Hom}({\pi }_1(Y,b),{\mathsf{F}}_{\kappa \left(d\right)})$.

Now, by Corollary 9, the claim follows. In particular, if ${\pi }_1\left(Y\right)$ has no nontrivial free images (say, ${\pi }_1\left(Y\right)$ is a finite group), the group ${\mathsf{Q}}_{d,d}^{\mathsf{emb}}(Y;\mathbf{c}\mathrm{\Theta };\mathbf{c}\mathrm{\Theta })$ is trivial.

See Figure 3 and [5,26] for more illustrations of the cases when ${\mathcal{P}}_d^{\mathbf{c}\mathrm{\Theta }}$ is a $K(\pi ,1)$-space. □

Proposition 15. 

Let ${\mathrm{\Theta }}^{\prime }=\mathrm{\Theta }{=}_{\mathsf{def}}{\{\omega :|\omega |}^{\prime }\ge k\}$, and $d^{\prime }\ge d>k>2$, $d^{\prime }\equiv dmod2$.

Then, assuming the Λ-condition (21), we get a group homomorphism

$$\begin{array}{c}\hfill {\mathrm{\Phi }}_{d,d^{\prime }}^{\mathsf{i}/\mathsf{e}}(n;\mathbf{c}\mathrm{\Theta };\mathbf{c}\mathrm{\Theta }):{\mathsf{G}}_{d,d^{\prime }}^{\mathsf{i}/\mathsf{e}}(n;\mathbf{c}\mathrm{\Theta };\mathbf{c}\mathrm{\Theta })⟶{\pi }_n\left({\mathcal{P}}_d^{\mathbf{c}\mathrm{\Theta }}\right)/ker\left({\left({ϵ}_{d,d^{\prime }}\right)}_{*}\right)\approx \\ \hfill \approx {\pi }_n\left(\underset{i=1}{\overset{A(d,k)}{\bigvee }}{S}_i^{k-1}\right)/ker\left\{{\pi }_n\left(\underset{i=1}{\overset{A(d,k)}{\bigvee }}{S}_i^{k-1}\right)\stackrel{{\left({\widetilde{ϵ}}_{d,d^{\prime }}\right)}_{*}}{⟶}{\pi }_n\left(\underset{j=1}{\overset{A(d^{\prime },k)}{\bigvee }}{S}_j^{k-1}\right)\right\},\end{array}$$

(51)

which is an isomorphism for the embeddings and an epimorphism for immersions. The homomorphism ${\left({\widetilde{ϵ}}_{d,d^{\prime }}\right)}_{*}$ in (51) is induced by the embedding ${ϵ}_{d,d^{\prime }}:{\mathcal{P}}_d^{\mathbf{c}\mathrm{\Theta }}\to {\mathcal{P}}_{d^{\prime }}^{\mathbf{c}\mathrm{\Theta }}$. The number $A(d,k):=A(d,k,0)$ has been introduced in (12).

For $n<k-1$, the group ${\mathsf{G}}_{d,d^{\prime }}^{\mathsf{emb}}(n;\mathbf{c}\mathrm{\Theta },\mathbf{c}\mathrm{\Lambda };\mathbf{c}\mathrm{\Theta })$ is trivial.

Proof. 

By Formula (31) from Theorem 10, we produce the map ${\mathrm{\Phi }}_{d,d^{\prime }}^{\mathsf{i}/\mathsf{e}}(n;\mathbf{c}\mathrm{\Theta };\mathbf{c}\mathrm{\Theta })$. By Corollary 9, it is a group epimomorphism for immersions and an isomorphism for the embeddings.

By Proposition 5 and the Alexander duality, the spaces ${\mathcal{P}}_d^{\mathbf{c}\mathrm{\Theta }}$ and ${\mathcal{P}}_{d^{\prime }}^{\mathbf{c}\mathrm{\Theta }}$ have the homology types of bouquets of $(k-1)$-spheres. Recall that a simply connected $CW$-complex whose torsion-free $\mathbb{Z}$-homology is concentrated in a single dimension q is homotopy equivalent to a bouquet of q-spheres (see [27], Theorem 4C.1). Therefore the spaces ${\mathcal{P}}_d^{\mathbf{c}\mathrm{\Theta }}$ and ${\mathcal{P}}_{d^{\prime }}^{\mathbf{c}\mathrm{\Theta }}$ have the homotopy types of bouquets of $(k-1)$-spheres, provided $k>2$. With the help of these homotopy equivalences, the homomorphism ${\left({\widetilde{ϵ}}_{d,d^{\prime }}\right)}_{*}:{\pi }_n\left({\bigvee }_{i=1}^{A(d,k)}{S}_i^{k-1}\right)\to {\pi }_n\left({\bigvee }_{j=1}^{A(d^{\prime },k)}{S}_j^{k-1}\right)$ is induced by the embedding ${ϵ}_{d,d^{\prime }}:{\mathcal{P}}_d^{\mathbf{c}\mathrm{\Theta }}\to {\mathcal{P}}_{d^{\prime }}^{\mathbf{c}\mathrm{\Theta }}$. This validates the first claim.

The last claim follows from the cellular approximation of a continuous map in its homotopy class. □

For $d^{\prime }=d$, we are able to compute the quasitopy classes of k-flat (see Definition 8) embeddings into $\mathbb{R}\times Y$. They correspond to the case $q=0$ in the following proposition.

Proposition 16. 

For $k\in [3,d-1]$ and $q\in [0,d]$, consider the closed subposet ${\mathrm{\Theta }}_{{|\sim |}^{\prime }\ge k}^{\left(q\right)}:=\left\{{\omega :\left|\omega \right|}^{\prime }\ge k,\left|\omega \right|\in [q,d]\right\}$. Assume the Λ-condition (21).

Then, for a compact smooth n-manifold Y with a boundary, the quasitopy set of embeddings is described by the formula

$${\mathsf{Q}}_{d,d}^{\mathsf{emb}}\left(Y;\mathbf{c}{\mathrm{\Theta }}_{{|\sim |}^{\prime }\ge k}^{\left(q\right)};\mathbf{c}{\mathrm{\Theta }}_{{|\sim |}^{\prime }\ge k}^{\left(q\right)}\right)\approx \left[(Y,\mathit{\partial }Y),(\underset{i=1}{\overset{A(d,k,q)}{\bigvee }}{S}_i^{k-1},★)\right],$$

where ★ is the apex of the bouquet, and the integer $A(d,k,q)$ is defined by (12).

In particular, the quasitopic classes of embeddings in the cylinder $\mathbb{R}\times D^n$ with the combinatorial patterns ω such that ${\left|\omega \right|}^{\prime }<k$ and $\left|\omega \right|\ge q$ are described by the group isomorphism

$${\mathsf{Q}}_{d,d}^{\mathsf{emb}}\left(D^n;\mathbf{c}{\mathrm{\Theta }}_{{|\sim |}^{\prime }\ge k}^{\left(q\right)};\mathbf{c}{\mathrm{\Theta }}_{{|\sim |}^{\prime }\ge k}^{\left(q\right)}\right)\approx {\pi }_n\left(\underset{i=1}{\overset{A(d,k,q)}{\bigvee }}{S}_i^{k-1},★\right).$$

Proof. 

The arguments are similar to the ones used in the proof of Proposition 15. To simplify notations, temporarily, put $\mathrm{\Theta }={\mathrm{\Theta }}_{{|\sim |}^{\prime }\ge k}^{\left(q\right)}$.

By Theorem 5, ${\overline{\mathcal{P}}}_d^{\mathrm{\Theta }}$ has the integral homology type of a bouquet of $A(d,k,q)$ many $(d-k)$-dimensional spheres ([6]). Since the space ${\overline{\mathcal{P}}}_d^{\mathrm{\Theta }}$ is $(d-k)$-dimensional $CW$-complex [5], for $k>2$, the space ${\mathcal{P}}_d^{\mathbf{c}\mathrm{\Theta }}$ is simply connected. By the Alexander duality, its integral homology is concentrated in the dimension $k-1$ and is isomorphic to ${\mathbb{Z}}^{A(d,k,q)}$. By Proposition 4C.1 from [27], ${\mathcal{P}}_d^{\mathbf{c}\mathrm{\Theta }}$ has the homotopy type of the bouquet ${\bigvee }_{i=1}^{A(d,k,q)}{S}_i^{k-1}$. Now, by Theorem 4, the claim follows. □

Theorem 6. 

Let Y be either a closed smooth n-manifold or a manifold with boundary, in which case, we assume the Λ-condition. We denote by $⟨\omega ⟩$ the closed subposet of ${\mathbf{\Omega }}_{⟨d]}$, consisting of elements ${\omega }^{\prime }⪯\omega$.

Then, for all $d\le 13$ and all ω such that ${\left|\omega \right|}^{\prime }>2$, the quasitopy ${\mathsf{Q}}_{d,d}^{\mathsf{emb}}(Y;\mathbf{c}⟨\omega ⟩;\mathbf{c}⟨\omega ⟩)$ either is trivial (consists of single element), or is isomorphic to the cohomotopy set ${\pi }^k\left(Y\right)$, where $k=k\left(\omega \right)\in \left[\right|\omega {|}^{\prime }-1,d-1]$.

For $d\le 13$, the List A1 in Appendix A lists all ω and the corresponding $k=k\left(\omega \right)$ for which ${\mathcal{P}}_d^{\mathbf{c}⟨\omega ⟩}$ is non-contractible (in fact, a homology k-sphere).

Proof. 

The claim follows by combining Theorem 4 with the List A1 in Appendix A. □

Example 5. 

Let $d=8$ and $\omega =\left(4\right)$. Then, for any closed Y, using the List A1 in Appendix A, we get a bijection ${\mathsf{Q}}_{8,8}^{\mathsf{emb}}(Y;\mathbf{c}⟨\left(4\right)⟩;\mathbf{c}⟨\left(4\right)⟩)\approx {\pi }^4\left(Y\right)$, the 4-cohomotopy set of Y. In particular, the we get the following group isomorphism:

$${\mathsf{Q}}_{8,8}^{\mathsf{emb}}(S^7;\mathbf{c}⟨\left(4\right)⟩;\mathbf{c}⟨\left(4\right)⟩)\approx {\pi }_7\left(S^4\right)\approx \mathbb{Z}\times {\mathbb{Z}}_{12}.$$

Let $d=12$ and $\omega =\left(11213\right)$. Then, for any closed Y, by (A1), we get a bijection

$${\mathsf{Q}}_{12,12}^{\mathsf{emb}}(Y;\mathbf{c}⟨\left(11213\right)⟩;\mathbf{c}⟨\left(11213\right)⟩)\approx {\pi }^6\left(Y\right).$$

In particular, we get an isomorphism ${\mathsf{Q}}_{12,12}^{\mathsf{emb}}(S^9;\mathbf{c}⟨\left(11213\right)⟩;\mathbf{c}⟨\left(11213\right)⟩)\approx {\pi }_9\left(S^6\right)\approx {\mathbb{Z}}_{24}$.

3.5. Relation Between Quasitopies and Inner Framed Cobordisms

For a compact smooth Y of dimension $n\ge k-1$, Proposition 16 below points to a peculiar connection between the quasitopies of embeddings ${\mathsf{Q}}_{d,d}^{\mathsf{emb}}\left(Y;\mathbf{c}{\mathrm{\Theta }}_{{|\sim |}^{\prime }\ge k}^{\left(q\right)};\mathbf{c}{\mathrm{\Theta }}_{{|\sim |}^{\prime }\ge k}^{\left(q\right)}\right)$ and the inner framed cobordisms ${\mathcal{FB}}_{\mathrm{\Xi }}^{k-1}\left(Y\right)$ of Y (see the definition below).

Definition 14. 

The cobordisms ${\mathcal{FB}}_{\mathrm{\Xi }}^{k-1}\left(Y\right)$ are based on codimension $k-1$ smooth closed submanifolds Z of Y of the form $Z={\coprod }_{\sigma =1}^{A(d,k,q)}{Z}_{\sigma }$. The normal bundle $\nu (Z,Y)$ is framed. The disjoint “components” ${\left\{Z_{\sigma }\right\}}_{\sigma }$ of Z are marked with different colors σ from a palletΞ of cardinality $A(k,d,q)$.

Two such submanifolds $Z_0,Z_1\subset Y$ are said to be inner cobordant if there exist codimension $k-1$ submanifold $W={\coprod }_{\sigma =1}^{A(d,k,q)}{W}_{\sigma }$ of $Y\times [0,1]$, such that $\mathit{\partial }W=(Z_0\times \left\{0\right\})\cup (Z_1\times \left\{1\right\})$; moreover, $\mathit{\partial }{W}_{\sigma }=\left({\left(Z_0\right)}_{\sigma }\times \left\{0\right\}\right)\coprod \left({\left(Z_1\right)}_{\sigma }\times \left\{1\right\}\right)$ for each color $\sigma \in \mathrm{\Xi }$. The normal bundle $\nu :=\nu (W,Y\times [0,1\left]\right)$ is framed, the restrictions ${\nu |}_{Y\times \left\{0\right\}}\approx \nu (Z_0,Y)$, ${\nu |}_{Y\times \left\{1\right\}}\approx \nu (Z_1,Y)$, and the framing of ν extends the framings of $\nu (Z_0,Y)$ and $\nu (Z_1,Y)$.

As with quasitopies of immersions, for any pair $Y_1$, $Y_2$ of compact smooth manifolds with boundary and any choice of ${\kappa }_1\in {\pi }_0(\mathit{\partial }{Y}_1)$, ${\kappa }_2\in {\pi }_0(\mathit{\partial }{Y}_2)$, an operation

$$\begin{array}{c}\hfill {\uplus }_{\mathcal{F}}:{\mathcal{FB}}_{\mathrm{\Xi }}^{k-1}\left(Y_1\right)\times {\mathcal{FB}}_{\mathrm{\Xi }}^{k-1}\left(Y_2\right)\to {\mathcal{FB}}_{\mathrm{\Xi }}^{k-1}\left(Y_1{\#}_{\mathit{\partial }}{Y}_2\right)\end{array}$$

(52)

may be defined in an obvious way as $Z_1\coprod Z_2\subset Y_1{\#}_{\mathit{\partial }}{Y}_2$. This operation ${\uplus }_{\mathcal{F}}$ converts the inner framed cobordisms ${\mathcal{FB}}_{\mathrm{\Xi }}^{k-1}\left(D^n\right)$ into a group. Choosing $\kappa \in {\pi }_0(\mathit{\partial }Y)$, we get a group action

$$\begin{array}{c}\hfill {\uplus }_{\mathcal{F}}:{\mathcal{FB}}_{\mathrm{\Xi }}^{k-1}\left(D^n\right)\times {\mathcal{FB}}_{\mathrm{\Xi }}^{k-1}\left(Y\right)\to {\mathcal{FB}}_{\mathrm{\Xi }}^{k-1}\left(Y\right).\end{array}$$

(53)

Proposition 17. 

Let a pallet Ξ be of the cardinality $A(d,k,q)$. For a compact smooth manifold Y of dimension $n\ge k-1$, where $k\in [3,d-1]$, there is a bijection

$$Th:{\mathcal{FB}}_{\mathrm{\Xi }}^{k-1}\left(Y\right)\approx {\mathsf{Q}}_{d,d}^{\mathsf{emb}}\left(Y;\mathbf{c}{\mathrm{\Theta }}_{{|\sim |}^{\prime }\ge k}^{\left(q\right)};\mathbf{c}{\mathrm{\Theta }}_{{|\sim |}^{\prime }\ge k}^{\left(q\right)}\right),$$

delivered by the Thom construction on the trivialized normal bundle $\nu (Z,Y)$, where $[Z\hookrightarrow Y]\in {\mathcal{FB}}_{\mathrm{\Xi }}^{k-1}\left(Y\right)$. The bijection $Th$ respects the operations ${\uplus }_{\mathcal{F}}$ and ⊎ in framed inner bordisms and in the quasitopies:

$$\begin{array}{c}\hfill Th\left(Z_1{\uplus }_{\mathcal{F}}{Z}_2\right)=Th\left(Z_1\right)\uplus Th\left(Z_2\right).\end{array}$$

(54)

Proof. 

Given a framed embedding $Z:={\coprod }_{\sigma =1}^{A(d,k,q)}{Z}_{\sigma }\hookrightarrow Y$ of a closed smooth Z of codimension $k-1$, the Thom construction on $\nu (Z,Y)$ produces a continuous map $T_Z:Y\to {\bigvee }_{\sigma =1}^{A(d,k,q)}{S}_{\sigma }^{k-1}$ to the bouquet. Since Z is closed, $\mathit{\partial }Y$ is mapped to the base point ★ of the bouquet. The homotopy class of $T_Z$ depends only on the inner cobordism class of $Z\subset Y$ in ${\mathcal{FB}}_{\mathrm{\Xi }}^{k-1}\left(Y\right)$.

Let us fix a homotopy equivalence $\tau :({\mathcal{P}}^{\mathbf{c}{\mathrm{\Theta }}_{{|\sim |}^{\prime }\ge k}^{\left(q\right)}},pt)\sim ({\bigvee }_{\sigma =1}^{A(d,k,q)}{S}_{\sigma }^{k-1},★)$. By Corollary 8, the homotopy class of the map ${\tilde{T}}_Z:={\tau }^{-1}\circ T_Z$ determines the quasitopy class of some embedding ${\beta }_{{\tilde{T}}_Z}:M\subset \mathbb{R}\times Y$, whose combinatorial tangency patterns to $\mathcal{L}$ belong to the poset $\mathbf{c}{\mathrm{\Theta }}_{{|\sim |}^{\prime }\ge k}^{\left(q\right)}$ and the tangency patterns of ${\beta }_{{\tilde{T}}_Z}:\mathit{\partial }M\to \mathbb{R}\times \mathit{\partial }Y$ to the poset $\mathbf{c}\mathrm{\Lambda }=(\varnothing ),\left(1\right)$. Thus the map $Th:Z⇝{\beta }_{{\tilde{T}}_Z}$ is well-defined.

To show that $Th$ is onto, we take any embedding $\beta :M\subset \mathbb{R}\times Y$ of a n-manifold M, whose tangency patterns reside in $\mathbf{c}{\mathrm{\Theta }}_{{|\sim |}^{\prime }\ge k}^{\left(q\right)}$ and such that the tangency patterns of $\beta :\mathit{\partial }M\subset \mathbb{R}\times \mathit{\partial }Y$ reside in $\mathbf{c}\mathrm{\Lambda }$ as above. We use $\beta$ to produce a map ${\mathrm{\Phi }}^{\beta }:(Y,\mathit{\partial }Y)\to ({\mathcal{P}}^{\mathbf{c}{\mathrm{\Theta }}_{{|\sim |}^{\prime }\ge k}^{\left(q\right)}},pt)$. Composing ${\mathrm{\Phi }}^{\beta }$ with the homotopy equivalence $\tau$, we get a map ${\tilde{\mathrm{\Phi }}}^{\beta }:=\tau \circ {\mathrm{\Phi }}^{\beta }$ from Y to the bouquet such that $\mathit{\partial }Y$ is mapped to the base point ★ of the bouquet. For each sphere $S_{\sigma }^{k-1}$ from the bouquet, we fix a point $b_{\sigma }\in S_{\sigma }^{k-1}$, different from ★, and a $(k-1)$-frame at $b_{\sigma }$. Perturbing ${\tilde{\mathrm{\Phi }}}^{\beta }$ within its homotopy class, we may assume that ${\tilde{\mathrm{\Phi }}}^{\beta }$ is transversal to each $b_{\sigma }$. Then, the closed framed submanifold $Z_{\beta }:={\left({\tilde{\mathrm{\Phi }}}^{\beta }\right)}^{-1}\left({\coprod }_{\sigma \in \mathrm{\Xi }}{b}_{\sigma }\right)\subset Y$ is an element of ${\mathcal{FB}}_{\mathrm{\Xi }}^{k-1}\left(Y\right)$. Moreover, for a given $\beta$, the map ${\tau }^{-1}\circ Th\left(Z_{\beta }\right)$ is in the homotopy class of ${\mathrm{\Phi }}^{\beta }$.

The injectivity of $Th$ has a similar validation, using the $(n+1)$-dimensional cobordism $B:N\to \mathbb{R}\times Y\times [0,1]$ that bounds an embedding $\beta :M\to \mathbb{R}\times Y$ which is quasitopic to the trivial embedding. Again, we perturb $\tau \circ {\mathrm{\Phi }}^B:Y\times [0,1]\to {\bigvee }_{\sigma =1}^{A(d,k,q)}{S}_{\sigma }^{k-1}$ to make it transversal to ${\coprod }_{\sigma \in \mathrm{\Xi }}{b}_{\sigma }$, thus producing a framed cobordism W in $Y\times [0,1]$ which bounds $Z_{\beta }$.

Finally, the validation of the property $Th\left(Z_1{\uplus }_{\mathcal{F}}{Z}_2\right)=Th\left(Z_1\right)\uplus Th\left(Z_2\right)$ is on the level of definitions. □

For $k>2$ and an oriented n-dimensional Y, where $\mathit{\partial }Y\ne \varnothing$, Proposition 17 gives a limited insight into the actions of the (abelian when $n\ge 2$) group ${\mathsf{G}}_{d,d}^{\mathsf{emb}}(n;\mathbf{c}{\mathrm{\Theta }}_{{|\sim |}^{\prime }\ge k}^{\left(q\right)};\mathbf{c}{\mathrm{\Theta }}_{{|\sim |}^{\prime }\ge k}^{\left(q\right)})$ on the set ${\mathsf{Q}}_{d,d}^{\mathsf{emb}}\left(Y;\mathbf{c}{\mathrm{\Theta }}_{{|\sim |}^{\prime }\ge k}^{\left(q\right)};\mathbf{c}{\mathrm{\Theta }}_{{|\sim |}^{\prime }\ge k}^{\left(q\right)}\right)$.

Here, is one useful observation: if $\beta :M\hookrightarrow \mathbb{R}\times Y$ is represented, via $T{h}^{-1}$, by a closed normally framed submanifold $Z_{\beta }={\coprod }_{\sigma \in \mathrm{\Xi }}{Z}_{\beta ,\sigma }\subset Y$, then the fundamental homology classes ${\{\left[Z_{\beta ,\sigma }\right]\in H_{n-k+1}(Y;\mathbb{Z})\}}_{\sigma \in \mathrm{\Xi }}$ are constant along the ${\mathsf{G}}_{d,d}^{\mathsf{emb}}(n;\mathbf{c}{\mathrm{\Theta }}_{{|\sim |}^{\prime }\ge k}^{\left(q\right)};\mathbf{c}{\mathrm{\Theta }}_{{|\sim |}^{\prime }\ge k}^{\left(q\right)})$-orbit through $Th\left(Z_{\beta }\right)$. Indeed, using the property $Th\left(Z_1{\uplus }_{\mathcal{F}}{Z}_2\right)=Th\left(Z_1\right)\uplus Th\left(Z_2\right)$, all the changes of $Z_{\beta }$, produced by the ${\uplus }_{\mathcal{F}}$-action, are incapsulated in a ball $B^n\subset Y$, and thus their fundamental classes are null-homologous in Y.

For a pallet $\mathrm{\Xi }$ of cardinality $A(d,k,q)$, consider the subset $H_{n-k+1}^{[\mathrm{\Xi }\sim fr]}(Y;\mathbb{Z})$ of the group ${\left(H_{n-k+1}(Y;\mathbb{Z})\right)}^{A(d,k,q)}$ that is realized by $A(d,k,q)$disjoint distinctly colored and normally framed closed submanifolds ${\left\{Z_{\sigma }\right\}}_{\sigma \in \mathrm{\Xi }}$ of Y, $dim{Z}_{\sigma }=n-k+1$. For $2k-2>n$, by a general position argument, $H_{n-k+1}^{[\mathrm{\Xi }\sim fr]}(Y;\mathbb{Z})$ is a subgroup of ${\left(H_{n-k+1}(Y;\mathbb{Z})\right)}^{A(d,k,q)}$.

Using Proposition 17 and tracing the correspondence $\left[\beta \right]⇝T{h}^{-1}\left(\left[\beta \right]\right)⇝{\left\{\left[Z_{\beta ,\sigma }\right]\right\}}_{\sigma }$, validates instantly to the following claim.

Proposition 18. 

Let Y be a compact smooth oriented n-manifold Y, where $n\ge k-1$ and $k\in [3,d-1]$. Assume that $\mathit{\partial }Y\ne \varnothing$. Then, the orbit-space of the ${\mathsf{G}}_{d,d}^{\mathsf{emb}}(n;\mathbf{c}{\mathrm{\Theta }}_{{|\sim |}^{\prime }\ge k}^{\left(q\right)};\mathbf{c}{\mathrm{\Theta }}_{{|\sim |}^{\prime }\ge k}^{\left(q\right)})$-action on the set ${\mathsf{Q}}_{d,d}^{\mathsf{emb}}\left(Y;\mathbf{c}{\mathrm{\Theta }}_{{|\sim |}^{\prime }\ge k}^{\left(q\right)};\mathbf{c}{\mathrm{\Theta }}_{{|\sim |}^{\prime }\ge k}^{\left(q\right)}\right)$ admits a surjection on the set $H_{n-k+1}^{[\mathrm{\Xi }\sim fr]}(Y;\mathbb{Z})$.

Example 6. 

Take $k=3$, $d=6$, $q=0$, and $n=3$. Then, $A(6,3,0)=10$ and $\#\mathrm{\Xi }=10$. Thus, we get a homotopy equivalence $\tau :{\mathcal{P}}_6^{\mathbf{c}{\mathrm{\Theta }}_{{|\sim |}^{\prime }\ge 3}}\sim {\bigvee }_{\sigma =1}^{10}{S}_{\sigma }^2$. For a compact oriented 3-manifold Y, any normally framed 1-dimensional submanifold Z acquires an orientation. Using the isomorphism

$$Th:{\mathcal{FB}}_{\mathrm{\Xi }}^2\left(Y\right)\approx {\mathsf{Q}}_{6,6}^{\mathsf{emb}}\left(Y;\mathbf{c}{\mathrm{\Theta }}_{{|\sim |}^{\prime }\ge 3};\mathbf{c}{\mathrm{\Theta }}_{{|\sim |}^{\prime }\ge 3}\right)$$

from Proposition 17, any collection of at most ten disjoint framed closed 1-dimensional submanifolds $Z_1,\dots Z_{10}\subset Y$ (that is, any framed link $Z\subset Y$, colored with 10 distinct colors at most) produces a quasitopy class of an embedding $\beta :M^3\to \mathbb{R}\times Y$, where M is closed. Its tangency patterns ω, with the exception of $(\varnothing )$, have only entries from the list $\{1,2,3\}$ so that no more than one 3 and no more than two 2’s are present in ω, while $\left|\omega \right|\le 6$.

For an orientable Y, the orbit-space of the ${\mathsf{G}}_{6,6}^{\mathsf{emb}}(3;\mathbf{c}{\mathrm{\Theta }}_{{|\sim |}^{\prime }\ge 3};\mathbf{c}{\mathrm{\Theta }}_{{|\sim |}^{\prime }\ge 3})$-action on ${\mathsf{Q}}_{6,6}^{\mathsf{emb}}\left(Y;\mathbf{c}{\mathrm{\Theta }}_{{|\sim |}^{\prime }\ge 3};\mathbf{c}{\mathrm{\Theta }}_{{|\sim |}^{\prime }\ge 3}\right)$ admits a surjection onto the group ${\left(H_1(Y;\mathbb{Z})\right)}^{10}$. For example, for $Y=T^3\setminus int\left(D^3\right)$, where $T^3$ is the 3-torus, the orbit-space is mapped onto the lattice ${\mathbb{Z}}^{30}$.

Corollary 14. 

We adopt the hypotheses of Proposition 16.

• For $dimY=k-1$ and any choice of $\kappa \in {\pi }_0(\mathit{\partial }Y)$, the group ${\mathsf{G}}_{d,d}^{\mathsf{emb}}(k-1;\mathbf{c}{\mathrm{\Theta }}_{{|\sim |}^{\prime }\ge k}^{\left(q\right)};\mathbf{c}{\mathrm{\Theta }}_{{|\sim |}^{\prime }\ge k}^{\left(q\right)})$ acts freely and transitively on the set ${\mathsf{Q}}_{d,d}^{\mathsf{emb}}\left(Y;\mathbf{c}{\mathrm{\Theta }}_{{|\sim |}^{\prime }\ge k}^{\left(q\right)};\mathbf{c}{\mathrm{\Theta }}_{{|\sim |}^{\prime }\ge k}^{\left(q\right)}\right)$. Thus both sets are in a 1-to-1 correspondence.
• For a simply connected Y, $dimY=k>4$, the group ${\mathsf{G}}_{d,d}^{\mathsf{emb}}\left(k;\mathbf{c}{\mathrm{\Theta }}_{{|\sim |}^{\prime }\ge k}^{\left(q\right)};\mathbf{c}{\mathrm{\Theta }}_{{|\sim |}^{\prime }\ge k}^{\left(q\right)}\right)$ acts freely and transitively on the set ${\mathsf{Q}}_{d,d}^{\mathsf{emb}}\left(Y;\mathbf{c}{\mathrm{\Theta }}_{{|\sim |}^{\prime }\ge k}^{\left(q\right)};\mathbf{c}{\mathrm{\Theta }}_{{|\sim |}^{\prime }\ge k}^{\left(q\right)}\right)$. Again, both sets are in a 1-to-1 correspondence.

Proof. 

By Proposition 18, there exists a bijection

$$Th:{\mathcal{FB}}_{\mathrm{\Xi }}^{k-1}\left(Y\right)\to {\mathsf{Q}}_{d,d}^{\mathsf{emb}}\left(Y;\mathbf{c}{\mathrm{\Theta }}_{{|\sim |}^{\prime }\ge k}^{\left(q\right)};\mathbf{c}{\mathrm{\Theta }}_{{|\sim |}^{\prime }\ge k}^{\left(q\right)}\right).$$

When $dimY=k-1$, the elements of ${\mathcal{FB}}_{\mathrm{\Xi }}^{k-1}\left(Y\right)$ are represented by finite sets Z of framed oriented singletons, marked with $\#\mathrm{\Xi }$ colors at most. (We may assume that no two singletons of the same color have opposite orientations.) Evidently, any such finite set Z can be incapsulated into a standard smooth ball $D^{k-1}\subset Y$ such that $\mathit{\partial }{D}^{k-1}\cap \mathit{\partial }Y=D^{k-2}$, a standard $(k-2)$-ball. Therefore Z belongs to the ${\mathcal{FB}}_{\mathrm{\Xi }}^{k-1}\left(D^{k-1}\right)$-orbit of the empty collection $Z_{\varnothing }$. By (54), $Th\left(Z\right)$ belongs to the ${\mathsf{G}}_{d,d}^{\mathsf{emb}}(k-1;\mathbf{c}{\mathrm{\Theta }}_{{|\sim |}^{\prime }\ge k}^{\left(q\right)};\mathbf{c}{\mathrm{\Theta }}_{{|\sim |}^{\prime }\ge k}^{\left(q\right)})$-orbit of the trivial embedding (the empty one for $d\equiv 0mod2$ and the embedding ${\beta }_{★}:Y\to \left\{0\right\}\times Y\subset \mathbb{R}\times Y$ for $d\equiv 1mod2$). This validates the first claim.

For a simply connected Y, $dimY=k>4$, again by Proposition 18, any element of ${\mathsf{Q}}_{d,d}^{\mathsf{emb}}\left(Y;\mathbf{c}{\mathrm{\Theta }}_{{|\sim |}^{\prime }\ge k}^{\left(q\right)};\mathbf{c}{\mathrm{\Theta }}_{{|\sim |}^{\prime }\ge k}^{\left(q\right)}\right)$ is represented by a framed collection Z of disjoint loops in Y, colored with $\#\mathrm{\Xi }$ colors at most. Using that ${\pi }_1\left(Y\right)=1$ and $dimY=k>4$, we can bound each loop $Z_{\sigma }$ by a regularly embedded smooth 2-disk $W_{\sigma }\subset int\left(Y\right)$ so that all $W_{\sigma }$’s are disjoint. Therefore, each loop $Z_{\sigma }$ is contained in a standard ball $D_{\sigma }^k$, the regular neighborhood of $W_{\sigma }$. By performing 1-surgeries on ${\coprod }_{\sigma }{D}_{\sigma }^k$, we construct a k-ball ${\tilde{B}}^k$ that contains all $Z_{\sigma }$’s. Adding a 1-handle $H\subset Y\setminus {\tilde{B}}^k$ that connects $\mathit{\partial }{\tilde{B}}^k$ with $\mathit{\partial }Y$, we exhibit a ball $B^k:={\tilde{B}}^k\cup H$ which contains all the loops and such that $\mathit{\partial }{B}^k\cap \mathit{\partial }Y$ is a $(k-1)$-dimensional ball. Therefore, Z is, once more, in the orbit of the empty collection $Z_{\varnothing }$ of loops. By (54), $Th\left(Z\right)$ belongs to the ${\mathsf{G}}_{d,d}^{\mathsf{emb}}(k;\mathbf{c}{\mathrm{\Theta }}_{{|\sim |}^{\prime }\ge k}^{\left(q\right)};\mathbf{c}{\mathrm{\Theta }}_{{|\sim |}^{\prime }\ge k}^{\left(q\right)})$-orbit of the trivial embedding.

In fact, this conclusion is also valid for 3-manifolds Y with a spherical boundary, but its validation is not as direct as for the case $k>4$. If ${\pi }_1\left(Y\right)=1$, by the Perelman’s solution of the Poincaré Conjecture [28,29,30], we conclude that Y is the standard ball $D^3$. Thus any $\mathrm{\Xi }$-colored and framed link $Z\subset Y$ is obviously contained in $D^3$.

As usual, the case $k=4$ seems to be challenging. □

3.6. More About the Stabilization of ${\mathcal{Q}}_{d,d^{\prime }}^{\mathsf{emb}}(Y,\mathit{\partial }Y;\mathbf{c}\mathrm{\Theta },\mathbf{c}\mathrm{\Lambda };\mathbf{c}{\mathrm{\Theta }}^{\prime })$ by the Degrees $d,d^{\prime }$

We start with the embeddings of 1-manifolds in the product $\mathbb{R}\times D^1$ and the forbidden poset $\mathrm{\Theta }$ that consists of $\omega$’s with the reduced norms $\ge 2$.

Proposition 19. 

Let $d^{\prime }\ge d+2$, $d^{\prime }\equiv dmod2$. For a closed subposet $\mathrm{\Theta }\subset {\mathbf{\Omega }}_{{⟨d],|\sim |}^{\prime }\ge 2}$, let ${\widehat{\mathrm{\Theta }}}_{\left\{d^{\prime }\right\}}$ be the smallest subposet in ${\mathbf{\Omega }}_{⟨d^{\prime }]}$ that contains Θ. Then, we get a stabilization by $d^{\prime }$:

$${\mathsf{Q}}_{d+2,d^{\prime }}^{\mathsf{emb}}(D^1;\mathbf{c}{\widehat{\mathrm{\Theta }}}_{\{d+2\}};\mathbf{c}{\widehat{\mathrm{\Theta }}}_{\left\{d^{\prime }\right\}})\approx {\pi }_1({\mathcal{P}}_{d+2}^{\mathbf{c}{\widehat{\mathrm{\Theta }}}_{\{d+2\}}},pt).$$

Proof. 

The claim follows from Theorem 4 by combining it with Theorem 6 (see also Theorem 2.15 from [5]), which claims that ${\left({ϵ}_{d+2,d^{\prime }}\right)}_{*}:{\pi }_1\left({\mathcal{P}}_{d+2}^{\mathbf{c}{\widehat{\mathrm{\Theta }}}_{\{d+2\}}}\right)\approx {\pi }_1\left({\mathcal{P}}_{d^{\prime }}^{\mathbf{c}{\mathrm{\Theta }}_{\left\{d^{\prime }\right\}}}\right)$ is an isomorphism, induced by the embedding ${ϵ}_{d+2,d^{\prime }}$ of the two spaces. See [5] for an explicit description of presentations of such fundamental groups ${\pi }_1\left({\mathcal{P}}_{d+2}^{\mathbf{c}{\widehat{\mathrm{\Theta }}}_{\{d+2\}}}\right)$. □

Theorem 7. 

Let Θ be a closed poset such that ${\left|\omega \right|}^{\prime }\ge 3$ for any $\omega \in \mathrm{\Theta }$. Let $d^{\prime }\ge d$ and $d^{\prime }\equiv dmod2$. Assume the Λ-condition (21).

For any compact smooth Y such that $dimY\le d+2-{\psi }_{\mathrm{\Theta }}(d+2)$ (see (9)) we get the classifying map

$$\begin{array}{c}\hfill {\mathrm{\Phi }}_{d,d+2}^{\mathsf{i}/\mathsf{e}}(Y;\mathbf{c}\mathrm{\Theta };\mathbf{c}\mathrm{\Theta }):{\mathsf{Q}}_{d,d+2}^{\mathsf{i}/\mathsf{e}}(Y;\mathbf{c}\mathrm{\Theta };\mathbf{c}\mathrm{\Theta })\to [(Y,\mathit{\partial }Y),({\mathcal{P}}_d^{\mathbf{c}\mathrm{\Theta }},pt)],\end{array}$$

(55)

which is bijective for embeddings and surjective for immersions.

For any profinite (in the sense of Definition 2) poset Θ and any Y, the set ${\mathsf{Q}}_{d,d^{\prime }}^{\mathsf{emb}}(Y;\mathbf{c}\mathrm{\Theta };\mathbf{c}\mathrm{\Theta })$ stabilizes for all sufficiently big d.

Proof. 

The argument is a bit similar to the one we used in the proof of Proposition 15.

Under the hypotheses, by Theorem 2, the homomorphism ${\left({ϵ}_{d,d^{\prime }}\right)}_{*}:H_j({\mathcal{P}}_d^{\mathbf{c}\mathrm{\Theta }};\mathbb{Z})\to H_j({\mathcal{P}}_{d+2}^{\mathbf{c}\mathrm{\Theta }};\mathbb{Z})$ is an isomorphism for all $j<d+2-{\psi }_{\mathrm{\Theta }}(d+2)$. Since ${\left|\omega \right|}^{\prime }\ge 3$ for any $\omega \in \mathrm{\Theta }$, all the spaces ${\left\{{\mathcal{P}}_{d^{\prime }}^{\mathbf{c}\mathrm{\Theta }}\right\}}_{d^{\prime }\ge d}$ are simply connected. Hence, ${ϵ}_{d,d+2}$ induces an isomorphism in the integral j-homology of ${\mathcal{P}}_d^{\mathbf{c}\mathrm{\Theta }}$ and of ${\mathcal{P}}_{d+2}^{\mathbf{c}\mathrm{\Theta }}$ for all $j<d+2-{\psi }_{\mathrm{\Theta }}(d+2)$. By the Whitehead Theorem (the inverse Hurewicz Theorem) (see Theorem (7.13) in [31]), ${ϵ}_{d,d+2}$ induces isomorphisms of the homotopy groups of ${\mathcal{P}}_d^{\mathbf{c}\mathrm{\Theta }}$ and of ${\mathcal{P}}_{d+2}^{\mathbf{c}\mathrm{\Theta }}$ in dimensions $\le d+2-{\psi }_{\mathrm{\Theta }}(d+2)$. By standard application of the obstruction theory, if $dimY\le d+2-{\psi }_{\mathrm{\Theta }}(d+2)$, no nontrivial element of $[(Y,\mathit{\partial }Y),({\mathcal{P}}_d^{\mathbf{c}\mathrm{\Theta }},pt)]$ becomes, via ${ϵ}_{d,d+2}$, null-homotopic in $[(Y,\mathit{\partial }Y),({\mathcal{P}}_{d+2}^{\mathbf{c}\mathrm{\Theta }},p{t}^{\prime })]$. Thus, for such Y, we get

$$\left[[(Y,\mathit{\partial }Y),{ϵ}_{d,d+2}:({\mathcal{P}}_d^{\mathbf{c}\mathrm{\Theta }},pt)\to ({\mathcal{P}}_{d+2}^{\mathbf{c}{\mathrm{\Theta }}^{\prime }},p{t}^{\prime })]\right]=[(Y,\mathit{\partial }Y),({\mathcal{P}}_d^{\mathbf{c}\mathrm{\Theta }},pt)].$$

By Lemma 4.3 from [6], for any closed profinite $\mathrm{\Theta }$, ${lim}_{d^{\prime }\to \infty }{d}^{\prime }-{\psi }_{\mathrm{\Theta }}\left(d^{\prime }\right)=+\infty$. Hence, repeating the previous arguments, we get a similar conclusion for all $d^{\prime }\ge d\gg dimY$.

Therefore, by Theorem 4, the all the claims of Theorem 7 follow. □

Example 7. 

Tracing these lines of arguments and using Vassiliev’s computation [4] of the cohomology ring $H^{*}({\mathcal{P}}^{\mathbf{c}{\mathrm{\Theta }}_{max\ge 4}},pt;\mathbb{Z})$, we get the following claim. For all $d\ge 4$ and any compact connected orientable surface Y, the quasitopies ${\mathsf{G}}_{d,d+2}^{\mathsf{emb}}(Y;\mathbf{c}{\mathrm{\Theta }}_{max\ge 4};\mathbf{c}{\mathrm{\Theta }}_{max\ge 4})$ of embeddings $\beta :M\to \mathbb{R}\times Y$, where M is a surface, are stable and isomorphic to $\mathbb{Z}$.

Example 8. 

Let $\mathrm{\Theta }=⟨\left(4\right),\left(33\right)⟩$. Then, by Theorem 7 and Example 1, we get a bijection

$$\begin{array}{c}\hfill {\mathrm{\Phi }}_{d,d+2}^{\mathsf{emb}}(Y;\mathbf{c}\mathrm{\Theta };\mathbf{c}\mathrm{\Theta }):{\mathsf{Q}}_{d,d+2}^{\mathsf{emb}}(Y;\mathbf{c}\mathrm{\Theta };\mathbf{c}\mathrm{\Theta })\to [(Y,\mathit{\partial }Y),({\mathcal{P}}_d^{\mathbf{c}\mathrm{\Theta }},pt)]\end{array}$$

(56)

for all $d\ge 2dim\left(Y\right)-4$. Thus, ${\mathsf{Q}}_{d,d+2}^{\mathsf{emb}}(Y;\mathbf{c}\mathrm{\Theta };\mathbf{c}\mathrm{\Theta })$ is stable for all $d\ge 2dim\left(Y\right)-4$.