Emergent Behavior and Computational Capabilities in Nonlinear Systems: Advancing Applications in Time Series Forecasting and Predictive Modeling †
Abstract
1. Introduction
2. Information-Based Metrics
2.1. Entropy Density
2.2. Effective Complexity Measure
2.3. Information Distance
2.4. Entropic Measures of Computational Complexity
3. Computational Capabilities in Nonlinear Systems
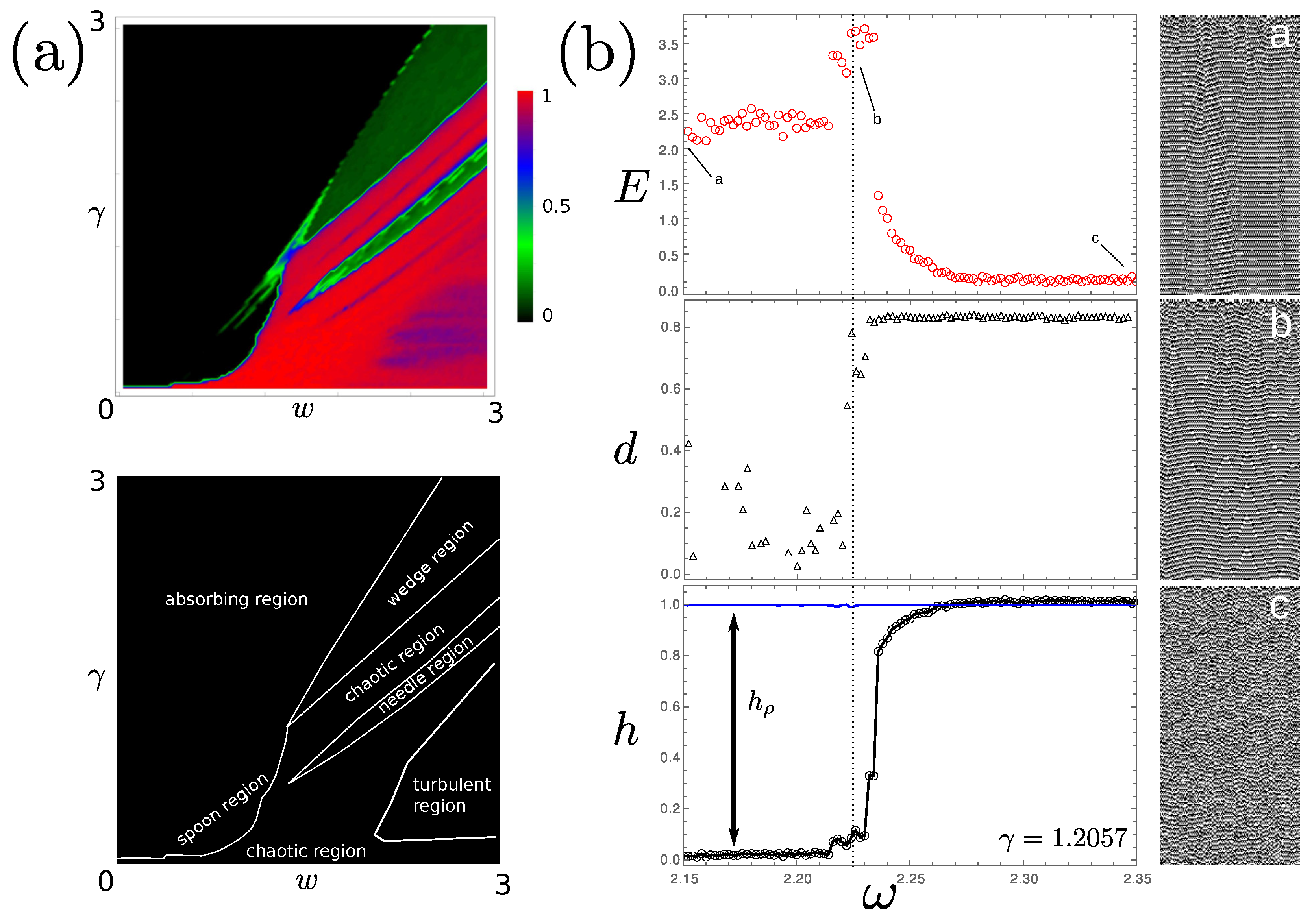
3.1. Local Phase-Dependent (LAP) Coupling
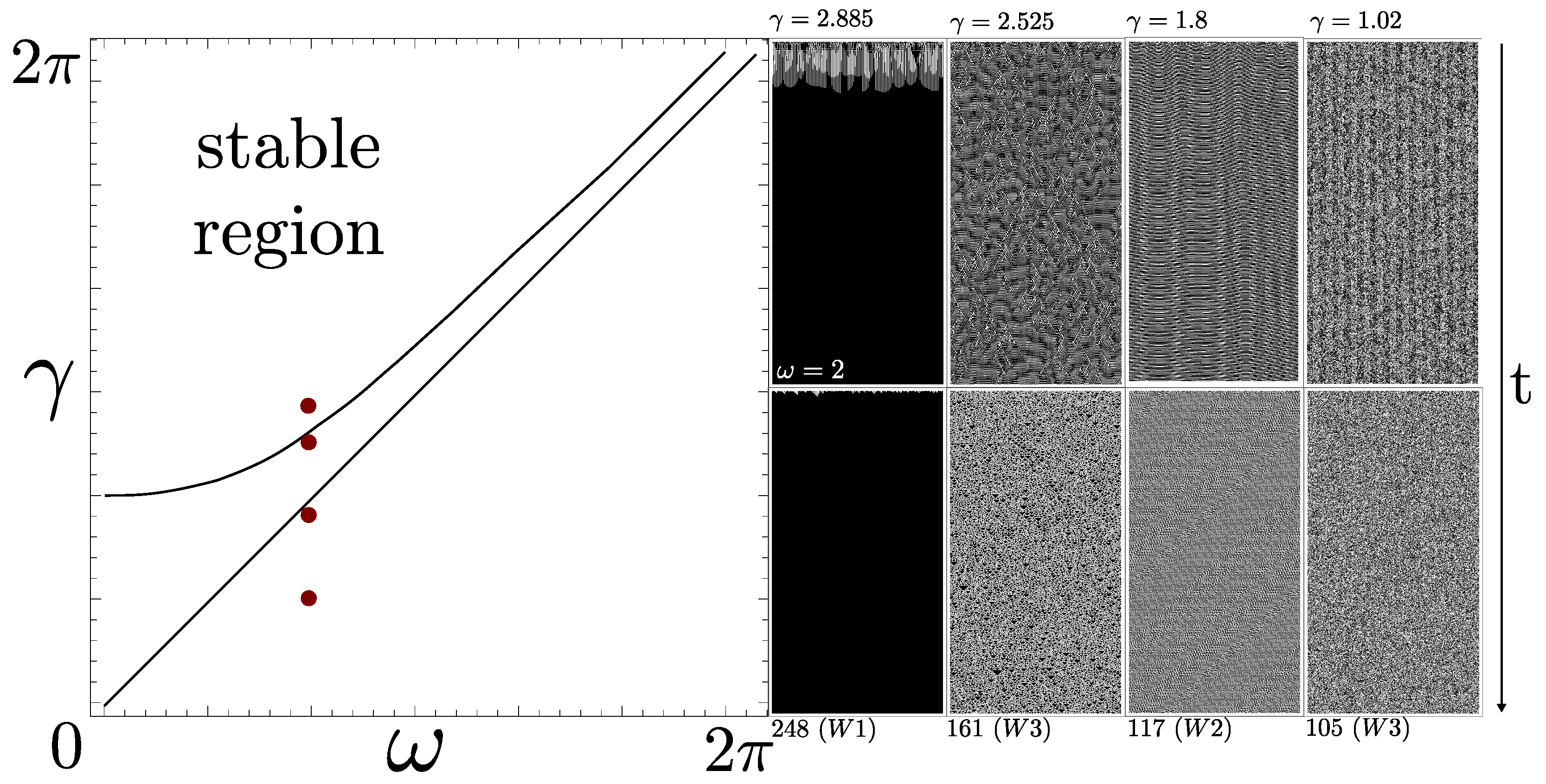
3.2. Kuramoto-like Local (LAK) Coupling
3.3. Edge of Chaos
4. Oscillators and Cellular Automata: A Comparison
4.1. Visual Comparison via Spatiotemporal Diagrams
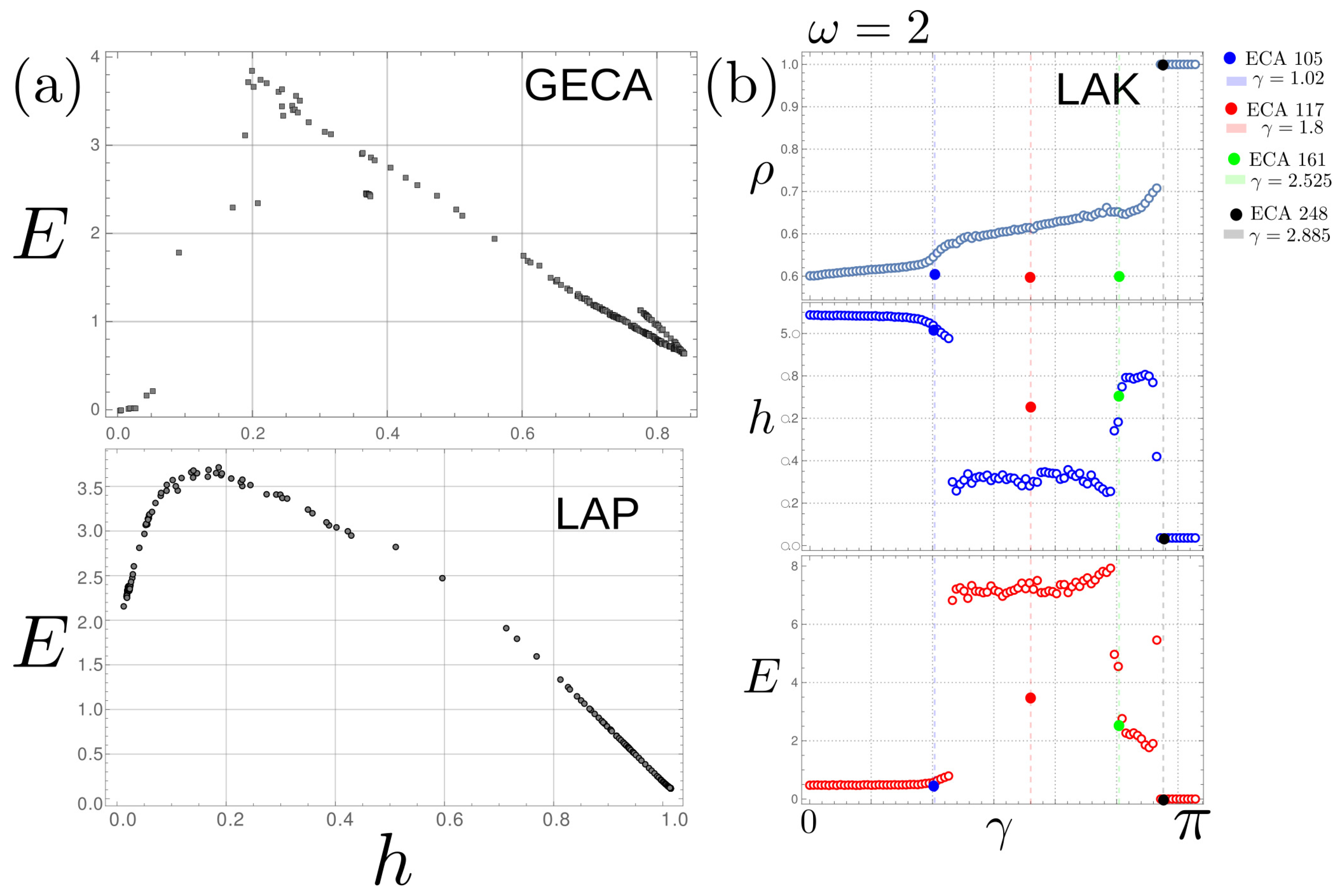
4.2. Quantitative Comparison via Entropic Measures
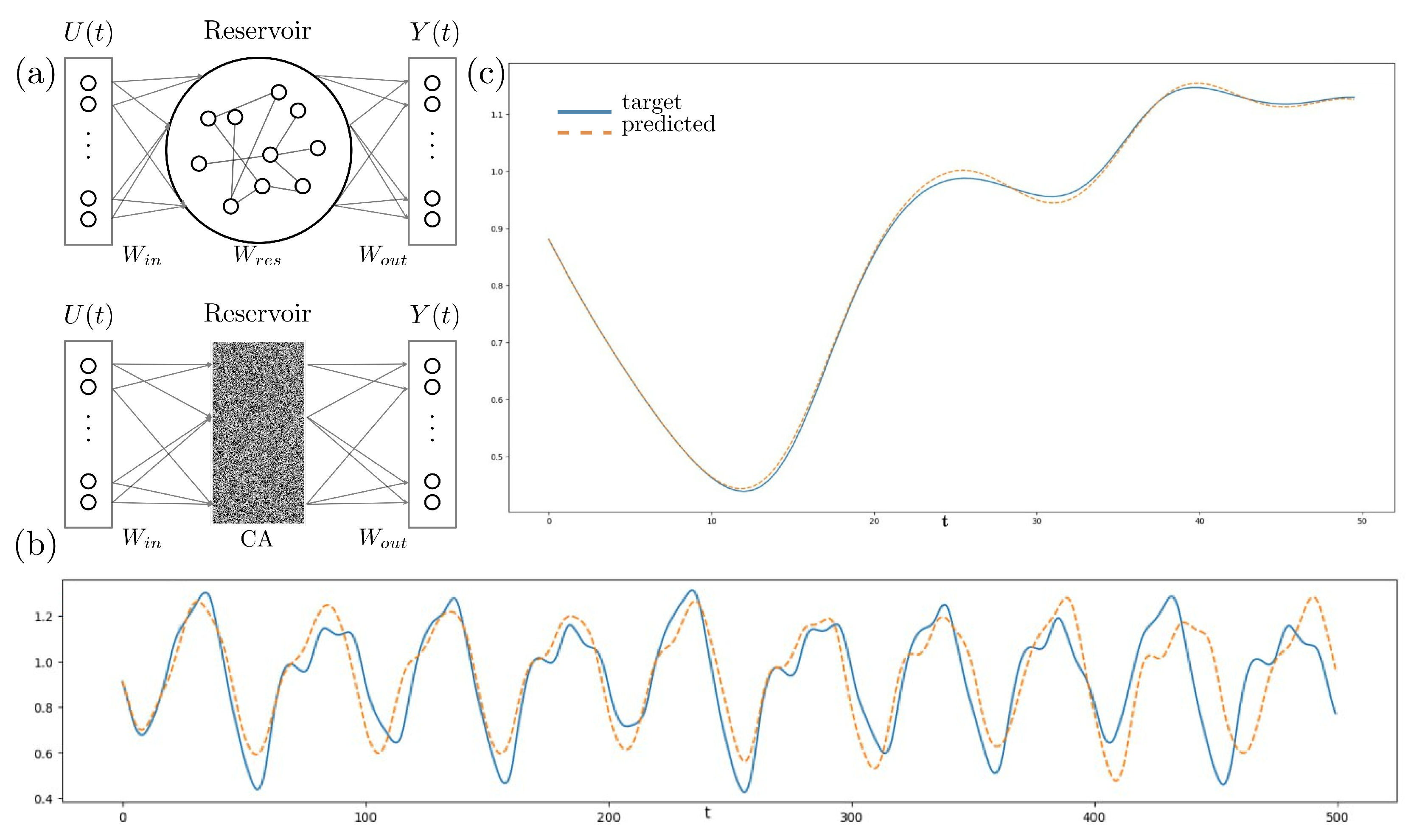
5. Dynamical Systems as Reservoirs in Echo State Networks
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Strogatz, S.H.; Stewart, I. Coupled Oscillators and Biological Synchronization. Sci. Am. 1993, 269, 102–109. [Google Scholar] [CrossRef]
- Strogatz, S. Nonlinear Dynamics and Chaos: With Applications to Physics, Biology, Chemistry, and Engineering, repr. ed.; Westview Press: Cambridge, MA, USA, 2007. [Google Scholar]
- Mora, T.; Bialek, W. Are Biological Systems Poised at Criticality? J. Stat. Phys. 2011, 144, 268–302. [Google Scholar] [CrossRef]
- Machta, J. Natural Complexity, Computational Complexity and Depth. Chaos Interdiscip. J. Nonlinear Sci. 2011, 21, 037111. [Google Scholar] [CrossRef]
- Ott, E.; Grebogi, C.; Yorke, J.A. Controlling Chaos. Phys. Rev. Lett. 1990, 64, 1196–1199. [Google Scholar] [CrossRef]
- Feali, M.S.; Hamidi, A. Dynamical Response of Autaptic Izhikevich Neuron Disturbed by Gaussian White Noise. J. Comput. Neurosci. 2023, 51, 59–69. [Google Scholar] [CrossRef]
- Acedo, L. A Cellular Automaton Model for Collective Neural Dynamics. Math. Comput. Model. 2009, 50, 717–725. [Google Scholar] [CrossRef]
- Bandini, S.; Mauri, G.; Serra, R. Cellular Automata: From a Theoretical Parallel Computational Model to Its Application to Complex Systems. Parallel Comput. 2001, 27, 539–553. [Google Scholar] [CrossRef]
- Dennunzio, A.; Formenti, E.; Kůrka, P. Cellular Automata Dynamical Systems. In Handbook of Natural Computing; Rozenberg, G., Bäck, T., Kok, J.N., Eds.; Springer: Berlin/Heidelberg, Germany, 2012; pp. 25–75. [Google Scholar] [CrossRef]
- Wolfram, S. Cellular Automata and Complexity: Collected Papers; Addison-Wesley Pub. Co.: Reading, MA, USA, 1994. [Google Scholar]
- Tisseur, P. Cellular Automata and Lyapunov Exponents. Nonlinearity 2000, 13, 1547–1560. [Google Scholar] [CrossRef]
- Estevez-Rams, E.; Estevez-Moya, D.; Garcia-Medina, K.; Lora-Serrano, R. Computational Capabilities at the Edge of Chaos for One Dimensional Systems Undergoing Continuous Transitions. Chaos Interdiscip. J. Nonlinear Sci. 2019, 29, 043105. [Google Scholar] [CrossRef]
- Estevez-Rams, E.; Estevez-Moya, D.; Aragón-Fernández, B. Phenomenology of Coupled Nonlinear Oscillators. Chaos Interdiscip. J. Nonlinear Sci. 2018, 28, 023110. [Google Scholar] [CrossRef]
- Estevez-Rams, E.; Garcia-Medina, K.; Aragón-Fernández, B. Correlation and Collective Behaviour in Adler-Type Locally Coupled Oscillators at the Edge of Chaos. Commun. Nonlinear Sci. Numer. Simul. 2024, 133, 107989. [Google Scholar] [CrossRef]
- García Medina, K.; Beltrán, J.L.; Estevez-Rams, E.; Kunka, D. Computational Capabilities of Adler Oscillators Under Weak Local Kuramoto-like Coupling. In Proceedings of the Progress in Artificial Intelligence and Pattern Recognition; Hernández Heredia, Y., Milián Núñez, V., Ruiz Shulcloper, J., Eds.; Lecture Notes in Computer Science; Springer: Cham, Switzerland, 2024; pp. 108–118. [Google Scholar] [CrossRef]
- Medina, K.G.; Estevez-Rams, E. Behavior of Circular Chains of Nonlinear Oscillators with Kuramoto-like Local Coupling. AIP Adv. 2023, 13, 035222. [Google Scholar] [CrossRef]
- García Medina, K.; Estevez-Rams, E.; Kunka, D. Non-Linear Oscillators with Kuramoto-like Local Coupling: Complexity Analysis and Spatiotemporal Pattern Generation. Chaos Solitons Fractals 2023, 175, 114056. [Google Scholar] [CrossRef]
- Alonso, L.M. Complex Behavior in Chains of Nonlinear Oscillators. Chaos Interdiscip. J. Nonlinear Sci. 2017, 27, 063104. [Google Scholar] [CrossRef]
- Schiff, J.L. Cellular Automata: A Discrete View of the World; John Wiley & Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
- Pedersen, J. Continuous Transitions of Cellular Automata. Complex Syst. 1990, 4, 653–665. [Google Scholar]
- Wolfram, S. Tables of Cellular Automaton Properties. Available online: https://content.wolfram.com/sw-publications/2020/07/cellular-automaton-properties.pdf (accessed on 30 July 2025).
- Jaeger, H. The “Echo State” Approach to Analysing and Training Recurrent Neural Networks; GMD Forschungszentrum Informationstechnik: Sankt Augustin, Germany, 2001. [Google Scholar] [CrossRef]
- Grassberger, P. Information and Complexity Measures in Dynamical Systems. In Information Dynamics; Atmanspacher, H., Scheingraber, H., Eds.; Springer: Boston, MA, USA, 1991; Volume 256, pp. 15–33. [Google Scholar] [CrossRef]
- Crutchfield, J.P.; Feldman, D.P. Regularities Unseen, Randomness Observed: Levels of Entropy Convergence. Chaos Interdiscip. J. Nonlinear Sci. 2003, 13, 25–54. [Google Scholar] [CrossRef]
- Li, M.; Chen, X.; Li, X.; Ma, B.; Vitanyi, P. The Similarity Metric. IEEE Trans. Inf. Theory 2004, 50, 3250–3264. [Google Scholar] [CrossRef]
- Vitányi, P.M.B.; Balbach, F.J.; Cilibrasi, R.L.; Li, M. Normalized Information Distance. In Information Theory and Statistical Learning; Emmert-Streib, F., Dehmer, M., Eds.; Springer: Boston, MA, USA, 2009; pp. 45–82. [Google Scholar] [CrossRef]
- Estevez-Rams, E.; Lora-Serrano, R.; Nunes, C.A.J.; Aragón-Fernández, B. Lempel-Ziv Complexity Analysis of One Dimensional Cellular Automata. Chaos Interdiscip. J. Nonlinear Sci. 2015, 25, 123106. [Google Scholar] [CrossRef] [PubMed]
- Winfree, A.T. Biological Rhythms and the Behavior of Populations of Coupled Oscillators. J. Theor. Biol. 1967, 16, 15–42. [Google Scholar] [CrossRef] [PubMed]
- Acebrón, J.A.; Bonilla, L.L.; Pérez Vicente, C.J.; Ritort, F.; Spigler, R. The Kuramoto Model: A Simple Paradigm for Synchronization Phenomena. Rev. Mod. Phys. 2005, 77, 137–185. [Google Scholar] [CrossRef]
- Wolfram, S. Computation Theory of Cellular Automata. Commun. Math. Phys. 1984, 96, 15–57. [Google Scholar] [CrossRef]
- Crutchfield, J.P. What Lies Between Order and Chaos? In Art and Complexity; Elsevier: Amsterdam, The Netherlands, 2003; pp. 31–45. [Google Scholar] [CrossRef]
- Crutchfield, J.P.; Young, K. Inferring Statistical Complexity. Phys. Rev. Lett. 1989, 63, 105–108. [Google Scholar] [CrossRef] [PubMed]
- Feldman, D.P.; McTague, C.S.; Crutchfield, J.P. The Organization of Intrinsic Computation: Complexity-Entropy Diagrams and the Diversity of Natural Information Processing. Chaos Interdiscip. J. Nonlinear Sci. 2008, 18, 043106. [Google Scholar] [CrossRef] [PubMed]
- Berezansky, L.; Braverman, E.; Idels, L. The Mackey–Glass Model of Respiratory Dynamics: Review and New Results. Nonlinear Anal. Theory Methods Appl. 2012, 75, 6034–6052. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
García-Medina, K.; Estevez-Moya, D.; Estevez-Rams, E.; Neder, R.B. Emergent Behavior and Computational Capabilities in Nonlinear Systems: Advancing Applications in Time Series Forecasting and Predictive Modeling. Comput. Sci. Math. Forum 2025, 11, 17. https://doi.org/10.3390/cmsf2025011017
García-Medina K, Estevez-Moya D, Estevez-Rams E, Neder RB. Emergent Behavior and Computational Capabilities in Nonlinear Systems: Advancing Applications in Time Series Forecasting and Predictive Modeling. Computer Sciences & Mathematics Forum. 2025; 11(1):17. https://doi.org/10.3390/cmsf2025011017
Chicago/Turabian StyleGarcía-Medina, Kárel, Daniel Estevez-Moya, Ernesto Estevez-Rams, and Reinhard B. Neder. 2025. "Emergent Behavior and Computational Capabilities in Nonlinear Systems: Advancing Applications in Time Series Forecasting and Predictive Modeling" Computer Sciences & Mathematics Forum 11, no. 1: 17. https://doi.org/10.3390/cmsf2025011017
APA StyleGarcía-Medina, K., Estevez-Moya, D., Estevez-Rams, E., & Neder, R. B. (2025). Emergent Behavior and Computational Capabilities in Nonlinear Systems: Advancing Applications in Time Series Forecasting and Predictive Modeling. Computer Sciences & Mathematics Forum, 11(1), 17. https://doi.org/10.3390/cmsf2025011017




