Comparison between Information Theoretic Measures to Assess Financial Markets

Abstract

Information theoretic measures were applied to the study of the randomness associations of different financial time series. We studied the level of similarities between information theoretic measures and the various tools of regression analysis, i.e., between Shannon entropy and the total sum of squares of the dependent variable, relative mutual information and coefficients of correlation, conditional entropy and residual sum of squares, etc. We observed that mutual information and its dynamical extensions provide an alternative approach with some advantages to study the association between several international stock indices. Furthermore, mutual information and conditional entropy are relatively efficient compared to the measures of statistical dependence.

1. Introduction

Financial markets are dynamic structures which exhibit nonlinear behavior. The correlation structure of time series data for financial securities incorporates important statistics for many real world applications such as portfolio diversification, risk measures, and asset pricing modeling [1,2]. Strict linear correlation studies are likely to neglect important financial system characteristics. Traditionally, non-linear correlations with higher order moments have been studied.

Some researchers considered the information measures theoretic approach to study this statistical dependence because of its potential to identify a stochastic relationship as a whole, including linearity and non-linearity (refer to [3,4,5,6]), and so making it a general approach. For example, network statistics based on mutual information can successfully replace statistics based on the coefficient of correlation [7]. Ormos et al. [8] defined continuous entropy as an alternative measure of risk in an asset pricing model. Mercurio et al. [9] introduced a new family of portfolio optimization problems called the return-entropy portfolio optimization (REPO), which simplifies the computation of portfolio entropy using a combinatorial approach. Novais et al. [10] described a new model for portfolio optimization (PO), using entropy and mutual information instead of variance and covariance as measurements of risk.

Ghosh et al. [11] presented a non-parametric estimate of the pricing kernel, extracted using an information-theoretic approach. This approach delivers smaller out-of-sample pricing errors and a better cross-sectional fit than leading factor models. Batra et al. [12] compared the efficiency of the traditional Mean-Variance (MV) portfolio model proposed by Markowitz with the models that incorporate diverse information theoretic measures such as Shannon entropy, Renyi entropy, Tsallis entropy, and two-parameter Varma entropy. Furthermore, they derived risk-neutral density functions of multi-asset to model the price of European options by incorporating a simple constrained minimization of the Kullback measure of relative information to evaluate the explicit solution of this multi-asset option pricing model [13].

In this paper, we propose a way of integrating non-linear dynamics and dependencies in the study of financial markets using several information entropic measures and some dynamical extensions using mutual information, such as the normalized mutual information measure, relative mutual information rate, and variation of information. We show that this approach leads to better results than other studies using a correlation-based approach on the basis of nine international stock indices which are traded continuously over eighteen years, i.e., (2001–2018).

The paper is divided into four sections. In Section 1, we give the theoretical framework of the information measures and methodology used. In Section 2, we describe financial market daily closing price data of some international stock indices with comparative results. In Section 3, we give a detailed comparative study with the help of tables and figures based on our analysis of the several international stock indices networks. In Section 4, we conclude the paper with a discussion.

2. Theoretical Framework: Entropy Measures

2.1. Shannon Entropy

Shannon [14] introduced the concept of entropy in the communication system. For the given probability distribution $p_i=P(X=x_i)$, $i=1,2...,n$ of a random variable X, the Shannon entropy $H\left(X\right)$ is given by

$$H\left(X\right)=-\sum _{i=1}^n{p}_{i}lo{g}_e{p}_i,0\le p_i\le 1\mathrm{and}\sum _{i=1}^n{p}_i=1.$$

(1)

This entropy has found many applications in various diversified fields specifically as a measure of volatility in financial market [15].

2.2. Joint Entropy

The joint entropy is the uncertainty measure allied with a joint probability distribution of two discrete random variables, say $X=\{x_1,x_2,x_3,...,x_s\}$ and $Y=\{y_1,y_2,y_3,...,y_t\}$, and is defined as

$$H(X,Y)=-\sum _{i=1}^s\sum _{j=1}^t{p}_{ij}lo{g}_e{p}_{ij},$$

where $p_{ij}=p(x_i,y_j)=P(X=x_i,Y=y_j)$ is the joint probability density function of random variables X and Y.

2.3. Conditional Entropy

The conditional entropy, also called the equivocation, of the random variable

$Y=\{y_1,y_2,y_3,...,y_t\}$ given $X=\{x_1,x_2,x_3,...,x_s\}$ is defined as

$$H\left(Y\right|X)=-\sum _{i=1}^s\sum _{j=1}^t{p}_{ij}lo{g}_e{p}_{j|i},$$

where $p_{j|i}=p\left(y_j\right|x_i)=P(Y=y_j|X=x_i)$ is the conditional probability of the random variable Y given $X=x_i$.

The joint and conditional entropy measures follow some properties as given below:

• $H\left(Y\right|X)\le H(Y)$
• $H(X,Y)\le H\left(X\right)+H\left(Y\right)$
• $H(X,Y)=H\left(X\right)+H\left(Y\right|X)=H(Y)+H(X\left|Y\right)$.

2.4. Mutual Information

The mutual information, also called the transinformation, of Y relative to X is defined as:

$$\begin{array}{cc}\hfill I\left(Y\right|X)=& H\left(Y\right)-H\left(Y\right|X)\hfill \\ \hfill =& H\left(Y\right)+H\left(X\right)-H(X,Y).\hfill \end{array}$$

This information measure follows some properties, as given below:

• Non-negative: $I\left(Y\right|X)\ge 0$
• Symmetric: $I\left(Y\right|X)=I(X\left|Y\right)$.

It is easy to see that

$$I\left(Y\right|X)=\sum _{i=1}^s\sum _{j=1}^t{p}_{ij}lo{g}_e\frac{p_{ij}}{p_i{q}_j},$$

where $p_i=P(X=x_i)$ and $q_j=P(Y=y_j)$ are marginal probability distributions of X and Y, respectively; and $p_{ij}=p(x_i,y_j)=P(X=x_i,Y=y_j)$ is the joint probability density function of X and Y.

Next, we can estimate the entropy of a specific stock X from the stock index Y, refer to [16], as

$$H\left(X\right)=I(X,Y)+H\left(X\right|Y);$$

(2)

Further, for Y as independent and X as dependent variables, the total variance of the stock can be subdivided into two parts: the explained sum of squares, i.e., systematic risk and the residual sum of squares, i.e., specific risk.

Next, we summarize some of the extensions of mutual information measure as follows:

2.4.1. Relative Mutual Information

The relative mutual information measure is directly comparable to the coefficient of determination ($R^2$), because both estimate the proportion of variability demonstrated by an independent variable in the dependent variable [16].

$$RM{I}_{XY}=\frac{I(X,Y)}{H\left(Y\right)}.$$

(3)

2.4.2. Normalized Mutual Information

For the two discrete random variables say, X and Y, the normalized mutual information is defined as:

$$NM{I}_{XY}=\frac{I(X,Y)}{\sqrt{H\left(X\right)H\left(Y\right)}}.$$

(4)

In addition to capturing strong linear relationships, this non-linear approach based on mutual information captures the non-linearity found in the volatile market data which could not be captured by the approach based on correlation coefficient [17].

2.4.3. Global Correlation Coefficient

This standardized measure of mutual information can be used as a predictability measure based on the distribution of empirical probability, and is defined as:

$${\lambda }_{XY}=\sqrt{1-e^{-2I(X,Y)}}.$$

(5)

It ranges from 0 to 1 and records the linear as well as the nonlinear dependence between two discrete random variables, say X and Y, and is easily comparable with the linear correlation coefficient [18].

$${\lambda }_{XY}=\left\{\begin{array}{cc}0,\hfill & \mathrm{if}\mathrm{X}\mathrm{contains}\mathrm{no}\mathrm{information}\mathrm{on}\mathrm{Y}\hfill \\ 1,\hfill & \mathrm{if}\mathrm{there}\mathrm{is}\mathrm{a}\mathrm{perfect}\mathrm{relationship}\mathrm{between}\mathrm{the}\mathrm{vectors}X\mathrm{and}Y.\hfill \end{array}\right.$$

(6)

2.5. Variation of Information

This information measure, denoted as $V{I}_{XY}$, is a true estimate of distance between two discrete random variables, say X and Y and, as such it obeys the triangle inequality [19]. Furthermore, it is closely related with mutual information measure and is given as

$$\begin{array}{cc}\hfill V{I}_{XY}=& H\left(X\right)+H\left(Y\right)-2I(X,Y)\hfill \\ \hfill =& H(X,Y)-I(X,Y)\hfill \\ \hfill =& H\left(X\right|Y)+H(Y\left|X\right).\hfill \end{array}$$

(7)

It is easy to see that

$$V{I}_{XY}=\{\begin{array}{cc}0,\hfill & \mathrm{when}\mathrm{X}\mathrm{is}\mathrm{equal}\mathrm{to}\mathrm{Y}\hfill \\ <H(X,Y),\hfill & \mathrm{when}\mathrm{X}\mathrm{and}\mathrm{Y}\mathrm{are}\mathrm{dependent}\hfill \\ H(X,Y),\hfill & \mathrm{when}\mathrm{X}\mathrm{and}\mathrm{Y}\mathrm{are}\mathrm{independent},\hfill \end{array}$$

(8)

where $H\left(X\right)$ is the entropy of the discrete random variable $X=\{x_1,x_2,x_3,...,x_s\}$ and $I(X,Y)$ is mutual information between two discrete random variables $X=\{x_1,x_2,x_3,...,x_s\}$ and $Y=\{y_1,y_2,y_3,...,y_t\}$ and $H(X,Y)$ is the joint entropy of X and Y.

3. Data and Result

The main objective of this paper is to show that information theoretic measures present a decent solution to the problem of dependence in the financial series data. For this purpose, we considered 14 time series comprising the daily closing price of the international stock indices and their selective stocks which were traded continuously between 1 January 2001 and 31 December 2018 (about 4433 observations in each time series).

To apply entropic measures in operation and to find their properties, we obtained daily closing price data over eighteen years of international stock market indices, namely IBOVESPA (Brazil), Hang Seng (Hong Kong), SSE Composite (China), Dow Jones Industrial Average (United States), CAC 40 (France), DAX (France), NASDAQ (United States), Nifty 50 (India) and BSE sensex (India), accessed on 1 August 2020 from in.finance.yahoo.com, the free financial data online platform. Furthermore, we make a comparison of two Indian market indices namely, NIFTY 50 and S&P BSE sensex with their common stocks. During the complete selection process, daily closing price data filtered to select stocks listed in their respective indices and as a result due to inadequate data, five stocks were selected from the study.

Our main emphasis is on determining the dependence level between each stock and its stock index, i.e., to select a stock which is more dependent on its relative index and this has been estimated by the information theoretic measures. Further, to compare two different indices with their stocks and measure their level of dependence, the concept of mutual information is used as analogous to covariance and normalized mutual information is calculated akin to the Pearson’s coefficient of correlation.

4. Tables and Figures

Figure 1 presents the allocation of the aforementioned Indian stock indices with their selected stocks. Figure 2 gives the details of the distribution of the aforementioned international stock indices; and Figure 3 gives the nature of indices with their stocks. Next, Figure 4, Figure 5, Figure 6 and Figure 7 represent the visual comparison of information and statistical measures. Furthermore, in Figure 4 and Figure 5 if we increases bin counts, entropy and TSS measures become inversely symmetric. We have presented equivalence between statistical measures and information theoretic measures, refer to Table 1. From the data given in Table 2, Table 3, Table 4 and Table 5, by using statistical software R (RStudio© 2021.09.1, 2009–2021 RStudio, Build 372, PBC, 250 Northern Ave, Boston, MA 02210), we present four correlation matrix plots of above-mentioned international indices with their stocks, refer to Figure 8 and Figure 9.

Figure 1. Distribution of Indian market indices with their stocks.

Figure 2. Distribution of International market indices.

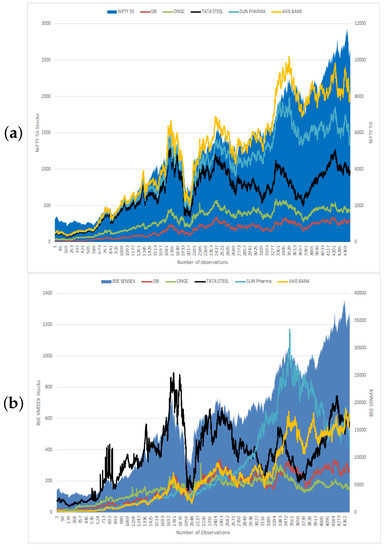
Figure 3. Nature of indices with their stocks. (a) NIFTY 50. (b) BSE SENSEX.

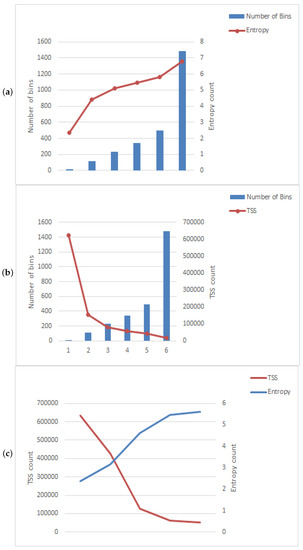
Figure 4. Comparison of Shannon entropy and Total sum of square of BSE sensex stocks. (a) Entropy with bins. (b) TSS with bins. (c) Entropy and TSS.

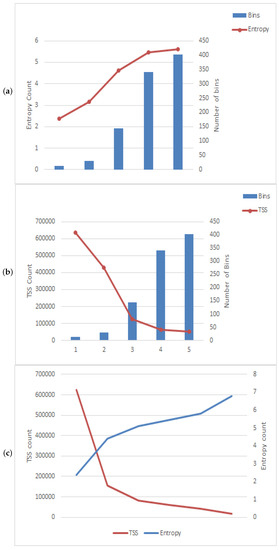
Figure 5. Comparison of Shannon entropy and Total sum of square of NIFTY 50 stocks. (a) Entropy with bins. (b) TSS with bins. (c) Entropy and TSS.

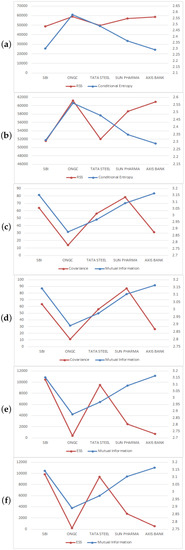
Figure 6. Comparison of information and statistical meaures of NIFTY 50 and BSE sensex stocks. (a) Conditional entropy and RSS with Nifty stocks. (b) Conditional entropy and RSS with BSE sensex stocks. (c) Mutual information and covariance with Nifty stocks. (d) Mutual information and covariance with BSE sensex stocks. (e) Mutual information and ESS with Nifty stocks. (f) Mutual information and ESS with BSE sensex stocks.

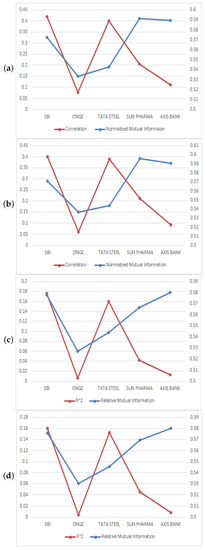
Figure 7. Comparison of information and statistical meaures of NIFTY 50 and BSE sensex stocks. (a) Correlation and Normalized mutual information with Nifty stocks. (b) Correlation and Normalized mutual information with BSE sensex stocks. (c) Relative mutual information and R2 with Nifty stocks. (d) Relative mutual information and R² with BSE sensex stocks.

Table 1. Equivalences between statistical measures and information theoretic measures.

Information Theoretical Measures	Statistical Measures
$H\left(Y\right)$ Entropy	(TSS) Total sum of squares
$H\left(Y\right|X)$ Conditional entropy	(RSS) Residual sum of squares
I(X,Y) Mutual information	cov(X,Y) Covariance or
	(ESS) Explained sum of squares
$NM{I}_{X,Y}$ Normalized mutual information	$R_{XY}$ Correlation
$RM{I}_{XY}$ Relative mutual information	$R_{XY}^2$ Coefficient of determination

Table 2. Correlation between NIFTY 50 index and its stocks with $R^2$ = 0.96765.

	NIFTY 50	SBI	ONGC	TATA STEEL	SUN PHARMA	AXIS BANK
NIFTY 50	1
SBI	0.91277	1
ONGC	0.75195	0.87759	1
TATA STEEL	0.62706	0.70924	0.72980	1
SUN PHARMA	0.84981	0.74144	0.63281	0.24771	1
AXIS BANK	0.96812	0.88938	0.68445	0.49662	0.90294	1

Table 3. Correlation between BSE sensex index and its stocks with $R^2$ = 0.96035.

	BSE Sensex	SBI	ONGC	TATA STEEL	SUN Pharma	AXIS BANK
BSE sensex	1
SBI	0.90630	1
ONGC	0.77082	0.85210	1
TATA STEEL	0.61634	0.69028	0.71104	1
SUN Pharma	0.84751	0.74785	0.63540	0.23767	1
AXIS BANK	0.96070	0.88372	0.67863	0.48074	0.90138	1

Table 4. Correlation between International Indices A.

	NIFTY 50	BSE Sensex	IBOVESPA	HANG SENG	SSE COMPOSITE
NIFTY 50	1
BSE sensex	0.99312	1
IBOVESPA	0.84651	0.85487	1
HANG SENG	0.90201	0.91444	0.91677	1
SSE COMPOSITE	0.62997	0.62134	0.66574	0.72005	1

Table 5. Correlation between International Indices B.

	DOW JONES	CAC 40	DAX	NASDAQ
DOW JONES	1
CAC 40	0.51827	1
DAX	0.94938	0.57404	1
NASDAQ	0.99037	0.46469	0.94892	1

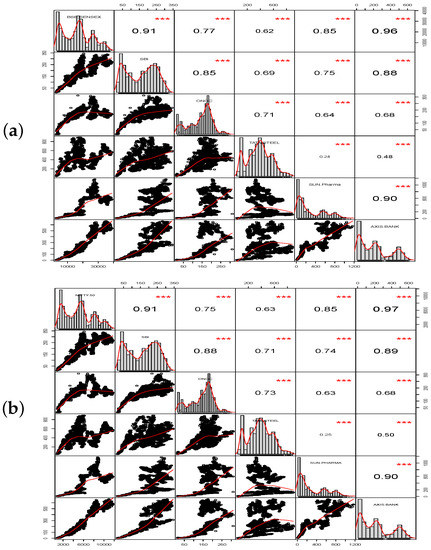
Figure 8. Correlation matrix plot of BSE sensex and Nifty 50 with their stocks SBI, ONGC, Tata Steel, Sun Pharma, and Axis Bank. (a) BSE sensex. (b) NIFTY 50. The distribution of each stock/index is shown on the diagonal; on the lower diagonal, the bi-variate scatter plots with the fitted higher order degree polynomial are shown and on the upper diagonal, the correlation value plus the significance level (p-values: 0.001) as stars (“***”).

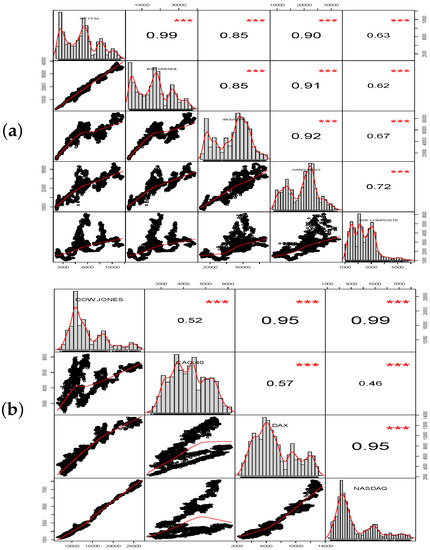
Figure 9. Correlation matrix plot of indices: Nifty 50 with BSE sensex, IBOVESPA, Hang Seng, and SSE Composite and Dow Jones with CAC 40, DAX, and NASDAQ. (a) Nifty 50. (b) Dow Jones. The distribution of each stock/index is shown on the diagonal; on the lower diagonal, the bi-variate scatter plots with the fitted higher order degree polynomial are shown and on the upper diagonal, the correlation value plus the significance level (p-values: 0.001) as stars (“***”).

We discussed the choice of bin counts for the nature of calculation of statistical and information theoretic measures, see Table 6, Table 7, Table 8, Table 9, Table 10 and Table 11. In general, the count of bins should be selected on the basis of availability of the number of observations of time series data. In Table 6 and Table 7 we show a count of total number of bins for the indices NIFTY 50 (342 bins) and BSE sensex (341 bins), respetively; we come to a conclusion that BSE sensex is more uncertain stock index as compared to NIFTY 50 and furthermore, Axis bank is the underlying stock which is more dependent compared with other stocks.

Table 6. NIFTY 50 and its stocks.

	Entropy	Conditional Entropy	RSS	Mutual Information	Covariance	TSS/ESS	Normalized Mutual Informaion	Correlation	Relative Mutual Information	${\mathit{R}}^2$	Global Correlation Coefficient	Beta	Joint Entropy	Variation of Information
Number of Bins: 13
NIFTY 50	2.36540					624,968.00000
SBI	2.45800	1.19399	525,211.40000	1.17139	14,421.80000	99,756.55000	0.48580	0.39952	0.49522	0.15962	0.95075	0.27691	3.65204	1.57500
ONGC	2.25030	1.27108	611,529.30000	1.09430	9615.42000	13,438.65000	0.47432	0.14664	0.46263	0.02150	0.94229	0.18463	3.52135	1.55790
TATA STEEL	2.31830	1.55828	271,045.30000	0.80710	39,897.10000	353,922.70000	0.34466	0.75253	0.34121	0.56631	0.89495	0.76606	3.87655	1.75198
SUN PHARMA	2.01200	1.24765	311,598.80000	1.11772	70,651.40000	313,369.20000	0.51235	0.70811	0.47253	0.50142	0.94501	1.35658	3.25969	1.46354
AXIS BANK	2.24080	0.95023	311,899.70000	1.41515	50,735.60000	313,068.3	0.61468	0.70777	0.59827	0.50093	0.97005	0.97417	3.19106	1.33263
Number of Bins: 114
NIFTY 50	4.40485					155,446.00000
SBI	4.51377	2.36359	109,584.07000	2.04125	602.40700	45,861.93000	0.45778	0.54317	0.45222	0.29503	0.99153	0.43791	6.87737	2.19911
ONGC	4.27008	2.54428	154,842.61420	1.86057	90.22120	603.38580	0.42900	0.06230	0.43572	0.00388	0.98782	0.06559	6.81436	2.22571
TATA STEEL	4.42332	2.63715	117,870.67000	1.76769	543.83200	37,575.33000	0.40046	0.49165	0.39963	0.24172	0.98531	0.39533	7.06047	2.30060
SUN PHARMA	4.01116	2.17026	141,939.42000	2.23459	756.63700	13,506.58000	0.53161	0.29476	0.55709	0.08688	0.99425	0.55003	6.18142	1.98666
AXIS BANK	4.22039	2.13511	152,160.01800	2.26973	324.84100	3285.98200	0.52642	0.14539	0.53780	0.02113	0.99464	0.23614	6.35551	2.02133
Number of Bins: 234
NIFTY 50	5.09440					82,294.00000
SBI	5.19725	2.41142	66,285.66000	2.68298	133.91900	16,008.34000	0.52141	0.44105	0.52665	0.19452	0.99766	0.37916	7.60868	2.21939
ONGC	4.95544	2.66188	81,787.85930	2.43251	29.42920	506.14070	0.48413	0.07842	0.47748	0.00615	0.99613	0.08332	7.61733	2.27701
TATA STEEL	5.12072	1.93975	68,218.60000	2.47435	117.95700	14,075.40000	0.48445	0.41356	0.48569	0.17103	0.99644	0.33397	7.06047	2.14152
SUN PHARMA	4.64187	2.37953	78,821.26900	2.71487	163.41200	3472.73100	0.55828	0.20542	0.53291	0.04219	0.99780	0.46267	7.02140	2.07521
AXIS BANK	4.91521	2.33849	80,765.57500	2.75591	76.24460	1528.42500	0.55074	0.13628	0.54096	0.01857	0.99797	0.21587	7.25371	2.12080
Number of Bins: 342
NIFTY 50	5.45397					59,342.00000
SBI	5.56269	2.30139	48,867.00000	3.15258	63.97360	10,474.90000	0.57235	0.42014	0.57803	0.17652	0.99908	0.36761	7.86408	2.17059
ONGC	5.32691	2.57858	58,991.00000	2.87539	13.99120	350.64500	0.53346	0.07687	0.52721	0.00591	0.99840	0.08040	7.90540	2.24278
TATA STEEL	5.48573	2.48593	49,847.00000	2.96804	56.51610	9495.09000	0.54262	0.40001	0.54419	0.16001	0.99867	0.32476	7.97166	2.23687
SUN PHARMA	5.00516	2.36412	56,861.00000	3.08985	78.31970	2480.87000	0.59138	0.20447	0.56653	0.04181	0.99896	0.45005	7.36928	2.06867
AXIS BANK	5.27565	2.29104	58,604.00000	3.16292	31.07630	738.05400	0.58965	0.11152	0.57993	0.01244	0.99910	0.17858	7.56670	2.09851
Number of Bins: 494
NIFTY 50	5.80256					42,468.00000
SBI	5.90688	2.14323	35,651.97000	3.65933	31.17240	6816.03000	0.62504	0.40062	0.61950	0.16049	0.99966	0.36187	8.05011	2.09542
ONGC	5.67248	2.42322	42,191.98000	3.37934	7.23935	276.02000	0.58902	0.08061	0.59574	0.00649	0.99941	0.08404	8.09570	2.17172
TATA STEEL	5.83876	2.29205	35,612.20000	3.51050	27.99800	6855.81000	0.60311	0.40178	0.60124	0.16143	0.99955	0.32502	8.13082	2.14949
SUN PHARMA	5.32343	2.31891	41,213.97000	3.48364	35.53140	1254.03000	0.62679	0.17183	0.65439	0.02952	0.99952	0.41248	7.64235	2.03929
AXIS BANK	5.61646	2.51435	41,923.79000	3.51050	15.80730	544.21300	0.61493	0.11320	0.62503	0.01281	0.99955	0.18350	8.13082	2.14949
Number of Bins: 1482
NIFTY 50	6.77728					17,490.00000
SBI	6.88017	1.43809	15,580.71000	5.33919	3.61783	1909.30000	0.78189	0.33040	0.77602	0.10916	0.99998	0.30635	8.31826	1.72599
ONGC	6.66510	1.67938	17,431.45000	5.09790	0.70358	58.55070	0.75850	0.05785	0.76486	0.00334	0.99998	0.05958	8.34448	1.80182
TATA STEEL	6.81970	1.52493	15,687.37000	5.25235	3.19311	1802.63000	0.77257	0.32103	0.77017	0.10306	0.99998	0.27038	8.34463	1.75848
SUN PHARMA	6.27082	1.85394	17,199.72000	4.92333	3.85145	290.28400	0.75521	0.12882	0.78511	0.01659	0.99997	0.32613	8.12477	1.78925
AXIS BANK	6.58587	1.63262	17,377.21000	5.14466	1.50709	112.79300	0.77005	0.08030	0.78116	0.00644	0.99998	0.12762	8.21849	1.75323

Table 7. BSE sensex and its stocks.

	Entropy	Conditional Entropy	RSS	Mutual Information	Covariance	TSS/ESS	Normalized Mutual Information	Correlation	Relative Mutual Information	${\mathit{R}}^2$	Global Correlation Coefficient	Beta	Joint Entropy	Variation of Information
Number of Bins: 13
BSE sensex	2.36610					63,4618.00000
SBI	2.45447	1.21135	507,692.90000	1.15475	16,513.00000	126,925.10000	0.47917	0.44721	0.48803	0.20000	0.94900	0.31224	3.66582	1.58463
ONGC	2.24806	1.26131	617,196.60000	1.10479	10,970.17000	17,421.43000	0.47902	0.16568	0.46692	0.02745	0.94353	0.20743	3.50937	1.55067
TATA STEEL	2.32674	1.56586	254,483.20000	0.80024	40,779.83000	380,134.80000	0.34105	0.77394	0.33821	0.59899	0.89342	0.77110	3.89260	1.75851
SUN PHARMA	2.00817	1.27706	332,931.90000	1.08904	69,300.58000	301,686.10000	0.49960	0.68947	0.46026	0.47538	0.94166	1.31040	3.28523	1.48195
AXIS BANK	2.22799	1.02924	329,834.50000	1.33686	50,682.83000	304,783.50000	0.58225	0.69301	0.56500	0.48026	0.96488	0.95836	3.25723	1.38577
Number of Bins: 31
BSE sensex	3.15224					427,756.00000
SBI	3.28062	1.68710	299,283.30000	1.46514	5517.76700	128,472.70000	0.45560	0.54800	0.46479	0.30034	0.97294	0.38698	4.96772	1.87151
ONGC	3.04249	1.75543	399,161.80000	1.39681	4018.90000	28,594.25000	0.45103	0.25854	0.44311	0.06684	0.96891	0.28185	4.79792	1.84421
TATA STEEL	3.15385	2.01077	306,297.50000	1.14147	6719.06700	121,458.50000	0.36202	0.53286	0.36211	0.28394	0.94763	0.47123	5.16463	2.00578
SUN PHARMA	2.79928	1.57570	197,588.50000	1.57654	18,222.33000	230,167.50000	0.53072	0.73354	0.50013	0.53808	0.97840	1.27799	4.37498	1.67285
AXIS BANK	3.04681	1.42946	203,804.30000	1.72278	12,906.50000	223,951.70000	0.55590	0.72356	0.54652	0.52355	0.98392	0.90517	4.47628	1.65936
Number of Bins: 143
BSE sensex	4.62278					127,290.00000
SBI	4.72456	2.42919	101,753.60000	2.19359	347.06340	25,536.36000	0.46937	0.44790	0.47451	0.20061	0.99376	0.38717	7.15375	2.22714
ONGC	4.49114	2.59902	125,777.00000	2.02375	101.78170	1513.03200	0.44414	0.10902	0.43777	0.01188	0.99122	0.11354	7.09017	2.25087
TATA STEEL	4.65221	2.64883	98,543.81000	1.97394	343.30990	28,746.19000	0.42565	0.47521	0.42700	0.22583	0.99030	0.38298	7.30105	2.30805
SUN PHARMA	4.19777	2.23328	118,472.40000	2.38949	472.82390	8817.57300	0.54243	0.26319	0.51689	0.06927	0.99578	0.52746	6.43106	2.01036
AXIS BANK	4.43235	2.24883	124,754.50000	2.37395	207.80280	2535.48800	0.52444	0.14113	0.51353	0.01991	0.99565	0.23181	6.68118	2.07538
Number of Bins: 341
BSE sensex	5.45260					61,410.00000
SBI	5.54762	2.31164	51,572.05000	3.14096	63.57059	9837.95000	0.57109	0.40025	0.57604	0.16020	0.99906	0.35196	7.85927	2.17216
ONGC	5.31997	2.56153	61,220.07650	2.89107	11.29412	189.92400	0.53678	0.06097	0.53021	0.00371	0.99845	0.06253	7.88151	2.23393
TATA STEEL	5.49089	2.47744	52,035.55100	2.97515	55.82941	9374.45000	0.54373	0.39070	0.54563	0.15265	0.99869	0.30910	7.96834	2.23454
SUN PHARMA	4.98351	2.34789	58,636.81300	3.10471	86.90882	2773.19000	0.59559	0.21250	0.56939	0.04515	0.99899	0.48117	7.33140	2.05589
AXIS BANK	5.26056	2.28971	60,892.79310	3.16289	26.05882	517.20700	0.59056	0.09177	0.58006	0.00842	0.99910	0.14427	7.55027	2.09460
Number of Bins: 403
BSE sensex	5.61651					51,504.00000
SBI	5.70792	2.25205	43,313.94000	3.36446	46.60945	8190.06000	0.59421	0.39877	0.59903	0.15901	0.99940	0.36379	7.95997	2.14371
ONGC	5.47974	2.49112	51,260.09620	3.12538	9.12437	243.90400	0.56336	0.06881	0.55646	0.00473	0.99903	0.07121	7.97086	2.20124
TATA STEEL	5.65151	2.40696	42,810.67900	3.20955	42.28607	8693.32000	0.56967	0.41083	0.57144	0.16878	0.99918	0.33005	8.05847	2.20202
SUN PHARMA	5.14687	2.32651	49,158.15900	3.28999	60.63433	2345.84000	0.61191	0.21341	0.58577	0.04554	0.99930	0.47326	7.47339	2.04533
AXIS BANK	5.41261	2.28429	51,126.86590	3.33221	17.46517	377.13400	0.60436	0.08557	0.59328	0.00732	0.99936	0.13631	7.69691	2.08918

Table 8. International market indices A.

	Entropy	Mutual Information	Correlation	Joint Entropy	Conditional Entropy	Relative Mutual Information
Number of Bins: 31
NIFTY 50	3.15029
BSE SNESEX	3.15202	2.11485	0.98778	4.18746	1.03544	0.67095
IBOVESPA	3.22630	1.51731	0.07871	4.85927	1.63298	0.47029
HANG SENG	3.20100	1.37211	−0.12990	4.97918	1.77818	0.42864
SSE COMPOSITE	2.95250	1.11249	0.44629	4.99030	2.03779	0.37679
Number of Bins: 143
NIFTY 50	4.61974
BSE SNESEX	4.62246	2.69859	0.95322	6.54361	1.92115	0.58379
IBOVESPA	4.71728	2.15750	0.10364	7.17952	2.46224	0.45736
HANG SENG	4.70464	2.05491	−0.10610	7.26947	2.56483	0.43678
SSE COMPOSITE	4.44981	1.89907	0.38445	7.17049	2.72067	0.42677
Number of Bins: 341
NIFTY 50	5.45048
BSE SNESEX	5.45222	3.37328	0.91252	7.52942	2.07720	0.61869
IBOVESPA	5.56159	3.06538	0.08978	7.94668	2.38509	0.55117
HANG SENG	5.54328	2.98039	−0.08060	8.01337	2.47009	0.53765
SSE COMPOSITE	5.28904	2.78918	0.34756	7.95034	2.66130	0.52735
Number of Bins: 403
NIFTY 50	5.60935
BSE SNESEX	5.61617	3.55583	0.9062	7.66968	2.05351	0.63314
IBOVESPA	5.72184	3.29735	0.08618	8.03383	2.31199	0.57627
HANG SENG	5.70409	3.20949	−0.08090	8.10395	2.39985	0.56266
SSE COMPOSITE	5.44616	3.02750	0.33483	8.02801	2.58184	0.55589

Table 9. International market indices B.

	Entropy	Mutual Information	Correlation	Joint Entropy	Conditional Entropy	Relative Mutual Information
Number of bins: 16
DOW JONES	2.39734
CAC 40	2.59322	0.74548	0.24985	4.24508	1.65186	0.28747
DAX	2.61923	1.23358	0.53358	3.78299	1.16376	0.47097
NASDAQ	2.35936	1.58996	0.76201	3.16674	0.80737	0.67389
Number of bins: 283
DOW JONES	5.13384
CAC 40	5.41487	2.42453	0.25323	8.12418	2.70930	0.44775
DAX	5.43041	2.63143	0.35362	7.93282	2.50241	0.48457
NASDAQ	5.14322	2.87793	0.58449	7.39913	2.25591	0.55955
Number of bins: 556
DOW JONES	5.79039
CAC 40	6.06928	3.52548	0.22600	8.33420	2.26491	0.58087
DAX	6.08881	3.61385	0.32142	8.26536	2.17654	0.59352
NASDAQ	5.79907	3.58918	0.55368	8.00029	2.20121	0.61892
Number of bins: 1132
DOW JONES	6.41815
CAC 40	6.69865	4.72292	0.19908	8.39388	1.69523	0.70505
DAX	6.71238	4.75384	0.28448	8.37669	1.66431	0.70821
NASDAQ	6.42275	4.54329	0.51441	8.29761	1.87486	0.70737

Table 10. Comparison of Shannon entropy and Total sum of square of BSE Sensex stocks.

	BSE SENSEX
Number of Bins	13	31	143	341	403
Entropy	2.36610	3.15224	4.62278	5.45260	5.61651
TSS	634,618.00000	427,756.00000	127,290.00000	61,410.00000	51,504.00000

Table 11. Comparison of Shannon entropy and Total sum of square of NIFTY 50 stocks.

	NIFTY 50
Number of Bins	13	114	234	342	494	1482
Entropy	2.36539	4.40485	5.09440	5.45397	5.80256	6.77728
TSS	624,968.00000	155,446.00000	82,294.00000	59,342.00000	42,468.00000	17,490.00000

In other words, by observing the Axis bank stock, more information about NIFTY 50 and BSE sensex can be obtained. Furthermore, by observing ONGC stock, remaining uncertainty about the aforementioned indices is greater than other stocks. We have also come to the conclusion that the measure of global correlation coefficient can be useful if a lower count of bins are considered, otherwise this measure gives a similar output to all stock variables. Thus, in this case, the large count of data bins would not be a reasonable choice for comparative analysis of information theoretic measures with statistical measures, as even in very small change in the prices no depth-patterns are to be found. The coefficient of correlation is a long-standing estimator of the degree of statistical dependence; however mutual information has advantages over it. Furthermore, it is evident from from Table 7 and Table 8 that the Shannon entropy, mutual information and the conditional entropy perform well in accordance with the systematic risk and the specific risk derived through the linear market model. Furthermore, from Table 8, as per maximum count of bins (i.e., 403), the index BSE sensex can be used as the appropriate variable for the dependency of the index NIFTY 50.

Furthermore, studies based on other stock market indices and foreign exchange markets can also be carried out to further examine the effectiveness of this approach. One cannot directly visualize dependency of a stock on its index using technical analysis; therefore the investor has to work on theoretical aspects too. In Table 9, as per maximum count of bins (i.e., 1132), the international index DAX can be used as the appropriate variable for the dependency of DOW Jones in comparison of other indices, such as CAC 40 and NASDAQ.

5. Discussion and Conclusions

5.1. Discussion

We find that the information measures such as mutual information is an ideal way to expand the financial networks of stock market indices based on statistical measures, while the measure of variation of information presents a different side of the markets but produces networks with troubling characteristics. The proposed methodology is sensitive to the choice of data bin counts in which the daily closing prices of market data are separated and require a large sample size. Furthermore, the comparison of entropy measures with statistical measures of dependent stock indices, such as Shannon entropy vs. variance of a stock, conditional entropy vs. residual sum of squares, coefficient of determination vs. the relative mutual information rate, and correlation vs. normalized mutual information measures indicate the further existence of non-linear relationships that are not identified by the statistical correlation measure and hence present a different aspect of market analysis.

Information measures such as Shannon entropy and one parametric entropy, such as Renyi and Tsallis entropies, were studied extensively by many researchers for analyzing volatility in financial markets. However, this concept can still be explored further using various two parametric entropy measures. The non-linear fluctuations in a variety of markets (i.e., stock, future, currency, commodity, and cryptocurrency) require powerful tools such as entropy for extracting information from the market that is otherwise not visible in standard statistical methods. Further, we can extend the information theoretic approach used in this paper to highly volatile financial markets.

5.2. Conclusions

This paper uses information theoretic concepts such as entropy, conditional entropy, and mutual information and their dynamic extensions to analyze the statistical dependence of the financial market. We checked some equivalences between information theoretic measures and statistical measures normally employed to capture the randomness in financial time series. This approach has the ability to check the non-linear dependence of market data without any specific probability distributions. We used different international stock indices to address our problem. Mutual information and conditional entropy were relatively efficient compared to the measures of statistical dependence. From the results obtained, it is inferred that the information theoretic approach observes the dependency effectively and can be considered to be an efficient approach to study financial markets. In addition, these measures can provide some additional information for financial market investors.