Abstract
In this work, we present a compact “adaptive downsampling” method that mitigates the nonlinearity problems associated with FPGA-based TDCs that utilize delay lines. Additionally, this generic method allows for trade-offs between resolution, linearity, and resource utilization. Since nonlinearity is one of the predominant issues regarding delay lines in FPGA-based TDCs, combined with the fact that delay lines are utilized for a wide range of TDC architectures (not limited to the delay-line TDC), other implementations (e.g., Vernier or wave union TDCs), also in different FPGA devices, can directly benefit from the proposed adaptive method, with no need for either custom routing or complex tuning of the converter. Furthermore, implementation-related challenges regarding clock skew, measurement uncertainty, and the placement of the TDC are discussed and we also propose an experimental setup that utilizes only FPGA resources in order to characterize the converter. Although the TDC in this work was implemented in a Xilinx Virtex-6 device and was characterized under different operational modes, we successfully optimized the converter’s nonlinearity and resource utilization while retaining single-shot precision. The best performing (in terms of linearity) implementation reached and values of 0.30 LSB and 0.45 LSB, respectively, and the single-shot precision () was 9.0 ps.
1. Introduction
Time measurement applications and methods have been and continue to be the subject of study in various fields of science and engineering and deal with the precise measurement of time events. Such precision time measurements are of the highest priority in applications such as nuclear and particle physics [1,2], biomedical systems [3], digital phase-locked loops [4,5], positron emission tomography [6,7], LiDAR [8], radio-frequency (RF) pulse detection [9], fluorescence lifetime measurements [10], time-of-flight measurements [11], time-over-threshold measurements [12], etc.
Time-to-Digital Converters (TDCs) are the fundamental building blocks that convert time-encoded data into digital information and feature several attractive characteristics. For instance, TDCs take advantage of technology scaling [13], since the ever-decreasing gate delays of transistors enable TDCs, and are implemented with newer CMOS processes to exhibit better resolution. As a result, the increasing TDC resolution paired with reasonably low power consumption calls for the time-domain processing of continuous signals [14,15] as an alternative to the traditional approach using voltage-domain processing.
TDCs can be implemented by employing both analog and digital architectures. However, analog designs of such converters include an ADC, and thus suffer from all the downfalls of analog circuits in deep sub-micron technologies such as lower SNR due to lower supply voltages stemming from technology scaling. Therefore, TDCs with no analog processing parts are the only way to avoid the aforementioned issues and take advantage of the benefits of digital circuits [13].
TDCs have been designed with many variations both in ASIC and FPGA forms. The former takes full advantage of the specialization that is possible with custom designs, and thus systems with very strict requirements are feasible, such as the TDCs reported in [16,17] with precision down to about 1 ps, whereas other works have reported measurement precision even below the picosecond boundary [5]. On the other hand, ASIC-based-TDCs also suffer from often long development times and costs, whereas FPGA-based-TDCs offer a good alternative and have attracted considerable focus due to their significant benefits such as fast prototyping and deployment, flexibility, as well as design portability compared to ASICs. FPGAs can also offer financial benefits since these devices are characterized by reasonably low costs for small to medium product volumes, and can thus be employed for addressing niche markets instead of massive ones. In effect, several FPGA-TDC architectures have been proposed in the literature [6,12,18,19,20,21,22,23,24,25,26,27].
The most important downside, however, is the predetermined architecture of FPGAs that cannot be optimized on a transistor level and thus results in relatively high nonlinearity regarding TDCs.
TDC architectures range from the traditional Tapped Delay Line (TDL) [18] to Vernier interpolation methods [19]. Furthermore, successive approximation methods [28,29] are also very popular in analog-to-digital converters (ADCs); multi-edge TDCs [23] have been employed to further improve their performance, whereas innovative methods such as wave union TDCs [21] aim to improve resolution at the expense of complex encoding schemes and larger area requirements.
The common denominator of many of the aforementioned TDC implementations is the use of delay lines as an integral component. In the case of FPGA-based implementations, delay lines are usually paired with nonlinearity, which is an inherent characteristic of their architecture. It could be argued that delay lines constitute the status quo for several TDC designs since these components can be employed to generate delayed instances of an arbitrary signal, which is the basis for constructing a TDC. Regarding FPGA-based TDCs, a delay line is usually employed when the implementation is based either on the traditional delay-line method [6,12,18,20,30] (which is also the most popular architecture among FPGA-based TDCs [31]) or on other more sophisticated techniques, for instance, Vernier [19,32,33], wave union [21,24,25], or multi-edge TDCs [23]. This indicates that the proposed methods can potentially be applicable to a multitude of FPGA-based TDC designs that employ delay lines, without the need for either custom routing or complex fine-tuning of the converter.
In the context of this work, we propose methods that mitigate issues regarding the nonlinearity of FPGA-based delay lines; discuss the trade-offs associated with the resolution, area, and linearity of the converter; and show, through a comparison with the results reported in the literature, that the proposed methods enable the improvement of the converter’s linearity by reducing the resource utilization. Furthermore, we propose a procedure in order to characterize the converter by employing only FPGA resources, thus alleviating the need for external delay generators, random pulse generators, or other complex characterization schemes. Even though the TDC implementations of this work build upon the methods in [20], we show that our TDC configurations, which utilize the downsampling method paired with heterogenous sampling, achieve lower resource usage and even superior linearity characteristics compared to [20] and other similar works reported in the literature.
The rest of the paper is organized as follows. In Section 2.1 and Section 2.2 the implementation-related challenges of the FPGA-based TDC design are outlined and in Section 2.3, the details of the proposed adaptive downsampling method are described in detail. Section 3 presents the experimental setup and discusses the results of the TDC’s characterization in various operational modes. The discussion of the proposed methods is given in Section 4 and Section 5 concludes the paper.
2. FPGA-TDC Methodology
The main target of any TDC system is the precise measurement of the arrival times of two pulses (e.g., START and STOP). The principle of operation with delay-line TDCs is quite straightforward and is illustrated in Figure 1. The tapped delay-line cell shown in Figure 1, comprises delay elements (implemented with CARRY4 primitives), sampling elements (flip-flops), and a ones-counter. The START signal drives the delay elements in a chain arrangement, whereas the STOP signal is used to drive the clock input of flip-flops (FFs) that sample the state of the delay line. Moreover, as the START input signal is asynchronous and often leads to setup and hold violations, we mitigated the metastability with a second line of FFs that added more robustness to the design. Although this design required equal delays for all delay elements in order to achieve maximum accuracy, these components also determined the resolution of the converter. In ASIC implementations, this design goal can be optimized by constructing a homogenous delay line. On the other hand, FPGAs are characterized by a predetermined architecture with configurable logic blocks (CLBs) that impose high nonlinearity as a result of unequal delay elements. In the following parts of this section, the methods employed for designing a TDL-based TDC system in FPGA devices are proposed and the means to compensate for their inherent nonlinearity are discussed.
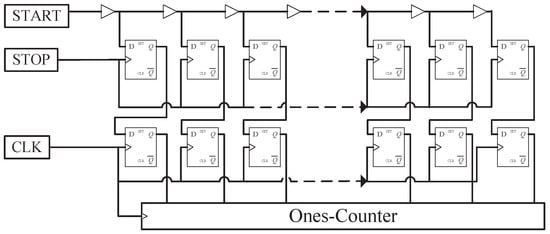
Figure 1.
Tapped Delay-Line Cell.
2.1. Tapped Delay-Line Architecture
The design process regarding TDL implementations began with the identification of the elements that would enable picosecond-level resolution and implement the delay elements in the corresponding chain of the tapped delay line. FPGAs feature fast carry chains that can be used as delay lines for precise time measurement. Specifically, the FPGA used in the current work (Xilinx Virtex-6) had CARRY4 primitives that are usually employed for the implementation of fast adders. This arithmetic component included four sum outputs and four carry outputs, referred to in this paper as S[3:0] and C[3:0], respectively (Figure 2). These elements were arranged vertically inside the 12 clock regions of the FGPA, with 40 vertical primitives in each clock region. Documentation regarding the CARRY4 primitive employed to construct the delay line and its implications can be found in [34]. As noted in the work of Machado et al. [31], CARRY primitives are the most used delay elements regarding FPGA-based delay lines.
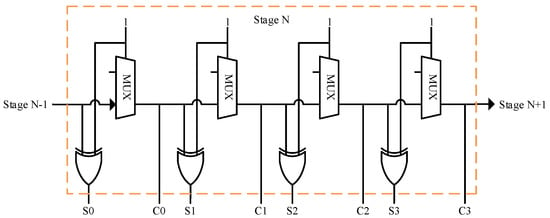
Figure 2.
CARRY4 primitive simplified schematic.
2.1.1. TDL Cell
FPGAs are divided into configurable logic blocks (CLBs), where each of these units of logic resources incorporates (for the FPGA used in this work) four look-up tables (LUTs), eight FFs, and one CARRY4 primitive, among others. In order to measure the time stamp of the delay line (i.e., the outputs of the CARRY4 primitives used for the delay-line implementation), we utilized the FFs that were located inside the same CLB with the corresponding CARRY4 primitives. Out of the eight FFs inside each CLB, only four can be driven by the CARRY4 cell, and thus the maximum number of usable outputs from the primitive is limited to four. If FFs from neighboring CLBs are used to sample the delay line, the signal skew would be intolerable and would significantly disturb the measurement and downgrade the performance of the converter.
Figure 2 illustrates a simplified schematic of the CARRY4 primitive, which consists of multiplexers (MUXs) and XOR gates. In order to implement the CARRY4 primitive in a delay-line configuration, the MUX select input is always activated so that the START signal is propagated through the primitive and, consequently, the delay line.
In Section 2.3, different sampling patterns are proposed for the construction of the delay line. The sampling pattern is defined as the combination of four or fewer outputs from the CARRY4 primitives that are used to construct a delay line. Regarding the patterns mentioned in this paper (e.g., CCCC), the most significant bit (i.e., the last output of the CARRY4 primitive) corresponds to the left-most bit and the least significant bit corresponds to the right-most bit. A downsampling pattern corresponds to a case where less than four outputs are used. As discussed later, the CCCC and SSSS patterns and their counterparts, CNCN and SNSN, and NCCC and NSSS, offered useful alternatives in cases where maximum resolution, minimum area, or minimum nonlinearity were desired. C and S denote the outputs of the CARRY4 primitive and N denotes an unused output. In addition, it should be noted that the LSB duration () varied according to the selected pattern, and thus the equivalent delays shown in Figure 1 also varied. The LSB duration is defined as the time difference between consecutive taps in the delay line. Furthermore, in order to implement a specific sampling pattern, the signals at the selected outputs of the CARRY4 primitives needed to be connected to the corresponding FFs. This was achieved with a custom “VHDL generate” statement for each delay-line implementation, without the need to add extra circuitry for selecting the CARRY4 outputs such as multiplexers.
2.1.2. Ones-Counter
The output of the delay line needed to be converted into a binary word indicating the number of taps that had been activated with the START signal. A leading one detector, which tracks the location of the first propagation bit in the delay line, offered a possible solution. In order to improve linearity, we implemented a pipelined ones-counter that automatically sorted the output taps in ascending order (depending on the switching time of each output) by counting the number of outputs that had been activated on the delay line [35]. As reported in the literature [18], this method improves the linearity of the converter, and specifically, as far as the proposed design is concerned, the (differential nonlinearity) was reduced by 0.13 LSB and 0.32 LSB for the CCCC and SSSS patterns, respectively. The difference in the performance of the aforementioned variations of the ones-counter was due to the fact that the delays were not uniform. Specifically, the outputs of the delay line did not switch linearly, meaning that some taps switched earlier than the ones located before them in the delay line. By sorting the outputs of the delay line with regard to the switching time, linearity was improved, as shown in the aforementioned comparison of the “ones-counter” and “leading-one” methods. For the following results, the ones-counter method was used. Furthermore, a possible alternative to the pipelined ones-counter is an RNS-based (residue number system) implementation [36] since such adders/counters can be used to efficiently count the number of ones by decreasing the length of the carry chain [37] while also sorting the output taps of the delay line.
2.2. Placement of the TDL
The proper placement of the delay line is critical due to the skew imposed by the FPGA architecture. As mentioned above, the FPGA resources were divided into clock regions that suffered from clock skew. The CARRY4 primitives were arranged vertically inside the FPGA, with each CLB incorporating one such primitive. The FPGA in this work consisted of 6 vertical clock regions on the left side of the FPGA and 6 vertical clock regions on the right side, amounting to a total of 12 regions. The clock signal distribution delay was different in the various regions, and was thus characterized by a higher skew in some specific regions and a lower skew in others (Figure 3), effectively degrading performance.
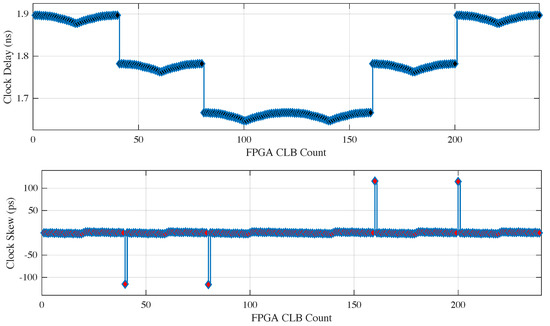
Figure 3.
Clock distribution delay and the corresponding skew.
By analyzing the timing reports (obtained from the Xilinx ISE software) of the FPGA (Xilinx Virtex-6 w/ML605 board), we concluded that the best choice was to use both central clock regions of the FPGA (clock regions 3 and 4 out of the 6 vertical ones). This choice constituted a trade-off between the length of the delay line and the imposed skew, which had a maximum absolute value of 116 ps, in the sense that the longer the delay line the higher the possibility of crossing two clock regions with high skew. Figure 3 illustrates the clock signal distribution delay to each of the 240 vertical CLBs that were used to build the longest delay line possible to implement in the FPGA. Each clock region consisted of 40 CLBs on the vertical axis, and thus clock regions 3 and 4 corresponded to the FPGA CLB numbers 81–160. The clock skew exhibited maximum/minimum values on the crossings from one clock region to another, as depicted in Figure 3. The only adjacent clock regions that featured minimal skew that was substantially lower than the rest were the two middle ones. The four maxima/minima of skew imposed high nonlinearities when the START signal crossed the clock regions along the delay line, with the exception of the two central ones. In theory, the rest of the clock regions could also be employed for the implementation of a delay line, but only across one single region with only half of the dynamic range of a delay line with respect to the two central ones.
For all patterns, the dynamic range for the single-shot measurements (a sole delay line is used) was about 3.2 ns, which was dictated by the fact that only the two central clock regions were suitable for a design with minimal skew effects. Depending on the sampling pattern, as discussed in the following section, the total number of used taps can be 320, 160, 80, or 40.
2.3. Adaptive Downsampling Method
As mentioned above, due to the predefined structure of the logic blocks of FPGAs, nonlinearity is inherent in FPGA-based TDCs and is an issue that severely degrades the performance of such systems.
As mentioned in the previous sections, the switching times of the outputs of the CARRY4 primitive are non-uniform, meaning that these switching times (e.g., the time needed for the START signal to trigger an output of the delay line after its arrival on the corresponding input) are not constant and in some cases, are also not linear. Thus, when computing their difference with respect to the subsequent outputs of the delay line, the results differed and took negative values. After analyzing the data illustrated in Figure 4, the switching times of the subsequent outputs ranged from +5.01 to −1.82 LSB and from +3.34 to −1.25 LSB regarding the CCCC and SSSS patterns, respectively. Figure 4 shows the discrepancy from the desired +1 LSB delay between taps, as well as the transfer functions for both the CCCC and SSSS patterns. This discrepancy resulted in the non-monotonicity of the transfer function between the time difference at the input and the bin count at the output of the TDL cell, as shown in the zoomed-in region in Figure 4, even after the outputs of the delay line had been sorted with the ones-counter. This characteristic was obtained from the Xilinx post-place and route simulations (as in [38]). The experimental results regarding the TDC characterization, nonlinearity estimation, and the corresponding experimental setup are presented in Section 3.
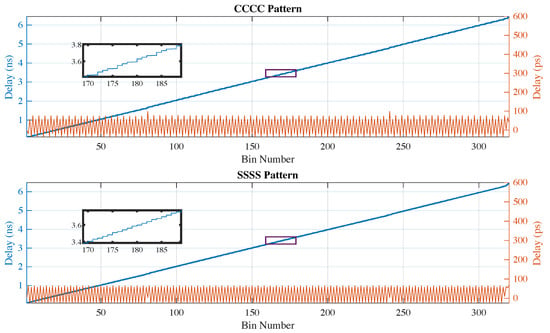
Figure 4.
Simulation results (post-place and route) regarding the transfer functions between the time difference at the input and the bin count at the output of the TDL cell (blue) and the delays of the subsequent tap transitions of the TDL cell (orange) for both maximum resolution patterns (CCCC and SSSS). Each delay line spans 80 CLBs and 2 clock regions.
When all the outputs of the CARRY4 primitive were used for the delay line (either the CCCC or the SSSS pattern), the effect of the non-uniform delays had an immediate impact on the nonlinearity of the TDC. In order to compensate for this inherent nonlinearity of FPGA-based TDCs, several solutions have been proposed. For example, in the work of Won and Lee [20], a heterogenous sampling technique was introduced (“tuned TDL”). Different combinations of the C- and S-outputs of the CARRY4 primitive were investigated while always utilizing four outputs of the primitive. In our attempt to further optimize for nonlinearities and area, we propose a new approach, the adaptive downsampling method, that considers all possible combinations of the C- and S-outputs for 4-tap, 3-tap, 2-tap, and 1-tap patterns. Patterns that include both C and S outputs are referred to hereafter as “tuned” patterns. As shown in table of Section 4, the proposed method offers significant improvements regarding the area and linearity of the TDC with respect to [20]. Although [20] investigated the 16 available 4-tap patterns, this paper also incorporates downsampled patterns, amounting to a total of 80 different patterns.
From the eight outputs of the CARRY4 primitive (shown in Figure 2) available to construct a delay line, we tested beyond the traditional CCCC and SSSS patterns all the different C and S combinations, amounting to a total of 16 4-tap patterns. Furthermore, by utilizing the adaptive downsampling method, we also implemented patterns that used only three, two, or one outputs of the CARRY4, including patterns that utilized only the C-outputs, S-outputs, or C and S combinations. This resulted in 32 3-tap patterns, 24 2-tap patterns, and 8 1-tap patterns. The results in Table 1 show the best-performing patterns in terms of both and (integral nonlinearity) in each category.

Table 1.
Nonlinearity as a function of the sampling pattern.
Although they did not exhibit the best linearity characteristics, the 4-tap patterns had the lowest , for example, the CCCC, SSSS, and SCCC ones. Furthermore, in order to optimize linearity and resource usage, a downsampled configuration can be chosen. For instance, the CCCN, SSSN, CSCN, or the CNCN, SNSN, NSCN patterns can be employed for improved linearity characteristics since these patterns offer the best (in terms of both DNL and INL) linearity metrics from the 3-tap and 2-tap patterns, respectively. The downsampled configurations also required fewer FPGA resources since both fewer FFs were required to sample the state of the delay line and fewer FPGA resources were needed for the implementation of the ones-counter. In an extreme case, where the minimization of resource usage of the design is the main objective, a 1-tap pattern can be employed. This aggressive downsampling configuration led to a much lower resolution, which was reduced by a factor of 4 compared to the 4-tap patterns. In this context, we also implemented all 1-tap configurations, with the NNNC and NNSN configurations exhibiting the best linearity characteristics.
The choice of the sampling pattern constituted a trade-off between resolution, linearity improvement, and resource utilization. On the one hand, more taps offered higher resolution and on the other hand, fewer taps reduced the overall area of the circuit, and the aim was that a specific pattern was chosen so that linearity also improved considerably. Overall, we propose a trade-off regarding the aforementioned parameters that can be employed in the design of any FPGA-based TDC that utilizes delay lines and is constructed of fixed building blocks with multiple outputs (CARRY primitives).
Area reduction is especially critical for the ones-counter and the sampling elements (FFs). For instance, the implementation of the ones-counter and the required FFs for two delay lines employing either of the 2-tap patterns requires the same area as the ones-counter and the FFs for only one delay line of either of the 4-tap configurations since the size of the modules is analogous to the number of taps of the delay line. The area requirements of the proposed sampling patterns are reported in table of Section 4. This area reduction has the potential to significantly reduce the area of the system, especially when multiple TDC channels are involved or when further signal processing of the TDC data needs to be locally executed inside the same FPGA, as, for instance, in our previous work [1], where beyond the fact that multiple channels were employed, the TDC was a separate module (an off-the-shelf component was used) and the FPGA was used for signal processing.
3. Results
3.1. Linearity Improvement
As discussed in Section 2.3, in an attempt to improve linearity, we investigated all possible downsampling patterns for the construction of a delay-line TDC. Specifically, we used the post-place and route simulation offered by the Xilinx tools. Table 1 illustrates the results from which the best (in terms of both DNL and INL) patterns, as discussed in Section 2.3, were selected. For instance, the best-performing 2-tap patterns in terms of linearity were the CNCN, SNSN, and NSCN (the NNCC pattern also exhibited similar performance). Linearity was significantly improved, for instance, regarding the CNCN and SNSN patterns compared with their 4-tap counterparts CCCC and SSSS, where the was improved from 0.63 to 0.12 LSB and from 0.33 to 0.19 LSB, respectively. Regarding , the above-mentioned patterns were also improved from 1.70 to 0.52 LSB and from 2.98 to 0.90 LSB. The final results for the best-performing patterns are illustrated in table of Section 3.3.
3.2. Effects of Nonidealities
Besides the inherent nonideality of the FPGA regarding its structure, other factors that degrade the performance of the TDC (translating to loss of linearity in our case) are the quantization error, clock jitter, input signal jitter, FF metastability, thermal noise, and supply noise jitter of the TDC. In order to determine the effects of the TDC’s nonidealities, we conducted a timing experiment for the measurement of the single-shot precision (SSP), i.e., the measurement uncertainty (standard deviation of the time intervals at the input of the TDC averaged over a range of delays) [18,20]. The experimental setup, as depicted in Figure 5, consisted of one clock signal and two TDC trigger signals that were used as the START and STOP TDC signals for the implemented converter. The aforementioned trigger and clock signals were generated by the Mixed Mode Clock Manager (MMCM) inside the FPGA.
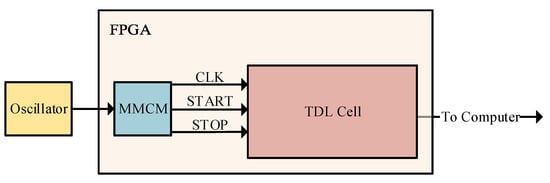
Figure 5.
Experimental setup.
In order to assess the SSP, we excited the TDL cell, which was implemented with various sampling pattern configurations in the aforementioned signals. A full characterization of a delay line with a specific sampling pattern corresponded to multiple runs of sample acquisitions. In each run, the phase difference of the trigger signals (START & STOP) was increased starting from a time value of ps and reaching a value of ns, which corresponded to the full dynamic range of the delay line. The phase difference of the trigger signals was increased in order to emulate different timing events, defined as the time difference (between the STOP and START signals) at the input of the TDL cell through the whole dynamic range of the delay line.
In our attempt to obtain reliable results (representative of the whole delay line), we used a phase increment of 125 ps by configuring the MMCM accordingly. The data were acquired by employing the integrated logic analyzer that is provided in the Xilinx Chipscope program. For each delay-line implementation, we collected data from 26 different timing events (sample acquisition runs), and for each phase difference, we obtained samples, leading to a total of 851,968 samples for one implementation. The results for each event were superimposed in order to assess the performance of the SSP in a holistic way. We conducted the experiment for the best-performing in terms of linearity 4-tap, 3-tap, 2-tap, and 1-tap patterns. Figure 6 illustrates the normalized histograms (with normal distribution data fits) of the superposition of the data from the timing experiments as a function of the uncertainty of the measurements and expressed as fractions. The histogram of the NNSN pattern has not been graphically reported for compactness.
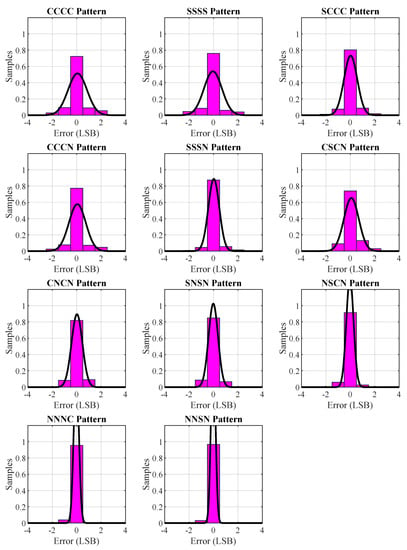
Figure 6.
Normalized histograms of the superposition of the experimental data regarding the measurement uncertainty of each sampling pattern with normal distribution fit.
Table 2 summarizes the experimental results for the various sampling patterns. For each pattern, the cumulative uncertainty of all the acquired data and the uncertainty of the worst-case scenario is shown. Specifically, the cumulative uncertainty corresponds to the superposition of all the acquired data regarding a delay line with a specific sampling pattern, whereas the worst-case scenario corresponds to the sample acquisition run that exhibited the worst standard deviation.

Table 2.
Measurement Uncertainty Summary.
Moreover, the LSB duration () was obtained from the experimental data and was approximately 10 ps, 13.33 ps, 20 ps, and 40 ps corresponding to the 4-tap, 3-tap, 2-tap, and 1-tap configurations, respectively. It should also be noted that when external signals drive the TDL cell, the MMCM can be employed as a “jitter filter” [39] in order to remove the jitter from the external START and STOP signals. Therefore, we can expect similar performance characteristics with the metrics reported in this paper in a case where external signals drive the TDL cell. The main insight of this experiment was the relationship between the number of used taps and measurement uncertainty and resolution. As shown in Figure 6, the more taps that were used in the delay line, the higher the uncertainty and standard deviation, as illustrated in Figure 6. In effect, the number of outputs used from the CARRY4 primitive was proportional to the intensity of the measurement uncertainty of the delay line (standard deviation and range) and inversely proportional to the resolution. This setup does not require either external delay generators [18], random pulse generators [6], or other components for the characterization of the TDC. By employing only internal FPGA resources, the proposed scheme can prove very useful and provide an alternative to other more complex characterization procedures, especially if the needed external components are not available, as in this work.
3.3. Total Estimated Nonlinearity
In order to obtain reliable results with respect to the overall nonlinearity, we combined the data from the Xilinx post-place and route simulation with the data we obtained from the aforementioned timing experiments. In detail, the effect of the measurement uncertainty was added to the data from the Xilinx post-place and route simulation, in accordance with the that was determined for each pattern in the previous sub-section. The DNL is calculated according to the formula (where is the switching time of the nth bin), whereas the INL is given by the cumulative sum of the DNL.
This process was performed for the best-performing 4-tap, 3-tap, 2-tap, and 1-tap patterns, which were used for the creation of Figure 7. The results illustrated in those figures show, as expected, improved performance regarding nonlinearity for the downsampled patterns. Table 3 reports the linearity characteristics of the tested patterns and Figure 7 shows a visual representation of the data. Specifically, the SCCC and SSSS patterns exhibited slightly better and worse compared with the CCCC pattern, which had the best overall linearity characteristics among the 4-tap patterns. Furthermore, although the SSSN pattern showed the best among the 3-tap configurations, its considerably inferior made the CCCN and CSCN patterns the most favorable choices. Although the CNCN pattern exhibited superior differential and integral nonlinearity to the other 2-tap configurations, the 1-tap configurations had characteristics similar to the NNNC pattern showing the best and the NNSN with the best . As shown in Table 3, the CNCN pattern’s nonlinearity characteristics were considerably superior compared to the other patterns, with the exception of the NSCN configuration, which had comparable metrics. Thus, by selecting the CNCN configuration, not only was the TDC’s performance significantly improved in terms of linearity but also its area was reduced considerably.
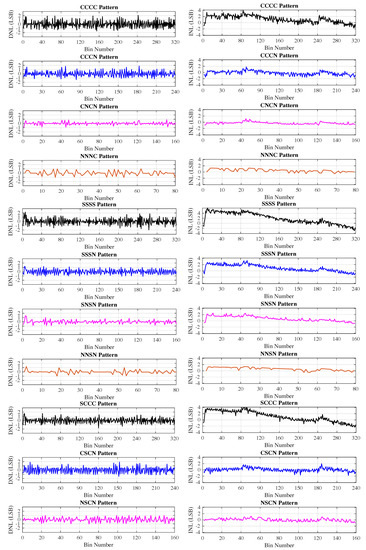
Figure 7.
DNL (left side) and INL (right side) as a function of the bin number for the C-patterns, S-patterns, and tuned patterns.

Table 3.
DNL and INL Summary.
4. Discussion
In this paper, a rigorous and adaptive downsampling method was proposed through which linearity was substantially improved, the area of the converter and other modules that may use the TDC’s output was reduced, and the SSP was retained. This generic method can be adapted to other FPGA-based TDC implementations since most FPGA-based TDCs employ delay lines that are constructed of fixed building blocks with multiple outputs (CARRY primitives). For example, the Xilinx 7 Series FPGAs (Spartan, Artix, Kintex, Virtex) incorporate the CARRY4 primitive [40], whereas the Xilinx UltraScale FPGAs (Kintex, Virtex, Zynq) incorporate the CARRY8 primitive, which is an advanced version of the CARRY4 with double the number of outputs (8 bits instead of 4) [41]. In order to employ the proposed method in a different device (e.g., the Xilinx 7 Series FPGAs), all adaptive downsampling patterns need to be tested again since the different device structures might translate to other adapted best-performing downsampling patterns. Furthermore, we quantified the uncertainty of the proposed TDC with a timing experiment that can be conducted through the employment of TDC clock signals without the need for external test equipment.
The performance of the TDC under various operational modes is illustrated in Table 4, with and reaching 6.0 ps and 9.0 ps regarding the CNCN pattern. As noted earlier, the proposed method offers a trade-off regarding the resolution, linearity, and area of the TDC. Either of the 4-tap configurations may offer the lowest value of 10 ps but not the best linearity. Thus, by selecting a downsampled pattern with good linearity characteristics, for instance, the CNCN pattern, linearity can be improved while the reducing area and retaining the SSP.

Table 4.
Performance Summary and Comparison.
Table 4 depicts the performance summary of the explored TDC implementations that are compared with similar works reported in the literature. Won and Lee [20] employed a Xilinx Virtex-6 FPGA in order to implement a delay-line TDC with different combinations of the four C- and four S-outputs and investigated the choice of the 4-tap sampling pattern (out of 16 possible implementations) that led to the best linearity characteristics. The performance of the TDC reported in our work is comparable to the results of [20], providing even superior performance regarding the nonlinearity metrics (CNCN pattern). Furthermore, the resources required for the implementation of one TDC channel in this work are considerably lower compared to [20] (considering both the FFs and LUTs). Moreover, the TDC reported in [26] (implemented in a Kintex-7 device) employed only the S-outputs of the CARRY4 cell (our TDCs use a combination of C- and S-outputs) in a bin decimation scheme and exhibited inferior performance regarding the SSP, and is thought to require more resources compared to this work. In addition, although [26] relied on the calibration of the TDC using the results of a code-density test, which is a more complex testing scheme and usually requires the use of a non-correlated oscillator or external testing equipment [6,18,20] (our implementation employs FPGA resources for testing), our design constitutes a more compact and rigorous method that can be employed for a multitude of FPGAs. Chen and Li employed a sub-TDL averaging topology (implemented in a Xilinx Virtex-7 FPGA) with histogram compensation (compensated TDC [30]) in order to improve linearity, adding an extra calibration scheme (calibrated TDC [30]). Their results regarding the compensated TDC [30] reported in Table 4 are comparable to the performance achieved in this work. However, their resource utilization is thought to be significantly higher. The second approach [30] (calibrated TDC) showed improved linearity in comparison with our work at the cost of a significantly increased resource utilization and design complexity (especially compared with the CNCN pattern). Table 4 also shows that the proposed TDC is comparable and even superior regarding certain metrics compared with other recent TDC implementations using TDL [18], Vernier interpolation [33], and wave union [21,25] methods. Additionally, the TDC implementation of [27] (Artix-7 device), employed the “tuned TDL” technique [20] with “real-time calibration” and exhibited inferior performance (SSP) compared to this work and more specifically the CNCN pattern. The lower usage of LUTs in [27] was due to the fact that their implementation used a delay line that was almost half the length of our implementation (48 CARRY4 cells instead of 80), resulting in more resources regarding both the delay line and the ones-counter of our design.
Consequently, the proposed adaptive downsampling method achieved the optimization (with respect to the literature) of both the linearity and area utilized by the TDC while retaining the SSP. Specifically, by employing the CNCN configuration it was possible to improve the and metrics by 0.47 LSB and 1.12 LSB and retain a comparable SSP compared to the CCCC pattern while using 50% fewer FFs and 33% fewer LUTs. This benefit can prove especially important when multiple TDC channels are implemented and resource utilization becomes critical. In a multi-channel design, emphasis needs to be given to the proper implementation and routing of delay lines in order to avoid timing errors and offsets, as well as potential interference from neighboring slices.
5. Conclusions
In this paper, we proposed a rigorous and adaptive method based on CARRY4 primitives in order to improve the performance of FPGA-based TDCs that utilize delay lines. By employing this method on a Xilinx Virtex-6 FPGA, we effectively improved the linearity of the converter and also reduced its area while retaining the SSP, offering a trade-off between the three crucial parameters of the TDC: linearity, area, and resolution. Firstly, downsampling resulted in fewer area requirements and improved linearity depending on the specific sampling pattern. Secondly, by testing all available adaptive patterns (for 4-tap, 3-tap, 2-tap, and 1-tap implementations), a further improvement in linearity was achieved. This technique can be employed in any FPGA-based TDC, which uses delay lines, constructed of fixed building blocks with multiple outputs, as in the case of the Xilinx-family FPGAs, which incorporate the CARRY4 and CARRY8 primitives.
Although this work proposes the optimization of TDL-based TDCs in FPGAs, superior performance in FPGA-based TDCs can also be achieved by employing more complex converter architectures, for instance, noise-shaping TDCs [42]. Since most TDC implementations incorporate a delay line, the proposed adaptive downsampling method can be applied to such complex TDC schemes, improving linearity with fewer FPGA resources.
Author Contributions
Conceptualization, E.D., M.B., and A.B.; methodology, E.D., M.B., and A.B.; software, E.D.; validation, E.D.; formal analysis, E.D.; investigation, E.D., M.B., and A.B.; data curation, E.D.; writing original draft preparation, E.D.; writing review and editing, E.D., M.B., and A.B.; visualization, E.D.; supervision, M.B., A.B.; project administration, M.B., A.B. All authors have read and agreed to the published version of the manuscript.
Funding
This work was partially supported by the EU—Horizon 2020—ENERMAN project (DT-FOF-09-2020) under Grant Agreement-958478.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Georgakopoulou, K.; Spathis, C.; Bourlis, G.; Tsirigotis, A.G.; Leisos, A.; Birbas, M.; Birbas, A.; Tzamarias, S.E. A 100 ps multi-time over threshold data acquisition system for cosmic ray detection. Meas. Sci. Technol. 2018, 29, 115001. [Google Scholar] [CrossRef]
- Christiansen, J. Picosecond Stopwatches: The Evolution of Time-to-Digital Converters. IEEE Solid-State Circuits Mag. 2012, 4, 55–59. [Google Scholar] [CrossRef]
- Moser, N.; Rodriguez-Manzano, J.; Lande, T.S.; Georgiou, P. A Scalable ISFET Sensing and Memory Array With Sensor Auto-Calibration for On-Chip Real-Time DNA Detection. IEEE Trans. Biomed. Circuits Syst. 2018, 12, 390–401. [Google Scholar] [CrossRef] [PubMed]
- Ho, C.; Chen, M.S. A Fractional-N DPLL with Calibration-Free Multi-Phase Injection-Locked TDC and Adaptive Single-Tone Spur Cancellation Scheme. IEEE Trans. Circuits Syst. I Regul. Pap. 2016, 63, 1111–1122. [Google Scholar] [CrossRef]
- Hussein, A.I.; Vasadi, S.; Paramesh, J. A 450 fs 65-nm CMOS Millimeter-Wave Time-to-Digital Converter Using Statistical Element Selection for All-Digital PLLs. IEEE J. Solid-State Circuits 2018, 53, 357–374. [Google Scholar] [CrossRef]
- Fishburn, M.; Menninga, L.H.; Favi, C.; Charbon, E. A 19.6 ps, FPGA-Based TDC with Multiple Channels for Open Source Applications. IEEE Trans. Nucl. Sci. 2013, 60, 2203–2208. [Google Scholar] [CrossRef]
- Venialgo, E.; Lusardi, N.; Garzetti, F.; Geraci, A.; Brunner, S.E.; Schaart, D.R.; Charbon, E. Toward a Full-Flexible and Fast-Prototyping TOF-PET Block Detector Based on TDC-on-FPGA. IEEE Trans. Radiat. Plasma Med. Sci. 2019, 3, 538–548. [Google Scholar] [CrossRef]
- Yoshioka, K.; Kubota, H.; Fukushima, T.; Kondo, S.; Ta, T.T.; Okuni, H.; Watanabe, K.; Hirono, M.; Ojima, Y.; Kimura, K.; et al. A 20-ch TDC/ADC Hybrid Architecture LiDAR SoC for 240 × 96 Pixel 200-m Range Imaging with Smart Accumulation Technique and Residue Quantizing SAR ADC. IEEE J. Solid-State Circuits 2018, 53, 3026–3038. [Google Scholar] [CrossRef]
- Jansson, J.; Koskinen, V.; Mantyniemi, A.; Kostamovaara, J. A Multichannel High-Precision CMOS Time-to-Digital Converter for Laser-Scanner-Based Perception Systems. IEEE Trans. Instrum. Meas. 2012, 61, 2581–2590. [Google Scholar] [CrossRef]
- Tyndall, D.; Rae, B.R.; Li, D.D.; Arlt, J.; Johnston, A.; Richardson, J.A.; Henderson, R.K. A High-Throughput Time-Resolved Mini-Silicon Photomultiplier With Embedded Fluorescence Lifetime Estimation in 0.13 μm CMOS. IEEE Trans. Biomed. Circuits Syst. 2012, 6, 562–570. [Google Scholar] [CrossRef]
- Palojarvi, P.; Maatta, K.; Kostamovaara, J. Integrated time-of-flight laser radar. IEEE Trans. Instrum. Meas. 1997, 46, 996–999. [Google Scholar] [CrossRef]
- Fan, H.H.; Cao, P.; Liu, S.B.; An, Q. TOT measurement implemented in FPGA TDC. Chin. Phys. C 2015, 39, 116101. [Google Scholar] [CrossRef]
- Henzler, S. Time-to-Digital Converters; Springer: Dordrecht, The Netherlands, 2010; Volume 1. [Google Scholar] [CrossRef]
- Kong, J.; Henzler, S.; Schmitt-Landsiedel, D.; Siek, L. A 9-bit, 1.08 ps resolution two-step time-to-digital converter in 65 nm CMOS for time-mode ADC. In Proceedings of the 2016 IEEE Asia Pacific Conference on Circuits and Systems (APCCAS), Jeju, Korea, 25–28 October 2016; pp. 348–351. [Google Scholar] [CrossRef]
- Roberts, G.W.; Ali-Bakhshian, M. A Brief Introduction to Time-to-Digital and Digital-to-Time Converters. IEEE Trans. Circuits Syst. II Express Briefs 2010, 57, 153–157. [Google Scholar] [CrossRef]
- Lee, M.; Abidi, A.A. A 9 b, 1.25 ps Resolution Coarse–Fine Time-to-Digital Converter in 90 nm CMOS that Amplifies a Time Residue. IEEE J. Solid-State Circuits 2008, 43, 769–777. [Google Scholar] [CrossRef]
- Keranen, P.; Maatta, K.; Kostamovaara, J. Wide-Range Time-to-Digital Converter with 1-ps Single-Shot Precision. IEEE Trans. Instrum. Meas. 2011, 60, 3162–3172. [Google Scholar] [CrossRef]
- Tontini, A.; Gasparini, L.; Pancheri, L.; Passerone, R. Design and Characterization of a Low-Cost FPGA-Based TDC. IEEE Trans. Nucl. Sci. 2018, 65, 680–690. [Google Scholar] [CrossRef]
- Cui, K.; Ren, Z.; Li, X.; Liu, Z.; Zhu, R. A High-Linearity, Ring-Oscillator-Based, Vernier Time-to-Digital Converter Utilizing Carry Chains in FPGAs. IEEE Trans. Nucl. Sci. 2017, 64, 697–704. [Google Scholar] [CrossRef]
- Won, J.Y.; Lee, J.S. Time-to-Digital Converter Using a Tuned-Delay Line Evaluated in 28-, 40-, and 45-nm FPGAs. IEEE Trans. Instrum. Meas. 2016, 65, 1678–1689. [Google Scholar] [CrossRef]
- Liu, C.; Wang, Y. A 128-Channel, 710 M Samples/Second, and Less Than 10 ps RMS Resolution Time-to-Digital Converter Implemented in a Kintex-7 FPGA. IEEE Trans. Nucl. Sci. 2015, 62, 773–783. [Google Scholar] [CrossRef]
- Bourdeauducq, S. A 26 ps RMS Time-to-Digital Converter Core for Spartan-6 FPGAs. 2013. Available online: https://arxiv.org/abs/1303.6840 (accessed on 25 October 2022).
- Wang, Y.; Zhou, X.; Song, Z.; Kuang, J.; Cao, Q. A 3.0-ps rms Precision 277-MSamples/s Throughput Time-to-Digital Converter Using Multi-Edge Encoding Scheme in a Kintex-7 FPGA. IEEE Trans. Nucl. Sci. 2019, 66, 2275–2281. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, C.; Cheng, X.; Li, D. Spartan-6 FPGA based 8-channel time-to-digital converters for TOF-PET systems. In Proceedings of the 2015 IEEE Nuclear Science Symposium and Medical Imaging Conference (NSS/MIC), 2015 IEEE Nuclear Science Symposium and Medical Imaging Conference (NSS/MIC), San Diego, CA, USA, 3–5 November 2015; pp. 1–3. [Google Scholar] [CrossRef]
- Ugur, C.; Bayer, E.; Kurz, N.; Traxler, M. A 16 channel high resolution (11 ps RMS) Time-to-Digital Converter in a Field Programmable Gate Array. J. Instrum. 2012, 7, C02004. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, C. A Nonlinearity Minimization-Oriented Resource-Saving Time-to-Digital Converter Implemented in a 28 nm Xilinx FPGA. IEEE Trans. Nucl. Sci. 2015, 62, 2003–2009. [Google Scholar] [CrossRef]
- Parsakordasiabi, M.; Vornicu, I.; Rodríguez-Vázquez, Á.; Carmona-Galán, R. A Low-Resources TDC for Multi-Channel Direct ToF Readout Based on a 28-nm FPGA. Sensors 2021, 21, 308. [Google Scholar] [CrossRef] [PubMed]
- Mantyniemi, A.; Rahkonen, T.; Kostamovaara, J. A CMOS Time-to-Digital Converter (TDC) Based On a Cyclic Time Domain Successive Approximation Interpolation Method. IEEE J. Solid-State Circuits 2009, 44, 3067–3078. [Google Scholar] [CrossRef]
- Ozawa, Y.; Ida, T.; Jiang, R.; Sakurai, S.; Takigami, S.; Tsukiji, N.; Shiota, R.; Kobayashi, H. SAR TDC Architecture with Self-Calibration Employing Trigger Circuit. In Proceedings of the 2017 IEEE 26th Asian Test Symposium (ATS), Taipei City, Taiwan, 27–30 November 2017; pp. 94–99. [Google Scholar] [CrossRef]
- Chen, H.; Li, D.D. Multichannel, Low Nonlinearity Time-to-Digital Converters Based on 20 and 28 nm FPGAs. IEEE Trans. Ind. Electron. 2019, 66, 3265–3274. [Google Scholar] [CrossRef]
- Machado, R.; Cabral, J.; Alves, F.S. Recent Developments and Challenges in FPGA-Based Time-to-Digital Converters. IEEE Trans. Instrum. Meas. 2019, 68, 4205–4221. [Google Scholar] [CrossRef]
- Cui, K.; Li, X.; Liu, Z.; Zhu, R. Toward Implementing Multichannels, Ring-Oscillator-Based, Vernier Time-to-Digital Converter in FPGAs: Key Design Points and Construction Method. IEEE Trans. Radiat. Plasma Med Sci. 2017, 1, 391–399. [Google Scholar] [CrossRef]
- Zhang, J.; Zhou, D. An 8.5-ps Two-Stage Vernier Delay-Line Loop Shrinking Time-to-Digital Converter in 130-nm Flash FPGA. IEEE Trans. Instrum. Meas. 2018, 67, 406–414. [Google Scholar] [CrossRef]
- Xilinx Inc. Virtex-6 Libraries Guide for HDL Designs, UG623. 2012. Available online: https://www.xilinx.com/support/documentation/sw_manuals/xilinx14_7/virtex6_hdl.pdf (accessed on 25 October 2022).
- Wang, Y.; Kuang, J.; Liu, C.; Cao, Q. A 3.9-ps RMS Precision Time-to-Digital Converter Using Ones-Counter Encoding Scheme in a Kintex-7 FPGA. IEEE Trans. Nucl. Sci. 2017, 64, 2713–2718. [Google Scholar] [CrossRef]
- Garner, H.L. The Residue Number System. IRE Trans. Electron. Comput. 1959, EC-8, 140–147. [Google Scholar] [CrossRef]
- Sousa, L. Nonconventional Computer Arithmetic Circuits, Systems and Applications. IEEE Circuits Syst. Mag. 2021, 21, 6–40. [Google Scholar] [CrossRef]
- Zhang, M.; Yang, K.; Chai, Z.; Wang, H.; Ding, Z.; Bao, W. High-Resolution Time-to-Digital Converters Implemented on 40-, 28-, and 20-nm FPGAs. IEEE Trans. Instrum. Meas. 2021, 70, 1–10. [Google Scholar] [CrossRef]
- Xilinx Inc. Virtex-6 FPGA Clocking Resources. 2014. Available online: https://docs.xilinx.com/v/u/en-US/ug362 (accessed on 25 October 2022).
- Xilinx Inc. 7 Series FPGAs Configurable Logic Block. 2016. Available online: https://docs.xilinx.com/v/u/LHd6SGNNCEUgQ~fLalm5Hg (accessed on 25 October 2022).
- Xilinx Inc. UltraScale Architecture Configurable Logic Block. 2017. Available online: https://docs.xilinx.com/v/u/en-US/ug574-ultrascale-clb (accessed on 25 October 2022).
- Wu, Y.; Lu, P.; Staszewski, R.B. A Time-Domain 147fsrms 2.5-MHz Bandwidth Two-Step Flash-MASH 1-1-1 Time-to-Digital Converter With Third-Order Noise-Shaping and Mismatch Correction. IEEE Trans. Circuits Syst. I Regul. Pap. 2020, 67, 2532–2545. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).