Calibrating for Precision Calorimetry in LArTPCs at ICARUS and SBN ^†

Abstract

The Short-Baseline Neutrino (SBN) Program at Fermilab consists of multiple Liquid Argon Time Projection Chamber (LArTPC) detectors in a single neutrino beam. SBN will have a broad physics program that includes GeV-scale neutrino cross section measurements and physics searches beyond the Standard Model including a search for short-baseline neutrino oscillations. Especially for the oscillation program at SBN (and, looking ahead, at DUNE) it is imperative to have accurate and precise energy measurements that can be related to the true neutrino energy. At ICARUS, we have developed a precise energy scale calibration procedure to match the needs of these physics goals. Two innovations are important here. First, diffusion plays a role in determining the energy scale in LArTPC calibration in a manner unappreciated by previous experiments. Second, incorporating systematic uncertainties into the energy scale calibration fit allows for a precise determination of the uncertainty of calorimetric measurements in a way that could be propogated to higher-level analyses. The result from the calibration procedure outlined herein is now being applied to neutrino beam data at ICARUS.

1. Motivating Precise Energy Scale Calibration in LArTPCs

Liquid Argon Time Projection Chamber (LArTPC) detectors such as ICARUS primarily leverage the charge deposited by charged particles for use in particle identification and calorimetric energy reconstruction. Reconstructing these quantities accurately is necessary to enable the physics goals for ICARUS, including a search for short-baseline neutrino oscillations as part of the Short-Baseline Neutrino Program at Fermilab [1,2]. The techniques developed for today’s LArTPC experiments will also enable the next generation long-baseline neutrino oscillation experiment—DUNE—where in particular obtaining an unbiased measure of neutrino energy has been shown to be very important [3].

In addition to ∼GeV physics measurements in neutrino oscillations, LArTPC detectors have also been shown to be sensitive to energy depositions in the ∼MeV range [4]. At the several kiloton size of the DUNE far detector, this sensitivity could enable a broad physics program alongside and supporting neutrino oscillation measurements [5]. Such measurements all rely on having an excellent measure of energy deposited in the detector.

A good measure of energy means that it is both precise (having a fine resolution) and accurate (having a small bias). The limits on the precision of LArTPC detectors are well understood and are intrinsic to the detector [6]. The accuracy of the energy measurement relies on its calibration. This work will describe the methodology we have applied thus far in the ICARUS experiment, techniques which will also be possible to leverage at DUNE.

2. Cosmic Muons as a Standard Candle

Operating at a short baseline in a neutrino beam and at the surface, ICARUS has both cosmic muons and charged particles in neutrino interactions available for calibrations. Of these, cosmic muons are more numerous: about one-million cosmic muons were used in the calibration work presented here. (The DUNE far detector will not have many neutrinos for calibration, but will have ∼4000 cosmics per day per module [7].) Cosmic muon energy loss is well understood and thus an excellent standard candle for energy scale calibration. At the energies relevant for cosmogenic particles, muons lose energy primarily through ionization loss. The mean energy loss of muons from this process is well described by the Bethe–Bloch theory [8]. However, the Landau–Vavilov nature of muon energy loss [9,10] means that it is challenging to reconstruct the mean energy loss, and so the most-probable-value (MPV) of energy loss is a better observable. For relativistic muons, this is equal to [11]

$${\frac{dE}{dx}}_{\mathrm{MPV}}=\overline{\frac{dE}{dx}}+\zeta T_{\max }\left(\log \left[\zeta t\right]+0.2+{\beta }^2\right),$$

(1)

where $\overline{\frac{dE}{dx}}$ is the mean energy loss, $\beta$ is the muon velocity, $T_{\max }$ is the maximum energy transfer to a single atomic electron and $\zeta$, with units of inverse length, encodes the rate of scattering (both as described by the Rutherford cross-section [11]), and t is the length of the muon observed by the wire. We call t the “wire-sensitive thickness” in this work.

That the most probable energy loss depends on the wire-sensitive thickness means that it (unlike the mean energy loss) is not an intrinsic property to the muon. In a LArTPC, it also depends on the angle of the muon to the wire plane measuring the ionization charge. It has also been shown that diffusion changes the wire-sensitive thickness [12,13] by smearing out the ionization charge observed by a wire. At ICARUS, for the first time in a LArTPC experiment, we have designed an energy calibration procedure that accounts for the effect of diffusion on the energy scale. To do this, we use the results of reference [12] to compute the wire-sensitive thickness for each muon energy deposition.

2.1. Uncertainties on the Energy Scale

The most probable energy loss in ICARUS has systematic uncertainties from unknown and uncertain properties of liquid argon. The mean energy loss depends on the mean excitation energy [11], which has only been measured in gaseous argon. We conservatively ascribe a ∼10% uncertainty on this value to account for possible differences due to the phase also observed in other materials [14]. The wire-sensitive thickness depends on the quantity of diffusion transverse to the electric field [12]. This quantity has never been measured in liquid argon close to the electric field strength of ICARUS. In this work, we apply a measurement of longitudinal diffusion in MicroBooNE [15] extrapolated to the ICARUS electric field strength [16] and propagated from longitudinal to transverse diffusion [17,18]. Due to the extrapolation involved, we assess a 50% uncertainty on this quantity.

Finally, we must consider the recombination of ionization electrons along the muon track. In a LArTPC, some ionization electrons will “recombine” with argon ions before they can be pulled away by the electric field [19]. A measurement of the $dE/dx$ dependent recombination is needed to understand how many ionization electrons a certain quantity of energy loss will produce [20,21]. We use the ArgoNeuT measurement here and apply its uncertainty. The quantities contributing systematic uncertainty are summarized in Table 1 alongside the results of the energy scale calibration.

Table 1. Results of calibration gain fit in each of the four ICARUS TPCs. Systematic parameters in the fit are included as pull terms (see Section 2.1 for a discussion).

Parameter	Prior	Posterior
Recombination $\alpha$ [20]	$0.93\pm 0.02$	$0.948\pm 0.010$
Recombination $\beta$ [cm${}^3$/g][cm/kV] [20]	$0.212\pm 0.05$	$0.212\pm 0.05$
Transverse Diffusion Constant [cm${}^2$/s] [15]	$8.8\pm 4.4$	$9.1\pm 2.2$
Mean Excitation Energy [eV] [14]	$188\pm 17$	$194\pm 15$
Gain TPC EE [e${}^{-}$/ADC]	–	$83.4\pm 2.0$
Gain TPC EW [e${}^{-}$/ADC]	–	$81.8\pm 2.0$
Gain TPC WE [e${}^{-}$/ADC]	–	$85.3\pm 2.0$
Gain TPC WW [e${}^{-}$/ADC]	–	$84.3\pm 2.0$

3. Energy Scale Calibration Procedure

To obtain the energy scale calibration, we first eliminate non-uniformities in the detector response to ionization charge and then measure the electronics gain. The detector non-uniformity we address here (in Section 3.1) is in the drift direction, where impurities in the argon can absorb ionization electrons and attenuate the signal. (E-field distortions in the drift direction can also in principle affect the detector response. These are small in ICARUS due to its short drift length, and we do not specifically address them here.) After dividing out the non-uniformity, we fit for the electronics gain as outlined in Section 3.2.

3.1. Charge Normalization in the Drift Direction

We use depositions from cosmic muons to normalize the detector response in ICARUS. By combining hits from enough muons, we can obtain distributions of energy loss that are constant across the drift direction. Then, any observed difference in the measured charge can be attributed to a detector non uniformity which can be divided out.

Importantly, the effect of diffusion described in Section 2 can bias this method. Diffusion increases with drift time, and thus so does the wire-sensitive thickness and therefore energy loss. Diffusion makes our standard candle no longer standard across the drift direction. We apply a novel procedure (suggested in [12]) to mitigate this bias. Instead of measuring charge hit-by-hit, we sum the charge from adjacent groups of 10 wires along a muon track. This makes the effective wire spacing much larger than the diffusion length, thus minimizing the impact of diffusion on energy loss.

We have been able to verify in our detector Monte Carlo that the 1-wire (hit-by-hit) measurement results in an underlying drift dependent $dE/dx$ (which we can access at truth level in the Monte Carlo), whereas the 10-wire (summed) measurements observes a flat one. Also, in data, we have observed different profiles of $dQ/dx$ from the 1-wire and 10-wire measurements across the detector. This is shown in Figure 1. Informed by the simulation, we apply the 10-wire measurement to estimate the detector response in the drift direction.

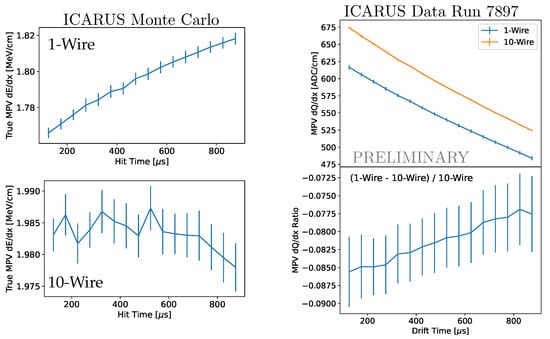
Figure 1. (Left) Profile of true most probable energy loss ($dE/dx$) for through-going cosmic muons as a function of drift time observed in ICARUS for the (biased) 1-wire measurement (top) and the (unbiased) 10-wire measurement (bottom). (Right) Profile of most-probable charge deposited ($dQ/dx$) from through-going cosmic muons in in ICARUS data as a function of drift time for the 1-wire and 10-wire measurements. In Monte Carlo, the energy loss of the 1-wire measurement increases with increasing drift time (due to the drift dependent effect of diffusion on wire-sensitive thickness). (The 10-wire measurement obtains a larger $dE/dx$ value (due to the higher wire-sensitive thickness from summing 10 adjacent wires) that is flat across the detector (because the 10-wire spacing dominates over the diffusion length). Correspondingly, in data the most probable value (MPV) of the 1-wire measurement increases relative to the 10-wire measurement with increasing drift time. We use the unbiased 10-wire measurement to extract the electron lifetime in the ICARUS calibration procedure.

3.2. Gain Measurement

After applying the detector normalization, we are ready to measure the electronics gain (in units of e${}^{-}$/ADC). As described in Section 2, we use energy loss from stopping cosmic muons for this measurement. We bin hits from cosmic muons in terms of the inputs to the most probable energy loss formula (Equation (1)): residual range, or the range of the muon track after that hit (to obtain the momentum), track angle to the wire plane, and drift time (both to obtain the wire-sensitive thickness). In each such bin, we fit a Landau distribution convolved with a Gaussian distribution to the histogram of $dQ/dx$ values to obtain the most probable value. We then fit the expected charge loss profile (applying the ArgoNeuT recombination measurement [20]), including the systematic uncertainties (described in Section 2.1) as pull terms. We measure the gain individually in each of the four ICARUS TPCs. The fit matches the profile well in each TPC. We show the fits from one of the TPCs in Figure 2. We summarize the results of the fit, including pull terms, in Table 1. No pull term has a value further than 1$\sigma$ away from the prior.

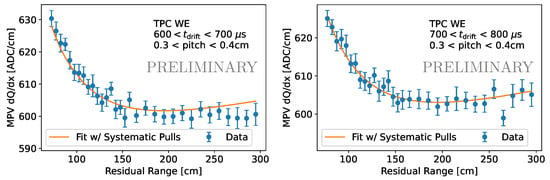
Figure 2. Example profile of $dQ/dx$ vs. residual range (a proxy for momentum) for cosmic muons in the gain measurement fit. Data are shown for one ICARUS TPC (WE) in two bins of drift time.

By including systematic uncertainties in the fit, we can obtain an uncertainty on the calibration. The size of the systematic uncertainty as a function of $dE/dx$ is shown in Figure 3. In obtaining the uncertainty, one has a choice of whether to consider only the uncertainty on the gain individually, or to marginalize the fit gain and recombination parameters together. The gain as measured by cosmic muons is very correlated with the recombination parameters, so by marginalizing over the two together one obtains a smaller systematic uncertainty in the energy. At ICARUS, we can use this parameterized uncertainty to understand the systematic uncertainty from effects such as recombination in higher-level analyses. This procedure would be less computationally intensive than, for example, the multi-sim method pursued by MicroBooNE [22].

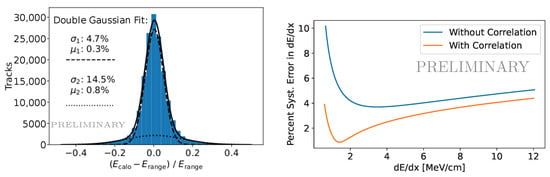
Figure 3. (Left) Comparison of calibrated calorimetric energy and range reconstructed energy for cosmic muons, fit to a double Gaussian. (Right) Systematic uncertainty in energy scale calibration with and without applying correlation between gain and recombination (see Section 3.2).

We have checked the energy scale calibration by comparing energy measurements for stopping cosmic muons done by summing calibrated energy depositions from the muon (“calo”) and done using range. This comparison is shown in Figure 3. The two energy measurements agree well with each other, demonstrating the accuracy of the calibration.

4. Future Work

The calibration described here is being used at ICARUS in preliminary studies of the neutrino data. We are also continuing to understand the detector uniformity, and to study the depositions from (highly ionizing) protons produced in beam neutrino interactions.