Analysis of Adiabatic Strain Localization Coupled to Ductile Fracture and Melting, with Application and Verification for Simple Shear

Abstract

Material failure by adiabatic shear is analyzed in viscoplastic metals that can demonstrate up to three distinct softening mechanisms: thermal softening, ductile fracture, and melting. An analytical framework is constructed for studying simple shear deformation with superposed static pressure. A continuum power-law viscoplastic formulation is coupled to a ductile damage model and a solid–liquid phase transition model in a thermodynamically consistent manner. Criteria for localization to a band of infinite shear strain are discussed. An analytical–numerical method for determining the critical average shear strain for localization and commensurate stress decay is devised. Averaged results for a high-strength steel agree reasonably well with experimental dynamic torsion data. Calculations probe possible effects of ductile fracture and melting on shear banding, and vice versa, including influences of cohesive energy, equilibrium melting temperature, and initial defects. A threshold energy density for localization onset is positively correlated to critical strain and inversely correlated to initial defect severity. Tensile pressure accelerates damage softening and increases defect sensitivity, promoting shear failure. In the present steel, melting is precluded by ductile fracture for loading conditions and material properties within realistic protocols. For this steel, if conduction, fracture, and damage softening are artificially suppressed, melting is confined to a narrow region in the core of the band. However, for other metals with vastly different physical properties, or for more diverse loading conditions, melting has not been unequivocally ruled out, even if fracture and conduction are permitted.

1. Introduction

Shear localization is a prevalent failure mode in solid materials that undergo strain-softening mechanisms. In crystalline metals deformed at high rates, near-adiabatic conditions are obtained, promoting a build up of local internal energy and temperature from plastic work, in turn leading to thermal softening as dislocation mobility increases with temperature. A mechanical instability ensues, beyond which localization into a thin band of very high shear strain and strain rate occurs [1,2]. Shear banding is often accompanied by damage mechanisms such as cracking and void growth [3,4,5,6,7], and melting is theoretically possible if temperatures become large enough [8]. In this work, “damage” and “ductile fracture” are used to refer changes in local material structure—distinct from phase transformation and deformation twinning and not captured by thermal softening alone in the context of continuum plasticity theory—that induce degradation of local strength.

Experiments and models on adiabatic shear spanning the previous four decades are reviewed in the monograph [1] and more recent article [2]. Most previous continuum modeling of adiabatic shear localization in metals, be it analytical [9,10,11,12,13,14,15,16,17] or numerical [18,19,20,21,22,23,24], did not explicitly address fracture or melting mechanisms. However, several continuum damage mechanics-type models for adiabatic shear [25,26,27,28] represented degradation distinctly from purely thermal softening. Mathematical analyses in Refs. [29,30] considered localization in strain-softening solids, without explicit thermal effects, that could be attributed to damage processes.

More recently, phase-field models [31,32,33,34,35,36,37], extending ideas for depicting brittle fracture and structural transformations in elastic solids [38,39,40,41,42,43], have addressed ductile fracture and adiabatic shear localization in elastic–plastic solids. A common element of many models is a contribution of some fraction of energy from plastic work to the net driving force for fracture [31,32,33,35,36,37,44], supported by experiments revealing the importance of microstructure- and damage-softening relative to thermal softening [45,46]. Furthermore, many continuum damage and ductile-fracture phase-field models include a threshold inelastic energy density at which damage nucleates [27,28,35,36,47], as opposed to classic phase-field fracture mechanics wherein any elastic energy can initiate diffuse cracks [43,48]. Timing of cracking or void nucleation relative to localized flow varies among metals with different compositions and microstructures [4,5,6,7,49,50]. Cited experiments usually suggest damage mechanisms accompany or follow localization, rather than precede it, since cracks and voids are scarcely seen outside shear bands in those materials tested.

Direct evidence of melting has been reported within dynamic shear bands in various titanium and steel alloys [49,51,52,53]. Known prior analyses of adiabatic shear did not include the thermodynamics of melting, even though local temperatures far exceeding the melting point of iron or steel can be predicted inside the shear band [8,11,14,54]. Phase-field models combining mechanics of elasticity and thermodynamics and kinetics of melting and solidification exist [55,56,57,58], but these do not consider plastic deformation or adiabatic shear. A continuum model described flowing material within a shear band using a Bingham model with Newtonian viscosity [59], at temperatures below the ambient melt temperature. Therein, the calibrated viscosity was so low for three different metallic systems that the constant, rate-independent part of the shear stress dominated.

A recent theoretical study [8] advanced the analyses of Molinari and Clifton [11,12,14] to account for influences of superposed pressure, external magnetic fields, and solid-solid phase transformations on adiabatic shear localization. Results showed how loading conditions and solid-solid phase transformations can promote or inhibit strain localization in iron and a high-strength Ni-Cr steel. Herein, treatments of Refs. [8,11,12,14] are further extended to account for damage (i.e., ductile shear fracture) and melting (i.e., solid–liquid transformation) processes. Criteria for localization into a band of infinite shear [11,12] are analyzed, and methods for calculating the average shear strain at which localization ensues are developed. The latter require numerical iteration and numerical integration, as closed-form expressions for critical strain cannot be derived analytically. A ductile fracture component of the model further addresses the additional “average” shear strain accommodated by the sample after localization, accounting for the effective shear displacement jump across the band whose shear strain approaches infinity and width approaches zero. This allows for representation of a gradual softening behavior in the macroscopic shear stress versus shear strain response as regularly witnessed experimentally [5,6,28,47,60]. Overly abrupt drops to zero stress upon localization [8,11,12] were criticized by Molinari and Clifton [12] as a notable deficiency of their original approach, therein speculated a result of poor resolution of defects.

As assumed or justified in prior works [1,8,12,61] for materials (e.g., steels) and average strain rates (e.g., 10³–10⁴/s) of present interest, regularization mechanisms of heat conduction and inertia are omitted to enable a tractable analysis without recourse to advanced numerical methods such as finite elements or finite differences. Similarly, to allow localization into a damaged region of infinitesimal thickness, the ductile fracture component of the formulation omits gradient regularization of phase-field theory [62], and Newtonian viscosity of molten material is likewise omitted in the limit of singular surfaces [8,11,12,63]. Any remaining (implicit) regularization is furnished by strain-rate sensitivity [64]. Apart from phase-field methods that introduce regularization via order parameter gradients, other generalized continuum theories, including various strain-gradient, micromorphic, and nonlocal types, can instill material length scales in solid mechanics problems (e.g., [29,30,65,66,67,68,69]). These generalized approaches, though promising with regard to stability and localization problems, are outside the scope of the current analysis. The present results are interpreted as a limiting case: predictions would be expected to underestimate conditions for localization given the absence of other regularization mechanisms [1,61]. An initial defect (e.g., strength perturbation) of greater intensity than imposed or predicted here and in Refs. [8,11,12] would seem needed to instill the same post-peak shear strain.

This article consists of seven more sections. In Section 2, a general 3D continuum framework is outlined, including constitutive fundamentals and thermodynamics. In Section 3, specialization of the framework to simple shear and pressure loading is undertaken. Constitutive model components for viscoelasticity, ductile fracture, and melting are introduced in this context. In Section 4, localization criteria are examined, and methods of calculation of critical shear strain and average stress-strain response are explained. In Section 5, properties and results are reported for a high-strength steel and compared to experimental observation. In Section 6, effects of variations in material parameters and loading conditions on localization behaviors are explored. In Section 7, modeling details, collective results, and limitations are discussed. In Section 8, conclusions consolidate the main developments. A list of notation precedes the bibliography. Standard conventions of continuum mechanics are used (e.g., Refs. [1,70]), with vectors and tensors in bold font and scalars and scalar components in italics. A single Cartesian frame of reference is sufficient for this work.

2. 3D Formulation

The general constitutive framework combines elements from Refs. [8,31,42,43,55,56,57,71]. Electromagnetic effects considered in Refs. [8,71] are excluded, but phase-field concepts for fracture [31,42,43,44] and melting [55,56,57] are now added. The material is isotropic in both solid polycrystalline and liquid amorphous states, and is assumed fully solid in its initial configuration.

Inertial dynamics, heat conduction, and surface energies are included the complete 3D theory, as are thermal expansion and finite elastic shear strain. These features are retained in Section 2 for generality and to facilitate identification and evaluation of successive approximations made later. Furthermore, retainment of such physics in the general formulation will allow a consistent implementation of the complete nonlinear theory in subsequent numerical simulations, for potential future comparison to the results of semi-analytical calculations reported in Section 5 and Section 6.

2.1. Constitutive Model

Denote the motion of a material particle at reference position $\mathbf{X}$ by spatial coordinates $\mathbf{x}$ = $\mathit{\phi }(\mathbf{X},t)$. Gradients with respect to $\mathbf{X}$ and $\mathbf{x}$ are written as ${\nabla }_0(·)$ and $\nabla (·)$, and a superposed dot denotes the time derivative at fixed $\mathbf{X}$. The deformation gradient $\mathbf{F}$ and its determinant J are decomposed into a product of three terms [70,72,73], with ${\mathbf{F}}^E$ thermoelastic deformation, ${\mathbf{F}}^P$ plastic deformation from dislocation motion, and ${\mathbf{F}}^I$ the total inelastic deformation from damage and melting:

$$\begin{array}{cc}\hfill & \mathbf{F}={\nabla }_0\mathit{\phi }={\mathbf{F}}^E{\mathbf{F}}^I{\mathbf{F}}^P,J=det\mathbf{F}=det{\mathbf{F}}^{E}det{\mathbf{F}}^{I}det{\mathbf{F}}^P=J^E{J}^I{J}^P>0.\hfill \end{array}$$

(1)

None of ${\mathbf{F}}^E,{\mathbf{F}}^I,{\mathbf{F}}^P$ need be individually integrable to a vector field [70]. Denote dimensionless order parameter fields for melting by $\xi (\mathbf{X},t)\in [0,1]$ and damage by $\varphi (\mathbf{X},t)\in [0,1]$, where

$$\begin{array}{c}\hfill \xi \left\{\begin{array}{cc}\hfill & =0\leftrightarrow \mathrm{solid}\mathrm{material},\hfill \\ \hfill & \in (0,1)\leftrightarrow \mathrm{mixed}\mathrm{phase}\mathrm{region},\hfill \\ \hfill & =1\leftrightarrow \mathrm{liquid}\mathrm{material};\hfill \end{array}\right.\varphi \left\{\begin{array}{cc}\hfill & =0\leftrightarrow \mathrm{undamaged}\mathrm{material},\hfill \\ \hfill & \in (0,1)\leftrightarrow \mathrm{partially}\mathrm{degraded}\mathrm{material},\hfill \\ \hfill & =1\leftrightarrow \mathrm{fully}\mathrm{degraded}\mathrm{material}.\hfill \end{array}\right.\end{array}$$

(2)

Deformations of solid and liquid phases are not tracked individually at a point $\mathbf{X}$, so each is effectively assigned the same overall deformation gradient $\mathbf{F}(\mathbf{X},t)$ at time t. Accordingly, $\xi$ is interpreted equivalently as the local mass fraction or local volume fraction of molten material. On the other hand, $\varphi$ need not represent the local volume fraction of voids or free volume, but rather is a generic indicator of local strength loss.

In a body of reference volume ${\Omega }_0$, reference conditions are $\xi \left(\mathbf{X}\right)=\varphi \left(\mathbf{X}\right)=0\forall \mathbf{X}\in {\Omega }_0$. Calculations do not consider bodies with initial liquid phases or with initial damage represented by nonzero values of $\xi (\mathbf{X},0)$ and $\varphi (\mathbf{X},0)$, respectively. If the material contains initial defects associated with damage entities (e.g., pores, micro-cracks, or other intrinsically weak zones), $\varphi (\mathbf{X},t)$ represents only the additional damage incurred after loading begins, potentially nonzero only for $t>0^{+}$. In Section 3.3, a relationship between initial strength perturbation $\delta {\chi }_0\left(\mathbf{X}\right)$ and an initial damage variable physically analogous to, but mathematically distinct from, $\varphi (\mathbf{X},0)=0$, is introduced.

Deformation ${\mathbf{F}}^I$ is a function of state (i.e., of order parameters), plasticity is isochoric, and symmetric thermoelastic deformation is measured by ${\mathbf{C}}^E$ with isochoric part ${\tilde{\mathbf{C}}}^E$:

$$\begin{array}{c}\hfill {\mathbf{F}}^I={\mathbf{F}}^I(\xi ,\varphi );J^P=det{\mathbf{F}}^P=1;{\mathbf{C}}^E={\left({\mathbf{F}}^E\right)}^{\mathrm{T}}{\mathbf{F}}^E,{\tilde{\mathbf{C}}}^E=J^{E-2/3}{\mathbf{C}}^E.\end{array}$$

(3)

Denote by $\chi (\mathbf{X},t)$ a scalar internal state variable field associated with plastic deformation processes (e.g., a dimensionless measure of dislocation density). Let $\theta (\mathbf{X},t)$ be absolute temperature. Helmholtz free energy per unit reference volume of the solid is $\psi$, consisting of thermoelastic strain energy W, thermal energy Q, microstructure energy R, and gradient surface energy $\Lambda$:

$$\begin{array}{c}\hfill \psi ({\mathbf{C}}^E,\theta ,\xi ,\varphi ,\chi ,{\nabla }_0\xi ,{\nabla }_0\varphi )=W({\mathbf{C}}^E,\theta ,\xi ,\varphi )+Q(\theta ,\xi )+R(\xi ,\varphi ,\chi )+\Lambda (\xi ,\varphi ,{\nabla }_0\xi ,{\nabla }_0\varphi ).\end{array}$$

(4)

Denoted by ${\theta }_0$ is a reference temperature, and $\Delta \theta =\theta -{\theta }_0$. Non-degraded isothermal bulk modulus $B_0$ is assumed the same in solid and liquid phases for neutral and compressive states wherein $ln{J}^E\le 0$. Volumetric coefficient of thermal expansion $A_0$ is assumed the same in solid and liquid. The non-degraded shear modulus of the solid is ${\mu }_0$. Thermoelastic strain energy combines a logarithmic equation of state [74] with a polyconvex shear contribution [62]:

$$\begin{array}{cc}\hfill & W(J^E,{\tilde{\mathbf{C}}}^E,\theta ,\xi ,\varphi )=\frac{1}{2}B(\xi ,\varphi ){(ln{J}^E)}^2[1-\frac{1}{3}(B_0^{\prime }-2)ln{J}^E]\hfill \\ & -A_{0}B\Delta \theta ln{J}^E+\frac{1}{2}\mu (\xi ,\varphi )(\mathrm{tr}{\tilde{\mathbf{C}}}^E-3).\hfill \end{array}$$

(5)

Let ${\iota }^{\xi }\left(\xi \right)\in [0,{\iota }_1^{\xi }]$ be an interpolation function between solid and liquid states satisfying ${\iota }^{\xi }\left(0\right)=1,{\iota }^{\xi }\left(1\right)={\iota }_1^{\xi }\in [0,1]$. Let $\overline{\omega }(\varphi ,J^E)=1+[\omega \left(\varphi \right)-1]\mathsf{H}(ln{J}^E)\in [0,1]$ be a degradation function satisfying $\omega \left(0\right)=1,\omega \left(1\right)={\omega }_1\in [0,1]$, where $\mathsf{H}(·)$ is the left-continuous Heaviside function. Moduli are interpolated as follows, noting as $\xi \to 1$ and $\varphi \to 1$, $B\to B_0{\omega }_1{\iota }_1^{\xi }$ in tension and $\mu \to {\mu }_0{\omega }_1{\iota }_1^{\xi }$:

$$B(\xi ,\varphi ,J^E)=B_0\overline{\omega }(\varphi ,J^E)[1+\{{\iota }^{\xi }\left(\xi \right)-1\}\mathsf{H}(ln{J}^E)],\mu (\xi ,\varphi )={\mu }_0\omega \left(\varphi \right){\iota }^{\xi }\left(\xi \right).$$

(6)

Constants ${\omega }_1$ or ${\iota }_1^{\xi }$, when nonzero, enable remnant strength when a material element is fully fractured or melted, and $B=B_0$ in compression. Cauchy pressure p and deviatoric Cauchy stress $\tilde{\mathit{\sigma }}$ then follow from (5), with ${\tilde{\mathbf{B}}}^E$ the spatial deviatoric lattice strain:

$$\begin{array}{cc}\hfill & \mathit{\sigma }=\tilde{\mathit{\sigma }}-p\mathbf{1};p=-{\displaystyle \frac{1}{3}}\mathrm{tr}\mathit{\sigma }=-{\displaystyle \frac{1}{J}}{\displaystyle \frac{\partial \psi }{\partial ln{J}^E}}=-{\displaystyle \frac{B}{J}}\{ln{J}^E[1-\frac{1}{2}(B_0^{\prime }-2)ln{J}^E]-A_0\Delta \theta \};\hfill \end{array}$$

(7)

$$\begin{array}{cc}\hfill & \tilde{\mathit{\sigma }}={\displaystyle \frac{2}{J}}{\mathbf{F}}^E{\displaystyle \frac{\partial \psi }{\partial {\tilde{\mathbf{C}}}^E}}:{\displaystyle \frac{\partial {\tilde{\mathbf{C}}}^E}{\partial {\mathbf{C}}^E}}{\left({\mathbf{F}}^E\right)}^{\mathrm{T}}={\displaystyle \frac{\mu }{J}}{\tilde{\mathbf{B}}}^E,{\tilde{\mathbf{B}}}^E={\left(J^E\right)}^{-2/3}{\mathbf{F}}^E{\left({\mathbf{F}}^E\right)}^{\mathrm{T}}-{\displaystyle \frac{1}{3}}\mathrm{tr}\left[{\left(J^E\right)}^{-2/3}{\mathbf{F}}^E{\left({\mathbf{F}}^E\right)}^{\mathrm{T}}\right]\mathbf{1}.\hfill \end{array}$$

(8)

Specific heat per unit volume $c_V$ is assumed the same for solid and liquid phases and is idealized as independent of $\theta$. Latent heat of fusion per unit reference volume of the solid is the constant $h_T$, positive for the usual case of higher internal energy of the liquid than the solid coexisting at the same $(p,\theta )$. Herein $h_T\ge 0$. An equilibrium transformation temperature is the constant ${\theta }_T$. At this temperature, in the absence of elastic deformation, stored energy of microstructure, and gradient surface energy, the free energy densities of solid and liquid phases are equal, whereby ${\theta }_T$ is interpreted as the melt temperature. Thermal energy is

$$\begin{array}{c}\hfill Q(\theta ,\xi )=-c_V[\theta ln(\theta /{\theta }_0)-\Delta \theta ]+\left[(h_T/{\theta }_T)(\theta -{\theta }_T)\right]{\iota }^{\xi }\left(\xi \right).\end{array}$$

(9)

Here ${\theta }_I\le {\theta }_T$ is a melt instability temperature, and constant $A_{\xi }=3h_T(1-{\theta }_I/{\theta }_T)\ge 0$ [55] .

Denote $E_C\ge 0$ as the cohesive energy per unit reference volume [42,62], presumed matching in solid and liquid phases here for simplicity. More generally, $E_C$ could depend on $\xi$ and $\theta$, to allow for different, temperature-dependent cavitation thresholds in solid and liquid. However, data to justify such generalizations, incurring additional driving and resistive forces for melting and fracture and increasing model complexity and computational burden, appear difficult to measure and do not seem to exist for the material analyzed in Section 5. Microstructure energy is

$$\begin{array}{c}\hfill R(\xi ,\varphi ,\chi )={\mu }_0[1-r_0^{\xi }\{1-{\iota }^{\xi }\left(\xi \right)\}]\overline{R}\left(\chi \right)+A_{\xi }{\xi }^2{(1-\xi )}^2+E_C{f}_{\varphi }\left(\varphi \right),\end{array}$$

(10)

with $\overline{R}$ a dimensionless function of $\chi$. The first term on the right in (10), for stored energy of dislocations, is scaled by the shear modulus [70], the second is a double well for phase boundaries [55,56,57], and the third, with $f_{\varphi }\left(\varphi \right)\in [0,1]$ a dimensionless function, is for homogeneous fracture [42,43]. Constant $r_{\xi }^0\in [0,1]$ is the fraction of stored energy of cold work released upon melting.

Let ${\Gamma }_{\xi }$ and ${\Gamma }_{\varphi }$ be surface energies for solid–liquid boundaries and cracks, respectively, and let $l_{\xi },l_{\varphi }$ be regularization length constants. Gradient energy of internal surfaces is then the usual sum of quadratic forms [43,55], where here surface energies can generally depend on order parameters:

$$\begin{array}{c}\hfill \Lambda (\xi ,\varphi ,{\nabla }_0\xi ,{\nabla }_0\varphi )={\Gamma }_{\xi }\left(\varphi \right)l_{\xi }|{\nabla }_0{\xi |}^2+{\Gamma }_{\varphi }\left(\xi \right)l_{\varphi }{\left|{\nabla }_0\varphi \right|}^2.\end{array}$$

(11)

Surface tension [55,56,57] is omitted from R and $\Lambda$ for brevity; it could be included by multiplying right sides of (10) and (11) by J and replacing ${\nabla }_0(·)$ with $\nabla (·)$ in (11).

For later use, define first Piola–Kirchhoff stress $\mathbf{P}$, elastic second Piola–Kirchhoff stress $\mathbf{S}$, Mandel stress $\overline{\mathbf{S}}$, and the thermoelastic entropy constitutive relation as

$$\begin{array}{cc}\hfill & \mathbf{P}=J\mathit{\sigma }{\mathbf{F}}^{-\mathrm{T}},\mathbf{S}=J{\left({\mathbf{F}}^E\right)}^{-1}\mathit{\sigma }{\left({\mathbf{F}}^E\right)}^{-\mathrm{T}}=2\partial \psi /\partial {\mathbf{C}}^E,\overline{\mathbf{S}}={\mathbf{C}}^E\mathbf{S},\eta =-\partial \psi /\partial \theta .\hfill \end{array}$$

(12)

With $\eta$ and U being entropy and internal energy per unit volume, $\mathbf{q}$ the referential heat flux, and $\kappa \ge 0$ isotropic Fourier conductivity generally dependent on temperature, phase, and damage, the following apply:

$$U=\psi +\theta \eta ,\mathbf{q}(\xi ,\varphi ,\theta ,{\nabla }_0\theta )=-\kappa (\xi ,\varphi ,\theta ){\nabla }_0\theta .$$

(13)

2.2. Balance Laws and Dissipation

Standard local forms [70,74] for conservation of mass and momentum are invoked, where ${\rho }_0$ and $\rho$ are referential (solid, undeformed and undamaged) and spatial (deformed, possibly molten, and possibly damaged) mass densities, $\mathbf{b}$ is body force per unit mass, and $\mathbf{\upsilon }=\dot{\mathbf{x}}$ is particle velocity:

$$\begin{array}{c}\hfill {\rho }_0=\rho J,\nabla ·\mathit{\sigma }+\rho \mathbf{b}=\rho \dot{\mathbf{\upsilon }},\mathit{\sigma }={\mathit{\sigma }}^{\mathrm{T}}.\end{array}$$

(14)

Let ${\mathbf{n}}_0$ be the outward normal to material body ${\Omega }_0$ on external boundary $\partial {\Omega }_0$. Global forms of the balance of energy and entropy inequality are as follows, the first extending classical continuum mechanics to account for surface energetics of order parameters [43,62,75]:

$$\begin{array}{cc}\hfill & {\displaystyle \frac{\mathrm{d}}{\mathrm{d}\mathrm{t}}}{\int }_{{\Omega }_0}U\mathrm{d}{\Omega }_0+{\displaystyle \frac{\mathrm{d}}{\mathrm{d}\mathrm{t}}}{\int }_{{\Omega }_0}{\displaystyle \frac{{\rho }_0}{2}}{\left|\mathbf{\upsilon }\right|}^2\mathrm{d}{\Omega }_0={\oint }_{\partial {\Omega }_0}(\mathbf{P}·{\mathbf{n}}_0)·\mathbf{\upsilon }\mathrm{d}\partial {\Omega }_0-{\oint }_{\partial {\Omega }_0}(\mathbf{q}·{\mathbf{n}}_0)\mathrm{d}\partial {\Omega }_0\hfill \end{array}$$

$$\begin{array}{c}\hfill +{\oint }_{\partial {\Omega }_0}\left({\displaystyle \frac{\partial \psi }{\partial {\nabla }_0\xi }}·{\mathbf{n}}_0\right)\dot{\xi }\mathrm{d}\partial {\Omega }_0+{\oint }_{\partial {\Omega }_0}\left({\displaystyle \frac{\partial \psi }{\partial {\nabla }_0\varphi }}·{\mathbf{n}}_0\right)\dot{\varphi }\mathrm{d}\partial {\Omega }_0,\end{array}$$

(15)

$$\begin{array}{cc}\hfill & {\displaystyle \frac{\mathrm{d}}{\mathrm{d}\mathrm{t}}}{\int }_{{\Omega }_0}\eta d{\Omega }_0+{\oint }_{\partial {\Omega }_0}{\displaystyle \frac{\mathbf{q}·{\mathbf{n}}_0}{\theta }}\mathrm{d}\partial {\Omega }_0\ge 0.\hfill \end{array}$$

(16)

The divergence theorem, (14), and differentiability give local versions of (15) and (16):

$$\begin{array}{cc}\hfill & \dot{U}=\mathbf{P}:\dot{\mathbf{F}}-{\nabla }_0·\mathbf{q}+{\nabla }_0·[(\partial \psi /\partial {\nabla }_0\xi )\dot{\xi }+(\partial \psi /\partial {\nabla }_0\varphi )\dot{\varphi }],\hfill \end{array}$$

(17)

$$\begin{array}{cc}\hfill & \theta \dot{\eta }+{\nabla }_0·\mathbf{q}-(\mathbf{q}·{\nabla }_0\theta )/\theta \ge 0.\hfill \end{array}$$

(18)

Define the internal dissipation as follows, applying the first of (13) and (17):

$$\begin{array}{c}\hfill \mathfrak{D}=\theta \dot{\eta }+{\nabla }_0·\mathbf{q}=\mathbf{P}:\dot{\mathbf{F}}+{\nabla }_0·[(\partial \psi /\partial {\nabla }_0\xi )\dot{\xi }+(\partial \psi /\partial {\nabla }_0\varphi )\dot{\varphi }]-\dot{\psi }-\dot{\theta }\eta .\end{array}$$

(19)

The second law (18) is, from (1), (3), (12), (13), and chain-rule differentiation of (4),

$$\begin{array}{cc}\hfill \mathfrak{D}& + {\displaystyle \frac{\kappa }{\theta }}{\left|{\nabla }_0\theta \right|}^2\ge 0;\mathfrak{D}=\left[{\left({\mathbf{F}}^I\right)}^{\mathrm{T}}\overline{\mathbf{S}}{\left({\mathbf{F}}^I\right)}^{-\mathrm{T}}\right]:{\mathbf{L}}^P+\varsigma \dot{\xi }+\zeta \dot{\varphi }+\vartheta \dot{\chi },{\mathbf{L}}^P={\dot{\mathbf{F}}}^P{\mathbf{F}}^{P-1};\hfill \\ \hfill \varsigma & =-\partial \psi /\partial \xi +{\nabla }_0·(\partial \psi /\partial {\nabla }_0\xi )+\mathbf{P}:(\partial \mathbf{F}/\partial \xi )\hfill \end{array}$$

(20)

$$\begin{array}{cc}\hfill & =-\partial (W+Q+R+\Lambda )/\partial \xi +2l_{\xi }{\nabla }_0·\left({\Gamma }_{\xi }{\nabla }_0\xi \right)+\left[\overline{\mathbf{S}}{\left({\mathbf{F}}^I\right)}^{-\mathrm{T}}\right]:(\partial {\mathbf{F}}^I/\partial \xi ),\hfill \\ \hfill \zeta & =-\partial \psi /\partial \varphi +{\nabla }_0·(\partial \psi /\partial {\nabla }_0\varphi )+\mathbf{P}:(\partial \mathbf{F}/\partial \varphi )\hfill \end{array}$$

(21)

$$\begin{array}{cc}\hfill & =-\partial (W+R+\Lambda )/\partial \varphi +2l_{\varphi }{\nabla }_0·\left({\Gamma }_{\varphi }{\nabla }_0\varphi \right)+\left[\overline{\mathbf{S}}{\left({\mathbf{F}}^I\right)}^{-\mathrm{T}}\right]:(\partial {\mathbf{F}}^I/\partial \varphi ),\hfill \end{array}$$

(22)

$$\begin{array}{cc}\hfill \vartheta & =-\partial \psi /\partial \chi =-{\mu }_0[1-(1-{\iota }^{\xi })r_0^{\xi }]\partial \overline{R}/\partial \chi .\hfill \end{array}$$

(23)

Expansion of $\dot{\eta }=-{\displaystyle \frac{\partial \dot{\psi }}{\partial \theta }}$ with (9), and (17), then give the temperature rate, where the specific heat per unit volume at constant volume obeys $c_V=-\theta {\displaystyle \frac{{\partial }^2\psi }{\partial {\theta }^2}}$:

$$\begin{array}{c}\hfill c_V\dot{\theta }=\mathfrak{D}+h_T{\displaystyle \frac{\theta }{{\theta }_T}}{\displaystyle \frac{\mathrm{d}{\iota }^{\xi }}{\mathrm{d}\xi }}\dot{\xi }-A_0\theta [B{\displaystyle \frac{{\dot{J}}^E}{J^E}}+ln{J}^E\{{\displaystyle \frac{\partial B}{\partial \xi }}\dot{\xi }+{\displaystyle \frac{\partial B}{\partial \varphi }}\dot{\varphi }\left\}\right]+{\nabla }_0·\left(\kappa {\nabla }_0\theta \right).\end{array}$$

(24)

3. Dynamic Shear with Pressure

The problem analyzed in Section 3, Section 4, Section 5 and Section 6 is similar to that of Ref. [8]. However, magnetization and magnetic fields considered in that work are omitted here, as are solid–solid phase transformations. Instead, solid–liquid transformations and ductile fracture are now included. It is possible to posit a reduced set of governing equations for shear band analysis from the outset, without referencing the full 3D constitutive model of Section 2 that encompasses thermoelasticity, conduction, gradient regularization, and inertia. However, that full formulation is used as a starting point here to clarify the simplifying assumptions needed for mathematically tractable limit analysis in later sections.

3.1. Geometry, Loading Conditions, and Governing Equations

Shown in Figure 1 is the transient boundary value problem of present study. Let $(X,Y,Z)$ and $(x,y,z)$ be Cartesian reference and spatial coordinates. The material domain ${\Omega }_0$ is of initial height $h_0$ and current height $h\left(t\right)$. The slab is infinitely extended in $X,x$- and $Z,z$- directions. The following mixed boundary conditions are invoked. Denote by ${\upsilon }_0={\upsilon }_x$ a constant velocity at $y=h$, with vanishing velocity ${\upsilon }_x=0$ at $y=0$. Constant pressure field $t_n=-p_0$ is applied as normal traction on all boundaries for $t\ge 0^{+}$. Though not depicted in Figure 1, tangential traction from ${\sigma }_{xy}$ at each cross section $x=\mathrm{constant}$ exists. Letting $(X,Y,Z)$ be coordinates minus application of $p_0$, $h_0$ can be unequal to the Y value of the planar boundary of the stress-free slab due to compressibility (i.e., $h_0$ depends on $p_0$). Pressure $p_0$ is applied slowly so is treated as an isothermal and quasi-static pre-loading. Then for dynamic shearing when $t\ge 0^{+}$, $y=0$ and $y=h$ are thermally insulated.

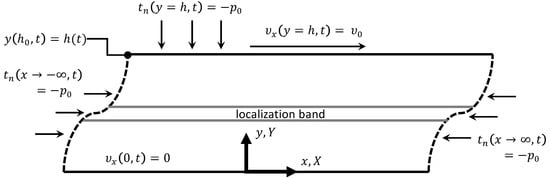
Figure 1. Boundary value problem for simple shear with superposed static pressure: tangential velocity at $y=h$ is ${\upsilon }_0$, normal traction $t_n$ is $p_0$, including $t_n(z\to \pm \infty ,t)=-p_0$. Slab is infinite in $X,x,Z,z$ directions; initial (current) height of slab is $h_0$ (h). Slab is thermally insulated: $\partial \theta /\partial y=0$ at $y=0$ and at $y=h$ for $t\ge 0^{+}$. Initial variable ${\chi }_0\left(y\right)=\chi (y,t=0)$ and temperature $\theta (y,t=0)$ can vary modestly over $y\in (0,h)$.

For $t>0^{+}$, while the body is shearing, h may displace from $h_0$ to maintain $p_0=\mathrm{constant}$ at $y=h$. This would occur if a volume-changing structural change such as melting or void growth is driven by shear. Note ${\upsilon }_0$ is constant for $t\ge 0^{+}$: acceleration from a resting state to an initial velocity gradient is not modeled. For $t\ge 0^{+}$, with infinite $x,z$ boundaries, spatial fields depend at most only on $(y,t)$, a common assumption in analytical studies of shear bands [1,11,12,13,76]:

$$\begin{array}{c}\hfill \mathit{\upsilon }=\mathit{\upsilon }(y,t),\mathbf{F}=\mathbf{F}(y,t),\mathit{\sigma }=\mathit{\sigma }(y,t),\theta =\theta (y,t),[t\ge 0^{+}].\end{array}$$

(25)

Any single localization band, within which $\mathbf{F}$ differs from most of the rest of the domain, is oriented as in Figure 1, but multiple parallel bands are allowable. Properties and initial temperature are constant with respect to x and z but need not so with respect to y. Perturbations in initial strength and temperature [14] can trigger localization at critical y locations.

Reference configuration covered by $(X,Y,Z)$ is a model construct for analysis and need not be attained in experimental practice. Pressure $p_0$ is removed instantly at fixed $\theta$ from an unsheared state, before ${\upsilon }_x={\upsilon }_0$ is applied. By construction, $\mathbf{F}={\mathbf{F}}^E={\mathbf{F}}^I={\mathbf{F}}^P=\mathbf{1}$, $\mathit{\sigma }=\mathbf{0}$, and $\varphi =\xi =0$ in this reference configuration. Almost everywhere, $\theta \approx {\theta }_0=\mathrm{constant}$ and $\chi \approx {\chi }_0=\mathrm{constant}$. Initial perturbations in $\theta$ and $\chi$ are permitted, with magnitudes so small that initial perturbations in J, p, $\varphi$, and $\xi$ can be omitted.

Since the constitutive model of Section 2 is isotropic, the only nonzero Cauchy stress components are ${\sigma }_{xx}$, ${\sigma }_{yy}$, ${\sigma }_{zz}$, and ${\sigma }_{xy}={\sigma }_{yx}$, and the nonzero heat flux component is $q_Y$. Taking $\mathbf{b}=\mathbf{0}$ henceforth and using (25), the second of (14) and heat conduction expressions in (13) and (24) are

$$\begin{array}{cc}\hfill & {\displaystyle \frac{\partial {\sigma }_{xy}}{\partial y}}=\rho {\dot{\upsilon }}_x,{\displaystyle \frac{\partial {\sigma }_{yy}}{\partial y}}=\rho {\dot{\upsilon }}_y;\hfill \end{array}$$

(26)

$$\begin{array}{cc}\hfill & q_Y=-\kappa F_{yY}{\displaystyle \frac{\partial \theta }{\partial y}},{\nabla }_0·\kappa {\nabla }_0\theta =F_{yY}{\displaystyle \frac{\partial }{\partial y}}\left(\kappa F_{yY}{\displaystyle \frac{\partial \theta }{\partial y}}\right).\hfill \end{array}$$

(27)

Regarding the deformation gradient, non-vanishing components of $\mathbf{F}\left(y\right(Y,t),t)$ are $F_{xX}$, $F_{yY}$, $F_{zZ}$, and $F_{xY}$. For generic differentiable function $f=f\left(y\right(Y,t),t)$ (e.g., (25)), $\partial f/\partial Y=(\partial f/\partial y)F_{yY}$, and $\partial f/\partial X=\partial f/\partial Z=0$. From the second of (25), compatibility conditions [70] ${\nabla }_0\times \mathbf{F}=\mathbf{0}$ necessitate

$$\begin{array}{c}\hfill \partial F_{xX}/\partial Y=\partial F_{xY}/\partial X=0,\partial F_{zZ}/\partial Y=\partial F_{zY}/\partial Z=0.\end{array}$$

(28)

Forms of $\mathit{\phi }$, ${\mathbf{F}}^E$, ${\mathbf{F}}^{\xi }$, and ${\mathbf{F}}^P$ satisfying (28) are postulated a priori [8], based on Figure 1. The reference configuration is unstressed, and ${\mathbf{F}}^E$ includes the isothermal elastic volume change from initial pressurization by $p_0$. Motion $\mathbf{x}=\mathit{\phi }(\mathbf{X},t)$ and deformation gradient terms, written in $3\times 3$ matrix format, are

$$\begin{array}{cc}\hfill & x=x(X,Y,t),y=y(Y,t),z=z(Z,t);\gamma =J^I{\gamma }^E+{\gamma }^I+{\gamma }^P;\hfill \end{array}$$

(29)

$$\begin{array}{cc}\hfill & \left[{\mathbf{F}}^E(Y,t)\right]={\left(J^E\left(t\right)\right)}^{1/3}\left[\begin{array}{ccc}1& {\gamma }^E(Y,t)& 0\\ 0& 1& 0\\ 0& 0& 1\end{array}\right],\left[{\mathbf{F}}^I(Y,t)\right]=\left[\begin{array}{ccc}1& {\gamma }^I(Y,t)& 0\\ 0& J^I(Y,t)& 0\\ 0& 0& 1\end{array}\right],\hfill \end{array}$$

(30)

$$\begin{array}{cc}\hfill & \left[{\mathbf{F}}^P(Y,t)\right]=\left[\begin{array}{ccc}1& {\gamma }^P(Y,t)& 0\\ 0& 1& 0\\ 0& 0& 1\end{array}\right],\left[\mathbf{F}(Y,t)\right]=\left[\begin{array}{ccc}1& \gamma (Y,t)& 0\\ 0& J^I(Y,t)& 0\\ 0& 0& 1\end{array}\right]{\left(J^E\left(t\right)\right)}^{1/3}.\hfill \end{array}$$

(31)

The thermoelastic term ${\mathbf{F}}^E$ contains spatially homogeneous volume change $J^E$ and shear ${\gamma }^E$. The total shear after thermoelastic volume change in the last of (31) is $\gamma$. Plastic deformation is a simple shear ${\gamma }^P$. Inelastic deformation from damage and melting consists of simple shear ${\gamma }^I$ and strain normal to the band, with volume change $J^I$, both interpolated as follows [41,43,55]:

$$\begin{array}{cc}\hfill & {\gamma }^I(\xi ,\varphi )={\gamma }^{\xi }\left(\xi \right)+{\gamma }^{\varphi }\left(\varphi \right),{\gamma }^{\xi }={\gamma }_0^{\xi }(1-{\iota }^{\xi }\left(\xi \right)),{\gamma }^{\varphi }={\gamma }_0^{\varphi }(1-{\iota }^{\varphi }\left(\varphi \right));\hfill \end{array}$$

(32)

$$\begin{array}{cc}\hfill & J^I(\xi ,\varphi )=J^{\xi }\left(\xi \right)J^{\varphi }\left(\varphi \right)={\displaystyle \frac{J^{\xi }\left(\xi \right)}{1/J^{\varphi }\left(\varphi \right)}}={\displaystyle \frac{1+{\delta }_0^{\xi }(1-{\iota }^{\xi }\left(\xi \right))}{1-{\delta }_0^{\varphi }(1-{\iota }^{\varphi }\left(\varphi \right))}};(1-{\iota }_1^{\xi }){\delta }_0^{\xi }={\displaystyle \frac{{\rho }^{\left(0\right)}}{{\rho }^{\left(1\right)}}}-1.\hfill \end{array}$$

(33)

Interpolation functions between solid and liquid, and between undamaged and failed states, are

$$\begin{array}{cc}\hfill & {\iota }^{\xi }\left(\xi \right)\in [0,{\iota }_1^{\xi }],{\iota }^{\varphi }\left(\varphi \right)\in [0,{\iota }_1^{\varphi }];\hfill \\ \hfill & {\iota }^{\xi }\left(0\right)={\iota }^{\varphi }\left(0\right)=1;{\iota }^{\xi }\left(1\right)={\iota }_1^{\xi }\in [0,1],{\iota }^{\varphi }\left(1\right)={\iota }_1^{\varphi }\in [0,1].\hfill \end{array}$$

(34)

Material constants are ${\gamma }_0^{\xi },{\gamma }_0^{\varphi },{\delta }_0^{\xi }$, and ${\delta }_0^{\varphi }$, any of which can be zero, positive, or negative. These constants are multiplied by $1-{\iota }_1^{\xi }$ or $1-{\iota }_1^{\varphi }$ to give any structure change-induced shear strains and volume changes at $\xi =1$ or $\varphi =1$. Mass densities of solid and fully liquid states are ${\rho }^{\left(0\right)}$ and ${\rho }^{\left(1\right)}$, respectively. When damage manifests physically as induced cavities or pores, then the quantity $(1-{\iota }_1^{\varphi }){\delta }_0^{\varphi }$ can be interpreted as the void volume fraction at the locally failed state. Notice that $J^{\varphi }$ accounts only for volume changes induced during deformation, and not for effects of initial defects (e.g., $J^{\varphi }$ does not account for initial porosity independent of $\varphi$ that is implicitly included in ${\rho }^{\left(0\right)}$).

Inserting ${\mathbf{F}}^E$ of (30), the Cauchy stress of (7) and (8) becomes

$$\begin{array}{cc}\hfill & \left[\mathit{\sigma }\right]={\displaystyle \frac{1}{J^E{J}^I}}\left[\begin{array}{cccc}& -\tilde{p}+{\displaystyle \frac{2}{3}}\mu {\left({\gamma }^E\right)}^2& \mu {\gamma }^E& 0\\ & \mu {\gamma }^E& -\tilde{p}-{\displaystyle \frac{1}{3}}\mu {\left({\gamma }^E\right)}^2& 0\\ & 0& 0& -\tilde{p}-{\displaystyle \frac{1}{3}}\mu {\left({\gamma }^E\right)}^2\end{array}\right],\hfill \end{array}$$

(35)

$$\begin{array}{cc}\hfill & \tilde{p}(J^E,\theta )=-B\{ln{J}^E[1-\frac{1}{2}(B_0^{\prime }-2)ln{J}^E]-A_0(\theta -{\theta }_0)\}.\hfill \end{array}$$

(36)

Three approximations are introduced to simplify (35) and (36) [8]. First, elastic shear is assumed small so terms of $O\left({\left({\gamma }^E\right)}^2\right)$ are negligible. Second, thermal expansion in $\tilde{p}$ is omitted (e.g., $A_0\to 0$), typical in analysis of shear bands [1,11,12,76]. Third, terms of $O\left({\delta }_0^{\xi }\right)$, $O\left({\delta }_0^{\varphi }\right)$ are omitted in the prefactor of (35). This implies local volume changes from melting and porosity remain small. For ferrous metals studied in Section 5 and Section 6, such volume changes, both expansive, cannot exceed $\approx 5$%, which would lead to overestimation of stress, at most, by the same percentage. Thus, (35) reduces to

$$\begin{array}{cc}\hfill & \left[\mathit{\sigma }\right]\approx \left[\begin{array}{ccc}-p_0& \mu {\gamma }^E/J^E& 0\\ \mu {\gamma }^E/J^E& -p_0& 0\\ 0& 0& -p_0\end{array}\right],J^E\approx \underset{{\widehat{J}}^E>0}{arg}\{p_0=-B_0{\displaystyle \frac{ln{\widehat{J}}^E}{{\widehat{J}}^E}}[1-\frac{1}{2}(B_0^{\prime }-2)ln{\widehat{J}}^E]\}.\hfill \end{array}$$

(37)

Since $p\approx p_0=\mathrm{constant}$, $J^E\left(p_0\right)=\mathrm{constant}$ for $t\ge 0^{+}$, consistent with (25).

Initial pressure, if tensile, is assumed small enough that no damage is incurred prior to shear loading, and subsequently, changes in B from shear-induced melting and fracture are ignored in the second of (37). Transient increases to $J^E$ that would be needed to offset reduction of B with increasing $\varphi$ when $p_0<0$ are omitted. Thus, (37) is most accurate for neutral or compressive states with $p_0\ge 0$. Since ${\sigma }_{yy}\approx -p_0$, the second of (26) is now obeyed unconditionally when ${\dot{\upsilon }}_y=0$. The first of (26) is $\partial \tau /\partial y\approx \partial \left(\mu {\gamma }^E\right)/\partial y=J^E\rho {\dot{\upsilon }}_x$. If $\tau \left(t\right)=J^E{\sigma }_{xy}\left(t\right)$ is independent of y, then inertial force is negligible.

Through (30)–(37), dissipation allotments from plastic and inelastic structure deformations of melting and fracture in the energy balance of (24) and entropy inequality of (20) are

$$\begin{array}{cc}\hfill & \left[{\left({\mathbf{F}}^I\right)}^{\mathrm{T}}\overline{\mathbf{S}}{\left({\mathbf{F}}^I\right)}^{-\mathrm{T}}\right]:{\mathbf{L}}^P=\tau {\dot{\gamma }}^P,\tau =J^E{\sigma }_{xy}=\mu {\gamma }^E/J^I\approx \mu {\gamma }^E,{\overline{p}}_0=J^E{p}_0;\hfill \end{array}$$

(38)

$$\begin{array}{cc}\hfill & \left[\overline{\mathbf{S}}{\left({\mathbf{F}}^I\right)}^{-\mathrm{T}}\right]:{\displaystyle \frac{\partial {\mathbf{F}}^I}{\partial \xi }}\dot{\xi }=-[\tau {\gamma }_0^{\xi }-{\displaystyle \frac{\{\tilde{p}-\frac{2}{3}\mu {\left({\gamma }^E\right)}^2\}{\delta }_0^{\xi }}{1+{\delta }_0^{\xi }(1-{\iota }^{\xi })}}]{\displaystyle \frac{\mathrm{d}{\iota }^{\xi }}{\mathrm{d}\xi }}\dot{\xi }\approx -[\tau {\gamma }_0^{\xi }-{\overline{p}}_0{\delta }_0^{\xi }]{\displaystyle \frac{\mathrm{d}{\iota }^{\xi }}{\mathrm{d}\xi }}\dot{\xi },\hfill \end{array}$$

(39)

$$\begin{array}{cc}\hfill & \left[\overline{\mathbf{S}}{\left({\mathbf{F}}^I\right)}^{-\mathrm{T}}\right]:{\displaystyle \frac{\partial {\mathbf{F}}^I}{\partial \varphi }}\dot{\varphi }=-[\tau {\gamma }_0^{\varphi }-{\displaystyle \frac{\{\tilde{p}-\frac{2}{3}\mu {\left({\gamma }^E\right)}^2\}{\delta }_0^{\varphi }}{1-{\delta }_0^{\varphi }(1-{\iota }^{\varphi })}}]{\displaystyle \frac{\mathrm{d}{\iota }^{\varphi }}{\mathrm{d}\varphi }}\dot{\varphi }\approx -[\tau {\gamma }_0^{\varphi }-{\overline{p}}_0{\delta }_0^{\varphi }]{\displaystyle \frac{\mathrm{d}{\iota }^{\varphi }}{\mathrm{d}\varphi }}\dot{\varphi }.\hfill \end{array}$$

(40)

Conjugate forces $\varsigma$ and $\zeta$ of (21) and (22) become, with ${\Gamma }_{\xi }$ and ${\Gamma }_{\varphi }$ constants for brevity,

$$\begin{array}{cc}\hfill \varsigma & \approx -{\mu }_0[\frac{1}{2}\omega (\mathrm{tr}{\tilde{\mathbf{C}}}^E-3)+r_0^{\xi }\overline{R}]{\displaystyle \frac{\mathrm{d}{\iota }^{\xi }}{\mathrm{d}\xi }}-2A_{\xi }\xi (1-\xi )(1-2\xi )-h_T[\theta /{\theta }_T-1]{\displaystyle \frac{\mathrm{d}{\iota }^{\xi }}{\mathrm{d}\xi }}\hfill \end{array}$$

$$\begin{array}{c}\hfill -[\tau {\gamma }_0^{\xi }-{\overline{p}}_0{\delta }_0^{\xi }]{\displaystyle \frac{\mathrm{d}{\iota }^{\xi }}{\mathrm{d}\xi }}+2l_{\xi }{\Gamma }_{\xi }{\nabla }_0^2\xi ,\end{array}$$

(41)

$$\begin{array}{cc}\hfill \zeta & \approx -{\mu }_0\left[\frac{1}{2}(\mathrm{tr}{\tilde{\mathbf{C}}}^E-3)\right]{\iota }^{\xi }{\displaystyle \frac{\mathrm{d}\omega }{\mathrm{d}\varphi }}-E_C{\displaystyle \frac{\mathrm{d}{f}_{\varphi }}{\mathrm{d}\varphi }}-[\tau {\gamma }_0^{\varphi }-{\overline{p}}_0{\delta }_0^{\varphi }]{\displaystyle \frac{\mathrm{d}{\iota }^{\varphi }}{\mathrm{d}\varphi }}+2l_{\varphi }{\Gamma }_{\varphi }{\nabla }_0^2\varphi .\hfill \end{array}$$

(42)

Temperature rate (24) becomes, with generally transient Taylor-Quinney factor $\beta \left(y\right(Y,t),t)$ [77,78] , $\theta =\theta \left(y\right(Y,t),t)$, ${\dot{J}}^E\left(p_0\right)=0$, $A_0=0$, and $\kappa =\mathrm{constant}$ for brevity and simplicity,

$$\begin{array}{cc}\hfill & c_V\dot{\theta }\approx \beta \tau {\dot{\gamma }}^P+[\varsigma +h_T{\displaystyle \frac{\theta }{{\theta }_T}}{\displaystyle \frac{\mathrm{d}{\iota }^{\xi }}{\mathrm{d}\xi }}]\dot{\xi }+\zeta \dot{\varphi }+\kappa {\displaystyle \frac{{\partial }^2\theta }{\partial Y^2}},\beta ={\displaystyle \frac{\tau {\dot{\gamma }}^P-{\mu }_0[1-(1-{\iota }^{\xi })r_0^{\xi }]\left(\frac{\partial \overline{R}}{\partial \chi }\right)\dot{\chi }}{\tau {\dot{\gamma }}^P}}.\hfill \end{array}$$

(43)

In (43), $\beta$ accounts for stored energy of cold work but not energies of fracture and melting.

Let an arbitrary rigid body rotation be ${\mathbf{R}}_0$. Strain energy W and stress $\mathit{\sigma }$ are unaffected by transformations of forms ${\mathbf{F}}^E\to {\mathbf{F}}^E{\mathbf{R}}_0^{\mathrm{T}}$ with ${\mathbf{F}}^I{\mathbf{F}}^P\to {\mathbf{R}}_0{\mathbf{F}}^I{\mathbf{F}}^P$. Different choices of ${\mathbf{R}}_0$ can affect partitioning of dissipation among inelastic deformation modes. Currently setting ${\mathbf{R}}_0=\mathbf{1}$, motivated by physics specific to Figure 1 and metal plasticity, is not arbitrary [70,79].

Note that hydrostatic pressure $p_0$ is fully applied before application of the shear velocity. Volumetric expansion or contraction in $J^E$ is time-independent during the shear process and does not affect the velocity field. The shear velocity and resulting shear displacement are independent of x and automatically fulfill periodicity conditions. Physically, the problem envisions a torsion or simple-shear experiment conducted in a pressurized chamber. In reality, $p_0$ is defined relative to atmospheric pressure ($\approx 101$ kPa); the standard Kolsky-bar experiment is not performed in vacuum. After $p_0$ is applied, the problem is plane strain with respect to the z coordinate.

3.2. Approximations and Reduced Governing Equations

The following additional assumptions are implemented later to facilitate analysis, in conjunction with prior assumptions that $A_0\to 0$, ${\delta }_0^{\xi }$ and ${\delta }_0^{\varphi }$ are small compared to unity, and $B\approx B_0=\mathrm{constant}$:

• Inertia is omitted (${\dot{\upsilon }}_x\to 0$), as in Refs. [8,11,12];
• The shearing response is idealized as rigid-viscoplastic, as in Refs. [1,8,11,12];
• Gradient regularization is omitted ($l_{\varphi }\to 0,l_{\xi }\to 0$) [42,62], and ${\theta }_I\to {\theta }_T\Rightarrow A_{\xi }\to 0$;
• Heat conduction is omitted ($\kappa \to 0$), as in Refs. [8,11,12];
• Taylor–Quinney factor is constant ($\beta {\dot{\gamma }}^P\to {\beta }_0\dot{\gamma },{\beta }_0=\mathrm{constant}\in (0,1]$); Refs. [8,11,12].

From the first assumption, the lone non-trivial equilibrium equation in the first of (26) becomes

$$\begin{array}{cc}\hfill & {\displaystyle \frac{\partial \tau (y,t)}{\partial y}}=0\Rightarrow {\displaystyle \frac{\partial \tau \left(y\right(Y,t),t)}{\partial Y}}=F_{yY}{\displaystyle \frac{\partial \tau }{\partial y}}=0\Rightarrow {\tau }_A=\tau (Y_A,t)=\tau (Y_B,t)={\tau }_B.\hfill \end{array}$$

(44)

Coordinates of any two material points the slab with shear stresses ${\tau }_A$, ${\tau }_B$ are written $Y_A$, $Y_B$. Recall $\tau =J^E{\sigma }_{xy}\approx \mu {\gamma }^E$ and from (30) and (31) that $F_{yY}(Y,t)={\left(J^E\right)}^{1/3}{J}^I(Y,t)>0$. Physical suitability of the first and fourth assumptions (i.e., omission of inertia and conduction) for materials and loading conditions of present interest, namely steels deformed in torsion at rates $\dot{\overline{\gamma }}\in [{10}^3$/s$,{10}^4$/s] is discussed in Refs. [1,8,11,12,61]. Limitations of these assumptions are reconsidered in Section 5.2 and Section 7. Acceleration is more important at much higher rates, conduction at much lower rates.

From the second assumption above, rigid viscoplasticity sets $\tau /\mu \to 0$ but $\tau$ can remain finite. Consistent with this limit, ${\gamma }^E\to 0$, $\tau /{\mu }_0\to 0$, $\tau \to 0$ as ${\iota }^{\xi }\omega \to 0$, and quadratic deviatoric strain energy $\mu (\mathrm{tr}{\tilde{\mathbf{C}}}^E-3)\to 0$. With $J^I$ on the order of unity, the shear strain and shear strain rate, with explicit viscoplastic and inelastic structural deformations, reduce to

$$\begin{array}{cc}\hfill & \gamma \approx {\gamma }^P+{\gamma }_0^{\xi }(1-{\iota }^{\xi })+{\gamma }_0^{\varphi }(1-{\iota }^{\varphi })\ge 0,\dot{\gamma }\approx {\dot{\gamma }}^P-{\gamma }_0^{\varphi }{\displaystyle \frac{\mathrm{d}{\iota }^{\varphi }}{\mathrm{d}\varphi }}\dot{\varphi }-{\gamma }_0^{\xi }{\displaystyle \frac{\mathrm{d}{\iota }^{\xi }}{\mathrm{d}\xi }}\dot{\xi }\ge 0.\hfill \end{array}$$

(45)

If ${\gamma }^{\xi }+{\gamma }^{\varphi }<0$, shearing from slip must exceed that from fracture and melting. If ${\gamma }^{\xi }+{\gamma }^{\varphi }>0$, then ${\gamma }^P<0$ is not impossible.

The third assumption discards some energetic contributions of boundary layers between solid and liquid and between undamaged and fully fractured material. While this assumption neglects certain physics resolved by phase-field theories of gradient type [43,55,56], it allows for modeling of spatial discontinuities in order parameters, and thus does not implicitly forbid jumps in shear strain $\gamma$ and temperature $\theta$ needed for the locally infinite-$\gamma$ description of adiabatic shear bands [8,11,12,14] invoked in Section 4, Section 5 and Section 6. Were the gradient energy contribution from $\xi$ included, a sharp spatial change or jump in $\xi$ would be impossible due to the nearly infinite or infinite energetic barrier from $\Lambda$ of (11). A similar remark applies for the gradient energy contribution from $\varphi$ in (11). Since primary driving forces for local increases in $\xi$ and $\varphi$ are later identified with $\theta$ and $\gamma$, respectively, the same barriers could restrict large increases in $\theta$ and $\gamma$ to zones or bands of finite width. A jump to an extreme value of $\theta$ or $\gamma$ for material in an infinitesimal-width band relative to its surroundings would engender a discontinuity in $\xi$ or $\varphi$ that is inadmissible in a gradient-regularized theory. Conductivity $\kappa >0$ would also restrict the minimum width of a shear band to avoid infinite contributions to dissipation in (20) and temperature rate in (43), as temperature gradients approach infinite magnitudes.

Combining the third assumption with the second,

$$\begin{array}{cc}\hfill \varsigma & \approx -[{\mu }_0{r}_0^{\xi }\overline{R}+h_T\{\theta /{\theta }_T-1\}+\tau {\gamma }_0^{\xi }-{\overline{p}}_0{\delta }_0^{\xi }]{\displaystyle \frac{\mathrm{d}{\iota }^{\xi }}{\mathrm{d}\xi }},\zeta \approx -E_C{\displaystyle \frac{\mathrm{d}{f}_{\varphi }}{\mathrm{d}\varphi }}-[\tau {\gamma }_0^{\varphi }-{\overline{p}}_0{\delta }_0^{\varphi }]{\displaystyle \frac{\mathrm{d}{\iota }^{\varphi }}{\mathrm{d}\varphi }}.\hfill \end{array}$$

(46)

Finally, from the fourth and fifth assumptions, the first inequality in (20), the first equality in (43), and the total cumulative plastic work $W^P$ are approximated, respectively, by

$$\begin{array}{cc}\hfill & {\beta }_0\tau \dot{\gamma }+\varsigma \dot{\xi }+\zeta \dot{\varphi }\gtrsim 0,c_V\dot{\theta }\approx {\beta }_0\tau \dot{\gamma }+[\varsigma +h_T{\displaystyle \frac{\theta }{{\theta }_T}}{\displaystyle \frac{\mathrm{d}{\iota }^{\xi }}{\mathrm{d}\xi }}]\dot{\xi }+\zeta \dot{\varphi },W^P\approx {\int }_0^t\tau \dot{\gamma }\mathrm{d}\widehat{t}={\int }_0^{\gamma }\tau \mathrm{d}\widehat{\gamma }.\hfill \end{array}$$

(47)

From (45) with ${\dot{\gamma }}^E=0$, if ${\gamma }_0^{\xi }\dot{\xi }\ne 0$ or ${\gamma }_0^{\varphi }\dot{\varphi }\ne 0$, then ${\dot{\gamma }}^P\ne \dot{\gamma }$. In that case, the fifth assumption implies $\beta =\beta \left(t\right)={\beta }_0(1+{\dot{\gamma }}^P/{\dot{\gamma }}^I)$ can be transient if ${\beta }_0=\mathrm{constant}$, the latter implicitly affected by dissipative contributions from inelastic structural shears. In Section 5 and Section 6, ${\gamma }_0^{\xi }={\gamma }_0^{\varphi }=0\Rightarrow \beta \to {\beta }_0$.

Models for plasticity, ductile damage, and melting following in Section 3.3, Section 3.4 and Section 3.5 are specialized to the dynamic, adiabatic, pressurized simple shear problem of Section 3.1, simplifying assumptions of Section 3.2, and relatively strong, ductile polycrystalline metals like structural steels. Different models would be needed for other loading regimes and material classes (e.g., quasi-statics, brittle solids).

3.3. Viscoplasticity

A power-law viscoplastic flow rule [8,11,12,13] relates $\dot{\gamma }$ to Kirchhoff shear stress $\tau =J^E{\sigma }_{xy}\ge 0$:

$$\begin{array}{cc}\hfill & \dot{\gamma }=\dot{{\gamma }_0}{(\tau /g)}^{1/m},g=g(\xi ,\varphi ,\chi ,\theta ;p_0)=g_Y(\xi ,\varphi ,p_0)h\left(\chi \right)\lambda \left(\theta \right).\hfill \end{array}$$

(48)

Denoted by ${\dot{\gamma }}_0=\mathrm{constant}\ge 0$ and $m=\mathrm{constant}>0$ are a reference strain rate and rate sensitivity. Flow stress $g\ge 0$ consists of pressure-, phase-, and damage-dependent static yield stress $g_Y\ge 0$, strain hardening (or softening) function $h\ge 0$, and thermal softening (or hardening) function $\lambda \ge 0$.

Internal state variable change $\chi \left(t\right)-{\chi }_0$ is associated with strain hardening, most often linked to increases in dislocation density [70,80]. For monotonically increasing $\gamma \left(t\right)$, the simplest realistic representation of $\chi$ associated with dislocations is, with initial value ${\chi }_0$ close to unity,

$$\begin{array}{c}\hfill \chi (y,t)={\chi }_0\left(Y(y,t)\right)+\gamma (y,t),{\chi }_0\approx 1;\dot{\chi }=\dot{\gamma }\Rightarrow \overline{R}\approx {\displaystyle \frac{1-{\beta }_0}{{\mu }_0}}{\int }_0^{\gamma }{\displaystyle \frac{\tau \mathrm{d}\widehat{\gamma }}{1-(1-{\iota }^{\xi })r_0^{\xi }}}+{\overline{R}}_0.\end{array}$$

(49)

In the rightmost expression, obtained from (43) and the fifth assumption of Section 3.2 with ${\beta }_0\approx \beta$, ${\overline{R}}_0\left(Y\right)\ge 0$ is an initial condition related to stored energy from initial dislocation density at Y.

Fractured or molten material is assumed to have degraded strength. Classical dislocation plasticity theory [70,80] presumes $g_Y$ is proportional to shear modulus $\mu$. Thus $g_Y$ is interpolated akin to $\mu$ in (6) via functions ${\iota }^{\xi }\left(\xi \right)$ and $\omega \left(\varphi \right)$. As in Refs. [8,11,12,13], h and $\lambda$ are power-law forms:

$$\begin{array}{cc}\hfill & g_Y(\xi ,\varphi ,p_0)=g_0\left(p_0\right){\iota }^{\xi }\left(\xi \right)\omega \left(\varphi \right),h\left(\chi \left(\gamma \right)\right)={\chi }_0{(1+\gamma /{\gamma }_0)}^n,\lambda \left(\theta \right)={(\theta /{\theta }_0)}^{\nu }.\hfill \end{array}$$

(50)

Here, $g_0\left(p_0\right)>0$ is strength of the solid with pressure scaling, while ${\gamma }_0$, n, and $\nu$ are dimensionless constants. Strength depends linearly on $p_0$ via the pressure derivative of shear modulus, ${\mu }^{\prime }$ [8]:

$$\begin{array}{c}\hfill g_0\left(p_0\right)=[1+({\mu }^{\prime }/{\mu }_0)p_0]g_0\left(0\right);{\mu }^{\prime }={(\partial \mu /\partial p)}_{\theta ={\theta }_0,p=0}.\end{array}$$

(51)

To avoid unnecessary complexity that would be eliminated by the rigid-viscoplastic assumption, pressure scaling of $\mu$ was omitted in elastic strain energy (5).

Flow stress $\tau$ is, inverting (48), as follows:

$$\begin{array}{cc}\hfill \tau (\gamma (y,t),\dot{\gamma }(y,t),\xi (y,t),\varphi (y,t),\theta (y,t);{\chi }_0\left(y\right),p_0)=& {\chi }_0{g}_0\left(p_0\right){\iota }^{\xi }\left(\xi \right)\omega \left(\varphi \right)\hfill \\ & \times (1+{\displaystyle \frac{\gamma }{{\gamma }_0}}{)}^n({\displaystyle \frac{\theta }{{\theta }_0}}{)}^{\nu }({\displaystyle \frac{\dot{\gamma }}{{\dot{\gamma }}_0}}{)}^m.\hfill \end{array}$$

(52)

In metals, the strain hardening exponent n is usually positive, and thermal softening exponent $\nu$ is usually negative. These conventions are not enforced a priori as restrictions in the theory, however.

The present power-law functions for strain hardening, strain-rate hardening, and thermal softening are sufficient for matching torsion data on steel analyzed in Section 5. Their simple forms facilitate mathematical analysis [8,11,12] while including the necessary basic physical ingredients. Sophisticated models are available elsewhere, for example in Refs. [1,81,82], that may be better-suited for modeling more complicated 3D deformation histories in ductile metals.

Accommodating usual degradation functions from continuum-damage [70,74] and phase-field mechanics [43] the function $\omega \left(\varphi \right)$ first introduced in (6) and now entering (50) is

$$\omega \left(\varphi \right)={\omega }_1+(1-{\omega }_1){(1-\varphi )}^k,\mathrm{d}\omega /\mathrm{d}\varphi =-k(1-{\omega }_1){(1-\varphi )}^{k-1}.$$

(53)

Material constants are $k\ge 1$ and ${\omega }_1\in [0,1]$, recalling the latter allows for remnant strength at $\varphi =1$.

Initial deviation $\delta {\chi }_0\left(Y\right)=1-{\chi }_0\left(Y\right)$, if positive as assigned by convention in Section 4, Section 5 and Section 6, accounts for strength defects. These could be initial micro-cracks, pores [83], texture variations, weak interfaces at grain boundaries [77], inclusions, or another microstructure feature that reduces strength. Deviation can be related to time-independent “damage” parameter ${\tilde{\varphi }}_0$ with linear degradation function ${\tilde{\omega }}_0$:

$$\begin{array}{c}\hfill \delta {\chi }_0\left(Y\right)=1-{\chi }_0\left(Y\right)={\tilde{\varphi }}_0\left(Y\right),{\tilde{\omega }}_0\left({\tilde{\varphi }}_0\right)=1-{\tilde{\varphi }}_0={\chi }_0.\end{array}$$

(54)

This is akin to (53) with $\varphi \to {\tilde{\varphi }}_0$, $k\to 1$, and ${\omega }_1\to 0$. In the present theory, it is advantageous to assign distinct values to ${\tilde{\varphi }}_0$ and ${\varphi }_0=\varphi (t=0)$, whereby ${\varphi }_0=0$ is used as the standard initial condition. This allows ${\tilde{\varphi }}_0$ and $\varphi$ to describe different weakening mechanisms (e.g., grains locally oriented favorably for easy slip, unrelated to ductile fracture).

If the solid has mild rate sensitivity (i.e., m small versus unity), an assumption used in some, but not all, steps of prior analyses [8,11,12] replaces local strain rate in (52) with average $\dot{\overline{\gamma }}$:

$$\begin{array}{cc}\hfill & \tau (\gamma ,\xi ,\varphi ,\theta ;\dot{\overline{\gamma }};{\chi }_0,p_0)\approx {\chi }_0{g}_0\left(p_0\right){\iota }^{\xi }\left(\xi \right)\omega \left(\varphi \right)(1+{\displaystyle \frac{\gamma }{{\gamma }_0}}{)}^n({\displaystyle \frac{\theta }{{\theta }_0}}{)}^{\nu }({\displaystyle \frac{\dot{\overline{\gamma }}}{{\dot{\gamma }}_0}}{)}^m,\dot{\overline{\gamma }}={\displaystyle \frac{{\upsilon }_0}{h_0}}.\hfill \end{array}$$

(55)

More accurate flow stress expression (52) is used in the momentum balance. Approximation (55) is used to estimate dissipative contributions to temperature [11,12] and structure kinetics [8] if $\dot{\gamma }(y,t)$ is unknown.

3.4. Shear Fracture

Classical, elastic-brittle phase-field fracture models [39,43,48,84] are inadequate for describing ductile failure in adiabatic shear bands because they do not account for coupling of plastic deformation to effective fracture toughness and fracture kinetics. Rather, similar to Refs. [31,32,35,36,37,44,85,86], here some fraction of plastic working is used as a driving force for shear fracture.

Let ${\alpha }_0\in [0,{\chi }_0]$ be a dimensionless constant quantifying this fraction. Degradation initiates when a threshold level of plastic work $W^{\varphi }$ has been attained [27,28,35,36,85,87]. Set $W^{\varphi }={\chi }_0{W}_0^{\varphi }[1+({\mu }^{\prime }/{\mu }_0)p_0]$, where $W_0^{\varphi }=\mathrm{constant}\ge 0$. Accordingly, initial defects and tensile pressure are assumed to linearly reduce threshold $W^{\varphi }$, analogously to static yield-strength terms h and $g_Y$ in (52) and (51).

Ensuring net non-negative dissipation from plastic work and ductile fracture, the following kinetic law for the order parameter rate, $\dot{\varphi }$, for dynamic shear degradation is postulated:

$$\begin{array}{cc}\hfill & \zeta \dot{\varphi }=-[{\alpha }_0{\beta }_0/{\chi }_0]\tau \dot{\gamma }\mathsf{H}(W^P-W^{\varphi })\mathsf{H}(1-\varphi )\hfill \\ & \Rightarrow {\beta }_0\tau \dot{\gamma }+\zeta \dot{\varphi }={\beta }_0\tau [1-({\alpha }_0/{\chi }_0)\mathsf{H}(W^P-W^{\varphi })\mathsf{H}(1-\varphi )]\dot{\gamma }\ge 0.\hfill \end{array}$$

(56)

Heaviside function $\mathsf{H}(1-\varphi )$ limits the solution to physical domain $\varphi \in [0,1]$. Substituting (46) into the first of (56) and enforcing $\mathrm{d}\varphi \ge 0$ gives a nonlinear differential equation at each $y\in [0,h]$:

$$\begin{array}{c}\hfill \left[⟨E_C{\displaystyle \frac{\mathrm{d}{f}_{\varphi }}{\mathrm{d}\varphi }}+\{\tau (\varphi ,·){\gamma }_0^{\varphi }-{\overline{p}}_0{\delta }_0^{\varphi }\}{\displaystyle \frac{\mathrm{d}{\iota }^{\varphi }\left(\varphi \right)}{\mathrm{d}\varphi }}⟩\right]\mathrm{d}\varphi =\left[{\displaystyle \frac{{\alpha }_0{\beta }_0}{{\chi }_0}}\tau (\varphi ,·)\mathsf{H}(W^P-W^{\varphi })\mathsf{H}(1-\varphi )\right]\mathrm{d}\gamma ,\end{array}$$

(57)

where $⟨(·)⟩={\displaystyle \frac{1}{2}}[(·)+|(·)\left|\right]$. The right side of (57) is non-negative since $\tau \ge 0$ and $\mathrm{d}\gamma \ge 0$. The $⟨(·)⟩$ operation on the left ensures $\mathrm{d}\varphi \ge 0$ (i.e., irreversible damage), and $\varphi \to 1$ by the $\mathsf{H}(1-\varphi )$ factor on the right when resistance $-\zeta$ within $⟨(·)⟩$ on the left is non-positive. This equation must usually be integrated numerically for $\varphi$ using (52) along with evolution equations for $\xi$ and $\theta$.

To demonstrate model features, apply (55) in each of (47) [8,11,12] and assume ${\gamma }_0^{\varphi }=0$, meaning no explicit inelastic shear strain from fracture. For monotonically increasing $\gamma (y,t)$, assume functional forms $\theta (y,t)=\theta \left(\gamma \right(y,t),y)$ and $\xi (y,t)=\xi \left(\gamma \right(y,t),y)$ exist. Denote ${\gamma }_f\left(y\right)$ as the value of $\gamma (y,t)$ at t when fracture initiates, as $W^P\to W^{\varphi }$. Then (57) is separable and can be integrated for $\varphi \left(\gamma \right)\in [0,1]$ at fixed ${\overline{p}}_0$, ${\chi }_0$, and y:

$$\begin{array}{c}\hfill {\int }_0^{\varphi }⟨{\displaystyle \frac{E_C}{\omega \left(\widehat{\varphi }\right)}}{\displaystyle \frac{\mathrm{d}{f}_{\varphi }}{\mathrm{d}\widehat{\varphi }}}-{\displaystyle \frac{{\overline{p}}_0{\delta }_0^{\varphi }}{\omega \left(\widehat{\varphi }\right)}}{\displaystyle \frac{\mathrm{d}{\iota }^{\varphi }}{\mathrm{d}\widehat{\varphi }}}⟩\mathrm{d}\widehat{\varphi }={\alpha }_0{\beta }_0{g}_0\left({\displaystyle \frac{\dot{\overline{\gamma }}}{{\dot{\gamma }}_0}}{)}^m{\int }_{{\gamma }_f}^{\gamma }{\iota }^{\xi }\left(\xi \left(\widehat{\gamma }\right)\right)\right(1+{\displaystyle \frac{\widehat{\gamma }}{{\gamma }_0}}{)}^n({\displaystyle \frac{\theta \left(\widehat{\gamma }\right)}{{\theta }_0}}{)}^{\nu }\mathrm{d}\widehat{\gamma }.\end{array}$$

(58)

Now take $f_{\varphi }=\varphi$, $k=1$ in (53), ${\iota }^{\varphi }=1-\varphi$, and assume $E_C+{\overline{p}}_0{\delta }_0^{\varphi }>0$. Then (58) produces

$$\begin{array}{c}\hfill \varphi \left(\gamma \right)=min\left[{\displaystyle \frac{1-exp\{-A_f{W}_f^P\left(\gamma \right)\}}{1-{\omega }_1}},1\right];A_f={\displaystyle \frac{{\alpha }_0{\beta }_0(1-{\omega }_1)}{{\chi }_0(E_C+{\overline{p}}_0{\delta }_0^{\varphi })}},W_f^P={\int }_{{\gamma }_f}^{\gamma }{\displaystyle \frac{\tau }{\omega }}\mathrm{d}\widehat{\gamma }.\end{array}$$

(59)

Plastic work $W_f^P\to \infty$, $\varphi \to 1$. When $\gamma (y,t)\le {\gamma }_f\left(y\right)$, the trivial solution is $\varphi (y,t)=0$, and $\mathrm{d}\varphi =0$ when $\tau =0$. Resistance to fracture at a given value of $\gamma$ is afforded by $E_C$; large ${\alpha }_0$, ${\beta }_0$ and defects $\delta {\chi }_0=1-{\chi }_0\ge 0$ promote fracture. If $E_C\le {\overline{p}}_0{\delta }_0^{\varphi }$, with ductile damage expansive (i.e., ${\delta }_0^{\varphi }>0$) tensile pressure $-{\overline{p}}_0\ge E_C/{\delta }_0^{\varphi }$ causes fracture as soon as $W^P>W^{\varphi }$ via $\varphi \to 1$ in (57).

Though not exercised in this work, the theory admits $W^{\varphi }$ to depend on $\theta$, $\chi$, and $\xi$ in addition to $p_0$. Temperature dependence may be useful to capture ductile–brittle transitions. Dependence on $\xi$ is likely redundant since $g_Y$ already reduces upon melting via ${\iota }^{\xi }$ in (50).

3.5. Melting

To ensure non-negative dissipation from melting or solidification, the Allen–Cahn or Ginzburg–Landau equation [55,56,57] is often invoked for kinetics of $\xi$, especially when modeling boundary layers of partially molten material. Here, since gradient regularization is omitted and solidification is less relevant, a linear relaxation model for phase transformations [71,88], also obeying non-negative dissipation, is instead adapted for melting. Letting $t_R^{\xi }\ge 0$ be a relaxation time constant,

$$\begin{array}{c}\hfill t_R^{\xi }\dot{\xi }=\left\{\begin{array}{cc}⟨\overline{\xi }-\xi ⟩,\hfill & (\varsigma >0),\hfill \\ -⟨\xi -\overline{\xi }⟩,\hfill & (\varsigma \le 0)\hfill \end{array}\right.\Rightarrow \varsigma \dot{\xi }\ge 0.\end{array}$$

(60)

The metastable melt fraction is $\overline{\xi }$. With ${\alpha }_{\xi }\ge 0$ and ${\beta }_{\xi }>0$ kinetic barriers, the following ordinary differential equation (ODE) is posited for melting but not solidification, akin to Refs. [71,88]:

$$\begin{array}{c}\hfill \mathrm{d}\overline{\xi }=-{\iota }^{\prime }\mathrm{d}\left[{\displaystyle \frac{⟨-\varsigma /{\iota }^{\prime }-{\alpha }_{\xi }⟩}{{\beta }_{\xi }}}\right]\mathsf{H}(1-\overline{\xi });{\iota }^{\prime }\left(\overline{\xi }\right)={\displaystyle \frac{\mathrm{d}{\iota }^{\xi }\left(\overline{\xi }\right)}{\mathrm{d}\overline{\xi }}}\le 0,{\iota }^{\prime }\left(1\right)=0.\end{array}$$

(61)

The Heaviside function restricts the solution to $\overline{\xi }\le 1$. This differential equation must generally be solved numerically for $\overline{\xi }$ since $\varsigma$ in (46) depends implicitly on $\overline{\xi }$. Dividing by ${\iota }^{\prime }$ and integrating,

$$\begin{array}{c}\hfill {\int }_0^{\overline{\xi }}{\displaystyle \frac{\mathrm{d}\xi }{{\iota }^{\prime }}}=-{\displaystyle \frac{1}{{\beta }_{\xi }}}⟨{\mu }_0{r}_0^{\xi }\overline{R}+{\displaystyle \frac{h_T}{{\theta }_T}}\{\theta -{\theta }_T\}+\{\tau {\gamma }_0^{\xi }-{\overline{p}}_0{\delta }_0^{\xi }\}-{\alpha }_{\xi }⟩,(\overline{\xi }\le 1).\end{array}$$

(62)

Consider another analytical example to illustrate concepts and model features. When $t_R^{\xi }\dot{\overline{\gamma }}\ll 1$, the left side of (60) is assumed to vanish, whereby $\xi \approx \overline{\xi }$. Assume such conditions hold, meaning melting completes at time scales that are fast relative to the loading time. Continuing to assume forms $\theta \left(\gamma \right(y,t),y)$ and $\varphi \left(\gamma \right(y,t),y)$ like those in (58) exist, and choosing

$$\begin{array}{c}\hfill {\iota }^{\xi }\left(\xi \right)={\iota }_1^{\xi }+(1-{\iota }_1^{\xi }){(1-\xi )}^2,{\iota }^{\prime }=\mathrm{d}{\iota }^{\xi }/\mathrm{d}\xi =-2(1-{\iota }_1^{\xi })(1-\xi )\in [-2(1-{\iota }_1^{\xi }),0],\end{array}$$

(63)

for example, (62) can be solved analytically as

$$\begin{array}{c}\hfill \xi \left(\gamma \right)=1-exp[-{\displaystyle \frac{2(1-{\iota }_1^{\xi })}{{\beta }_{\xi }}}⟨\mathsf{\Xi }\left(\gamma \right)⟩],\mathsf{\Xi }={\displaystyle \frac{h_T}{{\theta }_T}}\{\theta -{\theta }_T\}+{\mu }_0{r}_0^{\xi }\overline{R}+\tau {\gamma }_0^{\xi }-{\overline{p}}_0{\delta }_0^{\xi }-{\alpha }_{\xi }.\end{array}$$

(64)

If all terms except the first in $\mathsf{\Xi }$ vanish, then the local melt fraction $\xi =0$ for $\theta \le {\theta }_T$ and $\xi$ increases with $\theta$ for $\theta >{\theta }_T$. Solidification is possible (i.e., $\mathrm{d}\xi <0$) in that case if $\theta$ subsequently decreases. However, (61) with $\overline{\xi }\to \xi$ ensures non-negative dissipation $\varsigma \mathrm{d}\xi \ge 0$ only when $\mathrm{d}\xi \ge 0$, with $\varsigma <0\Rightarrow \mathrm{d}\xi =0$. The case $\mathrm{d}\xi <0$ when $\varsigma >0$ is not ruled out. In calculations, non-negative dissipation can be enforced by a constraint $\mathrm{d}\xi =⟨\mathrm{d}\overline{\xi }⟩$. Solidification is thereby eliminated. A different ODE involving some sign changes to (61) is needed to model dissipative, metastable reverse transitions (i.e., solidification) [71,88].

3.6. Temperature

Substituting (46), (55), and (56) into (47), for $\varphi \le 1$ and ${\gamma }_0^{\xi }=0$ as invoked in Section 4, Section 5 and Section 6, gives

$$\begin{array}{cc}\hfill \dot{\theta }& ={\displaystyle \frac{{\beta }_0}{c_V}}[1-{\displaystyle \frac{{\alpha }_0}{{\chi }_0}}\mathsf{H}(W^P-W^{\varphi })]{\chi }_0{g}_0\omega {\iota }^{\xi }(1+{\displaystyle \frac{\gamma }{{\gamma }_0}}{)}^n({\displaystyle \frac{\theta }{{\theta }_0}}{)}^{\nu }({\displaystyle \frac{\dot{\overline{\gamma }}}{{\dot{\gamma }}_0}}{)}^m\dot{\gamma }\hfill \\ & -{\displaystyle \frac{[{\mu }_0{r}_0^{\xi }\overline{R}-h_T-{\overline{p}}_0{\delta }_0^{\xi }]}{c_V}}{\displaystyle \frac{\mathrm{d}{\iota }^{\xi }}{\mathrm{d}\xi }}\dot{\xi }.\hfill \end{array}$$

(65)

This nonlinear differential equation must generally be solved numerically for $\theta (\gamma ,y)$ at each $y\in [0,h]$, in conjunction with (57) for $\varphi (\gamma ,y)$, (60) for $\xi (\gamma ,y)$, and (49) for $\overline{R}(\gamma ,y)$. If functional forms $\varphi \left(\gamma \right(y,t),y)$, $\xi \left(\gamma \right(y,t),y)$, and $\overline{R}(\gamma (y,t),y)$ exist, then at fixed y (65) gives

$$\begin{array}{cc}\hfill {\displaystyle \frac{\mathrm{d}\theta }{\mathrm{d}\gamma }}& ={\displaystyle \frac{{\beta }_0}{c_V}}[1-{\displaystyle \frac{{\alpha }_0}{{\chi }_0}}\mathsf{H}(W^P-W^{\varphi })]{\chi }_0{g}_0\omega {\iota }^{\xi }(1+{\displaystyle \frac{\gamma }{{\gamma }_0}}{)}^n({\displaystyle \frac{\theta }{{\theta }_0}}{)}^{\nu }({\displaystyle \frac{\dot{\overline{\gamma }}}{{\dot{\gamma }}_0}}{)}^m\hfill \\ & -{\displaystyle \frac{[{\mu }_0{r}_0^{\xi }\overline{R}-h_T-{\overline{p}}_0{\delta }_0^{\xi }]}{c_V}}{\displaystyle \frac{\mathrm{d}{\iota }^{\xi }}{\mathrm{d}\xi }}{\displaystyle \frac{\mathrm{d}\xi }{\mathrm{d}\gamma }}.\hfill \end{array}$$

(66)

This equation likewise must be solved numerically. But if melting never occurs, $\xi =0\Rightarrow {\iota }^{\xi }=1$, and, given function $\varphi \left(\gamma \right)$ at y, (66) can be separated and integrated from $\theta (y,0)={\theta }_i\left(y\right)$ as

$$\begin{array}{cc}\hfill & {\theta }^{-\nu }\mathrm{d}\theta =\left\{{\displaystyle \frac{{\beta }_0}{c_V{\theta }_0^{\nu }}}[1-({\alpha }_0/{\chi }_0)\mathsf{H}(W^P-W^{\varphi })]{\chi }_0{g}_0\omega \right(1+{\displaystyle \frac{\gamma }{{\gamma }_0}}{)}^n\left({\displaystyle \frac{\dot{\overline{\gamma }}}{{\dot{\gamma }}_0}}{)}^m\right\}\mathrm{d}\gamma \Rightarrow \hfill \\ \hfill & \theta \left(\gamma \right)=[{\theta }_i^{1-\nu }+{\displaystyle \frac{(1-\nu ){\beta }_0{\chi }_0{g}_0{\gamma }_0}{(1+n)c_V{\theta }_0^{\nu }}}({\displaystyle \frac{\dot{\overline{\gamma }}}{{\dot{\gamma }}_0}}{)}^m\left\{\right(1+{\displaystyle \frac{{\gamma }_f}{{\gamma }_0}}{)}^{1+n}-1\}\hfill \\ \hfill & +{\displaystyle \frac{(1-\nu )({\chi }_0-{\alpha }_0){\beta }_0{g}_0}{c_V{\theta }_0^{\nu }}}\left({\displaystyle \frac{\dot{\overline{\gamma }}}{{\dot{\gamma }}_0}}{)}^m{\int }_{{\gamma }_f}^{\gamma }\omega \left(\varphi \left(\widehat{\gamma }\right)\right)\right(1+{\displaystyle \frac{\widehat{\gamma }}{{\gamma }_0}}{)}^n\mathrm{d}\widehat{\gamma }{]}^{\frac{1}{1-\nu }},\left(\mathrm{if}\mathrm{no}\mathrm{melting}\right).\hfill \end{array}$$

(67)

The solution for $\theta \left(\gamma \right)$ in (67) presumes fracture occurs during the strain history, that is, $\gamma \ge {\gamma }_f$. If $\gamma <{\gamma }_f$, (67) holds with ${\gamma }_f\to \gamma$ such that the integral embedded on the right involving $\omega$ vanishes. In the latter case, the analytical solution matches Ref. [8] in the absence of phase transformations.

4. Localization and Numerical Methods

4.1. Failure Modes

Three different shear failure criteria are defined:

• Shear banding. This is the $L_{\infty }$ localization definition of Molinari and Clifton [11,12,14] also used in Ref. [8]. With reference to the last of (44), failure by localization of shear strain $\gamma (Y,t)$ occurs at material point B with $Y=Y_B$ and time $t_c$ when $\gamma (Y_B,t)/\gamma (Y_A,t)={\gamma }_B\left(t\right)/{\gamma }_A\left(t\right)\to \infty$ with increasing time $t\ge t_c$ for every point A with $Y_A\ne Y_B$. If $\dot{\gamma }$ remains bounded, $\tau \to 0$ as ${\gamma }_B\to \infty$, meaning shear stress vanishes at some time $t>t_c$.
• Shear fracture. As in phase-field and continuum damage mechanics, shear fracture occurs when order parameter $\varphi \to 1$. In the present analysis, shear fracture will generally occur earliest at a point $Y_B$ due to an initial defect. If ${\omega }_1=0$ in (53), then $\tau \to 0$ upon shear fracture. If ${\omega }_1>0$, some (small) fraction of strength can be maintained, depending on whether shear banding or melting take place concurrently.
• Melting. Failure by melting occurs when order parameter $\xi \to 1$. In the present analysis, melting will tend to occur first where temperature rise is largest, which correlates with high-strain regions triggered by initial defects (e.g., at point $Y_B$). In (63), $\tau \to 0$ as $\xi \to 1$ if ${\iota }_1^{\xi }=0$. But if ${\iota }_1^{\xi }>0$, then some fraction of strength can be maintained depending on whether shear banding or shear fracture occur simultaneously.

Shear band failure, by definition, requires infinite strain at $Y_B$. Shear fracture and melting may or may not mandate infinite strain, depending on assumptions and parameters entering their governing equations. For example, ${\gamma }_B\to \infty$ is required for $\varphi \to 1$ in (59) if ${\omega }_1=0$, but not if ${\omega }_1>0$. The model in (64) requires ${\gamma }_B\to \infty$ to approach infinite $\theta$ or $\overline{R}$ for $\xi \to 1$. If infinite strains are not required, fracture or melt failure can precede shear band failure. Depending on constitutive parameters for viscoplasticity, fracture, and melting, one or more failure modes may be impossible. Using a different theory, phase-field simulations [33] suggested a tendency for fracture to dominate shear band instability and failure in steel under dynamic torsion as applied strain rate increases.

First consider failure by shear banding. Equality ${\tau }_A^{1/m}={\tau }_B^{1/m}$ of (44) is integrated to any time $t=t_a>0$, with integration limits ${\gamma }_A=\gamma (Y_A,t_a)$ and ${\gamma }_B=\gamma (Y_B,t_a)$, initial conditions ${\chi }_{0A}={\chi }_0\left(Y_A\right)$, ${\chi }_{0B}={\chi }_0\left(Y_B\right)$, and flow stress function (52). Then changing variables and dividing by $g_0^{1/m}/{\dot{\gamma }}_0$, localization integrals are obtained by eliminating $\dot{\gamma }$:

$$\begin{array}{cc}\hfill & {\int }_0^{t_a}\left[g_0{\chi }_{0A}\omega \right(\varphi \left(\gamma (Y_A,t)\right){\iota }^{\xi }{\left(\xi \left(\gamma (Y_A,t)\right)\right]}^{1/m}{[1+\gamma (Y_A,t)/{\gamma }_0]}^{n/m}{[\theta \left(\gamma (Y_A,t)\right)/{\theta }_0]}^{\nu /m}{\dot{\gamma }}_0^{-1}\dot{\gamma }(Y_A,t)\mathrm{d}t\hfill \\ \hfill & ={\int }_0^{t_a}\left[g_0{\chi }_{0B}\omega \right(\varphi \left(\gamma (Y_B,t)\right){\iota }^{\xi }{\left(\xi \left(\gamma (Y_B,t)\right)\right]}^{1/m}{[1+\gamma (Y_B,t)/{\gamma }_0]}^{n/m}{[\theta \left(\gamma (Y_B,t)\right)/{\theta }_0]}^{\nu /m}{\dot{\gamma }}_0^{-1}\dot{\gamma }(Y_B,t)\mathrm{d}t\hfill \\ \hfill & \Rightarrow {\int }_0^{{\gamma }_A}{\chi }_{0A}^{1/m}{\left\{\omega \left(\varphi \left(\gamma \right)\right){\iota }^{\xi }\left(\xi \left(\gamma \right)\right)\right\}}^{1/m}{(1+\gamma /{\gamma }_0)}^{n/m}{[\theta \left(\gamma \right)/{\theta }_0]}^{\nu /m}\mathrm{d}\gamma \hfill \\ \hfill & ={\int }_0^{{\gamma }_B}{\chi }_{0B}^{1/m}{\left\{\omega \left(\varphi \left(\gamma \right)\right){\iota }^{\xi }\left(\xi \left(\gamma \right)\right)\right\}}^{1/m}{(1+\gamma /{\gamma }_0)}^{n/m}{[\theta \left(\gamma \right)/{\theta }_0]}^{\nu /m}\mathrm{d}\gamma .\hfill \end{array}$$

(68)

Dependence of $\xi$ and $\varphi$ on Y independently of $\gamma$ is permitted but is not written explicitly in (68). If $L_{\infty }$ localization occurs, $t_a\to t_c$, ${\gamma }_B\to \infty$, and ${\gamma }_A\to {\gamma }_{Ac}$, where ${\gamma }_{Ac}>0$ is finite:

$$\begin{array}{cc}\hfill & {\int }_0^{{\gamma }_{Ac}}{\chi }_{0A}^{1/m}{\left\{\omega \left(\varphi \left(\gamma \right)\right){\iota }^{\xi }\left(\xi \left(\gamma \right)\right)\right\}}^{1/m}{(1+\gamma /{\gamma }_0)}^{n/m}{[\theta \left(\gamma \right)/{\theta }_0]}^{\nu /m}\mathrm{d}\gamma \hfill \\ \hfill & =\underset{{\gamma }_B\to \infty }{lim}{\int }_0^{{\gamma }_B}{\chi }_{0B}^{1/m}{\left\{\omega \left(\varphi \left(\gamma \right)\right){\iota }^{\xi }\left(\xi \left(\gamma \right)\right)\right\}}^{1/m}{(1+\gamma /{\gamma }_0)}^{n/m}{[\theta \left(\gamma \right)/{\theta }_0]}^{\nu /m}\mathrm{d}\gamma \hfill \\ & =\underset{{\gamma }_B\to \infty }{lim}{\int }_0^{{\gamma }_B}I\left(\gamma \right)\mathrm{d}\gamma .\hfill \end{array}$$

(69)

As explained in Refs. [11,12], because ${\gamma }_{Ac}$ is finite by definition, the integrals on the left, and thus the right, sides of (69) must all be bounded. This means $L_{\infty }$ localization occurs if and only if $I\left(\gamma \right)$ is integrable as $\gamma \to \infty$. In Refs. [8,11,12], bounds on viscoplastic properties n, $\nu$, and m were derived for which $L_{\infty }$ localization (i.e., shear band failure) is possible. These prior derivations, based on power-law viscoplasticity and analytical solutions for $\theta =\theta \left(\gamma \right)$, did not consider shear fracture or melting. In the current setting, three possibilities emerge:

• Order parameters $\varphi$ or $\xi$ evolve with $\gamma$ as $\gamma \to \infty$. No definite criteria for the possibility of $L_{\infty }$ localization are derived since $\theta$, $\omega$, and ${\iota }^{\xi }$ depend on $\gamma$ in forms not known analytically.
• Either (or both of) $\varphi \to 1$ or $\xi \to 1$ occurs at finite ${\gamma }_B$ with ${\omega }_1=0$ or ${\iota }_1^{\xi }=0$. In this case, fracture or melt failure precedes shear band failure; the latter never occurs since ${\gamma }_B$ is finite.
• Both $\varphi$ and $\xi$ attain fixed terminal values less than unity, or attain unit values with ${\omega }_1>0$ and ${\iota }_1^{\xi }>0$, at finite ${\gamma }_B$. In this case, since $\varphi$ and $\xi$ cease to evolve, they do not influence behavior of $\theta \left(\gamma \right)$ in (67) as $\gamma \to \infty$, and $\omega$ and ${\iota }^{\varphi }$ become nonzero constants. Thus, the original criterion for the possibility of $L_{\infty }$ failure applies (see derivations in Refs. [8,11,12]):

  $$\begin{array}{c}\hfill \nu +n+(1-\nu )m<0,[\forall m>0,\nu <1],\end{array}$$

  (70)

  most valid for $m\ll 1$. A Newtonian fluid is recovered for $n=0$ and $m=1$, whereby (70) is violated. A slightly different analysis of non-hardening ($n=0$) materials [12] gives the localization criterion $\nu +m<0$, also violated for any Newtonian fluid with $\nu \ge -1$. Hence, Newtonian viscosity of molten material must be omitted for $L_{\infty }$ failure, as done herein.

Next consider failure by fracture in the context of (59). If ${\omega }_1>0$, shear fracture is possible at finite $\gamma$, necessarily preceding failure by shear banding or melting. However, as some strength is maintained when ${\omega }_1>0$, residual material can still fail by melting, and possibly, shear banding. If ${\omega }_1=0$, then $\gamma \to \infty \Rightarrow W_f^P\to \infty \Rightarrow \varphi \to 1$. Failure by shear fracture, melting, and potential shear banding can take place concurrently as $\gamma \to \infty$, but criterion (70) does not necessarily hold.

Lastly consider failure by melting in the context of heuristic model (64) with ${\gamma }_0^{\xi }=0$, $h_T>0$, and $a_{\xi }=\mathrm{constant}$. Since $\overline{R}$ is non-negative by (49), $\theta \left(\gamma \right)\to \infty \Rightarrow \mathsf{\Xi }\to \infty \Rightarrow \xi \to 1$. It is anticipated, but not proven, that melt failure occurs iff $\gamma \to \infty$ with $\omega >0$, meaning complete melting at infinite strain if complete strength loss from fracture has not occurred already. In contrast, if $\omega \to 0\Rightarrow \tau \to 0$ at finite $\gamma$, then failure by melting, like failure by shear banding, does not arise, since plastic dissipation supplying a temperature rise ceases and $\overline{R}$ becomes constant after shear fracture. If shear fracture does not occur at finite $\gamma$, then simultaneous shear banding, melt failure, and shear fracture are possible as $\gamma \to \infty$, but (70) need not necessarily apply for shear banding.

4.2. Homogeneous Solutions

Henceforth, the analysis allows non-uniform ${\chi }_0={\chi }_0\left(Y\right)$ and sets ${\theta }_i={\theta }_0=\mathrm{constant}$. All other physical properties are constant over ${\Omega }_0$. If ${\chi }_0$ is uniform, $L_{\infty }$ localization cannot occur: all points Y are indistinguishable so will share the same stress–strain–temperature history. Failure by shear fracture and melting remains possible. These could occur at finite or infinite $\gamma$. For homogeneous conditions, the entire slab would fracture or melt simultaneously. Average strain $\overline{\gamma }$ and defect parameter ${\overline{\chi }}_0$ in the slab, whose average strain rate is $\dot{\overline{\gamma }}$ since ${\upsilon }_0=\mathrm{constant}$, with $\widehat{y}={\left(J^E\right)}^{1/3}Y$, are

$$\begin{array}{c}\hfill \overline{\gamma }\left(t\right)={\displaystyle \frac{{\upsilon }_{0}t}{h_0}}={\displaystyle \frac{1}{h_0}}{\int }_0^{h_0}\gamma \left(Y\left(\widehat{y}\right)\right)\mathrm{d}\widehat{y},{\overline{\chi }}_0=1-\delta {\overline{\chi }}_0={\displaystyle \frac{1}{h_0}}{\int }_0^{h_0}{\chi }_0\left(Y\left(\widehat{y}\right)\right)\mathrm{d}\widehat{y}.\end{array}$$

(71)

Factor ${\left(J^E\right)}^{1/3}$ accounts for $h_0$ being the coordinate of the top of the slab after application of $p_0$ in Figure 1 and kinematic ansatz (29)–(31). If $p_0=0$, then $\widehat{y}=Y$.

For homogeneous conditions, stress from (52) is, at fixed $p_0$, $\dot{\gamma }=\dot{\overline{\gamma }}$, and ${\chi }_0={\overline{\chi }}_0$,

$$\begin{array}{c}\hfill \overline{\tau }(\overline{\gamma },\xi \left(\overline{\gamma }\right),\varphi \left(\overline{\gamma }\right),\theta \left(\overline{\gamma }\right))=g_0{\overline{\chi }}_0{\iota }^{\xi }\left(\xi \left(\overline{\gamma }\right)\right)\omega \left(\varphi \left(\overline{\gamma }\right)\right){(1+\overline{\gamma }/{\gamma }_0)}^n{[\theta \left(\overline{\gamma }\right)/{\theta }_0]}^{\nu }{[\dot{\overline{\gamma }}/{\dot{\gamma }}_0]}^m.\end{array}$$

(72)

Order parameters and temperature are uniform, but functions $\varphi \left(\gamma \right)$, $\xi \left(\gamma \right)$, and $\theta \left(\gamma \right)$ are not known analytically except in degenerate cases. Rather, (57), (61), and (66) comprise a set of three coupled ODEs to be integrated numerically, concurrently with (72), over the strain history $\gamma \left(t\right)$:

$$\begin{array}{c}\hfill \mathrm{d}\varphi /\mathrm{d}\gamma ={\mathcal{F}}_{\varphi }(\gamma ,\xi ,\varphi ,\theta ),\mathrm{d}\xi /\mathrm{d}\gamma ={\mathcal{F}}_{\xi }(\gamma ,\xi ,\varphi ,\theta ),\mathrm{d}\theta /\mathrm{d}\gamma ={\mathcal{F}}_{\theta }(\gamma ,\xi ,\varphi ,\theta ).\end{array}$$

(73)

Initial conditions prescribed for (73) are $\varphi \left(0\right)=\xi \left(0\right)={\overline{R}}_0=0$ and $\theta \left(0\right)={\theta }_0$.

4.3. Localization Calculations

Among all possible positions Y in the slab, localization ensues at the earliest possible $t_c$, at point $Y=Y_B$, for which the rightmost integral in (69) is a minimum [11,12]. Shear band failure, if occurring, commences at $Y_B=\mathrm{argmax}\left\{\delta {\chi }_0\right\}$ where ${\chi }_{0B}$ is a minimum. This follows from the integrand of ${\int }_0^{t_c}{\tau }^{1/m}\mathrm{d}t$ in (68) being non-negative and approaching zero only as $t\to t_c\iff {\gamma }_B\to \infty$ at B. This threshold integral for localization at $Y_B$ drops as ${\chi }_{0B}$ decreases because ${\chi }_0>0$ and $m>0$. For $m\ll 1$, the localization integral is very sensitive to the perturbation $\delta {\chi }_0$ [8,11,12].

A shear band approaches a singular surface at $Y_B$ across which displacement has a jump discontinuity as $\gamma \to \infty$. It is assumed that $\gamma$ and $\dot{\gamma }$ are continuous functions of Y except at singular point(s) $Y_B$ at $t\ge t_c$. In the shear band, from (68) and (69), ${\tau }^{1/m}/\dot{\gamma }\to 0$ at B as $t\to t_c$. At $t<t_c$, since $\gamma \left(Y\right)$ is continuous, ${\gamma }_A$ at at least one location $Y_A$ (that can in principle vary with t) must match $\overline{\gamma }={\upsilon }_{0}t/h_0$. If this $Y_A$ is time-independent, then ${\dot{\gamma }}_A=\dot{\overline{\gamma }}={\upsilon }_0/h_0$ identically. Stress exactly from (52) in that scenario, otherwise approximated by (55) at each $Y_A$, is given by (72) for $t<t_c$. From (44), this value of $\tau$ is equally valid for the entire Y-domain for $t<t_c$. Equations (73) are likewise valid to the same order of approximation for $t<t_c$, with estimate ${\chi }_0\approx {\overline{\chi }}_0$ in ${\mathcal{F}}_{\xi }$ and ${\mathcal{F}}_{\theta }$ [8,12,14], noting ${\mathcal{F}}_{\varphi }$ does not depend on ${\chi }_0$. With these assumptions, $\dot{\gamma }$ affects the solution only through $\tau$, and since $\tau$ is uniform over ${\Omega }_0$, it follows that $\theta$, $\varphi$, and $\xi$ are suitably approximate functions only of $\gamma$ at each point Y, for given loading and initial conditions ${\upsilon }_0$, $p_0$, and ${\overline{\chi }}_0$.

Computation of average localization strain ${\overline{\gamma }}_c$ proceeds as in Ref. [8]. Point $Y_B$ is that for which $Y_B=\mathrm{argmax}\left\{\delta {\chi }_0\left(Y\right)\right\}=\mathrm{argmin}\left\{{\chi }_0\left(Y\right)\right\}$. A numerical value of the right integral in (69) is found as ${\gamma }_B\to \infty$. This integral converges (diverges) if $L_{\infty }$ localization is possible (impossible). If converged, the left of (69) is set to this value at all $Y_A$ where ${\chi }_{0A}>{\chi }_{0B}$ and solved for ${\gamma }_{Ac}\left(Y\right)$ at each $Y\ne Y_B$. Critical strain ${\overline{\gamma }}_c$ is lastly found by integrating $\gamma ={\gamma }_{Ac}\left(Y\right)$ over Y in (71). Letting $I\left(\gamma \right(Y\left)\right)$ be any integrand in (69) and setting ${\gamma }_{Ac}\left(Y\right)=0$ at $Y=Y_B$ to exclude singularities [11,12],

$${\gamma }_{Ac}=\underset{{\gamma }_A\in (0,\infty )}{\arg 0}\left[{\int }_0^{{\gamma }_A}I\left(\gamma \left(Y_A\right)\right)\mathrm{d}\gamma -\underset{{\gamma }_B\to \infty }{lim}{\int }_0^{{\gamma }_B}I\left(\gamma \left(Y_B\right)\right)\mathrm{d}\gamma \right],{\overline{\gamma }}_c={\displaystyle \frac{1}{h_0}}{\int }_0^{h_0}{\gamma }_{Ac}\left(Y\left(\widehat{y}\right)\right)\mathrm{d}\widehat{y}.$$

(74)

Numerical iteration is used to solve the first of (74), and numerical integration to solve the second of (74). The localization threshold integral on the right of (69), and thus ${\overline{\gamma }}_c$ and $t_c$, are affected by transients in $\varphi$ and $\xi$; how so depends on properties and is not obvious from inspection. As strain in the vicinity of the band accommodates more of the average, $\gamma$ drops elsewhere for the same $\overline{\gamma }$.

Previous calculations [8,11,12] did not seek to model degradation and failure within the adiabatic shear band. Therein, $\overline{\gamma }={\overline{\gamma }}_c$ for $t\ge t_c$, and the drop to zero stress upon localization was modeled abruptly (e.g., $\overline{\tau }=0$ for $t>t_c$). A different approach is taken in the present work, similar to Refs. [27,28,47]. These studies likewise used plastic work-threshold-based damage models for adiabatic shear failure to capture gradual post-localization stress decay as witnessed in torsion experiments on iron and steels (e.g., [5,6,60]). Recall ${\overline{\gamma }}_c$ of (74) is the average strain in the slab that numerically excludes the contribution of the core of the fully formed shear band at $Y_B$: this core is infinitesimally wide but supports infinite shear strain ${\gamma }_{Bc}\to \infty$. The latter’s contribution, from a discrete zone wherein shear fracture tends to concentrate, is represented by effective jump in shear displacement ${\Delta }_{\varphi }\left(t\right)\ge 0$ that can be formally derived using Gauss’s theorem [73,77]:

$$\begin{array}{c}\hfill \overline{\gamma }\left(t\right)={\overline{\gamma }}_c+{\Delta }_{\varphi }\left(t\right)/h_0,[\forall t\ge t_c;{\Delta }_{\varphi }\left(t\right)=0\forall t\le t_c].\end{array}$$

(75)

Post-localization shear displacement jump ${\Delta }_{\varphi }$ need not be calculated explicitly, but it can be using $\overline{\gamma }={\upsilon }_{0}t/h_0$ and ${\overline{\gamma }}_c$ from (74). The average strain $\overline{\gamma }$ in (75) is identified with $\overline{\gamma }$ in (72) to calculate stress $\overline{\tau }$ for $t>t_c\leftrightarrow \overline{\gamma }>{\overline{\gamma }}_c$ and ${\overline{\chi }}_0<1$. Physical consistency of this post-localization stress calculation requires that ${\overline{\gamma }}_c$ match the applied strain needed for ductile shear fracture to initiate under macroscopically homogeneous deformation, as in (72) of Section 4.2. Only the average stress decay is continuously depicted for the time history $t>t_c$. Transients of local state variable fields $\gamma$, $\theta$, $\varphi$, and $\xi$ are not modeled for the entire time history $t>t_c$. However, the limit analysis does produce contours ${(·)}_c$ representing state variables at the final, failed material state as $\overline{\tau }\to 0$ and $t\gg t_c$.

In some demonstrative calculations of Section 5 and Section 6, ductile fracture is suppressed by setting threshold $W_0^{\varphi }\to \infty$. In those calculations, ${\Delta }_{\varphi }=0$ is imposed and local fields remain static for any $t>t_c$. For melt failure, this is consistent with neglecting viscosity of the liquid. For shear banding without resolution of ductile degradation, the predicted abrupt post-localization load drop is consistent with prior numerical implementations of the $L_{\infty }$ criterion [8,11,12].

Defect ${\tilde{\varphi }}_0\left(Y\right)=\delta {\chi }_0\left(Y\right)$, with a distribution assigned as in Refs. [8,76], instigates localization at a single point $Y_B$ at the midsection of the slab ${\Omega }_0$ in Figure 1. Recall $\widehat{y}$ is the coordinate at $t=0^{+}$ after application of $p_0$ but preceding shear by $\gamma \left(t\right)$. With $h_0$ identified in Figure 1, define $\tilde{y}$ having its coordinate origin at the midpoint of ${\Omega }_0$: $\widehat{y}={\displaystyle \frac{1}{2}}{h}_0\leftrightarrow \tilde{y}=0$. The initial defect distribution (i.e., yield strength perturbation) of intensity ${ϵ}_0$ and width ${\lambda }_0$ is prescribed in dimensionless form as [8,76]

$$\begin{array}{cc}\hfill & \delta {\chi }_0\left(\tilde{y}\left(Y\right)\right)={ϵ}_{0}exp[-{(2\tilde{y}/{\lambda }_0)}^2],[0<{\lambda }_0\le 1,{ϵ}_0\ge 0];\hfill \\ \hfill & \tilde{y}\left(Y\right)=(2/h_0)[\widehat{y}\left(Y\right)-h_0/2]=(2/h_0)[{\left(J^E\left(p_0\right)\right)}^{1/3}Y-h_0/2]\in [-1,1];\hfill \\ \hfill & \delta {\overline{\chi }}_0=1-{\overline{\chi }}_0={\displaystyle \frac{1}{2}}{\int }_{-1}^1\delta {\chi }_0\mathrm{d}\tilde{y}={\displaystyle \frac{\sqrt{\pi }}{4}}{ϵ}_0{\lambda }_0\mathrm{erf}\left[{\displaystyle \frac{2}{{\lambda }_0}}\right]\approx 0.4431{ϵ}_0{\lambda }_0.\hfill \end{array}$$

(76)

In calculations, $\gamma$ and y domains are discretized into dimensionless increments $\mathrm{d}\gamma$ and $\mathrm{d}\tilde{y}$. Taking $\mathrm{d}\gamma ,\mathrm{d}\tilde{y}\lesssim {10}^{-4}$ is generally sufficient for ${\overline{\gamma }}_c$ independent of grid size. In agreement with Refs. [8,11,12], results of the analytical–numerical scheme are grid-size independent so long as the grid is fine enough to evaluate the localization integral (e.g., (74)) over the shape of initial defect. If the initial defect is not too sharp, no special provisions are needed to mitigate mesh dependency. This contrasts with traditional dynamic finite element (FE) simulations lacking any gradient or nonlocal regularization where mesh dependency is problematic in the strain-softening regime. Strain-gradient plasticity and phase-field fracture methods are commonly used elsewhere in such numerical settings, at least in part, to alleviate this numerical issue that does not emerge for the present method of analysis.

With numerical integration limited by machine precision and an infinite number of increments $\mathrm{d}\gamma$ impossible, a large enough upper bound on ${\gamma }_B$ is consistently used in (74) to enable respectable convergence of ${\int }_0^{{\gamma }_B}I\left(\gamma \right)\mathrm{d}\gamma$ toward a constant value if enabled by properties (e.g., (70)) and loading conditions. Convergence quickens with fracture or melting: ${\left({\iota }^{\xi }\omega \right)}^{1/m}\to 0$ rapidly with $\gamma$ as $\varphi \left(\gamma \right)\to 1$ or $\xi \left(\gamma \right)\to 1$ for $m\ll 1$. In such cases, if failure by shear fracture or melting occurs, (74) is still used with singular point $Y_B$ excluded from ${\overline{\gamma }}_c$. Infinite strain remains possible at $Y_B$ if material has null strength there.

Numerical results include contours of ${\gamma }_c$, ${\theta }_c$, ${\varphi }_c$, and ${\xi }_c$, where subscript ${(·)}_c$ denotes a quantity as $t\gg t_c$ and $\overline{\tau }\to 0$. Contours are restricted to dimensionless $\tilde{y}$-space. They enable comparison of dimensionless widths of high-strain, high-temperature zones centered on singular bands at $\tilde{y}=0$. Absolute zone widths scale linearly with $h_0$ if $t_0=h_0/{\upsilon }_0$, ${ϵ}_0$, and ${\lambda }_0$ are all constants. Minimum widths tend to zero as $h_0\to 0$ at fixed ${\lambda }_0$ since gradient regularization, conduction, and inertia are not modeled. To account for regularizing physics and predict absolute shear band widths, more sophisticated numerical methods (e.g., finite difference [21] or FE [20,32]) are required.

5. Application to Steel

5.1. Properties and Parameters

Behavior of a high-strength, low C, Ni-Cr steel (i.e., a type of RHA steel) is analyzed. Mechanical properties follow from experimental studies of the 1970s–1990s [89,90,91,92,93], and for viscoplastic response, model calibrations to experimental data [8,94]. A typical composition [89,92] comprises Fe with 0.22 wt.% C, 1.06 wt.% Cr, 3.15 wt.% Ni, and other trace elements, rolled to a thickness of 0.5 in (12.7 mm). The dominant crystal structure at room temperature and atmospheric pressure is body centered cubic (BCC). As characterized in Ref. [92], the microstructure contains a mixture of martensite and bainite, heavily banded. Rolling can induce a slight anisotropy in plastic properties that is omitted in the current viscoplastic model and most others used for ballistic simulations of RHA [93,94]. The particular chemistry and processing history of the RHA tested in Ref. [6] are not listed in that reference, so the above characteristics are offered here as representative.

Material properties and parameters are listed in Table 1. Most properties, and most viscoplastic parameters, are repeated from Ref. [8] where original sources and calibrations can be found. Exceptions are static yield strength $g_0$ and rate sensitivity m. Values in Refs. [8,94] provided a best-fit to dynamic compression data optimized for strain rates of ${10}^4$/s. Experiments modeled in the present study [6] consider a Ni-Cr steel of RHA type, but at lower average rates (e.g., $\dot{\overline{\gamma }}\approx 3200$/s) and for which a lower flow stress was observed than is predicted via past values $g_0=0.693$ GPa and $m=0.065$. Iron and steels show increasing m for strain rates exceeding $\approx {10}^3$/s due to influences of phonon drag and relativistic mechanisms [17,70,80,95]. Logically, m is reduced to better represent rates $\lesssim {10}^4$/s; then, $g_0$ is adjusted to better match experimental torsion data [6] for $\overline{\gamma }<{\overline{\gamma }}_c$.

Table 1. Properties or model parameters for Ni-Cr steel (RHA), ${\theta }_0=300$ K.

Parameter [Units]	Definition	Value	Parameter [Units]	Definition	Value
${\rho }_0$ [g/cm3]	ambient mass density	7.84	$c_V$ [MPa/K]	specific heat	3.48
$B_0$ [GPa]	isotherm. bulk modulus	163	$h_T$ [GPa]	latent heat of fusion	2.09
$B_0^{\prime }$ [-]	pressure derivative of B	5.29	${\delta }_0^{\xi }$ [-]	melt volume change	0.052
${\mu }_0$ [GPa]	elastic shear modulus	80	${\theta }_T$ [K]	equilibrium melt	1800
${\mu }^{\prime }/{\mu }_0$ [1/GPa]	pressure variation of $\mu$	0.024	${\beta }_{\xi }$ [GPa]	melt kinetic barrier	0.18, 1.21
$g_0$ [GPa]	initial yield strength	0.40	$W_0^{\varphi }$ [GPa]	damage start threshold	0.45
${\gamma }_0$ [-]	reference plastic strain	0.01	${\alpha }_0$ [-]	fracture energy ratio	0.125
${\dot{\gamma }}_0$ [1/s]	reference strain rate	1.0	$E_C$ [GPa]	fracture cohesive energy	0.025
n [-]	strain harden. exponent	0.05	${\delta }_0^{\varphi }$ [-]	porosity at failure	0.05
m [-]	strain rate sensitivity	0.035	${\omega }_1$ [-]	residual strength factor	${10}^{-5}$
$\nu$ [-]	thermal softening	−0.33	${ϵ}_0$ [-]	nominal defect intensity	${10}^{-3}$
${\beta }_0$ [-]	Taylor-Quinney factor	0.8	${\lambda }_0$ [-]	initial defect width	0.5, 1.0

In particular, data used to inform n, $\nu$, and m primarily comprise uniaxial-stress tension experiments at lower rates [89] and uniaxial-stress compression experiments (i.e., Kolsky bar) at higher rates [93] over a range of initial temperatures. Test data and calibrations to Johnson–Cook [96] and power-law models are described in detail in Refs. [8,94]. Specifically, the reader is referred to Section 5.2, Table 1, and Figure 3a,b of Ref. [8] for assessment of the parameter calibrations for RHA (i.e., Ni-Cr steel). Implicit in consolidation of different stress states, parameters are assumed identical in tension, compression, and shear. Neither the standard Johnson–Cook model nor the power-law model, both based on standard $J_2$ flow theory, can discern differences in thermoplastic behaviors among tension, compression, and shear. Because torsion data across a wide range of rates and temperatures do not seem available for RHA, suitability of these assumptions for shear have not been verified. Data conversions among uniaxial tension/compression and shear are accomplished in terms of effective Von Mises stress ${\sigma }_V$ and its conjugate plastic strain rate ${\dot{ϵ}}_V^P$:

$$\begin{array}{cc}\hfill & {\sigma }_V={(\frac{3}{2}\tilde{\mathit{\sigma }}:\tilde{\mathit{\sigma }})}^{1/2}={\left(3J_2\right)}^{1/2},{\dot{ϵ}}_V^P={(\frac{2}{3}{\mathbf{d}}^P:{\mathbf{d}}^P:)}^{1/2};\hfill \\ \hfill & {\mathbf{d}}^P=\frac{1}{2}\{{\mathbf{F}}^E{\mathbf{L}}^P{\left({\mathbf{F}}^E\right)}^{-1}+{\left[{\mathbf{F}}^E{\mathbf{L}}^P{\left({\mathbf{F}}^E\right)}^{-1}\right]}^{\mathrm{T}}\}.\hfill \end{array}$$

(77)

Recall $\tilde{\mathit{\sigma }}$ is deviatoric Cauchy stress and ${\mathbf{L}}^P$ is the traceless plastic velocity gradient referred to the locally relaxed intermediate configuration. For uniaxial stress extension or compression, ${\sigma }_V$ is the magnitude of axial true stress and ${\dot{ϵ}}_V^P$ the axial true plastic strain rate. Correspondence to simple shear, including plastic work rate and recalling $\tau =J^E{\sigma }_{xy}$, is

$$\tau =J^E{\sigma }_V/\sqrt{3},{\dot{\gamma }}^P=\sqrt{3}\dot{{ϵ}_V^P};\tilde{\mathit{\sigma }}:{\mathbf{d}}^P={\sigma }_V^P{\dot{ϵ}}_V^P={\sigma }_{xy}{\dot{\gamma }}^P=\tau {\dot{\gamma }}^P/J^E.$$

(78)

For data or results conversions among different strain variables, time integration of (78) produces ${\gamma }^P=\sqrt{3}{ϵ}_V^P$.

Like pure Fe, the $\alpha$, $ϵ$, and $\gamma$ phases of this steel are BCC, HCP, and FCC. At $p=0$ and ${\theta }_0=300$ K, material is fully of $\alpha$ phase. Near ${\theta }_0$, $\alpha \to ϵ$ transformation occurs at $p\approx 13$ GPa, and near zero pressure, $\alpha \to \gamma$ transformation occurs at $\theta \approx 1000$ K (see Ref. [8] and works cited therein). The present treatment is restricted to $p_0<13$ GPa, but shear-induced $\alpha \to ϵ$ transformations, though not reported in known experiments on RHA, might be possible since they have been inferred for Fe [97]. Evidence of the $\alpha \to \gamma$ transition within shear bands has been noted in some experiments [3,98] and models [99], but not others [6,92]. To keep the analysis and interpretation of results tractable, $\alpha \to ϵ/\gamma$ transitions are not modeled herein. If solid–solid transformations do occur, the analysis amounts to assigning each solid phase the same properties and ignoring dissipation from transformations. See Refs. [8,99] for models quantifying solid transformations in shear bands.

For localization calculations, ${\lambda }_0$ follows from Ref. [8]. Effects of the initial defect width in (76) are explored in Section 5.2 by two choices ${\lambda }_0=0.5$ and ${\lambda }_0=1.0$. In Refs. [8,11,12], ranges of perturbation intensity spanning ${ϵ}_0\in [{10}^{-6},{10}^{-1}]$ were considered in parametric calculations on steels and Fe. Therein, ${\overline{\gamma }}_c$ decreased approximately linearly with ${log}_{10}{ϵ}_0$. In Table 1, ${ϵ}_0={10}^{-3}$, intermediate among prior cited values, is suitable in Section 5.2 for consistently matching ${\overline{\gamma }}_c$ to average shear at localization from experiment [6] when ${\lambda }_0=0.5$. However, as also shown in Section 5.2, ${ϵ}_0$ is not always a free parameter: ${ϵ}_0$, ${\lambda }_0$, $W_0^{\varphi }$, and ${\overline{\gamma }}_c$ are not all independent. As explained in Section 7, ${ϵ}_0$ can be assigned uniquely by calculations if ${\lambda }_0$ and $W_0^{\varphi }$ are prescribed a priori. In (70), $\nu +n+(1-\nu )m=-0.233<0$, so shear band failure is possible for this steel, at least in the absence of melting or fracture.

New parameters not repeated from Ref. [8] are those for the shear fracture model of Section 3.4 and the melting model of Section 3.5. For dynamic shear fracture, the simplest physically admissible choices entering (10), (53), and parameters consistent with experimental data [6] modeled in Section 5.2 are assumed. These include $f_{\varphi }=\varphi$, ${\omega }_1=0$, $k=1$, ${\iota }^{\varphi }=1-\varphi$, and ${\gamma }_0^{\varphi }=0$ as in example (59). The latter assumes isotropic ductile damage (e.g., spherical voids); detailed microscopy data would be needed to justify a nonzero value. The presently consulted data [6] do not allow independent calibration of ${\gamma }_0^{\varphi }$ and $E_C$; setting the former to zero is the simplest choice. The value $W_0^{\varphi }=450$ MPa is taken verbatim from Ref. [27] on RHA steel, with the caveat that values ranging from 20 to 350 MPa have been used elsewhere for various structural steels [35,37]. Phase-field studies [31,32,35,37] consistently assign 10% of the plastic work to energy consumed by fracture, giving ${\alpha }_0{\beta }_0=0.1$ in Table 1. Cohesive energy $E_C$ is unknown a priori for the specific steel of present study; the value $E_C=25$ MPa in Table 1 is calibrated in Section 5.2 to the post-localization stress-strain data of Ref. [6]. Values ranging anywhere from 10 to 1600 MPa can be inferred from experimental and phase-field studies on other high-strength steels [4,31,32,35,37]. Induced porosity at fracture quantified by ${\delta }_0^{\varphi }$ is difficult to quantify precisely for dynamic shear, but voids and cracks have been observed inside shear bands in experiments on steels [3,4,6]. A representative value of 0.05 from Ref. [71] on Fe and other steels is used, most valid for lower or tensile $p_0$. With this choice and the value of $E_C$ in Table 1, tensile pressure that would induce rupture is $-p_0\approx E_C/{\delta }_0^{\xi }=0.5$ GPa. The corresponding uniaxial tensile stress would be $\approx 1.5$ GPa. For reference, the static ultimate tensile strength of RHA ranges from 0.8 to 1.2 GPa [7,89], and spall strengths of Fe and steels range from 0.7 to 3.7 GPa [100].

For melting, $\xi \to \overline{\xi }$, ${\gamma }_0^{\xi }=0$, and (63) is used. Metastable equilibrium, $t_R^{\xi }\dot{\overline{\gamma }}\ll 1$, is justified by suitability of shock-wave experiments that complete at timescales on the order of μs to determine melting curves of Fe [101,102]. Omission of ${\gamma }_0^{\xi }$ is the usual assumption [56,57], satisfactory in the limit of sharp interfaces [55,103]. A nonzero value could be important for modeling nanoscale physics in a regularized phase-field theory [55], but calibration to nm scale data from experiments or atomic simulations is needed. The equilibrium melt temperature at ambient pressure, ${\theta }_T$, is around 1800 K in Fe [104] and the present class of steels [93,94]. Unknown for the current Ni-Cr steel, values of $h_T$ and ${\delta }_0^{\xi }$ for Fe [104] are used as a substitute. The model can be considered reasonably accurate only for $p_0\lesssim 10$ GPa since a near-linear dependence of melt start temperature on pressure is predicted by (63). At higher $p_0$, experiments and atomic simulation data show highly nonlinear melt curves for Fe [101,102]. Such data also show mixed-phase regions where liquid and solid coexist at a given $\theta$ and $p_0$. The width of the mixed-phase region, and dissipation from melting, are controlled by ${\beta }_{\xi }$, for which precise values are unknown. Assumed in Table 1 are two choices for ${\beta }_{\xi }$: one, for “fast melting” with ${\beta }_{\xi }=0.18$ GPa, one for “slow melting” with ${\beta }_{\xi }=1.21$ GPa. For the former, under purely thermal loading, $\xi =0.99$ at ${\displaystyle \frac{\theta }{{\theta }_T}}=1.2$. For the latter, $\xi =0.5$ at ${\displaystyle \frac{\theta }{{\theta }_T}}=1.2$. Redundant in the present setting, null values $a_{\xi }=0$ and ${\iota }_1^{\xi }=0$ are assigned. Admissible minimum and maximum values of $r_0^{\xi }$ are explored in calculations: $r_0^{\xi }=0$ and $r_0^{\xi }=1$.

5.2. Numerical Results

Outcomes of calculations invoking methods of Section 4.2 and Section 4.3, with baseline properties of Ni-Cr steel in Table 1, are reported next. Results in Section 5.2 consider only null external pressure (i.e., $p_0=0\iff J^E=1$). Results are compared with dynamic torsion data of Ref. [6], specifically data from the experiment on specimen labeled “B6”. In that work [6], a torsional split Hopkinson (i.e., Kolsky) bar was used to determine average dynamic shear stress versus shear strain behavior, and local strains and strain rates were calculated by analyzing high-speed photographs taken in situ on portions of specimens marked beforehand with regularly spaced grids. Data for six specimens of 2 mm length were reported, but local strain distributions were only shown for B6 (hence the reason for first modeling that particular sample; B2 is also modeled later). Among the six samples, average wall thickness varied by $\approx 10$%, mean strain rates varied up to a factor of around two, and localization was observed in four of the six experiments. Strains at localization onset were consistent for three of these four. As the material is not extremely rate sensitive, test-to-test variations are attributed to different initial defects that could possibly be linked to thickness perturbations [8,11,12]. Though possible, no attempts were made to customize shapes of initial strength defect distributions (e.g., ${\lambda }_0$, ${ϵ}_0$) to better fit results of multiple tests.

Recall the shearing rate of the present framework is $\dot{\gamma }=2\dot{ϵ}$, where in the absence of dilatation, the true local strain rate is $\dot{ϵ}={\dot{ϵ}}_{xy}={\displaystyle \frac{1}{2}}(\partial {\upsilon }_x/\partial y+\partial {\upsilon }_y/\partial x)$. The mean shearing rate for test B6 is taken as $\dot{\overline{\gamma }}=3200$/s, depicting the average reported by the Hopkinson bar analysis [6]. The strain measure reported in Ref. [6] is interpreted here as true strain; it is not mathematically defined in that work. If, instead, it is interpreted as nominal strain (with rotation), then experimental values of $\gamma$ and $\overline{\gamma }$ as quoted herein should be multiplied by ${\displaystyle \frac{1}{2}}$. Threshold energy $W_0^{\varphi }$ would be similarly reduced. The present true-strain interpretation is supported by consistency of the current model and parameters (i.e., Table 1) with the value of $W_0^{\varphi }$ for RHA quoted in Ref. [27] and the Von Mises equivalent strain $\gamma /\sqrt{3}$ up to onset of localization for the same steel reported in Figure 3 of Ref. [28]

After localization begins, the mean shear strain rate remains reasonably constant according to the Hopkinson bar analysis, but image analysis suggests it could vary [6]. The former experimental result is used herein; the framework in Section 4 requires $\dot{\overline{\gamma }}=\mathrm{constant}$, and further omits inertial effects that would seem more prominent if the average, in addition to local, strain rate fluctuated strongly in time. Total average strain from experiment B6 is converted from a start time $t=0$ when the experimental load-time history provided by the Hopkinson bar begins. During the early part of the test (i.e., first $\approx 20\mu$s [6]), the stress response is overly compliant and highly oscillatory because the sample has neither loaded fully nor achieved equilibrium needed for a (nearly) uniform stress-strain state [105]. Thus, the oscillatory quasi-elastic offset “strain” ${\gamma }_o=3200\times 20\times {10}^{-6}=0.064$ contributes to the total calculated this way. For comparison of average stress-strain data with results of the rigid-viscoplastic framework of Section 3 and Section 4, this offset must equivalently be subtracted from the experimental record or added to the model reference datum, since prior to 20 μs, the bulk of the sample has not plastically yielded. Fine-scale oscillations are omitted [28].

Average stress-strain behaviors are compared in Figure 2a. The model result is offset by ${\gamma }_o$ as it necessarily excludes the oscillatory elastic ramp-up. Because of its rigid-viscoplasticity assumption (e.g., [1,12]), the model is overly stiff in the small-strain regime where the elastic contribution to strain is omitted by definition. The rapid load drop corresponding to the onset of localization appears at $\overline{\gamma }={\overline{\gamma }}_c=0.753$. Recall from Section 5.1 that the model, with prescribed ${ϵ}_0={10}^{-3}$, is able to accurately match the experimental stress-strain record with calibration of only two parameters: (i) initial yield strength $g_0$ for average stress up to localization and (ii) cohesive energy $E_C$ for the rate of post-localization stress decay. Shown in parametric calculations of Section 6, the stress drop becomes more abrupt as $E_C$ is reduced or as tensile pressure is increased. Resulting from the damage model of Section 3.4, shear stress $\overline{\tau }$ decays exponentially, asymptotically approaching zero at large strain. A drop to absolute zero stress at finite strain is not captured. This limitation can be rectified by using a cut-off failure criterion ${\varphi }_F$, whereby flow resistance $g_Y(\xi ,\varphi ,p_0)\to 0$ for $\varphi \ge {\varphi }_F$. The final fracture strain inferred from data in Figure 2a can be matched by setting ${\varphi }_F\approx 0.98$.

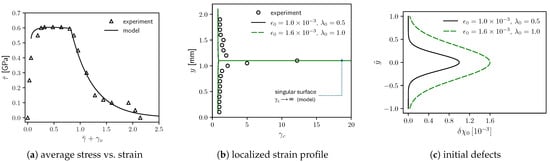
Figure 2. Model results and experimental torsion data [6]: (a) average shear stress $\overline{\tau }$ vs. average shear strain $\overline{\gamma }$ (strain in rigid-plastic model shifted by ${\gamma }_o$ to compensate for oscillatory elastic ramp-up in experiments, not resolved) (b) localized strain distribution $\gamma$, specimen size $h_0=2$ mm (c) two initial defect profiles (${ϵ}_0,{\lambda }_0$). Experimental points sample continuous (a) or discrete (b) data from Ref. [6]. Nominal shear strain $\gamma$ here in (b), with rotation, is defined as twice the numerical value of strain (e.g., $ϵ$) in Figure 17 of Ref. [6].

Physically, a monotonic reduction in stress after damage onset is expected. However, data in Figure 2a show a horizontal plateau within a total strain domain between 1.5 and 2. Reasons for this are indefinite in Ref. [6]. A possible explanation is that damage initiates non-uniformly over the circumference of the specimen, then requires a finite time to propagate before the load drop is registered by the experimental apparatus [106]. The simple shear treatment of Section 3.1, in contrast, assumes damage $\varphi$ and strain $\gamma$ are independent of x and z coordinates and thus uniform around the circumference.

Localized strain distributions from model ($\gamma ={\gamma }_c$) and experiment ($t=613\mu$s) are compared in Figure 2b. Model results are shifted upward by $\Delta y=0.1$ mm so that locations of the centers of the shear bands coincide. This is permissible since $\gamma$-contours are nearly independent of $\tilde{y}$ for $|\tilde{y}|\gtrsim 0.9$. Local strains are similarly uniform far from the core at $y=1.1$ mm, but the model does not capture the strain bulge surrounding the core of the band seen in the experiment. Post-localization strain within the modeled band is depicted by a finite displacement jump ${\Delta }_{\varphi }$ via (75) over a zero-width (i.e., singular) surface. In the experimental record, the band is of finite width, but cracks not evident in the data profile were seen around at least some of the perimeter [6]. Discrepancies can be attributed to missing regularization mechanism(s) in the model (e.g., no conduction, inertia, or gradient surface energies) and limits of experimental resolution emphasized in Ref. [6]. Differences between model and experiment are an inherent restriction of the $L_{\infty }$ method that cannot predict the true band width. Average shear strain is mainly accommodated by slip on the singular surface in Figure 2b rather than more broadly distributed as in the experiment. Adjustments to the model parameters and initial defect shape cannot resolve these fundamental differences.

The mean stress-strain behavior is the same when a less concentrated initial defect profile is prescribed, but of higher peak intensity, as depicted in Figure 2c. The value of ${ϵ}_0=1.6\times {10}^{-3}$ must be tuned in this case to produce the same value of ${\overline{\gamma }}_c=0.753$: a less sharp defect requires a larger magnitude to induce the same average localization strain.

Effects of the two defect profiles on critical strain, temperature, and ductile fracture parameter distributions are further examined in Figure 3a–c. As anticipated, a more diffuse defect produces a wider strain, temperature, and damage distribution away from the infinite-strain band centered at $\tilde{y}=0$ than a narrower initial defect. Maximum temperature ${\theta }_c$ does not reach 500 K in either case. Damage-softening from fracture in the shear band reduces $\tau$ to such a low value that plastic working ceases to affect the $\theta$ by any pragmatically calculable amount as $\gamma \to \infty$. Calculations verify temperature rise is insufficient to induce melting, even at the core of the shear band, recalling ${\theta }_T=1800$ K. It also appears insufficient to induce $\alpha \to \gamma$ phase transformation (not enabled in the framework of Section 2, Section 3 and Section 4) that occurs at $\approx 1000$ K [8,92]. In the band center, ${\varphi }_c\to 1$.

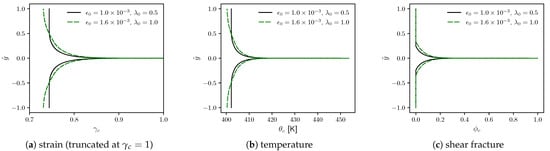
Figure 3. Model results for two initial defect profiles (${ϵ}_0,{\lambda }_0$) vs. normalized spatial position $\tilde{y}$: (a) post-localization strain ${\gamma }_c$ (b) temperature ${\theta }_c$ (c) fracture order parameter ${\varphi }_c$

Calculations from the full model, fracture suppressed, and both fracture and melting suppressed are considered in Figure 4. In the full model, labeled “fracture” in Figure 4a, melting never occurs; results here are repeated with experimental data from Figure 2a. Cases in which fracture is deactivated but melting enabled are denoted “fast melt” and “slow melt” for respective small and large values of kinetic factor ${\beta }_{\xi }$ in Table 1. Different choices of ${\beta }_{\xi }$ and $r_0^{\xi }$ produce modest differences in the total strain at which localization ensues, beyond which the drop in average stress $\overline{\tau }$ is abrupt per assumptions in Section 4.3. The largest critical localization strain is predicted when both softening mechanisms (i.e., fracture and melting) are suppressed. Figure 4b–d compare predictions of model renditions under homogeneous deformations (i.e., no initial defects: ${ϵ}_0=0\leftrightarrow \delta {\chi }_0=0$). When stored energy of cold work fuels melting, then melting begins at $\overline{\gamma }\approx 7.0$. When it does not, melting begins at $\overline{\gamma }\approx 13.3$. Subsequently, melting occurs at a faster rate with respect to $\overline{\gamma }$ for the lower value of ${\beta }_{\xi }$, as evidenced by the homogeneous melt fraction $\overline{\xi }$ in Figure 4d. Shear stress decays with increasing $\overline{\xi }$ in Figure 4b. Homogeneous temperature $\overline{\theta }$ increases monotonically when melting is suppressed. Since melting consumes energy ($h_T>0$), the rate of temperature increase is reduced during solid-to-liquid transformation. As seen in Figure 4c, for the case of fast melting fueled by energy from dissolution of dislocations, $\overline{\theta }$ can even decrease.

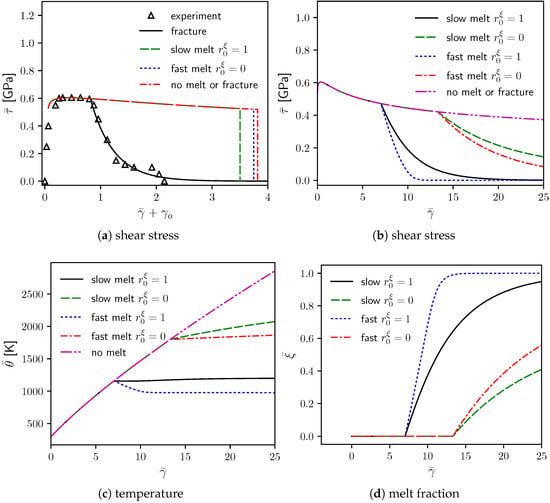
Figure 4. Model results with features activated or suppressed: (a) average shear stress $\overline{\tau }$ vs. average shear strain $\overline{\gamma }$ and experimental torsion data [6]; (b–d) homogeneous solutions for average shear stress, temperature $\overline{\theta }$, and melt order parameter $\overline{\xi }$ to extreme shear strain. Slow and fast melt correspond to respective large and small values of ${\beta }_{\xi }$ in Table 1; $r_0^{\xi }$ is fraction of stored energy of cold work released upon melting.

Contours of localized shear strain, temperature, and melt fraction are compared in Figure 5 for different renditions with fracture suppressed. These correspond to any post-localization time $t>t_c$. In Figure 5a, local strain ${\gamma }_c$ differs very little whether or not melting occurs. Differences are larger among the two different choices of ${\lambda }_0$. Similar trends are observed for local temperature ${\theta }_c$ in Figure 5b, noting that in the core of the shear band at $\tilde{y}=0$, ${\theta }_c$ can exceed 2400 K. Accordingly, as seen in Figure 5c, complete melting ${\xi }_c\to 1$ is possible in the core. However, temperature and other driving forces (e.g., $\overline{R}$) are not large enough outside the core to induce appreciable melting. Even partially liquified material is always confined to a very narrow region near the center of the band.

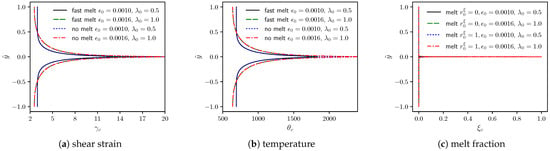
Figure 5. Model results without fracture for two initial defect profiles (${ϵ}_0,{\lambda }_0$) vs. normalized spatial position $\tilde{y}$: (a,b) strain ${\gamma }_c$, temperature ${\theta }_c$ for $r_0^{\xi }=0$ or melt suppressed (c) melt parameter ${\xi }_c$ for $r_0^{\xi }=0,1$.

Outcomes of calculations of Section 5.2 are summarized in Table 2, specifically the average stress ${\overline{\tau }}_c$ computed at $t=t_c^{-}$ (i.e., immediately preceding the load drop associated with localization) and the critical average strain from (74) as $t\to t_c$ that, by definition, excludes the contribution ${\Delta }_{\varphi }$ of (75). Since the steel is already thermal softening prior to any localization, lower ${\overline{\gamma }}_c$ always correlates with larger ${\overline{\tau }}_c$. A more diffuse defect with larger ${\lambda }_0$ tends to delay localization. For the same initial defect profile, critical localization strain is reduced 80% by ductile shear fracture, but by no more than 12% by melting. For the considered ranges of material parameters and loading conditions in these calculations, melting never occurs when shear fracture is permitted.

Table 2. Results summary for high-strength steel, $p_0=0$, ${\theta }_0=300$ K, $\dot{\overline{\gamma }}=3200$/s.

Physics	${\mathit{W}}_0^{\mathit{\varphi }}$ [MPa]	${\mathit{\theta }}_{\mathit{T}}$ [K]	${\mathit{ϵ}}_0$ [${10}^{-3}$]	${\mathit{\lambda }}_0$	${\mathit{\beta }}_{\mathit{\xi }}$ [GPa]	${\mathit{r}}_0^{\mathit{\xi }}$	${\overline{\mathit{\tau }}}_{\mathit{c}}$ [MPa]	${\overline{\mathit{\gamma }}}_{\mathit{c}}$
Fracture	450	1800	1.0	0.5	0.182	1	597	0.753
(full model)			1.6	1.0	0.182	1	596	0.753
Melting	∞	1800	1.0	0.5	0.182	1	526	3.432
(no fracture)			1.6	1.0	0.182	1	524	3.515
			1.0	0.5	1.207	1	525	3.437
			1.6	1.0	1.207	1	524	3.521
			1.0	0.5	0.182	0	521	3.681
			1.6	1.0	0.182	0	517	3.874
			1.0	0.5	1.207	0	521	3.683
			1.6	1.0	1.207	0	517	3.877
No fracture	∞	∞	1.0	0.5	0.182	1	519	3.751
or melting			1.6	1.0	0.182	1	515	3.983

6. Parameter Variations

Parametric calculations next investigate influences of pressure $p_0$ and values of $W_0^{\varphi }$ and $E_C$ entering the ductile fracture theory of Section 3.4. In all calculations of Section 6, the defect width ${\lambda }_0=0.5$ per Table 1, but the intensity ${ϵ}_0$ can depart from its nominal value of ${10}^{-3}$ in Table 1. Quantities labeled by an asterisk ${(·)}^{*}$ correspond to nominal property values from Table 1 or to results obtained from calculations using such nominal property values. Pressures are always limited to $|p_0|\le 5$ GPa.

For calculations reported in Figure 6, the full model with fracture and possible melting is invoked, but melting never occurs in these predictions because fracture always takes place first. As in Section 5.2, upon shear fracture, stress drops too quickly to enable a large enough temperature rise from stress power to initiate melting, even in the center of the shear band.

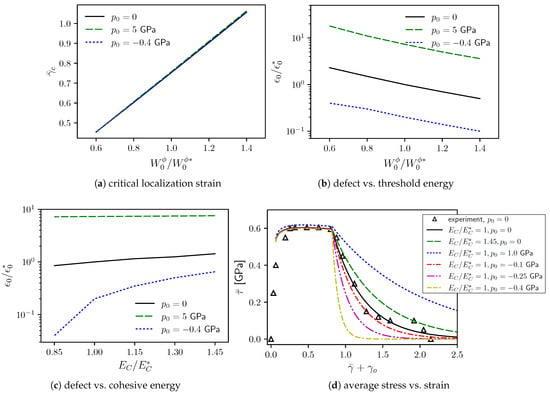
Figure 6. Effects of threshold fracture energy $W_0^{\varphi }$, cohesive energy $E_C$, and pressure $p_0$ on (a) average strain for localization ${\overline{\gamma }}_c$ and (b,c) initial defect magnitude ${ϵ}_0$ consistent with $\overline{{\gamma }_c}$ (d) average stress $\overline{\tau }$ vs. strain $\overline{\gamma }$ at $W_0^{\varphi }=W_0^{\varphi *}$ with experimental torsion data [6]. Baseline ($W_0^{\varphi *},E_C^{*},{ϵ}_0^{*}$) from Table 1.

Effects of threshold energy $W_0^{\varphi }$ on critical localization strain ${\overline{\gamma }}_c$, at fixed $E_C$, are shown in Figure 6a. Three values of applied pressure are considered: zero, 5 GPa compression, and 0.4 GPa tension. Recall from Section 5.1 that a tensile pressure approaching 0.5 GPa would induce instant cavitation and rupture, so larger tensile pressures not modeled here. The magnitude of each initial defect ${ϵ}_0$ needed to achieve the corresponding ${\overline{\gamma }}_c$ is shown in Figure 6b. Critical average strain increases near linearly with $W_0^{\varphi }$ but scantly increases (decreases) with compressive (tensile) pressure at fixed $W_0^{\varphi }$. Initial defect intensity in Figure 6b, in contrast, decreases significantly as tensile stress increases at fixed threshold $W_0^{\varphi }$. Furthermore, perturbation strength must decrease to enable larger threshold energy at fixed pressure. Results are physically viable: sensitivity to defects is greater in tension than compression, and threshold energy drops for sharper defects. Threshold energy and initial defects should not be prescribed independently because results show the two are intrinsically coupled, as discussed more in Section 7. The maximum local temperature in the core of the shear band, among all cases reported in Figure 6, arises for $W_0^{\varphi }/W_0^{\varphi *}=1.4$ and $p_0=5$ GPa, with a post-localization value $\theta =782$ K. Maximum core temperature increases as $W_0^{\varphi }$, $E_C$, and $p_0$ increase: threshold energy, cohesive energy, and compressive stress all delay final failure from damage-softening and fracture.

Effects of cohesive energy on defect intensity needed to produce a consistent value of ${\overline{\gamma }}_c\approx 0.75$, at fixed $W_0^{\varphi }=W_0^{\varphi *}$, are reported in Figure 6c. At any value of $E_C$, a larger defect intensity ${ϵ}_0$ is required in compression, a smaller defect strength in tension. Pressure sensitivity increases for lower values of $E_C$. At fixed $p_0$, a larger $E_C$ requires a more severe defect to engender the same ${\overline{\gamma }}_c$, especially under tensile stress. For $p_0=5$ GPa, ${\overline{\gamma }}_c=0.757$, whereas ${\overline{\gamma }}_c=0.753$ for $p_0=0$ and $-0.4$ GPa. Cohesive energy and perturbation strength are nearly independent at high compressive pressure. Effects of $p_0$ and increased $E_C$ are compared with experiment [6] in Figure 6d, where ${ϵ}_0$ is prescribed to give ${\overline{\gamma }}_c=0.753$ in all cases shown. Stress decay for $\overline{\gamma }>{\overline{\gamma }}_c$ accelerates under tensile pressure and decelerates when $E_C$ increases. Compressive pressure slows damage progression because of resistance to void expansion or crack opening.

Barring activation of some catastrophic defect or change in microstructure, adiabatic shear localization should follow, but not precede, instability in a viscoplastic solid [1,10,13,14,107,108]. Therefore, as the shear fracture model of Section 3.4 seeks to represent material degradation within a shear band, a pragmatic lower bound on the threshold plastic work $W_0^{\varphi }$, written as ${\tilde{W}}_0^{\varphi }$, corresponds to the plastic work accumulated up to the instability strain ${\tilde{\gamma }}_c$, that, in homogeneous simple shear, is determined from the condition $\mathrm{d}\tau /\mathrm{d}\gamma =0$ under adiabatic conditions at a given initial temperature ${\theta }_i$, loading rate $\dot{\gamma }=\dot{\overline{\gamma }}$, and pressure $p_0$. This bound is implicit in prior modeling [28,47] that used a similar threshold energy density for the onset of damage softening. In the absence of melting, and with ${\theta }_i={\theta }_0$, the power-law flow model of (52) with analytical temperature solution of (67) (${\gamma }_f\to \gamma$) yields the following implicit solution for minimum localization strain ${\tilde{\gamma }}_c$ and energy ${\tilde{W}}_0^{\varphi }$:

$$\begin{array}{cc}\hfill & {\tilde{\gamma }}_c=\underset{\gamma \ge 0}{\arg 0}\left[{\displaystyle \frac{n}{\nu A_c}}+{\displaystyle \frac{{(1+\frac{\gamma }{{\gamma }_0})}^{1+n}}{1+A_c\left(\frac{1-\nu }{1+n}\right)\{{(1+\frac{\gamma }{{\gamma }_0})}^{1+n}-1\}}}\right],A_c={\displaystyle \frac{{\beta }_0{\chi }_0{g}_0{\gamma }_0}{c_V{\theta }_0}}({\displaystyle \frac{\dot{\overline{\gamma }}}{{\dot{\gamma }}_0}}{)}^m;\hfill \end{array}$$

(79)

$$\begin{array}{cc}\hfill & {\tilde{W}}_0^{\varphi }={\int }_0^{{\tilde{\gamma }}_c}\tau (\gamma ,\theta \left(\gamma \right))\mathrm{d}\gamma ={\displaystyle \frac{c_V{\theta }_0}{{\beta }_0}}\left[\right\{1+A_c\left({\displaystyle \frac{1-\nu }{1+n}}\right)\left[\right(1+{\displaystyle \frac{{\tilde{\gamma }}_c}{{\gamma }_0}}{)}^{1+n}-1]{\}}^{{\displaystyle \frac{1}{1-\nu }}}-1].\hfill \end{array}$$

(80)

Parameters from Table 1, $\dot{\overline{\gamma }}=3200$/s, and $p_0=0$ give ${\tilde{\gamma }}_c=0.372$ and ${\tilde{W}}_0^{\varphi }=0.221$ GPa. The former can be compared with Culver’s critical strain ${\widehat{\gamma }}_c=-{\displaystyle \frac{n{c}_V\theta }{\nu \tau }}$ (e.g., [7]), where ${\widehat{\gamma }}_c=0.306$ for calculated peak stress $\tau =0.605$ GPa and $\theta =351$ K.

Effects of n, $\nu$, m, and $g_0$ on ${\tilde{\gamma }}_c$ and ${\tilde{W}}_0^{\varphi }$ are shown in Figure 7a,b. Both ${\tilde{\gamma }}_c$ and ${\tilde{W}}_0^{\varphi }$ increase nearly linearly with increasing strain hardening exponent n. Both decrease nonlinearly with decreasing (more strongly negative) $\nu$, corresponding to more thermal softening. While ${\tilde{\gamma }}_c$ decreases modestly and nearly linearly with increasing rate sensitivity m, the minimum threshold energy ${\tilde{W}}_0^{\varphi }$ is negligibly affected by m. The latter is likewise insensitive to initial static yield strength $g_0$, but ${\tilde{\gamma }}_c$ decreases nonlinearly with increasing $g_0$. The latter decrease is a result of proportionally more plastic dissipation and temperature rise, leading to thermal softening that overtakes strain hardening at a lower applied strain.

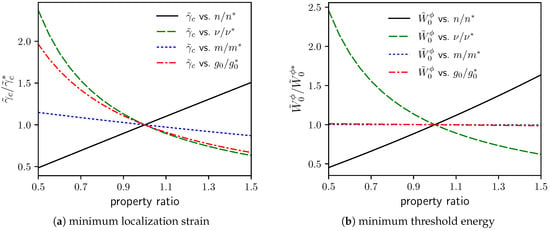
Figure 7. Effects of viscoplastic parameters for strain hardening $n>0$, thermal softening $\nu <0$, rate sensitivity $m>0$, and yield strength $g_0>0$ on minimum localization (i.e., instability) strain ${\tilde{\gamma }}_c$ and corresponding threshold energy ${\tilde{W}}_0^{\varphi }$. Baseline ($n^{*},{\nu }^{*},m^{*},g_0^{*}$) from Table 1 produce ${\tilde{\gamma }}_c^{*}=0.372$ and ${\tilde{W}}_0^{\varphi *}=0.221$ GPa.

Implications of varying the equilibrium melt temperature ${\theta }_T$ are also investigated. Parametric calculations reported in Figure 8a study hypothetical cases when fracture is suppressed (i.e., $W_0^{\varphi }\to \infty$). Here, the defect profile is fixed at nominal values from Table 1: ${ϵ}_0={10}^{-3},{\lambda }_0=0.5$. Influences of compressive or tensile pressure $p_0=\pm 5$ GPa are considered, where large tensile pressure is admissible since fracture and cavitation are suppressed. Melt temperature ${\theta }_T$ ranges from 450 to 2250 K in Figure 8a. In all cases, ${\overline{\gamma }}_c$ increases with increasing ${\theta }_T$ at fixed $p_0$: loss of shear strength is delayed as the requisite temperature rise for melting increases. In Figure 8a, ${\overline{\gamma }}_c$ decreases (increases) in tension (compression) at low ${\theta }_T$, with the opposite trend at high ${\theta }_T$. The effect of $p_0$ is greater at high ${\theta }_T$. Opposing effects ensue: compression resists melting due to ${\overline{p}}_0{\delta }_0^{\xi }>0$ in (64), but $p_0$ increases strength via (51) and thus dissipative temperature rise that promotes melting.

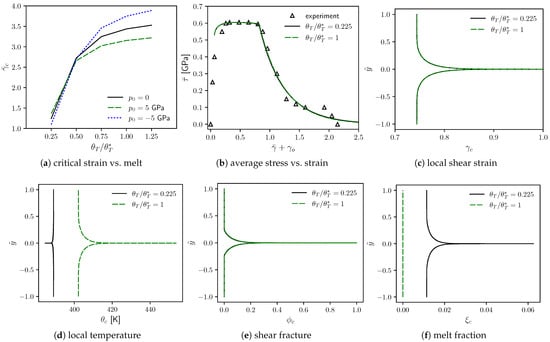
Figure 8. Model results for (a) effects of equilibrium melt temperature ${\theta }_T$ and pressure $p_0$ on critical localization strain ${\overline{\gamma }}_c$ with fracture suppressed (b) average stress vs. strain for reduced and realistic (${\theta }_T^{*}$ from Table 1) melt temperatures (fracture enabled) and experimental data [6] (c–f) post-localization strain ${\gamma }_c$, temperature ${\theta }_c$, fracture parameter ${\varphi }_c$, melt parameter ${\xi }_c$ for reduced and realistic melt temperatures.

A theoretical case in which fracture and melting take place concurrently is now studied. In this case, ${\theta }_T=0.225{\theta }_T^{*}=405$ K is low enough that melting begins in the core of the shear band even when the fracture model is enabled. Here, all parameters except ${\theta }_T$ and ${ϵ}_0$ are nominal values from Table 1, including the set (${\lambda }_0=0.5,{\beta }_{\xi }=1.21$GPa$,r_0^{\xi }=1$). The value ${ϵ}_0=7\times {10}^{-4}$ is reduced from ${10}^{-3}$ so that localization always ensues at ${\overline{\gamma }}_c=0.753$. Average stress-strain behavior differs little in Figure 8b between the nominal case and reduced melting temperature. Contours of local shear strain ${\gamma }_c$ and damage order parameter ${\varphi }_c$ are also hardly affected by ${\theta }_T$ in Figure 8c,e. The material only partially melts, with nonzero ${\xi }_c$ limited to a narrow region near the core of the shear band in Figure 8f. Temperature ${\theta }_c$ in Figure 8d decreases slightly, relative to surrounding material, in the core where this transition occurs, as thermal energy is consumed by latent heat.

Results in Figure 8 confirm melting is possible prior to, or in concert with, fracture if equilibrium melting temperature ${\theta }_T$ is artificially lowered. Similarly, melting with the true value of ${\theta }_T$ can precede fracture if threshold energy $W_0^{\varphi }$ is artificially raised. Taking ${\beta }_{\xi }=0.182$ GPa and $r_0^{\xi }=1$ from Table 2, melting initiates simultaneously with fracture when $W_0^{\varphi }=3.73$ GPa, or $8.3$ times its physical value of 450 MPa in Table 1. Artificially increasing $E_C$ could likewise induce melting simultaneously with damage, since dissipation during a slower fracture kinetic process would increase temperature enough for melting. However, determination of a lower bound on $E_C$ for this to occur requires a nested iterative computational scheme that exceeds current capabilities.

Evaluation of model performance at different nominal strain rates $\dot{\overline{\gamma }}={\upsilon }_0/h_0$ and initial temperatures ${\theta }_i$ is of interest. Effects of variations in these loading parameters are now explored with material properties held fixed at their nominal values in Table 1. It is emphasized that the present approach should be limited to applied rates not much lower than $\approx {10}^3$/s and not much higher than $\approx {10}^4$/s because heat conduction and inertia are omitted. Conduction can notably increase the critical localization strain at low rates and inertia can delay localization at high rates [1,61,109]. Given these domain limits, it is not essential that the model and parameters have as high accuracy for low-strain rate problems. Results for two different strain rates are compared in Figure 9a with experimental data from Ref. [6], namely tests B2 and B6, over the same ratio of test conditions, all at initial temperature ${\theta }_i={\theta }_0=300$K. Model results concur with experimental trends in these data that average localization strain and failure behaviors (e.g., exponential stress decay) are similar when strain rate varies by a factor of around two. Test B2 shows some oscillatory rises in peak stress that are more likely due to specimen variations (e.g., higher wall thickness noted in Ref. [6]) than rate sensitivity.

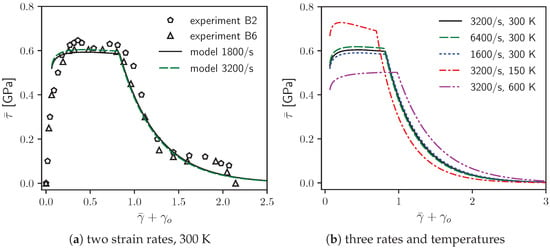
Figure 9. Effects of applied strain rate $\dot{\overline{\gamma }}$ and initial temperature ${\theta }_i$ on average stress $\overline{\tau }$: (a) model results at two nominal rates and data from experiments B2 and B6 of Ref. [6] over the same strain-rate ratio and at starting temperature ${\theta }_0$ (b) model results for three strain rates and three initial temperatures. Parameters from Table 1 are used.

High-rate torsion data at initial temperatures differing from room temperature were not found in existing literature on RHA steel. High- and low-temperature dynamic torsion data exist for other alloys [110,111,112], but such investigations tend to focus on quantifying the flow strength at different rates and temperatures rather than closely tracking strain localization and failure as in Ref. [6]. In those representative publications, stress-strain data are truncated prior to complete load collapse; the present framework cannot be applied toward the shear band problem, as data are insufficient to calibrate parameter $E_C$, for example. Some other alloys also show behaviors inconsistent with the present constitutive theory, for example, different strain-rate sensitivity at different test temperatures [111] or increasing ductility as temperature is reduced [110]. The present theory would less accurately model these cases. As a compromise, Figure 9b shows model predictions for RHA steel over a range of ${\theta }_i$ and strain rates, relaxing the previous assumption that ${\theta }_i={\theta }_0$. Results show increasing (decreasing) ductility and decreasing (increasing) peak stress as ${\theta }_i$ is increased (decreased) by successive factors of two. Similar qualitative trends are witnessed when strain rate is decreased (increased) by the same ratios, though a factor two decrease in strain rate has a much smaller effect on ductility than a twofold increase in temperature.

7. Discussion

A power-law viscoplastic flow rule with a single hardening variable $\chi$ has been used, with governing equations in Section 3.3. This class of model is thought sufficient for analyzing localization under shear-dominant dynamic loading in high-strength steels, as it has been used for this purpose in prior studies [1,12,83]. Importantly, the separable multiplicative form with power-law rate sensitivity is essential for application of the $L_{\infty }$ criterion in Section 4. Other forms of rate sensitivity do not allow elimination of strain rate in (68), but analytical solutions have been derived for different kinds of thermal softening functions [11,12]. For the former reason, the Johnson–Cook model [96], convenient for fitting stress-strain data on many metals, has not been used in this study because its logarithmic form of rate sensitivity is incompatible with the present method of solution. Other models having a stronger basis in metal physics, for example accounting for dislocation mechanics [80,113], dynamic recrystallization (DRX, though not necessarily occurring in the present steel) [114,115], and crystal lattice orientations [116], offer more insight into effects of microstructure. Their complexity, however, precludes implementation in the current mathematical approach and generally necessitates advanced numerical techniques. Differences in results are possible depending on what additional mechanisms are included in these more sophisticated models; for example, DRX [114,117] might precede, complement, or accelerate damage softening in a shear band.

In the plasticity framework of Section 3.3, the flow stress comprises a product of strain hardening, thermal softening, and strain rate hardening terms in power law form. Each contribution is assumed independent. The strain hardening exponent n, thermal softening exponent $\nu$, and rate sensitivity exponent m are assumed to be constants. A similar multiplicative decoupling appears in the standard Johnson–Cook model [96]. Both the power-law and Johnson–Cook formulations are widely used to describe RHA and other high-strength steels [12,83,93,94]. Therefore, the present decoupled model is assumed sufficient in this study, noting that a more complicated model might be more accurate for certain problems at the expense of analytical tractability.

The constitutive framework and analysis techniques of Section 3 and Section 4 are limited to pressurized simple shear. The theory must be generalized to address arbitrary 3D boundary value problems. For isotropic materials, formulation of plasticity and damage models in terms of scalar effective stress (e.g., Von Mises stress) and effective strain rate defined in (77) and (78) is a standard approach for generic stress-strain states. Representative works with guidelines on this topic include Refs. [1,81,118,119].

The framework idealizes the fully formed core of a shear band as a singular region of infinitesimal width and infinite strain. Thus, experimentally measured widths and magnitudes of the band in a continuous sample are necessarily under- and over-predicted, respectively, when experimental profiles do not account for singularities (e.g., shear cracks). Realistic absolute widths cannot be calculated since the analysis includes no material length scale: presently, calculated widths are proportional to specimen size for an a priori, normalized initial perturbation profile. To accurately calculate the absolute width, a complete theoretical model with heat conduction, inertia, and phase-field (i.e., damage order-parameter) gradient regularization should be implemented in a numerical scheme with full space-time discretization. The governing equations for such a complete theoretical model have already been included in the theory outlined in Section 2 of this work, but certain material constants have been zeroed out to allow use of the infinite-strain, singular-point localization criterion (i.e., $L_{\infty }$) pioneered by Molinari and Clifton [11,12,14].

Gradient regularization is contrary to the $L_{\infty }$ criterion so is not invoked. Fourier conduction and standard gradient or phase field models for damage do not allow infinitesimal-width mechanisms (i.e., jumps in field variables such as strain and temperature) because energetic changes are penalized by extreme gradients. The localization integral (68) also requires shear stress uniformity that is incompatible with inertia. The general constitutive theory of Section 2 allows regularization and inertia, but the analytical–numerical solution method of Section 4 does not. A much more computationally demanding FE scheme with explicit dynamics would be needed to implement gradient regularization, heat conduction, and inertia, for example Refs. [33,35,37]. Besides the noted inability to predict the absolute shear band width, omission of regularization is likely to lead to underestimation of localization and failure thresholds for the same initial perturbation. High defect sensitivity inherent in the $L_{\infty }$ criterion should be reduced in a regularized theoretical–numerical setting: a stronger initial perturbation is expected to be needed to overcome energetic resistance from presently omitted regularization mechanisms. Heat conduction and inertia have been shown in prior studies on metals with physical properties representative of steel to increase the critical localization strain at applied shear strain rates below $\approx {10}^3$/s and above $\approx {10}^4$/s, respectively [1,61,109].

Reintroduction of regularization mechanisms, especially heat conduction, is not expected to alter the conclusion that ductile fracture precludes melting in the present RHA steel in a standard torsional Kolsky-bar experiment. Conduction would draw heat away from the core of the band, limiting its maximum temperature. Computational studies [35,37] of torsion-type tests with heat conduction, phase field damage regularization, and inertia consistently predict maximum temperatures far below ambient melt temperature in other alloys. However, the current model and those other works [35,37] do not resolve micron and sub-micron scale mechanisms such as frictional dissipation at asperities of fractured surfaces that could induce highly localized melting [120].

As shown in Figure 6, coupling exists among initial perturbation strength ${ϵ}_0$, threshold energy $W_0^{\varphi }$, and critical strain ${\overline{\gamma }}_c$. This implies $W_0^{\varphi }$ and ${ϵ}_0$ are not strictly independent, so care must be taken with their prescription. The onset of damage correlates with the beginning of the severe load drop witnessed in an experiment at applied strain ${\gamma }_f$. From (47) and (56), $W_0^{\varphi }\approx W^P\left({\gamma }_f\right)$ where $W^P$ is cumulative plastic work, very close to the area under the torsional stress-strain curve for small elastic strain. This definition agrees with Refs. [27,28,47]. If this value is nearly constant for a given material, as claimed in prior works [27,28,47] and reasonably demonstrated in Figure 9a for data at two rates on the same RHA, then defect strength ${ϵ}_0$ can also be presumed relatively constant among similar test conditions. The magnitude of ${ϵ}_0$ in the analysis, unfortunately, cannot be ascertained from experimental stress-strain data alone, nor can the shape and width (${\lambda }_0$) of the profile as in Figure 2c. Here, ${\lambda }_0$ is assumed a priori, and ${ϵ}_0$ uniquely calculated such that the localization strain predictions concur with experimental stress-strain data. This is not deemed a material property calibration, but rather a consistency check necessitated by the method of analysis. From the scale in Figure 6b, at fixed ${\overline{\gamma }}_c$, threshold energy varies nearly linearly with logarithm of defect strength. This trend, in combination with Figure 6a, agrees with Refs. [8,12] that show logarithmic dependence of localization strain on ${ϵ}_0$. Therefore, an extremely precise characterization of ${ϵ}_0$ may not be needed. While determination of the initial defect is a limitation of the method, the current procedures confirm that if a stronger defect is introduced, stress collapse should begin sooner, so threshold energy should be lower. If data indicate $W_0^{\varphi }$ depends on $\theta$, its functional form can be calibrated from experiments at different ${\theta }_i$, with ${ϵ}_0$ determined for each case via the procedure above.

Cohesive energy $E_C$ is calibrated to match stress decay upon localization witnessed in data (e.g., Figure 2a). The larger the value of $E_C$, the slower the damage accumulation and softening with subsequent strain. Though $E_C$ is an adjusted parameter in this setting, its value should be related to fracture toughness, for example shear-band toughness ${\Gamma }_C$ of Ref. [121] that in turn appears roughly correlated to mode-II toughness $J_{IIC}$ in metals. One can take $E_C{l}_C\approx {\Gamma }_C$, where $l_C$ is a characteristic length and ${\Gamma }_C$ half the shear-band toughness. In phase field implementations of this idea, ranges of characteristic length and surface energy for steels can vary by orders of magnitude [31,32,35,37]. Regardless, since behavior is more brittle as $E_C$ decreases, a logical assumption is $E_C\propto J_{IIC}$.

The ductile fracture model in (57) and (59) includes a resistance ${\overline{p}}_0{\delta }_0^{\varphi }$, namely, the product of compressive pressure and maximum volumetric expansion from crack opening or porosity. Parameter ${\delta }_0^{\varphi }$ is a constant for simplicity to enable analysis, limiting physical generality. If ${\delta }_0^{\varphi }$ is finite, damage progression is inhibited at high compressive pressures as in Figure 6d. If a material is known to undergo mode II fracture under extreme high pressure-shear, then ${\delta }_0^{\varphi }\to 0$ should more realistically be assigned. Physically, this would allow cracks to close and voids to collapse at high pressure. The threshold pressure at which nominal choice ${\delta }_0^{\varphi }=0.05$ in Table 1 becomes invalid would need to be determined from seemingly unavailable experimental data on pressure-shear fracture in this steel. Similarly, validity of prescribed value of $W_0^{\varphi }$, also assumed a material constant [27,28,47], remains to be confirmed from data spanning a wider range of experimental conditions.

The model matches experimental stress-strain data in Figure 2a and Figure 9a but does not match the shape profile in Figure 2b. This is an inherent limitation of the $L_{\infty }$ method that cannot predict the true band width. Average shear strain is mainly accommodated by slip on the singular surface rather than more broadly distributed as in the experiment. Were a phase field model with gradient terms such as in (11) implemented in a more costly numerical method, such terms should establish the final band width, rather than characteristics ${ϵ}_0$ and ${\lambda }_0$ of the initial perturbation. This has been shown in Refs. [35,37] and broad applications of phase-field fracture mechanics whereby the regularization length $l_{\varphi }$ controls the equilibrium width of the damage surface. Prior studies have also indicated, in the absence of a gradient-damage model, that thermal diffusivity can instill a steady-state shear band width [1,121]. If phase field damage and conduction are invoked simultaneously, width should be determined by the dominant length scale that emerges from material properties and loading conditions. An initial defect still affects initiation of localization for the simple shear problem even with regularization enabled, since without any perturbation, the homogeneous solution that contains no gradients of field variables remains valid.

The present framework has only been applied to RHA steel. The approach should be straightforward to adapt to other metals so long as sufficient data exist to calibrate their flow, fracture, and melt parameters. Besides conventional properties in Table 1, the threshold energy $W_0^{\varphi }$, cohesive energy $E_C$, and initial perturbation ${ϵ}_0$ should be obtained consistently with failure behavior observed in a dynamic torsion experiment, as discussed already. Determination of $E_C$ is likely most challenging because Kolsky-bar data are often truncated prior to complete load collapse. This is understandable if such experiments only seek plastic flow properties. Alterations to the ductile damage model of Section 3.4 can be anticipated if late-stage stress-strain data do not follow a consistent exponential decay.

8. Conclusions

An analytical–numerical framework has been advanced to study interplay among adiabatic shear localization, ductile fracture, and melting in viscoplastic solids. The problem studied is adiabatic simple shear with uniform external pressure. Localization initiates when a threshold energy density from cumulative plastic work is attained in the context of a dynamic shear fracture model. Post-localization stress decay is modulated by the cohesive energy (related to the shear-band fracture toughness), with the decay rate increased (decreased) by tensile (compressive) stress. Localization concludes when a band of infinitesimal thickness and infinite shear strain is admitted by solutions to the governing equations. Threshold energy, initial defects (e.g., local strength perturbations), and critical average strain at which localization begins are not independent. Larger threshold energy implies a larger critical strain and a defect of lesser intensity or broader distribution. Sharp intense defects are most deleterious; defect sensitivity increases with tensile pressure. Following the usual convention that instability is a necessary condition for localization, the threshold energy logically increases with strain hardening propensity and decreases with more thermal softening.

The model is exercised using properties for a high-strength steel (i.e., RHA). Calculated results for average stress-strain behavior, including post-localization response, accurately match experimental data from dynamic torsion using a literature value of threshold energy density for steel. Nearly all material parameters are obtained from cited research. Calibration is required only for initial yield strength and cohesive energy. The latter’s value is within bounds suggested by experiments and prior phase-field studies. Model features and current parameters, with fracture enabled, are thought to limit accurate calculations to maximum compressive pressures of ≈5–10 GPa and tensile pressures under 0.5 GPa.

Calculations suggest that melting is unimportant for shear localization this steel under dynamic torsion at rates on the order of 10³–10⁴/s. Shear fracture progresses faster than the temperature rise needed for melt initiation. Maximum predicted temperatures in the core of the band are presumably elevated due to omission of thermal diffusion; however, it is possible that the intentionally simple damage model implemented herein omits dissipative structural processes that could competitively increase local temperature. The temperature rise within the shear-softened zone likewise appears insufficient for $\alpha \to \gamma$ phase transition in this steel. It is not impossible than an $\alpha \to ϵ$ transformation could occur, but this transformation has not been confirmed in known experiments on RHA at low pressures (e.g., $p\le 5$ GPa as studied here). If much higher pressures, or if metals with greater intrinsic resistance to local shear fracture (i.e., much larger threshold or cohesive energies), are considered, then higher temperatures can be attained. Therefore, the present inferences of low importance of melting and phase transitions should not be unduly extrapolated to more extreme pressure states, other (e.g., multi-axial) stress-strain histories, nor to all kinds of steels.