Symmetry Solutions and Conserved Quantities of a Generalized (2+1)-Dimensional Nonlinear Wave Equation

Abstract

In this paper, we scrutinize a generalized (2+1)-dimensional nonlinear wave equation (NWE) which describes the waves propagation in plasma physics by utilizing Lie group analysis, Lie point symmetry are obtained and thereafter symmetry reductions are performed which lead to nonlinear ordinary differential equations (NODEs). These NODEs are then solved using various methods that includes the direct integration method. This then leads us to explicit exact solutions of NWE. Graphical representation of the achieved results is given to have a good understanding of the nature of solutions obtained. In conclusion, we construct conserved vectors of the NWE by invoking Ibragimov’s theorem.

1. Introduction

Nonlinear partial differential equations are an important branch of modern mathematics and are used to describe nonlinear physical phenomena in the fields of mechanics, communication engineering, ocean engineering, chemistry, chemical circulation systems, plasma physics, solid state physics and so on [1,2,3,4,5,6]. Solving these nonlinear partial differential equations are often tough and time consuming with the already known conventional methods. In order to understand the dynamics of the systems described by the concerned equation, numerous technical approaches have been introduced by various researchers in mathematics and physics by which one can obtain the exact solutions of nonlinear partial differential equations, such as extended simplest equation method [7], homotopy perturbation technique [8], the sine-cosine method [9], Bäcklund transformation [10], variation of parameters approach [11], Hirota’s technique [12], Lie group analysis [13], Darboux transformation [14], F-expansion technique [15], bifurcation technique [16], Kudryashov’s technique [17], sine-Gordon expanded equation approach [18], multi-exponential function technique [19] homogeneous balance approach [20], the $(G^{\prime }/G)—$expansion method [21], as well as the inverse scattering transform [22], to mention but a few.

Lie group analysis, initiated by the Norwegian mathematician Marius Sophus Lie (1842–1899), is a mathematical technique that can be employed to solve differential equations, which depend on first finding symmetries of the equation. These symmetries may help in simplifying the equation and eventually finding its special solutions [23,24,25,26,27].

Conservation laws are basic rules in physics which state that certain quantifiable properties of a closed system remain unchanged over time, no matter what is happening within the system. These laws contemplate deep symmetries in nature and play a vital role in the comprehension of the physical systems. Conservation laws are crucial for exploring integrability and for initiating existence and uniqueness of solutions. They are also utilized in stability and global aspects of solutions. Furthermore, they play a pivotal role in the evolution of numerical methods [28,29,30,31,32,33,34,35,36].

In [37], the authors worked on the interplay behaviour connected to a generalized (2+1)-dimensional Hirota bilinear equation

$$\begin{array}{c}\left(D_t{D}_y+c_1{\left(D^3\right)}_x{D}_y+c_2{\left(D^2\right)}_y\right)f·f\hfill \\ =2\left[f_{yt}f-f_y{f}_t+c_1(f_{xxxy}f-3f_{xxy}{f}_x+3f_{xy}{f}_{xx}-f_y{f}_{xxx})+c_2(f_{yy}f-{f^2}_y)\right]=0,\hfill \end{array}$$

(1)

which is associated with

$$\begin{array}{c}\hfill u_{yt}+c_1\left[u_{xxxy}+3(2u_x{u}_y+u_{xy}u)+3u_{xx}{\int }_{-\infty }^x{u}_{y}d{x}^{\prime }\right]+c_2{u}_{yy}=0,\end{array}$$

(2)

via the transformation $u=2{[lnf(x,y,t)]}_{xx}$, with $c_1$, $c_2$ being constants. Two kinds of interaction solutions were derived for Equation (2) that included the lump-kink and lump-soliton solutions. Later on the authors of [38], utilized the simplified Hirota’s method along with various ansatz methods and retrieved a class of rational wave structures like multiple soliton solutions, breather, rational, and complexiton solutions. In order to generalize (2) and investigate the model with more complex dynamical behaviour, the authors Zhao and He of [39] introduced the generalized (2+1)-dimensional nonlinear wave (2DNW) equation

$$\begin{array}{c}\hfill u_{yt}+c_1\left[u_{xxxy}+3(2u_x{u}_y+u_{xy}u)+3u_{xx}{\int }_{-\infty }^x{u}_{y}d{x}^{\prime }\right]+c_2{u}_{yy}+c_3{u}_{xx}=0,\end{array}$$

(3)

with $c_3$ being an arbitrary constant. For the details of physics of the 2DNW Equation (3) the reader is refereed to the reference [39]. Zhao and He obtained N-soliton solutions. M-Lump solutions were investigated by applying the long wave limit to the N-soliton solutions. High-order breather and the dynamical behaviour of the hybrid solutions were systematically analyzed via numerical simulations [39].

Zhao et al. investigated the integrability and various solutions of the 2DNW Equation (3) in [40]. Mixed rogue-periodic and rogue-solitary wave solutions were achieved. Also, interconnections between the solitary waves and rogue waves, and interplays between the periodic waves and rogue waves were investigated [40].

He et al. studied the 2DNW Equation (3) and investigated the resonance Y-type solutions and interaction between different types of resonance soliton solutions. The hybrid solutions containing resonance Y-type solitons, breathers and lumps were explored. Furthermore, one- and two-period wave solutions were derived. The relationship between soliton solutions and the quasi-periodic wave solutions were analyzed [41].

In [42], the authors presented the solution of the 2DNW Equation (3) by analyzing the eigenfunctions and Green’s functions of their Lax representations as well as the inverse spectral transformations.

Li et al. studied the generalized (2+1)-dimensional nonlinear wave (g2DNW) equation [43]

$$\begin{array}{c}\hfill u_{ty}+\alpha u_{xxxy}+\beta u_x{u}_y+\lambda u{u}_{xy}+\delta u_{xx}{\int }_{-\infty }^x{u}_{y}dx+ϵu_{yy}+\theta u_{xx}=0,\end{array}$$

(4)

with $\beta =\lambda +\delta$, and $\alpha$, $\beta$, $\gamma$, $ϵ$, $\theta$, being arbitrary constants. Equation (4) has similar physical significance to the KdV equation and represents non-linear waves in plasma physics, fluid dynamics, and weakly dispersion media. Modified hyperbolic function expansion method was successfully invoked to obtain the trigonometric function solutions, the positive hyperbolic function solutions and the hyperbolic trigonometric function solutions in [43].

In this paper, we study the g2DNW Equation (4) from the Lie symmetry standpoint. We first eliminate the integral sign in the equation by introducing the transformation $u(t,x,y)=q_x(t,x,y)$. This transforms Equation (4) into the nonlinear fifth-order wave equation

$$\begin{array}{c}\hfill q_{txy}+\alpha q_{xxxxy}+\beta q_{xx}{q}_{xy}+\lambda q_x{q}_{xxy}+\delta q_{xxx}{q}_y+ϵq_{xyy}+\theta q_{xxx}=0.\end{array}$$

(5)

The paper is organized as follows. In Section 2, we construct new exact solutions of Equation (5) by implementing Lie group analysis along with certain other techniques. Conservation laws are derived in Section 3 using the theorem due to Ibragimov. Finally, concluding remarks are presented in Section 4.

2. Exact Solutions of Equation (5)

We work out Lie symmetries and perform symmetry reductions of the NWE Equation (5). On top of that, we construct travelling wave solution of (5) through integration.

2.1. Lie Point Symmetries of (5)

Lie symmetries of (5) will be acquired by the use of vector field

$$\begin{array}{c}\hfill {\displaystyle X=\tau (t,x,y,q)\frac{\partial }{\partial t}+\xi (t,x,y,q)\frac{\partial }{\partial x}+\varphi (t,x,y,q)\frac{\partial }{\partial y}+\eta (t,x,y,q)\frac{\partial }{\partial q},}\end{array}$$

(6)

where $\tau$, $\xi$, $\varphi$ and $\eta$ are infinitesimals to be determined. The vector field X generates all Lie point symmetries of (5) if

$$\begin{array}{c}\hfill X^{\left[5\right]}{F|}_{F=0}=0,\end{array}$$

(7)

where $F\equiv q_{ty}+\alpha q_{xxxxy}+\beta q_{xx}{q}_{xy}+\lambda q_x{q}_{xxy}+\delta q_{xxxx}{q}_y+ϵq_{xyy}+\theta q_{xxx}$, and $X^{\left[5\right]}$ is the fifth extension of X. For details, see Appendix A.

Expanding (7) and splitting on derivatives of q, we obtain an overdetermined system of linear partial differential equations, which on solving yields the following seven Lie point symmetries:

$$\begin{array}{cc}\hfill & X_1={\displaystyle \frac{\partial }{\partial t}},X_2={\displaystyle \frac{\partial }{\partial x}},X_3={\displaystyle \frac{\partial }{\partial y}},X_4={\displaystyle \frac{\partial }{\partial q}},X_5=\lambda t{\displaystyle \frac{\partial }{\partial x}}+x{\displaystyle \frac{\partial }{\partial q}},\hfill \\ \hfill & X_6=3t{\displaystyle \frac{\partial }{\partial t}}+x{\displaystyle \frac{\partial }{\partial x}}+(4ϵt-y){\displaystyle \frac{\partial }{\partial y}}-q{\displaystyle \frac{\partial }{\partial q}},X_7=\delta {\displaystyle \frac{\partial }{\partial y}}-\theta {\displaystyle \frac{\partial }{\partial q}},\hfill \end{array}$$

with the respective group actions

$$\begin{array}{cc}\hfill & (\overline{t},\overline{x},\overline{y},\overline{q})⟶(t+a,x,y,q),\hfill \\ \hfill & (\overline{t},\overline{x},\overline{y},\overline{q})⟶(t,x+a,y,q),\hfill \\ \hfill & (\overline{t},\overline{x},\overline{y},\overline{q})⟶(t,x,y+a,q),\hfill \\ \hfill & (\overline{t},\overline{x},\overline{y},\overline{q})⟶(t,x,y,q+a),\hfill \\ \hfill & (\overline{t},\overline{x},\overline{y},\overline{q})⟶(t,x+\lambda at,y,q+ax+{\displaystyle \frac{1}{2}}\lambda a^{2}t),\hfill \\ \hfill & (\overline{t},\overline{x},\overline{y},\overline{q})⟶(t{e}^{3a},x{e}^a,e^{-a}(y-ϵt)+ϵt{e}^{4a},q{e}^{-a}),\hfill \\ \hfill & (\overline{t},\overline{x},\overline{y},\overline{q})⟶(t,x,y+a\delta ,q-a\theta )\hfill \end{array}$$

in terms of a parameter a. Accordingly, if $q=H(t,x,y)$ is the solution of nonlinear wave Equation (5), then so are

$$\begin{array}{cc}\hfill q_1=& H(t-a,x,y),\hfill \\ \hfill q_2=& H(t,x-a,y),\hfill \\ \hfill q_3=& H(t,x,y-a),\hfill \\ \hfill q_4=& a+H(t,x,y),\hfill \\ \hfill q_5=& ax+{\displaystyle \frac{1}{2}}\lambda a^{2}t+H(t,x-\lambda at,y),\hfill \\ \hfill q_6=& e^{-a}H(t{e}^{-3a},x{e}^{-a},y{e}^a+ϵt-ϵt{e}^{5a}),\hfill \\ \hfill q_7=& H(t,x,y-a\delta )-a\theta .\hfill \end{array}$$

2.2. Symmetry Reductions and Invariant Solutions of (5)

We derive multiple group-invariant solutions of (5) in this section by carrying out Lie symmetry reductions via the characteristic equations.

2.2.1. Solution Using Translation Symmetries $X_1$, $X_2$ and $X_3$

In this subsection, we construct the travelling wave solution of (5) using the translation symmetries $X_1$, $X_2$ and $X_3$. Thus, we take $q(t,x,y)=Q\left(\xi \right)$, where $\xi =ax+by+ct$ with $a,b$ and c being arbitrary constants. Substituting $Q\left(\xi \right)$ in (5), one gets

$$\begin{array}{c}\hfill (bc+ϵb^2+\theta a^2)Q^{\prime \prime \prime }+\alpha a^{3}b{Q}^{\prime \prime \prime \prime \prime }+a^{2}b\beta {\left(Q^{\prime \prime }\right)}^2+(\lambda +\delta )a^{2}b{Q}^{\prime }{Q}^{\prime \prime \prime }=0.\end{array}$$

(8)

To integrate the above equation we take $\beta =\lambda +\delta$, and get

$$\begin{array}{c}\hfill (bc+ϵb^2+\theta a^2)Q^{\prime \prime \prime }+\alpha a^{3}b{Q}^{\prime \prime \prime \prime \prime }+a^{2}b\beta \left\{Q^{\prime }{Q}^{\prime \prime \prime }+Q^{\prime \prime }{Q}^{\prime \prime }\right\}=0,\end{array}$$

(9)

which we rewrite as

$$\begin{array}{c}\hfill A{Q}^{\prime \prime \prime }+B\left\{Q^{\prime }{Q}^{\prime \prime \prime }+Q^{\prime \prime }{Q}^{\prime \prime }\right\}+C{Q}^{\prime \prime \prime \prime \prime }=0,\end{array}$$

(10)

where $A=bc+ϵb^2+\theta a^2,B=a^{2}b\beta$ and $C=\alpha a^{3}b$. Integrating (10) we get

$$\begin{array}{c}\hfill A{Q}^{\prime \prime }+B{Q}^{\prime }{Q}^{\prime \prime }+C{Q}^{\prime \prime \prime \prime }=C_1,\end{array}$$

where $C_1$ is a constant. To integrate further, we take $C_1=0$. Thus, integrating we get

$$\begin{array}{c}\hfill A{Q}^{\prime }+{\displaystyle \frac{1}{2}}B{Q}^{\prime 2}+C{Q}^{\prime \prime \prime }=C_2,\end{array}$$

where $C_2$ is an arbitrary constant. Multiplying the above equation by $Q^{\prime \prime }$ and integrating it once, we get

$$\begin{array}{c}\hfill {\displaystyle \frac{1}{2}}A{Q}^{\prime 2}+{\displaystyle \frac{1}{6}}B{Q}^{\prime 3}+{\displaystyle \frac{1}{2}}C{Q}^{\prime \prime 2}=C_2{Q}^{\prime }+C_3,\end{array}$$

where $C_3$ is a constant of integration. Let $Q^{\prime }=P$, then the above equation becomes

$$\begin{array}{c}\hfill {\displaystyle \frac{1}{2}}A{P}^2+{\displaystyle \frac{1}{6}}B{P}^3+{\displaystyle \frac{1}{2}}C{P}^{\prime 2}=C_{2}P+C_3.\end{array}$$

(11)

If the algebraic equation

$$\begin{array}{c}\hfill P^3+{\displaystyle \frac{3A}{B}}{P}^2-{\displaystyle \frac{6C_2}{B}}P-{\displaystyle \frac{6C_3}{B}}=0\end{array}$$

has real roots $m_1,m_2,m_3$ such that $m_1>m_2>m_3$, then Equation (11) becomes

$$\begin{array}{c}\hfill P^{\prime 2}=-{\displaystyle \frac{B}{3C}}(P-m_1)(P-m_2)(P-m_3),\end{array}$$

whose solution is [44,45]

$$\begin{array}{c}\hfill P\left(\xi \right)=m_2+(m_1-m_2){\mathrm{cn}}^2\left(\sqrt{{\displaystyle \frac{B(m_1-m_3)}{12C}}}\xi |T^2\right),T^2={\displaystyle \frac{m_1-m_2}{m_1-m_3}},\end{array}$$

(12)

where cn represents the cosine elliptic function. Since $P=Q^{\prime }$ we integrate the above expression with respect to $\xi$. Thereafter, reverting to the original variables, we obtain the solution of Equation (5) as

$$\begin{array}{cc}\hfill q(t,x,y)=& \sqrt{{\displaystyle \frac{12C{(m_1-m_2)}^2}{B(m_1-m_3)T^8}}}\left\{\mathrm{EllipticE}\left[\mathrm{sn}\left(\sqrt{{\displaystyle \frac{B(m_1-m_3)}{12C}}}\xi |T^2\right),T^2\right]\right\}\hfill \\ \hfill & +\left\{m_2-(m_1-m_2){\displaystyle \frac{1-T^4}{T^4}}\right\}\xi +k_3,\hfill \end{array}$$

(13)

where $\xi =ax+by+ct$, $k_3$ is a constant, $A=bc+ϵb^2+\theta a^2,B=a^{2}b(\lambda +\delta )$ and

$$\begin{array}{c}\hfill \mathrm{EllipticE}[p,z]={\int }_0^p\sqrt{{\displaystyle \frac{1-z^2{m}^2}{1-m^2}}}dm\end{array}$$

is the incomplete elliptic integral [45]. The profile of the solution (13) is depicted in Figure 1.

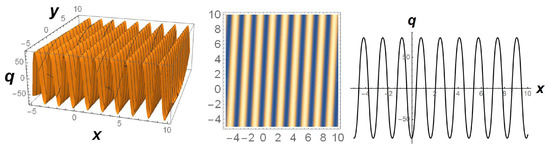
Figure 1. Periodic wave profile of solution (13) in $xy$-axis with $-5\le x,y\le 10$, $t=-14$, $a=-4$, $c=0.6$, $b=0.2$, $m_1=60$, $m_2=30$, $m_3=5$ and $k_3=1$.

2.2.2. Invariant Solution of Equation (5) Using $X_5$

In this subsection, we construct an invariant solution of (5) using Lie point symmetry $X_5=\lambda t{\displaystyle \frac{\partial }{\partial x}}+x{\displaystyle \frac{\partial }{\partial q}}$. This symmetry gives us three invariants

$$\begin{array}{c}\hfill J_1=t,J_2=y,F=q-{\displaystyle \frac{1}{2\lambda t}}{x}^2,\end{array}$$

(14)

which implies that

$$\begin{array}{c}\hfill q(t,x,y)={\displaystyle \frac{x^2}{2\lambda t}}+F(t,y),\end{array}$$

(15)

is the solution of the Equation (5) under $X_5$. Here $F(t,y)$ ia an arbitrary function of t and y. The profile of the solution (15) is presented in Figure 2.

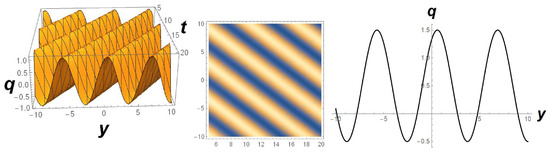
Figure 2. Exhibition of periodic wave profile of solution (15) in $ty$-axis with the choice of $F(t,y)=sin(y+t)$, $5\le t\le 20$, $-10\le y\le 10$, using $\lambda =\alpha =\beta =1$ and $x=1$.

2.2.3. Invariant Solution of Equation (5) Using $X_6$

The symmetry $X_6=3t{\displaystyle \frac{\partial }{\partial t}}+x{\displaystyle \frac{\partial }{\partial x}}+(4ϵt-y){\displaystyle \frac{\partial }{\partial y}}-q{\displaystyle \frac{\partial }{\partial q}}$ gives three invariants, namely

$$\begin{array}{c}\hfill f=x{t}^{-{\displaystyle \frac{1}{3}}},g=t^{{\displaystyle \frac{1}{3}}}(y-ϵt),G(f,g)=q{t}^{{\displaystyle \frac{1}{3}}}.\end{array}$$

(16)

Using these invariants Equation (5) leads to the nonlinear partial differential equation

$$\begin{array}{c}\hfill g{G}_{fgg}-G_{fg}+3\beta G_{fg}{G}_{ff}-f{G}_{ffg}+3\gamma G_f{G}_{ffg}+3\theta G_{fff}+3\delta G_g{G}_{fff}+3\alpha G_{ffffg}=0.\end{array}$$

(17)

The above equation has three Lie point symmetries, viz.,

$$\begin{array}{cc}\hfill & L_1=3\lambda {\displaystyle \frac{\partial }{\partial f}}+f{\displaystyle \frac{\partial }{\partial G}},L_2=\theta g{\displaystyle \frac{\partial }{\partial G}}-\delta g{\displaystyle \frac{\partial }{\partial g}},L_3={\displaystyle \frac{\partial }{\partial G}}.\hfill \end{array}$$

Using the symmetry $L_1$, we get two invariants $r=g$, $H\left(r\right)={\displaystyle \frac{1}{2}}{f}^2-3\lambda G$, and we see that Equation (17) is satisfied for arbitrary H. Hence, going back to original variables, the invariant solution of Equation (5) under the symmetry $X_6$ is

$$\begin{array}{c}\hfill q(t,x,y)={\displaystyle \frac{x^2}{6\lambda t}}-{\displaystyle \frac{1}{3\lambda t^{\frac{1}{3}}}}H\left(t^{{\displaystyle \frac{1}{3}}}(y-ϵt)\right),\end{array}$$

(18)

where H is an arbitrary function of its argument. The profile of the solution (18) is depicted in Figure 3.

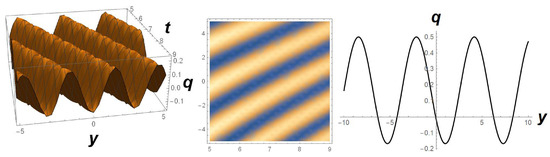
Figure 3. Periodic wave profile representing solution (18) with $H(t,y)=cos\left(t^{{\displaystyle \frac{1}{3}}}(y-ϵt)\right)$ in $ty$-axis with $5\le t\le 9$, $-5\le y\le 5$, $\lambda =\beta =\alpha =ϵ=1$ and $x=1$.

Similarly, symmetry $L_2$ gives us two invariants $k=f$ and $M\left(f\right)={\displaystyle \frac{\theta }{\delta }}g-G$, satisfied the Equation (17) for arbitrary M. Hence, going back to original variables, one can get the invariant solution of Equation (5) stated as

$$\begin{array}{c}\hfill q(t,x,y)=-{\displaystyle \frac{1}{\delta }}\theta (y-ϵt)+{\displaystyle \frac{1}{t^{\frac{1}{3}}}}M\left({\displaystyle \frac{x}{t^{\frac{1}{3}}}}\right),\end{array}$$

(19)

where M is an arbitrary function of its argument. The profile of the solution (19) is exhibited in Figure 4.

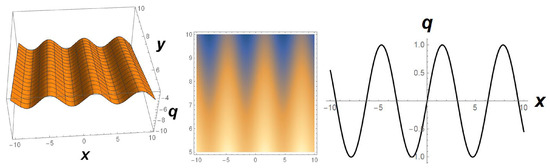
Figure 4. Exhibition of periodic wave solution of (19) in $xy$-axis, with the choice of $M(t,x)=sin\left(x/t^{1/3}\right)$, $-10\le x\le 10$, $5\le y\le 10$, $\lambda =\alpha =\beta =ϵ=\delta =\theta =1$ and $t=1$.

2.2.4. Invariant Solution of Equation (5) Using $X_7$

Symmetry $X_7=\delta {\displaystyle \frac{\partial }{\partial y}}-\theta {\displaystyle \frac{\partial }{\partial q}}$ gives us three invariants, namely

$$\begin{array}{c}\hfill J_1=t,J_2=x,F=q+{\displaystyle \frac{\theta }{\delta }}y,\end{array}$$

(20)

which provide the solution of Equation (5) as

$$\begin{array}{c}\hfill q(t,x,y)=F(t,x)-{\displaystyle \frac{\theta }{\delta }}y,\end{array}$$

(21)

where $F(t,x)$ is an arbitrary function of t and x. The profile of the solution (21) is depicted in Figure 5.

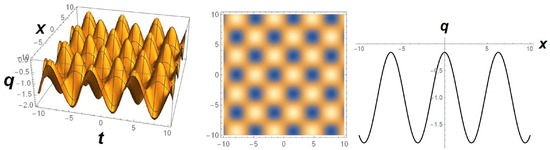
Figure 5. Periodic wave profile of solution (21) in $tx$-axis with the choice of $F(t,x)=sintcosx$, $-10\le t,x\le 10$, using $\delta =\theta =\alpha =\beta =1$ and $y=1$.

3. Conserved Vectors via Ibragimov’s Theorem

In this section, we compute conserved vectors of Equation (5) using Ibragimov’s theorem [36]. We first gain the adjoint equation of (5) stated as

$$\begin{array}{c}\hfill F^{*}\equiv {\displaystyle \frac{\delta }{\delta q}}\left\{v(q_{txy}+\theta q_{xxx}+\alpha q_{xxxxy}+\beta q_{xx}{q}_{xy}+\delta q_{xxx}{q}_y+\lambda q_x{q}_{xxy}+ϵq_{xyy})\right\},\end{array}$$

(22)

with a new introduced variable $v=v(t,x,y)$ and Euler operator

$$\begin{array}{cc}\hfill {\displaystyle \frac{\delta }{\delta q}}=& {\displaystyle \frac{\partial }{\partial q}}-D_x{\displaystyle \frac{\partial }{\partial q_x}}-D_y{\displaystyle \frac{\partial }{\partial q_y}}+D_x^2{\displaystyle \frac{\partial }{\partial q_{xx}}}+D_x{D}_y{\displaystyle \frac{\partial }{\partial q_{xy}}}-D_t{D}_x{D}_y{\displaystyle \frac{\partial }{\partial q_{txy}}}\hfill \\ \hfill & -D_x^3{\displaystyle \frac{\partial }{\partial q_{xxx}}}-D_x^2{D}_y{\displaystyle \frac{\partial }{\partial q_{xxy}}}-D_x{D}_y^2{\displaystyle \frac{\partial }{\partial q_{xyy}}}-D_x^4{D}_y{\displaystyle \frac{\partial }{\partial q_{xxxxy}}}.\hfill \end{array}$$

The expansion of adjoint Equation (22) gives the adjoint $F^{*}$ as

$$\begin{array}{cc}\hfill F^{*}\equiv & 2\beta q_{xxxy}v-2\delta q_{xxxy}v-2\lambda q_{xxxy}v-v_{txy}+(\beta -2\lambda )q_{xx}{v}_{xy}+\beta v_{xx}{q}_{xy}\hfill \\ \hfill & +3\beta v_x{q}_{xxy}+\beta q_{xxx}{v}_y-3\delta v_{xx}{q}_{xy}-3\delta v_x{q}_{xxy}-\delta q_{xxx}{v}_y-\delta q_y{v}_{xxx}\hfill \\ \hfill & -\lambda v_{xx}{q}_{xy}-3\lambda v_x{q}_{xxy}-\lambda q_x{v}_{xxy}-\lambda q_{xxx}{v}_y-\theta v_{xxx}-\alpha v_{xxxxy}-ϵv_{xyy}=0.\hfill \end{array}$$

(23)

According to [36], Equation (5) considered alongside its adjoint possesses the Lagrangian represented by $\mathcal{L}$ and expressed as

$$\begin{array}{c}\hfill \mathcal{L}\equiv vF=v(q_{txy}+\theta q_{xxx}+\alpha q_{xxxxy}+\beta q_{xx}{q}_{xy}+\delta q_{xxx}{q}_y+\lambda q_x{q}_{xxy}+ϵq_{xyy}).\end{array}$$

(24)

One can use the given formula to calculate the conserved vectors for NWE (5)

$$\begin{array}{cc}\hfill T^i=& {\xi }^i\mathcal{L}+W^{\alpha }\left[{\displaystyle \frac{\partial \mathcal{L}}{\partial u_i^{\alpha }}}-D_j{\displaystyle \frac{\partial \mathcal{L}}{\partial u_{ij}^{\alpha }}}+D_j{D}_k{\displaystyle \frac{\partial \mathcal{L}}{\partial u_{ijk}^{\alpha }}}-\dots \right]\hfill \\ \hfill & +D_j\left(W^{\alpha }\right)\left[{\displaystyle \frac{\partial \mathcal{L}}{\partial u_{ij}^{\alpha }}}-D_k{\displaystyle \frac{\partial \mathcal{L}}{\partial u_{ijk}^{\alpha }}}+\dots \right]+D_j{D}_k\left(W^{\alpha }\right)\left[{\displaystyle \frac{\partial \mathcal{L}}{\partial u_{ijk}^{\alpha }}}-\dots \right],\hfill \end{array}$$

(25)

where $\mathcal{L}$ is the Lagrangian given by Equation (23) and $W^{\alpha }$ is the Lie characteristic function given by $W^{\alpha }={\eta }^{\alpha }-{\xi }^i{q}_j^{\alpha }.$

Case 1. The conserved vector $(T_1^t,T_1^x,T_1^y)$ of the system of Equations (5) and (23), associated with $X_1=\delta /\delta t$, is given by

$$\begin{array}{cc}\hfill T_1^t=& \alpha q_{xxxxy}v+\beta q_{xx}{q}_{xy}v+\delta q_{xxx}{q}_{y}v+\theta q_{xxx}v+\lambda q_x{q}_{xxy}v+ϵq_{xyy}v+{\displaystyle \frac{2}{3}}v{q}_{txy}-{\displaystyle \frac{1}{3}}{q}_t{v}_{xy}\hfill \\ \hfill & +{\displaystyle \frac{1}{6}}{v}_x{q}_{ty}+{\displaystyle \frac{1}{6}}{v}_y{q}_{tx},\hfill \\ \hfill T_1^x=& {\displaystyle \frac{3}{2}}\beta q_t{q}_{xxy}v-\theta q_t{v}_{xx}+\beta q_t{v}_x{q}_{xy}+{\displaystyle \frac{1}{2}}\beta q_t{q}_{xx}{v}_y-2\delta q_t{v}_x{q}_{xy}-\delta q_t{q}_y{v}_{xx}-{\displaystyle \frac{2}{3}}\lambda q_t{v}_x{q}_{xy}\hfill \\ \hfill & -{\displaystyle \frac{2}{3}}\lambda q_t{q}_x{v}_{xy}-{\displaystyle \frac{2}{3}}\lambda q_t{q}_{xx}{v}_y-{\displaystyle \frac{1}{3}}ϵq_t{v}_{yy}-{\displaystyle \frac{1}{2}}\beta q_{xx}{q}_{ty}v-\delta q_t{q}_{xxy}v-{\displaystyle \frac{5}{3}}\lambda q_t{q}_{xxy}v\hfill \\ \hfill & +{\displaystyle \frac{1}{3}}\lambda q_{xx}{q}_{ty}v-{\displaystyle \frac{4}{5}}\alpha q_t{v}_{xxxy}+{\displaystyle \frac{1}{5}}\alpha v_{xxx}{q}_{ty}+{\displaystyle \frac{1}{3}}\lambda q_x{v}_x{q}_{ty}+{\displaystyle \frac{1}{3}}ϵv_y{q}_{ty}+{\displaystyle \frac{1}{6}}{v}_t{q}_{ty}\hfill \\ \hfill & +\delta q_{tx}{q}_{xy}v+{\displaystyle \frac{1}{3}}\lambda q_{tx}{q}_{xy}v-{\displaystyle \frac{1}{3}}ϵq_{tyy}v+\theta v_x{q}_{tx}+{\displaystyle \frac{3}{5}}\alpha q_{tx}{v}_{xxy}+\delta q_y{v}_x{q}_{tx}+{\displaystyle \frac{1}{3}}\lambda q_x{v}_y{q}_{tx}\hfill \\ \hfill & -{\displaystyle \frac{1}{3}}{q}_t{v}_{ty}-{\displaystyle \frac{4}{5}}\alpha v{q}_{txxxy}-\delta q_y{q}_{txx}v-\theta q_{txx}v-{\displaystyle \frac{2}{3}}\lambda q_{x}v{q}_{txy}-{\displaystyle \frac{1}{3}}{q}_{tty}v-{\displaystyle \frac{2}{5}}\alpha v_{xx}{q}_{txy}\hfill \\ \hfill & -{\displaystyle \frac{2}{5}}\alpha q_{txx}{v}_{xy}+{\displaystyle \frac{3}{5}}\alpha v_x{q}_{txxy}+{\displaystyle \frac{1}{5}}\alpha v_y{q}_{txxx}+{\displaystyle \frac{1}{6}}{q}_{tt}{v}_y-\beta q_{tx}{q}_{xy}v,\hfill \\ \hfill T_1^y=& {\displaystyle \frac{1}{2}}\beta q_t{q}_{xxx}v-\delta q_t{q}_{xxx}v-{\displaystyle \frac{1}{3}}\lambda q_t{q}_{xxx}v-{\displaystyle \frac{1}{5}}\alpha q_t{v}_{xxxx}+{\displaystyle \frac{1}{2}}\beta q_t{q}_{xx}{v}_x-{\displaystyle \frac{2}{3}}\lambda q_t{q}_{xx}{v}_x\hfill \\ \hfill & -{\displaystyle \frac{1}{3}}\lambda q_t{q}_x{v}_{xx}-{\displaystyle \frac{2}{3}}ϵq_t{v}_{xy}-{\displaystyle \frac{1}{2}}\beta q_{xx}{q}_{tx}v+{\displaystyle \frac{1}{3}}\lambda q_{xx}{q}_{tx}v+{\displaystyle \frac{1}{5}}\alpha v_{xxx}{q}_{tx}+{\displaystyle \frac{1}{3}}\lambda q_x{v}_x{q}_{tx}\hfill \\ \hfill & +{\displaystyle \frac{1}{3}}ϵv_x{q}_{ty}+{\displaystyle \frac{1}{3}}ϵv_y{q}_{tx}+{\displaystyle \frac{1}{6}}{v}_t{q}_{tx}-{\displaystyle \frac{1}{3}}{q}_t{v}_{tx}-{\displaystyle \frac{1}{5}}\alpha q_{txxxx}v-{\displaystyle \frac{1}{3}}\lambda q_x{q}_{txx}v-{\displaystyle \frac{2}{3}}ϵv{q}_{txy}\hfill \\ \hfill & -{\displaystyle \frac{1}{3}}{q}_{ttx}v-{\displaystyle \frac{1}{5}}\alpha v_{xx}{q}_{txx}+{\displaystyle \frac{1}{5}}\alpha v_x{q}_{txxx}+{\displaystyle \frac{1}{6}}{q}_{tt}{v}_x.\hfill \end{array}$$

Case 2. The conserved vector $(T_2^t,T_2^x,T_2^y)$ of the system of Equations (5) and (23), associated with $X_2=\delta /\delta x$ is

$$\begin{array}{cc}\hfill T_2^t=& -{\displaystyle \frac{1}{3}}{q}_{xxy}v+{\displaystyle \frac{1}{6}}{v}_x{q}_{xy}-{\displaystyle \frac{1}{3}}{q}_x{v}_{xy}+{\displaystyle \frac{1}{6}}{q}_{xx}{v}_y,\hfill \\ \hfill T_2^x=& {\displaystyle \frac{2}{3}}ϵq_{xyy}v+\theta q_{xx}{v}_x+\beta q_x{v}_x{q}_{xy}+{\displaystyle \frac{1}{2}}\beta q_{xx}{q}_x{v}_y-2\delta q_x{v}_x{q}_{xy}-{\displaystyle \frac{2}{3}}\lambda {q_x}^2{v}_{xy}-{\displaystyle \frac{1}{3}}\lambda q_x{v}_x{q}_{xy}\hfill \\ \hfill & -{\displaystyle \frac{1}{3}}\lambda q_{xx}{q}_x{v}_y-{\displaystyle \frac{1}{3}}ϵq_x{v}_{yy}+{\displaystyle \frac{1}{3}}ϵv_y{q}_{xy}-{\displaystyle \frac{1}{2}}\beta q_{xx}{q}_{xy}v+{\displaystyle \frac{3}{2}}\beta q_x{q}_{xxy}v+\delta q_{xx}{q}_{xy}v\hfill \\ \hfill & -\delta q_x{q}_{xxy}v+{\displaystyle \frac{2}{3}}\lambda q_{xx}{q}_{xy}v-{\displaystyle \frac{4}{3}}\lambda q_x{q}_{xxy}v-\theta q_x{v}_{xx}+\delta q_{xx}{q}_y{v}_x-\delta q_x{q}_y{v}_{xx}{\displaystyle \frac{1}{5}}\alpha q_{xxxxy}v\hfill \\ \hfill & +{\displaystyle \frac{2}{3}}v{q}_{txy}+{\displaystyle \frac{1}{6}}{v}_t{q}_{xy}-{\displaystyle \frac{1}{3}}{q}_x{v}_{ty}+{\displaystyle \frac{1}{6}}{v}_y{q}_{tx}-{\displaystyle \frac{2}{5}}\alpha v_{xx}{q}_{xxy}+{\displaystyle \frac{3}{5}}\alpha q_{xx}{v}_{xxy}-{\displaystyle \frac{2}{5}}\alpha q_{xxx}{v}_{xy}\hfill \\ \hfill & +{\displaystyle \frac{1}{5}}\alpha v_{xxx}{q}_{xy}+{\displaystyle \frac{3}{5}}\alpha v_x{q}_{xxxy}-{\displaystyle \frac{4}{5}}\alpha q_x{v}_{xxxy}+{\displaystyle \frac{1}{5}}\alpha q_{xxxx}{v}_y,\hfill \\ \hfill T_2^y=& -{\displaystyle \frac{1}{5}}\alpha q_{xxxxx}v+{\displaystyle \frac{1}{2}}\beta q_{xxx}{q}_{x}v-{\displaystyle \frac{1}{2}}\beta {q_{xx}}^{2}v-\delta q_{xxx}{q}_{x}v-{\displaystyle \frac{2}{3}}\lambda q_{xxx}{q}_{x}v+{\displaystyle \frac{1}{3}}\lambda {q_{xx}}^{2}v\hfill \\ \hfill & -{\displaystyle \frac{2}{3}}ϵq_{xxy}v-{\displaystyle \frac{1}{3}}{q}_{txx}v-{\displaystyle \frac{1}{3}}{q}_x{v}_{tx}+{\displaystyle \frac{1}{6}}{v}_t{q}_{xx}+{\displaystyle \frac{1}{6}}{v}_x{q}_{tx}-{\displaystyle \frac{1}{5}}\alpha q_x{v}_{xxxx}-{\displaystyle \frac{1}{5}}\alpha q_{xxx}{v}_{xx}\hfill \\ \hfill & +{\displaystyle \frac{1}{5}}\alpha q_{xx}{v}_{xxx}+{\displaystyle \frac{1}{5}}\alpha q_{xxxx}{v}_x+{\displaystyle \frac{1}{2}}\beta q_{xx}{q}_x{v}_x-{\displaystyle \frac{1}{3}}\lambda {q_x}^2{v}_{xx}-{\displaystyle \frac{1}{3}}\lambda q_{xx}{q}_x{v}_x-{\displaystyle \frac{2}{3}}ϵq_x{v}_{xy}\hfill \\ \hfill & +{\displaystyle \frac{1}{3}}ϵv_x{q}_{xy}+{\displaystyle \frac{1}{3}}ϵq_{xx}{v}_y.\hfill \end{array}$$

Case 3. The conserved vector $(T_3^t,T_3^x,T_3^y)$ of Equations (5) and (23), associated with $X_3=\delta /\delta y$, has components given by

$$\begin{array}{cc}\hfill T_3^t=& -{\displaystyle \frac{1}{3}}{q}_{xyy}v+{\displaystyle \frac{1}{6}}{q}_{yy}{v}_x+{\displaystyle \frac{1}{6}}{v}_y{q}_{xy}-{\displaystyle \frac{1}{3}}{q}_y{v}_{xy},\hfill \\ \hfill T_3^x=& -\delta v_{xx}{q_y}^2-{\displaystyle \frac{1}{3}}ϵv_{yy}{q}_y+\beta v_x{q}_{xy}{q}_y-\delta v_x{q}_{xy}{q}_y-{\displaystyle \frac{2}{3}}\lambda v_x{q}_{xy}{q}_y-{\displaystyle \frac{2}{3}}\lambda q_x{v}_{xy}{q}_y\hfill \\ \hfill & +{\displaystyle \frac{1}{2}}\beta v_y{q}_{xx}{q}_y-{\displaystyle \frac{2}{3}}\lambda v_y{q}_{xx}{q}_y-\theta v_{xx}{q}_y+{\displaystyle \frac{3}{2}}\beta v{q}_{xxy}{q}_y-2\delta v{q}_{xxy}{q}_y-{\displaystyle \frac{5}{3}}\lambda v{q}_{xxy}{q}_y\hfill \\ \hfill & -{\displaystyle \frac{4}{5}}\alpha v_{xxxy}{q}_y-{\displaystyle \frac{1}{3}}{v}_{ty}{q}_y-\beta v{q_{xy}}^2+\delta v{q_{xy}}^2+{\displaystyle \frac{1}{3}}\lambda v{q_{xy}}^2+{\displaystyle \frac{1}{3}}ϵv_y{q}_{yy}-{\displaystyle \frac{1}{3}}ϵv{q}_{yyy}\hfill \\ \hfill & +{\displaystyle \frac{1}{3}}\lambda q_{yy}{q}_x{v}_x+{\displaystyle \frac{1}{3}}\lambda v_y{q}_x{q}_{xy}+\theta v_x{q}_{xy}-{\displaystyle \frac{2}{3}}\lambda v{q}_x{q}_{xyy}-{\displaystyle \frac{1}{2}}\beta q_{yy}{q}_{xx}+{\displaystyle \frac{1}{3}}\lambda v{q}_{yy}{q}_{xx}\hfill \\ \hfill & -{\displaystyle \frac{2}{5}}\alpha q_{xyy}{v}_{xx}-\theta v{q}_{xxy}-{\displaystyle \frac{2}{5}}\alpha v_{xy}{q}_{xxy}+{\displaystyle \frac{3}{5}}\alpha q_{xy}{v}_{xxy}+{\displaystyle \frac{3}{5}}\alpha v_x{q}_{xxyy}+{\displaystyle \frac{1}{5}}\alpha q_{yy}{v}_{xxx}\hfill \\ \hfill & +{\displaystyle \frac{1}{5}}\alpha v_y{q}_{xxxy}-{\displaystyle \frac{4}{5}}\alpha v{q}_{xxxyy}+{\displaystyle \frac{1}{6}}{q}_{yy}{v}_t+{\displaystyle \frac{1}{6}}{v}_y{q}_{ty}-{\displaystyle \frac{1}{3}}v{q}_{tyy},\hfill \\ \hfill T_3^y=& {\displaystyle \frac{4}{5}}\alpha q_{xxxxy}v+{\displaystyle \frac{1}{2}}\beta q_{xx}{q}_{xy}v+{\displaystyle \frac{1}{2}}\beta q_{xxx}{q}_{y}v+\theta q_{xxx}v+{\displaystyle \frac{1}{3}}\lambda q_{xx}{q}_{xy}v+{\displaystyle \frac{2}{3}}\lambda q_x{q}_{xxy}v\hfill \\ \hfill & -{\displaystyle \frac{1}{3}}\lambda q_{xxx}{q}_{y}v+{\displaystyle \frac{1}{3}}ϵq_{xyy}v+{\displaystyle \frac{2}{3}}v{q}_{txy}+{\displaystyle \frac{1}{6}}{v}_x{q}_{ty}+{\displaystyle \frac{1}{6}}{v}_t{q}_{xy}-{\displaystyle \frac{1}{3}}{q}_y{v}_{tx}+{\displaystyle \frac{1}{5}}\alpha v_x{q}_{xxxy}\hfill \\ \hfill & -{\displaystyle \frac{1}{5}}\alpha v_{xx}{q}_{xxy}+{\displaystyle \frac{1}{5}}\alpha v_{xxx}{q}_{xy}-{\displaystyle \frac{1}{5}}\alpha q_y{v}_{xxxx}+{\displaystyle \frac{1}{2}}\beta q_{xx}{q}_y{v}_x+{\displaystyle \frac{1}{3}}\lambda q_x{v}_x{q}_{xy}-{\displaystyle \frac{2}{3}}\lambda q_{xx}{q}_y{v}_x\hfill \\ \hfill & -{\displaystyle \frac{1}{3}}\lambda q_x{q}_y{v}_{xx}+{\displaystyle \frac{1}{3}}ϵq_{yy}{v}_x+{\displaystyle \frac{1}{3}}ϵv_y{q}_{xy}-{\displaystyle \frac{2}{3}}ϵq_y{v}_{xy}.\hfill \end{array}$$

Case 4. The conserved vector $(T_4^t,T_4^x,T_4^y)$ of (5) and (23), associated with $X_4=\delta /\delta u$ is

$$\begin{array}{cc}\hfill T_4^t=& {\displaystyle \frac{1}{3}}{v}_{xy},\hfill \\ \hfill T_4^x=& -{\displaystyle \frac{3}{2}}\beta q_{xxy}v+\delta q_{xxy}v+{\displaystyle \frac{5}{3}}\lambda q_{xxy}v-{\displaystyle \frac{1}{2}}\beta q_{xx}{v}_y-\beta v_x{q}_{xy}+2\delta v_x{q}_{xy}+\delta q_y{v}_{xx}\hfill \\ \hfill & +{\displaystyle \frac{2}{3}}\lambda q_{xx}{v}_y+{\displaystyle \frac{2}{3}}\lambda v_x{q}_{xy}+{\displaystyle \frac{2}{3}}\lambda q_x{v}_{xy}+{\displaystyle \frac{4}{5}}\alpha v_{xxxy}+\theta v_{xx}+{\displaystyle \frac{1}{3}}ϵv_{yy}+{\displaystyle \frac{1}{3}}{v}_{ty}-{\displaystyle \frac{1}{6}}{v}_y,\hfill \\ \hfill T_4^y=& -{\displaystyle \frac{1}{2}}\beta q_{xxx}v+\delta q_{xxx}v+{\displaystyle \frac{1}{3}}\lambda q_{xxx}v-{\displaystyle \frac{1}{2}}\beta q_{xx}{v}_x+{\displaystyle \frac{2}{3}}\lambda q_{xx}{v}_x+{\displaystyle \frac{1}{3}}\lambda q_x{v}_{xx}+{\displaystyle \frac{2}{3}}ϵv_{xy}\hfill \\ \hfill & +{\displaystyle \frac{1}{5}}\alpha v_{xxxx}+{\displaystyle \frac{1}{3}}{v}_{tx}-{\displaystyle \frac{1}{6}}{v}_x.\hfill \end{array}$$

Case 5. The conserved vector $(T_5^t,T_5^x,T_5^y)$ of the system of Equations (5) and (23), associated with symmetry $X_5=\lambda t{\displaystyle \frac{\partial }{\partial x}}+x{\displaystyle \frac{\partial }{\partial q}}$ is

$$\begin{array}{cc}\hfill T_5^t=& -{\displaystyle \frac{1}{3}}\lambda q_{xxy}v+{\displaystyle \frac{1}{6}}\lambda q_{xx}{v}_y+{\displaystyle \frac{1}{6}}\lambda v_x{q}_{xy}-{\displaystyle \frac{1}{3}}\lambda q_x{v}_{xy}+{\displaystyle \frac{1}{3}}x{v}_{xy}-{\displaystyle \frac{1}{6}}{v}_y,\hfill \\ \hfill T_5^x=& -{\displaystyle \frac{1}{3}}{q}_x{v}_x{q}_{xy}{\lambda }^2-{\displaystyle \frac{2}{3}}{q_x}^2{v}_{xy}{\lambda }^2-{\displaystyle \frac{1}{3}}{v}_y{q}_x{q}_{xx}{\lambda }^2+{\displaystyle \frac{2}{3}}v{q}_{xy}{q}_{xx}{\lambda }^2-{\displaystyle \frac{4}{3}}v{q}_x{q}_{xxy}{\lambda }^2-{\displaystyle \frac{1}{6}}{v}_y{q}_x\lambda \hfill \\ \hfill & -{\displaystyle \frac{1}{3}}ϵv_{yy}{q}_x\lambda -{\displaystyle \frac{2}{3}}v{q}_{xy}\lambda +{\displaystyle \frac{1}{3}}ϵv_y{q}_{xy}\lambda +{\displaystyle \frac{2}{3}}x{v}_x{q}_{xy}\lambda +\beta q_x{v}_x{q}_{xy}\lambda -2\delta q_x{v}_x{q}_{xy}\lambda \hfill \\ \hfill & +{\displaystyle \frac{2}{3}}x{q}_x{v}_{xy}-\theta v_x\lambda +{\displaystyle \frac{2}{3}}ϵv{q}_{xyy}\lambda +{\displaystyle \frac{2}{3}}x{v}_y{q}_{xx}\lambda +{\displaystyle \frac{1}{2}}\beta v_y{q}_x{q}_{xx}\lambda +\theta v_x{q}_{xx}\lambda \hfill \\ \hfill & +\delta q_y{v}_x{q}_{xx}\lambda -{\displaystyle \frac{1}{2}}\beta v{q}_{xy}{q}_{xx}\lambda +\delta v{q}_{xy}{q}_{xx}\lambda -\theta q_x{v}_{xx}\lambda +{\displaystyle \frac{5}{3}}xv{q}_{xxy}\lambda +{\displaystyle \frac{3}{2}}\beta v{q}_x{q}_{xxy}\lambda \hfill \\ \hfill & -\delta v{q}_x{q}_{xxy}\lambda -{\displaystyle \frac{2}{5}}\alpha v_{xx}{q}_{xxy}\lambda +{\displaystyle \frac{3}{5}}\alpha q_{xx}{v}_{xxy}\lambda -{\displaystyle \frac{2}{5}}\alpha v_{xy}{q}_{xxx}\lambda +{\displaystyle \frac{1}{5}}\alpha q_{xy}{v}_{xxx}\lambda \hfill \\ \hfill & +{\displaystyle \frac{3}{5}}\alpha v_x{q}_{xxxy}\lambda -{\displaystyle \frac{4}{5}}\alpha q_x{v}_{xxxy}\lambda +{\displaystyle \frac{1}{5}}\alpha v_y{q}_{xxxx}\lambda +{\displaystyle \frac{1}{5}}\alpha v{q}_{xxxxy}\lambda +{\displaystyle \frac{1}{6}}{q}_{xy}{v}_t\lambda \hfill \\ \hfill & -{\displaystyle \frac{1}{3}}{q}_x{v}_{ty}\lambda +{\displaystyle \frac{1}{6}}{v}_y{q}_{tx}\lambda +{\displaystyle \frac{2}{3}}v{q}_{txy}\lambda -{\displaystyle \frac{1}{6}}x{v}_y+{\displaystyle \frac{1}{3}}xϵv_{yy}-\delta q_y{v}_x+\beta v{q}_{xy}-\delta v{q}_{xy}\hfill \\ \hfill & -x\beta v_x{q}_{xy}+2x\delta v_x{q}_{xy}-{\displaystyle \frac{1}{2}}x\beta v_y{q}_{xx}+x\theta v_{xx}+x\delta q_y{v}_{xx}-{\displaystyle \frac{3}{2}}x\beta v{q}_{xxy}\hfill \\ \hfill & +x\delta v{q}_{xxy}-{\displaystyle \frac{3}{5}}\alpha v_{xxy}+{\displaystyle \frac{4}{5}}x\alpha v_{xxxy}+{\displaystyle \frac{1}{3}}x{v}_{ty}-\delta q_y{q}_x{v}_{xx}\lambda ,\hfill \\ \hfill T_5^y=& {\displaystyle \frac{1}{3}}v{q_{xx}}^2{\lambda }^2-{\displaystyle \frac{1}{3}}{q}_x{v}_x{q}_{xx}{\lambda }^2-{\displaystyle \frac{1}{3}}{q_x}^2{v}_{xx}{\lambda }^2-{\displaystyle \frac{2}{3}}v{q}_x{q}_{xxx}{\lambda }^2-{\displaystyle \frac{1}{2}}\beta v{q_{xx}}^2\lambda -{\displaystyle \frac{1}{6}}{q}_x{v}_x\lambda \hfill \\ \hfill & +{\displaystyle \frac{1}{3}}ϵv_x{q}_{xy}\lambda -{\displaystyle \frac{2}{3}}ϵq_x{v}_{xy}\lambda -{\displaystyle \frac{2}{3}}v{q}_{xx}\lambda +{\displaystyle \frac{1}{3}}ϵv_y{q}_{xx}\lambda +{\displaystyle \frac{2}{3}}x{v}_x{q}_{xx}\lambda +{\displaystyle \frac{1}{2}}\beta q_x{v}_x{q}_{xx}\lambda \hfill \\ \hfill & +{\displaystyle \frac{1}{3}}x{q}_x{v}_{xx}\lambda +{\displaystyle \frac{1}{3}}xv{q}_{xxx}\lambda +{\displaystyle \frac{1}{2}}\beta v{q}_x{q}_{xxx}\lambda -\delta v{q}_x{q}_{xxx}\lambda -{\displaystyle \frac{1}{5}}\alpha v_{xx}{q}_{xxx}\lambda \hfill \\ \hfill & +{\displaystyle \frac{1}{5}}\alpha q_{xx}{v}_{xxx}\lambda +{\displaystyle \frac{1}{5}}\alpha v_x{q}_{xxxx}\lambda -{\displaystyle \frac{1}{5}}\alpha q_x{v}_{xxxx}\lambda -{\displaystyle \frac{1}{5}}\alpha v{q}_{xxxxx}\lambda +{\displaystyle \frac{1}{6}}{q}_{xx}{v}_t\lambda \hfill \\ \hfill & +{\displaystyle \frac{1}{6}}{v}_x{q}_{tx}\lambda -{\displaystyle \frac{1}{3}}{q}_x{v}_{tx}\lambda -{\displaystyle \frac{1}{3}}v{q}_{txx}\lambda +{\displaystyle \frac{1}{3}}v-{\displaystyle \frac{1}{6}}x{v}_x+{\displaystyle \frac{2}{3}}xϵv_{xy}+{\displaystyle \frac{1}{2}}\beta v{q}_{xx}\hfill \\ \hfill & -{\displaystyle \frac{1}{2}}x\beta v_x{q}_{xx}-{\displaystyle \frac{1}{2}}x\beta v{q}_{xxx}+x\delta v{q}_{xxx}-{\displaystyle \frac{1}{5}}\alpha v_{xxx}+{\displaystyle \frac{1}{5}}x\alpha v_{xxxx}-{\displaystyle \frac{1}{6}}{v}_t+{\displaystyle \frac{1}{3}}x{v}_{tx}\hfill \\ \hfill & -{\displaystyle \frac{2}{3}}ϵv{q}_{xxy}\lambda -{\displaystyle \frac{1}{3}}ϵv_y.\hfill \end{array}$$

Case 6. The conserved vector $(T_6^t,T_6^x,T_6^y)$ of (5) and (23) associated with $X_6=3t{\displaystyle \frac{\partial }{\partial t}}+x{\displaystyle \frac{\partial }{\partial x}}+(4ϵt-y){\displaystyle \frac{\partial }{\partial y}}-q{\displaystyle \frac{\partial }{\partial q}}$ has components given by

$$\begin{array}{cc}\hfill T_6^t=& 3\alpha t{q}_{xxxxy}v+3\beta t{q}_{xx}{q}_{xy}v+3\delta t{q}_{xxx}{q}_{y}v+3\theta t{q}_{xxx}v+3\lambda t{q}_x{q}_{xxy}v+{\displaystyle \frac{5}{3}}tϵq_{xyy}v\hfill \\ \hfill & -{\displaystyle \frac{1}{3}}{q}_{xy}v-{\displaystyle \frac{1}{3}}{v}_{xy}q+{\displaystyle \frac{1}{3}}y{q}_{xyy}v-{\displaystyle \frac{1}{3}}x{q}_{xxy}v+2tv{q}_{txy}+{\displaystyle \frac{2}{3}}tϵq_{yy}{v}_x+{\displaystyle \frac{2}{3}}tϵv_y{q}_{xy}\hfill \\ \hfill & -{\displaystyle \frac{4}{3}}tϵq_y{v}_{xy}-t{q}_t{v}_{xy}+{\displaystyle \frac{1}{2}}t{v}_x{q}_{ty}+{\displaystyle \frac{1}{2}}t{v}_y{q}_{tx}+{\displaystyle \frac{1}{3}}{q}_x{v}_y-{\displaystyle \frac{1}{3}}x{q}_x{v}_{xy}-{\displaystyle \frac{1}{6}}y{q}_{yy}{v}_x\hfill \\ \hfill & -{\displaystyle \frac{1}{6}}y{v}_y{q}_{xy}+{\displaystyle \frac{1}{6}}x{v}_x{q}_{xy}+{\displaystyle \frac{1}{3}}y{q}_y{v}_{xy}+{\displaystyle \frac{1}{6}}x{q}_{xx}{v}_y,\hfill \\ \hfill T_6^x=& {\displaystyle \frac{4}{3}}t{v}_y{q}_{yy}{ϵ}^2-{\displaystyle \frac{4}{3}}t{q}_y{v}_{yy}{ϵ}^2-{\displaystyle \frac{4}{3}}tv{q}_{yyy}{ϵ}^2-4t\beta v{q_{xy}}^2ϵ+4t\delta v{q_{xy}}^2ϵ+{\displaystyle \frac{4}{3}}t\lambda v{q_{xy}}^2ϵ\hfill \\ \hfill & -v{q}_{yy}ϵ-{\displaystyle \frac{1}{3}}y{v}_y{q}_{yy}ϵ-{\displaystyle \frac{1}{3}}q{v}_{yy}ϵ+{\displaystyle \frac{1}{3}}y{q}_y{v}_{yy}ϵ+{\displaystyle \frac{1}{3}}yv{q}_{yyy}ϵ-{\displaystyle \frac{1}{3}}x{v}_{yy}{q}_xϵ\hfill \\ \hfill & +{\displaystyle \frac{1}{3}}x{v}_y{q}_{xy}ϵ+{\displaystyle \frac{4}{3}}t\lambda v_y{q}_x{q}_{xy}ϵ+4t\theta v_x{q}_{xy}ϵ+4t\beta q_y{v}_x{q}_{xy}ϵ-4t\delta q_y{v}_x{q}_{xy}ϵ\hfill \\ \hfill & -{\displaystyle \frac{8}{3}}t\lambda q_y{v}_x{q}_{xy}ϵ-{\displaystyle \frac{8}{3}}t\lambda q_y{q}_x{v}_{xy}ϵ+{\displaystyle \frac{2}{3}}xv{q}_{xyy}ϵ-{\displaystyle \frac{8}{3}}t\lambda v{q}_x{q}_{xyy}ϵ+2t\beta q_y{v}_y{q}_{xx}ϵ\hfill \\ \hfill & -{\displaystyle \frac{8}{3}}t\lambda q_y{v}_y{q}_{xx}ϵ-2t\beta v{q}_{yy}{q}_{xx}ϵ+{\displaystyle \frac{4}{3}}t\lambda v{q}_{yy}{q}_{xx}ϵ-4t\delta {q_y}^2{v}_{xx}ϵ-4t\theta q_y{v}_{xx}ϵ\hfill \\ \hfill & -{\displaystyle \frac{8}{5}}t\alpha q_{xyy}{v}_{xx}ϵ-4t\theta v{q}_{xxy}ϵ+6t\beta v{q}_y{q}_{xxy}ϵ-8t\delta v{q}_y{q}_{xxy}ϵ-{\displaystyle \frac{20}{3}}t\lambda v{q}_y{q}_{xxy}ϵ\hfill \\ \hfill & -{\displaystyle \frac{8}{5}}t\alpha v_{xy}{q}_{xxy}ϵ+{\displaystyle \frac{12}{5}}t\alpha q_{xy}{v}_{xxy}ϵ+{\displaystyle \frac{12}{5}}t\alpha v_x{q}_{xxyy}ϵ+{\displaystyle \frac{4}{5}}t\alpha q_{yy}{v}_{xxx}ϵ+{\displaystyle \frac{4}{5}}t\alpha v_y{q}_{xxxy}ϵ\hfill \\ \hfill & -{\displaystyle \frac{16}{5}}t\alpha q_y{v}_{xxxy}ϵ-{\displaystyle \frac{16}{5}}t\alpha v{q}_{xxxyy}ϵ-t{v}_{yy}{q}_tϵ+{\displaystyle \frac{2}{3}}t{q}_{yy}{v}_tϵ+{\displaystyle \frac{5}{3}}t{v}_y{q}_{ty}ϵ-{\displaystyle \frac{4}{3}}t{q}_y{v}_{ty}ϵ\hfill \\ \hfill & -{\displaystyle \frac{7}{3}}tv{q}_{tyy}ϵ+{\displaystyle \frac{2}{3}}\lambda v_y{q_x}^2+y\beta v{q_{xy}}^2-y\delta v{q_{xy}}^2-{\displaystyle \frac{1}{3}}y\lambda v{q_{xy}}^2+2\theta q_x{v}_x+2\delta q_y{q}_x{v}_x\hfill \\ \hfill & -{\displaystyle \frac{1}{3}}y\lambda q_{yy}{q}_x{v}_x-2\beta v{q}_x{q}_{xy}+2\delta v{q}_x{q}_{xy}-{\displaystyle \frac{1}{3}}y\lambda v_y{q}_x{q}_{xy}-y\theta v_x{q}_{xy}+\beta q{v}_x{q}_{xy}\hfill \\ \hfill & -2\delta q{v}_x{q}_{xy}-{\displaystyle \frac{2}{3}}\lambda q{v}_x{q}_{xy}-y\beta q_y{v}_x{q}_{xy}+y\delta q_y{v}_x{q}_{xy}+{\displaystyle \frac{2}{3}}y\lambda q_y{v}_x{q}_{xy}+x\beta q_x{v}_x{q}_{xy}\hfill \\ \hfill & -2x\delta q_x{v}_x{q}_{xy}-{\displaystyle \frac{1}{3}}x\lambda q_x{v}_x{q}_{xy}-{\displaystyle \frac{2}{3}}x\lambda {q_x}^2{v}_{xy}-{\displaystyle \frac{2}{3}}\lambda q{q}_x{v}_{xy}+{\displaystyle \frac{2}{3}}y\lambda q_y{q}_x{v}_{xy}\hfill \\ \hfill & +{\displaystyle \frac{2}{3}}y\lambda v{q}_x{q}_{xyy}-3\theta v{q}_{xx}-3\delta v{q}_y{q}_{xx}+{\displaystyle \frac{1}{2}}\beta q{v}_y{q}_{xx}-{\displaystyle \frac{2}{3}}\lambda q{v}_y{q}_{xx}-{\displaystyle \frac{1}{2}}y\beta q_y{v}_y{q}_{xx}\hfill \\ \hfill & +{\displaystyle \frac{2}{3}}y\lambda q_y{v}_y{q}_{xx}+{\displaystyle \frac{1}{2}}y\beta v{q}_{yy}{q}_{xx}-{\displaystyle \frac{1}{3}}y\lambda v{q}_{yy}{q}_{xx}+{\displaystyle \frac{1}{2}}x\beta v_y{q}_x{q}_{xx}-{\displaystyle \frac{1}{3}}x\lambda v_y{q}_x{q}_{xx}\hfill \\ \hfill & +x\theta v_x{q}_{xx}+x\delta q_y{v}_x{q}_{xx}-{\displaystyle \frac{1}{2}}x\beta v{q}_{xy}{q}_{xx}+x\delta v{q}_{xy}{q}_{xx}+{\displaystyle \frac{2}{3}}x\lambda v{q}_{xy}{q}_{xx}-{\displaystyle \frac{6}{5}}\alpha v_{xy}{q}_{xx}\hfill \\ \hfill & +y\delta {q_y}^2{v}_{xx}-\theta q{v}_{xx}+y\theta q_y{v}_{xx}-\delta q{q}_y{v}_{xx}-x\theta q_x{v}_{xx}-x\delta q_y{q}_x{v}_{xx}-{\displaystyle \frac{2}{5}}\alpha q_{xy}{v}_{xx}\hfill \\ \hfill & +{\displaystyle \frac{2}{5}}y\alpha q_{xyy}{v}_{xx}+y\theta v{q}_{xxy}+{\displaystyle \frac{3}{2}}\beta qv{q}_{xxy}-\delta qv{q}_{xxy}-{\displaystyle \frac{5}{3}}\lambda qv{q}_{xxy}-{\displaystyle \frac{3}{2}}y\beta v{q}_y{q}_{xxy}\hfill \\ \hfill & +2y\delta v{q}_y{q}_{xxy}+{\displaystyle \frac{5}{3}}y\lambda v{q}_y{q}_{xxy}+{\displaystyle \frac{3}{2}}x\beta v{q}_x{q}_{xxy}-x\delta v{q}_x{q}_{xxy}-{\displaystyle \frac{4}{3}}x\lambda v{q}_x{q}_{xxy}\hfill \\ \hfill & +{\displaystyle \frac{6}{5}}\alpha v_x{q}_{xxy}+{\displaystyle \frac{2}{5}}y\alpha v_{xy}{q}_{xxy}-{\displaystyle \frac{2}{5}}x\alpha v_{xx}{q}_{xxy}+{\displaystyle \frac{6}{5}}\alpha q_x{v}_{xxy}-{\displaystyle \frac{3}{5}}y\alpha q_{xy}{v}_{xxy}\hfill \\ \hfill & +{\displaystyle \frac{3}{5}}x\alpha q_{xx}{v}_{xxy}-{\displaystyle \frac{3}{5}}y\alpha v_x{q}_{xxyy}+{\displaystyle \frac{4}{5}}\alpha v_y{q}_{xxx}-{\displaystyle \frac{2}{5}}x\alpha v_{xy}{q}_{xxx}-{\displaystyle \frac{1}{5}}y\alpha q_{yy}{v}_{xxx}\hfill \\ \hfill & +{\displaystyle \frac{1}{5}}x\alpha q_{xy}{v}_{xxx}-{\displaystyle \frac{12}{5}}\alpha v{q}_{xxxy}-{\displaystyle \frac{1}{5}}y\alpha v_y{q}_{xxxy}+{\displaystyle \frac{3}{5}}x\alpha v_x{q}_{xxxy}-{\displaystyle \frac{4}{5}}\alpha q{v}_{xxxy}\hfill \\ \hfill & +{\displaystyle \frac{4}{5}}y\alpha q_y{v}_{xxxy}-{\displaystyle \frac{4}{5}}x\alpha q_x{v}_{xxxy}+{\displaystyle \frac{4}{5}}y\alpha v{q}_{xxxyy}+{\displaystyle \frac{1}{5}}x\alpha v_y{q}_{xxxx}+{\displaystyle \frac{1}{5}}x\alpha v{q}_{xxxxy}\hfill \end{array}$$

$$\begin{array}{cc}\hfill & +3t\beta v_x{q}_{xy}{q}_t-6t\delta v_x{q}_{xy}{q}_t-2t\lambda v_x{q}_{xy}{q}_t-2t\lambda q_x{v}_{xy}{q}_t+{\displaystyle \frac{3}{2}}t\beta v_y{q}_{xx}{q}_t\hfill \\ \hfill & -3t\delta q_y{v}_{xx}{q}_t+{\displaystyle \frac{9}{2}}t\beta v{q}_{xxy}{q}_t-3t\delta v{q}_{xxy}{q}_t-5t\lambda v{q}_{xxy}{q}_t-{\displaystyle \frac{12}{5}}t\alpha v_{xxxy}{q}_t\hfill \\ \hfill & +{\displaystyle \frac{1}{6}}x{q}_{xy}{v}_t-v{q}_{ty}-{\displaystyle \frac{1}{6}}y{v}_y{q}_{ty}+t\lambda q_x{v}_x{q}_{ty}-{\displaystyle \frac{3}{2}}t\beta v{q}_{xx}{q}_{ty}+t\lambda v{q}_{xx}{q}_{ty}\hfill \\ \hfill & +{\displaystyle \frac{1}{2}}t{v}_t{q}_{ty}-{\displaystyle \frac{1}{3}}q{v}_{ty}+{\displaystyle \frac{1}{3}}y{q}_y{v}_{ty}-{\displaystyle \frac{1}{3}}x{q}_x{v}_{ty}-t{q}_t{v}_{ty}+{\displaystyle \frac{1}{3}}yv{q}_{tyy}+{\displaystyle \frac{1}{6}}x{v}_y{q}_{tx}\hfill \\ \hfill & +3t\theta v_x{q}_{tx}+3t\delta q_y{v}_x{q}_{tx}-3t\beta v{q}_{xy}{q}_{tx}+3t\delta v{q}_{xy}{q}_{tx}+t\lambda v{q}_{xy}{q}_{tx}+{\displaystyle \frac{9}{5}}t\alpha v_{xxy}{q}_{tx}\hfill \\ \hfill & +{\displaystyle \frac{2}{3}}xv{q}_{txy}-2t\lambda v{q}_x{q}_{txy}-{\displaystyle \frac{6}{5}}t\alpha v_{xx}{q}_{txy}-3t\theta v{q}_{txx}-3t\delta v{q}_y{q}_{txx}-{\displaystyle \frac{6}{5}}t\alpha v_{xy}{q}_{txx}\hfill \\ \hfill & +{\displaystyle \frac{9}{5}}t\alpha v_x{q}_{txxy}+{\displaystyle \frac{3}{5}}t\alpha v_y{q}_{txxx}-{\displaystyle \frac{12}{5}}t\alpha v{q}_{txxxy}+{\displaystyle \frac{1}{2}}t{v}_y{q}_{tt}-tv{q}_{tty}-3t\theta v_{xx}{q}_t+{\displaystyle \frac{2}{3}}{q}_y{v}_yϵ\hfill \\ \hfill & +{\displaystyle \frac{4}{3}}t\lambda q_{yy}{q}_x{v}_xϵ+{\displaystyle \frac{2}{3}}{v}_y{q}_t+t\lambda v_y{q}_x{q}_{tx}+{\displaystyle \frac{3}{5}}t\alpha v_{xxx}{q}_{ty}-{\displaystyle \frac{1}{6}}y{q}_{yy}{v}_t-2t\lambda v_y{q}_{xx}{q}_t,\hfill \\ \hfill T_6^y=& {\displaystyle \frac{4}{3}}t{q}_{yy}{v}_x{ϵ}^2+{\displaystyle \frac{4}{3}}t{v}_y{q}_{xy}{ϵ}^2-{\displaystyle \frac{8}{3}}t{q}_y{v}_{xy}{ϵ}^2+{\displaystyle \frac{4}{3}}tv{q}_{xyy}{ϵ}^2+{\displaystyle \frac{2}{3}}{v}_y{q}_xϵ+{\displaystyle \frac{2}{3}}{q}_y{v}_xϵ-{\displaystyle \frac{1}{3}}y{q}_{yy}{v}_xϵ\hfill \\ \hfill & -2v{q}_{xy}ϵ-{\displaystyle \frac{1}{3}}y{v}_y{q}_{xy}ϵ+{\displaystyle \frac{1}{3}}x{v}_x{q}_{xy}ϵ+{\displaystyle \frac{4}{3}}t\lambda q_x{v}_x{q}_{xy}ϵ-{\displaystyle \frac{2}{3}}q{v}_{xy}ϵ+{\displaystyle \frac{2}{3}}y{q}_y{v}_{xy}ϵ\hfill \\ \hfill & -{\displaystyle \frac{1}{3}}yv{q}_{xyy}ϵ+{\displaystyle \frac{1}{3}}x{v}_y{q}_{xx}ϵ+2t\beta q_y{v}_x{q}_{xx}ϵ-{\displaystyle \frac{8}{3}}t\lambda q_y{v}_x{q}_{xx}ϵ+2t\beta v{q}_{xy}{q}_{xx}ϵ\hfill \\ \hfill & -{\displaystyle \frac{4}{3}}t\lambda q_y{q}_x{v}_{xx}ϵ-{\displaystyle \frac{2}{3}}xv{q}_{xxy}ϵ+{\displaystyle \frac{8}{3}}t\lambda v{q}_x{q}_{xxy}ϵ-{\displaystyle \frac{4}{5}}t\alpha v_{xx}{q}_{xxy}ϵ+4t\theta v{q}_{xxx}ϵ\hfill \\ \hfill & -{\displaystyle \frac{4}{3}}t\lambda v{q}_y{q}_{xxx}ϵ+{\displaystyle \frac{4}{5}}t\alpha q_{xy}{v}_{xxx}ϵ+{\displaystyle \frac{4}{5}}t\alpha v_x{q}_{xxxy}ϵ-{\displaystyle \frac{4}{5}}t\alpha q_y{v}_{xxxx}ϵ+{\displaystyle \frac{16}{5}}t\alpha v{q}_{xxxxy}ϵ\hfill \\ \hfill & -2t{v}_{xy}{q}_tϵ+{\displaystyle \frac{2}{3}}t{q}_{xy}{v}_tϵ+{\displaystyle \frac{5}{3}}t{v}_x{q}_{ty}ϵ+t{v}_y{q}_{tx}ϵ-{\displaystyle \frac{4}{3}}t{q}_y{v}_{tx}ϵ+{\displaystyle \frac{2}{3}}tv{q}_{txy}ϵ-{\displaystyle \frac{1}{2}}x\beta v{q_{xx}}^2\hfill \\ \hfill & +{\displaystyle \frac{1}{3}}x\lambda v{q_{xx}}^2+{\displaystyle \frac{2}{3}}\lambda {q_x}^2{v}_x-{\displaystyle \frac{1}{3}}y\lambda q_x{v}_x{q}_{xy}-\beta v{q}_x{q}_{xx}-{\displaystyle \frac{1}{3}}\lambda v{q}_x{q}_{xx}+{\displaystyle \frac{1}{2}}\beta q{v}_x{q}_{xx}\hfill \\ \hfill & -{\displaystyle \frac{2}{3}}\lambda q{v}_x{q}_{xx}-{\displaystyle \frac{1}{2}}y\beta q_y{v}_x{q}_{xx}+{\displaystyle \frac{2}{3}}y\lambda q_y{v}_x{q}_{xx}+{\displaystyle \frac{1}{2}}x\beta q_x{v}_x{q}_{xx}-{\displaystyle \frac{1}{3}}x\lambda q_x{v}_x{q}_{xx}\hfill \\ \hfill & -{\displaystyle \frac{1}{2}}y\beta v{q}_{xy}{q}_{xx}-{\displaystyle \frac{1}{3}}y\lambda v{q}_{xy}{q}_{xx}-{\displaystyle \frac{1}{3}}x\lambda {q_x}^2{v}_{xx}-{\displaystyle \frac{1}{3}}\lambda q{q}_x{v}_{xx}+{\displaystyle \frac{1}{3}}y\lambda q_y{q}_x{v}_{xx}\hfill \\ \hfill & -{\displaystyle \frac{2}{3}}y\lambda v{q}_x{q}_{xxy}+{\displaystyle \frac{1}{5}}y\alpha v_{xx}{q}_{xxy}-y\theta v{q}_{xxx}+{\displaystyle \frac{1}{2}}\beta qv{q}_{xxx}-\delta qv{q}_{xxx}-{\displaystyle \frac{1}{3}}\lambda uv{q}_{xxx}\hfill \\ \hfill & -{\displaystyle \frac{1}{2}}y\beta v{q}_y{q}_{xxx}+{\displaystyle \frac{1}{3}}y\lambda v{q}_y{q}_{xxx}+{\displaystyle \frac{1}{2}}x\beta v{q}_x{q}_{xxx}-x\delta v{q}_x{q}_{xxx}-{\displaystyle \frac{2}{3}}x\lambda v{q}_x{q}_{xxx}\hfill \\ \hfill & -{\displaystyle \frac{1}{5}}x\alpha v_{xx}{q}_{xxx}+{\displaystyle \frac{2}{5}}\alpha q_x{v}_{xxx}-{\displaystyle \frac{1}{5}}y\alpha q_{xy}{v}_{xxx}+{\displaystyle \frac{1}{5}}x\alpha q_{xx}{v}_{xxx}-{\displaystyle \frac{1}{5}}y\alpha v_x{q}_{xxxy}\hfill \\ \hfill & +{\displaystyle \frac{1}{5}}x\alpha v_x{q}_{xxxx}-{\displaystyle \frac{1}{5}}\alpha q{v}_{xxxx}+{\displaystyle \frac{1}{5}}y\alpha q_y{v}_{xxxx}-{\displaystyle \frac{1}{5}}x\alpha q_x{v}_{xxxx}-{\displaystyle \frac{4}{5}}y\alpha v{q}_{xxxxy}\hfill \\ \hfill & +{\displaystyle \frac{2}{3}}{v}_x{q}_t+{\displaystyle \frac{3}{2}}t\beta v_x{q}_{xx}{q}_t-2t\lambda v_x{q}_{xx}{q}_t-t\lambda q_x{v}_{xx}{q}_t+{\displaystyle \frac{3}{2}}t\beta v{q}_{xxx}{q}_t-3t\delta v{q}_{xxx}{q}_t\hfill \\ \hfill & -t\lambda v{q}_{xxx}{q}_t-{\displaystyle \frac{3}{5}}t\alpha v_{xxxx}{q}_t+{\displaystyle \frac{1}{3}}{q}_x{v}_t-{\displaystyle \frac{1}{6}}y{q}_{xy}{v}_t+{\displaystyle \frac{1}{6}}x{q}_{xx}{v}_t-{\displaystyle \frac{1}{6}}y{v}_x{q}_{ty}-{\displaystyle \frac{5}{3}}v{q}_{tx}\hfill \\ \hfill & +{\displaystyle \frac{1}{6}}x{v}_x{q}_{tx}+t\lambda q_x{v}_x{q}_{tx}-{\displaystyle \frac{3}{2}}t\beta v{q}_{xx}{q}_{tx}+t\lambda v{q}_{xx}{q}_{tx}+{\displaystyle \frac{3}{5}}t\alpha v_{xxx}{q}_{tx}+{\displaystyle \frac{1}{2}}t{v}_t{q}_{tx}\hfill \\ \hfill & +{\displaystyle \frac{1}{3}}y{q}_y{v}_{tx}-{\displaystyle \frac{1}{3}}x{q}_x{v}_{tx}-t{q}_t{v}_{tx}-{\displaystyle \frac{2}{3}}yv{q}_{txy}-{\displaystyle \frac{1}{3}}xv{q}_{txx}-t\lambda v{q}_x{q}_{txx}-{\displaystyle \frac{3}{5}}t\alpha v_{xx}{q}_{txx}\hfill \\ \hfill & +{\displaystyle \frac{3}{5}}t\alpha v_x{q}_{txxx}-{\displaystyle \frac{3}{5}}t\alpha v{q}_{txxxx}+{\displaystyle \frac{1}{2}}t{v}_x{q}_{tt}-tv{q}_{ttx}-{\displaystyle \frac{2}{3}}x{q}_x{v}_{xy}ϵ+{\displaystyle \frac{4}{3}}t\lambda v{q}_{xy}{q}_{xx}ϵ\hfill \\ \hfill & +2t\beta v{q}_y{q}_{xxx}ϵ-{\displaystyle \frac{3}{5}}\alpha q_{xx}{v}_{xx}+{\displaystyle \frac{4}{5}}\alpha v_x{q}_{xxx}-\alpha v{q}_{xxxx}-{\displaystyle \frac{1}{5}}x\alpha v{q}_{xxxxx}-{\displaystyle \frac{1}{3}}q{v}_{tx}.\hfill \end{array}$$

Case 7. The conserved vector $(T_7^t,T_7^x,T_7^y)$ of the system of Equations (5) and (23), associated with the symmetry $X_7=\delta {\displaystyle \frac{\partial }{\partial y}}-\theta {\displaystyle \frac{\partial }{\partial q}}$ has components

$$\begin{array}{cc}\hfill T_7^t=& -{\displaystyle \frac{1}{3}}\delta q_{xyy}v+{\displaystyle \frac{1}{6}}\delta q_{yy}{v}_x+{\displaystyle \frac{1}{6}}\delta v_y{q}_{xy}-{\displaystyle \frac{1}{3}}\delta q_y{v}_{xy}-{\displaystyle \frac{1}{3}}\theta v_{xy},\hfill \\ \hfill T_7^x=& v{q_{xy}}^2{\delta }^2-q_y{v}_x{q}_{xy}{\delta }^2-{q_y}^2{v}_{xx}{\delta }^2-2v{q}_y{q}_{xxy}{\delta }^2-\beta v{q_{xy}}^2\delta +{\displaystyle \frac{1}{3}}\lambda v{q_{xy}}^2\delta \hfill \\ \hfill & +{\displaystyle \frac{1}{6}}ϵq_y{v}_y\delta -{\displaystyle \frac{1}{3}}ϵv{q}_{yy}\delta +{\displaystyle \frac{1}{3}}ϵv_y{q}_{yy}\delta -{\displaystyle \frac{1}{3}}ϵq_y{v}_{yy}\delta -{\displaystyle \frac{1}{3}}ϵv{q}_{yyy}\delta +{\displaystyle \frac{1}{3}}\lambda q_y{q}_x{v}_x\delta \hfill \\ \hfill & +{\displaystyle \frac{1}{3}}\lambda q_{yy}{q}_x{v}_x\delta -{\displaystyle \frac{2}{3}}\lambda v{q}_x{q}_{xy}\delta +{\displaystyle \frac{1}{3}}\lambda v_y{q}_x{q}_{xy}\delta -\theta v_x{q}_{xy}\delta +\beta q_y{v}_x{q}_{xy}\delta -{\displaystyle \frac{2}{3}}\lambda q_y{v}_x{q}_{xy}\delta \hfill \\ \hfill & -{\displaystyle \frac{2}{3}}\lambda q_y{q}_x{v}_{xy}\delta -{\displaystyle \frac{2}{3}}\lambda v{q}_x{q}_{xyy}\delta -{\displaystyle \frac{1}{2}}\beta v{q}_y{q}_{xx}\delta +{\displaystyle \frac{1}{3}}\lambda v{q}_y{q}_{xx}\delta +{\displaystyle \frac{1}{2}}\beta q_y{v}_y{q}_{xx}\delta \hfill \\ \hfill & -{\displaystyle \frac{2}{3}}\lambda q_y{v}_y{q}_{xx}\delta -{\displaystyle \frac{1}{2}}\beta v{q}_{yy}{q}_{xx}\delta +{\displaystyle \frac{1}{3}}\lambda v{q}_{yy}{q}_{xx}\delta -2\theta q_y{v}_{xx}\delta -{\displaystyle \frac{2}{5}}\alpha q_{xy}{v}_{xx}\delta \hfill \\ \hfill & -{\displaystyle \frac{2}{5}}\alpha q_{xyy}{v}_{xx}\delta -2\theta v{q}_{xxy}\delta +{\displaystyle \frac{3}{2}}\beta v{q}_y{q}_{xxy}\delta -{\displaystyle \frac{5}{3}}\lambda v{q}_y{q}_{xxy}\delta +{\displaystyle \frac{3}{5}}\alpha v_x{q}_{xxy}\delta \hfill \\ \hfill & -{\displaystyle \frac{2}{5}}\alpha v_{xy}{q}_{xxy}\delta +{\displaystyle \frac{3}{5}}\alpha q_{xy}{v}_{xxy}\delta +{\displaystyle \frac{3}{5}}\alpha v_x{q}_{xxyy}\delta +{\displaystyle \frac{1}{5}}\alpha q_y{v}_{xxx}\delta +{\displaystyle \frac{1}{5}}\alpha q_{yy}{v}_{xxx}\delta \hfill \\ \hfill & -{\displaystyle \frac{4}{5}}\alpha v{q}_{xxxy}\delta +{\displaystyle \frac{1}{5}}\alpha v_y{q}_{xxxy}\delta -{\displaystyle \frac{4}{5}}\alpha q_y{v}_{xxxy}\delta -{\displaystyle \frac{4}{5}}\alpha v{q}_{xxxyy}\delta +{\displaystyle \frac{1}{6}}{q}_y{v}_t\delta -{\displaystyle \frac{1}{3}}v{q}_{ty}\delta \hfill \\ \hfill & +{\displaystyle \frac{1}{6}}{v}_y{q}_{ty}\delta -{\displaystyle \frac{1}{3}}{q}_y{v}_{ty}\delta -{\displaystyle \frac{1}{3}}v{q}_{tyy}\delta -{\displaystyle \frac{1}{3}}ϵ\theta v_{yy}+{\displaystyle \frac{1}{3}}\theta \lambda q_x{v}_x+\beta \theta v_x{q}_{xy}-{\displaystyle \frac{2}{3}}\theta \lambda v_x{q}_{xy}\hfill \\ \hfill & -{\displaystyle \frac{2}{3}}\theta \lambda q_x{v}_{xy}-{\displaystyle \frac{1}{2}}\beta \theta v{q}_{xx}+{\displaystyle \frac{1}{3}}\theta \lambda v{q}_{xx}+{\displaystyle \frac{1}{2}}\beta \theta v_y{q}_{xx}-{\displaystyle \frac{2}{3}}\theta \lambda v_y{q}_{xx}-{\theta }^2{v}_{xx}+{\displaystyle \frac{3}{2}}\beta \theta v{q}_{xxy}\hfill \\ \hfill & +{\displaystyle \frac{1}{5}}\alpha \theta v_{xxx}-{\displaystyle \frac{4}{5}}\alpha \theta v_{xxxy}+{\displaystyle \frac{1}{6}}\theta v_t-{\displaystyle \frac{1}{3}}\theta v_{ty}+{\displaystyle \frac{1}{6}}{q}_{yy}{v}_t\delta +{\displaystyle \frac{1}{6}}ϵ\theta v_y-{\displaystyle \frac{5}{3}}\theta \lambda v{q}_{xxy},\hfill \\ \hfill T_7^y=& {\displaystyle \frac{1}{6}}ϵ\theta v_x+{\displaystyle \frac{1}{6}}\delta ϵq_y{v}_x+{\displaystyle \frac{1}{3}}\delta ϵq_{yy}{v}_x+{\displaystyle \frac{1}{3}}\delta \lambda q_x{q}_{xy}{v}_x+{\displaystyle \frac{1}{2}}\beta \theta q_{xx}{v}_x-{\displaystyle \frac{2}{3}}\theta \lambda q_{xx}{v}_x\hfill \\ \hfill & +{\displaystyle \frac{1}{2}}\beta \delta q_y{q}_{xx}{v}_x-{\displaystyle \frac{2}{3}}\delta \lambda q_y{u}_{xx}{v}_x+{\displaystyle \frac{1}{5}}\alpha \delta q_{xxxy}{v}_x+{\displaystyle \frac{1}{6}}\delta q_{ty}{v}_x-{\displaystyle \frac{1}{3}}\delta ϵv{q}_{xy}+{\displaystyle \frac{1}{3}}\delta ϵv_y{q}_{xy}\hfill \\ \hfill & -{\displaystyle \frac{2}{3}}ϵ\theta v_{xy}-{\displaystyle \frac{2}{3}}\delta ϵq_y{v}_{xy}+{\displaystyle \frac{1}{3}}\delta ϵv{q}_{xyy}+{\displaystyle \frac{1}{2}}\beta \delta v{q}_{xy}{q}_{xx}+{\displaystyle \frac{1}{3}}\delta \lambda v{q}_{xy}{q}_{xx}-{\displaystyle \frac{1}{3}}\theta \lambda q_x{v}_{xx}\hfill \\ \hfill & -{\displaystyle \frac{1}{3}}\delta \lambda q_y{q}_x{v}_{xx}+{\displaystyle \frac{2}{3}}\delta \lambda v{q}_x{q}_{xxy}-{\displaystyle \frac{1}{5}}\alpha \delta v_{xx}{q}_{xxy}+{\displaystyle \frac{1}{2}}\beta \theta v{q}_{xxx}-{\displaystyle \frac{1}{3}}\theta \lambda v{q}_{xxx}+{\displaystyle \frac{1}{2}}\beta \delta v{q}_y{q}_{xxx}\hfill \\ \hfill & -{\displaystyle \frac{1}{3}}\delta \lambda v{q}_y{q}_{xxx}+{\displaystyle \frac{1}{5}}\alpha \delta q_{xy}{v}_{xxx}-{\displaystyle \frac{1}{5}}\alpha \theta v_{xxxx}-{\displaystyle \frac{1}{5}}\alpha \delta q_y{v}_{xxxx}+{\displaystyle \frac{4}{5}}\alpha \delta v{q}_{xxxxy}+{\displaystyle \frac{1}{6}}\delta q_{xy}{v}_t\hfill \\ \hfill & -{\displaystyle \frac{1}{3}}\theta v_{tx}-{\displaystyle \frac{1}{3}}\delta q_y{v}_{tx}+{\displaystyle \frac{2}{3}}\delta v{q}_{txy}.\hfill \end{array}$$

4. Concluding Remarks

In this paper, we studied the (2+1)-dimensional nonlinear wave equation by utilizing Lie group analysis. We first computed the Lie point symmetries and by employing the Lie equations with initial conditions, we obtain one-parameter group of transformations. Travelling wave solution was obtained by using the three translation symmetries and the solution (13) was presented in terms of an incomplete elliptic integral. Furthermore, various other exact solutions were obtained under the Lie symmetries of the equation. Graphical presentation for each obtained solution was provided to understand the behaviour of the solutions. Finally, we constructed seven conserved vectors for the Equation (5) by invoking the theorem due to Ibragimov. These included the conservation of energy and momentum.